breeze/LeetCode-Book
1
0
Fork 0
mirror of https://github.com/krahets/LeetCode-Book.git synced 2026-01-12 00:19:02 +08:00
Code Issues Packages Projects Releases Wiki Activity

Add documents of leetbook IOA and

Browse Source 
selected coding interview.
This commit is contained in:
krahets
2023-10-10 20:22:09 +08:00
parent 6def47ca3f
commit de1a505d63
175 changed files with 23813 additions and 0 deletions
Download Patch File Download Diff File Expand all files Collapse all files

26
leetbook_ioa/docs/# 0 引言.md Executable file
View File

@@ -0,0 +1,26 @@
# 引言
《图解算法数据结构》面向算法初学者、互联网求职者设计，主要内容包括：
### 精选面试题图文解析
- 图文详解 75 道题目，覆盖主要算法知识点，非常适合作为算法学习的 **第一份题库**。
- 题库活跃于各大互联网公司招聘中，可使笔面试准备事半功倍。
- 致力于行文深入浅出、图文搭配，提供简洁的 **Python, Java, C++** 解题代码。
- 笔者整理了 **题目分类** 和 **刷题计划** ，让刷题有迹可循。
### 数据结构与算法专栏
- **基础知识：** 时间复杂度、空间复杂度等算法知识。
- **数据结构：** 数组、链表、字符串、栈、队列、哈希表、树、图、堆。
- **算法专题：** 搜索与回溯、分治、动态规划、贪心、排序、位运算、模拟、数学。
## 配套代码
为方便各位 Debug 算法题目，笔者整理了本 LeetBook 的配套代码，包括：
- 「题解代码」提供 Python, Java, C++ 语言。
- 「测试样例」与运行调用代码。
- 「数据结构」封装，提升 LeetCode 刷题效率。
与本 LeetBook 配合食用更佳，仓库链接：https://github.com/krahets/LeetCode-Book

14
leetbook_ioa/docs/# 0.1 刷题建议.md Executable file
View File

@@ -0,0 +1,14 @@
# 刷题建议
本书专为算法初学者设计，特别针对有意进入互联网行业的求职者。内容覆盖如下主题：
- **算法**：搜索、查找、排序、双指针、回溯、分治、动态规划、贪心、位运算、数学等。
- **数据结构**：数组、栈、队列、字符串、链表、树、图、堆、哈希表等。
所有题目已经进行分类，并按照难易程度排序。对于初学者，这里提供几条刷题建议：
1. 建议每日刷 2~3 题。若能轻松完成，可以尝试增加至 5～8 题，但请记住：刷题的质量远重要于数量。务必确保你真正理解了每个题目的解法及背后的算法原理。
2. 建议你按照目录顺序逐题解答。如果碰到某些难以解决的题目，可以先跳过，稍后回顾时再挑战。
3. 很多题目都有不止一种解法，请你注意比较和探讨各种方法的特点和适用情况。
4. 如果你发现自己忘记了某个题目的解法，不必灰心。艾宾浩斯遗忘曲线指出，为了真正掌握一个知识点，通常需要复习至少3次。
5. 行百里者半九十。坚持至关重要，加油，相信你可以做到！

81
leetbook_ioa/docs/# 0.2 题目分类.md Executable file
View File

@@ -0,0 +1,81 @@
# 题目分类
题目可能存在多种解法，下表仅列举最优解法（时间与空间复杂度最低）的算法和数据结构分类。
| 题目 | 算法分类 | 数据结构分类 |
| -------------------------------- | ---------------- | -------------- |
| 寻找文件副本 | 查找 | 数组 |
| 寻找目标值 - 二维数组 | 查找 | 数组 |
| 路径加密 | | 字符串 |
| 图书整理 I | | 栈与队列，链表 |
| 推理二叉树 | 分治 | 树，哈希表 |
| 图书整理 II | | 栈与队列 |
| 斐波那契数 | 动态规划 | 数组 |
| 跳跃训练 | 动态规划 | 数组 |
| 库存管理 I | 查找 | 数组 |
| 字母迷宫 | 回溯，搜索 | 数组，图 |
| 衣橱整理 | 回溯，搜索 | 数组，图 |
| 砍竹子 I | 贪心，数学 | |
| 砍竹子 II | 贪心，分治，数学 | |
| 位 1 的个数 | 位运算 | |
| Pow(x, n) | 分治，位运算 | |
| 报数 | | 数组 |
| 删除链表节点 | 双指针 | 链表 |
| 模糊搜索验证 | 动态规划 | 字符串 |
| 有效数字 | | 字符串 |
| 训练计划 I | 双指针 | 数组 |
| 训练计划 II | 双指针 | 链表 |
| 训练计划 III | 双指针 | 链表 |
| 训练计划 IV | 双指针 | 链表 |
| 子结构判断 | 搜索 | 树 |
| 翻转二叉树 | 搜索 | 栈与队列，树 |
| 判断对称二叉树 | 搜索 | 树 |
| 螺旋遍历二维数组 | 模拟 | 数组 |
| 最小栈 | 排序 | 栈与队列 |
| 验证图书取出顺序 | 模拟 | 栈与队列 |
| 彩灯装饰记录 I | 搜索 | 栈与队列，树 |
| 彩灯装饰记录 II | 搜索 | 栈与队列，树 |
| 彩灯装饰记录 III | 搜索 | 栈与队列，树 |
| 验证二叉搜索树的后序遍历序列 | 分治 | 栈与队列，树 |
| 二叉树中和为目标值的路径 | 回溯，搜索 | 树 |
| 随机链表的复制 | | 链表 |
| 将二叉搜索树转化为排序的双向链表 | 搜索，双指针 | 树 |
| 序列化与反序列化二叉树 | 搜索 | 树 |
| 套餐内商品的排列顺序 | 回溯 | 字符串，哈希表 |
| 库存管理 II | | 数组 |
| 库存管理 III | 排序 | 数组，堆 |
| 数据流中的中位数 | 排序 | 堆 |
| 连续天数的最高销售额 | 动态规划 | 数组 |
| 数字 1 的个数 | 数学 | |
| 找到第 k 位数字 | 数学 | |
| 破解闯关密码 | 排序 | 字符串 |
| 解密数字 | 动态规划 | 字符串 |
| 珠宝的最高价值 | 动态规划 | 数组 |
| 招式拆解 I | 动态规划，双指针 | 哈希表 |
| 丑数 | 动态规划 | |
| 招式拆解 II | | 哈希表 |
| 交易逆序对的总数 | 分治 | 数组 |
| 训练计划 V | 双指针 | 链表 |
| 统计目标成绩的出现次数 | 查找 | 数组 |
| 点名 | 查找 | 数组 |
| 寻找二叉搜索树中的目标节点 | 搜索 | 树 |
| 计算二叉树的深度 | 搜索 | 树 |
| 判断是否为平衡二叉树 | 搜索 | 树 |
| 撞色搭配 | 位运算 | 数组 |
| 训练计划 VI | 位运算 | 数组 |
| 查找总价格为目标值的两个商品 | 双指针 | 数组 |
| 文件组合 | 双指针 | 数组 |
| 字符串中的单词反转 | 双指针 | 字符串 |
| 动态口令 | | 字符串 |
| 望远镜中最高的海拔 | 排序 | 数组，栈与队列 |
| 设计自助结算系统 | 排序 | 数组，栈与队列 |
| 统计结果概率 | 动态规划 | |
| 文物朝代判断 | 排序 | 数组，哈希表 |
| 破冰游戏 | 数学 | |
| 买卖芯片的最佳时机 | 动态规划 | 数组 |
| 设计机械累加器 | | |
| 加密运算 | 位运算 | |
| 按规则计算统计结果 | 数学 | 数组 |
| 不使用库函数的字符串转整数 | | 字符串 |
| 求二叉搜索树的最近公共祖先 | 搜索 | 树 |
| 寻找二叉树的最近公共祖先 | 搜索 | 树 |

629
leetbook_ioa/docs/# 1.1 数据结构简介.md Executable file
View File

@@ -0,0 +1,629 @@
# 数据结构简介
数据结构是为实现对计算机数据有效使用的各种数据组织形式，服务于各类计算机操作。不同的数据结构具有各自对应的适用场景，旨在降低各种算法计算的时间与空间复杂度，达到最佳的任务执行效率。
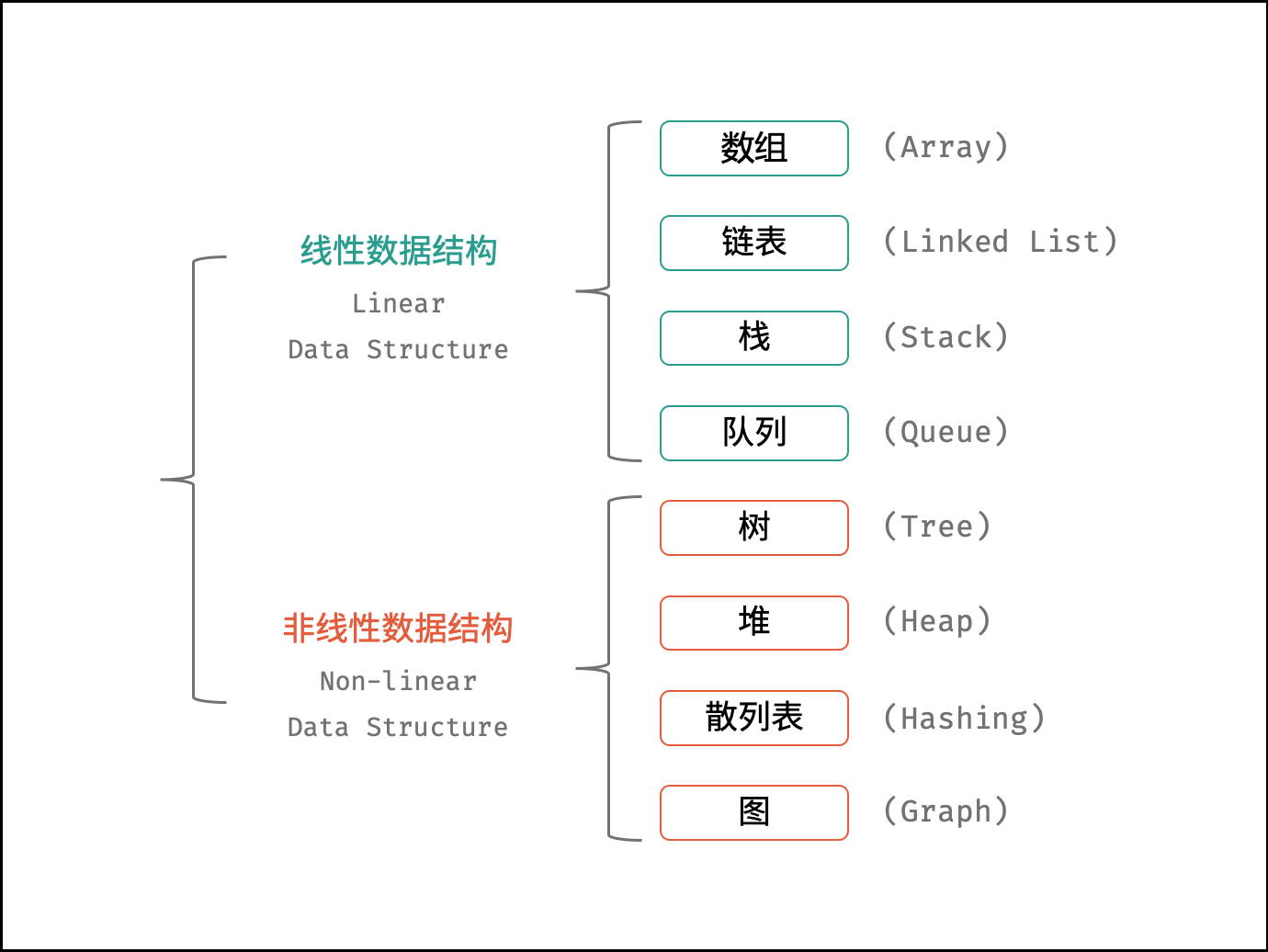
如下图所示，常见的数据结构可分为「线性数据结构」与「非线性数据结构」，具体为：「数组」、「链表」、「栈」、「队列」、「树」、「图」、「散列表」、「堆」。
![Picture1.png](https://pic.leetcode-cn.com/1599638810-SZDwfK-Picture1.png){:width=500}
从零开始学习算法的同学对数据结构的使用方法可能尚不熟悉，本节将初步介绍各数据结构的基本特点，与 Python3 , Java , C++ 语言中各数据结构的初始化与构建方法。
> 代码运行可使用本地 IDE 或 [力扣 PlayGround](https://leetcode-cn.com/playground/) 。
---
## 数组
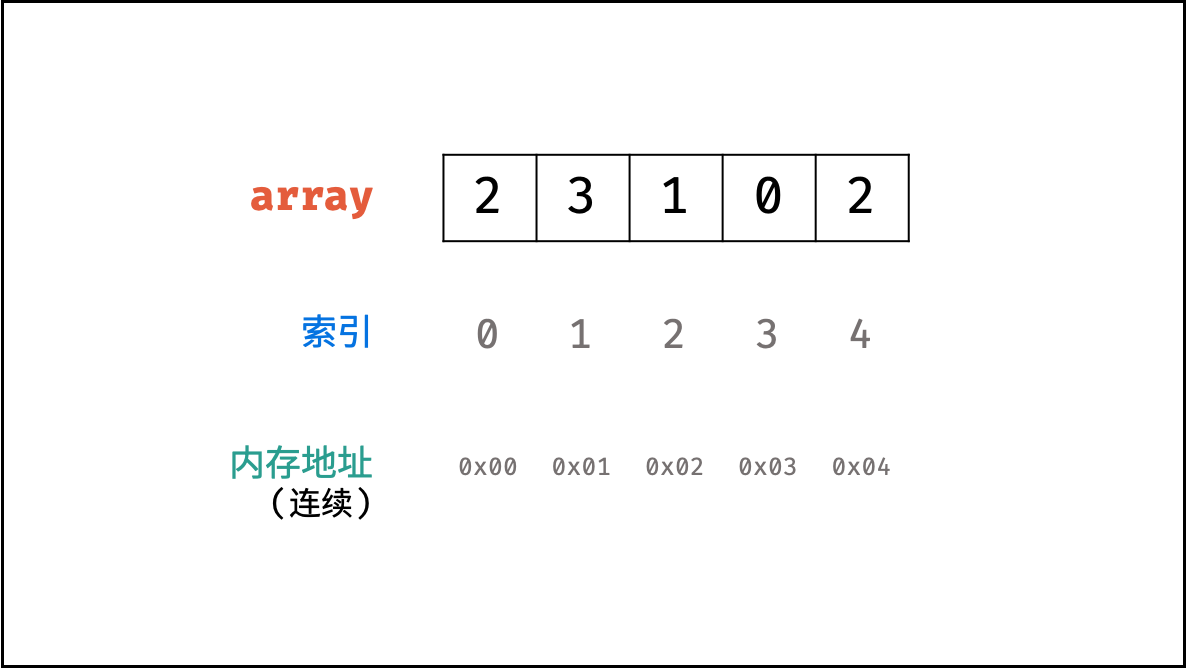
数组是将相同类型的元素存储于连续内存空间的数据结构，其长度不可变。
如下图所示，构建此数组需要在初始化时给定长度，并对数组每个索引元素赋值，代码如下：
```Java []
// 初始化一个长度为 5 的数组 array
int[] array = new int[5];
// 元素赋值
array[0] = 2;
array[1] = 3;
array[2] = 1;
array[3] = 0;
array[4] = 2;
```
```C++ []
// 初始化一个长度为 5 的数组 array
int array[5];
// 元素赋值
array[0] = 2;
array[1] = 3;
array[2] = 1;
array[3] = 0;
array[4] = 2;
```
或者可以使用直接赋值的初始化方式，代码如下：
```Java []
int[] array = {2, 3, 1, 0, 2};
```
```C++ []
int array[] = {2, 3, 1, 0, 2};
```
![Picture2.png](https://pic.leetcode-cn.com/1599587176-JAxwpf-Picture2.png){:width=500}
「可变数组」是经常使用的数据结构，其基于数组和扩容机制实现，相比普通数组更加灵活。常用操作有：访问元素、添加元素、删除元素。
```Java []
// 初始化可变数组
List<Integer> array = new ArrayList<>();
// 向尾部添加元素
array.add(2);
array.add(3);
array.add(1);
array.add(0);
array.add(2);
```
```Python []
# 初始化可变数组
array = []
# 向尾部添加元素
array.append(2)
array.append(3)
array.append(1)
array.append(0)
array.append(2)
```
```C++ []
// 初始化可变数组
vector<int> array;
// 向尾部添加元素
array.push_back(2);
array.push_back(3);
array.push_back(1);
array.push_back(0);
array.push_back(2);
```
---
## 链表
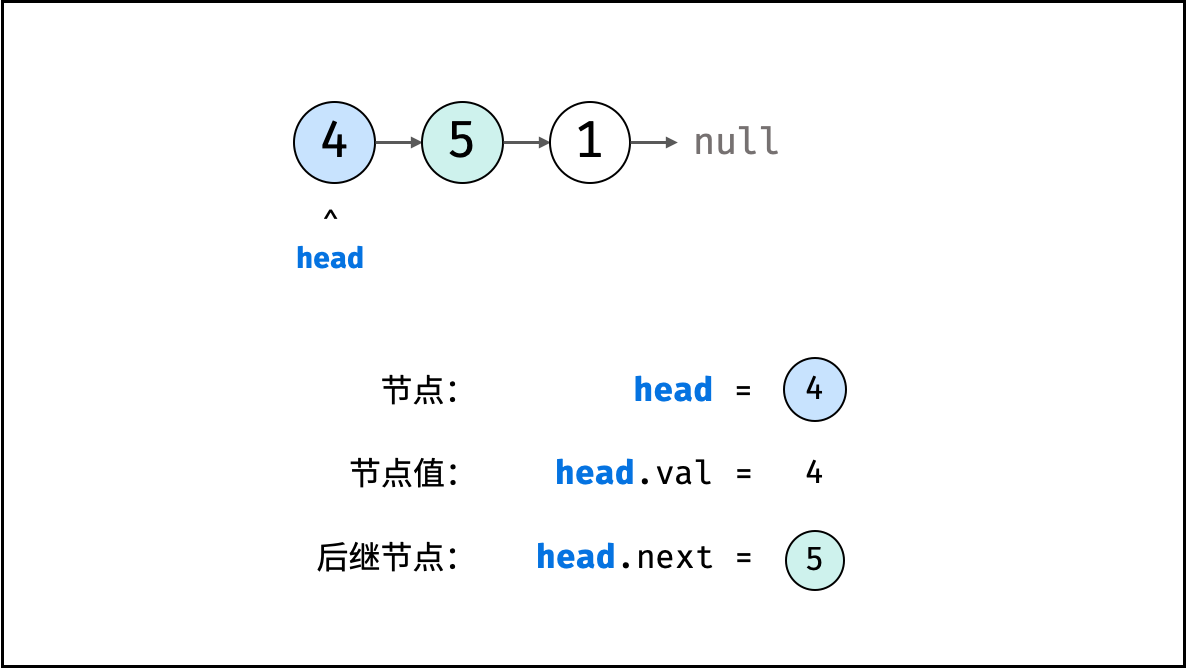
链表以节点为单位，每个元素都是一个独立对象，在内存空间的存储是非连续的。链表的节点对象具有两个成员变量：「值 `val`」，「后继节点引用 `next`」 。
```Java []
class ListNode {
int val; // 节点值
ListNode next; // 后继节点引用
ListNode(int x) { val = x; }
}
```
```Python []
class ListNode:
def __init__(self, x):
self.val = x # 节点值
self.next = None # 后继节点引用
```
```C++ []
struct ListNode {
int val; // 节点值
ListNode *next; // 后继节点引用
ListNode(int x) : val(x), next(NULL) {}
};
```
如下图所示，建立此链表需要实例化每个节点，并构建各节点的引用指向。
```Java []
// 实例化节点
ListNode n1 = new ListNode(4); // 节点 head
ListNode n2 = new ListNode(5);
ListNode n3 = new ListNode(1);
// 构建引用指向
n1.next = n2;
n2.next = n3;
```
```Python []
# 实例化节点
n1 = ListNode(4) # 节点 head
n2 = ListNode(5)
n3 = ListNode(1)
# 构建引用指向
n1.next = n2
n2.next = n3
```
```C++ []
// 实例化节点
ListNode *n1 = new ListNode(4); // 节点 head
ListNode *n2 = new ListNode(5);
ListNode *n3 = new ListNode(1);
// 构建引用指向
n1->next = n2;
n2->next = n3;
```
![Picture3.png](https://pic.leetcode-cn.com/1599578767-zgLjYw-Picture3.png){:width=500}
---
## 栈
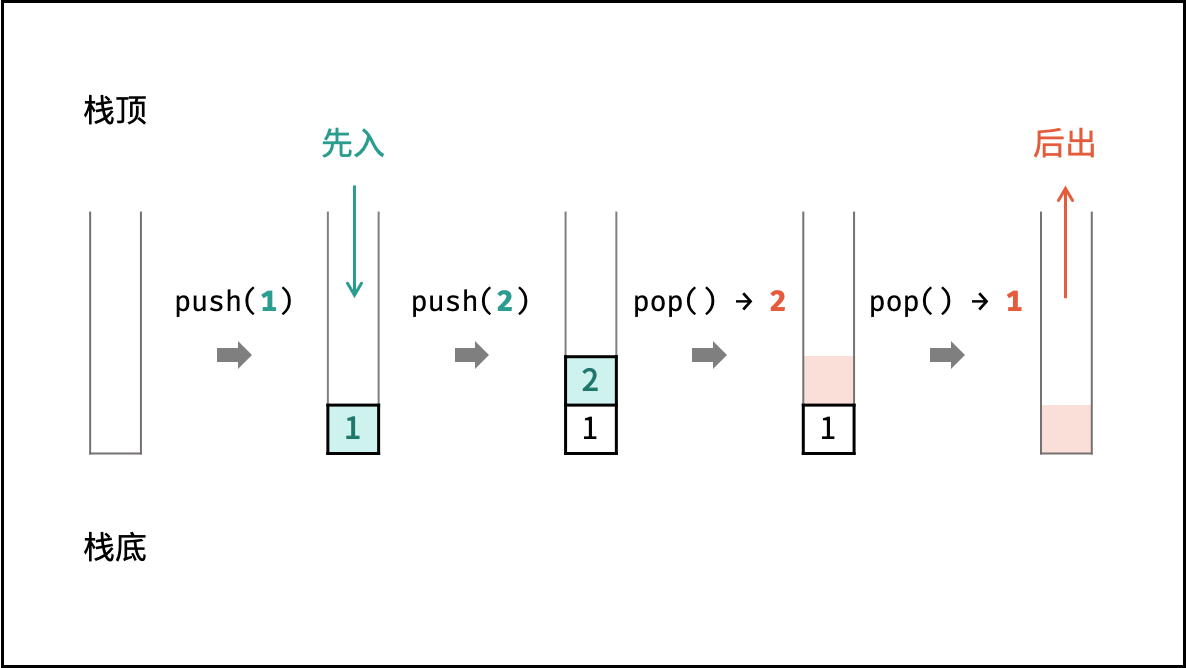
栈是一种具有 「先入后出」 特点的抽象数据结构，可使用数组或链表实现。
```Java []
Stack<Integer> stack = new Stack<>();
```
```Python []
stack = [] # Python 可将列表作为栈使用
```
```C++ []
stack<int> stk;
```
如下图所示，通过常用操作「入栈 `push()`」,「出栈 `pop()`」，展示了栈的先入后出特性。
```Java []
stack.push(1); // 元素 1 入栈
stack.push(2); // 元素 2 入栈
stack.pop(); // 出栈 -> 元素 2
stack.pop(); // 出栈 -> 元素 1
```
```Python []
stack.append(1) # 元素 1 入栈
stack.append(2) # 元素 2 入栈
stack.pop() # 出栈 -> 元素 2
stack.pop() # 出栈 -> 元素 1
```
```C++ []
stk.push(1); // 元素 1 入栈
stk.push(2); // 元素 2 入栈
stk.pop(); // 出栈 -> 元素 2
stk.pop(); // 出栈 -> 元素 1
```
![Picture4.png](https://pic.leetcode-cn.com/1599578767-ZifMEX-Picture4.png){:width=500}
> 注意：通常情况下，不推荐使用 Java 的 `Vector` 以及其子类 `Stack` ，而一般将 `LinkedList` 作为栈来使用。详细说明请见：[Stack，ArrayDeque，LinkedList 的区别](https://blog.csdn.net/cartoon_/article/details/87992743) 。
```Java []
LinkedList<Integer> stack = new LinkedList<>();
stack.addLast(1); // 元素 1 入栈
stack.addLast(2); // 元素 2 入栈
stack.removeLast(); // 出栈 -> 元素 2
stack.removeLast(); // 出栈 -> 元素 1
```
---
## 队列
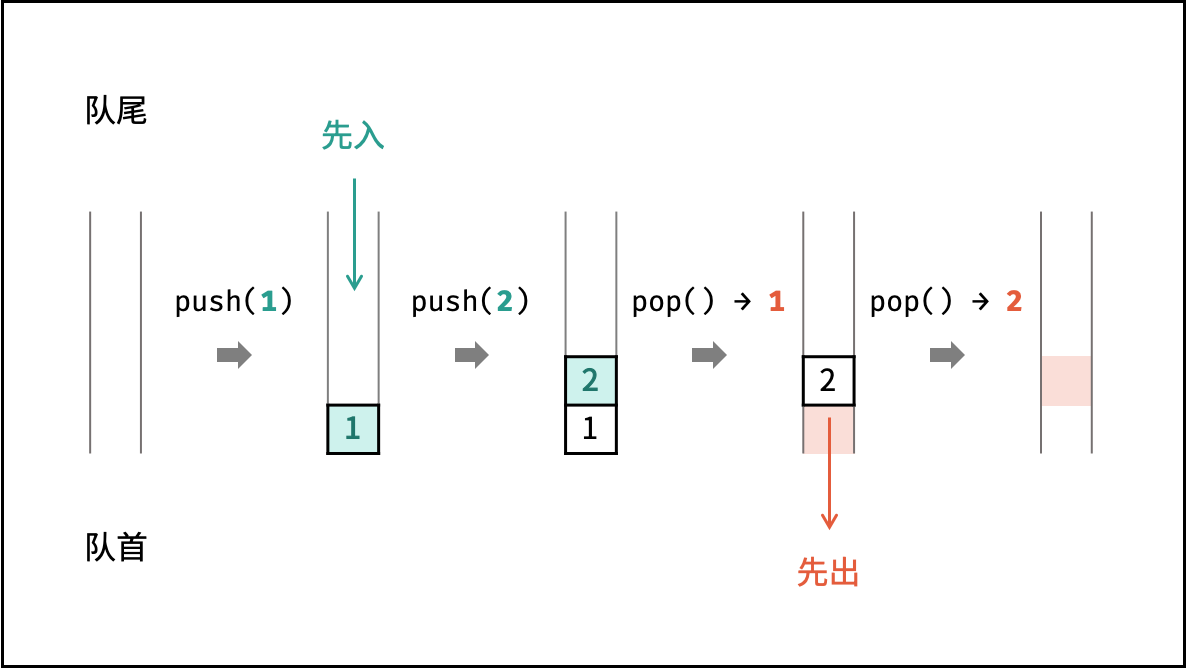
队列是一种具有 「先入先出」 特点的抽象数据结构，可使用链表实现。
```Java []
Queue<Integer> queue = new LinkedList<>();
```
```Python []
# Python 通常使用双端队列 collections.deque
from collections import deque
queue = deque()
```
```C++ []
queue<int> que;
```
如下图所示，通过常用操作「入队 `push()`」,「出队 `pop()`」，展示了队列的先入先出特性。
```Java []
queue.offer(1); // 元素 1 入队
queue.offer(2); // 元素 2 入队
queue.poll(); // 出队 -> 元素 1
queue.poll(); // 出队 -> 元素 2
```
```Python []
queue.append(1) # 元素 1 入队
queue.append(2) # 元素 2 入队
queue.popleft() # 出队 -> 元素 1
queue.popleft() # 出队 -> 元素 2
```
```C++ []
que.push(1); // 元素 1 入队
que.push(2); // 元素 2 入队
que.pop(); // 出队 -> 元素 1
que.pop(); // 出队 -> 元素 2
```
![Picture5.png](https://pic.leetcode-cn.com/1599588416-Majmwh-Picture5.png){:width=500}
---
## 树
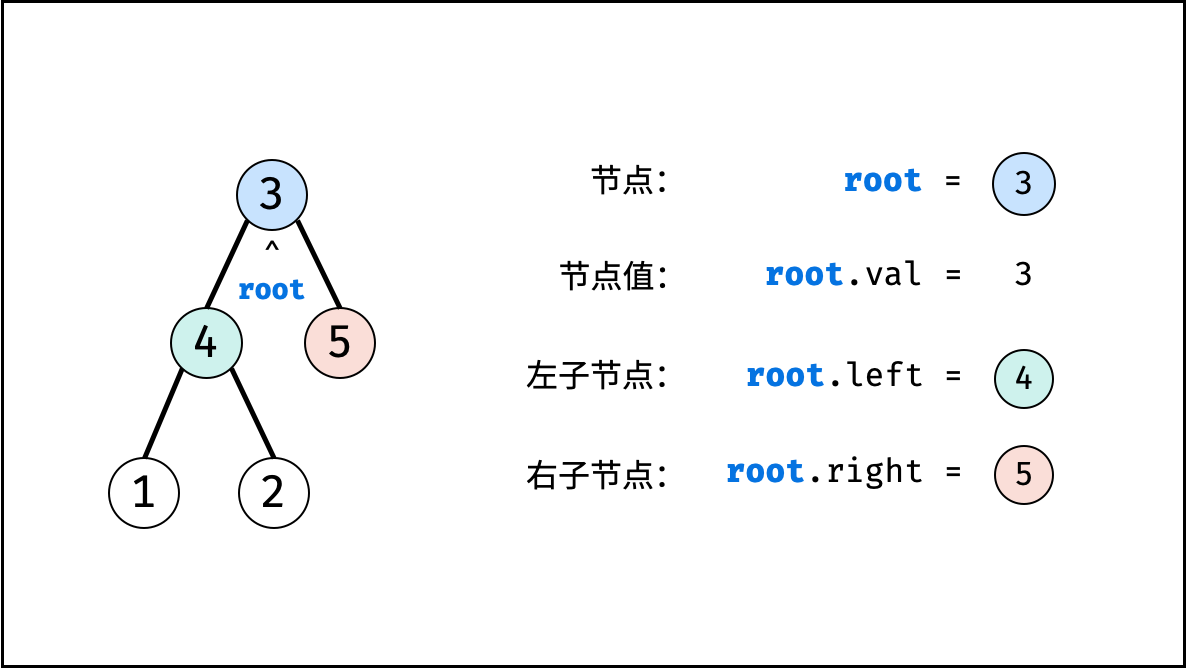
树是一种非线性数据结构，根据子节点数量可分为 「二叉树」 和 「多叉树」，最顶层的节点称为「根节点 `root`」。以二叉树为例，每个节点包含三个成员变量：「值 `val`」、「左子节点 `left`」、「右子节点 `right`」 。
```Java []
class TreeNode {
int val; // 节点值
TreeNode left; // 左子节点
TreeNode right; // 右子节点
TreeNode(int x) { val = x; }
}
```
```Python []
class TreeNode:
def __init__(self, x):
self.val = x # 节点值
self.left = None # 左子节点
self.right = None # 右子节点
```
```C++ []
struct TreeNode {
int val; // 节点值
TreeNode *left; // 左子节点
TreeNode *right; // 右子节点
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
```
如下图所示，建立此二叉树需要实例化每个节点，并构建各节点的引用指向。
```Java []
// 初始化节点
TreeNode n1 = new TreeNode(3); // 根节点 root
TreeNode n2 = new TreeNode(4);
TreeNode n3 = new TreeNode(5);
TreeNode n4 = new TreeNode(1);
TreeNode n5 = new TreeNode(2);
// 构建引用指向
n1.left = n2;
n1.right = n3;
n2.left = n4;
n2.right = n5;
```
```Python []
# 初始化节点
n1 = TreeNode(3) # 根节点 root
n2 = TreeNode(4)
n3 = TreeNode(5)
n4 = TreeNode(1)
n5 = TreeNode(2)
# 构建引用指向
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
```
```C++ []
// 初始化节点
TreeNode *n1 = new TreeNode(3); // 根节点 root
TreeNode *n2 = new TreeNode(4);
TreeNode *n3 = new TreeNode(5);
TreeNode *n4 = new TreeNode(1);
TreeNode *n5 = new TreeNode(2);
// 构建引用指向
n1->left = n2;
n1->right = n3;
n2->left = n4;
n2->right = n5;
```
![Picture6.png](https://pic.leetcode-cn.com/1599579136-bBARpC-Picture6.png){:width=500}
---
## 图
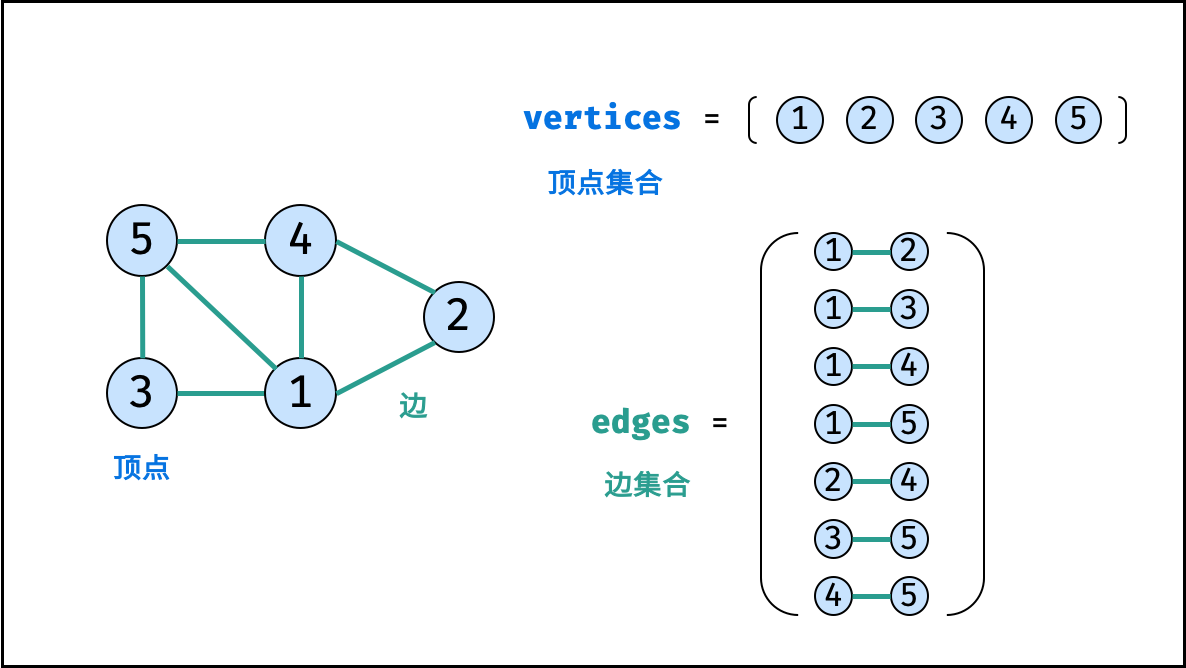
图是一种非线性数据结构，由「节点（顶点）`vertex`」和「边 `edge`」组成，每条边连接一对顶点。根据边的方向有无，图可分为「有向图」和「无向图」。本文 **以无向图为例** 开展介绍。
如下图所示，此无向图的 **顶点** 和 **边** 集合分别为：
- 顶点集合： `vertices = {1, 2, 3, 4, 5}`
- 边集合： `edges = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 4), (3, 5), (4, 5)}`
![Picture7.png](https://pic.leetcode-cn.com/1599579136-Fxseew-Picture7.png){:width=500}
表示图的方法通常有两种：
1. **邻接矩阵：** 使用数组 $vertices$ 存储顶点，邻接矩阵 $edges$ 存储边； $edges[i][j]$ 代表节点 $i + 1$ 和 节点 $j + 1$ 之间是否有边。
$$
vertices = [1, 2, 3, 4, 5] \\
edges = \left[ \begin{matrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 \\ \end{matrix} \right]
$$
```Python []
vertices = [1, 2, 3, 4, 5]
edges = [[0, 1, 1, 1, 1],
[1, 0, 0, 1, 0],
[1, 0, 0, 0, 1],
[1, 1, 0, 0, 1],
[1, 0, 1, 1, 0]]
```
```Java []
int[] vertices = {1, 2, 3, 4, 5};
int[][] edges = {{0, 1, 1, 1, 1},
{1, 0, 0, 1, 0},
{1, 0, 0, 0, 1},
{1, 1, 0, 0, 1},
{1, 0, 1, 1, 0}};
```
```C++ []
int vertices[5] = {1, 2, 3, 4, 5};
int edges[5][5] = {{0, 1, 1, 1, 1},
{1, 0, 0, 1, 0},
{1, 0, 0, 0, 1},
{1, 1, 0, 0, 1},
{1, 0, 1, 1, 0}};
```
2. **邻接表：** 使用数组 $vertices$ 存储顶点，邻接表 $edges$ 存储边。 $edges$ 为一个二维容器，第一维 $i$ 代表顶点索引，第二维 $edges[i]$ 存储此顶点对应的边集和；例如 $edges[0] = [1, 2, 3, 4]$ 代表 $vertices[0]$ 的边集合为 $[1, 2, 3, 4]$ 。
$$
vertices = [1, 2, 3, 4, 5] \\
edges = \left[ \begin{matrix} [ & 1 & 2 & 3 & 4 & ] \\ [ & 0 & 3 & ] \\ [ & 0 & 4 & ] \\ [ & 0 & 1 & 4 & ] \\ [ & 0 & 2 & 3 & ] \end{matrix} \right]
$$
```Python []
vertices = [1, 2, 3, 4, 5]
edges = [[1, 2, 3, 4],
[0, 3],
[0, 4],
[0, 1, 4],
[0, 2, 3]]
```
```Java []
int[] vertices = {1, 2, 3, 4, 5};
List<List<Integer>> edges = new ArrayList<>();
List<Integer> edge_1 = new ArrayList<>(Arrays.asList(1, 2, 3, 4));
List<Integer> edge_2 = new ArrayList<>(Arrays.asList(0, 3));
List<Integer> edge_3 = new ArrayList<>(Arrays.asList(0, 4));
List<Integer> edge_4 = new ArrayList<>(Arrays.asList(0, 1, 4));
List<Integer> edge_5 = new ArrayList<>(Arrays.asList(0, 2, 3));
edges.add(edge_1);
edges.add(edge_2);
edges.add(edge_3);
edges.add(edge_4);
edges.add(edge_5);
```
```C++ []
int vertices[5] = {1, 2, 3, 4, 5};
vector<vector<int>> edges;
vector<int> edge_1 = {1, 2, 3, 4};
vector<int> edge_2 = {0, 3};
vector<int> edge_3 = {0, 4};
vector<int> edge_4 = {0, 1, 4};
vector<int> edge_5 = {0, 2, 3};
edges.push_back(edge_1);
edges.push_back(edge_2);
edges.push_back(edge_3);
edges.push_back(edge_4);
edges.push_back(edge_5);
```
> **邻接矩阵 VS 邻接表 ：**
>
> 邻接矩阵的大小只与节点数量有关，即 $N^2$ ，其中 $N$ 为节点数量。因此，当边数量明显少于节点数量时，使用邻接矩阵存储图会造成较大的内存浪费。
> 因此，**邻接表** 适合存储稀疏图（顶点较多、边较少）； **邻接矩阵** 适合存储稠密图（顶点较少、边较多）。
---
## 散列表
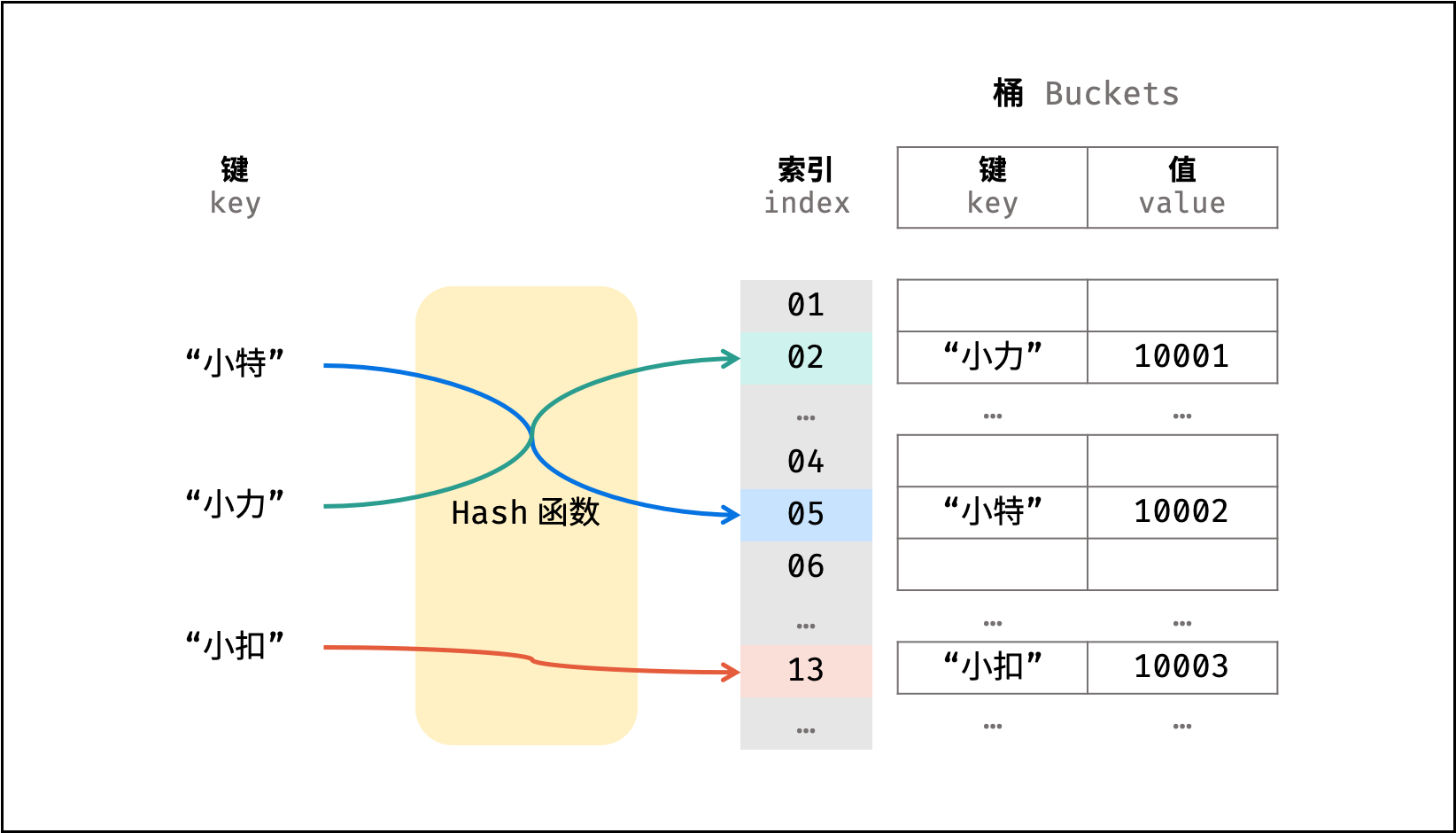
散列表是一种非线性数据结构，通过利用 Hash 函数将指定的「键 `key`」映射至对应的「值 `value`」，以实现高效的元素查找。
> 设想一个简单场景：小力、小特、小扣的学号分别为 10001, 10002, 10003 。
> 现需求从「姓名」查找「学号」。
则可通过建立姓名为 `key` ，学号为 `value` 的散列表实现此需求，代码如下：
```Java []
// 初始化散列表
Map<String, Integer> dic = new HashMap<>();
// 添加 key -> value 键值对
dic.put("小力", 10001);
dic.put("小特", 10002);
dic.put("小扣", 10003);
// 从姓名查找学号
dic.get("小力"); // -> 10001
dic.get("小特"); // -> 10002
dic.get("小扣"); // -> 10003
```
```Python []
# 初始化散列表
dic = {}
# 添加 key -> value 键值对
dic["小力"] = 10001
dic["小特"] = 10002
dic["小扣"] = 10003
# 从姓名查找学号
dic["小力"] # -> 10001
dic["小特"] # -> 10002
dic["小扣"] # -> 10003
```
```C++ []
// 初始化散列表
unordered_map<string, int> dic;
// 添加 key -> value 键值对
dic["小力"] = 10001;
dic["小特"] = 10002;
dic["小扣"] = 10003;
// 从姓名查找学号
dic.find("小力")->second; // -> 10001
dic.find("小特")->second; // -> 10002
dic.find("小扣")->second; // -> 10003
```
![Picture8.png](https://pic.leetcode-cn.com/1599811794-ruXMOV-Picture8.png){:width=550}
### Hash 函数设计示例 ：
> 假设需求：从「学号」查找「姓名」。
将三人的姓名存储至以下数组中，则各姓名在数组中的索引分别为 0, 1, 2 。
```Java []
String[] names = { "小力", "小特", "小扣" };
```
```Python []
names = [ "小力", "小特", "小扣" ]
```
```C++ []
string names[] = { "小力", "小特", "小扣" };
```
此时，我们构造一个简单的 Hash 函数（ $\%$ 为取余符号 ），公式和封装函数如下所示：
$$
hash(key) = (key - 1) \% 10000
$$
```Java []
int hash(int id) {
int index = (id - 1) % 10000;
return index;
}
```
```Python []
def hash(id):
index = (id - 1) % 10000
return index
```
```C++ []
int hash(int id) {
int index = (id - 1) % 10000;
return index;
}
```
则我们构建了以学号为 `key` 、姓名对应的数组索引为 `value` 的散列表。利用此 Hash 函数，则可在 $O(1)$ 时间复杂度下通过学号查找到对应姓名，即：
```Java
names[hash(10001)] // 小力
names[hash(10002)] // 小特
names[hash(10003)] // 小扣
```
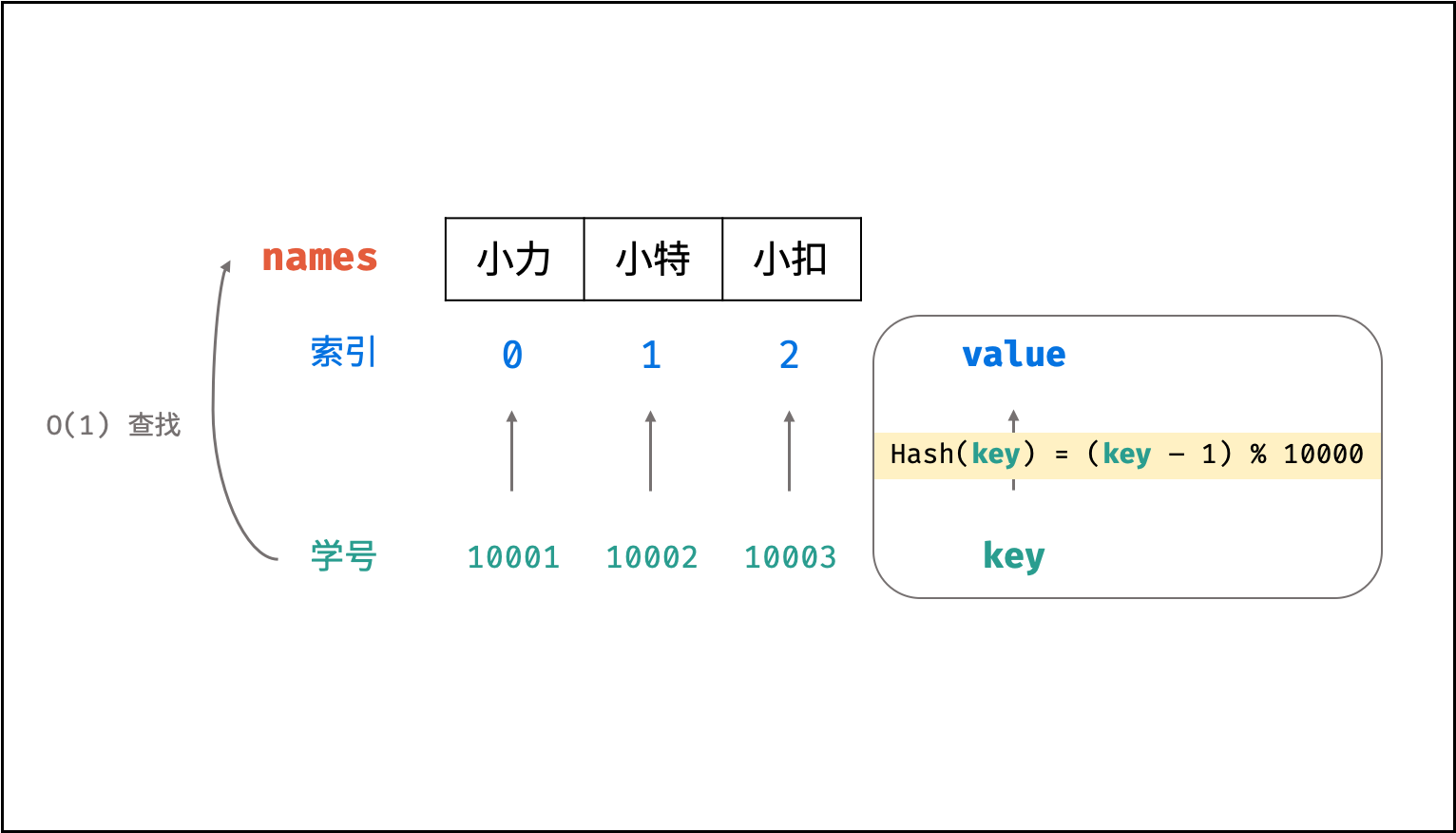![Picture8-1.png](https://pic.leetcode-cn.com/1599811794-NfbpfW-Picture8-1.png){:width=550}
以上设计只适用于此示例，实际的 Hash 函数需保证低碰撞率、 高鲁棒性等，以适用于各类数据和场景。
---
## 堆：
堆是一种基于「完全二叉树」的数据结构，可使用数组实现。以堆为原理的排序算法称为「堆排序」，基于堆实现的数据结构为「优先队列」。堆分为「大顶堆」和「小顶堆」，大（小）顶堆：任意节点的值不大于（小于）其父节点的值。
> **完全二叉树定义：** 设二叉树深度为 $k$ ，若二叉树除第 $k$ 层外的其它各层（第 $1$ 至 $k-1$ 层）的节点达到最大个数，且处于第 $k$ 层的节点都连续集中在最左边，则称此二叉树为完全二叉树。
如下图所示，为包含 `1, 4, 2, 6, 8` 元素的小顶堆。将堆（完全二叉树）中的结点按层编号，即可映射到右边的数组存储形式。
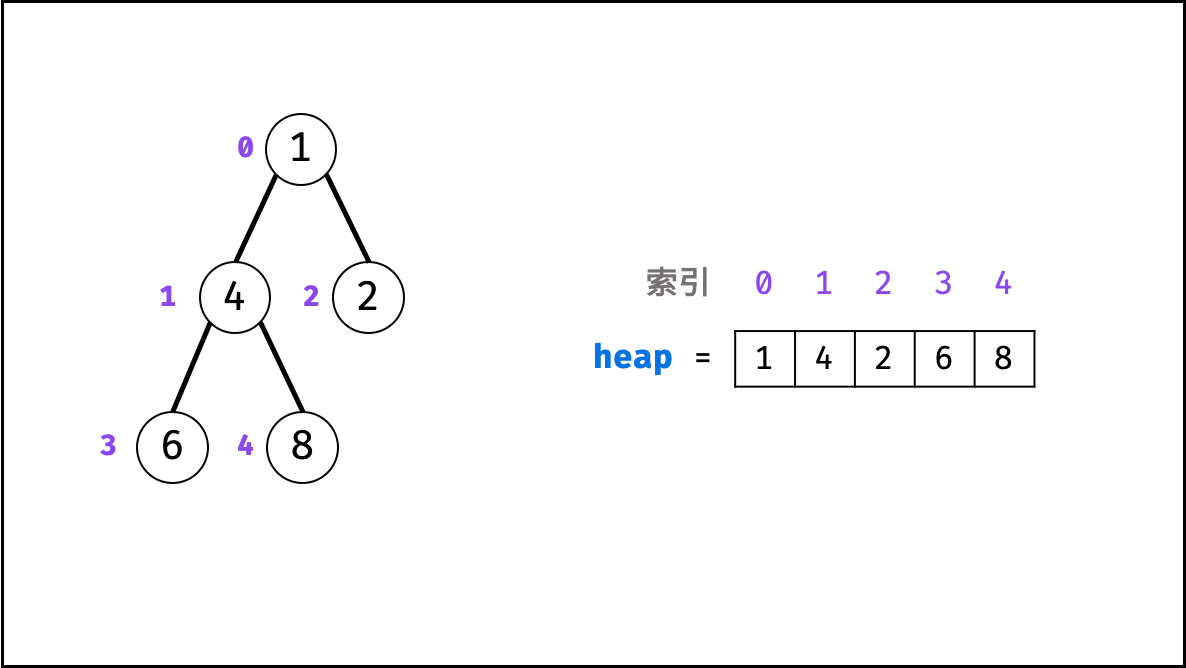![Picture9.png](https://pic.leetcode-cn.com/1599584901-xoiGEQ-Picture9.png){:width=550}
通过使用「优先队列」的「压入 `push()`」和「弹出 `pop()`」操作，即可完成堆排序，实现代码如下：
```Java []
// 初始化小顶堆
Queue<Integer> heap = new PriorityQueue<>();
// 元素入堆
heap.add(1);
heap.add(4);
heap.add(2);
heap.add(6);
heap.add(8);
// 元素出堆（从小到大）
heap.poll(); // -> 1
heap.poll(); // -> 2
heap.poll(); // -> 4
heap.poll(); // -> 6
heap.poll(); // -> 8
```
```Python []
from heapq import heappush, heappop
# 初始化小顶堆
heap = []
# 元素入堆
heappush(heap, 1)
heappush(heap, 4)
heappush(heap, 2)
heappush(heap, 6)
heappush(heap, 8)
# 元素出堆（从小到大）
heappop(heap) # -> 1
heappop(heap) # -> 2
heappop(heap) # -> 4
heappop(heap) # -> 6
heappop(heap) # -> 8
```
```C++ []
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> heap;
// 元素入堆
heap.push(1);
heap.push(4);
heap.push(2);
heap.push(6);
heap.push(8);
// 元素出堆（从小到大）
heap.pop(); // -> 1
heap.pop(); // -> 2
heap.pop(); // -> 4
heap.pop(); // -> 6
heap.pop(); // -> 8
```

15
leetbook_ioa/docs/# 1.2 算法复杂度.md Executable file
View File

@@ -0,0 +1,15 @@
# 算法复杂度
算法复杂度旨在计算在输入数据量 $N$ 的情况下，算法的「时间使用」和「空间使用」情况；体现算法运行使用的时间和空间随「数据大小 $N$ 」而增大的速度。
算法复杂度主要可从 **时间** 、**空间** 两个角度评价：
- **时间：** 假设各操作的运行时间为固定常数，统计算法运行的「计算操作的数量」 ，以代表算法运行所需时间；
- **空间：** 统计在最差情况下，算法运行所需使用的「最大空间」；
「输入数据大小 $N$ 」指算法处理的输入数据量；根据不同算法，具有不同定义，例如：
- **排序算法：** $N$ 代表需要排序的元素数量；
- **搜索算法：** $N$ 代表搜索范围的元素总数，例如数组大小、矩阵大小、二叉树节点数、图节点和边数等；
接下来，我们将分别从概念定义、符号表示、常见种类、时空权衡、示例解析、示例题目等角度入手，学习「时间复杂度」和「空间复杂度」。

514
leetbook_ioa/docs/# 1.3 时间复杂度.md Executable file
View File

@@ -0,0 +1,514 @@
# 时间复杂度
根据定义，时间复杂度指输入数据大小为 $N$ 时，算法运行所需花费的时间。需要注意：
- 统计的是算法的「计算操作数量」，而不是「运行的绝对时间」。计算操作数量和运行绝对时间呈正相关关系，并不相等。算法运行时间受到「编程语言 、计算机处理器速度、运行环境」等多种因素影响。例如，同样的算法使用 Python 或 C++ 实现、使用 CPU 或 GPU 、使用本地 IDE 或力扣平台提交，运行时间都不同。
- 体现的是计算操作随数据大小 $N$ 变化时的变化情况。假设算法运行总共需要「 $1$ 次操作」、「 $100$ 次操作」，此两情况的时间复杂度都为常数级 $O(1)$ ；需要「 $N$ 次操作」、「 $100N$ 次操作」的时间复杂度都为 $O(N)$ 。
---
## 符号表示
根据输入数据的特点，时间复杂度具有「最差」、「平均」、「最佳」三种情况，分别使用 $O$ , $\Theta$ , $\Omega$ 三种符号表示。以下借助一个查找算法的示例题目帮助理解。
> **题目：** 输入长度为 $N$ 的整数数组 `nums` ，判断此数组中是否有数字 $7$ ，若有则返回 `true` ，否则返回 $\text{false}$ 。
>
> **解题算法：** 线性查找，即遍历整个数组，遇到 $7$ 则返回 `true` 。
>
> **代码：**
>
> ```Python []
> def find_seven(nums):
> for num in nums:
> if num == 7:
> return True
> return False
> ```
>
> ```Java []
> boolean findSeven(int[] nums) {
> for (int num : nums) {
> if (num == 7)
> return true;
> }
> return false;
> }
> ```
>
> ```C++ []
> bool findSeven(vector<int>& nums) {
> for (int num : nums) {
> if (num == 7)
> return true;
> }
> return false;
> }
> ```
- **最佳情况 $\Omega(1)$ ：** `nums = [7, a, b, c, ...]` ，即当数组首个数字为 $7$ 时，无论 `nums` 有多少元素，线性查找的循环次数都为 $1$ 次；
- **最差情况 $O(N)$ ：** `nums = [a, b, c, ...]` 且 `nums` 中所有数字都不为 $7$ ，此时线性查找会遍历整个数组，循环 $N$ 次；
- **平均情况 $\Theta$ ：** 需要考虑输入数据的分布情况，计算所有数据情况下的平均时间复杂度；例如本题目，需要考虑数组长度、数组元素的取值范围等；
> 大 $O$ 是最常使用的时间复杂度评价渐进符号，下文示例与本 LeetBook 题目解析皆使用 $O$ 。
---
## 常见种类
根据从小到大排列，常见的算法时间复杂度主要有：
$$
O(1) < O(\log N) < O(N) < O(N\log N) < O(N^2) < O(2^N) < O(N!)
$$
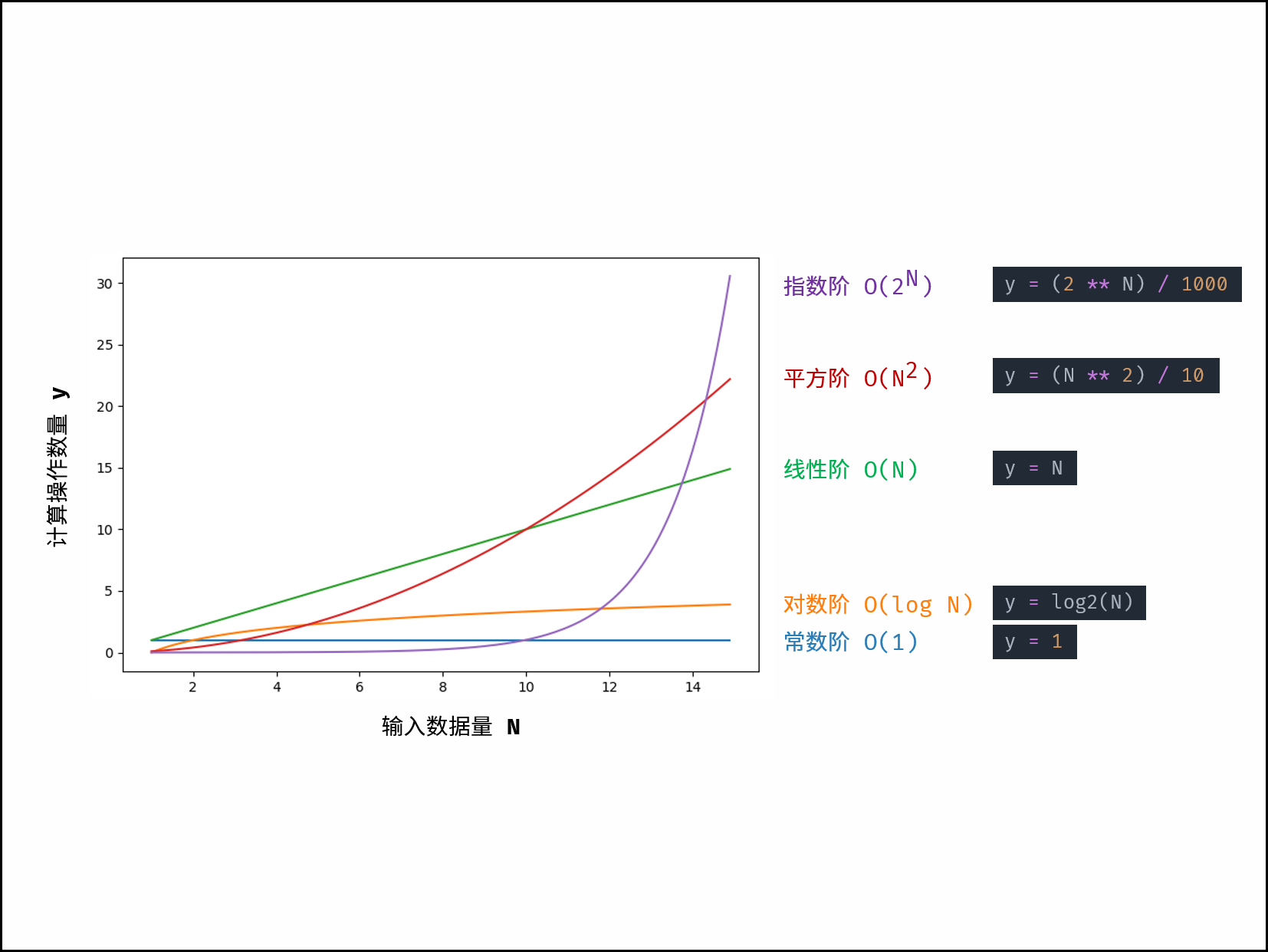
![Picture1.png](https://pic.leetcode-cn.com/1623519242-UTNefQ-Picture1.png)
对于以下所有示例，设输入数据大小为 $N$ ，计算操作数量为 $count$ 。图中每个「**蓝色方块**」代表一个单元计算操作。
### 常数 $O(1)$ ：
运行次数与 $N$ 大小呈常数关系，即不随输入数据大小 $N$ 的变化而变化。
```Python []
def algorithm(N):
a = 1
b = 2
x = a * b + N
return 1
```
```Java []
int algorithm(int N) {
int a = 1;
int b = 2;
int x = a * b + N;
return 1;
}
```
```C++ []
int algorithm(int N) {
int a = 1;
int b = 2;
int x = a * b + N;
return 1;
}
```
对于以下代码，无论 $a$ 取多大，都与输入数据大小 $N$ 无关，因此时间复杂度仍为 $O(1)$ 。
```Python []
def algorithm(N):
count = 0
a = 10000
for i in range(a):
count += 1
return count
```
```Java []
int algorithm(int N) {
int count = 0;
int a = 10000;
for (int i = 0; i < a; i++) {
count++;
}
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
int a = 10000;
for (int i = 0; i < a; i++) {
count++;
}
return count;
}
```
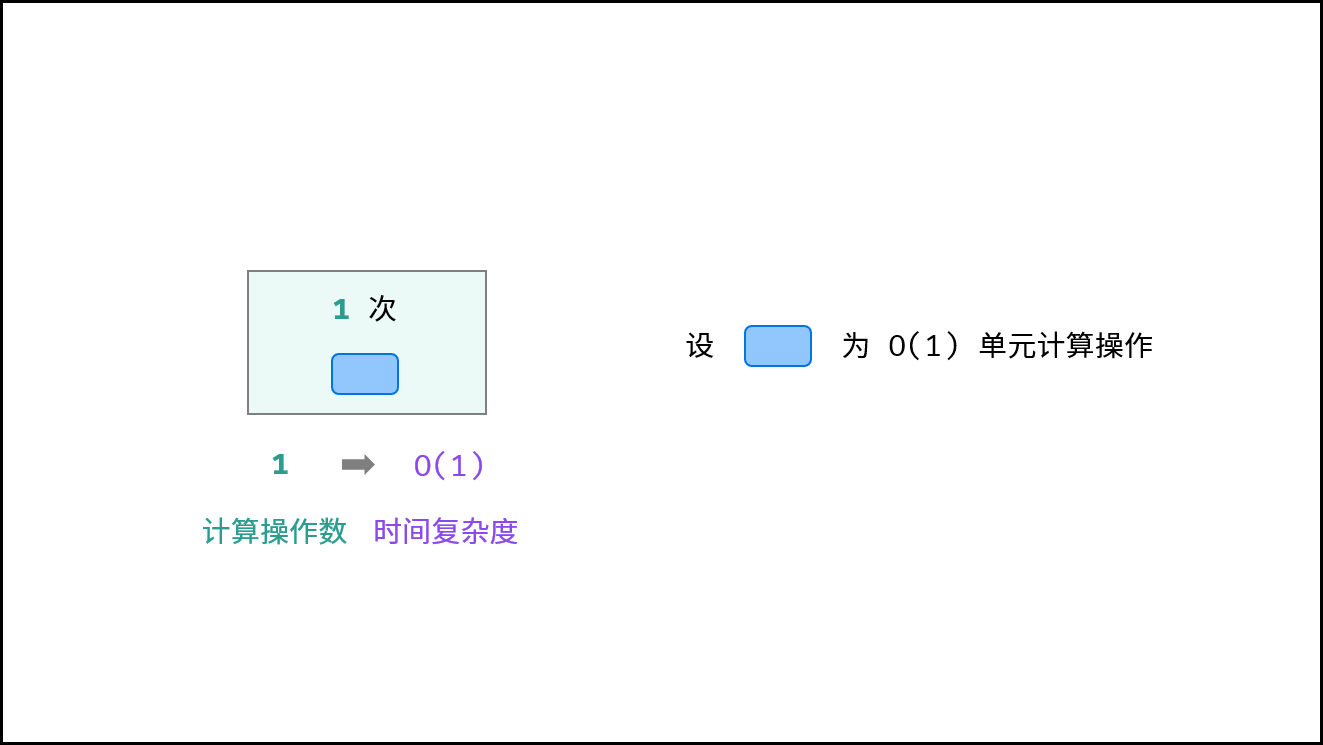![Picture2.png](https://pic.leetcode-cn.com/1623779241-lViysV-Picture2.png){:width=500}
### 线性 $O(N)$ ：
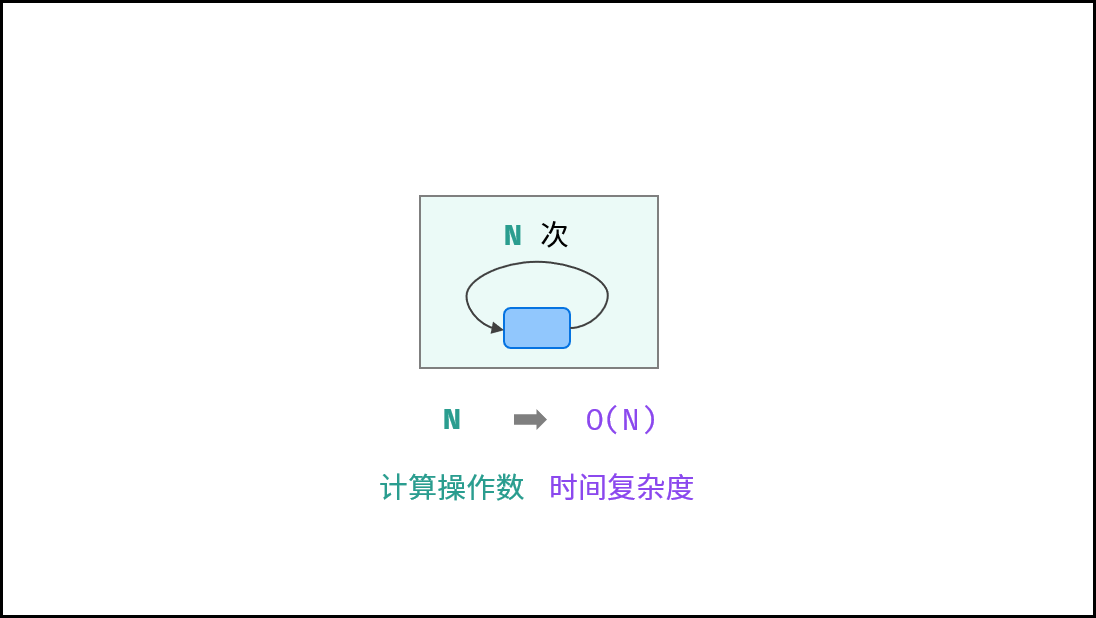
循环运行次数与 $N$ 大小呈线性关系，时间复杂度为 $O(N)$ 。
```Python []
def algorithm(N):
count = 0
for i in range(N):
count += 1
return count
```
```Java []
int algorithm(int N) {
int count = 0;
for (int i = 0; i < N; i++)
count++;
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
for (int i = 0; i < N; i++)
count++;
return count;
}
```
对于以下代码，虽然是两层循环，但第二层与 $N$ 大小无关，因此整体仍与 $N$ 呈线性关系。
```Python []
def algorithm(N):
count = 0
a = 10000
for i in range(N):
for j in range(a):
count += 1
return count
```
```Java []
int algorithm(int N) {
int count = 0;
int a = 10000;
for (int i = 0; i < N; i++) {
for (int j = 0; j < a; j++) {
count++;
}
}
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
int a = 10000;
for (int i = 0; i < N; i++) {
for (int j = 0; j < a; j++) {
count++;
}
}
return count;
}
```
![Picture3.png](https://pic.leetcode-cn.com/1623519242-AhnqvJ-Picture3.png){:width=500}
### 平方 $O(N^2)$ ：
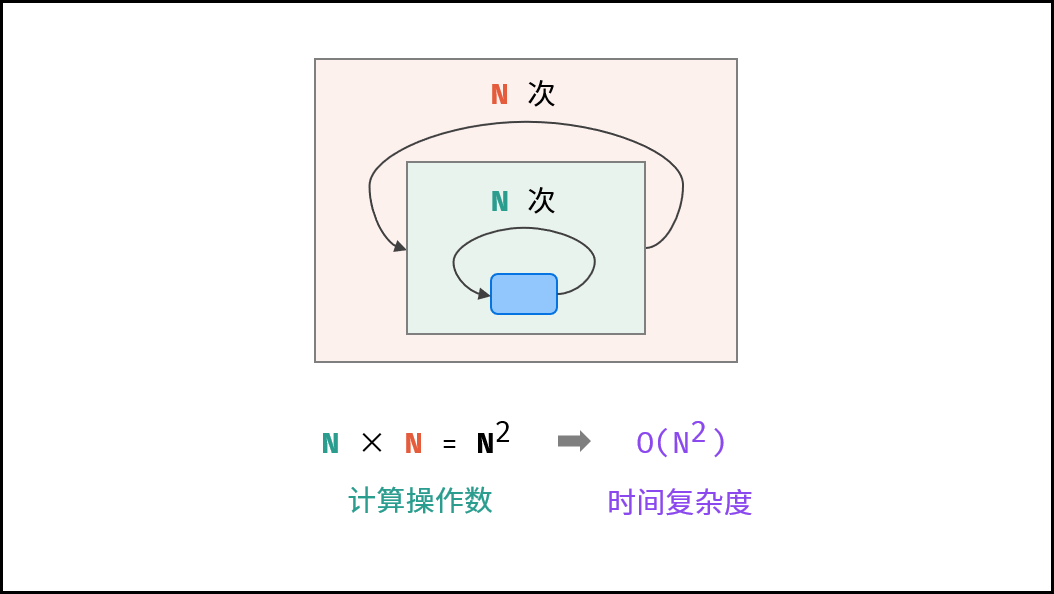
两层循环相互独立，都与 $N$ 呈线性关系，因此总体与 $N$ 呈平方关系，时间复杂度为 $O(N^2)$ 。
```Python []
def algorithm(N):
count = 0
for i in range(N):
for j in range(N):
count += 1
return count
```
```Java []
int algorithm(int N) {
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
count++;
}
}
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
count++;
}
}
return count;
}
```
以「冒泡排序」为例，其包含两层独立循环：
1. 第一层复杂度为 $O(N)$ ；
2. 第二层平均循环次数为 $\frac{N}{2}$ ，复杂度为 $O(N)$ ，推导过程如下：
$$
O(\frac{N}{2}) = O(\frac{1}{2})O(N) = O(1)O(N) = O(N)
$$
因此，冒泡排序的总体时间复杂度为 $O(N^2)$ ，代码如下所示。
```Python []
def bubble_sort(nums):
N = len(nums)
for i in range(N - 1):
for j in range(N - 1 - i):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
return nums
```
```Java []
int[] bubbleSort(int[] nums) {
int N = nums.length;
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
return nums;
}
```
```C++ []
vector<int> bubbleSort(vector<int>& nums) {
int N = nums.size();
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
}
}
}
return nums;
}
```
![Picture4.png](https://pic.leetcode-cn.com/1623519242-piiPrs-Picture4.png){:width=450}
### 指数 $O(2^N)$ ：
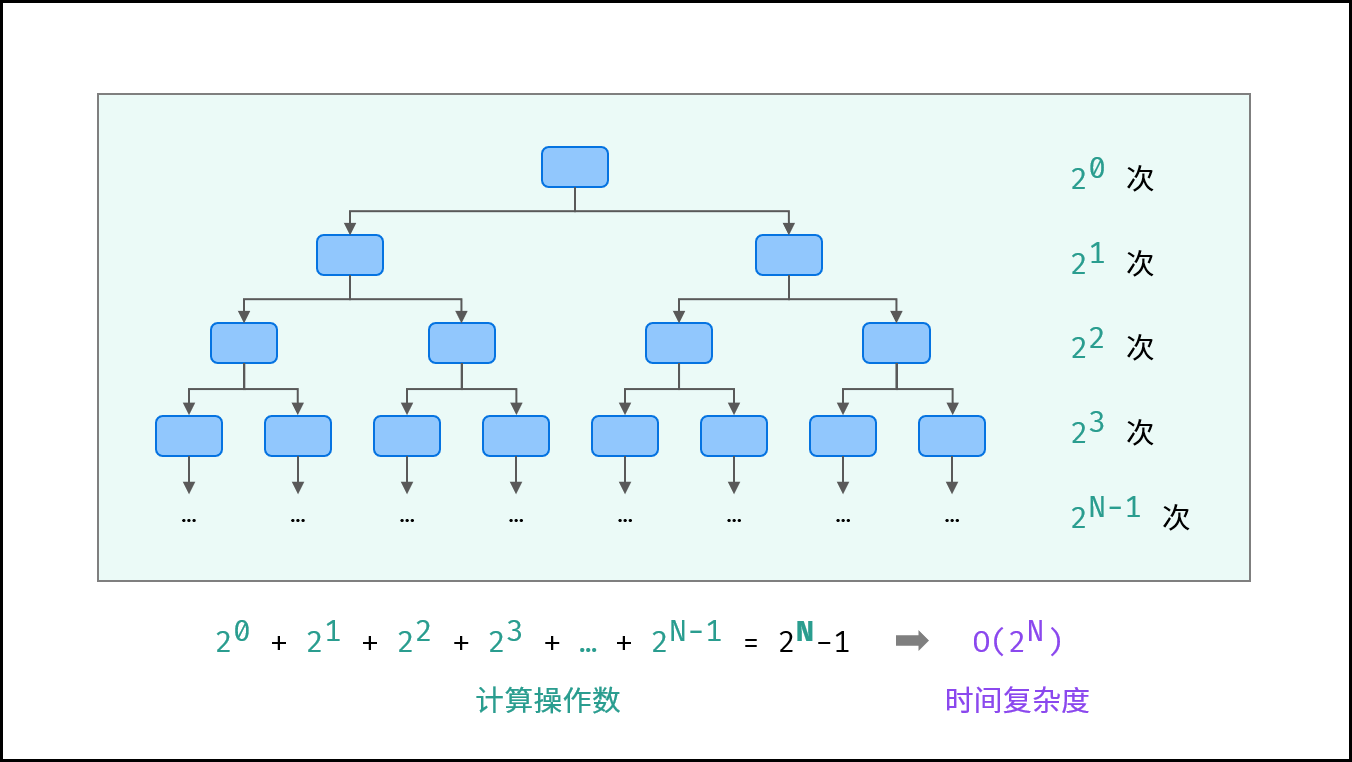
生物学科中的 “细胞分裂” 即是指数级增长。初始状态为 $1$ 个细胞，分裂一轮后为 $2$ 个，分裂两轮后为 $4$ 个，……，分裂 $N$ 轮后有 $2^N$ 个细胞。
算法中，指数阶常出现于递归，算法原理图与代码如下所示。
```Python []
def algorithm(N):
if N <= 0: return 1
count_1 = algorithm(N - 1)
count_2 = algorithm(N - 1)
return count_1 + count_2
```
```Java []
int algorithm(int N) {
if (N <= 0) return 1;
int count_1 = algorithm(N - 1);
int count_2 = algorithm(N - 1);
return count_1 + count_2;
}
```
```C++ []
int algorithm(int N) {
if (N <= 0) return 1;
int count_1 = algorithm(N - 1);
int count_2 = algorithm(N - 1);
return count_1 + count_2;
}
```
![Picture5.png](https://pic.leetcode-cn.com/1623519242-XLBkIT-Picture5.png){:width=600}
### 阶乘 $O(N!)$ ：
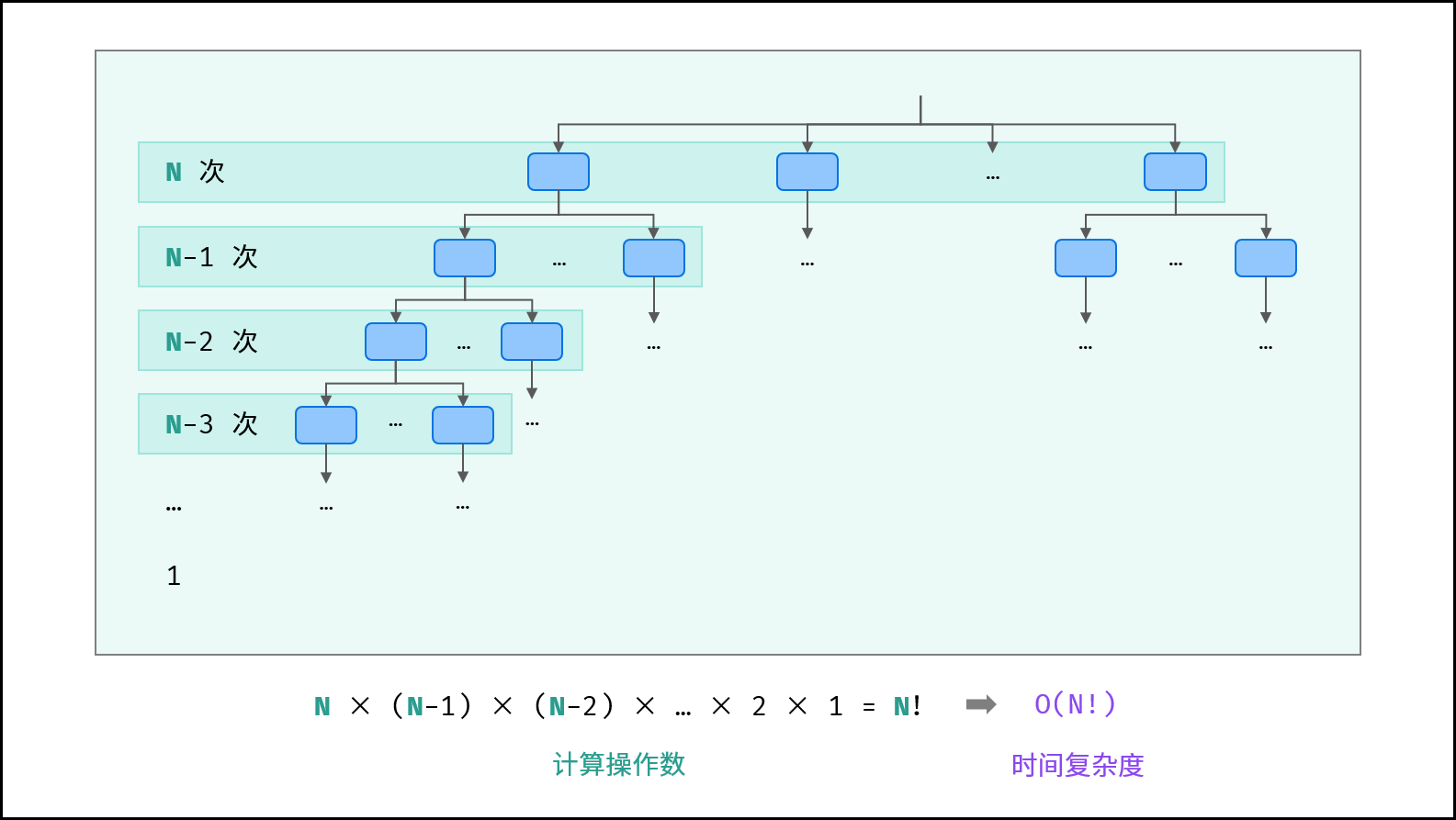
阶乘阶对应数学上常见的 “全排列” 。即给定 $N$ 个互不重复的元素，求其所有可能的排列方案，则方案数量为：
$$
N \times (N - 1) \times (N - 2) \times \cdots \times 2 \times 1 = N!
$$
如下图与代码所示，阶乘常使用递归实现，算法原理：第一层分裂出 $N$ 个，第二层分裂出 $N - 1$ 个，…… ，直至到第 $N$ 层时终止并回溯。
```Python []
def algorithm(N):
if N <= 0: return 1
count = 0
for _ in range(N):
count += algorithm(N - 1)
return count
```
```Java []
int algorithm(int N) {
if (N <= 0) return 1;
int count = 0;
for (int i = 0; i < N; i++) {
count += algorithm(N - 1);
}
return count;
}
```
```C++ []
int algorithm(int N) {
if (N <= 0) return 1;
int count = 0;
for (int i = 0; i < N; i++) {
count += algorithm(N - 1);
}
return count;
}
```
![Picture6.png](https://pic.leetcode-cn.com/1623519242-AFSqrK-Picture6.png){:width=600}
### 对数 $O(\log N)$ ：
对数阶与指数阶相反，指数阶为 “每轮分裂出两倍的情况” ，而对数阶是 “每轮排除一半的情况” 。对数阶常出现于「二分法」、「分治」等算法中，体现着 “一分为二” 或 “一分为多” 的算法思想。
设循环次数为 $m$ ，则输入数据大小 $N$ 与 $2 ^ m$ 呈线性关系，两边同时取 $log_2$ 对数，则得到循环次数 $m$ 与 $\log_2 N$ 呈线性关系，即时间复杂度为 $O(\log N)$ 。
```Python []
def algorithm(N):
count = 0
i = N
while i > 1:
i = i / 2
count += 1
return count
```
```Java []
int algorithm(int N) {
int count = 0;
float i = N;
while (i > 1) {
i = i / 2;
count++;
}
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
float i = N;
while (i > 1) {
i = i / 2;
count++;
}
return count;
}
```
如以下代码所示，对于不同 $a$ 的取值，循环次数 $m$ 与 $\log_a N$ 呈线性关系 ，时间复杂度为 $O(\log_a N)$ 。而无论底数 $a$ 取值，时间复杂度都可记作 $O(\log N)$ ，根据对数换底公式的推导如下：
$$
O(\log_a N) = \frac{O(\log_2 N)}{O(\log_2 a)} = O(\log N)
$$
```Python []
def algorithm(N):
count = 0
i = N
a = 3
while i > 1:
i = i / a
count += 1
return count
```
```Java []
int algorithm(int N) {
int count = 0;
float i = N;
int a = 3;
while (i > 1) {
i = i / a;
count++;
}
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
float i = N;
int a = 3;
while (i > 1) {
i = i / a;
count++;
}
return count;
}
```
> 如下图所示，为二分查找的时间复杂度示意图，每次二分将搜索区间缩小一半。
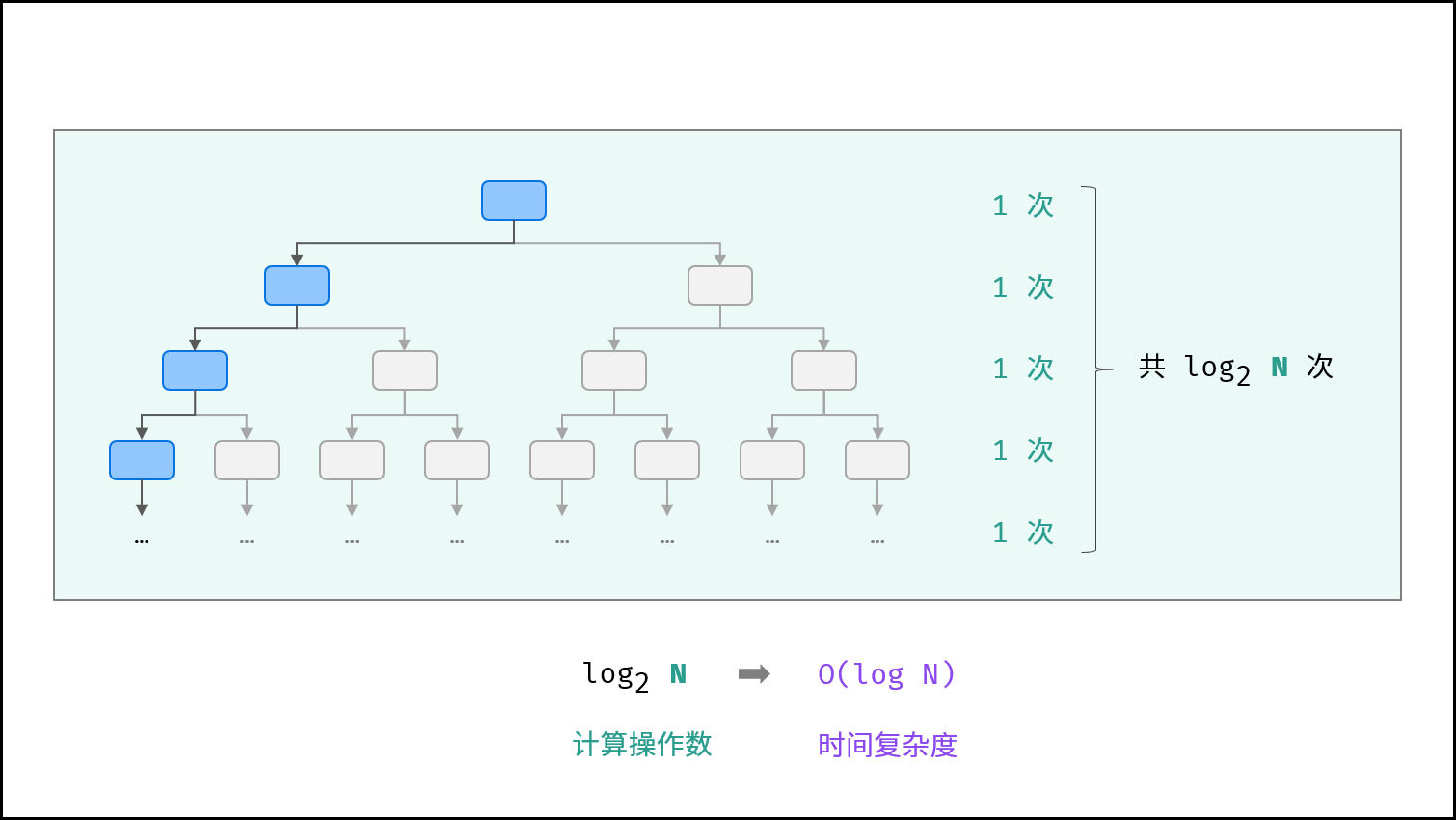![Picture7.png](https://pic.leetcode-cn.com/1623519242-WthaZa-Picture7.png){:width=600}
### 线性对数 $O(N \log N)$ ：
两层循环相互独立，第一层和第二层时间复杂度分别为 $O(\log N)$ 和 $O(N)$ ，则总体时间复杂度为 $O(N \log N)$ ；
```Python []
def algorithm(N):
count = 0
i = N
while i > 1:
i = i / 2
for j in range(N):
count += 1
```
```Java []
int algorithm(int N) {
int count = 0;
float i = N;
while (i > 1) {
i = i / 2;
for (int j = 0; j < N; j++)
count++;
}
return count;
}
```
```C++ []
int algorithm(int N) {
int count = 0;
float i = N;
while (i > 1) {
i = i / 2;
for (int j = 0; j < N; j++)
count++;
}
return count;
}
```
线性对数阶常出现于排序算法，例如「快速排序」、「归并排序」、「堆排序」等，其时间复杂度原理如下图所示。
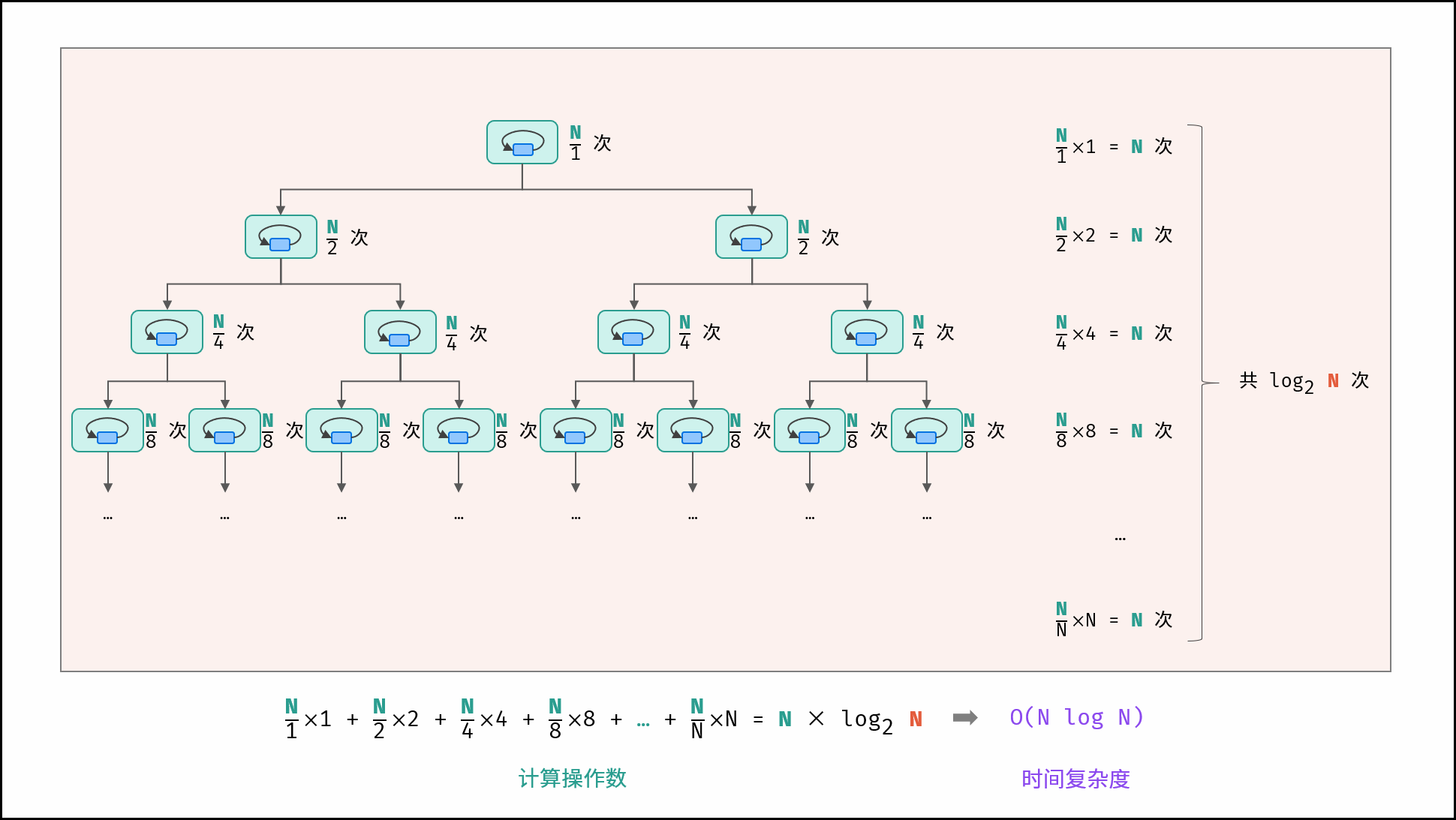
![Picture8.png](https://pic.leetcode-cn.com/1623519242-rhCOIh-Picture8.png)
---
## 示例题目
以下列举本 LeetBook 中各时间复杂度的对应示例题解，以帮助加深理解。
| 时间复杂度 | 示例题解 |
| ------------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- |
| $O(1)$ | [砍竹子 I](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5vyva2/)、[文物朝代判断](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/572x9r/) |
| $O(\log N)$ | [Pow(x, n)](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/57p2pv/)、[统计目标成绩的出现次数](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/58lgr7/) |
| $O(N)$ | [训练计划 III](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/9p7s17/)、[斐波那契数](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50fji7/) |
| $O(N \log N)$ | [破解闯关密码](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/59ceyt/)、[交易逆序对的总数](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/o53yjd/) |
| $O(N^2)$ | [验证二叉搜索树的后序遍历序列](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5vwbf6/)、[招式拆解 I](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5dz9di/) |
| $O(N!)$ | [套餐内商品的排列顺序](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50hah3/) |

547
leetbook_ioa/docs/# 1.4 空间复杂度.md Executable file
View File

@@ -0,0 +1,547 @@
# 空间复杂度
空间复杂度涉及的空间类型有：
- **输入空间：** 存储输入数据所需的空间大小；
- **暂存空间：** 算法运行过程中，存储所有中间变量和对象等数据所需的空间大小；
- **输出空间：** 算法运行返回时，存储输出数据所需的空间大小；
通常情况下，空间复杂度指在输入数据大小为 $N$ 时，算法运行所使用的「暂存空间」+「输出空间」的总体大小。
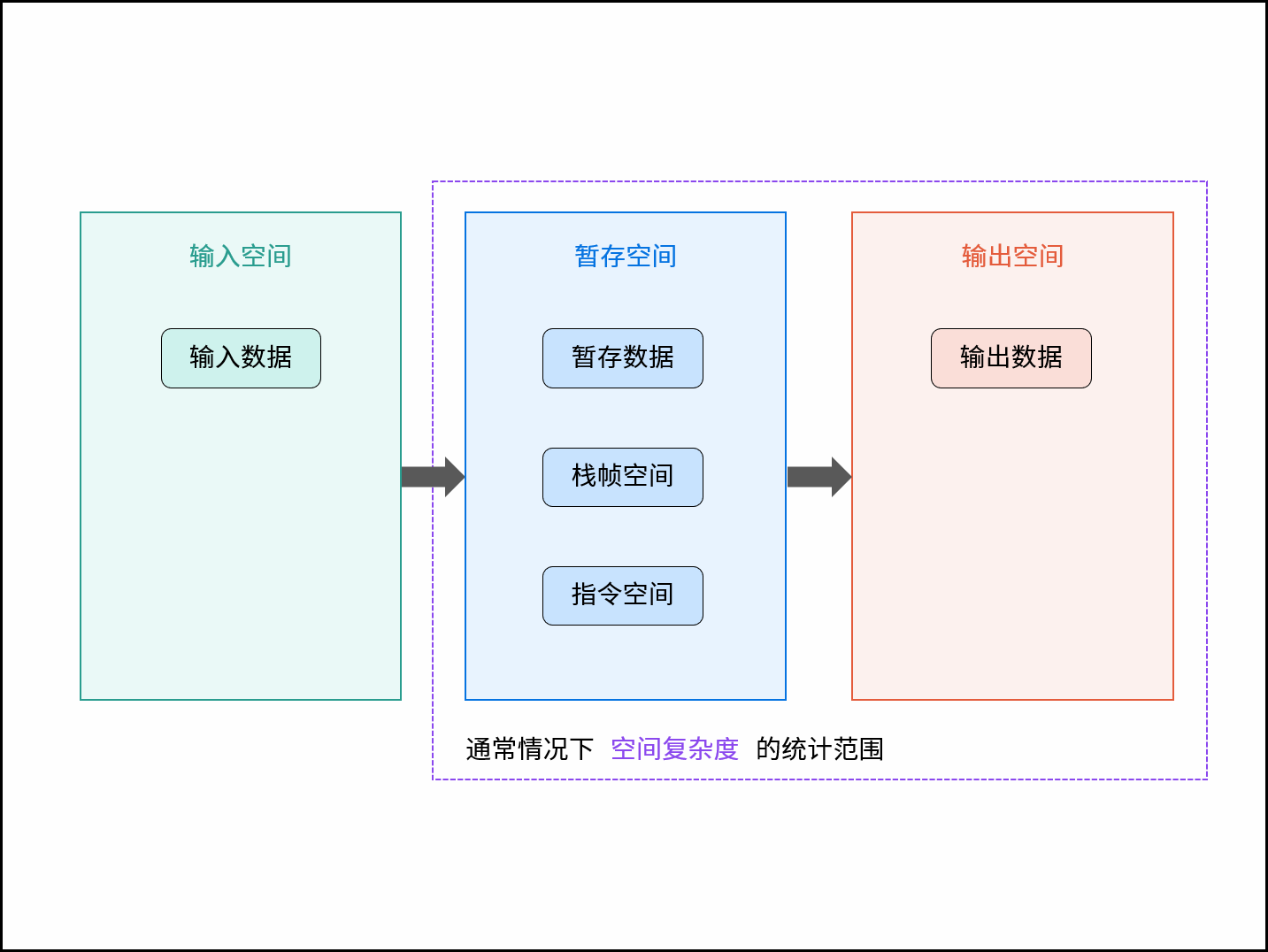![Picture1.png](https://pic.leetcode-cn.com/1623769147-NnmTbL-Picture1.png){:width=500}
而根据不同来源，算法使用的内存空间分为三类：
**指令空间：**
编译后，程序指令所使用的内存空间。
**数据空间：**
算法中的各项变量使用的空间，包括：声明的常量、变量、动态数组、动态对象等使用的内存空间。
```Python []
class Node:
def __init__(self, val):
self.val = val
self.next = None
def algorithm(N):
num = N # 变量
nums = [0] * N # 动态数组
node = Node(N) # 动态对象
```
```Java []
class Node {
int val;
Node next;
Node(int x) { val = x; }
}
void algorithm(int N) {
int num = N; // 变量
int[] nums = new int[N]; // 动态数组
Node node = new Node(N); // 动态对象
}
```
```C++ []
struct Node {
int val;
Node *next;
Node(int x) : val(x), next(NULL) {}
};
void algorithm(int N) {
int num = N; // 变量
int nums[N]; // 动态数组
Node* node = new Node(N); // 动态对象
}
```
**栈帧空间：**
程序调用函数是基于栈实现的，函数在调用期间，占用常量大小的栈帧空间，直至返回后释放。如以下代码所示，在循环中调用函数，每轮调用 `test()` 返回后，栈帧空间已被释放，因此空间复杂度仍为 $O(1)$ 。
```Python []
def test():
return 0
def algorithm(N):
for _ in range(N):
test()
```
```Java []
int test() {
return 0;
}
void algorithm(int N) {
for (int i = 0; i < N; i++) {
test();
}
}
```
```C++ []
int test() {
return 0;
}
void algorithm(int N) {
for (int i = 0; i < N; i++) {
test();
}
}
```
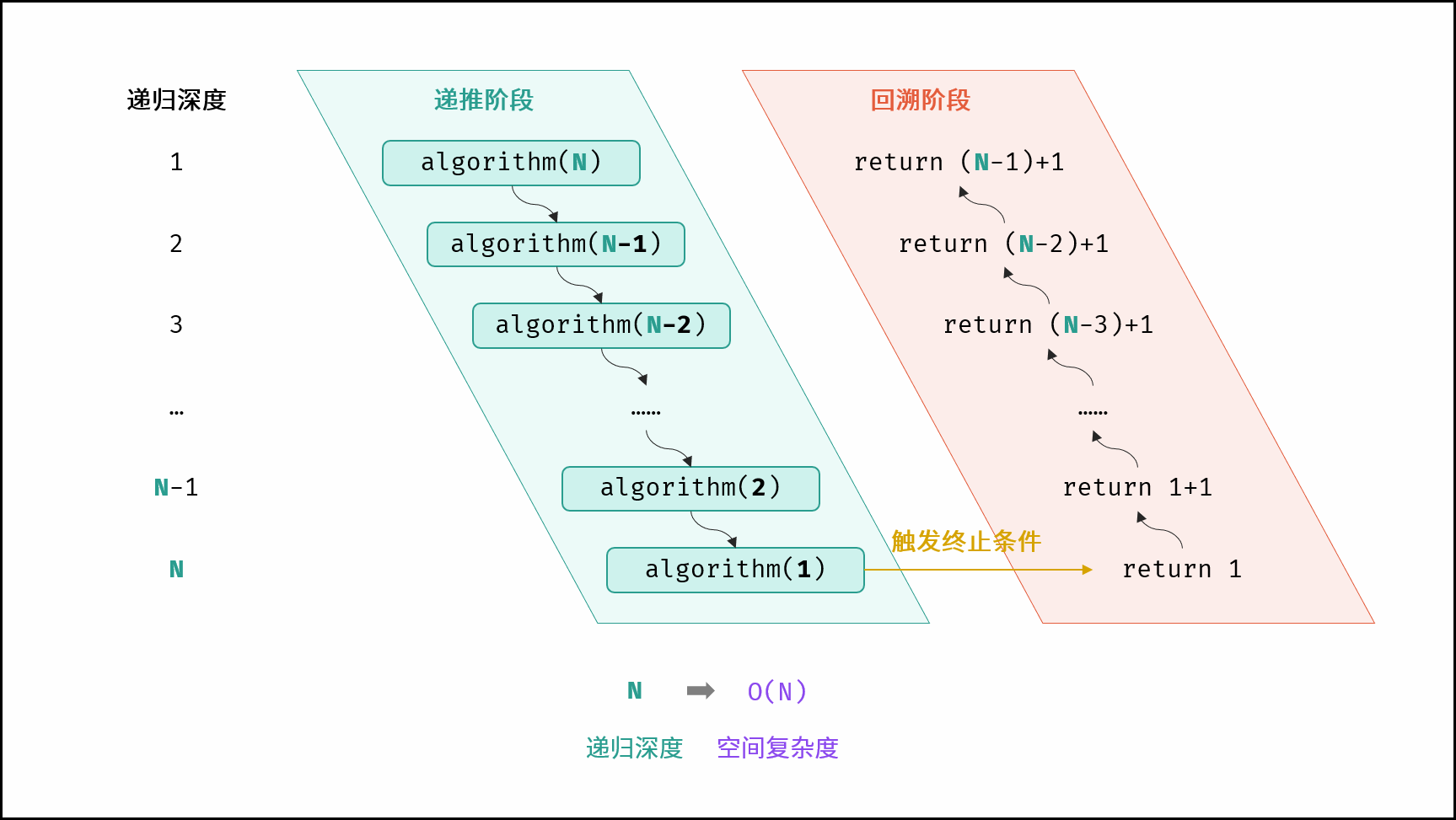
算法中，栈帧空间的累计常出现于递归调用。如以下代码所示，通过递归调用，会同时存在 $N$ 个未返回的函数 `algorithm()` ，此时累计使用 $O(N)$ 大小的栈帧空间。
```Python []
def algorithm(N):
if N <= 1: return 1
return algorithm(N - 1) + 1
```
```Java []
int algorithm(int N) {
if (N <= 1) return 1;
return algorithm(N - 1) + 1;
}
```
```C++ []
int algorithm(int N) {
if (N <= 1) return 1;
return algorithm(N - 1) + 1;
}
```
---
## 符号表示
通常情况下，空间复杂度统计算法在 “最差情况” 下使用的空间大小，以体现算法运行所需预留的空间量，使用符号 $O$ 表示。
最差情况有两层含义，分别为「最差输入数据」、算法运行中的「最差运行点」。例如以下代码：
> 输入整数 $N$ ，取值范围 $N \geq 1$ ；
- **最差输入数据：** 当 $N \leq 10$ 时，数组 `nums` 的长度恒定为 10 ，空间复杂度为 $O(10) = O(1)$ ；当 $N > 10$ 时，数组 $nums$ 长度为 $N$ ，空间复杂度为 $O(N)$ ；因此，空间复杂度应为最差输入数据情况下的 $O(N)$ 。
- **最差运行点：** 在执行 `nums = [0] * 10` 时，算法仅使用 $O(1)$ 大小的空间；而当执行 `nums = [0] * N` 时，算法使用 $O(N)$ 的空间；因此，空间复杂度应为最差运行点的 $O(N)$ 。
```Python []
def algorithm(N):
num = 5 # O(1)
nums = [0] * 10 # O(1)
if N > 10:
nums = [0] * N # O(N)
```
```Java []
void algorithm(int N) {
int num = 5; // O(1)
int[] nums = new int[10]; // O(1)
if (N > 10) {
nums = new int[N]; // O(N)
}
}
```
```C++ []
void algorithm(int N) {
int num = 5; // O(1)
vector<int> nums(10); // O(1)
if (N > 10) {
nums.resize(N); // O(N)
}
}
```
---
## 常见种类
根据从小到大排列，常见的算法空间复杂度有：
$$
O(1) < O(\log N) < O(N) < O(N^2) < O(2^N)
$$
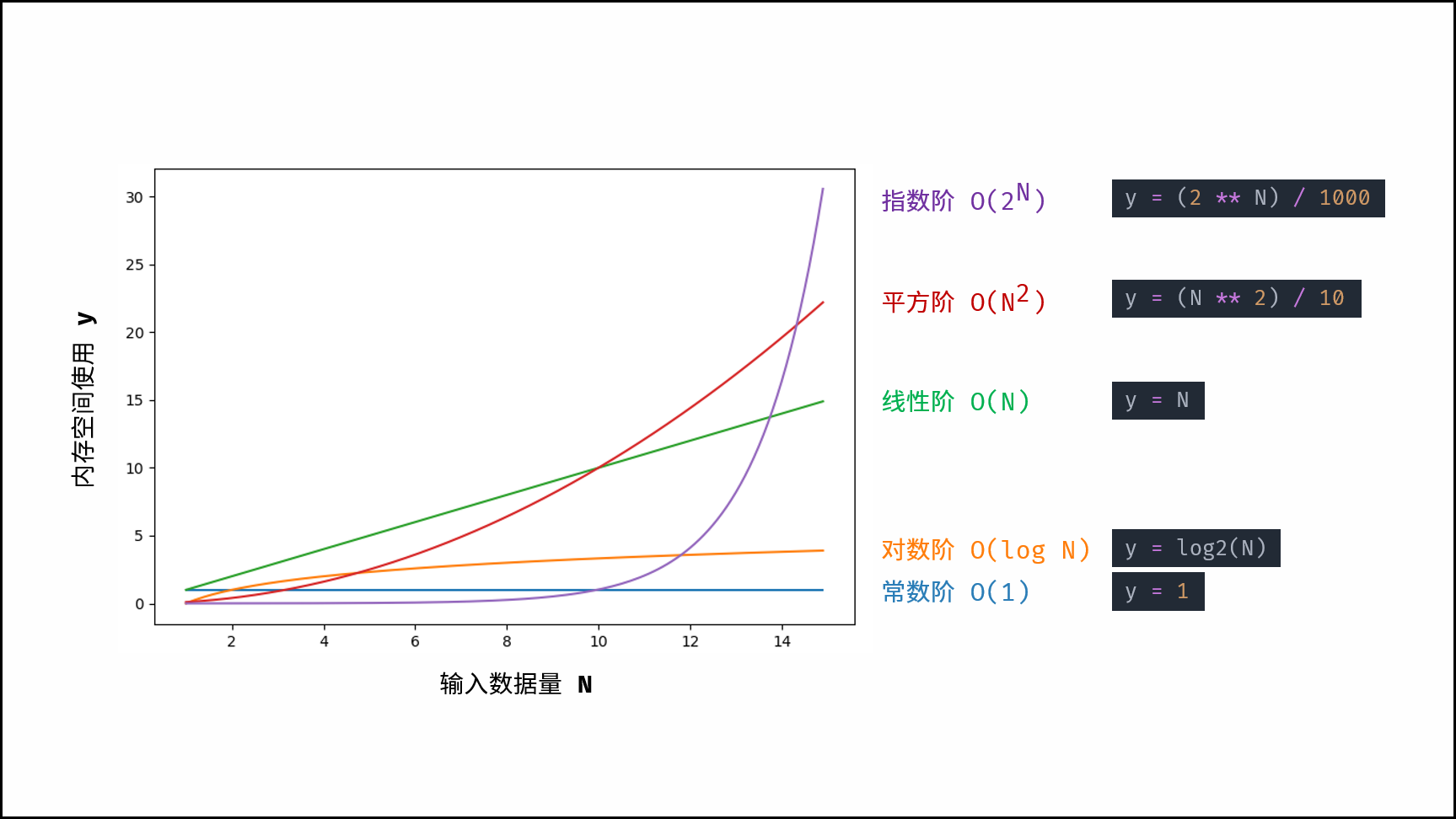
![Picture2.png](https://pic.leetcode-cn.com/1623769147-SyWGvV-Picture2.png)
对于以下所有示例，设输入数据大小为正整数 $N$ ，节点类 `Node` 、函数 `test()` 如以下代码所示。
```Python []
# 节点类 Node
class Node:
def __init__(self, val):
self.val = val
self.next = None
# 函数 test()
def test():
return 0
```
```Java []
// 节点类 Node
class Node {
int val; // 变量
Node next; // 动态数组
Node(int x) { val = x; } // 动态对象
}
// 函数 test()
int test() {
return 0;
}
```
```C++ []
// 节点类 Node
struct Node {
int val;
Node *next;
Node(int x) : val(x), next(NULL) {}
};
// 函数 test()
int test() {
return 0;
}
```
### 常数 $O(1)$ ：
普通常量、变量、对象、元素数量与输入数据大小 $N$ 无关的集合，皆使用常数大小的空间。
```Python []
def algorithm(N):
num = 0
nums = [0] * 10000
node = Node(0)
dic = { 0: '0' }
```
```Java []
void algorithm(int N) {
int num = 0;
int[] nums = new int[10000];
Node node = new Node(0);
Map<Integer, String> dic = new HashMap<>() {{ put(0, "0"); }};
}
```
```C++ []
void algorithm(int N) {
int num = 0;
int nums[10000];
Node* node = new Node(0);
unordered_map<int, string> dic;
dic.emplace(0, "0");
}
```
如以下代码所示，虽然函数 `test()` 调用了 $N$ 次，但每轮调用后 `test()` 已返回，无累计栈帧空间使用，因此空间复杂度仍为 $O(1)$ 。
```Python []
def algorithm(N):
for _ in range(N):
test()
```
```Java []
void algorithm(int N) {
for (int i = 0; i < N; i++) {
test();
}
}
```
```C++ []
void algorithm(int N) {
for (int i = 0; i < N; i++) {
test();
}
}
```
### 线性 $O(N)$ ：
元素数量与 $N$ 呈线性关系的任意类型集合（常见于一维数组、链表、哈希表等），皆使用线性大小的空间。
```Python []
def algorithm(N):
nums_1 = [0] * N
nums_2 = [0] * (N // 2)
nodes = [Node(i) for i in range(N)]
dic = {}
for i in range(N):
dic[i] = str(i)
```
```Java []
void algorithm(int N) {
int[] nums_1 = new int[N];
int[] nums_2 = new int[N / 2];
List<Node> nodes = new ArrayList<>();
for (int i = 0; i < N; i++) {
nodes.add(new Node(i));
}
Map<Integer, String> dic = new HashMap<>();
for (int i = 0; i < N; i++) {
dic.put(i, String.valueOf(i));
}
}
```
```C++ []
void algorithm(int N) {
int nums_1[N];
int nums_2[N / 2 + 1];
vector<Node*> nodes;
for (int i = 0; i < N; i++) {
nodes.push_back(new Node(i));
}
unordered_map<int, string> dic;
for (int i = 0; i < N; i++) {
dic.emplace(i, to_string(i));
}
}
```
如下图与代码所示，此递归调用期间，会同时存在 $N$ 个未返回的 `algorithm()` 函数，因此使用 $O(N)$ 大小的栈帧空间。
```Python []
def algorithm(N):
if N <= 1: return 1
return algorithm(N - 1) + 1
```
```Java []
int algorithm(int N) {
if (N <= 1) return 1;
return algorithm(N - 1) + 1;
}
```
```C++ []
int algorithm(int N) {
if (N <= 1) return 1;
return algorithm(N - 1) + 1;
}
```
![Picture3.png](https://pic.leetcode-cn.com/1623771937-urjBWX-Picture3.png)
### 平方 $O(N^2)$ ：
元素数量与 $N$ 呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间。
```Python []
def algorithm(N):
num_matrix = [[0 for j in range(N)] for i in range(N)]
node_matrix = [[Node(j) for j in range(N)] for i in range(N)]
```
```Java []
void algorithm(int N) {
int num_matrix[][] = new int[N][N];
List<List<Node>> node_matrix = new ArrayList<>();
for (int i = 0; i < N; i++) {
List<Node> nodes = new ArrayList<>();
for (int j = 0; j < N; j++) {
nodes.add(new Node(j));
}
node_matrix.add(nodes);
}
}
```
```C++ []
void algorithm(int N) {
vector<vector<int>> num_matrix;
for (int i = 0; i < N; i++) {
vector<int> nums;
for (int j = 0; j < N; j++) {
nums.push_back(0);
}
num_matrix.push_back(nums);
}
vector<vector<Node*>> node_matrix;
for (int i = 0; i < N; i++) {
vector<Node*> nodes;
for (int j = 0; j < N; j++) {
nodes.push_back(new Node(j));
}
node_matrix.push_back(nodes);
}
}
```
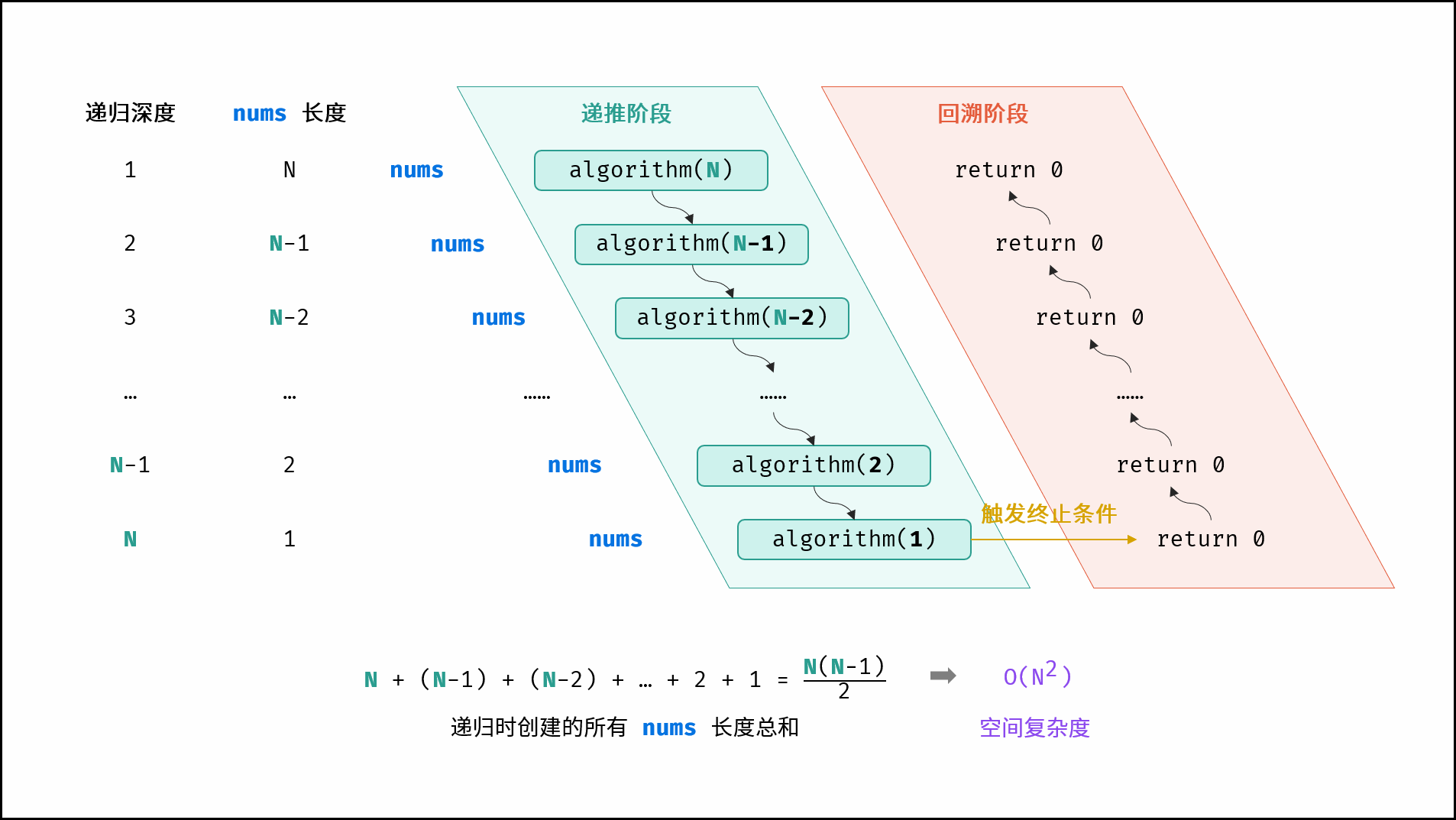
如下图与代码所示，递归调用时同时存在 $N$ 个未返回的 `algorithm()` 函数，使用 $O(N)$ 栈帧空间；每层递归函数中声明了数组，平均长度为 $\frac{N}{2}$ ，使用 $O(N)$ 空间；因此总体空间复杂度为 $O(N^2)$ 。
```Python []
def algorithm(N):
if N <= 0: return 0
nums = [0] * N
return algorithm(N - 1)
```
```Java []
int algorithm(int N) {
if (N <= 0) return 0;
int[] nums = new int[N];
return algorithm(N - 1);
}
```
```C++ []
int algorithm(int N) {
if (N <= 0) return 0;
int nums[N];
return algorithm(N - 1);
}
```
![Picture4.png](https://pic.leetcode-cn.com/1623769147-PYKjhh-Picture4.png)
### 指数 $O(2^N)$ ：
指数阶常见于二叉树、多叉树。例如，高度为 $N$ 的「满二叉树」的节点数量为 $2^N$ ，占用 $O(2^N)$ 大小的空间；同理，高度为 $N$ 的「满 $m$ 叉树」的节点数量为 $m^N$ ，占用 $O(m^N) = O(2^N)$ 大小的空间。
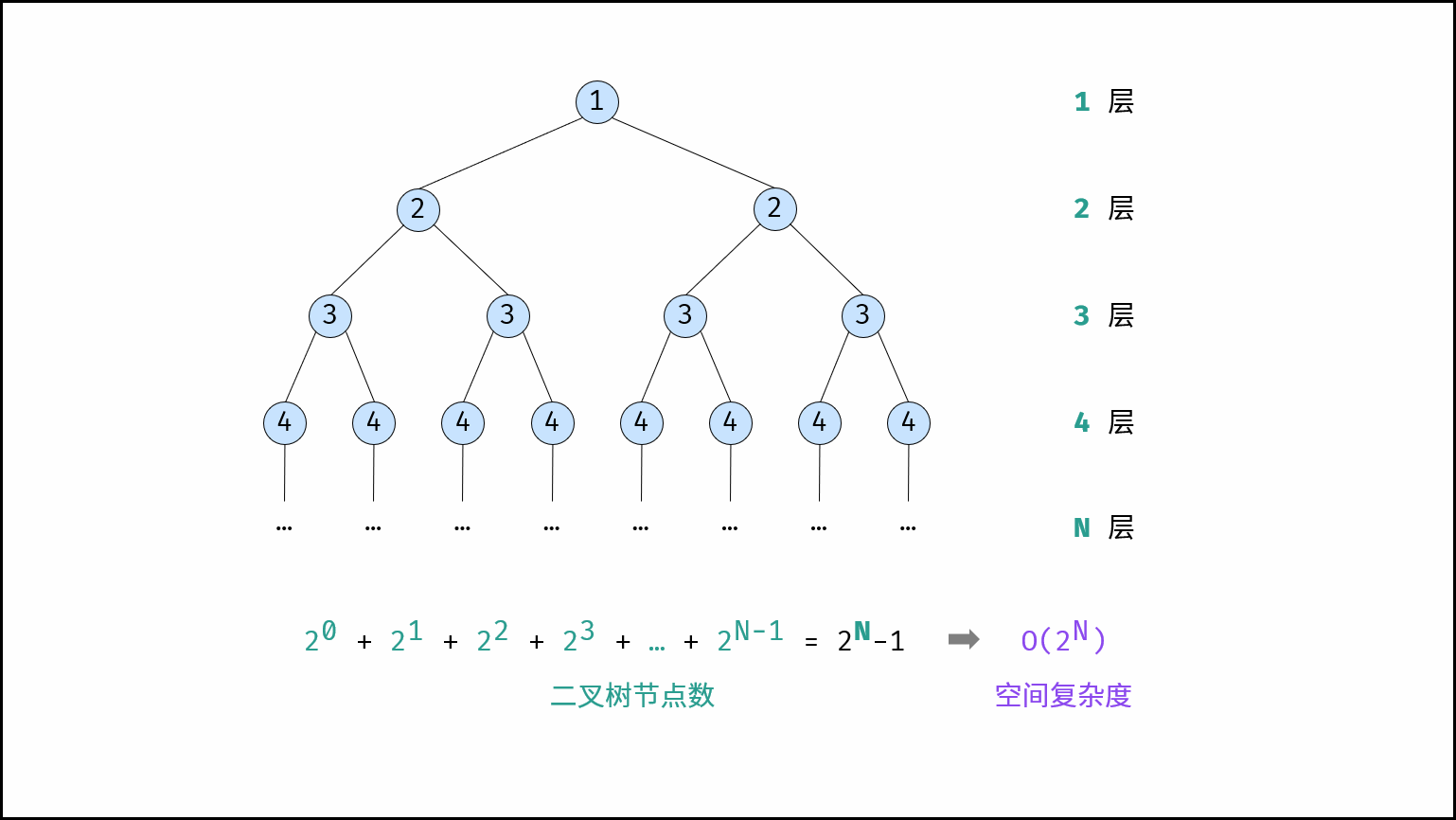![Picture5.png](https://pic.leetcode-cn.com/1623769147-FLxBQi-Picture5.png){:width=600}
### 对数 $O(\log N)$ ：
对数阶常出现于分治算法的栈帧空间累计、数据类型转换等，例如：
- **快速排序** ，平均空间复杂度为 $\Theta(\log N)$ ，最差空间复杂度为 $O(N)$ 。拓展知识：通过应用 [尾递归优化](https://stackoverflow.com/questions/310974/what-is-tail-call-optimization) ，可以将快速排序的最差空间复杂度限定至 $O(N)$ 。
- **数字转化为字符串** ，设某正整数为 $N$ ，则字符串的空间复杂度为 $O(\log N)$ 。推导如下：正整数 $N$ 的位数为 $log_{10} N$ ，即转化的字符串长度为 $\log_{10} N$ ，因此空间复杂度为 $O(\log N)$ 。
---
## 时空权衡
对于算法的性能，需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性，即时间和空间复杂度皆较低。而实际上，对于某个算法问题，同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度，往往是以提升空间复杂度为代价的，反之亦然。
> 由于当代计算机的内存充足，通常情况下，算法设计中一般会采取「空间换时间」的做法，即牺牲部分计算机存储空间，来提升算法的运行速度。
以 LeetCode 全站第一题 [两数之和](https://leetcode-cn.com/problems/two-sum/) 为例，「暴力枚举」和「辅助哈希表」分别为「空间最优」和「时间最优」的两种算法。
### 方法一：暴力枚举
时间复杂度 $O(N^2)$ ，空间复杂度 $O(1)$ ；属于「时间换空间」，虽然仅使用常数大小的额外空间，但运行速度过慢。
```Python []
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums) - 1):
for j in range(i + 1, len(nums)):
if nums[i] + nums[j] == target:
return i, j
return
```
```Java []
class Solution {
public int[] twoSum(int[] nums, int target) {
int size = nums.length;
for (int i = 0; i < size - 1; i++) {
for (int j = i + 1; j < size; j++) {
if (nums[i] + nums[j] == target)
return new int[] { i, j };
}
}
return new int[0];
}
}
```
```C++ []
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int size = nums.size();
for (int i = 0; i < size - 1; i++) {
for (int j = i + 1; j < size; j++) {
if (nums[i] + nums[j] == target)
return { i, j };
}
}
return {};
}
};
```
### 方法二：辅助哈希表
时间复杂度 $O(N)$ ，空间复杂度 $O(N)$ ；属于「空间换时间」，借助辅助哈希表 `dic` ，通过保存数组元素值与索引的映射来提升算法运行效率，是本题的最佳解法。
```Python []
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
dic = {}
for i in range(len(nums)):
if target - nums[i] in dic:
return dic[target - nums[i]], i
dic[nums[i]] = i
return []
```
```Java []
class Solution {
public int[] twoSum(int[] nums, int target) {
int size = nums.length;
Map<Integer, Integer> dic = new HashMap<>();
for (int i = 0; i < size; i++) {
if (dic.containsKey(target - nums[i])) {
return new int[] { dic.get(target - nums[i]), i };
}
dic.put(nums[i], i);
}
return new int[0];
}
}
```
```C++ []
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int size = nums.size();
unordered_map<int, int> dic;
for (int i = 0; i < size; i++) {
if (dic.find(target - nums[i]) != dic.end()) {
return { dic[target - nums[i]], i };
}
dic.emplace(nums[i], i);
}
return {};
}
};
```
---
## 示例题目
在 LeetCode 题目中，「输入空间」和「输出空间」往往是固定的，是必须使用的内存空间。因希望专注于算法性能对比，本 LeetBook 的题目解析的空间复杂度仅统计「暂存空间」大小。
| 空间复杂度 | 示例题解 |
| ----------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ |
| $O(1)$ | [斐波那契数](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50fji7/)、[训练计划 III](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/9p7s17/) |
| $O(\log N)$ | [库存管理 III](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/ohwddh/)、[找到第 k 位数字](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/57w6b3/) |
| $O(N)$ | [图书整理 I](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5d8831/)、[动态口令](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/58eckc/) |
| $O(N^2)$ | [衣橱整理](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/9hka9c/)、[套餐内商品的排列顺序](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50hah3/) |

482
leetbook_ioa/docs/# 11.1 动态规划解题框架.md Executable file
View File

@@ -0,0 +1,482 @@
# 动态规划解题框架
动态规划是算法与数据结构的重难点之一，其包含了「分治思想」、「空间换时间」、「最优解」等多种基石算法思想，常作为笔面试中的中等困难题出现。为帮助读者全面理解动态规划，知晓其来龙去脉，本文将从以下几个角度切入介绍：
1. 动态规划问题特点，**动态规划**和**分治算法**的联系与区别；
2. 借助例题介绍**重叠子问题**和**最优子结构**分别是什么，以及动态规划是如何解决它们的；
3. 动态规划的**解题框架**总结；
4. 动态规划的**练习例题**，从易到难排序；
---
## 动态规划特点
「分治」是算法中的一种基本思想，其通过**将原问题分解为子问题**，不断递归地将子问题分解为更小的子问题，并通过**组合子问题的解**来得到原问题的解。
类似于分治算法，「动态规划」也通过组合子问题的解得到原问题的解。不同的是，适合用动态规划解决的问题具有「重叠子问题」和「最优子结构」两大特性。
### 重叠子问题
动态规划的子问题是有**重叠的**，即各个子问题中包含**重复的更小子问题**。若使用暴力法穷举，求解这些相同子问题会产生大量的重复计算，效率低下。
动态规划在第一次求解某子问题时，会将子问题的解保存；后续遇到重叠子问题时，则直接通过查表获取解，保证每个**独立子问题只被计算一次**，从而降低算法的时间复杂度。
### 最优子结构
如果一个问题的最优解可以由其子问题的最优解组合构成，并且这些子问题可以独立求解，那么称此问题具有最优子结构。
动态规划从基础问题的解开始，不断迭代**组合、选择子问题的最优解**，最终得到原问题最优解。
---
## 重叠子问题示例：斐波那契数列
> 斐波那契数形成的数列为 $[0, 1, 1, 2, 3, 5, 8, 13, \cdots]$ ，数学定义如下：
> $$
> \begin{aligned}
> & F_0 = 0 \\
> & F_1 = 1 \\
> & F_n = F_{n-1} + F_{n-2}
> \end{aligned}
> $$
> **题目：** 求取第 $n$ 个斐波那契数（从第 0 个斐波那契数开始）。
以下，本文从「暴力递归」$\rightarrow$「记忆化递归」$\rightarrow$「动态规划」三种解法，介绍**重叠子问题**的概念与解决方案。
### 方法一：暴力递归
设斐波那契数列第 $n$ 个数字为 $f(n)$ 。根据数列定义，可得 $f(n) = f(n - 1) + f(n - 2)$ ，且第 0 , 1 个斐波那契数分别为 $f(0) = 0$ , $f(1) = 1$ 。
我们很容易联想到使用分治思想来求取 $f(n)$ ，即将求原问题 $f(n)$ 分解为求子问题 $f(n-1)$ 和 $f(n-2)$ ，向下递归直至已知的 $f(0)$ 和 $f(1)$ ，最终组合这些子问题求取原问题 $f(n)$ 。
```Python []
# 求第 n 个斐波那契数
def fibonacci(n):
if n == 0: return 0 # 返回 f(0)
if n == 1: return 1 # 返回 f(1)
return fibonacci(n - 1) + fibonacci(n - 2) # 分解为两个子问题求解
```
```Java []
// 求第 n 个斐波那契数
int fibonacci(int n) {
if (n == 0) return 0; // 返回 f(0)
if (n == 1) return 1; // 返回 f(1)
return fibonacci(n - 1) + fibonacci(n - 2); // 分解为两个子问题求解
}
```
```C++ []
int fibonacci(int n) {
if (n == 0) return 0; // 返回 f(0)
if (n == 1) return 1; // 返回 f(1)
return fibonacci(n - 1) + fibonacci(n - 2); // 分解为两个子问题求解
}
```
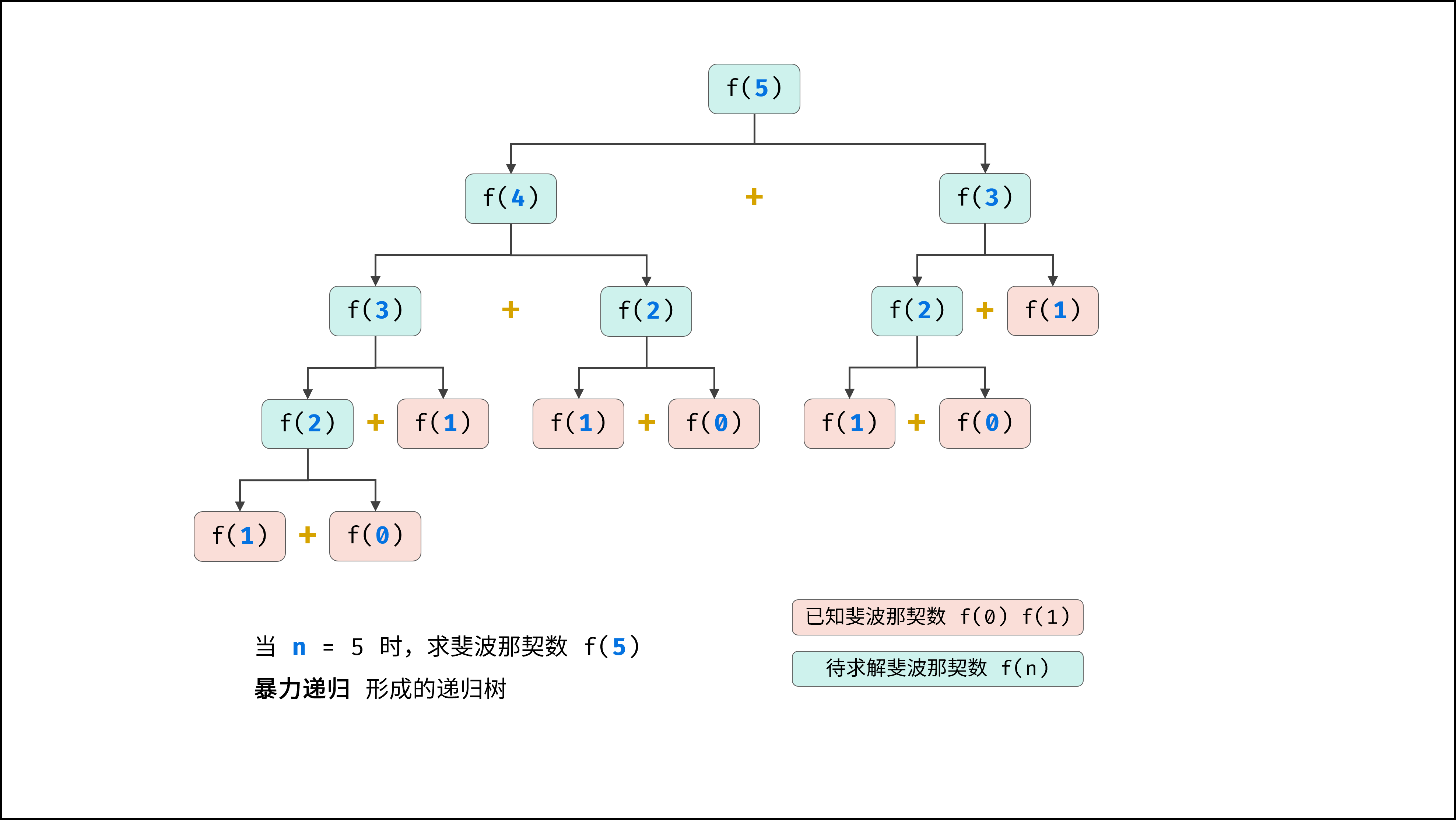
![Picture1.png](https://pic.leetcode-cn.com/1635075778-GADtbi-Picture1.png)
如上图所示，为暴力递归求斐波那契数 $f(5)$ 形成的二叉树，树中的每个节点代表着执行了一次 `fibonacci()` 函数，且有：
- 执行一次 `fibonacci()` 函数的时间复杂度为 $O(1)$ ；
- 二叉树节点数为指数级 $O(2^n)$ ；
因此，暴力递归的总体时间复杂度为 $O(2^n)$ 。此方法效率低下，随着 $n$ 的增长产生指数级爆炸。
### 方法二：记忆化递归
观察发现，暴力递归中的子问题多数都是**重叠子问题**，即：
$$
\begin{aligned}
& f(n) = f(n - 1) + f(n - 2) & 包含 f(n - 2) \\
& f(n - 1) = f(n - 2) + f(n - 3) & 重复 f(n - 2) \\
& f(n - 2) = f(n - 3) + f(n - 4) & 重复 f(n - 3) \\
& \cdots &以此类推
\end{aligned}
$$
这些重叠子问题产生了大量的递归树节点，其**不应被重复计算**。实际上，可以在递归中**第一次求解子问题**时，就将它们**保存**；后续递归中再次遇到相同子问题时，直接访问内存赋值即可。记忆化递归的代码如下所示。
```Python []
def fibonacci(n, dp):
if n == 0: return 0 # 返回 f(0)
if n == 1: return 1 # 返回 f(1)
if dp[n] != 0: return dp[n] # 若 f(n) 以前已经计算过，则直接返回记录的解
dp[n] = fibonacci(n - 1, dp) + fibonacci(n - 2, dp) # 将 f(n) 则记录至 dp
return dp[n]
# 求第 n 个斐波那契数
def fibonacci_memorized(n):
dp = [0] * (n + 1) # 用于保存 f(0) 至 f(n) 问题的解
return fibonacci(n, dp)
```
```Java []
int fibonacci(int n, int[] dp) {
if (n == 0) return 0; // 返回 f(0)
if (n == 1) return 1; // 返回 f(1)
if (dp[n] != 0) return dp[n]; // 若 f(n) 以前已经计算过，则直接返回记录的解
dp[n] = fibonacci(n - 1, dp) + fibonacci(n - 2, dp); // 将 f(n) 则记录至 dp
return dp[n];
}
// 求第 n 个斐波那契数
int fibonacciMemorized(int n) {
int[] dp = new int[n + 1]; // 用于保存 f(0) 至 f(n) 问题的解
return fibonacci(n, dp);
}
```
```C++ []
int fibonacci(int n, vector<int> dp) {
if (n == 0) return 0; // 返回 f(0)
if (n == 1) return 1; // 返回 f(1)
if (dp[n] != 0) return dp[n]; // 若 f(n) 以前已经计算过，则直接返回记录的解
dp[n] = fibonacci(n - 1, dp) + fibonacci(n - 2, dp); // 将 f(n) 则记录至 dp
return dp[n];
}
// 求第 n 个斐波那契数
int fibonacciMemorized(int n) {
vector<int> dp(n + 1, 0); // 用于保存 f(0) 至 f(n) 问题的解
return fibonacci(n, dp);
}
```
如下图所示，应用记忆化递归方法后，递归树中绝大部分节点被**剪枝**。此时，`fibonacci()` 函数的调用次数从 $O(2^n)$ 指数级别降低至 $O(n)$ 线性级别，时间复杂度大大降低。
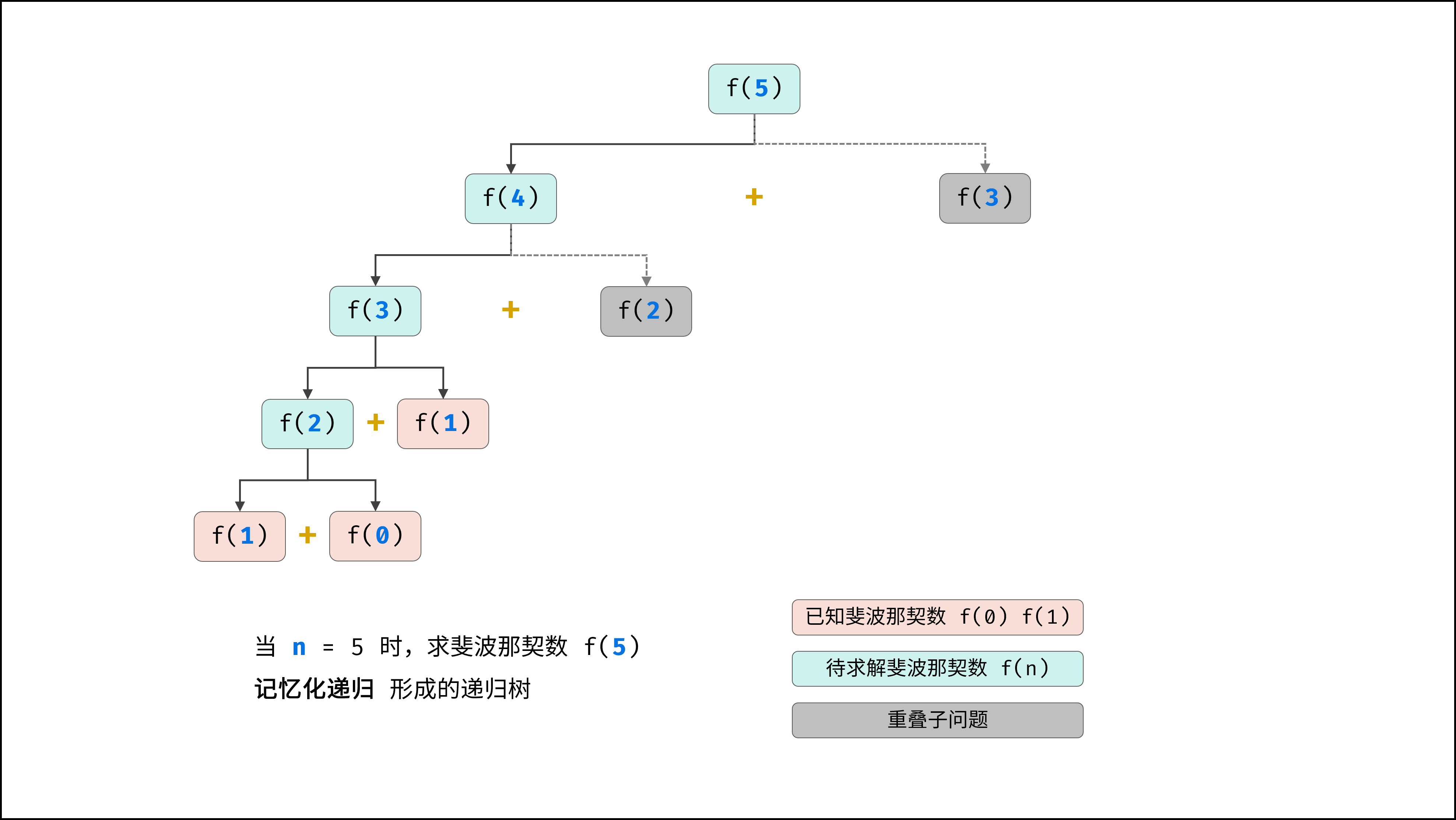
![Picture2.png](https://pic.leetcode-cn.com/1635075778-pJXkPc-Picture2.png)
### 方法三：动态规划
递归本质上是基于分治思想的从顶至底的解法。借助记忆化递归思想，可应用动态规划从底至顶求取 $f(n)$ ，代码如下所示。
```Python []
# 求第 n 个斐波那契数
def fibonacci(n):
if n == 0: return 0 # 若求 f(0) 则直接返回 0
dp = [0] * (n + 1) # 初始化 dp 列表
dp[0], dp[1] = 0, 1 # 初始化 f(0), f(1)
for i in range(2, n + 1): # 状态转移求取 f(2), f(3), ..., f(n)
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n] # 返回 f(n)
```
```Java []
// 求第 n 个斐波那契数
int fibonacci(int n) {
if (n == 0) return 0; // 若求 f(0) 则直接返回 0
int[] dp = new int[n + 1]; // 初始化 dp 列表
dp[1] = 1; // 初始化 f(0), f(1)
for (int i = 2; i <= n; i++) { // 状态转移求取 f(2), f(3), ..., f(n)
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n]; // 返回 f(n)
}
```
```C++ []
// 求第 n 个斐波那契数
int fibonacci(int n) {
if (n == 0) return 0; // 若求 f(0) 则直接返回 0
vector<int> dp(n + 1, 0); // 初始化 dp 列表
dp[1] = 1; // 初始化 f(0), f(1)
for (int i = 2; i <= n; i++) { // 状态转移求取 f(2), f(3), ..., f(n)
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n]; // 返回 f(n)
}
```
如下图所示，为动态规划求解 $f(5)$ 的迭代流程，其是转移方程 $f(n) = f(n - 1) + f(n - 2)$ 的体现。
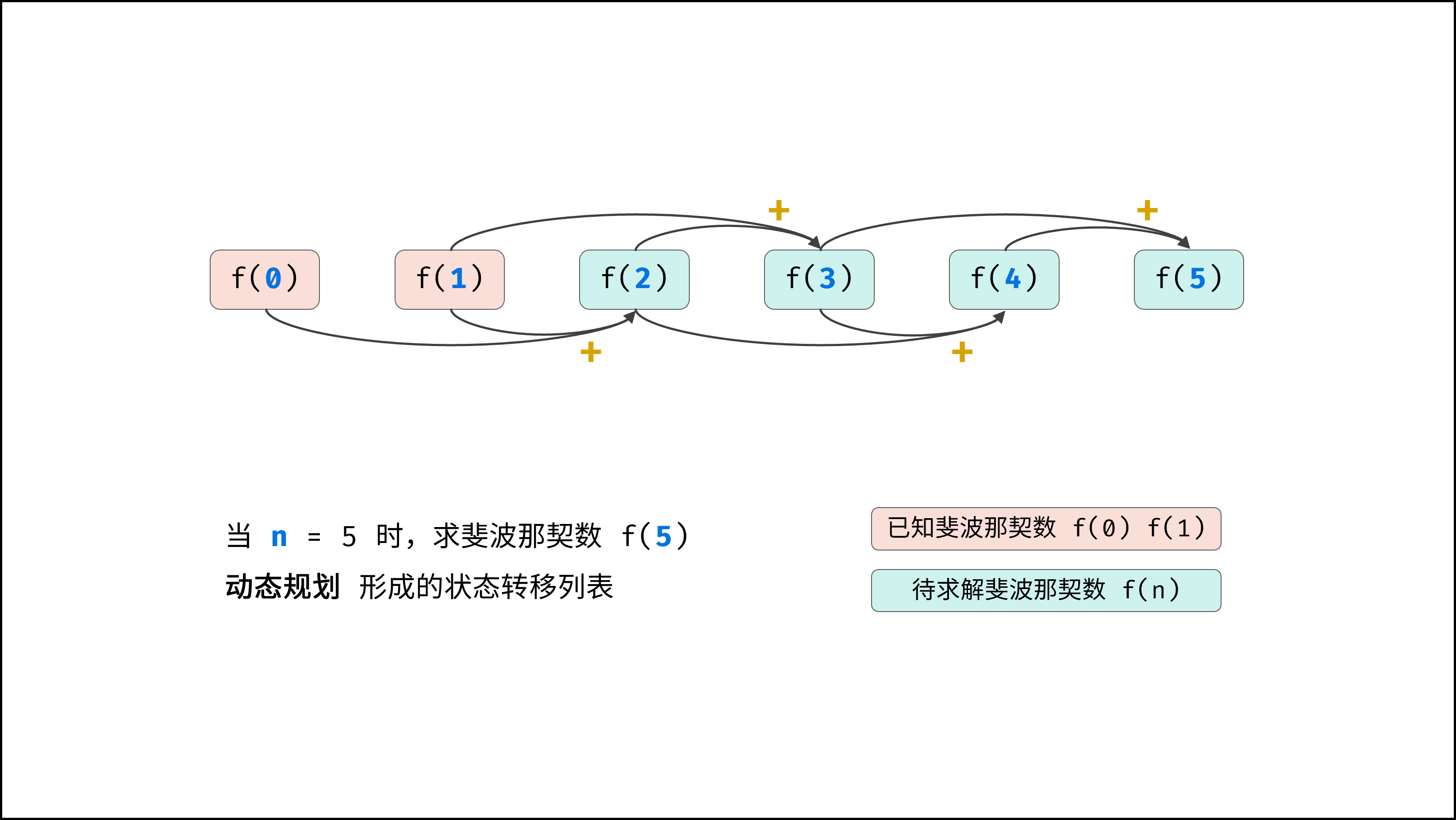
![Picture3.png](https://pic.leetcode-cn.com/1635075778-EeBEoS-Picture3.png)
上述动态规划解法借助了一个 `dp` 数组保存子问题的解，其空间复杂度为 $O(N)$ 。而由于 $f(n)$ 只与 $f(n - 1)$ 和 $f(n - 2)$ 有关，因此我们可以仅使用两个变量 $a$ , $b$ 交替前进计算即可。此时动态规划的空间复杂度降低至 $O(1)$ ，代码如下所示。
```Python []
# 求第 n 个斐波那契数
def fibonacci(n):
if n == 0: return 0 # 若求 f(0) 则直接返回 0
a, b = 0, 1 # 初始化 f(0), f(1)
for i in range(2, n + 1): # 状态转移求取 f(2), f(3), ..., f(n)
a, b = b, a + b
return b # 返回 f(n)
```
```Java []
// 求第 n 个斐波那契数
int fibonacci(int n) {
if (n == 0) return 0; // 若求 f(0) 则直接返回 0
int a = 0, b = 1; // 初始化 f(0), f(1)
for (int i = 2; i <= n; i++) { // 状态转移求取 f(2), f(3), ..., f(n)
int tmp = a;
a = b;
b = tmp + b;
}
return b; // 返回 f(n)
}
```
```C++ []
// 求第 n 个斐波那契数
int fibonacci(int n) {
if (n == 0) return 0; // 若求 f(0) 则直接返回 0
int a = 0, b = 1; // 初始化 f(0), f(1)
for (int i = 2; i <= n; i++) { // 状态转移求取 f(2), f(3), ..., f(n)
int tmp = a;
a = b;
b = tmp + b;
}
return b; // 返回 f(n)
}
```
### 示例小结
记忆化递归和动态规划的本质思想是一致的，是对斐波那契数列定义的不同表现形式：
- **记忆化递归 — 从顶至低：** 求 $f(n)$ 需要 $f(n - 1)$ 和 $f(n - 2)$ ； $\cdots$ ；求 $f(2)$ 需要 $f(1)$ 和 $f(0)$ ；而 $f(1)$ 和 $f(0)$ 已知；
- **动态规划 — 从底至顶：** 将已知 $f(0)$ 和 $f(1)$ 组合得到 $f(2)$ ；$\cdots$ ；将 $f(n - 2)$ 和 $f(n - 1)$ 组合得到 $f(n)$ ；
斐波那契数列问题不包含「最优子结构」，只需计算每个子问题的解，避免重复计算即可，并不需要从子问题组合中**选择最优组合**。接下来，本文借助「最高蛋糕售价方案」，介绍动态规划的**最优子结构**概念。
---
## 最优子结构示例：蛋糕最高售价
> 小力开了一家蛋糕店，并针对不同重量的蛋糕设定了不同售价，分别为：
>
> | 蛋糕重量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
> | :------: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
> | 售价 | 0 | 2 | 3 | 6 | 7 | 11 | 15 |
>
> **问题：** 现给定一个重量为 $n$ 的蛋糕，问小力应该如何切分蛋糕，达到最高的蛋糕总售价。
设重量为 $n$ 蛋糕的售价为 $p(n)$ ，切分的最高总售价为 $f(n)$ 。
- **子问题：** $f(n)$ 的子问题包括 $f(0), f(1), f(2), \cdots, f(n - 1)$ ，分别代表重量为 $0, 1, 2, \cdots, n - 1$ 蛋糕的最高售价。 已知无蛋糕时 $f(0) = 0$ ，蛋糕重量为 1 时不可切分 $f(1) = p(1)$ ；
- **最优子结构：**
- **定义：** 如果一个问题最优解可以由其子问题最优解组合构成，那么称此问题具有最优子结构。
- **对于本题：** 重量为 $n$ 的蛋糕的总售价可切分为 $n$ 种组合，即重量为 $0, 1, 2, ..., n - 1$ 蛋糕**最高售价**加上 $n, n - 1, n - 2, \cdots, 1$ 剩余重量蛋糕的**售价**；从这些组合中，售价最高的组合便是原问题的解 $f(n)$ ，这便是本题的最优子结构。
- **状态转移方程：** 找出最优子结构后，易构建出如下的状态转移方程。
$$
f(n) = \max_{0 \leq i < n} (f(i) + p(n - i))
$$
根据以上推导，本题也能使用「暴力递归」$\rightarrow$「记忆化递归」$\rightarrow$「动态规划」三种方法解决。
### 方法一：暴力递归
暴力递归解法的代码如下，其时间复杂度为指数级 $O(2^n)$ 。
```Python []
# 输入蛋糕价格列表 price_list ，求重量为 n 蛋糕的最高售价
def max_cake_price(n, price_list):
if n <= 1: return price_list[n] # 蛋糕重量 <= 1 时直接返回
f_n = 0
for i in range(n): # 从 n 种组合种选择最高售价的组合作为 f(n)
f_n = max(f_n, max_cake_price(i, price_list) + price_list[n - i])
return f_n # 返回 f(n)
max_cake_price(4, [0, 2, 3, 6, 7, 11, 15])
```
```Java []
// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, int[] priceList) {
if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
int f_n = 0;
for (int i = 0; i < n; i++) // 从 n 种组合种选择最高售价的组合作为 f(n)
f_n = Math.max(f_n, maxCakePrice(i, priceList) + priceList[n - i]);
return f_n; // 返回 f(n)
}
```
```C++ []
// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, vector<int> priceList) {
if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
int f_n = 0;
for (int i = 0; i < n; i++) // 从 n 种组合种选择最高售价的组合作为 f(n)
f_n = max(f_n, maxCakePrice(i, priceList) + priceList[n - i]);
return f_n; // 返回 f(n)
}
```
如下图所示，为暴力递归求解 $f(4)$ 形成的多叉树。
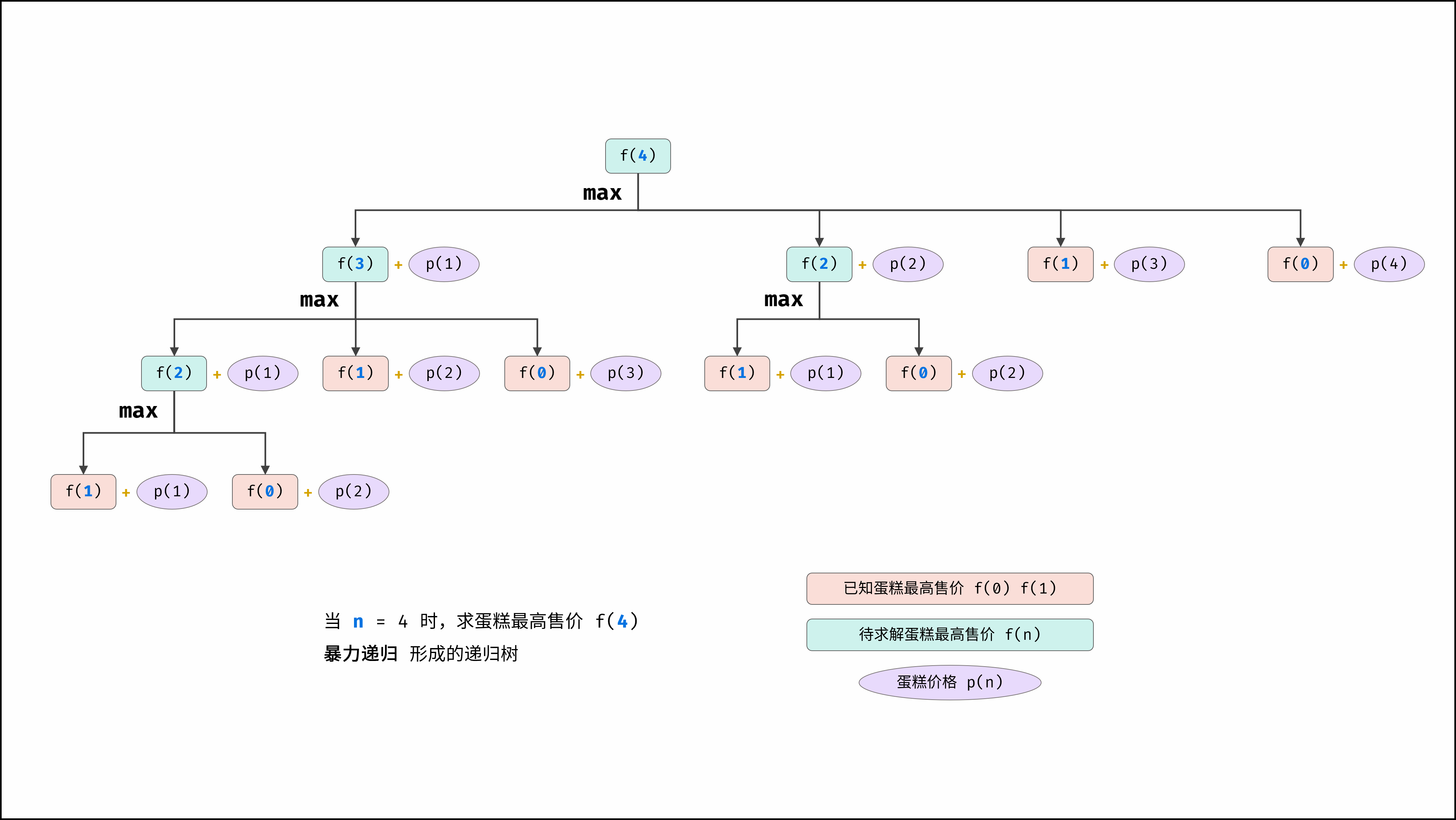
![Picture4.png](https://pic.leetcode-cn.com/1635075778-AljQEJ-Picture4.png)
### 方法二：记忆化递归
观察发现，递归树中存在大量**重叠子问题**，可通过记忆化处理避免重复计算。记忆化递归的算法的时间复杂度为 $O(n^2)$ ，包括：
- $f(2)$ 至 $f(n)$ 共 $n - 1$ 个待计算子问题，使用 $O(n)$ 时间；
- 计算某 $f(i)$ 需遍历 $i - 1$ 种子问题组合，使用 $O(n)$ 时间；
```Python []
# 输入蛋糕价格列表 price_list ，求重量为 n 蛋糕的最高售价
def max_cake_price(n, price_list, dp):
if n <= 1: return price_list[n] # 蛋糕重量 <= 1 时直接返回
f_n = 0
for i in range(n): # 从 n 种组合种选择最高售价的组合作为 f(n)
# 若 f(i) 以前已经计算过，则调取记录的解；否则，递归计算 f(i)
f_i = dp[i] if dp[i] != 0 else max_cake_price(i, price_list, dp)
f_n = max(f_n, f_i + price_list[n - i])
dp[n] = f_n # 记录 f(n) 至 dp 数组
return f_n # 返回 f(n)
def max_cake_price_memorized(n, price_list):
dp = [0] * (n + 1)
return max_cake_price(n, price_list, dp)
```
```Java []
// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, int[] priceList, int[] dp) {
if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
int f_n = 0;
for (int i = 0; i < n; i++) { // 从 n 种组合种选择最高售价的组合作为 f(n)
int f_i = dp[i] != 0 ? dp[i] : maxCakePrice(i, priceList, dp);
f_n = Math.max(f_n, f_i + priceList[n - i]);
}
dp[n] = f_n; // 记录 f(n) 至 dp 数组
return f_n; // 返回 f(n)
}
int maxCakePriceMemorized(int n, int[] priceList) {
int[] dp = new int[n + 1];
return maxCakePrice(n, priceList, dp);
}
```
```C++ []
// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, vector<int> &priceList, vector<int> dp) {
if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
int f_n = 0;
for (int i = 0; i < n; i++) { // 从 n 种组合种选择最高售价的组合作为 f(n)
int f_i = dp[i] != 0 ? dp[i] : maxCakePrice(i, priceList, dp);
f_n = max(f_n, f_i + priceList[n - i]);
}
dp[n] = f_n; // 记录 f(n) 至 dp 数组
return f_n; // 返回 f(n)
}
int maxCakePriceMemorized(int n, vector<int> priceList) {
vector<int> dp(n + 1, 0);
return maxCakePrice(n, priceList, dp);
}
```
如下图所示，为记忆化递归求解 $f(4)$ 形成的多叉树。观察得知，重叠子问题皆被**剪枝**。
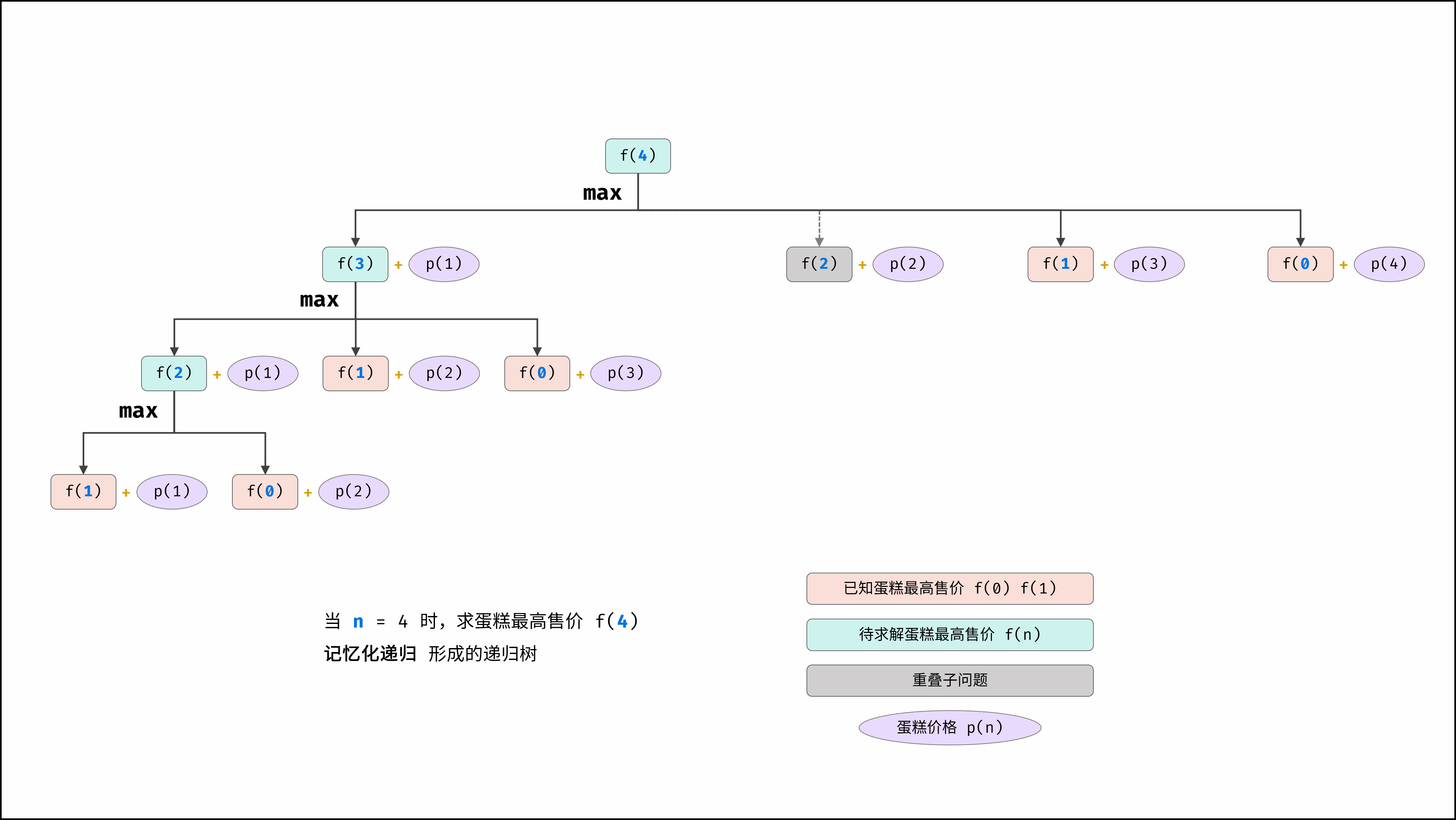
![Picture5.png](https://pic.leetcode-cn.com/1635075778-tsDBrs-Picture5.png)
### 方法三：动态规划
相较于记忆化递归的从顶至底方法，易得动态规划的从底至顶方法，代码如下所示。
```Python []
# 输入蛋糕价格列表 price_list ，求重量为 n 蛋糕的最高售价
def max_cake_price(n, price_list):
if n <= 1: return price_list[n] # 蛋糕重量 <= 1 时直接返回
dp = [0] * (n + 1) # 初始化 dp 列表
for j in range(1, n + 1): # 按顺序计算 f(1), f(2), ..., f(n)
for i in range(j): # 从 j 种组合种选择最高售价的组合作为 f(j)
dp[j] = max(dp[j], dp[i] + price_list[j - i])
return dp[n]
```
```Java []
// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, int[] priceList) {
if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
int[] dp = new int[n + 1]; // 初始化 dp 列表
for (int j = 1; j <= n; j++) { // 按顺序计算 f(1), f(2), ..., f(n)
for (int i = 0; i < j; i++) // 从 j 种组合种选择最高售价的组合作为 f(j)
dp[j] = Math.max(dp[j], dp[i] + priceList[j - i]);
}
return dp[n];
}
```
```C++ []
// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, vector<int> priceList) {
if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
vector<int> dp(n + 1, 0); // 初始化 dp 列表
for (int j = 1; j <= n; j++) { // 按顺序计算 f(1), f(2), ..., f(n)
for (int i = 0; i < j; i++) // 从 j 种组合种选择最高售价的组合作为 f(j)
dp[j] = max(dp[j], dp[i] + priceList[j - i]);
}
return dp[n];
}
```
如下图所示，为动态规划求解 $f(4)$ 的迭代流程，其是转移方程 $f(n) = \max_{0 \leq i < n} (f(i) + p(n - i))$ 的体现。
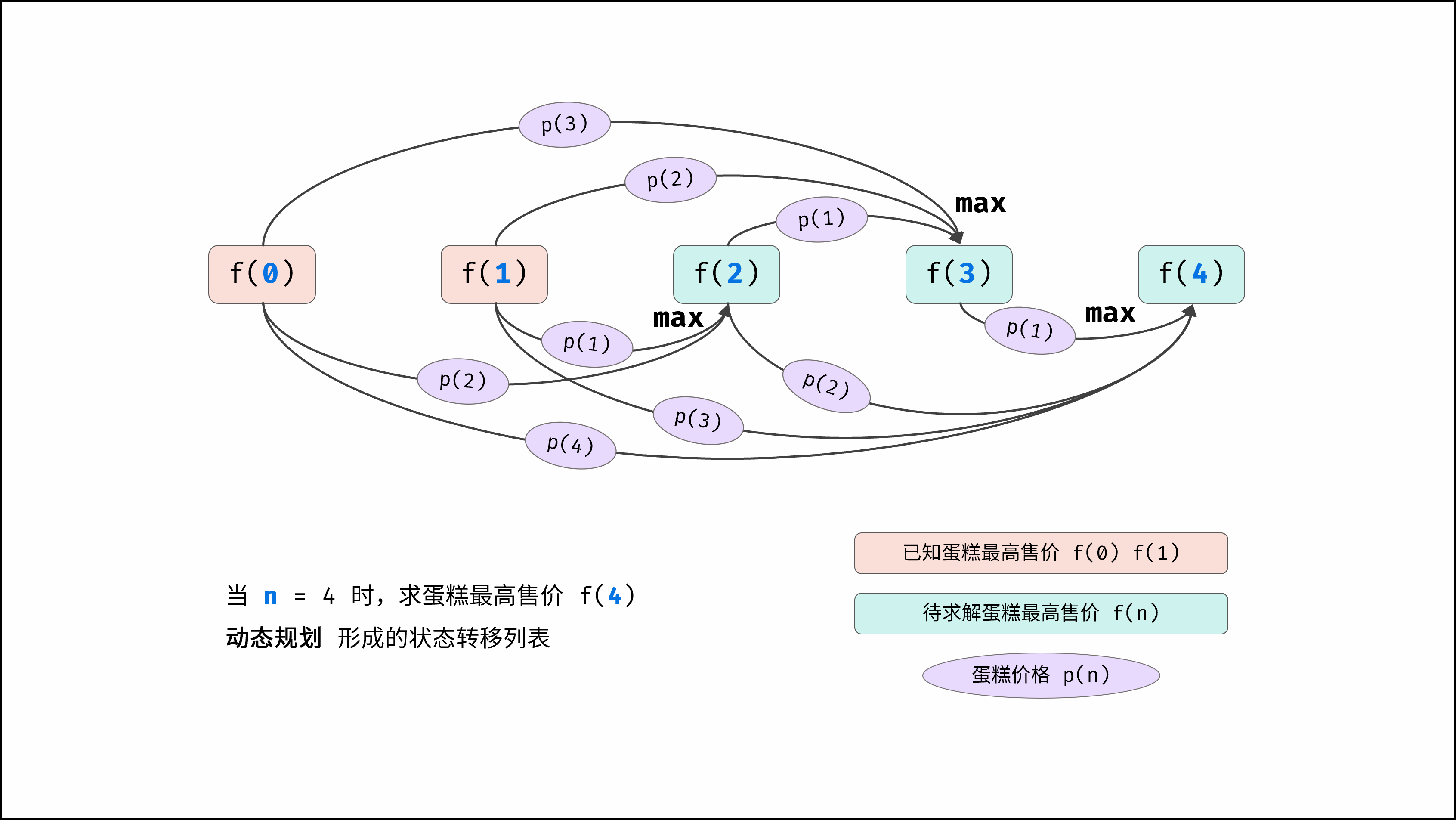
![Picture6.png](https://pic.leetcode-cn.com/1635075778-PBtyyB-Picture6.png)
### 示例小结
本题同时包含「重叠子问题」和「最优子结构」，为动态规划的典型问题。动态规划通过填表避免了重复计算问题，并通过状态转移方程、初始状态实现对问题的迭代求解。
普遍来看，**求最值** 的问题一般都具有「重叠子问题」和「最优子结构」特点，因此此类问题往往适合用动态规划解决。
---
## 动态规划解题框架
若确定给定问题具有重叠子问题和最优子结构，那么就可以使用动态规划求解。总体上看，求解可分为四步：
1. **状态定义：** 构建问题最优解模型，包括问题**最优解的定义**、有哪些**计算解的自变量**；
2. **初始状态：** 确定**基础子问题的解**（即已知解），原问题和子问题的解都是以基础子问题的解为起始点，在迭代计算中得到的；
3. **转移方程：** 确定原问题的解与子问题的解之间的关系是什么，以及使用何种**选择规则**从子问题最优解组合中选出原问题最优解；
4. **返回值：** 确定应返回的问题的解是什么，即动态规划**在何处停止迭代**；
完成以上步骤后，便容易写出对应的解题代码。
### 示例：斐波那契数列
- 状态定义：一维 $dp$ 列表，设第 $i$ 个斐波那契数为 $dp[i]$ ；
- 初始状态：已知第 $0$ , $1$ 个斐波那契数分别为 $dp[0] = 0$ , $dp[1] = 1$ ；
- 转移方程：后一个数字等于前两个数字之和，即
$$
dp[i] = dp[i - 1] + dp[i - 2]
$$
- 返回值：需求取的第 $n$ 个斐波那契数 $dp[n]$ ；
### 示例：蛋糕最高售价
- 状态定义：一维 $dp$ 列表，设重量为 $i$ 蛋糕的售价为 $p(i)$ ，重量为 $i$ 蛋糕切分后的最高售价为 $dp[i]$ ；
- 初始状态：已知重量为 0 蛋糕的最高售价为 0 ，重量为 1 的蛋糕最高售价为 $p(1)$ ；
- 转移方程：$dp[n]$ 为 $n$ 种切分组合中的最高售价组合，即
$$
dp[n] = \max_{0 \leq i < n} (dp[i] + p(n - i))
$$
- 返回值：需求取的重量为 $n$ 的蛋糕最高售价 $dp[n]$ ；
---
## 例题练习
动态规划的问题种类多，难度跨度较大，需要充足练习、熟能生巧。以下给出若干典型例题，供读者巩固理解本文内容。
| 题目 | 难度 | 描述 |
| ----------------------------------------------------------------------------------------------- | ---- | ----------------------------------------------------------------------- |
| [跳跃训练](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/57hyl5/) | 简单 | 与本文的斐波那契数列例题等价 |
| [连续天数的最高销售额](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/59gq9c/) | 简单 | 求最大值问题，关键点在于状态定义 |
| [珠宝的最高价值](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5vokvr/) | 简单 | 求最大值问题，特点是其 $dp$ 列表是二维的 |
| [统计结果概率](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/ozzl1r/) | 中等 | 容易想到暴力枚举方法，难点为列出状态转移方程，且正向递推方法比较 tricky |
| [模糊搜索验证](https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/9a1ypc/) | 困难 | 状态定义容易得出，但状态转移方程复杂、选择规则分支多 |

136
leetbook_ioa/docs/# 7.1 排序算法简介.md Executable file
View File

@@ -0,0 +1,136 @@
# 排序算法简介
排序算法用作实现列表的排序，列表元素可以是整数，也可以是浮点数、字符串等其他数据类型。生活中有许多需要排序算法的场景，例如：
- **整数排序：** 对于一个整数数组，我们希望将所有数字从小到大排序；
- **字符串排序：** 对于一个姓名列表，我们希望将所有单词按照字符先后排序；
- **自定义排序：** 对于任意一个 **已定义比较规则** 的集合，我们希望将其按规则排序；
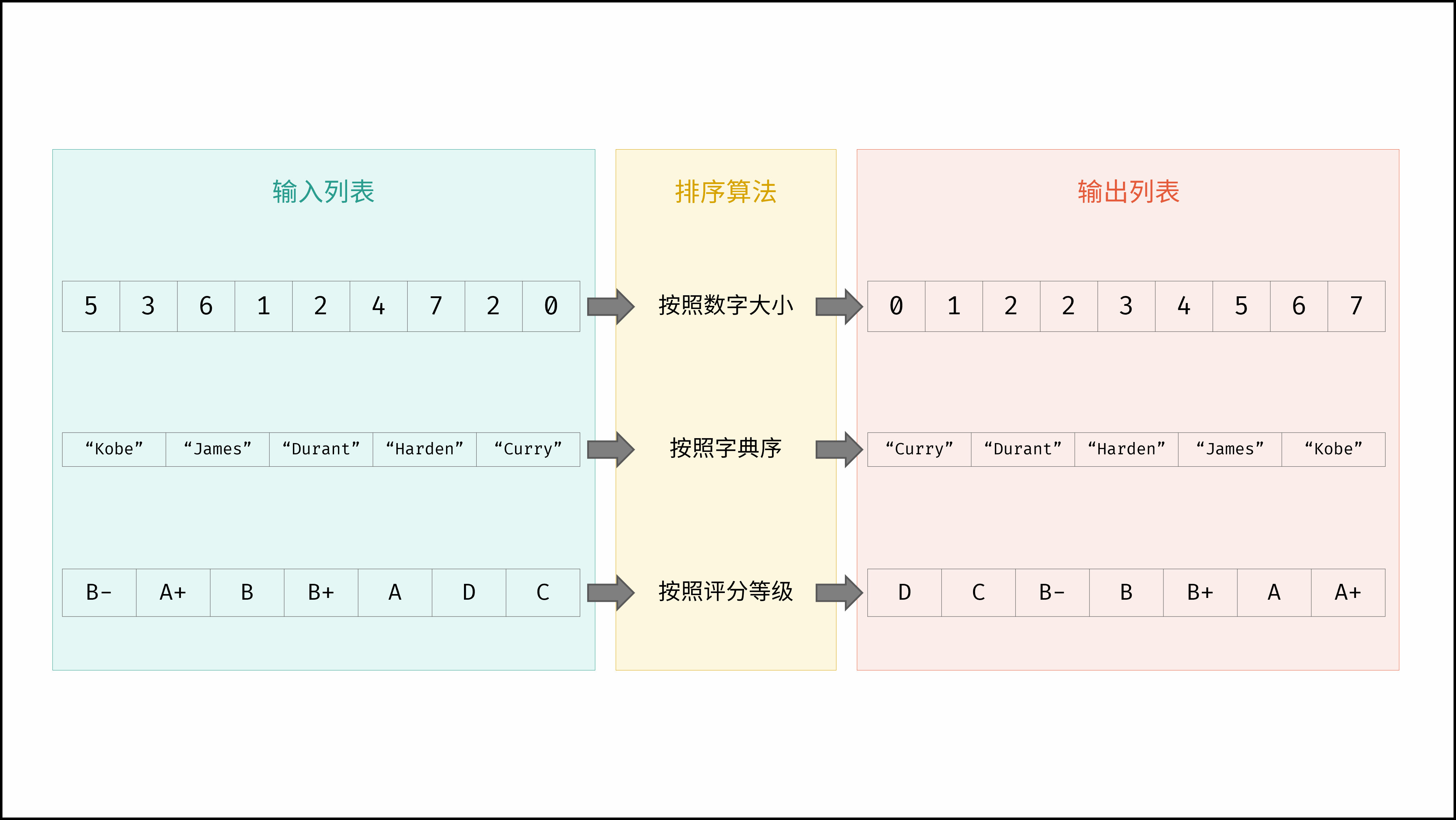
![Picture1.png](https://pic.leetcode-cn.com/1629483616-HHvvqY-Picture1.png)
同时，某些算法需要在排序算法的基础上使用（即在排序数组上运行），例如：
- **二分查找：** 根据数组已排序的特性，才能每轮确定排除两部分中的哪一部分；
- **双指针：** 例如合并两个排序链表，根据已排序特性，才能通过双指针移动在线性时间内将其合并为一个排序链表。
> 接下来，本文将从「常见排序算法」、「分类方法」、「时间与空间复杂度」三方面入手，简要介绍排序算法。「各排序算法详细介绍」请见后续专栏文章。
---
## 常见算法
常见排序算法包括「冒泡排序」、「插入排序」、「选择排序」、「快速排序」、「归并排序」、「堆排序」、「基数排序」、「桶排ss序」。如下图所示，为各排序算法的核心特性与时空复杂度总结。
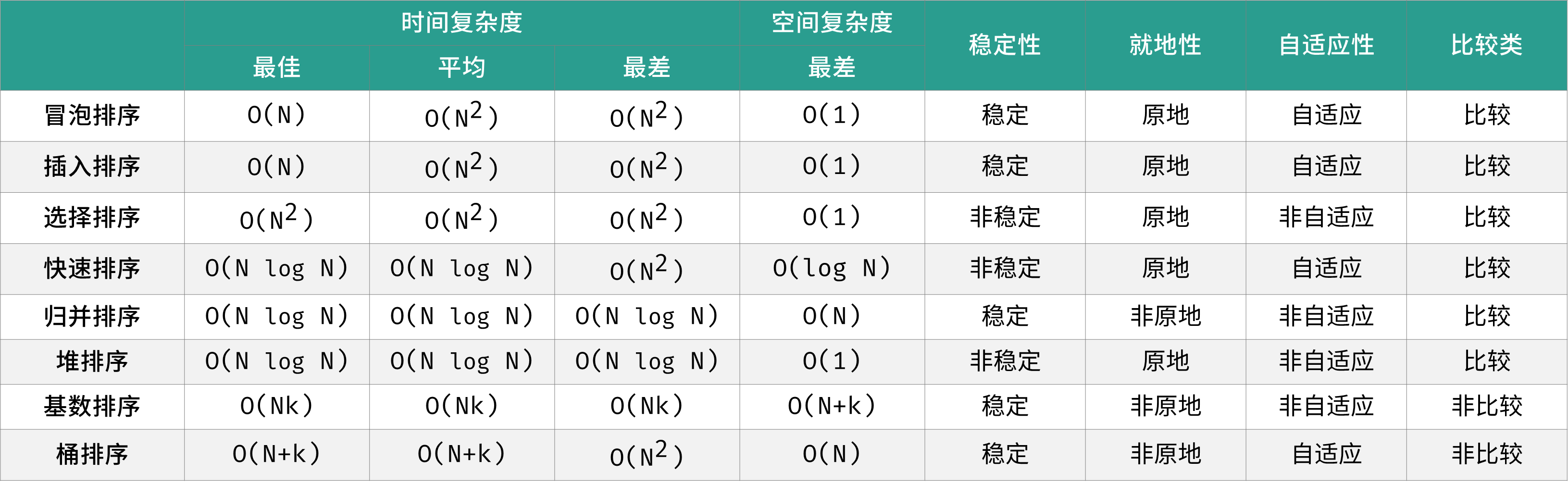
![Picture2.png](https://pic.leetcode-cn.com/1629483637-tmENTT-Picture2.png)
如下图所示，为在 「随机乱序」、「接近有序」、「完全倒序」、「少数独特」四类输入数据下，各常见排序算法的排序过程。
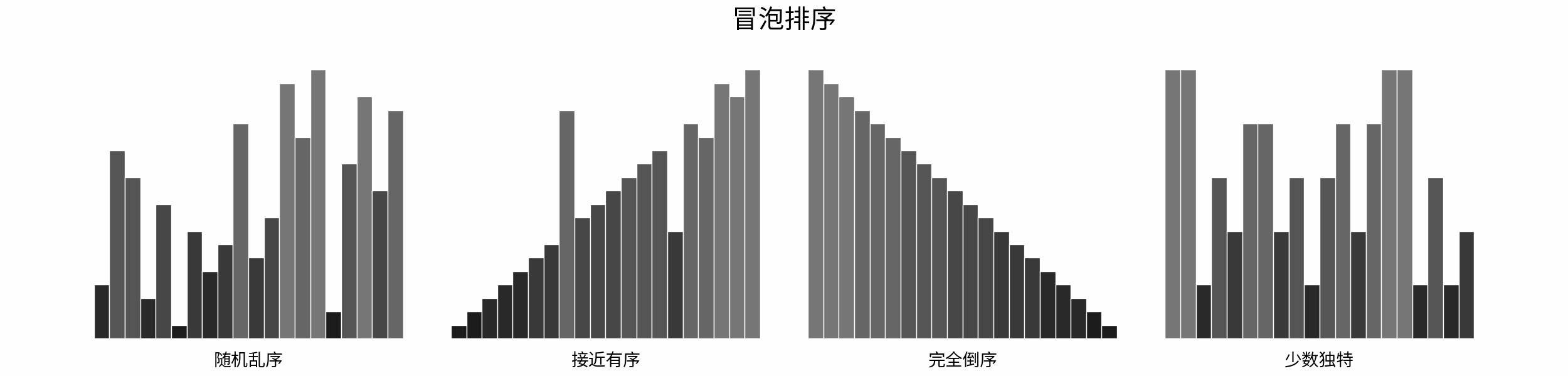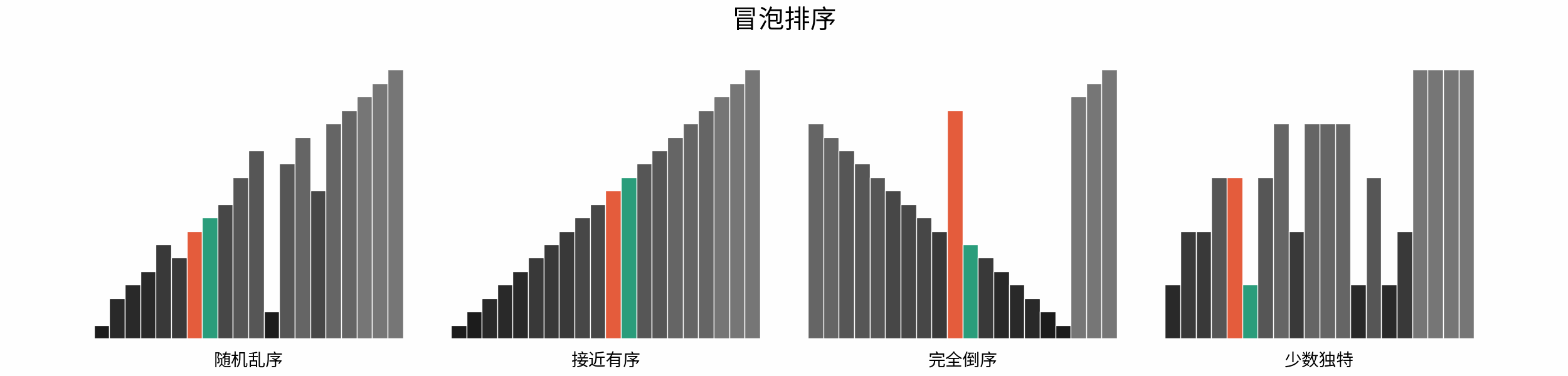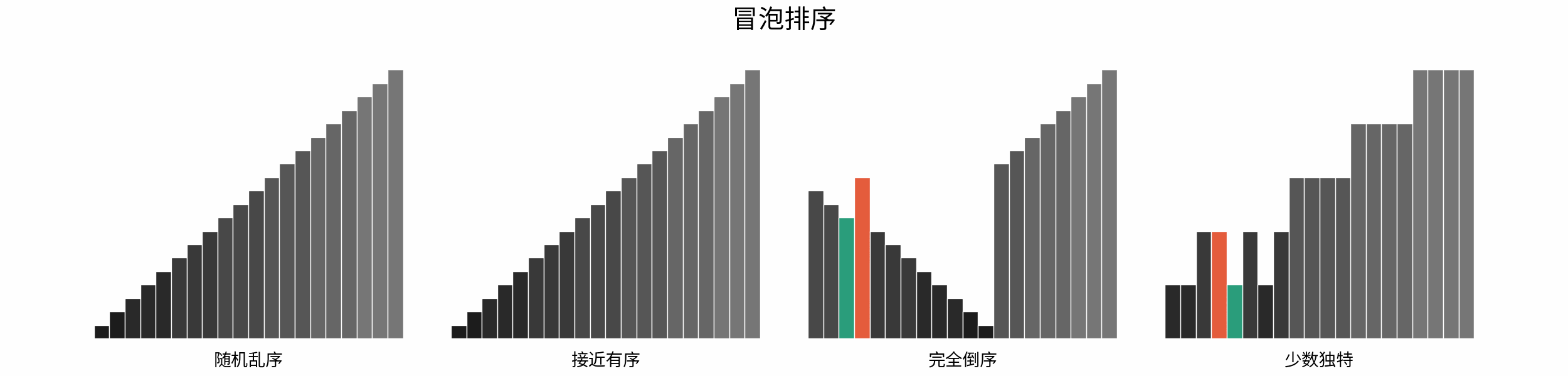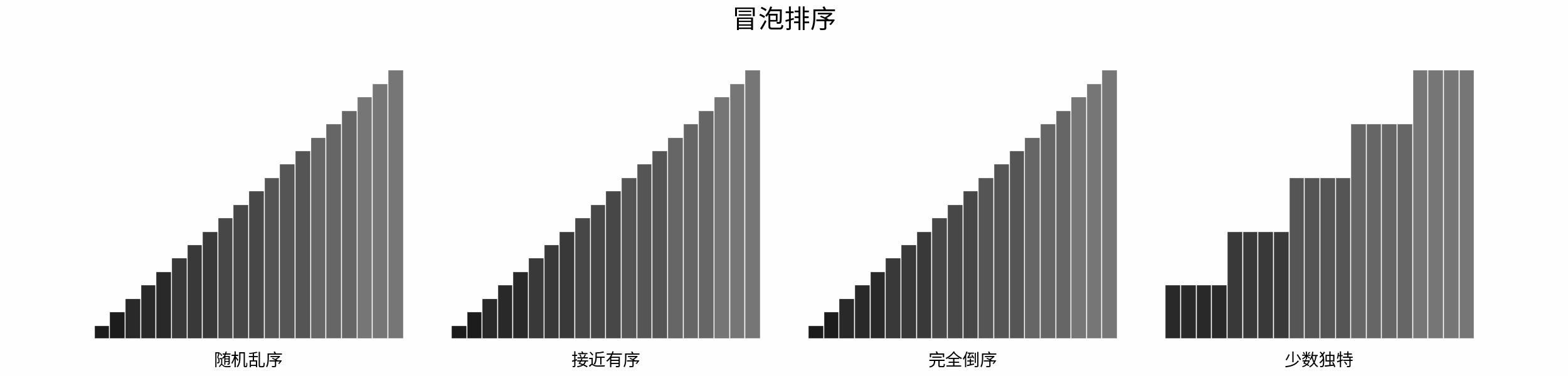
![krahets-bubble-sort.gif](https://pic.leetcode-cn.com/1629482805-alxVCi-krahets-bubble-sort.gif)
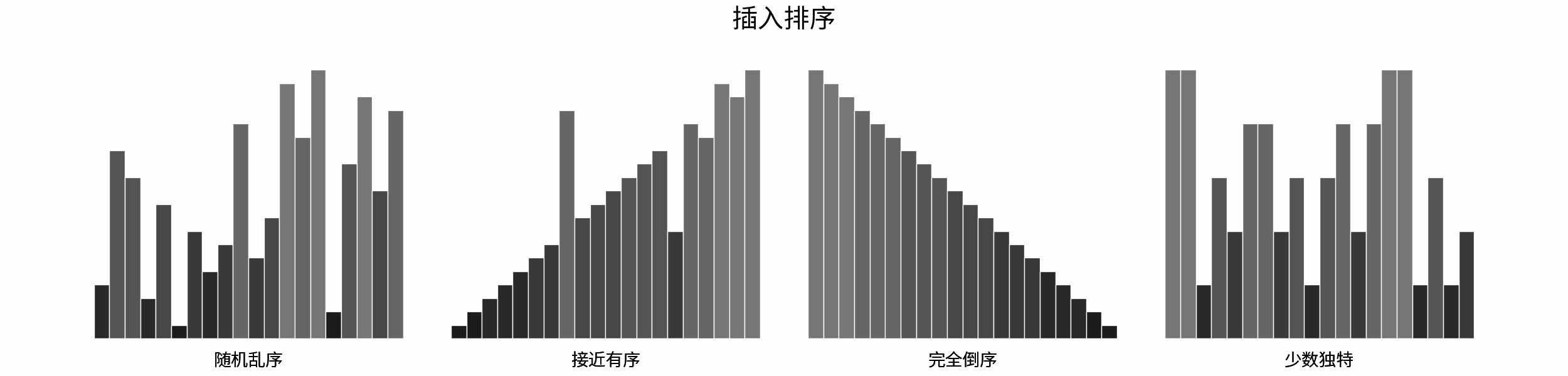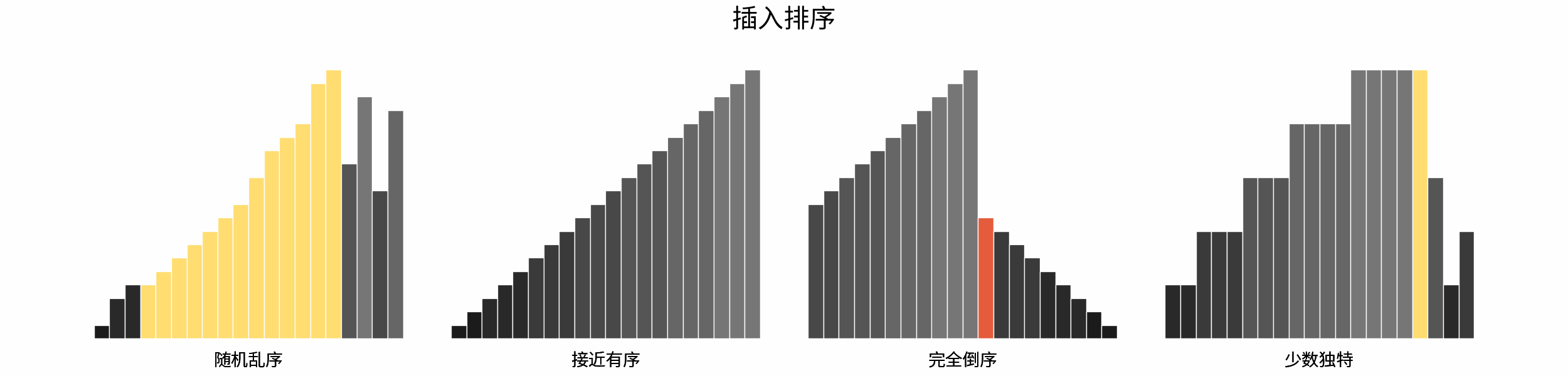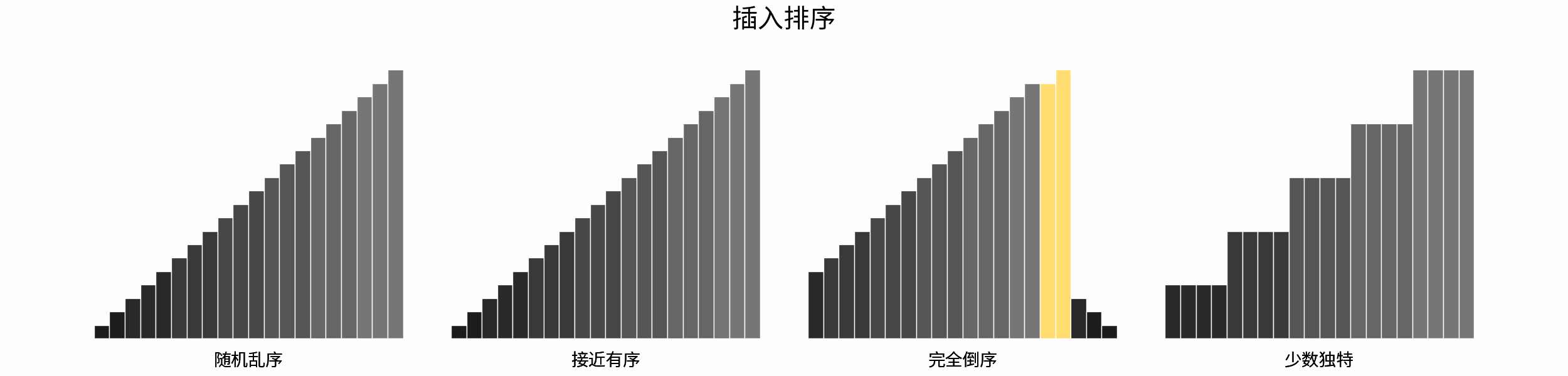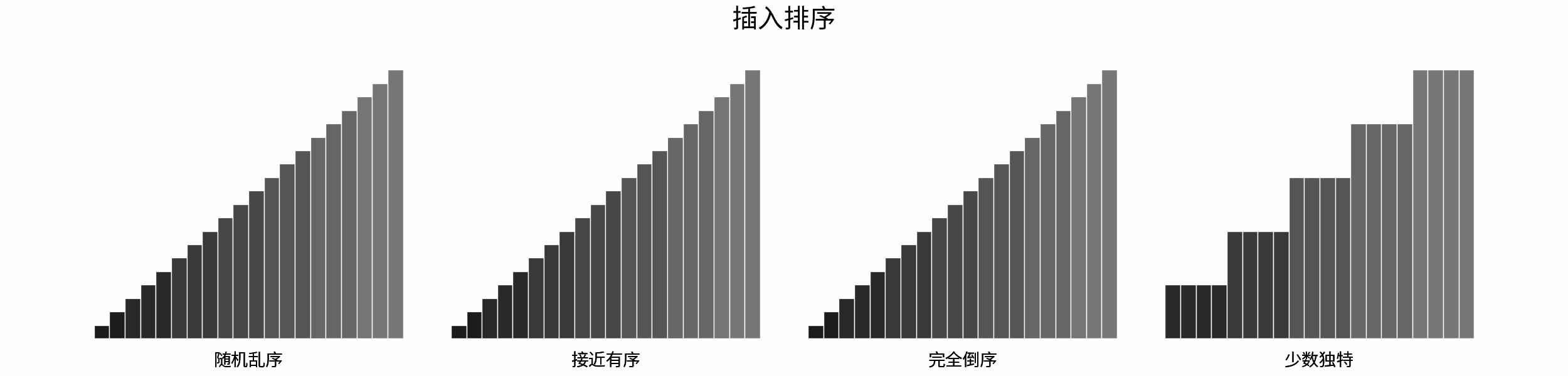
![krahets-insertion-sort.gif](https://pic.leetcode-cn.com/1629482805-MMIXPp-krahets-insertion-sort.gif)
![krahets-selection-sort.gif](https://pic.leetcode-cn.com/1629482805-vdWamx-krahets-selection-sort.gif)
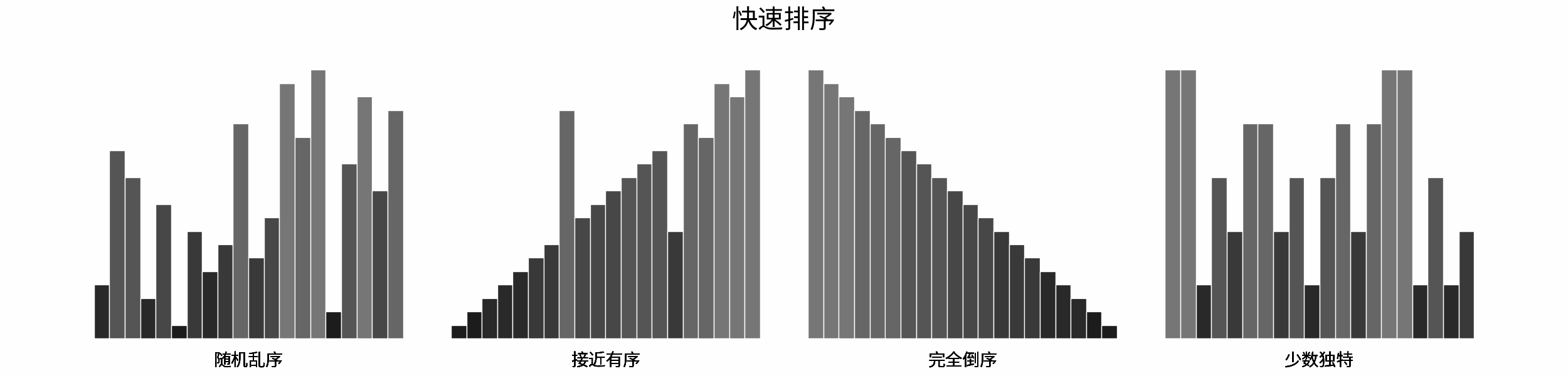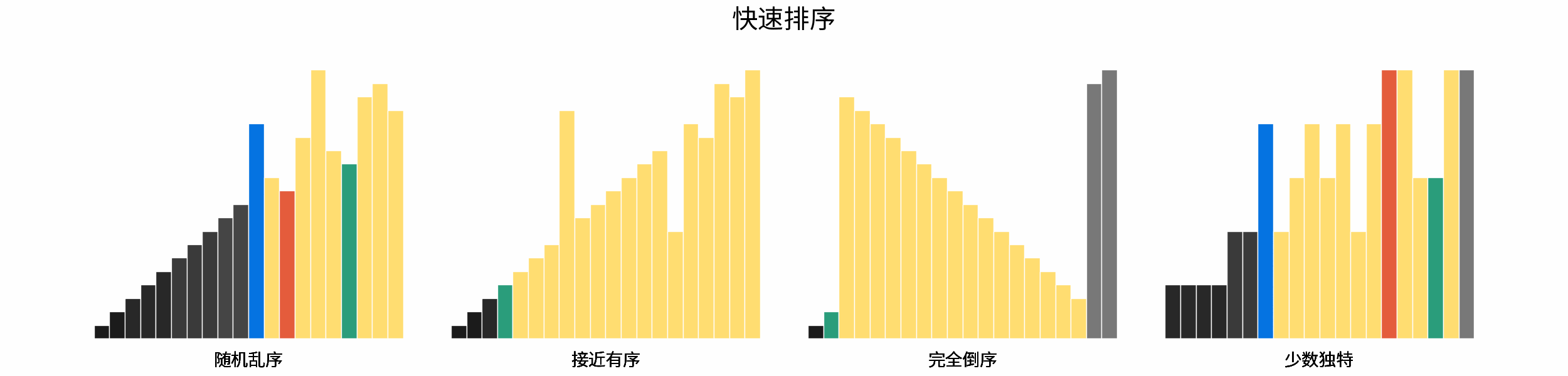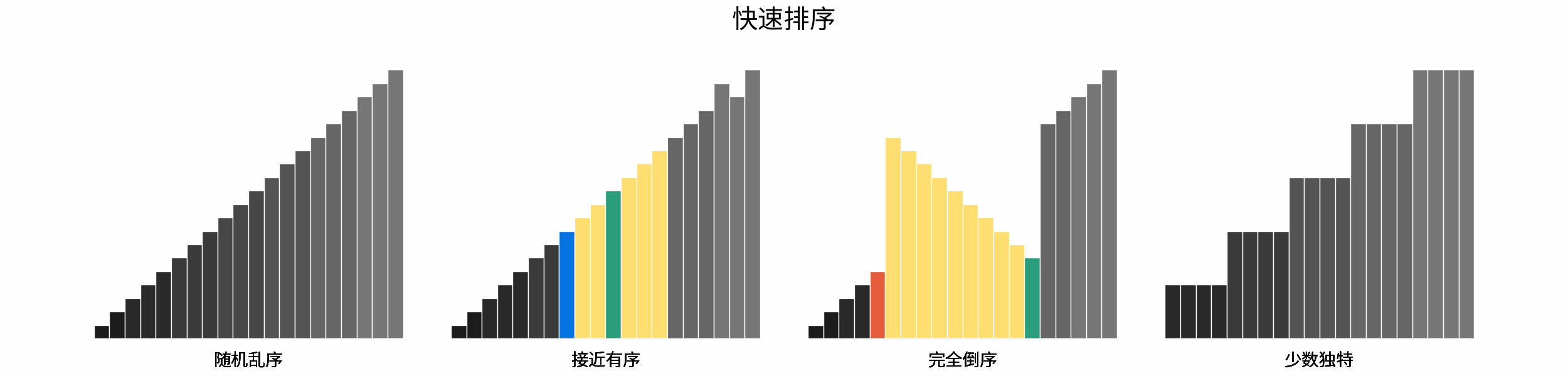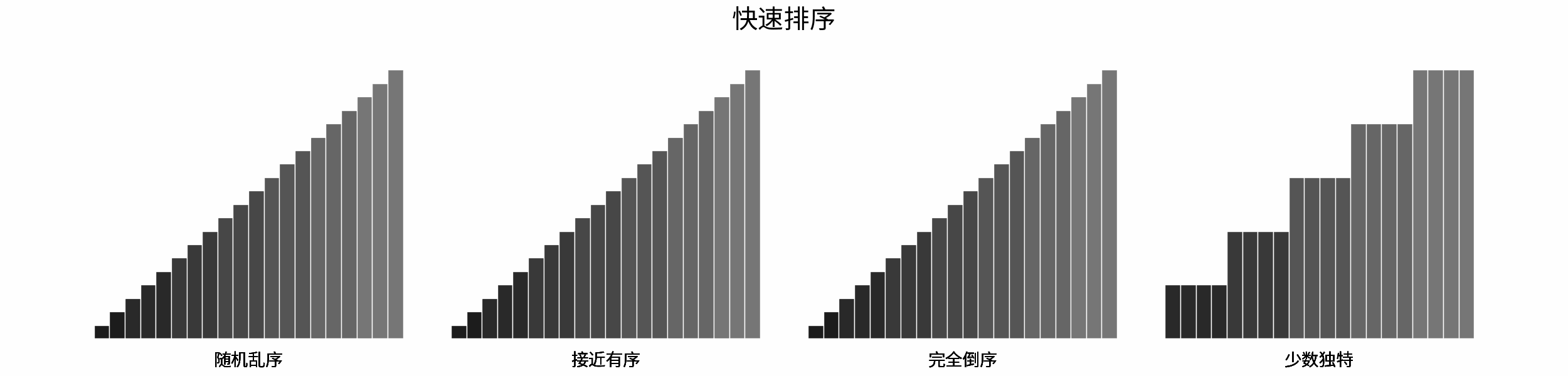
![krahets-quick-sort.gif](https://pic.leetcode-cn.com/1629482805-DYNZPE-krahets-quick-sort.gif)
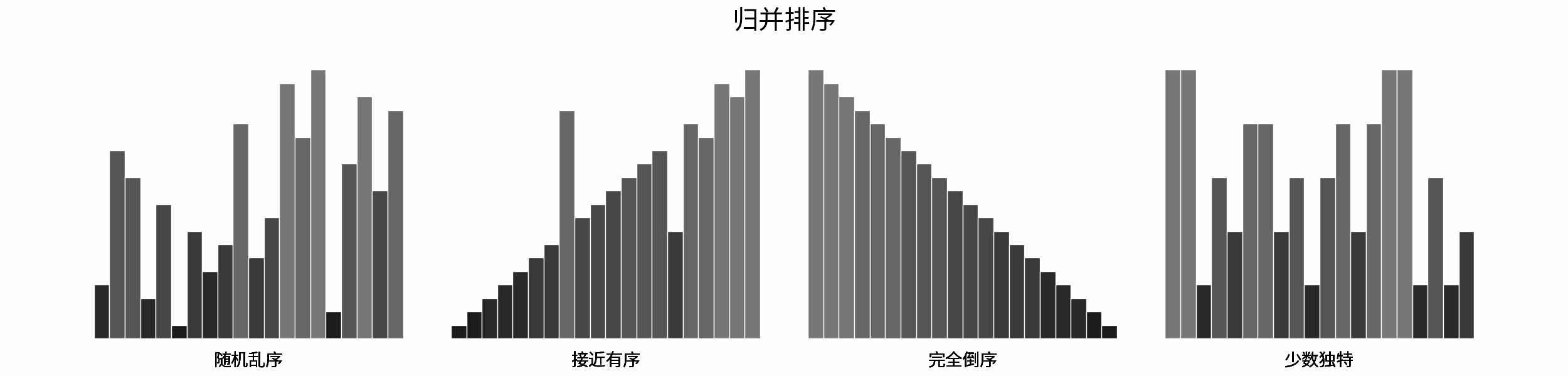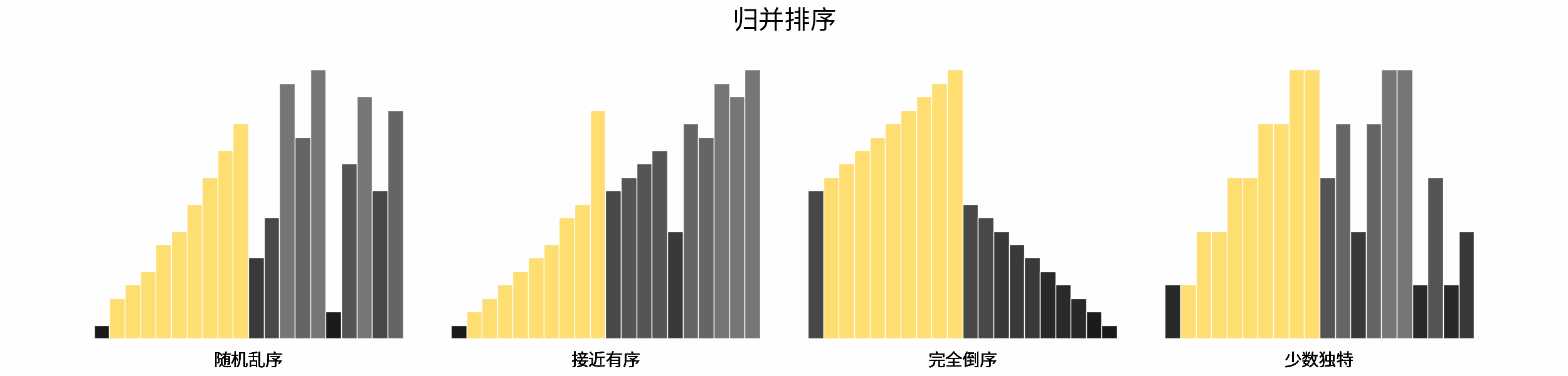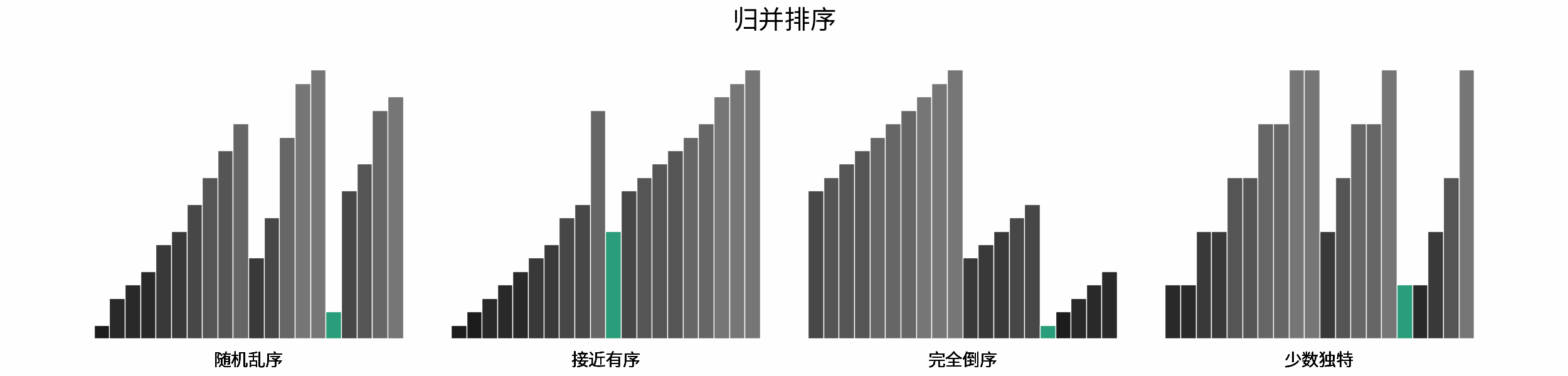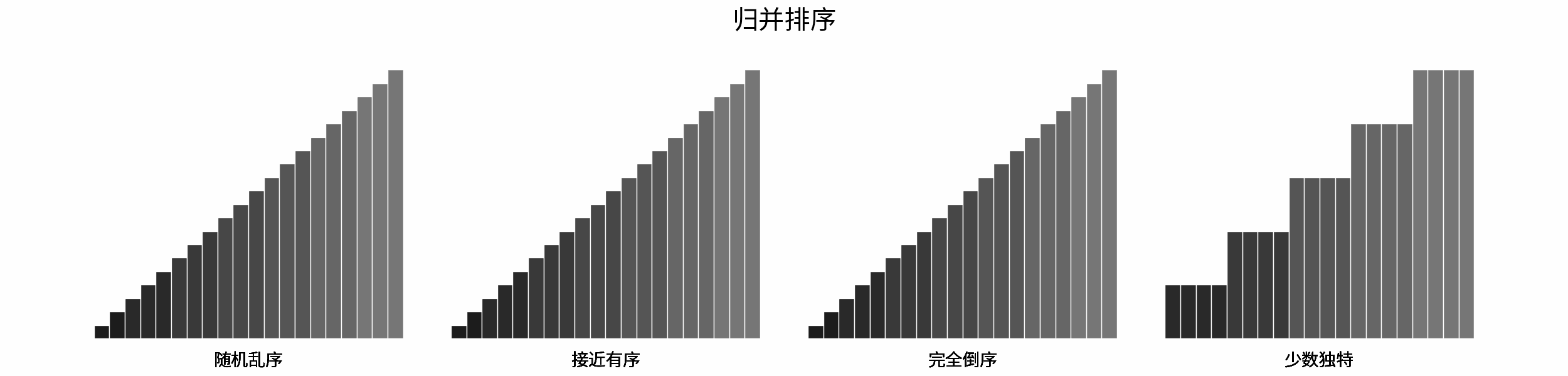
![krahets-merge-sort.gif](https://pic.leetcode-cn.com/1629482805-IjWwSz-krahets-merge-sort.gif)
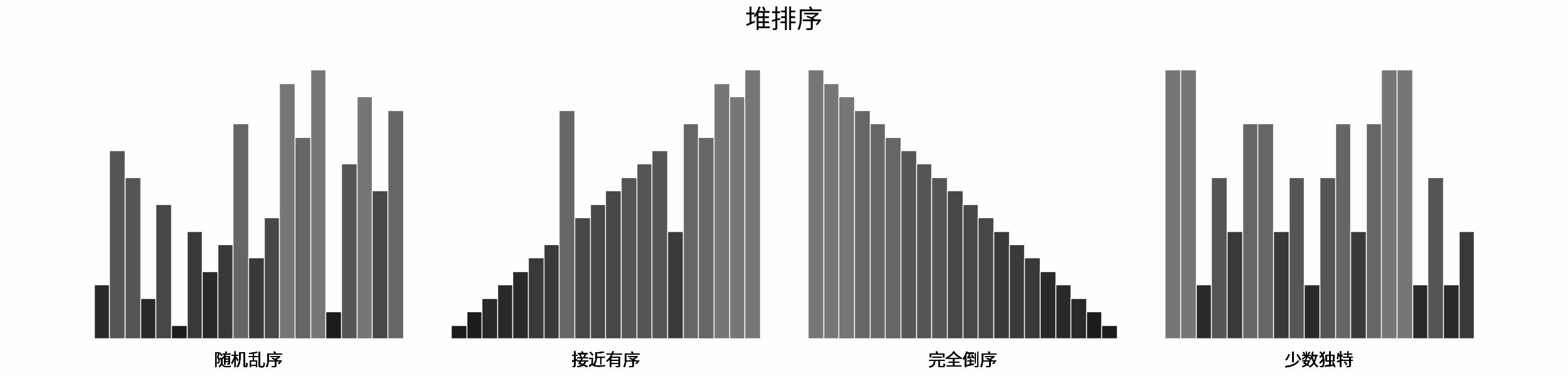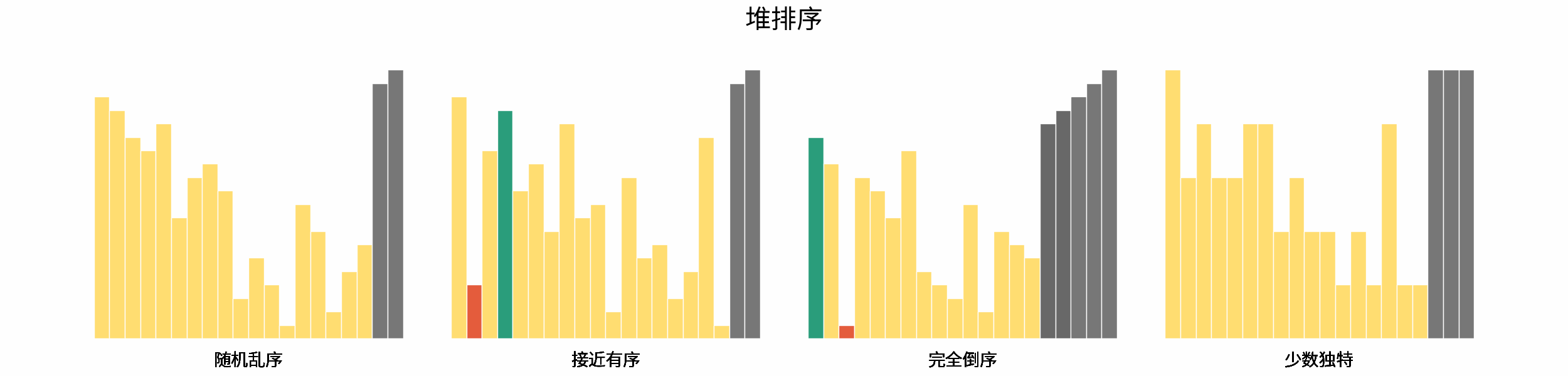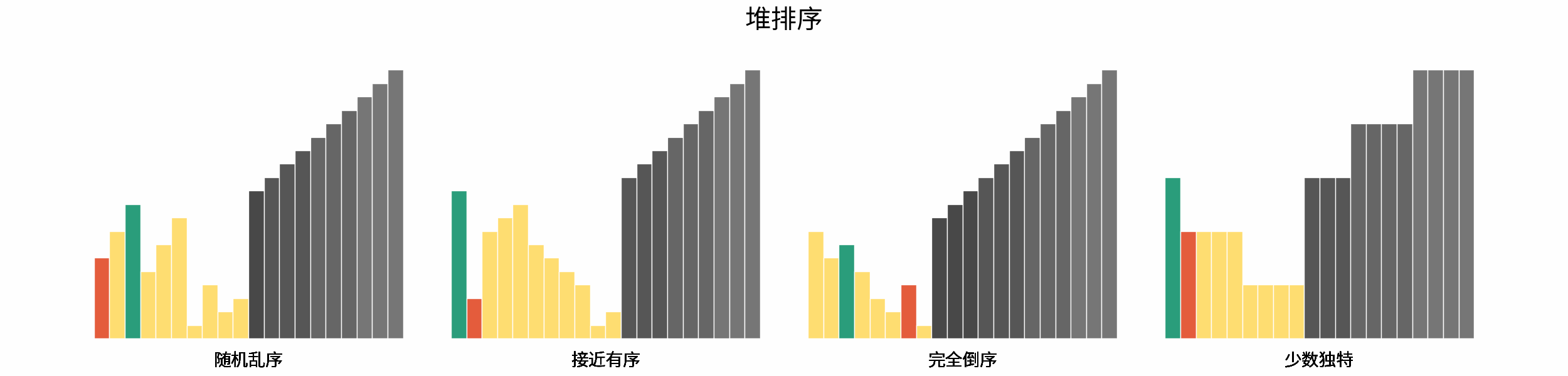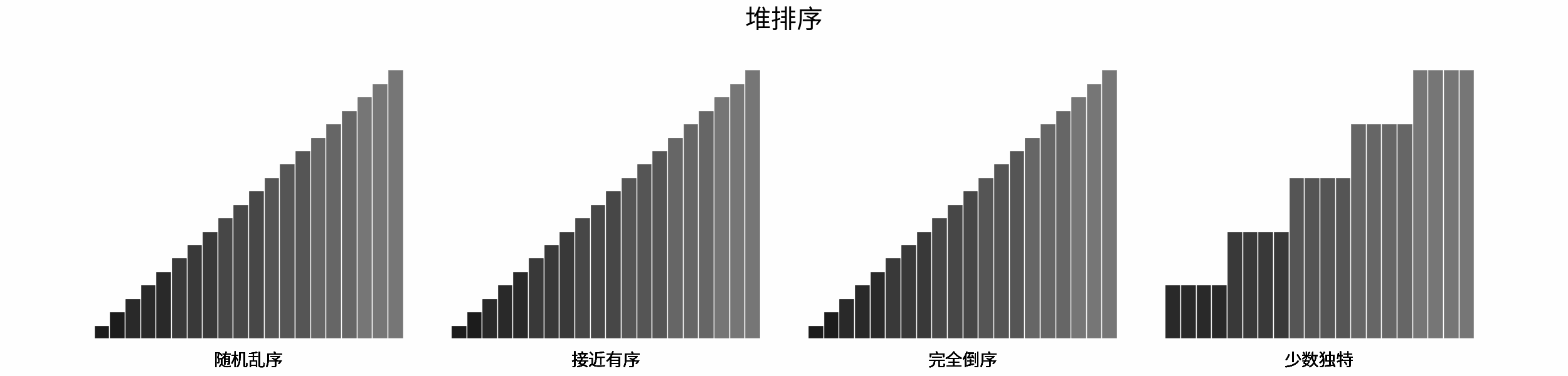
![krahets-heap-sort.gif](https://pic.leetcode-cn.com/1629482805-apljJY-krahets-heap-sort.gif)
---
## 分类方法
排序算法主要可根据 **稳定性** 、**就地性** 、**自适应性** 分类。理想的排序算法具有以下特性：
- 具有稳定性，即相等元素的相对位置不变化；
- 具有就地性，即不使用额外的辅助空间；
- 具有自适应性，即时间复杂度受元素分布影响；
特别地，任意排序算法都 **不同时具有以上所有特性** 。因此，排序算法的选型使用取决于具体的列表类型、元素数量、元素分布情况等应用场景特点。
### 稳定性：
根据 **相等元素** 在数组中的 **相对顺序** 是否被改变，排序算法可分为「稳定排序」和「非稳定排序」两类。
- 「稳定排序」在完成排序后，**不改变** 相等元素在数组中的相对顺序。例如：冒泡排序、插入排序、归并排序、基数排序、桶排序。
- 「非稳定排序」在完成排序后，相等素在数组中的相对位置 **可能被改变**。例如：选择排序、快速排序、堆排序。
> **何时需考虑排序算法的稳定性？**
>
> 数组排序中，由于元素皆为数字，因此稳定和非稳定排序皆可输出相同结果，此时无需考虑排序算法的稳定性。
>
> 非稳定排序会改变相等元素的相对次序，这在实际应用场景中可能是不能接受的。如以下代码所示，非稳定排序破坏了输入列表 `people` 按姓名排序的性质。
>
> ```Python
> # 人 = (姓名, 年龄) ，按姓名排序
> people = [
> ('A', 19),
> ('B', 18),
> ('C', 21),
> ('D', 19),
> ('E', 23)
> ]
>
> # 非稳定排序（按年龄）
> sort_by_age(people)
>
> # 人 = (姓名, 年龄) ，按年龄排序
> people = [
> ('B', 18),
> ('D', 19), # ('D', 19) 和 ('A', 19) 的相对位置改变，输入时按姓名排序的性质丢失
> ('A', 19),
> ('C', 21),
> ('E', 23)
> ]
> ```
### 就地性：
根据排序过程中 **是否使用额外内存（辅助数组）**，排序算法可分为「原地排序」和「异地排序」两类。一般地，由于不使用外部内存，原地排序相比非原地排序的执行效率更高。
- 「原地排序」不使用额外辅助数组，例如：冒泡排序、插入排序、选择排序、快速排序、堆排序。
- 「非原地排序」使用额外辅助数组，例如：归并排序、基数排序、桶排序。
### 自适应性：
根据算法 **时间复杂度** 是否 **受待排序数组的元素分布影响** ，排序算法可分为「自适应排序」和「非自适应排序」两类。
- 「自适应排序」的时间复杂度受元素分布影响；例如：冒泡排序、插入排序、快速排序、桶排序。
- 「非自适应排序」的时间复杂度恒定；例如：选择排序、归并排序、堆排序、基数排序。
### 是否基于比较：
比较类排序基于元素之间的 **比较算子**（小于、相等、大于）来决定元素的相对顺序；相对的，非比较排序则不基于比较算子实现。
- 「基于比较排序」基于元素之间的比较完成排序，例如：冒泡排序、插入排序、选择排序、快速排序、归并排序、堆排序。
- 「非基于比较排序」不基于元素之间的比较完成排序，例如：基数排序、桶排序。
> 基于比较的排序算法的平均时间复杂度最优为 $O(N \log N)$ ，而非比较排序算法可以达到线性级别的时间复杂度。
---
## 时空复杂度
总体上看，排序算法追求时间与空间复杂度最低。而即使某些排序算法的时间复杂度相等，但实际性能还受 **输入列表性质、元素数量、元素分布等** 等因素影响。
> 设输入列表元素数量为 $N$ ，常见排序算法的「时间复杂度」和「空间复杂度」如下图所示。
| 算法 | 最佳时间 | 平均时间 | 最差时间 | 最差空间 |
| :------: | :-----------------: | :----------------: | :-----------: | :---------: |
| 冒泡排序 | $\Omega(N)$ | $\Theta(N^2)$ | $O(N^2)$ | $O(1)$ |
| 插入排序 | $\Omega(N)$ | $\Theta(N^2)$ | $O(N^2)$ | $O(1)$ |
| 选择排序 | $\Omega(N^2)$ | $\Theta(N^2)$ | $O(N^2)$ | $O(1)$ |
| 快速排序 | $\Omega(N \log N )$ | $\Theta(N \log N)$ | $O(N^2)$ | $O(\log N)$ |
| 归并排序 | $\Omega(N \log N)$ | $\Theta(N \log N)$ | $O(N \log N)$ | $O(N)$ |
| 堆排序 | $\Omega(N \log N)$ | $\Theta(N \log N)$ | $O(N \log N)$ | $O(1)$ |
| 基数排序 | $\Omega(Nk)$ | $\Theta(Nk)$ | $O(Nk)$ | $O(N + k)$ |
| 桶排序 | $\Omega(N + k)$ | $\Theta(N + k)$ | $O(N^2)$ | $O(N)$ |
对于上表，需要特别注意：
- 「基数排序」适用于正整数、字符串、特定格式的浮点数排序，$k$ 为最大数字的位数；「桶排序」中 $k$ 为桶的数量。
- 普通「冒泡排序」的最佳时间复杂度为 $O(N^2)$ ，通过增加标志位实现 **提前返回** ，可以将最佳时间复杂度降低至 $O(N)$ 。
- 在输入列表完全倒序下，普通「快速排序」的空间复杂度劣化至 $O(N)$ ，通过代码优化 **尾递归优化** 保持算法递归较短子数组，可以将最差递归深度降低至 $\log N$ 。
- 普通「快速排序」总以最左或最右元素为基准数，因此在输入列表有序或倒序下，时间复杂度劣化至 $O(N^2)$ ；通过 **随机选择基准数** ，可极大减少此类最差情况发生，尽可能地保持 $O(N \log N)$ 的时间复杂度。
- 若输入列表是数组，则归并排序的空间复杂度为 $O(N)$ ；而若排序 **链表** ，则「归并排序」不需要借助额外辅助空间，空间复杂度可以降低至 $O(1)$ 。

125
leetbook_ioa/docs/# 7.2 冒泡排序.md Executable file
View File

@@ -0,0 +1,125 @@
# 冒泡排序
冒泡排序是最基础的排序算法，由于其直观性，经常作为首个介绍的排序算法。其原理为：
- **内循环：** 使用相邻双指针 `j` , `j + 1` 从左至右遍历，依次比较相邻元素大小，若左元素大于右元素则将它们交换；遍历完成时，**最大元素会被交换至数组最右边** 。
- **外循环：** 不断重复「内循环」，每轮将当前最大元素交换至 **剩余未排序数组最右边** ，直至所有元素都被交换至正确位置时结束。
如下图所示，首轮「内循环」后，数组最大元素已被交换至数组最右边；接下来，只需要完成数组剩余 $N - 1$ 个元素的排序即可（设数组元素数量为 $N$ ）。同理，对剩余 $N - 1$ 个元素执行「内循环」，可将第二大元素交换至剩余数组最右端，以此类推……
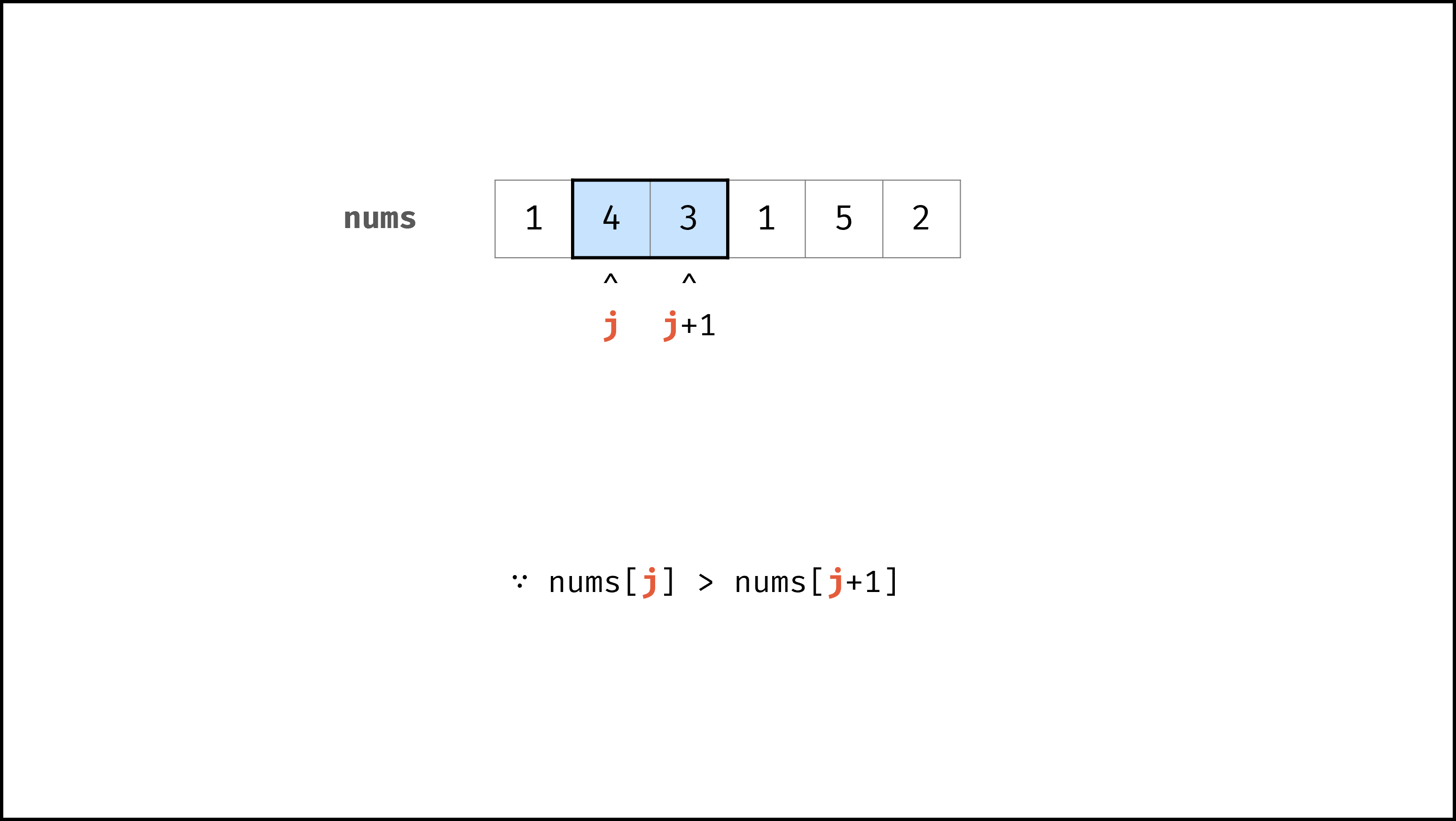<![Picture41.png](https://pic.leetcode-cn.com/1628617783-TRYTrM-Picture41.png),![Picture32.png](https://pic.leetcode-cn.com/1628617558-qhIrsx-Picture32.png),![Picture33.png](https://pic.leetcode-cn.com/1628617558-ittLRv-Picture33.png),![Picture34.png](https://pic.leetcode-cn.com/1628617558-BksXHQ-Picture34.png),![Picture35.png](https://pic.leetcode-cn.com/1628617558-KwAJiL-Picture35.png),![Picture36.png](https://pic.leetcode-cn.com/1628617558-DeEUpW-Picture36.png),![Picture37.png](https://pic.leetcode-cn.com/1628617558-zFJvRA-Picture37.png),![Picture38.png](https://pic.leetcode-cn.com/1628617558-aIxOzm-Picture38.png),![Picture39.png](https://pic.leetcode-cn.com/1628617558-FPPYAH-Picture39.png),![Picture40.png](https://pic.leetcode-cn.com/1628617558-ZGLsvZ-Picture40.png)>
如下图所示，冒泡排序的「外循环」共 $N - 1$ 轮，每轮「内循环」都将当前最大元素交换至数组最右边，从而完成对整个数组的排序。
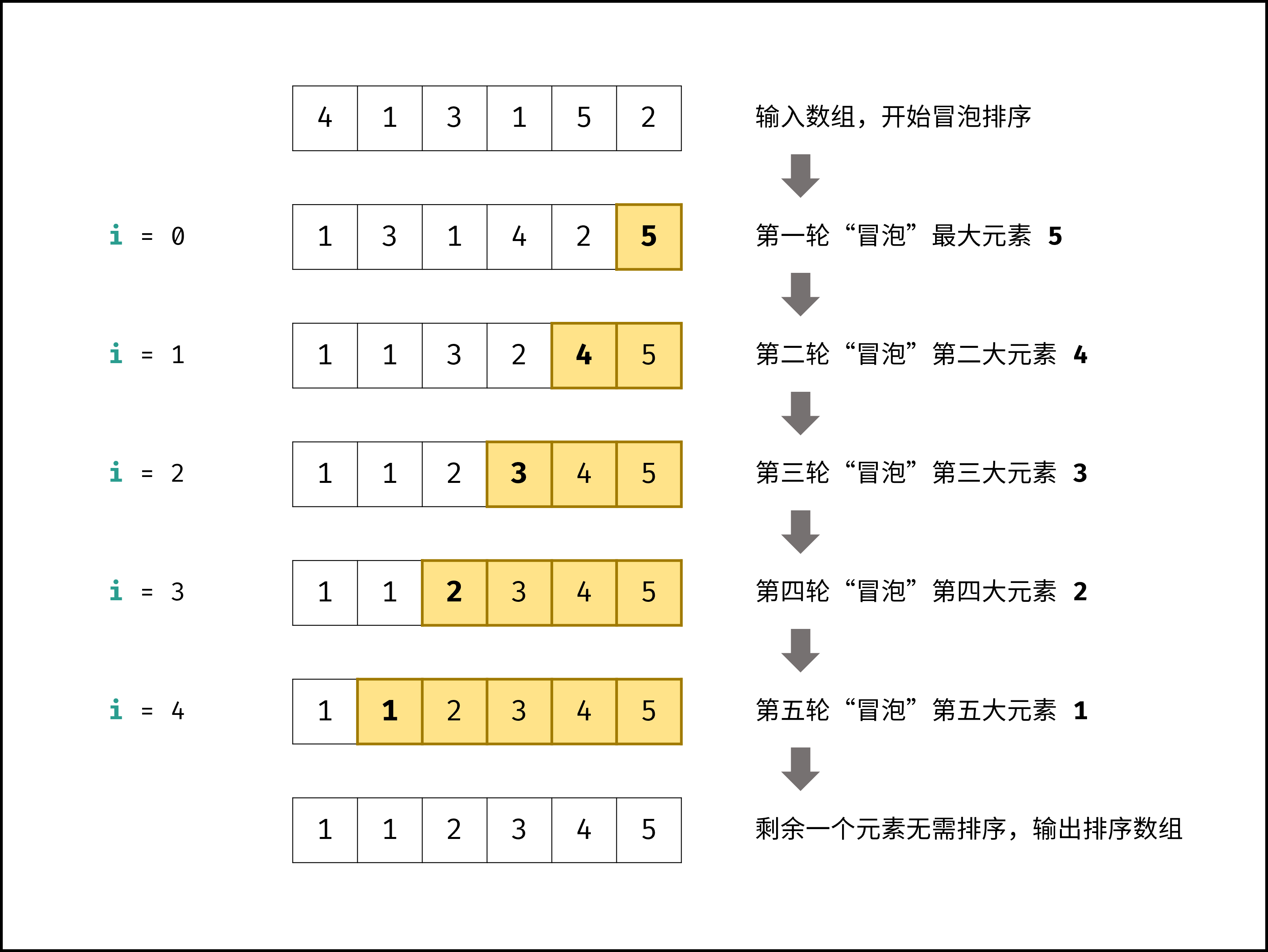![Picture1.png](https://pic.leetcode-cn.com/1628616643-PvqWBM-Picture1.png){:width=550}
如下图所示，为示例数组 `nums = [4, 1, 3, 1, 5, 2]` 的冒泡排序算法运行过程。
<![Picture2.png](https://pic.leetcode-cn.com/1628616643-WpzPBX-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1628616643-TtwECa-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1628616643-sCpIbT-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1628616643-dwjmfo-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1628616643-UqsBRU-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1628616643-zuIEGr-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1628616643-ZHOCyb-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1628616643-MrkmoX-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1628616643-tGgDta-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1628616643-wapMMy-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1628616643-hQjyzQ-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1628616643-UNVHcU-Picture13.png),![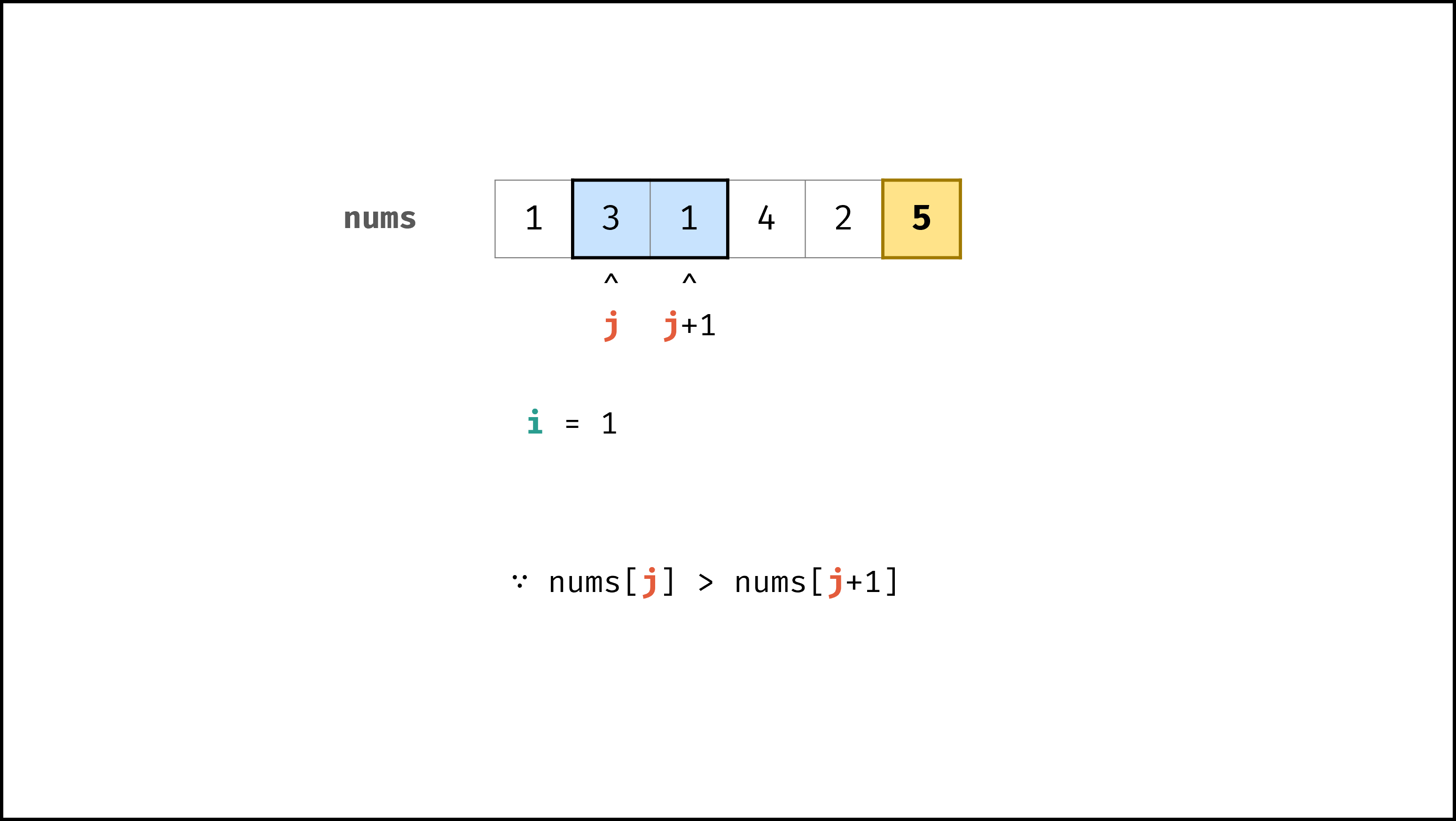Picture14.png](https://pic.leetcode-cn.com/1628616643-bXSWDP-Picture14.png),![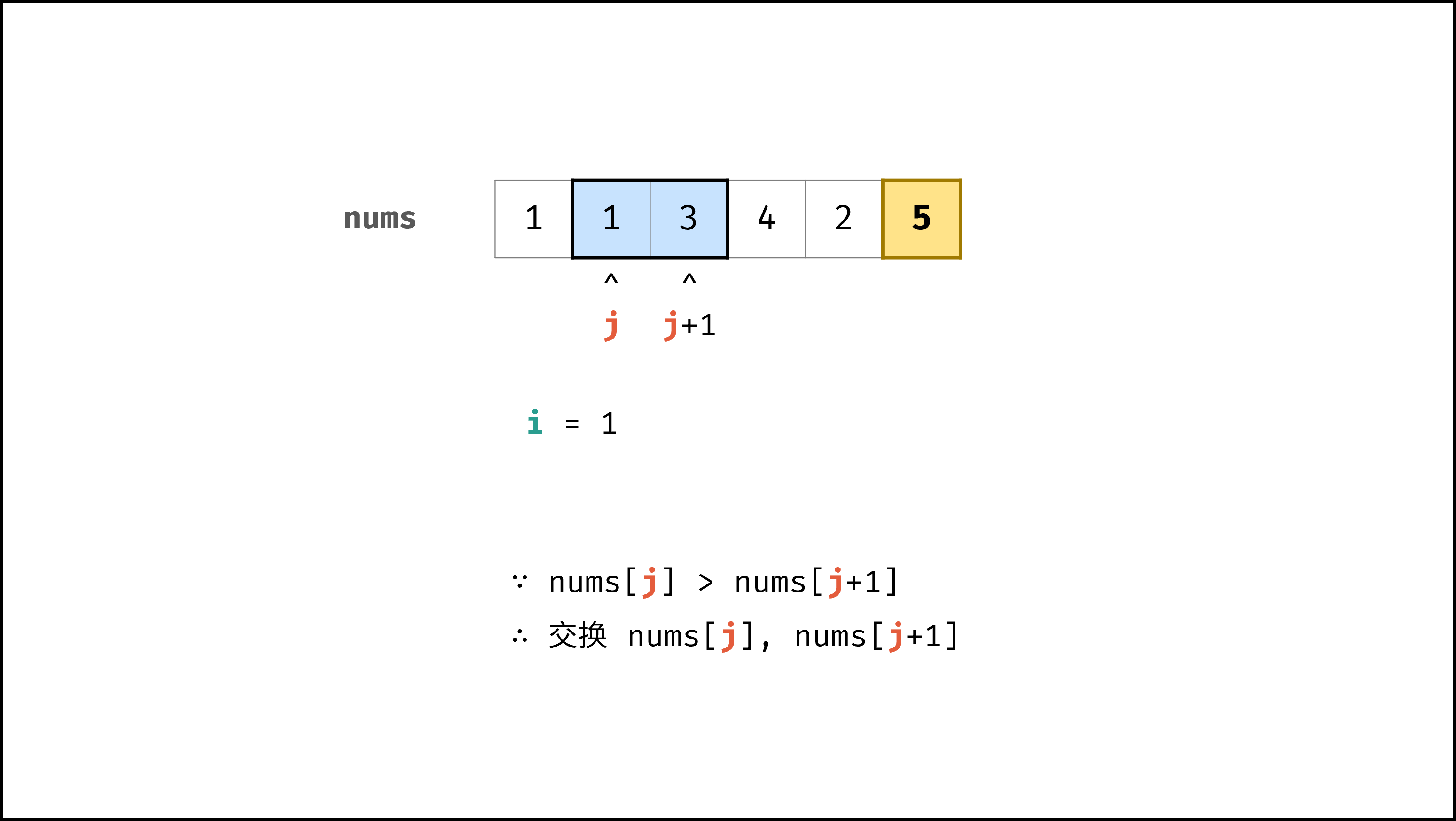Picture15.png](https://pic.leetcode-cn.com/1628616643-UPLFgg-Picture15.png),![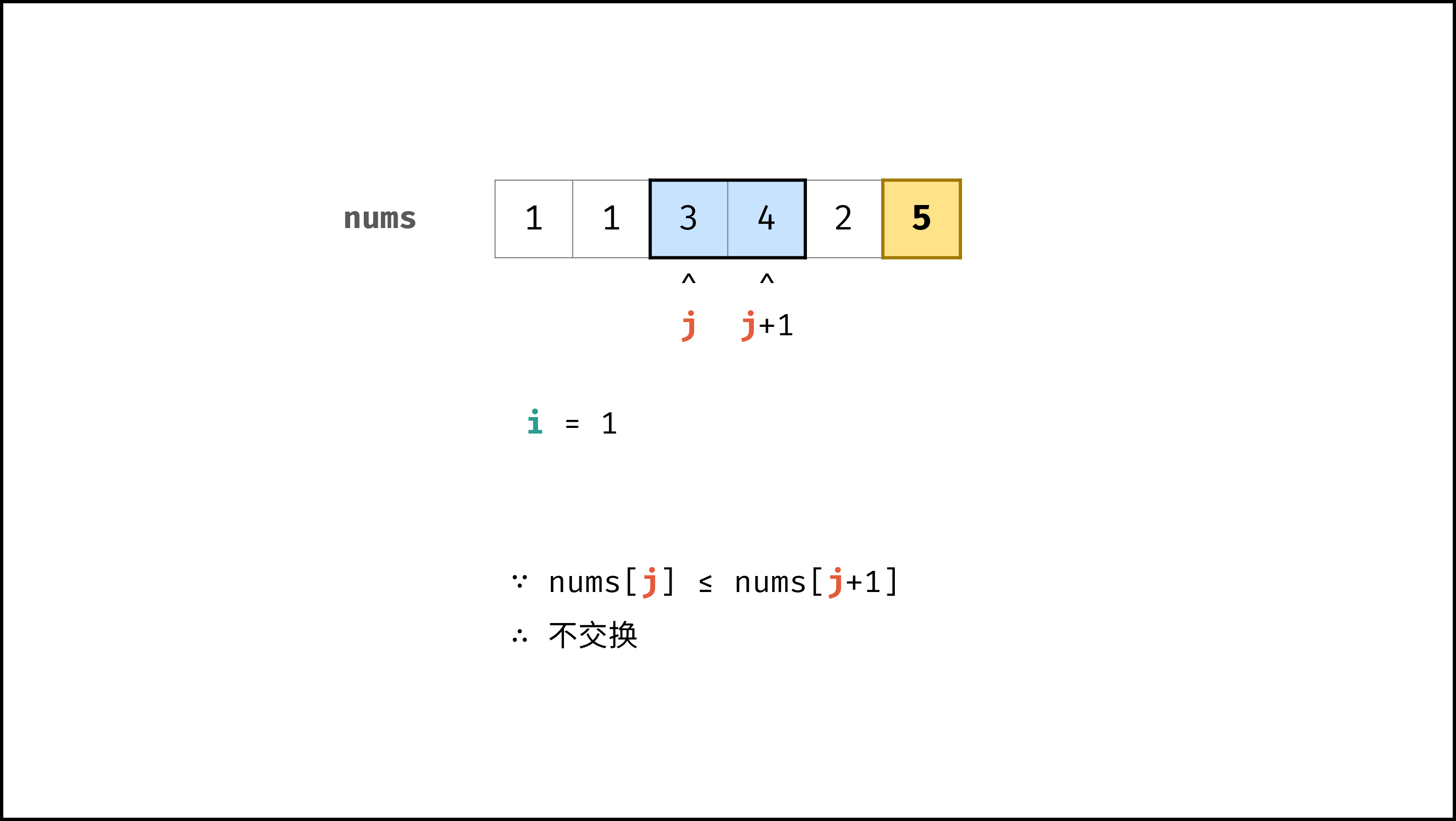Picture16.png](https://pic.leetcode-cn.com/1628616643-aKpsRI-Picture16.png),![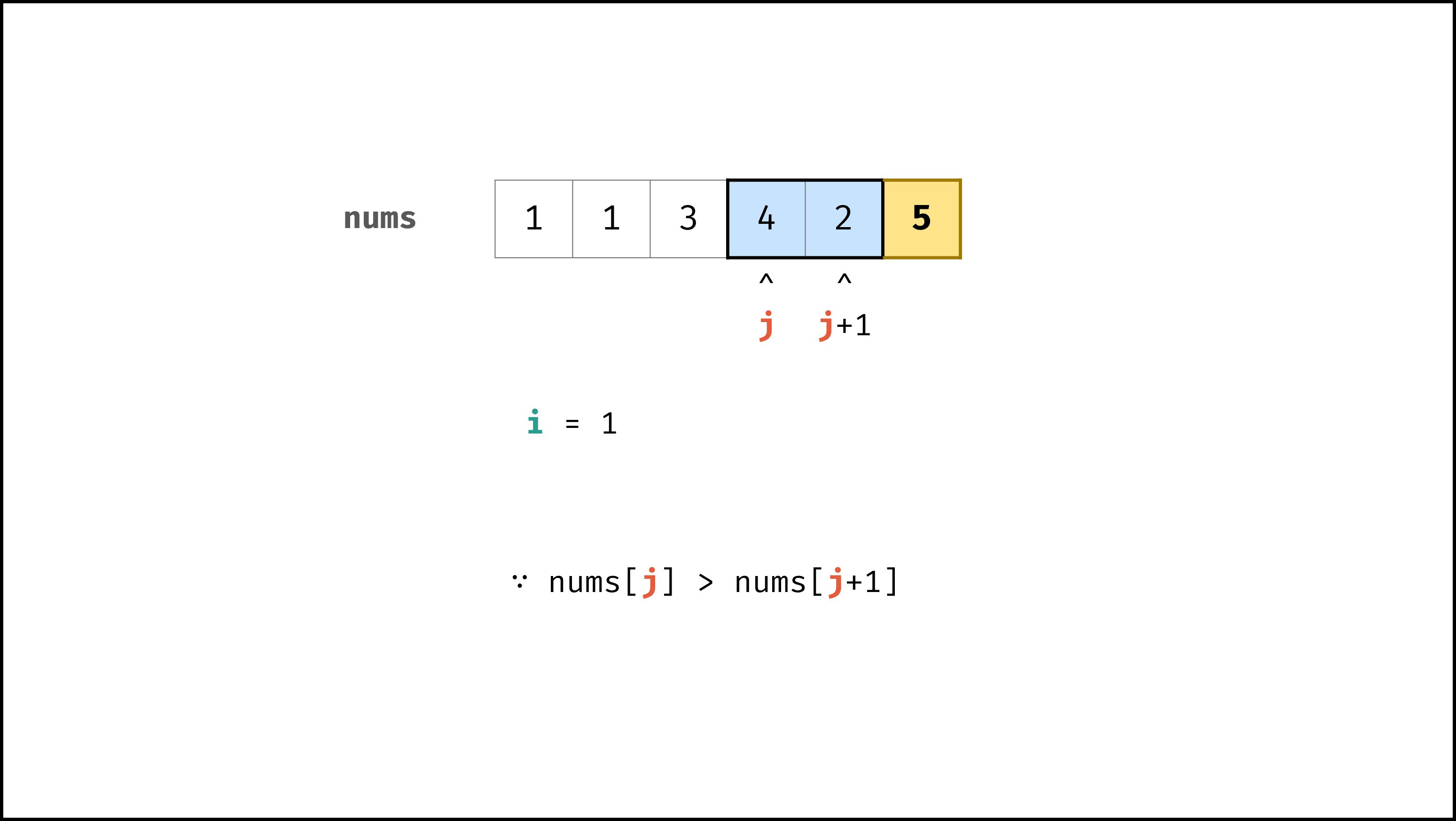Picture17.png](https://pic.leetcode-cn.com/1628616643-GmDQBC-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1628616643-iHXhIo-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1628616643-kXamhB-Picture19.png),![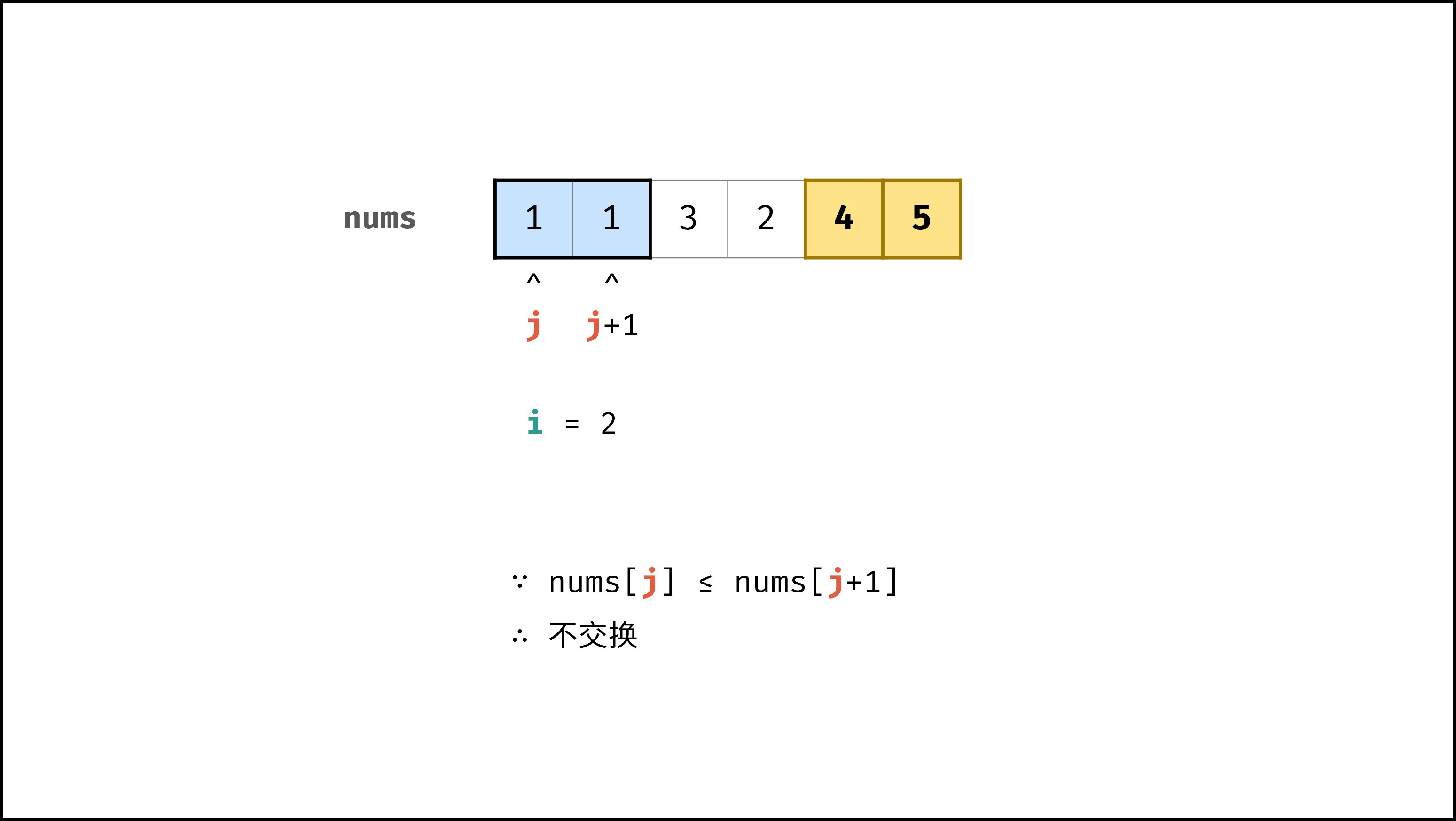Picture20.png](https://pic.leetcode-cn.com/1628616643-wiIbgD-Picture20.png),![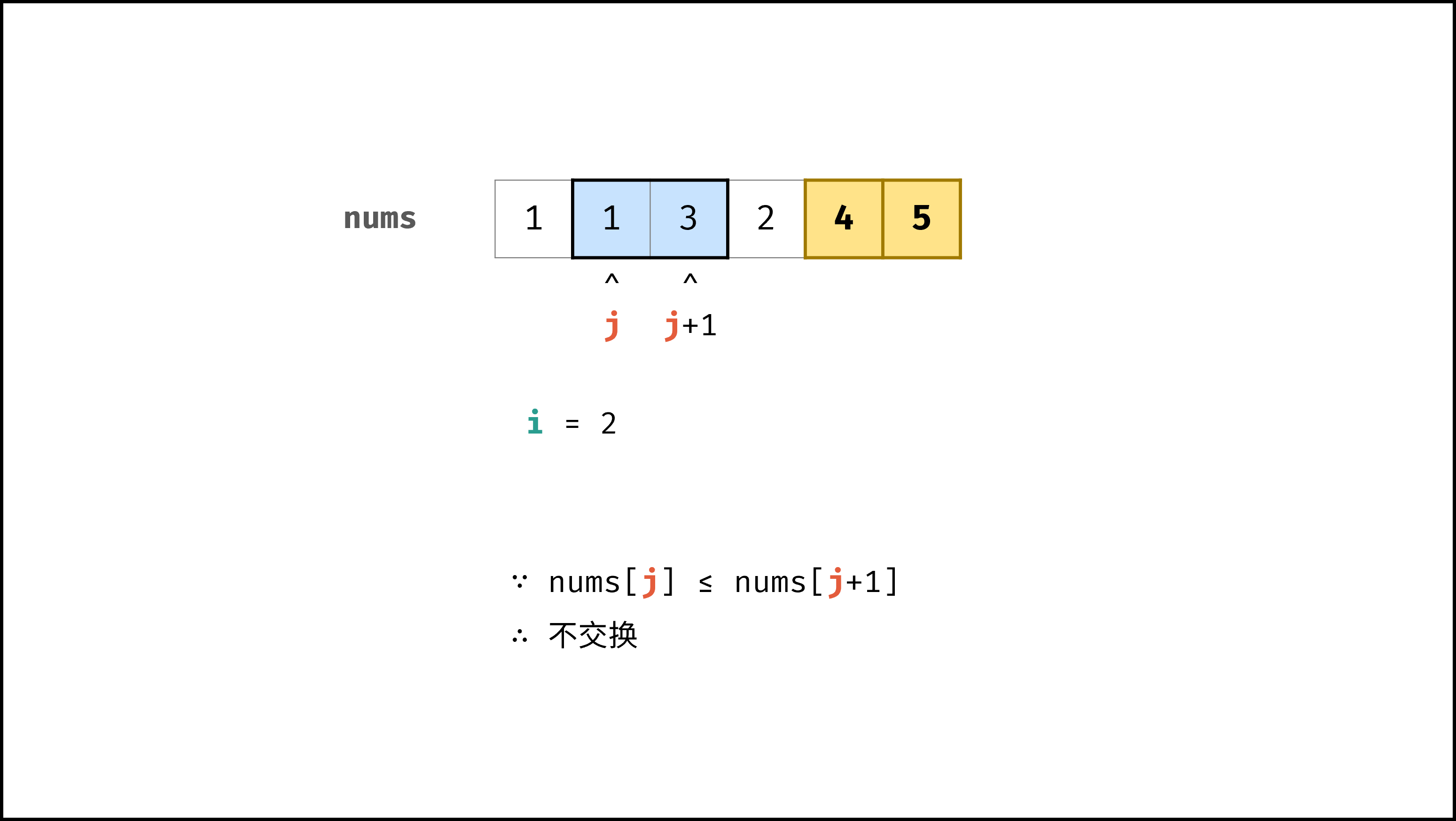Picture21.png](https://pic.leetcode-cn.com/1628616643-TUaEPM-Picture21.png),![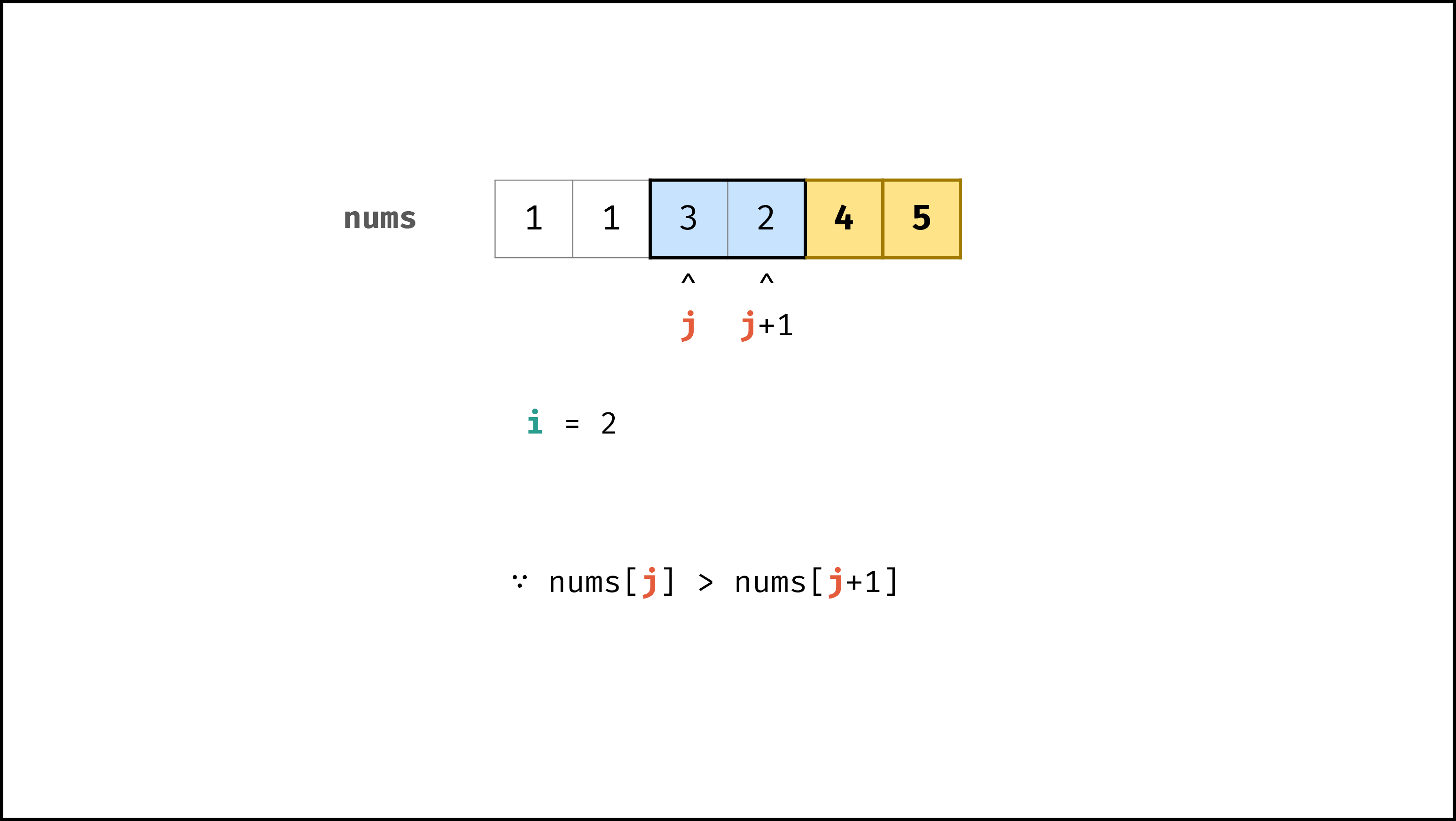Picture22.png](https://pic.leetcode-cn.com/1628616643-ovdBtR-Picture22.png),![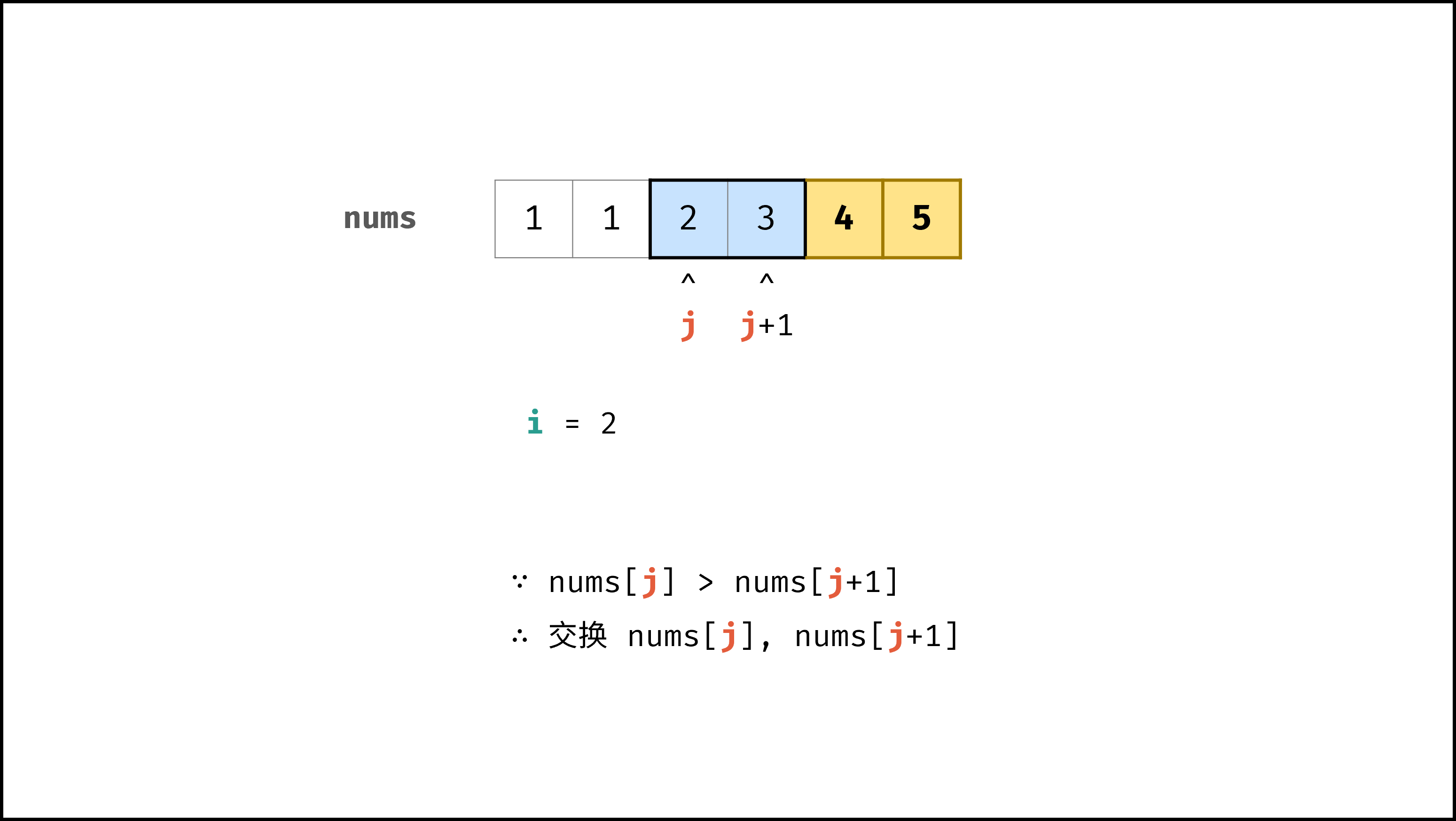Picture23.png](https://pic.leetcode-cn.com/1628616643-lotSjf-Picture23.png),![Picture24.png](https://pic.leetcode-cn.com/1628616643-FCYmSX-Picture24.png),![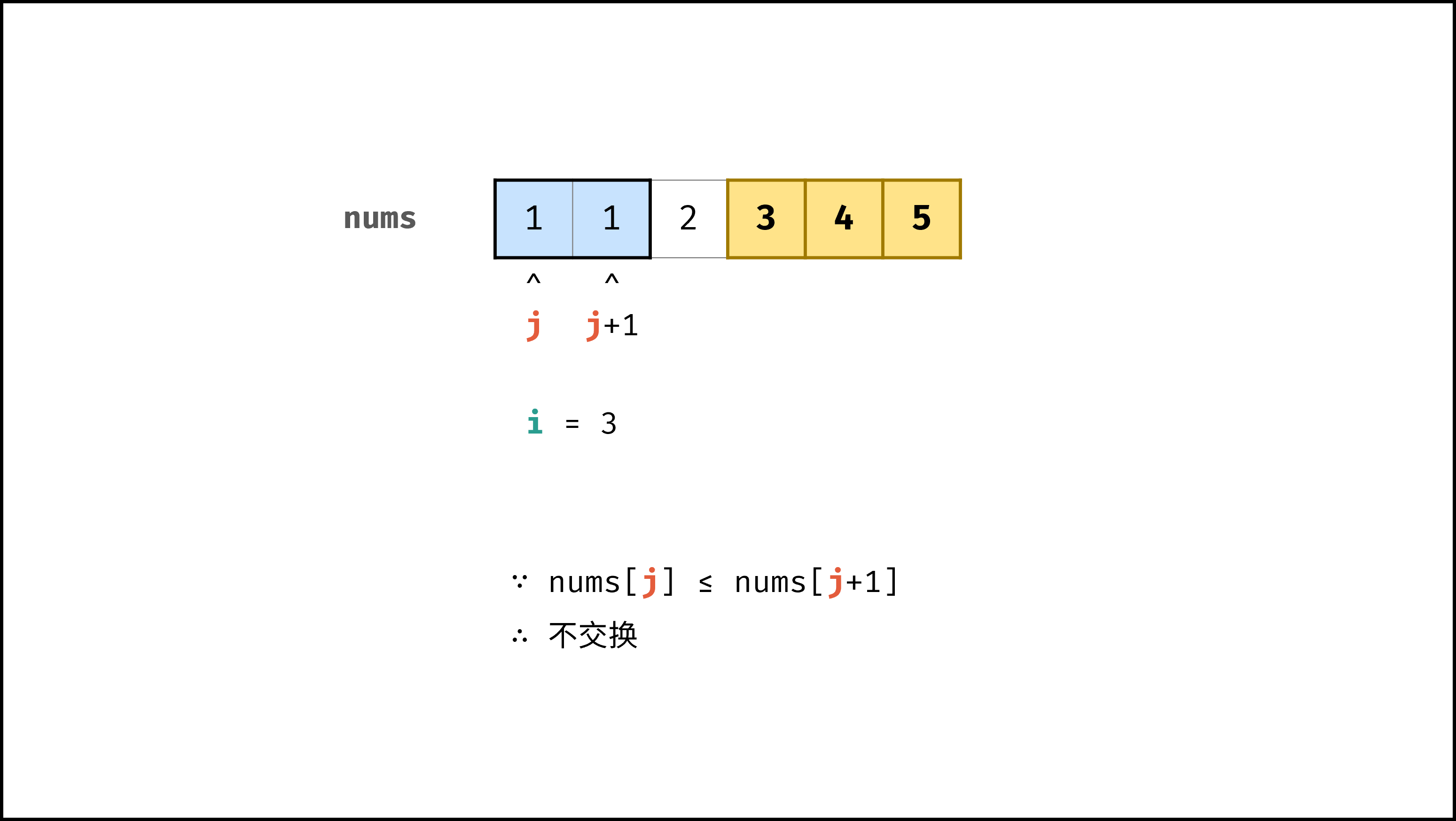Picture25.png](https://pic.leetcode-cn.com/1628616643-gdaGaw-Picture25.png),![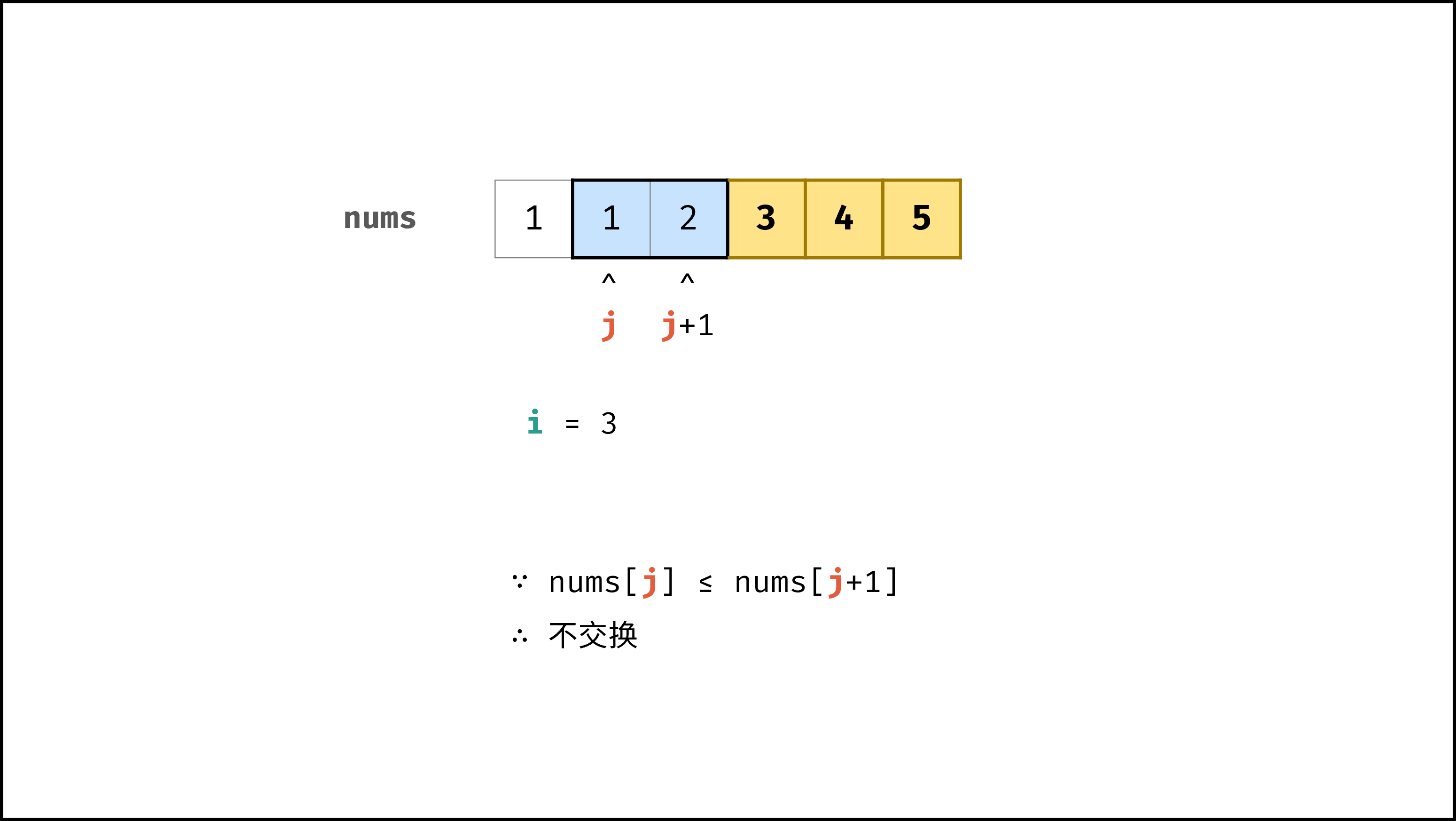Picture26.png](https://pic.leetcode-cn.com/1628616643-iWnCmb-Picture26.png),![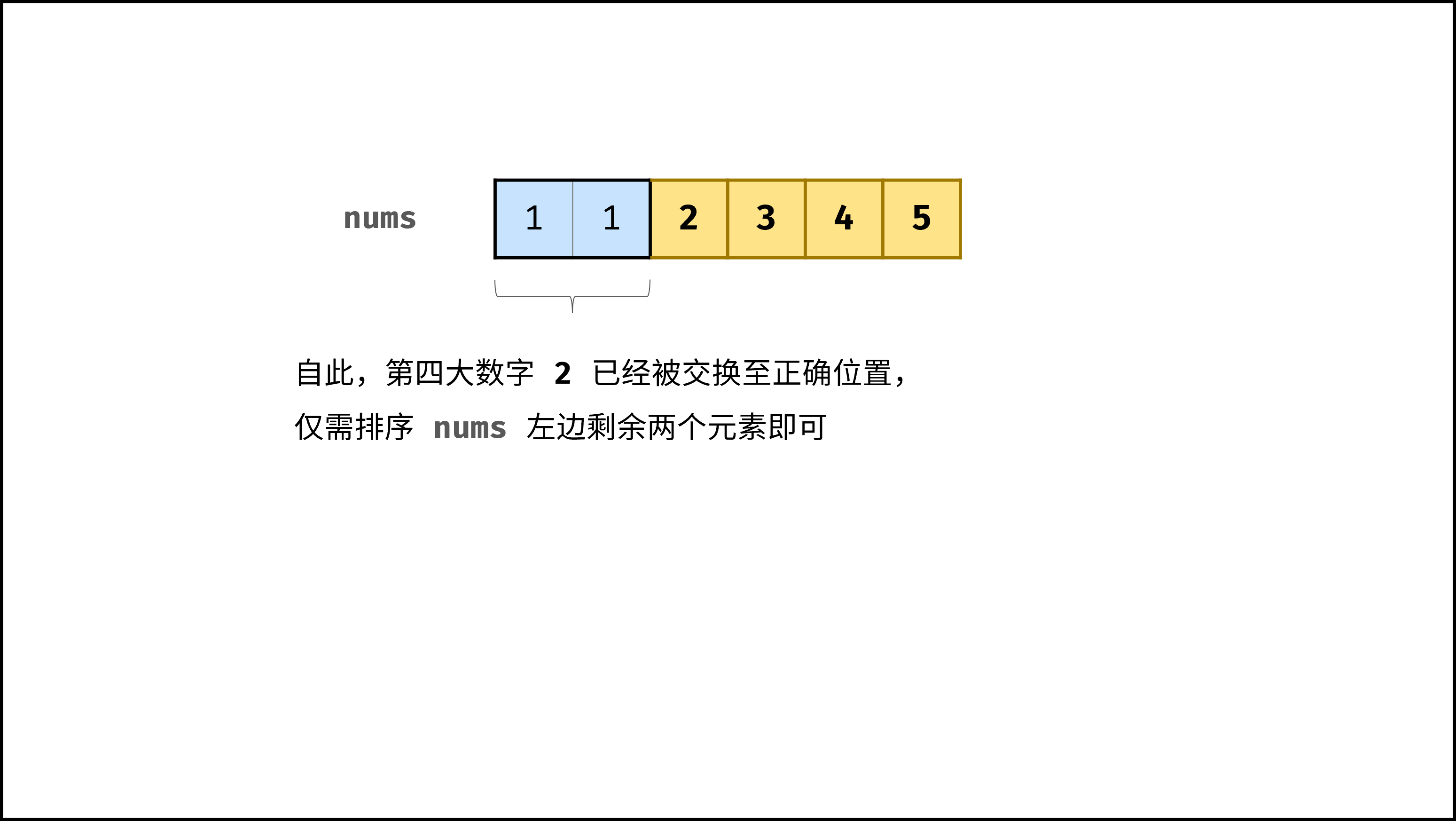Picture27.png](https://pic.leetcode-cn.com/1628616643-YPjzsI-Picture27.png),![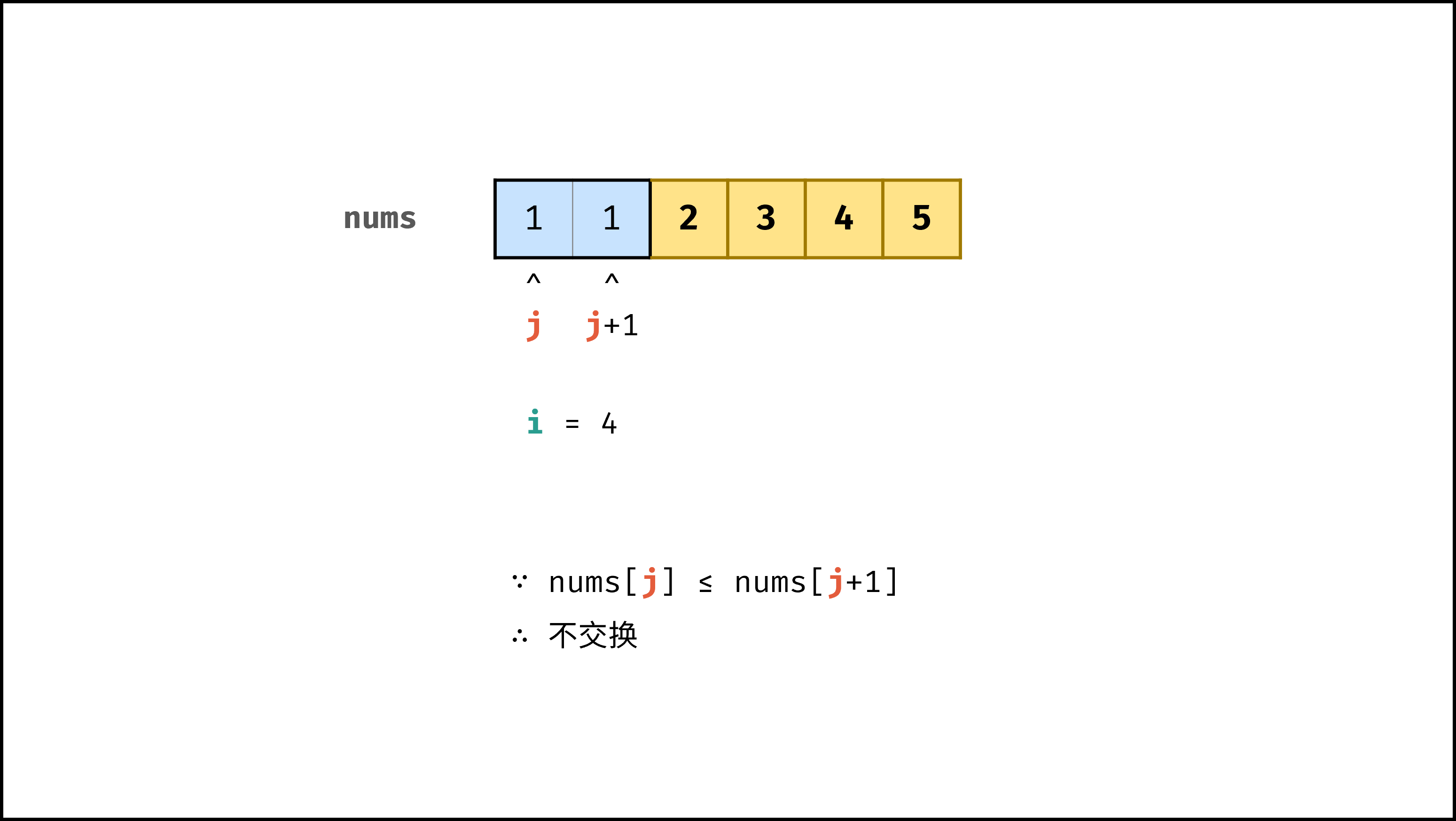Picture28.png](https://pic.leetcode-cn.com/1628616643-AFSnYn-Picture28.png),![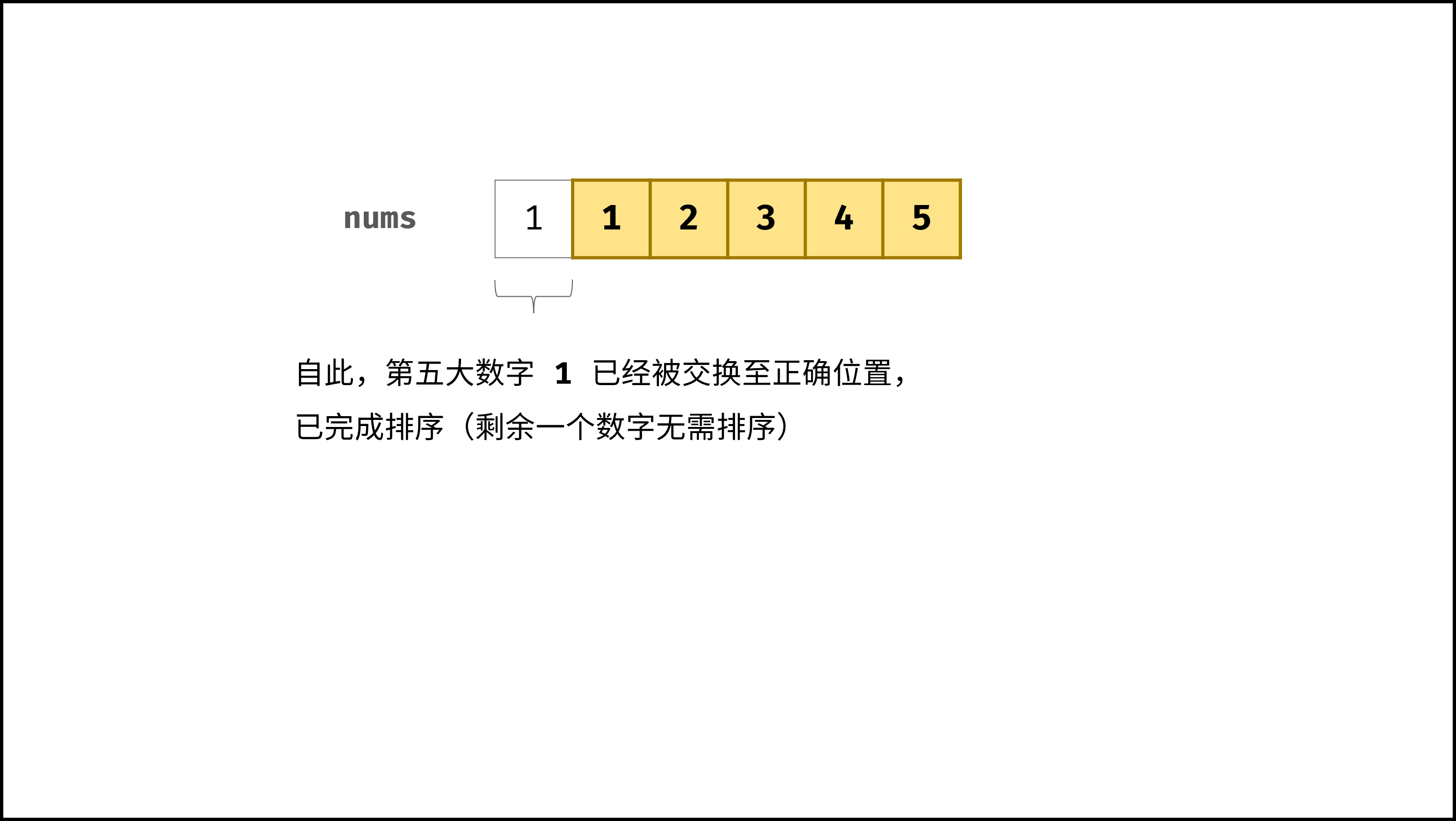Picture29.png](https://pic.leetcode-cn.com/1628616643-yCLeAx-Picture29.png),![Picture30.png](https://pic.leetcode-cn.com/1628616643-HikxcK-Picture30.png)>
## 代码
```Python []
def bubble_sort(nums):
N = len(nums)
for i in range(N - 1): # 外循环
for j in range(N - i - 1): # 内循环
if nums[j] > nums[j + 1]:
# 交换 nums[j], nums[j + 1]
nums[j], nums[j + 1] = nums[j + 1], nums[j]
```
```Java []
void bubbleSort(int[] nums) {
int N = nums.length;
for (int i = 0; i < N - 1; i++) { // 外循环
for (int j = 0; j < N - i - 1; j++) { // 内循环
if (nums[j] > nums[j + 1]) {
// 交换 nums[j], nums[j + 1]
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
}
```
```C++ []
void bubbleSort(vector<int> &nums) {
int N = nums.size();
for (int i = 0; i < N - 1; i++) { // 外循环
for (int j = 0; j < N - i - 1; j++) { // 内循环
if (nums[j] > nums[j + 1]) {
// 交换 nums[j], nums[j + 1]
swap(nums[j], nums[j + 1]);
}
}
}
}
```
## 算法特性
- **时间复杂度 $O(N^2)$ ：**
- **最佳 $\Omega(N)$ ：** 普通冒泡排序的时间复杂度恒为 $O(N^2)$ ，对于近似排序数组，通过加入标志位可实现提前返回（详情请见下文）。
- **平均与最差 $O(N^2)$ ：**「外循环」共 $N - 1$ 轮，使用 $O(N)$ 时间；每轮「内循环」分别遍历 $N - 1$ , $N - 2$ , $\cdots$ , $2$ , $1$ 次，平均 $\frac{N}{2}$ 次，使用 $O(\frac{N}{2}) = O(N)$ 时间；因此，总体时间复杂度为 $O(N^2)$ 。
- **空间复杂度 $O(1)$ ：** 只需原地交换元素，使用常数大小的额外空间。
- 冒泡排序是通过不断 **交换元素** 实现排序（交换 2 个元素需要 3 次赋值操作），因此速度较慢；
- **原地：** 指针变量仅使用常数大小额外空间，空间复杂度为 $O(1)$ ；
- **稳定：** 元素值相同时不交换，因此不会改变相同元素的相对位置；
- **自适应：** 通过增加一个标志位 `flag` ，若某轮内循环未执行任何交换操作时，说明已经完成排序，因此直接返回。此优化使冒泡排序的最优时间复杂度达到 $O(N)$（当输入数组已排序时）；
## 标志位优化
> 普通冒泡排序的时间复杂度恒为 $O(N^2)$​ ，与输入数组的元素分布无关。
通过增加一个标志位 `flag` ，若在某轮「内循环」中未执行任何交换操作，则说明数组已经完成排序，直接返回结果即可。
优化后的冒泡排序的最差和平均时间复杂度仍为 $O(N^2)$ ；在输入数组 **已排序** 时，达到 **最佳时间复杂度** $\Omega(N)$ 。
```Python []
def bubble_sort(nums):
N = len(nums)
for i in range(N - 1):
flag = False # 初始化标志位
for j in range(N - i - 1):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
flag = True # 记录交换元素
if not flag: break # 内循环未交换任何元素，则跳出
```
```Java []
void bubbleSort(int[] nums) {
int N = nums.length;
for (int i = 0; i < N - 1; i++) {
boolean flag = false; // 初始化标志位
for (int j = 0; j < N - i - 1; j++) {
if (nums[j] > nums[j + 1]) {
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
flag = true; // 记录交换元素
}
}
if (!flag) break; // 内循环未交换任何元素，则跳出
}
}
```
```C++ []
void bubbleSort(vector<int> &nums) {
int N = nums.size();
for (int i = 0; i < N - 1; i++) {
bool flag = false; // 初始化标志位
for (int j = 0; j < N - i - 1; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
flag = true; // 记录交换元素
}
}
if (!flag) break; // 内循环未交换任何元素，则跳出
}
}
```

244
leetbook_ioa/docs/# 7.3 快速排序.md Executable file
View File

@@ -0,0 +1,244 @@
# 快速排序
快速排序算法有两个核心点，分别为 **哨兵划分** 和 **递归** 。
**哨兵划分**：以数组某个元素（一般选取首元素）为 **基准数** ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。
> 下图展示了哨兵划分操作流程。经过一轮 **哨兵划分** ，可将数组排序问题拆分为 **两个较短数组的排序问题** （本文称之为左（右）子数组）。
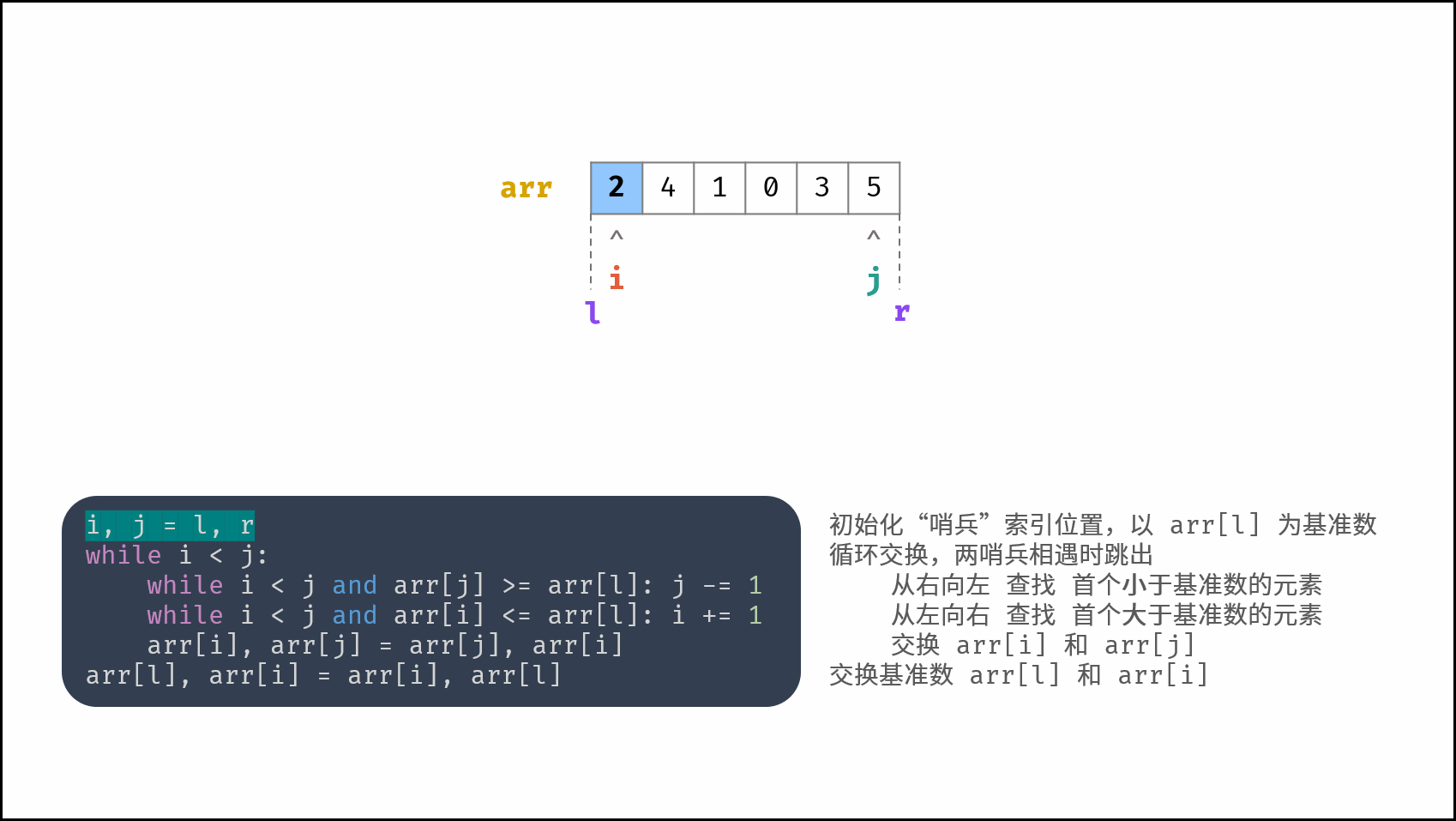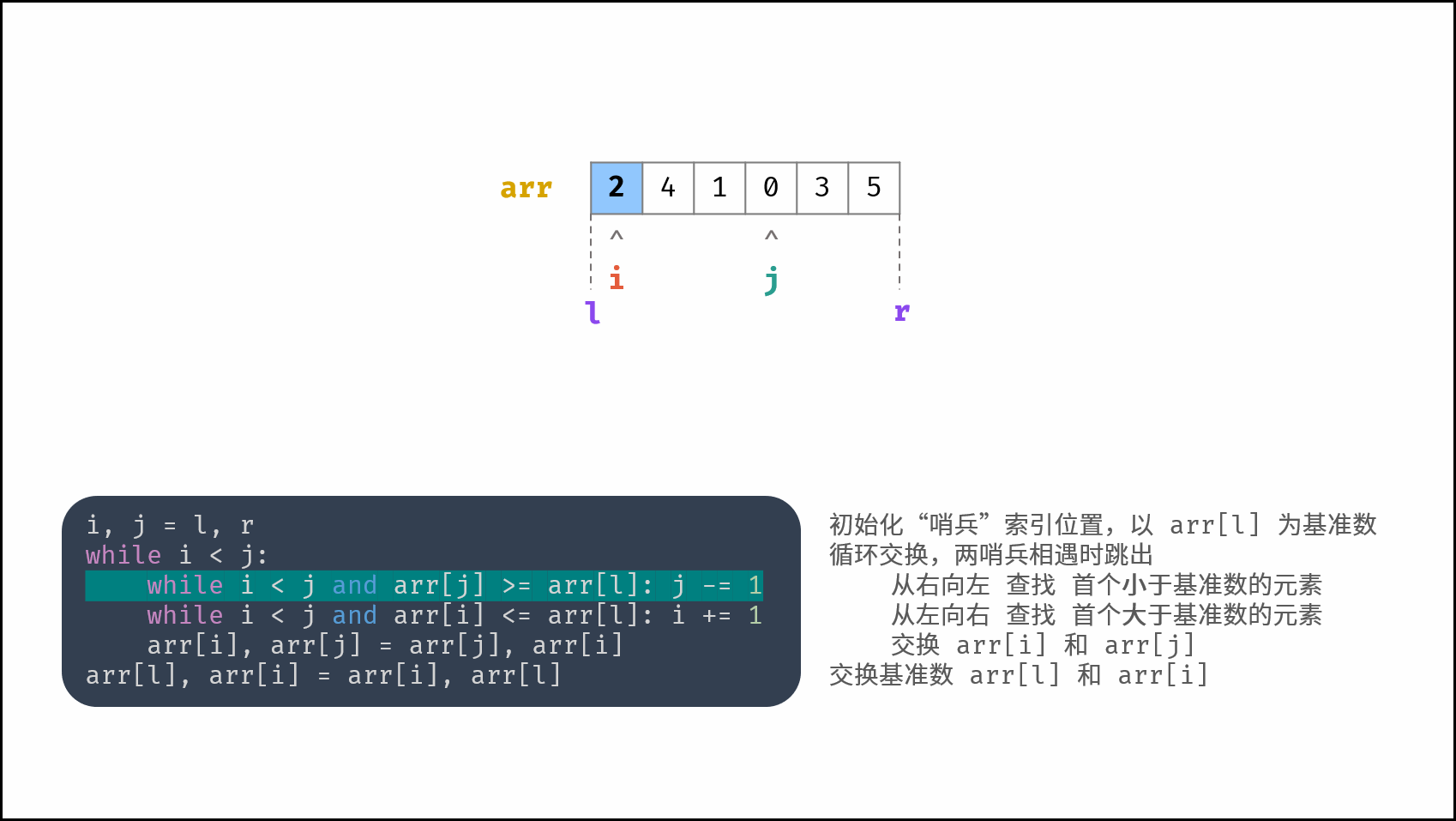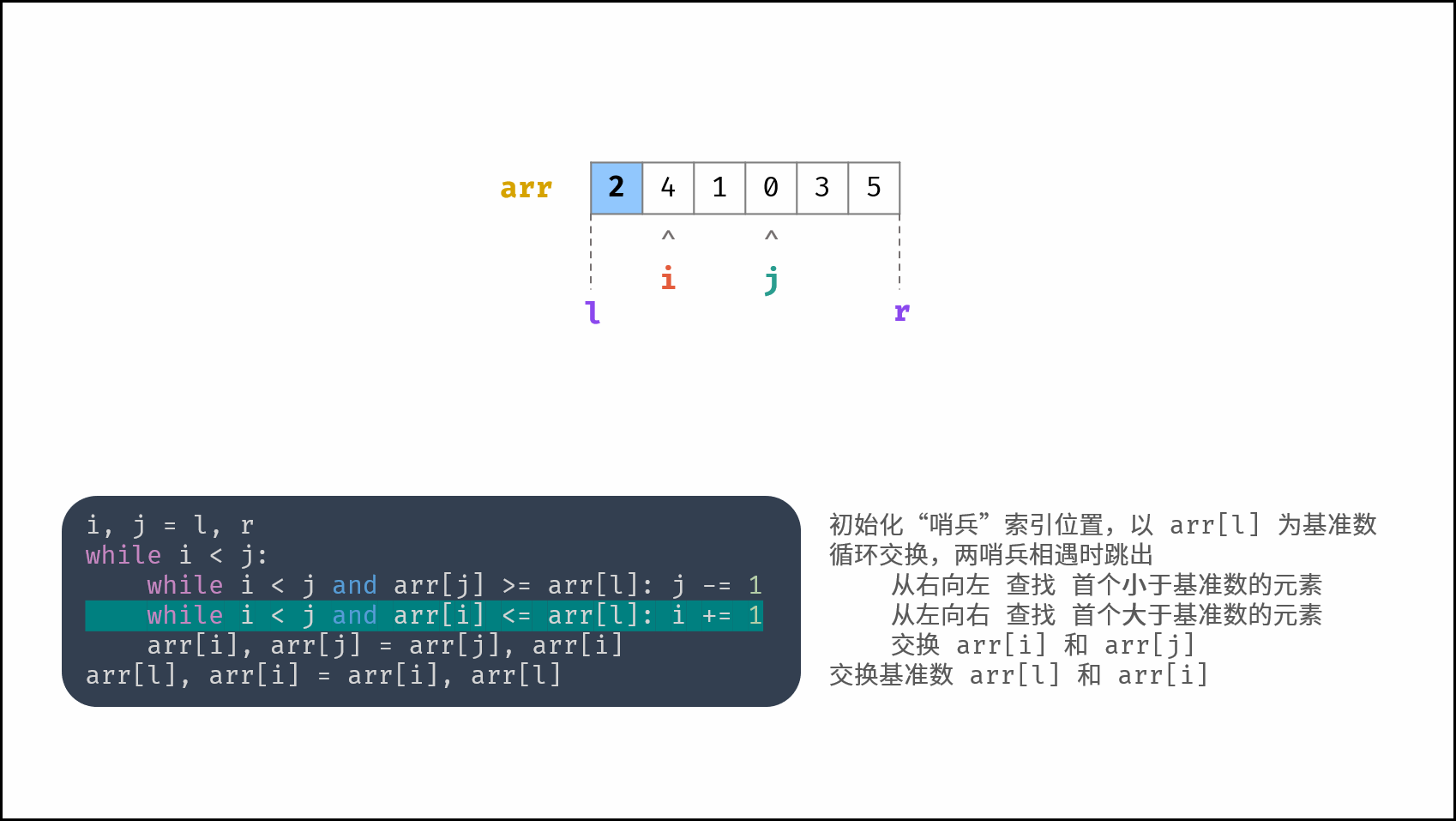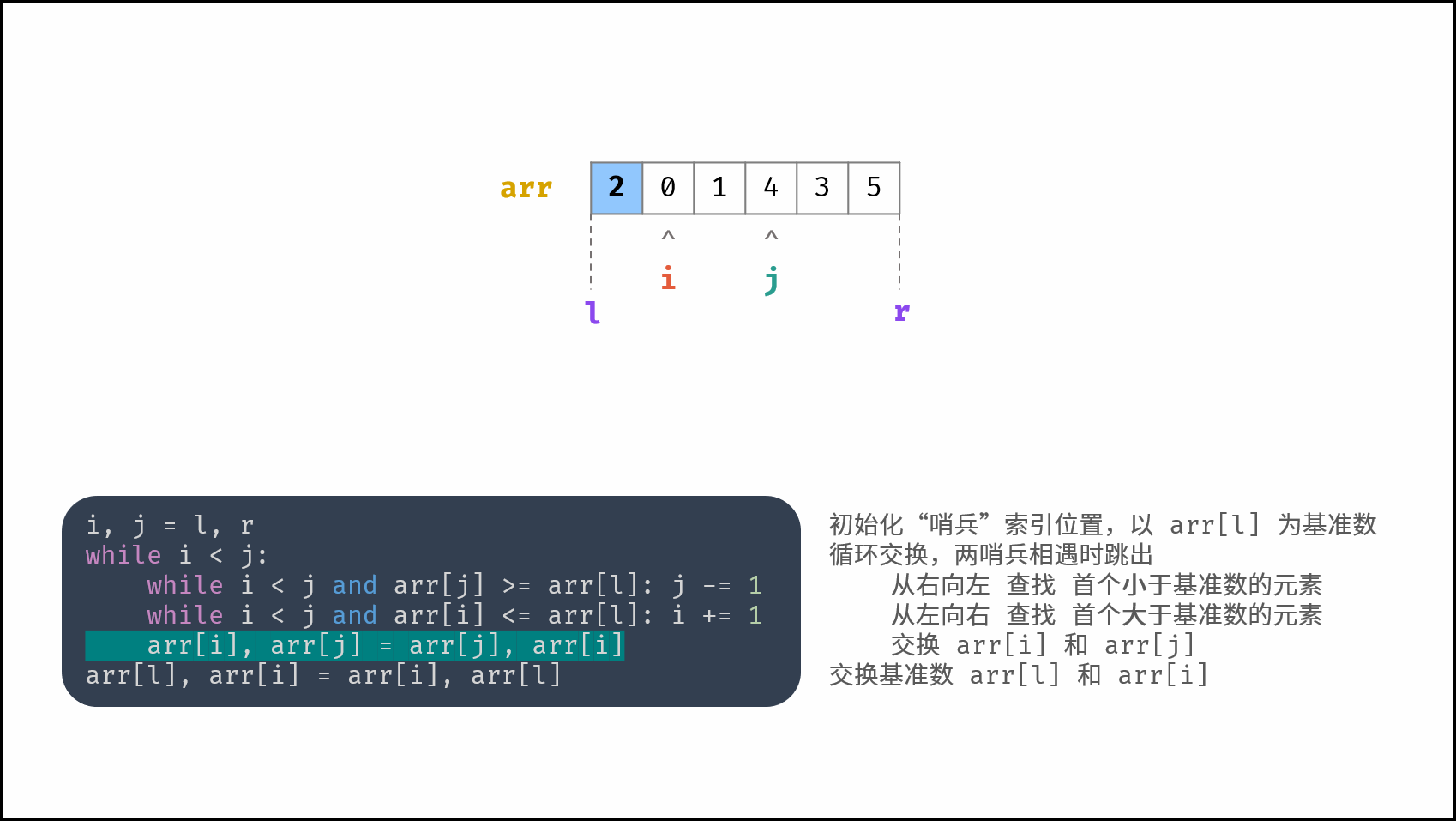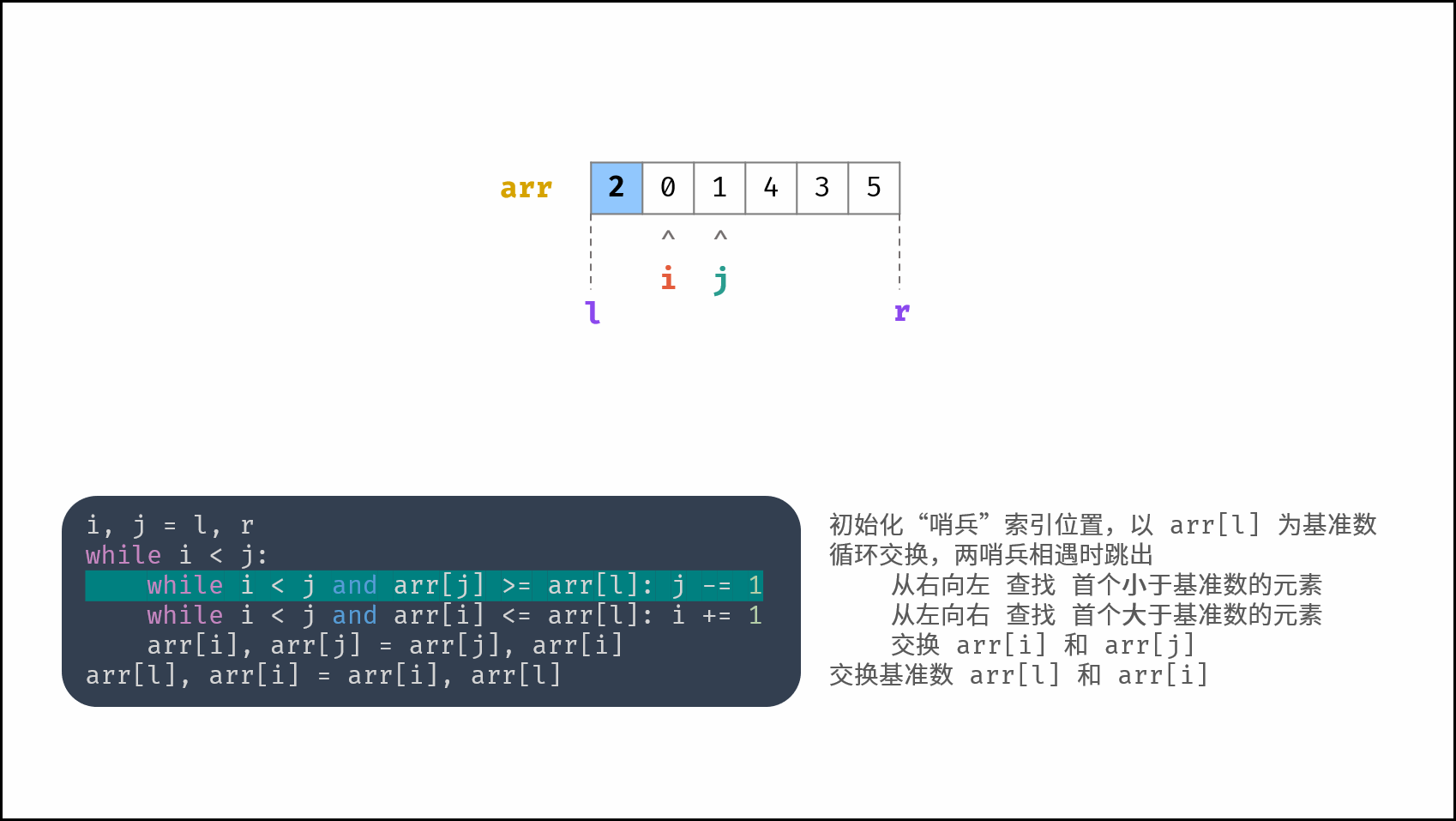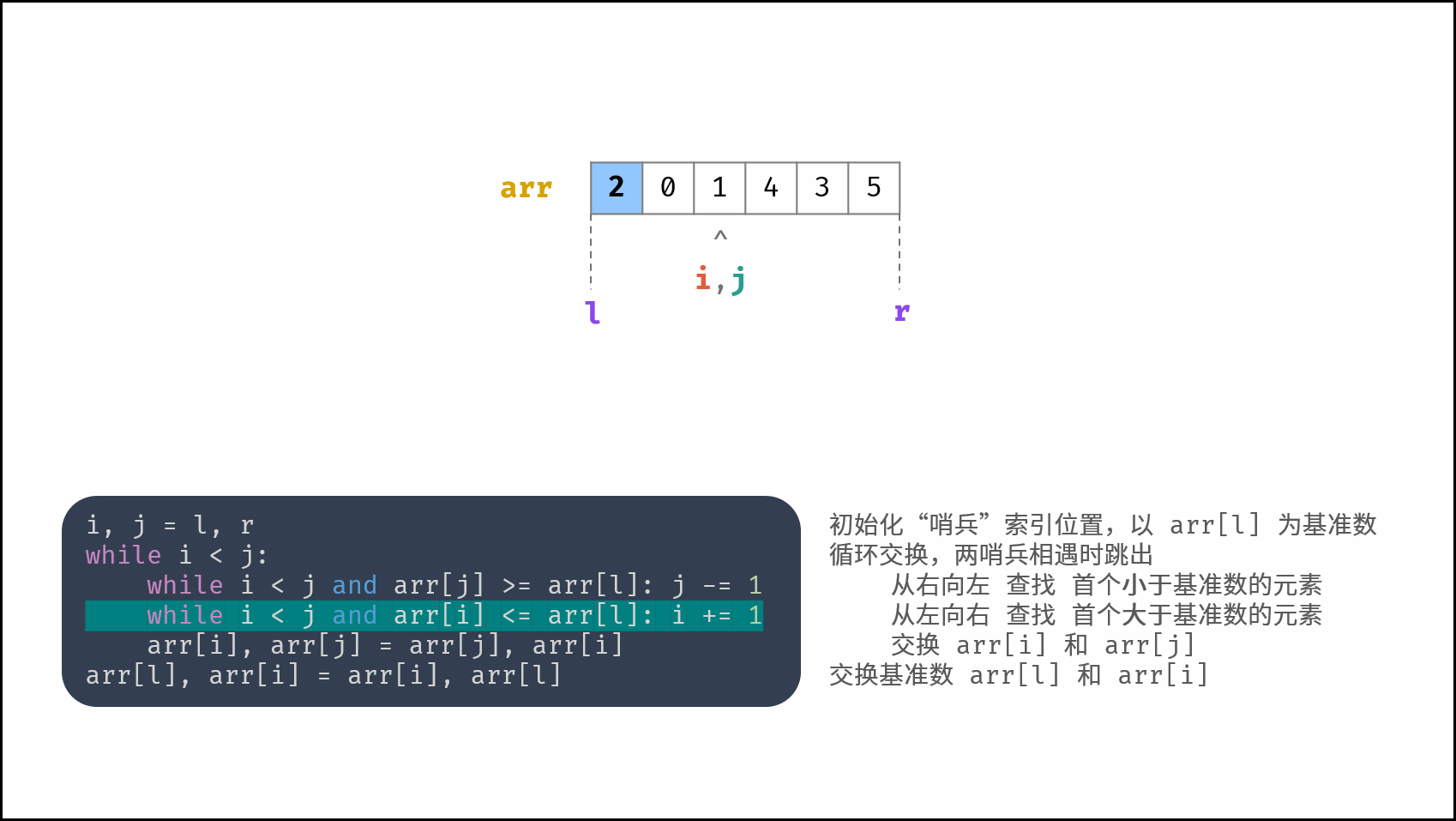<![Picture2.png](https://pic.leetcode-cn.com/1612615167-etrYaH-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1612615167-PHsLgY-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1612615167-aMCCrd-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1612615167-smzuGu-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1612615167-WXDRIU-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1612615167-lWmBlA-Picture7.png),![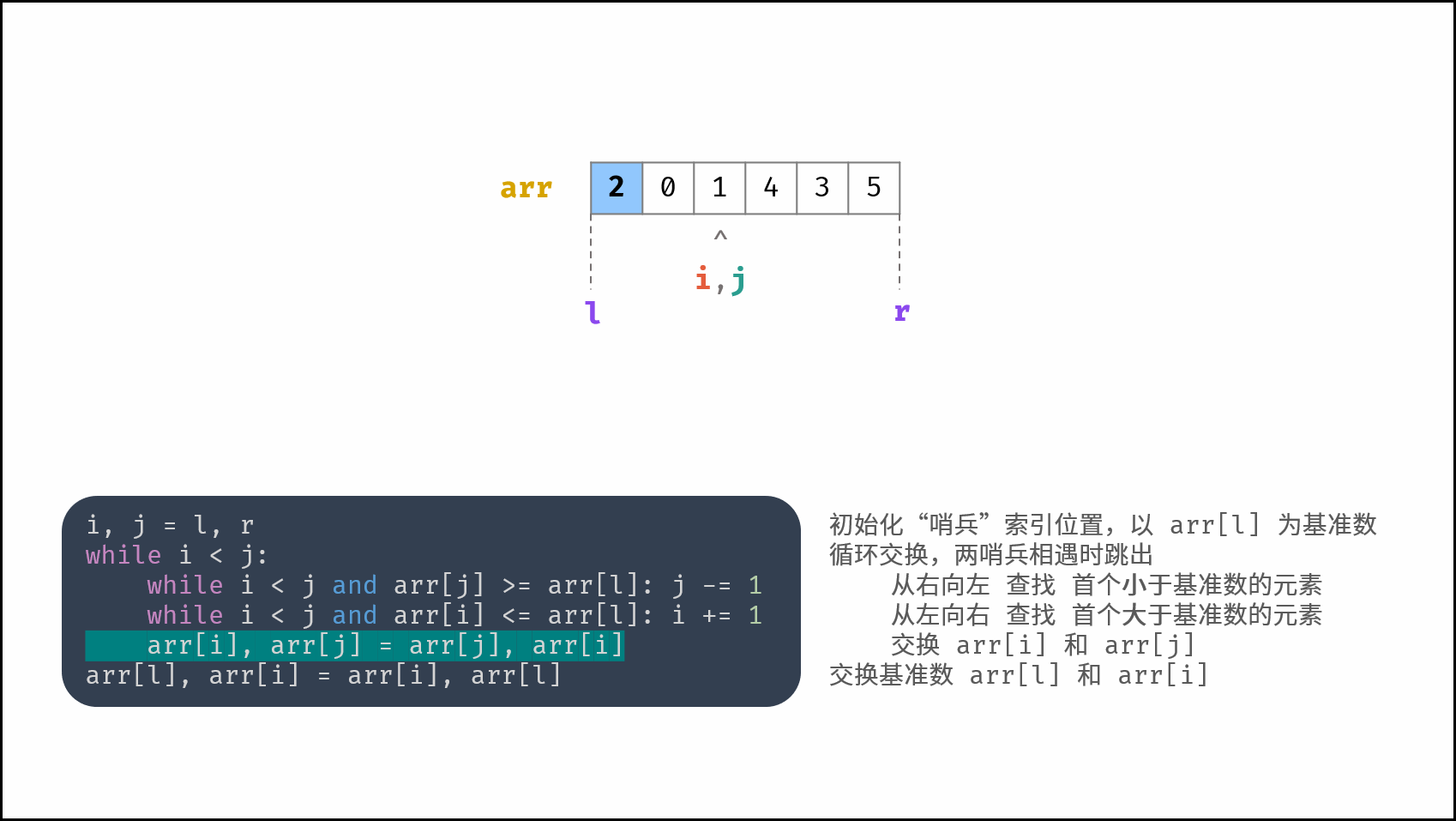Picture8.png](https://pic.leetcode-cn.com/1612615167-ghPekO-Picture8.png),![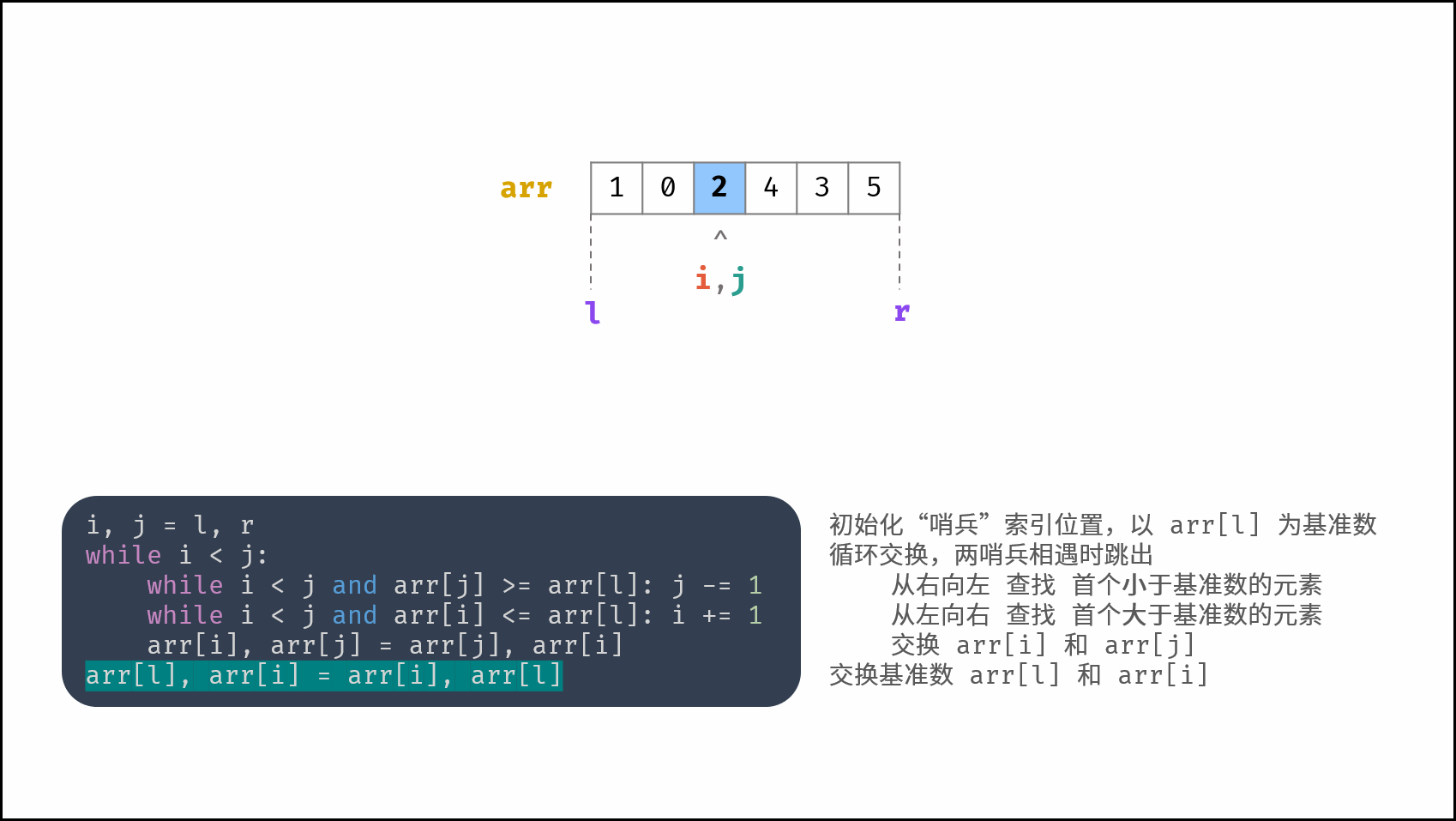Picture9.png](https://pic.leetcode-cn.com/1612615167-azMHYj-Picture9.png),![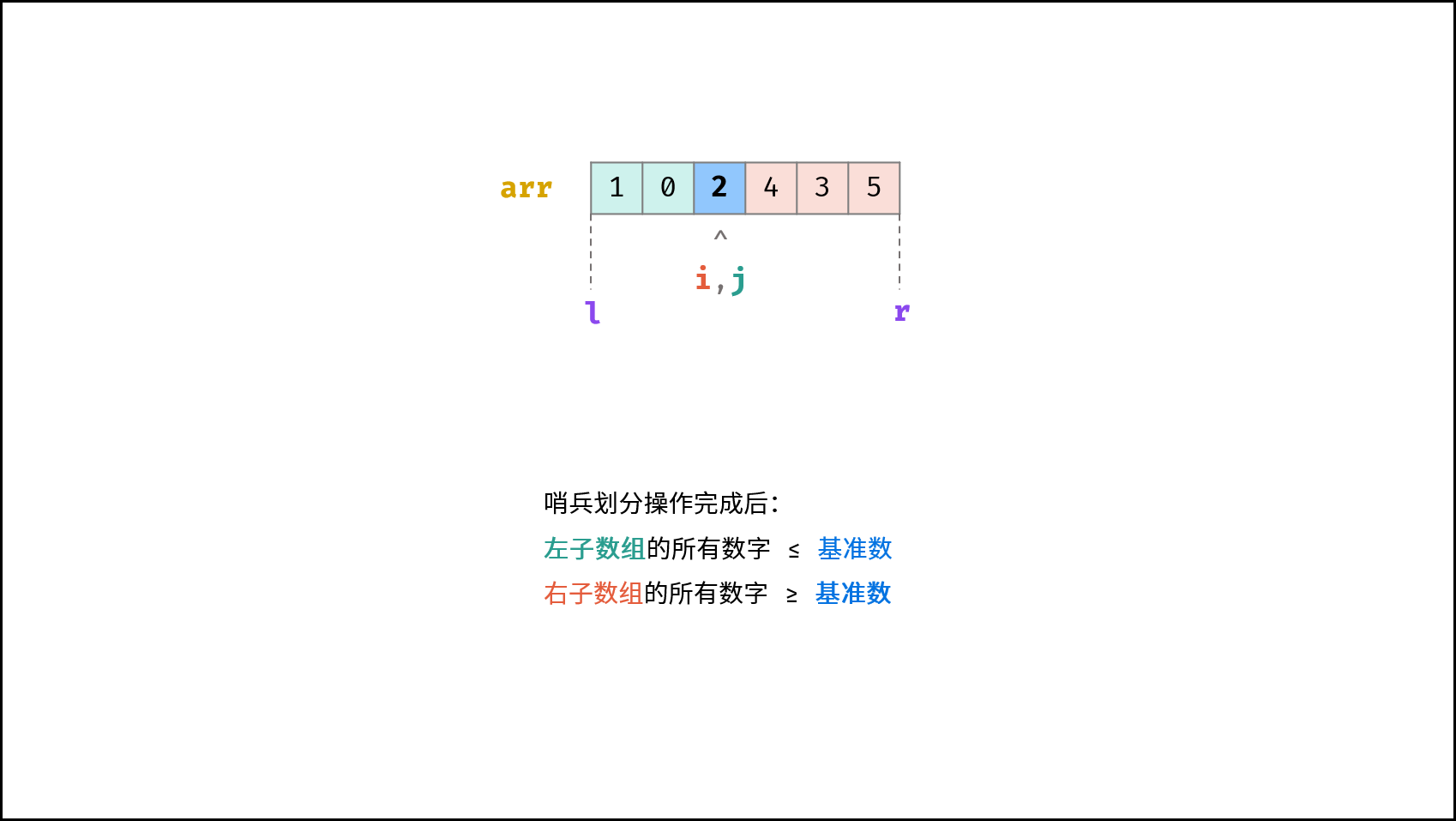Picture10.png](https://pic.leetcode-cn.com/1623073951-BKkDwO-Picture10.png)>
**递归**：对 **左子数组** 和 **右子数组** 分别递归执行 **哨兵划分**，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。
> 下图展示了数组 `[2,4,1,0,3,5]` 的快速排序流程。观察发现，快速排序和 **二分法** 的原理类似，都是以 $\log$ 时间复杂度实现搜索区间缩小。
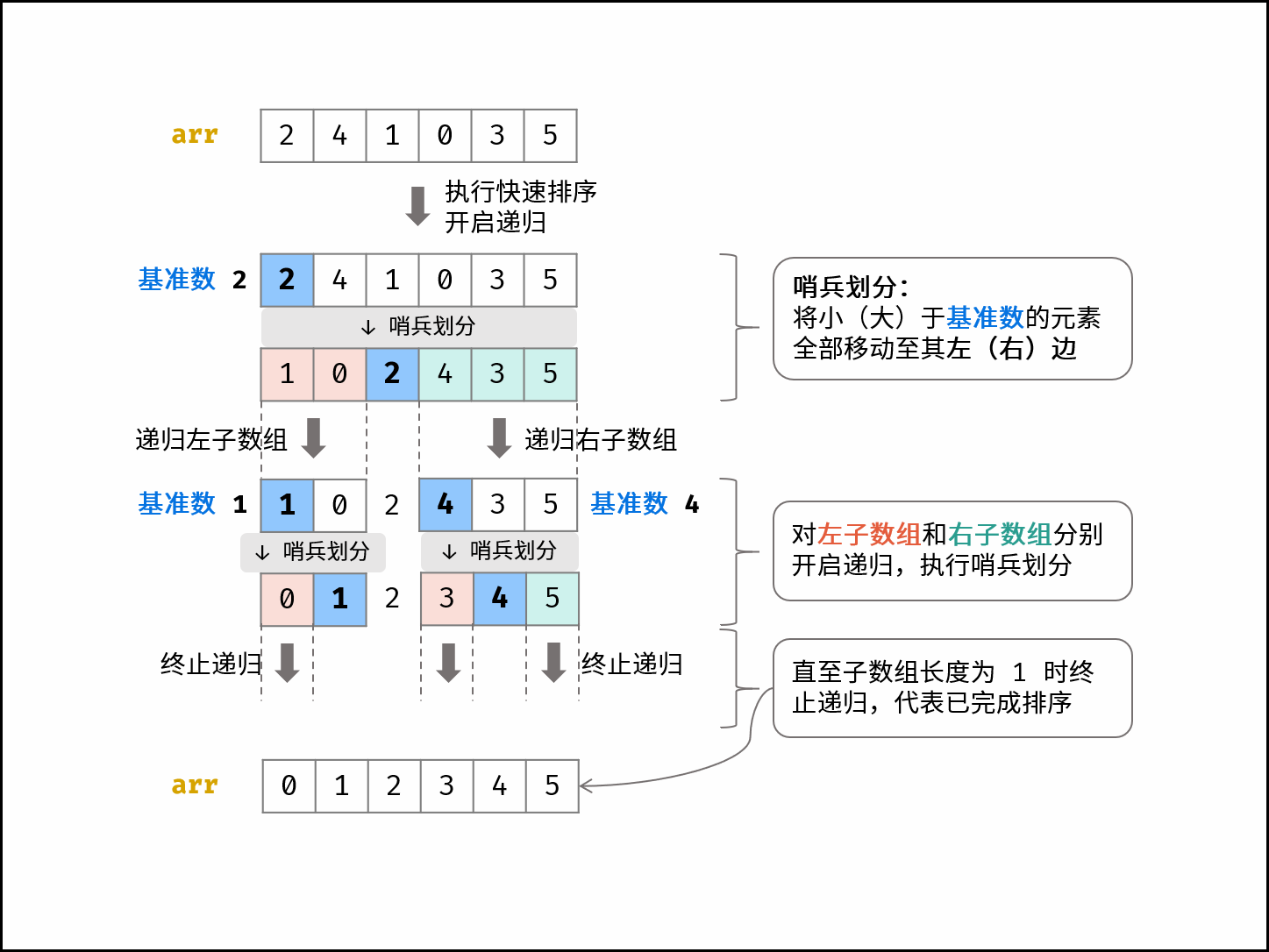![Picture1.png](https://pic.leetcode-cn.com/1612615552-rifQwI-Picture1.png){:width=550}
## 代码
```Python []
def quick_sort(nums, l, r):
# 子数组长度为 1 时终止递归
if l >= r: return
# 哨兵划分操作
i = partition(nums, l, r)
# 递归左（右）子数组执行哨兵划分
quick_sort(nums, l, i - 1)
quick_sort(nums, i + 1, r)
def partition(nums, l, r):
# 以 nums[l] 作为基准数
i, j = l, r
while i < j:
while i < j and nums[j] >= nums[l]: j -= 1
while i < j and nums[i] <= nums[l]: i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[l], nums[i] = nums[i], nums[l]
return i
# 调用
nums = [3, 4, 1, 5, 2]
quick_sort(nums, 0, len(nums) - 1)
```
```Java []
void quickSort(int[] nums, int l, int r) {
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作
int i = partition(nums, l, r);
// 递归左（右）子数组执行哨兵划分
quickSort(nums, l, i - 1);
quickSort(nums, i + 1, r);
}
int partition(int[] nums, int l, int r) {
// 以 nums[l] 作为基准数
int i = l, j = r;
while (i < j) {
while (i < j && nums[j] >= nums[l]) j--;
while (i < j && nums[i] <= nums[l]) i++;
swap(nums, i, j);
}
swap(nums, i, l);
return i;
}
void swap(int[] nums, int i, int j) {
// 交换 nums[i] 和 nums[j]
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
// 调用
int[] nums = { 4, 1, 3, 2, 5 };
quickSort(nums, 0, nums.length - 1);
```
```C++ []
int partition(vector<int>& nums, int l, int r) {
// 以 nums[l] 作为基准数
int i = l, j = r;
while (i < j) {
while (i < j && nums[j] >= nums[l]) j--;
while (i < j && nums[i] <= nums[l]) i++;
swap(nums[i], nums[j]);
}
swap(nums[i], nums[l]);
return i;
}
void quickSort(vector<int>& nums, int l, int r) {
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作
int i = partition(nums, l, r);
// 递归左（右）子数组执行哨兵划分
quickSort(nums, l, i - 1);
quickSort(nums, i + 1, r);
}
// 调用
vector<int> nums = { 4, 1, 3, 2, 5, 1 };
quickSort(nums, 0, nums.size() - 1);
```
## 算法特性
- **时间复杂度：**
- **最佳 $\Omega(N \log N )$ ：** 最佳情况下， 每轮哨兵划分操作将数组划分为等长度的两个子数组；哨兵划分操作为线性时间复杂度 $O(N)$ ；递归轮数共 $O(\log N)$ 。
- **平均 $\Theta(N \log N)$ ：** 对于随机输入数组，哨兵划分操作的递归轮数也为 $O(\log N)$ 。
- **最差 $O(N^2)$ ：** 对于某些特殊输入数组，每轮哨兵划分操作都将长度为 $N$ 的数组划分为长度为 $1$ 和 $N - 1$ 的两个子数组，此时递归轮数达到 $N$ 。
> 通过 「随机选择基准数」优化，可尽可能避免出现最差情况，详情请见下文。
- **空间复杂度 $O(N)$ ：** 快速排序的递归深度最好与平均皆为 $\log N$ ；输入数组完全倒序下，达到最差递归深度 $N$ 。
> 通过「尾递归」优化，可将最差空间复杂度降低至 $O(\log N)$ ，详情请见下文。
- 虽然平均时间复杂度与「归并排序」和「堆排序」一致，但在实际使用中快速排序 **效率更高** ，这是因为：
- **最差情况稀疏性：** 虽然快速排序的最差时间复杂度为 $O(N^2)$ ，差于归并排序和堆排序，但统计意义上看，这种情况出现的机率很低。大部分情况下，快速排序以 $O(N \log N)$ 复杂度运行。
- **缓存使用效率高：** 哨兵划分操作时，将整个子数组加载入缓存中，访问元素效率很高；堆排序需要跳跃式访问元素，因此不具有此特性。
- **常数系数低：** 在提及的三种算法中，快速排序的 **比较**、**赋值**、**交换** 三种操作的综合耗时最低（类似于插入排序快于冒泡排序的原理）。
- **原地：** 不用借助辅助数组的额外空间，递归仅使用 $O(\log N)$ 大小的栈帧空间。
- **非稳定：** 哨兵划分操作可能改变相等元素的相对顺序。
- **自适应：** 对于极少输入数据，每轮哨兵划分操作都将长度为 $N$ 的数组划分为长度 $1$ 和 $N - 1$ 两个子数组，此时时间复杂度劣化至 $O(N^2)$ 。
## 算法优化
快速排序的常见优化手段有「尾递归」和「随机基准数」两种。
### 尾递归：
由于普通快速排序每轮选取「子数组最左元素」作为「基准数」，因此在输入数组 **完全倒序** 时， `partition()` 的递归深度会达到 $N$ ，即 **最差空间复杂度** 为 $O(N)$ 。
每轮递归时，仅对 **较短的子数组** 执行哨兵划分 `partition()` ，就可将最差的递归深度控制在 $O(\log N)$ （每轮递归的子数组长度都 $\leq$ 当前数组长度 $/ 2$ ），即实现最差空间复杂度 $O(\log N)$ 。
> 代码仅需修改 `quick_sort()` 方法，其余方法不变，在此省略。
```Python []
def quick_sort(nums, l, r):
# 子数组长度为 1 时终止递归
while l < r:
# 哨兵划分操作
i = partition(nums, l, r)
# 仅递归至较短子数组，控制递归深度
if i - l < r - i:
quick_sort(nums, l, i - 1)
l = i + 1
else:
quick_sort(nums, i + 1, r)
r = i - 1
```
```Java []
void quickSort(int[] nums, int l, int r) {
// 子数组长度为 1 时终止递归
while (l < r) {
// 哨兵划分操作
int i = partition(nums, l, r);
// 仅递归至较短子数组，控制递归深度
if (i - l < r - i) {
quickSort(nums, l, i - 1);
l = i + 1;
} else {
quickSort(nums, i + 1, r);
r = i - 1;
}
}
}
```
```C++ []
void quickSort(vector<int>& nums, int l, int r) {
// 子数组长度为 1 时终止递归
while (l < r) {
// 哨兵划分操作
int i = partition(nums, l, r);
// 仅递归至较短子数组，控制递归深度
if (i - l < r - i) {
quickSort(nums, l, i - 1);
l = i + 1;
} else {
quickSort(nums, i + 1, r);
r = i - 1;
}
}
}
```
### 随机基准数：
同样地，由于快速排序每轮选取「子数组最左元素」作为「基准数」，因此在输入数组 **完全有序** 或 **完全倒序** 时， `partition()` 每轮只划分一个元素，达到最差时间复杂度 $O(N^2)$ 。
因此，可使用 **随机函数** ，每轮在子数组中随机选择一个元素作为基准数，这样就可以极大概率避免以上劣化情况。
值得注意的是，由于仍然可能出现最差情况，因此快速排序的最差时间复杂度仍为 $O(N^2)$ 。
> 代码仅需修改 `partition()` 方法，其余方法不变，在此省略。
```Python []
def partition(nums, l, r):
# 在闭区间 [l, r] 随机选取任意索引，并与 nums[l] 交换
ra = random.randrange(l, r + 1)
nums[l], nums[ra] = nums[ra], nums[l]
# 以 nums[l] 作为基准数
i, j = l, r
while i < j:
while i < j and nums[j] >= nums[l]: j -= 1
while i < j and nums[i] <= nums[l]: i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[l], nums[i] = nums[i], nums[l]
return i
```
```Java []
int partition(int[] nums, int l, int r) {
// 在闭区间 [l, r] 随机选取任意索引，并与 nums[l] 交换
int ra = (int)(l + Math.random() * (r - l + 1));
swap(nums, l, ra);
// 以 nums[l] 作为基准数
int i = l, j = r;
while (i < j) {
while (i < j && nums[j] >= nums[l]) j--;
while (i < j && nums[i] <= nums[l]) i++;
swap(nums, i, j);
}
swap(nums, i, l);
return i;
}
```
```C++ []
int partition(vector<int>& nums, int l, int r) {
// 在闭区间 [l, r] 随机选取任意索引，并与 nums[l] 交换
int ra = l + rand() % (r - l + 1);
swap(nums[l], nums[ra]);
// 以 nums[l] 作为基准数
int i = l, j = r;
while (i < j) {
while (i < j && nums[j] >= nums[l]) j--;
while (i < j && nums[i] <= nums[l]) i++;
swap(nums[i], nums[j]);
}
swap(nums[i], nums[l]);
return i;
}
```

130
leetbook_ioa/docs/# 7.4 归并排序.md Executable file
View File

@@ -0,0 +1,130 @@
# 归并排序
归并排序体现了 “分而治之” 的算法思想，具体为：
- **「分」：** 不断将数组从 **中点位置** 划分开，将原数组的排序问题转化为子数组的排序问题；
- **「治」：** 划分到子数组长度为 1 时，开始向上合并，不断将 **左右两个较短排序数组** 合并为 **一个较长排序数组**，直至合并至原数组时完成排序；
> 如下图所示，为数组 `[7,3,2,6,0,1,5,4]` 的归并排序过程。
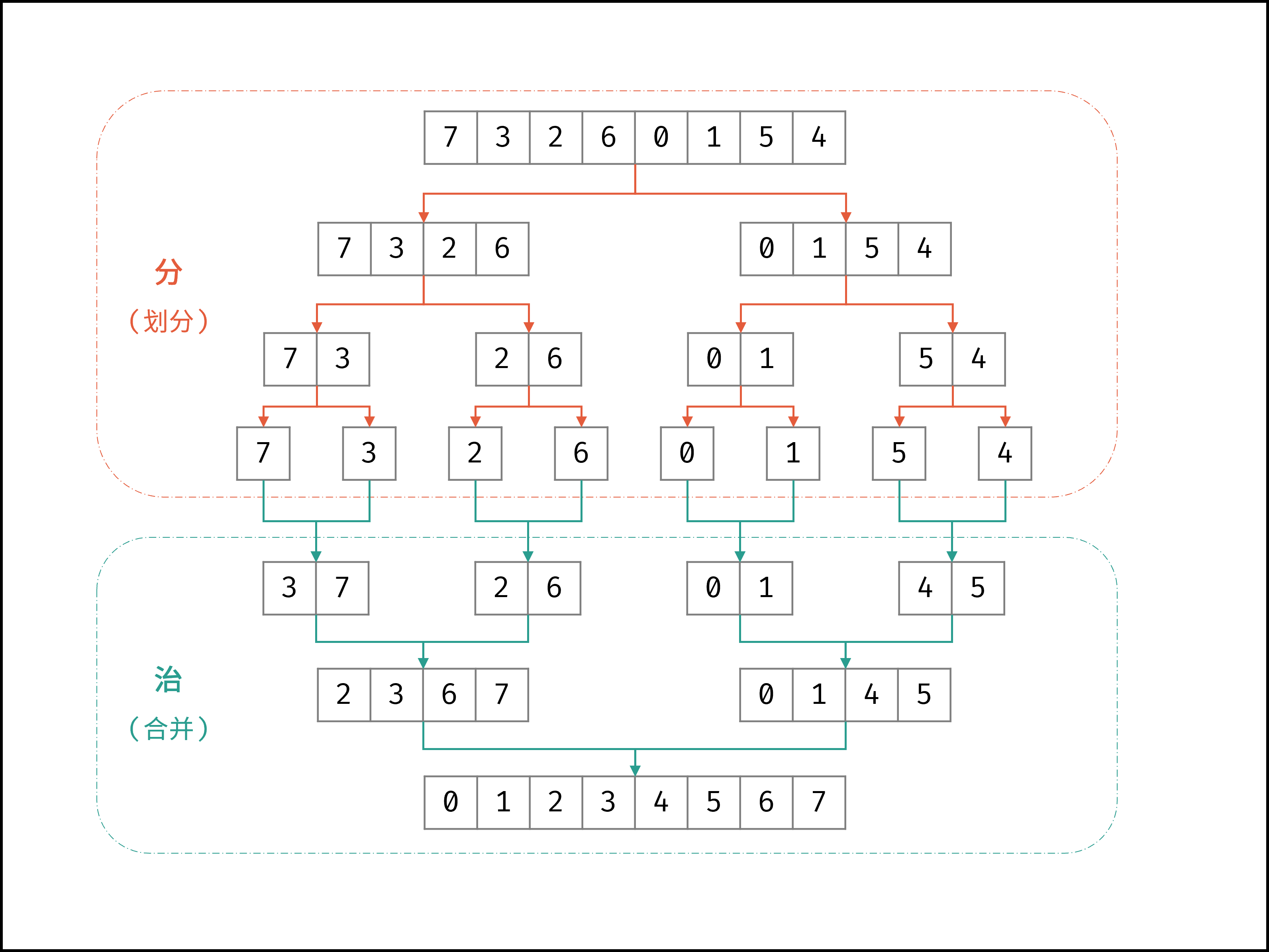![Picture1.png](https://pic.leetcode-cn.com/1632675739-CNHaOu-Picture1.png){:width=500}
## 算法流程
1. **递归划分：**
1. 计算数组中点 $m$ ，递归划分左子数组 `merge_sort(l, m)` 和右子数组 `merge_sort(m + 1, r)` ；
2. 当 $l \geq r$ 时，代表子数组长度为 1 或 0 ，此时 **终止划分** ，开始合并；
2. **合并子数组：**
1. 暂存数组 $nums$ 闭区间 $[l, r]$ 内的元素至辅助数组 $tmp$ ；
2. **循环合并：** 设置双指针 $i$ , $j$ 分别指向 $tmp$ 的左 / 右子数组的首元素；
> **注意：** $nums$ 子数组的左边界、中点、右边界分别为 $l$ , $m$ , $r$ ，而辅助数组 $tmp$ 中的对应索引为 $0$ , $m - l$ , $r - l$ ；
- **当 $i == m - l + 1$ 时：** 代表左子数组已合并完，因此添加右子数组元素 $tmp[j]$ ，并执行 $j = j + 1$ ；
- **否则，当 $j == r - l + 1$ 时：** 代表右子数组已合并完，因此添加左子数组元素 $tmp[i]$ ，并执行 $i = i + 1$ ；
- **否则，当 $tmp[i] \leq tmp[j]$ 时：** 添加左子数组元素 $tmp[i]$ ，并执行 $i = i + 1$ ；
- **否则（即当 $tmp[i] > tmp[j]$ 时）：** 添加右子数组元素 $tmp[j]$ ，并执行 $j = j + 1$ ；
> 如下动图所示，为数组 `[7,3,2,6]` 的归并排序过程。
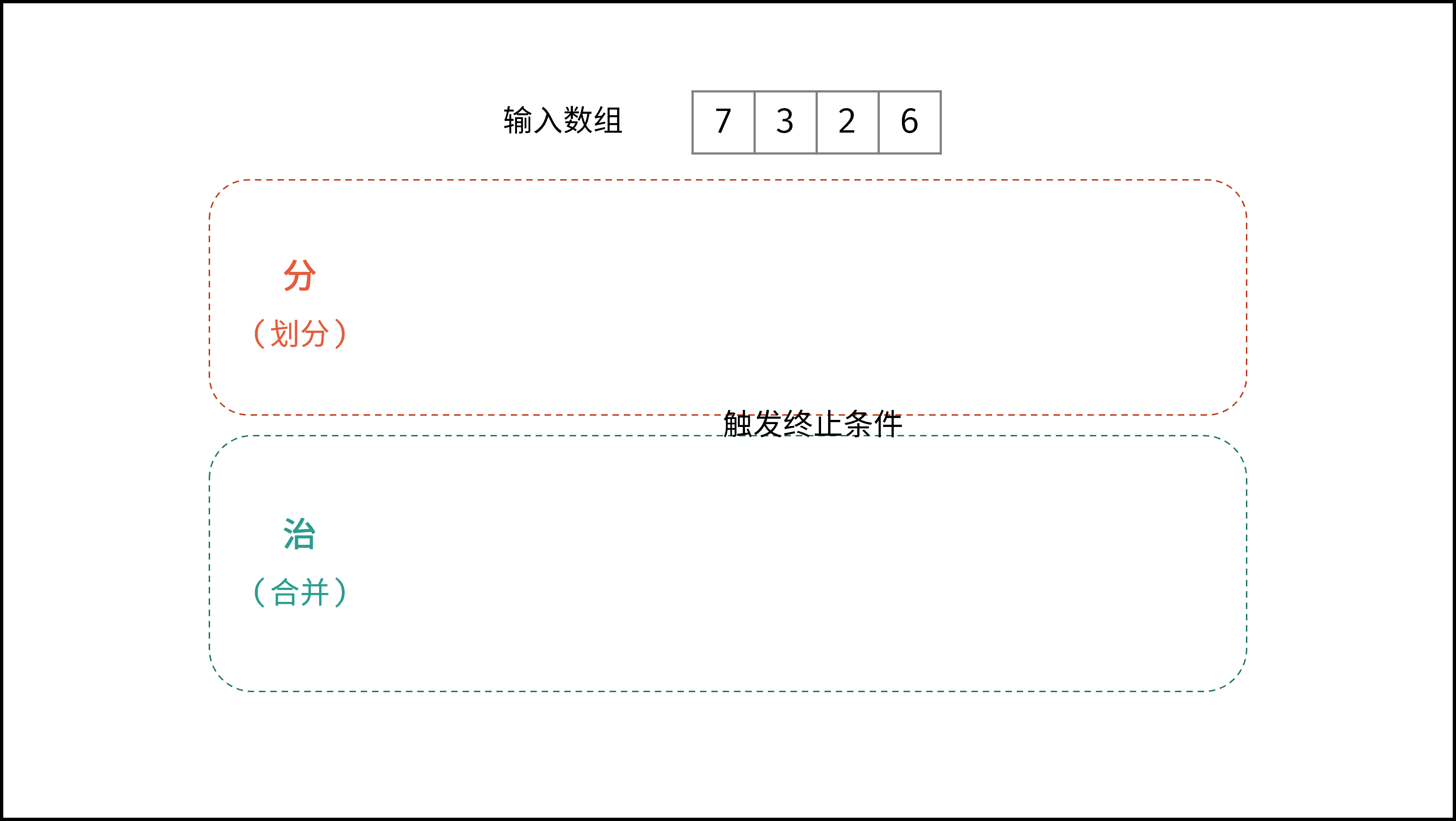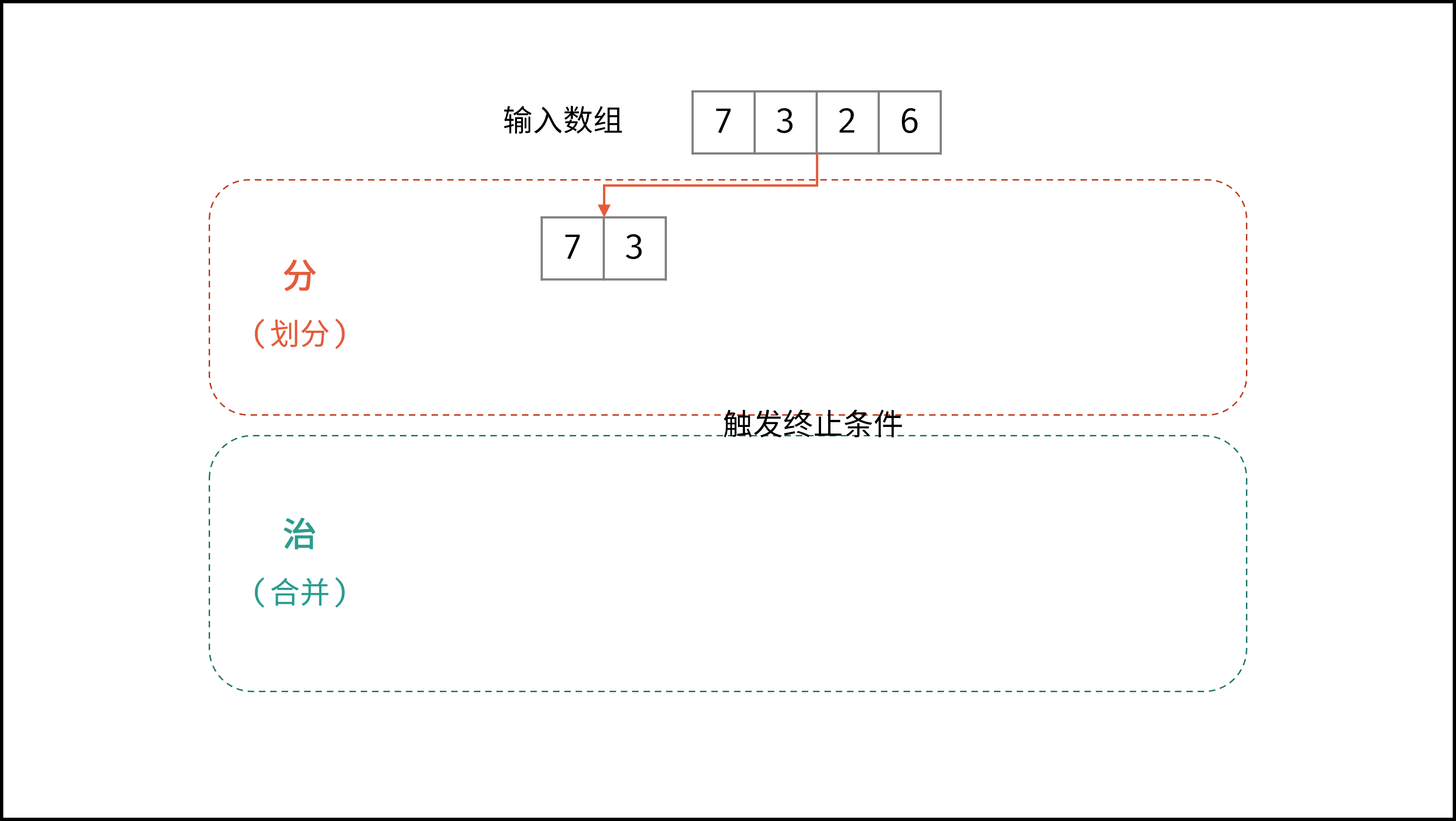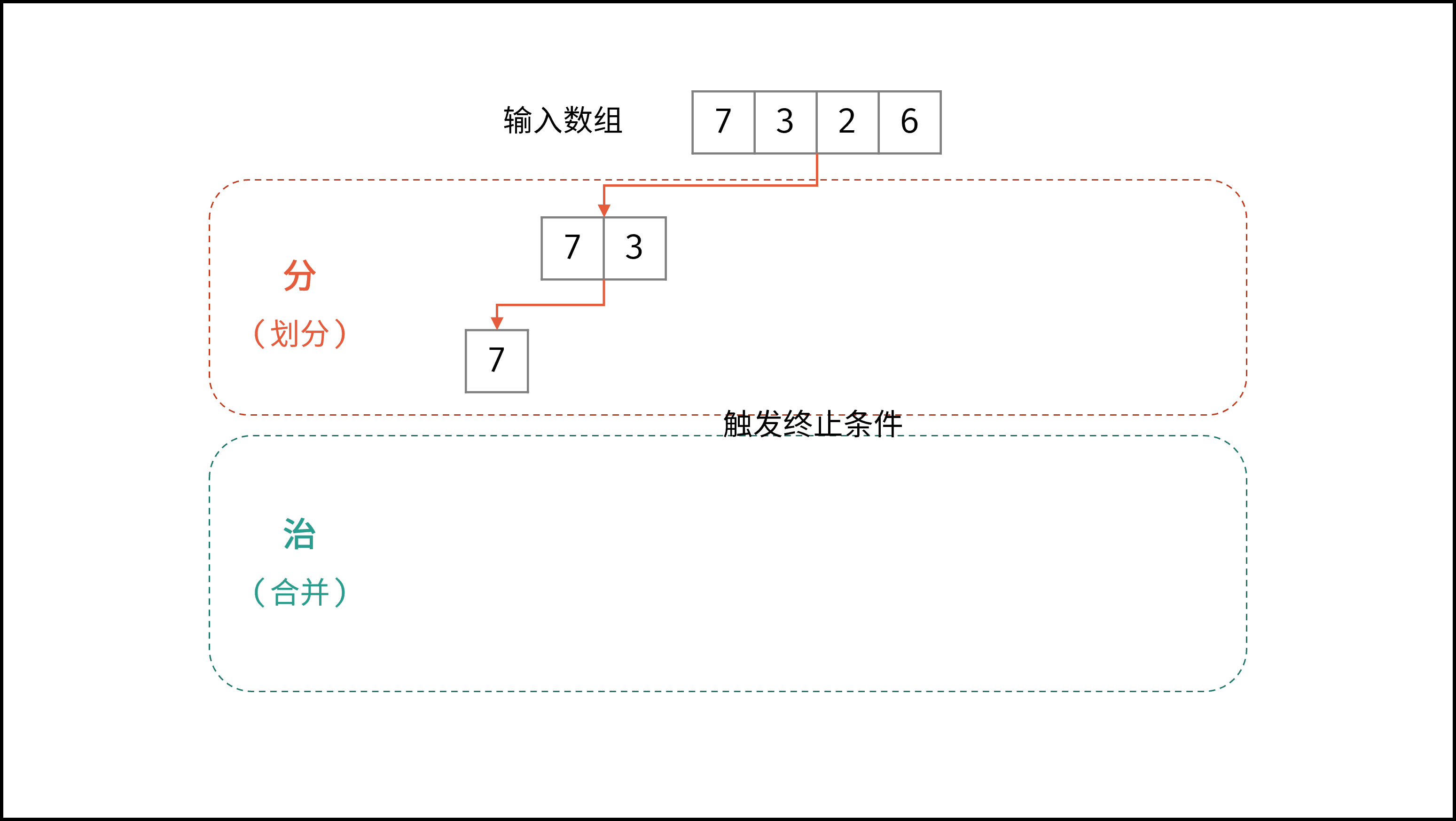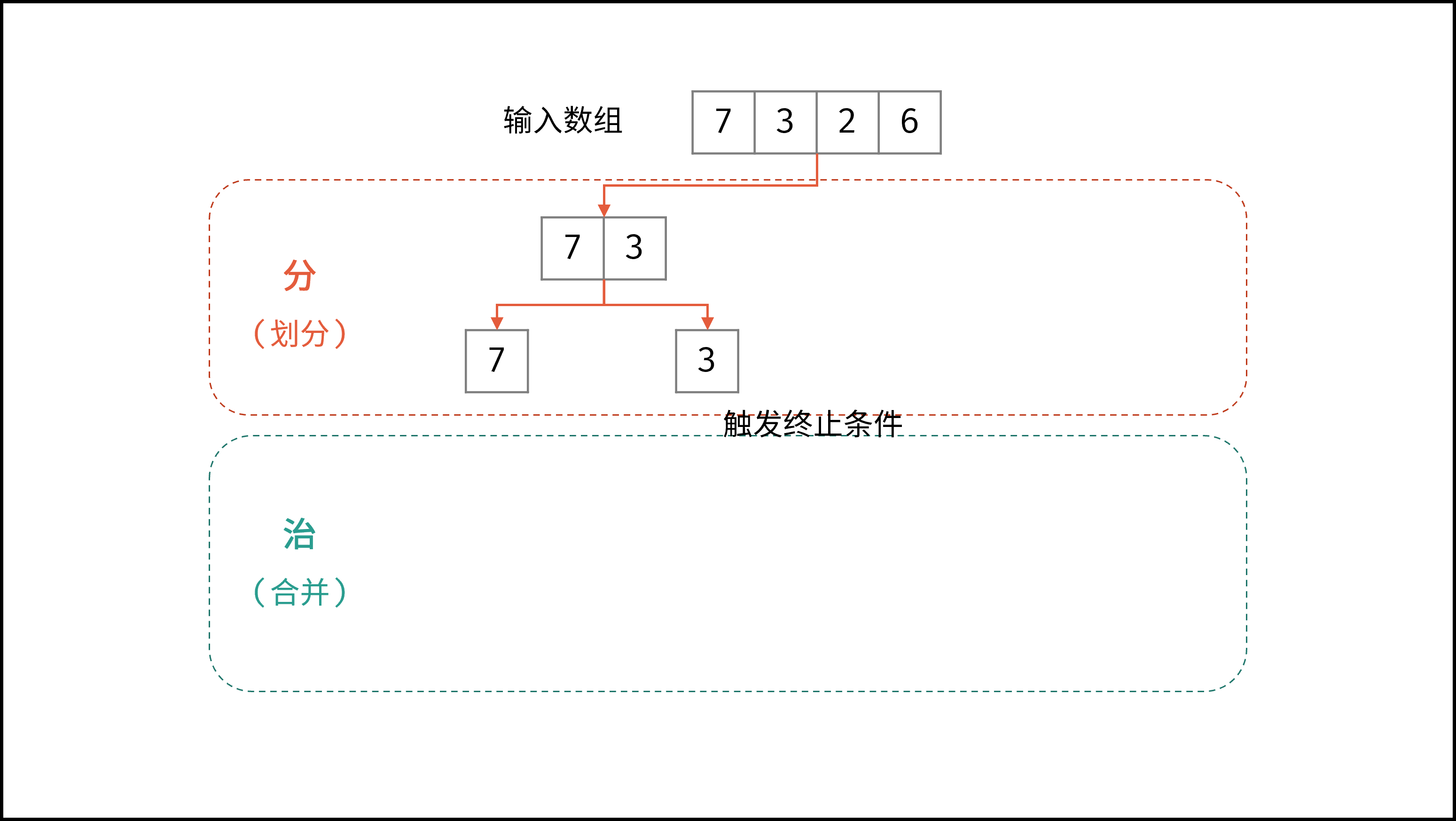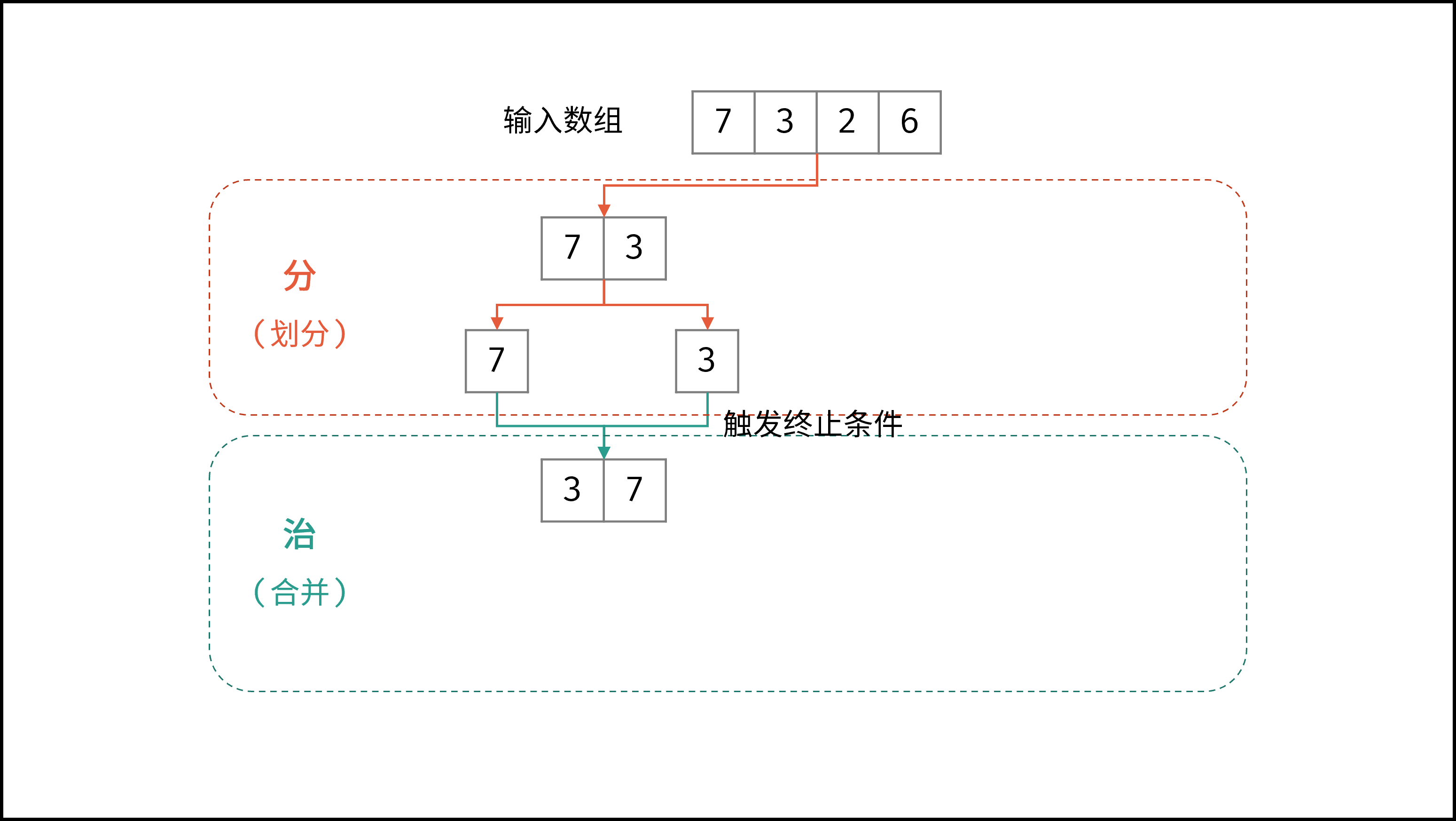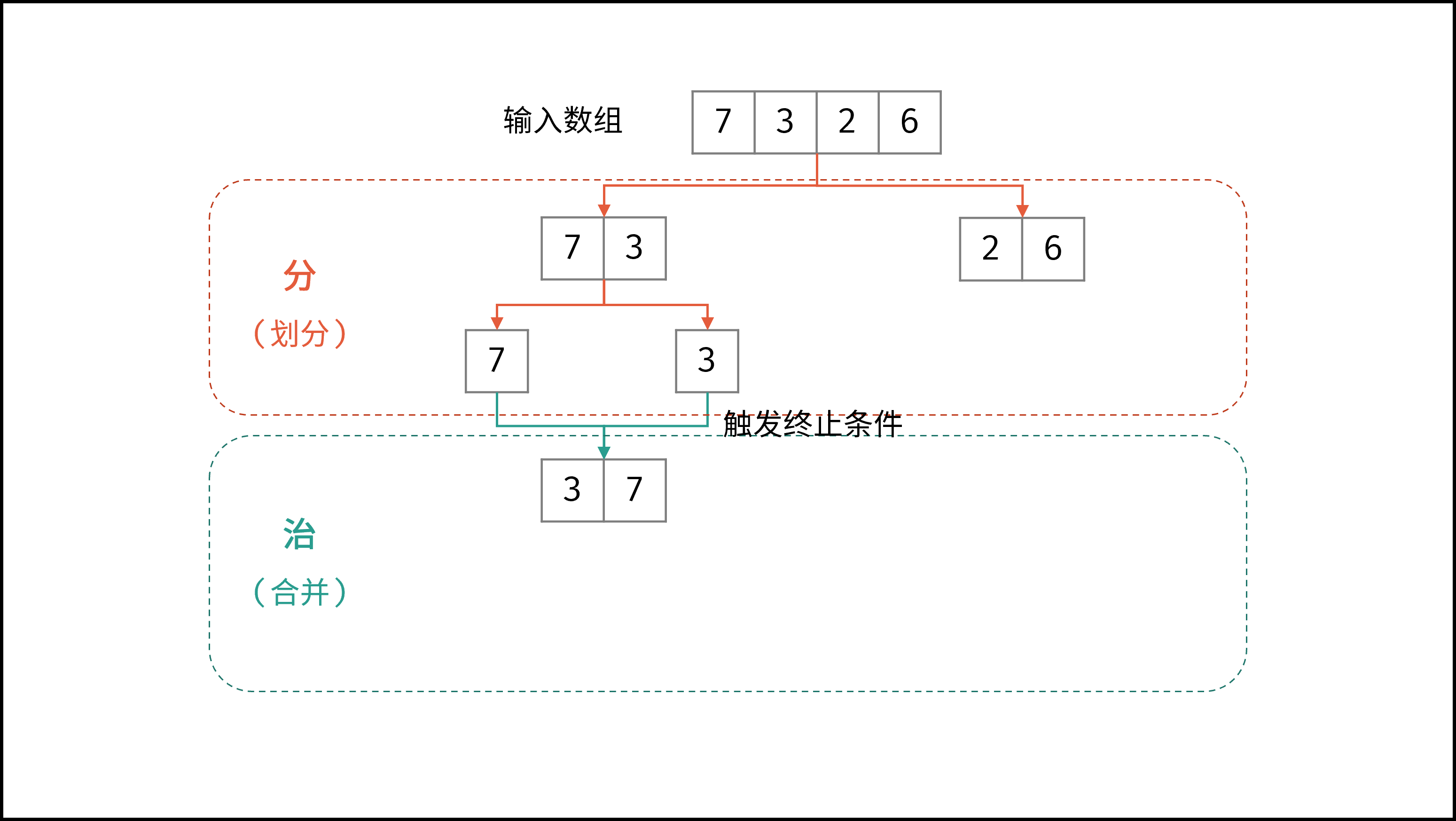<![Picture2.png](https://pic.leetcode-cn.com/1632675858-cJeqUR-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1632675727-PPgpZZ-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1632675727-UVoxsJ-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1632675727-dfjbJY-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1632675727-UJRCIE-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1632675727-YDhFvj-Picture7.png),![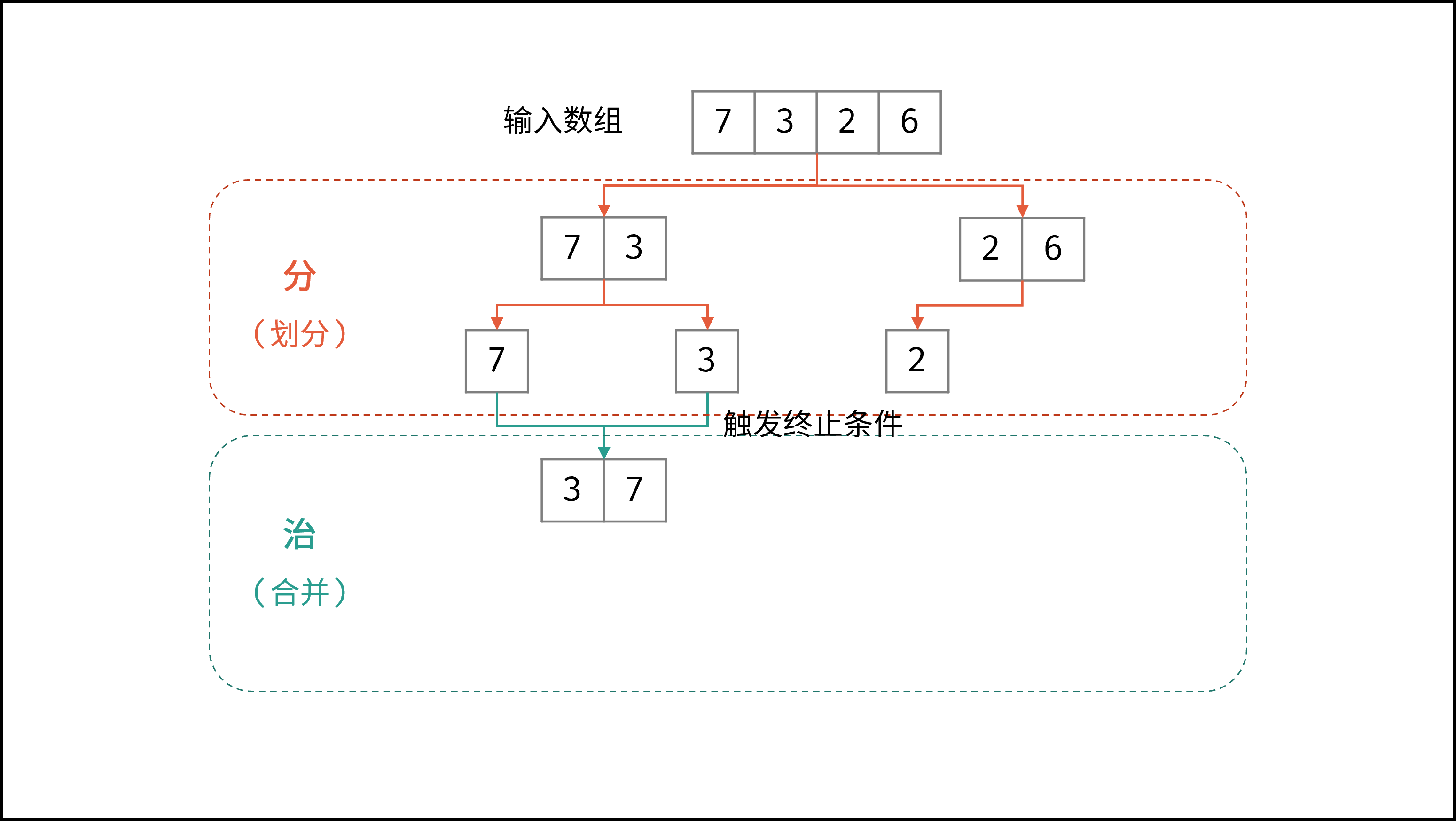Picture8.png](https://pic.leetcode-cn.com/1632675727-hjJlql-Picture8.png),![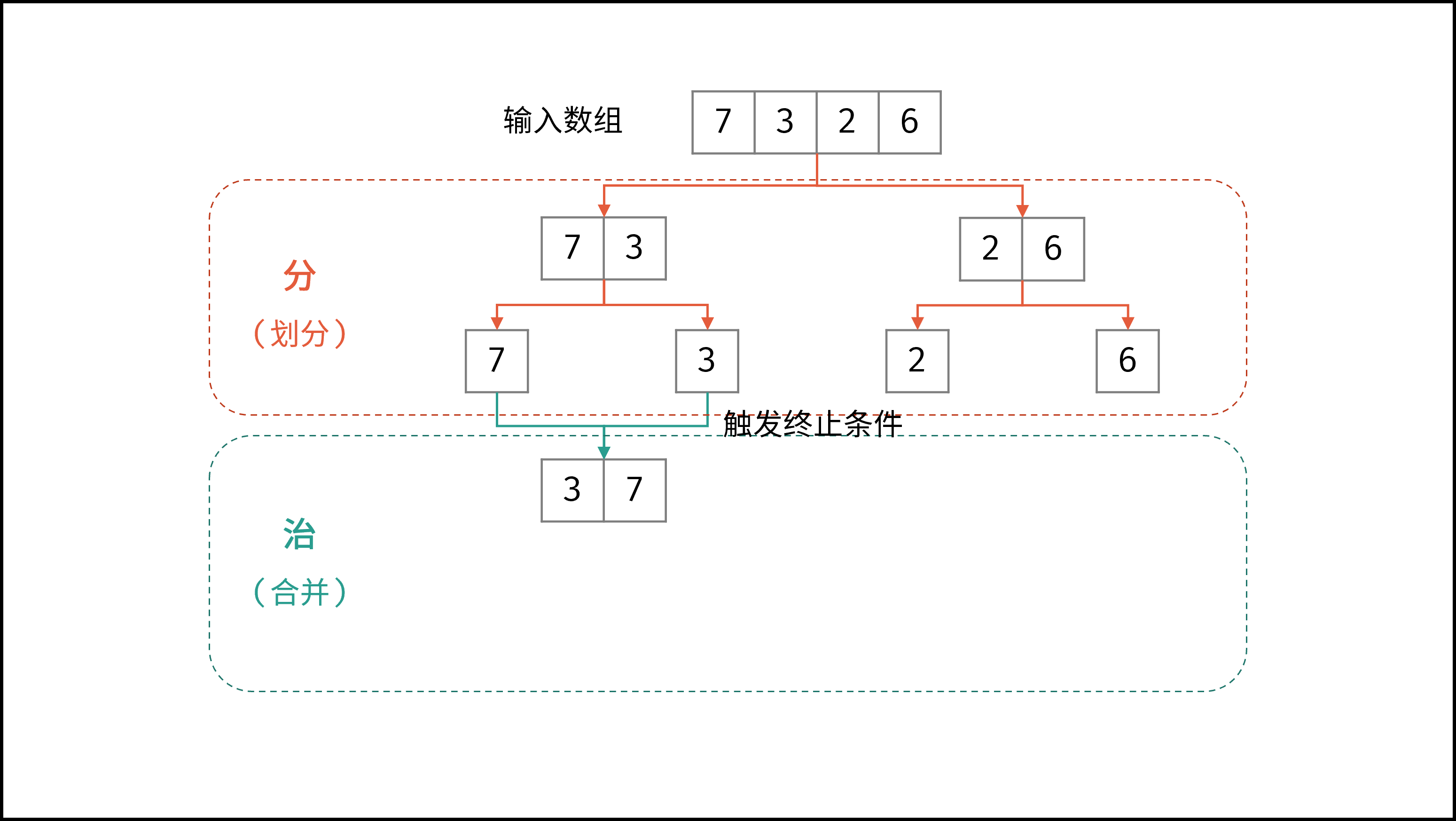Picture9.png](https://pic.leetcode-cn.com/1632675727-FYTodg-Picture9.png),![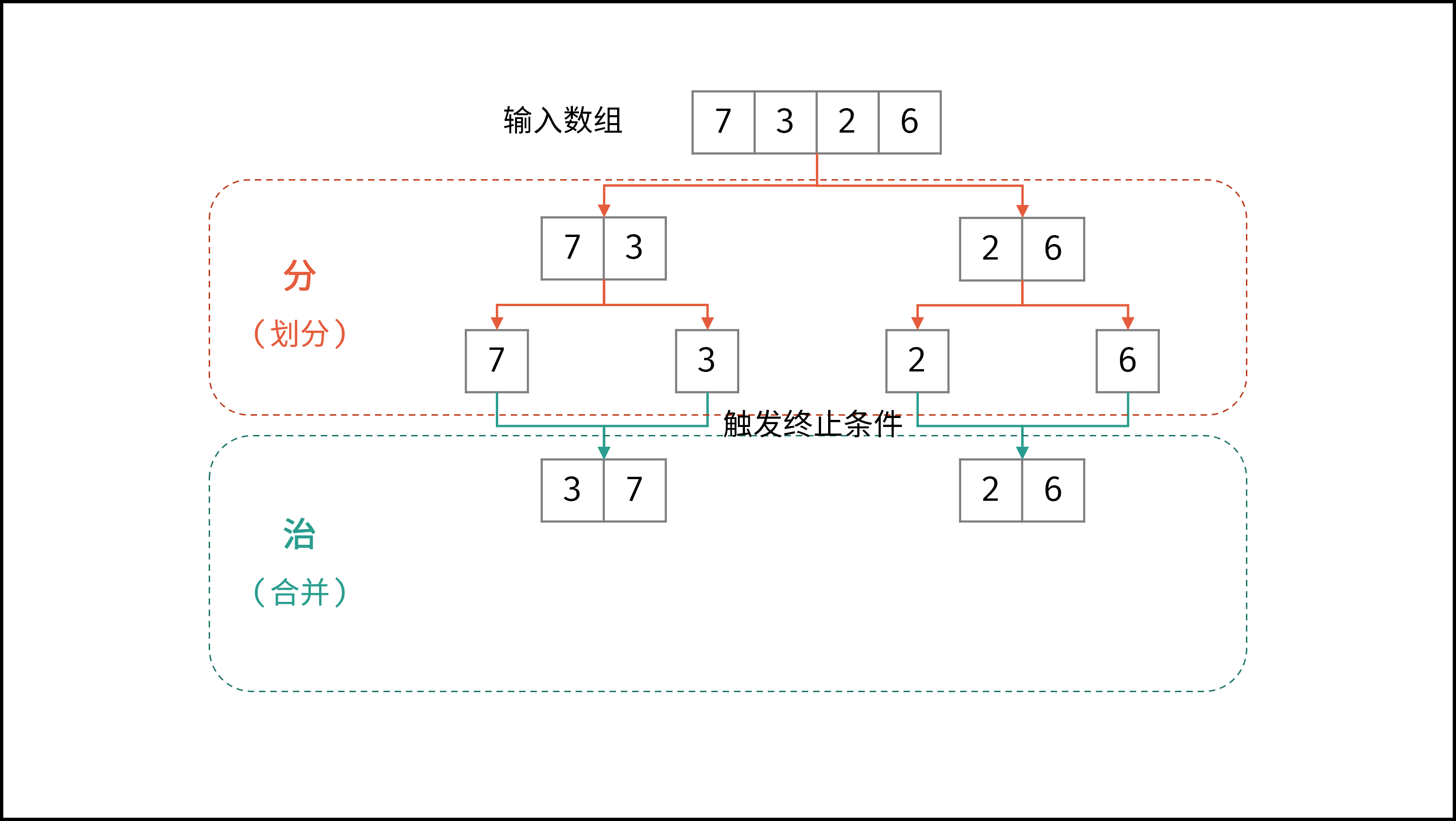Picture10.png](https://pic.leetcode-cn.com/1632675727-dAGnBR-Picture10.png),![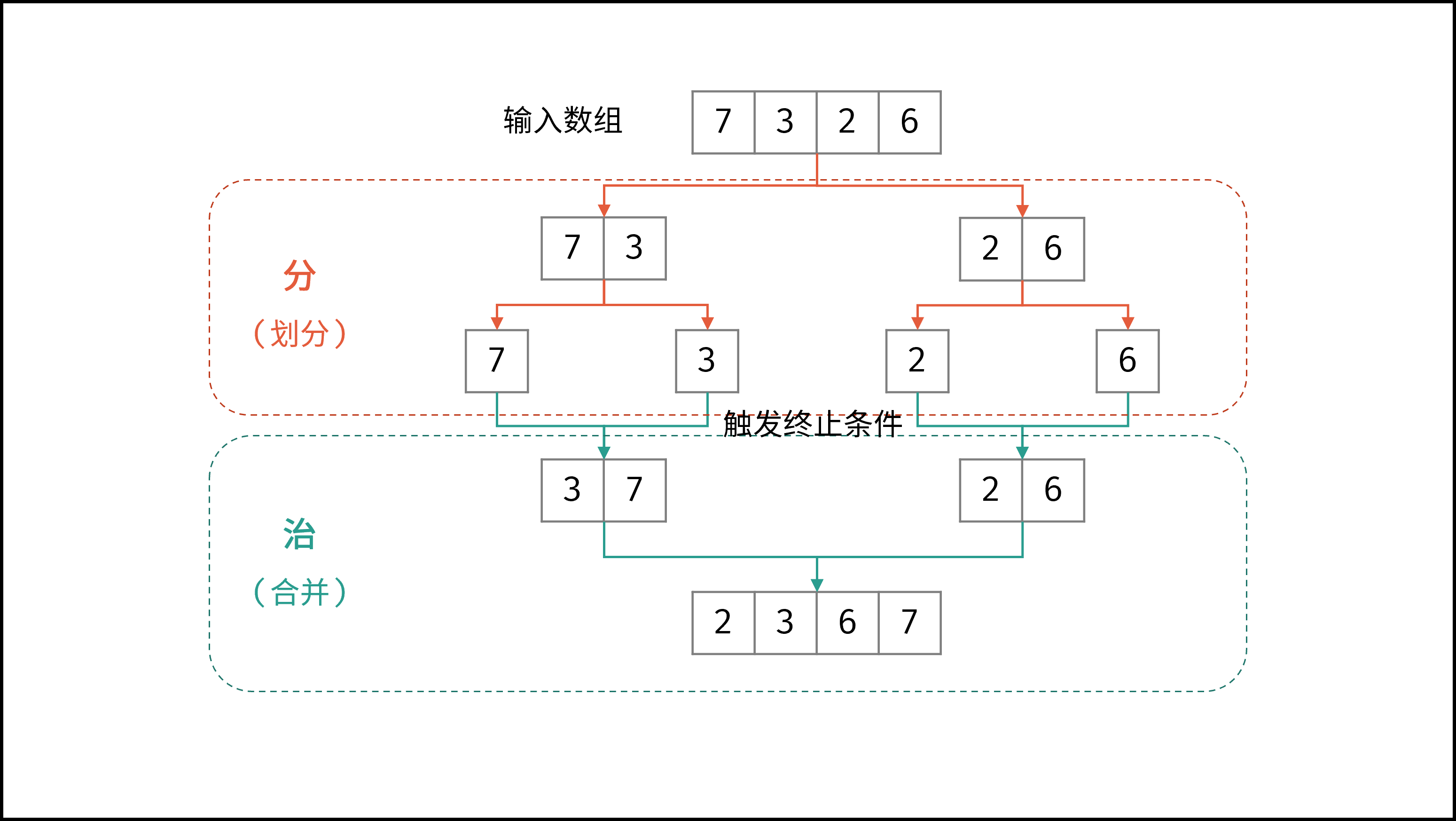Picture11.png](https://pic.leetcode-cn.com/1632675727-VVDNmq-Picture11.png)>
## 代码
为简化代码，「当 $j = r + 1$ 时」 与 「当 $tmp[i] \leq tmp[j]$ 时」 两判断项可合并。
```Python []
def merge_sort(nums, l, r):
# 终止条件
if l >= r: return
# 递归划分数组
m = (l + r) // 2
merge_sort(nums, l, m)
merge_sort(nums, m + 1, r)
# 合并子数组
tmp = nums[l:r + 1] # 暂存需合并区间元素
i, j = 0, m - l + 1 # 两指针分别指向左/右子数组的首个元素
for k in range(l, r + 1): # 遍历合并左/右子数组
if i == m - l + 1:
nums[k] = tmp[j]
j += 1
elif j == r - l + 1 or tmp[i] <= tmp[j]:
nums[k] = tmp[i]
i += 1
else:
nums[k] = tmp[j]
j += 1
# 调用
nums = [3, 4, 1, 5, 2, 1]
merge_sort(0, len(nums) - 1)
```
```Java []
void mergeSort(int[] nums, int l, int r) {
// 终止条件
if (l >= r) return;
// 递归划分
int m = (l + r) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, r);
// 合并子数组
int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
for (int k = l; k <= r; k++)
tmp[k - l] = nums[k];
int i = 0, j = m - l + 1; // 两指针分别指向左/右子数组的首个元素
for (int k = l; k <= r; k++) { // 遍历合并左/右子数组
if (i == m - l + 1)
nums[k] = tmp[j++];
else if (j == r - l + 1 || tmp[i] <= tmp[j])
nums[k] = tmp[i++];
else {
nums[k] = tmp[j++];
}
}
}
// 调用
int[] nums = { 3, 4, 1, 5, 2, 1 };
mergeSort(nums, 0, len(nums) - 1);
```
```C++ []
void mergeSort(vector<int>& nums, int l, int r) {
// 终止条件
if (l >= r) return;
// 递归划分
int m = (l + r) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, r);
// 合并阶段
int tmp[r - l + 1]; // 暂存需合并区间元素
for (int k = l; k <= r; k++)
tmp[k - l] = nums[k];
int i = 0, j = m - l + 1; // 两指针分别指向左/右子数组的首个元素
for (int k = l; k <= r; k++) { // 遍历合并左/右子数组
if (i == m - l + 1)
nums[k] = tmp[j++];
else if (j == r - l + 1 || tmp[i] <= tmp[j])
nums[k] = tmp[i++];
else {
nums[k] = tmp[j++];
}
}
}
// 调用
vector<int> nums = { 4, 1, 3, 2, 5, 1 };
mergeSort(nums, 0, nums.size() - 1);
```
## 算法特性
- **时间复杂度：** 最佳 $\Omega(N \log N )$ ，平均 $\Theta(N \log N)$ ，最差 $O(N \log N)$ 。
- **空间复杂度 $O(N)$ ：** 合并过程中需要借助辅助数组 $tmp$ ，使用 $O(N)$ 大小的额外空间；划分的递归深度为 $\log N$ ，使用 $O(\log N)$ 大小的栈帧空间。
- 若输入数据是 **链表** ，则归并排序的空间复杂度可被优化至 $O(1)$ ，这是因为：
- 通过应用「双指针法」，可在 $O(1)$ 空间下完成两个排序链表的合并，省去辅助数组 $tmp$ 使用的额外空间；
- 通过使用「迭代」代替「递归划分」，可省去递归使用的栈帧空间；
> 详情请参考：[148. 排序链表](https://leetcode-cn.com/problems/sort-list/solution/sort-list-gui-bing-pai-xu-lian-biao-by-jyd/)
- **非原地：** 辅助数组 $tmp$ 需要使用额外空间。
- **稳定：** 归并排序不改变相等元素的相对顺序。
- **非自适应：** 对于任意输入数据，归并排序的时间复杂度皆相同。

140
leetbook_ioa/docs/LCR 120. 寻找文件副本.md Executable file
View File

@@ -0,0 +1,140 @@
## 方法一：哈希表
利用数据结构特点，容易想到使用哈希表（Set）记录数组的各个数字，当查找到重复数字则直接返回。
### 算法流程：
1. 初始化： 新建 HashSet ，记为 $hmap$ ；
2. 遍历数组 $documents$ 中的每个数字 $doc$ ：
1. 当 $doc$ 在 $hmap$ 中，说明重复，直接返回 $doc$ ；
2. 将 $doc$ 添加至 $hmap$ 中；
3. 返回 $-1$ 。本题中一定有重复数字，因此这里返回多少都可以。
> 下图中的 `nums` 对应本题的 `documents` 。
<![Picture1.png](https://pic.leetcode-cn.com/b73933d9cafbbed2d3b3cc3353f2ef7e9af2614d623c7e87f7bc6d8fbaf27f40-Picture1.png),![Picture2.png](https://pic.leetcode-cn.com/e97aa100bcab08166e04da36bc9f3537d2cde0f7cc4e027e12b4765fd3c0f042-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/3e40c3d2c2d5b36522d7884c685029720dffb787d4c2dd12b70596d4cedf8120-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/b5a77688e2c989573786fa7b6b1b30026f9ffe0070d0b1760cf8931573545462-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/29528f65ea95425b032c3039a8c80d9e2ae4f9cac89eef3a8c19bfc668abb546-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/23d093dbd8fd248e9075fbee511483adaef103fb072d18eec3a8d3d00c870512-Picture6.png)>
### 代码：
```Python []
class Solution:
def findRepeatDocument(self, documents: List[int]) -> int:
hmap = set()
for doc in documents:
if doc in hmap: return doc
hmap.add(doc)
return -1
```
```Java []
class Solution {
public int findRepeatDocument(int[] documents) {
Set<Integer> hmap = new HashSet<>();
for(int doc : documents) {
if(hmap.contains(doc)) return doc;
hmap.add(doc);
}
return -1;
}
}
```
```C++ []
class Solution {
public:
int findRepeatDocument(vector<int>& documents) {
unordered_map<int, bool> map;
for(int doc : documents) {
if(map[doc]) return doc;
map[doc] = true;
}
return -1;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 遍历数组使用 $O(N)$ ，HashSet 添加与查找元素皆为 $O(1)$ 。
- **空间复杂度 $O(N)$ ：** HashSet 占用 $O(N)$ 大小的额外空间。
## 方法二：原地交换
题目说明尚未被充分使用，即 `在一个长度为 n 的数组 documents 里的所有数字都在 0 ~ n-1 的范围内` 。 此说明含义：数组元素的 **索引** 和 **值** 是 **一对多** 的关系。
因此，可遍历数组并通过交换操作，使元素的 **索引** 与 **值** 一一对应（即 $documents[i] = i$ ）。因而，就能通过索引映射对应的值，起到与字典等价的作用。
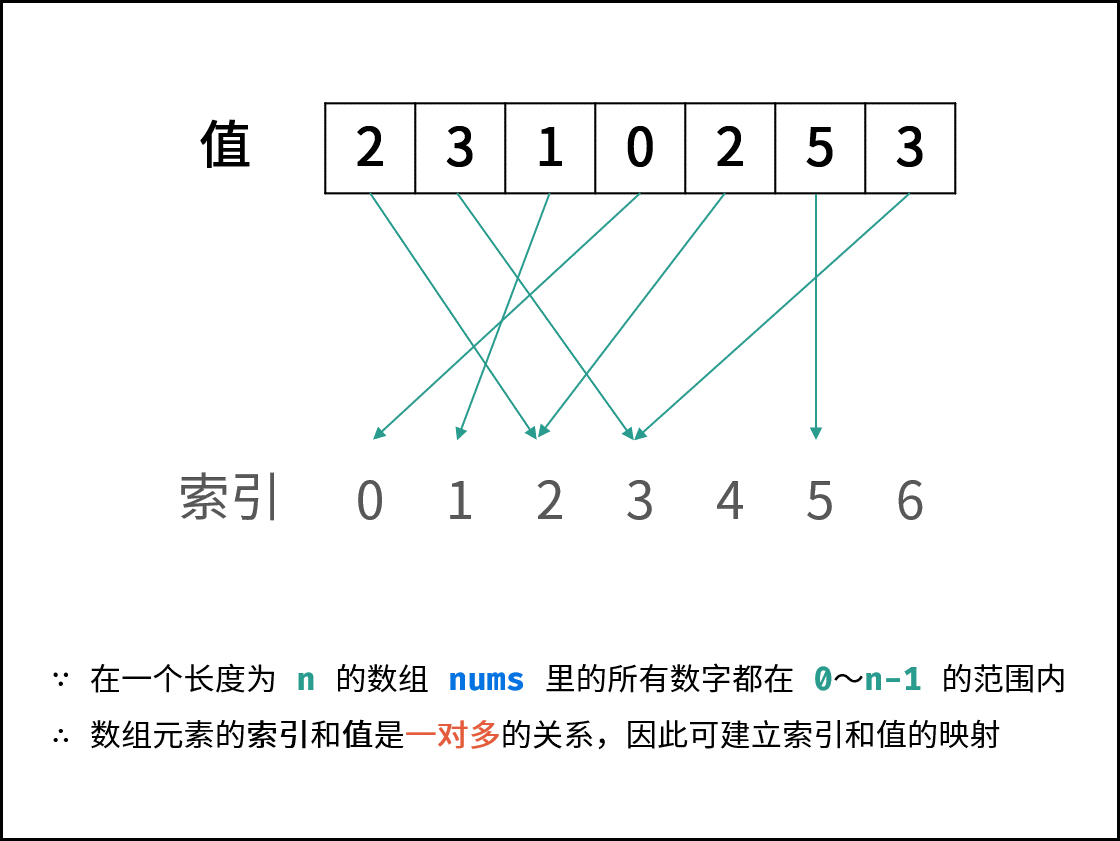![Picture0.png](https://pic.leetcode-cn.com/1618146573-bOieFQ-Picture0.png){:align=center width=500}
遍历中，第一次遇到数字 $x$ 时，将其交换至索引 $x$ 处；而当第二次遇到数字 $x$ 时，一定有 $documents[x] = x$ ，此时即可得到一组重复数字。
### 算法流程：
1. 遍历数组 $documents$ ，设索引初始值为 $i = 0$ :
1. **若 $documents[i] = i$ ：** 说明此数字已在对应索引位置，无需交换，因此跳过；
2. **若 $documents[documents[i]] = documents[i]$ ：** 代表索引 $documents[i]$ 处和索引 $i$ 处的元素值都为 $documents[i]$ ，即找到一组重复值，返回此值 $documents[i]$ ；
3. **否则：** 交换索引为 $i$ 和 $documents[i]$ 的元素值，将此数字交换至对应索引位置。
2. 若遍历完毕尚未返回，则返回 $-1$ 。
<![Picture7.png](https://pic.leetcode-cn.com/45a6303cd3ab50036a99ae89e2b0458f9b4885bb9d089997dfc0e5851a6a6300-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/58905a586575382e51096a5ce3e9e098ef8df215723174b4ac1d042e10a95c01-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/68a992b40bd5781a388c4fe811cd7a7c9b8dbb659089ed7473605323df76d241-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/98fd49b23dbb73cba6c551faaabfaaf5b3bbaed5f50f6c11ac42496bdfd2eba1-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/e6089e2d686fb1e76feb4f065ed14f7d2c02eadcdbfb6d4e2e9b6843f64914c3-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/80f2f1df8c43f56d63d09118fcb49c6c9d834aa743b01e9f8fd2b1ac9ce85403-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/64c97efd298d010e91b89eb18c7eb961538d6c1da400495c328dd92de3b47648-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/eaf0db1a4b0e0869d29fa789a234888d45dfffc5d1d13c5fb1c237a0b1bc5389-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/82ea50d1915609e368839cac6d4e0e615ff8297138aff645d0c2aba79e6a7b7e-Picture15.png)>
### 代码：
Python 中，$a, b = c, d$ 操作的原理是先暂存元组 $(c, d)$ ，然后 “按左右顺序” 赋值给 a 和 b 。
因此，若写为 $documents[i], documents[documents[i]] = documents[documents[i]], documents[i]$ ，则 $documents[i]$ 会先被赋值，之后 $documents[documents[i]]$ 指向的元素则会出错。
```Python []
class Solution:
def findRepeatDocument(self, documents: List[int]) -> int:
i = 0
while i < len(documents):
if documents[i] == i:
i += 1
continue
if documents[documents[i]] == documents[i]: return documents[i]
documents[documents[i]], documents[i] = documents[i], documents[documents[i]]
return -1
```
```Java []
class Solution {
public int findRepeatDocument(int[] documents) {
int i = 0;
while(i < documents.length) {
if(documents[i] == i) {
i++;
continue;
}
if(documents[documents[i]] == documents[i]) return documents[i];
int tmp = documents[i];
documents[i] = documents[tmp];
documents[tmp] = tmp;
}
return -1;
}
}
```
```C++ []
class Solution {
public:
int findRepeatDocument(vector<int>& documents) {
int i = 0;
while(i < documents.size()) {
if(documents[i] == i) {
i++;
continue;
}
if(documents[documents[i]] == documents[i])
return documents[i];
swap(documents[i],documents[documents[i]]);
}
return -1;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 遍历数组使用 $O(N)$ ，每轮遍历的判断和交换操作使用 $O(1)$ 。
- **空间复杂度 $O(1)$ ：** 使用常数复杂度的额外空间。

72
leetbook_ioa/docs/LCR 121. 寻找目标值 - 二维数组.md Executable file
View File

@@ -0,0 +1,72 @@
## 解题思路：
> 若使用暴力法遍历矩阵 `plants` ，则时间复杂度为 $O(NM)$ 。暴力法未利用矩阵 **“从上到下递增、从左到右递增”** 的特点，显然不是最优解法。
如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 **二叉搜索树** ，即对于每个元素，其左分支元素更小、右分支元素更大。
因此，考虑从 “根节点” 开始搜索，遇到比 `target` 大的元素就向左，反之向右，即可找到目标值 `target` 。
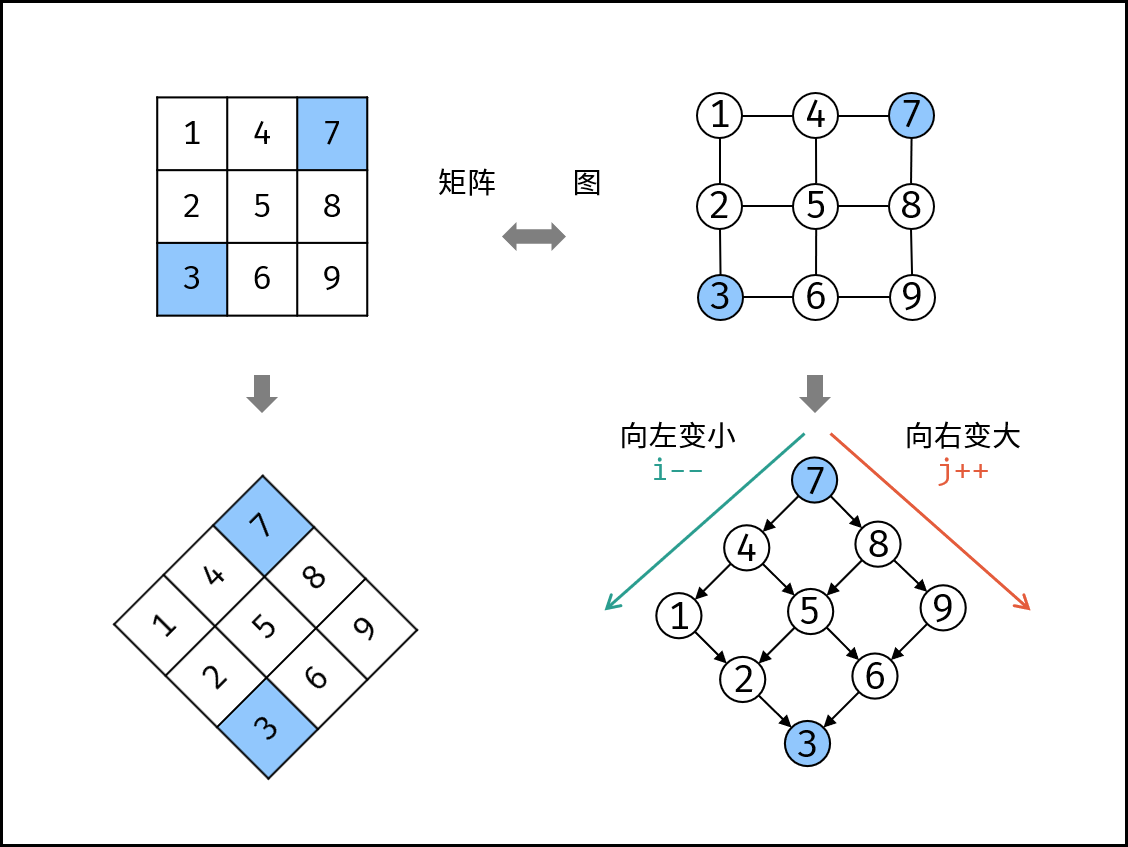![Picture1.png](https://pic.leetcode-cn.com/6584ea93812d27112043d203ea90e4b0950117d45e0452d0c630fcb247fbc4af-Picture1.png){:align=center width=450}
### 算法流程：
“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素。以 `plants` 中的 **左下角元素** 为起始点，则有:
1. 从矩阵 `plants` 左下角元素（索引设为 `(i, j)` ）开始遍历，并与目标值对比：
- 当 `plants[i][j] > target` 时，执行 `i--` ，即消去第 `i` 行元素；
- 当 `plants[i][j] < target` 时，执行 `j++` ，即消去第 `j` 列元素；
- 当 `plants[i][j] = target` 时，返回 $\text{true}$ ，代表找到目标值。
2. 若行索引或列索引越界，则代表矩阵中无目标值，返回 $\text{false}$ 。
> 每轮 `i` 或 `j` 移动后，相当于生成了“消去一行（列）的新矩阵”， 索引`(i,j)` 指向新矩阵的左下角元素，因此可重复使用以上性质消去行（列）。
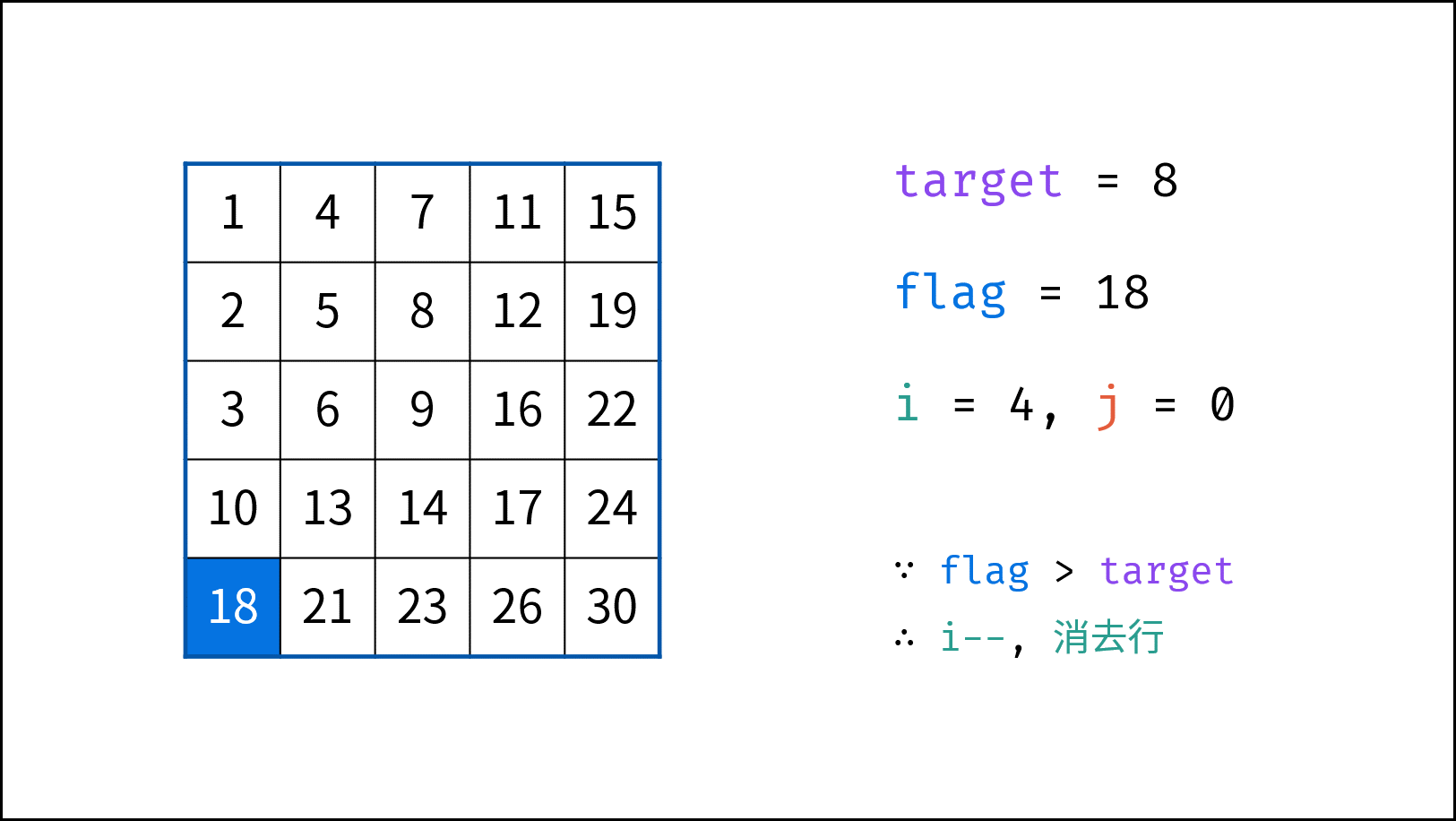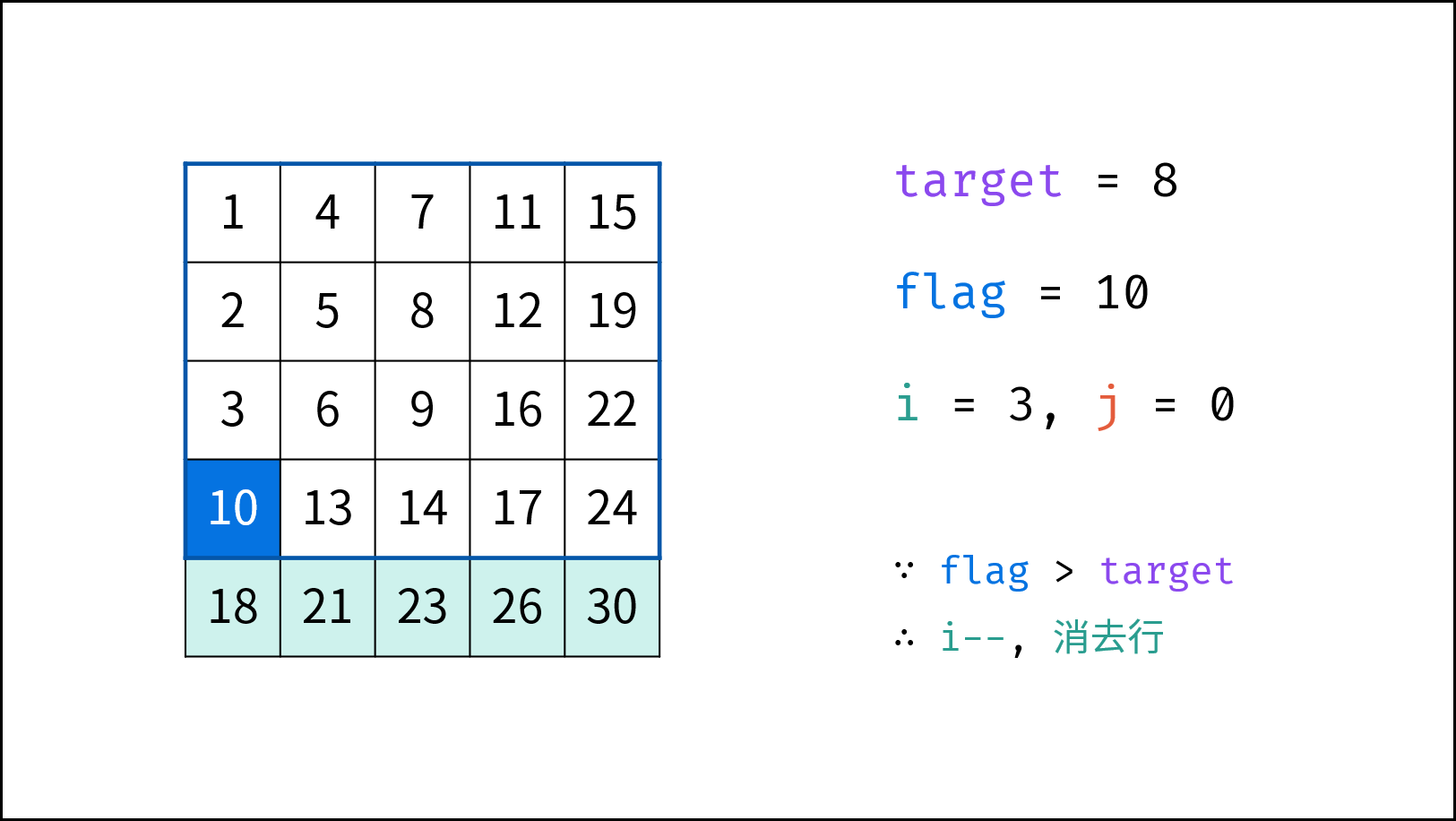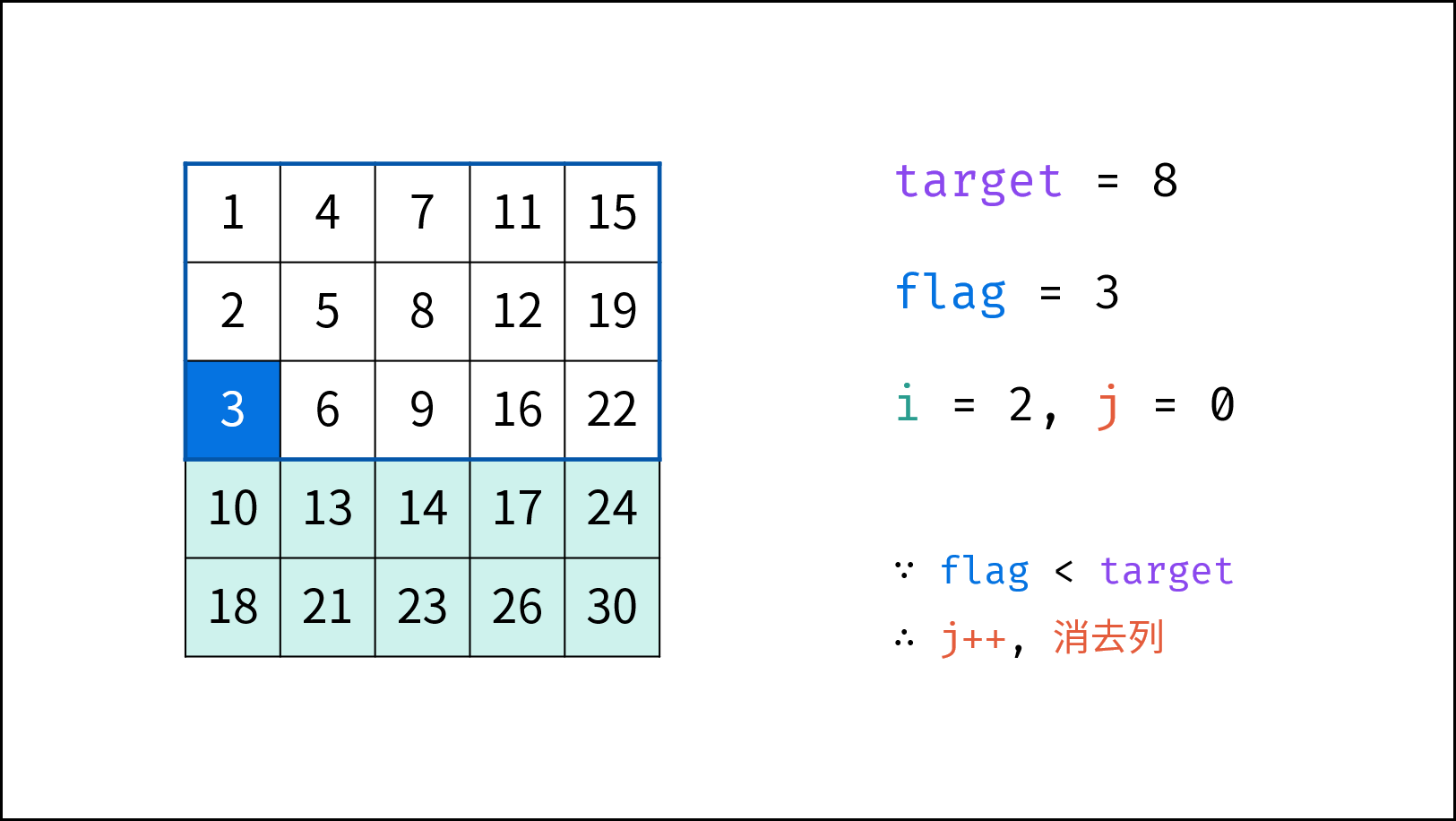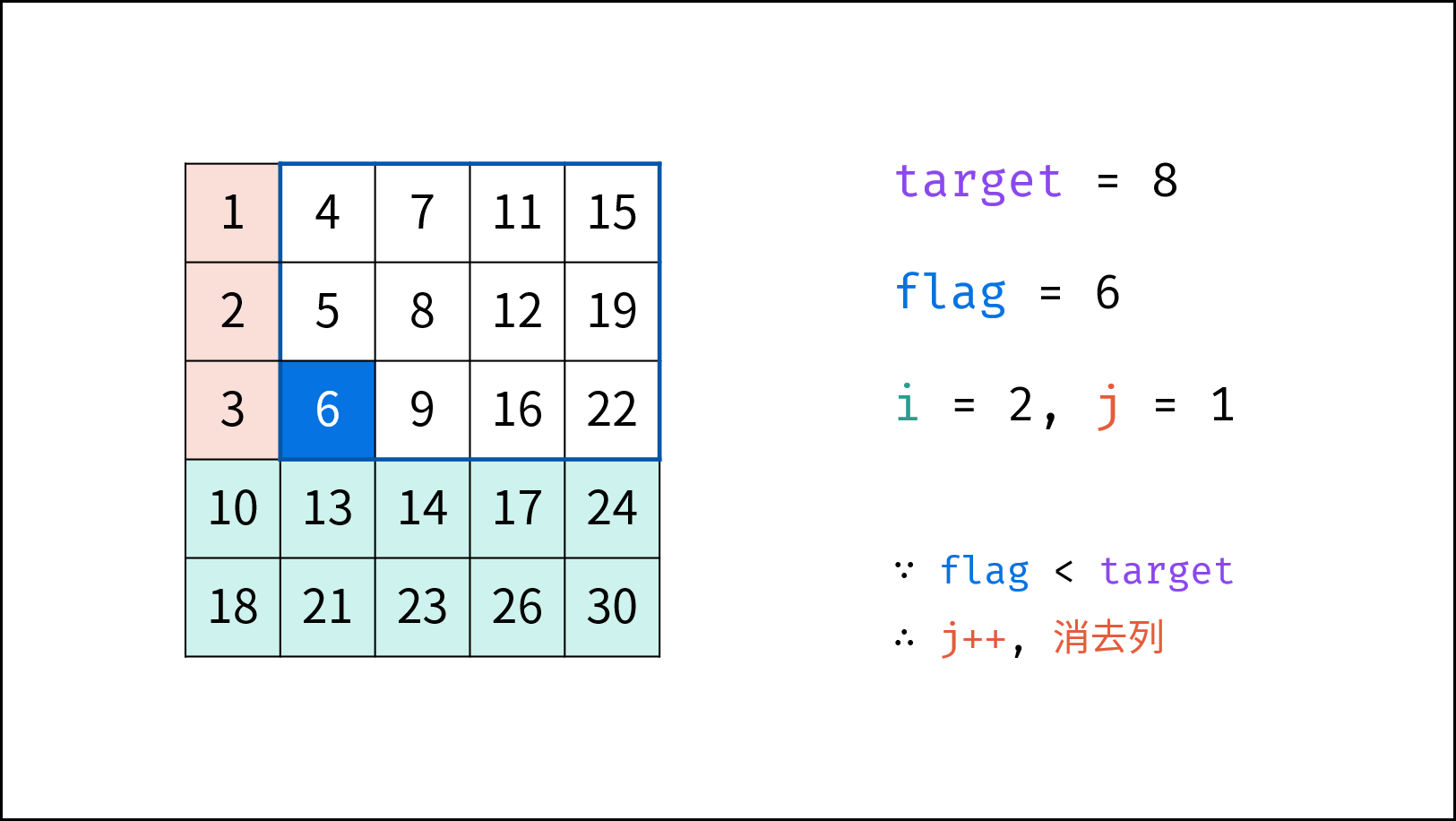<![Picture2.png](https://pic.leetcode-cn.com/6a083897417b51e94ed84e3483d334078d851e691eb8655b45432372ecdea9d6-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/c301ea07f6081e95d06c07cc23fb0419e67ffdd92c2511201f72c3f86f18c928-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/3f1f6c8af23c89cd3179f486cfb932322ea4fa08ab707dc5e20b9adb243278e9-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/533c0eba70d25e5f7a1930186389a38feae15a91eea771fd388edd1eecc0b129-Picture5.png),![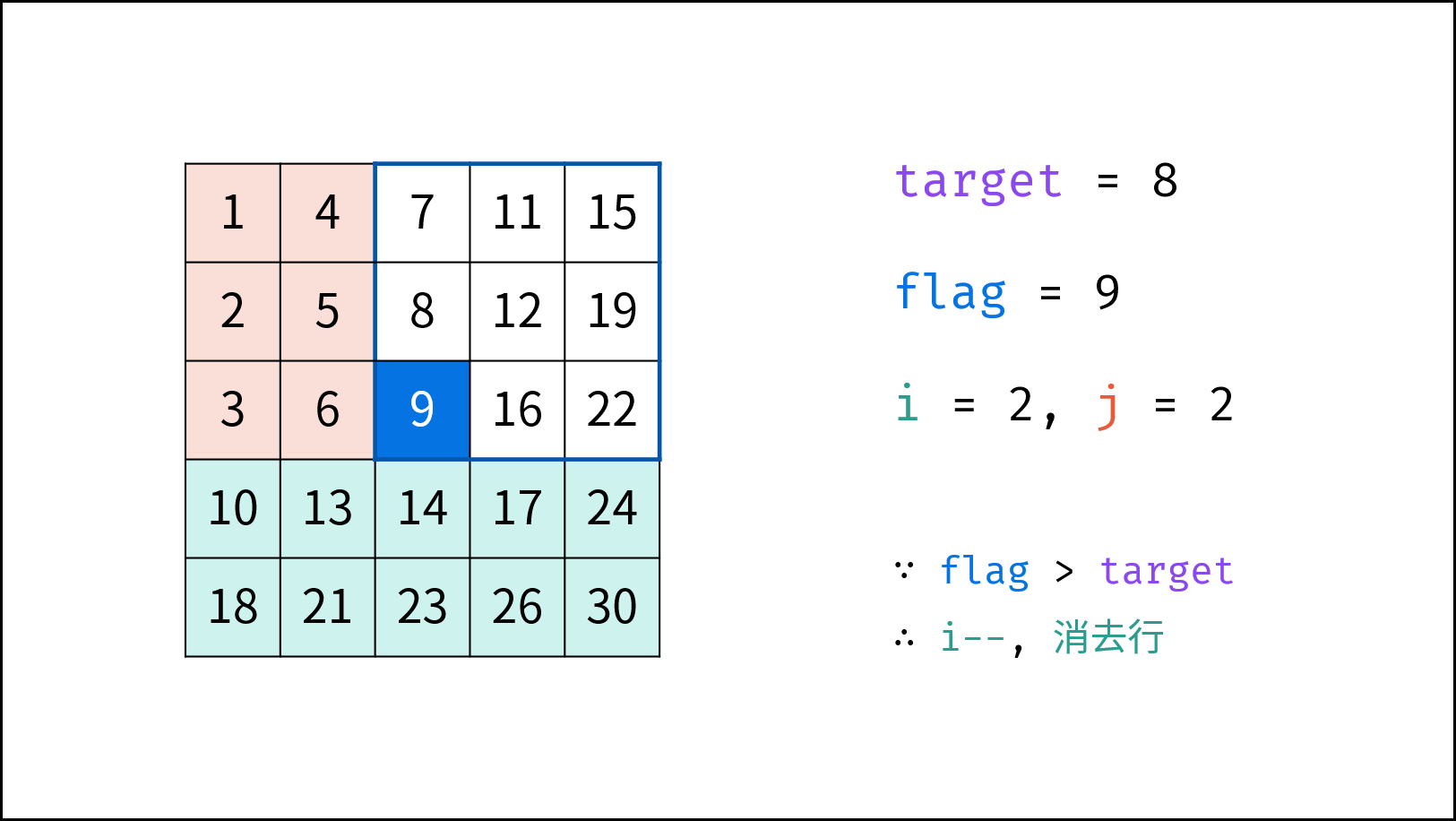Picture6.png](https://pic.leetcode-cn.com/116704601a28972d17b32cc641485a1ab707930504a720160e121b092e9f7084-Picture6.png),![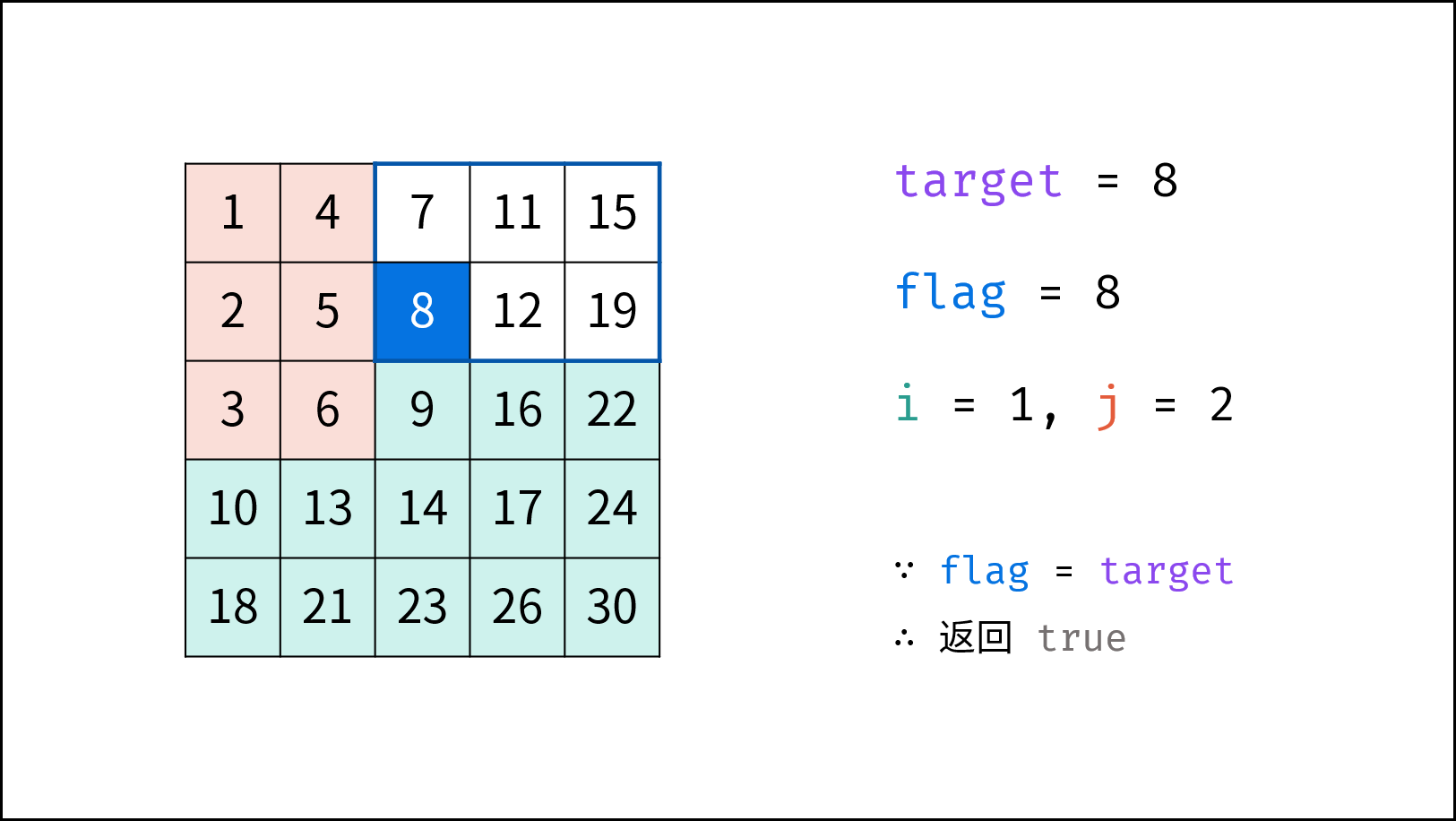Picture7.png](https://pic.leetcode-cn.com/7db0cca850374644eff397880d5cdb3be17a3558a306162955a7ffb31bbf4e5c-Picture7.png)>
## 代码：
```Python []
class Solution:
def findTargetIn2DPlants(self, plants: List[List[int]], target: int) -> bool:
i, j = len(plants) - 1, 0
while i >= 0 and j < len(plants[0]):
if plants[i][j] > target: i -= 1
elif plants[i][j] < target: j += 1
else: return True
return False
```
```Java []
class Solution {
public boolean findTargetIn2DPlants(int[][] plants, int target) {
int i = plants.length - 1, j = 0;
while(i >= 0 && j < plants[0].length)
{
if(plants[i][j] > target) i--;
else if(plants[i][j] < target) j++;
else return true;
}
return false;
}
}
```
```C++ []
class Solution {
public:
bool findTargetIn2DPlants(vector<vector<int>>& plants, int target) {
int i = plants.size() - 1, j = 0;
while(i >= 0 && j < plants[0].size())
{
if(plants[i][j] > target) i--;
else if(plants[i][j] < target) j++;
else return true;
}
return false;
}
};
```
### 复杂度分析：
- 时间复杂度 $O(M+N)$ ：其中，$N$ 和 $M$ 分别为矩阵行数和列数，此算法最多循环 $M+N$ 次。
- 空间复杂度 $O(1)$ : `i`, `j` 指针使用常数大小额外空间。

46
leetbook_ioa/docs/LCR 122. 路径加密.md Executable file
View File

@@ -0,0 +1,46 @@
## 方法一：遍历添加
在 Python 和 Java 等语言中，字符串都被设计成「不可变」的类型，即无法直接修改字符串的某一位字符，需要新建一个字符串实现。
### 算法流程：
1. 初始化一个 `list` (Python) 或 `StringBuilder` (Java) ，记为 `res` ；
2. 遍历列表 `path` 中的每个字符 `c` ：
- 当 `c` 为空格时：向 `res` 后添加空格 " " ；
- 当 `c` 不为空格时：向 `res` 后添加字符 `c` ；
3. 将列表 `res` 转化为字符串并返回。
> 下图中的 `s` 对应本题的 `path` 。
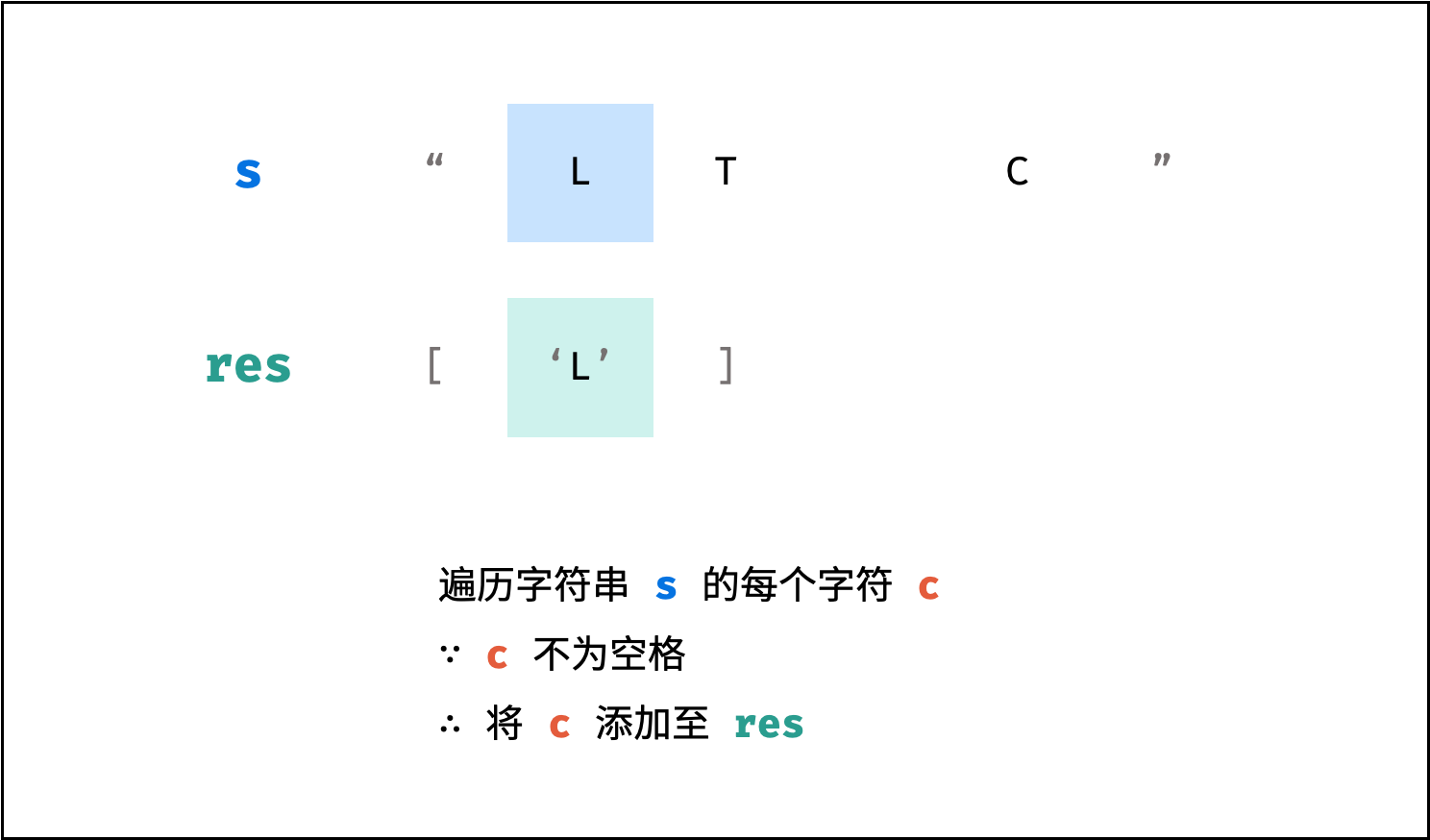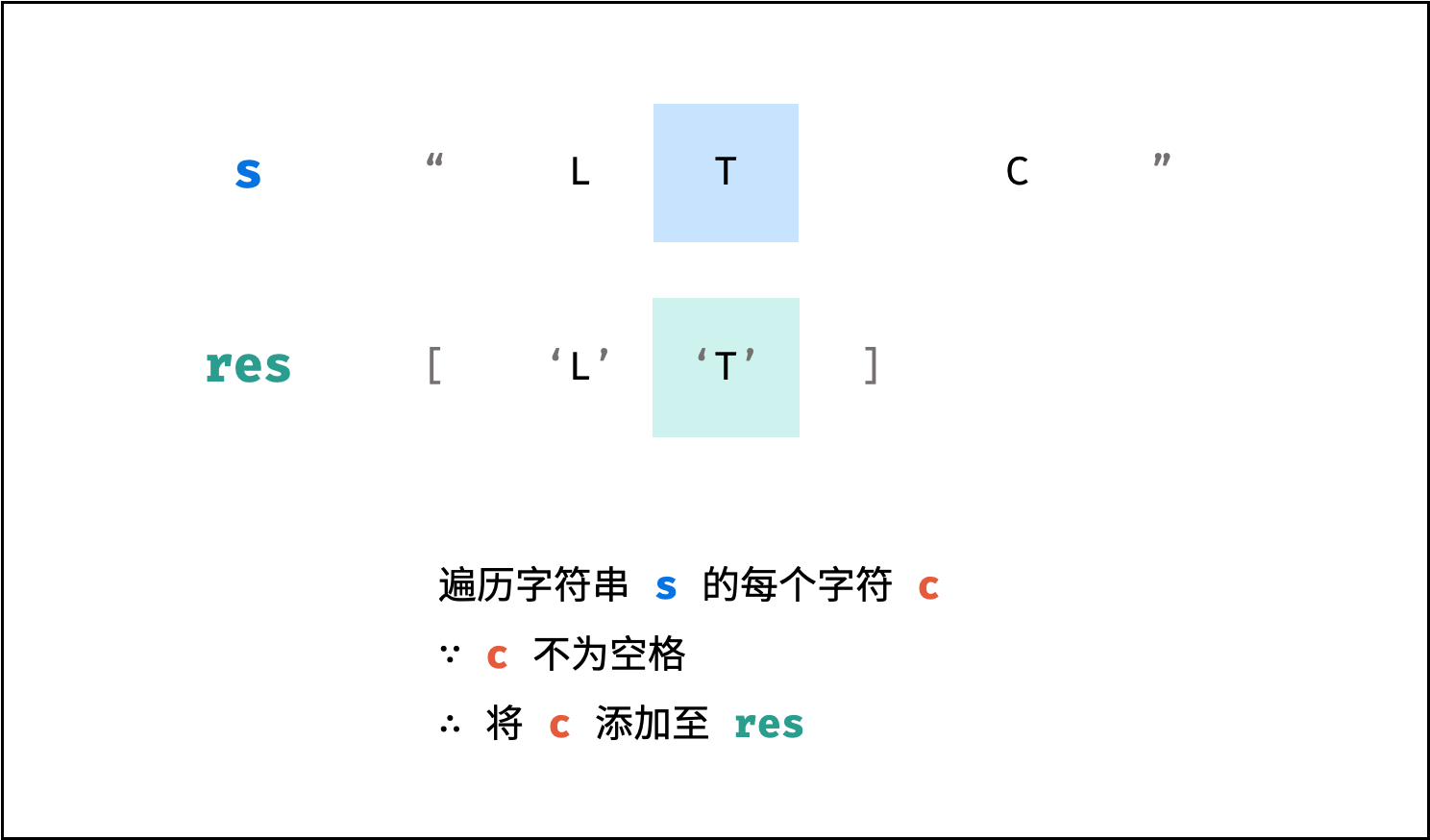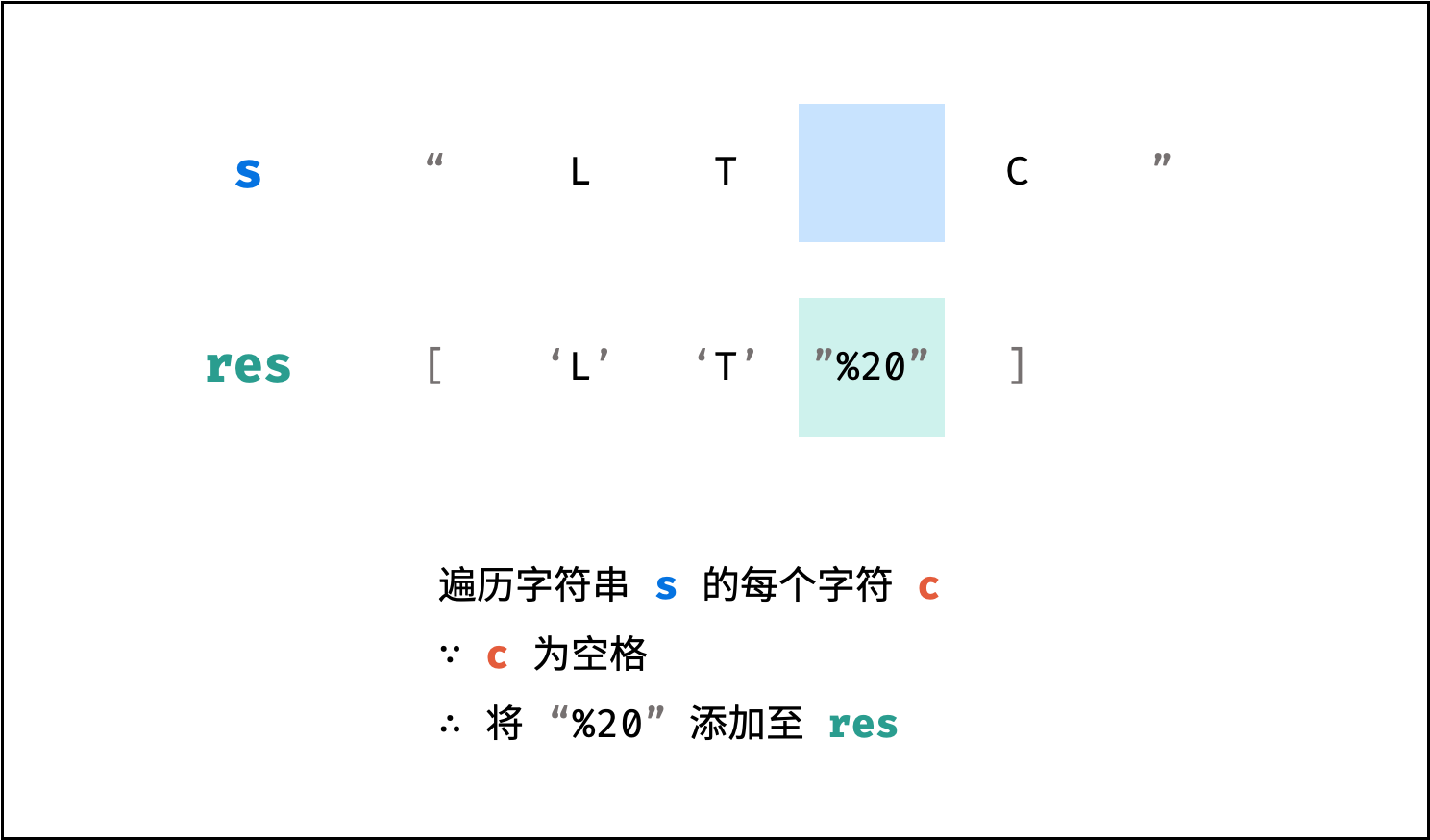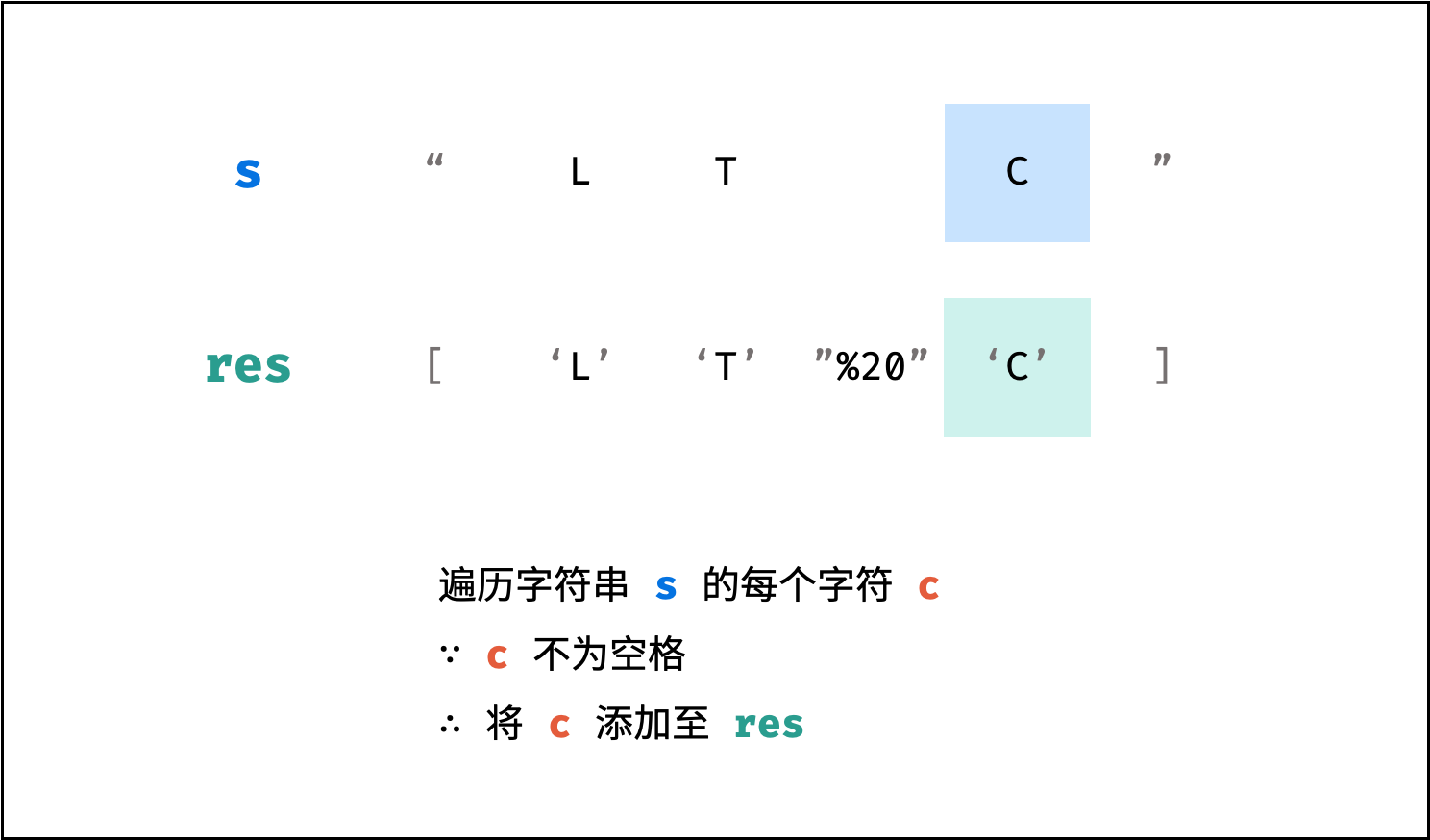<![Picture1.png](https://pic.leetcode-cn.com/1599931882-pLqBGE-Picture1.png),![Picture2.png](https://pic.leetcode-cn.com/1599931882-qBgBNr-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599931882-pzDKEt-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599931882-IEnADl-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599931882-LvchKo-Picture5.png)>
## 代码：
```Python []
class Solution:
def pathEncryption(self, path: str) -> str:
res = []
for c in path:
if c == '.': res.append(' ')
else: res.append(c)
return "".join(res)
```
```Java []
class Solution {
public String pathEncryption(String path) {
StringBuilder res = new StringBuilder();
for(Character c : path.toCharArray())
{
if(c == '.') res.append(' ');
else res.append(c);
}
return res.toString();
}
}
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 遍历使用 $O(N)$ ，每轮添加（修改）字符操作使用 $O(1)$ ；
- **空间复杂度 $O(N)$ ：** Python 新建的 list 和 Java 新建的 StringBuilder 都使用了线性大小的额外空间。

126
leetbook_ioa/docs/LCR 123. 图书整理 I.md Executable file
View File

@@ -0,0 +1,126 @@
## 方法一：递归
利用递归，先递推至链表末端；回溯时，依次将节点值加入列表，即可实现链表值的倒序输出。
1. **终止条件：** 当 `head == None` 时，代表越过了链表尾节点，则返回空列表；
2. **递推工作：** 访问下一节点 `head.next` ；
3. **回溯阶段：**
- **Python：** 返回 `当前 list + 当前节点值 [head.val]` ；
- **Java / C++：** 将当前节点值 `head.val` 加入列表 `tmp` ；
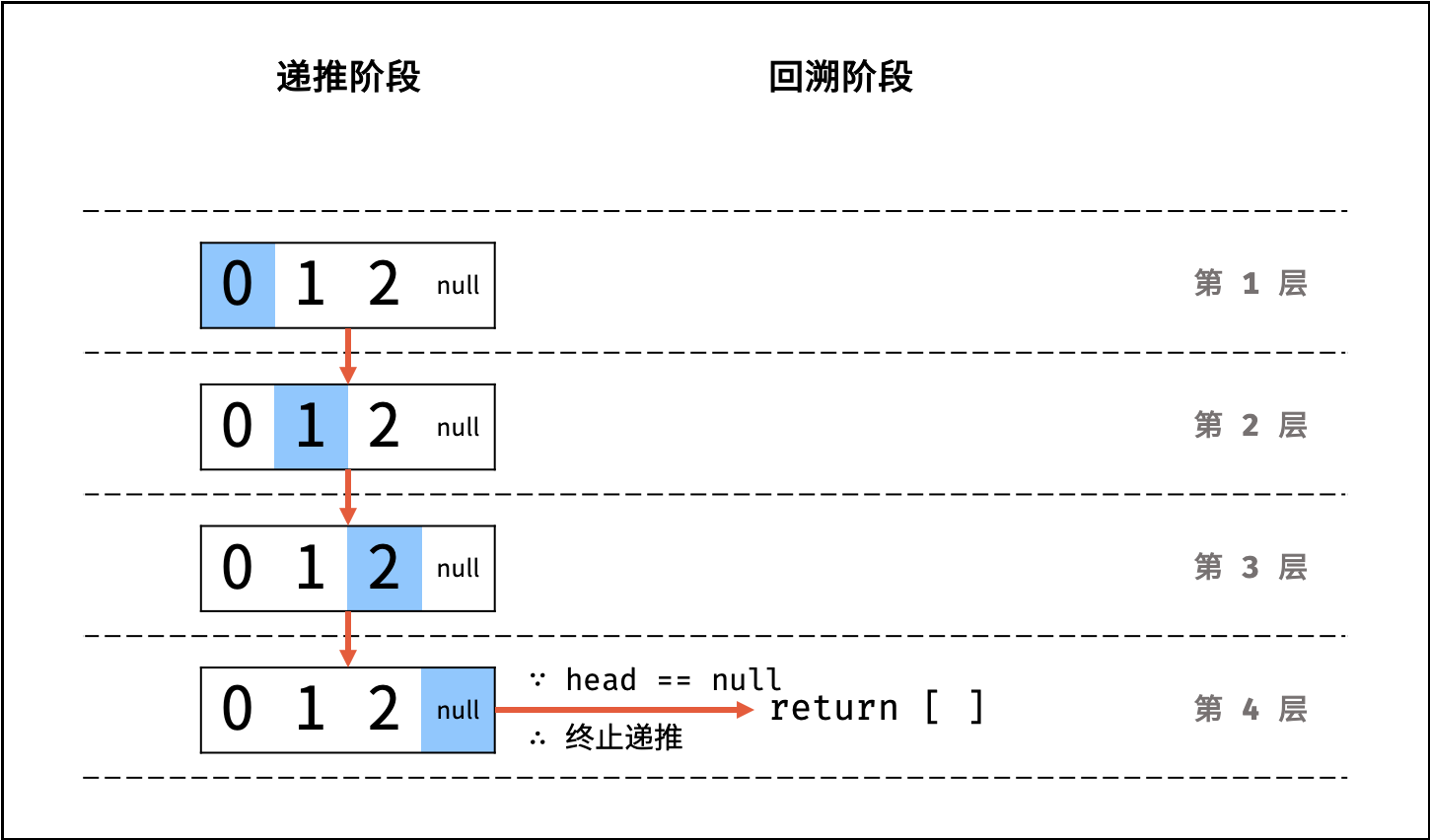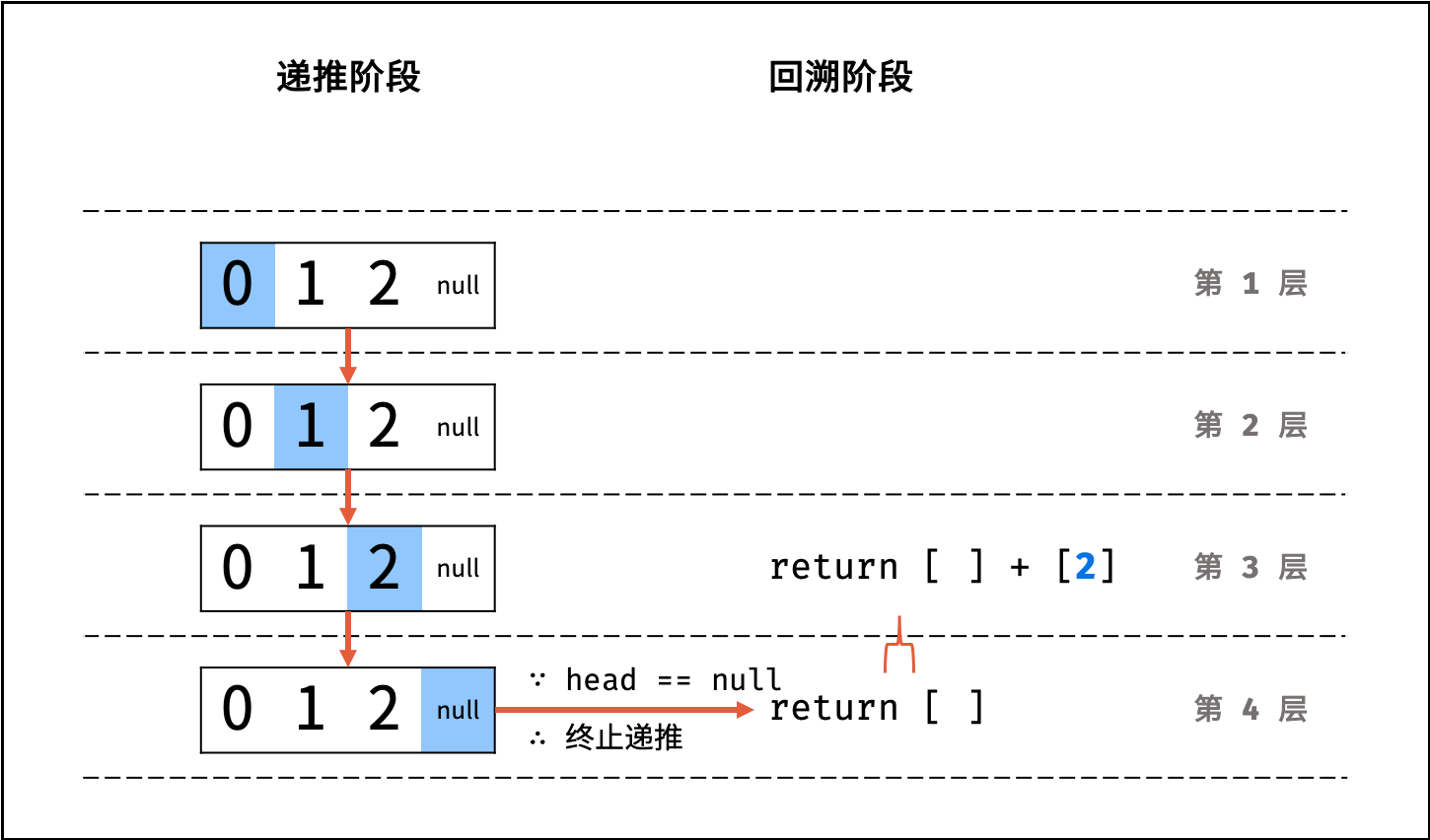<![Picture1.png](https://pic.leetcode-cn.com/1599284309-ongbxB-Picture1.png),![Picture2.png](https://pic.leetcode-cn.com/1599284309-sNAjgz-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599284309-lsJzwg-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599284309-WEexSa-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599284309-aAAzfv-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599284309-AwHMnh-Picture6.png),![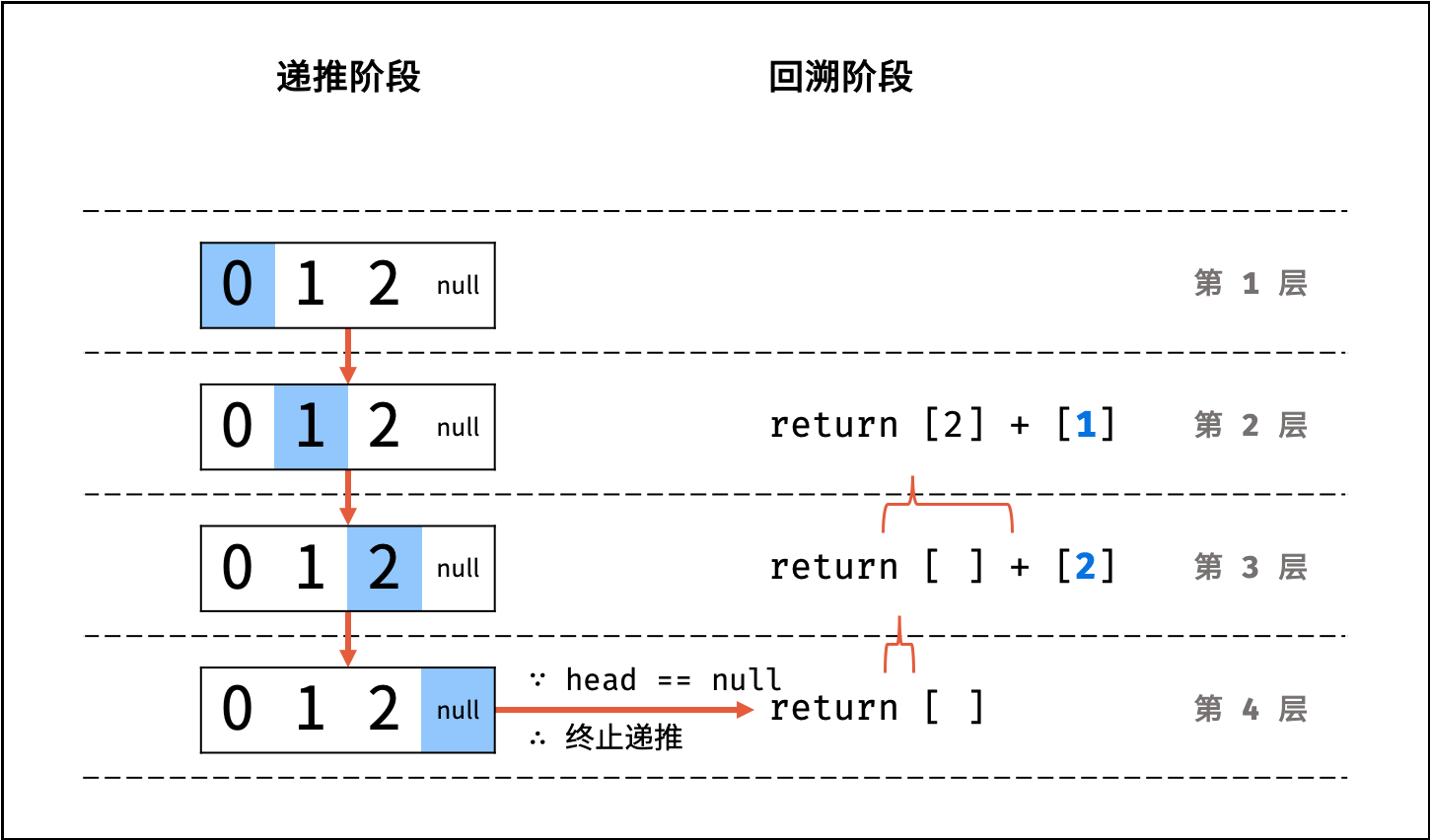Picture7.png](https://pic.leetcode-cn.com/1599284309-TPcwUZ-Picture7.png),![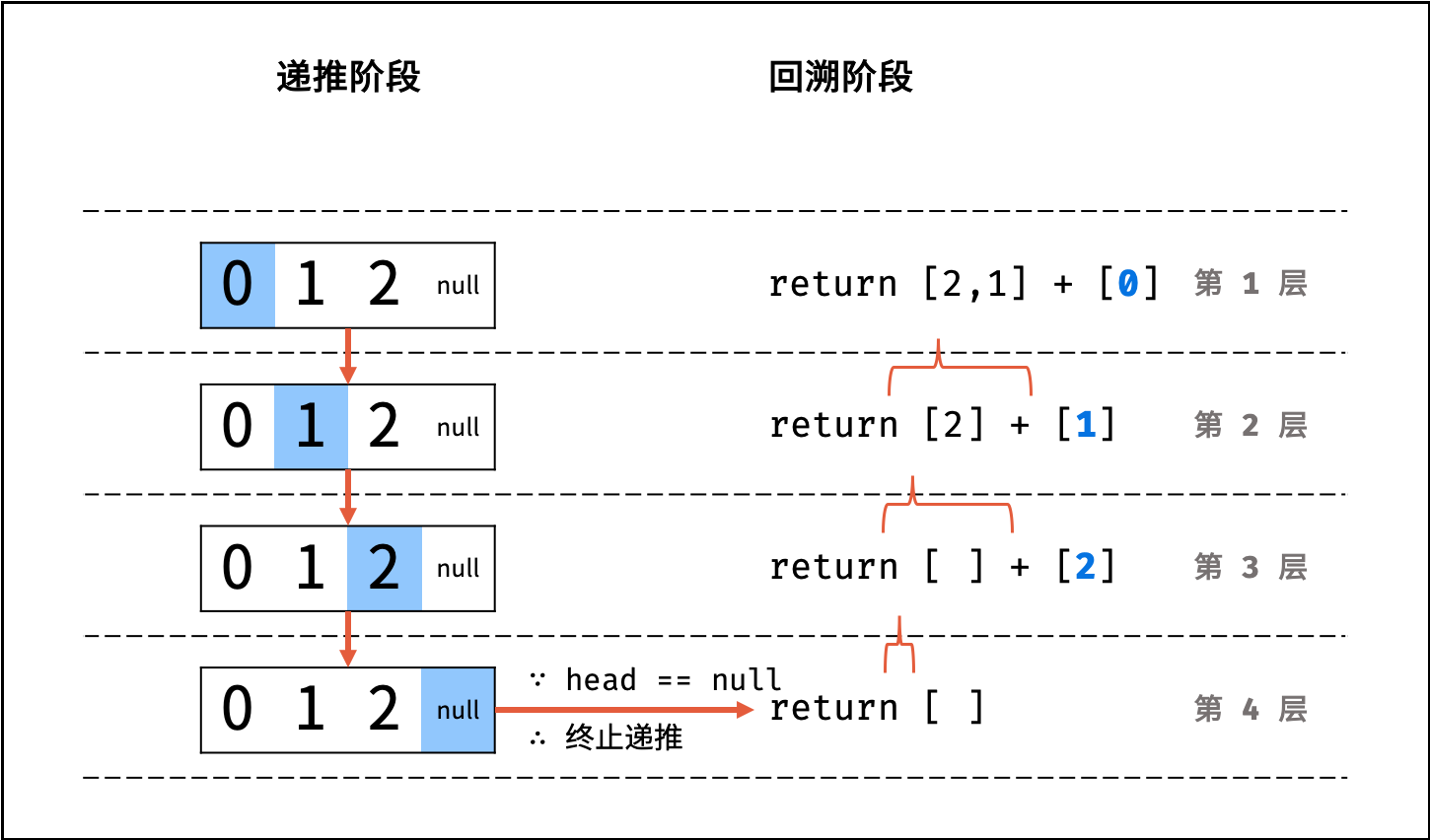Picture8.png](https://pic.leetcode-cn.com/1599284309-sBtikj-Picture8.png),![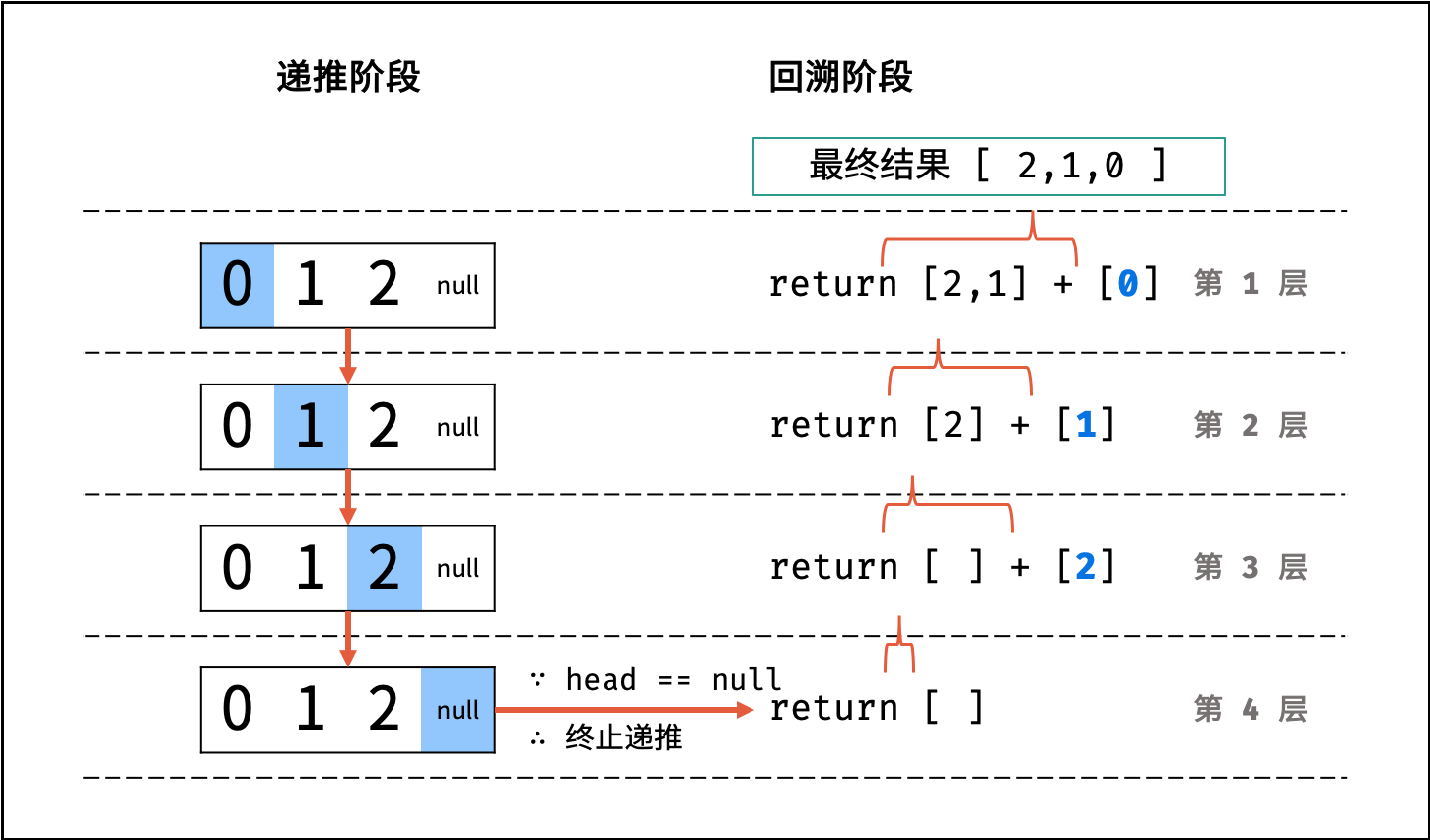Picture8-1.png](https://pic.leetcode-cn.com/1599284504-Zuewmm-Picture8-1.png)>
### 代码：
```Python []
class Solution:
def reverseBookList(self, head: Optional[ListNode]) -> List[int]:
return self.reverseBookList(head.next) + [head.val] if head else []
```
```Java []
class Solution {
ArrayList<Integer> tmp = new ArrayList<Integer>();
public int[] reverseBookList(ListNode head) {
recur(head);
int[] res = new int[tmp.size()];
for(int i = 0; i < res.length; i++)
res[i] = tmp.get(i);
return res;
}
void recur(ListNode head) {
if(head == null) return;
recur(head.next);
tmp.add(head.val);
}
}
```
```C++ []
class Solution {
public:
vector<int> reverseBookList(ListNode* head) {
recur(head);
return res;
}
private:
vector<int> res;
void recur(ListNode* head) {
if(head == nullptr) return;
recur(head->next);
res.push_back(head->val);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$：** 遍历链表，递归 $N$ 次。
- **空间复杂度 $O(N)$：** 系统递归需要使用 $O(N)$ 的栈空间。
## 方法二：辅助栈法
链表只能 **从前至后** 访问每个节点，而题目要求 **倒序输出** 各节点值，这种 **先入后出** 的需求可以借助 **栈** 来实现。
### 算法流程：
1. **入栈：** 遍历链表，将各节点值 `push` 入栈。
2. **出栈：** 将各节点值 `pop` 出栈，存储于数组并返回。
> 图解以 Java 代码为例，Python 无需将 `stack` 转移至 `res`，而是直接返回倒序数组。
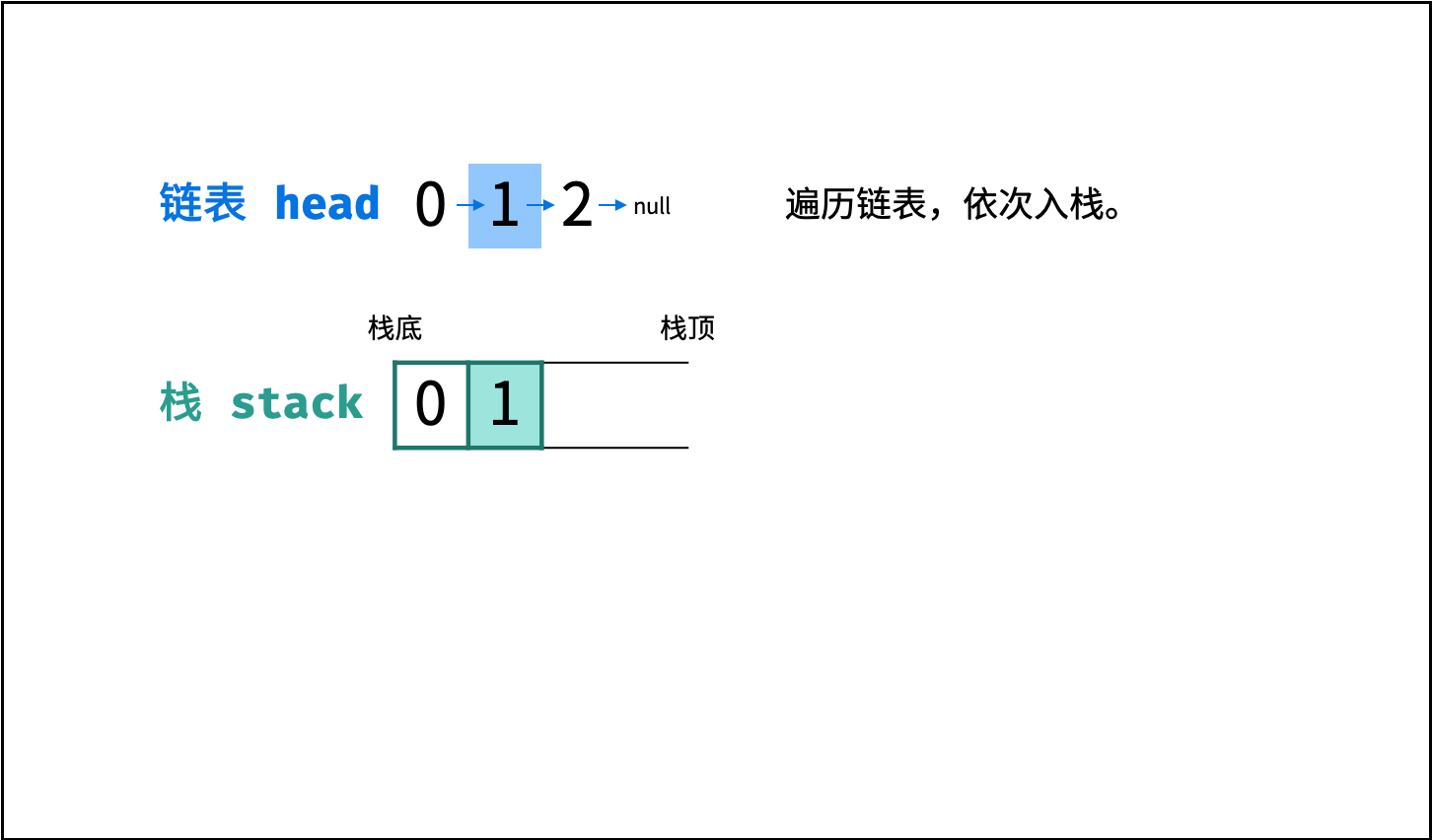<![Picture9.png](https://pic.leetcode-cn.com/1599284309-uVDdUn-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599284309-bkTHcM-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1599284309-pjcVQL-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1599284309-CdJEZQ-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1599284309-hpDDSU-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1599284309-BTfQdQ-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1599284309-RplwUC-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1599284309-JIonvw-Picture16.png)>
### 代码：
Java 数组长度不可变，因此使用 List 先存储，再转为数组并返回。
```Python []
class Solution:
def reverseBookList(self, head: ListNode) -> List[int]:
stack = []
while head:
stack.append(head.val)
head = head.next
return stack[::-1]
```
```Java []
class Solution {
public int[] reverseBookList(ListNode head) {
LinkedList<Integer> stack = new LinkedList<Integer>();
while(head != null) {
stack.addLast(head.val);
head = head.next;
}
int[] res = new int[stack.size()];
for(int i = 0; i < res.length; i++)
res[i] = stack.removeLast();
return res;
}
}
```
```C++ []
class Solution {
public:
vector<int> reverseBookList(ListNode* head) {
stack<int> stk;
while(head != nullptr) {
stk.push(head->val);
head = head->next;
}
vector<int> res;
while(!stk.empty()) {
res.push_back(stk.top());
stk.pop();
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$：** 入栈和出栈共使用 $O(N)$ 时间。
- **空间复杂度 $O(N)$：** 辅助栈 `stack` 和数组 `res` 共使用 $O(N)$ 的额外空间。

117
leetbook_ioa/docs/LCR 124. 推理二叉树.md Executable file
View File

@@ -0,0 +1,117 @@
## 解题思路：
前序遍历性质： 节点按照 `[ 根节点 | 左子树 | 右子树 ]` 排序。
中序遍历性质： 节点按照 `[ 左子树 | 根节点 | 右子树 ]` 排序。
> 以题目示例为例：
>
> - 前序遍历划分 `[ 3 | 9 | 20 15 7 ]`
> - 中序遍历划分 `[ 9 | 3 | 15 20 7 ]`
根据以上性质，可得出以下推论：
1. 前序遍历的首元素 为 树的根节点 `node` 的值。
2. 在中序遍历中搜索根节点 `node` 的索引 ，可将 中序遍历 划分为 `[ 左子树 | 根节点 | 右子树 ]` 。
3. 根据中序遍历中的左（右）子树的节点数量，可将 前序遍历 划分为 `[ 根节点 | 左子树 | 右子树 ] ` 。
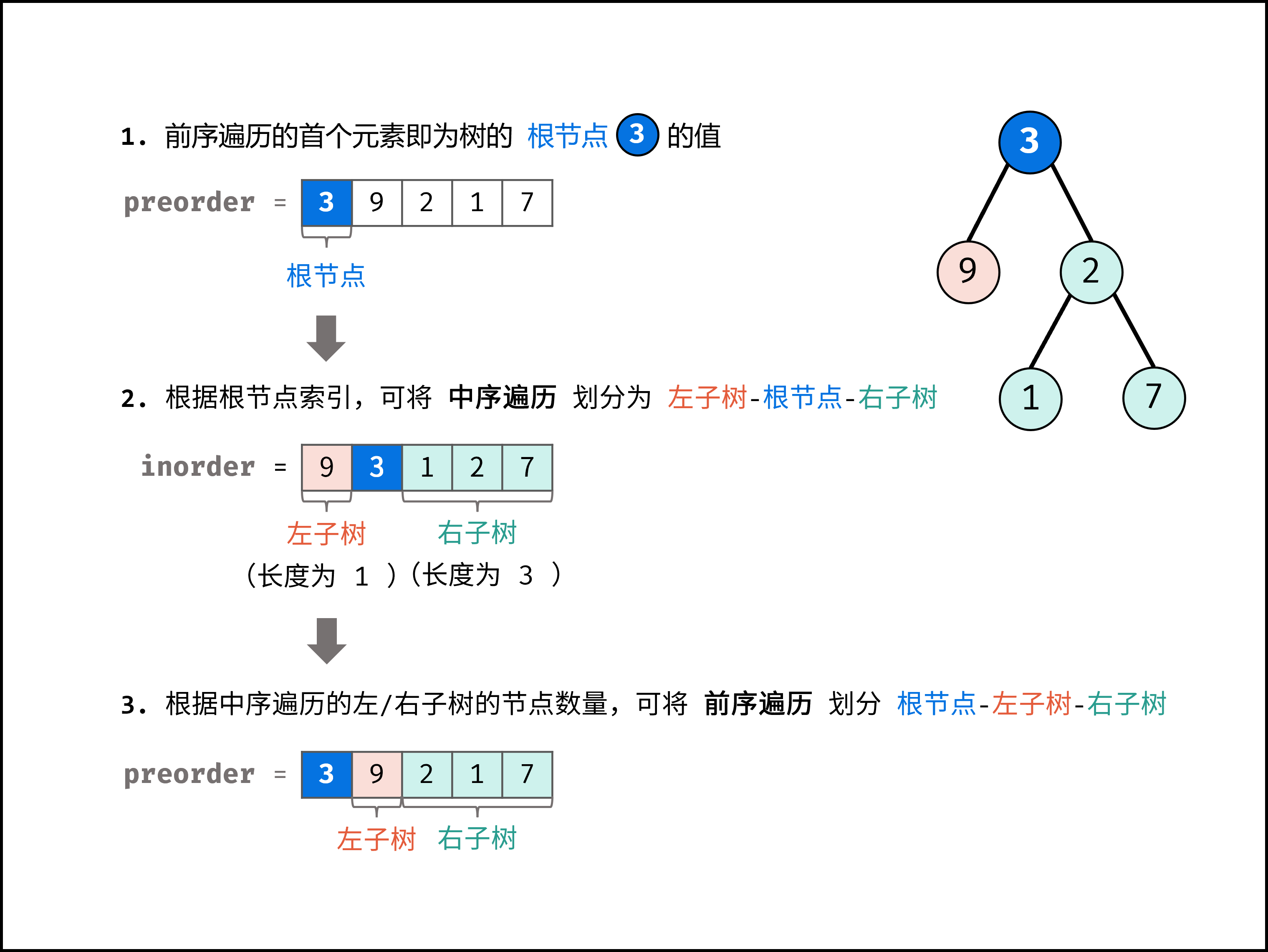![Picture1.png](https://pic.leetcode-cn.com/1629825510-roByLr-Picture1.png){:align=center width=550}
通过以上三步，可确定 **三个节点** ：1.树的根节点、2.左子树根节点、3.右子树根节点。
根据「分治算法」思想，对于树的左、右子树，仍可复用以上方法划分子树的左右子树。
### 分治解析：
**递推参数：** 根节点在前序遍历的索引 `root` 、子树在中序遍历的左边界 `left` 、子树在中序遍历的右边界 `right` ；
**终止条件：** 当 `left > right` ，代表已经越过叶节点，此时返回 $\text{null}$ ；
**递推工作：**
1. **建立根节点 `node` ：** 节点值为 `preorder[root]` ；
2. **划分左右子树：** 查找根节点在中序遍历 `inorder` 中的索引 `i` ；
> 为了提升效率，本文使用哈希表 `hmap` 存储中序遍历的值与索引的映射，查找操作的时间复杂度为 $O(1)$ ；
3. **构建左右子树：** 开启左右子树递归；
| | 根节点索引 | 中序遍历左边界 | 中序遍历右边界 |
| ---------- | --------------------- | -------------- | -------------- |
| **左子树** | `root + 1` | `left` | `i - 1` |
| **右子树** | `i - left + root + 1` | `i + 1` | `right` |
> **TIPS：** `i - left + root + 1`含义为 `根节点索引 + 左子树长度 + 1`
**返回值：** 回溯返回 `node` ，作为上一层递归中根节点的左 / 右子节点；
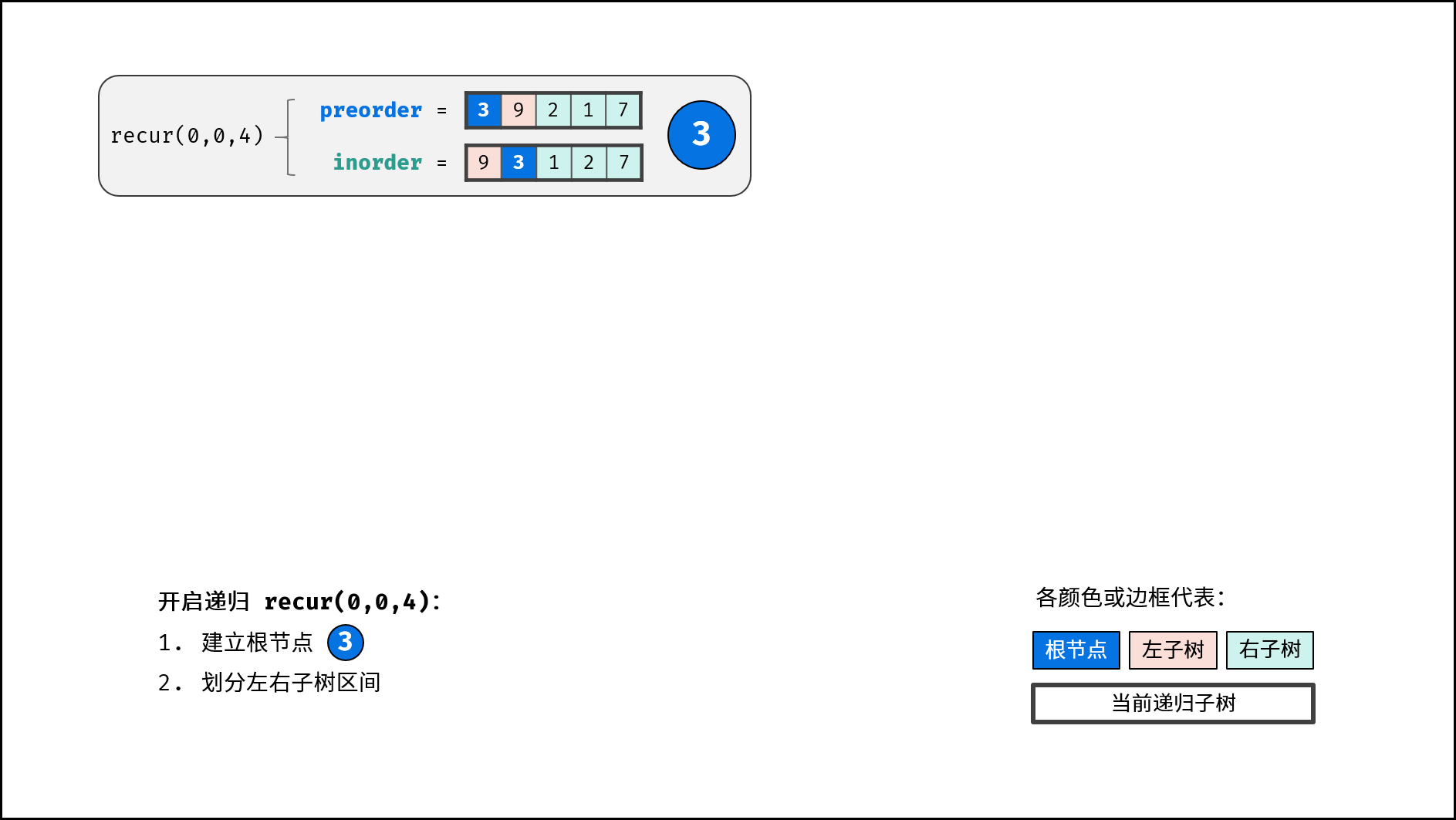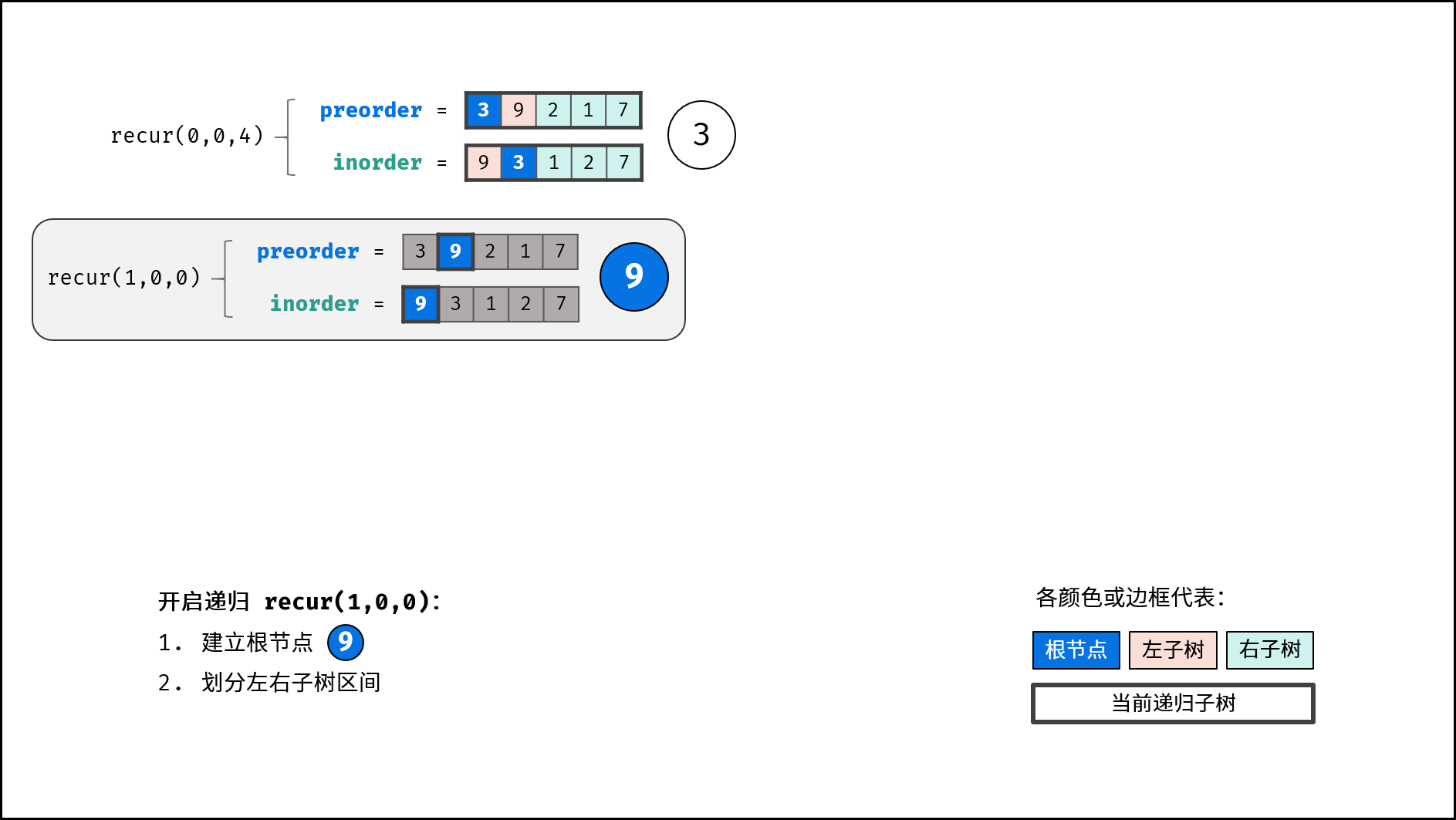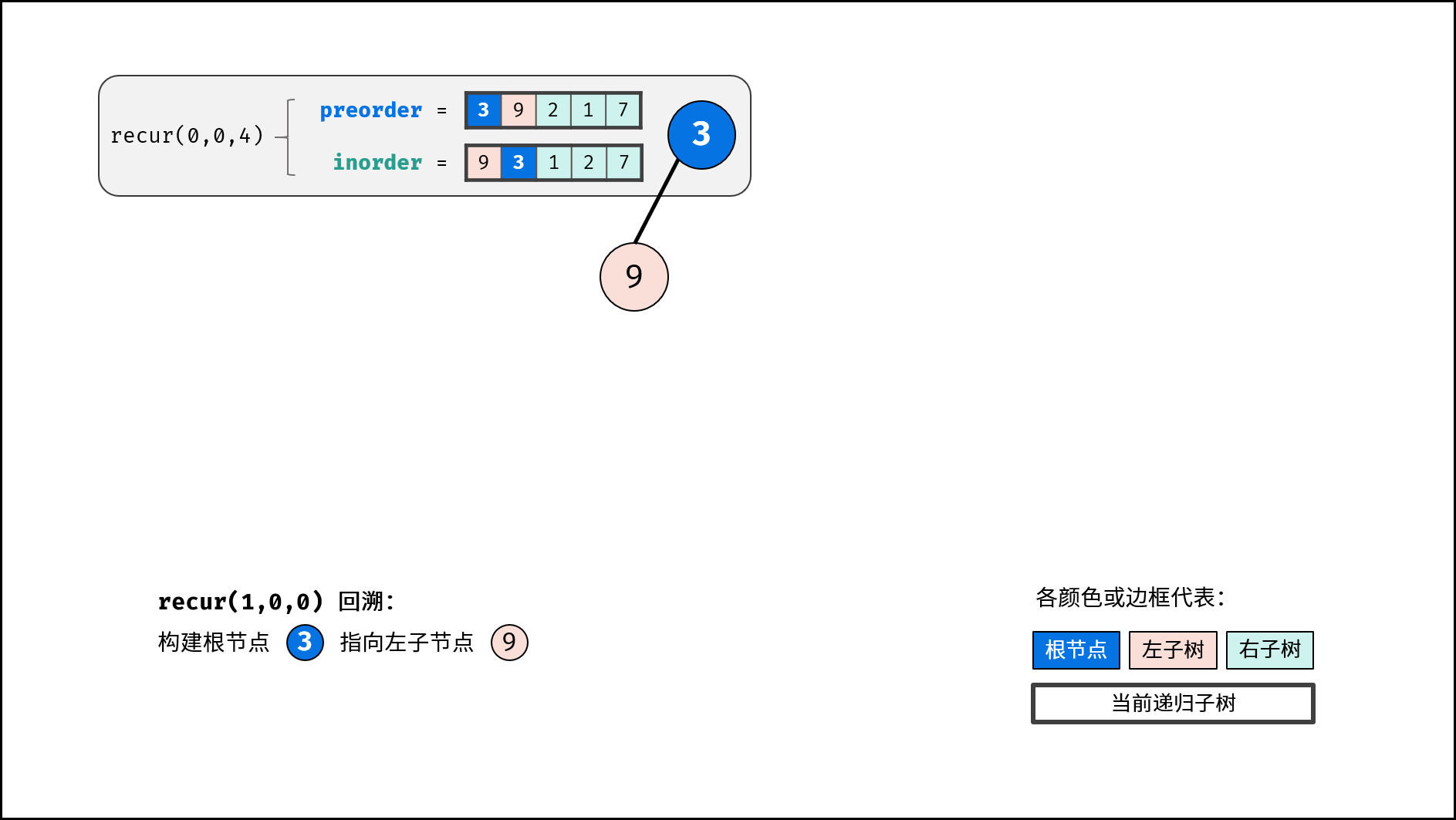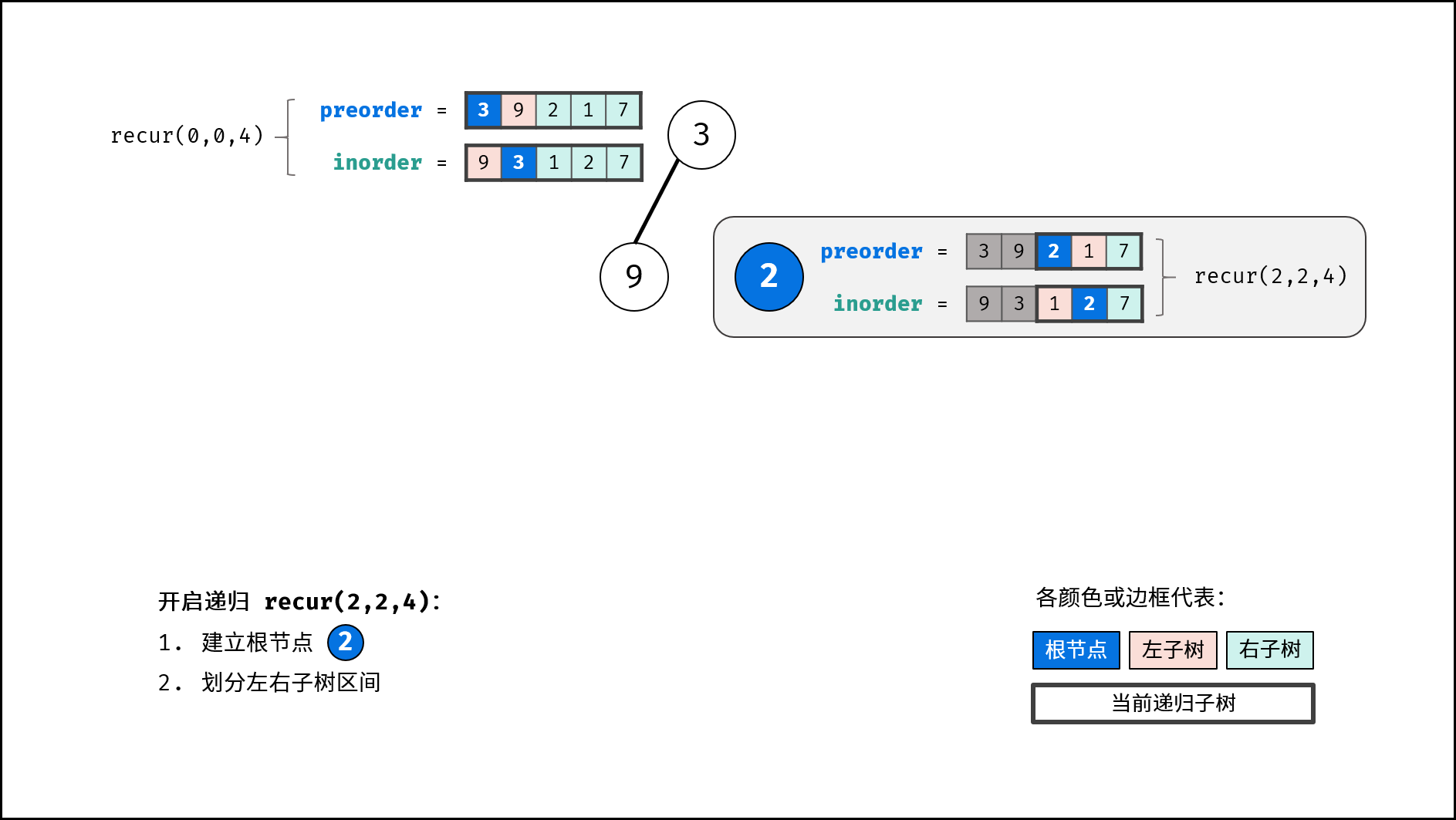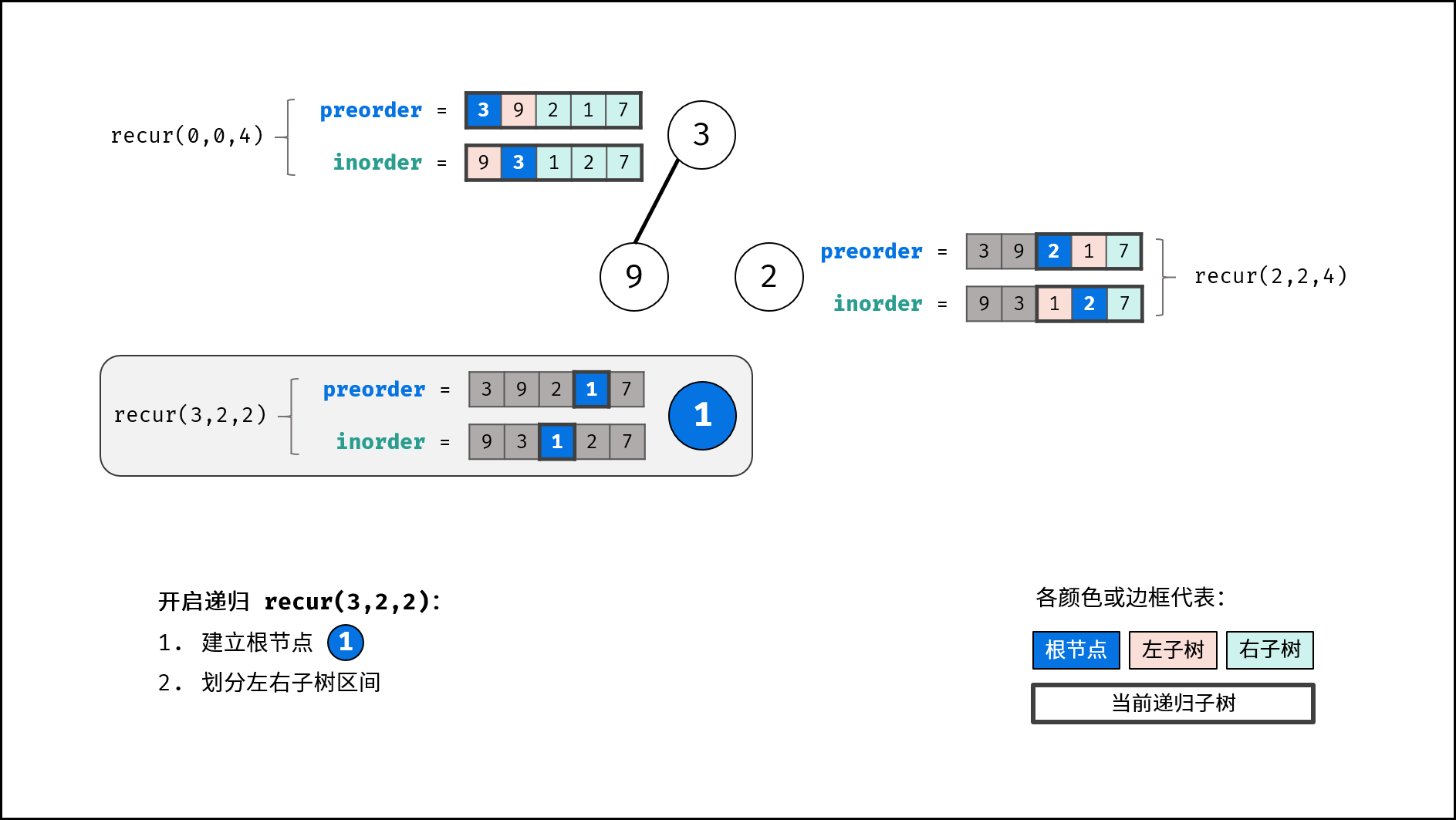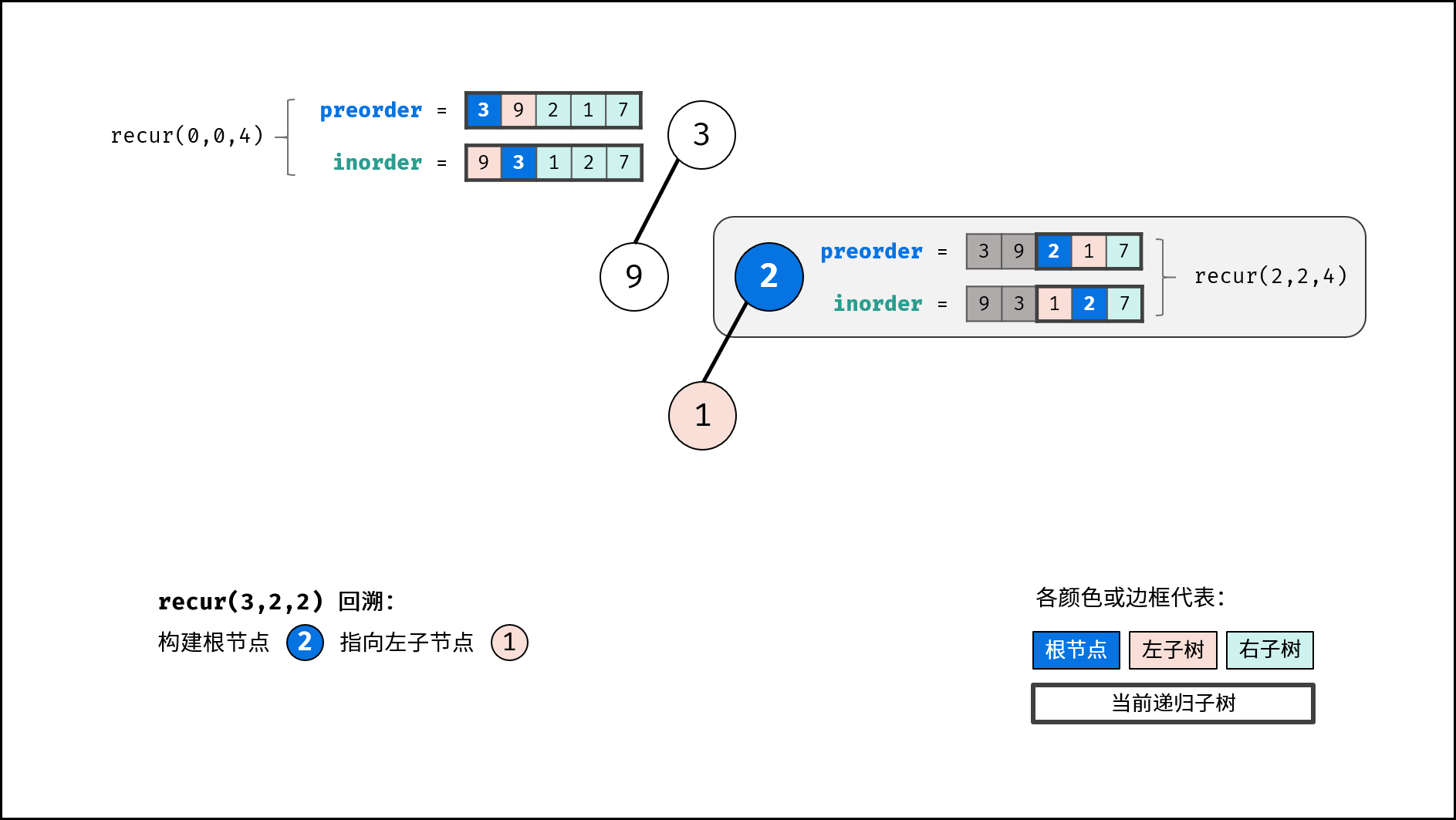<![Picture2.png](https://pic.leetcode-cn.com/1603644245-DwefAv-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603644377-aJTwyJ-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603644377-rGvUqA-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603644245-OrFteB-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603644245-RBtYMS-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603644245-ZlaMmX-Picture7.png),![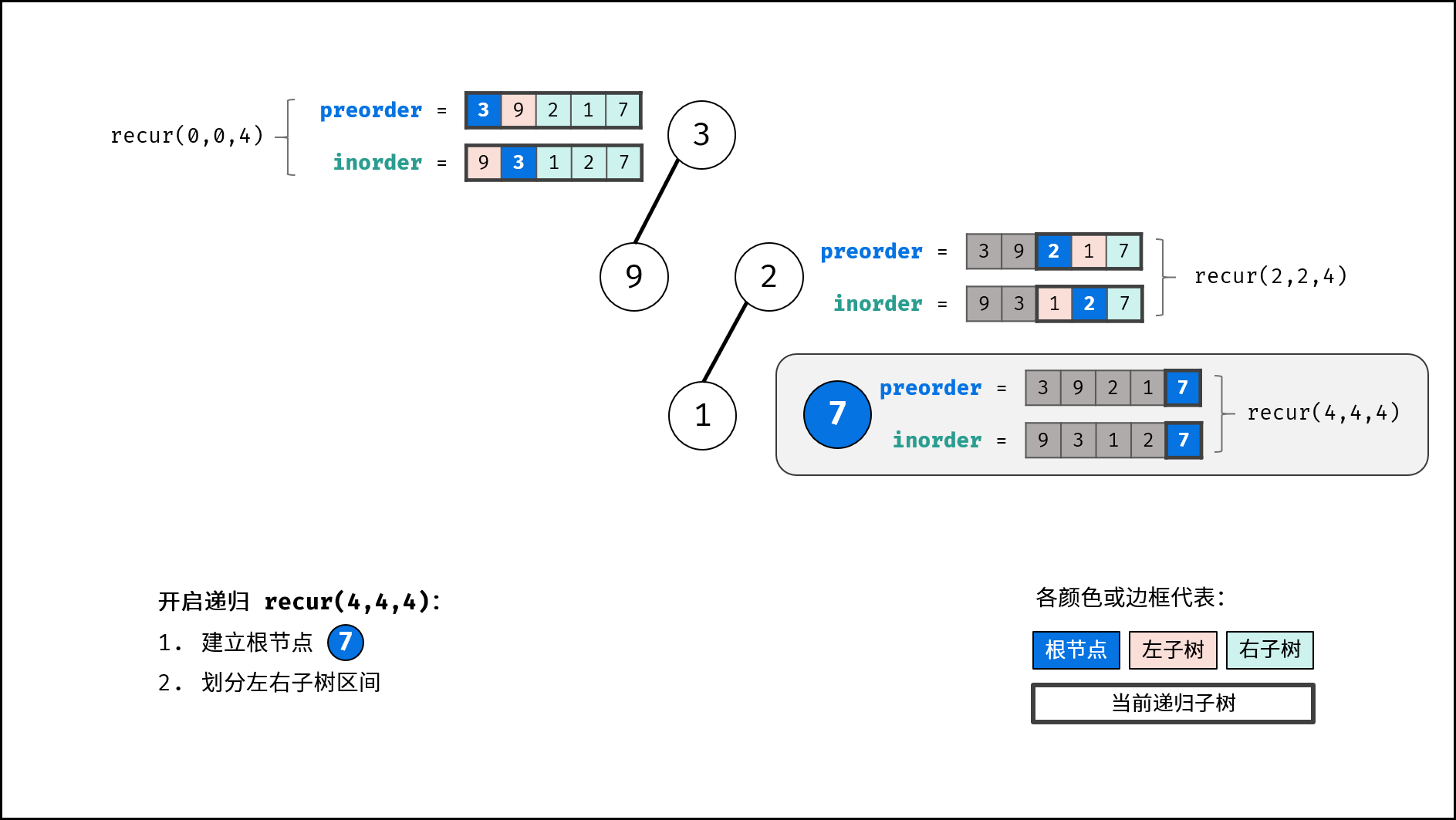Picture8.png](https://pic.leetcode-cn.com/1603644245-leDZaF-Picture8.png),![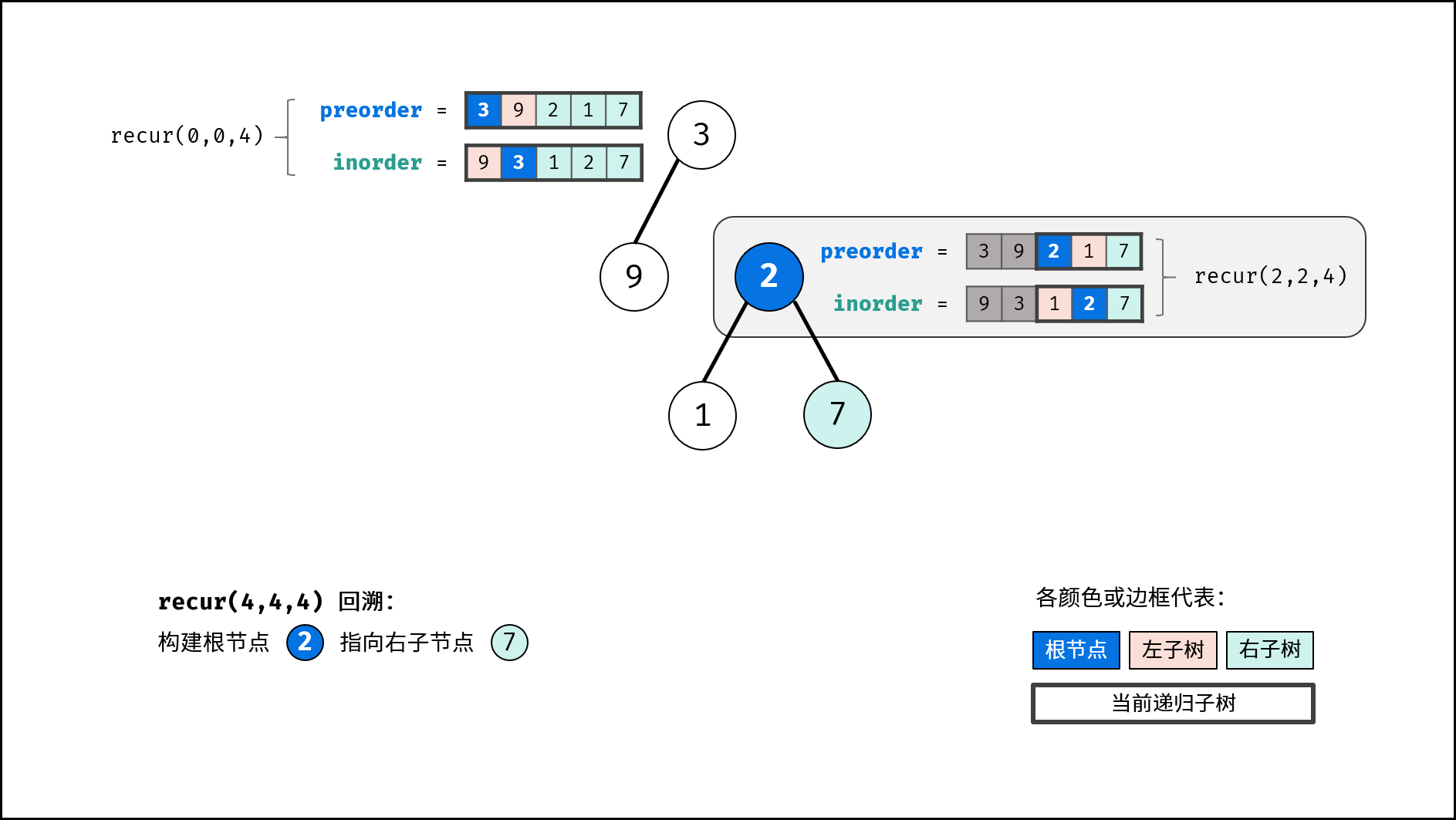Picture9.png](https://pic.leetcode-cn.com/1603644245-KtWHlj-Picture9.png),![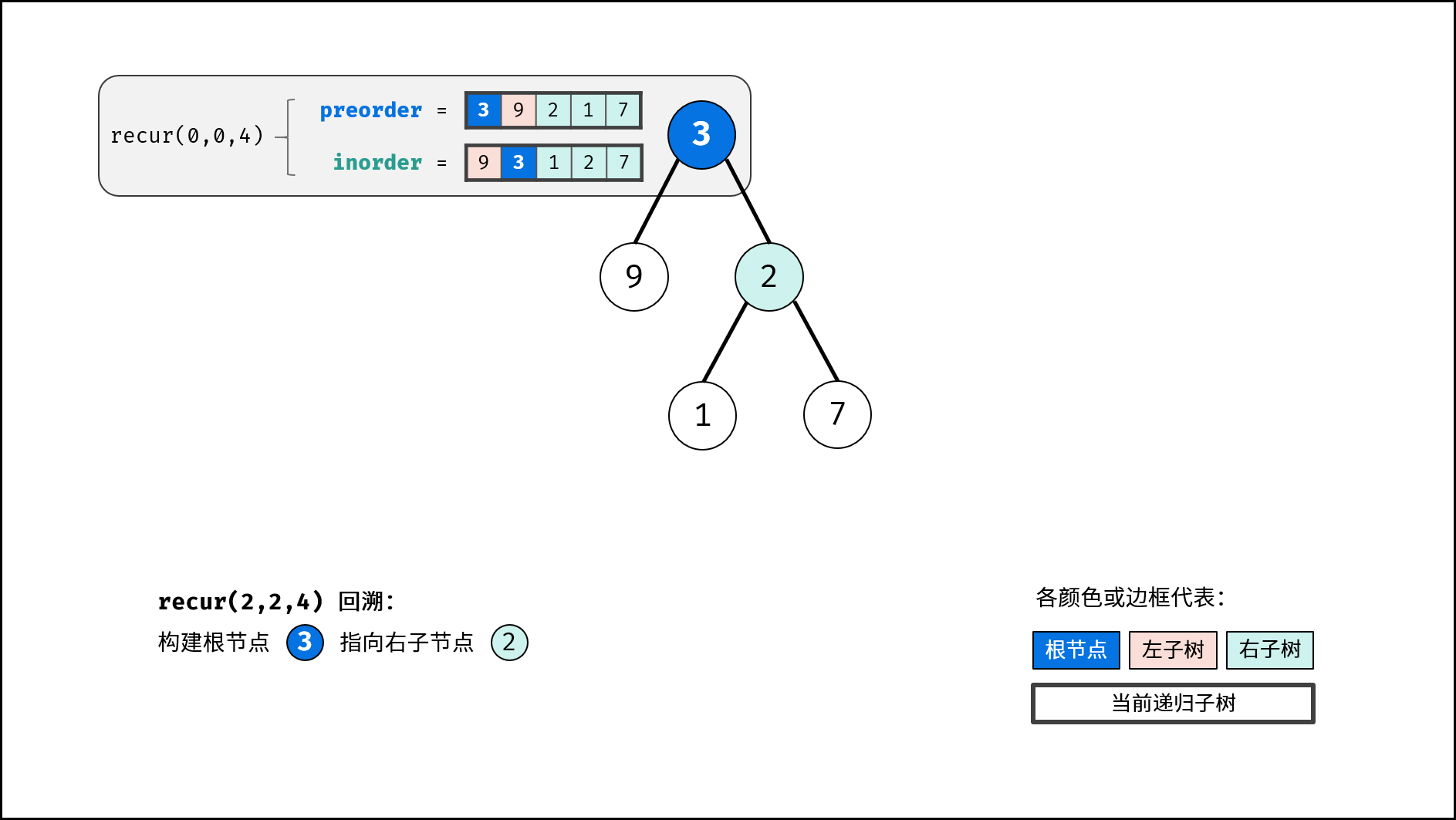Picture10.png](https://pic.leetcode-cn.com/1603644245-tYOIfd-Picture10.png),![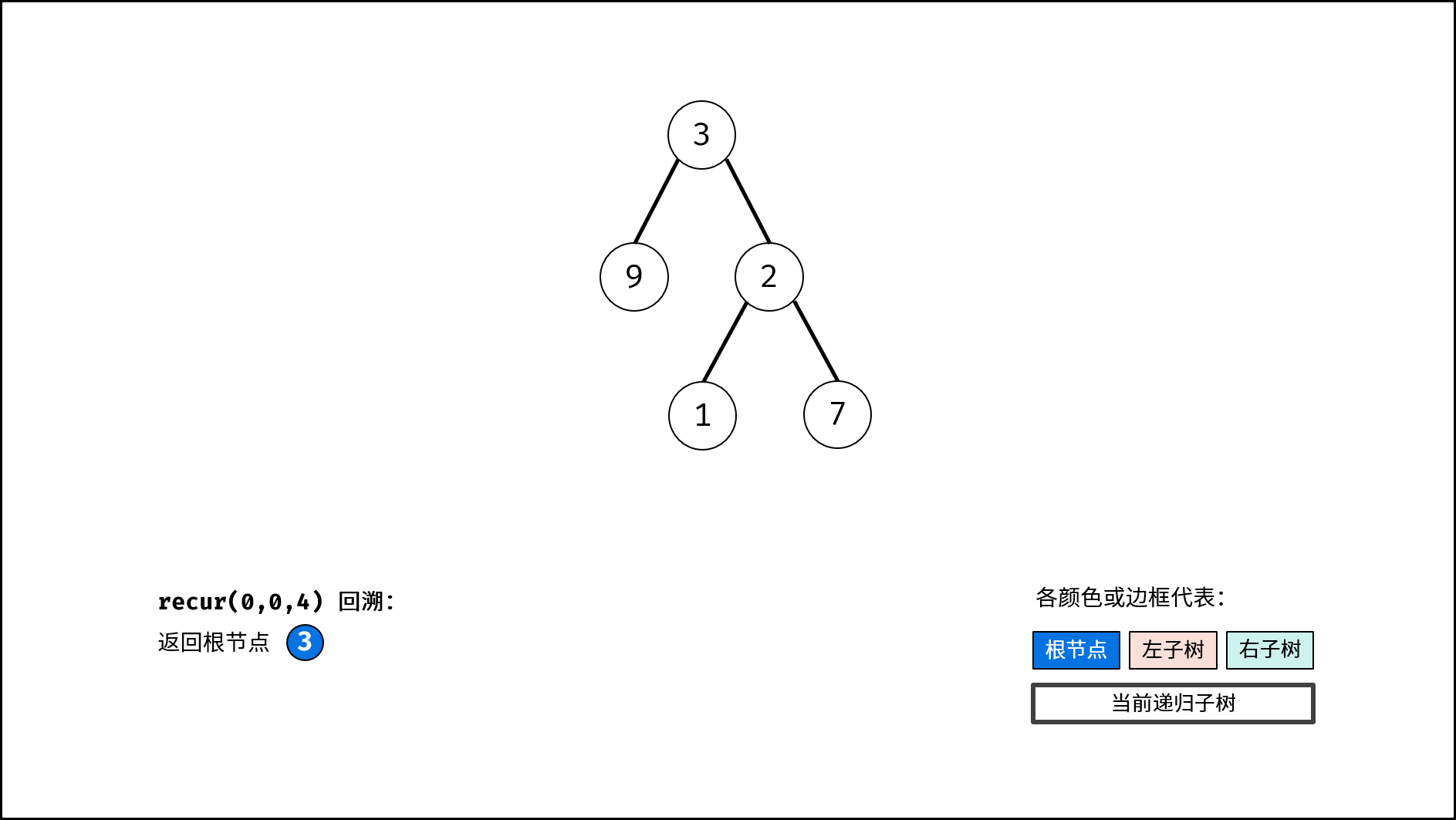Picture11.png](https://pic.leetcode-cn.com/1603644245-IAznrm-Picture11.png),![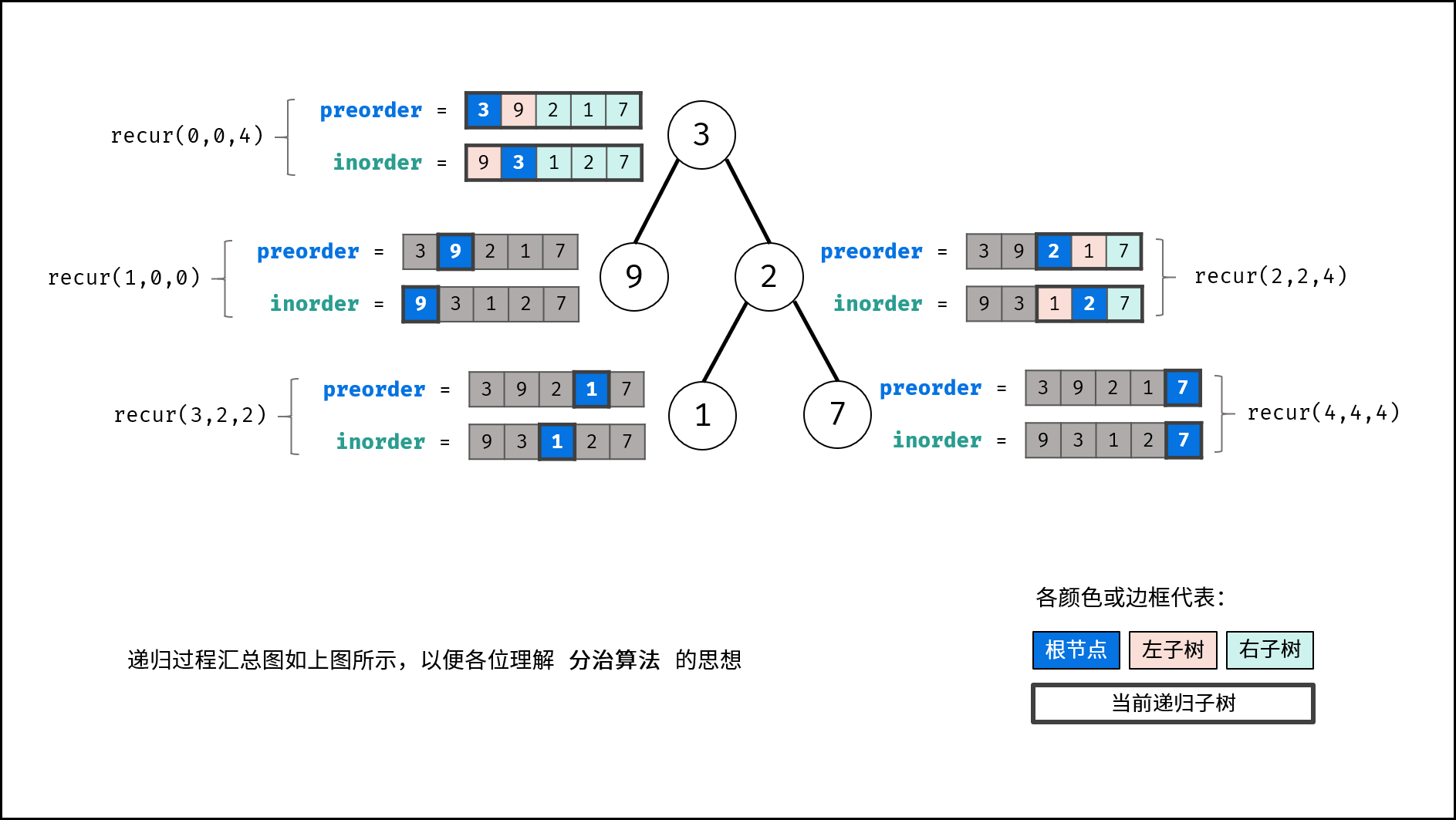Picture12.png](https://pic.leetcode-cn.com/1603644245-oLIgwn-Picture12.png)>
## 代码：
> 注意：本文方法只适用于 “无重复节点值” 的二叉树。
```Python []
class Solution:
def deduceTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
def recur(root, left, right):
if left > right: return # 递归终止
node = TreeNode(preorder[root]) # 建立根节点
i = hmap[preorder[root]] # 划分根节点、左子树、右子树
node.left = recur(root + 1, left, i - 1) # 开启左子树递归
node.right = recur(i - left + root + 1, i + 1, right) # 开启右子树递归
return node # 回溯返回根节点
hmap, preorder = {}, preorder
for i in range(len(inorder)):
hmap[inorder[i]] = i
return recur(0, 0, len(inorder) - 1)
```
```Java []
class Solution {
int[] preorder;
HashMap<Integer, Integer> hmap = new HashMap<>();
public TreeNode deduceTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
for(int i = 0; i < inorder.length; i++)
hmap.put(inorder[i], i);
return recur(0, 0, inorder.length - 1);
}
TreeNode recur(int root, int left, int right) {
if(left > right) return null; // 递归终止
TreeNode node = new TreeNode(preorder[root]); // 建立根节点
int i = hmap.get(preorder[root]); // 划分根节点、左子树、右子树
node.left = recur(root + 1, left, i - 1); // 开启左子树递归
node.right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归
return node; // 回溯返回根节点
}
}
```
```C++ []
class Solution {
public:
TreeNode* deduceTree(vector<int>& preorder, vector<int>& inorder) {
this->preorder = preorder;
for(int i = 0; i < inorder.size(); i++)
hmap[inorder[i]] = i;
return recur(0, 0, inorder.size() - 1);
}
private:
vector<int> preorder;
unordered_map<int, int> hmap;
TreeNode* recur(int root, int left, int right) {
if(left > right) return nullptr; // 递归终止
TreeNode* node = new TreeNode(preorder[root]); // 建立根节点
int i = hmap[preorder[root]]; // 划分根节点、左子树、右子树
node->left = recur(root + 1, left, i - 1); // 开启左子树递归
node->right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归
return node; // 回溯返回根节点
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为树的节点数量。初始化 HashMap 需遍历 `inorder` ，占用 $O(N)$ 。递归共建立 $N$ 个节点，每层递归中的节点建立、搜索操作占用 $O(1)$ ，因此使用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** HashMap 使用 $O(N)$ 额外空间；最差情况下（输入二叉树为链表时），递归深度达到 $N$ ，占用 $O(N)$ 的栈帧空间；因此总共使用 $O(N)$ 空间。

97
leetbook_ioa/docs/LCR 125. 图书整理 II.md Executable file
View File

@@ -0,0 +1,97 @@
## 解题思路：
> 我们可将两个书车看作两个“栈”，本题可被转化为“用两个栈实现一个队列”。
栈实现队列的出队操作效率低下：栈底元素（对应队首元素）无法直接删除，需要将上方所有元素出栈。
列表倒序操作可使用双栈实现：设有含三个元素的栈 `A = [1,2,3]` 和空栈 `B = []` 。若循环执行 `A` 元素出栈并添加入栈 `B` ，直到栈 `A` 为空，则 `A = []` , `B = [3,2,1]` ，即栈 `B` 元素为栈 `A` 元素倒序。
利用栈 `B` 删除队首元素：倒序后，`B` 执行出栈则相当于删除了 `A` 的栈底元素，即对应队首元素。
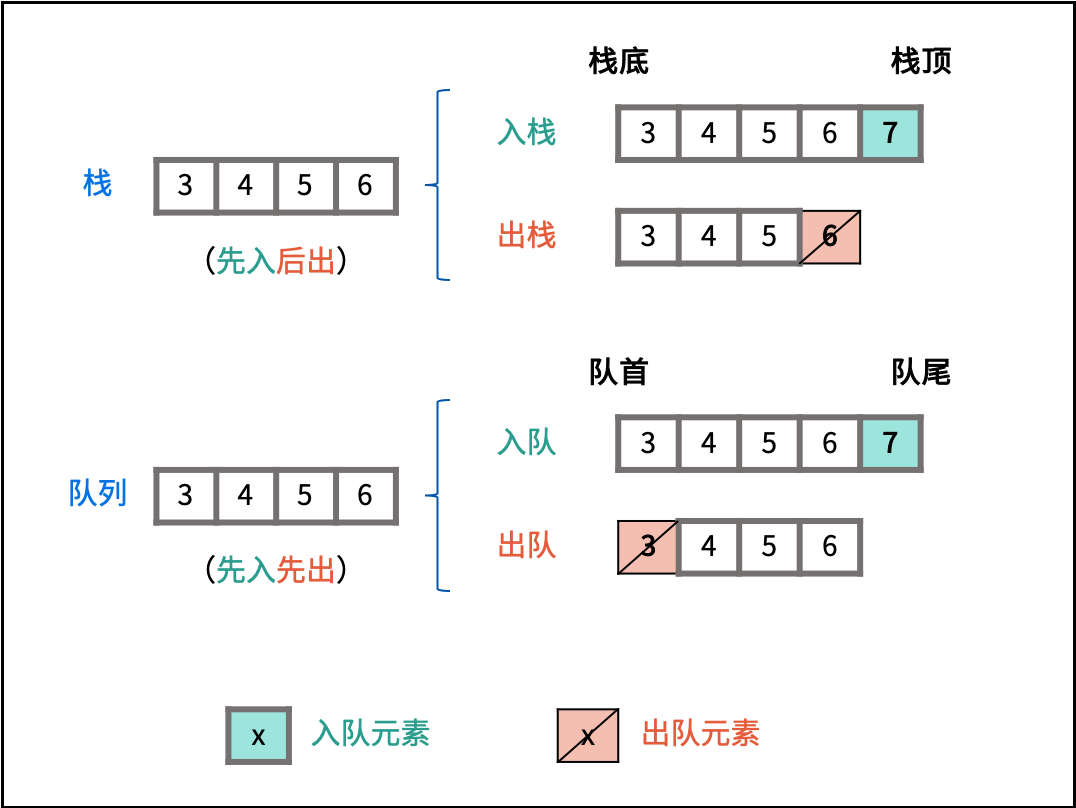![Picture1.png](https://pic.leetcode-cn.com/1599286207-HnnMhX-Picture1.png){:align=center width=500}
题目要求实现 **加入队尾**`appendTail()` 和 **删除队首**`deleteHead()` 两个函数的正常工作。因此，可以设计栈 `A` 用于加入队尾操作，栈 `B` 用于将元素倒序，从而实现删除队首元素。
### 函数设计：
1. **加入队尾 `appendTail()` ：** 将数字 `val` 加入栈 `A` 即可。
2. **删除队首`deleteHead()` ：** 有以下三种情况。
1. **当栈 `B` 不为空：** `B`中仍有已完成倒序的元素，因此直接返回 `B` 的栈顶元素。
2. **否则，当 `A` 为空：** 即两个栈都为空，无元素，因此返回 -1 。
3. **否则：** 将栈 `A` 元素全部转移至栈 `B` 中，实现元素倒序，并返回栈 `B` 的栈顶元素。
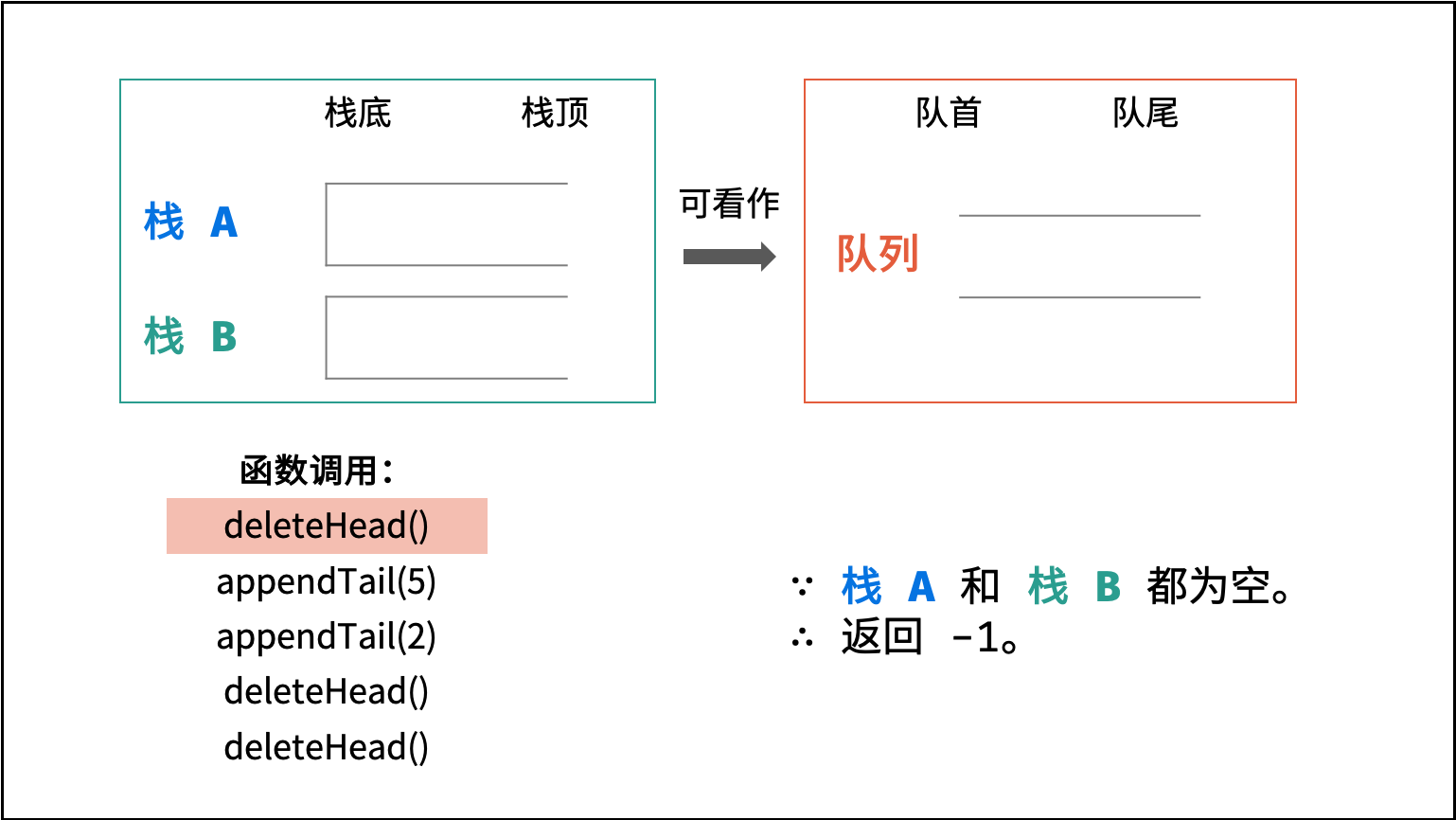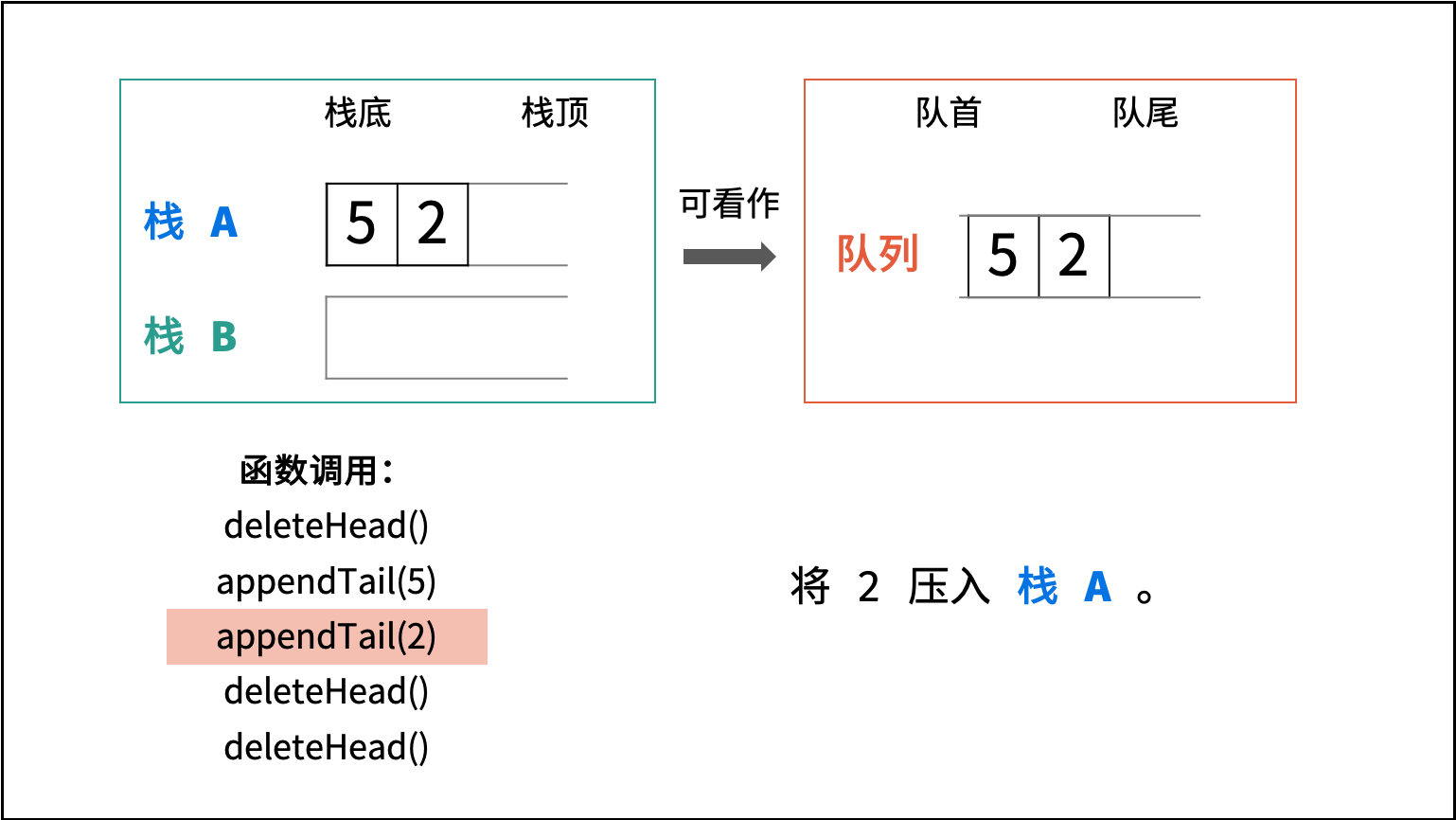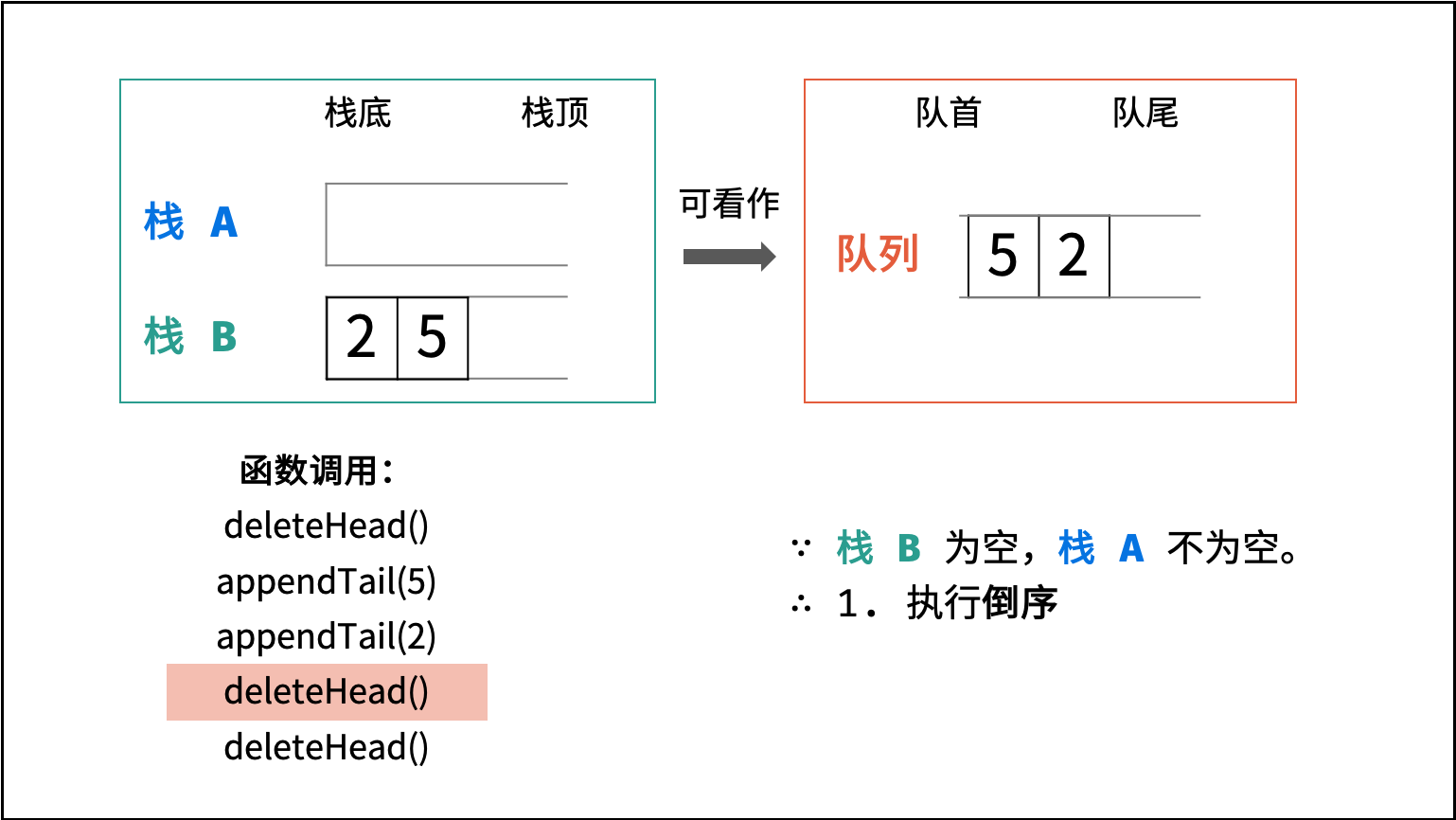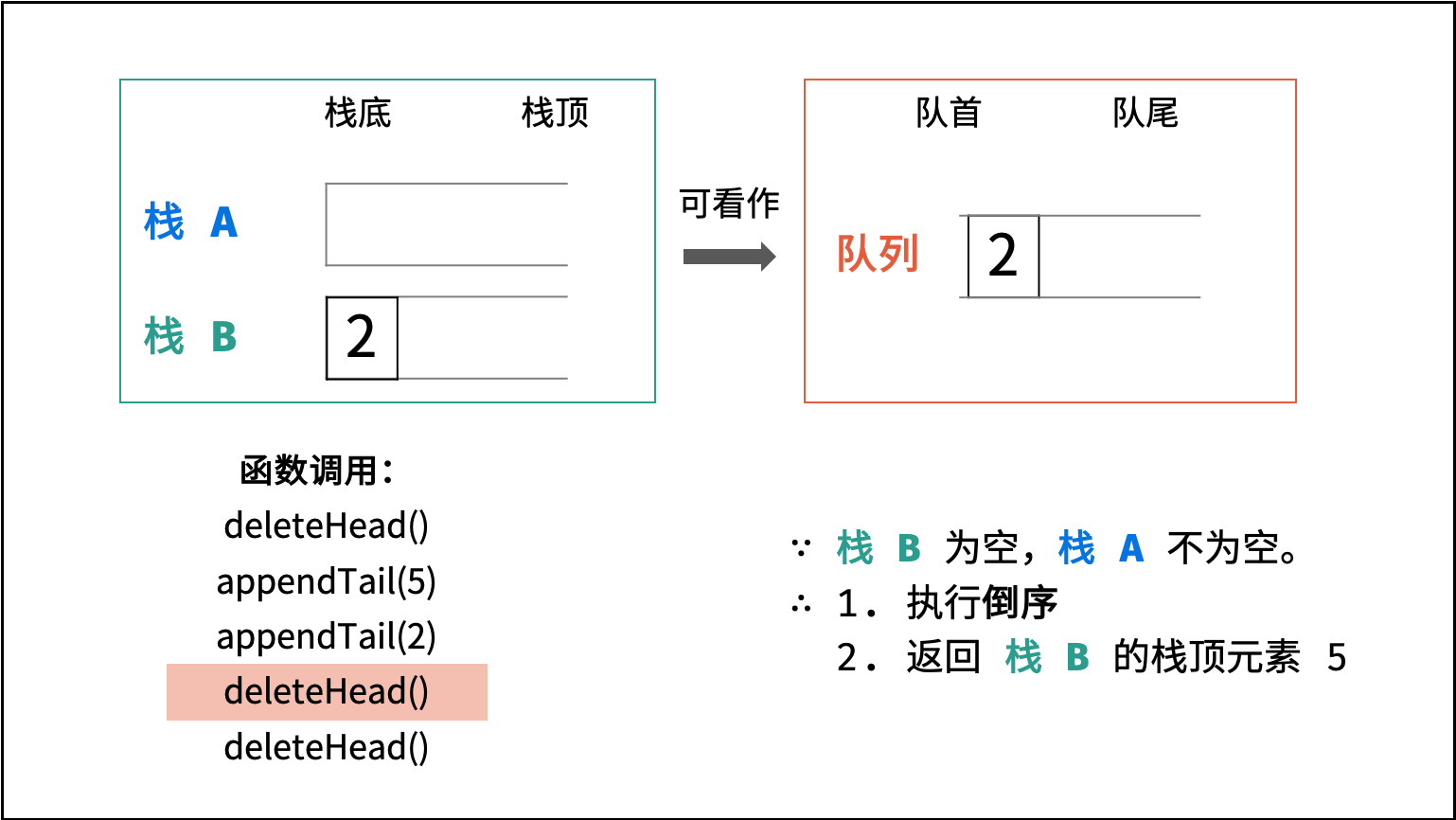<![Picture2.png](https://pic.leetcode-cn.com/1599286207-iyRyBk-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599286207-CGxWnt-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599286207-tULpWB-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599286207-aEsTfK-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599286207-VdXYtf-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599286207-heDHcK-Picture7.png),![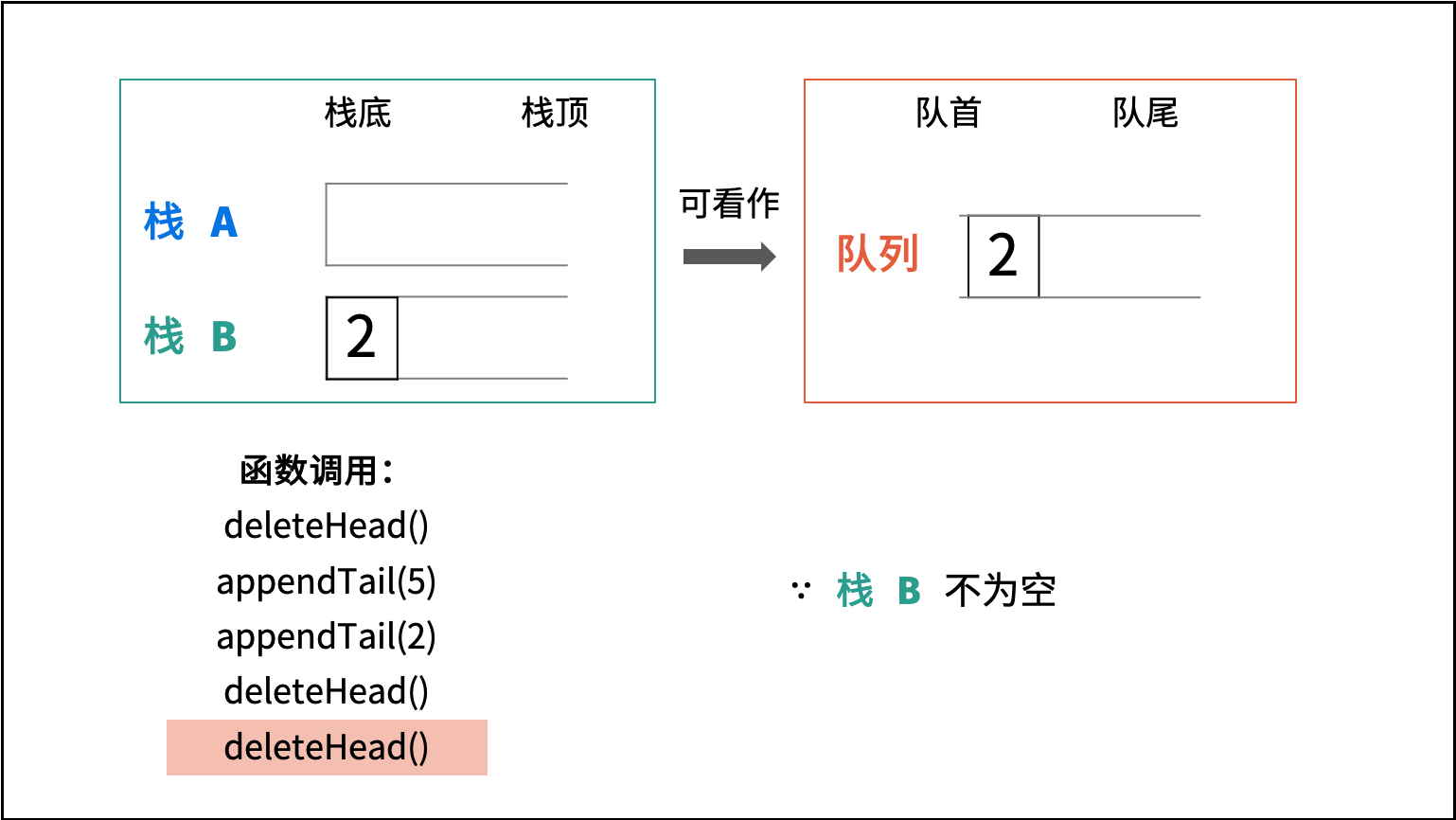Picture8.png](https://pic.leetcode-cn.com/1599286207-gwMjUh-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1599286207-xInqcE-Picture9.png)>
## 代码：
Python 和 Java 的栈的 `pop()` 函数返回栈顶元素，而 C++ 不返回；因此对于 C++ ，需要先使用 `top()` 方法暂存栈顶元素，再执行 `pop()` 出栈操作。
```Python []
class CQueue:
def __init__(self):
self.A, self.B = [], []
def appendTail(self, value: int) -> None:
self.A.append(value)
def deleteHead(self) -> int:
if self.B: return self.B.pop()
if not self.A: return -1
while self.A:
self.B.append(self.A.pop())
return self.B.pop()
```
```Java []
class CQueue {
LinkedList<Integer> A, B;
public CQueue() {
A = new LinkedList<Integer>();
B = new LinkedList<Integer>();
}
public void appendTail(int value) {
A.addLast(value);
}
public int deleteHead() {
if(!B.isEmpty()) return B.removeLast();
if(A.isEmpty()) return -1;
while(!A.isEmpty())
B.addLast(A.removeLast());
return B.removeLast();
}
}
```
```C++ []
class CQueue {
public:
stack<int> A, B;
CQueue() {}
void appendTail(int value) {
A.push(value);
}
int deleteHead() {
if(!B.empty()) {
int tmp = B.top();
B.pop();
return tmp;
}
if(A.empty()) return -1;
while(!A.empty()) {
int tmp = A.top();
A.pop();
B.push(tmp);
}
int tmp = B.top();
B.pop();
return tmp;
}
};
```
### 复杂度分析：
> 以下分析仅满足添加 $N$ 个元素并删除 $N$ 个元素，即栈初始和结束状态下都为空的情况。
- **时间复杂度：** `appendTail()`函数为 $O(1)$ ；`deleteHead()` 函数在 $N$ 次队首元素删除操作中总共需完成 $N$ 个元素的倒序。
- **空间复杂度 $O(N)$ ：** 最差情况下，栈 `A` 和 `B` 共保存 $N$ 个元素。

97
leetbook_ioa/docs/LCR 126. 斐波那契数.md Executable file
View File

@@ -0,0 +1,97 @@
## 解题思路：
斐波那契数列的定义是 $f(n + 1) = f(n) + f(n - 1)$ ，生成第 $n$ 项的做法有以下几种：
1. **递归：**
- **原理：** 把 $f(n)$ 问题的计算拆分成 $f(n-1)$ 和 $f(n-2)$ 两个子问题的计算，并递归，以 $f(0)$ 和 $f(1)$ 为终止条件。
- **缺点：** 大量重复的递归计算，例如 $f(n)$ 和 $f(n - 1)$ 两者向下递归需要 **各自计算** $f(n - 2)$ 的值。
2. **记忆化递归：**
- **原理：** 在递归的基础上，新建一个长度为 $n$ 的数组，用于在递归时存储 $f(0)$ 至 $f(n)$ 的数字值，重复遇到某数字则直接从数组取用，避免了重复的递归计算。
- **缺点：** 记忆化存储需要使用 $O(N)$ 的额外空间。
3. **动态规划：**
- **原理：** 以斐波那契数列性质 $f(n + 1) = f(n) + f(n - 1)$ 为转移方程。
- 从计算效率、空间复杂度上看，动态规划是本题的最佳解法。
> 下图帮助理解递归的 “重复计算” 概念。
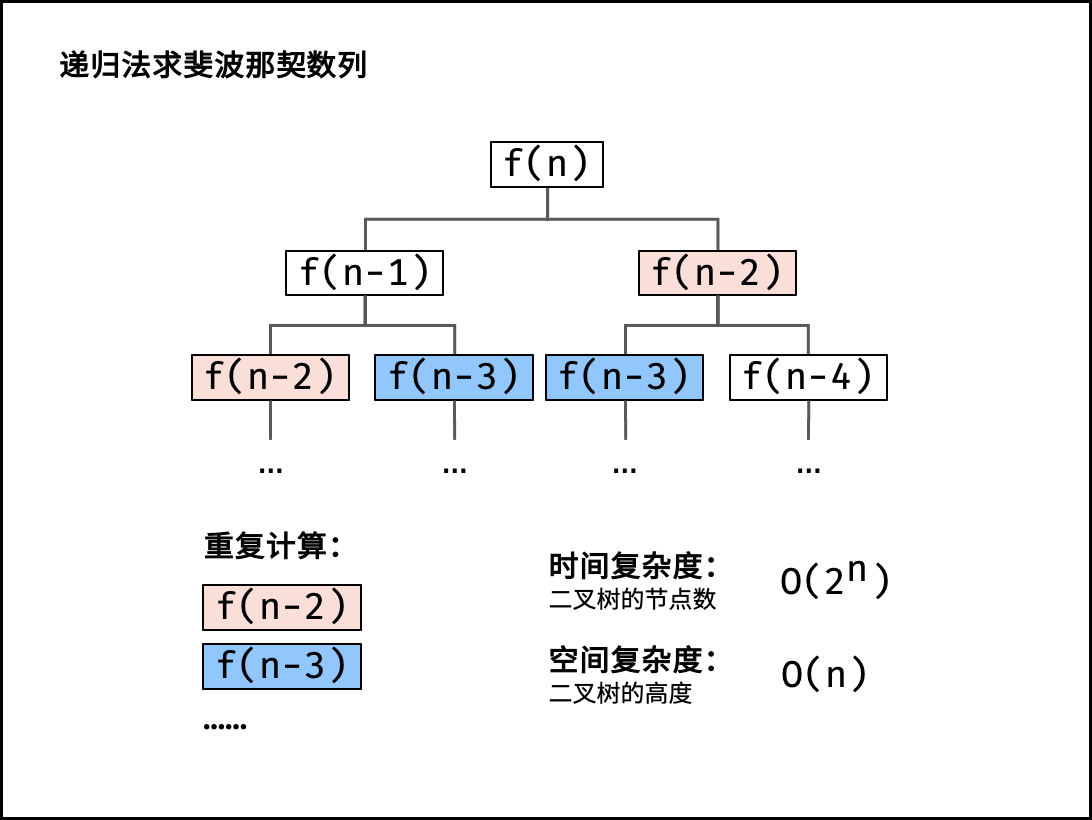![Picture1.png](https://pic.leetcode-cn.com/1599882883-mtYecf-Picture1.png){:align=center width=500}
### 动态规划解析：
- **状态定义：** 设 $dp$ 为一维数组，其中 $dp[i]$ 的值代表 斐波那契数列第 $i$ 个数字 。
- **转移方程：** $dp[i + 1] = dp[i] + dp[i - 1]$ ，即对应数列定义 $f(n + 1) = f(n) + f(n - 1)$ ；
- **初始状态：** $dp[0] = 0$, $dp[1] = 1$ ，即初始化前两个数字；
- **返回值：** $dp[n]$ ，即斐波那契数列的第 $n$ 个数字。
### 空间优化：
> 若新建长度为 $n$ 的 $dp$ 列表，则空间复杂度为 $O(N)$ 。
- 由于 $dp$ 列表第 $i$ 项只与第 $i-1$ 和第 $i-2$ 项有关，因此只需要初始化三个整形变量 `sum`, `a`, `b` ，利用辅助变量 $sum$ 使 $a, b$ 两数字交替前进即可 *（具体实现见代码）* 。
- 节省了 $dp$ 列表空间，因此空间复杂度降至 $O(1)$ 。
### 循环求余法：
> **大数越界：** 随着 $n$ 增大, $f(n)$ 会超过 `Int32` 甚至 `Int64` 的取值范围，导致最终的返回值错误。
- **求余运算规则：** 设正整数 $x, y, p$ ，求余符号为 $\odot$ ，则有 $(x + y) \odot p = (x \odot p + y \odot p) \odot p$ 。
- **解析：** 根据以上规则，可推出 $f(n) \odot p = [f(n-1) \odot p + f(n-2) \odot p] \odot p$ ，从而可以在循环过程中每次计算 $sum = (a + b) \odot 1000000007$ ，此操作与最终返回前取余等价。
<![Picture2.png](https://pic.leetcode-cn.com/1599882883-jbnPaZ-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599882883-ZIXjom-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599882883-UHnEEL-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599882883-UHtjpA-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599882883-jXtHXx-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599882883-ppWbXc-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599882883-lyXbyd-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1599882883-vhrJxv-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599882883-cIpqVP-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1599882883-NmQlPg-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1599882883-coycTs-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1599882883-FZVjJi-Picture13.png)>
## 代码：
```Python []
class Solution:
def fib(self, n: int) -> int:
a, b = 0, 1
for _ in range(n):
a, b = b, (a + b) % 1000000007
return a
```
```Java []
class Solution {
public int fib(int n) {
int a = 0, b = 1, sum;
for(int i = 0; i < n; i++){
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
}
```
```C++ []
class Solution {
public:
int fib(int n) {
int a = 0, b = 1, sum;
for(int i = 0; i < n; i++){
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
};
```
由于 Python 中整形数字的大小限制取决计算机的内存（可理解为无限大），因此也可不考虑大数越界问题；但当数字很大时，加法运算的效率也会降低，因此不推荐此方法。
```Python []
# 不考虑大数越界问题
class Solution:
def fib(self, n: int) -> int:
a, b = 0, 1
for _ in range(n):
a, b = b, a + b
return a % 1000000007
```
### 复杂度分析：
- **时间复杂度 $O(n)$ ：** 计算 $f(n)$ 需循环 $n$ 次，每轮循环内计算操作使用 $O(1)$ 。
- **空间复杂度 $O(1)$ ：** 几个标志变量使用常数大小的额外空间。

93
leetbook_ioa/docs/LCR 127. 跳跃训练.md Executable file
View File

@@ -0,0 +1,93 @@
## 解题思路：
设跳上 $n$ 级平台有 $f(n)$ 种跳法。在所有跳法中，青蛙的最后一步只有两种情况： **跳上 $1$ 级或 $2$ 级平台**。
1. **当为 $1$ 级平台：** 剩 $n-1$ 个平台，此情况共有 $f(n-1)$ 种跳法；
2. **当为 $2$ 级平台：** 剩 $n-2$ 个平台，此情况共有 $f(n-2)$ 种跳法。
即 $f(n)$ 为以上两种情况之和，即 $f(n)=f(n-1)+f(n-2)$ ，以上递推性质为斐波那契数列。因此，本题可转化为 **求斐波那契数列第 $n$ 项的值** ，唯一的不同在于起始数字不同。
- 跳跃训练问题： $f(0)=1$ , $f(1)=1$ , $f(2)=2$ ；
- 斐波那契数列问题： $f(0)=0$ , $f(1)=1$ , $f(2)=1$ 。
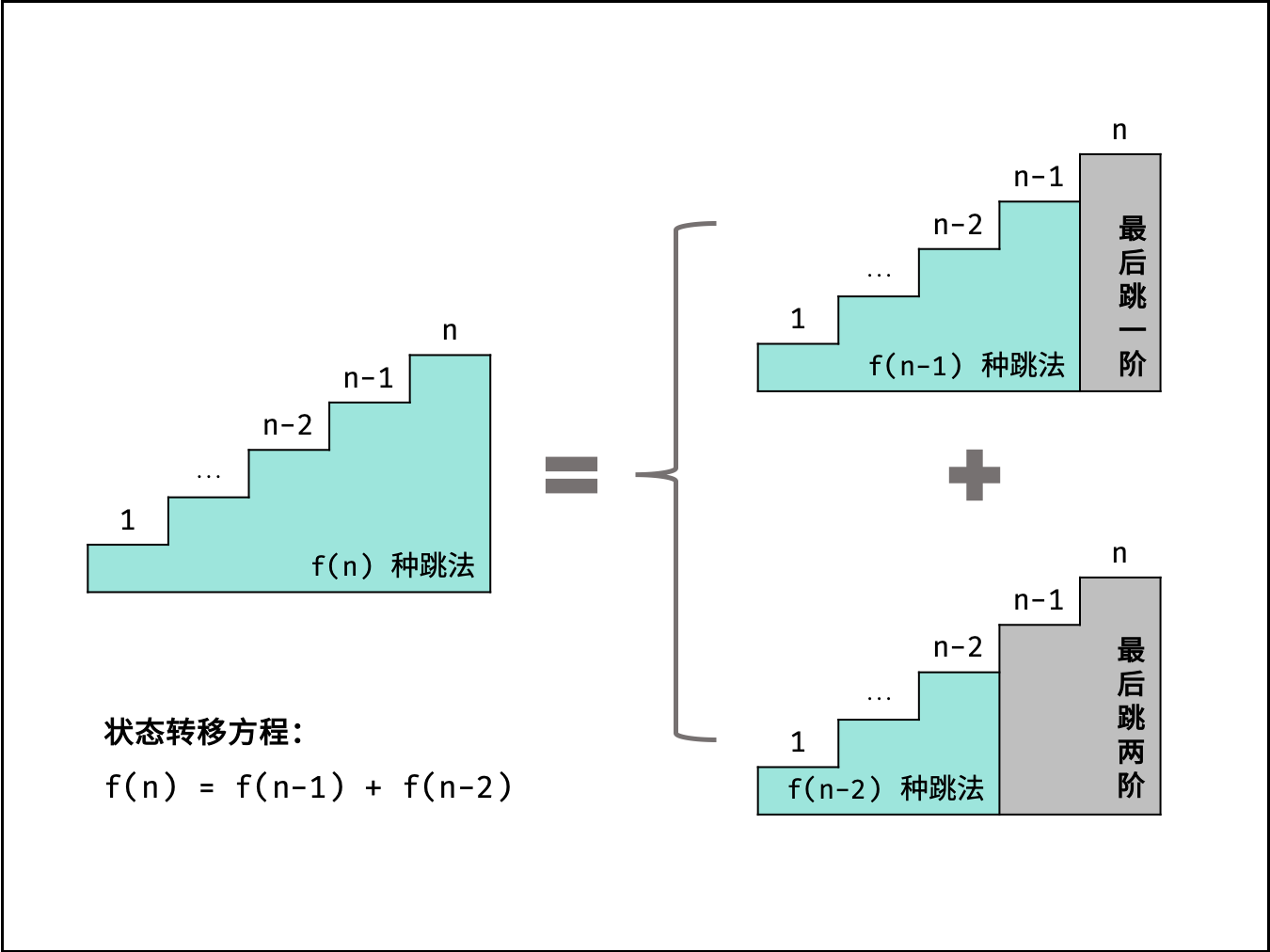![Picture1.png](https://pic.leetcode-cn.com/1599883153-UckfTw-Picture1.png){:align=center width=500}
### 动态规划解析：
- **状态定义：** 设 $dp$ 为一维数组，其中 $dp[i]$ 的值代表斐波那契数列的第 $i$ 个数字。
- **转移方程：** $dp[i + 1] = dp[i] + dp[i - 1]$ ，即对应数列定义 $f(n + 1) = f(n) + f(n - 1)$ ；
- **初始状态：** $dp[0] = 1$, $dp[1] = 1$ ，即初始化前两个数字；
- **返回值：** $dp[n]$ ，即斐波那契数列的第 $n$ 个数字。
### 空间优化：
> 若新建长度为 $n$ 的 $dp$ 列表，则空间复杂度为 $O(N)$ 。
- 由于 $dp$ 列表第 $i$ 项只与第 $i-1$ 和第 $i-2$ 项有关，因此只需要初始化三个整形变量 `sum`, `a`, `b` ，利用辅助变量 $sum$ 使 $a, b$ 两数字交替前进即可 *（具体实现见代码）* 。
- 因为节省了 $dp$ 列表空间，因此空间复杂度降至 $O(1)$ 。
### 循环求余法：
> **大数越界：** 随着 $n$ 增大, $f(n)$ 会超过 `Int32` 甚至 `Int64` 的取值范围，导致最终的返回值错误。
- **求余运算规则：** 设正整数 $x, y, p$ ，求余符号为 $\odot$ ，则有 $(x + y) \odot p = (x \odot p + y \odot p) \odot p$ 。
- **解析：** 根据以上规则，可推出 $f(n) \odot p = [f(n-1) \odot p + f(n-2) \odot p] \odot p$ ，从而可以在循环过程中每次计算 $sum = a + b \odot 1000000007$ ，此操作与最终返回前取余等价。
<![Picture2.png](https://pic.leetcode-cn.com/1599883153-iXEZvr-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599883153-MjJsdM-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599883153-kMaCBQ-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599883153-jVtBVj-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599883153-EsemaN-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599883153-wznsCe-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599883153-mVlvjo-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1599883153-zzFSWJ-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599883153-LmZgWM-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1599883153-jSUeMz-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1599883153-kRKefY-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1599883153-vEYzWk-Picture13.png)>
## 代码：
```Python []
class Solution:
def trainWays(self, num: int) -> int:
a, b = 1, 1
for _ in range(num):
a, b = b, (a + b) % 1000000007
return a
```
```Java []
class Solution {
public int trainWays(int num) {
int a = 1, b = 1, sum;
for(int i = 0; i < num; i++){
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
}
```
```C++ []
class Solution {
public:
int trainWays(int num) {
int a = 1, b = 1, sum;
for(int i = 0; i < num; i++){
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
};
```
由于 Python 中整形数字的大小限制取决计算机的内存（可理解为无限大），因此也可不考虑大数越界问题；但当数字很大时，加法运算的效率也会降低，因此不推荐此方法。
```Python []
# 不考虑大数越界问题
class Solution:
def trainWays(self, num: int) -> int:
a, b = 1, 1
for _ in range(num):
a, b = b, a + b
return a % 1000000007
```
### 复杂度分析：
- **时间复杂度 $O(n)$ ：** 计算 $f(n)$ 需循环 $n$ 次，每轮循环内计算操作使用 $O(1)$ 。
- **空间复杂度 $O(1)$ ：** 几个标志变量使用常数大小的额外空间。

161
leetbook_ioa/docs/LCR 128. 库存管理 I.md Executable file
View File

@@ -0,0 +1,161 @@
## 解题思路：
如下图所示，寻找旋转数组的最小元素即为寻找 **右排序数组** 的首个元素 $stock[x]$ ，称 $x$ 为 **旋转点** 。
> 下图中的 `numbers` 对应本题的 `stock` 。
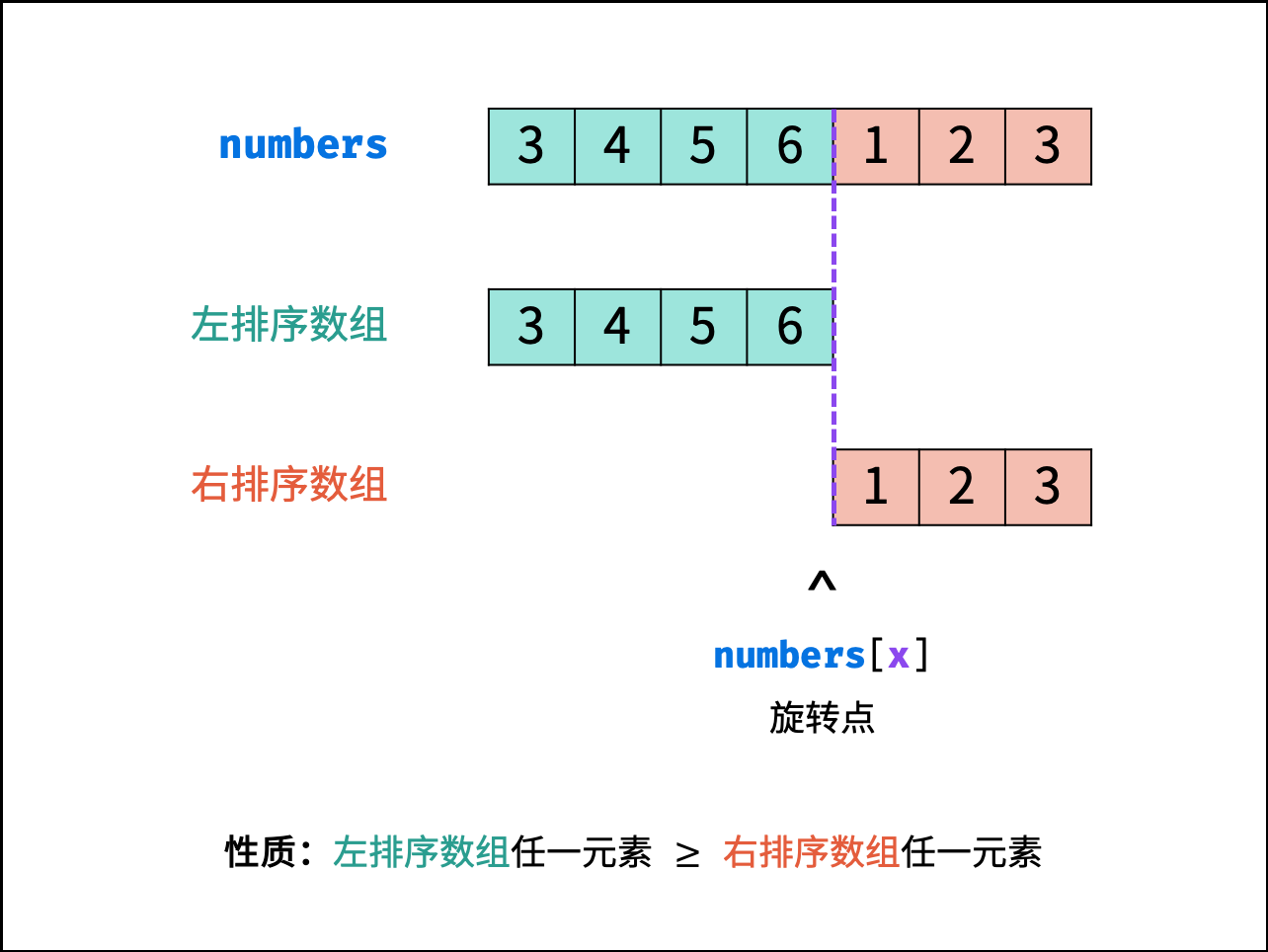![Picture1.png](https://pic.leetcode-cn.com/1599404042-JMvjtL-Picture1.png){:align=center width=450}
排序数组的查找问题首先考虑使用 **二分法** 解决，其可将 **遍历法** 的 **线性级别** 时间复杂度降低至 **对数级别** 。
### 算法流程：
1. **初始化：** 声明 $i$, $j$ 双指针分别指向 $stock$ 数组左右两端；
2. **循环二分：** 设 $m = (i + j) / 2$ 为每次二分的中点（ "`/`" 代表向下取整除法，因此恒有 $i \leq m < j$ ），可分为以下三种情况：
1. **当 $stock[m] > stock[j]$ 时：** $m$ 一定在 左排序数组 中，即旋转点 $x$ 一定在 $[m + 1, j]$ 闭区间内，因此执行 $i = m + 1$；
2. **当 $stock[m] < stock[j]$ 时：** $m$ 一定在 右排序数组 中，即旋转点 $x$ 一定在$[i, m]$ 闭区间内，因此执行 $j = m$；
3. **当 $stock[m] = stock[j]$ 时：** 无法判断 $m$ 在哪个排序数组中，即无法判断旋转点 $x$ 在 $[i, m]$ 还是 $[m + 1, j]$ 区间中。**解决方案：** 执行 $j = j - 1$ 缩小判断范围，分析见下文。
3. **返回值：** 当 $i = j$ 时跳出二分循环，并返回 **旋转点的值** $stock[i]$ 即可。
### 正确性证明：
当 $stock[m] = stock[j]$ 时，无法判定 $m$ 在左（右）排序数组，自然也无法通过二分法安全地缩小区间，因为其会导致旋转点 $x$ 不在区间 $[i, j]$ 内。举例如下：
> 设以下两个旋转点值为 $0$ 的示例数组，则当 $i = 0$, $j = 4$ 时 $m = 2$ ，两示例结果不同。
> 示例一 $[1, 0, 1, 1, 1]$ ：旋转点 $x = 1$ ，因此 $m = 2$ 在 **右排序数组** 中。
> 示例二 $[1, 1, 1, 0, 1]$ ：旋转点 $x = 3$ ，因此 $m = 2$ 在 **左排序数组** 中。
而证明 $j = j - 1$ 正确（缩小区间安全性），需分为两种情况：
1. **当 $x < j$ 时：** 易得执行 $j = j - 1$ 后，旋转点 $x$ 仍在区间 $[i, j]$ 内。
2. **当 $x = j$ 时：** 执行 $j = j - 1$ 后越过（丢失）了旋转点 $x$ ，但最终返回的元素值 $stock[i]$ 仍等于旋转点值 $stock[x]$ 。
1. 由于 $x = j$ ，因此 $stock[x] = stock[j] = stock[m] \leq number[i]$ ;
2. 又由于 $i \leq m <j$ 恒成立，因此有 $m < x$ ，即此时 $m$ 一定在左排序数组中，因此 $stock[m] \geq stock[i]$ ;
综合 `1.` , `2.` ，可推出 $stock[i] = stock[m]$ ，且区间 $[i, m]$ 内所有元素值相等，即有：
$$
stock[i] = stock[i+1] = \cdots = stock[m] = stock[x]
$$
此时，执行 $j = j - 1$ 后虽然丢失了旋转点 $x$ ，但之后区间 $[i, j]$ 只包含左排序数组，二分下去返回的一定是本轮的 $stock[i]$ ，而其与 $stock[x]$ 相等。
> 综上所述，此方法可以保证返回值 $stock[i]$ 等于旋转点值 $stock[x]$ ，但在少数特例下 $i \ne x$ ；而本题目只要求返回 “旋转点的值” ，因此本方法正确。
**补充思考：** 为什么本题二分法不用 $stock[m]$ 和 $stock[i]$ 作比较？
二分目的是判断 $m$ 在哪个排序数组中，从而缩小区间。而在 $stock[m] > stock[i]$情况下，无法判断 $m$ 在哪个排序数组中。本质上是由于 $j$ 初始值肯定在右排序数组中；$i$ 初始值无法确定在哪个排序数组中。举例如下：
> 对于以下两示例，当 $i = 0, j = 4, m = 2$ 时，有 `stock[m] > stock[i]` ，而结果不同。
> $[1, 2, 3, 4 ,5]$ 旋转点 $x = 0$ ： $m$ 在右排序数组（此示例只有右排序数组）；
> $[3, 4, 5, 1 ,2]$ 旋转点 $x = 3$ ： $m$ 在左排序数组。
<![Picture2.png](https://pic.leetcode-cn.com/1599404042-VzHrmU-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599404042-fNXpQJ-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599404042-qbOflt-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599404042-sBLuCR-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599404042-lYmLFN-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599404042-HkRBZW-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599404366-eOwigV-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1599404366-ngPDoD-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599404438-qzDKAI-Picture10.png)>
### 复杂度分析：
- **时间复杂度 $O(\log N)$ ：** 在特例情况下（例如 $[1, 1, 1, 1]$），会退化到 $O(N)$。
- **空间复杂度 $O(1)$ ：** $i$ , $j$ , $m$ 变量使用常数大小的额外空间。
## 代码：
```Python []
class Solution:
def stockManagement(self, stock: List[int]) -> int:
i, j = 0, len(stock) - 1
while i < j:
m = (i + j) // 2
if stock[m] > stock[j]: i = m + 1
elif stock[m] < stock[j]: j = m
else: j -= 1
return stock[i]
```
```Java []
class Solution {
public int stockManagement(int[] stock) {
int i = 0, j = stock.length - 1;
while (i < j) {
int m = (i + j) / 2;
if (stock[m] > stock[j]) i = m + 1;
else if (stock[m] < stock[j]) j = m;
else j--;
}
return stock[i];
}
}
```
```C++ []
class Solution {
public:
int stockManagement(vector<int>& stock) {
int i = 0, j = stock.size() - 1;
while (i < j) {
int m = (i + j) / 2;
if (stock[m] > stock[j]) i = m + 1;
else if (stock[m] < stock[j]) j = m;
else j--;
}
return stock[i];
}
};
```
实际上，当出现 $stock[m] = stock[j]$ 时，一定有区间 $[i, m]$ 内所有元素相等 或 区间 $[m, j]$ 内所有元素相等（或两者皆满足）。对于寻找此类数组的最小值问题，可直接放弃二分查找，而使用线性查找替代。
```Python []
class Solution:
def stockManagement(self, stock: List[int]) -> int:
i, j = 0, len(stock) - 1
while i < j:
m = (i + j) // 2
if stock[m] > stock[j]: i = m + 1
elif stock[m] < stock[j]: j = m
else: return min(stock[i:j])
return stock[i]
```
```Java []
class Solution {
public int stockManagement(int[] stock) {
int i = 0, j = stock.length - 1;
while (i < j) {
int m = (i + j) / 2;
if (stock[m] > stock[j]) i = m + 1;
else if (stock[m] < stock[j]) j = m;
else {
int x = i;
for(int k = i + 1; k < j; k++) {
if(stock[k] < stock[x]) x = k;
}
return stock[x];
}
}
return stock[i];
}
}
```
```C++ []
class Solution {
public:
int stockManagement(vector<int>& stock) {
int i = 0, j = stock.size() - 1;
while (i < j) {
int m = (i + j) / 2;
if (stock[m] > stock[j]) i = m + 1;
else if (stock[m] < stock[j]) j = m;
else {
int x = i;
for(int k = i + 1; k < j; k++) {
if(stock[k] < stock[x]) x = k;
}
return stock[x];
}
}
return stock[i];
}
};
```

103
leetbook_ioa/docs/LCR 129. 字母迷宫.md Executable file
View File

@@ -0,0 +1,103 @@
## 解题思路：
本问题是典型的回溯问题，可使用 **深度优先搜索（DFS）+ 剪枝** 解决。
- **深度优先搜索：** 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
- **剪枝：** 在搜索中，遇到 `这条路不可能和目标字符串匹配成功` 的情况（*例如：此矩阵元素和目标字符不同、此元素已被访问）*，则应立即返回，称之为 `可行性剪枝` 。
> 下图中的 `word` 对应本题的 `target` 。
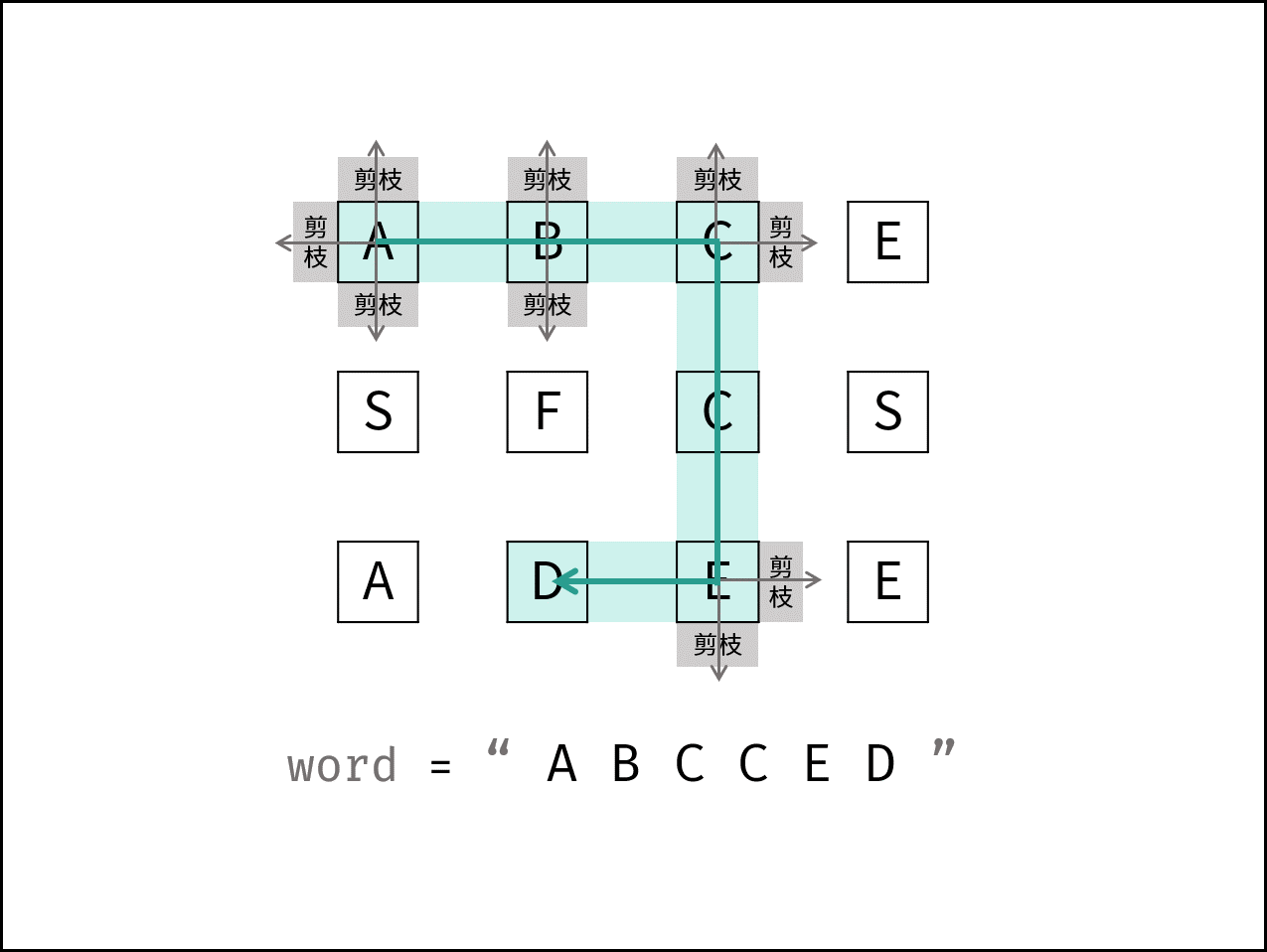![Picture0.png](https://pic.leetcode-cn.com/1604944042-glmqJO-Picture0.png){:align=center width=500}
### DFS 解析：
- **递归参数：** 当前元素在矩阵 `grid` 中的行列索引 `i` 和 `j` ，当前目标字符在 `target` 中的索引 `k` 。
- **终止条件：**
1. 返回 $\text{false}$ ： (1) 行或列索引越界 **或** (2) 当前矩阵元素与目标字符不同 **或** (3) 当前矩阵元素已访问过 （ (3) 可合并至 (2) ） 。
2. 返回 $\text{true}$ ： `k = len(target) - 1` ，即字符串 `target` 已全部匹配。
- **递推工作：**
1. 标记当前矩阵元素： 将 `grid[i][j]` 修改为 **空字符** `''` ，代表此元素已访问过，防止之后搜索时重复访问。
2. 搜索下一单元格： 朝当前元素的 **上、下、左、右** 四个方向开启下层递归，使用 `或` 连接 （代表只需找到一条可行路径就直接返回，不再做后续 DFS ），并记录结果至 `res` 。
3. 还原当前矩阵元素： 将 `grid[i][j]` 元素还原至初始值，即 `target[k]` 。
- **返回值：** 返回布尔量 `res` ，代表是否搜索到目标字符串。
> 使用空字符（Python: `''` , Java/C++: `'\0'` ）做标记是为了防止标记字符与矩阵原有字符重复。当存在重复时，此算法会将矩阵原有字符认作标记字符，从而出现错误。
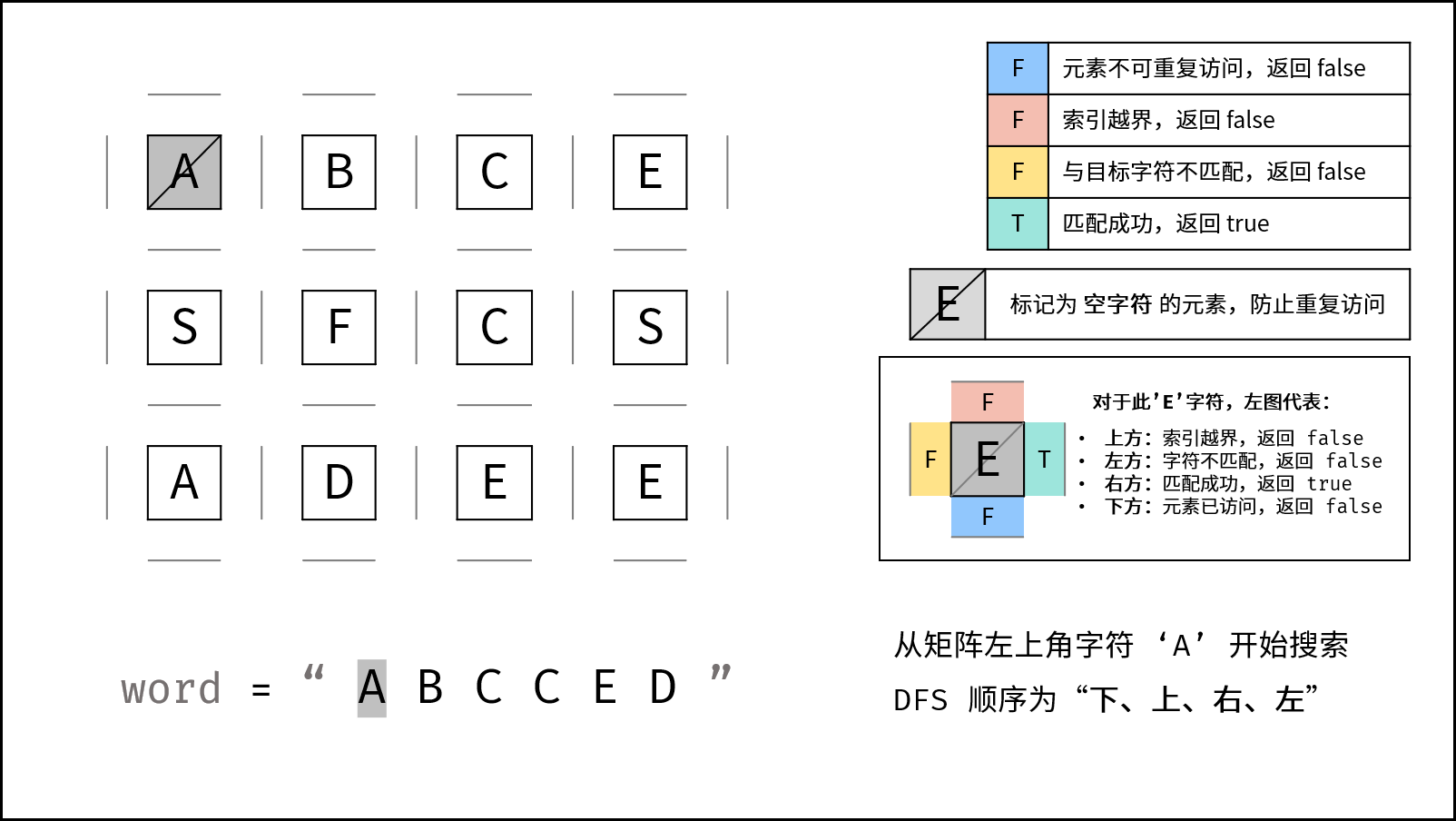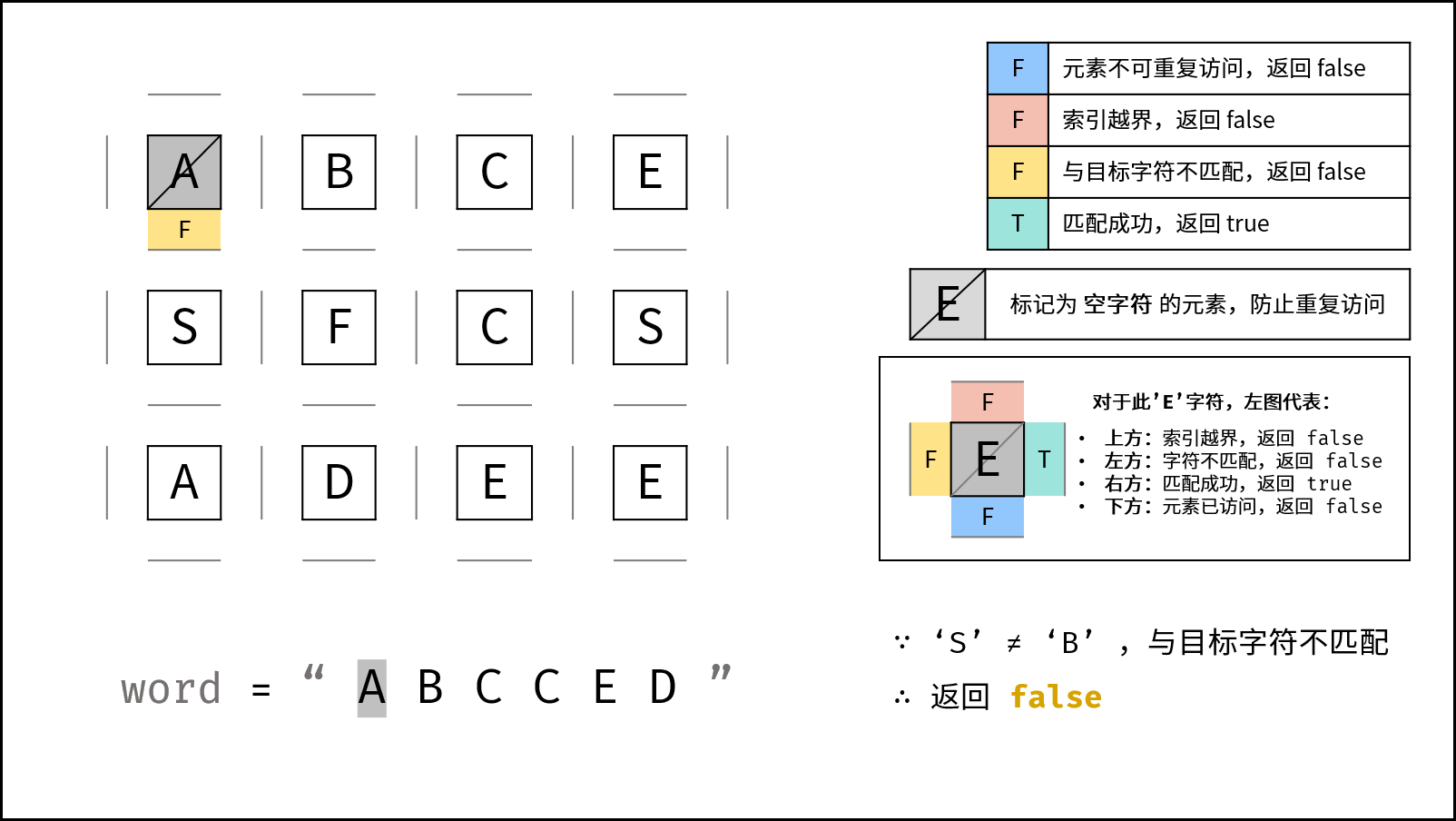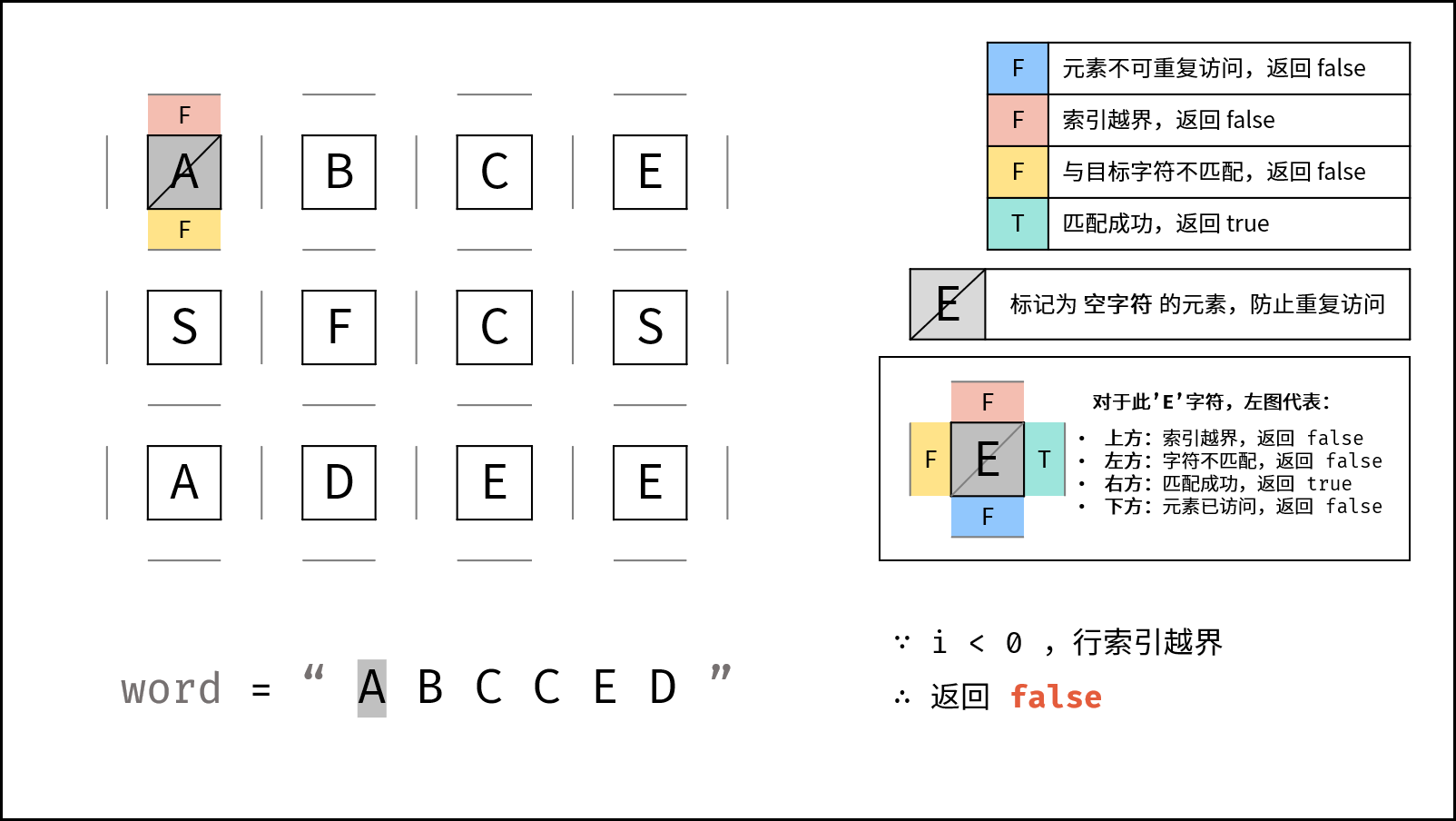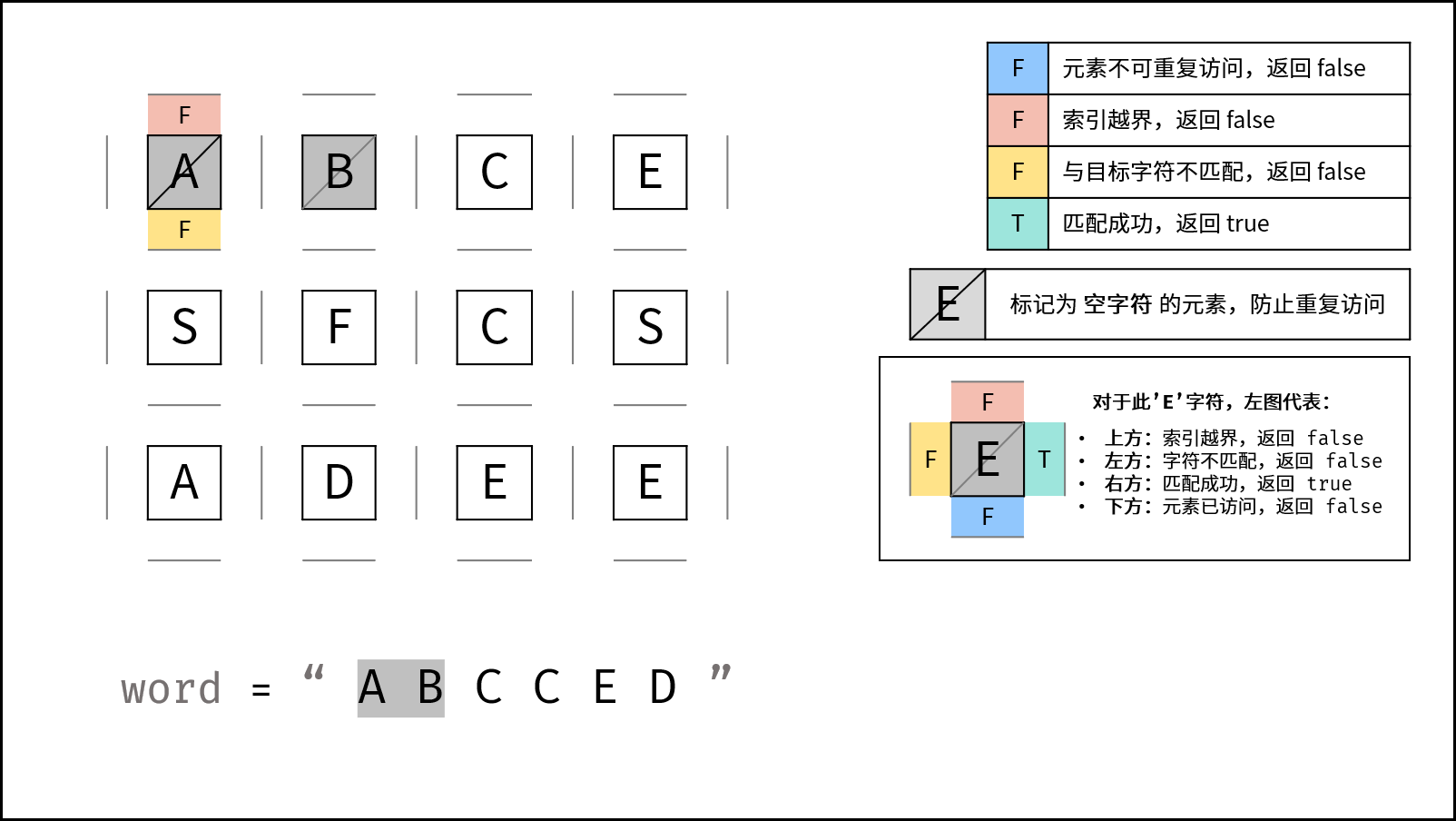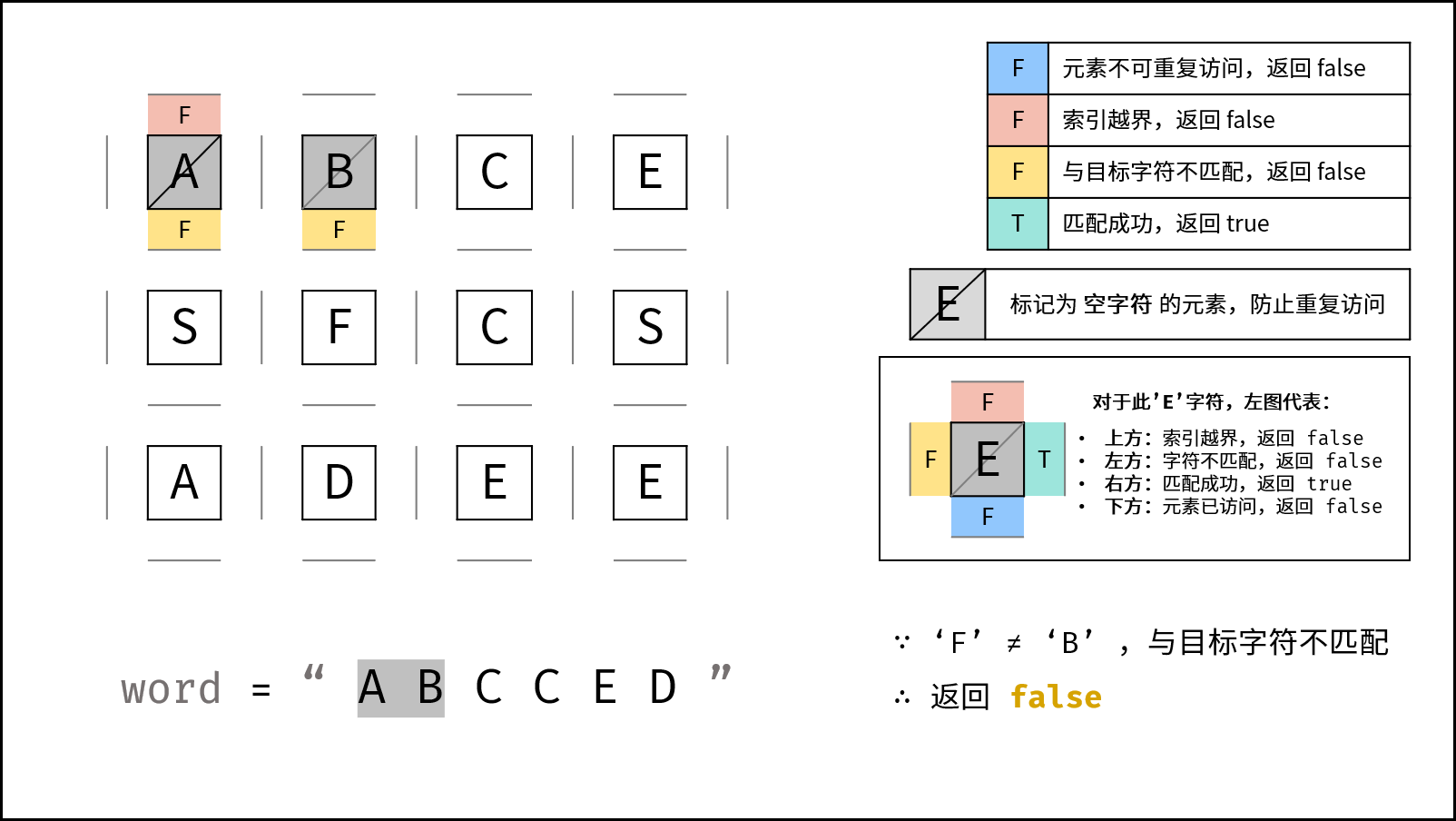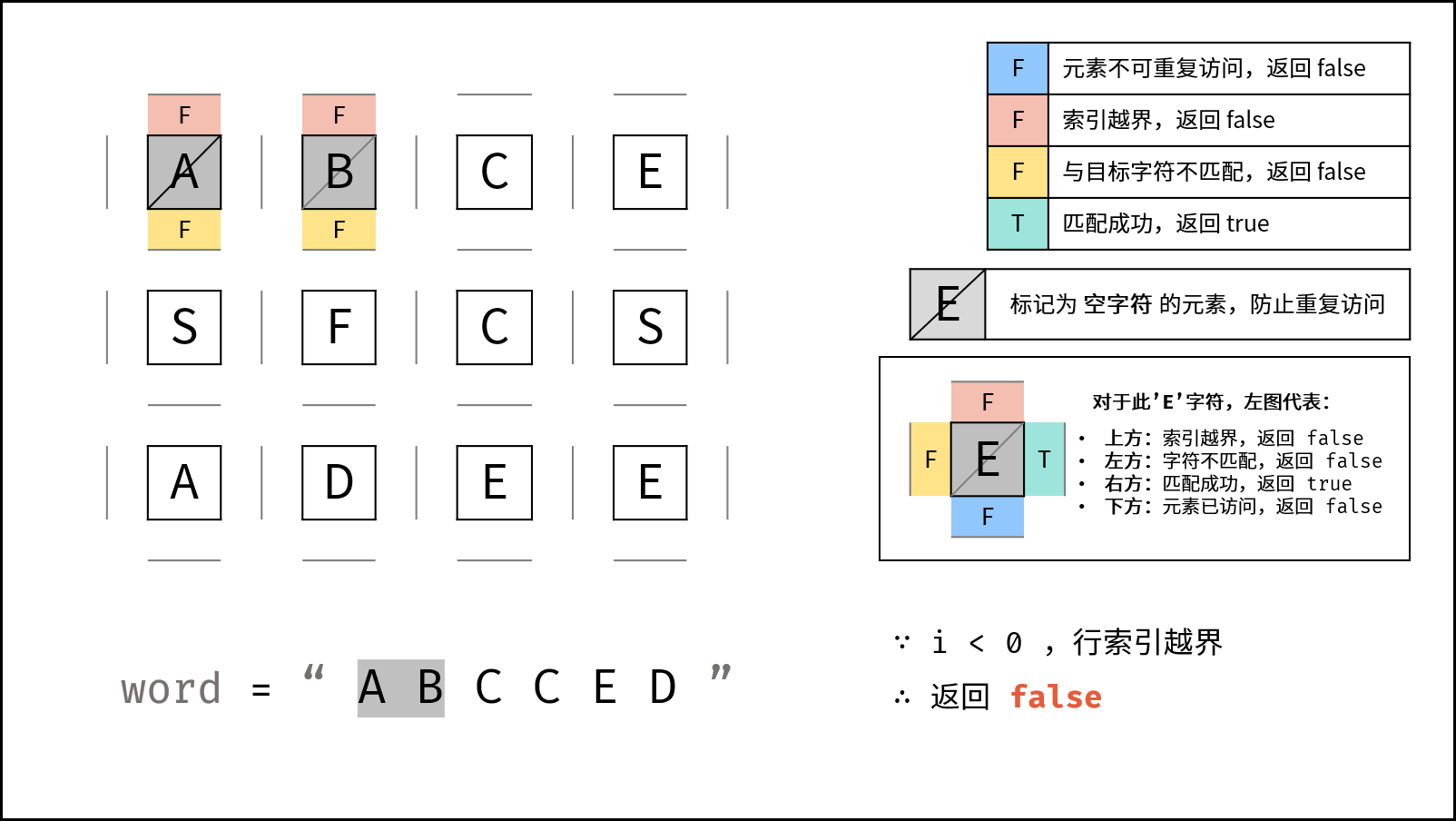<![Picture1.png](https://pic.leetcode-cn.com/1600793567-fPZPYj-Picture1.png),![Picture2.png](https://pic.leetcode-cn.com/1600793567-hVwomN-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600793567-yoOQer-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600793567-qyZcNF-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600793567-pvxYVP-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600793567-izfBtb-Picture6.png),![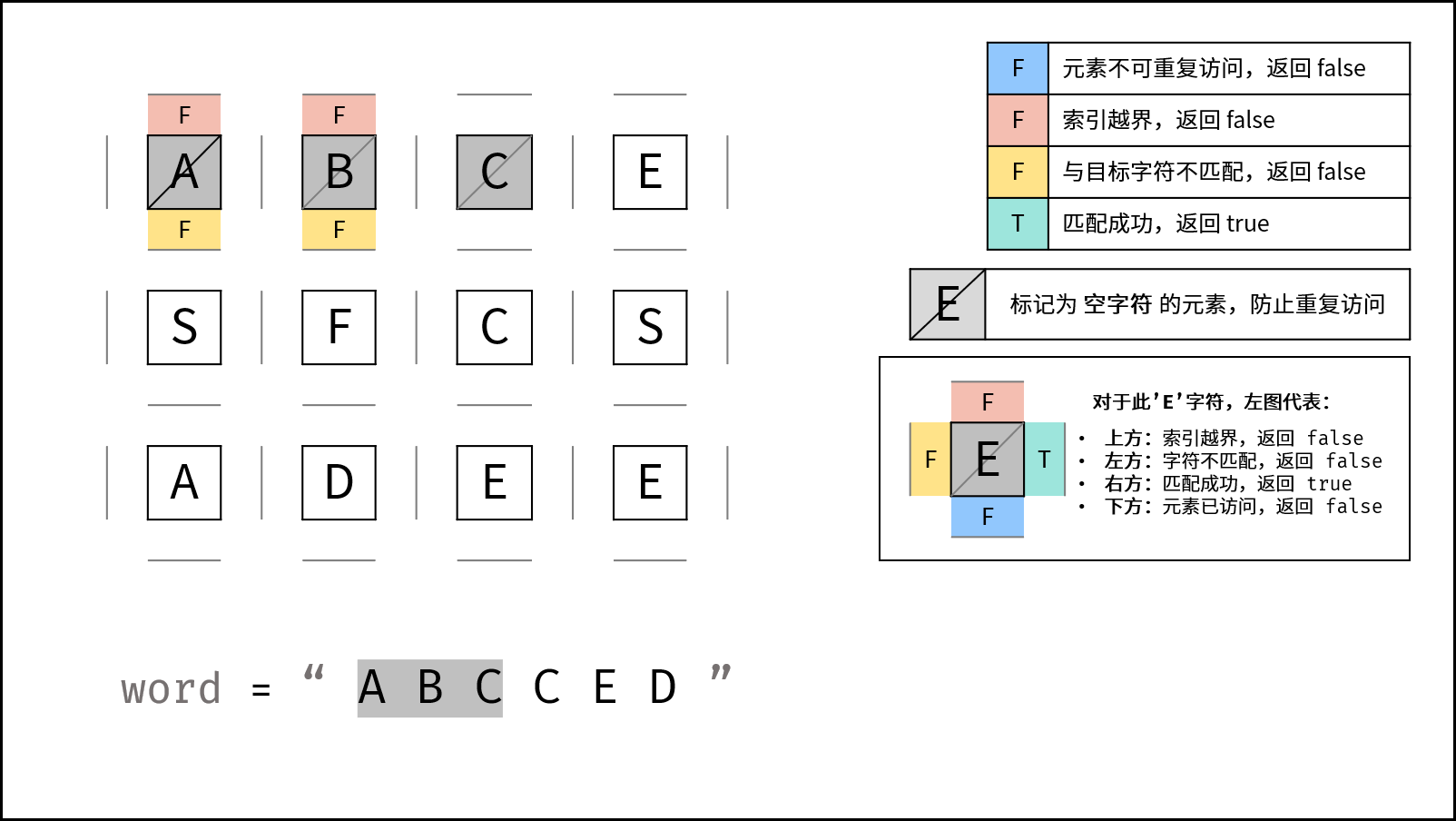Picture7.png](https://pic.leetcode-cn.com/1600793567-bwnSPQ-Picture7.png),![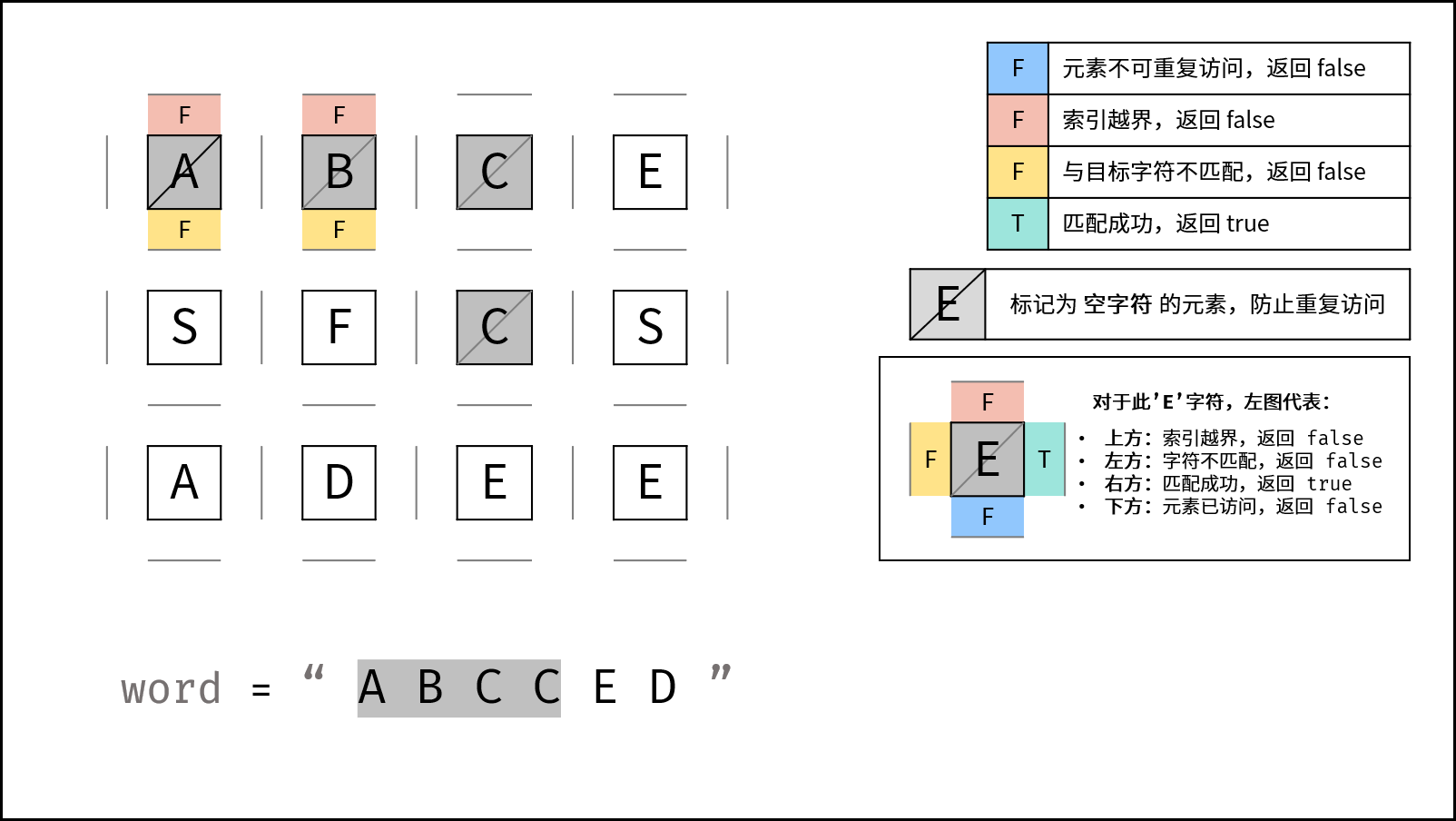Picture8.png](https://pic.leetcode-cn.com/1600793567-pnRRIE-Picture8.png),![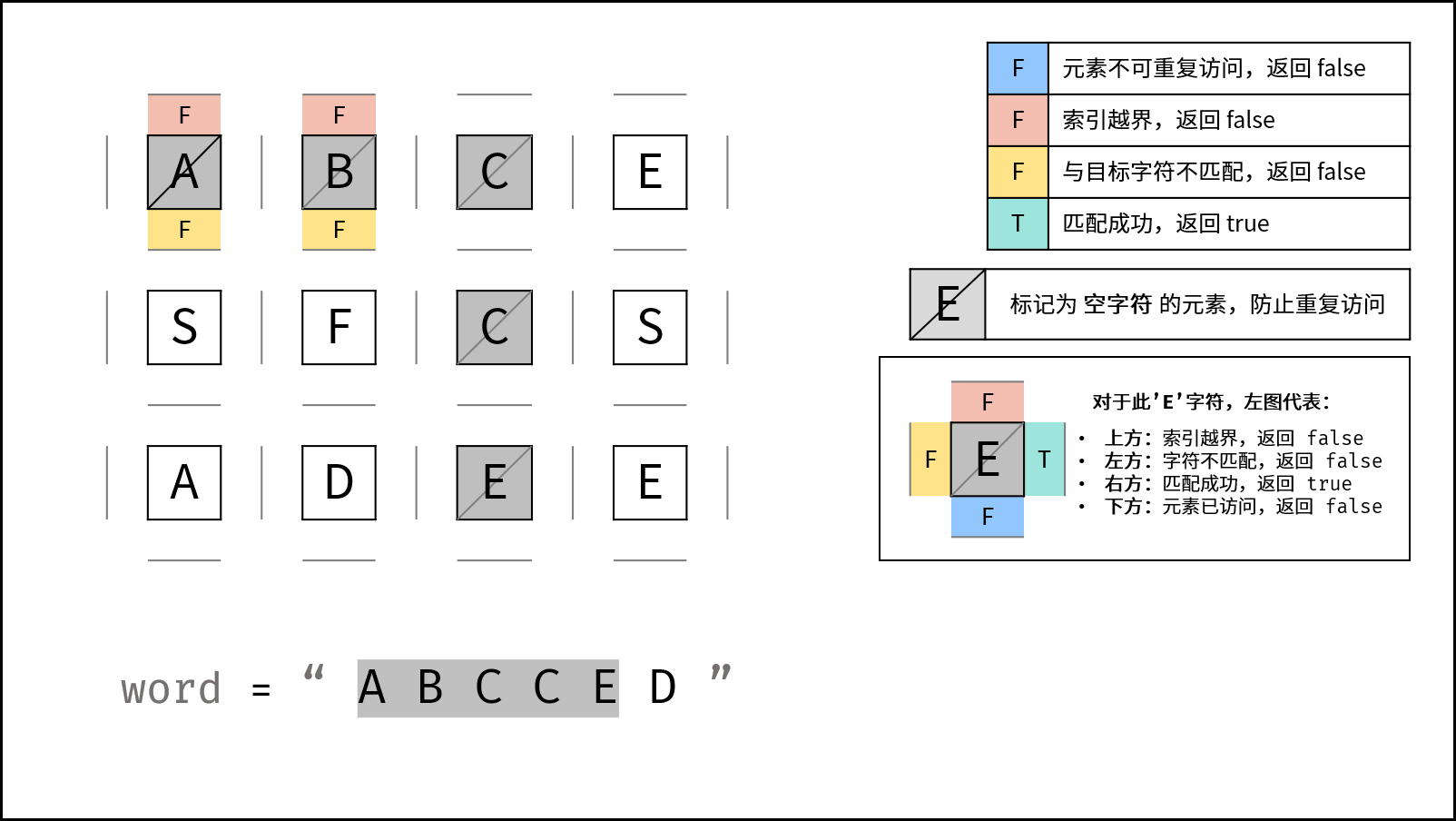Picture9.png](https://pic.leetcode-cn.com/1600793567-yQNohz-Picture9.png),![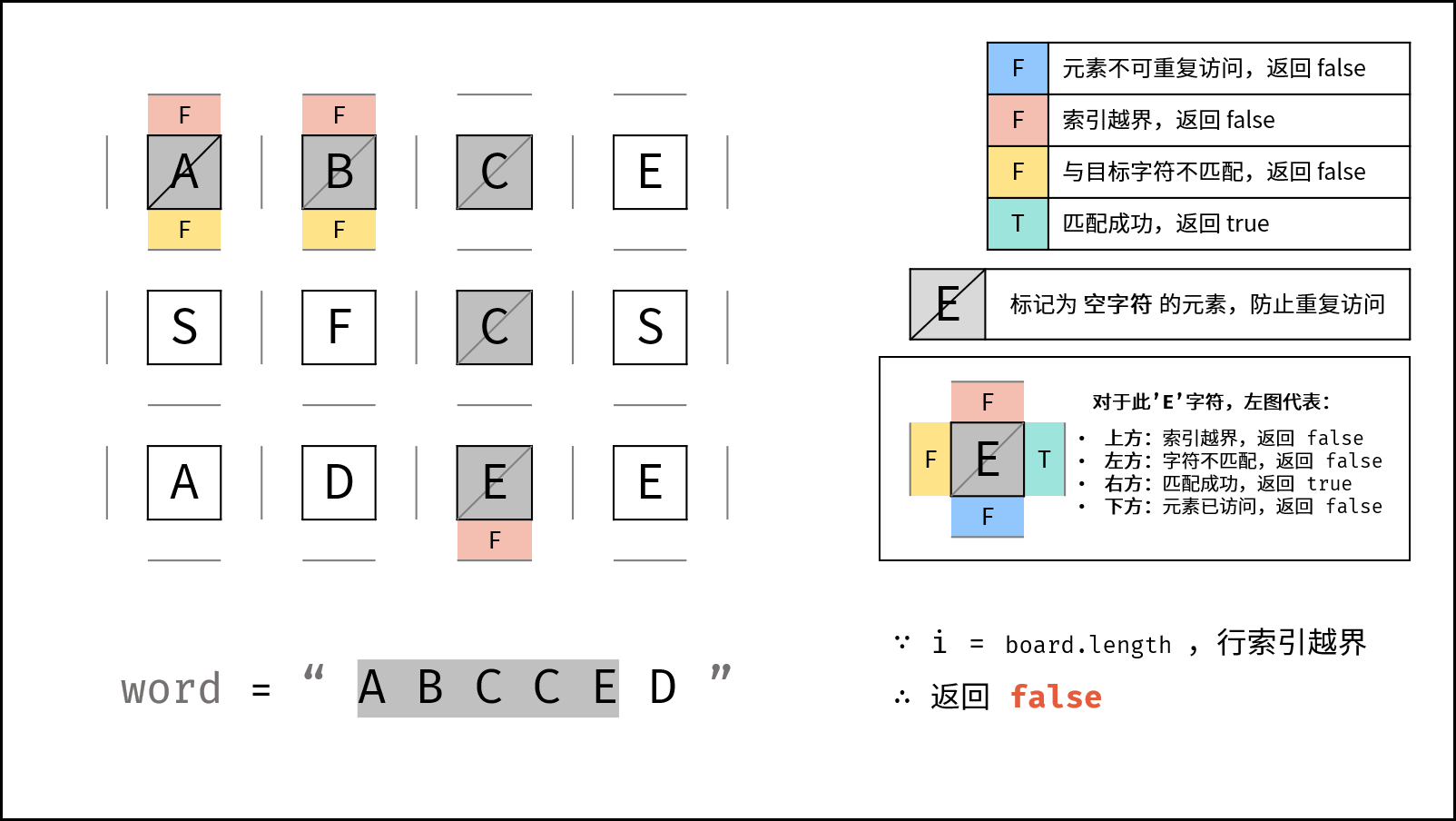Picture10.png](https://pic.leetcode-cn.com/1600793567-zLOKmi-Picture10.png),![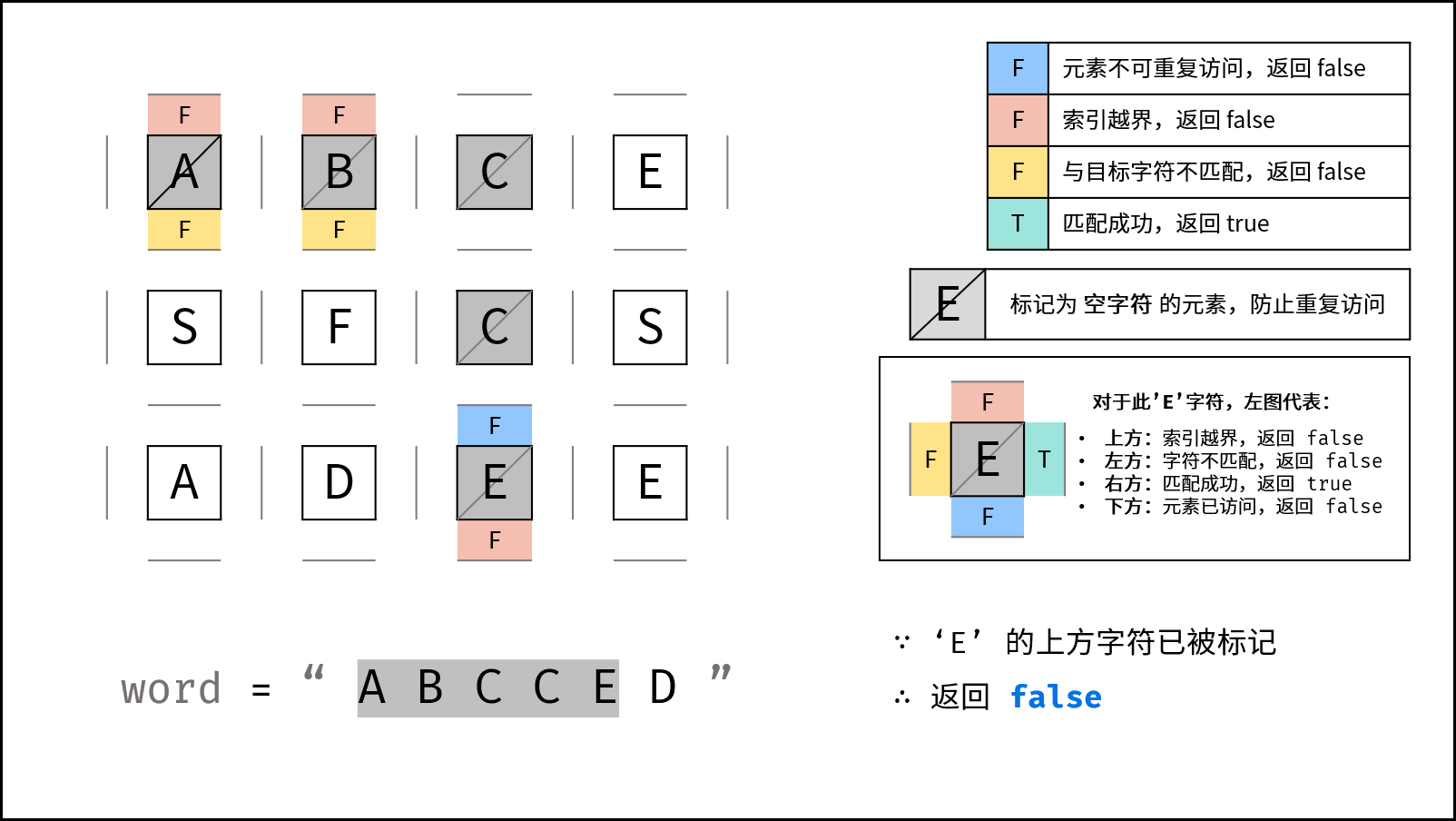Picture11.png](https://pic.leetcode-cn.com/1600793567-neMJnx-Picture11.png),![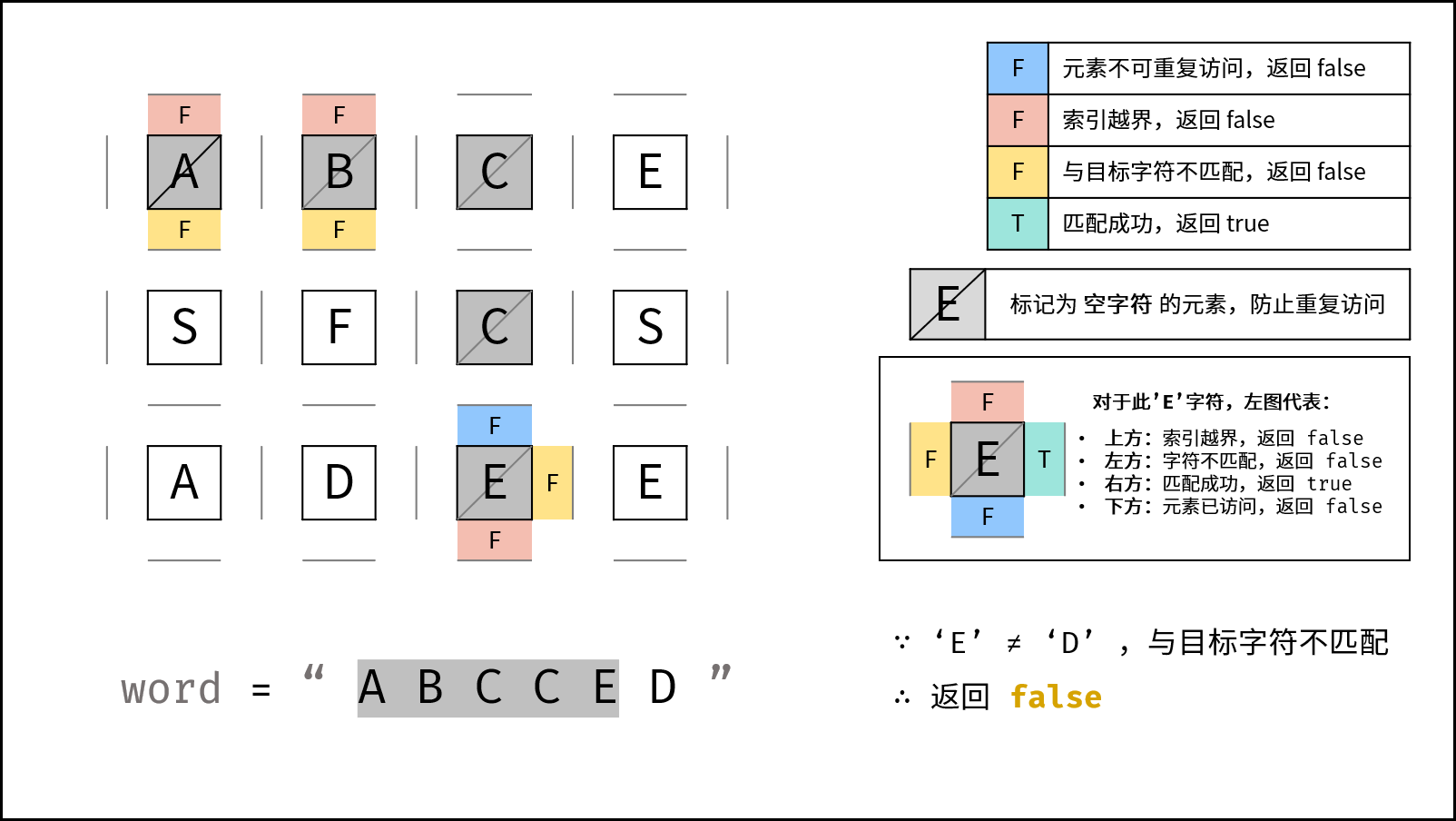Picture12.png](https://pic.leetcode-cn.com/1600793567-dyuEzg-Picture12.png),![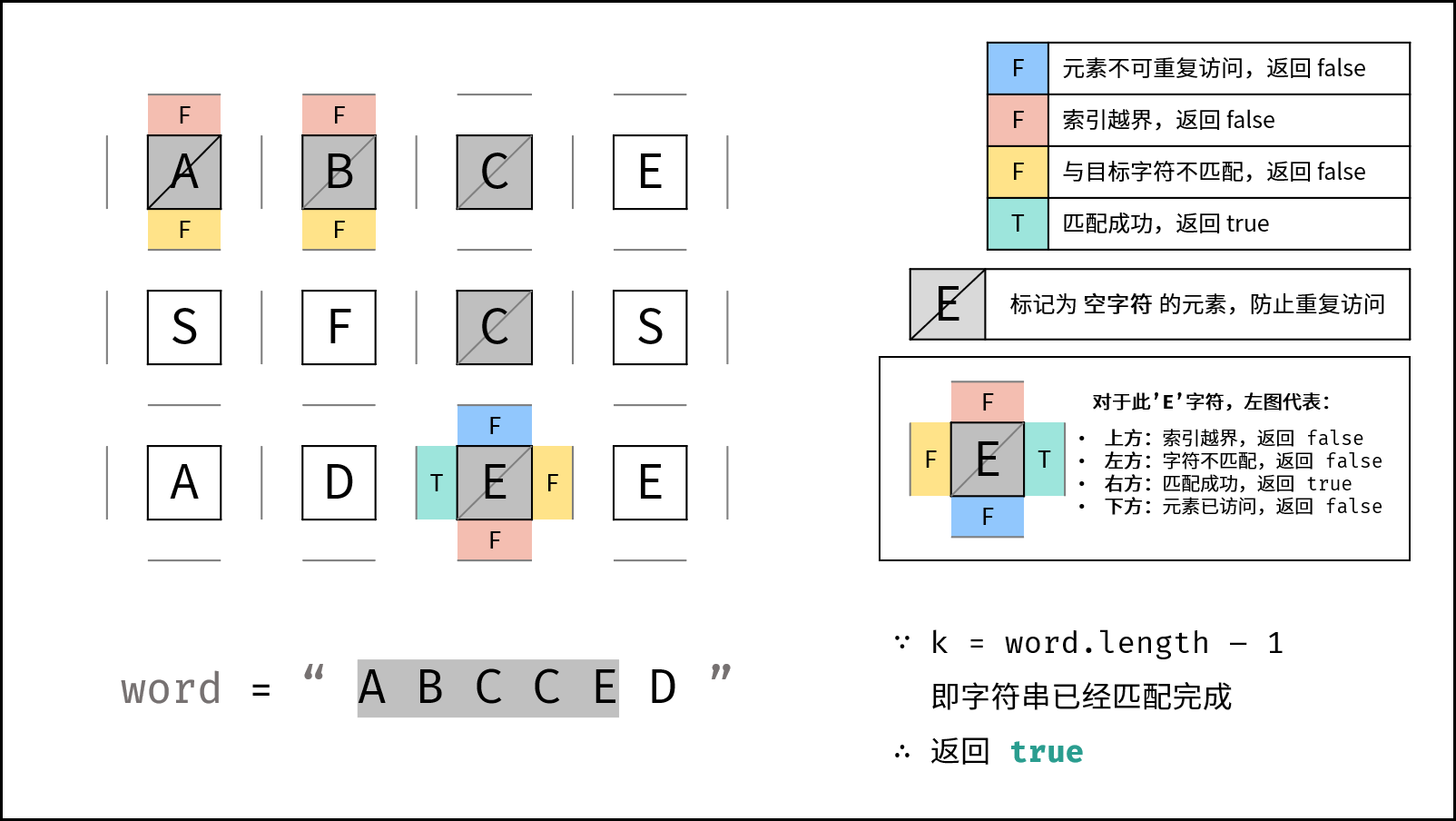Picture13.png](https://pic.leetcode-cn.com/1600793567-lnVDIT-Picture13.png),![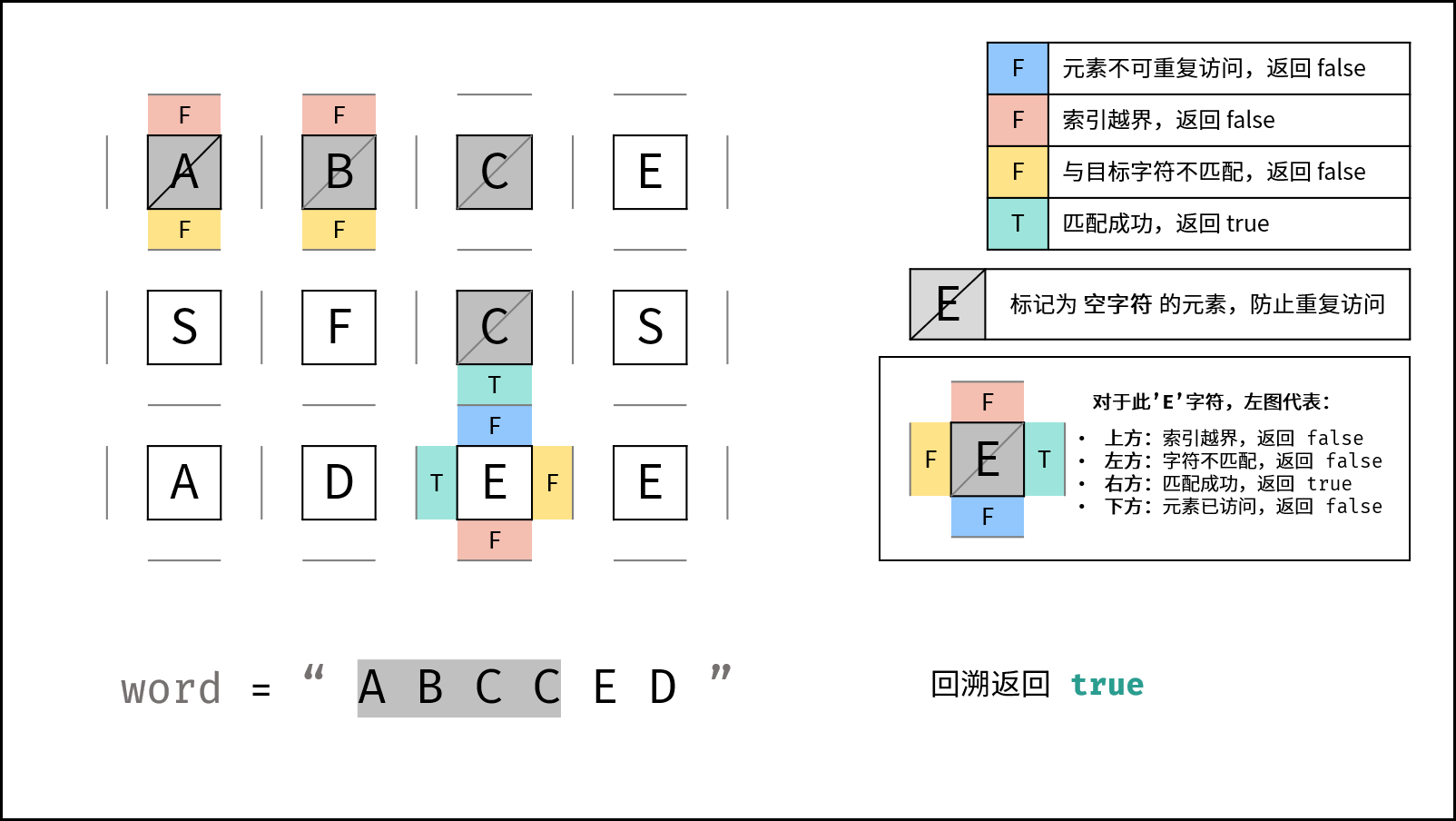Picture14.png](https://pic.leetcode-cn.com/1600793567-tLXXgg-Picture14.png),![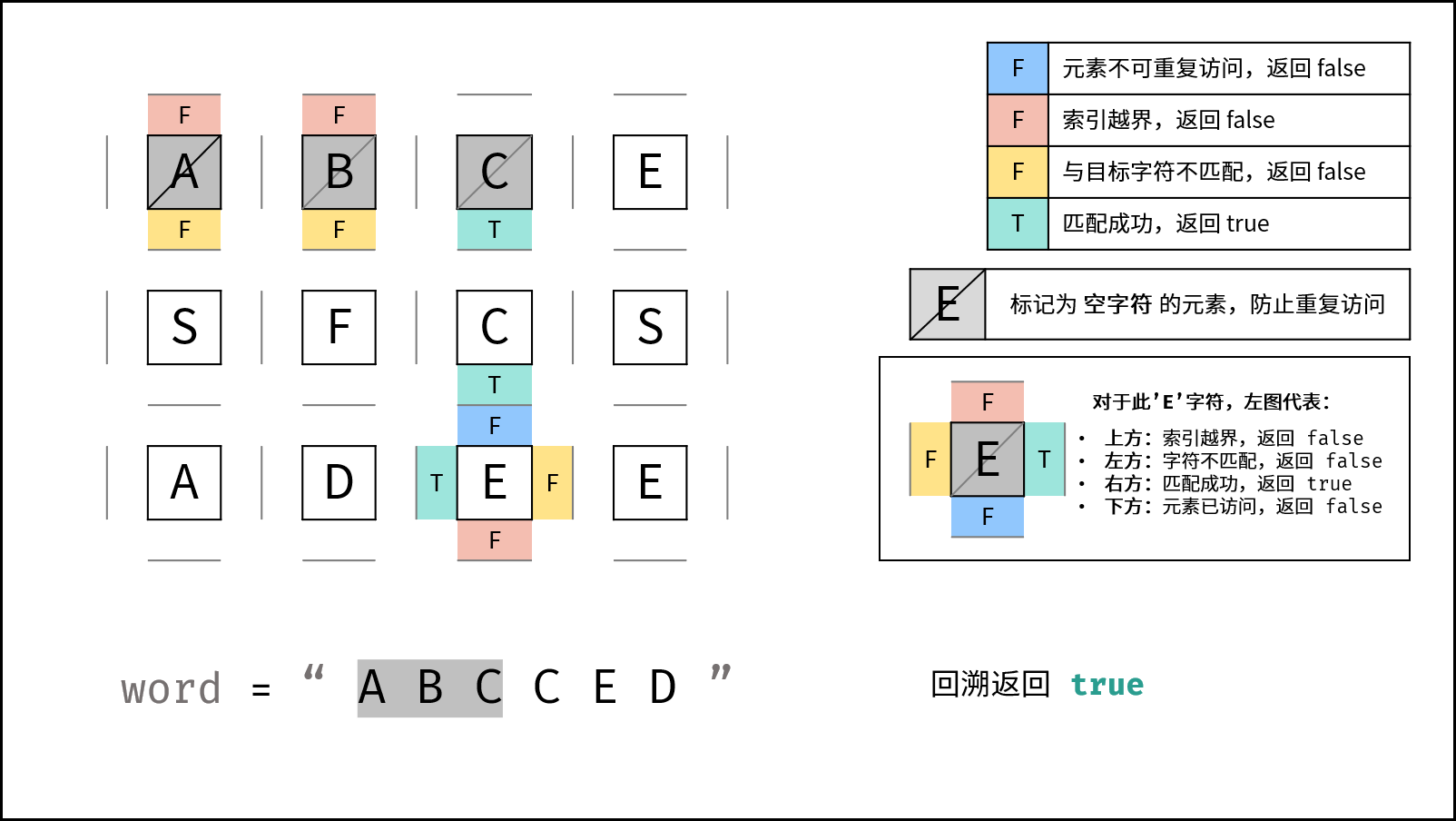Picture15.png](https://pic.leetcode-cn.com/1600793567-VwCJGV-Picture15.png),![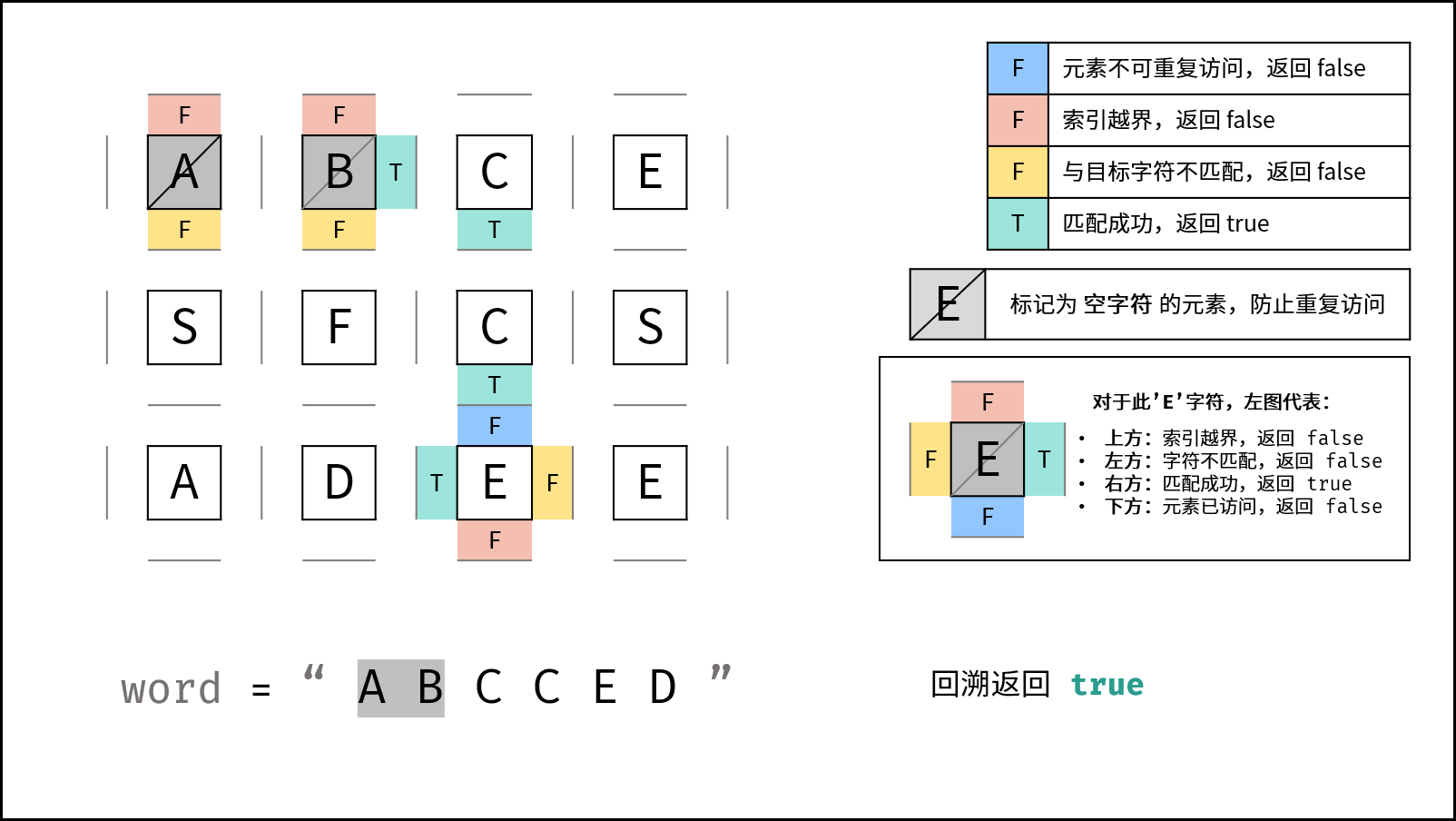Picture16.png](https://pic.leetcode-cn.com/1600793567-aNgVtM-Picture16.png),![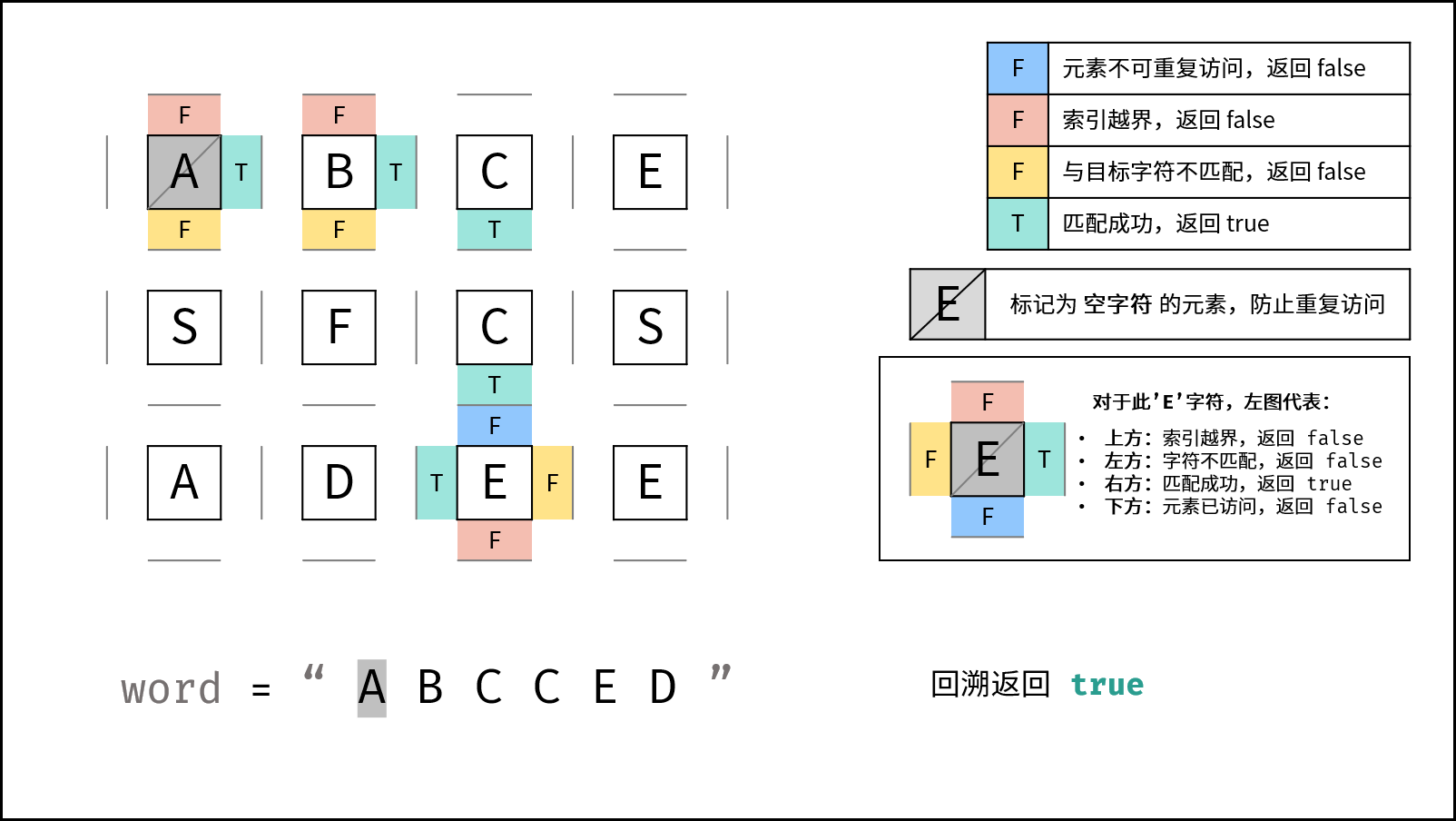Picture17.png](https://pic.leetcode-cn.com/1600793567-EcdfJE-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1600793793-PrBQdk-Picture18.png)>
## 代码：
```Python []
class Solution:
def wordPuzzle(self, grid: List[List[str]], target: str) -> bool:
def dfs(i, j, k):
if not 0 <= i < len(grid) or not 0 <= j < len(grid[0]) or grid[i][j] != target[k]: return False
if k == len(target) - 1: return True
grid[i][j] = ''
res = dfs(i + 1, j, k + 1) or dfs(i - 1, j, k + 1) or dfs(i, j + 1, k + 1) or dfs(i, j - 1, k + 1)
grid[i][j] = target[k]
return res
for i in range(len(grid)):
for j in range(len(grid[0])):
if dfs(i, j, 0): return True
return False
```
```Java []
class Solution {
public boolean wordPuzzle(char[][] grid, String target) {
char[] words = target.toCharArray();
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(dfs(grid, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] grid, char[] target, int i, int j, int k) {
if(i >= grid.length || i < 0 || j >= grid[0].length || j < 0 || grid[i][j] != target[k]) return false;
if(k == target.length - 1) return true;
grid[i][j] = '\0';
boolean res = dfs(grid, target, i + 1, j, k + 1) || dfs(grid, target, i - 1, j, k + 1) ||
dfs(grid, target, i, j + 1, k + 1) || dfs(grid, target, i , j - 1, k + 1);
grid[i][j] = target[k];
return res;
}
}
```
```C++ []
class Solution {
public:
bool wordPuzzle(vector<vector<char>>& grid, string target) {
rows = grid.size();
cols = grid[0].size();
for(int i = 0; i < rows; i++) {
for(int j = 0; j < cols; j++) {
if(dfs(grid, target, i, j, 0)) return true;
}
}
return false;
}
private:
int rows, cols;
bool dfs(vector<vector<char>>& grid, string target, int i, int j, int k) {
if(i >= rows || i < 0 || j >= cols || j < 0 || grid[i][j] != target[k]) return false;
if(k == target.size() - 1) return true;
grid[i][j] = '\0';
bool res = dfs(grid, target, i + 1, j, k + 1) || dfs(grid, target, i - 1, j, k + 1) ||
dfs(grid, target, i, j + 1, k + 1) || dfs(grid, target, i , j - 1, k + 1);
grid[i][j] = target[k];
return res;
}
};
```
### 复杂度分析：
> $M, N$ 分别为矩阵行列大小，$K$ 为字符串 `target` 长度。
- **时间复杂度 $O(3^KMN)$ ：** 最差情况下，需要遍历矩阵中长度为 $K$ 字符串的所有方案，时间复杂度为 $O(3^K)$；矩阵中共有 $MN$ 个起点，时间复杂度为 $O(MN)$ 。
- **方案数计算：** 设字符串长度为 $K$ ，搜索中每个字符有上、下、左、右四个方向可以选择，舍弃回头（上个字符）的方向，剩下 $3$ 种选择，因此方案数的复杂度为 $O(3^K)$ 。
- **空间复杂度 $O(K)$ ：** 搜索过程中的递归深度不超过 $K$ ，因此系统因函数调用累计使用的栈空间占用 $O(K)$ （因为函数返回后，系统调用的[栈空间会释放](https://leetcode-cn.com/explore/orignial/card/recursion-i/259/complexity-analysis/1223/)）。最坏情况下 $K = MN$ ，递归深度为 $MN$ ，此时系统栈使用 $O(MN)$ 的额外空间。

242
leetbook_ioa/docs/LCR 130. 衣橱整理.md Executable file
View File

@@ -0,0 +1,242 @@
## 解题思路：
为提升回溯的计算效率，首先讲述两项前置工作： **数位之和计算** 、 **可达解分析** 。
### 数位之和计算：
设一数字 $x$ ，向下取整除法符号 $//$ ，求余符号 $\odot$ ，则有：
- $x \odot 10$ ：得到 $x$ 的个位数字；
- $x // 10$ ： 令 $x$ 的十进制数向右移动一位，即删除个位数字。
因此，可通过循环求得数位和 $s$ ，数位和计算的封装函数如下所示：
```Python []
def sums(x):
s = 0
while x != 0:
s += x % 10
x = x // 10
return s
```
```Java []
int sums(int x)
int s = 0;
while(x != 0) {
s += x % 10;
x = x / 10;
}
return s;
```
```C++ []
int sums(int x)
int s = 0;
while(x != 0) {
s += x % 10;
x = x / 10;
}
return s;
```
由于机器人每次只能移动一格（即只能从 $x$ 运动至 $x \pm 1$），因此每次只需计算 $x$ 到 $x \pm 1$ 的**数位和增量**。本题说明 $1 \leq n,m \leq 100$ ，以下公式仅在此范围适用。
**数位和增量公式：** 设 $x$ 的数位和为 $s_x$ ，$x+1$ 的数位和为 $s_{x+1}$ ；
1. **当 $(x + 1) \odot 10 = 0$ 时：** $s_{x+1} = s_x - 8$ ，例如 $19, 20$ 的数位和分别为 $10, 2$ ；
2. **当 $(x + 1) \odot 10 \neq 0$ 时：** $s_{x+1} = s_x + 1$ ，例如 $1, 2$ 的数位和分别为 $1, 2$ 。
> 以下代码为增量公式的三元表达式写法，将整合入最终代码中。
```Python []
s_x + 1 if (x + 1) % 10 else s_x - 8
```
```Java []
(x + 1) % 10 != 0 ? s_x + 1 : s_x - 8;
```
```C++ []
(x + 1) % 10 != 0 ? s_x + 1 : s_x - 8;
```
### 可达解分析：
根据数位和增量公式得知，数位和每逢 **进位** 突变一次。根据此特点，矩阵中 **满足数位和的解** 构成的几何形状形如多个 **等腰直角三角形** ，每个三角形的直角顶点位于 $0, 10, 20, ...$ 等数位和突变的矩阵索引处 。
三角形内的解虽然都满足数位和要求，但由于机器人每步只能走一个单元格，而三角形间不一定是连通的，因此机器人不一定能到达，称之为 **不可达解** ；同理，可到达的解称为 **可达解** *（本题求此解）* 。
> 下图展示了 $n,m = 20$ ，$cnt \in [6, 19]$ 的可达解、不可达解、非解，以及连通性的变化。其中 $k$ 对应本题的 $cnt$ 。
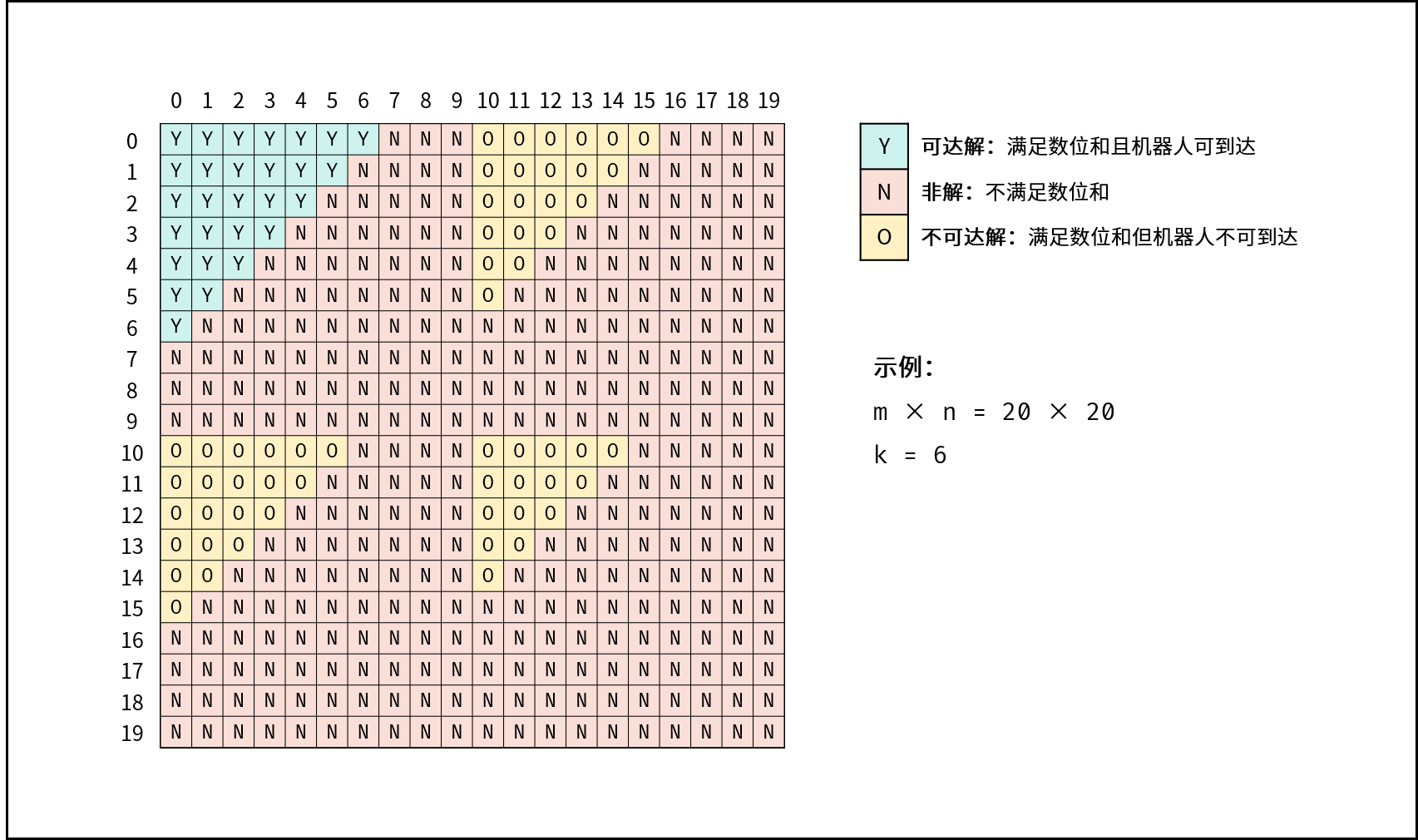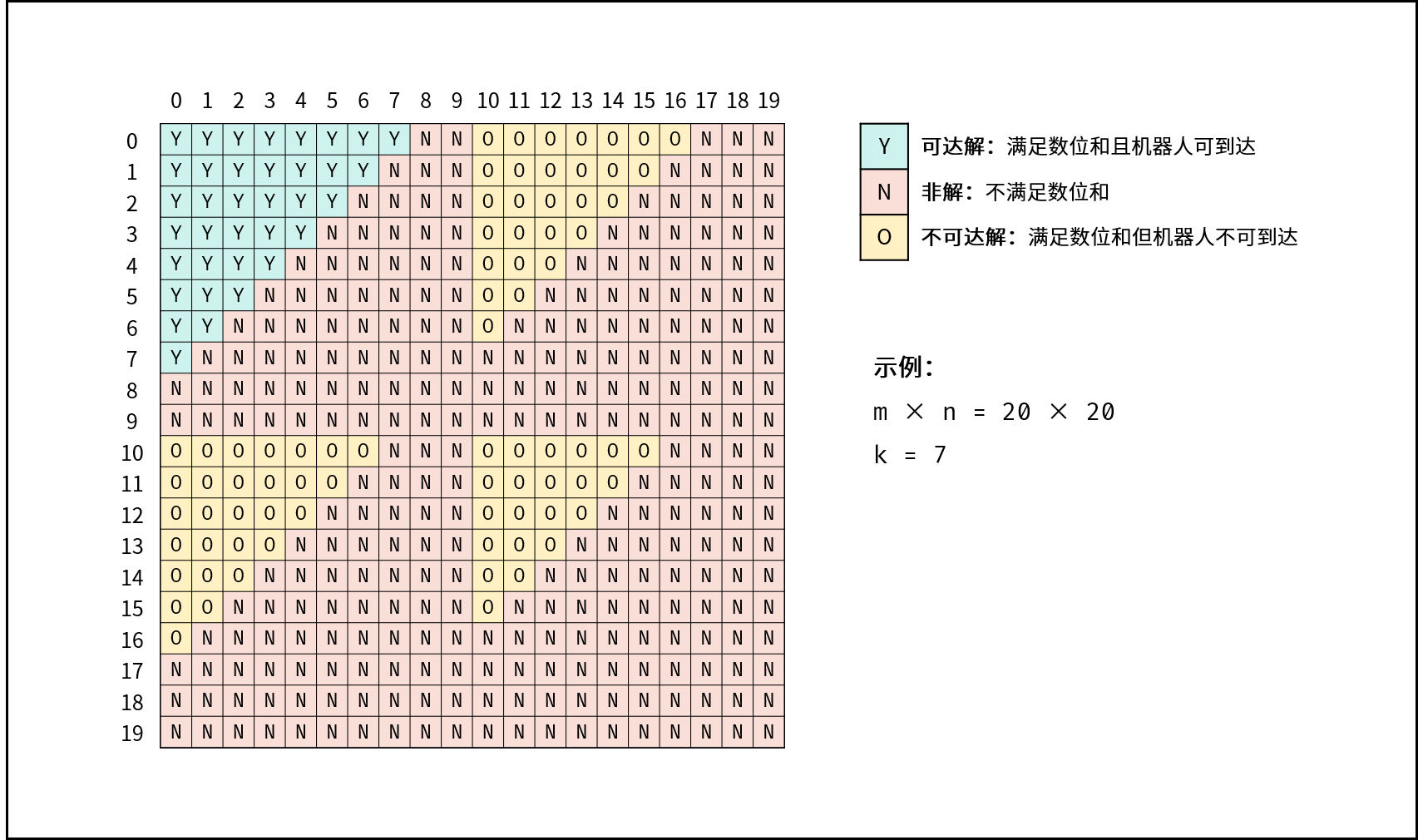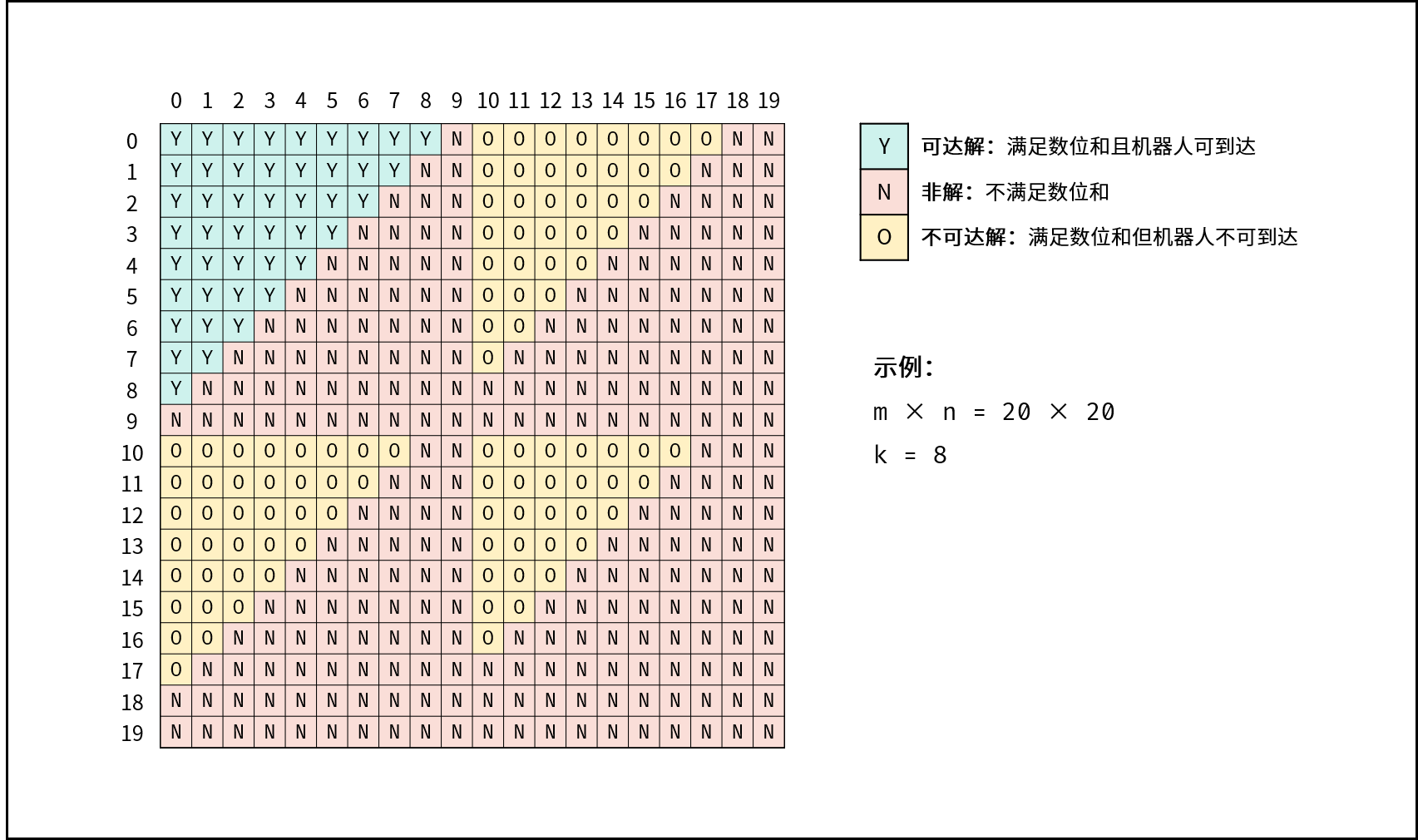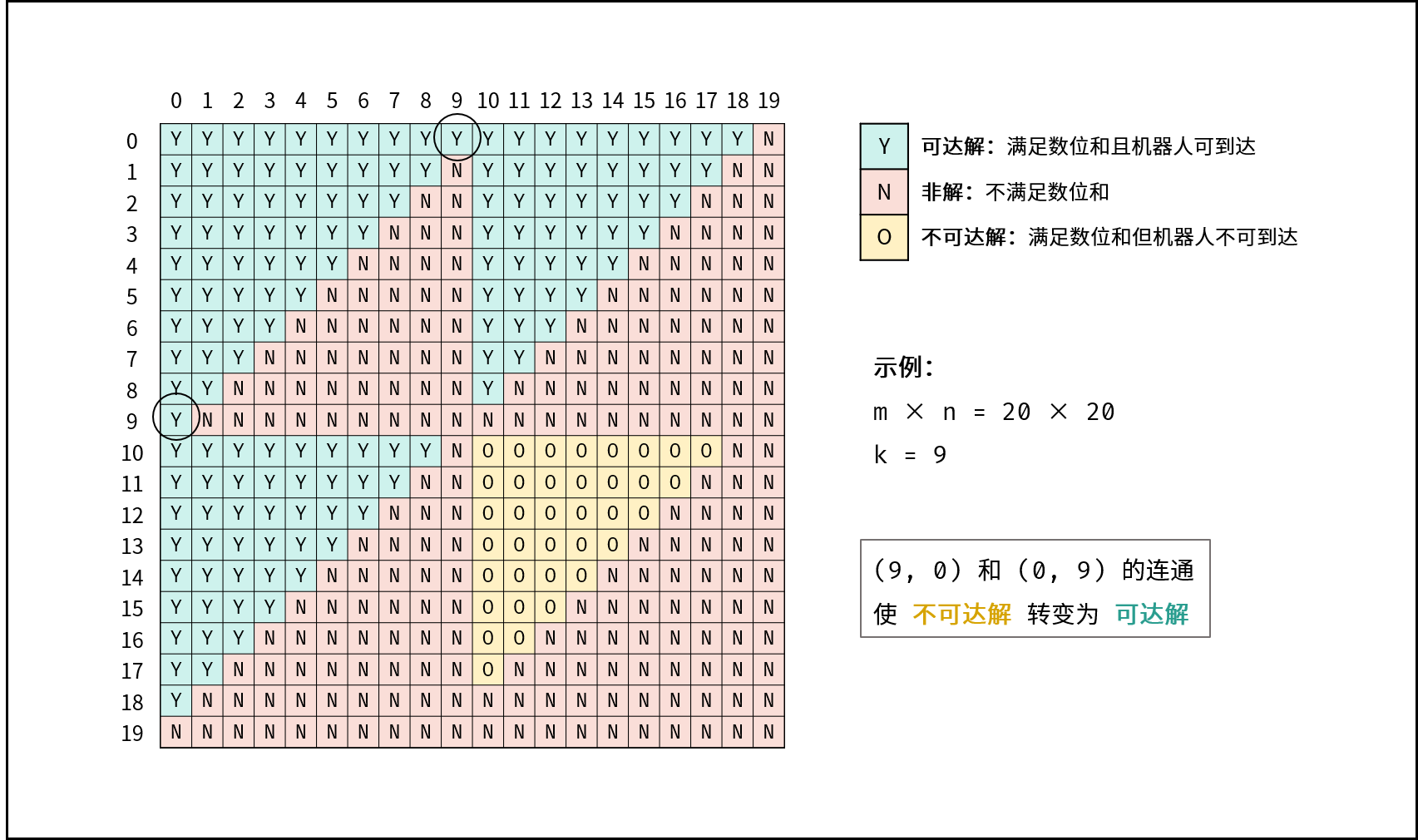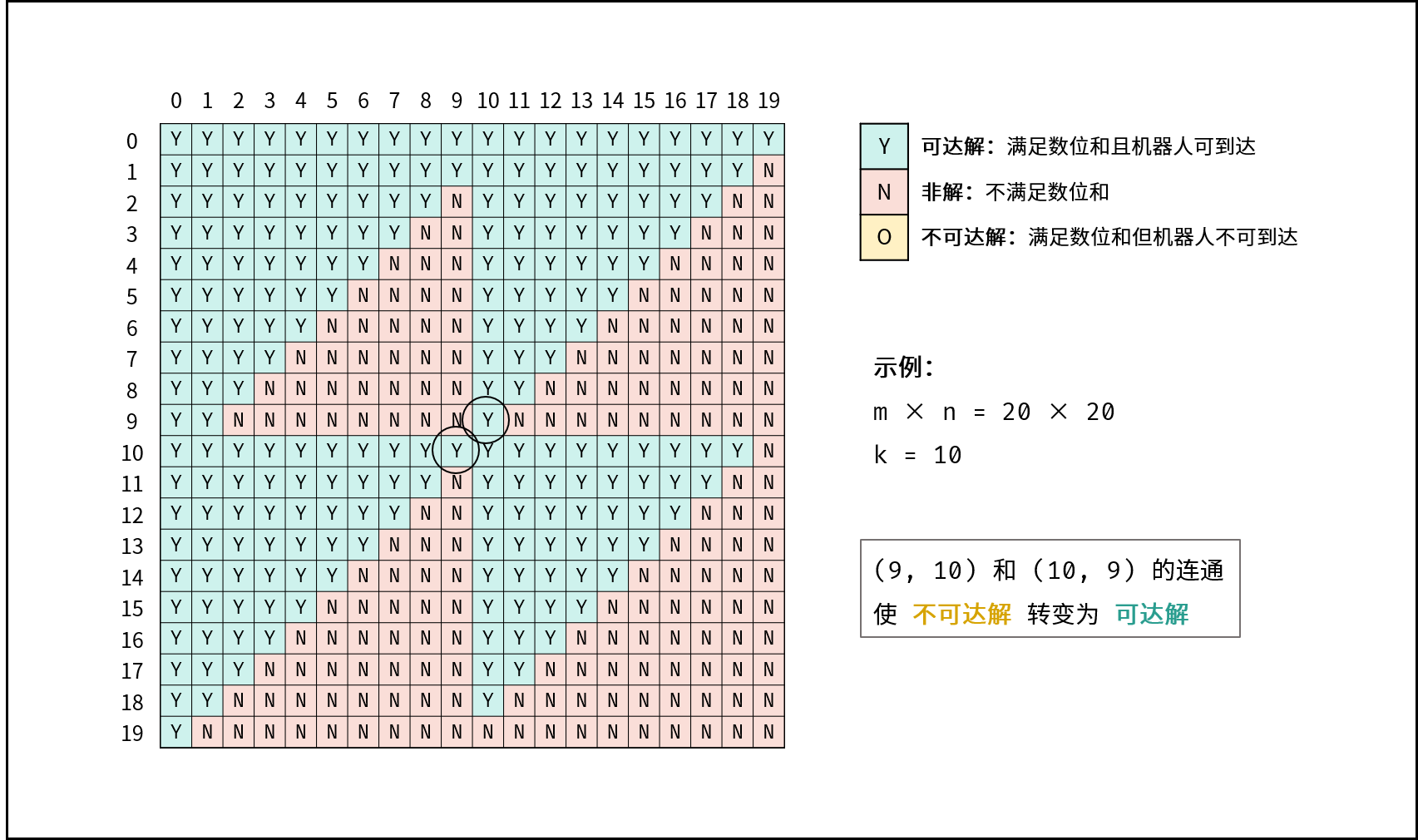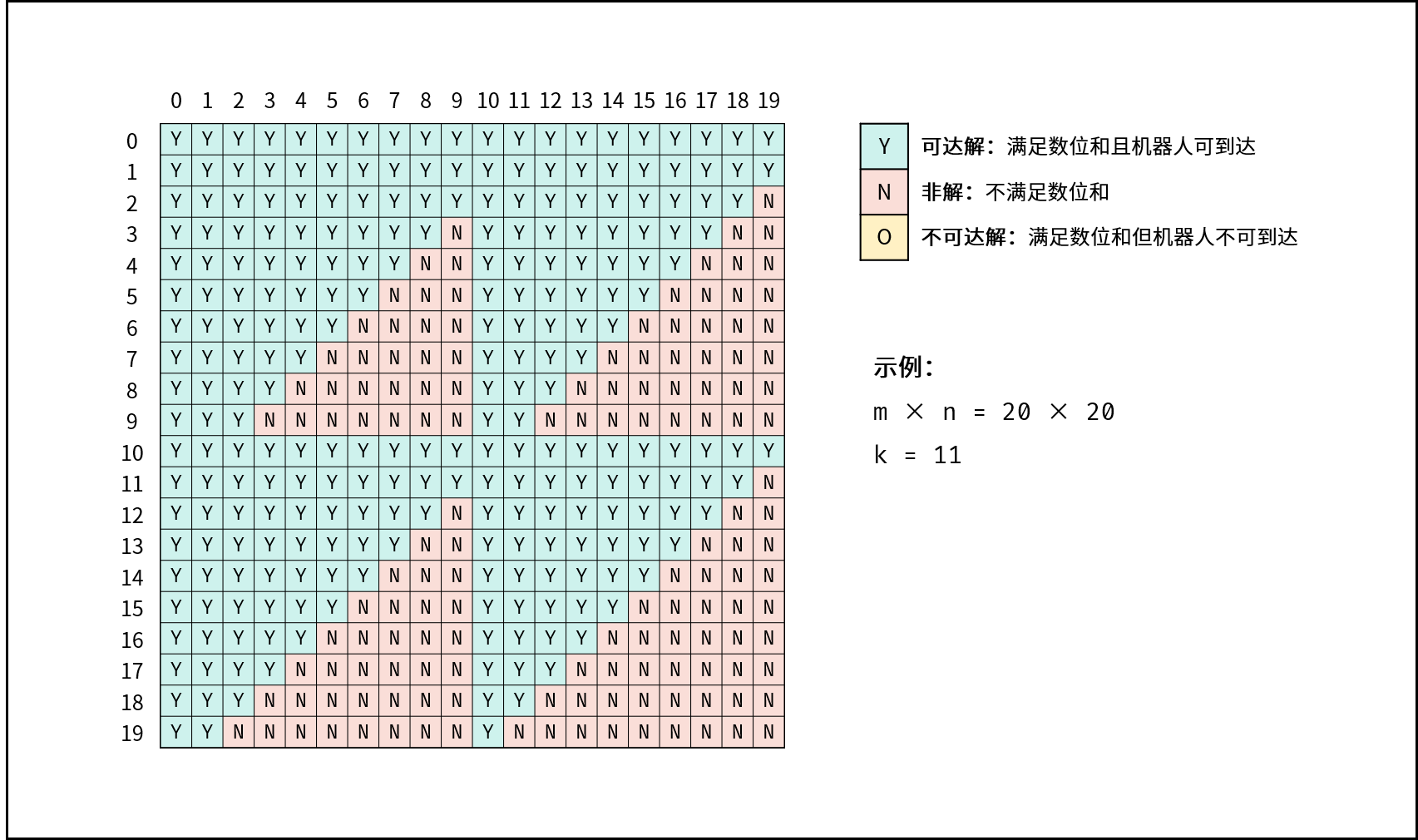<![Picture1.png](https://pic.leetcode-cn.com/1603026306-OdpwLi-Picture1.png),![Picture2.png](https://pic.leetcode-cn.com/1603026306-jCBpqd-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603026306-aEEvfM-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603026306-daxIuh-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603026306-HAMNPH-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603026306-IUKeMt-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603026306-YxlxXI-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1603026306-JLhUWz-Picture8.png)>
根据可达解的结构和连通性，易推出机器人可 **仅通过向右和向下移动，访问所有可达解** 。
- **三角形内部：** 全部连通，易证；
- **两三角形连通处：** 若某三角形内的解为可达解，则必与其左边或上边的三角形连通（即相交），即机器人必可从左边或上边走进此三角形。
![Picture9.png](https://pic.leetcode-cn.com/1603024999-XMpudY-Picture9.png){:align=center width=500}
## 方法一：深度优先遍历（DFS）
**深度优先搜索：** 可以理解为暴力法模拟机器人在矩阵中的所有路径。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
**剪枝：** 在搜索中，遇到数位和超出目标值、此元素已访问，则应立即返回，称之为 `可行性剪枝` 。
### 算法解析：
- **递归参数：** 当前元素在矩阵中的行列索引 `i` 和 `j` ，两者的数位和 `si`, `sj` 。
- **终止条件：** 当 (1) 行列索引越界 **或** (2) 数位和超出目标值 `cnt` **或** (3) 当前元素已访问过 时，返回 $0$ ，代表不计入可达解。
- **递推工作：**
1. **标记当前单元格** ：将索引 `(i, j)` 存入 Set `visited` 中，代表此单元格已被访问过。
2. **搜索下一单元格：** 计算当前元素的 **下、右** 两个方向元素的数位和，并开启下层递归 。
- **回溯返回值：** 返回 `1 + 右方搜索的可达解总数 + 下方搜索的可达解总数`，代表从本单元格递归搜索的可达解总数。
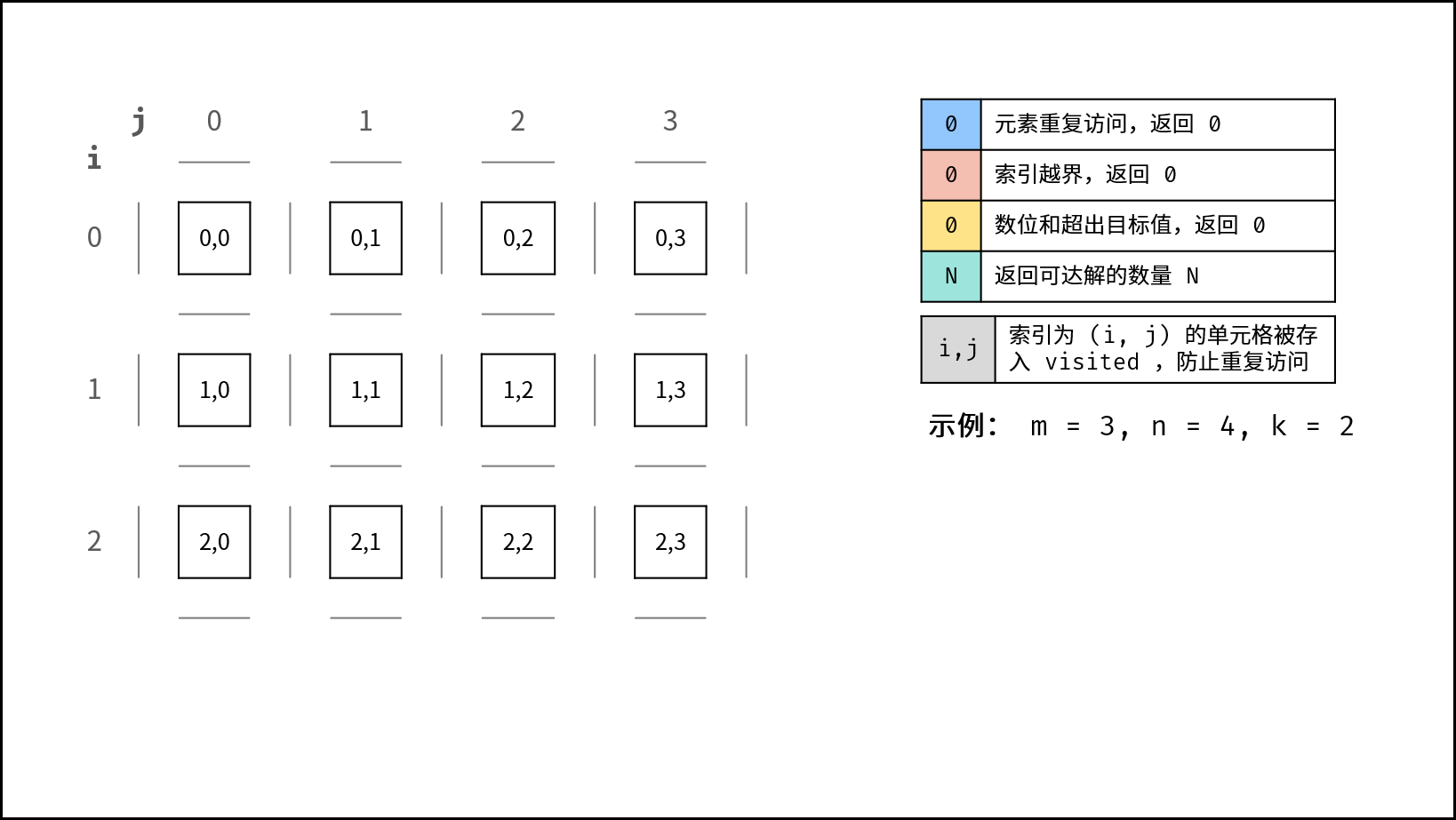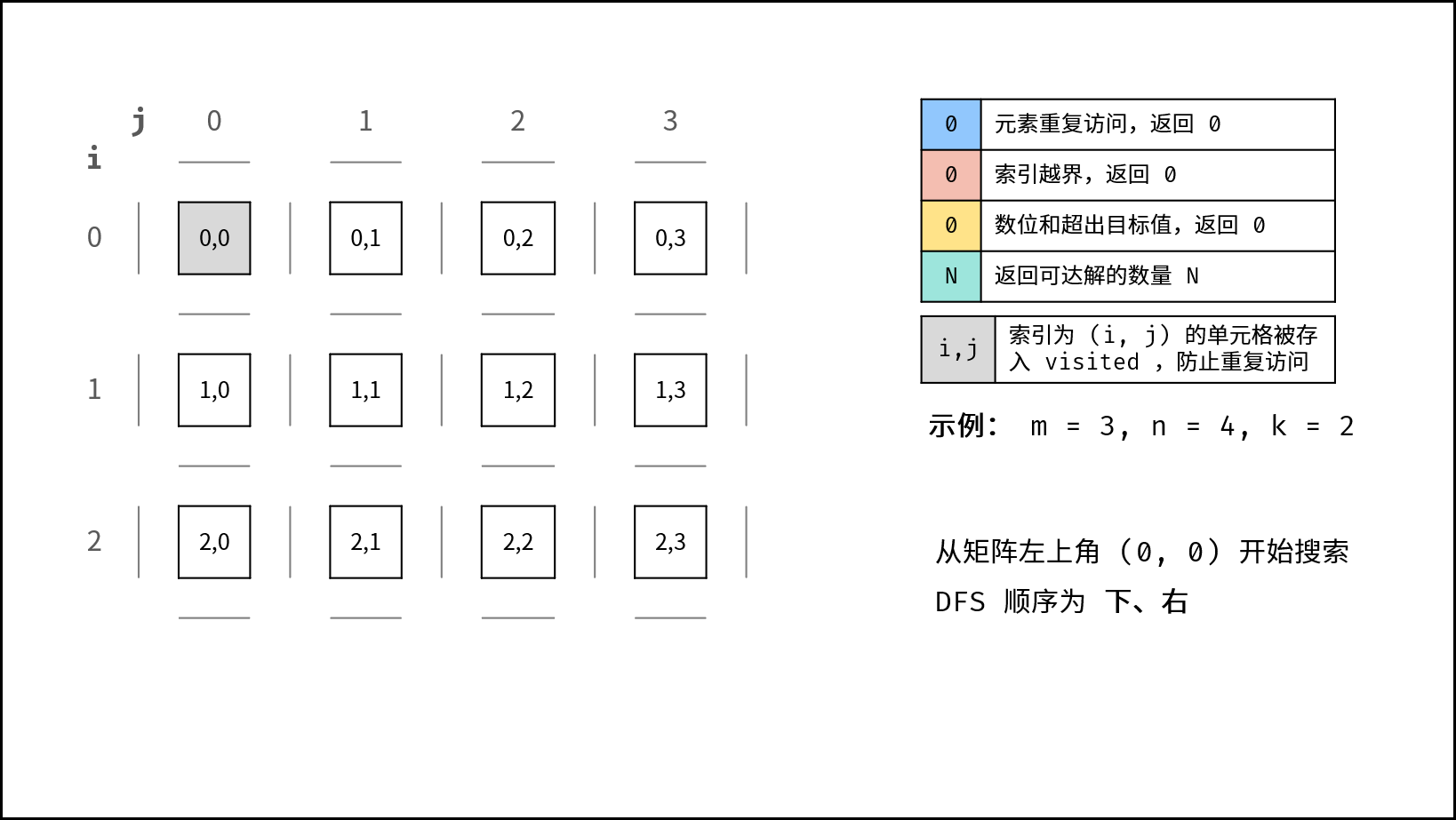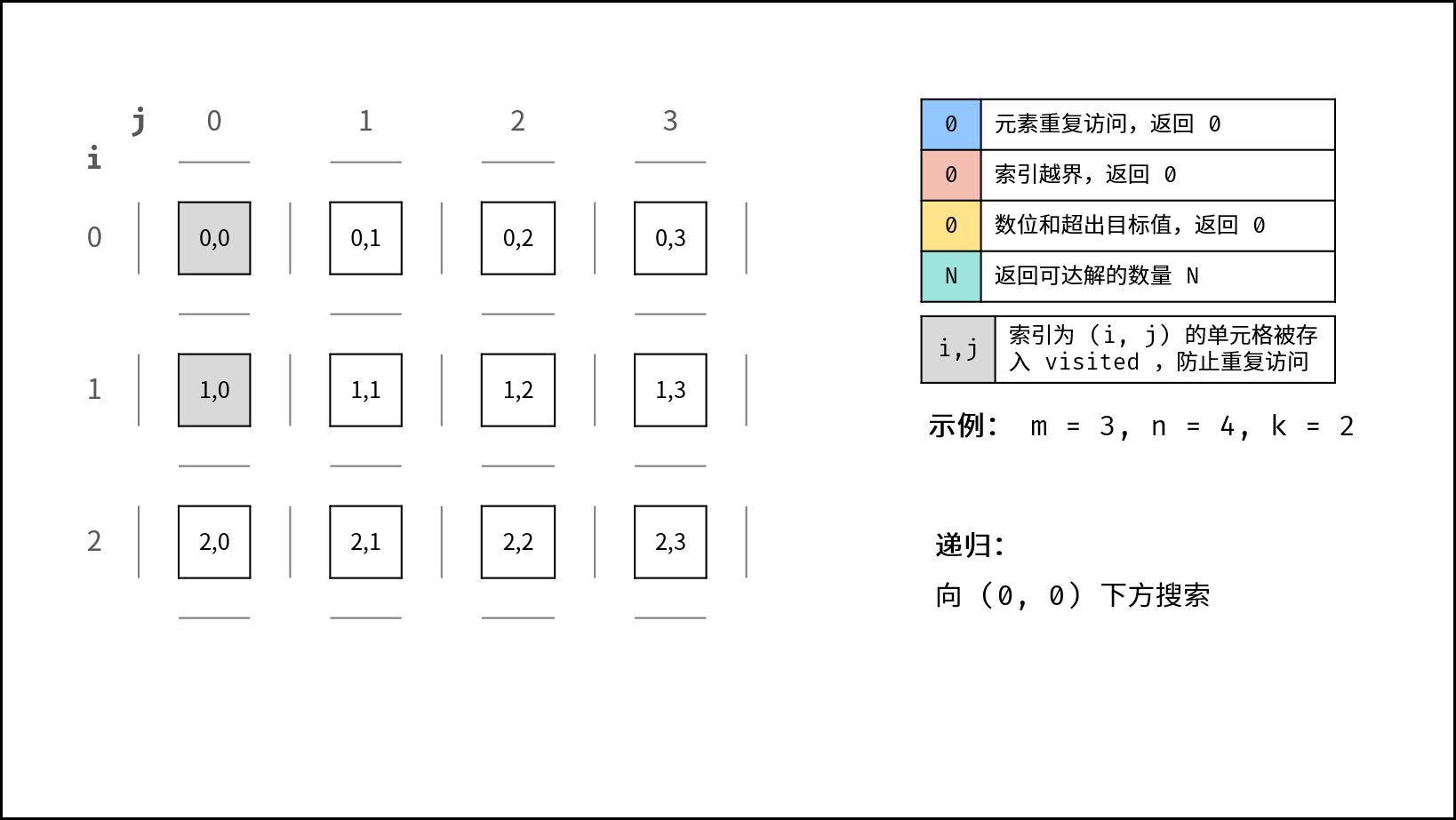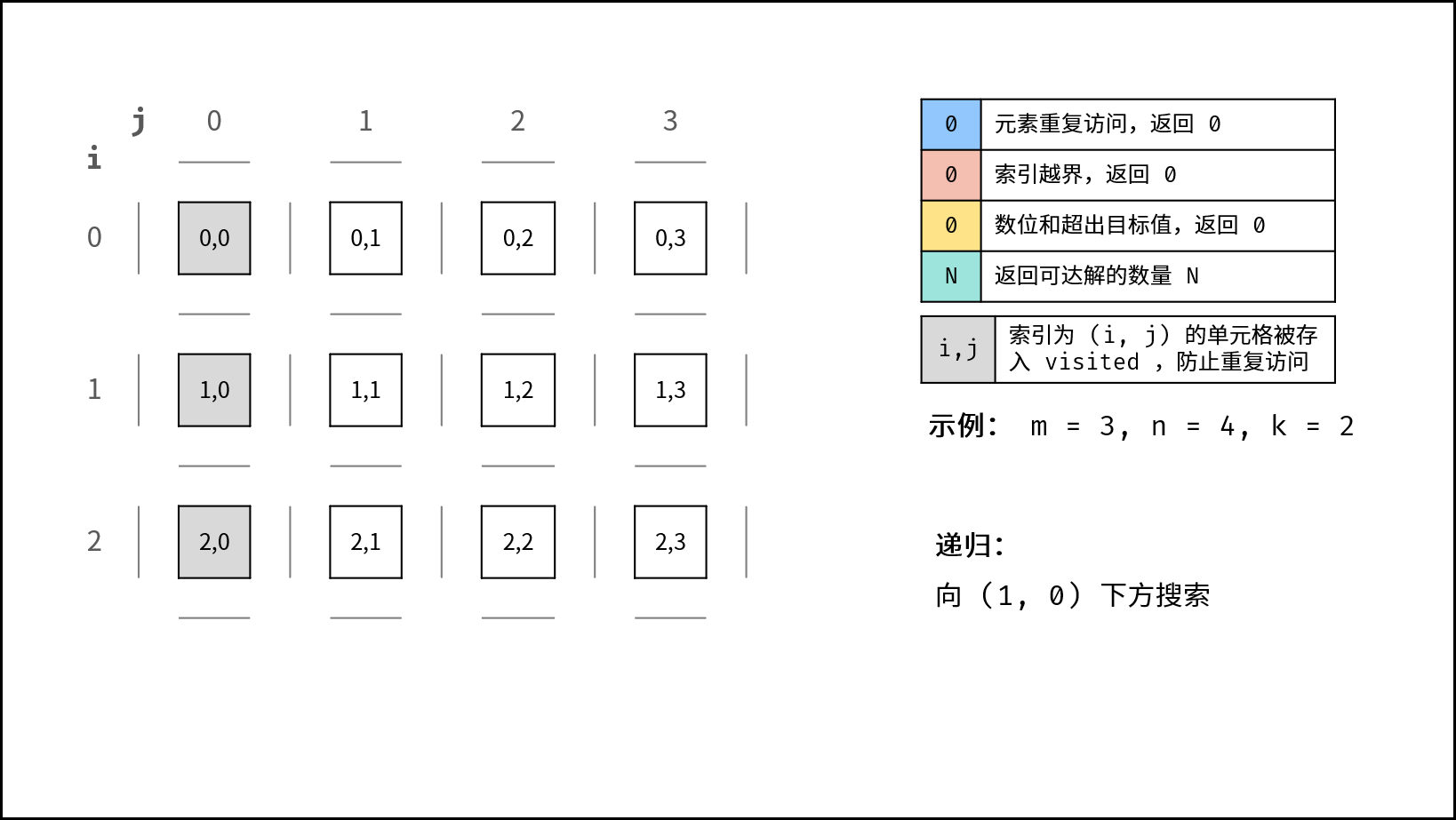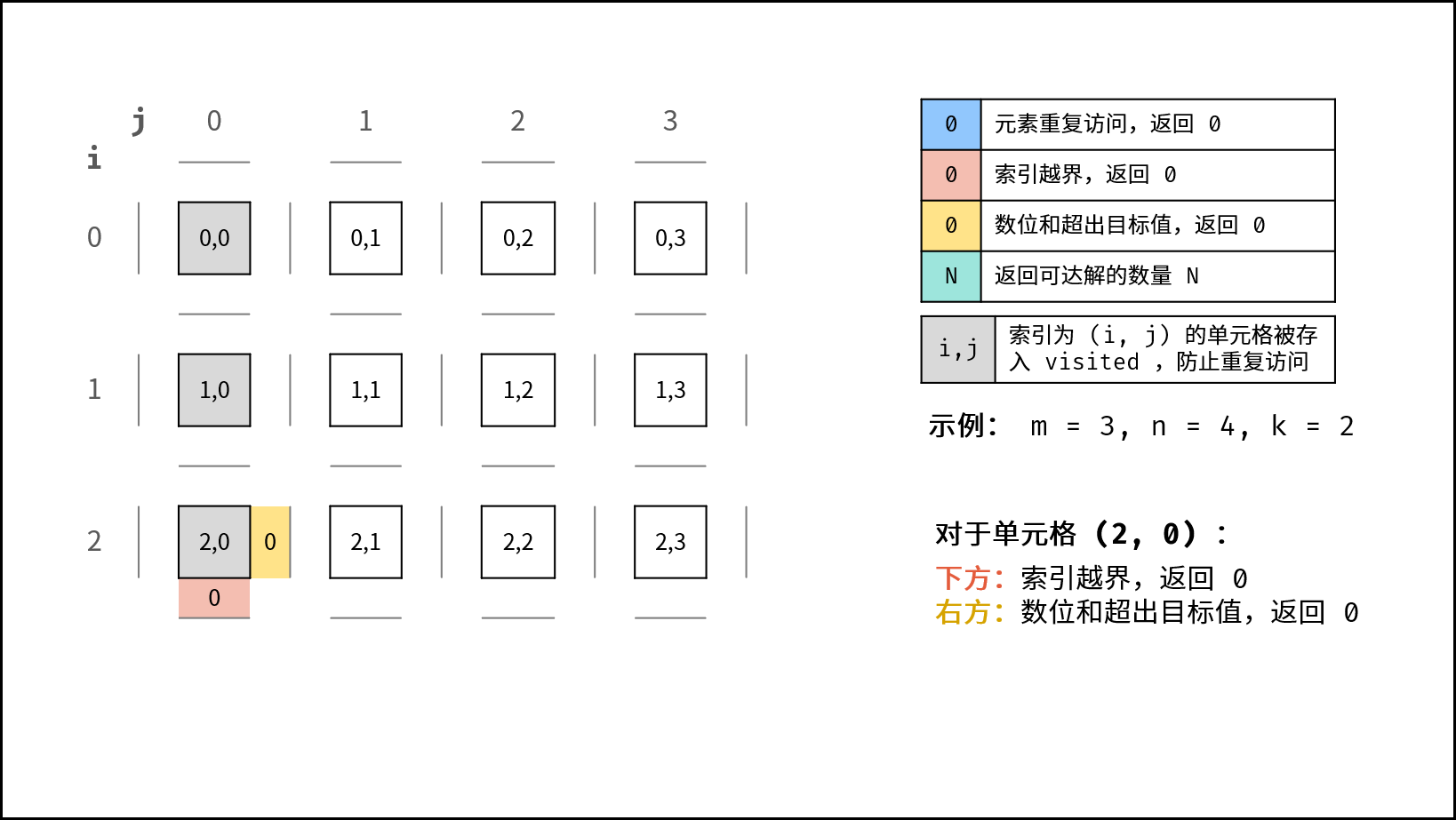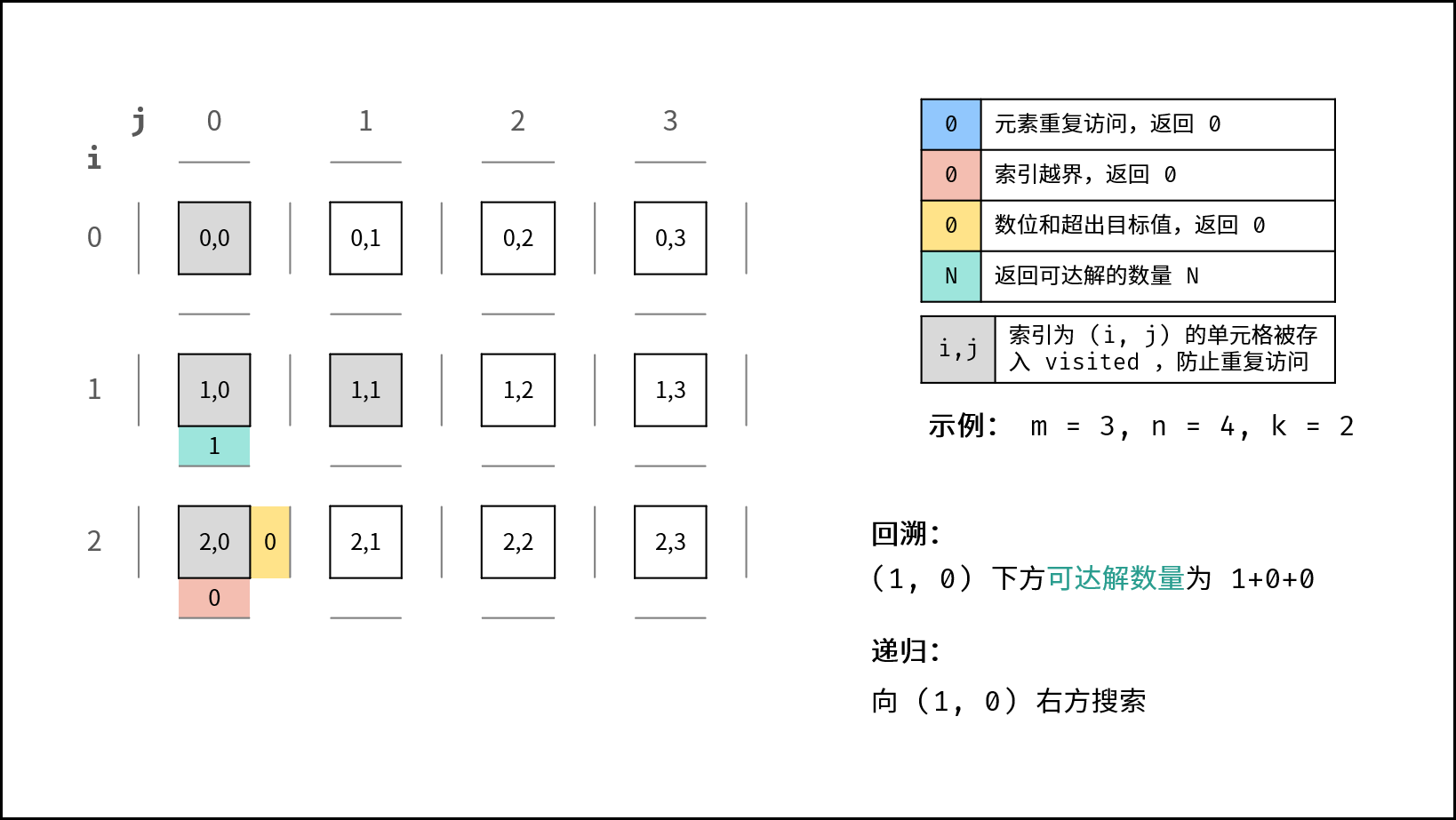<![Picture10.png](https://pic.leetcode-cn.com/1603024999-URYkbB-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1603024999-XyKkZo-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1603024999-eQXMnv-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1603024999-mcujIe-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1603024999-dXOdEJ-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1603024999-ApTwow-Picture15.png),![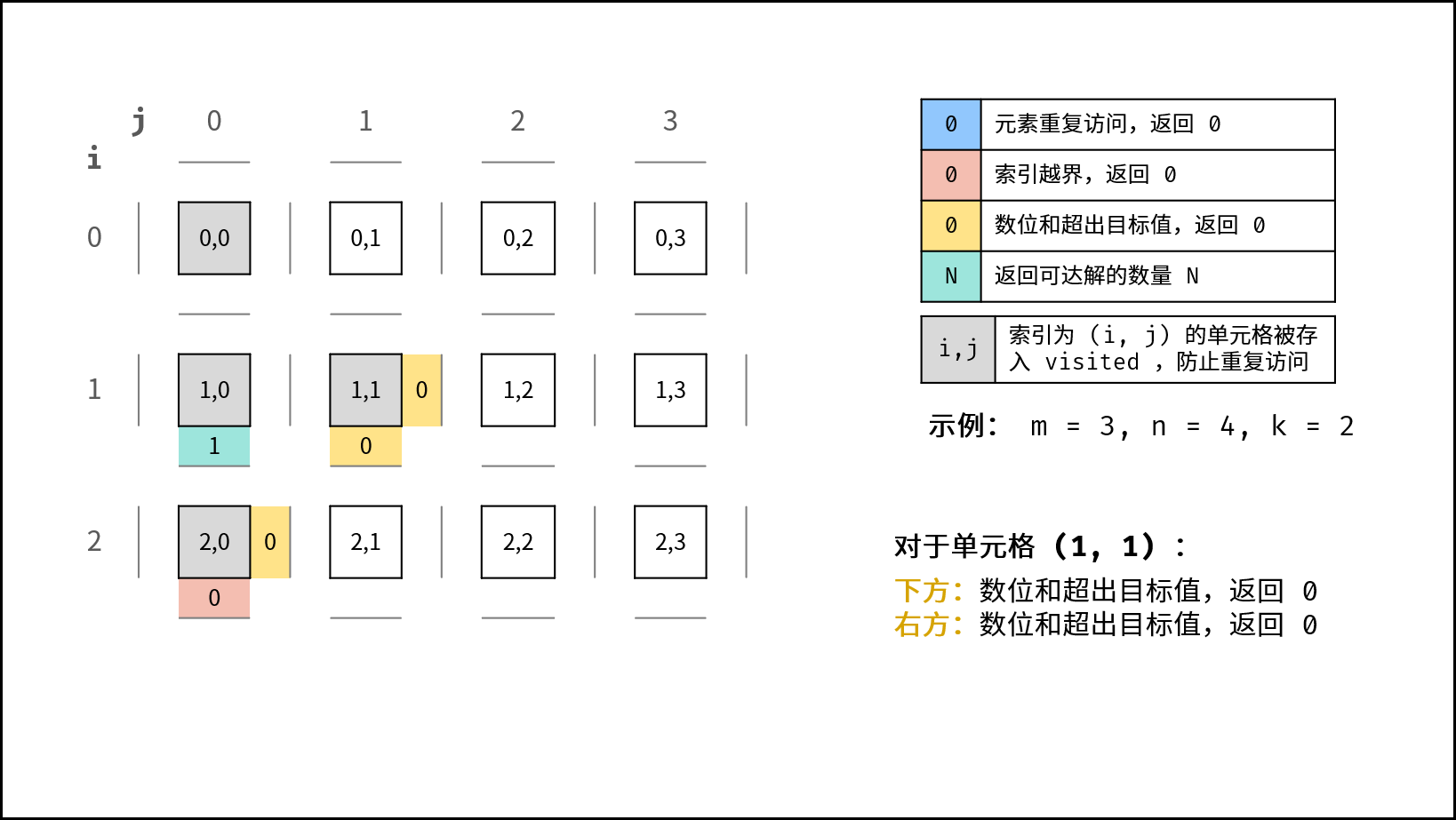Picture16.png](https://pic.leetcode-cn.com/1603024999-krgMMb-Picture16.png),![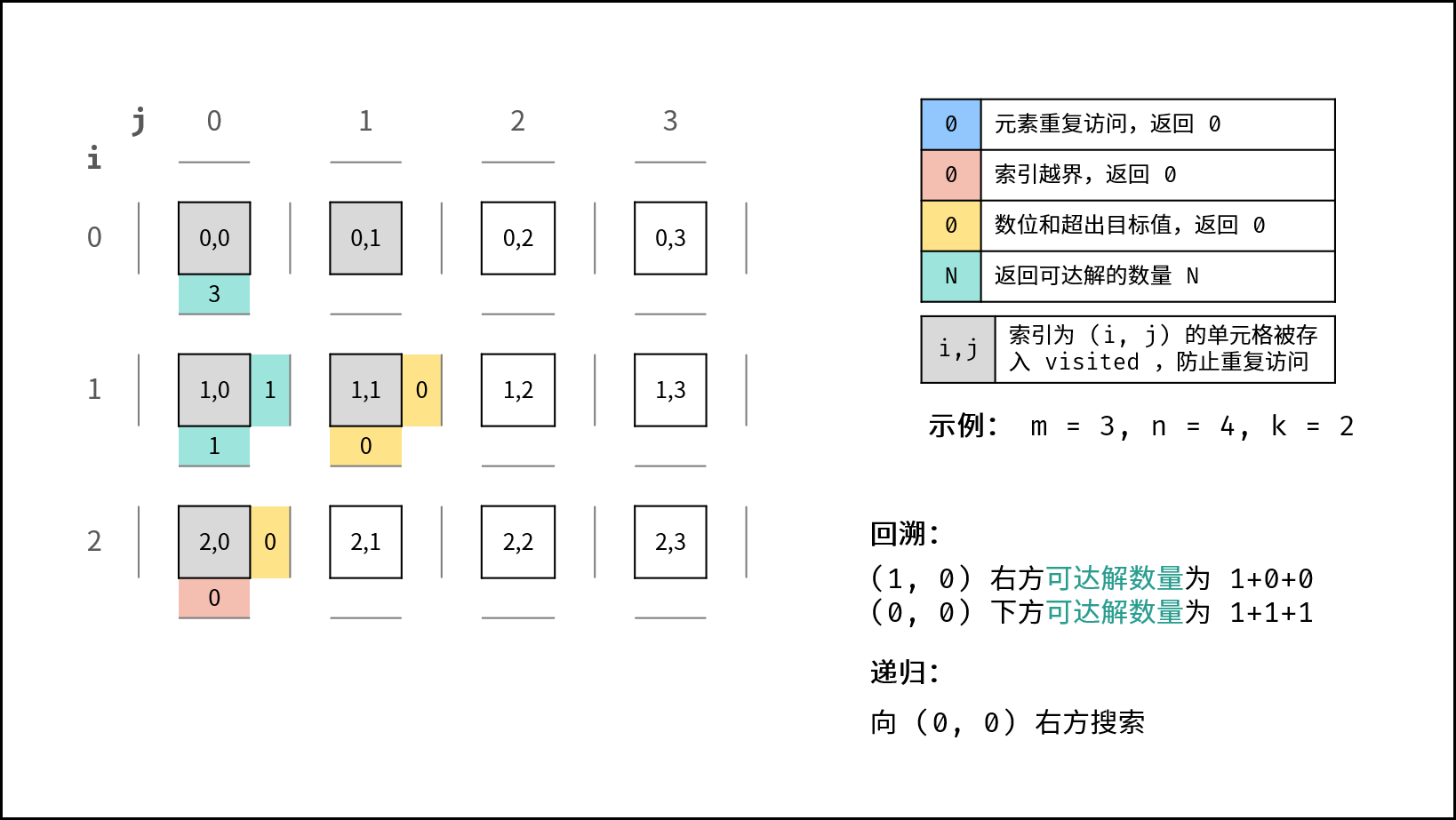Picture17.png](https://pic.leetcode-cn.com/1603024999-JCGqrp-Picture17.png),![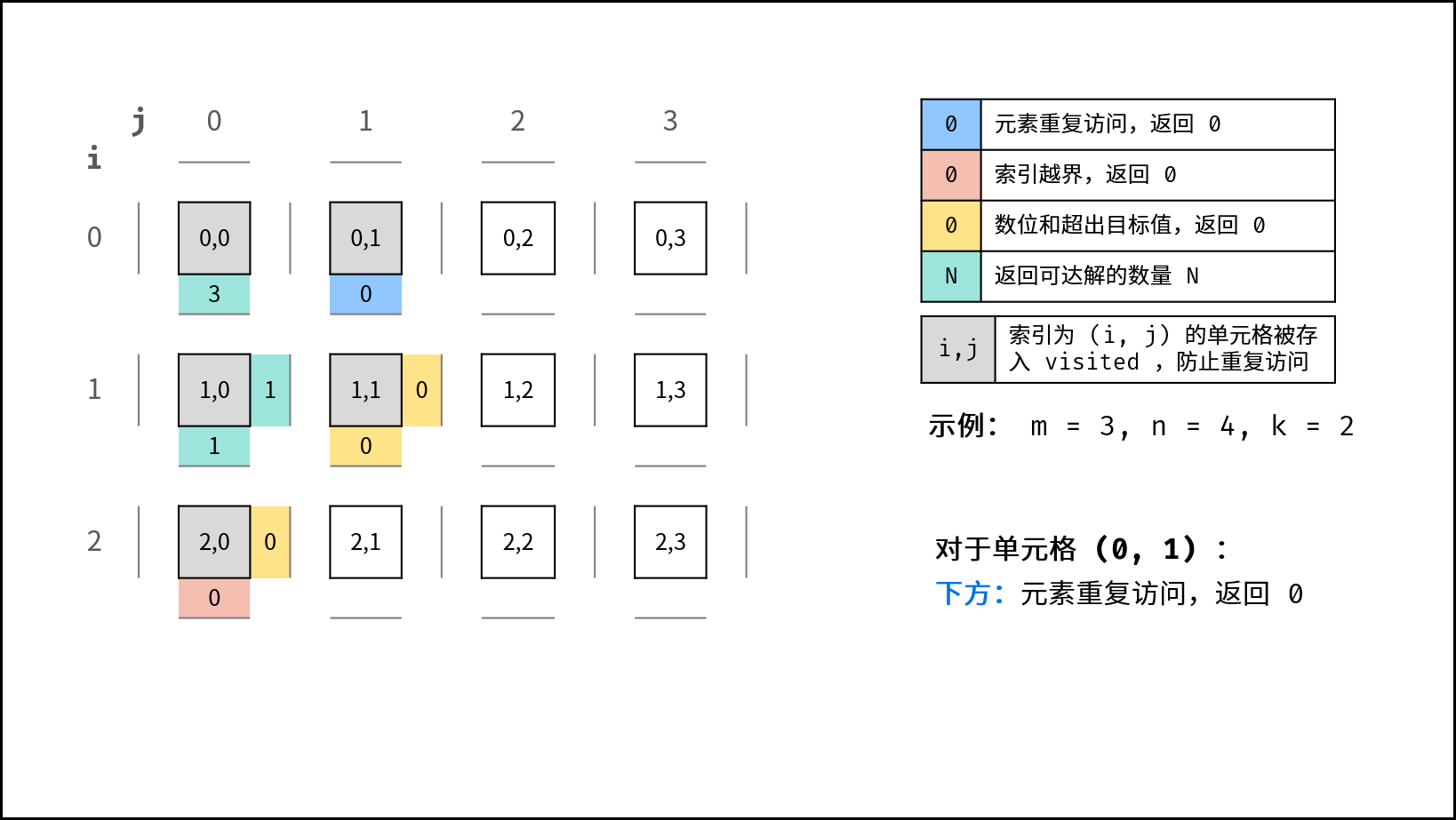Picture18.png](https://pic.leetcode-cn.com/1603024999-jYYavg-Picture18.png),![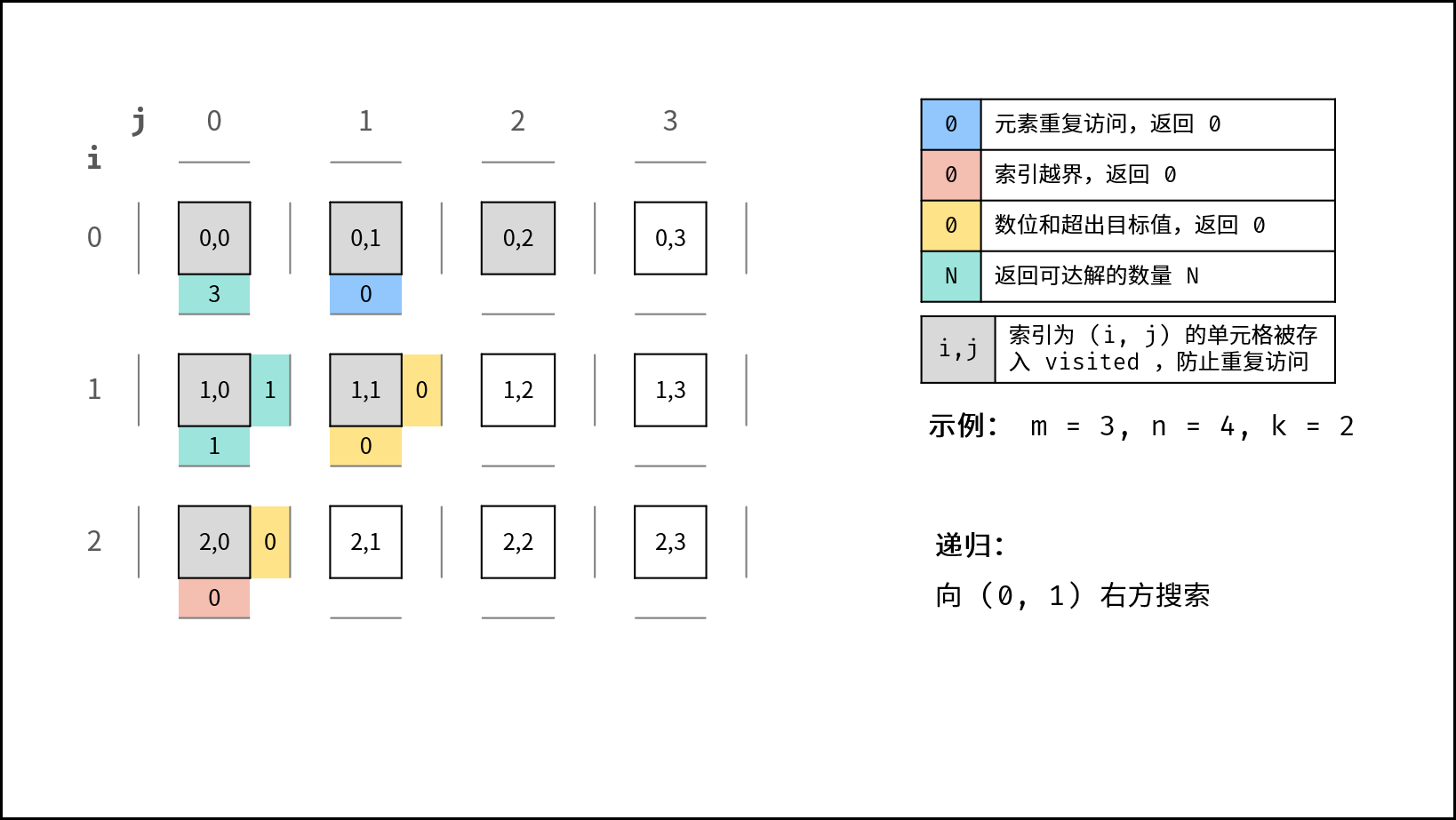Picture19.png](https://pic.leetcode-cn.com/1603024999-RRZCbl-Picture19.png),![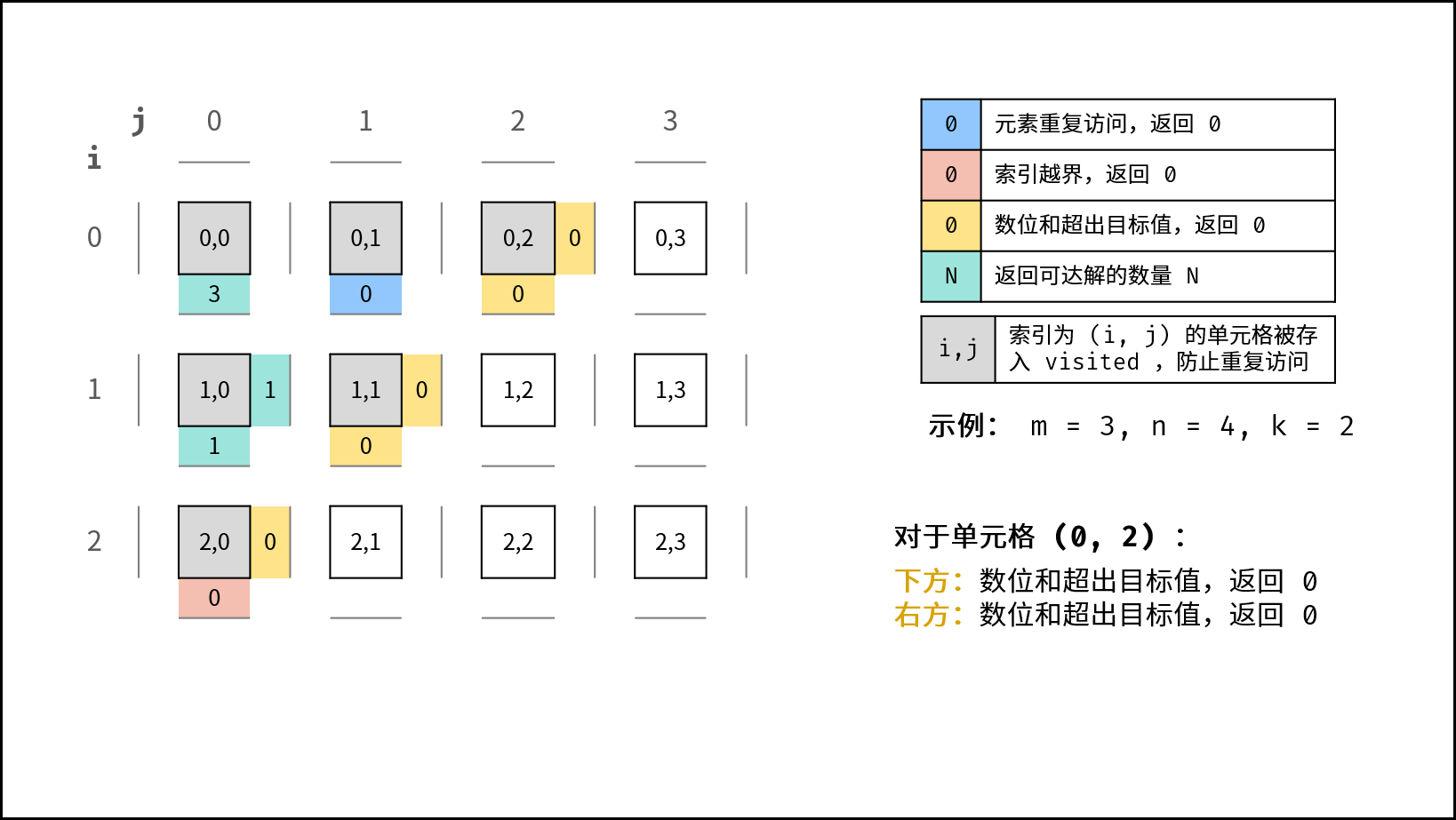Picture20.png](https://pic.leetcode-cn.com/1603024999-HBTzMV-Picture20.png),![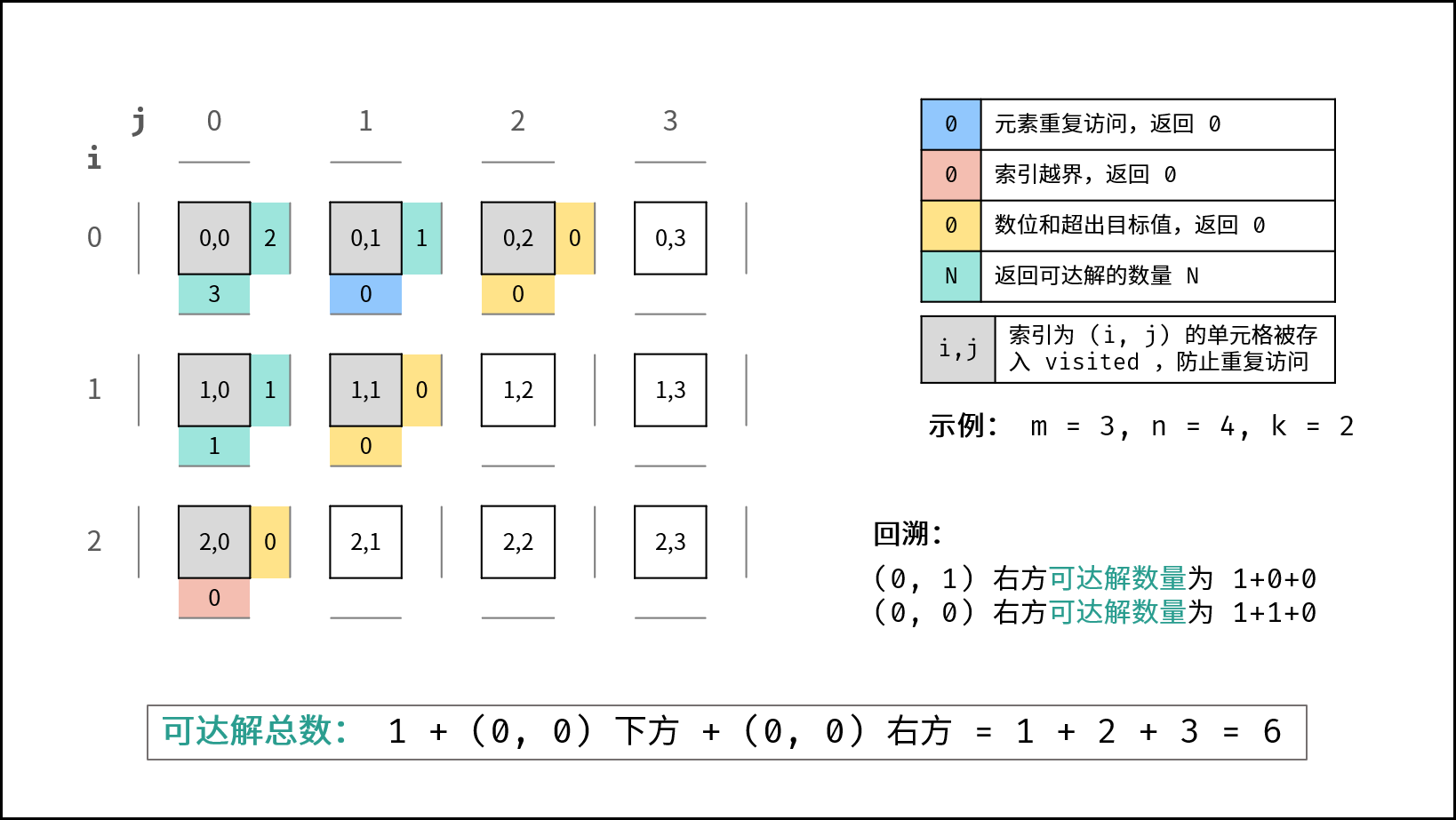Picture21.png](https://pic.leetcode-cn.com/1603024999-iYtADx-Picture21.png)>
### 代码：
> Java/C++ 代码中 `visited` 为辅助矩阵，Python 中为 Set 。
```Python []
class Solution:
def wardrobeFinishing(self, m: int, n: int, cnt: int) -> int:
def dfs(i, j, si, sj):
if i >= m or j >= n or cnt < si + sj or (i, j) in visited: return 0
visited.add((i,j))
return 1 + dfs(i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj) + dfs(i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8)
visited = set()
return dfs(0, 0, 0, 0)
```
```Java []
class Solution {
int m, n, cnt;
boolean[][] visited;
public int wardrobeFinishing(int m, int n, int cnt) {
this.m = m; this.n = n; this.cnt = cnt;
this.visited = new boolean[m][n];
return dfs(0, 0, 0, 0);
}
public int dfs(int i, int j, int si, int sj) {
if(i >= m || j >= n || cnt < si + sj || visited[i][j]) return 0;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) + dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
}
}
```
```C++ []
class Solution {
public:
int wardrobeFinishing(int m, int n, int cnt) {
vector<vector<bool>> visited(m, vector<bool>(n, 0));
return dfs(0, 0, 0, 0, visited, m, n, cnt);
}
private:
int dfs(int i, int j, int si, int sj, vector<vector<bool>> &visited, int m, int n, int cnt) {
if(i >= m || j >= n || cnt < si + sj || visited[i][j]) return 0;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj, visited, m, n, cnt) +
dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8, visited, m, n, cnt);
}
};
```
### 复杂度分析：
> 设矩阵行列数分别为 $M, N$ 。
- **时间复杂度 $O(MN)$ ：** 最差情况下，机器人遍历矩阵所有单元格，此时时间复杂度为 $O(MN)$ 。
- **空间复杂度 $O(MN)$ ：** 最差情况下，Set `visited` 内存储矩阵所有单元格的索引，使用 $O(MN)$ 的额外空间。
## 方法二：广度优先遍历（BFS）
BFS 和 DFS 的目标都是遍历整个矩阵，不同点在于搜索顺序不同。DFS 是朝一个方向走到底，再回退，以此类推；BFS 则是按照“平推”的方式向前搜索。
**BFS 实现：** 通常利用队列实现广度优先遍历。
### 算法解析：
- **初始化：** 将机器人初始点 $(0, 0)$ 加入队列 `queue` ；
- **迭代终止条件：** `queue` 为空。代表已遍历完所有可达解。
- **迭代工作：**
1. **单元格出队：** 将队首单元格的 索引、数位和 弹出，作为当前搜索单元格。
2. **判断是否跳过：** 若 (1) 行列索引越界 **或** (2) 数位和超出目标值 `cnt` **或** (3) 当前元素已访问过 时，执行 `continue` 。
3. **标记当前单元格** ：将单元格索引 `(i, j)` 存入 Set `visited` 中，代表此单元格 **已被访问过** 。
4. **单元格入队：** 将当前元素的 **下方、右方** 单元格的 **索引、数位和** 加入 `queue` 。
- **返回值：** Set `visited` 的长度 `len(visited)` ，即可达解的数量。
> Java/C++ 使用了辅助变量 `res` 统计可达解数量； Python 直接返回 Set 的元素数 `len(visited)` 即可。
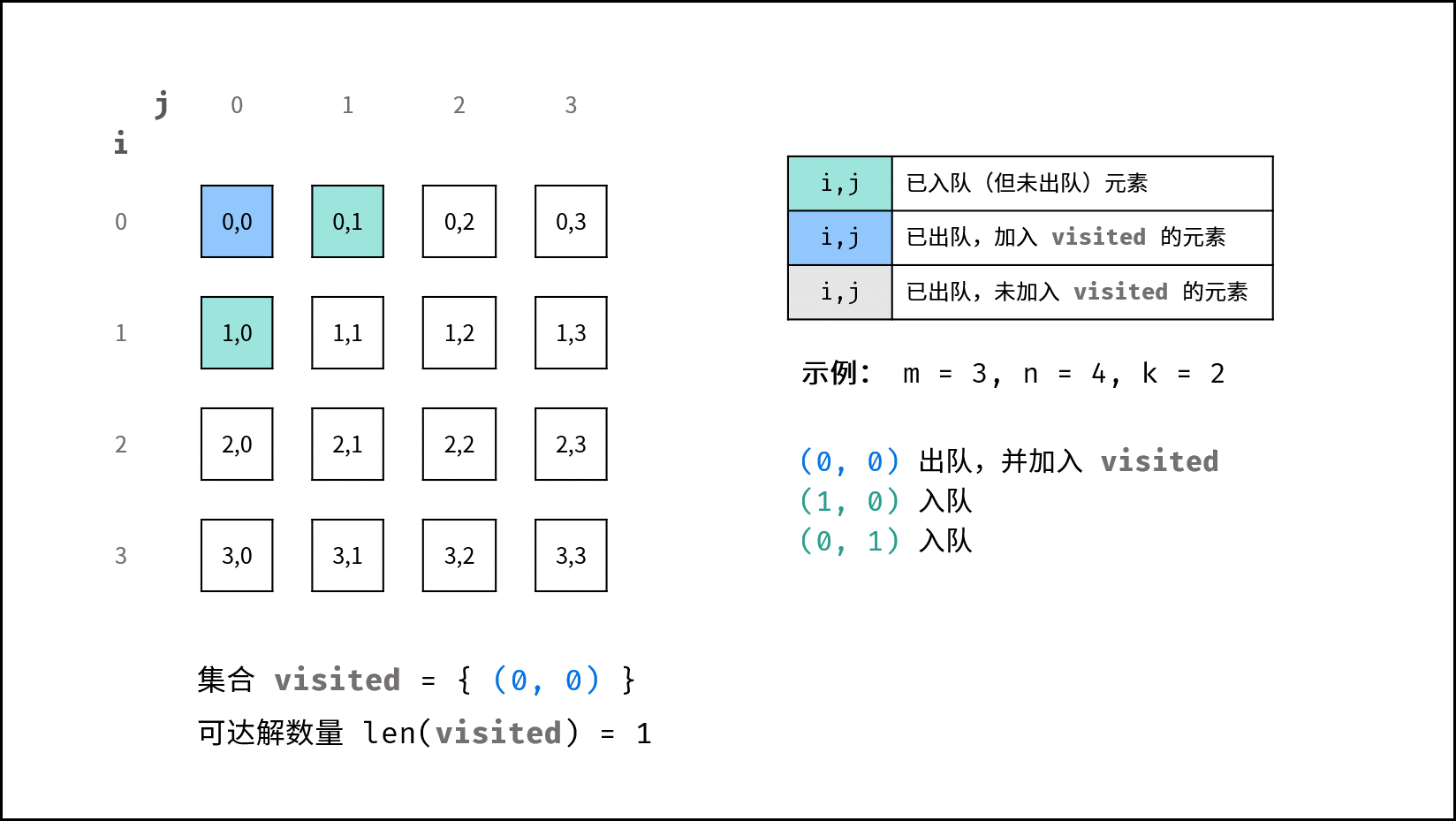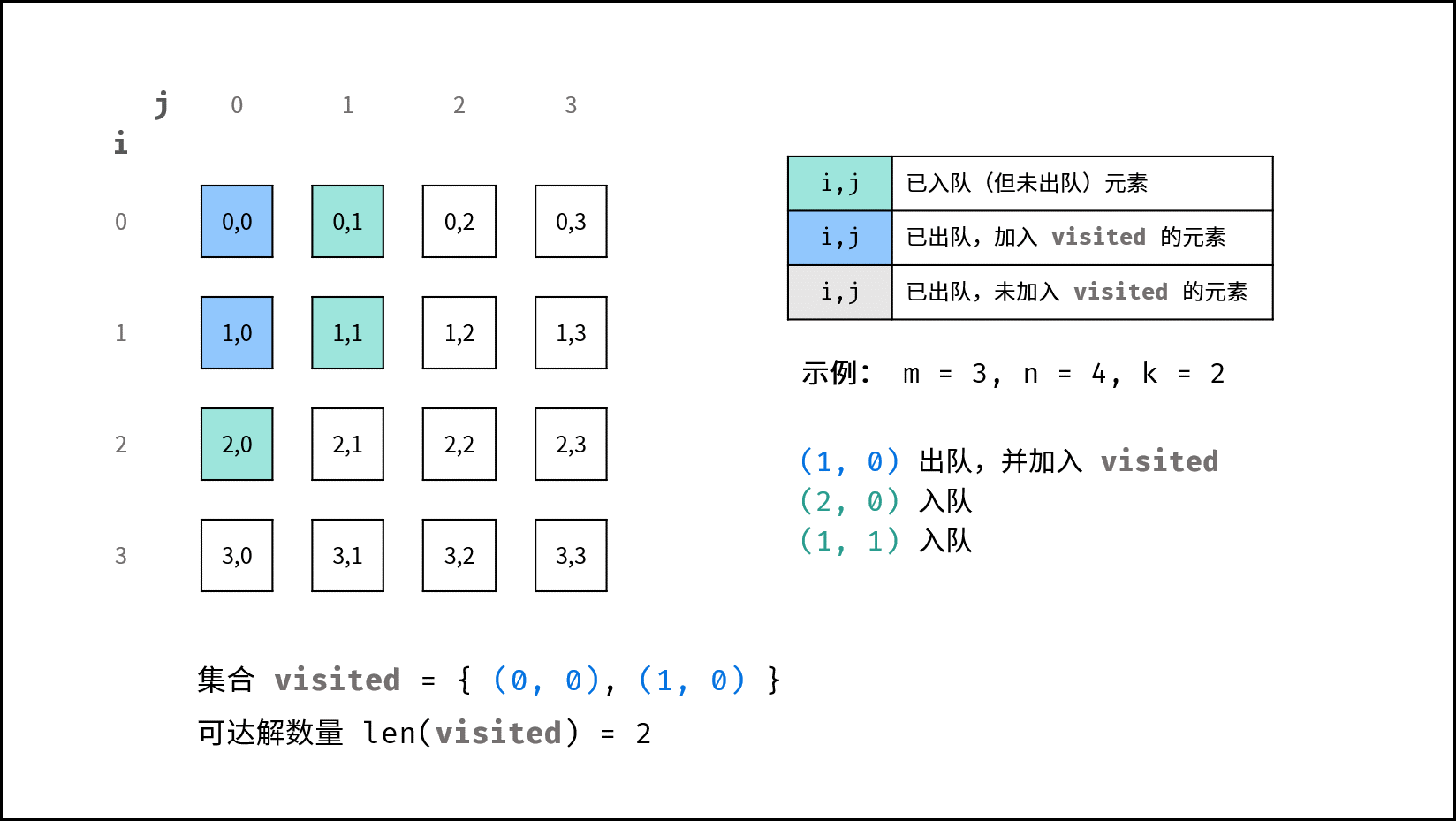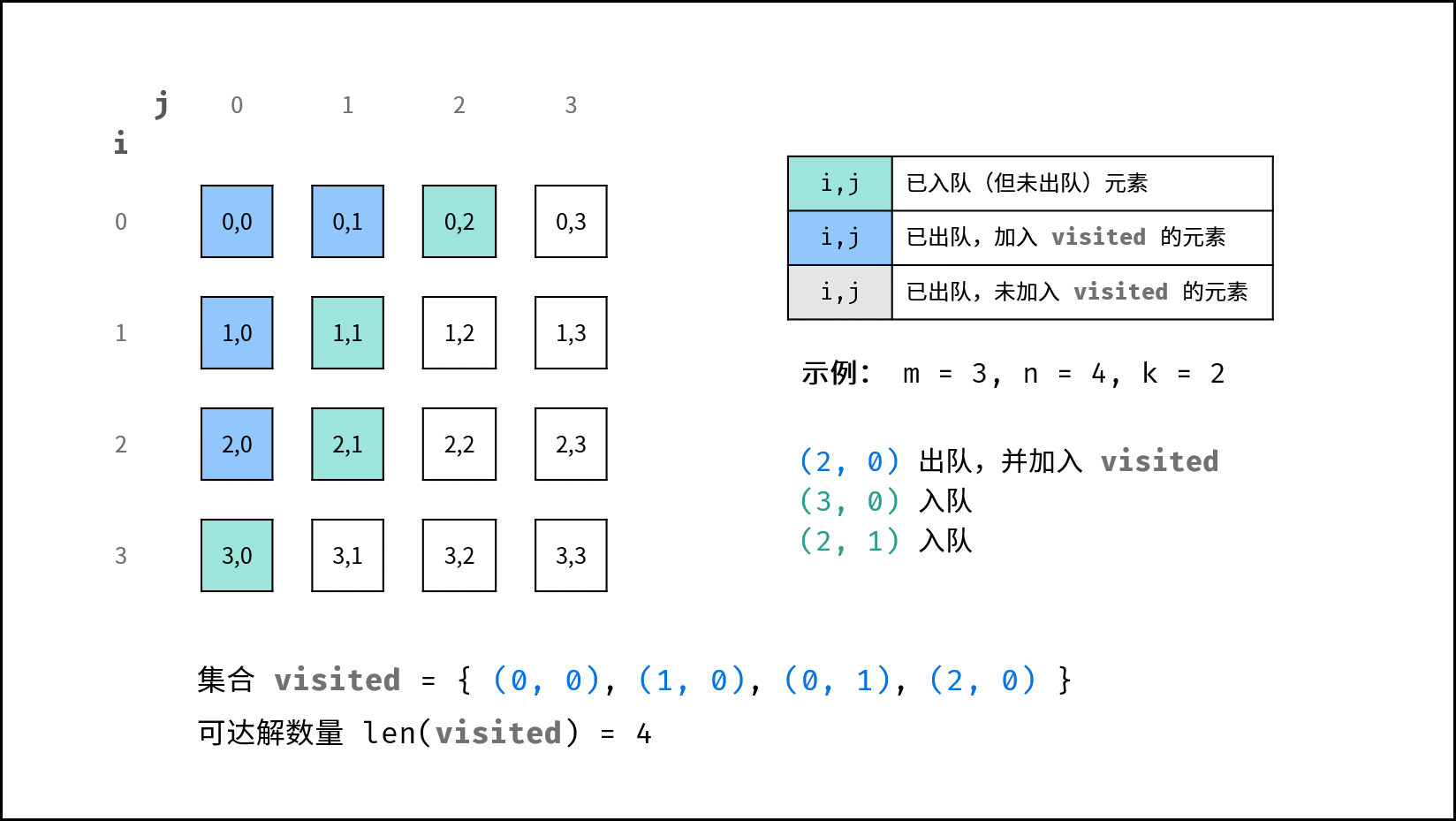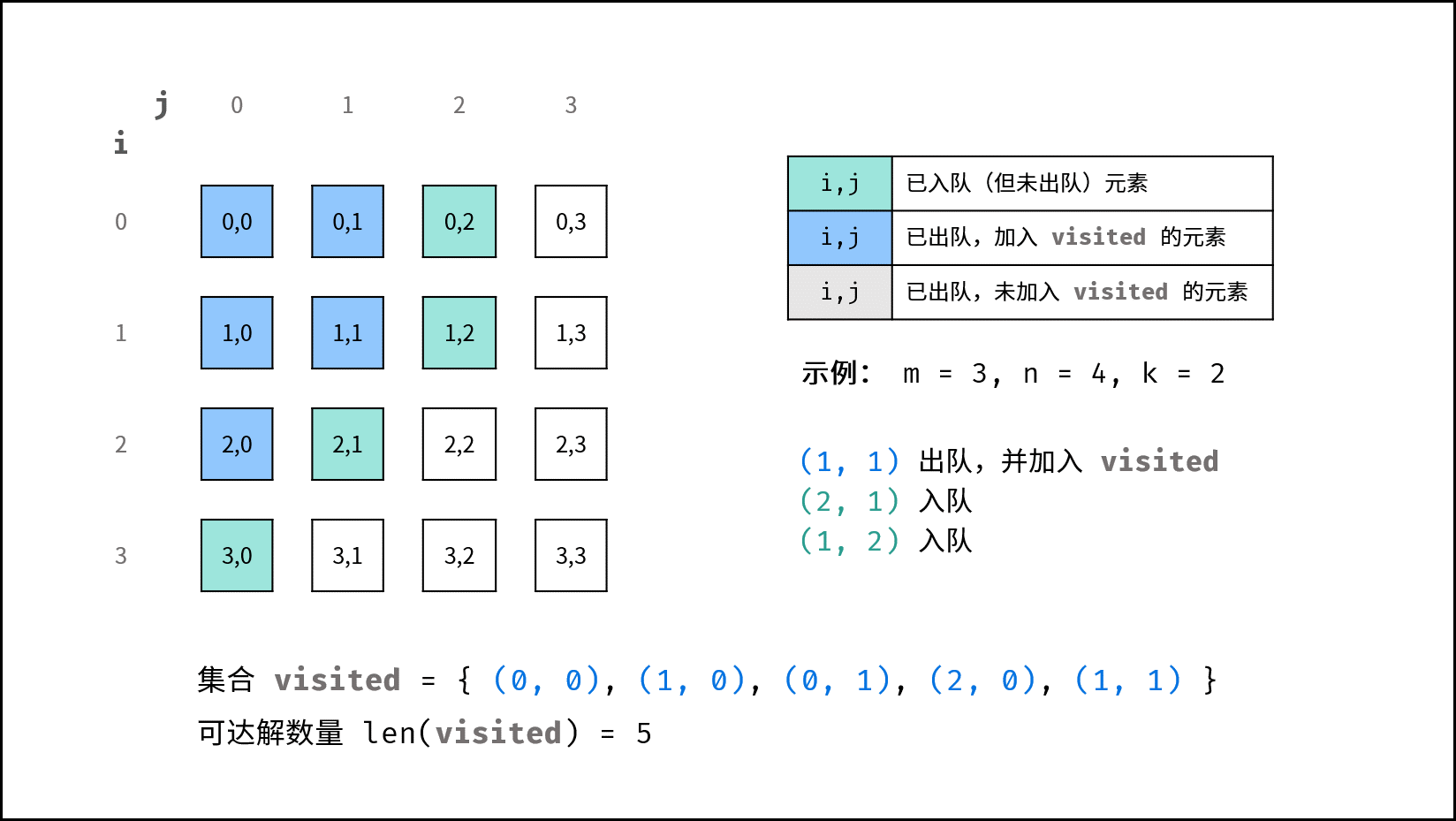<![Picture22.png](https://pic.leetcode-cn.com/1603024999-EKiknO-Picture22.png),![Picture23.png](https://pic.leetcode-cn.com/1603024999-hEnxrs-Picture23.png),![Picture24.png](https://pic.leetcode-cn.com/1603024999-goUtpL-Picture24.png),![Picture25.png](https://pic.leetcode-cn.com/1603024999-BwmmIl-Picture25.png),![Picture26.png](https://pic.leetcode-cn.com/1603024999-bQyxbG-Picture26.png),![Picture27.png](https://pic.leetcode-cn.com/1603024999-tjBCbi-Picture27.png),![Picture28.png](https://pic.leetcode-cn.com/1603024999-MBLwqu-Picture28.png),![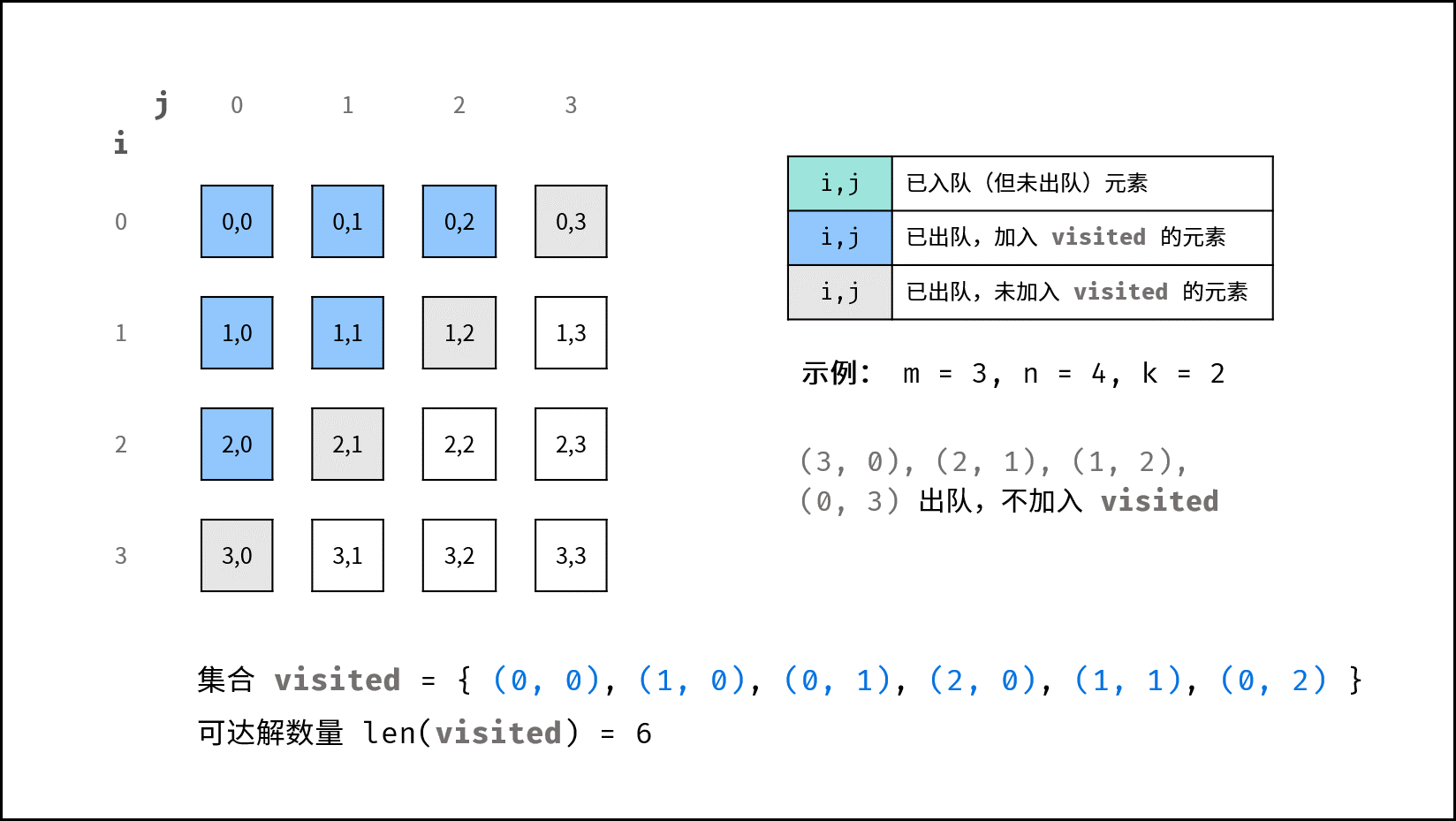Picture29.png](https://pic.leetcode-cn.com/1603024999-NYKszu-Picture29.png),![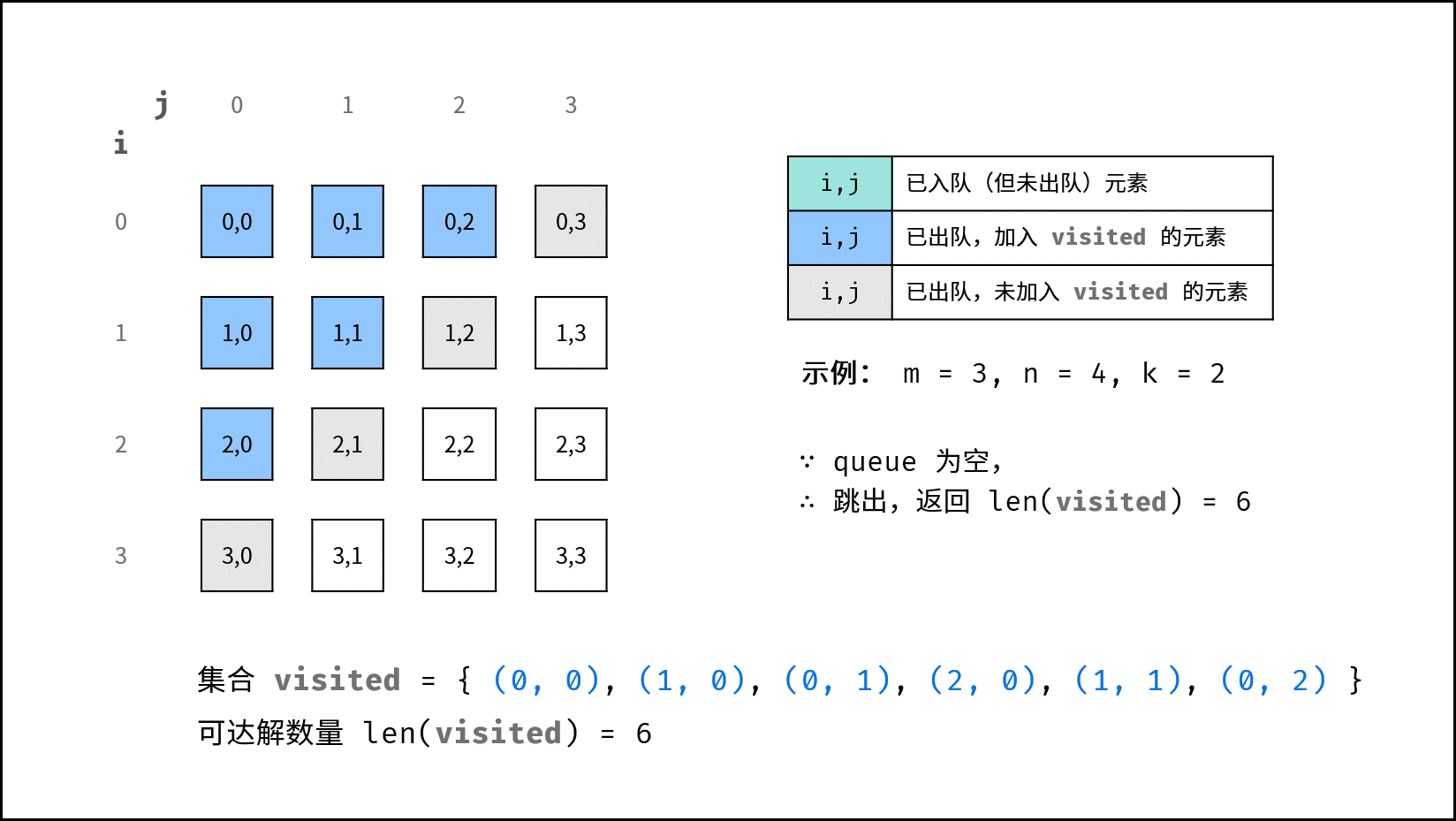Picture30.png](https://pic.leetcode-cn.com/1603024999-aMYSTi-Picture30.png)>
### 代码：
> Java/C++ 代码中 `visited` 为辅助矩阵，Python 中为 Set 。
```Python []
class Solution:
def wardrobeFinishing(self, m: int, n: int, cnt: int) -> int:
queue, visited = [(0, 0, 0, 0)], set()
while queue:
i, j, si, sj = queue.pop(0)
if i >= m or j >= n or cnt < si + sj or (i, j) in visited: continue
visited.add((i,j))
queue.append((i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj))
queue.append((i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8))
return len(visited)
```
```Java []
class Solution {
public int wardrobeFinishing(int m, int n, int cnt) {
boolean[][] visited = new boolean[m][n];
int res = 0;
Queue<int[]> queue= new LinkedList<int[]>();
queue.add(new int[] { 0, 0, 0, 0 });
while(queue.size() > 0) {
int[] x = queue.poll();
int i = x[0], j = x[1], si = x[2], sj = x[3];
if(i >= m || j >= n || cnt < si + sj || visited[i][j]) continue;
visited[i][j] = true;
res ++;
queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
}
return res;
}
}
```
```C++ []
class Solution {
public:
int wardrobeFinishing(int m, int n, int cnt) {
vector<vector<bool>> visited(m, vector<bool>(n, 0));
int res = 0;
queue<vector<int>> que;
que.push({ 0, 0, 0, 0 });
while(que.size() > 0) {
vector<int> x = que.front();
que.pop();
int i = x[0], j = x[1], si = x[2], sj = x[3];
if(i >= m || j >= n || cnt < si + sj || visited[i][j]) continue;
visited[i][j] = true;
res++;
que.push({ i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
que.push({ i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
}
return res;
}
};
```
### 复杂度分析：
> 设矩阵行列数分别为 $M, N$ 。
- **时间复杂度 $O(MN)$ ：** 最差情况下，机器人遍历矩阵所有单元格，此时时间复杂度为 $O(MN)$ 。
- **空间复杂度 $O(MN)$ ：** 最差情况下，Set `visited` 内存储矩阵所有单元格的索引，使用 $O(MN)$ 的额外空间。

164
leetbook_ioa/docs/LCR 131. 砍竹子 I.md Executable file
View File

@@ -0,0 +1,164 @@
## 解题思路：
设将长度为 $n$ 的竹子切为 $a$ 段：
$$
n = n_1 + n_2 + ... + n_a
$$
本题等价于求解：
$$
\max(n_1 \times n_2 \times ... \times n_a)
$$
> 以下数学推导总体分为两步：(1) 当所有绳段长度相等时，乘积最大。(2) 最优的绳段长度为 $3$ 。
### 数学推导：
以下公式为“算术几何均值不等式” ，等号当且仅当 $n_1 = n_2 = ... = n_a$ 时成立。
$$
\frac{n_1 + n_2 + ... + n_a}{a} \geq \sqrt[a]{n_1 n_2 ... n_a}
$$
> **推论一：** 将竹子 **以相等的长度等分为多段** ，得到的乘积最大。
设将竹子按照 $x$ 长度等分为 $a$ 段，即 $n = ax$ ，则乘积为 $x^a$ 。观察以下公式，由于 $n$ 为常数，因此当 $x^{\frac{1}{x}}$ 取最大值时， 乘积达到最大值。
$$
x^a = x^{\frac{n}{x}} = (x^{\frac{1}{x}})^n
$$
根据分析，可将问题转化为求 $y = x^{\frac{1}{x}}$ 的极大值，因此对 $x$ 求导数。
$$
\begin{aligned}
\ln y & = \frac{1}{x} \ln x & \text{取对数} \\
\frac{1}{y} \dot {y} & = \frac{1}{x^2} - \frac{1}{x^2} \ln x & \text{对 $x$ 求导} \\
& = \frac{1 - \ln x}{x^2} \\
\dot {y} & = \frac{1 - \ln x}{x^2} x^{\frac{1}{x}} & \text{整理得}
\end{aligned}
$$
令 $\dot {y} = 0$ ，则 $1 - \ln x = 0$ ，易得驻点为 $x_0 = e \approx 2.7$ ；根据以下公式，可知 $x_0$ 为极大值点。
$$
\dot {y}
\begin{cases}
> 0 & , x \in [- \infty, e) \\
< 0 & , x \in (e, \infty] \\
\end{cases}
$$
由于切分长度 $x$ 必须为整数，最接近 $e$ 的整数为 $2$ 或 $3$ 。如下式所示，代入 $x = 2$ 和 $x = 3$ ，得出 $x = 3$ 时，乘积达到最大。
$$
y(3) = 3^{1/3} \approx 1.44 \\
y(2) = 2^{1/2} \approx 1.41
$$
口算对比方法：给两数字同时取 $6$ 次方，再对比。
$$
y(3)^6 = (3^{1/3})^6 = 9 \\
y(2)^6 = (2^{1/2})^6 = 8
$$
> **推论二：** 尽可能将竹子以长度 $3$ 等分为多段时，乘积最大。
### 切分规则：
1. **最优：** $3$ 。把竹子尽可能切为多个长度为 $3$ 的片段，留下的最后一段竹子的长度可能为 $0,1,2$ 三种情况。
2. **次优：** $2$ 。若最后一段竹子长度为 $2$ ；则保留，不再拆为 $1+1$ 。
3. **最差：** $1$ 。若最后一段竹子长度为 $1$ ；则应把一份 $3 + 1$ 替换为 $2 + 2$，因为 $2 \times 2 > 3 \times 1$。
### 算法流程：
1. 当 $n \leq 3$ 时，按照规则应不切分，但由于题目要求必须剪成 $m>1$ 段，因此必须剪出一段长度为 $1$ 的竹子，即返回 $n - 1$ 。
2. 当 $n>3$ 时，求 $n$ 除以 $3$ 的 整数部分 $a$ 和 余数部分 $b$ （即 $n = 3a + b$ ），并分为以下三种情况：
- 当 $b = 0$ 时，直接返回 $3^a$；
- 当 $b = 1$ 时，要将一个 $1 + 3$ 转换为 $2+2$，因此返回 $3^{a-1} \times 4$；
- 当 $b = 2$ 时，返回 $3^a \times 2$。
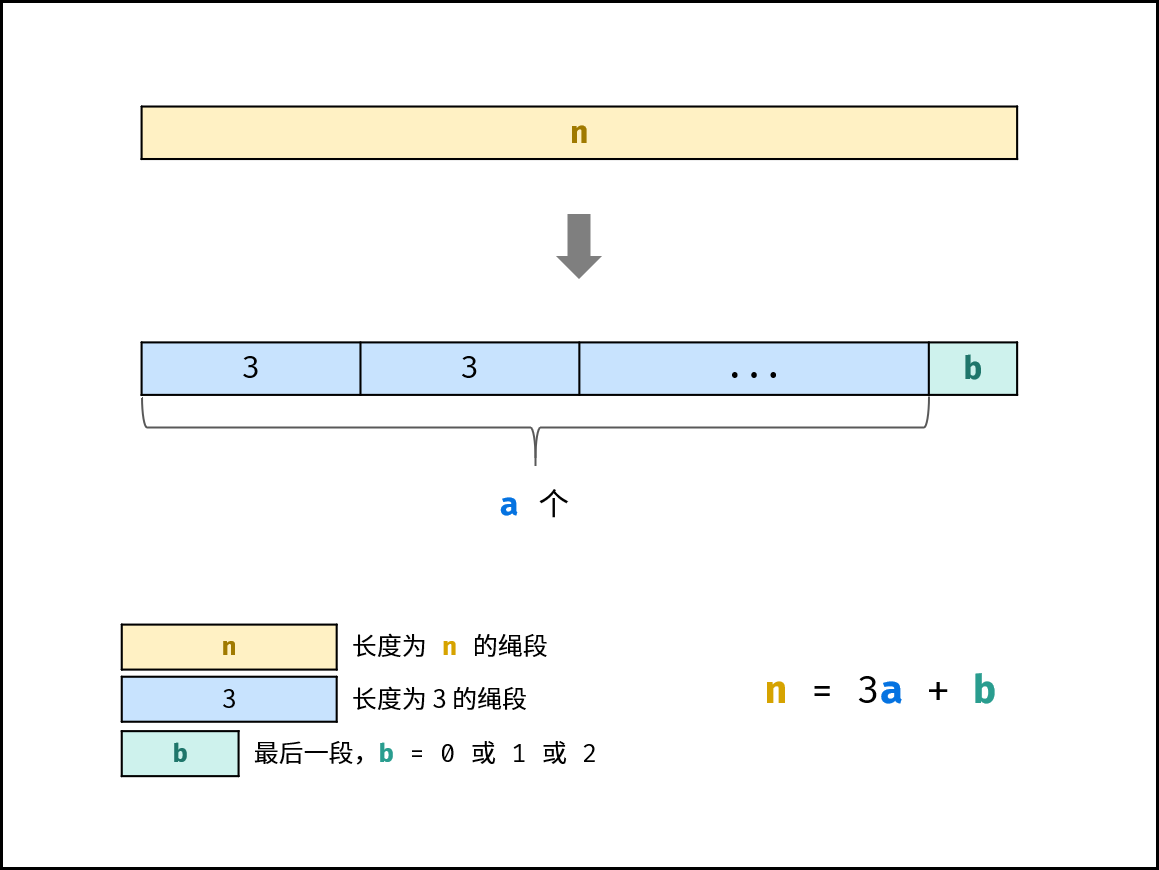![Picture1.png](https://pic.leetcode-cn.com/1f9adeaa7b9fff0ab19c9d29e3a8f98749011d22dc162d67bdbe223f1a38119f-Picture1.png){:align=center width=600}
## 代码：
> Python 中常见有三种幂计算函数： **`*`** 和 **`pow()`** 的时间复杂度均为 $O(\log a)$ ；而 **`math.pow()`** 始终调用 C 库的 `pow()` 函数，其执行浮点取幂，时间复杂度为 $O(1)$ 。
```Python []
class Solution:
def cuttingBamboo(self, bamboo_len: int) -> int:
if bamboo_len <= 3: return bamboo_len - 1
a, b = bamboo_len // 3, bamboo_len % 3
if b == 0: return int(math.pow(3, a))
if b == 1: return int(math.pow(3, a - 1) * 4)
return int(math.pow(3, a) * 2)
```
```Java []
class Solution {
public int cuttingBamboo(int bamboo_len) {
if(bamboo_len <= 3) return bamboo_len - 1;
int a = bamboo_len / 3, b = bamboo_len % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
```
```C++ []
class Solution {
public:
int cuttingBamboo(int bamboo_len) {
if(bamboo_len <= 3) return bamboo_len - 1;
int a = bamboo_len / 3, b = bamboo_len % 3;
if(b == 0) return pow(3, a);
if(b == 1) return pow(3, a - 1) * 4;
return pow(3, a) * 2;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(1)$ ：** 仅有求整、求余、次方运算。
- [求整和求余运算](https://stackoverflow.com/questions/35189851/time-complexity-of-modulo-operator-in-python)：资料提到不超过机器数的整数可以看作是 $O(1)$ ；
- [幂运算](https://stackoverflow.com/questions/32418731/java-math-powa-b-time-complexity)：查阅资料，提到浮点取幂为 $O(1)$ 。
- **空间复杂度 $O(1)$ ：** 变量 `a` 和 `b` 使用常数大小额外空间。
## 贪心思路：
数学推导需要一定的知识基础，贪心算法的思路更加适合快速解题。
> 设一竹子长度为 $n$ ( $n>1$ )，则其必可被切分为两段 $n=n_1+n_2$ 。
> 根据经验推测，切分的两数字乘积往往原数字更大，即往往有 $n_1 \times n_2 > n_1 + n_2 = n$ 。
>
> - **例如竹子长度为 $6$ ：** $6 = 3 + 3 < 3 \times 3 = 9$ ；
> - **也有少数反例，例如 $2$ ：** $2 = 1 + 1 > 1 \times 1 = 1$ 。
- **推论一：** 合理的切分方案可以带来更大的乘积。
> 设一竹子长度为 $n$ ( $n>1$ )，**切分为两段** $n=n_1+n_2$ ，**切分为三段** $n=n_1+n_2+n_3$ 。
> 根据经验推测，**三段** 的乘积往往更大，即往往有 $n_1 n_2 n_3 > n_1 n_2$ 。
>
> - **例如竹子长度为 $9$ ：** 两段 $9=4+5$ 和 三段 $9=3+3+3$，则有 $4 \times 5 < 3 \times 3 \times 3$ 。
> - **也有少数反例，例如 $6$ ：** 两段 $6=3+3$ 和 三段 $6=2+2+2$，则有 $3 \times 3 > 2 \times 2 \times 2$ 。
- **推论二：** 若切分方案合理，竹子段切分的越多，乘积越大。
> 总体上看，貌似长竹子切分为越多段乘积越大，但其实到某个长度分界点后，乘积到达最大值，就不应再切分了。
> **问题转化：** 是否有**优先级最高的长度** $x$ 存在？若有，则应该尽可能把竹子以 $x$ 长度切为多段，以获取最大乘积。
- **推论三：** 为使乘积最大，只有长度为 $2$ 和 $3$ 的竹子不应再切分，且 $3$ 比 $2$ 更优 *（详情见下表）* 。
| 竹子切分方案 | 乘积 | 结论 |
| ------------- | ------------------------------------------ | ----------------------------------------------------------------- |
| $2 = 1 + 1$ | $1 \times 1 = 1$ | $2$ 不应切分 |
| $3=1+2$ | $1 \times 2 = 2$ | $3$ 不应切分 |
| $4=2+2=1+3$ | $2 \times 2 = 4 > 1 \times 3 = 3$ | $4$ 和 $2$ 等价，且 $2+2$ 比 $1+3$ 更优 |
| $5=2+3=1+4$ | $2 \times 3 = 6 > 1 \times 4 = 4$ | $5$ 应切分为 $2+3$ |
| $6=3+3=2+2+2$ | $3 \times 3 = 9 > 2 \times 2 \times 2 = 8$ | $6$ 应切分为 $3+3$ ，进而**推出 $3$ 比 $2$ 更优** |
| $>7$ | ... | **长绳**（长度>7）可转化为多个**短绳**（长度1~6），因此肯定应切分 |

166
leetbook_ioa/docs/LCR 132. 砍竹子 II.md Executable file
View File

@@ -0,0 +1,166 @@
## 解题思路：
> 切分规则的推导流程请见上一题「砍竹子 I」。
### 切分规则：
1. **最优：** $3$ 。把竹子尽可能切为多个长度为 $3$ 的片段，留下的最后一段竹子的长度可能为 $0,1,2$ 三种情况。
2. **次优：** $2$ 。若最后一段竹子长度为 $2$ ；则保留，不再拆为 $1+1$ 。
3. **最差：** $1$ 。若最后一段竹子长度为 $1$ ；则应把一份 $3 + 1$ 替换为 $2 + 2$，因为 $2 \times 2 > 3 \times 1$。
### 算法流程：
1. 当 $n \leq 3$ 时，按照规则应不切分，但由于题目要求必须剪成 $m>1$ 段，因此必须剪出一段长度为 $1$ 的竹子，即返回 $n - 1$ 。
2. 当 $n>3$ 时，求 $n$ 除以 $3$ 的 整数部分 $a$ 和 余数部分 $b$ （即 $n = 3a + b$ ），并分为以下三种情况（设求余操作符号为 "$\odot$" ）：
- 当 $b = 0$ 时，直接返回 $3^a \odot 1000000007$；
- 当 $b = 1$ 时，要将一个 $1 + 3$ 转换为 $2+2$，因此返回 $(3^{a-1} \times 4)\odot 1000000007$；
- 当 $b = 2$ 时，返回 $(3^a \times 2) \odot 1000000007$。
![Picture1.png](https://pic.leetcode-cn.com/1f9adeaa7b9fff0ab19c9d29e3a8f98749011d22dc162d67bdbe223f1a38119f-Picture1.png){:align=center width=600}
### 大数求余解法：
**大数越界：** 当 $a$ 增大时，最后返回的 $3^a$ 大小以指数级别增长，可能超出 `int32` 甚至 `int64` 的取值范围，导致返回值错误。
**大数求余问题：** 在仅使用 `int32` 类型存储的前提下，正确计算 $x^a$ 对 $p$ 求余（即 $x^a \odot p$ ）的值。
**解决方案：** *循环求余* 、 *快速幂求余* ，其中后者的时间复杂度更低，两种方法均基于以下求余运算规则推出：
$$
(xy) \odot p = [(x \odot p)(y \odot p)] \odot p
$$
### 1. 循环求余：
根据求余运算性质推出（∵ 本题中 $x<p$，∴ $x \odot p = x$ ）：
$$
x^a \odot p = [(x ^{a-1} \odot p)(x \odot p)] \odot p=[(x ^{a-1} \odot p)x] \odot p
$$
利用此公式，可通过循环操作依次求 $x^1, x^2, ..., x^{a-1}, x^a$ 对 $p$ 的余数，保证每轮中间值 `rem` 都在 `int32` 取值范围中。封装方法代码如下所示。
```Python []
# 求 (x^a) % p —— 循环求余法
def remainder(x, a, p):
rem = 1
for _ in range(a):
rem = (rem * x) % p
return rem
```
**时间复杂度 $O(N)$ ：** 其中 $N=a$ ，即循环的线性复杂度。
### 2. 快速幂求余：
根据求余运算性质可推出：
$$
x^a \odot p = (x^2)^{a/2} \odot p = (x^2 \odot p)^{a / 2} \odot p
$$
当 $a$ 为奇数时 $a/2$ 不是整数，因此分为以下两种情况（ ''$//$'' 代表向下取整的除法）：
$$
{x^a \odot p = }
\begin{cases}
(x^2 \odot p)^{a // 2} \odot p & \text{, $a$ 为偶数} \\
{[(x \odot p)(x ^{a-1} \odot p)] \odot p = [x(x^2 \odot p)^{a//2}] \odot p} & \text{, $a$ 为奇数} \\
\end{cases}
$$
**解析：** 利用以上公式，可通过循环操作每次把指数 $a$ 问题降低至指数 $a//2$ 问题，只需循环 $\log_2(N)$ 次，因此可将复杂度降低至对数级别。封装方法代码如下所示。
```Python []
# 求 (x^a) % p —— 快速幂求余
def remainder(x, a, p):
rem = 1
while a > 0:
if a % 2: rem = (rem * x) % p
x = x ** 2 % p
a //= 2
return rem
```
**帮助理解：** 根据下表， 初始状态 $rem=1$, $x=3$, $a=19$, $p=1000000007$ ，最后会将 $rem \times (x^a \odot p)$ 化为 $rem \times (x^0 \odot p) = rem \times 1$ 的形式，即 $rem$ 为余数答案。
| $n$ | $rem \times (x^a \odot p)$ | $rem_n=rem_{n-1} \times x_{n-1} \odot p$ | $x_n=x_{n-1}^2 \odot p$ | $a_n=a_{n-1}//2$ |
| --- | -----------------------------------------: | ---------------------------------------: | -----------------------------: | :--------------: |
| $1$ | $1 \times (3^{19} \odot p)$ | $1$ | $3$ | $19$ |
| $2$ | $3 \times (9^{9} \odot p)$ | $3=1\times3\odot p$ | $9=3^2 \odot p$ | $9=19//2$ |
| $3$ | $27 \times (81^{4} \odot p)$ | $27 = 3 \times 9 \odot p$ | $81=9^2\odot p$ | $4=9//2$ |
| $4$ | $27 \times (6561^{2} \odot p)$ | $27$ | $6561=81^2 \odot p$ | $2=4//2$ |
| $5$ | $27 \times (43046721^{1} \odot p)$ | $27$ | $43046721=6561^2 \odot p$ | $1=2//2$ |
| $6$ | $162261460 \times (175880701^{0} \odot p)$ | $162261460=27 \times 43046721 \odot p$ | $175880701=43046721^2 \odot p$ | $0=1//2$ |
## 代码：
**Python 代码：** 由于语言特性，理论上 Python 中的变量取值范围由系统内存大小决定（无限大），因此在 Python 中其实不用考虑大数越界问题。
**Java/C++ 代码：** 根据二分法计算原理，至少要保证变量 `x` 和 `rem` 可以正确存储 $1000000007^2$ ，而 $2^{64} > 1000000007^2 > 2^{32}$ ，因此我们选取 `long` 类型。
```Python []
class Solution:
def cuttingBamboo(self, bamboo_len: int) -> int:
if bamboo_len <= 3: return bamboo_len - 1
a, b, p, x, rem = bamboo_len // 3 - 1, bamboo_len % 3, 1000000007, 3 , 1
while a > 0:
if a % 2: rem = (rem * x) % p
x = x ** 2 % p
a //= 2
if b == 0: return (rem * 3) % p # = 3^(a+1) % p
if b == 1: return (rem * 4) % p # = 3^a * 4 % p
return (rem * 6) % p # = 3^(a+1) * 2 % p
```
```Java []
class Solution {
public int cuttingBamboo(int bamboo_len) {
if(bamboo_len <= 3) return bamboo_len - 1;
int b = bamboo_len % 3, p = 1000000007;
long rem = 1, x = 3;
for(int a = bamboo_len / 3 - 1; a > 0; a /= 2) {
if(a % 2 == 1) rem = (rem * x) % p;
x = (x * x) % p;
}
if(b == 0) return (int)(rem * 3 % p);
if(b == 1) return (int)(rem * 4 % p);
return (int)(rem * 6 % p);
}
}
```
```C++ []
class Solution {
public:
int cuttingBamboo(int bamboo_len) {
if(bamboo_len <= 3) return bamboo_len - 1;
int b = bamboo_len % 3, p = 1000000007;
long rem = 1, x = 3;
for(int a = bamboo_len / 3 - 1; a > 0; a /= 2) {
if(a % 2 == 1) rem = (rem * x) % p;
x = (x * x) % p;
}
if(b == 0) return (int)(rem * 3 % p);
if(b == 1) return (int)(rem * 4 % p);
return (int)(rem * 6 % p);
}
};
```
```Python []
# 由于语言特性，Python 可以不考虑大数越界问题
class Solution:
def cuttingBamboo(self, bamboo_len: int) -> int:
if bamboo_len <= 3: return bamboo_len - 1
a, b, p = bamboo_len // 3, bamboo_len % 3, 1000000007
if b == 0: return 3 ** a % p
if b == 1: return 3 ** (a - 1) * 4 % p
return 3 ** a * 2 % p
```
### 复杂度分析：
> 以下为 **二分求余法** 的复杂度。
- **时间复杂度 $O(\log N)$ ：** 其中 $N=a$ ，二分法为对数级别复杂度，每轮仅有求整、求余、次方运算。
- [求整和求余运算](https://stackoverflow.com/questions/35189851/time-complexity-of-modulo-operator-in-python)：资料提到不超过机器数的整数可以看作是 $O(1)$ ；
- [幂运算](https://stackoverflow.com/questions/32418731/java-math-powa-b-time-complexity)：查阅资料，提到浮点取幂为 $O(1)$ 。
- **空间复杂度 $O(1)$ ：** 变量 `a, b, p, x, rem` 使用常数大小额外空间。

126
leetbook_ioa/docs/LCR 133. 位 1 的个数.md Executable file
View File

@@ -0,0 +1,126 @@
## 方法一：逐位判断
根据 **与运算** 定义，设二进制数字 $n$ ，则有：
- 若 $n \& 1 = 0$ ，则 $n$ 二进制 **最右一位** 为 $0$ ；
- 若 $n \& 1 = 1$ ，则 $n$ 二进制 **最右一位** 为 $1$ 。
根据以上特点，考虑以下 **循环判断** ：
1. 判断 $n$ 最右一位是否为 $1$ ，根据结果计数。
2. 将 $n$ 右移一位（本题要求把数字 $n$ 看作无符号数，因此使用 **无符号右移** 操作）。
### 算法流程：
1. 初始化数量统计变量 $res = 0$ 。
2. 循环逐位判断： 当 $n = 0$ 时跳出。
1. **`res += n & 1` ：** 若 $n \& 1 = 1$ ，则统计数 $res$ 加一。
2. **`n >>= 1` ：** 将二进制数字 $n$ 无符号右移一位（ Java 中无符号右移为 "$>>>$" ） 。
3. 返回统计数量 $res$ 。
<![Picture2.png](https://pic.leetcode-cn.com/196a1e24f89c3291d8462f1a2bdab87dde8590d4c04d964d503db8dcaf5fda72-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/4f4d43ed85b87c9dba12e0b3f3f3a8760f90e8e23d33d19ebabb3ad3c8149897-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/8f054e5ba19053365563577f339343bb635591381b1d8c950624bd9390309c71-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/20f8471b079eaa94d0f09b7627c94e64f541b85f660d3f20b14fd2fa1e3b1f92-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/6312b1569a40d74174f0c31fcfb8cc9836e0c2ab6c0ade144ab74f009ae0560d-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/eee12d1995aa0aa24757dcb10e1c8829ef72f685aa3baad74bf001d9f8cd7e54-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/9f734c501f50afaaee0d9ea0fe3c42f3af68eaaff1c9c5563295bbe1ac2a3110-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/ad1934398b309e369cbaa83f21a88a672ae9025460a3c93ec94439574620e1de-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/aae3da9131792c0103f9b24b35abebadb30b47d92441c5927546036066e5614b-Picture10.png)>
### 代码：
```Python []
class Solution:
def hammingWeight(self, n: int) -> int:
res = 0
while n:
res += n & 1
n >>= 1
return res
```
```Java []
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res += n & 1;
n >>>= 1;
}
return res;
}
}
```
```C++ []
class Solution {
public:
int hammingWeight(uint32_t n) {
unsigned int res = 0; // c++ 使用无符号数
while(n != 0) {
res += n & 1;
n >>= 1;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(\log_2 n)$ ：** 此算法循环内部仅有 **移位、与、加** 等基本运算，占用 $O(1)$ ；逐位判断需循环 $log_2 n$ 次，其中 $\log_2 n$ 代表数字 $n$ 最高位 $1$ 的所在位数（例如 $\log_2 4 = 2$, $\log_2 16 = 4$）。
- **空间复杂度 $O(1)$ ：** 变量 $res$ 使用常数大小额外空间。
## 方法二：巧用 $n \& (n - 1)$
- **$(n - 1)$ 解析：** 二进制数字 $n$ 最右边的 $1$ 变成 $0$ ，此 $1$ 右边的 $0$ 都变成 $1$ 。
- **$n \& (n - 1)$ 解析：** 二进制数字 $n$ 最右边的 $1$ 变成 $0$ ，其余不变。
![Picture1.png](https://pic.leetcode-cn.com/f23d9ef4fcfd65d7fbe29e477cbf36110b2f34558020e8cff09a1e13c0275c43-Picture1.png){:align=center width=450}
### 算法流程：
1. 初始化数量统计变量 $res$ 。
2. 循环消去最右边的 $1$ ：当 $n = 0$ 时跳出。
1. **`res += 1` ：** 统计变量加 $1$ ；
2. **`n &= n - 1` ：** 消去数字 $n$ 最右边的 $1$ 。
3. 返回统计数量 $res$ 。
<![Picture11.png](https://pic.leetcode-cn.com/d16a9a6cfdba918c655679373632afc8ddeaf9b64912aa1fbf7b57371736ccaa-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/a6c05d83742bdf0cc50f9e4f1cc05833b3fca1b33abad88cf82c30459964bfa1-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/19f7add30dac42e0785de28909579b0f961122cbfd673a44230b3a1c4fe89f80-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/016ca059d0eb893b9a5f1c0b3ff013ffbd42424f8cd0cc1f9a76624dcbd87c41-Picture14.png)>
### 代码：
```Python []
class Solution:
def hammingWeight(self, n: int) -> int:
res = 0
while n:
res += 1
n &= n - 1
return res
```
```Java []
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res++;
n &= n - 1;
}
return res;
}
}
```
```C++ []
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while(n != 0) {
res++;
n &= n - 1;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(M)$ ：** $n \& (n - 1)$ 操作仅有减法和与运算，占用 $O(1)$ ；设 $M$ 为二进制数字 $n$ 中 $1$ 的个数，则需循环 $M$ 次（每轮消去一个 $1$ ），占用 $O(M)$ 。
- **空间复杂度 $O(1)$ ：** 变量 $res$ 使用常数大小额外空间。

134
leetbook_ioa/docs/LCR 134. Pow(x, n).md Executable file
View File

@@ -0,0 +1,134 @@
## 解题思路：
求 $x^n$ 最简单的方法是通过循环将 $n$ 个 $x$ 乘起来，依次求 $x^1, x^2, ..., x^{n-1}, x^n$ ，时间复杂度为 $O(n)$ 。
**快速幂法** 可将时间复杂度降低至 $O(\log n)$ ，以下从 「分治法」 和 「二进制」 两个角度解析快速幂法。
### 快速幂解析（分治法角度）：
> 快速幂实际上是分治思想的一种应用。
**二分推导：** $x^n = x^{n/2} \times x^{n/2} = (x^2)^{n/2}$ ，令 $n/2$ 为整数，则需要分为奇偶两种情况（设向下取整除法符号为 "$//$" ）：
$$
x^n =
\begin{cases}
(x^2)^{n//2} & , n 为偶数 \\
x(x^2)^{n//2} & , n 为奇数 \\
\end{cases}
$$
> 观察发现，当 $n$ 为奇数时，二分后会多出一项 $x$ 。
**幂结果获取：**
- 根据推导，可通过循环 $x = x^2$ 操作，每次把幂从 $n$ 降至 $n//2$ ，直至将幂降为 $0$ ；
- 设 $res=1$ ，则初始状态 $x^n = x^n \times res$ 。在循环二分时，每当 $n$ 为奇数时，将多出的一项 $x$ 乘入 $res$ ，则最终可化至 $x^n = x^0 \times res = res$ ，返回 $res$ 即可。
![Picture2.png](https://pic.leetcode-cn.com/1599885604-YzlkAN-Picture2.png){:align=center width=500}
**转化为位运算：**
- 向下整除 $n // 2$ **等价于** 右移一位 $n >> 1$ ；
- 取余数 $n \mod 2$ **等价于** 判断二进制最右位 $n \& 1$ ；
### 快速幂解析（二进制角度）：
> 利用十进制数字 $n$ 的二进制表示，可对快速幂进行数学化解释。
对于任何十进制正整数 $n$ ，设其二进制为 "$b_m...b_3b_2b_1$"（ $b_i$ 为二进制某位值，$i \in [1,m]$ ），则有：
- **二进制转十进制：** $n = 1b_1 + 2b_2 + 4b_3 + ... + 2^{m-1}b_m$ *（即二进制转十进制公式）* ；
- **幂的二进制展开：** $x^n = x^{1b_1 + 2b_2 + 4b_3 + ... + 2^{m-1}b_m} = x^{1b_1}x^{2b_2}x^{4b_3}...x^{2^{m-1}b_m}$ ；
根据以上推导，可把计算 $x^n$ 转化为解决以下两个问题：
- **计算 $x^1, x^2, x^4, ..., x^{2^{m-1}}$ 的值：** 循环赋值操作 $x = x^2$ 即可；
- **获取二进制各位 $b_1, b_2, b_3, ..., b_m$ 的值：** 循环执行以下操作即可。
1. **$n \& 1$ （与操作）：** 判断 $n$ 二进制最右一位是否为 $1$ ；
2. **$n>>1$ （移位操作）：** $n$ 右移一位（可理解为删除最后一位）。
因此，应用以上操作，可在循环中依次计算 $x^{2^{0}b_1}, x^{2^{1}b_2}, ..., x^{2^{m-1}b_m}$ 的值，并将所有 $x^{2^{i-1}b_i}$ 累计相乘即可，其中：
$$
x^{2^{i-1}b_i}=
\begin{cases}
1 & , b_i = 0 \\
x^{2^{i-1}} & , b_i = 1 \\
\end{cases}
$$
![Picture1.png](https://pic.leetcode-cn.com/1599885604-yDzVYK-Picture1.png){:align=center width=500}
### 算法流程：
1. 当 $x = 0.0$ 时：直接返回 $0.0$ ，以避免后续 $1$ 除以 $0$ 操作报错。**分析：** 数字 $0$ 的正数次幂恒为 $0$ ；$0$ 的 $0$ 次幂和负数次幂没有意义，因此直接返回 $0.0$ 即可。
2. 初始化 $res = 1$ 。
3. 当 $n < 0$ 时：把问题转化至 $n \geq 0$ 的范围内，即执行 $x = 1/x$ ，$n = - n$ 。
4. 循环计算：当 $n = 0$ 时跳出。
1. 当 $n \& 1 = 1$ 时：将当前 $x$ 乘入 $res$ （即 $res *= x$ ）。
2. 执行 $x = x^2$ （即 $x *= x$ ）。
3. 执行 $n$ 右移一位（即 $n >>= 1$）。
5. 返回 $res$ 。
## 代码：
Java 中 int32 变量区间 $n \in [-2147483648, 2147483647]$ ，因此当 $n = -2147483648$ 时执行 $n = -n$ 会因越界而赋值出错。解决方法是先将 $n$ 存入 long 变量 $b$ ，后面用 $b$ 操作即可。
```Python []
class Solution:
def myPow(self, x: float, n: int) -> float:
if x == 0.0: return 0.0
res = 1
if n < 0: x, n = 1 / x, -n
while n:
if n & 1: res *= x
x *= x
n >>= 1
return res
```
```Java []
class Solution {
public double myPow(double x, int n) {
if(x == 0.0f) return 0.0d;
long b = n;
double res = 1.0;
if(b < 0) {
x = 1 / x;
b = -b;
}
while(b > 0) {
if((b & 1) == 1) res *= x;
x *= x;
b >>= 1;
}
return res;
}
}
```
```C++ []
class Solution {
public:
double myPow(double x, int n) {
if(x == 0.0f) return 0.0;
long b = n;
double res = 1.0;
if(b < 0) {
x = 1 / x;
b = -b;
}
while(b > 0) {
if((b & 1) == 1) res *= x;
x *= x;
b >>= 1;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(\log n)$ ：** 二分的时间复杂度为对数级别。
- **空间复杂度 $O(1)$ ：** $res$, $b$ 等变量占用常数大小额外空间。

269
leetbook_ioa/docs/LCR 135. 报数.md Executable file
View File

@@ -0,0 +1,269 @@
## 解题思路：
题目要求打印 “从 $1$ 至 $cnt$ 的数字” ，因此需考虑以下两个问题：
1. **最大的 $cnt$ 位数（记为 $end$ ）和位数 $cnt$ 的关系：** 例如最大的 $1$ 位数是 $9$ ，最大的 $2$ 位数是 $99$ ，最大的 $3$ 位数是 $999$ 。则可推出公式：
$$
end = 10^{cnt} - 1
$$
2. **大数越界问题：** 当 $cnt$ 较大时，$end$ 会超出 $int32$ 整型的取值范围，超出取值范围的数字无法正常存储。但由于本题要求返回 int 类型数组，相当于默认所有数字都在 int32 整型取值范围内，因此不考虑大数越界问题。
因此，只需定义区间 $[1, 10^{cnt} - 1]$ 和步长 $1$ ，通过 $for$ 循环生成结果列表 $res$ 并返回即可。
### 代码：
```Python []
class Solution:
def countNumbers(self, cnt: int) -> List[int]:
res = []
for i in range(1, 10 ** cnt):
res.append(i)
return res
```
```Java []
class Solution {
public int[] countNumbers(int cnt) {
int end = (int)Math.pow(10, cnt) - 1;
int[] res = new int[end];
for(int i = 0; i < end; i++)
res[i] = i + 1;
return res;
}
}
```
利用 Python 的语言特性，可以简化代码：先使用 `range()` 方法生成可迭代对象，再使用 `list()` 方法转化为列表并返回即可。
```Python
class Solution:
def countNumbers(self, cnt: int) -> List[int]:
return list(range(1, 10 ** cnt))
```
### 复杂度分析：
- **时间复杂度 $O(10^{cnt})$ ：** 生成长度为 $10^{cnt}$ 的列表需使用 $O(10^{cnt})$ 时间。
- **空间复杂度 $O(1)$ ：** 建立列表需使用 $O(1)$ 大小的额外空间（ 列表作为返回结果，不计入额外空间 ）。
## 大数打印拓展：
实际上，本题的主要考点是大数越界情况下的打印。需要解决以下三个问题：
**1. 表示大数的变量类型：**
- 无论是 short / int / long ... 任意变量类型，数字的取值范围都是有限的。因此，大数的表示应用字符串 String 类型。
**2. 生成数字的字符串集：**
- 使用 int 类型时，每轮可通过 $+1$ 生成下个数字，而此方法无法应用至 String 类型。并且， String 类型的数字的进位操作效率较低，例如 `"9999"` 至 `"10000"` 需要从个位到千位循环判断，进位 4 次。
- 观察可知，生成的列表实际上是 $cnt$ 位 $0$ - $9$ 的 **全排列** ，因此可避开进位操作，通过递归生成数字的 String 列表。
**3. 递归生成全排列：**
- 基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 $cnt = 2$ 时（数字范围 $1 - 99$ ），固定十位为 $0$ - $9$ ，按顺序依次开启递归，固定个位 $0$ - $9$ ，终止递归并添加数字字符串。
> 下图中的 `n` 对应本题中的 `cnt` 。
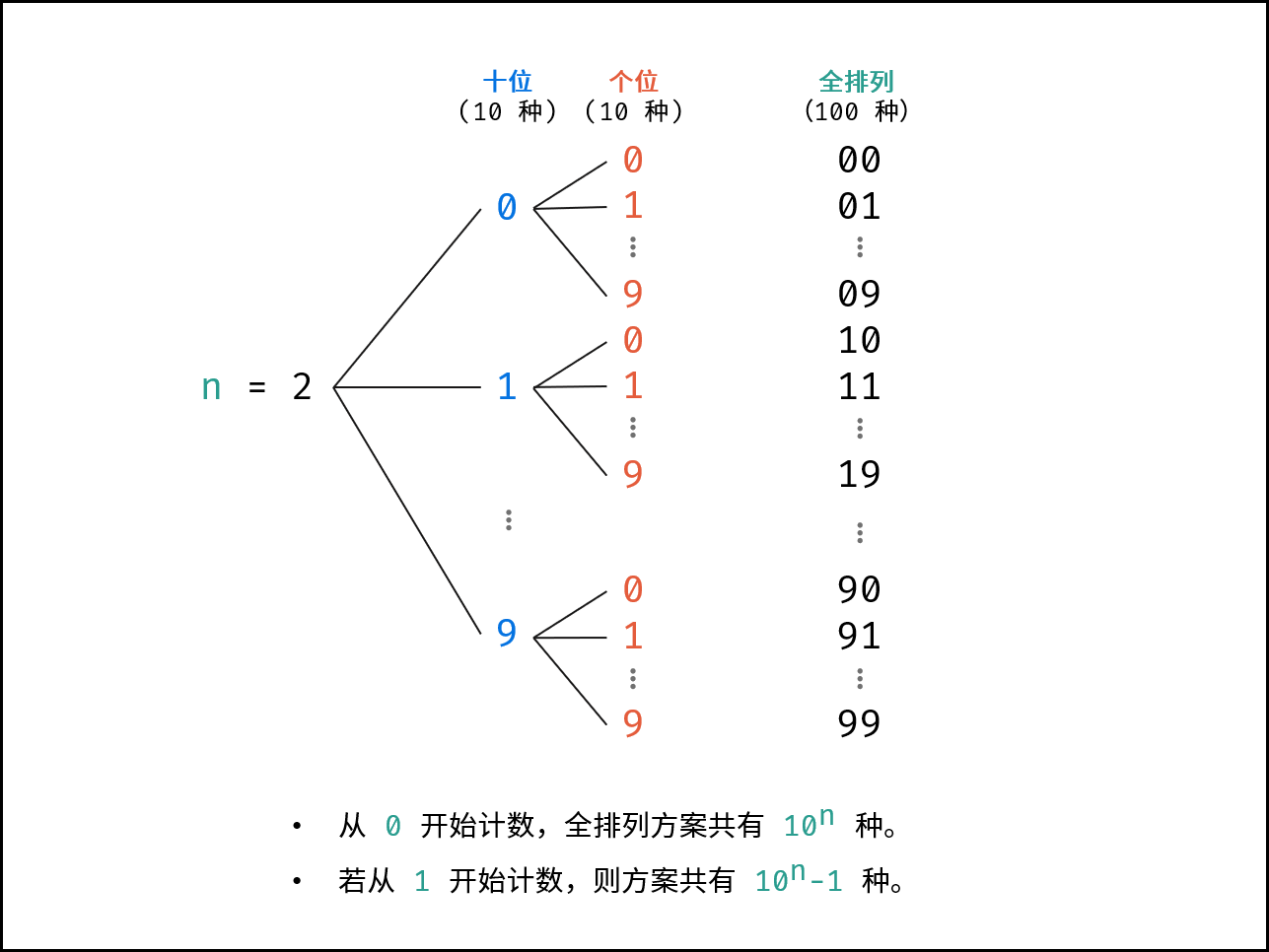![Picture1.png](https://pic.leetcode-cn.com/83f4b5930ddc1d42b05c724ea2950ee7f00427b11150c86b45bd88405f8c7c87-Picture1.png){:align=center width=500}
根据以上方法，可初步编写全排列代码：
```Python []
class Solution:
def countNumbers(self, cnt: int) -> [int]:
def dfs(x):
if x == cnt: # 终止条件：已固定完所有位
res.append(''.join(num)) # 拼接 num 并添加至 res 尾部
return
for i in range(10): # 遍历 0 - 9
num[x] = str(i) # 固定第 x 位为 i
dfs(x + 1) # 开启固定第 x + 1 位
num = ['0'] * cnt # 起始数字定义为 cnt 个 0 组成的字符列表
res = [] # 数字字符串列表
dfs(0) # 开启全排列递归
return ','.join(res) # 拼接所有数字字符串，使用逗号隔开，并返回
```
```Java []
class Solution {
StringBuilder res;
int count = 0, cnt;
char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
public String countNumbers(int cnt) {
this.cnt = cnt;
res = new StringBuilder(); // 数字字符串集
num = new char[cnt]; // 定义长度为 cnt 的字符列表
dfs(0); // 开启全排列递归
res.deleteCharAt(res.length() - 1); // 删除最后多余的逗号
return res.toString(); // 转化为字符串并返回
}
void dfs(int x) {
if(x == cnt) { // 终止条件：已固定完所有位
res.append(String.valueOf(num) + ","); // 拼接 num 并添加至 res 尾部，使用逗号隔开
return;
}
for(char i : loop) { // 遍历 ‘0‘ - ’9‘
num[x] = i; // 固定第 x 位为 i
dfs(x + 1); // 开启固定第 x + 1 位
}
}
}
```
在此方法下，各数字字符串被逗号隔开，共同组成长字符串。返回的数字集字符串如下所示：
```yaml
输入：n = 1
输出："0,1,2,3,4,5,6,7,8,9"
输入：n = 2
输出："00,01,02,...,10,11,12,...,97,98,99"
输入：n = 3
输出："000,001,002,...,100,101,102,...,997,998,999"
```
观察可知，当前的生成方法仍有以下问题：
1. 诸如 $00, 01, 02, \cdots$ 应显示为 $0, 1, 2, \cdots$ ，即应 **删除高位多余的 $0$** ;
2. 此方法从 $0$ 开始生成，而题目要求 **列表从 $1$ 开始** ；
以上两个问题的解决方法如下：
**1. 删除高位多余的 $0$ ：**
- **字符串左边界定义：** 声明变量 $start$ 规定字符串的左边界，以保证添加的数字字符串 `num[start:]` 中无高位多余的 $0$ 。例如当 $cnt = 2$ 时，$1 - 9$ 时 $start = 1$ ，$10 - 99$ 时 $start = 0$ 。
- **左边界 $start$ 变化规律：** 观察可知，当输出数字的所有位都是 $9$ 时，则下个数字需要向更高位进 $1$ ，此时左边界 $start$ 需要减 $1$ （即高位多余的 $0$ 减少一个）。例如当 $cnt = 3$ （数字范围 $1 - 999$ ）时，左边界 $start$ 需要减 $1$ 的情况有： "009" 进位至 "010" ， "099" 进位至 "100" 。设数字各位中 $9$ 的数量为 $nine$ ，所有位都为 $9$ 的判断条件可用以下公式表示：
$$
cnt - start = nine
$$
- **统计 $nine$ 的方法：** 固定第 $x$ 位时，当 $i = 9$ 则执行 $nine = nine + 1$ ，并在回溯前恢复 $nine = nine - 1$ 。
**2. 列表从 $1$ 开始：**
- 在以上方法的基础上，添加数字字符串前判断其是否为 `"0"` ，若为 `"0"` 则直接跳过。
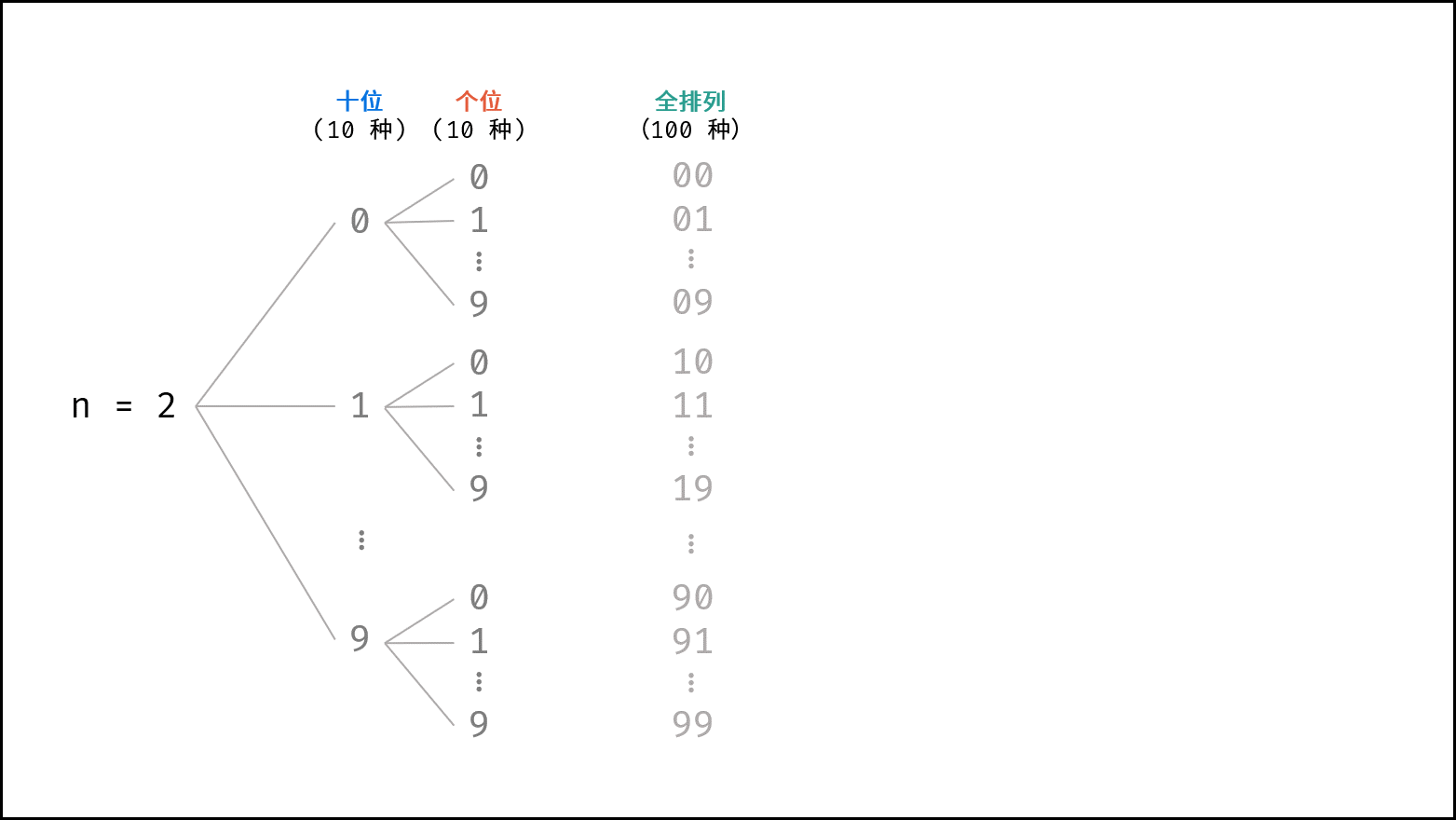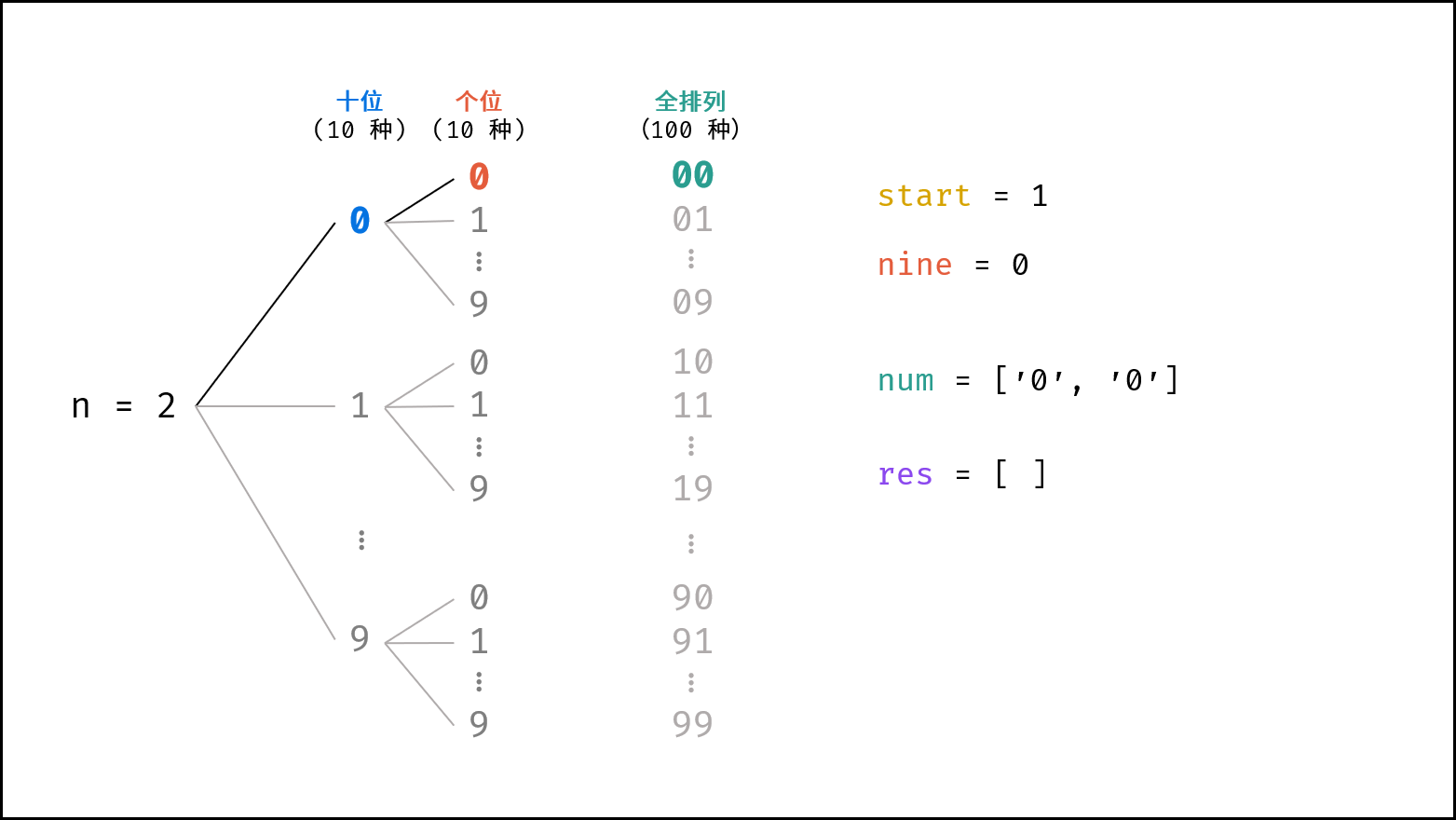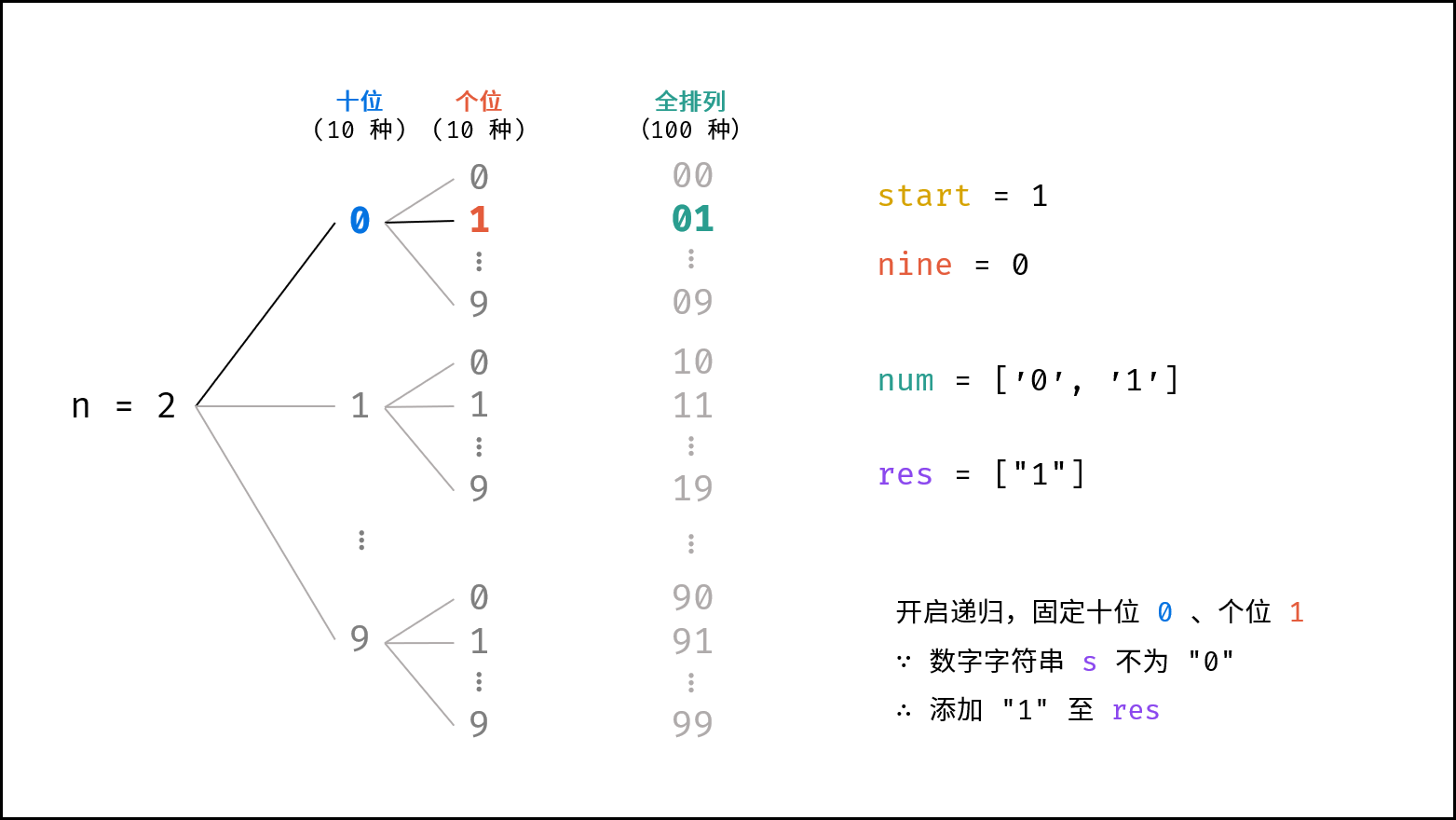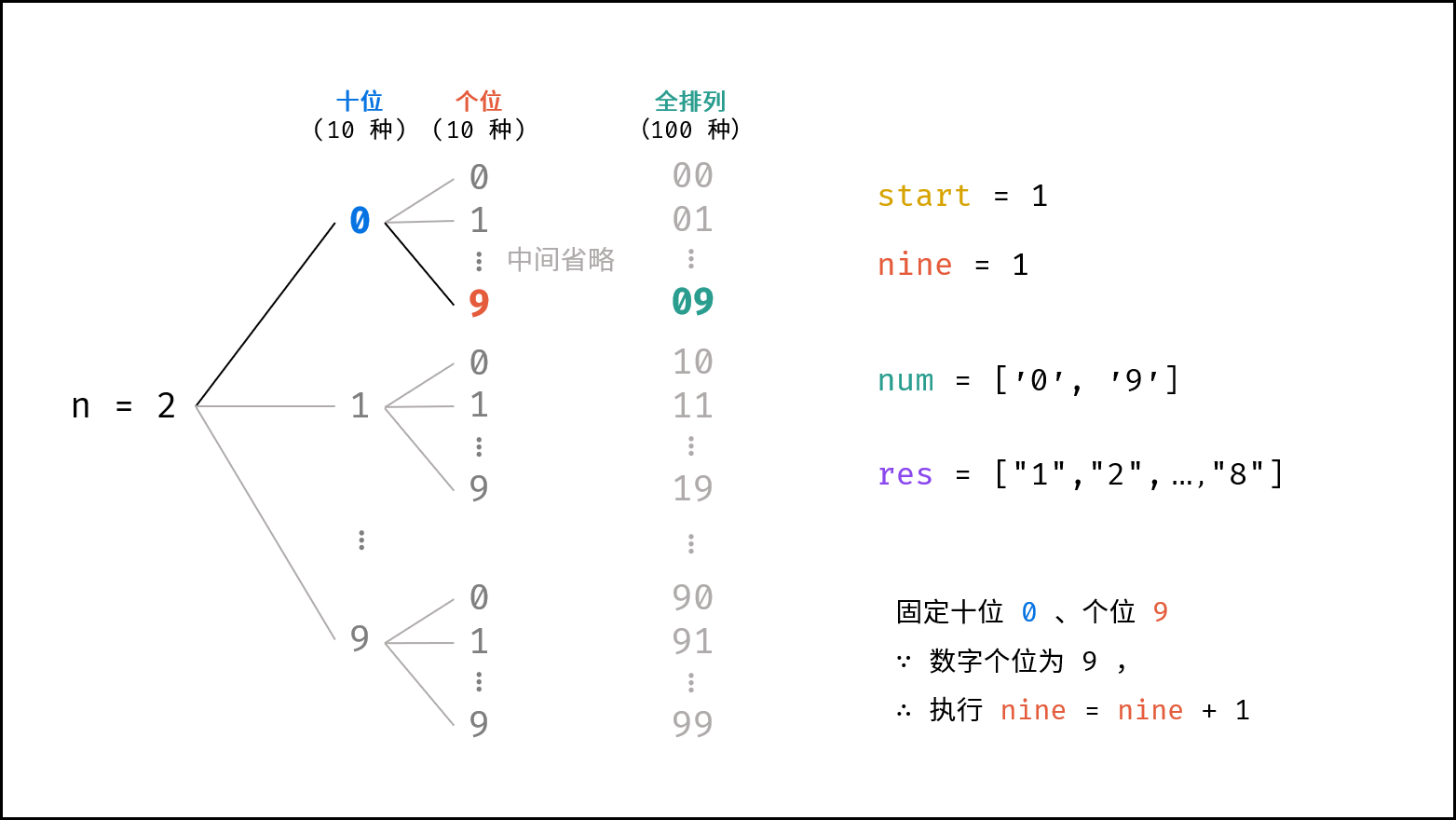<![Picture2.png](https://pic.leetcode-cn.com/bb0fc4784a72a8faad53689b0990f81e4d05ec49944045ed8aa9135361c40900-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/97c09f1a09ecc9ecb4bd07e979a237b17fbd4d0df573f373a3870aa5ba9ee646-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/a5172aa7252a4faccbc784ace848cd6a22de5f12bd05a390684e11149a367d19-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/a39c50b23a277472678dfea21bdce694ea8fe1ba53cd88d539042dc79bded1c6-Picture5.png),![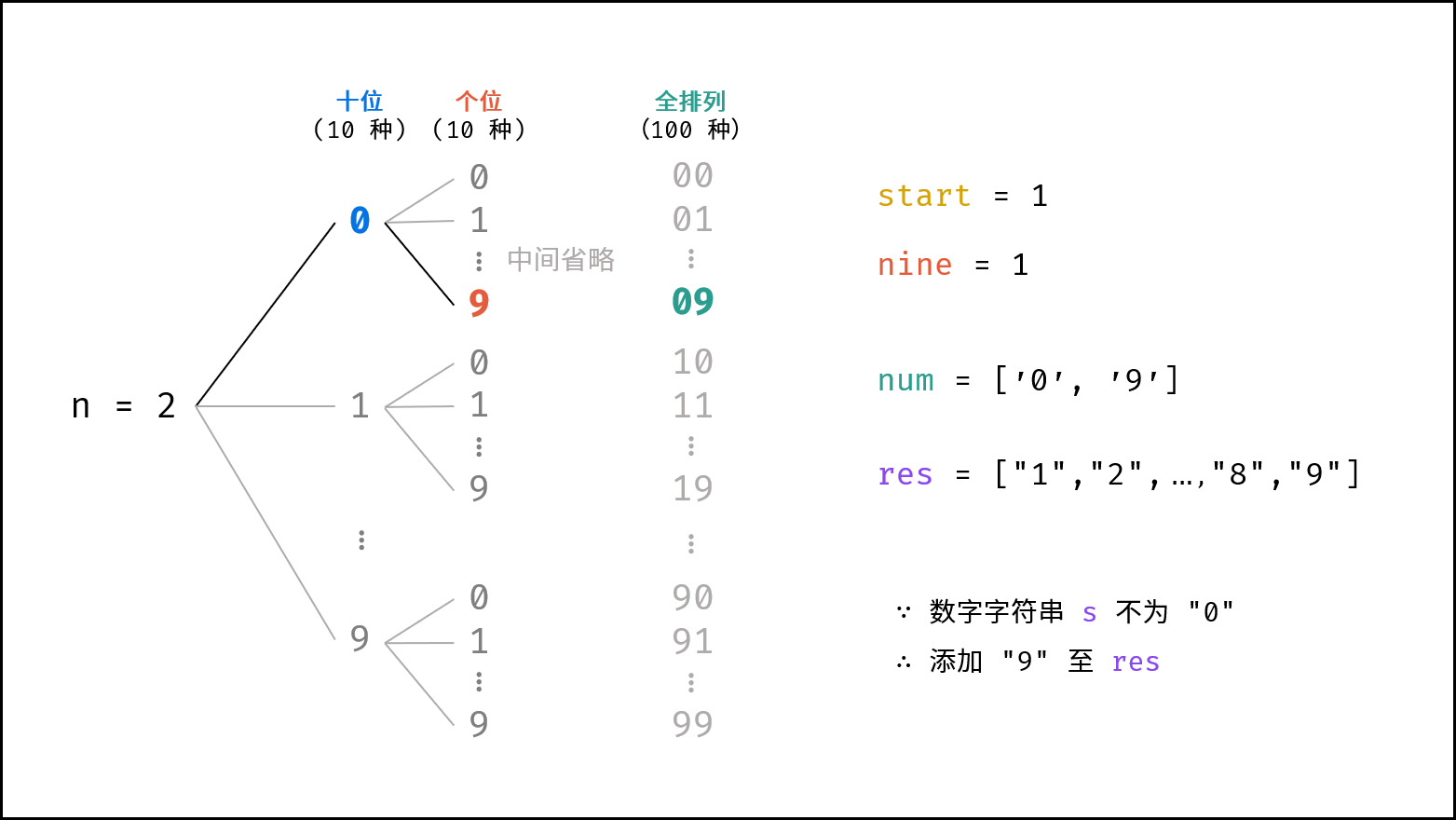Picture6.png](https://pic.leetcode-cn.com/5141d4ee38c38126c5a4ee9180a7d3de3f78aef2df49e4219a5a7eb048bc6945-Picture6.png),![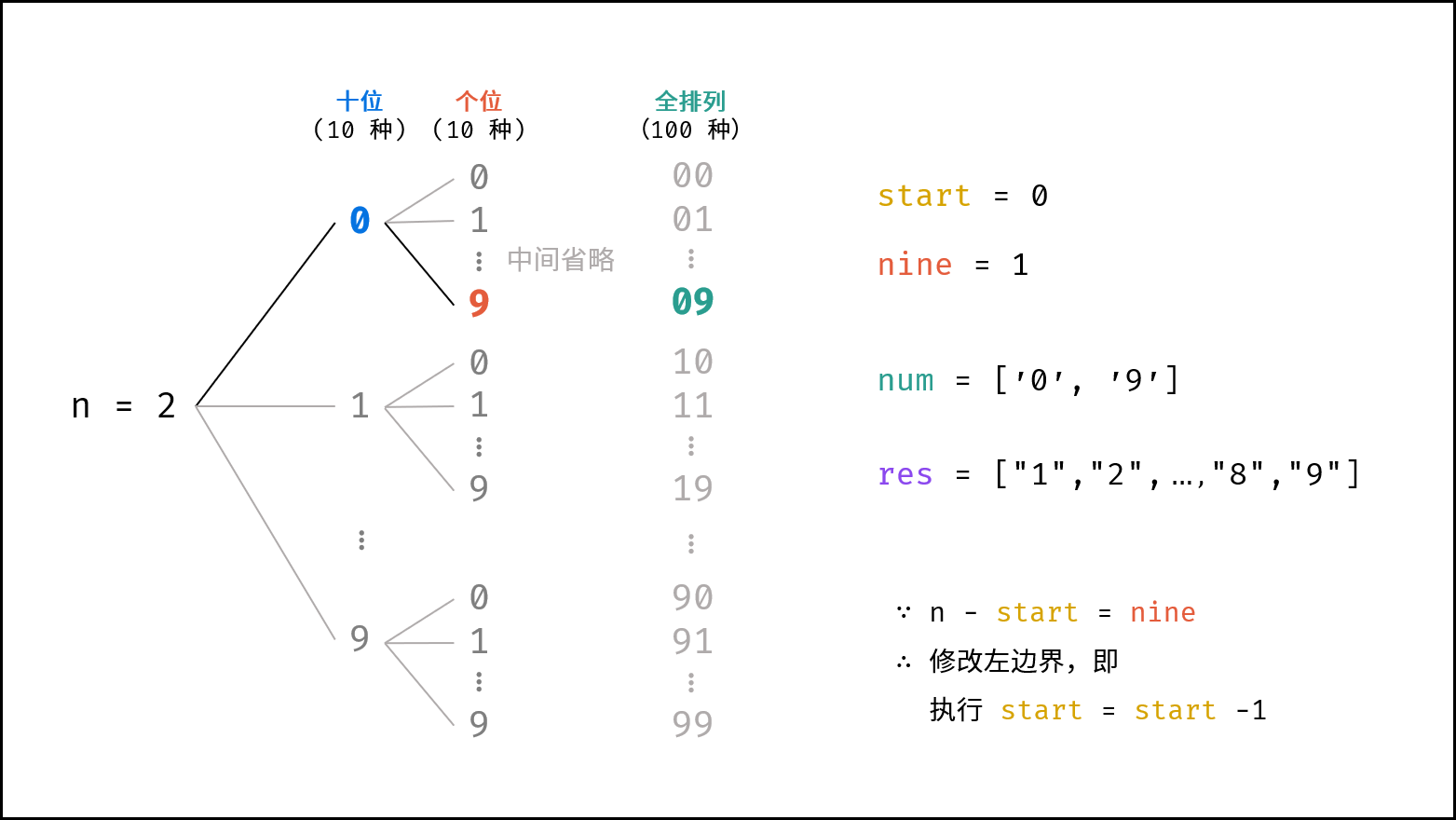Picture7.png](https://pic.leetcode-cn.com/78503ed898575813a65c53d6af335e5ff6e21aaf8bfac3d8a47ff8b5b461c0a6-Picture7.png),![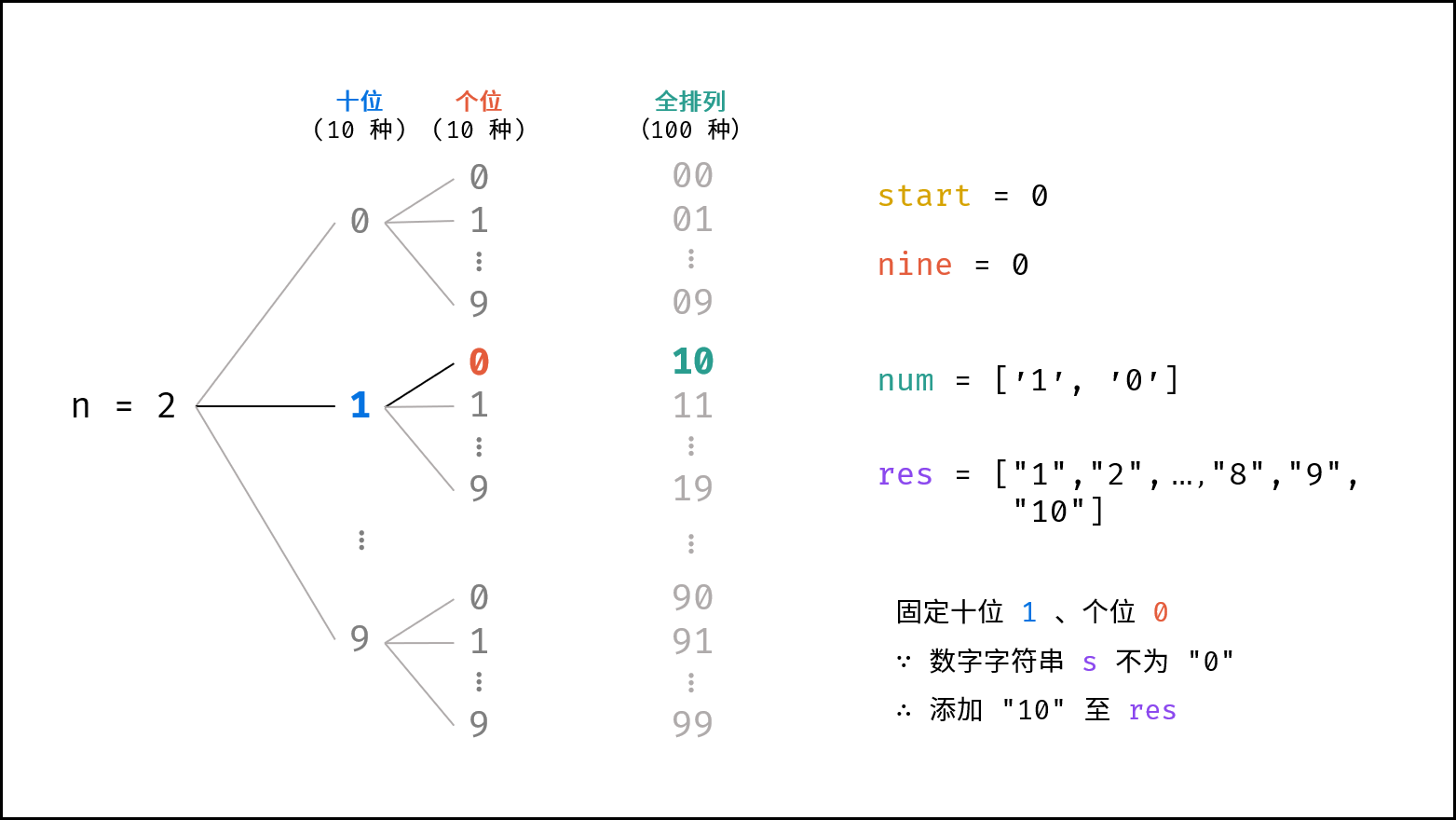Picture8.png](https://pic.leetcode-cn.com/94c3fb5cc91bd94980d73d5c3f41b8a9c0e28621b30077dacc1477be09ea123c-Picture8.png),![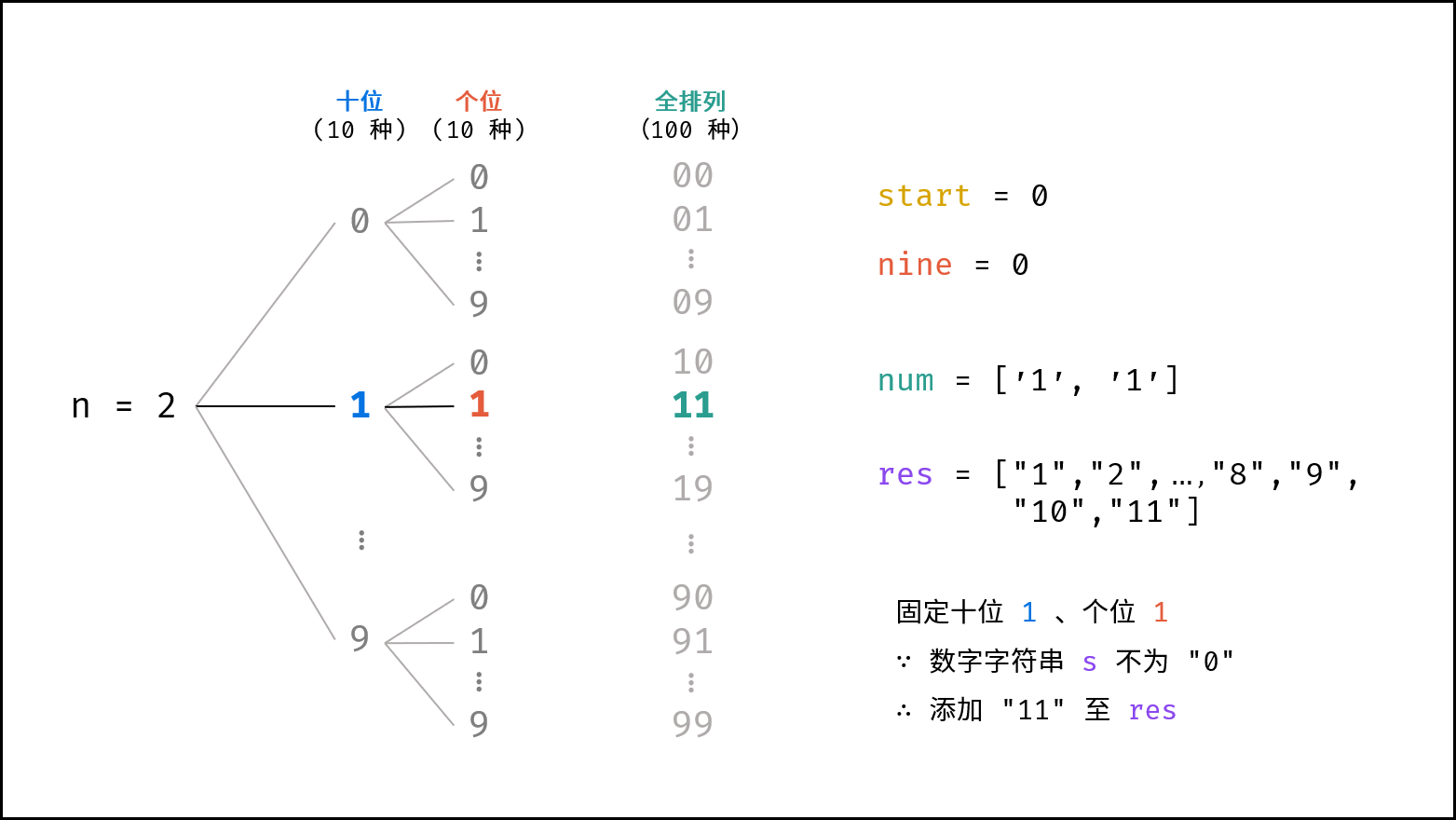Picture9.png](https://pic.leetcode-cn.com/0a75909b073c50769c09c9d0ab26fe9c74db406c52611b824b1cc04dae7a19ed-Picture9.png),![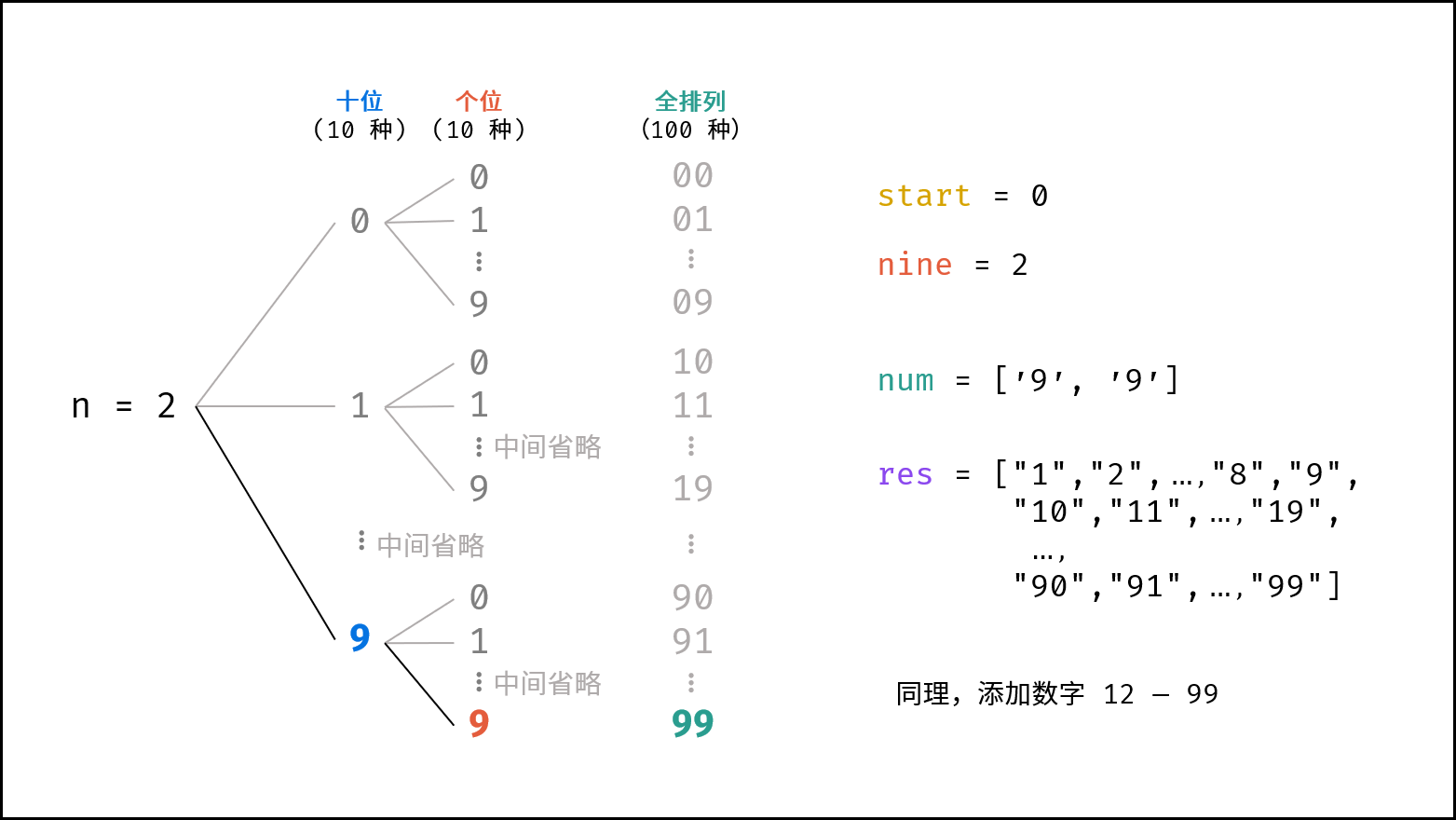Picture10.png](https://pic.leetcode-cn.com/98054fcc5e43d84baba54224be52c5cd35b23fcc8dca3594e1068e6095f7b79a-Picture10.png),![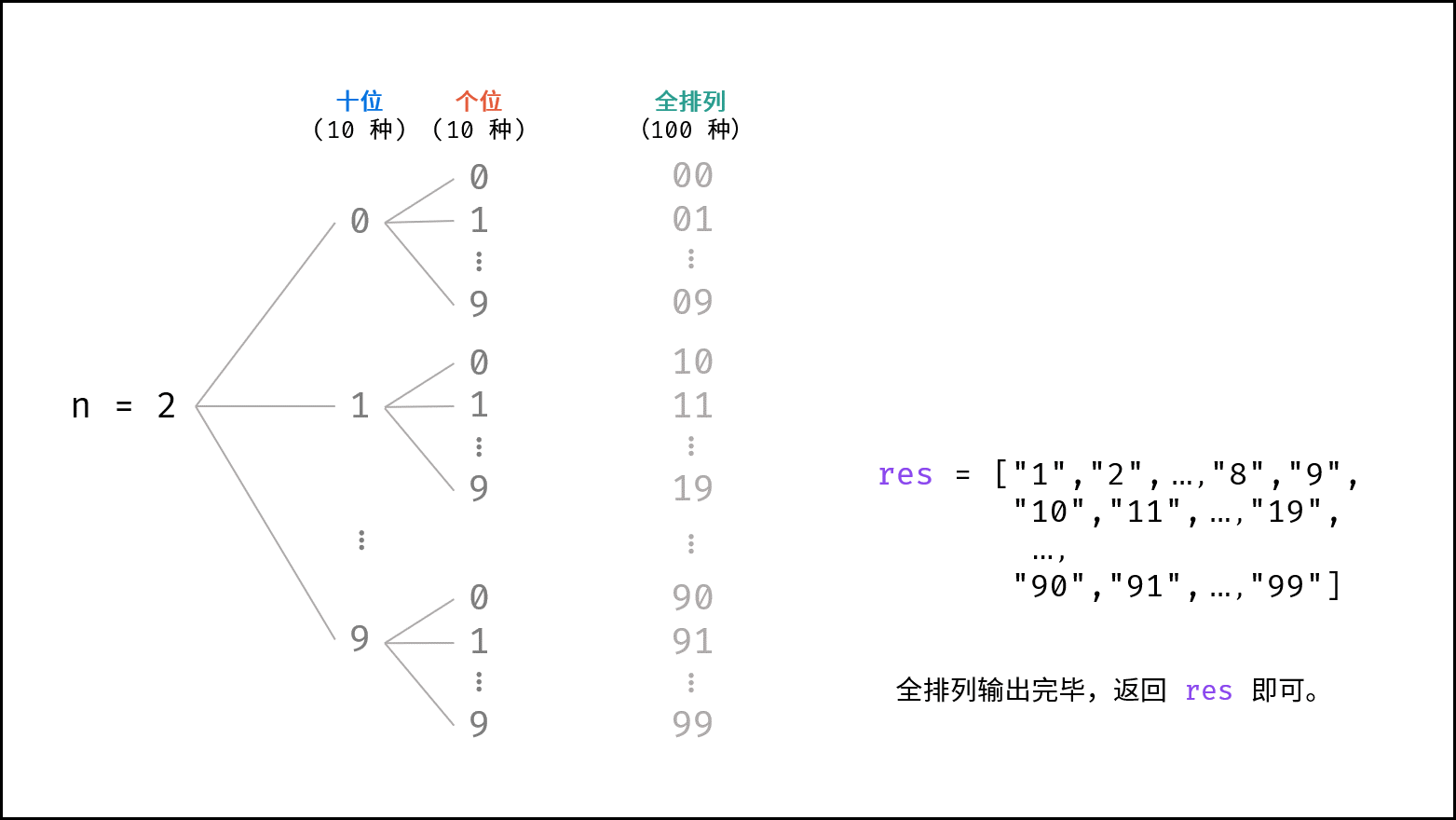Picture11.png](https://pic.leetcode-cn.com/ff49da44975c30a260e15136b21e21c3e615f077cd6a3ae923c077a1e0a485c5-Picture11.png)>
### 代码：
为 **正确表示大数** ，以下代码的返回值为数字字符串集拼接而成的长字符串。
```Python []
class Solution:
def countNumbers(self, cnt: int) -> [int]:
def dfs(x):
if x == cnt:
s = ''.join(num[self.start:])
if s != '0': res.append(s)
if cnt - self.start == self.nine: self.start -= 1
return
for i in range(10):
if i == 9: self.nine += 1
num[x] = str(i)
dfs(x + 1)
self.nine -= 1
num, res = ['0'] * cnt, []
self.nine = 0
self.start = cnt - 1
dfs(0)
return ','.join(res)
```
```Java []
class Solution {
StringBuilder res;
int nine = 0, count = 0, start, cnt;
char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
public String countNumbers(int cnt) {
this.cnt = cnt;
res = new StringBuilder();
num = new char[cnt];
start = cnt - 1;
dfs(0);
res.deleteCharAt(res.length() - 1);
return res.toString();
}
void dfs(int x) {
if(x == cnt) {
String s = String.valueOf(num).substring(start);
if(!s.equals("0")) res.append(s + ",");
if(cnt - start == nine) start--;
return;
}
for(char i : loop) {
if(i == '9') nine++;
num[x] = i;
dfs(x + 1);
}
nine--;
}
}
```
本题要求输出 int 类型数组。为 **运行通过** ，可在添加数字字符串 $s$ 前，将其转化为 int 类型。代码如下所示：
```Python []
class Solution:
def countNumbers(self, cnt: int) -> [int]:
def dfs(x):
if x == cnt:
s = ''.join(num[self.start:])
if s != '0': res.append(int(s))
if cnt - self.start == self.nine: self.start -= 1
return
for i in range(10):
if i == 9: self.nine += 1
num[x] = str(i)
dfs(x + 1)
self.nine -= 1
num, res = ['0'] * cnt, []
self.nine = 0
self.start = cnt - 1
dfs(0)
return res
```
```Java []
class Solution {
int[] res;
int nine = 0, count = 0, start, cnt;
char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
public int[] countNumbers(int cnt) {
this.cnt = cnt;
res = new int[(int)Math.pow(10, cnt) - 1];
num = new char[cnt];
start = cnt - 1;
dfs(0);
return res;
}
void dfs(int x) {
if(x == cnt) {
String s = String.valueOf(num).substring(start);
if(!s.equals("0")) res[count++] = Integer.parseInt(s);
if(cnt - start == nine) start--;
return;
}
for(char i : loop) {
if(i == '9') nine++;
num[x] = i;
dfs(x + 1);
}
nine--;
}
}
```
### 复杂度分析：
- **时间复杂度 $O(10^{cnt})$ ：** 递归的生成的排列的数量为 $10^{cnt}$ 。
- **空间复杂度 $O(10^{cnt})$ ：** 结果列表 $res$ 的长度为 $10^{cnt} - 1$ ，各数字字符串的长度区间为 $1, 2, ..., cnt$ ，因此占用 $O(10^{cnt})$ 大小的额外空间。

69
leetbook_ioa/docs/LCR 136. 删除链表节点.md Executable file
View File

@@ -0,0 +1,69 @@
## 解题思路：
本题删除值为 `val` 的节点分需为两步：定位节点、修改引用。
1. **定位节点：** 遍历链表，直到 `head.val == val` 时跳出，即可定位目标节点。
2. **修改引用：** 设节点 `cur` 的前驱节点为 `pre` ，后继节点为 `cur.next` ；则执行 `pre.next = cur.next` ，即可实现删除 `cur` 节点。
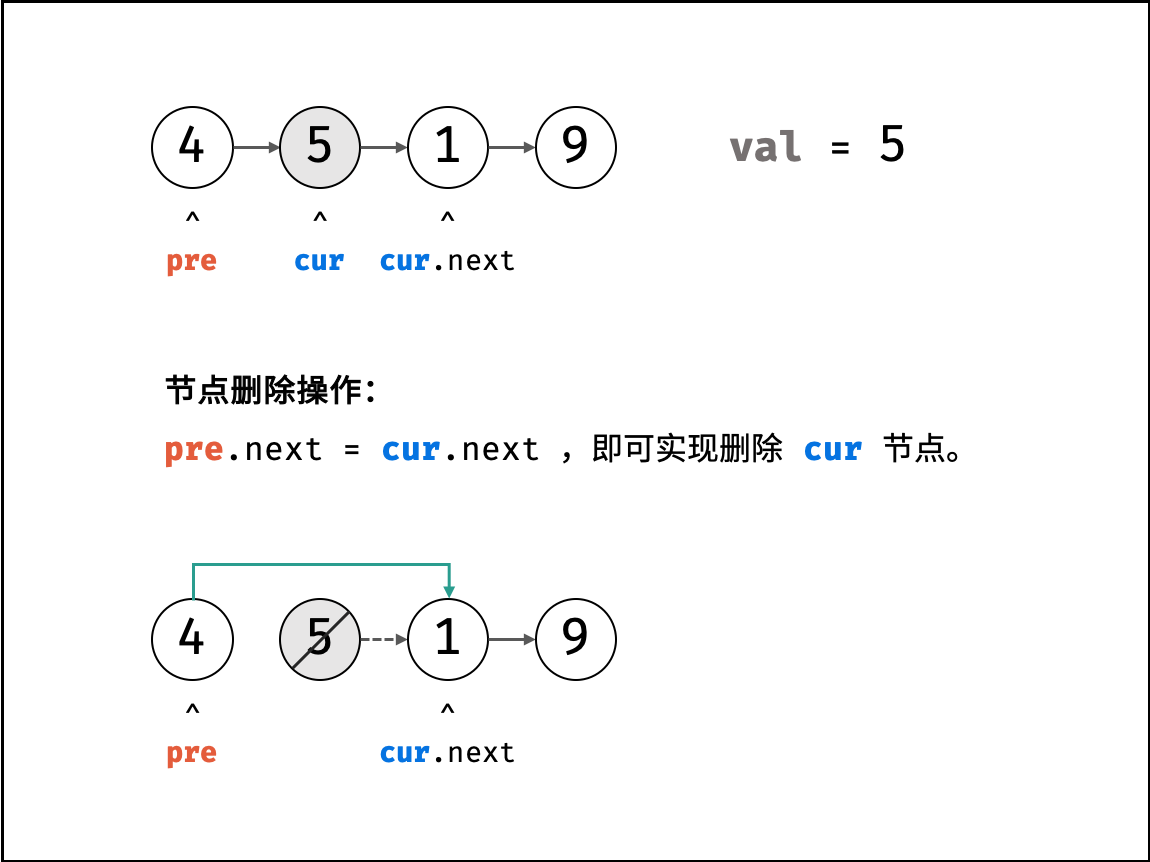![Picture1.png](https://pic.leetcode-cn.com/1613757478-NBOvjn-Picture1.png){:align=center width=450}
### 算法流程：
1. **特例处理：** 当应删除头节点 `head` 时，直接返回 `head.next` 即可。
2. **初始化：** `pre = head` , `cur = head.next` 。
3. **定位节点：** 当 `cur` 为空 **或** `cur` 节点值等于 `val` 时跳出。
1. 保存当前节点索引，即 `pre = cur` 。
2. 遍历下一节点，即 `cur = cur.next` 。
4. **删除节点：** 若 `cur` 指向某节点，则执行 `pre.next = cur.next` ；若 `cur` 指向 $\text{null}$ ，代表链表中不包含值为 `val` 的节点。
5. **返回值：** 返回链表头部节点 `head` 即可。
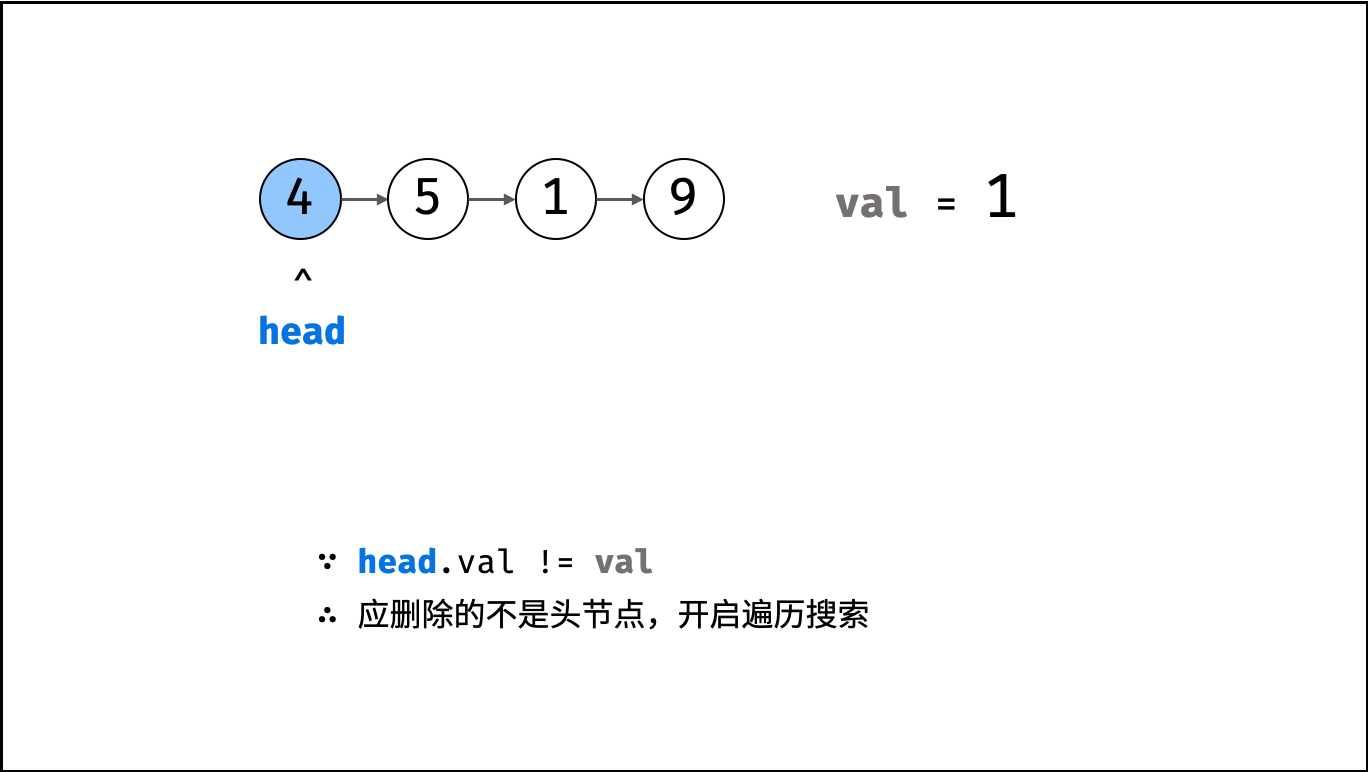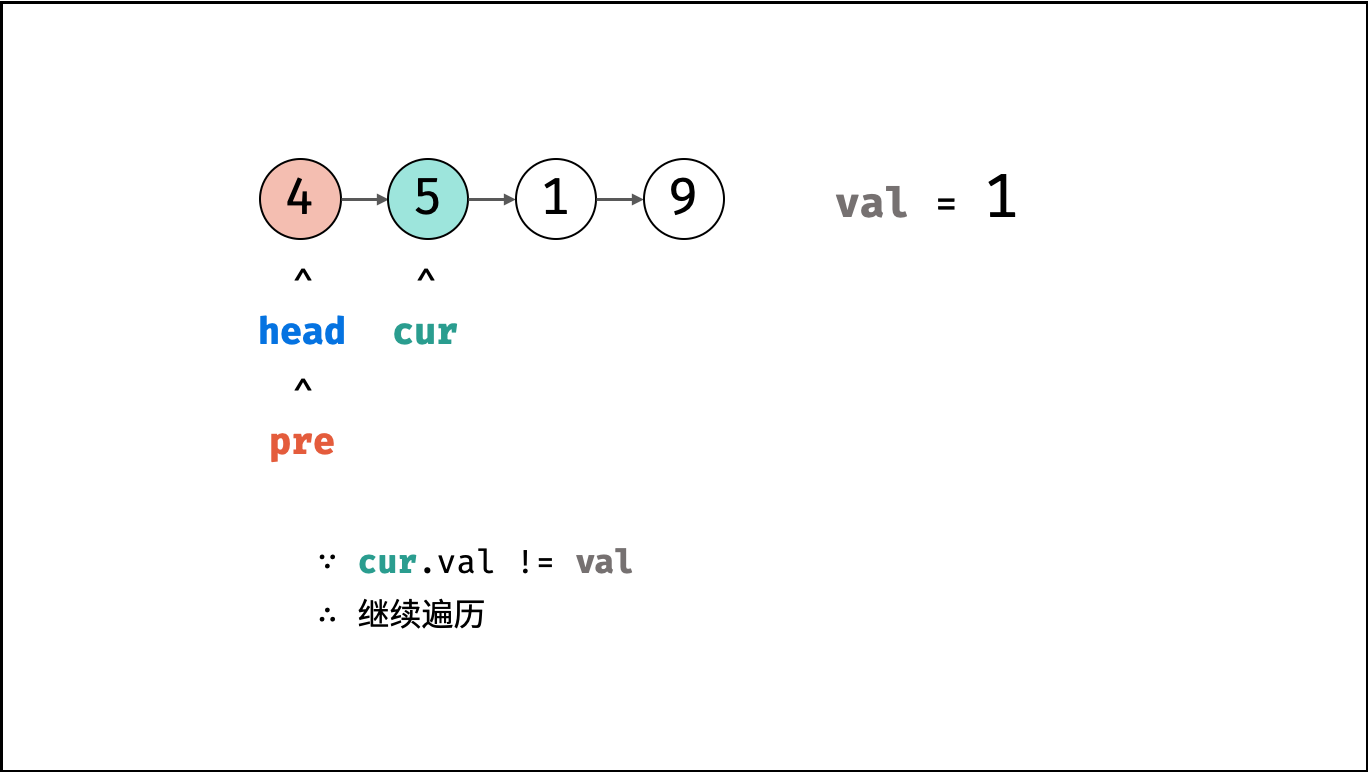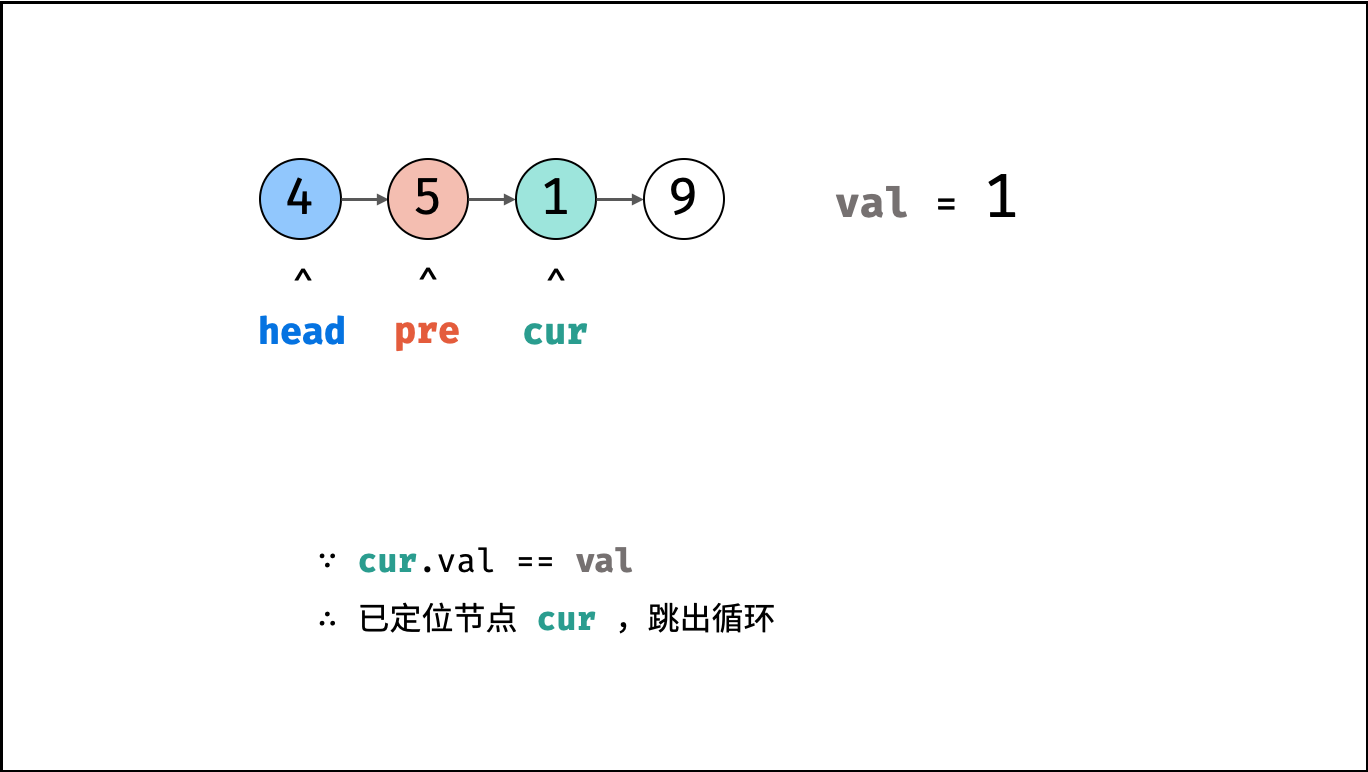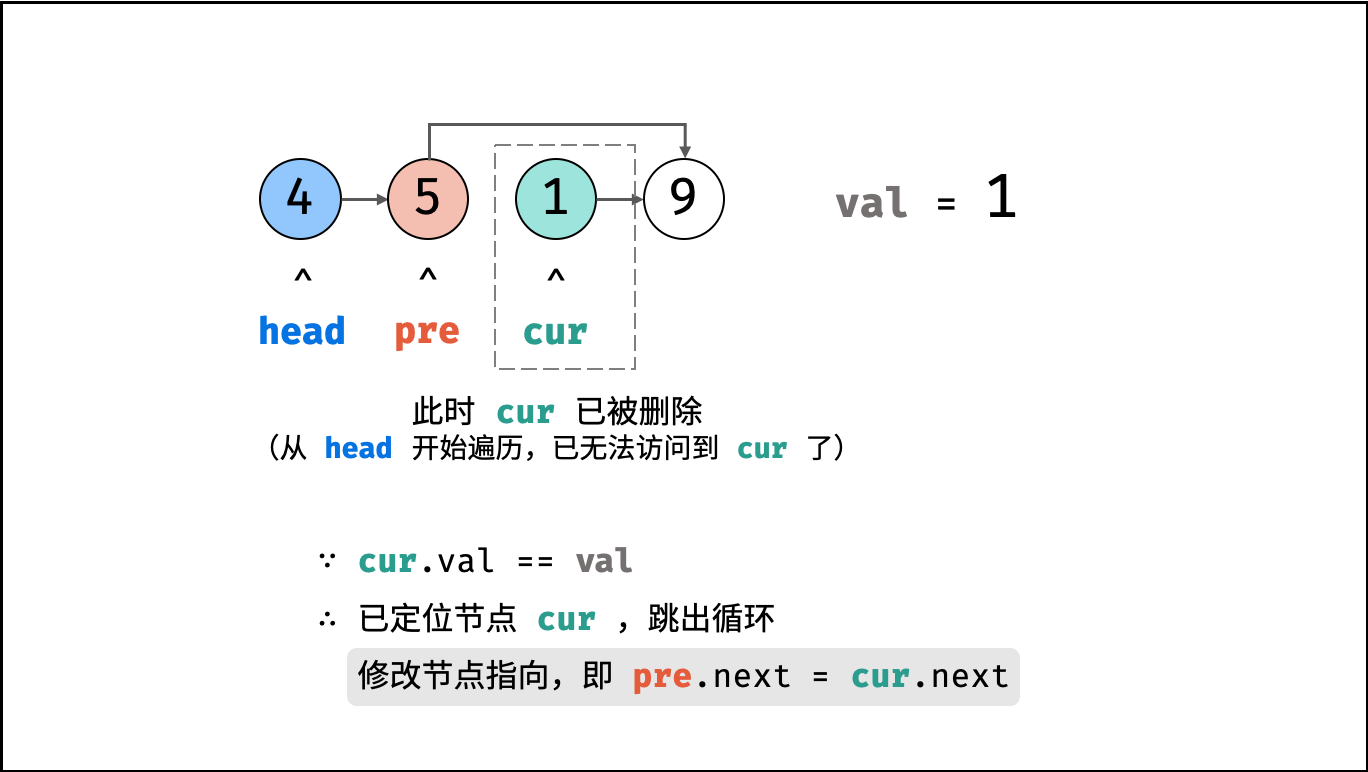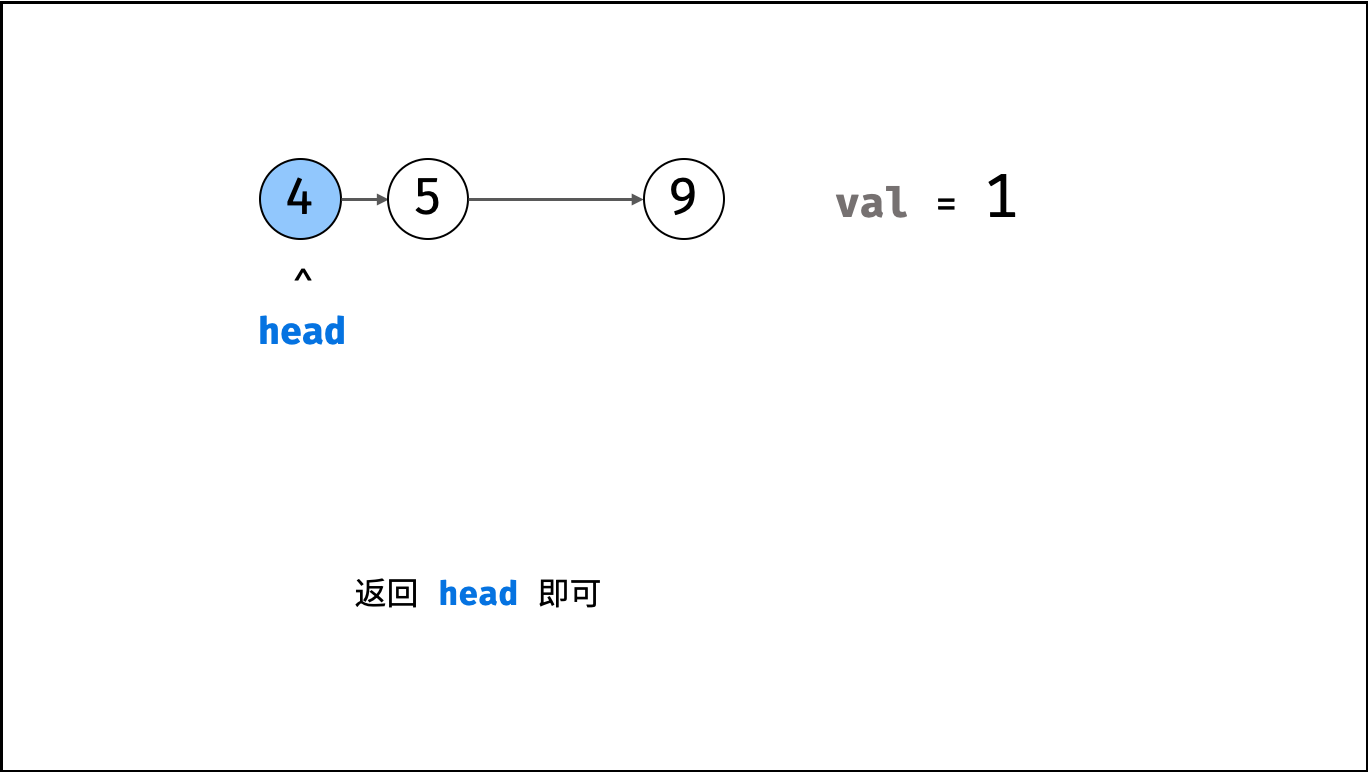<![Picture2.png](https://pic.leetcode-cn.com/1599417705-BpuWiY-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599417705-RNAPbt-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599417705-dIljCU-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599417705-nRNZwN-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599417705-XmugFY-Picture6.png)>
## 代码：
```Python []
class Solution:
def deleteNode(self, head: ListNode, val: int) -> ListNode:
if head.val == val: return head.next
pre, cur = head, head.next
while cur and cur.val != val:
pre, cur = cur, cur.next
if cur: pre.next = cur.next
return head
```
```Java []
class Solution {
public ListNode deleteNode(ListNode head, int val) {
if(head.val == val) return head.next;
ListNode pre = head, cur = head.next;
while(cur != null && cur.val != val) {
pre = cur;
cur = cur.next;
}
if(cur != null) pre.next = cur.next;
return head;
}
}
```
```C++ []
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(head->val == val) return head->next;
ListNode *pre = head, *cur = head->next;
while(cur != nullptr && cur->val != val) {
pre = cur;
cur = cur->next;
}
if(cur != nullptr) pre->next = cur->next;
return head;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为链表长度，删除操作平均需循环 $N/2$ 次，最差 $N$ 次。
- **空间复杂度 $O(1)$ ：** `cur`, `pre` 占用常数大小额外空间。

185
leetbook_ioa/docs/LCR 137. 模糊搜索验证.md Executable file
View File

@@ -0,0 +1,185 @@
## 解题思路：
> 设 $s$ 的长度为 $n$ ，$p$ 的长度为 $m$ ；将 $s$ 的第 $i$ 个字符记为 $s_i$ ，$p$ 的第 $j$ 个字符记为 $p_j$ ，将 $s$ 的前 $i$ 个字符组成的子字符串记为 $s[:i]$ , 同理将 $p$ 的前 $j$ 个字符组成的子字符串记为 $p[:j]$ 。
>
> 因此，本题可转化为求 $s[:n]$ 是否能和 $p[:m]$ 匹配。
总体思路是从 $s[:1]$ 和 $p[:1]$ 是否能匹配开始判断，每轮添加一个字符并判断是否能匹配，直至添加完整个字符串 $s$ 和 $p$ 。展开来看，假设 $s[:i]$ 与 $p[:j]$ 可以匹配，那么下一状态有两种：
1. 添加一个字符 $s_{i+1}$ 后是否能匹配？
2. 添加字符 $p_{j+1}$ 后是否能匹配？
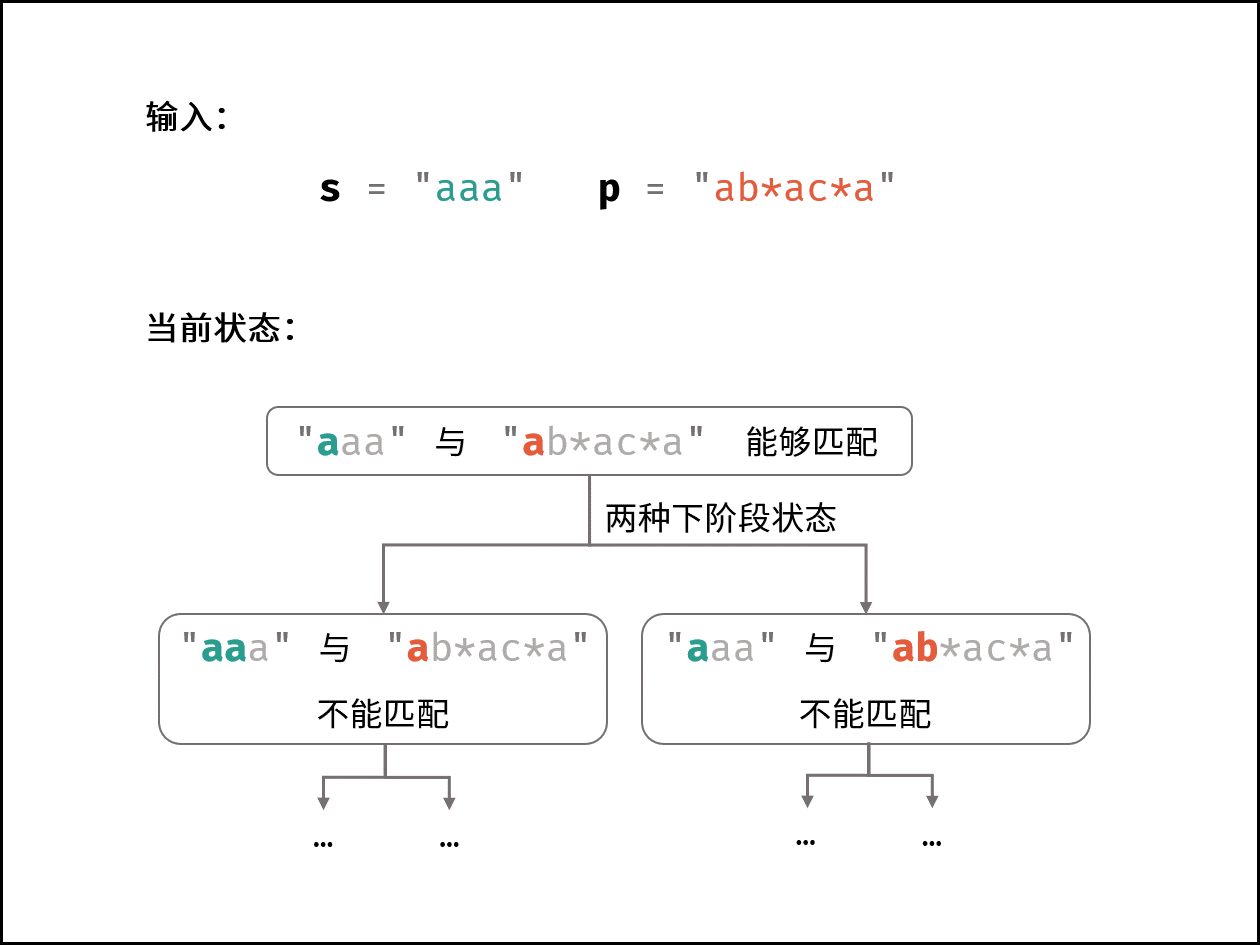![Picture1.png](https://pic.leetcode-cn.com/1614516402-HyzAil-Picture1.png){:align=center width=500}
因此，本题的状态共有 $m \times n$ 种，应定义状态矩阵 $dp$ ，$dp[i][j]$ 代表 $s[:i]$ 与 $p[:j]$ 是否可以匹配。
做好状态定义，接下来就是根据 「`普通字符`」 , 「`.`」 , 「`*`」三种字符的功能定义，分析出动态规划的转移方程。
### 动态规划解析：
**状态定义：** 设动态规划矩阵 `dp` ，`dp[i][j]` 代表字符串 `s` 的前 `i` 个字符和 `p` 的前 `j` 个字符能否匹配。
**转移方程：** 需要注意，由于 `dp[0][0]` 代表的是空字符的状态， 因此 `dp[i][j]` 对应的添加字符是 `s[i - 1]` 和 `p[j - 1]` 。
- 当 `p[j - 1] = '*'` 时，`dp[i][j]` 在当以下任一情况为 $\text{true}$ 时等于 $\text{true}$ ：
1. **`dp[i][j - 2]`：** 即将字符组合 `p[j - 2] *` 看作出现 0 次时，能否匹配；
2. **`dp[i - 1][j]` 且 `s[i - 1] = p[j - 2]`:** 即让字符 `p[j - 2]` 多出现 1 次时，能否匹配；
3. **`dp[i - 1][j]` 且 `p[j - 2] = '.'`:** 即让字符 `'.'` 多出现 1 次时，能否匹配；
- 当 `p[j - 1] != '*'` 时，`dp[i][j]` 在当以下任一情况为 $\text{true}$ 时等于 $\text{true}$ ：
1. **`dp[i - 1][j - 1]` 且 `s[i - 1] = p[j - 1]`：** 即让字符 `p[j - 1]` 多出现一次时，能否匹配；
2. **`dp[i - 1][j - 1]` 且 `p[j - 1] = '.'`：** 即将字符 `.` 看作字符 `s[i - 1]` 时，能否匹配；
**初始化：** 需要先初始化 `dp` 矩阵首行，以避免状态转移时索引越界。
- **`dp[0][0] = true`：** 代表两个空字符串能够匹配。
- **`dp[0][j] = dp[0][j - 2]` 且 `p[j - 1] = '*'`：** 首行 `s` 为空字符串，因此当 `p` 的偶数位为 `*` 时才能够匹配（即让 `p` 的奇数位出现 0 次，保持 `p` 是空字符串）。因此，循环遍历字符串 `p` ，步长为 2（即只看偶数位）。
**返回值：** `dp` 矩阵右下角字符，代表字符串 `s` 和 `p` 能否匹配。
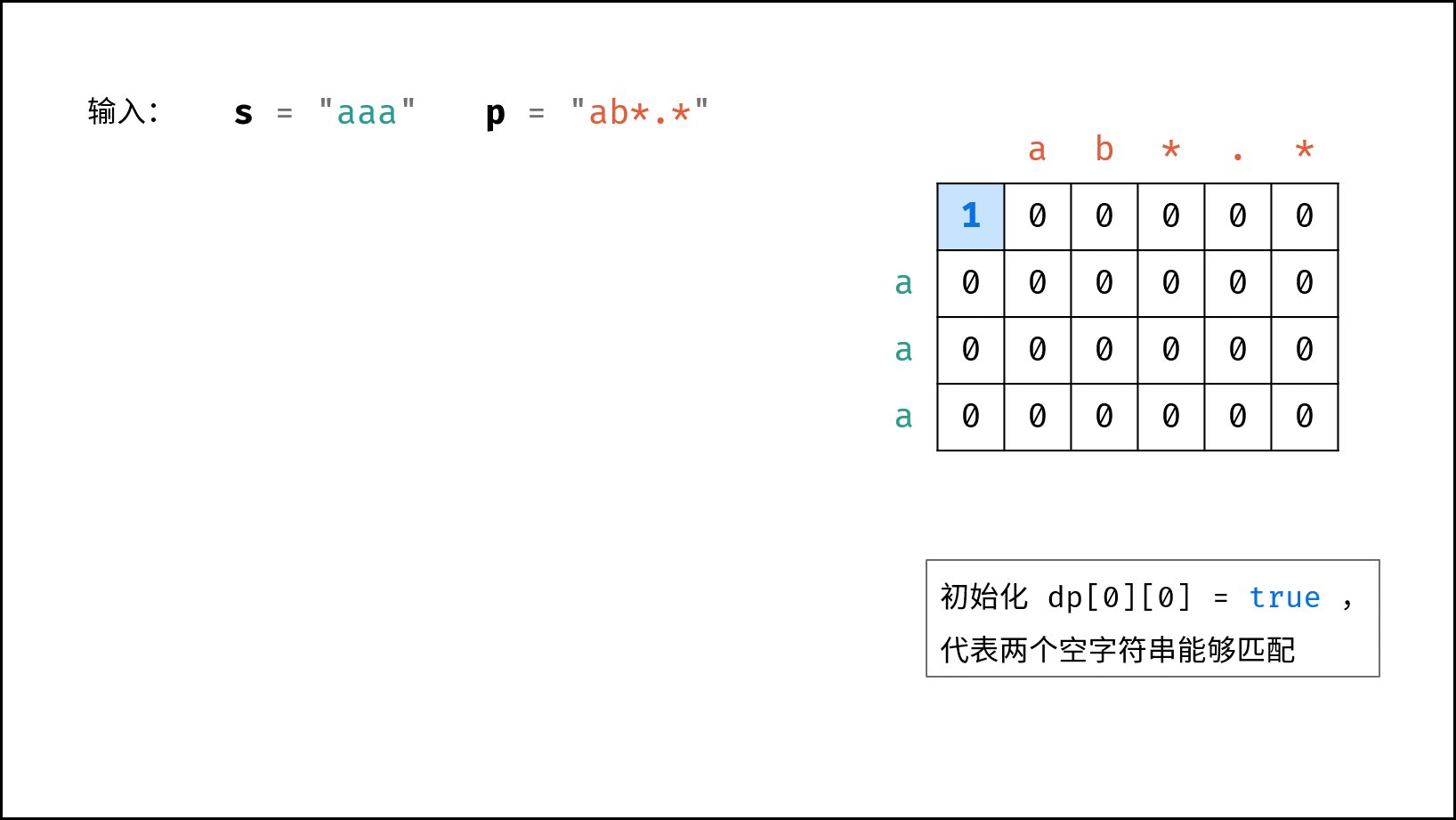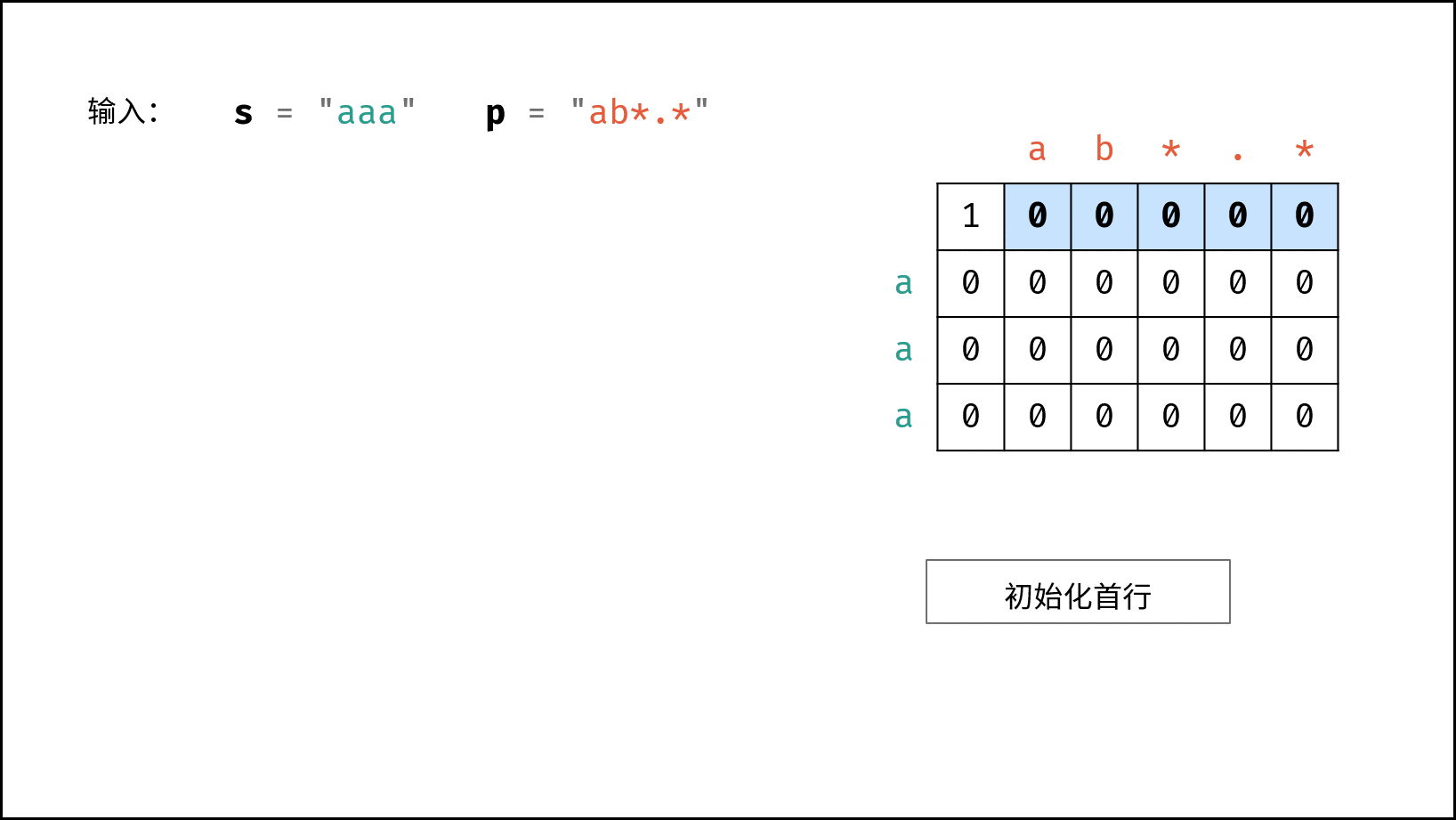<![Picture2.png](https://pic.leetcode-cn.com/1614516402-hHLAeA-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1614516402-KnJpAF-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1614516402-MacqQq-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1614516402-rFRAGU-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1614516402-ATFWBt-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1614516402-OeJlxq-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1614516402-oqHduu-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1614516402-ETWYMx-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1614516402-NXXjya-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1614516402-uMxtXN-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1614516402-HHmdNJ-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1614516402-bBdFaG-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1614516402-EsgHuc-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1614516402-YlyLPO-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1614516402-VpcAnO-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1614516402-CmmPpZ-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1614516402-ibjjpB-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1614516402-gBEUfu-Picture19.png)>
## 代码：
```Python []
class Solution:
def articleMatch(self, s: str, p: str) -> bool:
m, n = len(s) + 1, len(p) + 1
dp = [[False] * n for _ in range(m)]
dp[0][0] = True
for j in range(2, n, 2):
dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i][j - 2] or dp[i - 1][j] and (s[i - 1] == p[j - 2] or p[j - 2] == '.') \
if p[j - 1] == '*' else \
dp[i - 1][j - 1] and (p[j - 1] == '.' or s[i - 1] == p[j - 1])
return dp[-1][-1]
```
```Java []
class Solution {
public boolean articleMatch(String s, String p) {
int m = s.length() + 1, n = p.length() + 1;
boolean[][] dp = new boolean[m][n];
dp[0][0] = true;
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
dp[i][j] = p.charAt(j - 1) == '*' ?
dp[i][j - 2] || dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') :
dp[i - 1][j - 1] && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1));
}
}
return dp[m - 1][n - 1];
}
}
```
```C++ []
class Solution {
public:
bool articleMatch(string s, string p) {
int m = s.size() + 1, n = p.size() + 1;
vector<vector<bool>> dp(m, vector<bool>(n, false));
dp[0][0] = true;
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p[j - 1] == '*';
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
dp[i][j] = p[j - 1] == '*' ?
dp[i][j - 2] || dp[i - 1][j] && (s[i - 1] == p[j - 2] || p[j - 2] == '.'):
dp[i - 1][j - 1] && (p[j - 1] == '.' || s[i - 1] == p[j - 1]);
}
}
return dp[m - 1][n - 1];
}
};
```
以上代码利用布尔运算实现简短长度，若阅读不畅，可先理解以下代码，与文中内容一一对应：
```Python []
class Solution:
def articleMatch(self, s: str, p: str) -> bool:
m, n = len(s) + 1, len(p) + 1
dp = [[False] * n for _ in range(m)]
dp[0][0] = True
# 初始化首行
for j in range(2, n, 2):
dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
# 状态转移
for i in range(1, m):
for j in range(1, n):
if p[j - 1] == '*':
if dp[i][j - 2]: dp[i][j] = True # 1.
elif dp[i - 1][j] and s[i - 1] == p[j - 2]: dp[i][j] = True # 2.
elif dp[i - 1][j] and p[j - 2] == '.': dp[i][j] = True # 3.
else:
if dp[i - 1][j - 1] and s[i - 1] == p[j - 1]: dp[i][j] = True # 1.
elif dp[i - 1][j - 1] and p[j - 1] == '.': dp[i][j] = True # 2.
return dp[-1][-1]
```
```Java []
class Solution {
public boolean articleMatch(String s, String p) {
int m = s.length() + 1, n = p.length() + 1;
boolean[][] dp = new boolean[m][n];
dp[0][0] = true;
// 初始化首行
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
// 状态转移
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if(p.charAt(j - 1) == '*') {
if(dp[i][j - 2]) dp[i][j] = true; // 1.
else if(dp[i - 1][j] && s.charAt(i - 1) == p.charAt(j - 2)) dp[i][j] = true; // 2.
else if(dp[i - 1][j] && p.charAt(j - 2) == '.') dp[i][j] = true; // 3.
} else {
if(dp[i - 1][j - 1] && s.charAt(i - 1) == p.charAt(j - 1)) dp[i][j] = true; // 1.
else if(dp[i - 1][j - 1] && p.charAt(j - 1) == '.') dp[i][j] = true; // 2.
}
}
}
return dp[m - 1][n - 1];
}
}
```
```C++ []
class Solution {
public:
bool articleMatch(string s, string p) {
int m = s.size() + 1, n = p.size() + 1;
vector<vector<bool>> dp(m, vector<bool>(n, false));
dp[0][0] = true;
// 初始化首行
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p[j - 1] == '*';
// 状态转移
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if(p[j - 1] == '*') {
if(dp[i][j - 2]) dp[i][j] = true; // 1.
else if(dp[i - 1][j] && s[i - 1] == p[j - 2]) dp[i][j] = true; // 2.
else if(dp[i - 1][j] && p[j - 2] == '.') dp[i][j] = true; // 3.
} else {
if(dp[i - 1][j - 1] && s[i - 1] == p[j - 1]) dp[i][j] = true; // 1.
else if(dp[i - 1][j - 1] && p[j - 1] == '.') dp[i][j] = true; // 2.
}
}
}
return dp[m - 1][n - 1];
}
};
```
### 复杂度分析：
- **时间复杂度 $O(MN)$ ：** 其中 $M, N$ 分别为 `s` 和 `p` 的长度，状态转移需遍历整个 `dp` 矩阵。
- **空间复杂度 $O(MN)$ ：** 状态矩阵 `dp` 使用 $O(MN)$ 的额外空间。

112
leetbook_ioa/docs/LCR 138. 有效数字.md Executable file
View File

@@ -0,0 +1,112 @@
## 解题思路：
本题使用有限状态自动机。根据字符类型和合法数值的特点，先定义状态，再画出状态转移图，最后编写代码即可。
**字符类型：**
空格 「 」、数字「 $0—9$ 」 、正负号 「 $+$, $-$ 」 、小数点 「 $.$ 」 、幂符号 「 $e$, $E$ 」 。
**状态定义：**
按照字符串从左到右的顺序，定义以下 9 种状态。
0. 开始的空格
1. 幂符号前的正负号
2. 小数点前的数字
3. 小数点、小数点后的数字
4. 当小数点前为空格时，小数点、小数点后的数字
5. 幂符号
6. 幂符号后的正负号
7. 幂符号后的数字
8. 结尾的空格
**结束状态：**
合法的结束状态有 2, 3, 7, 8 。
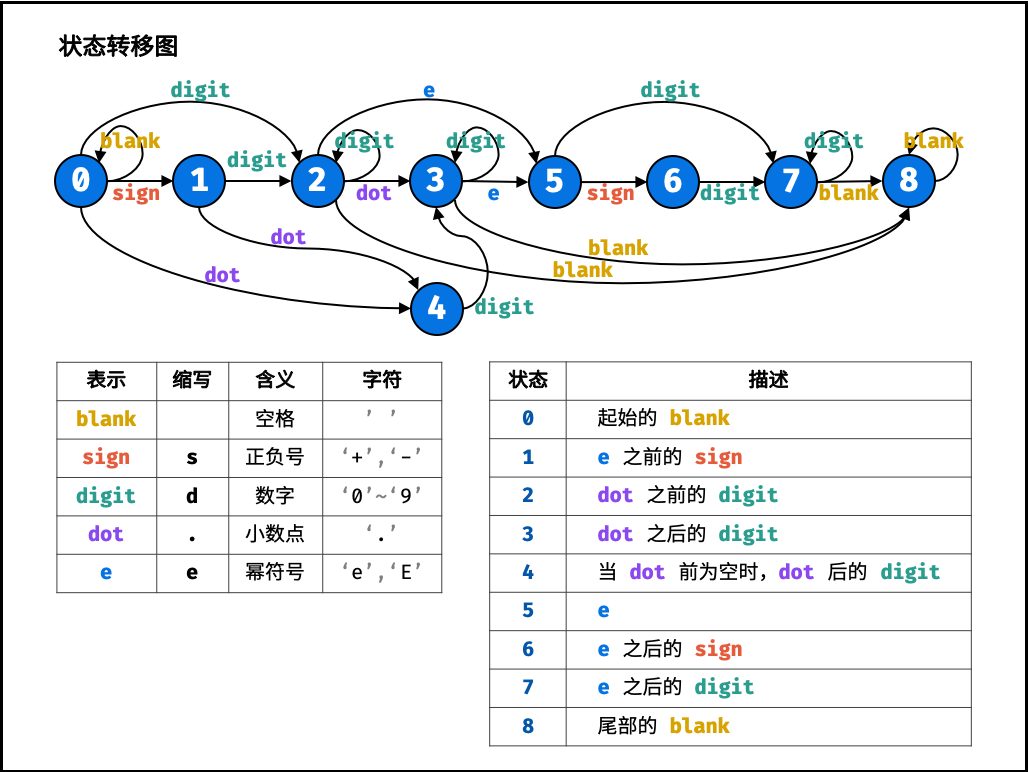![Picture1.png](https://pic.leetcode-cn.com/1599283151-YmPMis-Picture1.png){:align=center width=650}
### 算法流程：
1. **初始化：**
1. **状态转移表 `states` ：** 设 `states[i]` ，其中 `i` 为所处状态，`states[i]` 使用哈希表存储可转移至的状态。键值对 `(key, value)` 含义：输入字符 `key` ，则从状态 `i` 转移至状态 `value` 。
2. **当前状态 `p` ：** 起始状态初始化为 `p = 0` 。
2. **状态转移循环：** 遍历字符串 `s` 的每个字符 `c` 。
1. **记录字符类型 `t` ：** 分为四种情况。
- 当 `c` 为正负号时，执行 `t = 's'` ;
- 当 `c` 为数字时，执行 `t = 'd'` ;
- 当 `c` 为 `e` 或 `E` 时，执行 `t = 'e'` ;
- 当 `c` 为 `.` 或 `空格` 时，执行 `t = c` （即用字符本身表示字符类型）;
- 否则，执行 `t = '?'` ，代表为不属于判断范围的非法字符，后续直接返回 $\text{false}$ 。
2. **终止条件：** 若字符类型 `t` 不在哈希表 `states[p]` 中，说明无法转移至下一状态，因此直接返回 $\text{false}$ 。
3. **状态转移：** 状态 `p` 转移至 `states[p][t]` 。
3. **返回值：** 跳出循环后，若状态 `p` $\in {2, 3, 7, 8}$ ，说明结尾合法，返回 $\text{true}$ ，否则返回 $\text{false}$ 。
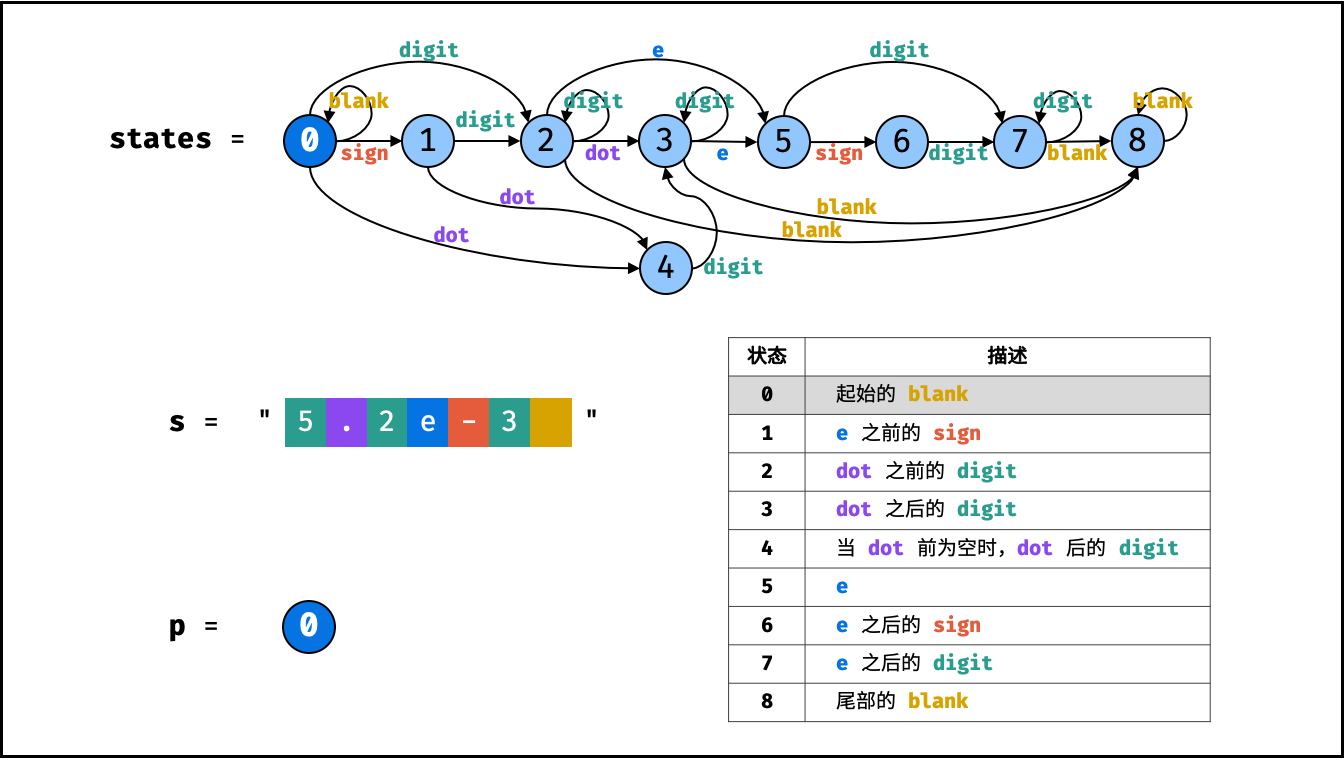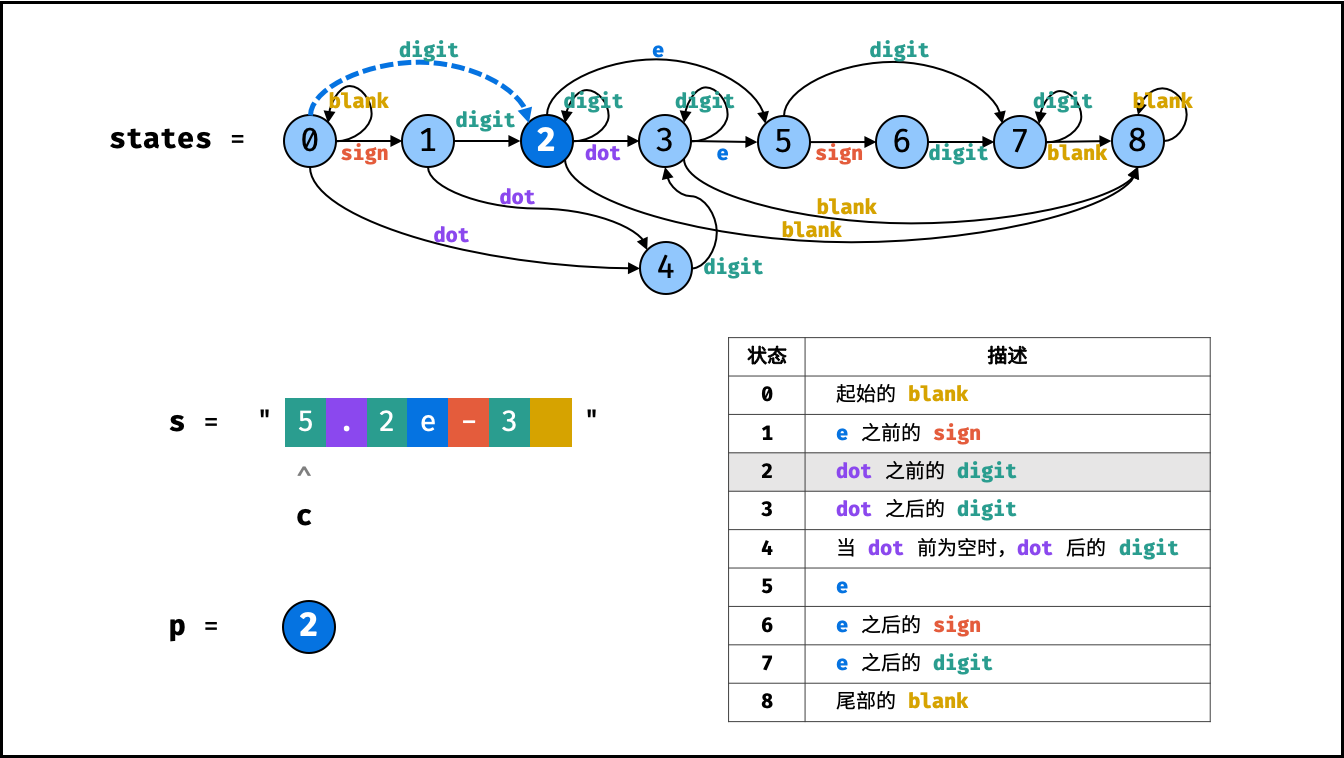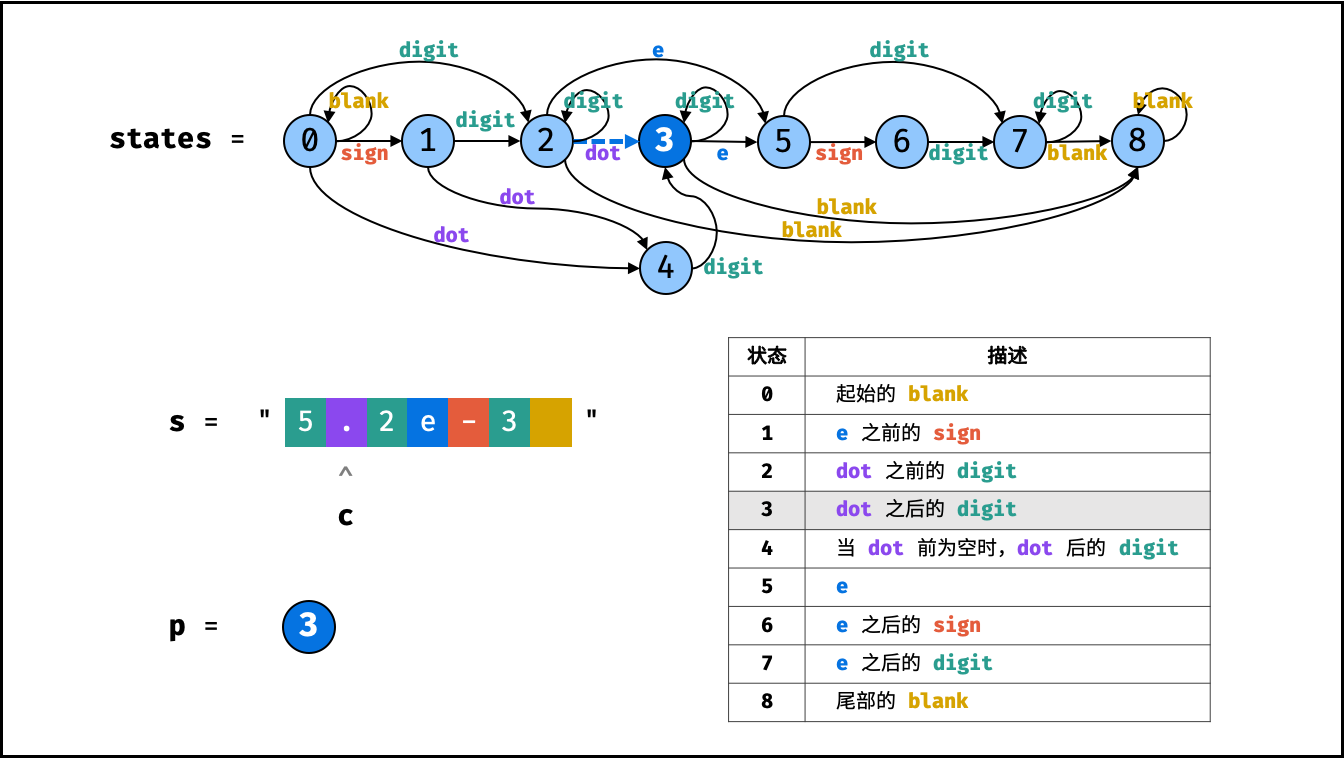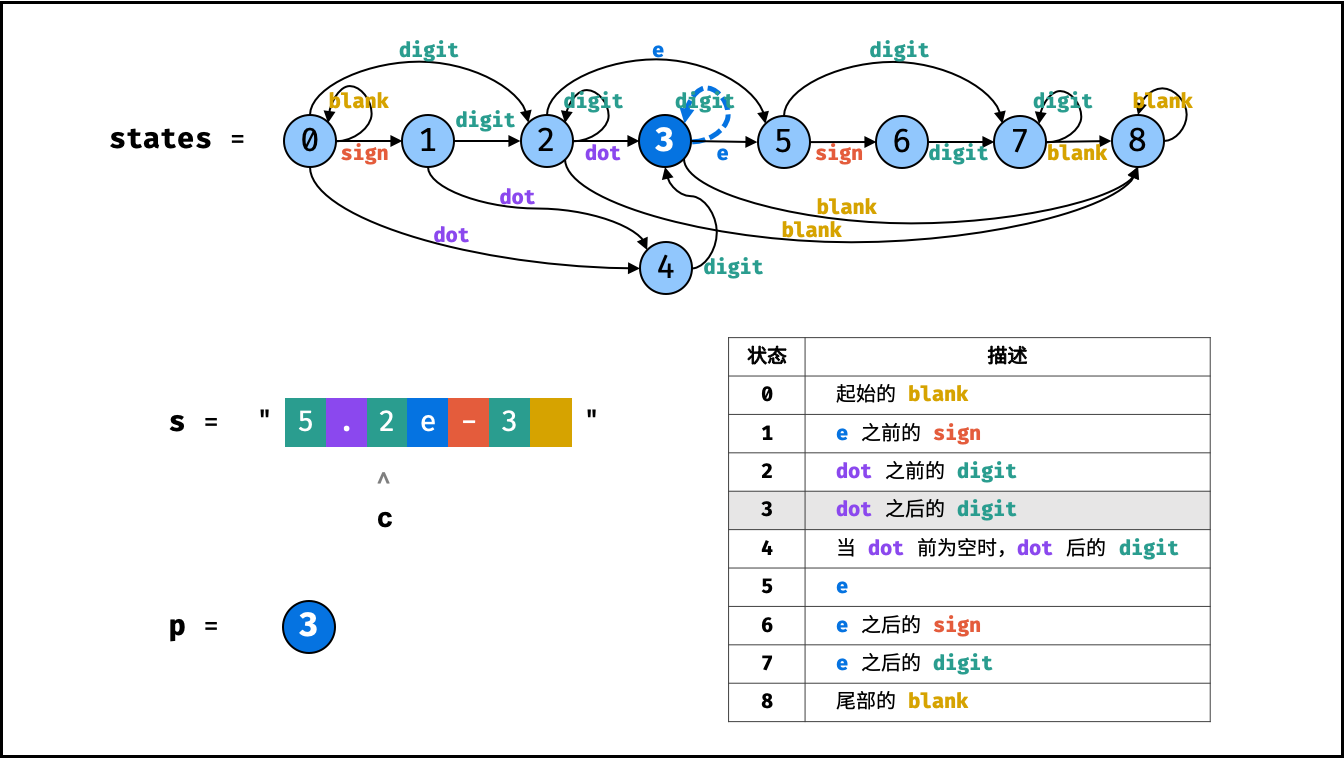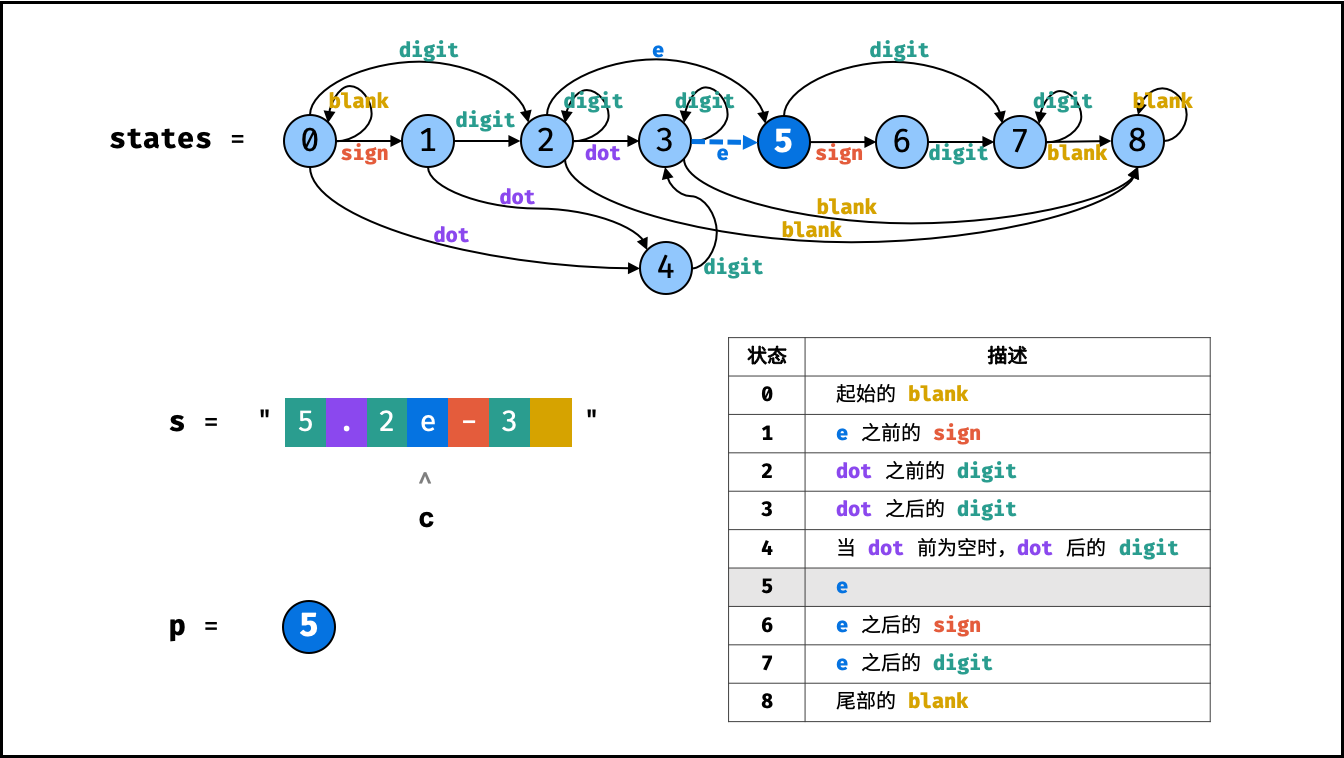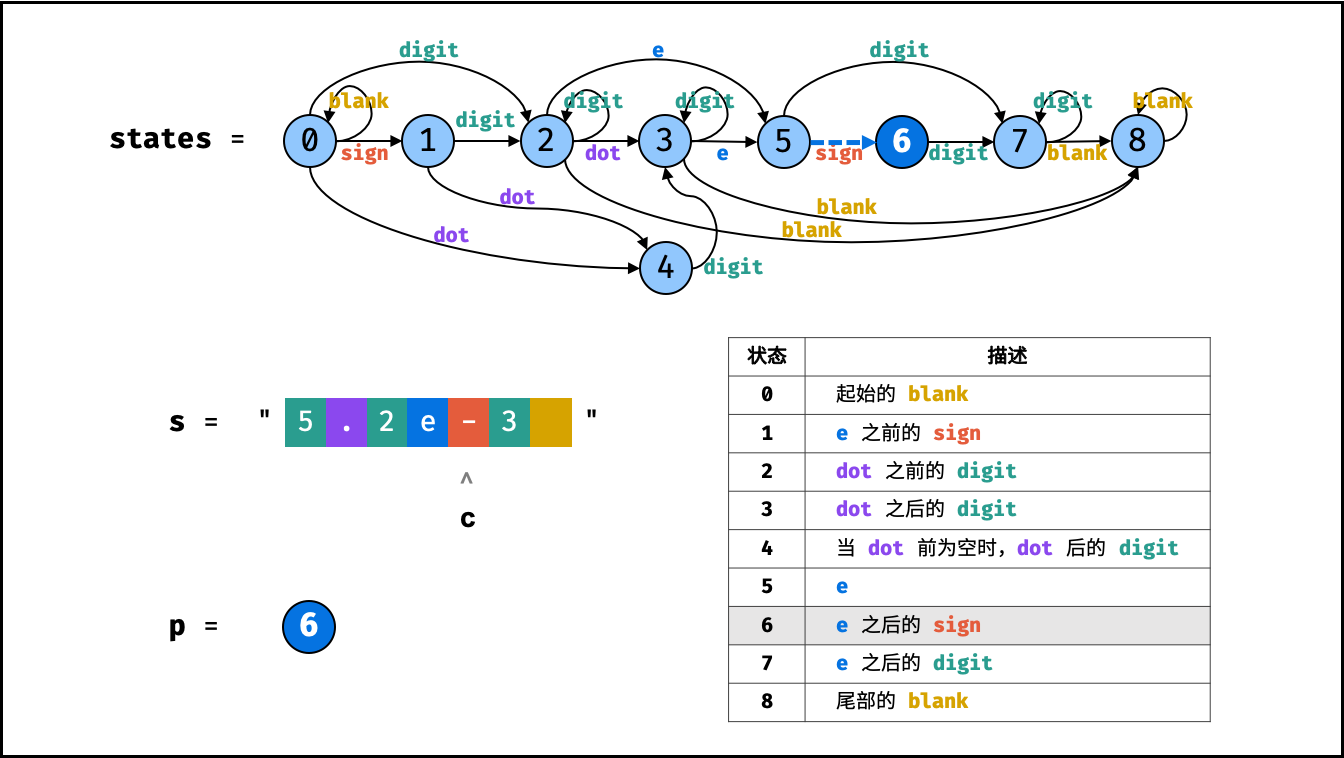<![Picture2.png](https://pic.leetcode-cn.com/1599283163-NYRJuG-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599283166-EeQMXb-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599283171-UsxiTn-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599283169-vZtZhA-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599283174-EjrKZh-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599283177-PHaNOb-Picture7.png),![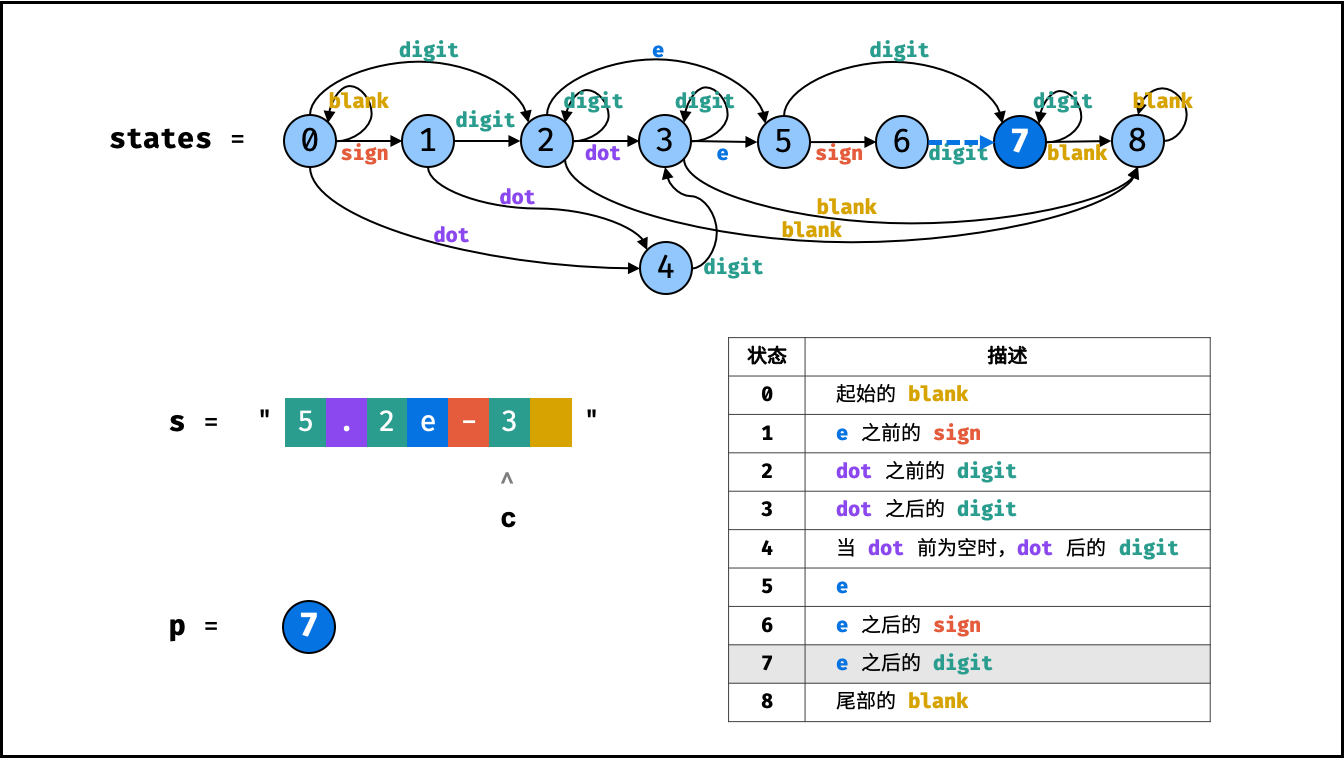Picture8.png](https://pic.leetcode-cn.com/1599283183-QAjXuu-Picture8.png),![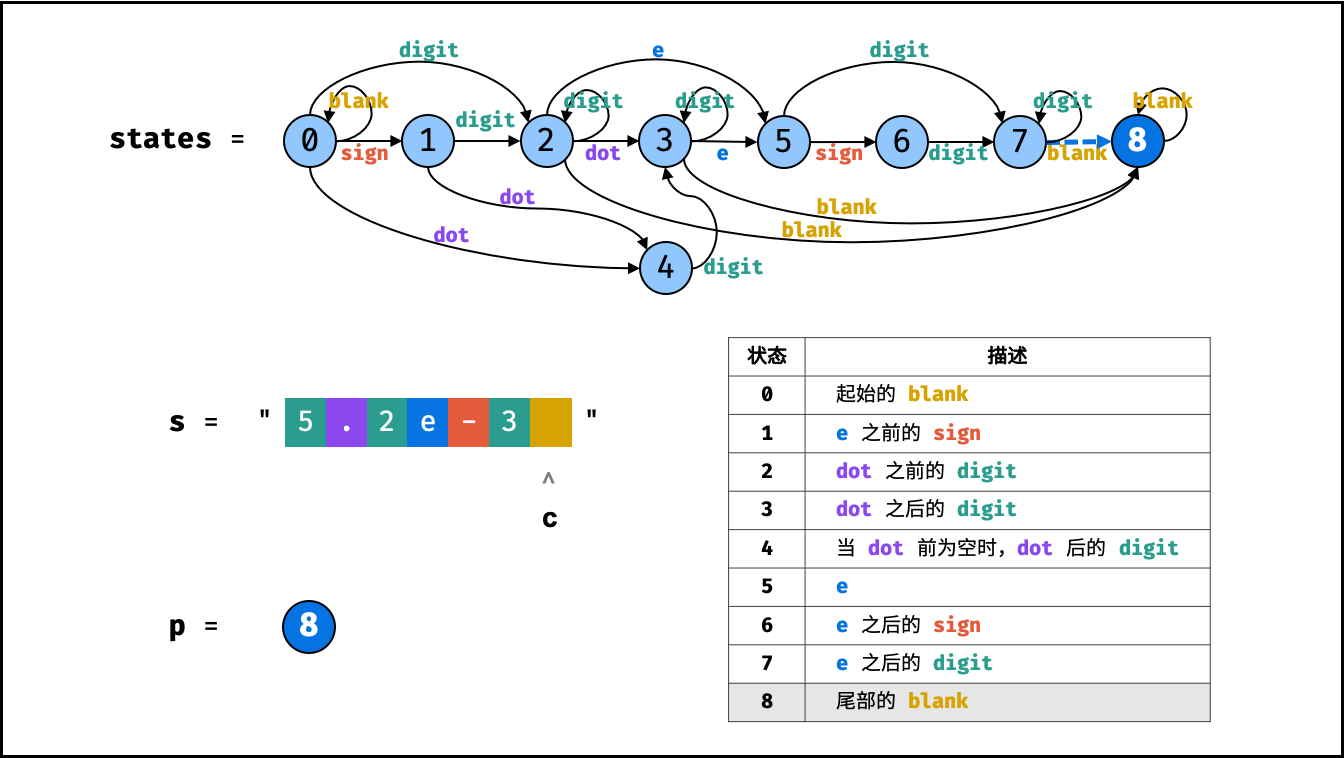Picture9.png](https://pic.leetcode-cn.com/1599283186-RNpWas-Picture9.png),![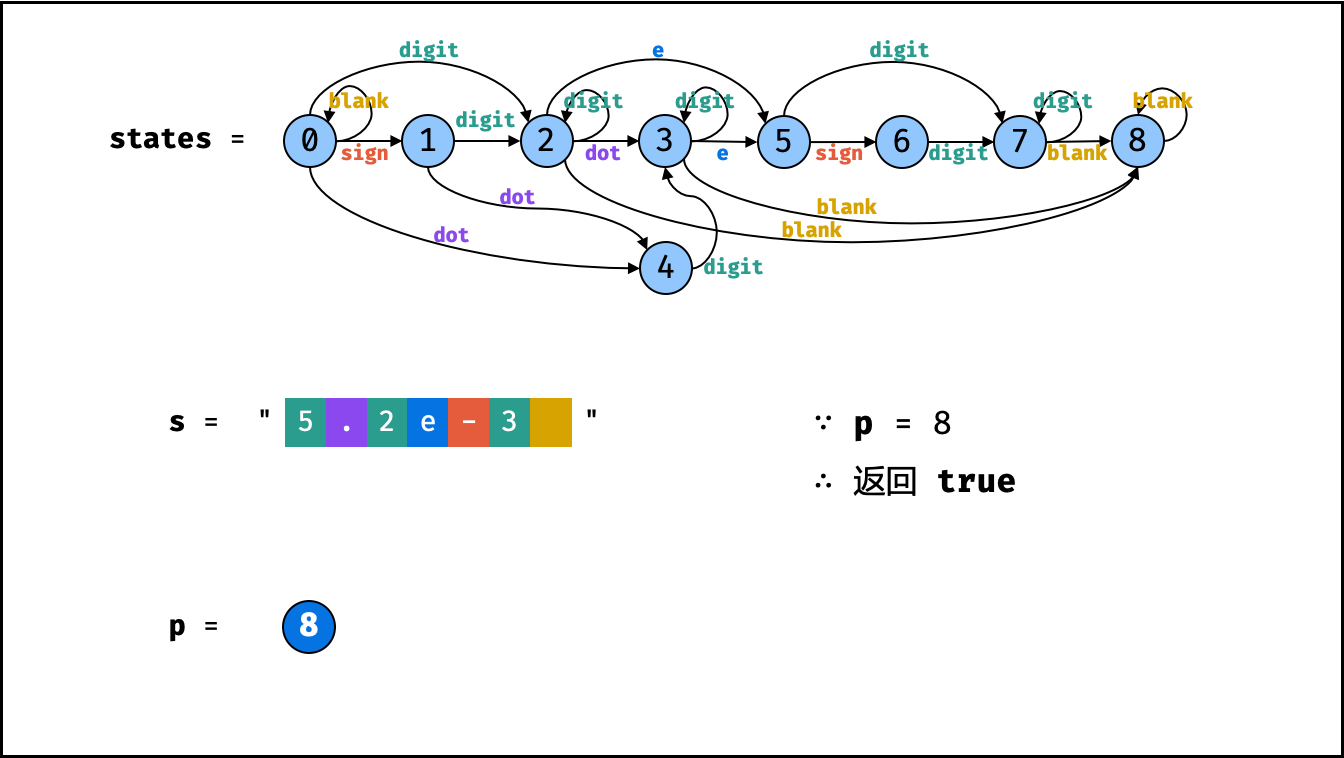Picture10.png](https://pic.leetcode-cn.com/1599283190-JizpdM-Picture10.png)>
## 代码：
Java 的状态转移表 `states` 使用 Map[] 数组存储。
```Python []
class Solution:
def validNumber(self, s: str) -> bool:
states = [
{ ' ': 0, 's': 1, 'd': 2, '.': 4 }, # 0. start with 'blank'
{ 'd': 2, '.': 4 } , # 1. 'sign' before 'e'
{ 'd': 2, '.': 3, 'e': 5, ' ': 8 }, # 2. 'digit' before 'dot'
{ 'd': 3, 'e': 5, ' ': 8 }, # 3. 'digit' after 'dot'
{ 'd': 3 }, # 4. 'digit' after 'dot' (‘blank’ before 'dot')
{ 's': 6, 'd': 7 }, # 5. 'e'
{ 'd': 7 }, # 6. 'sign' after 'e'
{ 'd': 7, ' ': 8 }, # 7. 'digit' after 'e'
{ ' ': 8 } # 8. end with 'blank'
]
p = 0 # start with state 0
for c in s:
if '0' <= c <= '9': t = 'd' # digit
elif c in "+-": t = 's' # sign
elif c in "eE": t = 'e' # e or E
elif c in ". ": t = c # dot, blank
else: t = '?' # unknown
if t not in states[p]: return False
p = states[p][t]
return p in (2, 3, 7, 8)
```
```Java []
class Solution {
public boolean validNumber(String s) {
Map[] states = {
new HashMap<>() {{ put(' ', 0); put('s', 1); put('d', 2); put('.', 4); }}, // 0.
new HashMap<>() {{ put('d', 2); put('.', 4); }}, // 1.
new HashMap<>() {{ put('d', 2); put('.', 3); put('e', 5); put(' ', 8); }}, // 2.
new HashMap<>() {{ put('d', 3); put('e', 5); put(' ', 8); }}, // 3.
new HashMap<>() {{ put('d', 3); }}, // 4.
new HashMap<>() {{ put('s', 6); put('d', 7); }}, // 5.
new HashMap<>() {{ put('d', 7); }}, // 6.
new HashMap<>() {{ put('d', 7); put(' ', 8); }}, // 7.
new HashMap<>() {{ put(' ', 8); }} // 8.
};
int p = 0;
char t;
for(char c : s.toCharArray()) {
if(c >= '0' && c <= '9') t = 'd';
else if(c == '+' || c == '-') t = 's';
else if(c == 'e' || c == 'E') t = 'e';
else if(c == '.' || c == ' ') t = c;
else t = '?';
if(!states[p].containsKey(t)) return false;
p = (int)states[p].get(t);
}
return p == 2 || p == 3 || p == 7 || p == 8;
}
}
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为字符串 `s` 的长度，判断需遍历字符串，每轮状态转移的使用 $O(1)$ 时间。
- **空间复杂度 $O(1)$ ：** `states` 和 `p` 使用常数大小的额外空间。

77
leetbook_ioa/docs/LCR 139. 训练计划 I.md Executable file
View File

@@ -0,0 +1,77 @@
## 解题思路：
考虑定义双指针 $i$ , $j$ 分列数组左右两端，循环执行：
1. 指针 $i$ 从左向右寻找偶数；
2. 指针 $j$ 从右向左寻找奇数；
3. 将 偶数 $actions[i]$ 和 奇数 $actions[j]$ 交换。
可始终保证： 指针 $i$ 左边都是奇数，指针 $j$ 右边都是偶数 。
> 下图中的 `nums` 对应本题的 `actions` 。
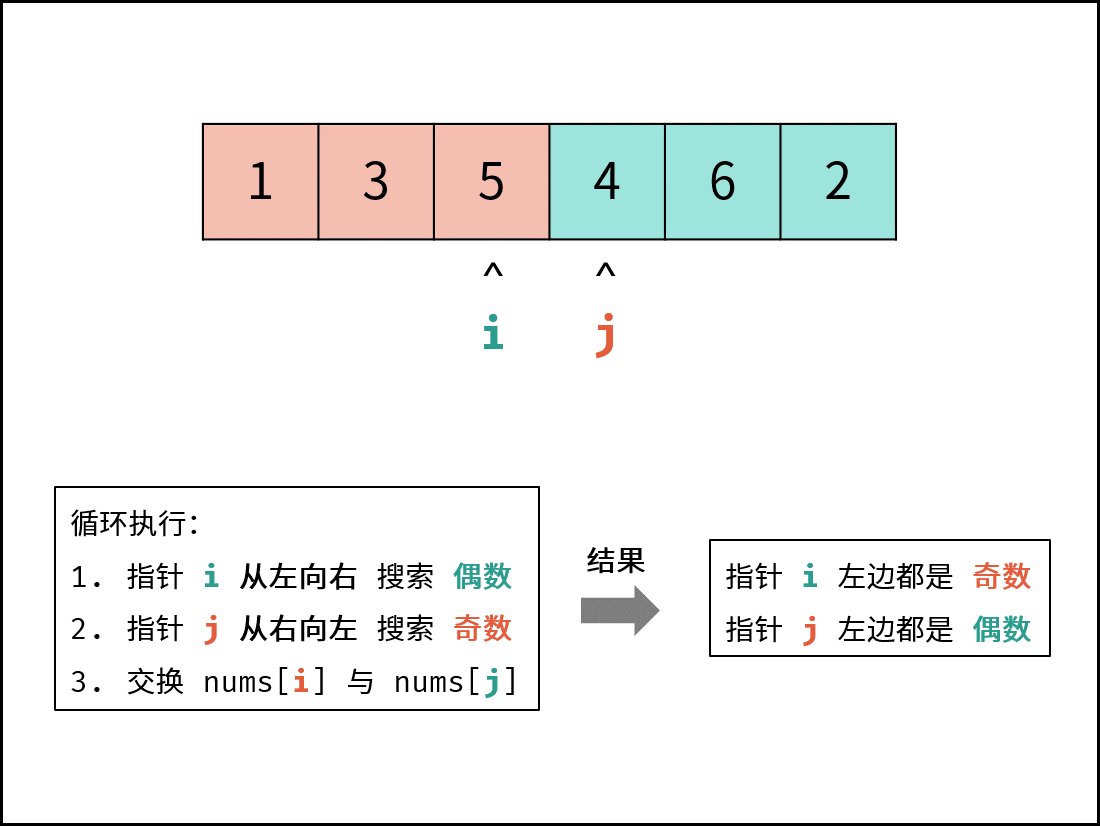![Picture1.png](https://pic.leetcode-cn.com/43e965485da89efa688947bc108232f10b65b5ba5c0dbd6a68227a82c7e451e4-Picture1.png){:align=center width=450}
### 算法流程：
1. **初始化：** $i$ , $j$ 双指针，分别指向数组 $actions$ 左右两端；
2. **循环交换：** 当 $i = j$ 时跳出；
1. 指针 $i$ 遇到奇数则执行 $i = i + 1$ 跳过，直到找到偶数；
2. 指针 $j$ 遇到偶数则执行 $j = j - 1$ 跳过，直到找到奇数；
3. 交换 $actions[i]$ 和 $actions[j]$ 值；
3. **返回值：** 返回已修改的 $actions$ 数组。
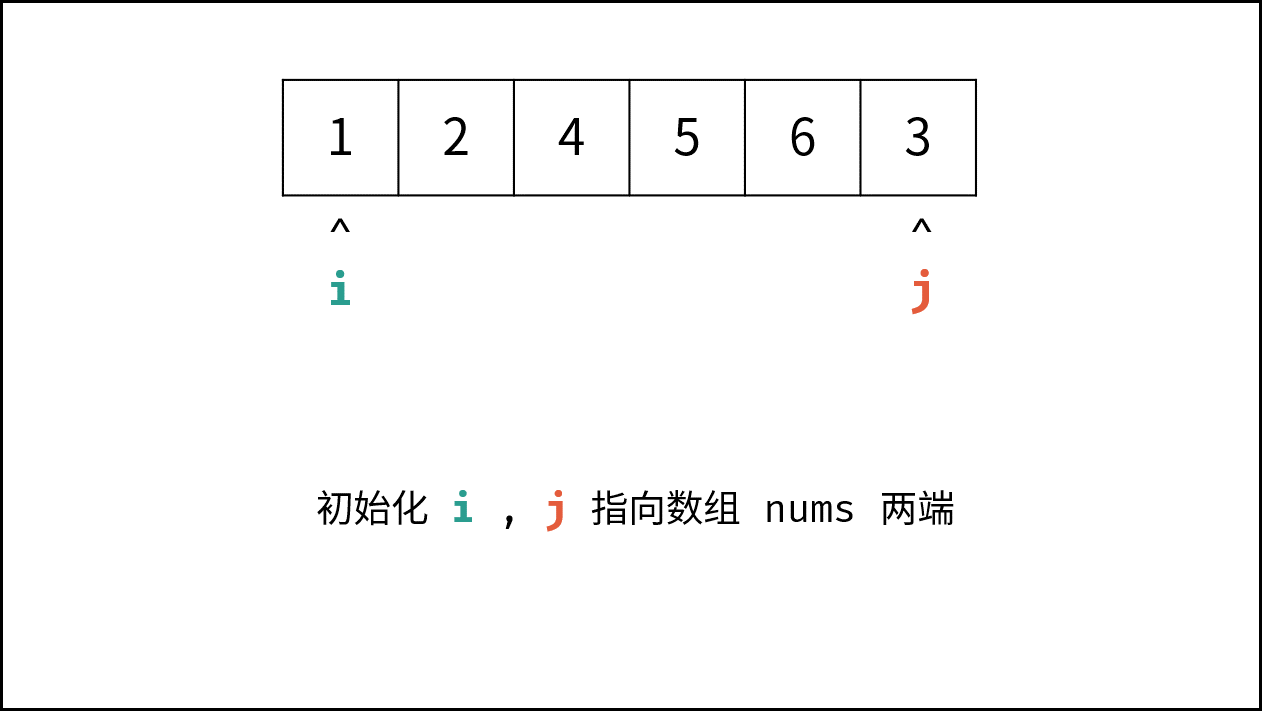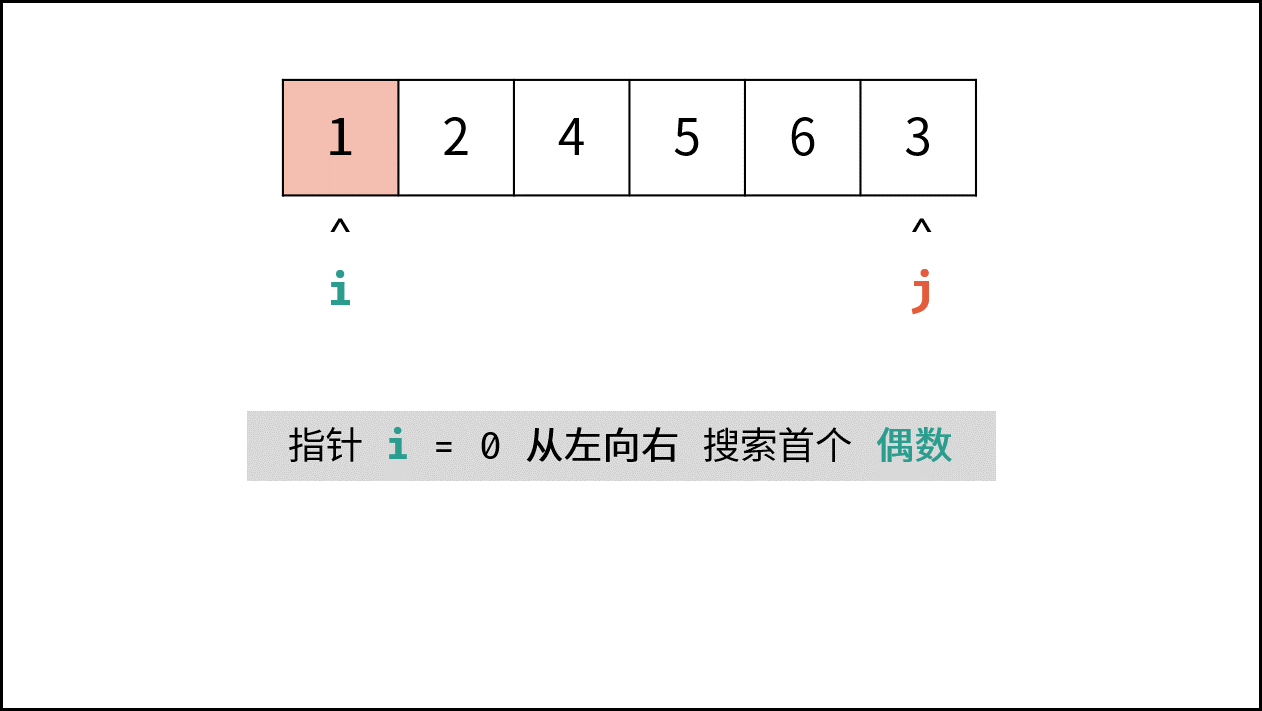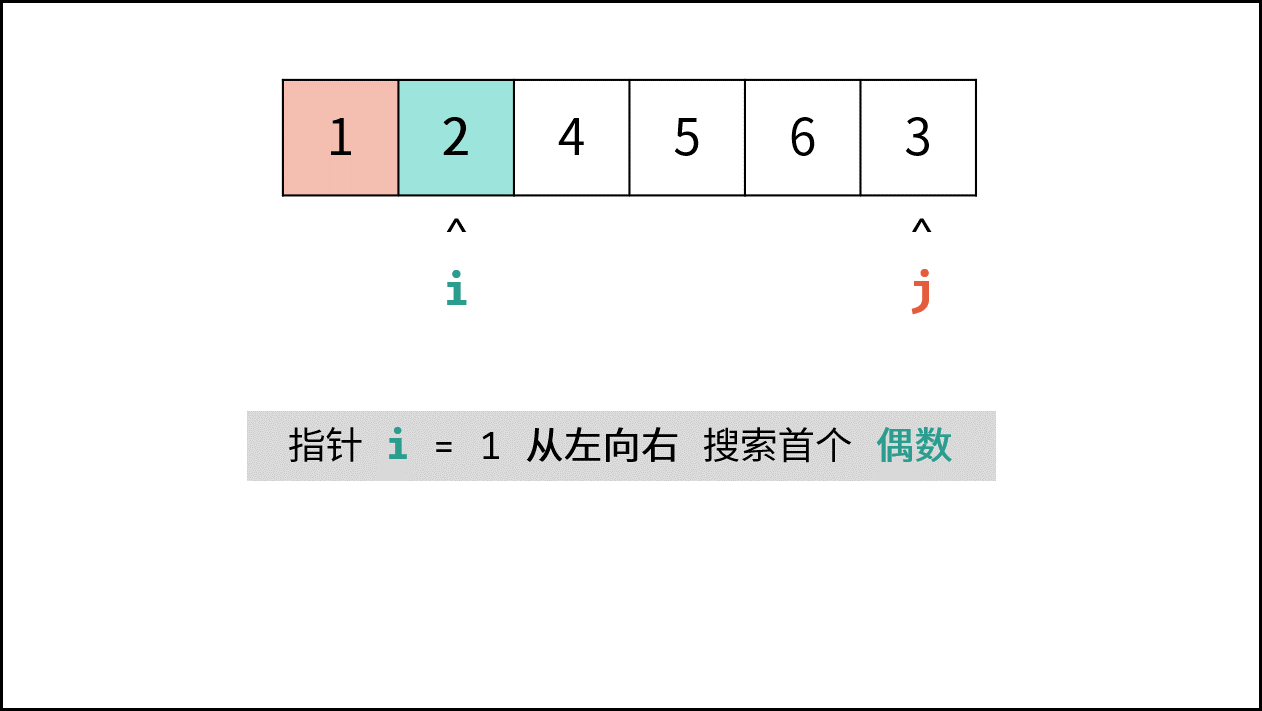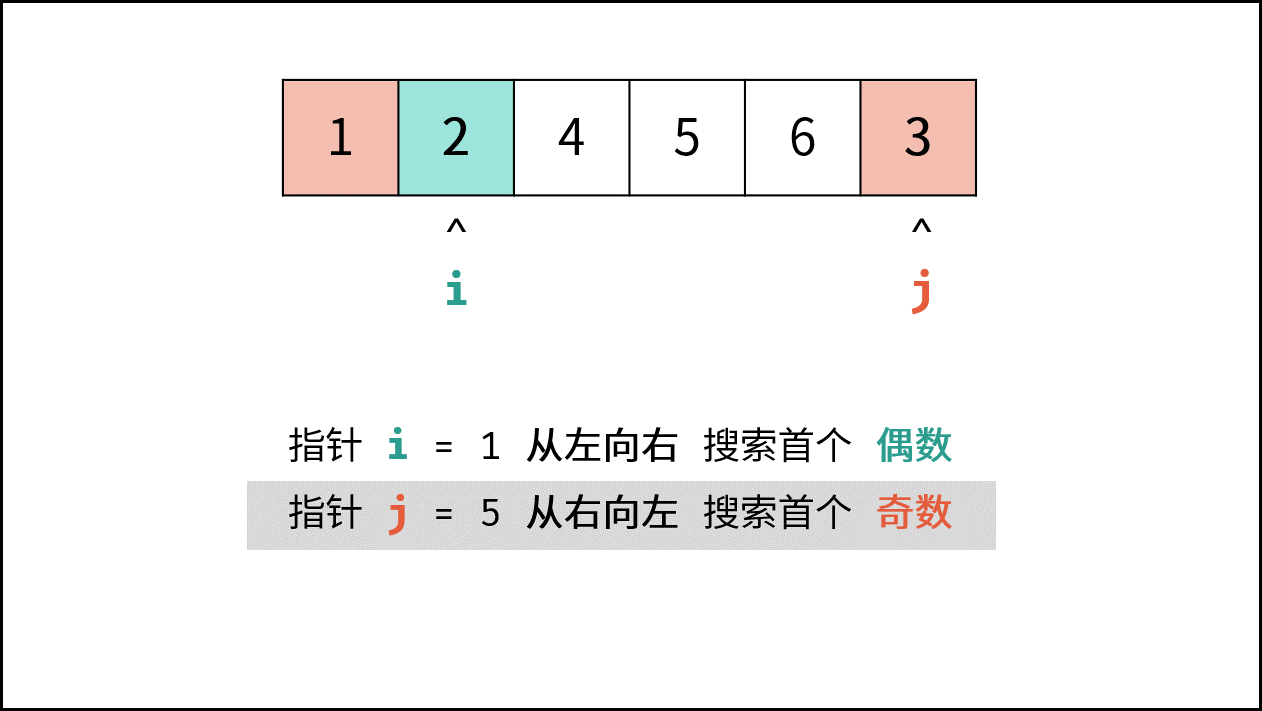<![Picture2.png](https://pic.leetcode-cn.com/da0888dfd73a7acd81e0e90589fe9d64f3505ea50bd5912b91d69a8da7198f34-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/d7f2d1d374e8c49a070d741ca7c56e07a79d7e4e956843c7743f57a836129b3b-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/df55f9254945072e0a2527c34557407a2543d60c1522bfc8a2455c156f4858cd-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/4d55b6e14518172f0a0b182bcb4fd2da1486ce25d9c73614e531786ed7f34901-Picture5.png),![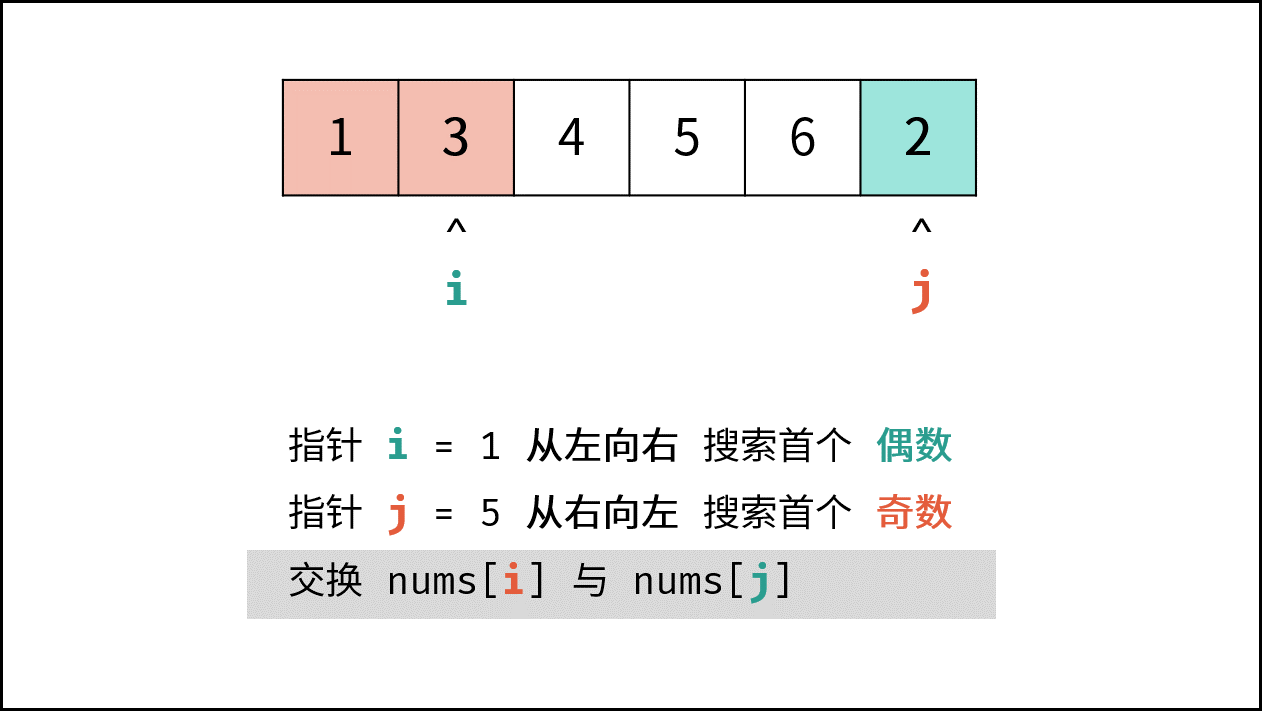Picture6.png](https://pic.leetcode-cn.com/dbe233642580b0cde66172b2016eeb8b0e5d68497d1397a718d8d269be52769d-Picture6.png),![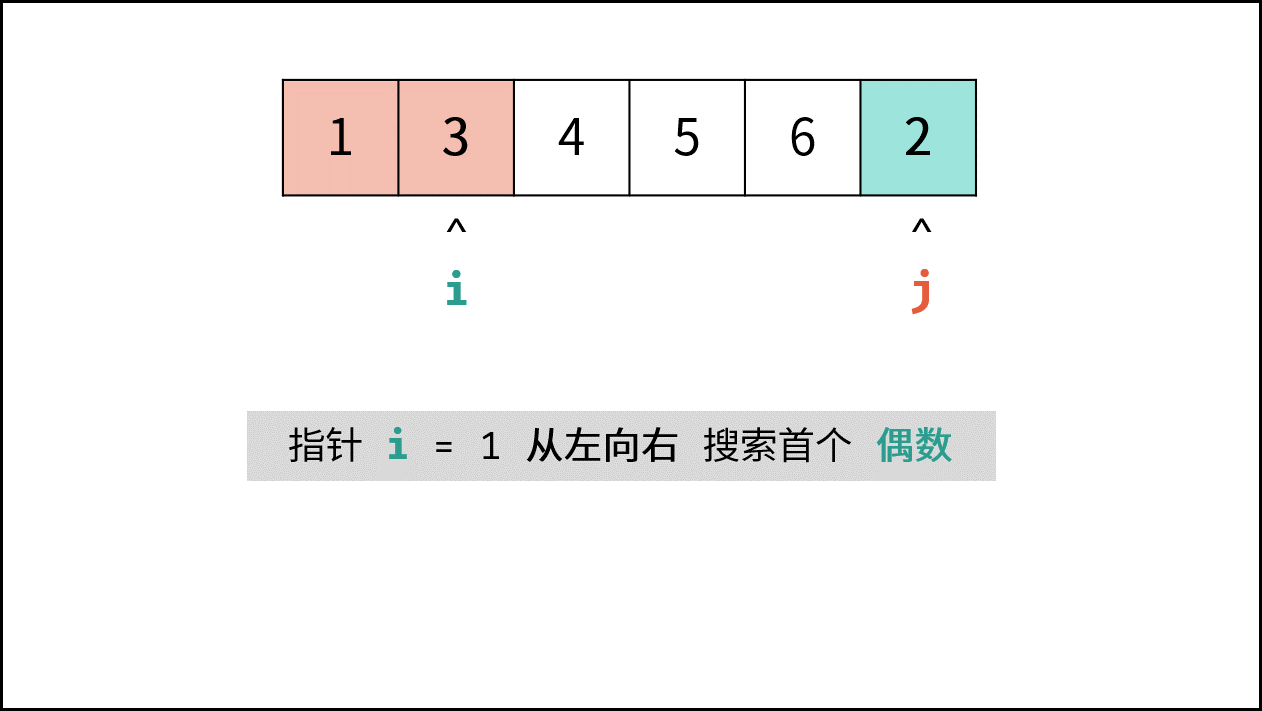Picture7.png](https://pic.leetcode-cn.com/821bd0f6c76673e9bd2f80ef9b05a6fa46e9c469174e910337731ed848559e88-Picture7.png),![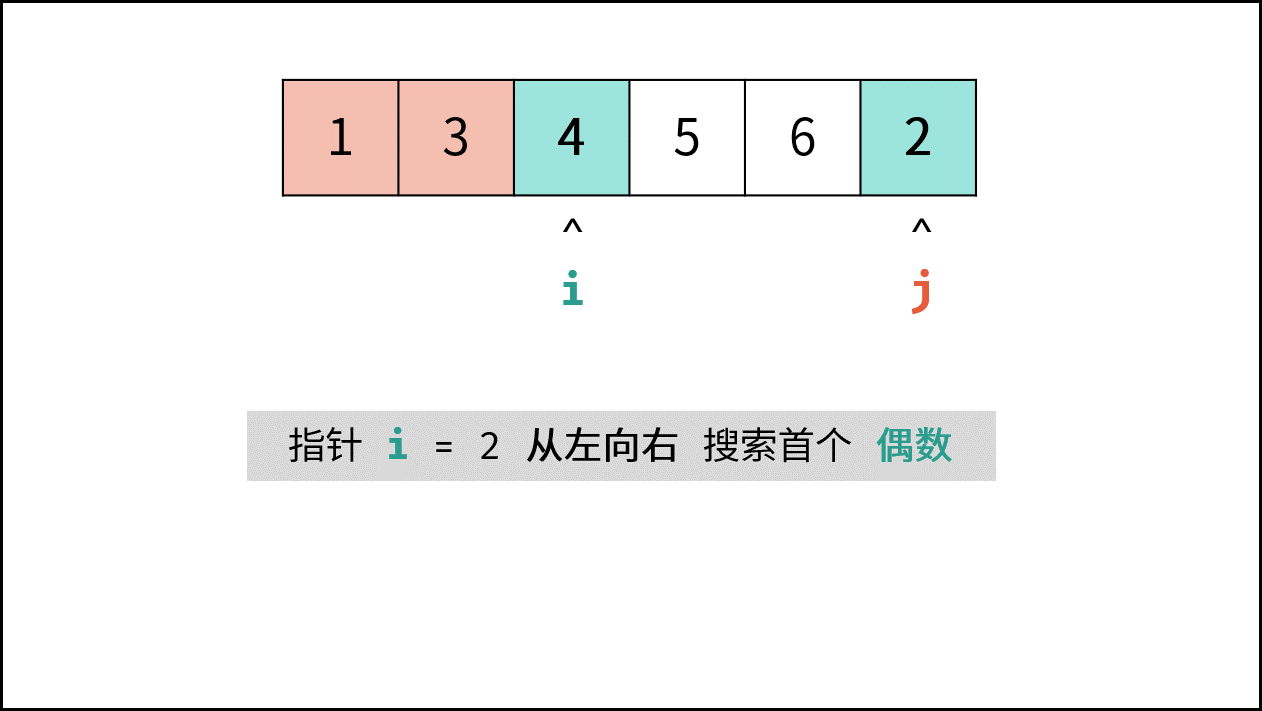Picture8.png](https://pic.leetcode-cn.com/3963804db077b70f679e5e49ce9918121bf7c561c497fc9eb2c18db424cb4ac6-Picture8.png),![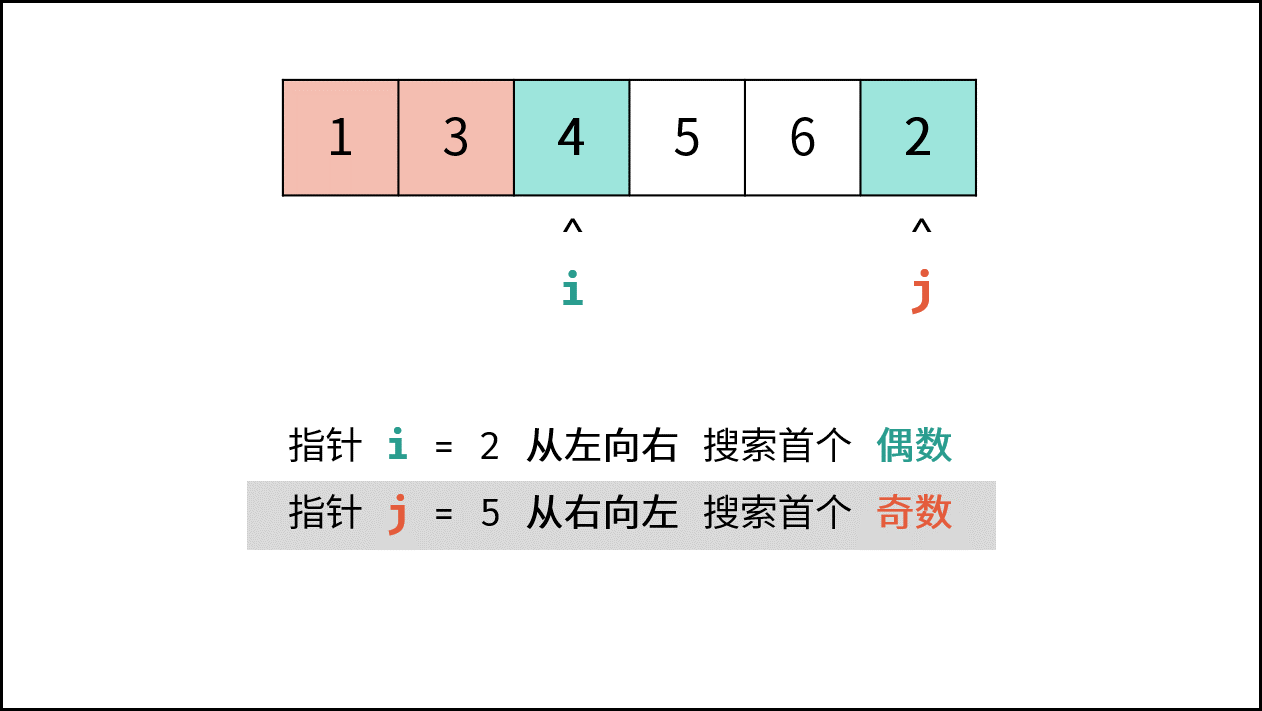Picture9.png](https://pic.leetcode-cn.com/0bcd7a450477531fceda531d14c5b447162194eaf907bf382de9f9ea7042e332-Picture9.png),![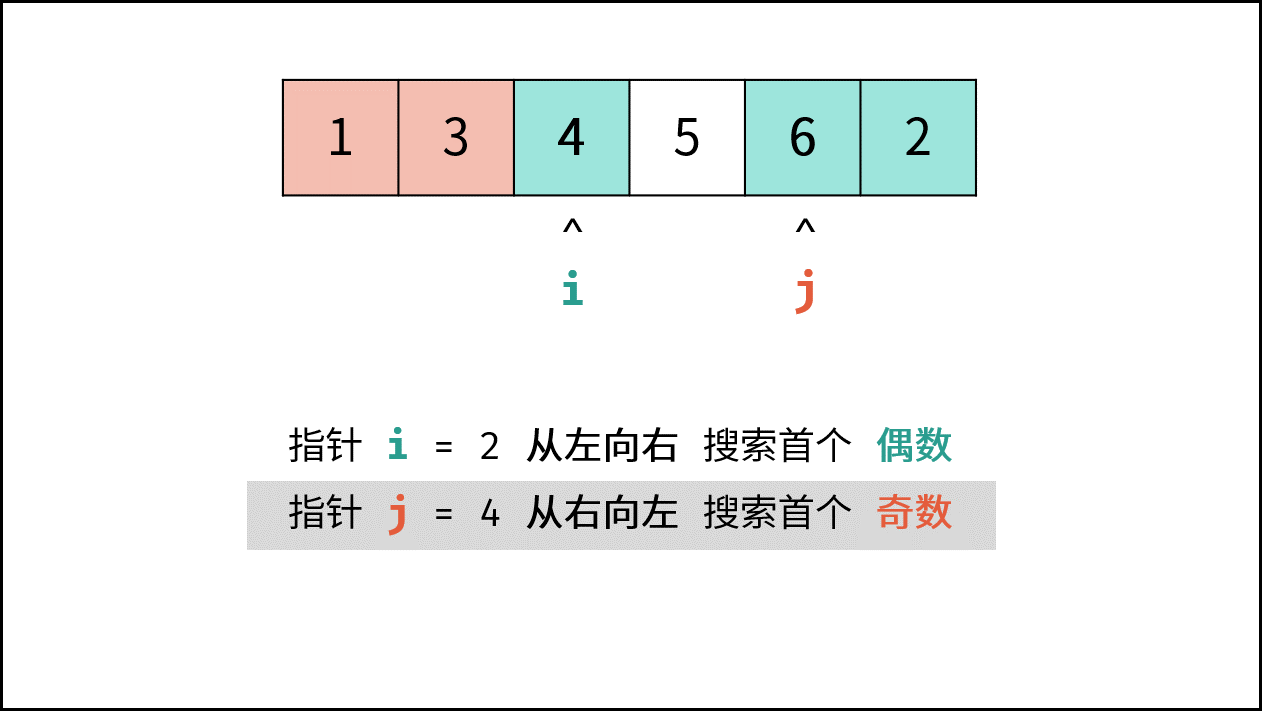Picture10.png](https://pic.leetcode-cn.com/86065c3426a6b850aa6f2be5bf68168017d125c58b8684a9f452608246ea69cb-Picture10.png),![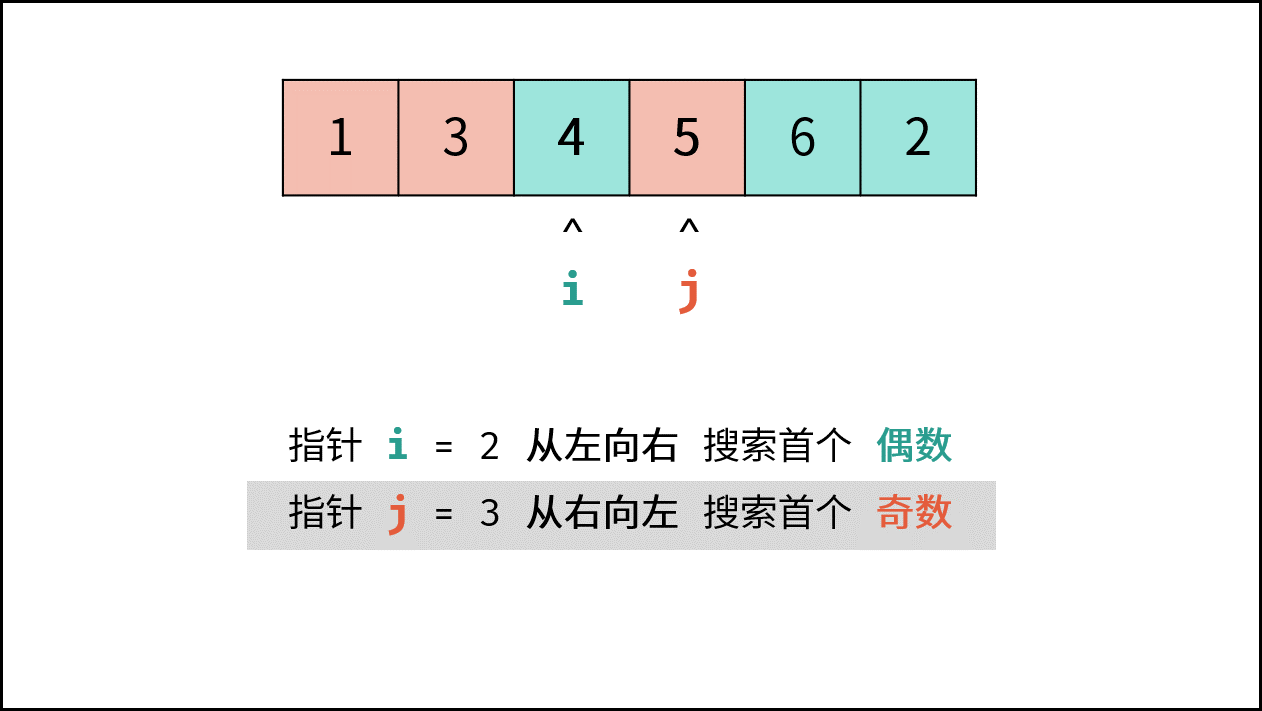Picture11.png](https://pic.leetcode-cn.com/24b9340b86b30c96aa9a3941e2fc2e95c110ac4b09c2c846f5db041c7d334a86-Picture11.png),![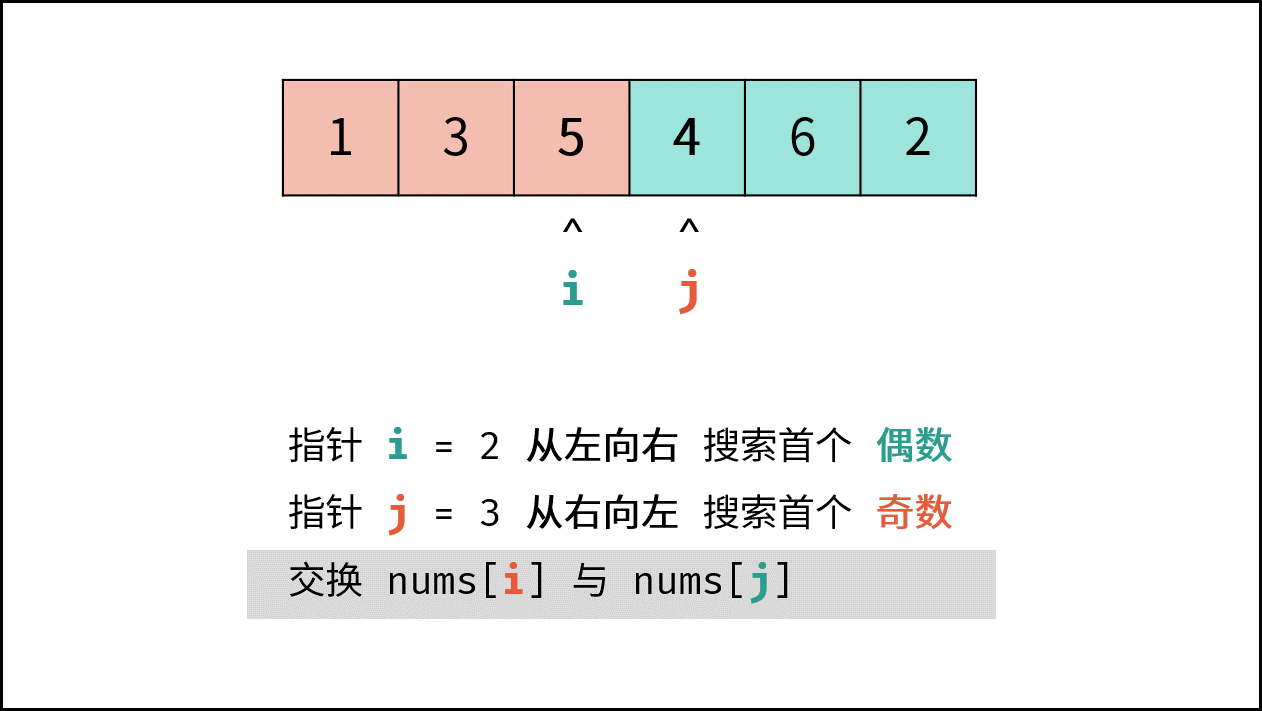Picture12.png](https://pic.leetcode-cn.com/3443ed25feeda4e3acc652668ee28b727f371f87b1c0754c9d3de21e0a44a1b1-Picture12.png),![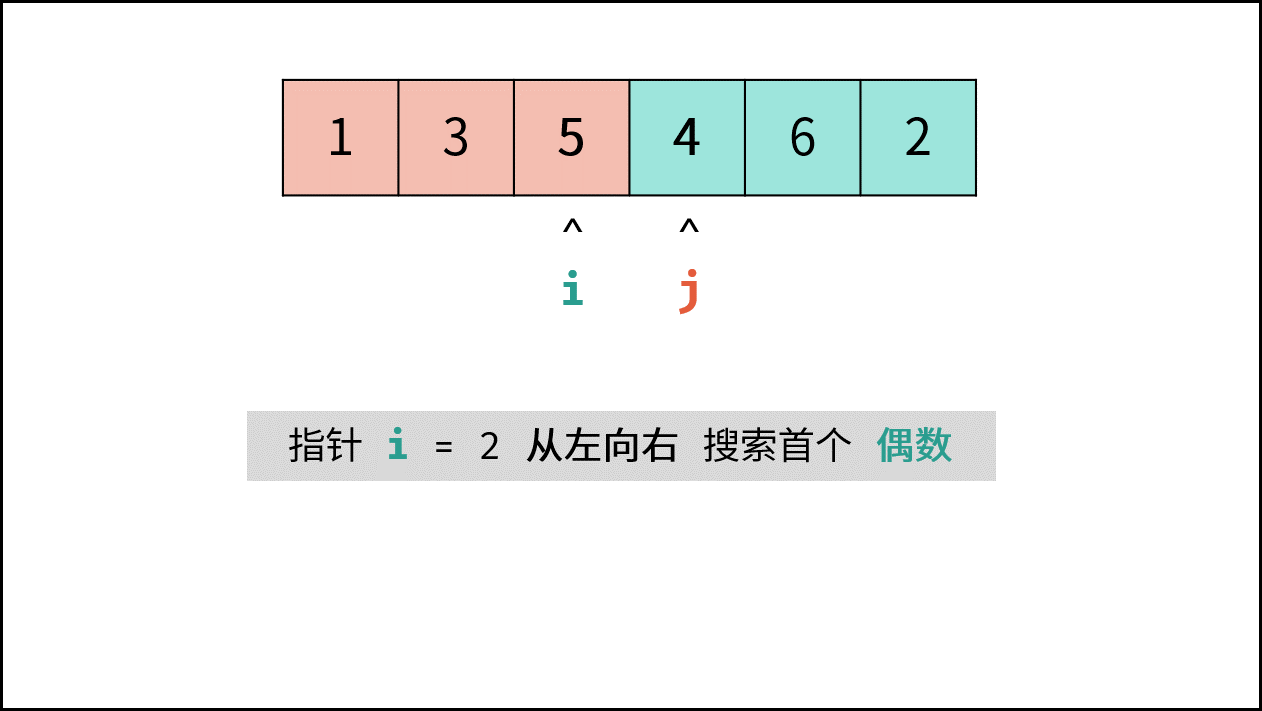Picture13.png](https://pic.leetcode-cn.com/9d018e7094a1de7aac217185675bb04d2b20a04c3a97de78f5abcc047f796172-Picture13.png),![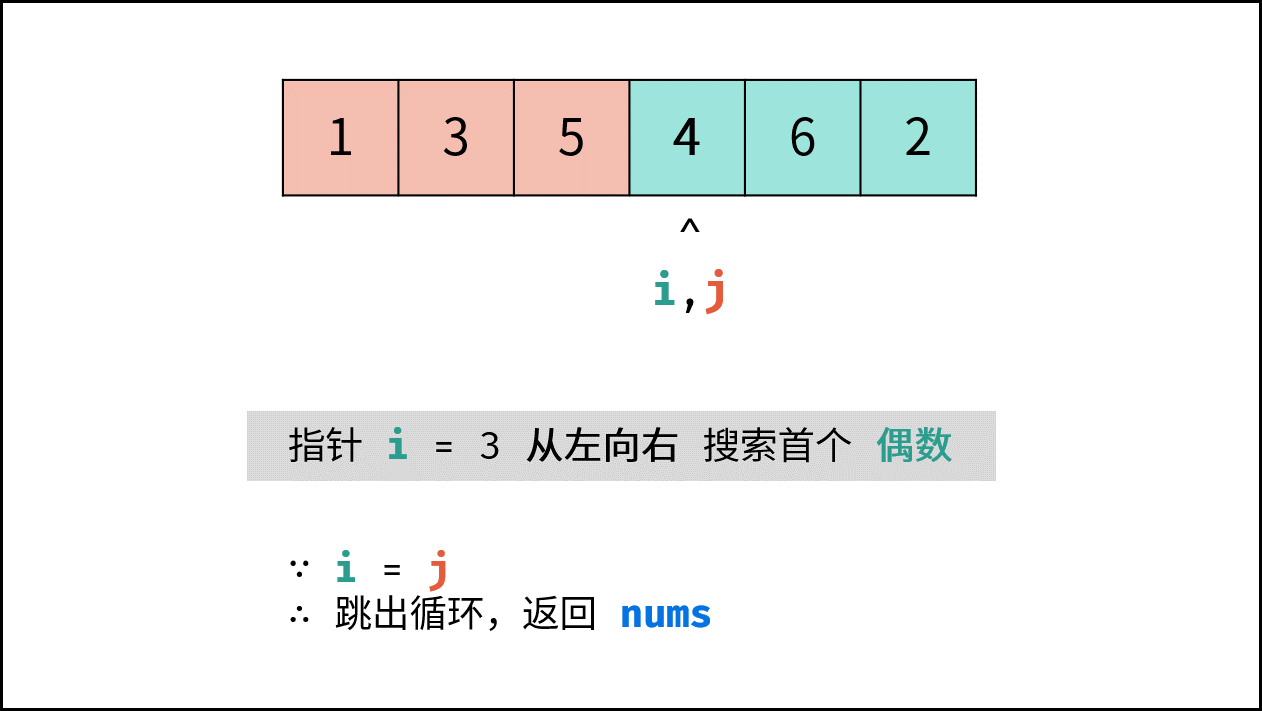Picture14.png](https://pic.leetcode-cn.com/3562063179aec9dce30b083d43ff55f8e4e4260787975d2f5138b86081f47f99-Picture14.png)>
## 代码：
$x \& 1$ 位运算 等价于 $x \mod 2$ 取余运算，即皆可用于判断数字奇偶性。
```Python []
class Solution:
def trainingPlan(self, actions: List[int]) -> List[int]:
i, j = 0, len(actions) - 1
while i < j:
while i < j and actions[i] & 1 == 1: i += 1
while i < j and actions[j] & 1 == 0: j -= 1
actions[i], actions[j] = actions[j], actions[i]
return actions
```
```Java []
class Solution {
public int[] trainingPlan(int[] actions) {
int i = 0, j = actions.length - 1, tmp;
while(i < j) {
while(i < j && (actions[i] & 1) == 1) i++;
while(i < j && (actions[j] & 1) == 0) j--;
tmp = actions[i];
actions[i] = actions[j];
actions[j] = tmp;
}
return actions;
}
}
```
```C++ []
class Solution {
public:
vector<int> trainingPlan(vector<int>& actions)
{
int i = 0, j = actions.size() - 1;
while (i < j)
{
while(i < j && (actions[i] & 1) == 1) i++;
while(i < j && (actions[j] & 1) == 0) j--;
swap(actions[i], actions[j]);
}
return actions;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为数组 $actions$ 长度，双指针 $i$, $j$ 共同遍历整个数组。
- **空间复杂度 $O(1)$ ：** 双指针 $i$, $j$ 使用常数大小的额外空间。

119
leetbook_ioa/docs/LCR 140. 训练计划 II.md Executable file
View File

@@ -0,0 +1,119 @@
## 解题思路：
第一时间想到的解法：
1. 先遍历统计链表长度，记为 $n$ ；
2. 设置一个指针走 $(n-cnt)$ 步，即可找到链表倒数第 $cnt$ 个节点；
使用双指针则可以不用统计链表长度。
> 下图中的 `k` 对应本题的 `cnt` 。
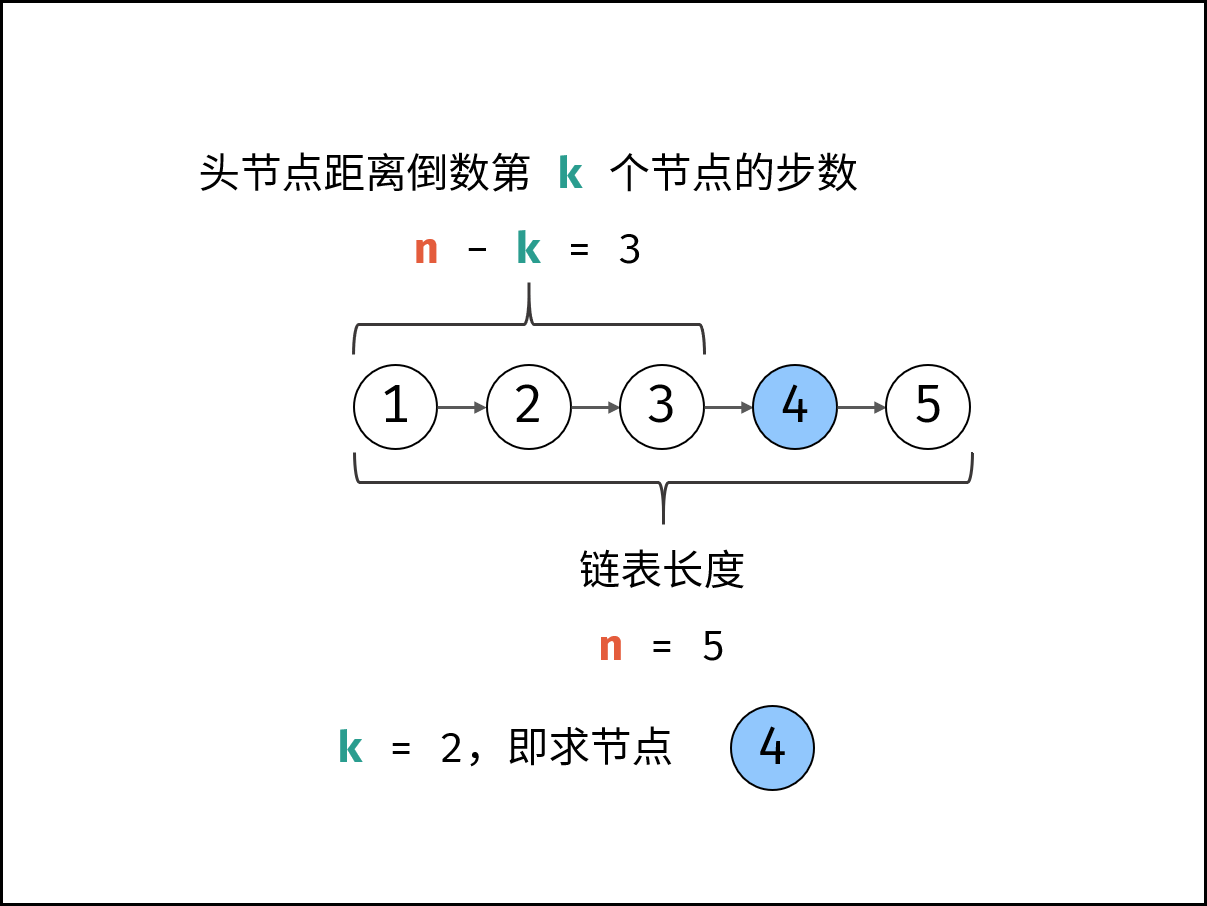![Picture1.png](https://pic.leetcode-cn.com/1600794523-AAMvoP-Picture1.png){:align=center width=450}
### 算法流程：
1. **初始化：** 前指针 `former` 、后指针 `latter` ，双指针都指向头节点 `head​` 。
2. **构建双指针距离：** 前指针 `former` 先向前走 $cnt$ 步（结束后，双指针 `former` 和 `latter` 间相距 $cnt$ 步）。
3. **双指针共同移动：** 循环中，双指针 `former` 和 `latter` 每轮都向前走一步，直至 `former` 走过链表 **尾节点** 时跳出（跳出后，`latter` 与尾节点距离为 $cnt-1$，即 `latter` 指向倒数第 $cnt$ 个节点）。
4. **返回值：** 返回 `latter` 即可。
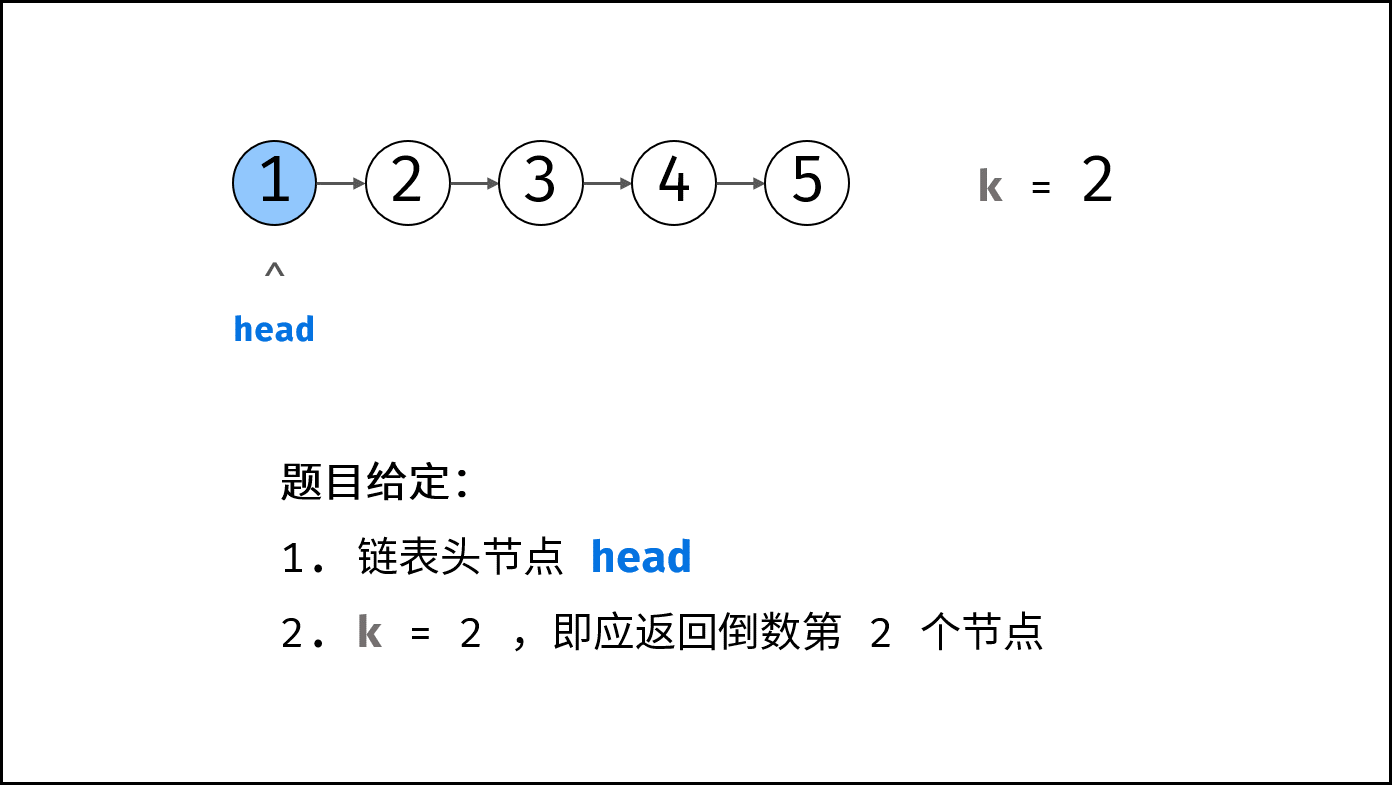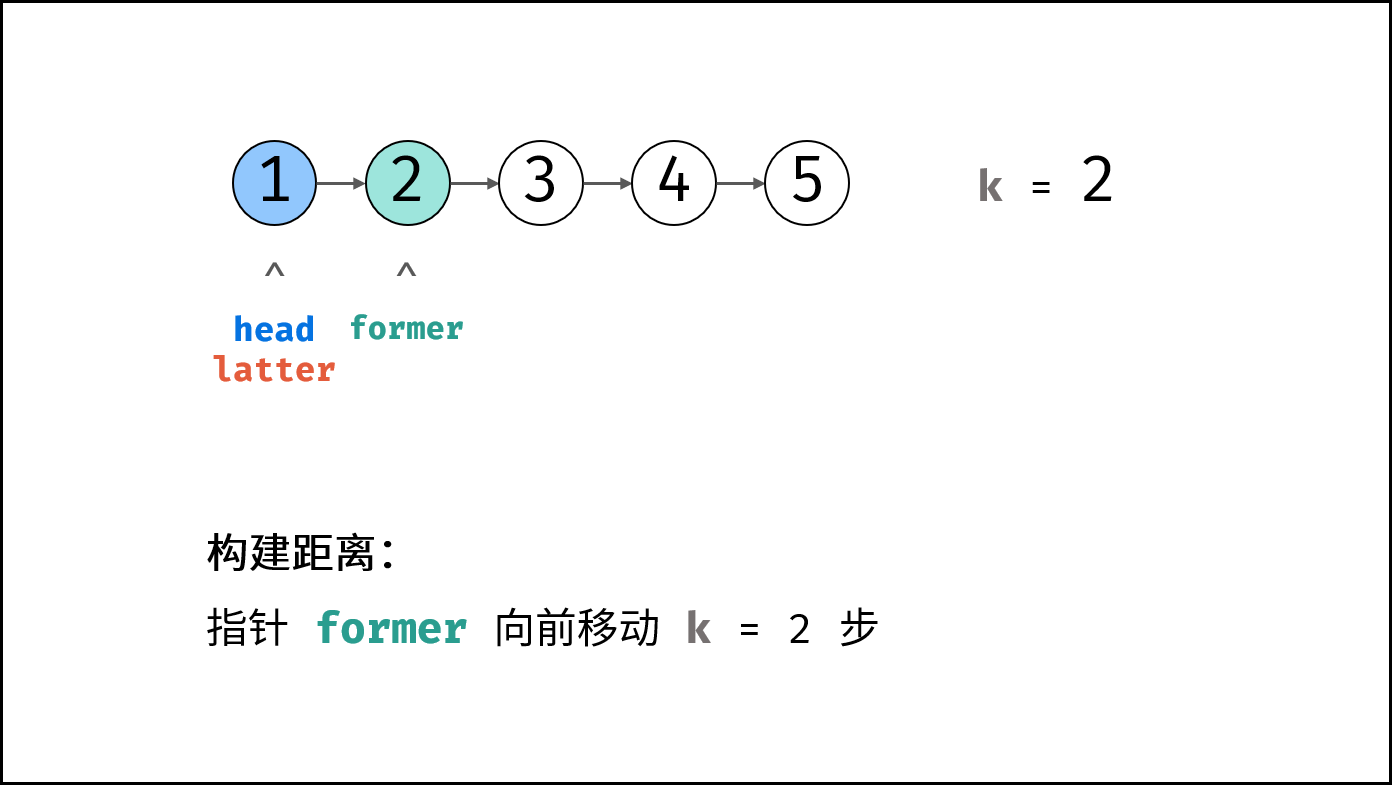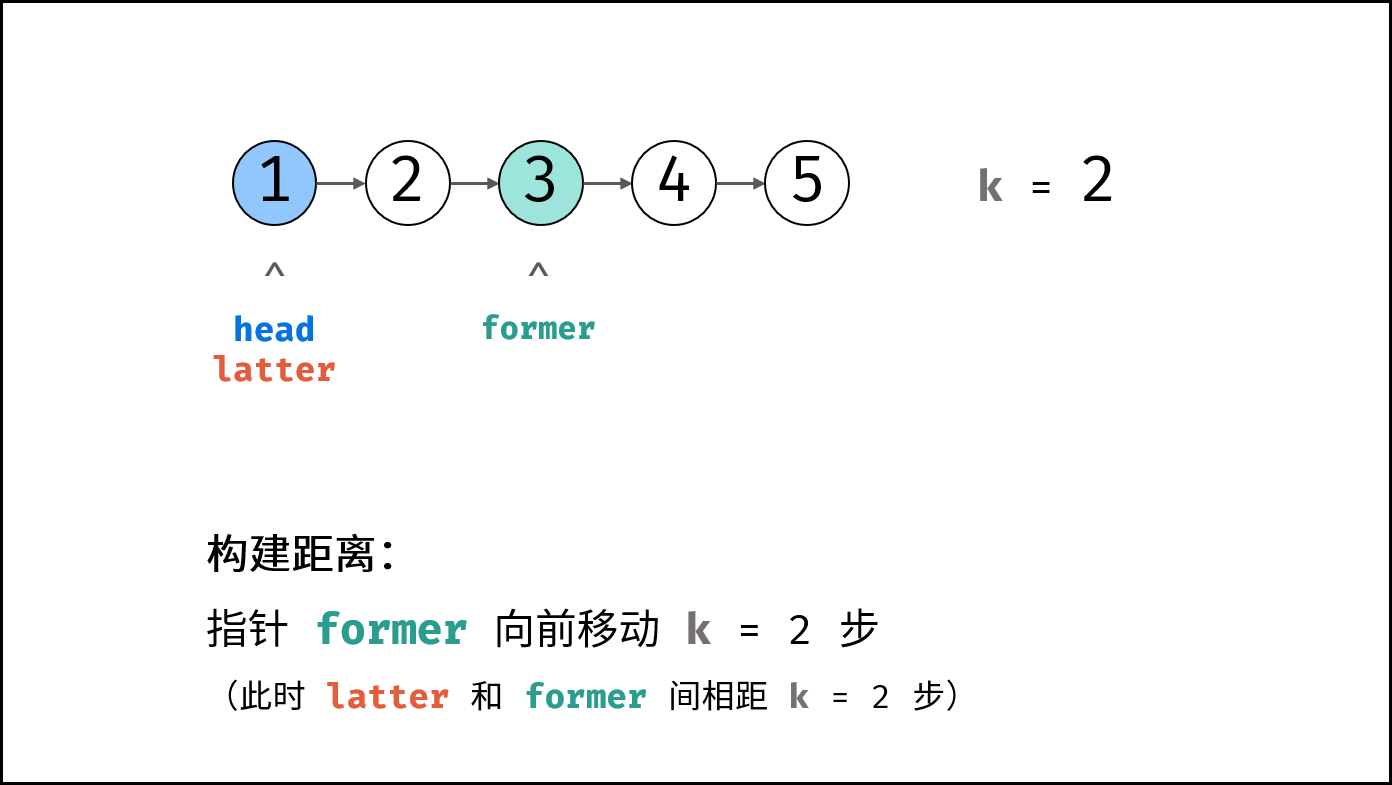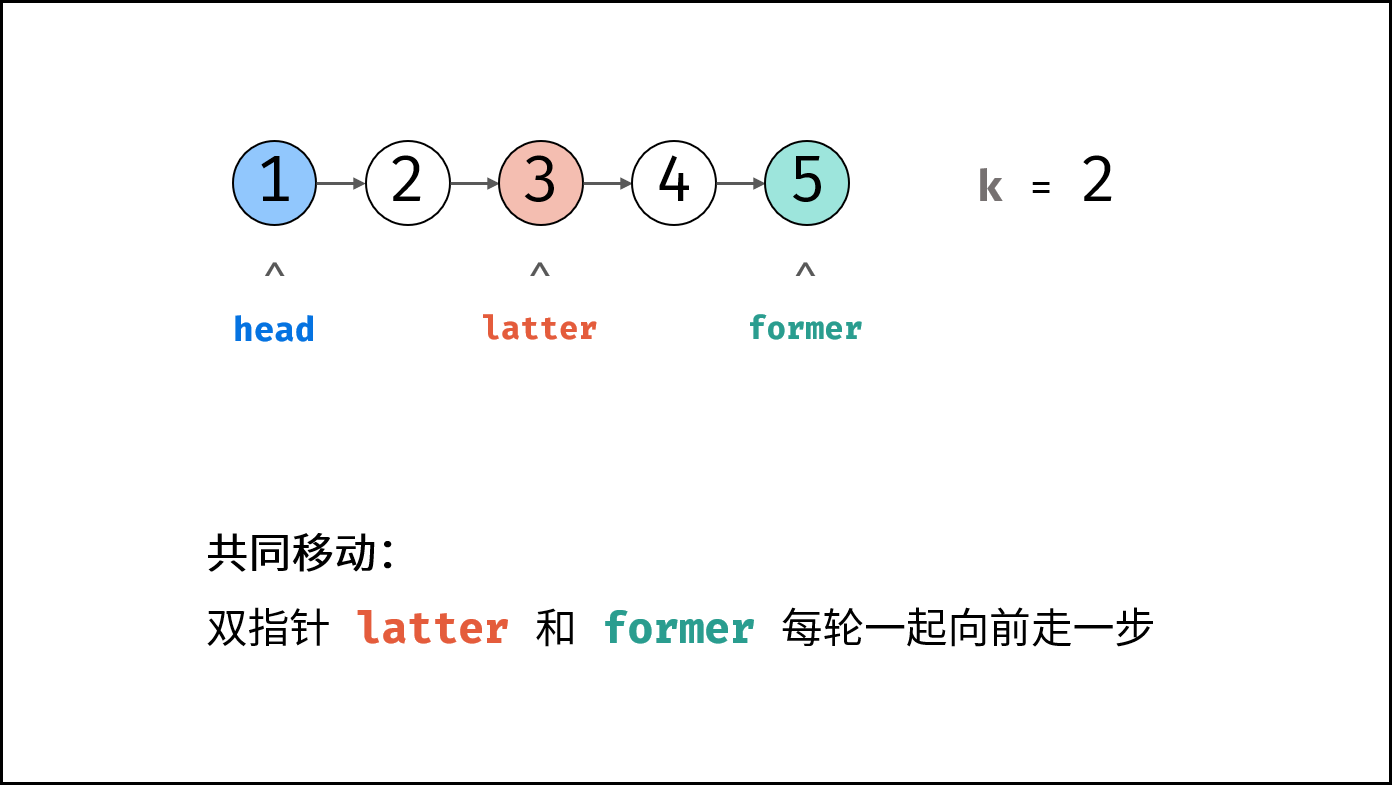<![Picture2.png](https://pic.leetcode-cn.com/1600794523-rIzxRa-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600794523-uBYNOH-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600794523-DUsoIo-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600794523-KeuJNd-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600794523-wGInQX-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600794523-zzxWkh-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1600794523-NHOoqg-Picture8.png),![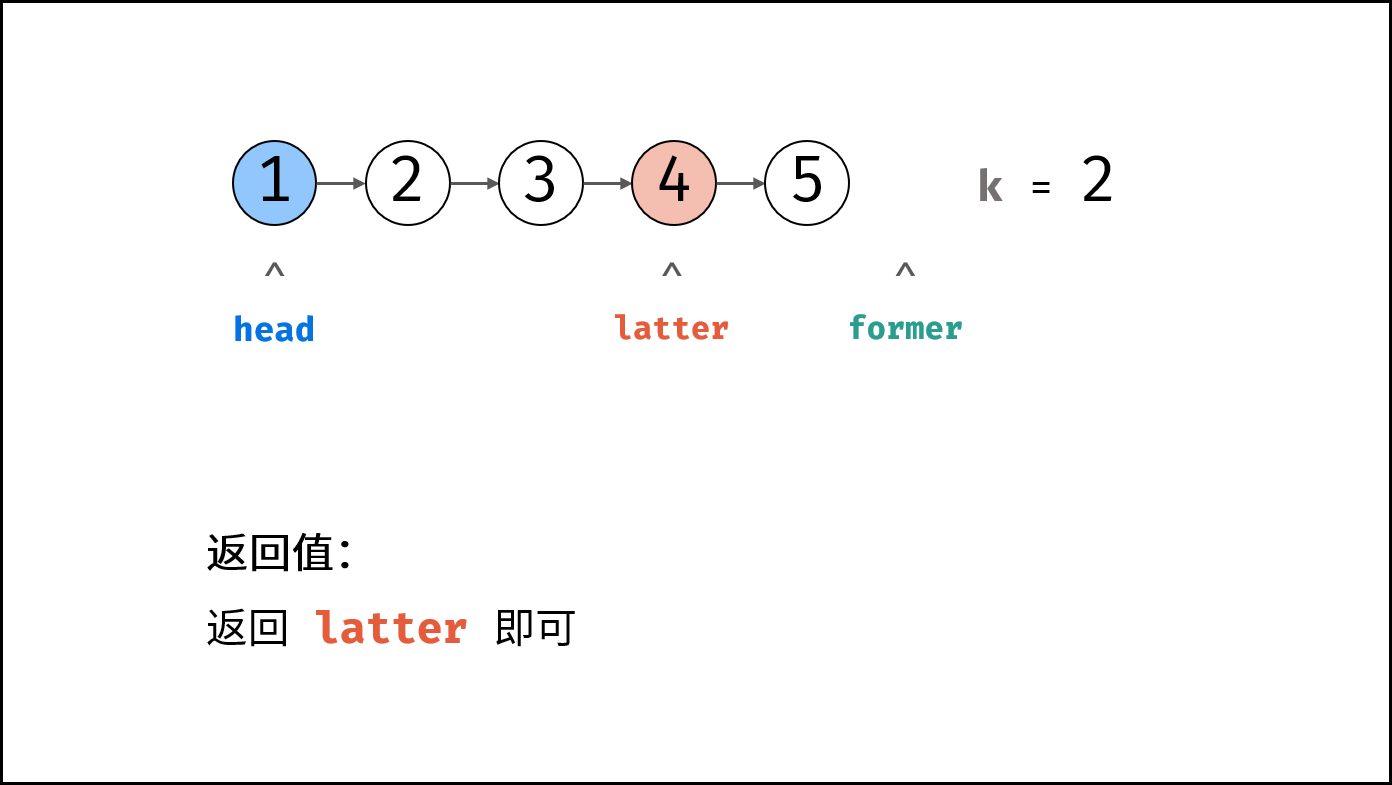Picture9.png](https://pic.leetcode-cn.com/1600794523-vBjirm-Picture9.png)>
## 代码：
```Python []
class Solution:
def trainingPlan(self, head: ListNode, cnt: int) -> ListNode:
former, latter = head, head
for _ in range(cnt):
former = former.next
while former:
former, latter = former.next, latter.next
return latter
```
```Java []
class Solution {
public ListNode trainingPlan(ListNode head, int cnt) {
ListNode former = head, latter = head;
for(int i = 0; i < cnt; i++)
former = former.next;
while(former != null) {
former = former.next;
latter = latter.next;
}
return latter;
}
}
```
```C++ []
class Solution {
public:
ListNode* trainingPlan(ListNode* head, int cnt) {
ListNode *former = head, *latter = head;
for(int i = 0; i < cnt; i++)
former = former->next;
while(former != nullptr) {
former = former->next;
latter = latter->next;
}
return latter;
}
};
```
本题没有 $cnt>$ 链表长度的测试样例 ，因此不用考虑越界。考虑越界问题的代码如下：
```Python []
class Solution:
def trainingPlan(self, head: ListNode, cnt: int) -> ListNode:
former, latter = head, head
for _ in range(cnt):
if not former: return
former = former.next
while former:
former, latter = former.next, latter.next
return latter
```
```Java []
class Solution {
public ListNode trainingPlan(ListNode head, int cnt) {
ListNode former = head, latter = head;
for(int i = 0; i < cnt; i++) {
if(former == null) return null;
former = former.next;
}
while(former != null) {
former = former.next;
latter = latter.next;
}
return latter;
}
}
```
```C++ []
class Solution {
public:
ListNode* trainingPlan(ListNode* head, int cnt) {
ListNode *former = head, *latter = head;
for(int i = 0; i < cnt; i++) {
if(former == nullptr) return nullptr;
former = former->next;
}
while(former != nullptr) {
former = former->next;
latter = latter->next;
}
return latter;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(n)$ ：** $n$ 为链表长度；总体看，`former` 走了 $n$ 步，`latter` 走了 $(-cnt)$ 步。
- **空间复杂度 $O(1)$ ：** 双指针 `former` , `latter` 使用常数大小的额外空间。

127
leetbook_ioa/docs/LCR 141. 训练计划 III.md Executable file
View File

@@ -0,0 +1,127 @@
## 解题思路：
如下图所示，题目要求将链表反转。本文介绍迭代（双指针）、递归两种实现方法。
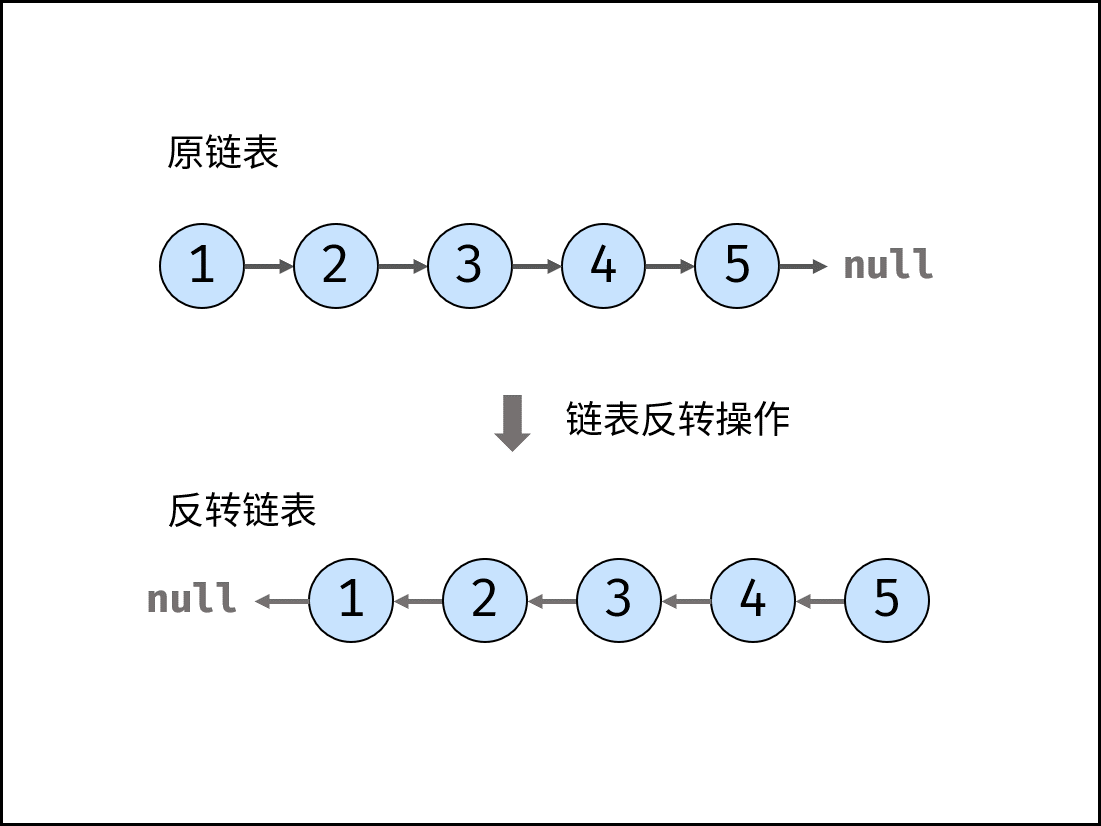![Picture1.png](https://pic.leetcode-cn.com/1604779288-WXygqL-Picture1.png){:align=center width=450}
## 方法一：迭代（双指针）
考虑遍历链表，并在访问各节点时修改 `next` 引用指向，算法流程见注释。
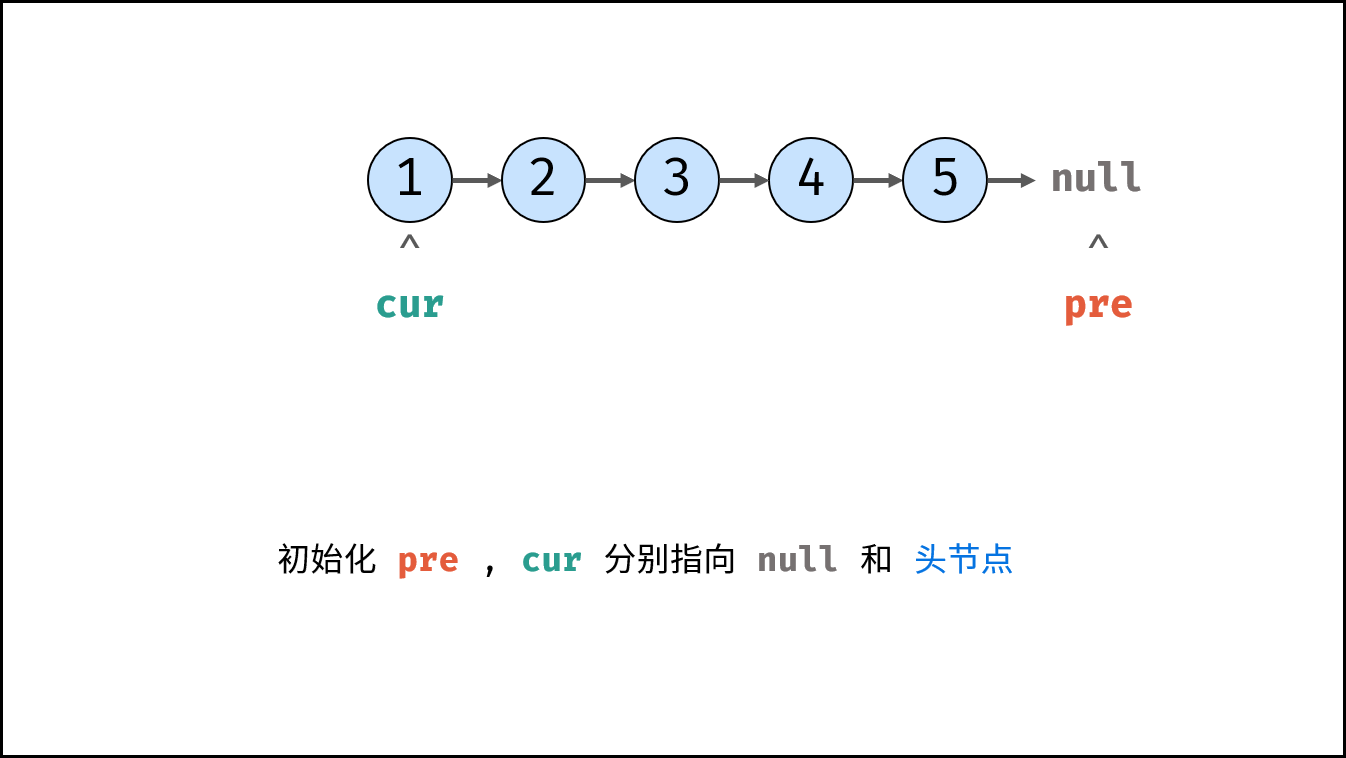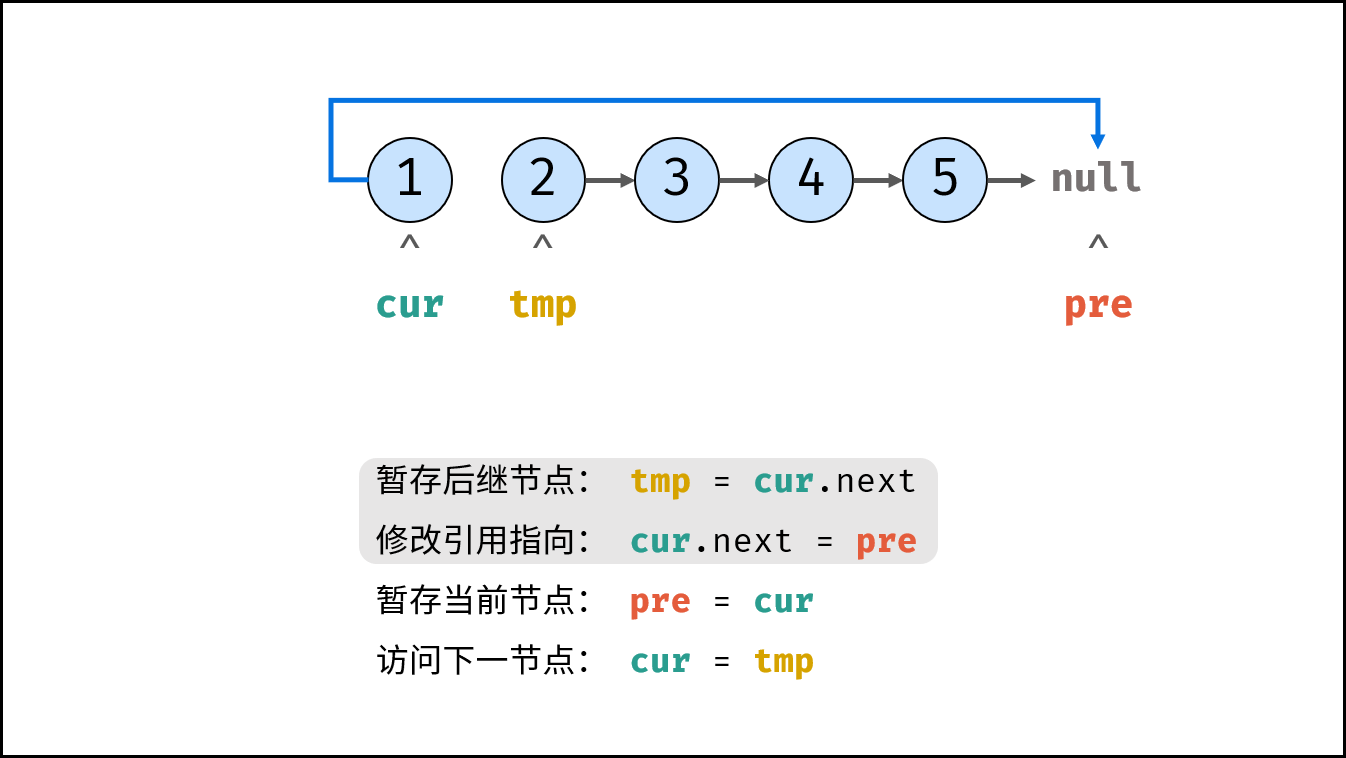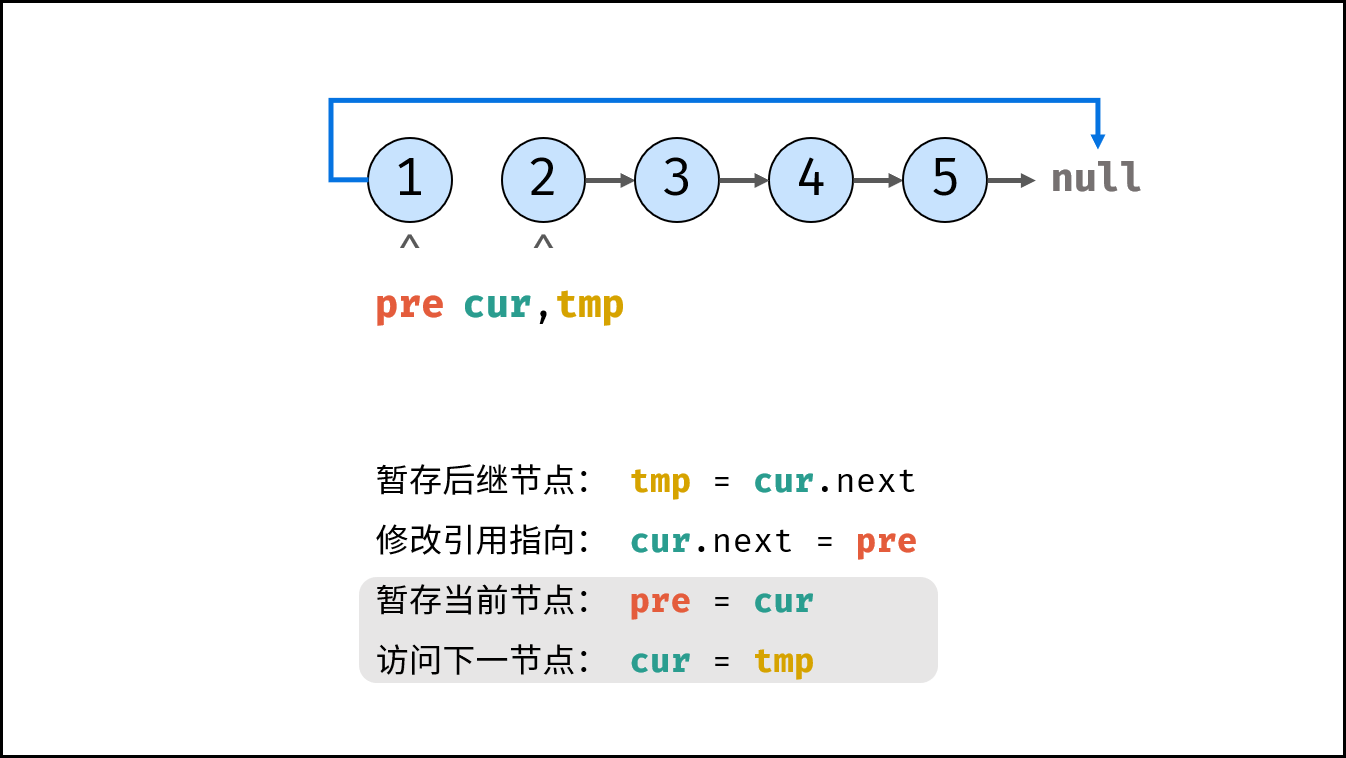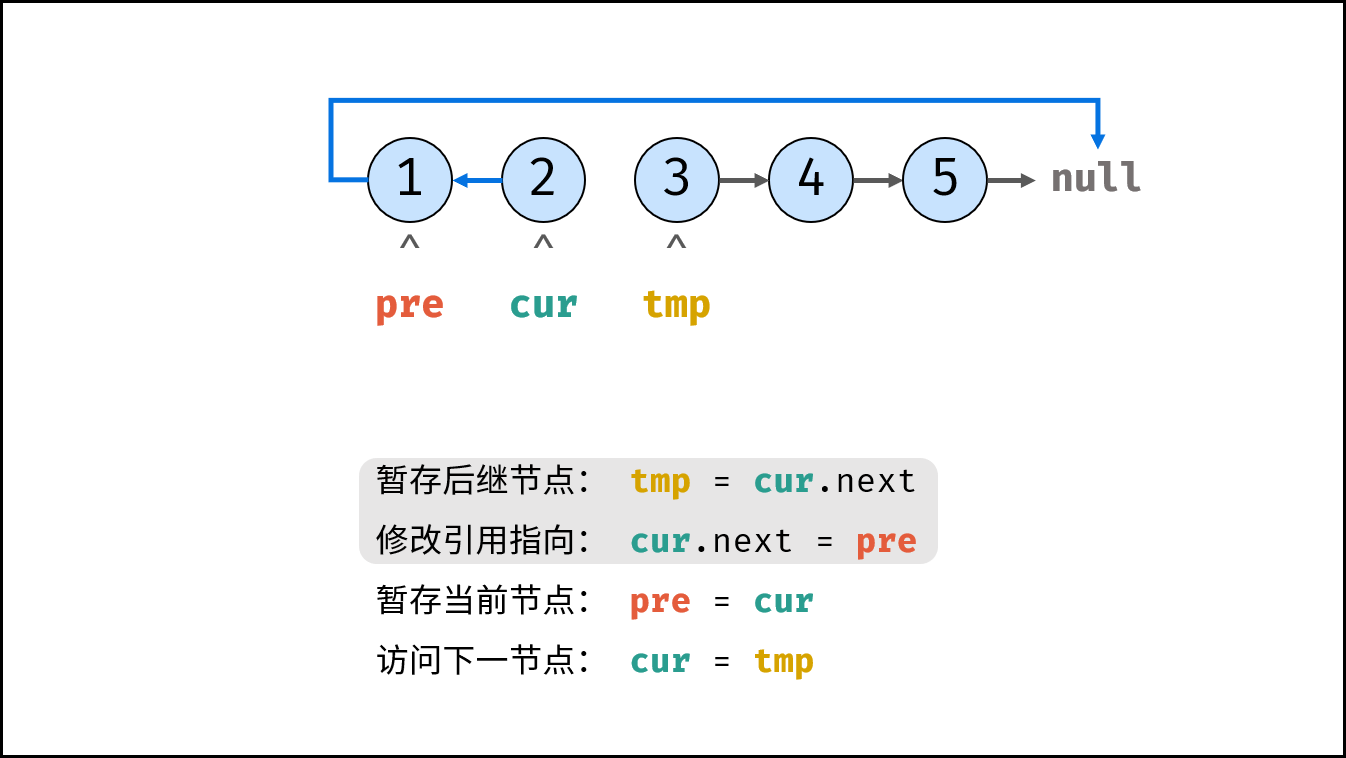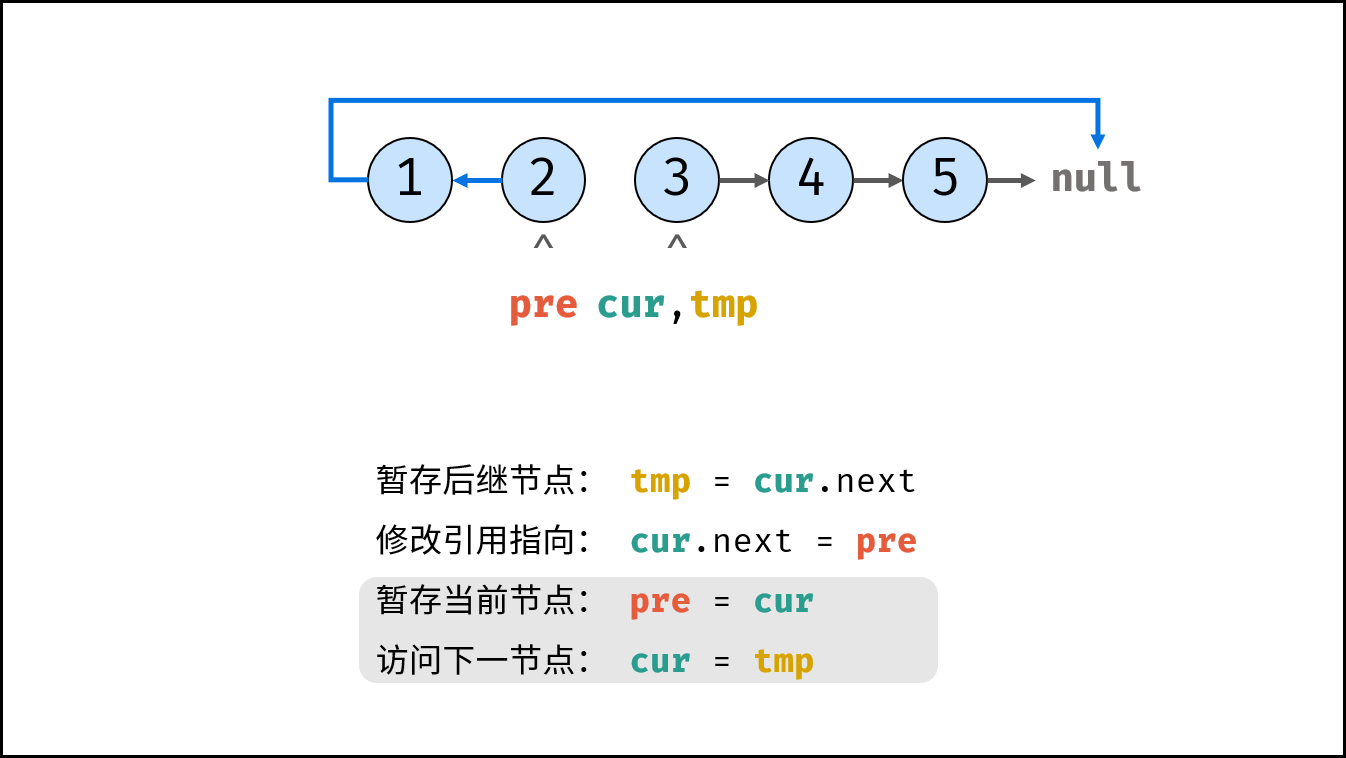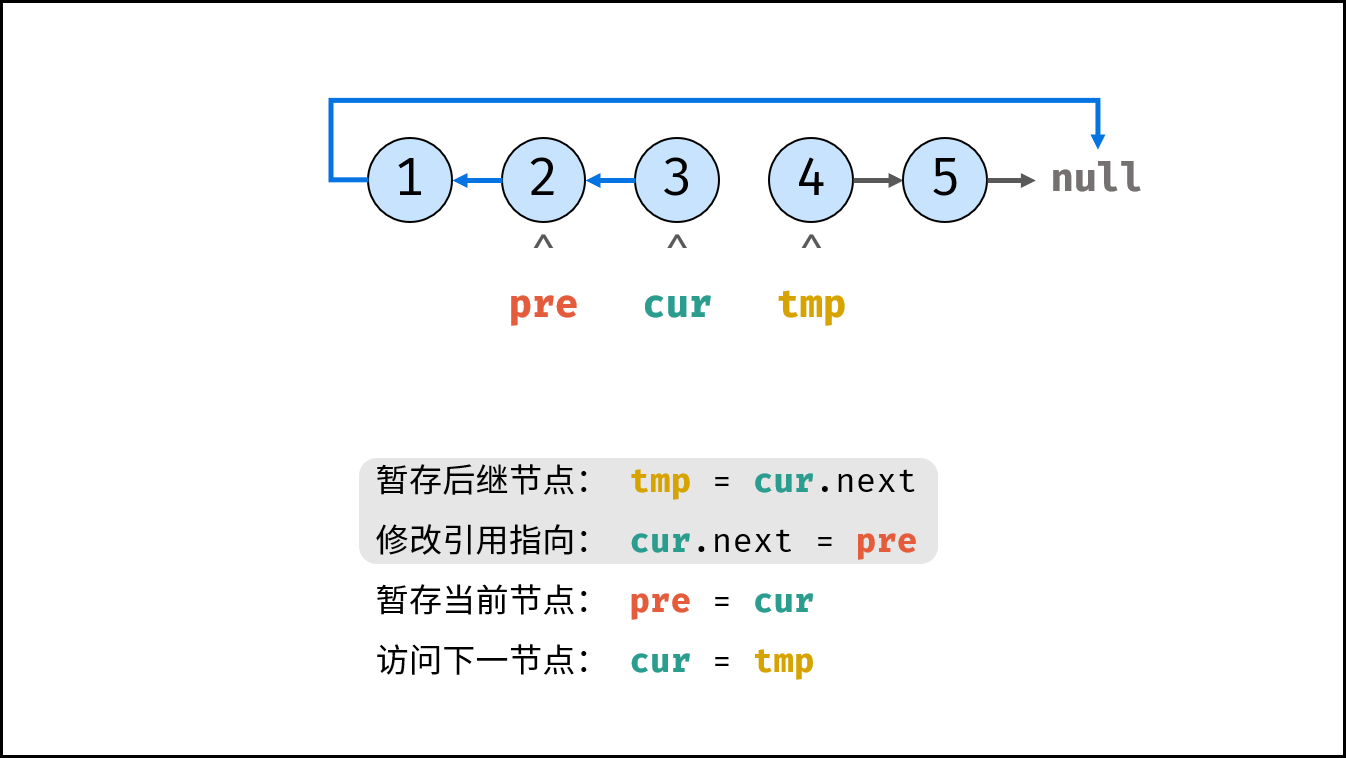<![Picture2.png](https://pic.leetcode-cn.com/1604779288-fMPcDn-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1604779288-jExDGV-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1604779444-fENrGT-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1604779288-GaydTj-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1604779288-gowIkz-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1604779288-VWjYQd-Picture7.png),![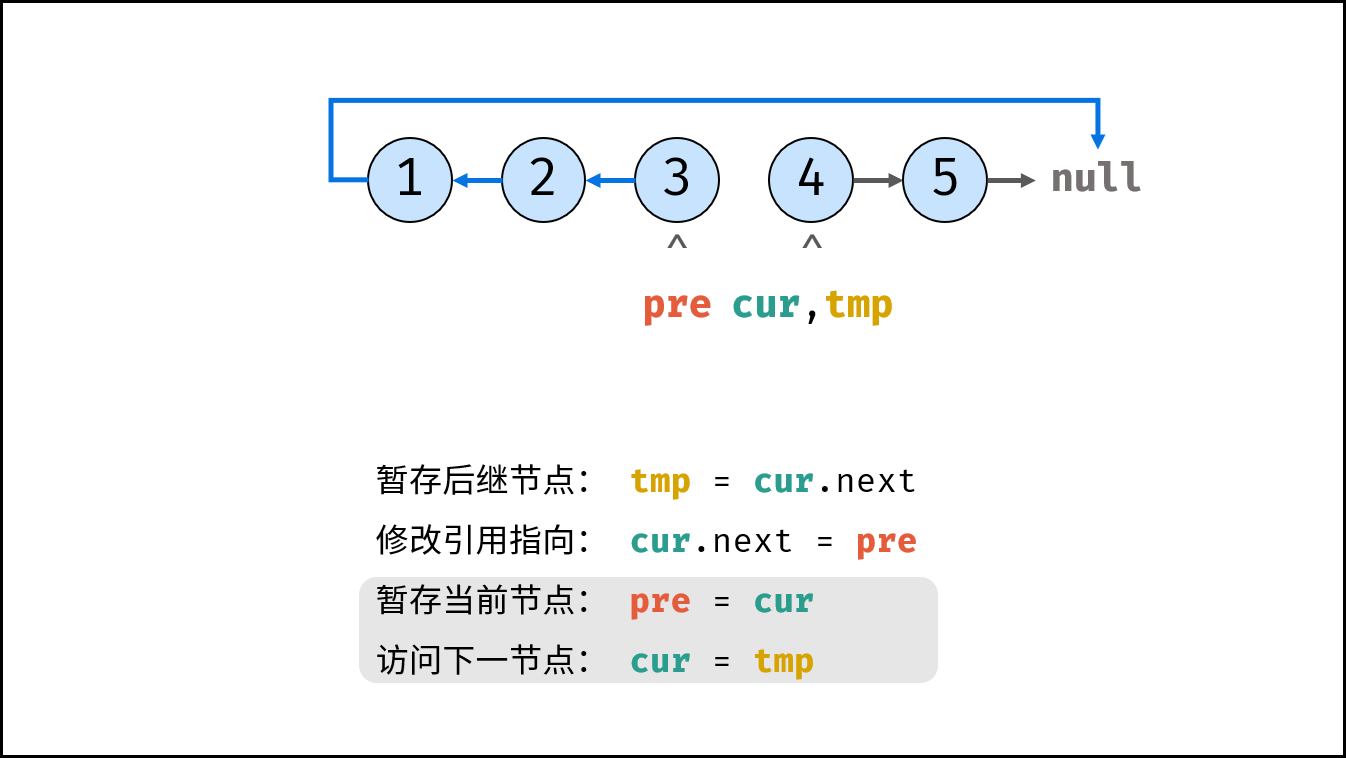Picture8.png](https://pic.leetcode-cn.com/1604779288-DyVPZm-Picture8.png),![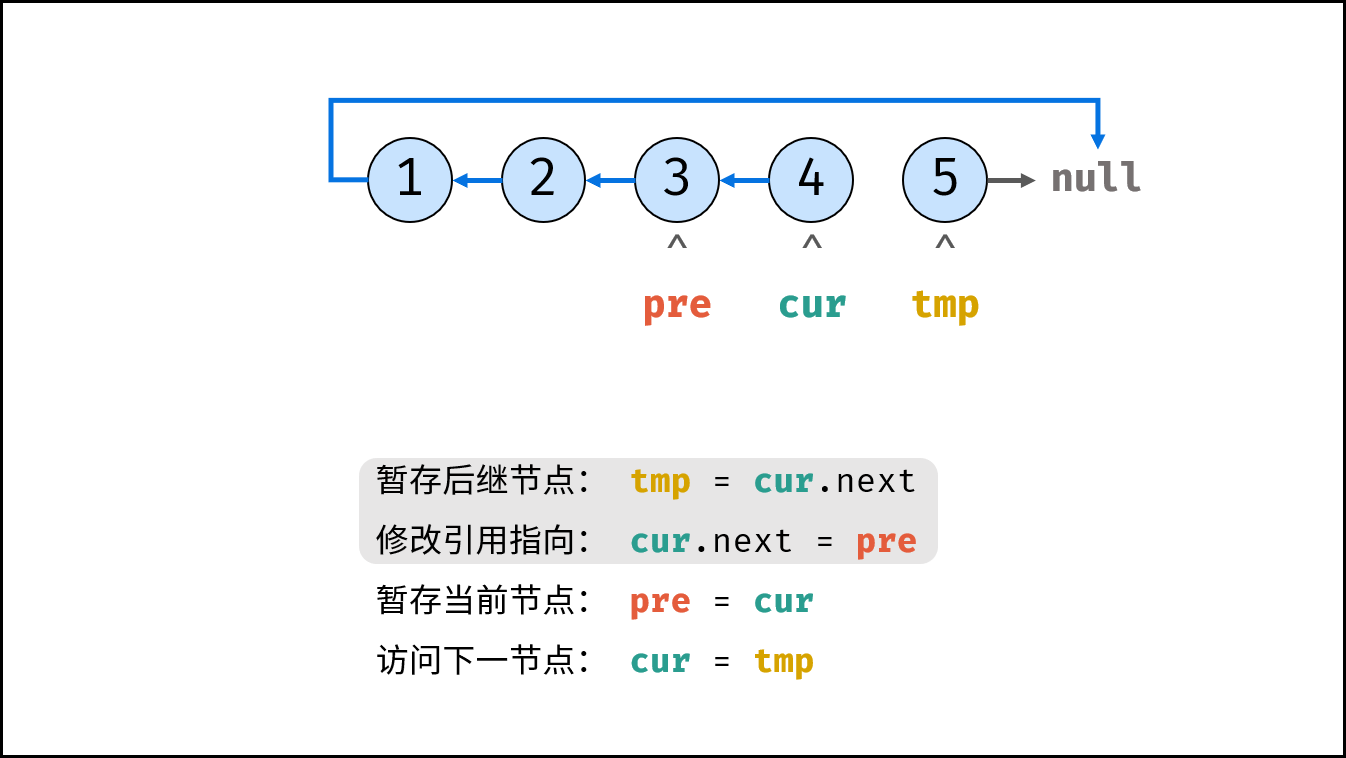Picture9.png](https://pic.leetcode-cn.com/1604779288-yyhJIv-Picture9.png),![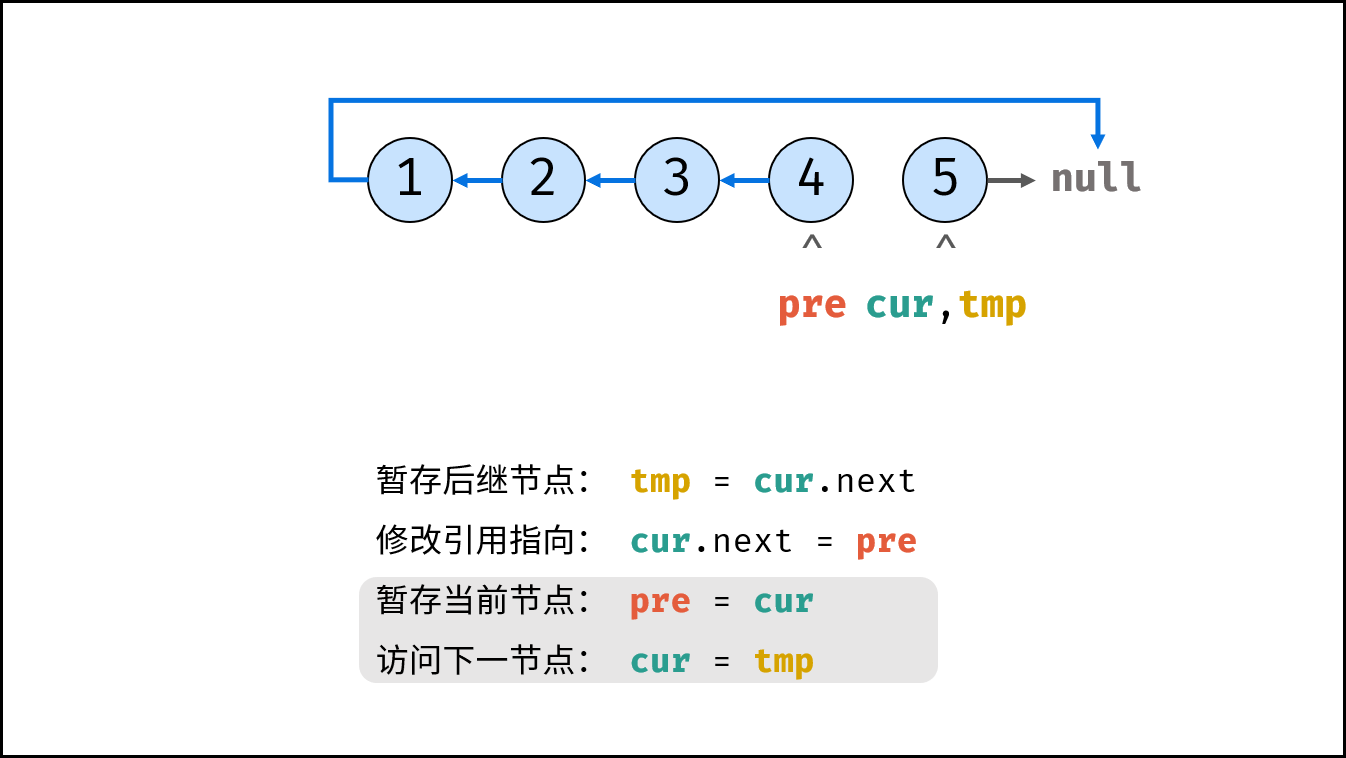Picture10.png](https://pic.leetcode-cn.com/1604779288-nZLbad-Picture10.png),![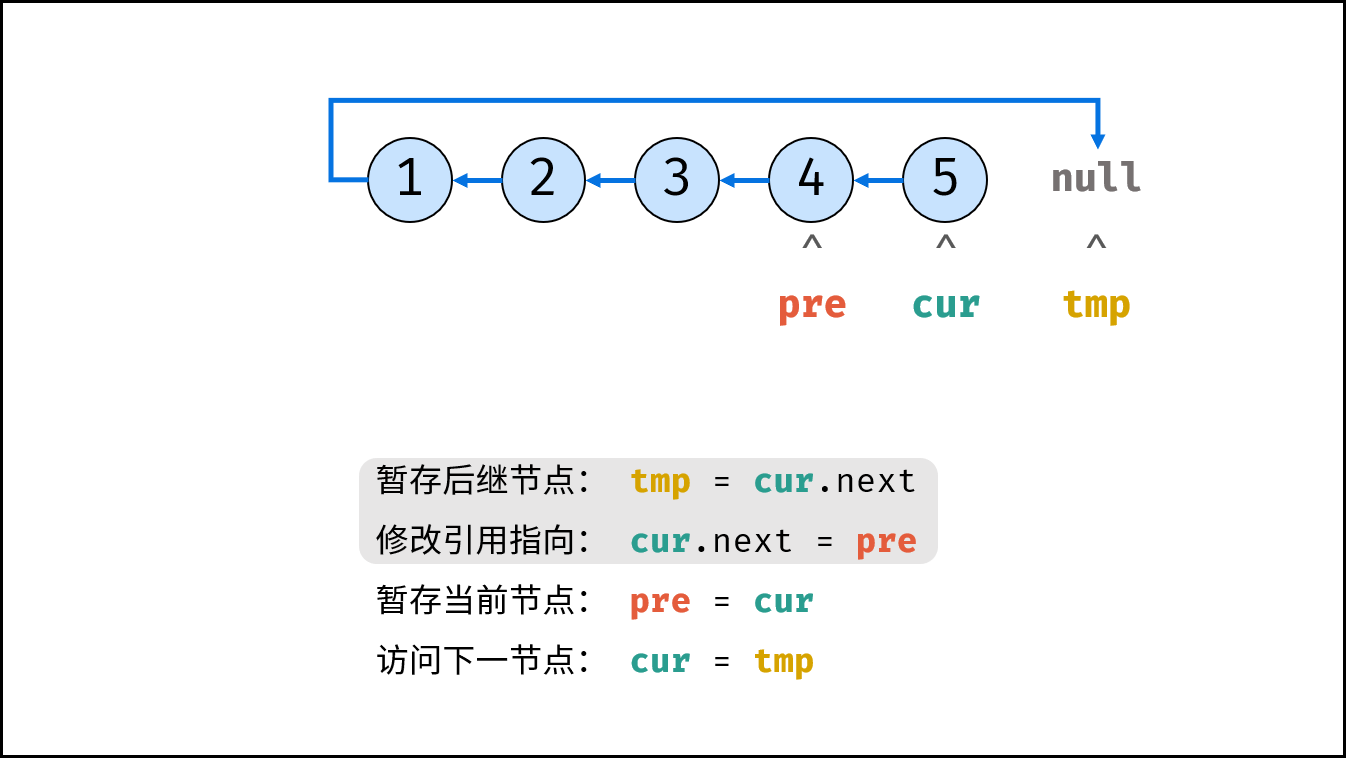Picture11.png](https://pic.leetcode-cn.com/1604779288-OLQNEW-Picture11.png),![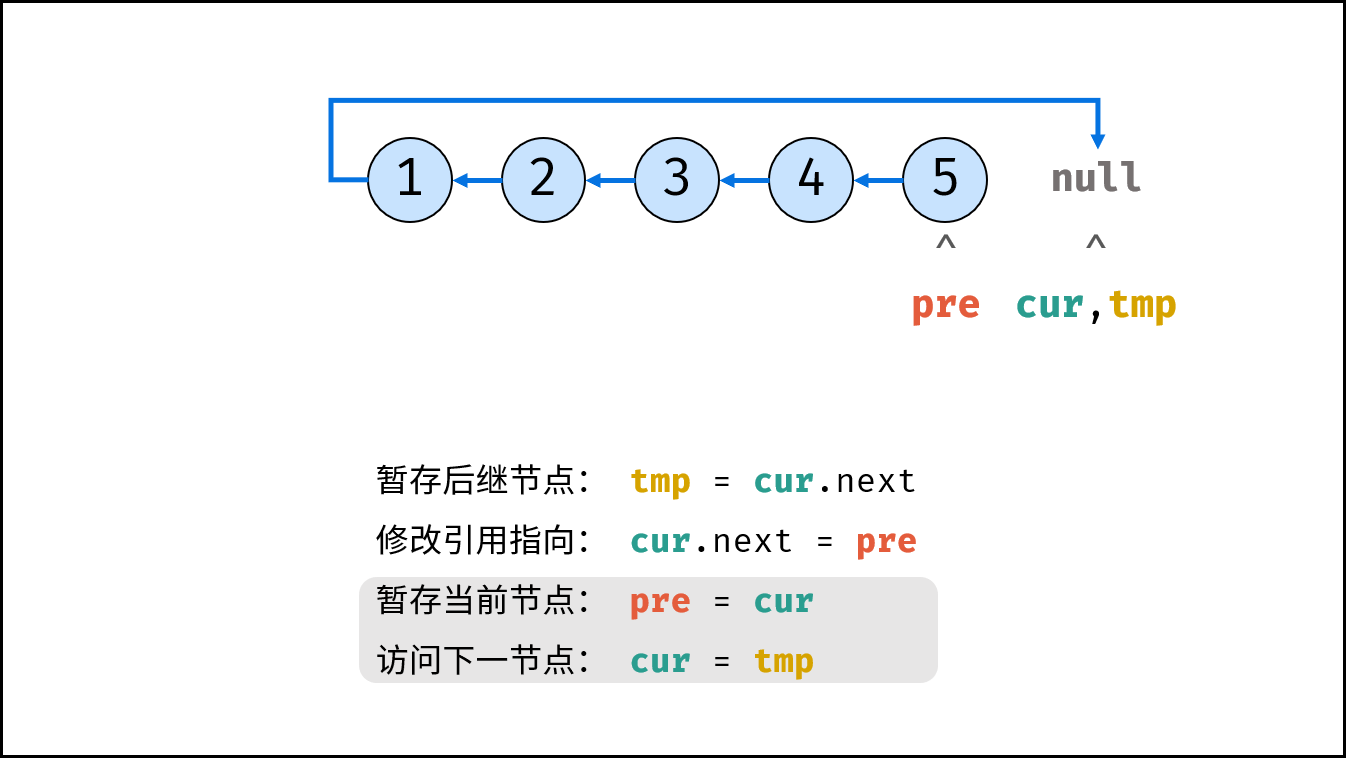Picture12.png](https://pic.leetcode-cn.com/1604779288-MHParU-Picture12.png),![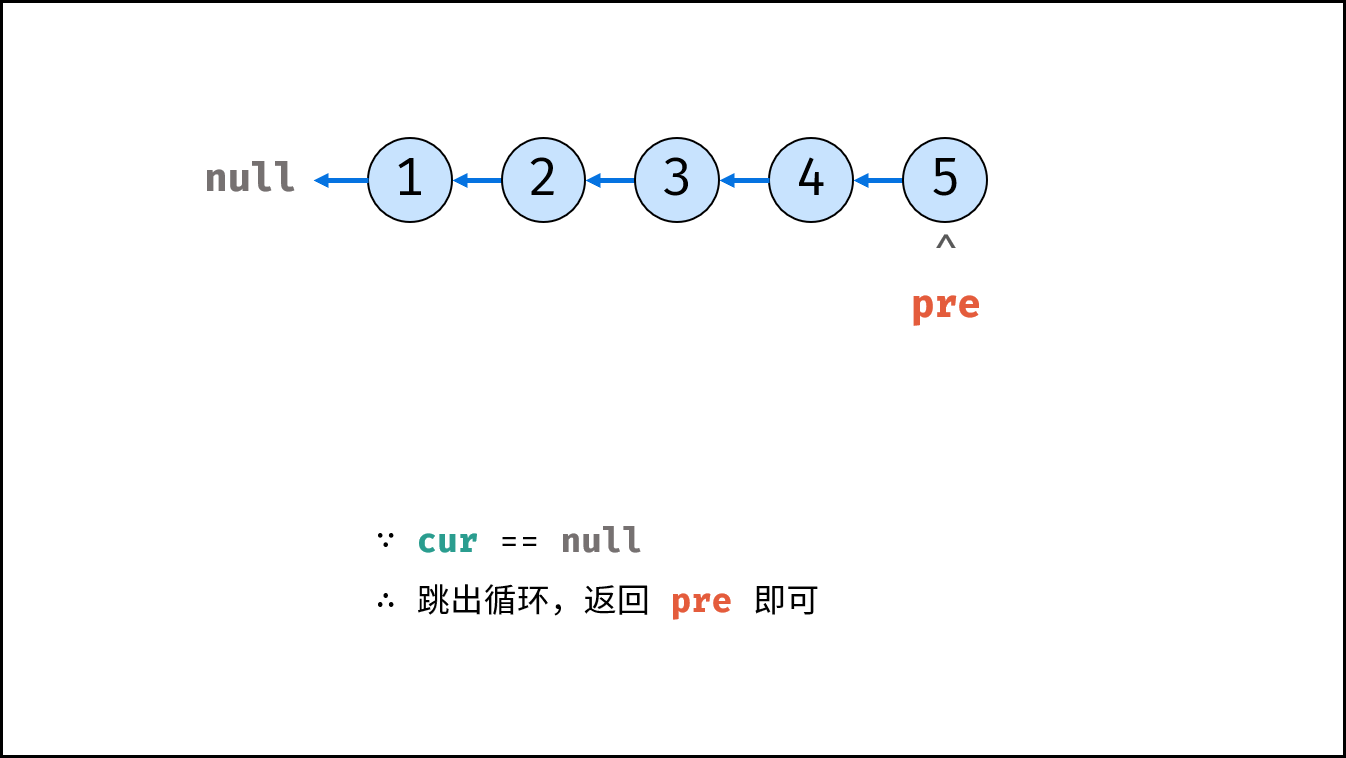Picture13.png](https://pic.leetcode-cn.com/1604779288-CaAUfb-Picture13.png)>
### 代码：
```Python []
class Solution:
def trainningPlan(self, head: ListNode) -> ListNode:
cur, pre = head, None
while cur:
tmp = cur.next # 暂存后继节点 cur.next
cur.next = pre # 修改 next 引用指向
pre = cur # pre 暂存 cur
cur = tmp # cur 访问下一节点
return pre
```
```Java []
class Solution {
public ListNode trainningPlan(ListNode head) {
ListNode cur = head, pre = null;
while(cur != null) {
ListNode tmp = cur.next; // 暂存后继节点 cur.next
cur.next = pre; // 修改 next 引用指向
pre = cur; // pre 暂存 cur
cur = tmp; // cur 访问下一节点
}
return pre;
}
}
```
```C++ []
class Solution {
public:
ListNode* trainningPlan(ListNode* head) {
ListNode *cur = head, *pre = nullptr;
while(cur != nullptr) {
ListNode* tmp = cur->next; // 暂存后继节点 cur.next
cur->next = pre; // 修改 next 引用指向
pre = cur; // pre 暂存 cur
cur = tmp; // cur 访问下一节点
}
return pre;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 遍历链表使用线性大小时间。
- **空间复杂度 $O(1)$ ：** 变量 `pre` 和 `cur` 使用常数大小额外空间。
## 方法二：递归
考虑使用递归遍历链表，当越过尾节点后终止递归，在回溯时修改各节点的 `next` 引用指向。
### `recur(cur, pre)` 递归函数：
1. 终止条件：当 `cur` 为空，则返回尾节点 `pre` （即反转链表的头节点）；
2. 递归后继节点，记录返回值（即反转链表的头节点）为 `res` ；
3. 修改当前节点 `cur` 引用指向前驱节点 `pre` ；
4. 返回反转链表的头节点 `res` ；
### `trainningPlan(head)` 函数：
调用并返回 `recur(head, null)` 。传入 `null` 是因为反转链表后，`head` 节点指向 `null` ；
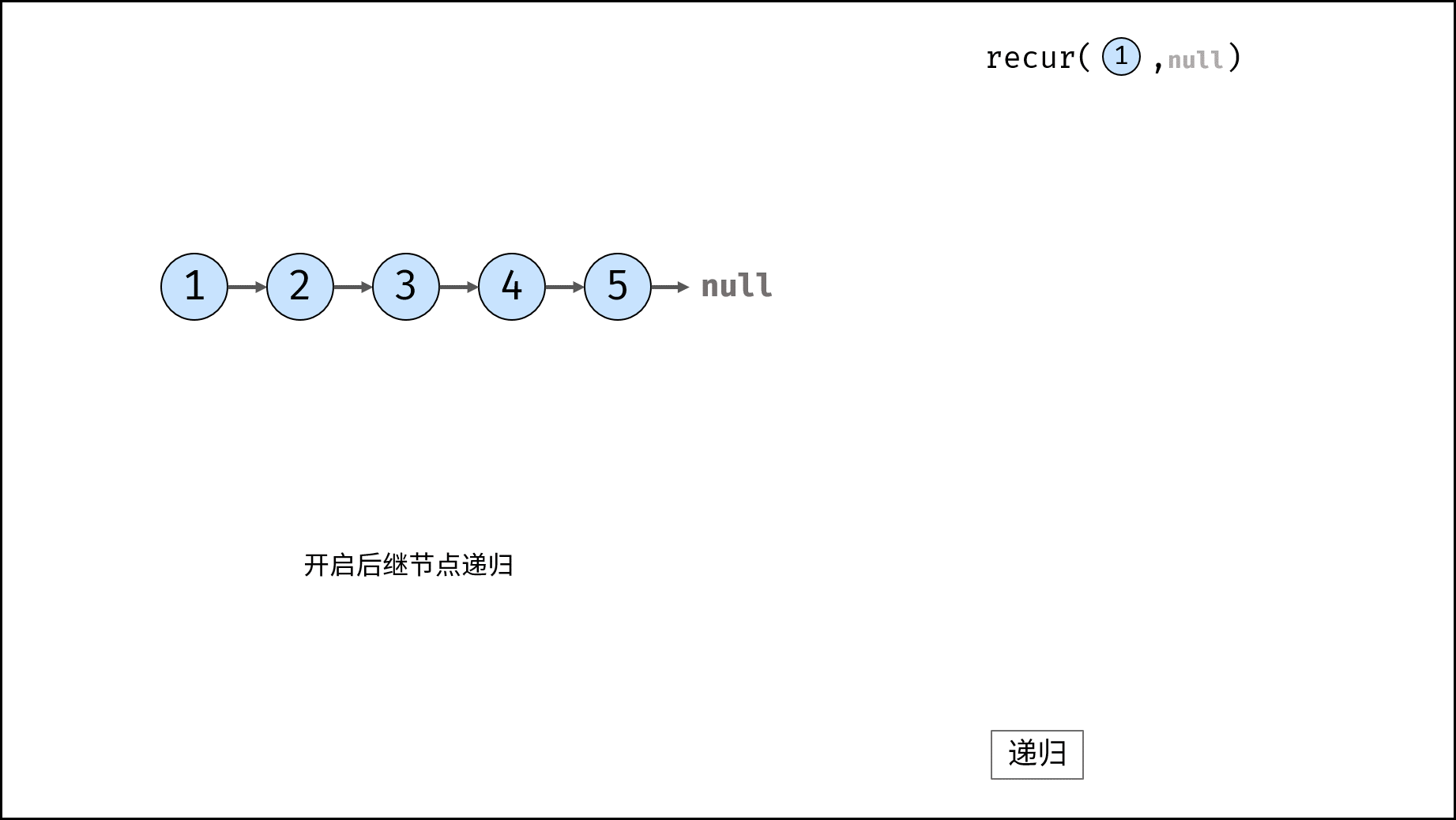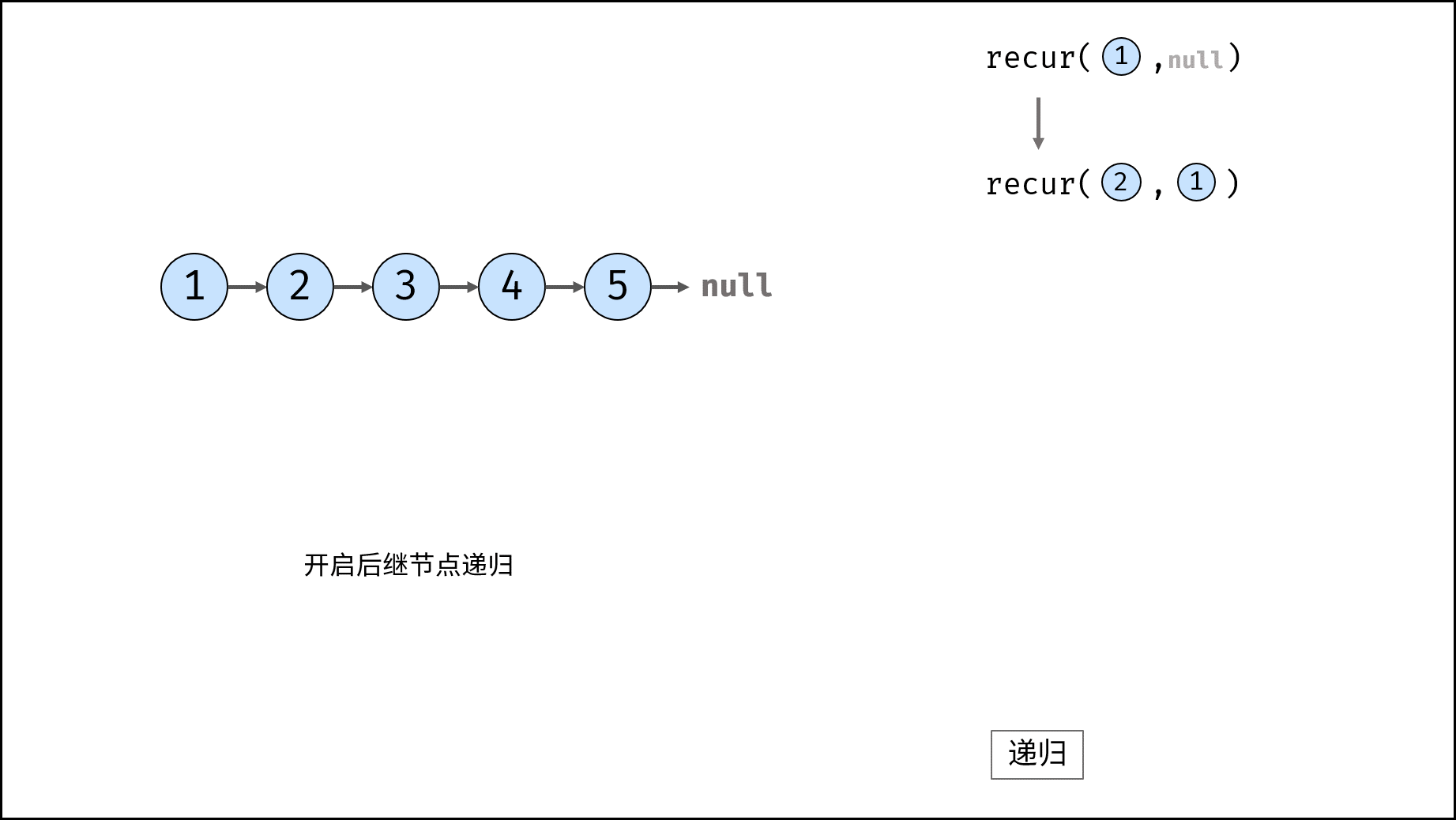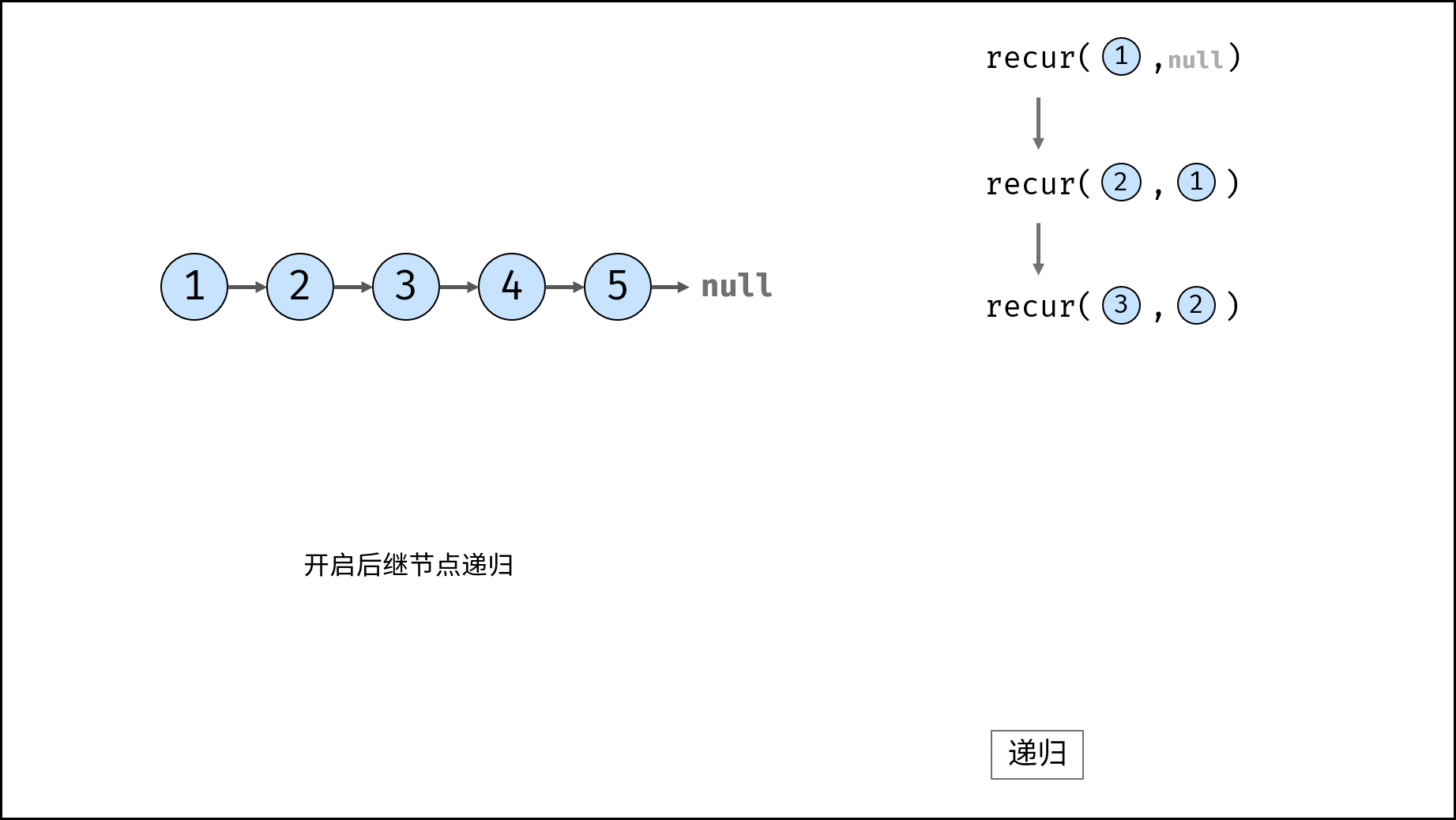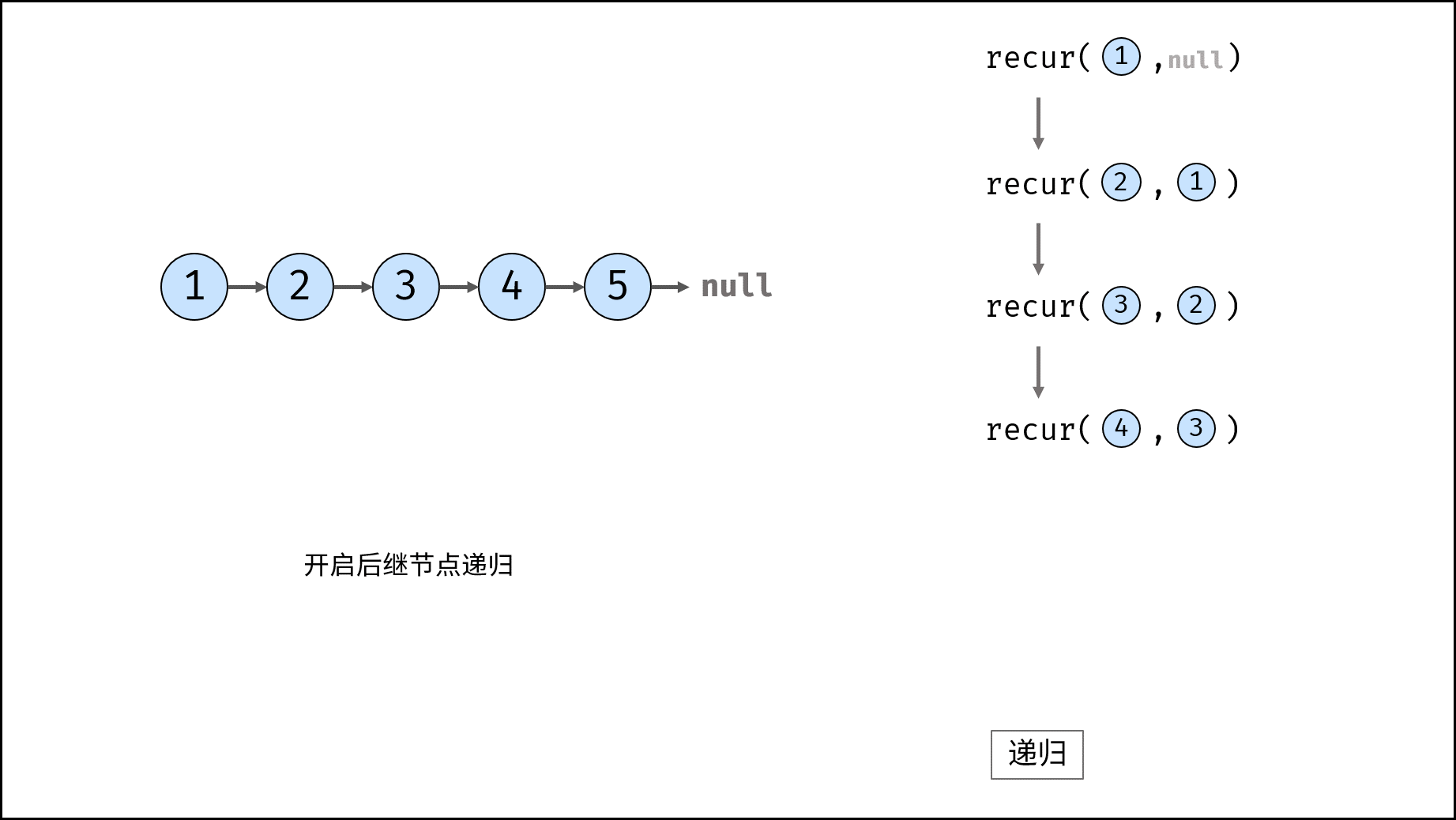<![Picture14.png](https://pic.leetcode-cn.com/1604779288-qqLwjR-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1604779288-ZENdRv-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1604779288-seTNVj-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1604779288-sLdyLs-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1604779288-jxqzsM-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1604779288-ezRpYf-Picture19.png),![Picture20.png](https://pic.leetcode-cn.com/1604779288-CupRFr-Picture20.png),![Picture21.png](https://pic.leetcode-cn.com/1604779288-fEyTvV-Picture21.png),![Picture22.png](https://pic.leetcode-cn.com/1604779288-ZoKASJ-Picture22.png),![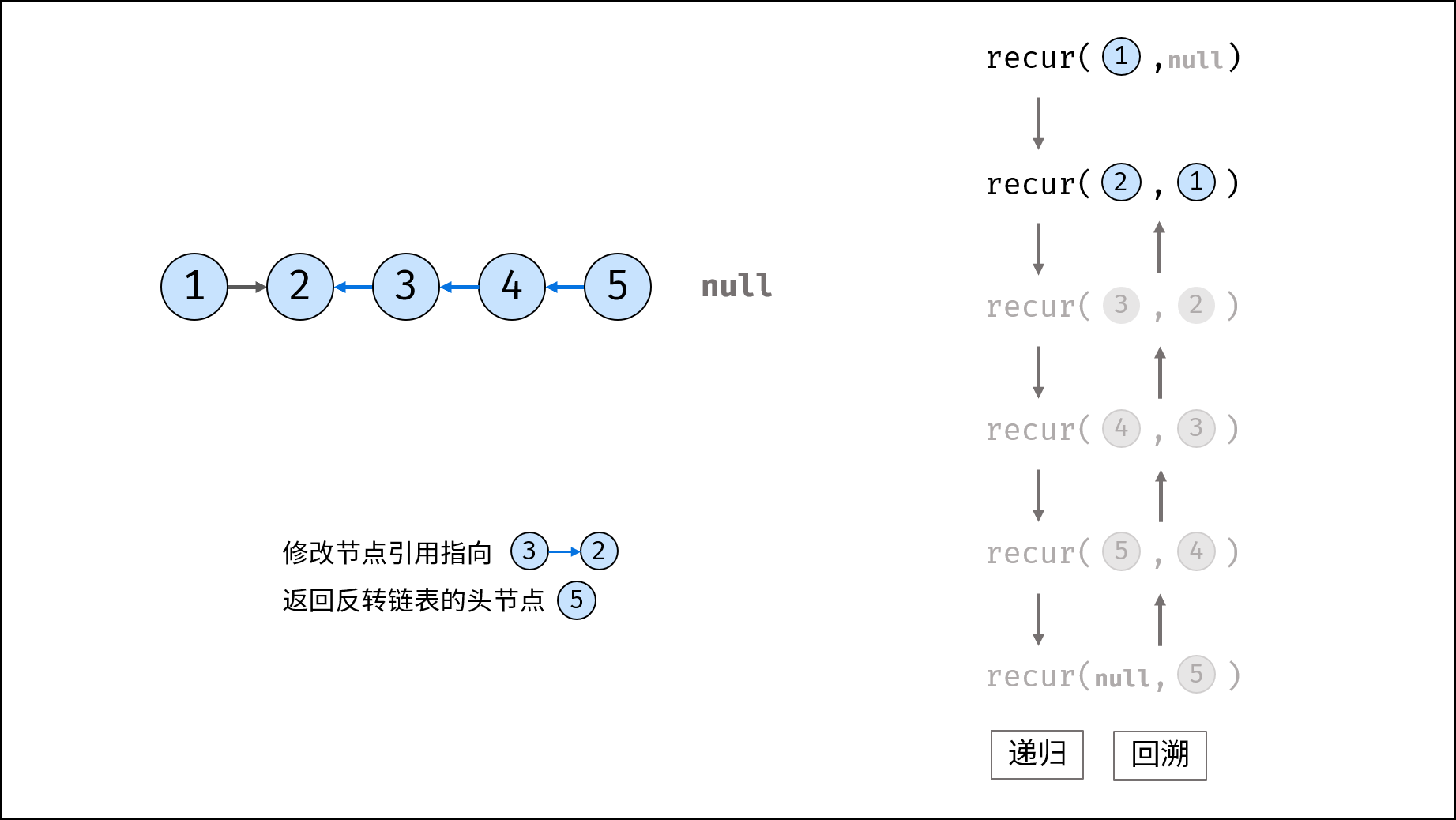Picture23.png](https://pic.leetcode-cn.com/1604779700-EVamXi-Picture23.png),![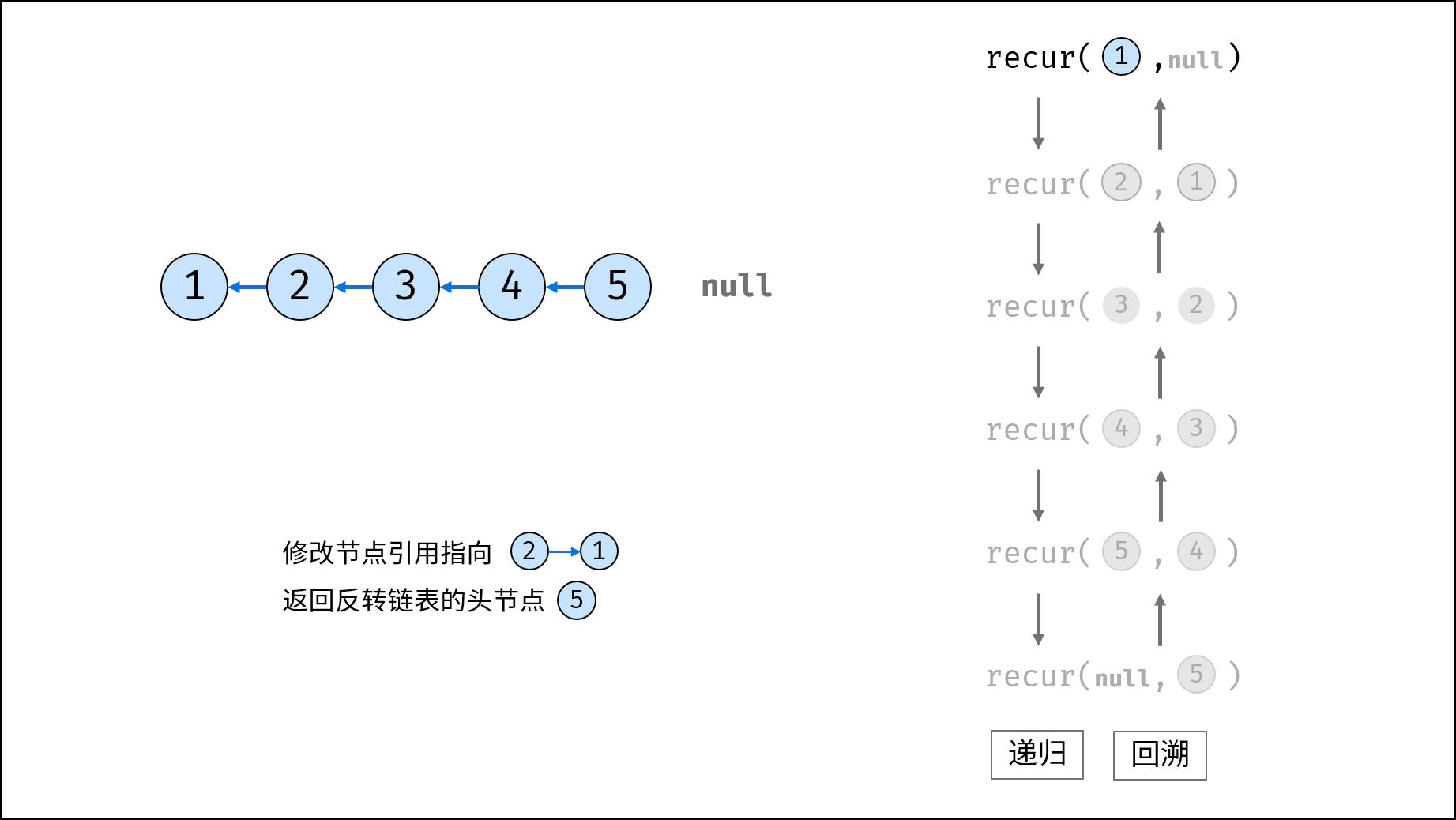Picture24.png](https://pic.leetcode-cn.com/1604779700-APVBqI-Picture24.png),![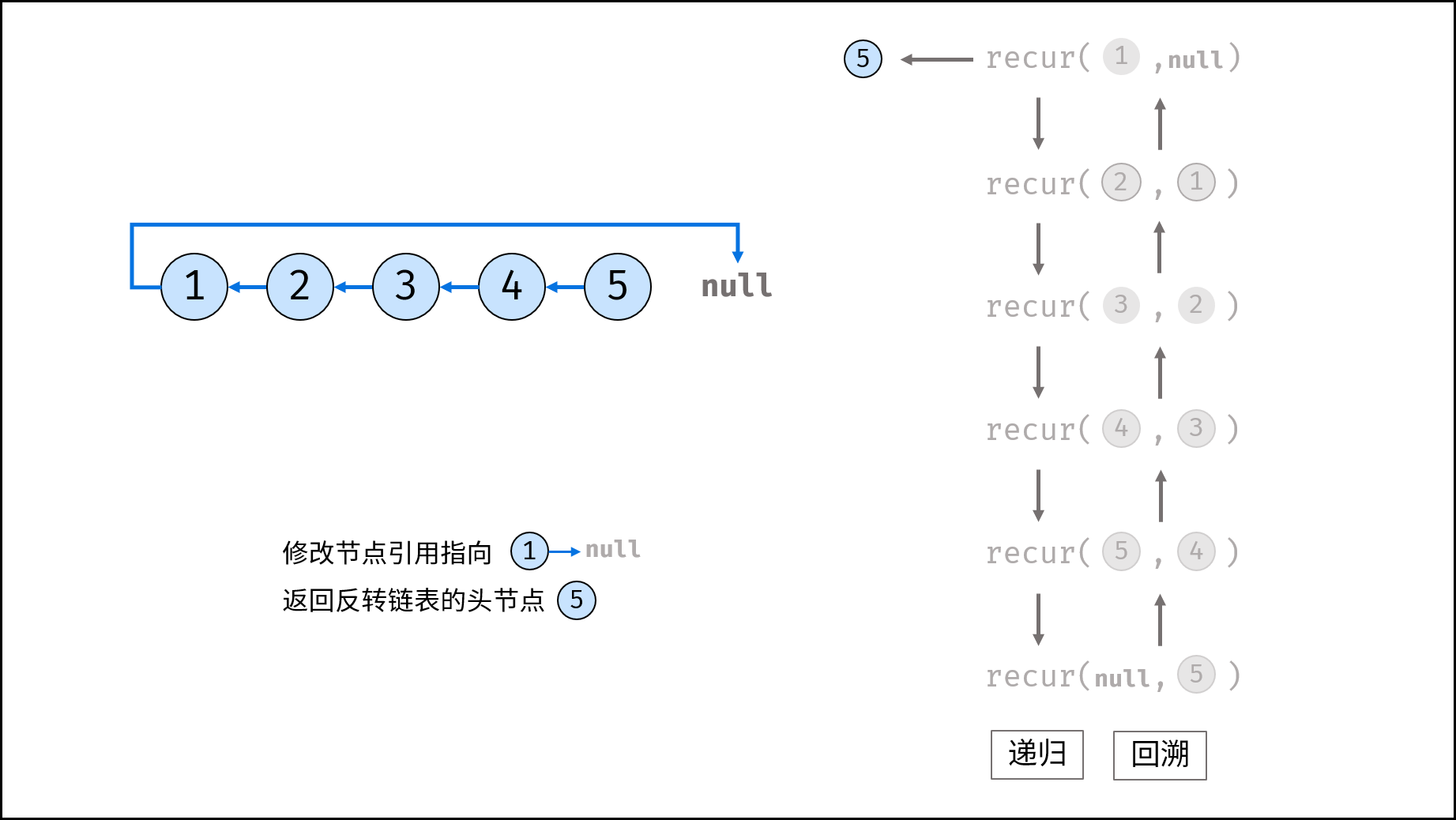Picture25.png](https://pic.leetcode-cn.com/1604779700-zBKSUx-Picture25.png)>
### 代码：
```Python []
class Solution:
def trainningPlan(self, head: ListNode) -> ListNode:
def recur(cur, pre):
if not cur: return pre # 终止条件
res = recur(cur.next, cur) # 递归后继节点
cur.next = pre # 修改节点引用指向
return res # 返回反转链表的头节点
return recur(head, None) # 调用递归并返回
```
```Java []
class Solution {
public ListNode trainningPlan(ListNode head) {
return recur(head, null); // 调用递归并返回
}
private ListNode recur(ListNode cur, ListNode pre) {
if (cur == null) return pre; // 终止条件
ListNode res = recur(cur.next, cur); // 递归后继节点
cur.next = pre; // 修改节点引用指向
return res; // 返回反转链表的头节点
}
}
```
```C++ []
class Solution {
public:
ListNode* trainningPlan(ListNode* head) {
return recur(head, nullptr); // 调用递归并返回
}
private:
ListNode* recur(ListNode* cur, ListNode* pre) {
if (cur == nullptr) return pre; // 终止条件
ListNode* res = recur(cur->next, cur); // 递归后继节点
cur->next = pre; // 修改节点引用指向
return res; // 返回反转链表的头节点
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 遍历链表使用线性大小时间。
- **空间复杂度 $O(N)$ ：** 遍历链表的递归深度达到 $N$ ，系统使用 $O(N)$ 大小额外空间。

88
leetbook_ioa/docs/LCR 142. 训练计划 IV.md Executable file
View File

@@ -0,0 +1,88 @@
## 解题思路：
根据题目描述， 链表 `l1` , `l2` 是 **递增** 的，因此容易想到使用双指针 `l1` 和 `l2` 遍历两链表，根据 `l1.val` 和 `l2.val` 的大小关系确定节点添加顺序，两节点指针交替前进，直至遍历完毕。
**引入伪头节点：** 由于初始状态合并链表中无节点，因此循环第一轮时无法将节点添加到合并链表中。解决方案：初始化一个辅助节点 `dum` 作为合并链表的伪头节点，将各节点添加至 `dum` 之后。
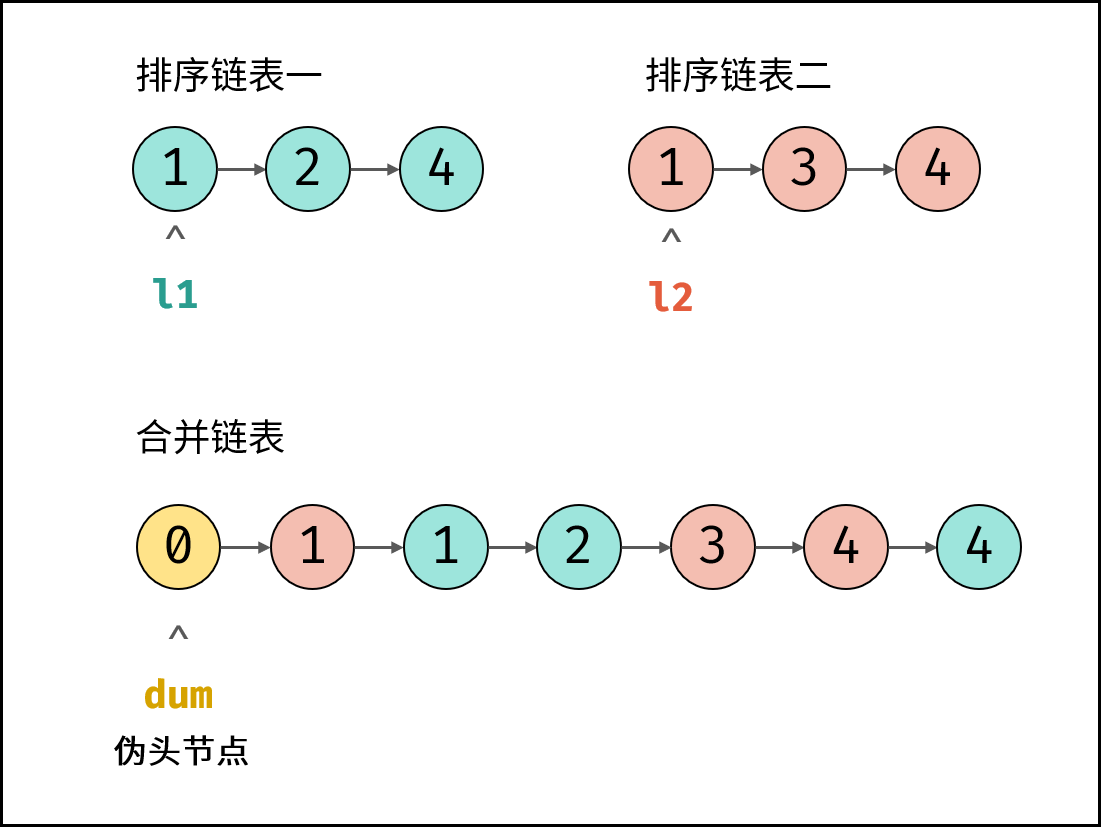![Picture1.png](https://pic.leetcode-cn.com/e4c8c97883da50d81498fd1f1e6cdd575429bd65f9f2babb00dc2b709f7ad8b2-Picture1.png){:align=center width=450}
### 算法流程：
1. **初始化：** 伪头节点 `dum` ，节点 `cur` 指向 `dum` 。
2. **循环合并：** 当 `l1` 或 `l2` 为空时跳出；
1. 当 `l1.val < l2.val` 时： `cur` 的后继节点指定为 `l1` ，并 `l1` 向前走一步；
2. 当 `l1.val >= l2.val` 时： `cur` 的后继节点指定为 `l2` ，并 `l2` 向前走一步 ；
3. 节点 `cur` 向前走一步，即 `cur = cur.next` 。
3. **合并剩余尾部：** 跳出时有两种情况，即 `l1` 为空 **或** `l2` 为空。
1. 若 `l1 != null` ： 将 `l1` 添加至节点 `cur` 之后；
2. 否则： 将 `l2` 添加至节点 `cur` 之后。
4. **返回值：** 合并链表在伪头节点 `dum` 之后，因此返回 `dum.next` 即可。
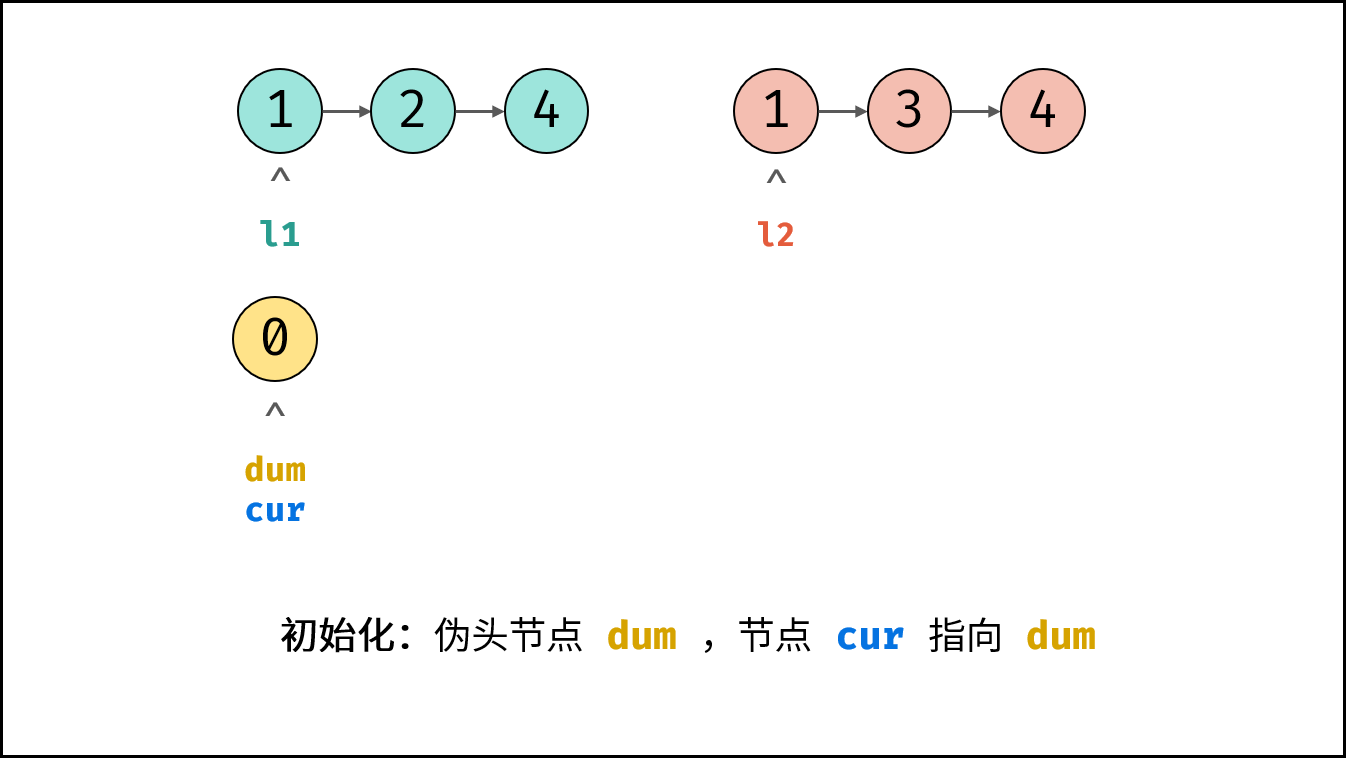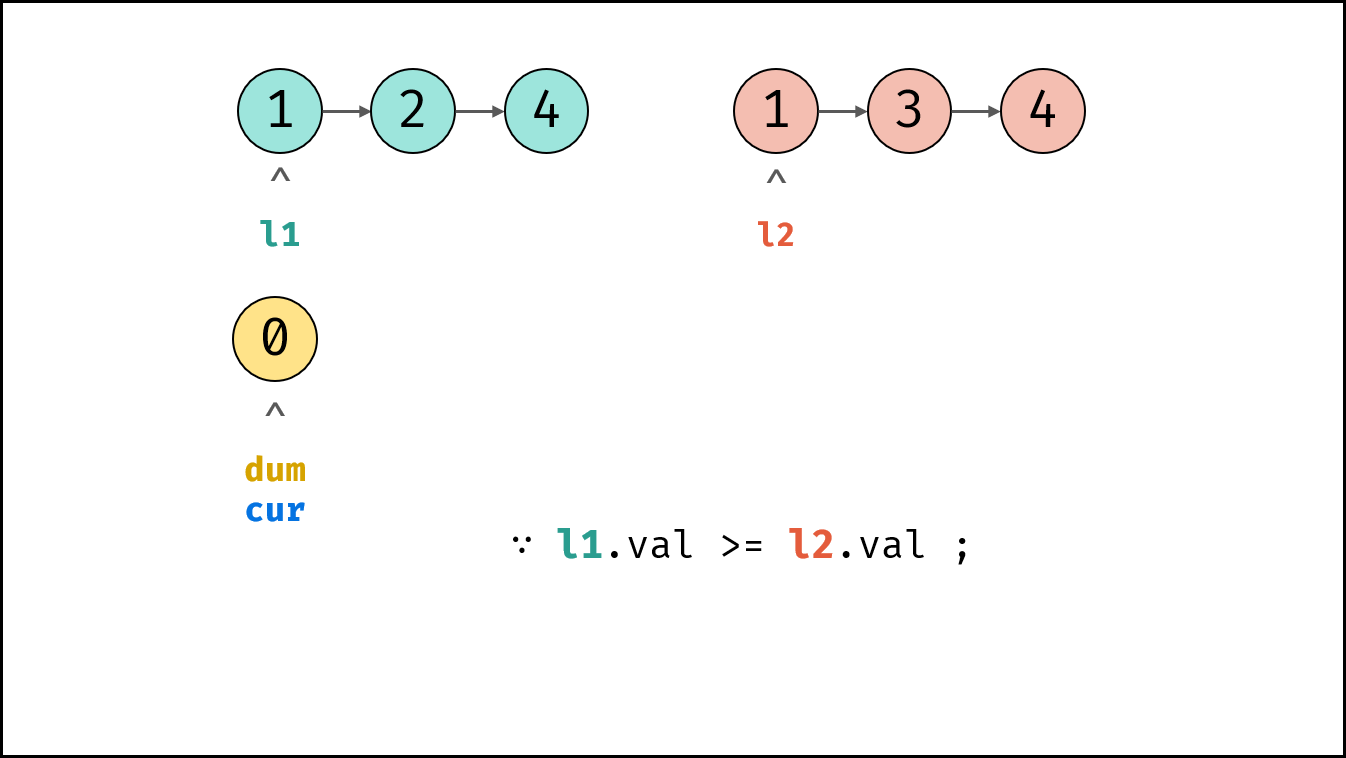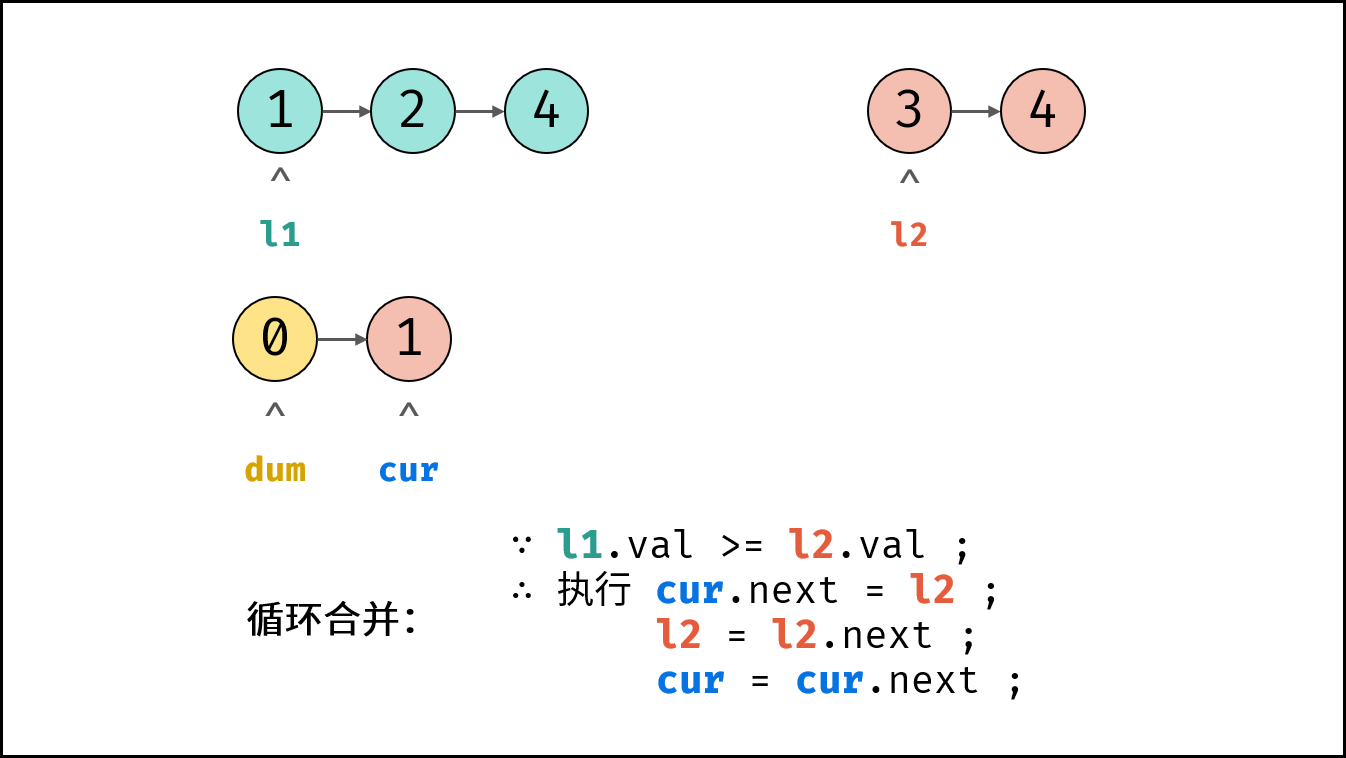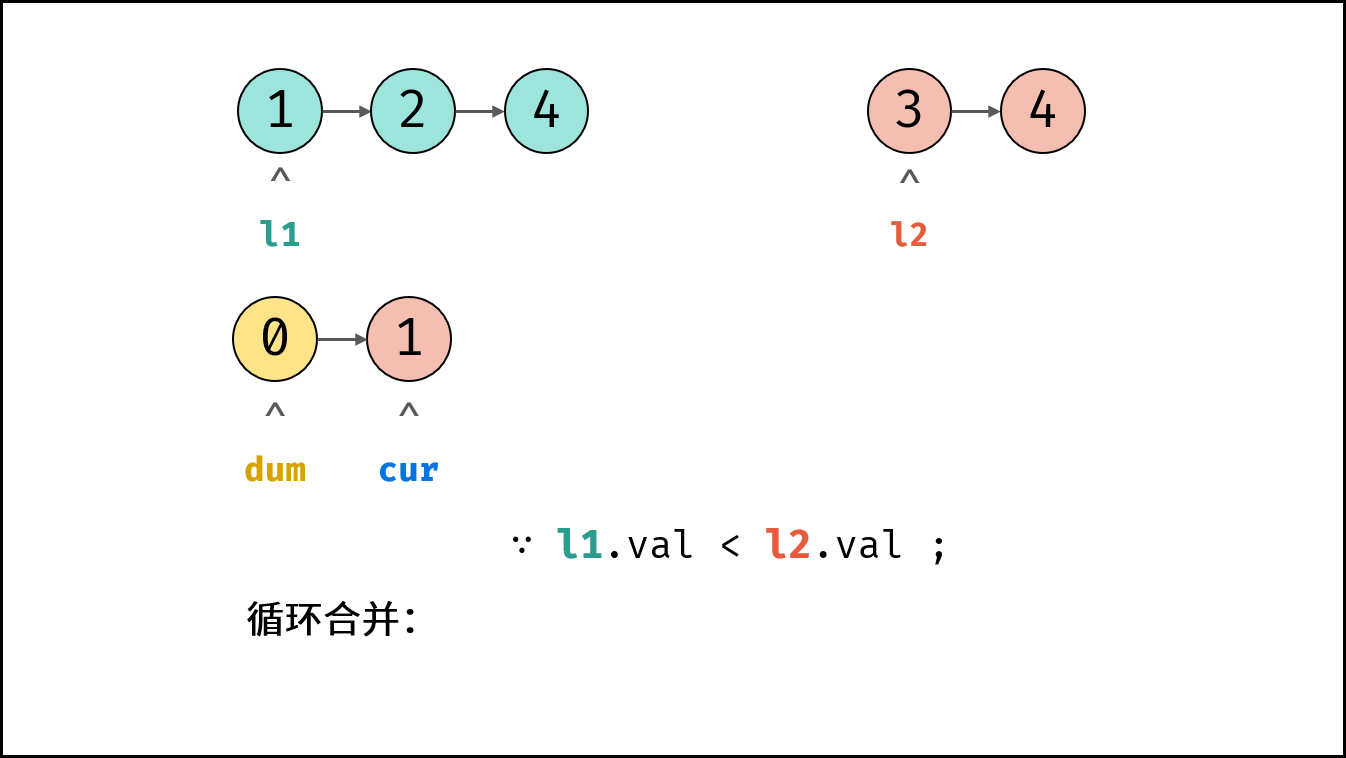<![Picture3.png](https://pic.leetcode-cn.com/05455e3fb731d5a7648e37c8c8457b0ceb150de3b0527a78f634b7a860c18027-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/e3ffa4ba33af05fcf44ea49f25c9e60aef5b3c3d3354153a28e4bfa4d1dc8efc-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/9129290dd20a1e08204ee2163827d1a8221504e793925706bd222c2bf6c0cf73-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/9f8886d4cee6c5388bf0bd6fb10cbdf221cda2d5ef0658cafd59b5ee40b8cf76-Picture6.png),![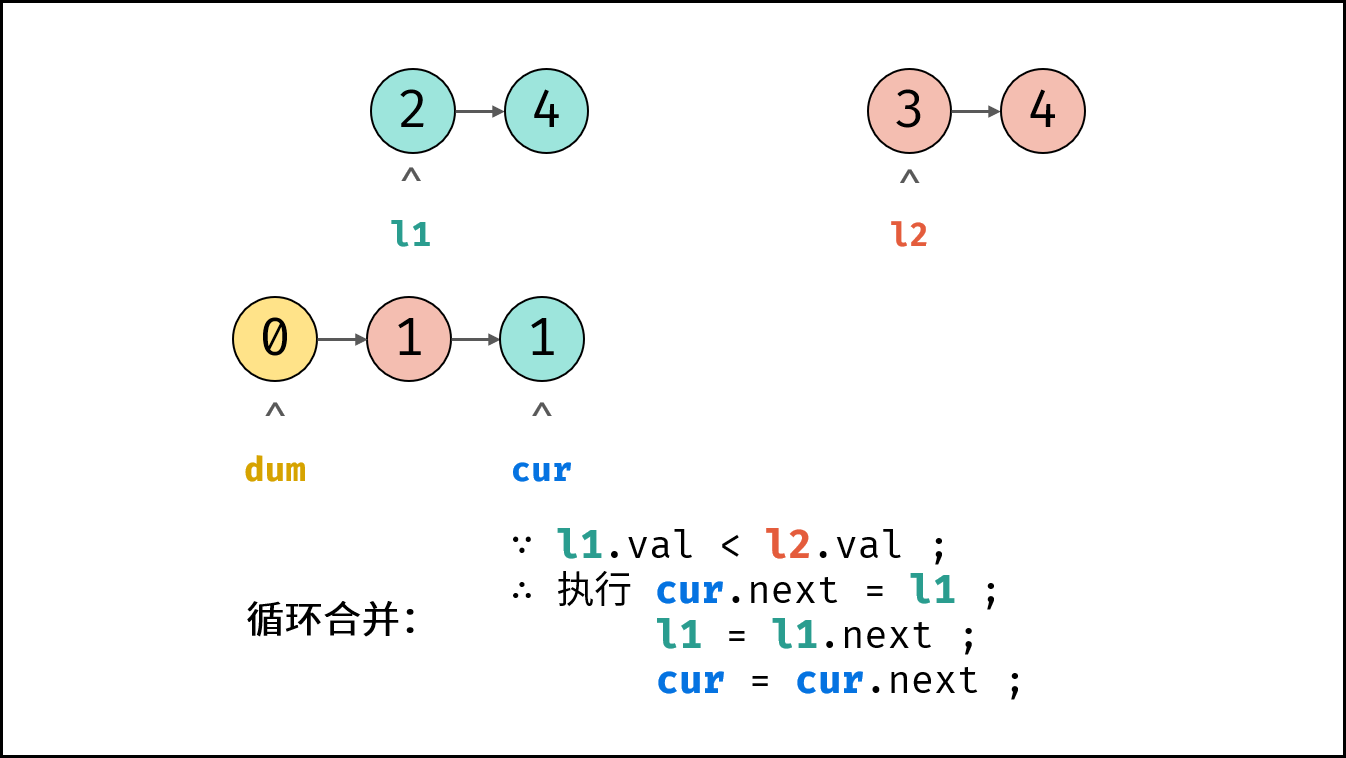Picture7.png](https://pic.leetcode-cn.com/cb95607fe27ce4d33f0be29e3654fb493b3ef30a021b873224557e653b25c83e-Picture7.png),![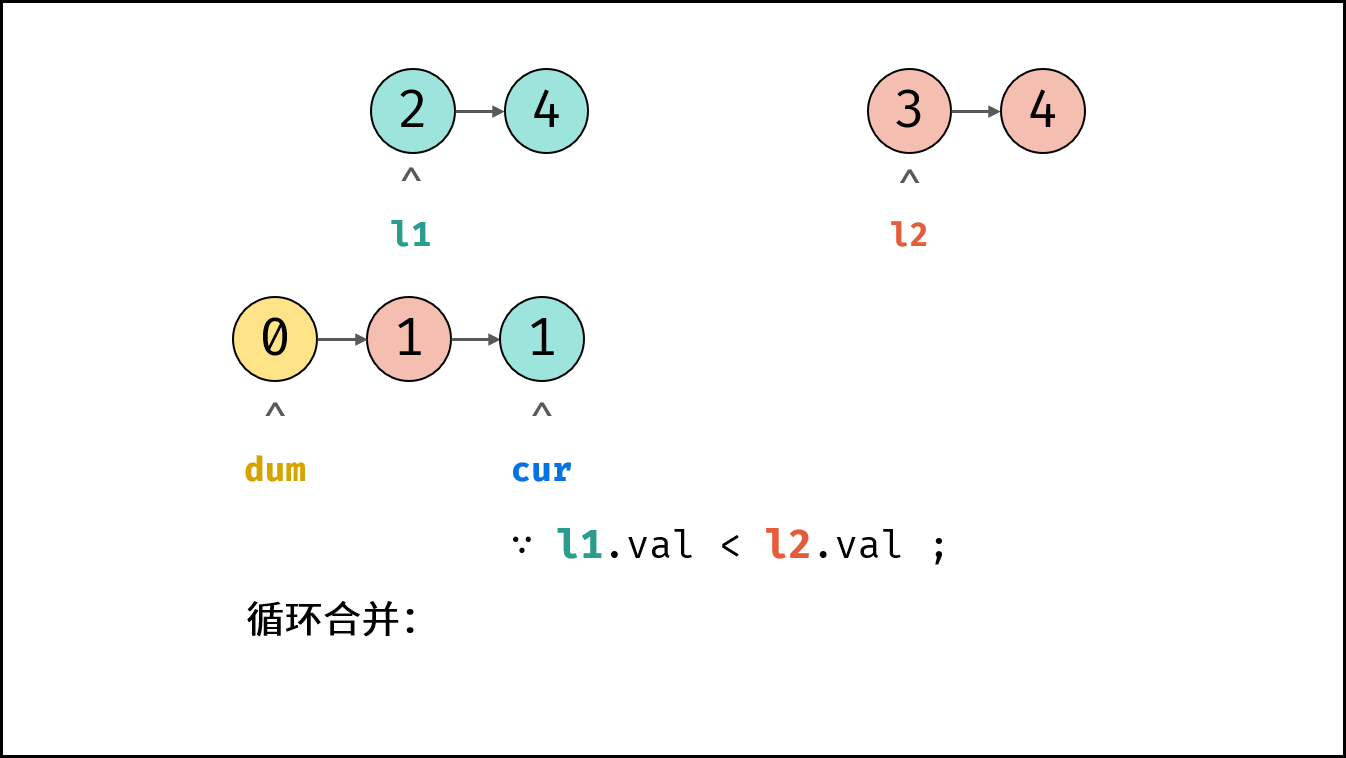Picture8.png](https://pic.leetcode-cn.com/2522ef8e15165bf431023944c21415aacdd5bb5f3a326e054afe719f381a5b7c-Picture8.png),![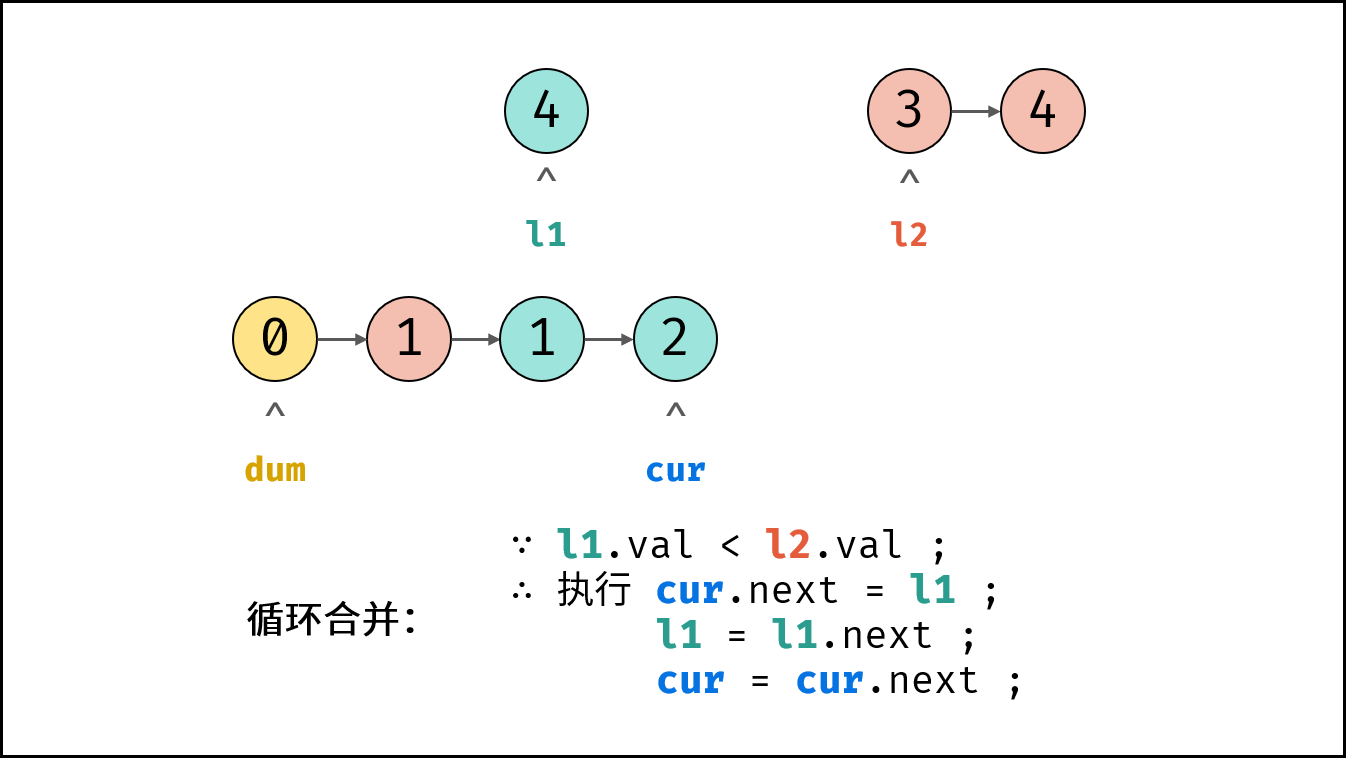Picture9.png](https://pic.leetcode-cn.com/847b824db3b595061ef654d4f0371df28e7a8f1c659c171599272aab737b0aff-Picture9.png),![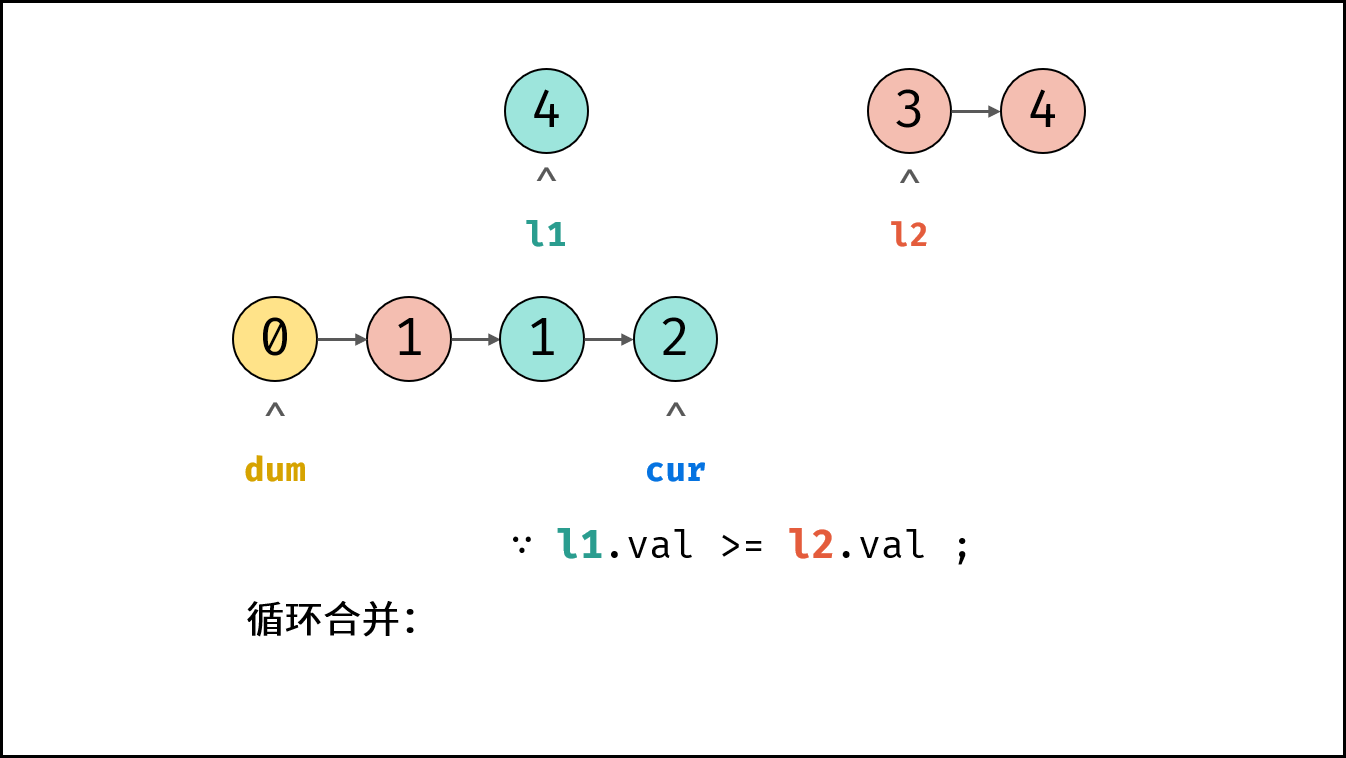Picture10.png](https://pic.leetcode-cn.com/37df2fe55b9cb1f1014a545a5342a1612f7960c45058cc2ed1c11126008c2e76-Picture10.png),![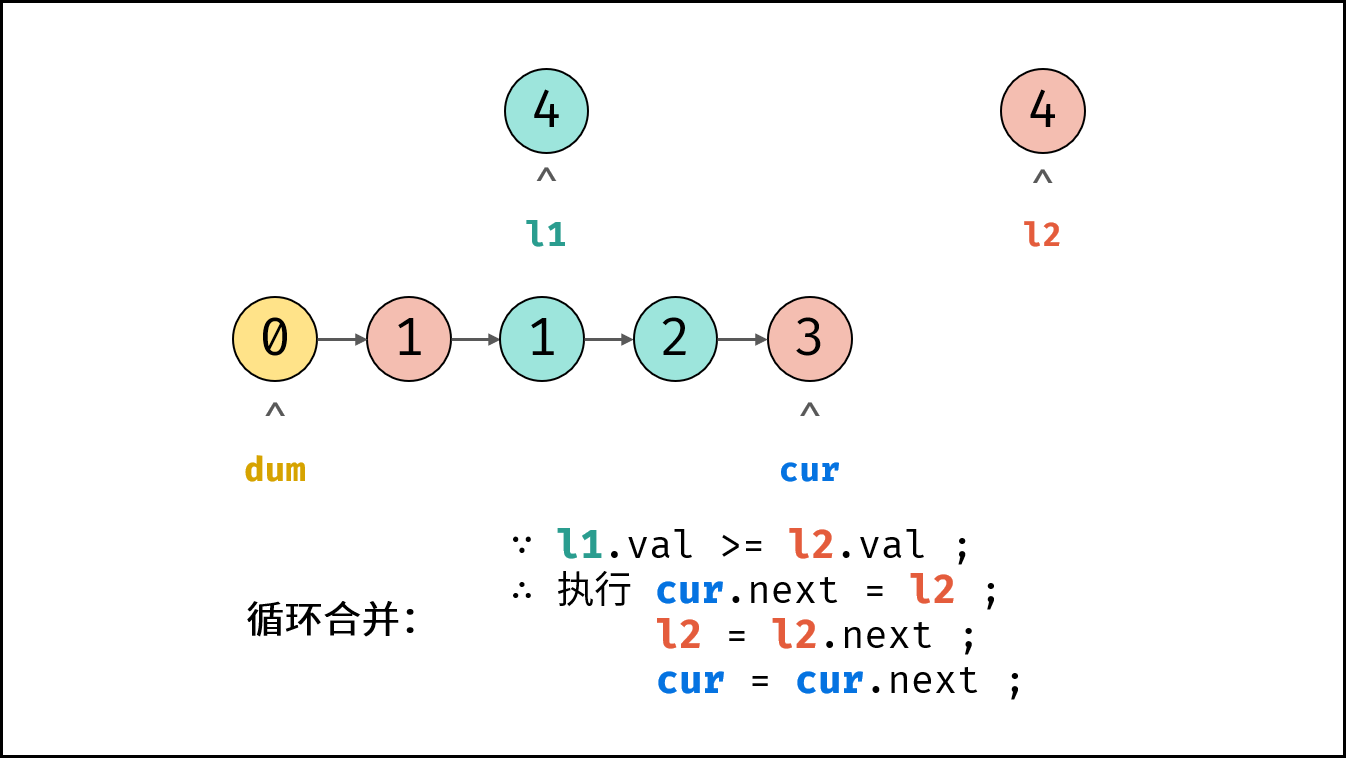Picture11.png](https://pic.leetcode-cn.com/07fd5c0b5fca93187466b8243dd43a16eed603c53a3e6582b7e7eaa1fe32c74c-Picture11.png),![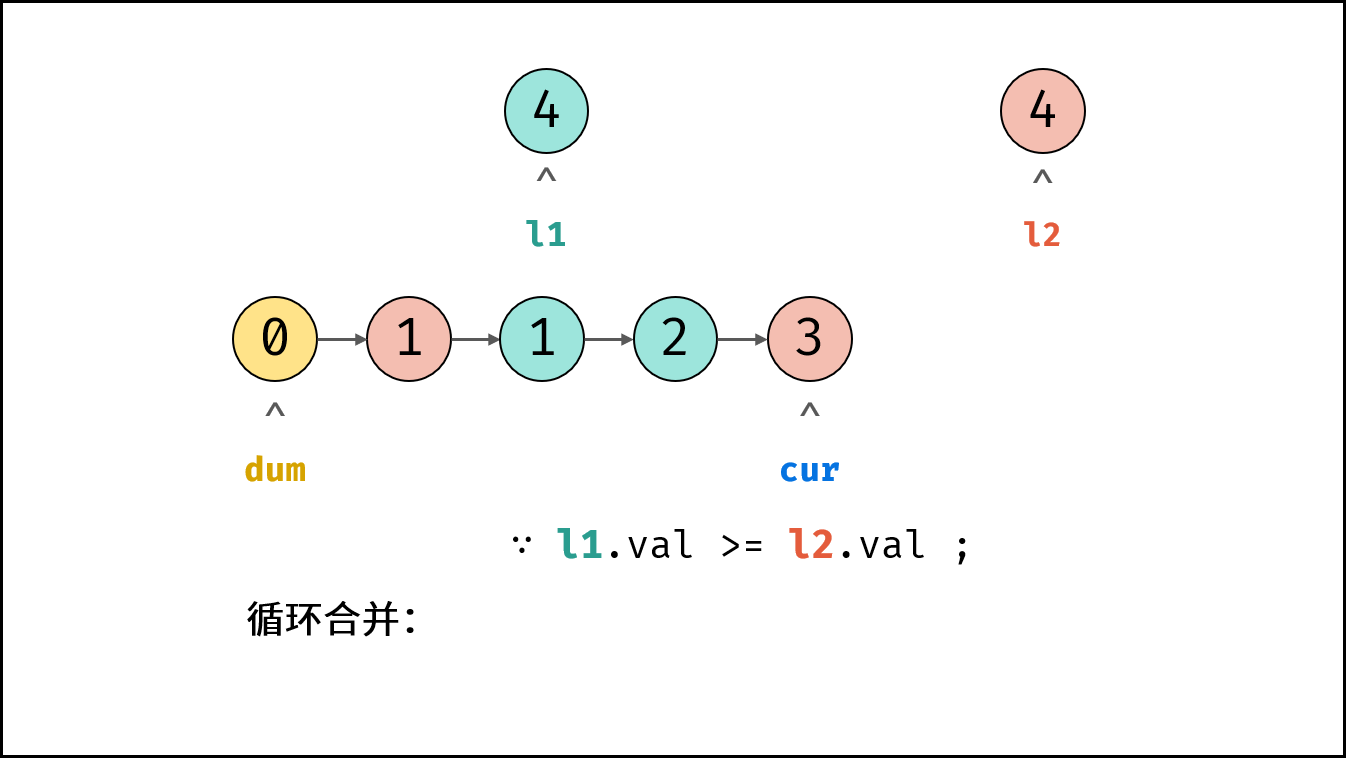Picture12.png](https://pic.leetcode-cn.com/3b7c0eb170a0cbcb6b82f3f1f8d6847edaaa9a7a92c3cb7a6c7c2e48f5fa8e9f-Picture12.png),![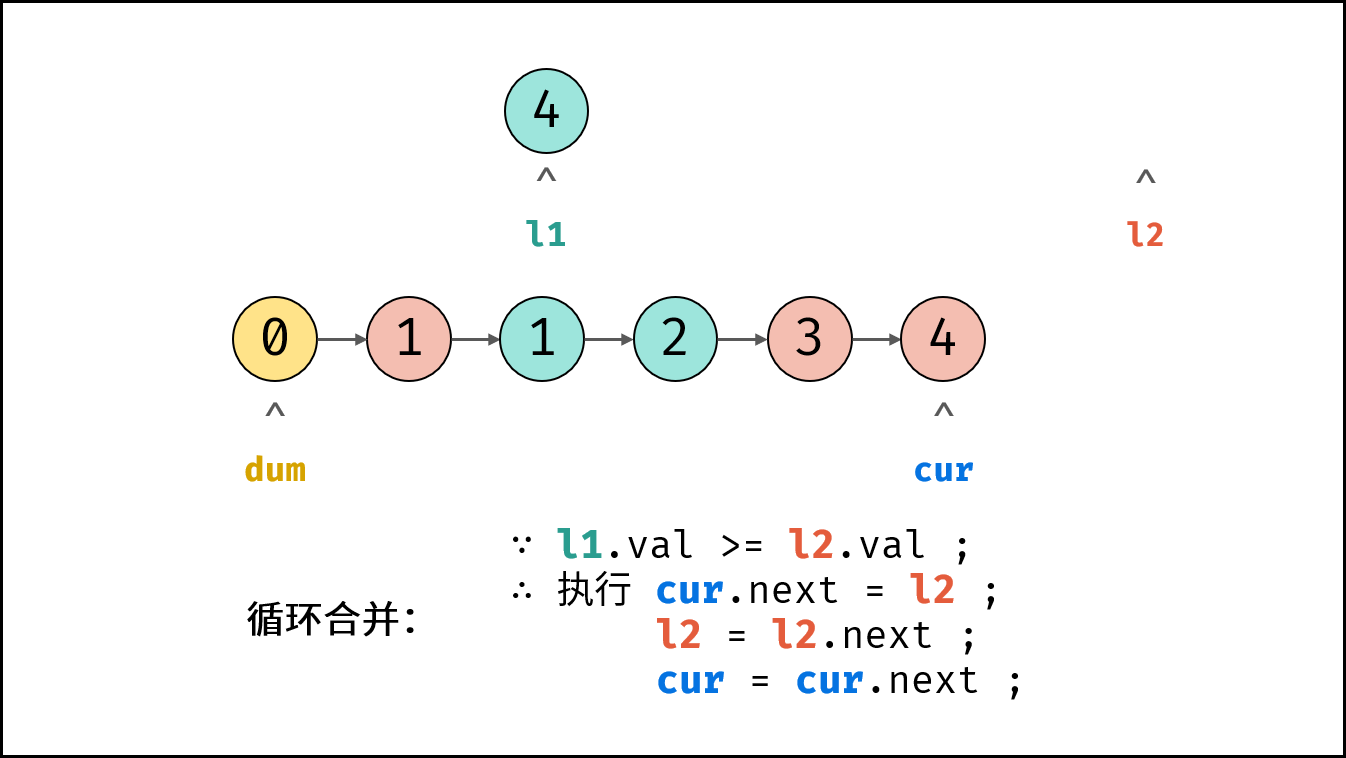Picture13.png](https://pic.leetcode-cn.com/a205af9de048c533b61719f86f64b3df6b91ad3b61343d6111439dca86e65110-Picture13.png),![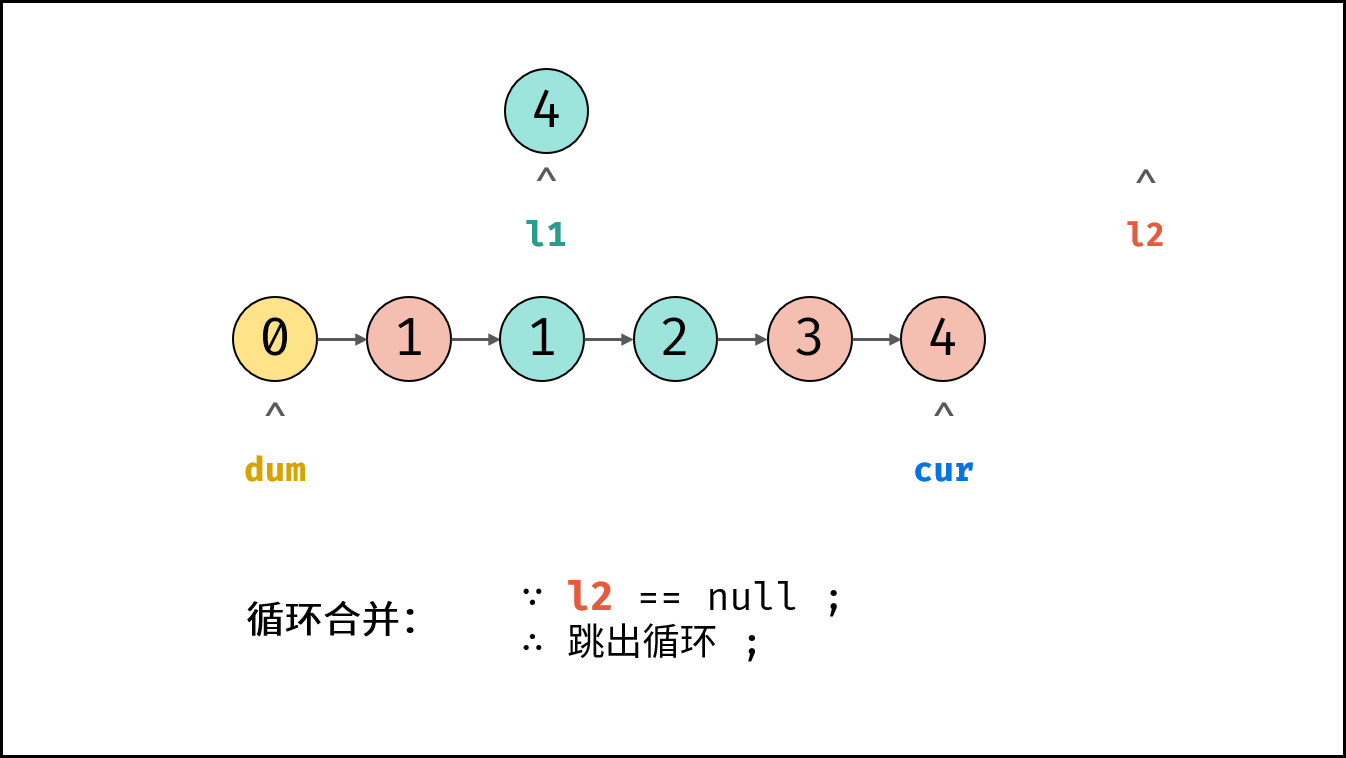Picture14.png](https://pic.leetcode-cn.com/a92a8e0154079d0aafed45c6a5a5f72079bf05c2246c9655f9c7e593eaebdaf1-Picture14.png),![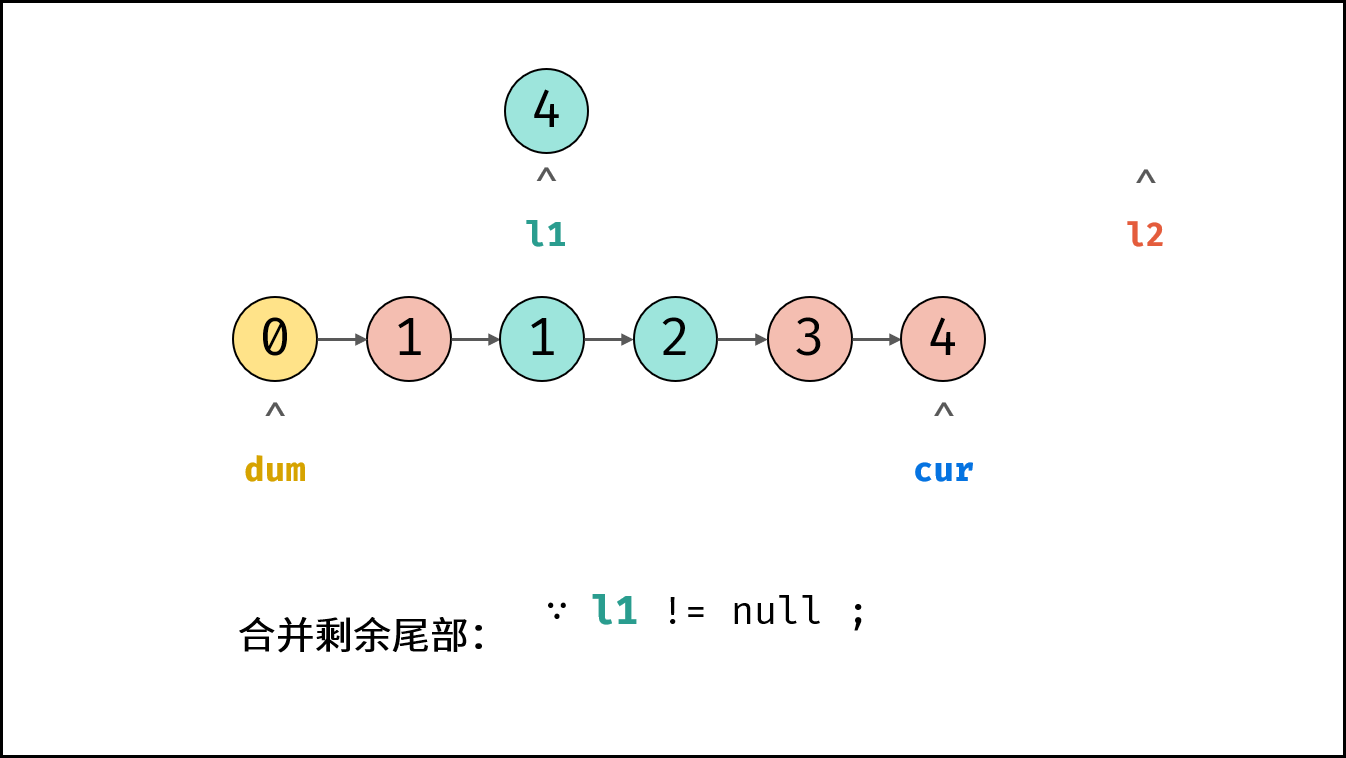Picture15.png](https://pic.leetcode-cn.com/e3f9ea9e458d4fbe1e79002648df4b317c14a56426baa3b417078ead13b1537b-Picture15.png),![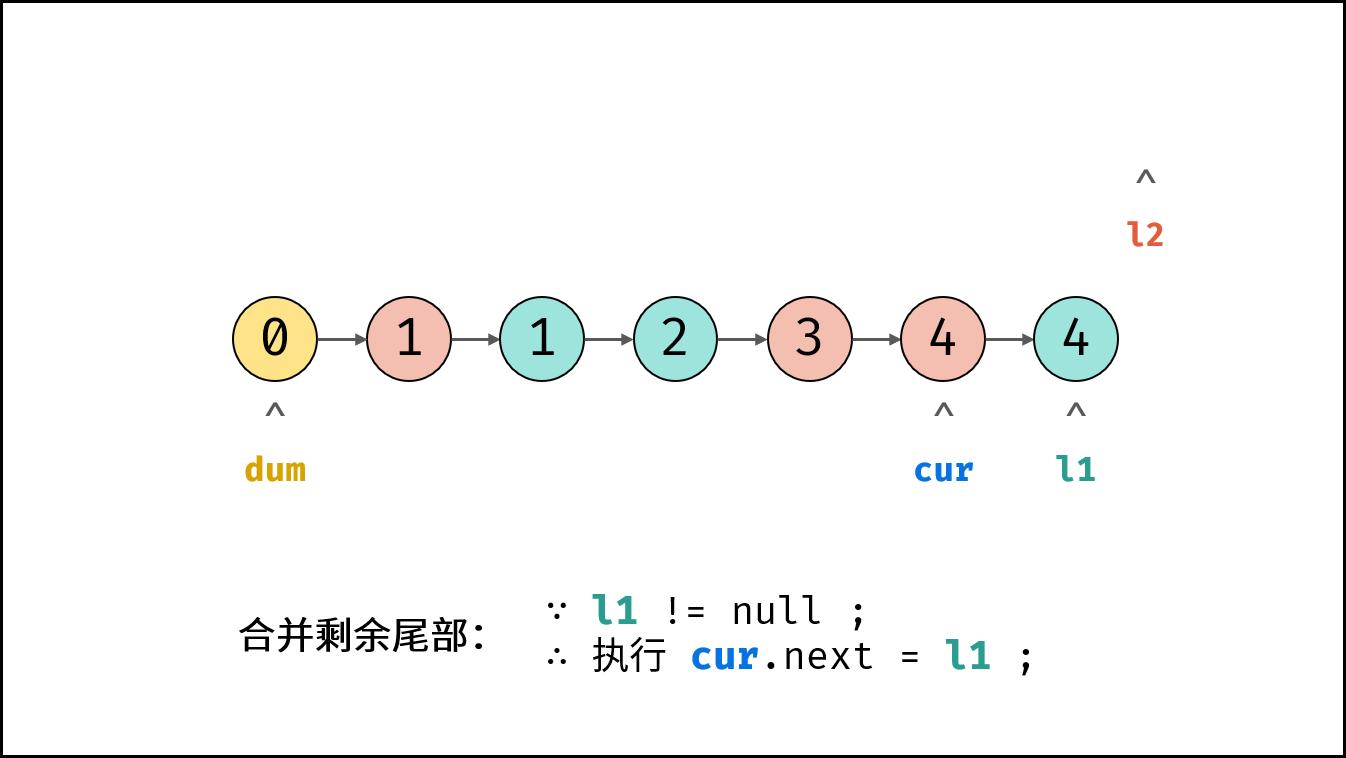Picture16.png](https://pic.leetcode-cn.com/16d64263051da9ac16aafec27694f8c925c5f4f0cc854e494ce21b3065f4411f-Picture16.png),![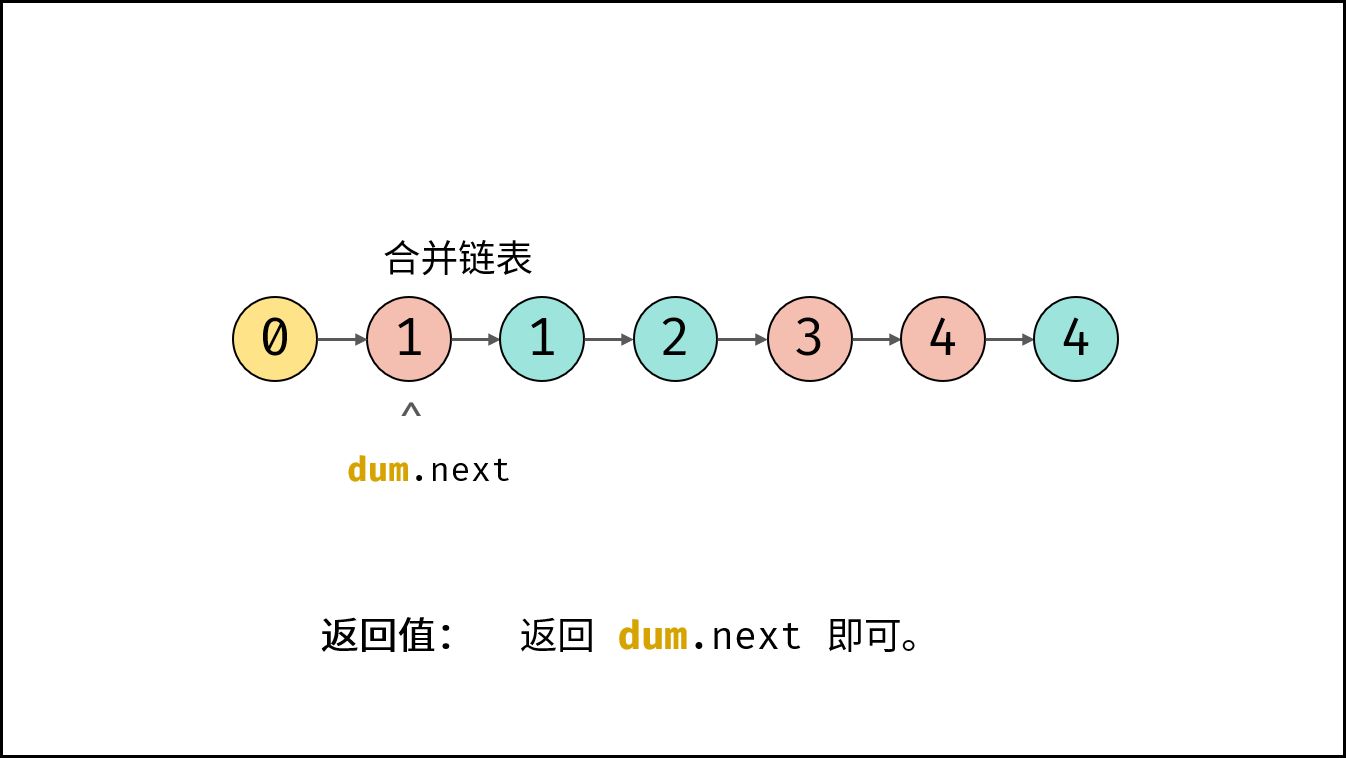Picture17.png](https://pic.leetcode-cn.com/e6716316657e534835459fb5c3df99c5b8873da3a67af1eb1b9e27837245087e-Picture17.png)>
## 代码：
Python 三元表达式写法 `A if x else B` ，代表当 `x = True` 时执行 `A` ，否则执行 `B` 。
```Python []
class Solution:
def trainningPlan(self, l1: ListNode, l2: ListNode) -> ListNode:
cur = dum = ListNode(0)
while l1 and l2:
if l1.val < l2.val:
cur.next, l1 = l1, l1.next
else:
cur.next, l2 = l2, l2.next
cur = cur.next
cur.next = l1 if l1 else l2
return dum.next
```
```Java []
class Solution {
public ListNode trainningPlan(ListNode l1, ListNode l2) {
ListNode dum = new ListNode(0), cur = dum;
while(l1 != null && l2 != null) {
if(l1.val < l2.val) {
cur.next = l1;
l1 = l1.next;
}
else {
cur.next = l2;
l2 = l2.next;
}
cur = cur.next;
}
cur.next = l1 != null ? l1 : l2;
return dum.next;
}
}
```
```C++ []
class Solution {
public:
ListNode* trainningPlan(ListNode* l1, ListNode* l2) {
ListNode* dum = new ListNode(0);
ListNode* cur = dum;
while(l1 != nullptr && l2 != nullptr) {
if(l1->val < l2->val) {
cur->next = l1;
l1 = l1->next;
}
else {
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
cur->next = l1 != nullptr ? l1 : l2;
return dum->next;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(M+N)$ ：** $M$ , $N$ 分别为链表 `l1`, `l2` 的长度，合并操作需遍历两链表。
- **空间复杂度 $O(1)$ ：** 节点引用 `dum` , `cur` 使用常数大小的额外空间。

78
leetbook_ioa/docs/LCR 143. 子结构判断.md Executable file
View File

@@ -0,0 +1,78 @@
## 解题思路：
若树 `B` 是树 `A` 的子结构，则子结构的根节点可能为树 `A` 的任意一个节点。因此，判断树 `B` 是否是树 `A` 的子结构，需完成以下两步工作：
1. 先序遍历树 `A` 中的每个节点 `node` ；（对应函数 `isSubStructure(A, B)`）
2. 判断树 `A` 中以 `node` 为根节点的子树是否包含树 `B` 。（对应函数 `recur(A, B)`）
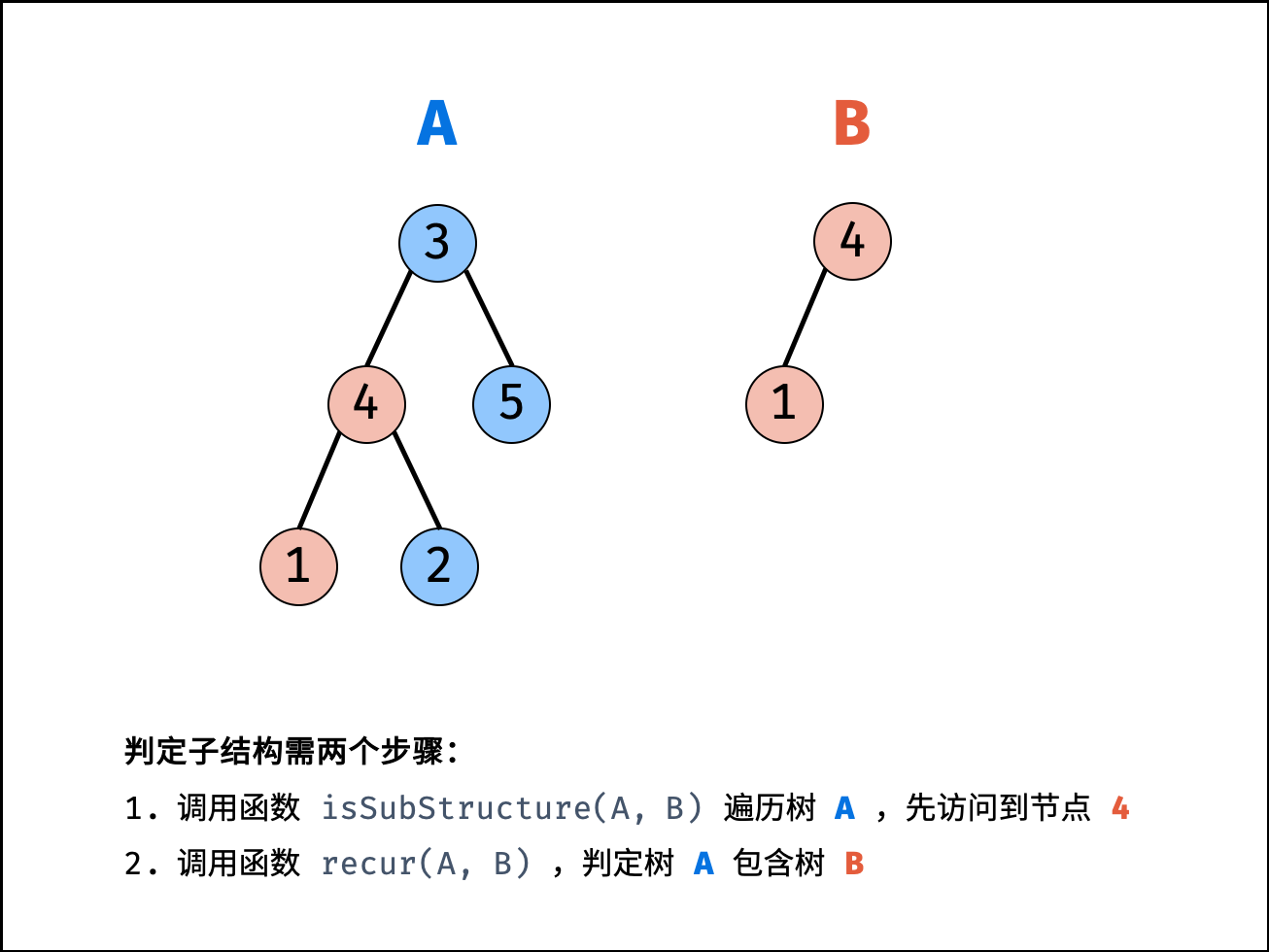![Picture1.png](https://pic.leetcode-cn.com/1599290566-VhWsiQ-Picture1.png){:align=center width=500}
### 算法流程：
本文名词规定：**树 `A`** 的根节点记作 **节点 `A`** ，**树 `B`** 的根节点称为 **节点 `B`** 。
**`recur(A, B)` 函数：**
1. **终止条件：**
1. 当节点 `B` 为空：说明树 `B` 已匹配完成（越过叶子节点），因此返回 $\text{true}$ ；
2. 当节点 `A` 为空：说明已经越过树 `A` 的叶节点，即匹配失败，返回 $\text{false}$ ；
3. 当节点 `A` 和 `B` 的值不同：说明匹配失败，返回 $\text{false}$ ；
2. **返回值：**
1. 判断 `A` 和 `B` 的 **左子节点** 是否相等，即 `recur(A.left, B.left)` ；
2. 判断 `A` 和 `B` 的 **右子节点** 是否相等，即 `recur(A.right, B.right)` ；
**`isSubStructure(A, B)` 函数：**
1. **特例处理：** 当 树 `A` 为空 **或** 树 `B` 为空 时，直接返回 $\text{false}$ ；
2. **返回值：** 若树 `B` 是树 `A` 的子结构，则必满足以下三种情况之一，因此用或 `||` 连接；
1. 以 **节点 `A` 为根节点的子树** 包含树 `B` ，对应 `recur(A, B)`；
2. 树 `B` 是 **树 `A` 左子树** 的子结构，对应 `isSubStructure(A.left, B)`；
3. 树 `B` 是 **树 `A` 右子树** 的子结构，对应 `isSubStructure(A.right, B)`；
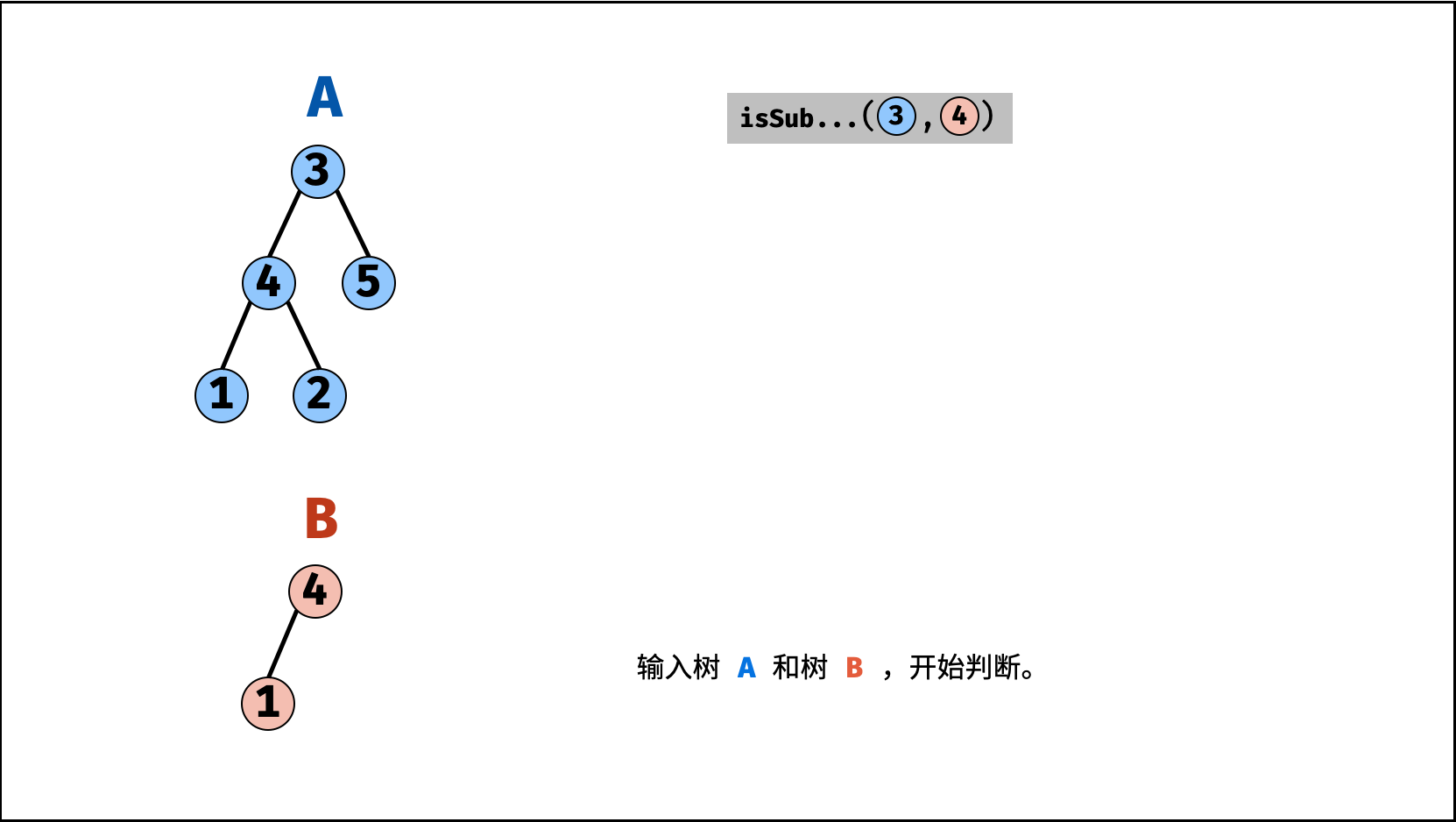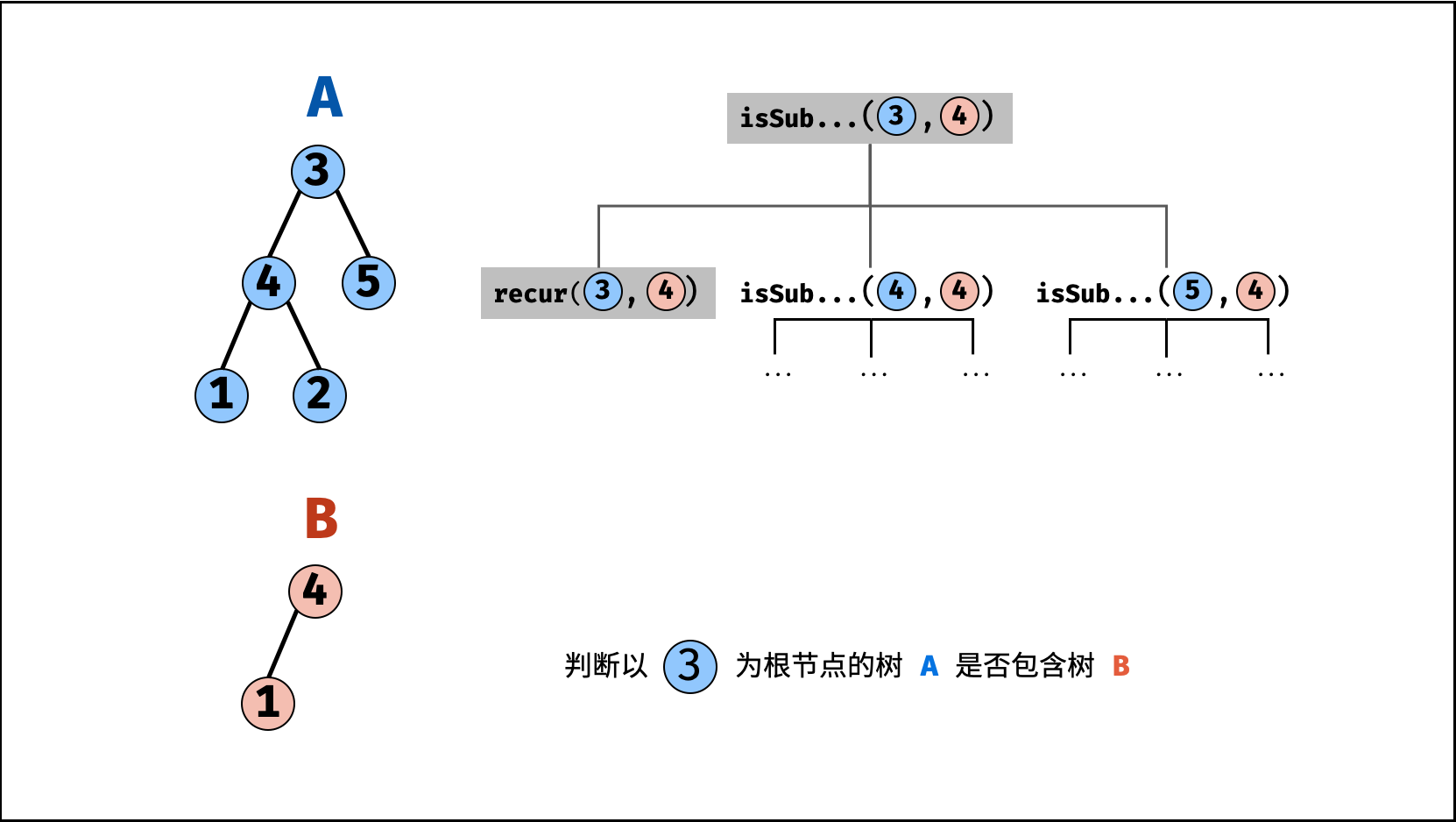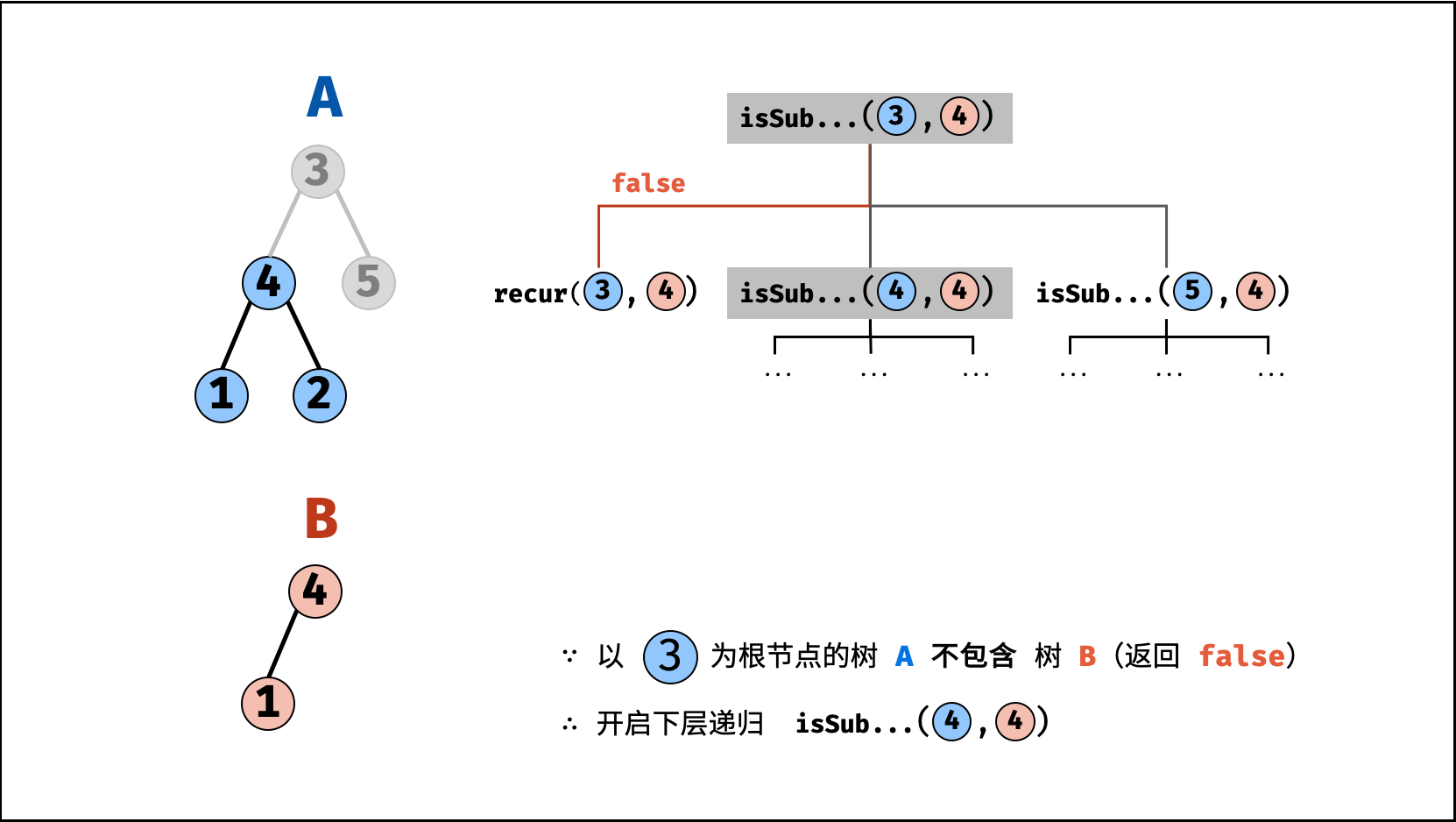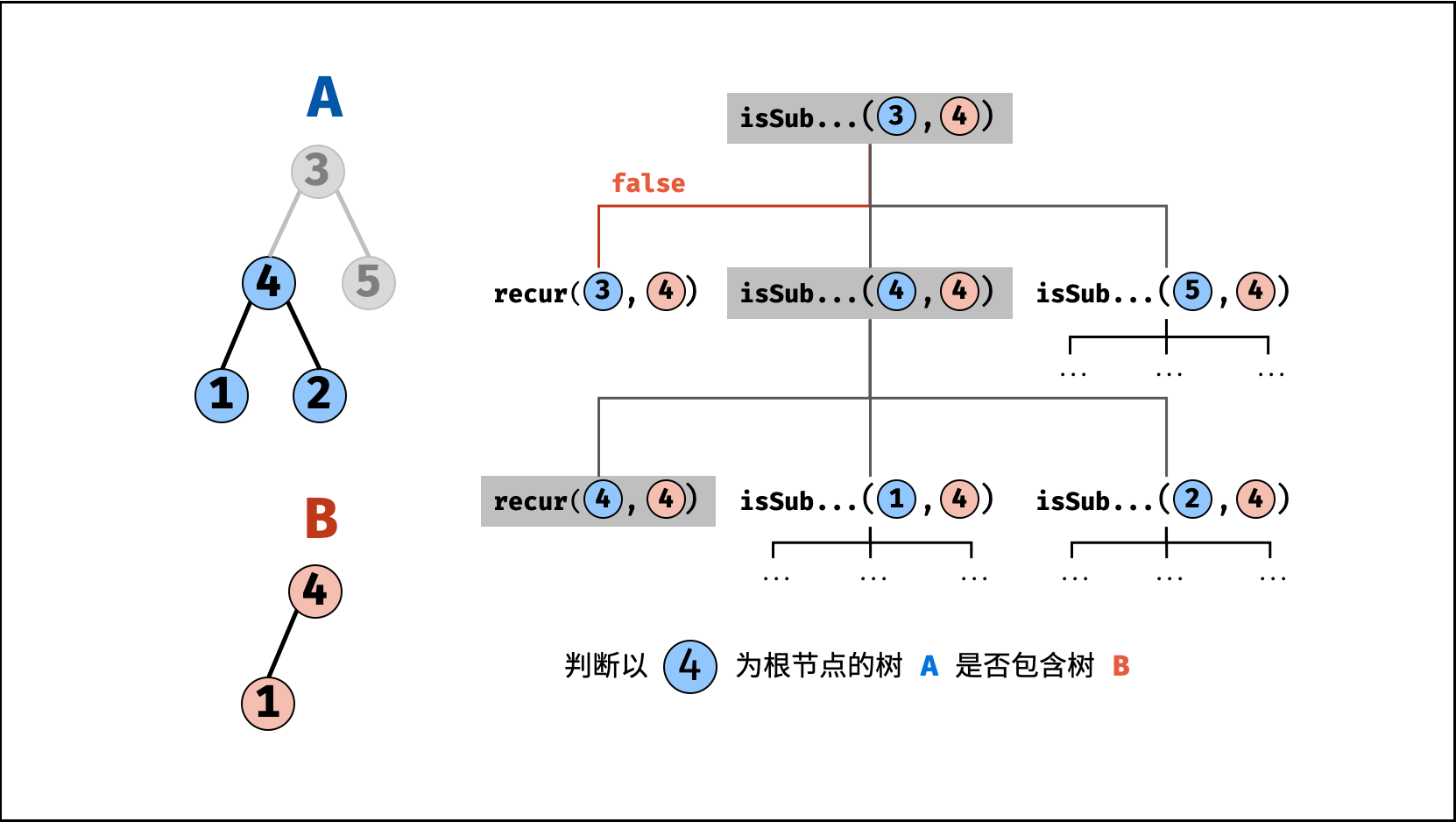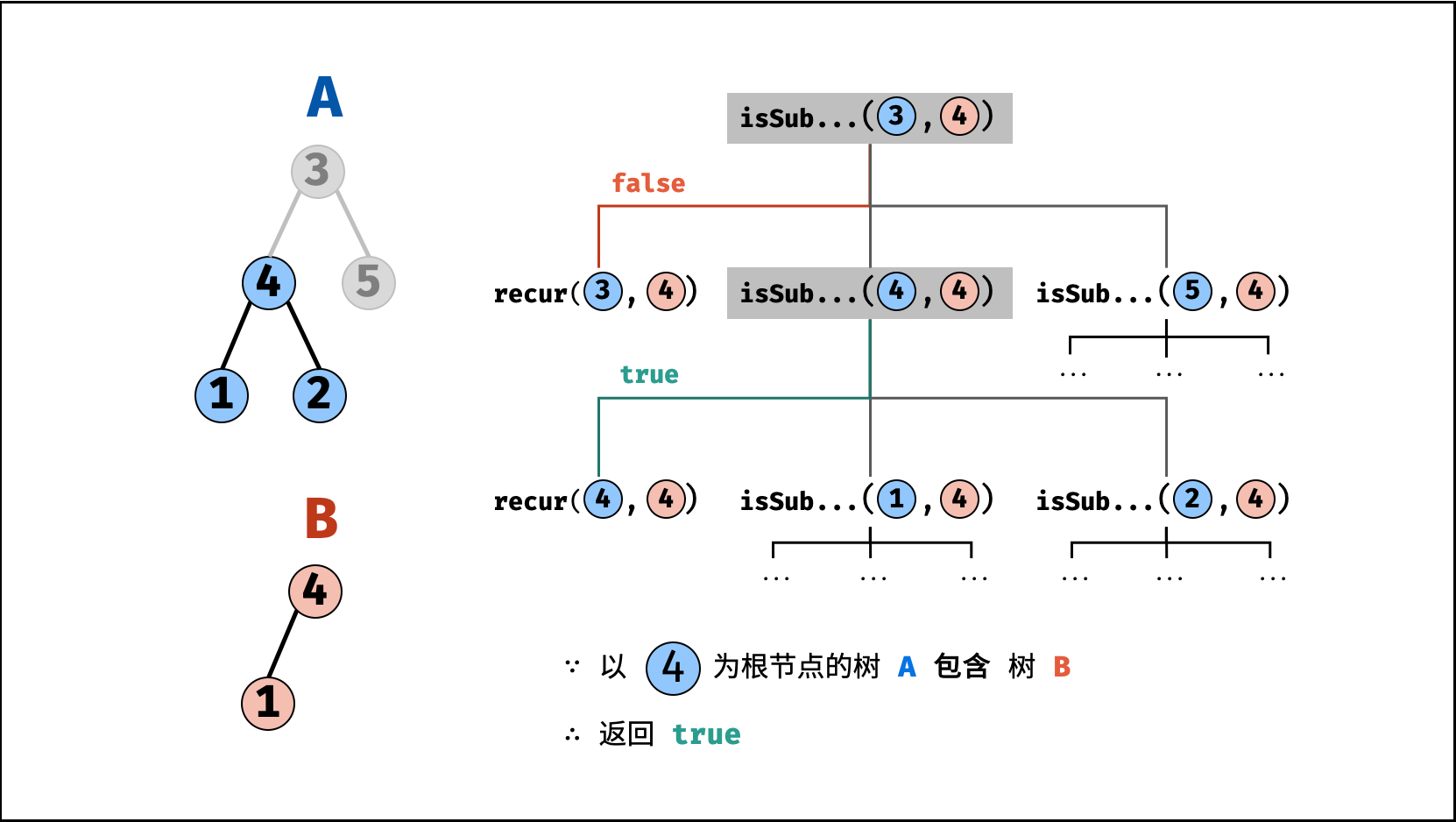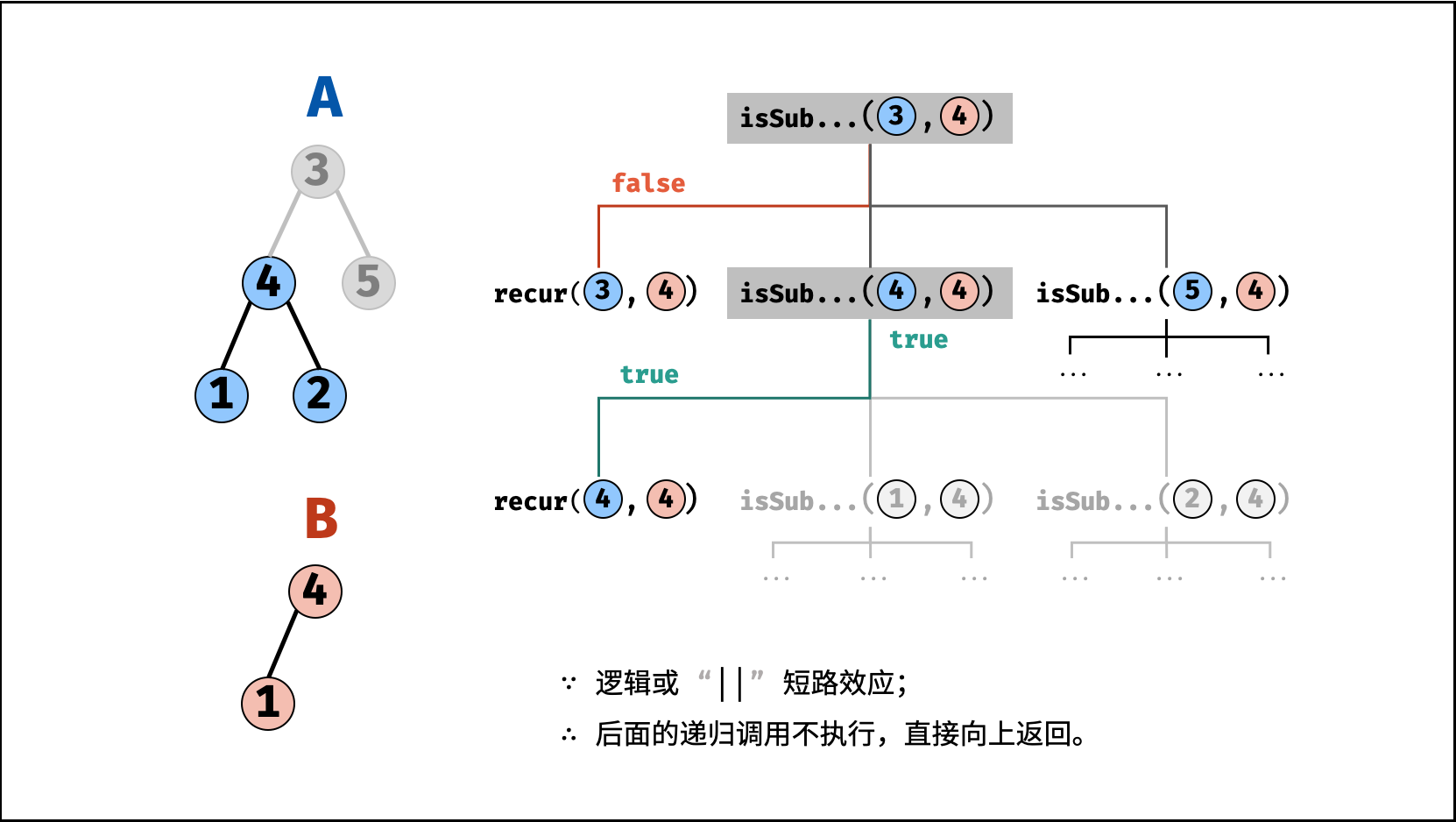<![Picture2.png](https://pic.leetcode-cn.com/1599290566-wdnbCE-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599290566-xOoQYJ-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599290566-WFqwOB-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599290566-qTdycS-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599290566-beTqAX-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599290566-JKuHpD-Picture7.png),![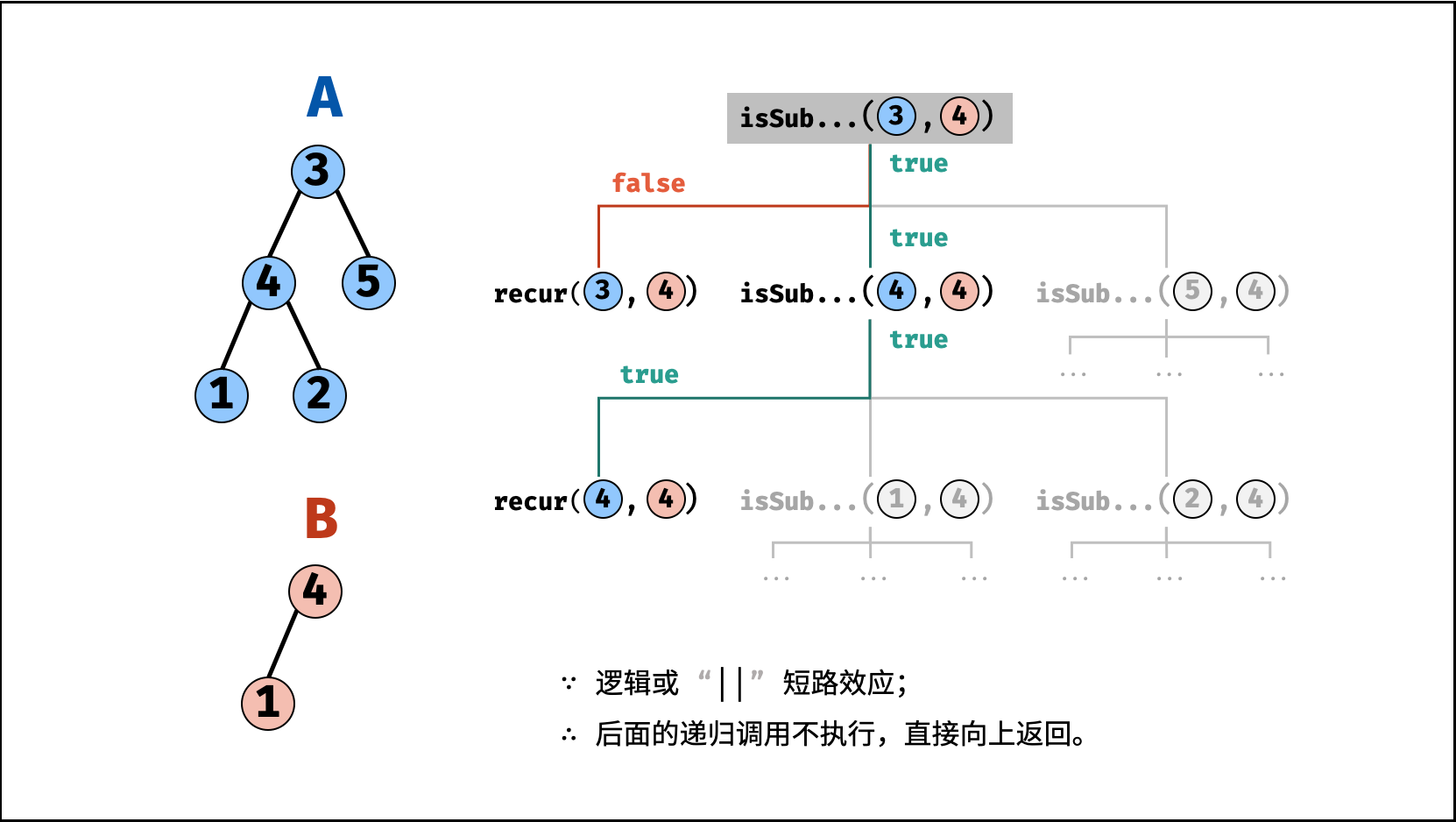Picture8.png](https://pic.leetcode-cn.com/1599290566-wdAXGL-Picture8.png),![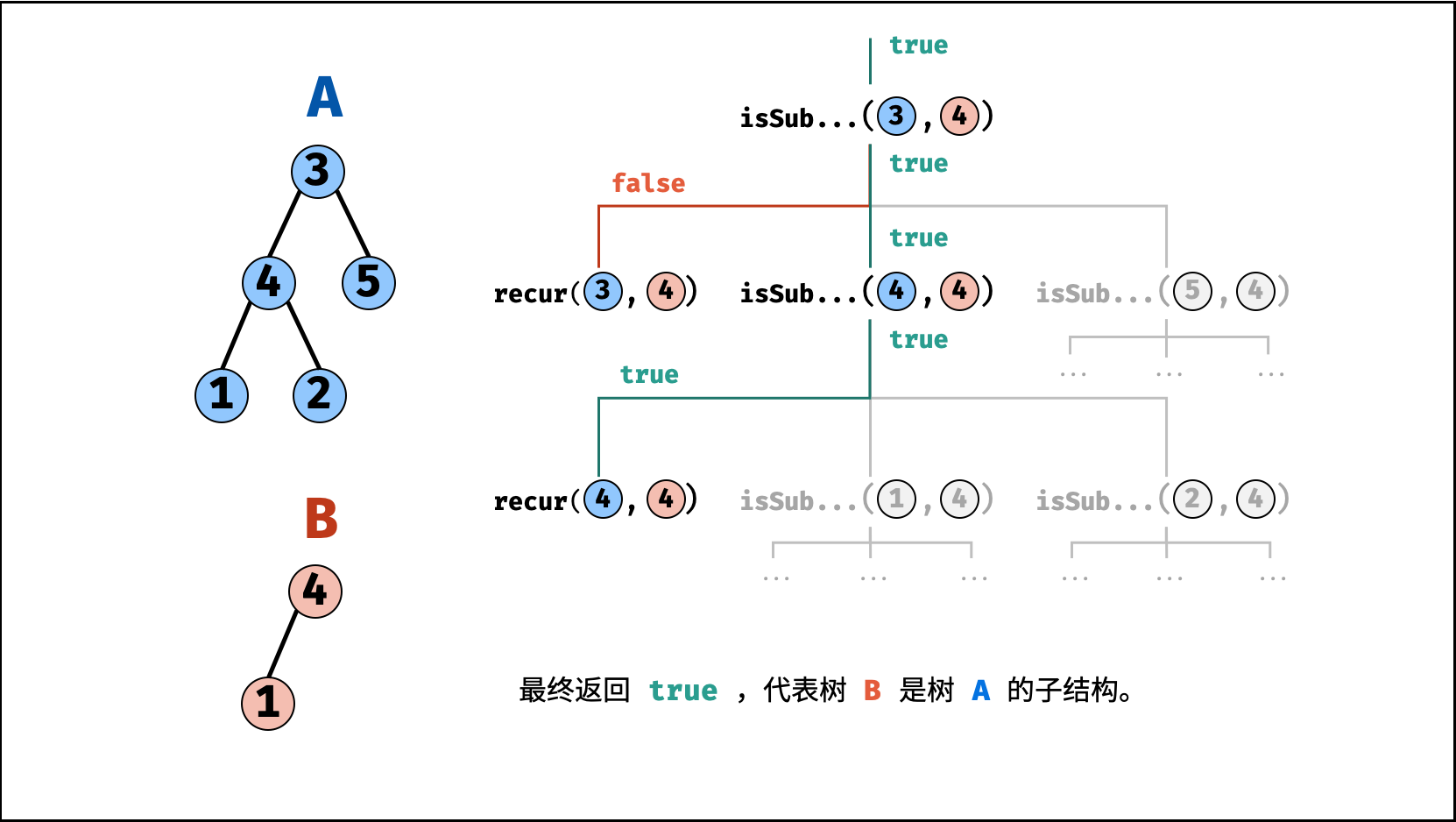Picture9.png](https://pic.leetcode-cn.com/1599290566-JOToTY-Picture9.png)>
## 代码：
```Python []
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
def recur(A, B):
if not B: return True
if not A or A.val != B.val: return False
return recur(A.left, B.left) and recur(A.right, B.right)
return bool(A and B) and (recur(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B))
```
```Java []
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
return (A != null && B != null) && (recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B));
}
boolean recur(TreeNode A, TreeNode B) {
if(B == null) return true;
if(A == null || A.val != B.val) return false;
return recur(A.left, B.left) && recur(A.right, B.right);
}
}
```
```C++ []
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
return (A != nullptr && B != nullptr) && (recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
}
private:
bool recur(TreeNode* A, TreeNode* B) {
if(B == nullptr) return true;
if(A == nullptr || A->val != B->val) return false;
return recur(A->left, B->left) && recur(A->right, B->right);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(MN)$ ：** 其中 $M, N$ 分别为树 `A` 和 树 `B` 的节点数量；先序遍历树 `A` 占用 $O(M)$ ，每次调用 `recur(A, B)` 判断占用 $O(N)$ 。
- **空间复杂度 $O(M)$ ：** 当树 `A` 和树 `B` 都退化为链表时，递归调用深度最大。当 $M \leq N$ 时，遍历树 `A` 与递归判断的总递归深度为 $M$ ；当 $M>N$ 时，最差情况为遍历至树 `A` 的叶节点，此时总递归深度为 $M$。

153
leetbook_ioa/docs/LCR 144. 翻转二叉树.md Executable file
View File

@@ -0,0 +1,153 @@
## 解题思路：
**二叉树镜像定义：** 对于二叉树中任意节点 `root` ，设其左 / 右子节点分别为 `left` , `right` ；则在二叉树的镜像中的对应 `root` 节点，其左 / 右子节点分别为 `right` , `left` 。
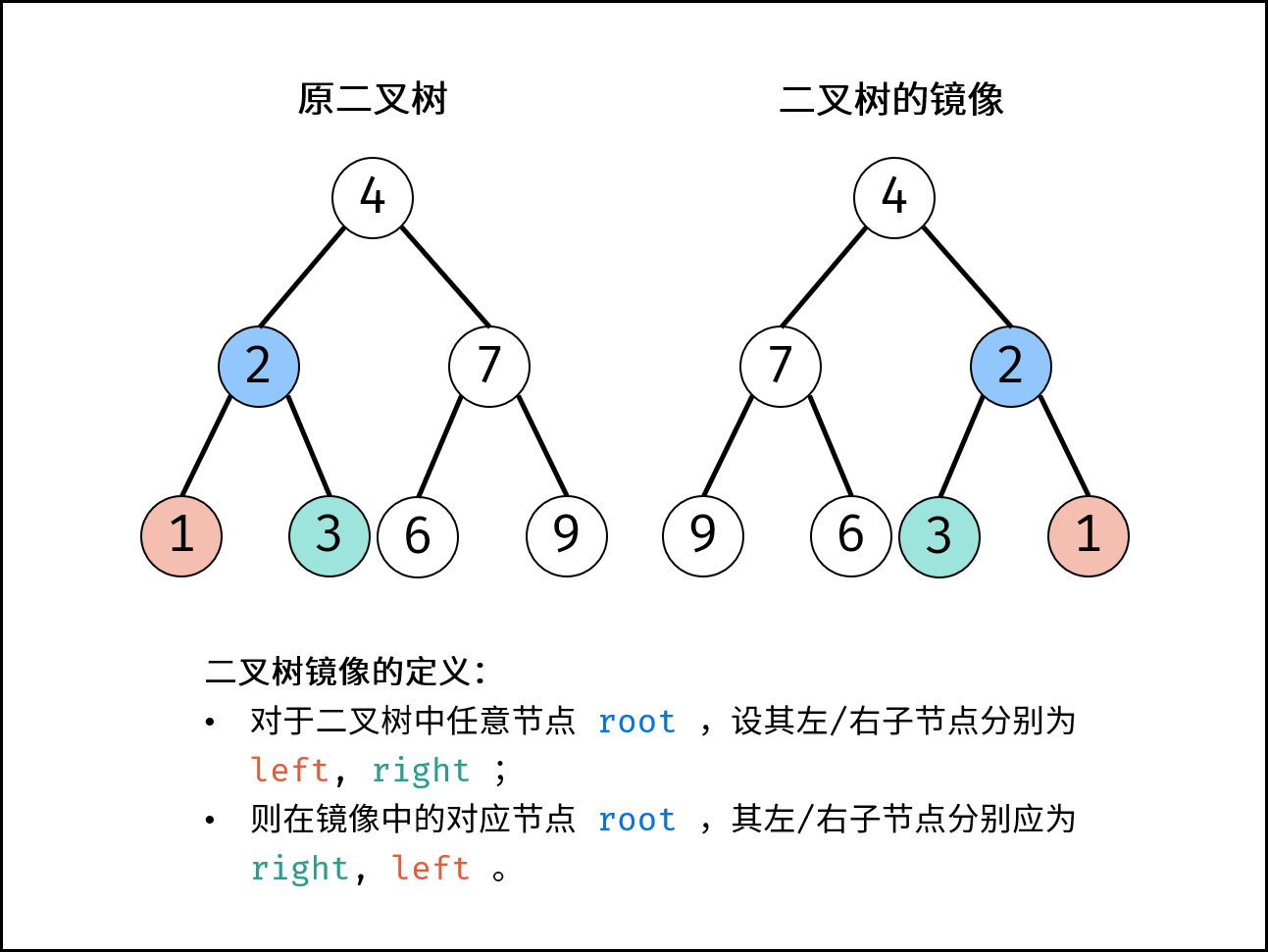![Picture1.png](https://pic.leetcode-cn.com/20717714d97fa04d509e4f0525a3089efefc2ea02cc08ce92b77978e9b51f15f-Picture1.png){:align=center width=450}
## 方法一：递归
根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。
### 递归解析：
1. **终止条件：** 当节点 `root` 为空时（即越过叶节点），则返回 $\text{null}$ ；
2. **递推工作：**
1. 初始化节点 `tmp` ，用于暂存 `root` 的左子节点；
2. 开启递归 **右子节点** `mirrorTree(root.right)` ，并将返回值作为 `root` 的 **左子节点** 。
3. 开启递归 **左子节点** `mirrorTree(tmp)` ，并将返回值作为 `root` 的 **右子节点** 。
3. **返回值：** 返回当前节点 `root` ；
> **Q：** 为何需要暂存 `root` 的左子节点？
> **A：** 在递归右子节点 “`root.left = mirrorTree(root.right)`” 执行完毕后，`root.left` 的值已经发生改变，此时递归左子节点 `mirrorTree(root.left)` 则会出问题。
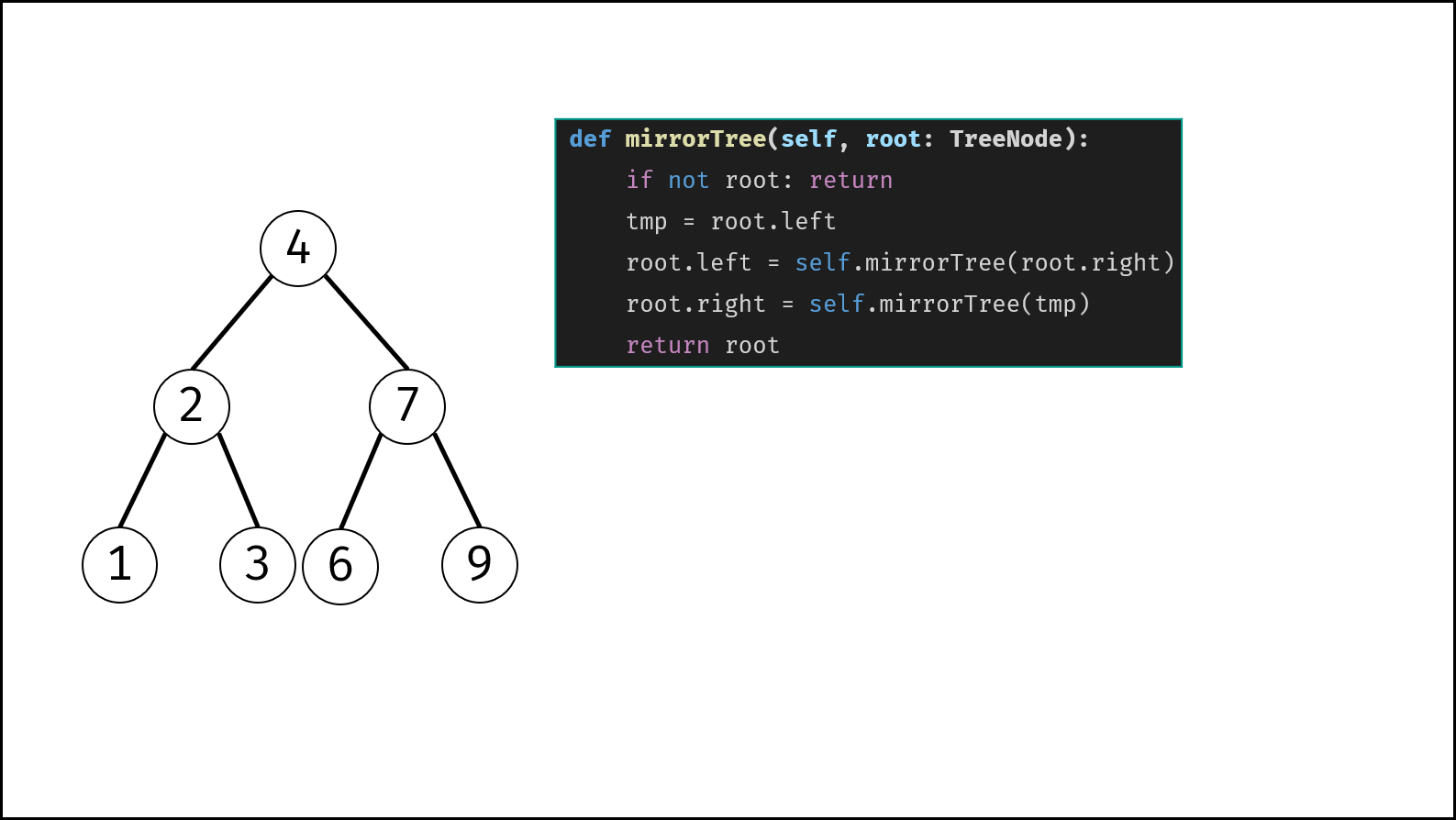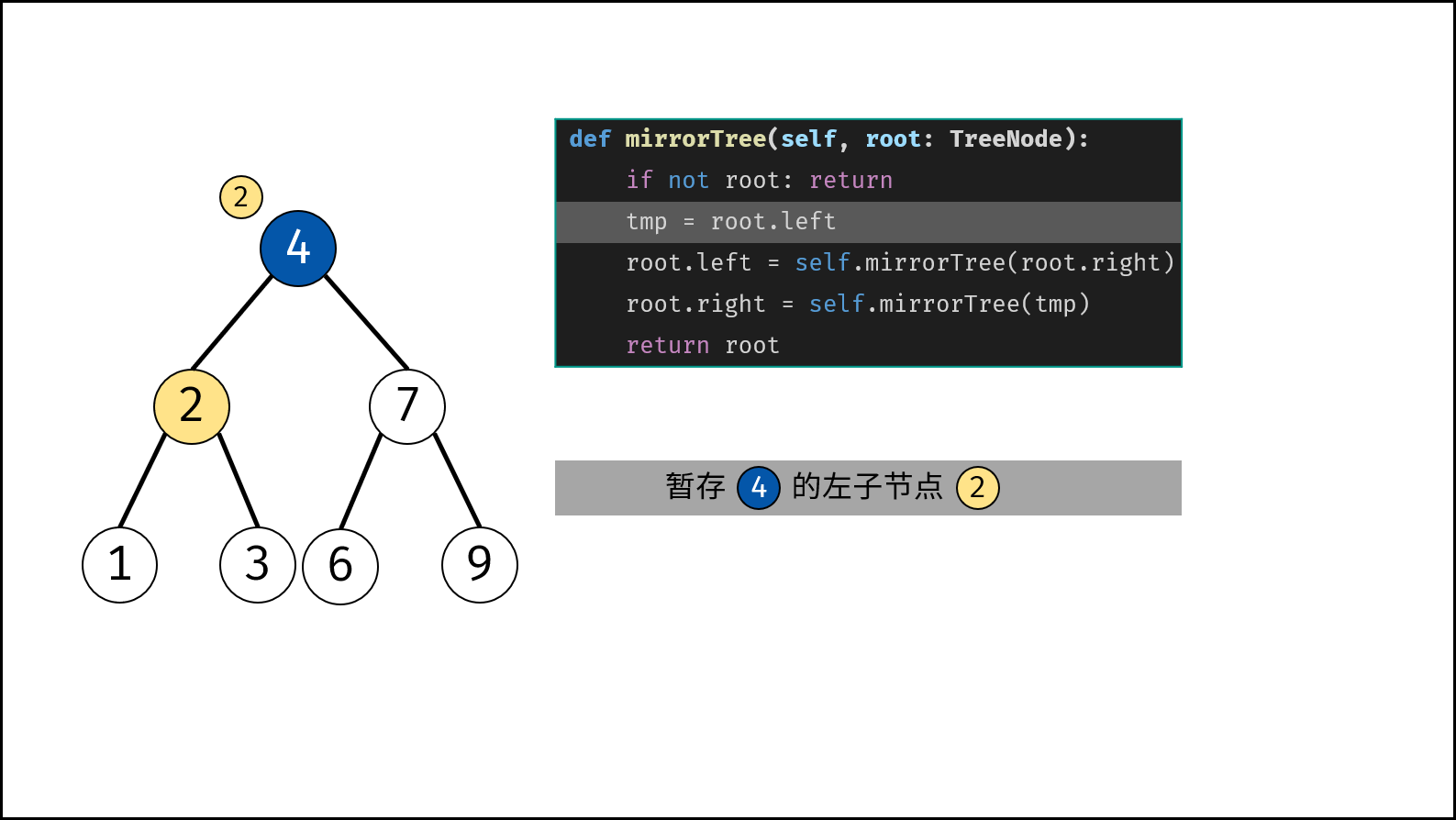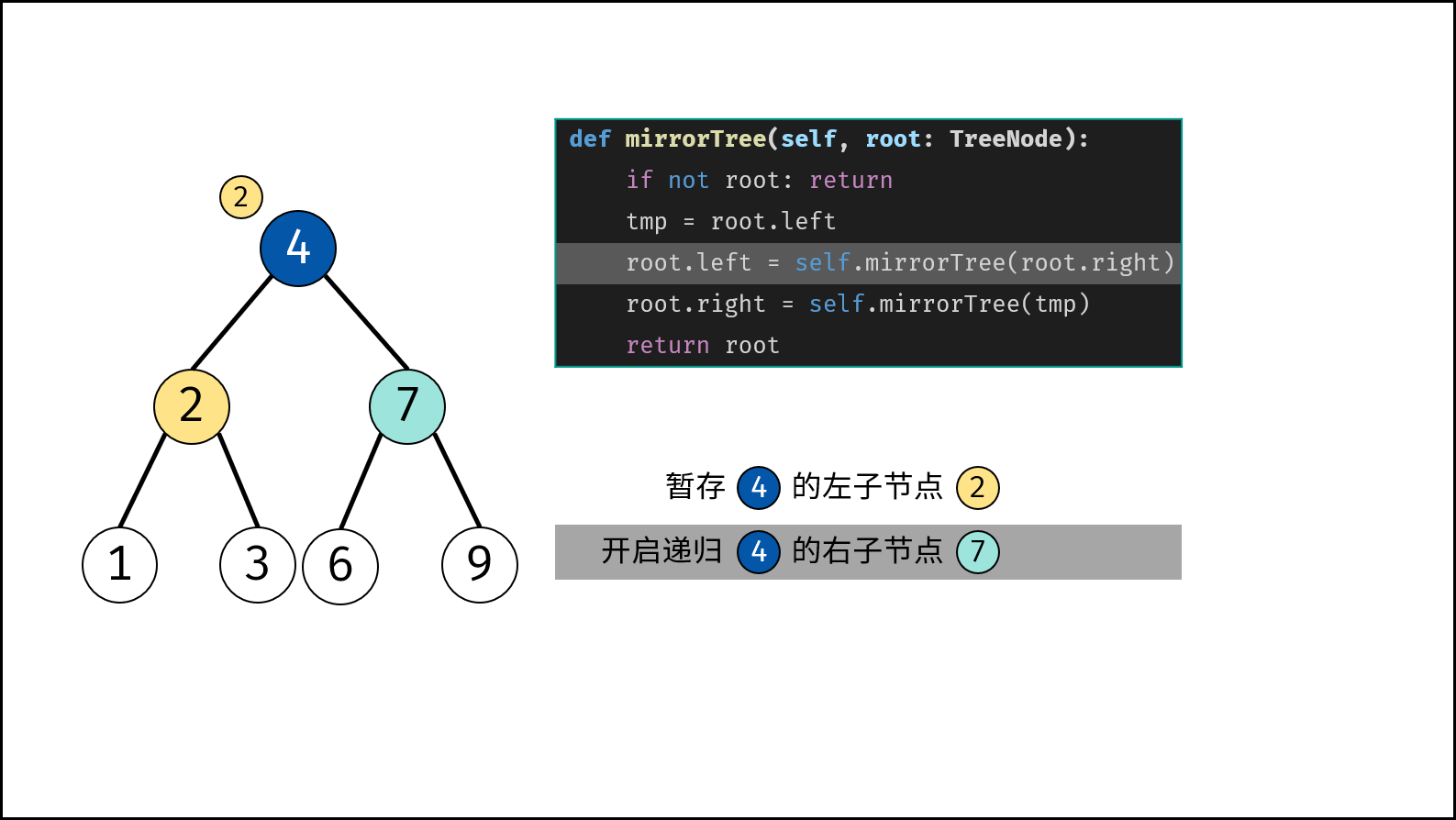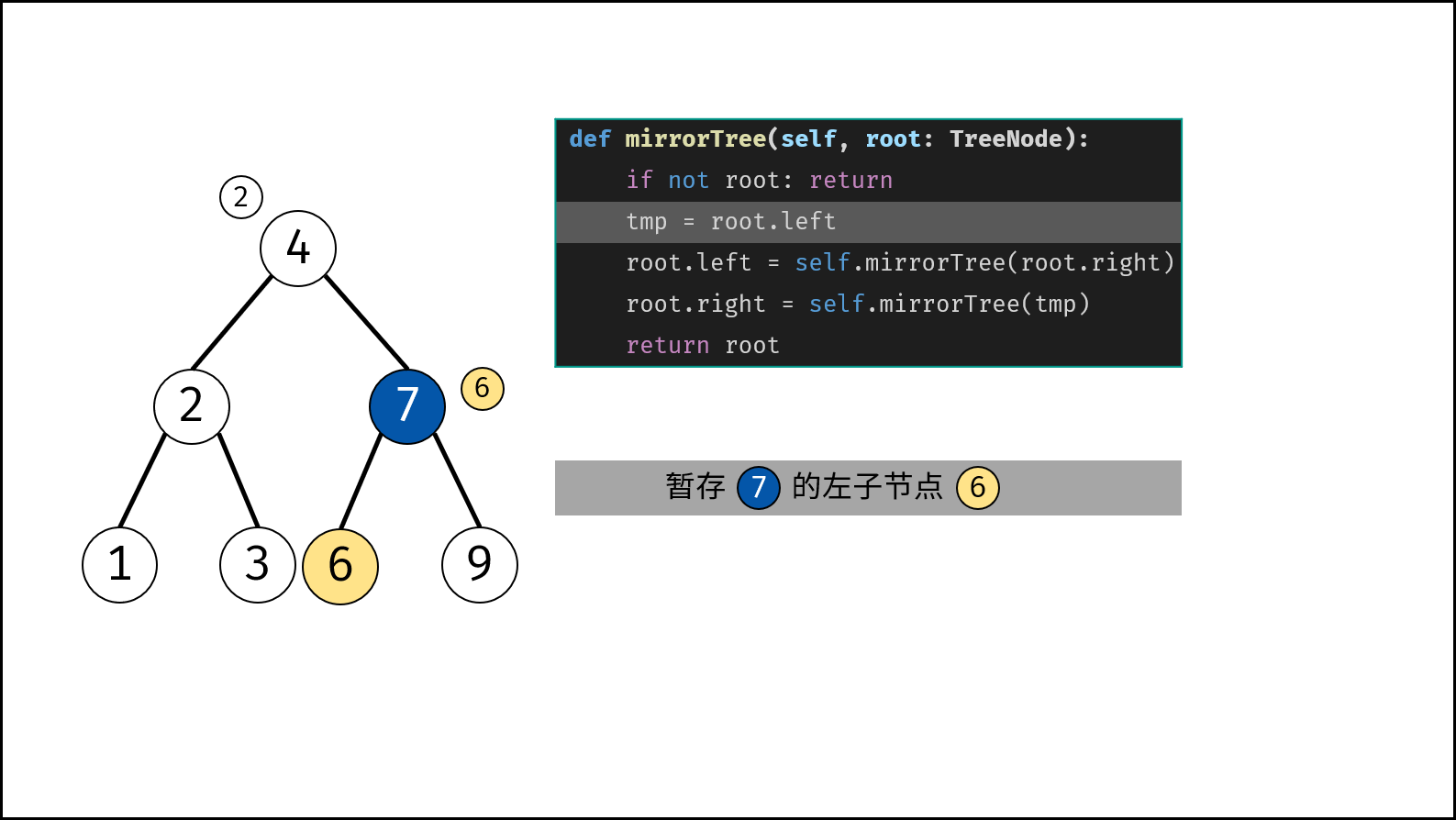<![Picture2.png](https://pic.leetcode-cn.com/c252a2c9792a0998d0560be8e882db3ad1f2e106b0d56c76fdfef219e55e4ea3-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/3cbcd2849f6ff770d6da0b833b12e301cc5f0a7f9ac6bd42cb10d05485c2d556-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/cd0030363c59130f0148c10ae2429315df94ad0784eb770d7754ee6dc7c18a99-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/bb5609047b8d25d3ecd025788f91cf20c32dcdb2c1567ec765d47aa75b5e4312-Picture5.png),![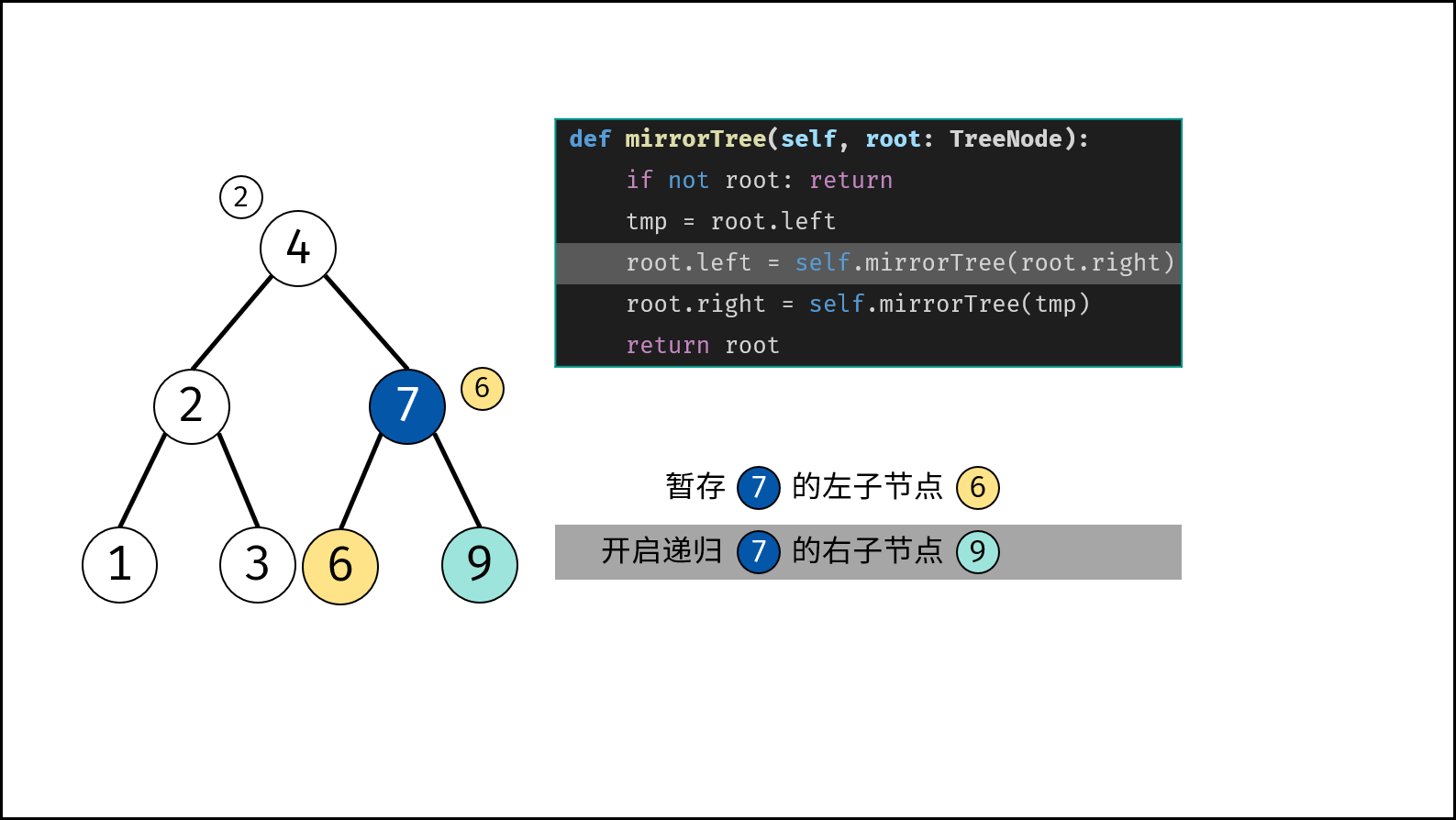Picture6.png](https://pic.leetcode-cn.com/43eece405220d52a5e988d521858b80f26974157fa2e8a8a9ae4be24ad516e3c-Picture6.png),![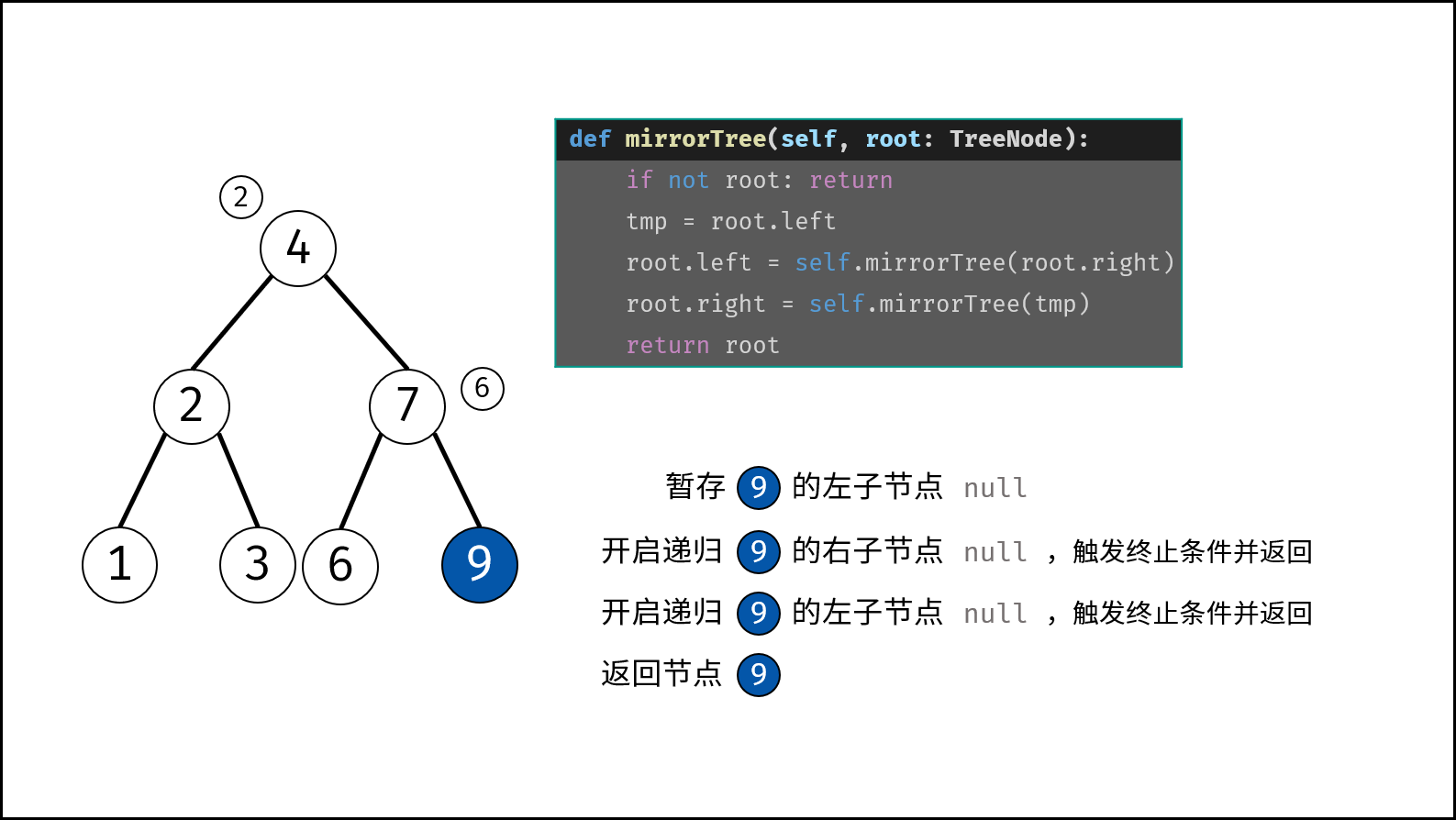Picture7.png](https://pic.leetcode-cn.com/507baf32a66f6c69eaba911c177e69591f1e7fed82d5c0cd31632d03b6d0cb73-Picture7.png),![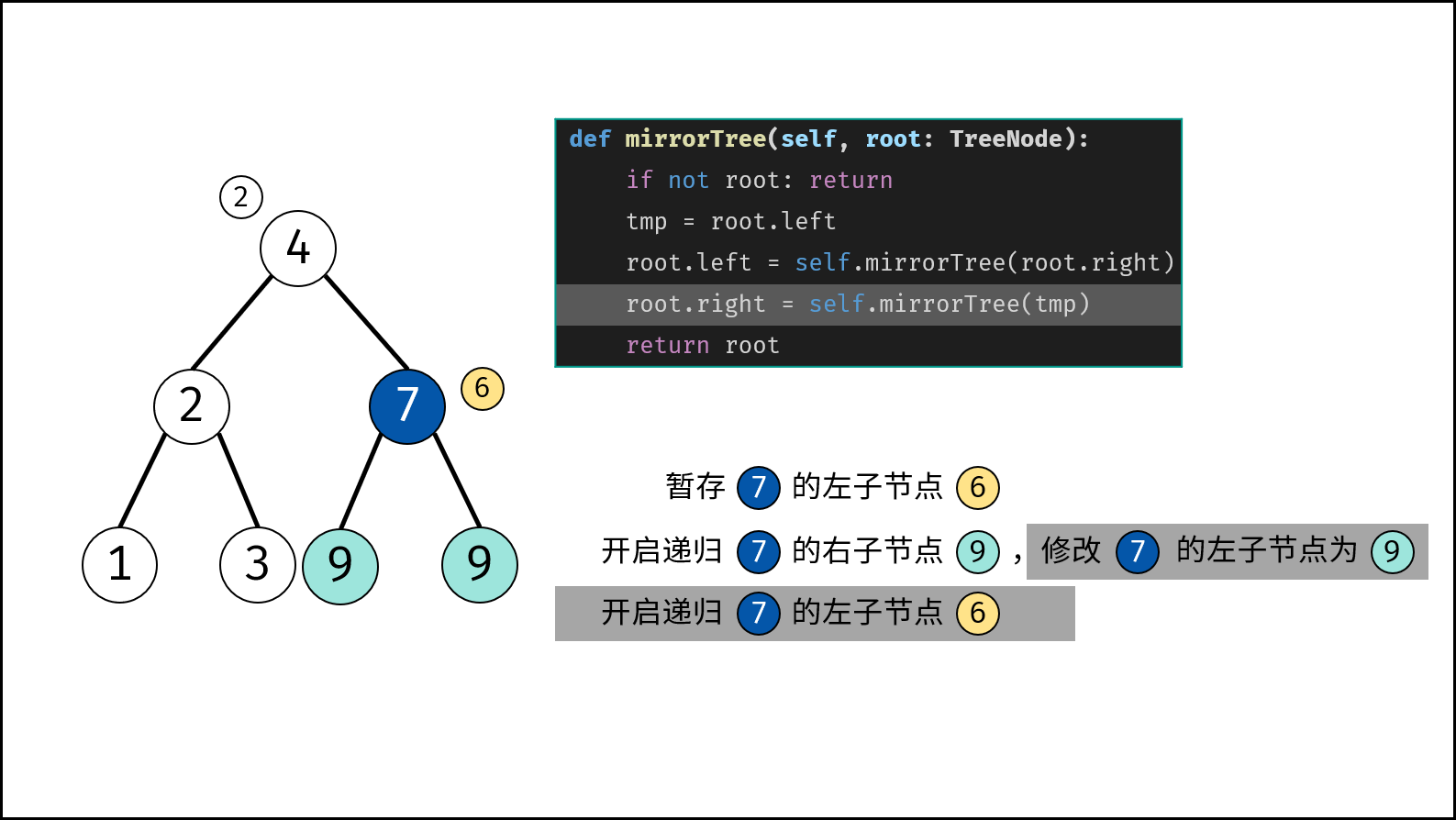Picture8.png](https://pic.leetcode-cn.com/fe80c840e08c4c2778f1fc784729721212bf5a626c94f13828c5bd13ff834646-Picture8.png),![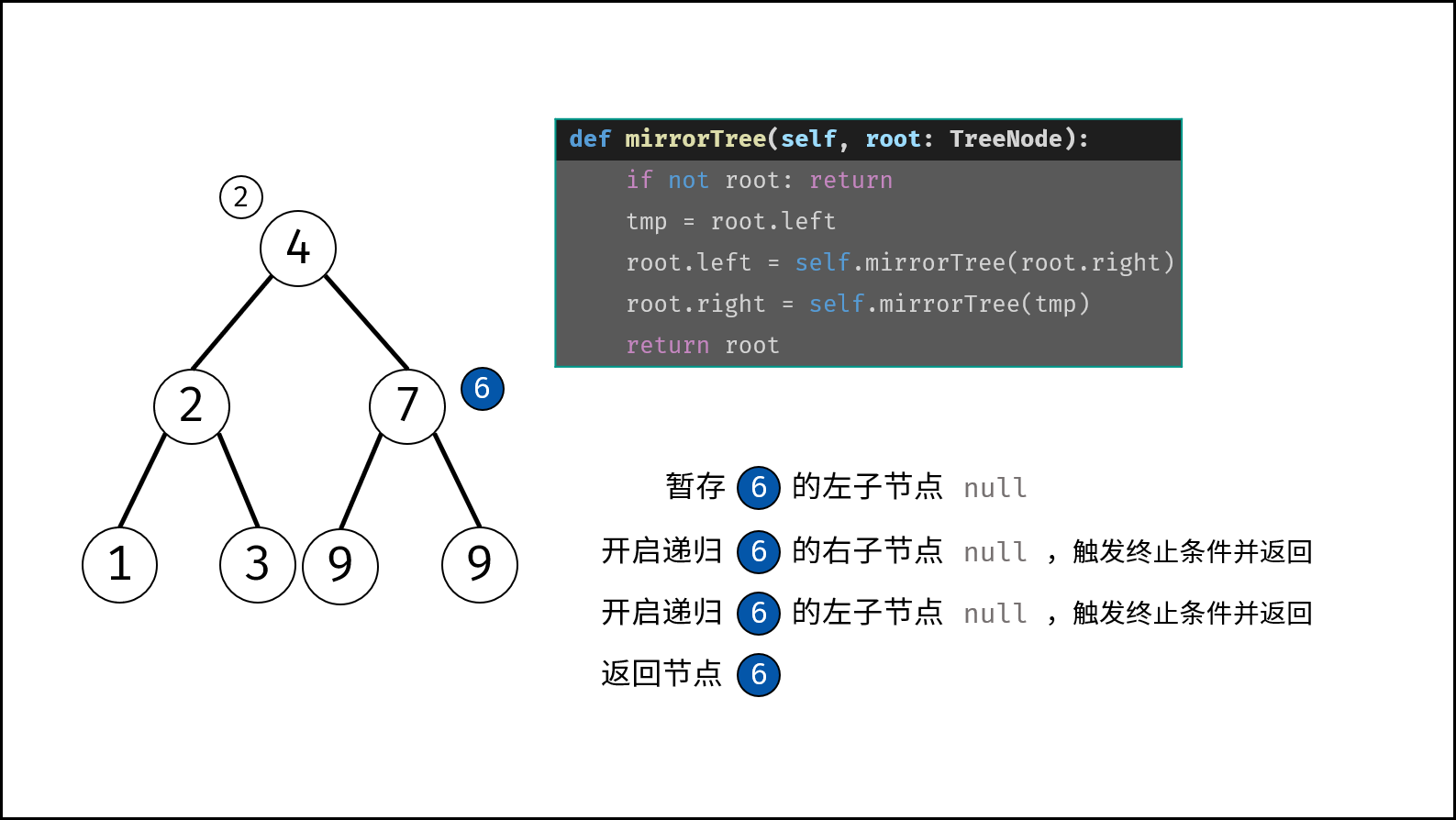Picture9.png](https://pic.leetcode-cn.com/44d8152ca5f18dcefa70eae07ca544ce45c83dd3d6bed5a8954e5bf2b0591b82-Picture9.png),![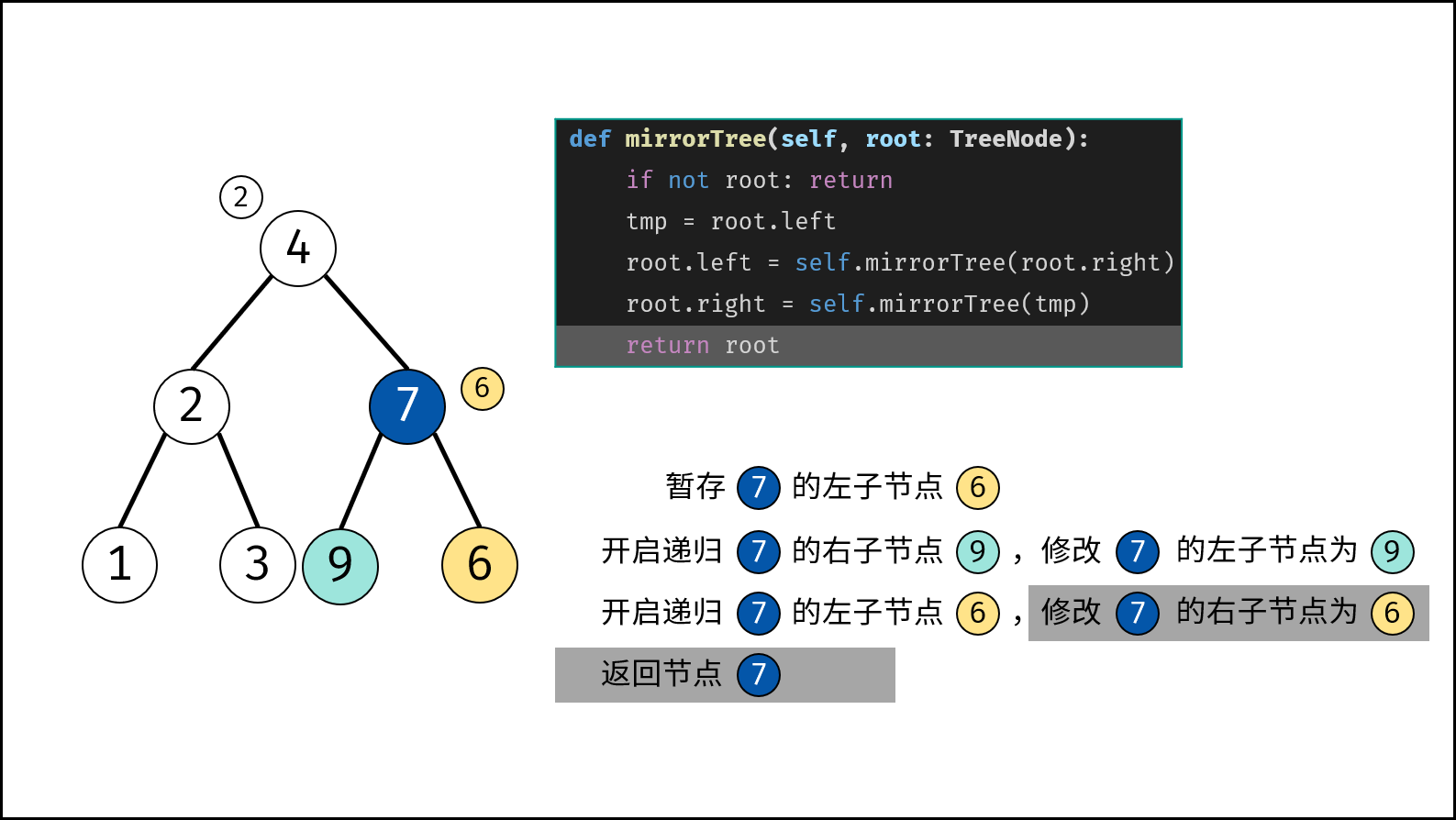Picture10.png](https://pic.leetcode-cn.com/9f1205d9bf6419c18e88de1494ca67d1328184d7fc3a7b10ea2d18b2f192831c-Picture10.png),![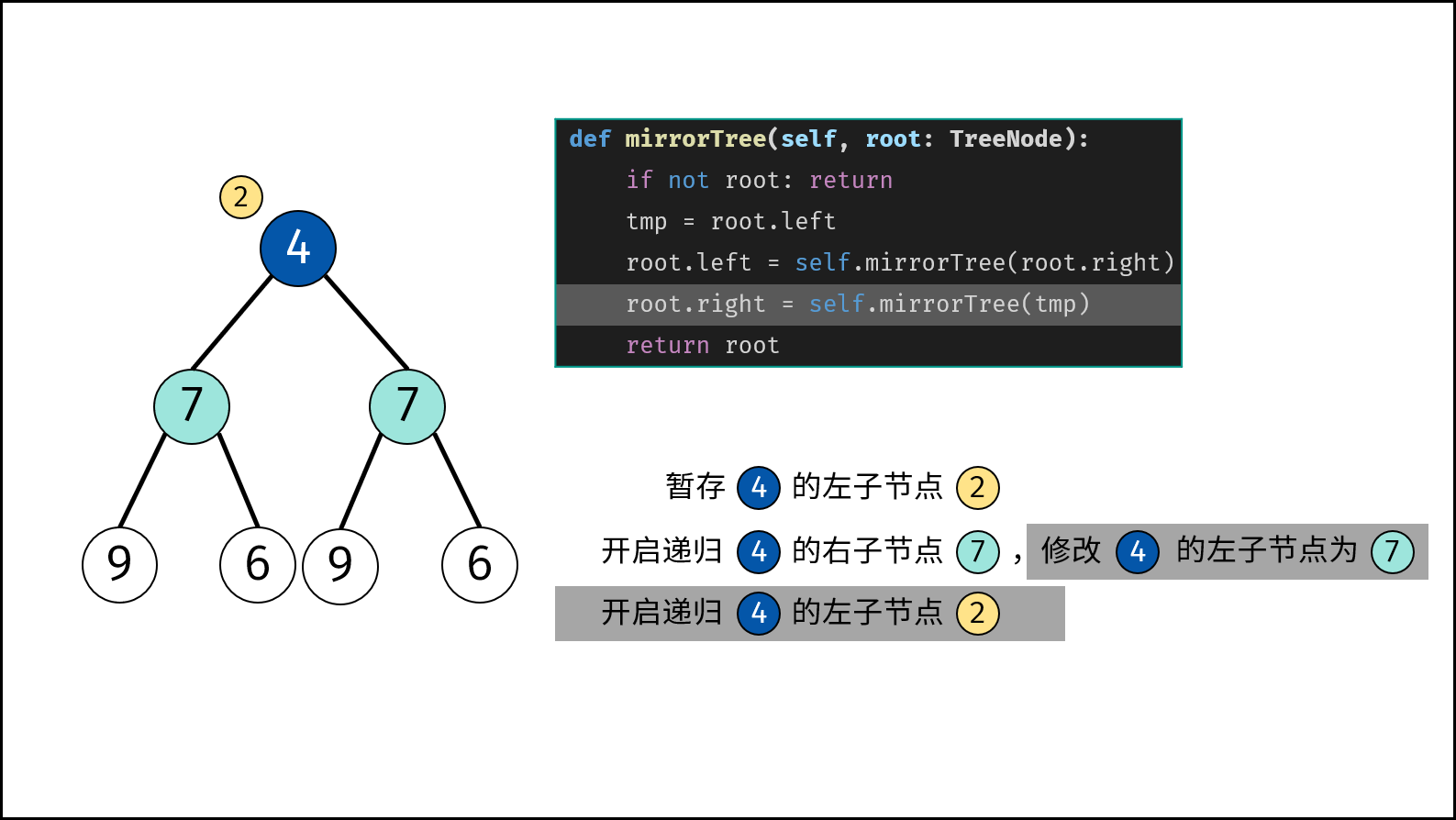Picture11.png](https://pic.leetcode-cn.com/c15e0ee4b1aaf37219c05c1663947159d92ce8315cd08e373db72ed76a8faf28-Picture11.png),![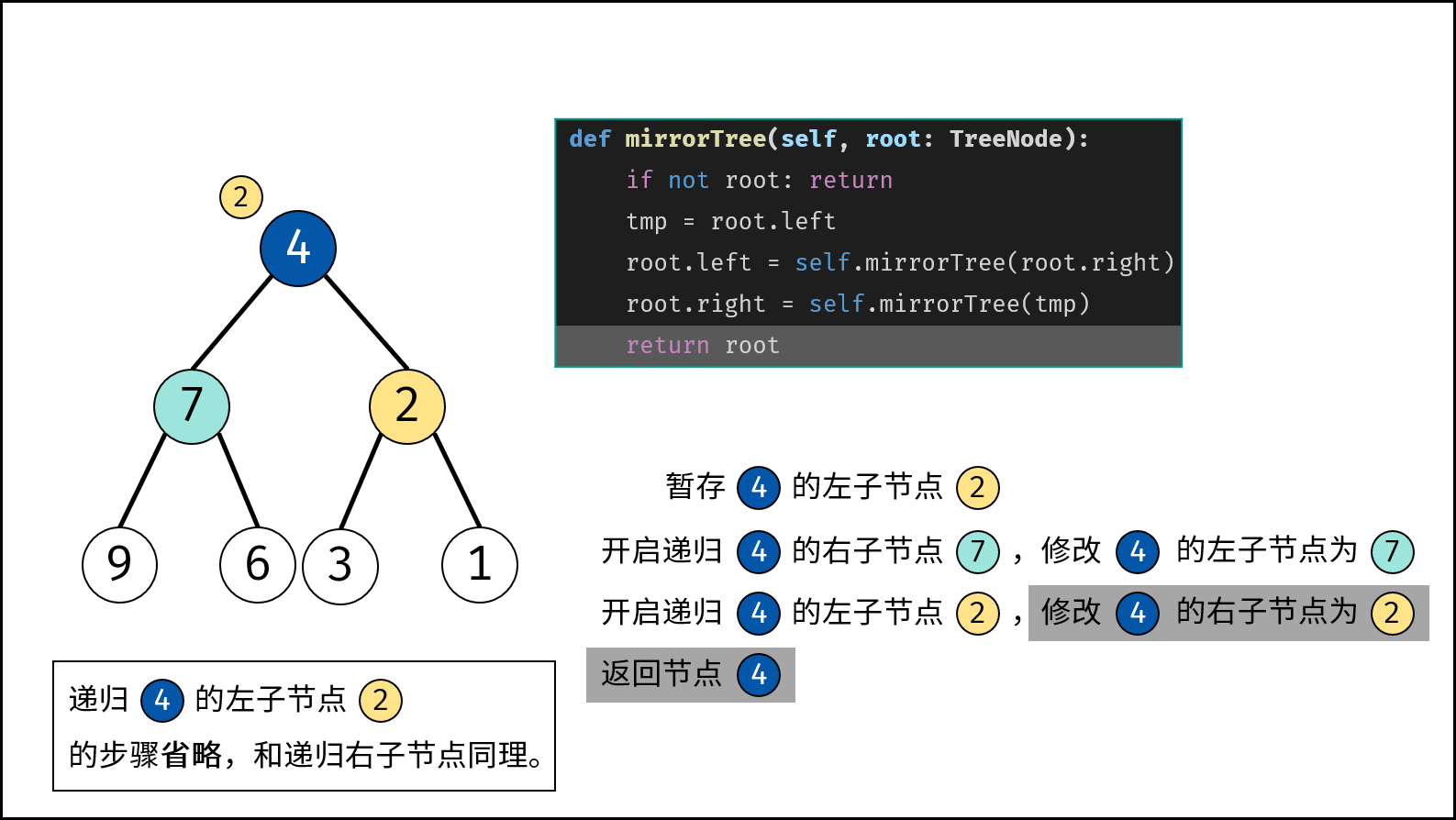Picture12.png](https://pic.leetcode-cn.com/8004f1d71e6cdf27463fd4b88fffa73570bcfc59b368e7b45c71d63cfbb57c22-Picture12.png)>
## 代码：
```Python []
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
if not root: return
tmp = root.left
root.left = self.mirrorTree(root.right)
root.right = self.mirrorTree(tmp)
return root
```
```Java []
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return null;
TreeNode tmp = root.left;
root.left = mirrorTree(root.right);
root.right = mirrorTree(tmp);
return root;
}
}
```
```C++ []
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if (root == nullptr) return nullptr;
TreeNode* tmp = root->left;
root->left = mirrorTree(root->right);
root->right = mirrorTree(tmp);
return root;
}
};
```
Python 利用平行赋值的写法（即 `a, b = b, a` ），可省略暂存操作。其原理是先将等号右侧打包成元组 `(b,a)` ，再序列地分给等号左侧的 `a, b` 序列。
```Python []
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
if not root: return
root.left, root.right = self.mirrorTree(root.right), self.mirrorTree(root.left)
return root
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** 最差情况下（当二叉树退化为链表），递归时系统需使用 $O(N)$ 大小的栈空间。
## 方法二：辅助栈（或队列）
利用栈（或队列）遍历树的所有节点 `node` ，并交换每个 `node` 的左 / 右子节点。
### 算法流程：
1. **特例处理：** 当 `root` 为空时，直接返回 $null$ ；
2. **初始化：** 栈（或队列），本文用栈，并加入根节点 `root` 。
3. **循环交换：** 当栈 `stack` 为空时跳出；
1. **出栈：** 记为 `node` ；
2. **添加子节点：** 将 `node` 左和右子节点入栈；
3. **交换：** 交换 `node` 的左 / 右子节点。
4. **返回值：** 返回根节点 `root` 。
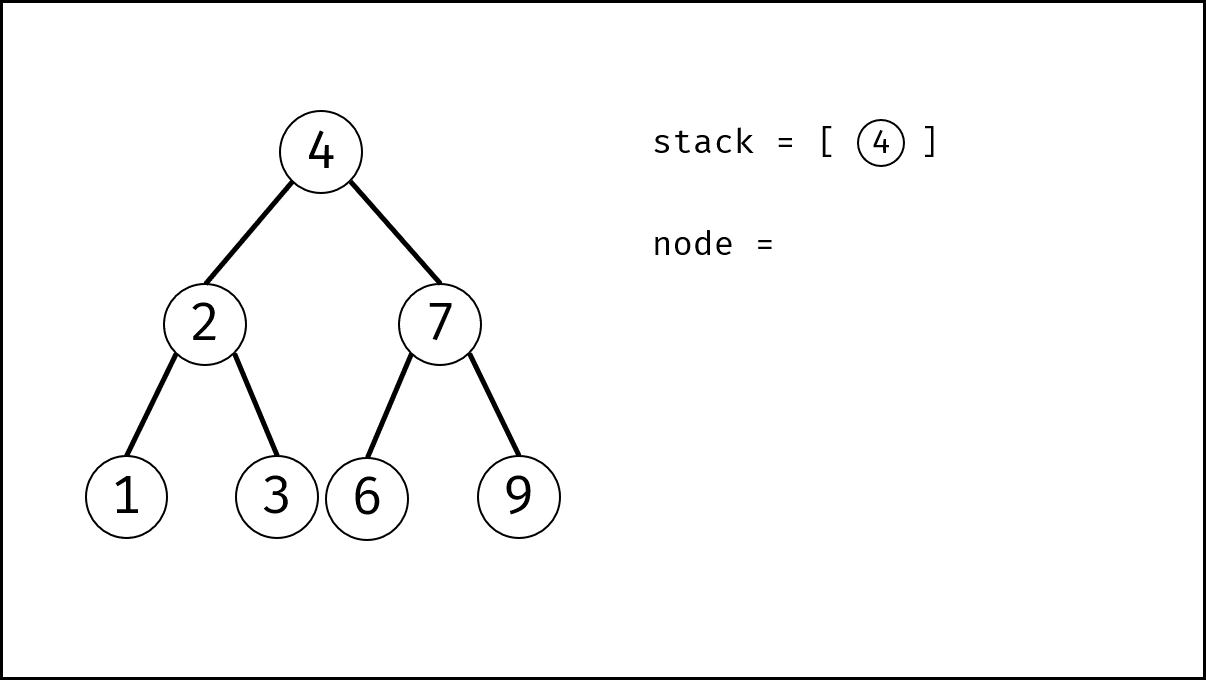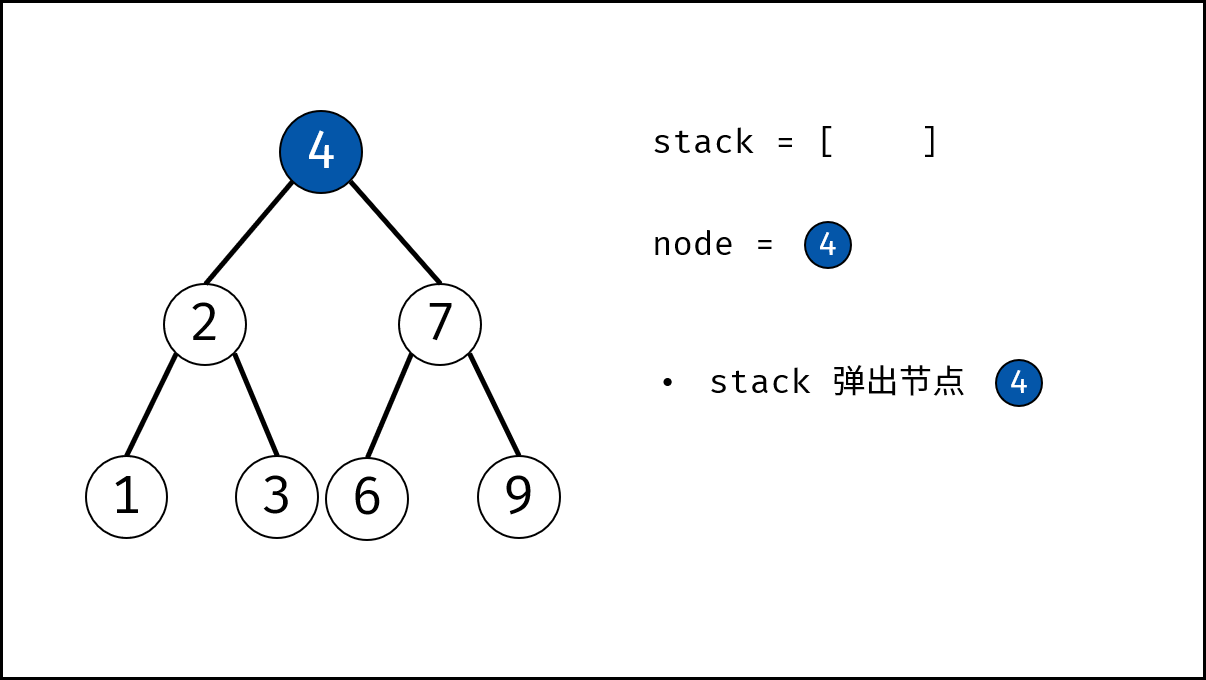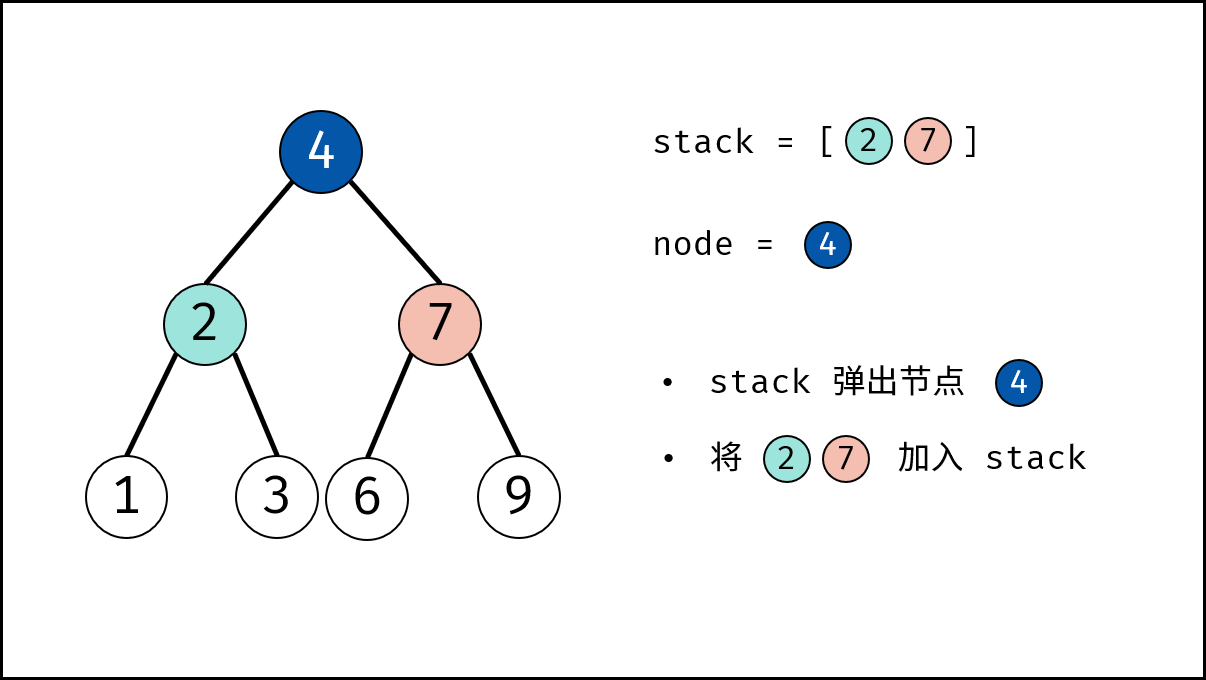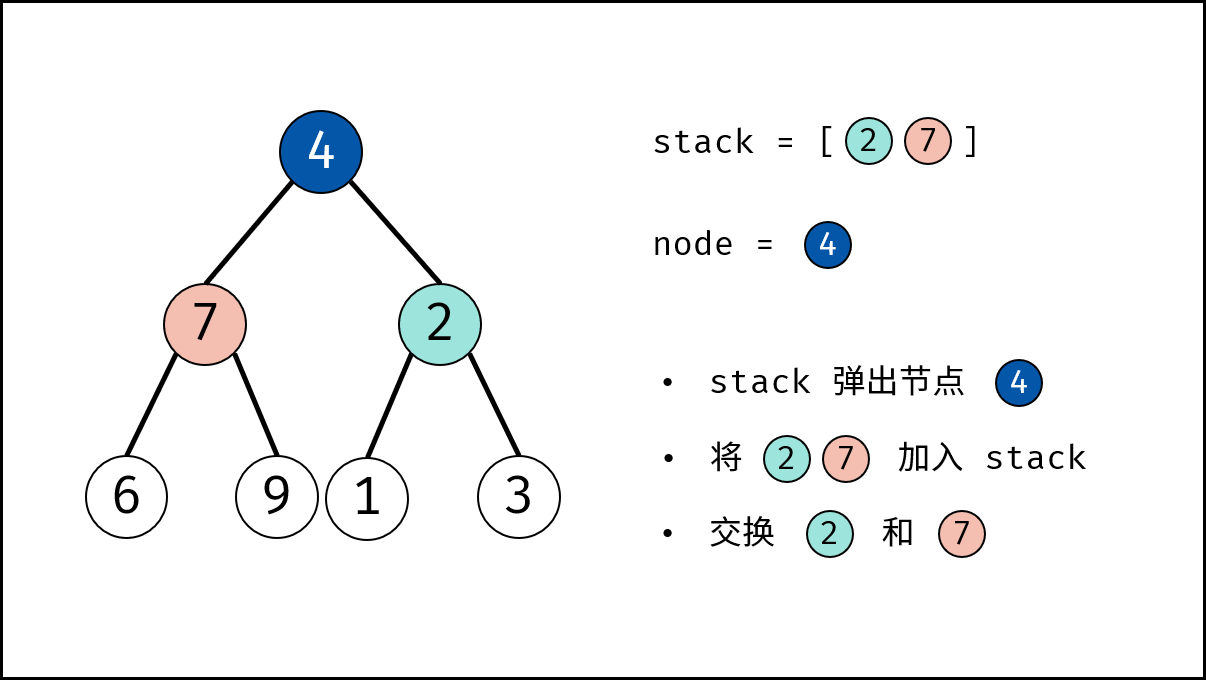<![Picture13.png](https://pic.leetcode-cn.com/81331bdc63b4c5d6c86463656ba00132496eaf099575b2e18221d6e048661d37-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/99b4c84f372970f8d80c06f34fba5f0749595bdac93778a50053be6f541cfa0d-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/5503d4ed061383c4e2c01434ce1915d1f8c6fe3c4012cdf4abcdfc3ec86060e2-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/d9f0b2915de7a92e085ea02560b07b415fd037ac7eefb75771210662ed8f78b4-Picture16.png),![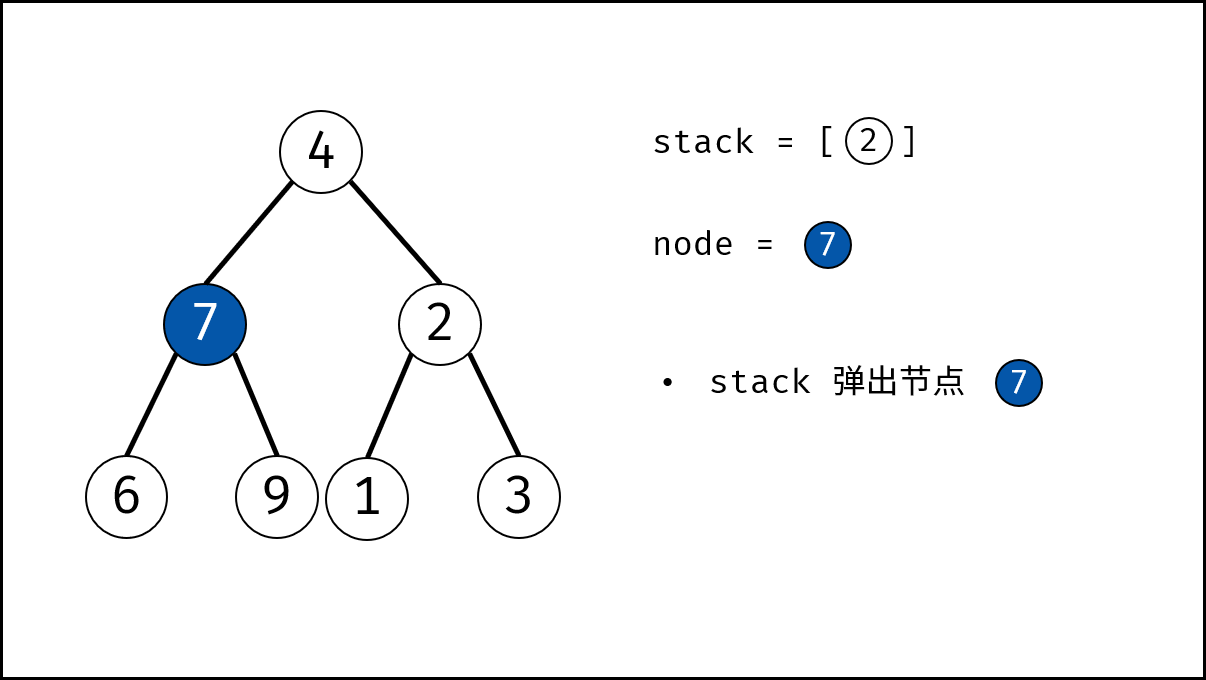Picture17.png](https://pic.leetcode-cn.com/c8153b754fafb628ad4c1ed9c18e3aabc5f90d21edf5a44ec0ced28fd7d47ac6-Picture17.png),![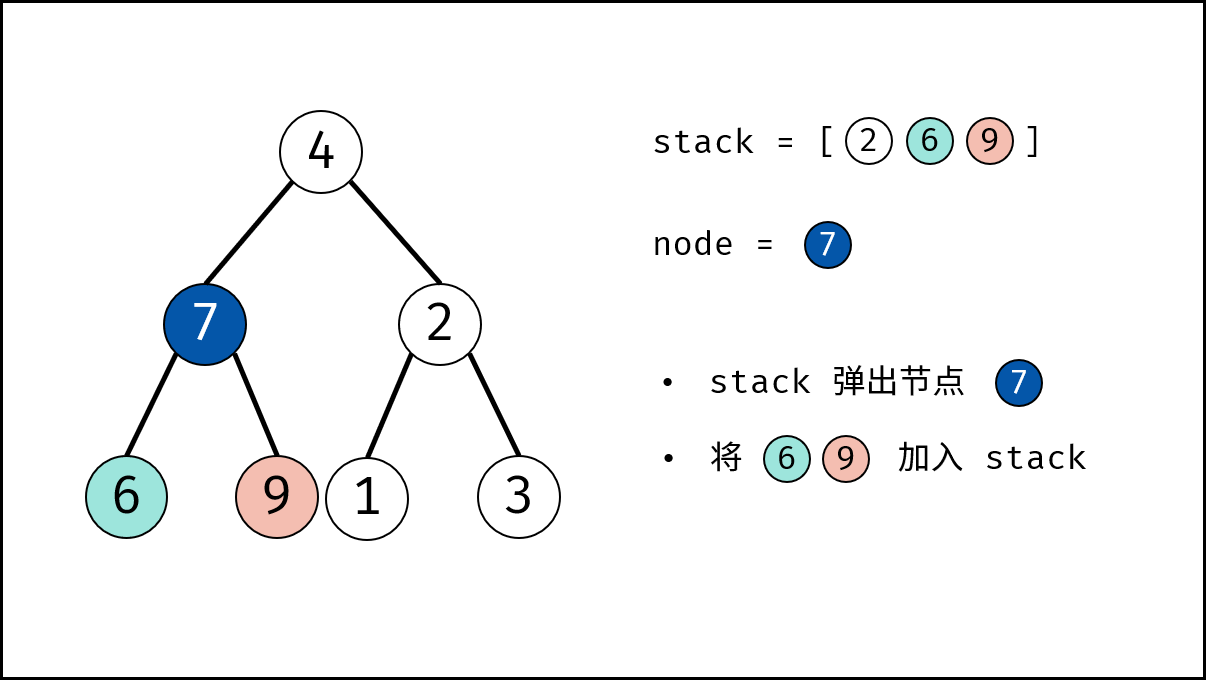Picture18.png](https://pic.leetcode-cn.com/861a0a9ba4447757052e2c3e5024fb1cc22b51b851e0adf529c98a9c81127302-Picture18.png),![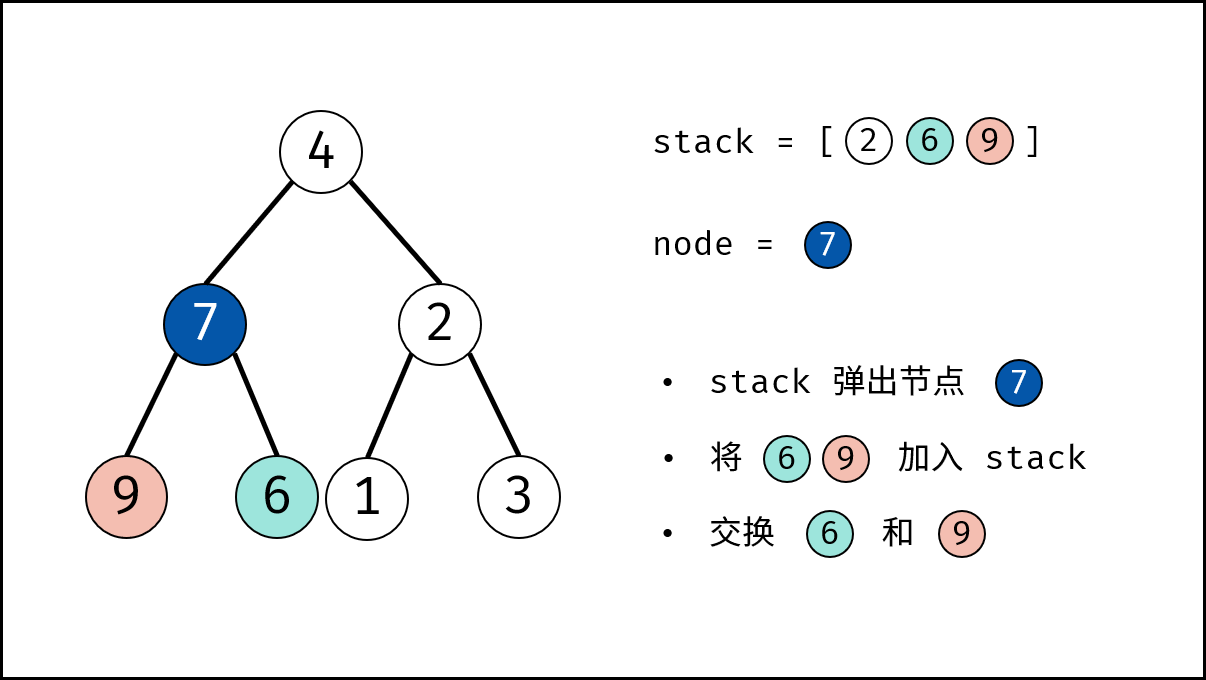Picture19.png](https://pic.leetcode-cn.com/7f8cee99b8b07eda3e6e1eb492e046a001081fe50ea41d69856c8997a456afbc-Picture19.png),![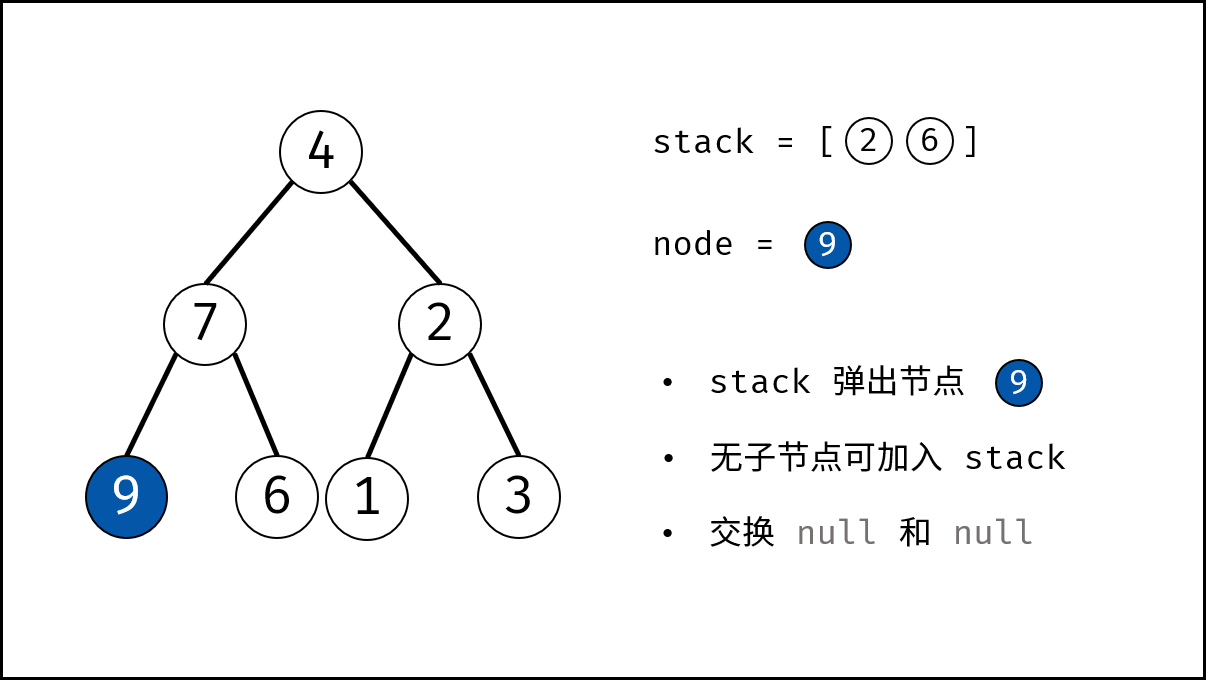Picture20.png](https://pic.leetcode-cn.com/ead0526a3bce7844986c50ba9d8b84b88e5de99f3cf24bc8f875b09388f9c10e-Picture20.png),![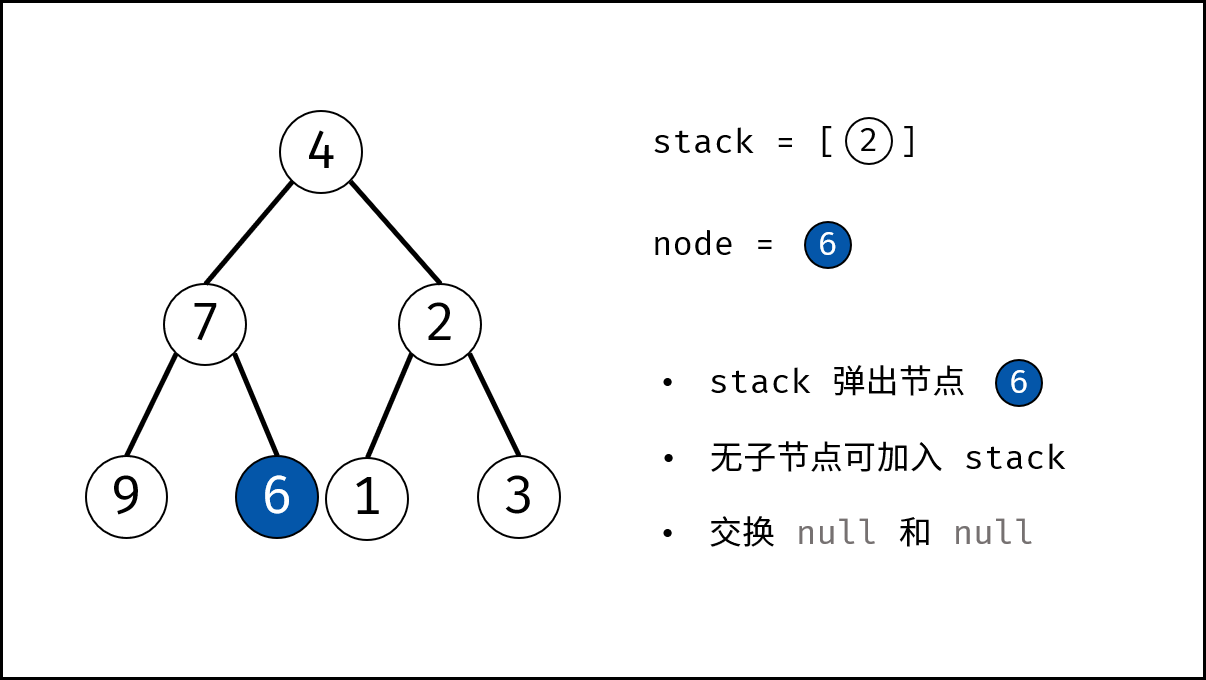Picture21.png](https://pic.leetcode-cn.com/d760f2955e791989e7bea2c8cf5215cc3f37174d7549cc9568624297d9454e80-Picture21.png),![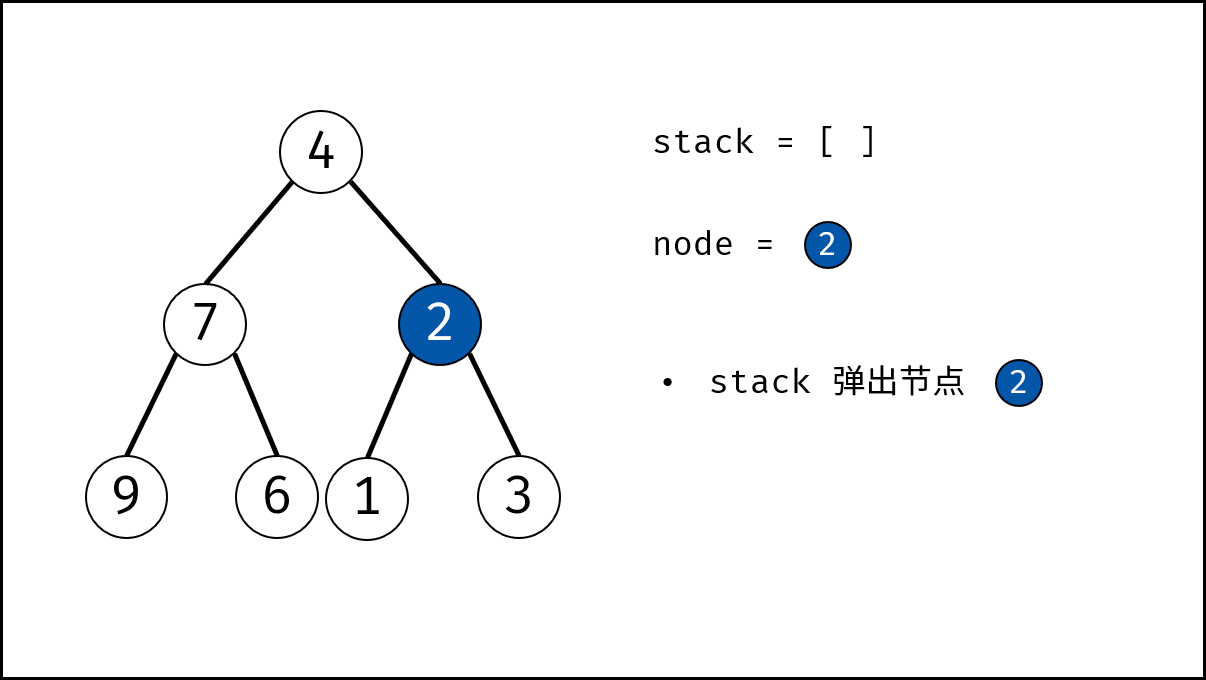Picture22.png](https://pic.leetcode-cn.com/c45fbb856ba6dc8e482eefad674ce762fb5051a9ddcf04c20d7d95765aa0d268-Picture22.png),![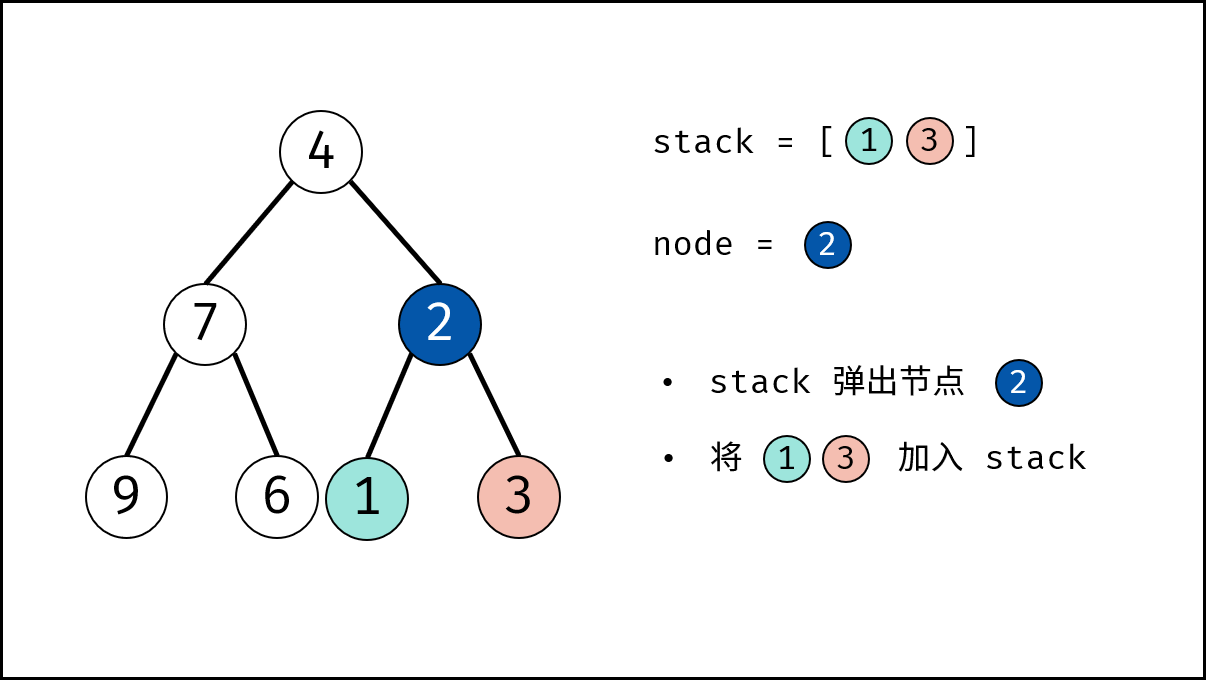Picture23.png](https://pic.leetcode-cn.com/b0c2b30dbfff1f95c6c23346ee4a7be585d6e6e88316de09f6ea26af175f3d02-Picture23.png),![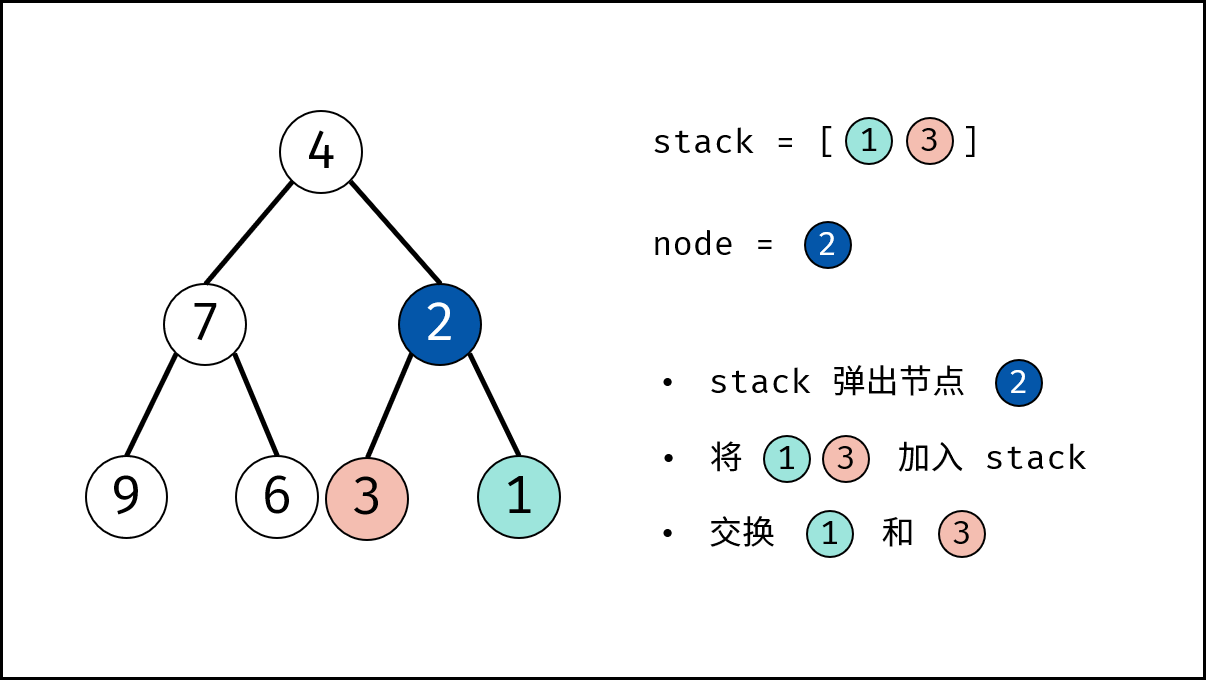Picture24.png](https://pic.leetcode-cn.com/5f53c023643258091591e0b9b59140592bbb295a64729f479f5c9381e2be6d68-Picture24.png),![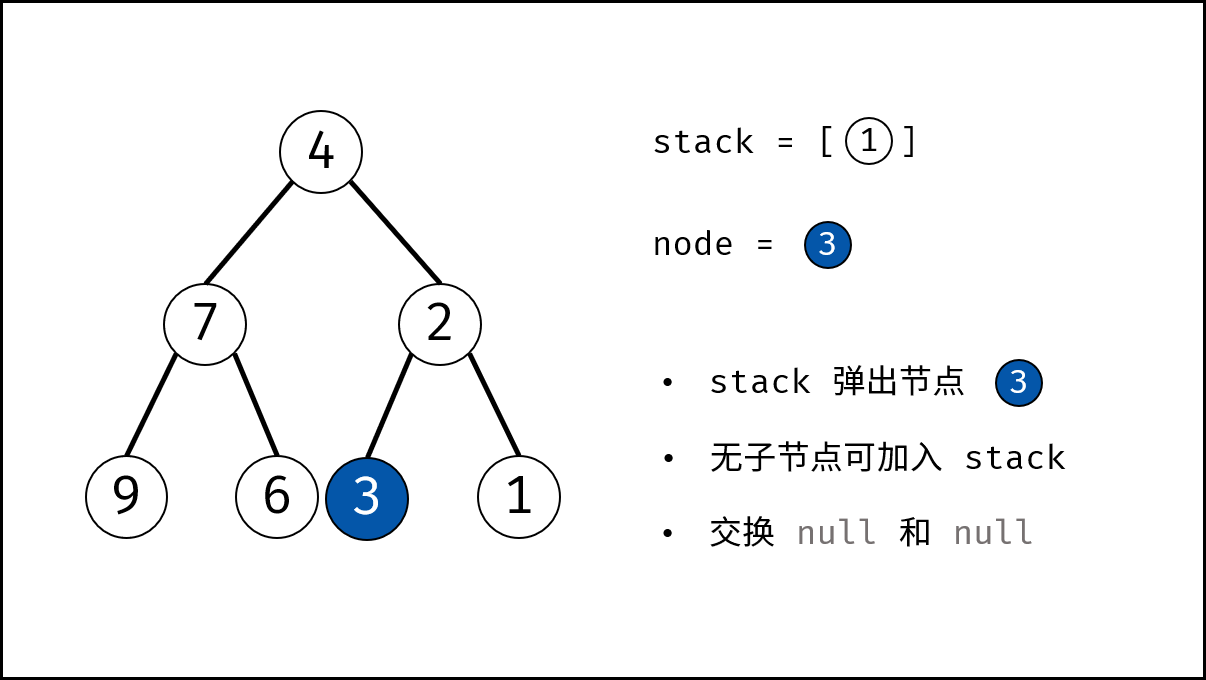Picture25.png](https://pic.leetcode-cn.com/e70dfd905f7f6940675941ef3380cf6fbf46bea448fbfba79b781816f78c841e-Picture25.png),![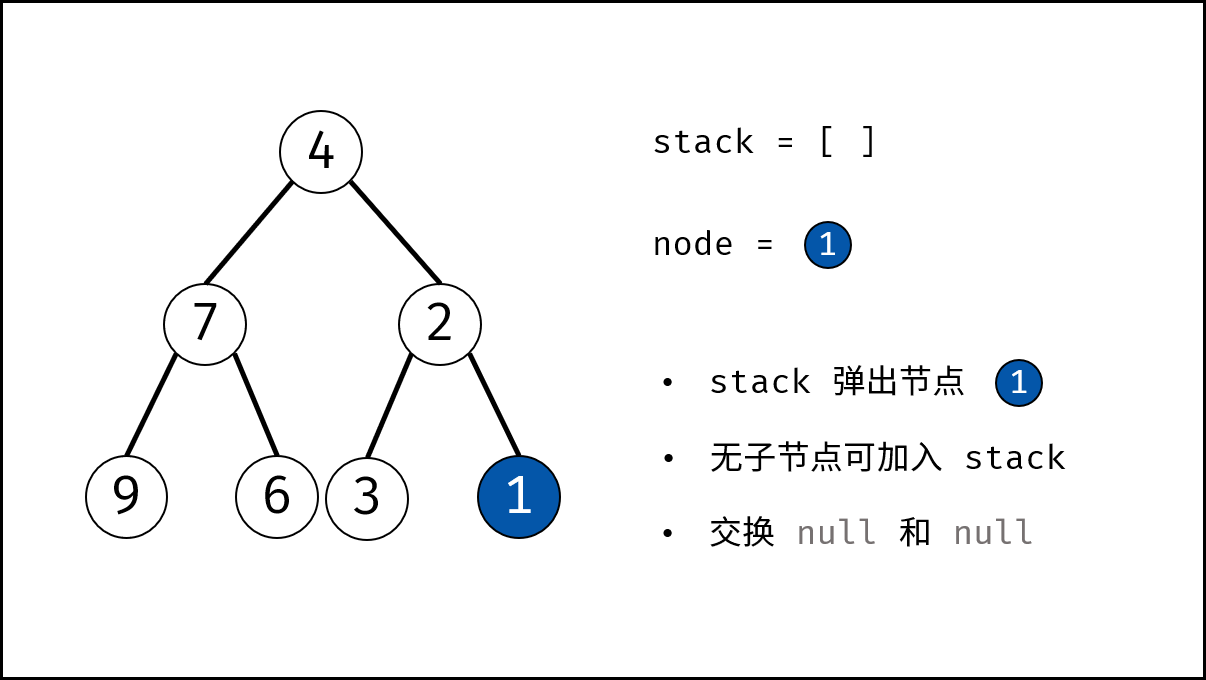Picture26.png](https://pic.leetcode-cn.com/08705f9b4b36ee742cb09aca06303f458699b029dfba1b520f2374d7909322ee-Picture26.png),![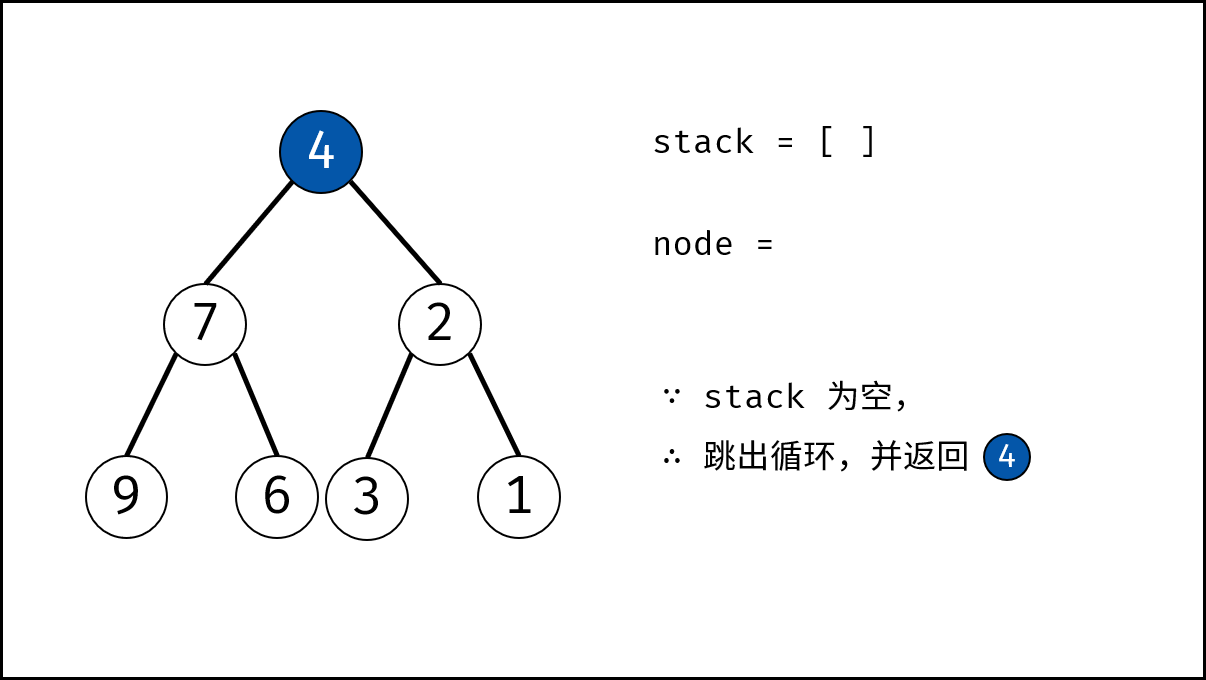Picture27.png](https://pic.leetcode-cn.com/d2f65256baa602a1b85e0d92c5a93c239ca96a1119196eda4140b1dfbbb4f1d3-Picture27.png)>
### 代码：
```Python []
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
if not root: return
stack = [root]
while stack:
node = stack.pop()
if node.left: stack.append(node.left)
if node.right: stack.append(node.right)
node.left, node.right = node.right, node.left
return root
```
```Java []
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return null;
Stack<TreeNode> stack = new Stack<>() {{ add(root); }};
while(!stack.isEmpty()) {
TreeNode node = stack.pop();
if(node.left != null) stack.add(node.left);
if(node.right != null) stack.add(node.right);
TreeNode tmp = node.left;
node.left = node.right;
node.right = tmp;
}
return root;
}
}
```
```C++ []
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(root == nullptr) return nullptr;
stack<TreeNode*> stack;
stack.push(root);
while (!stack.empty())
{
TreeNode* node = stack.top();
stack.pop();
if (node->left != nullptr) stack.push(node->left);
if (node->right != nullptr) stack.push(node->right);
TreeNode* tmp = node->left;
node->left = node->right;
node->right = tmp;
}
return root;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** 如下图所示，最差情况下，栈 `stack` 最多同时存储 $\frac{N + 1}{2}$ 个节点，占用 $O(N)$ 额外空间。
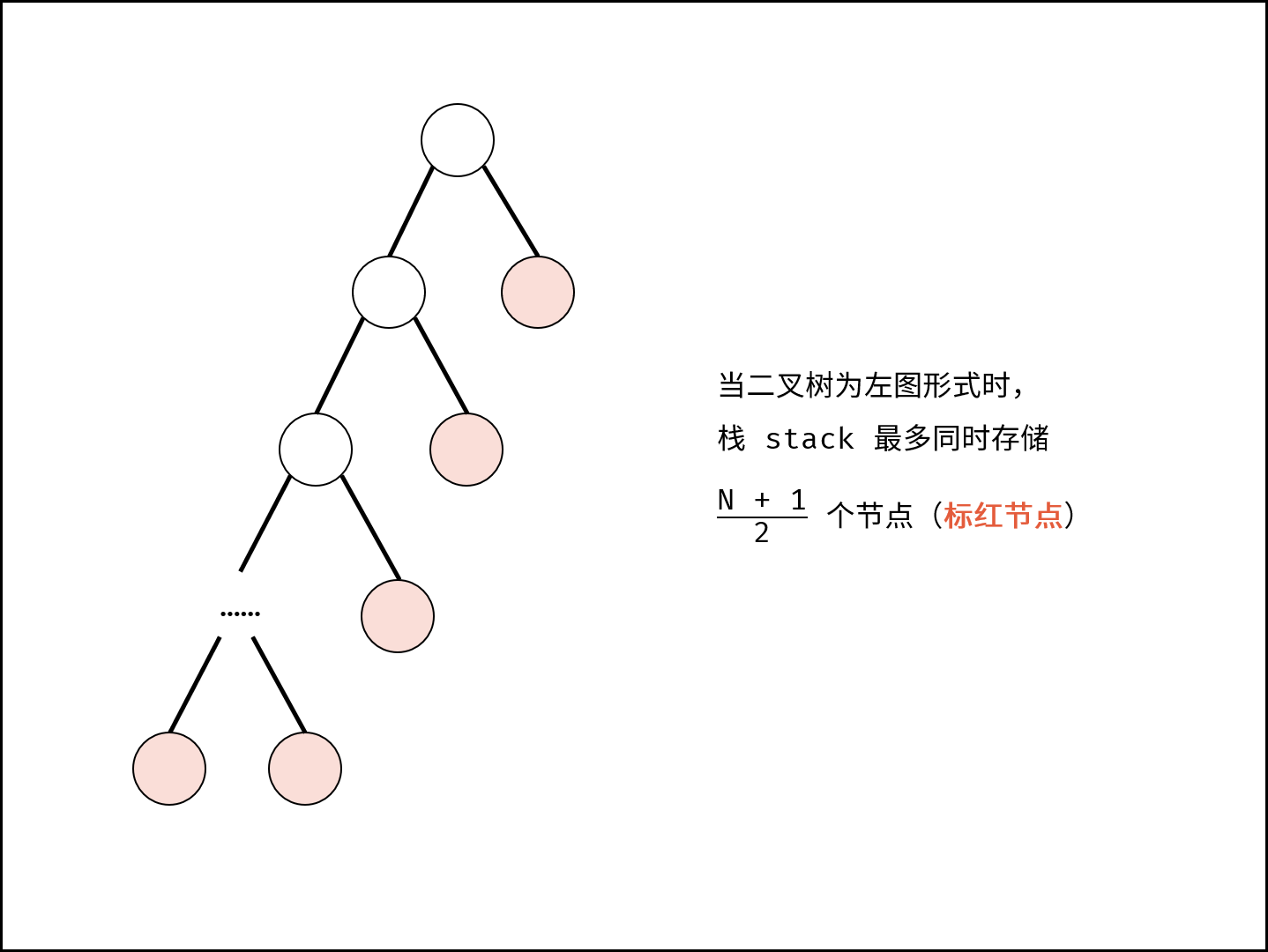![Picture0.png](https://pic.leetcode-cn.com/1614450330-bTAcyj-Picture0.png){:align=center width=450}

79
leetbook_ioa/docs/LCR 145. 判断对称二叉树.md Executable file
View File

@@ -0,0 +1,79 @@
## 解题思路：
**对称二叉树定义：** 对于树中 **任意两个对称节点** `L` 和 `R `，一定有：
- `L.val = R.val` ：即此两对称节点值相等。
- `L.left.val = R.right.val` ：即 $L$ 的 左子节点 和 $R$ 的 右子节点 对称；
- `L.right.val = R.left.val` ：即 $L$ 的 右子节点 和 $R$ 的 左子节点 对称。
根据以上规律，考虑从顶至底递归，判断每对左右节点是否对称，从而判断树是否为对称二叉树。
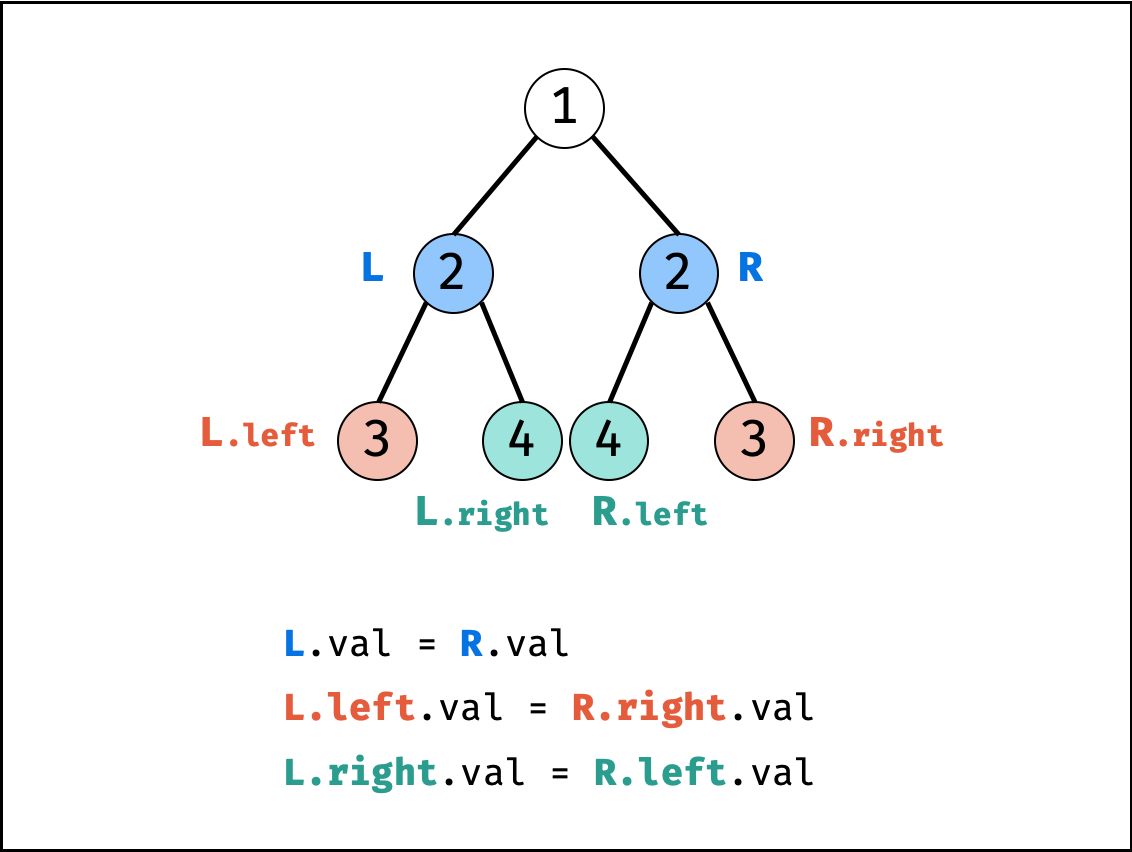![Picture1.png](https://pic.leetcode-cn.com/1599398062-PbkpuX-Picture1.png){:align=center width=450}
### 算法流程：
**`checkSymmetricTree(root)` ：**
- **特例处理：** 若根节点 `root` 为空，则直接返回 $\text{true}$ 。
- **返回值：** 即 `recur(root.left, root.right)` ;
**`recur(L, R)` ：**
- **终止条件：**
- 当 `L` 和 `R` 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 $\text{true}$ ；
- 当 `L` 或 `R` 中只有一个越过叶节点： 此树不对称，因此返回 $\text{false}$ ；
- 当节点 `L` 值 $\ne$ 节点 `R` 值： 此树不对称，因此返回 $\text{false}$ ；
- **递推工作：**
- 判断两节点 `L.left` 和 `R.right` 是否对称，即 `recur(L.left, R.right)` ；
- 判断两节点 `L.right` 和 `R.left` 是否对称，即 `recur(L.right, R.left)` ；
- **返回值：** 两对节点都对称时，才是对称树，因此用与逻辑符 `&&` 连接。
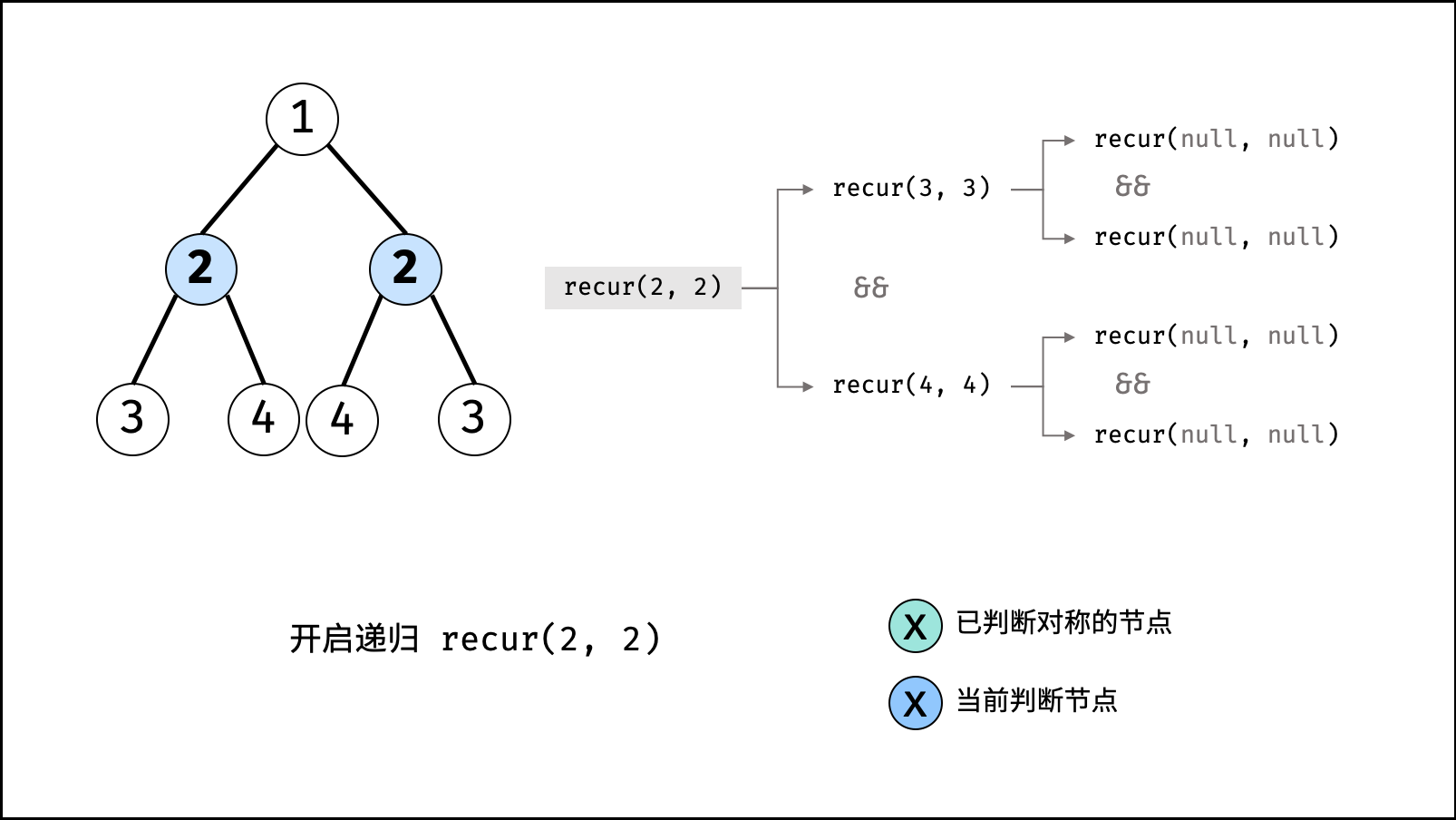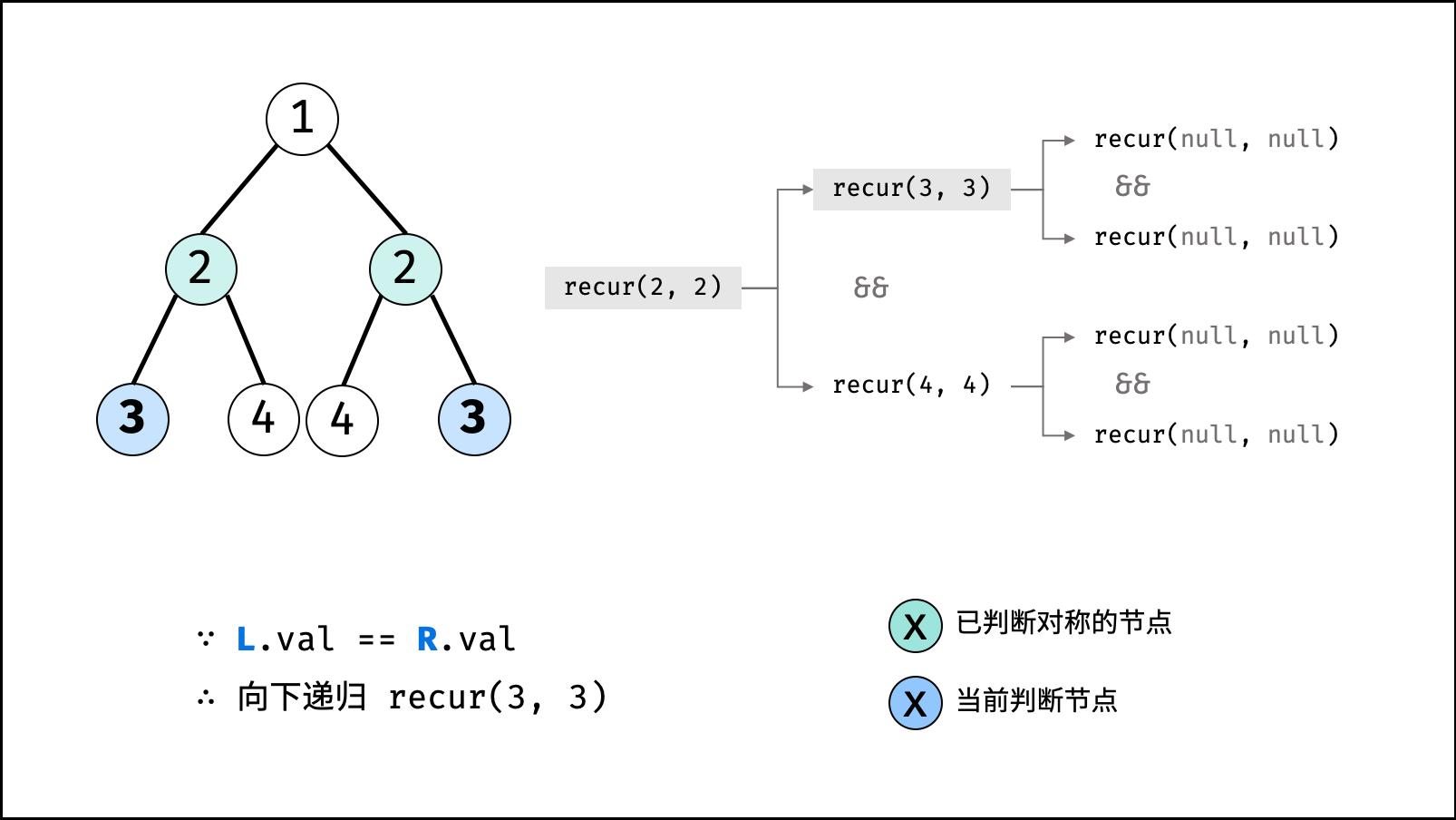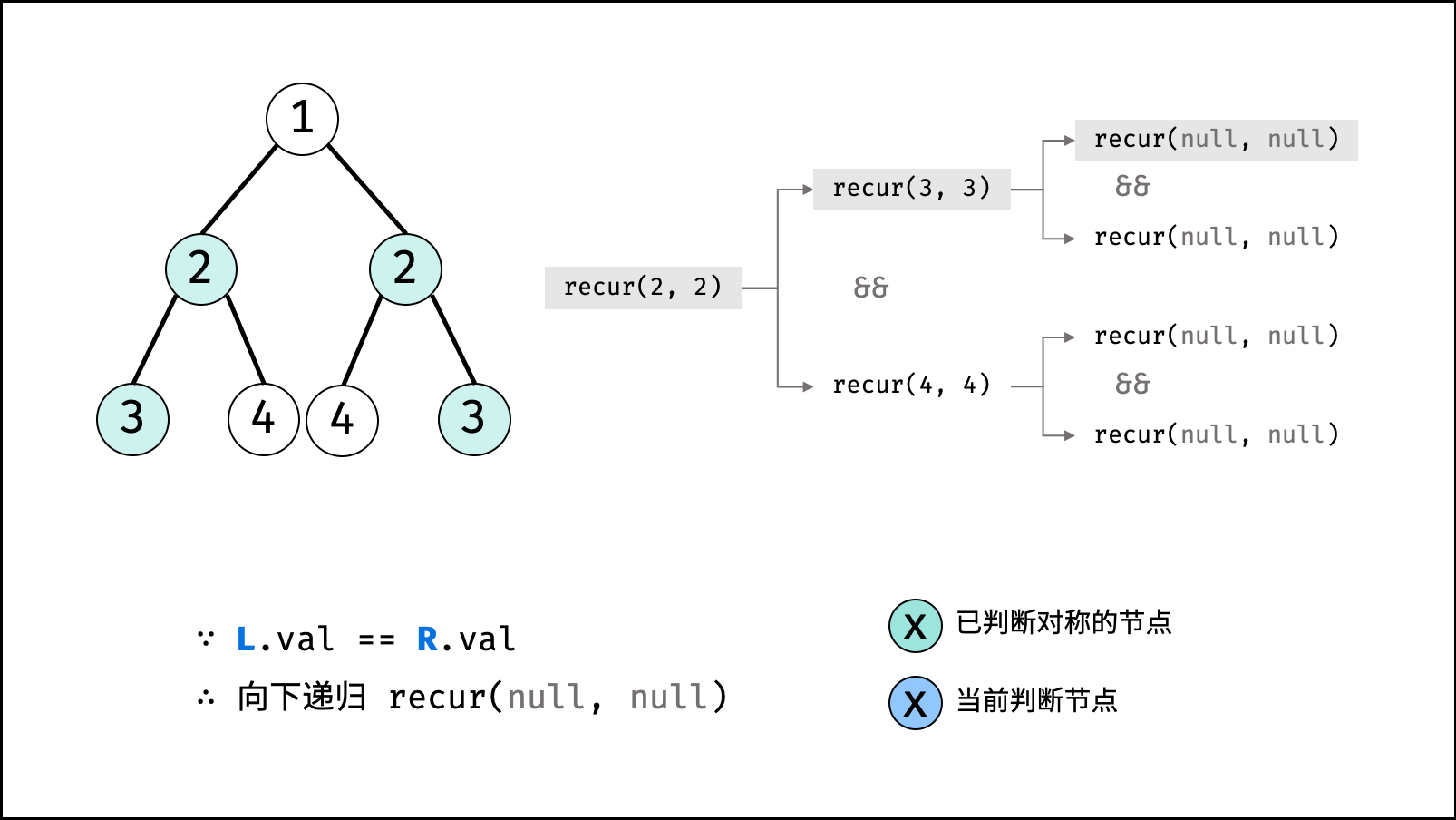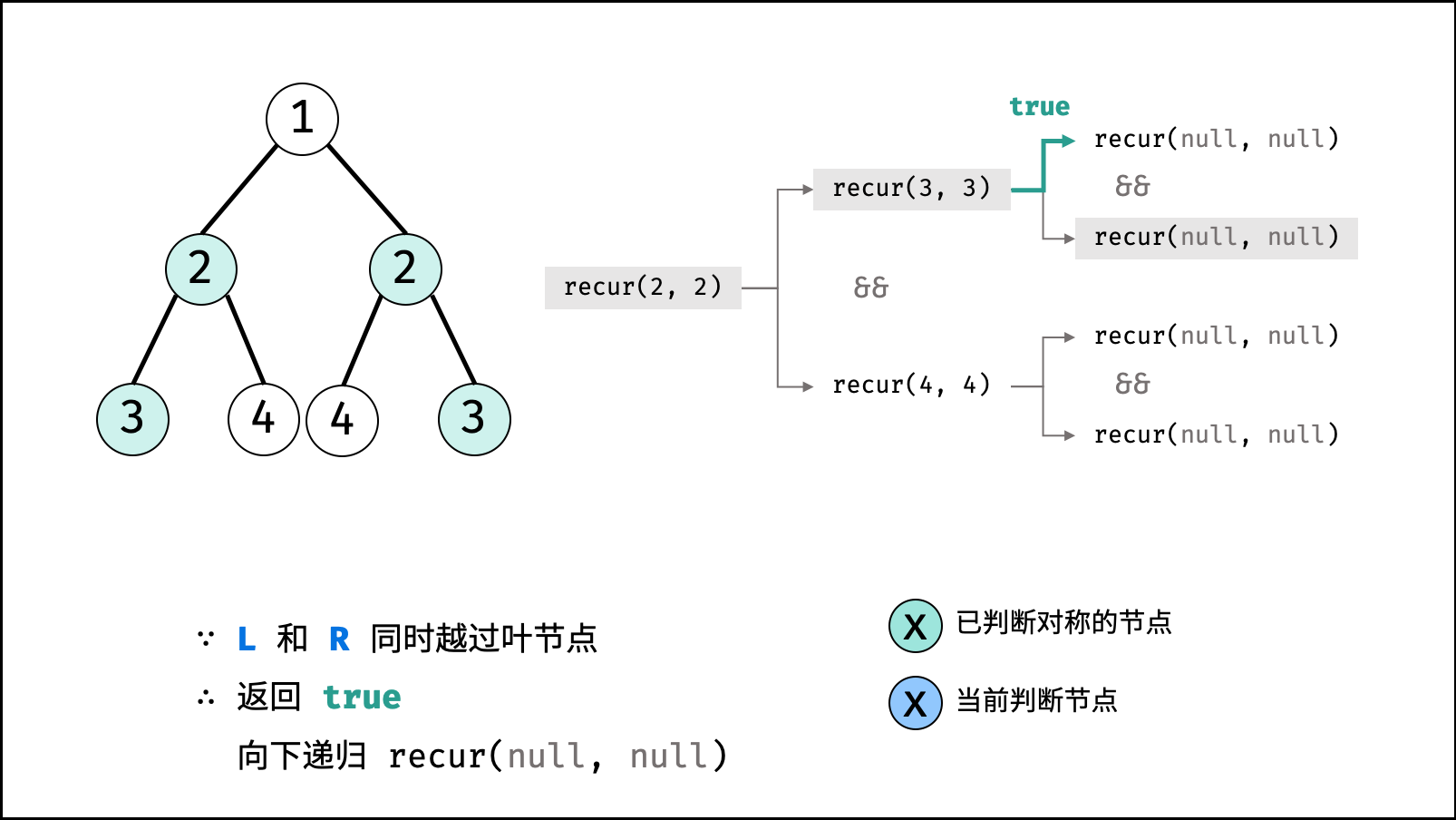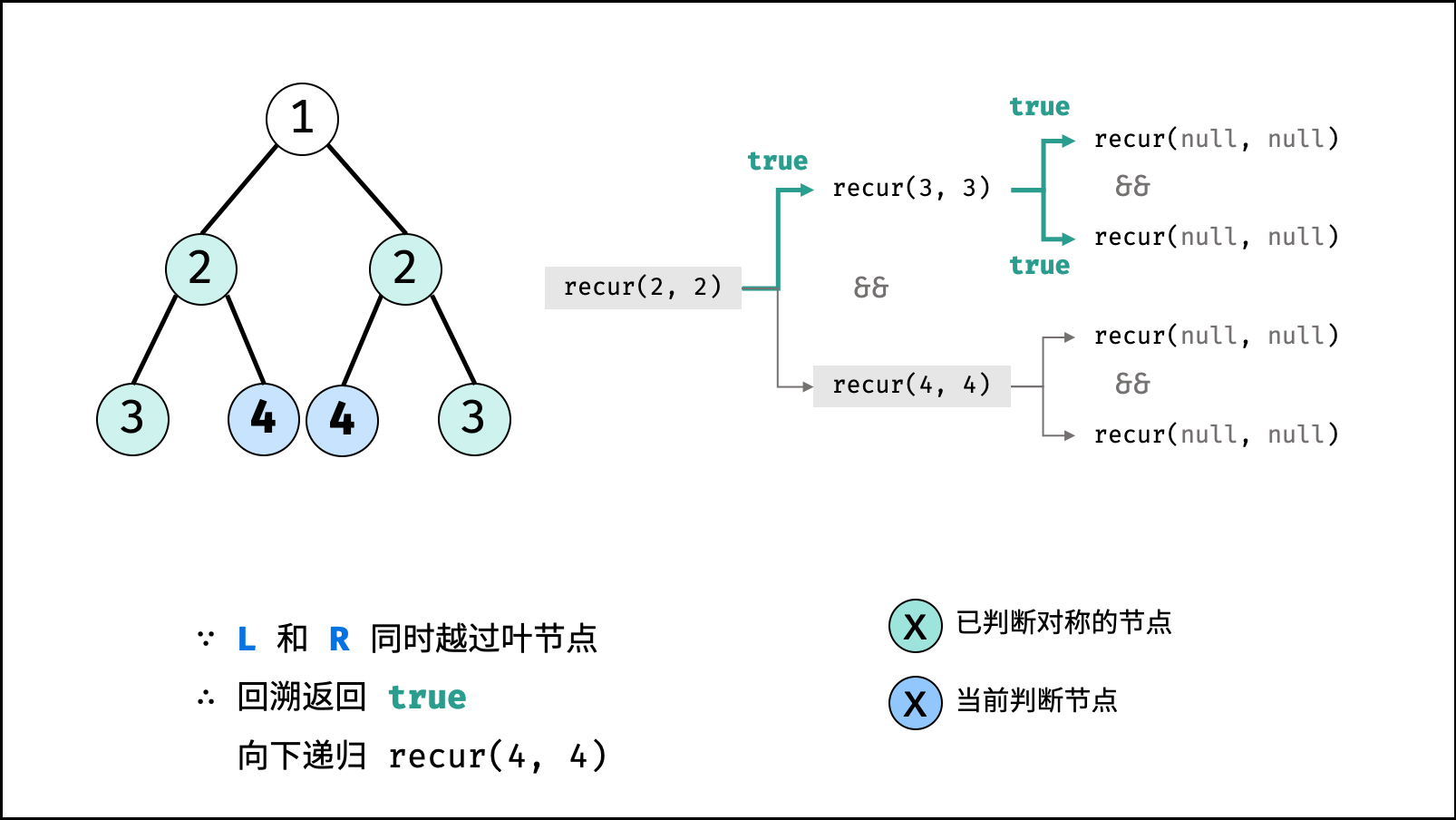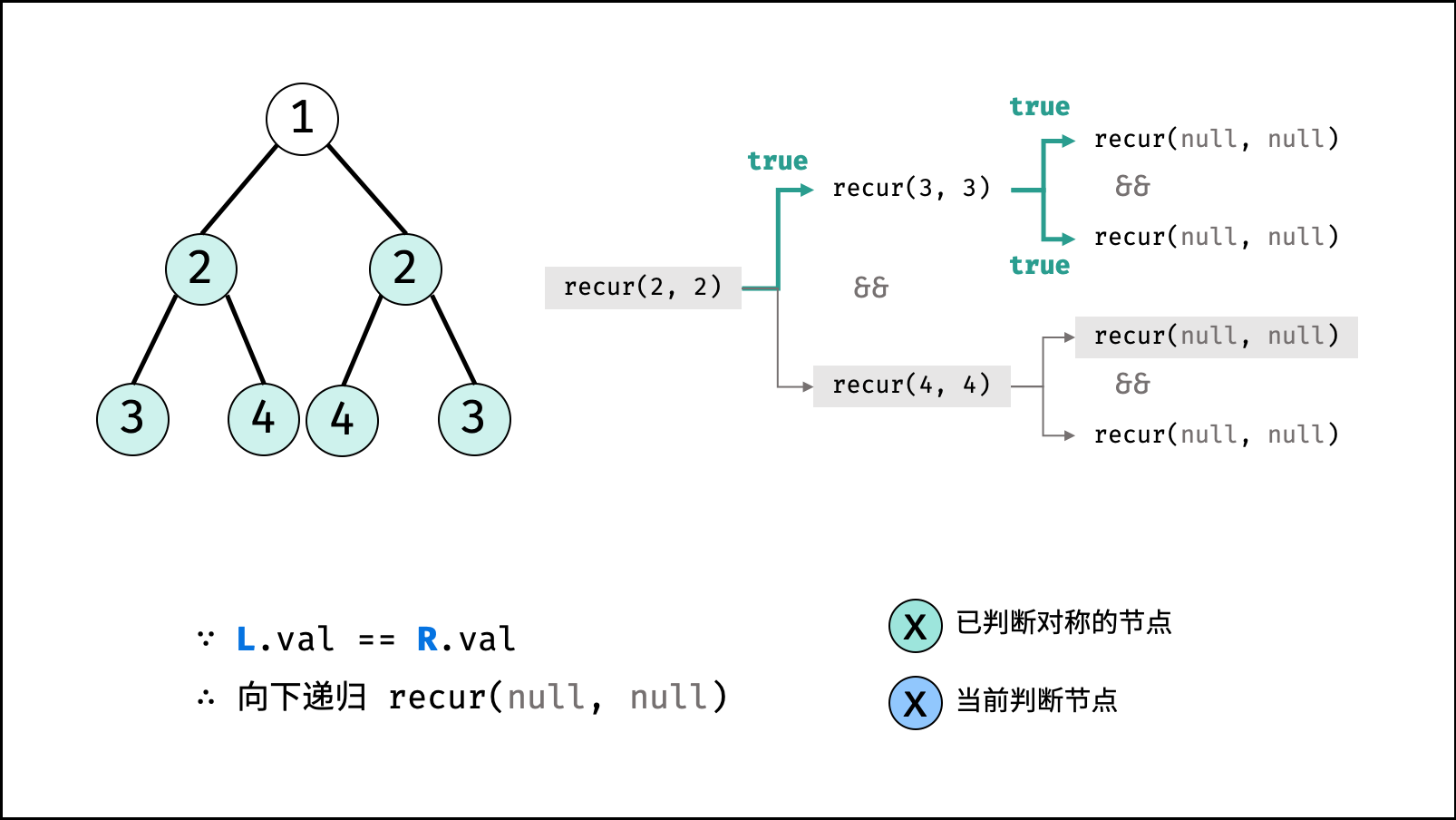<![Picture3.png](https://pic.leetcode-cn.com/1599398062-NdosHq-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599398062-AQIJat-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599398062-VpQoLn-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599398062-LdDcFl-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599398062-fkGmWS-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599398062-NxoTTP-Picture8.png),![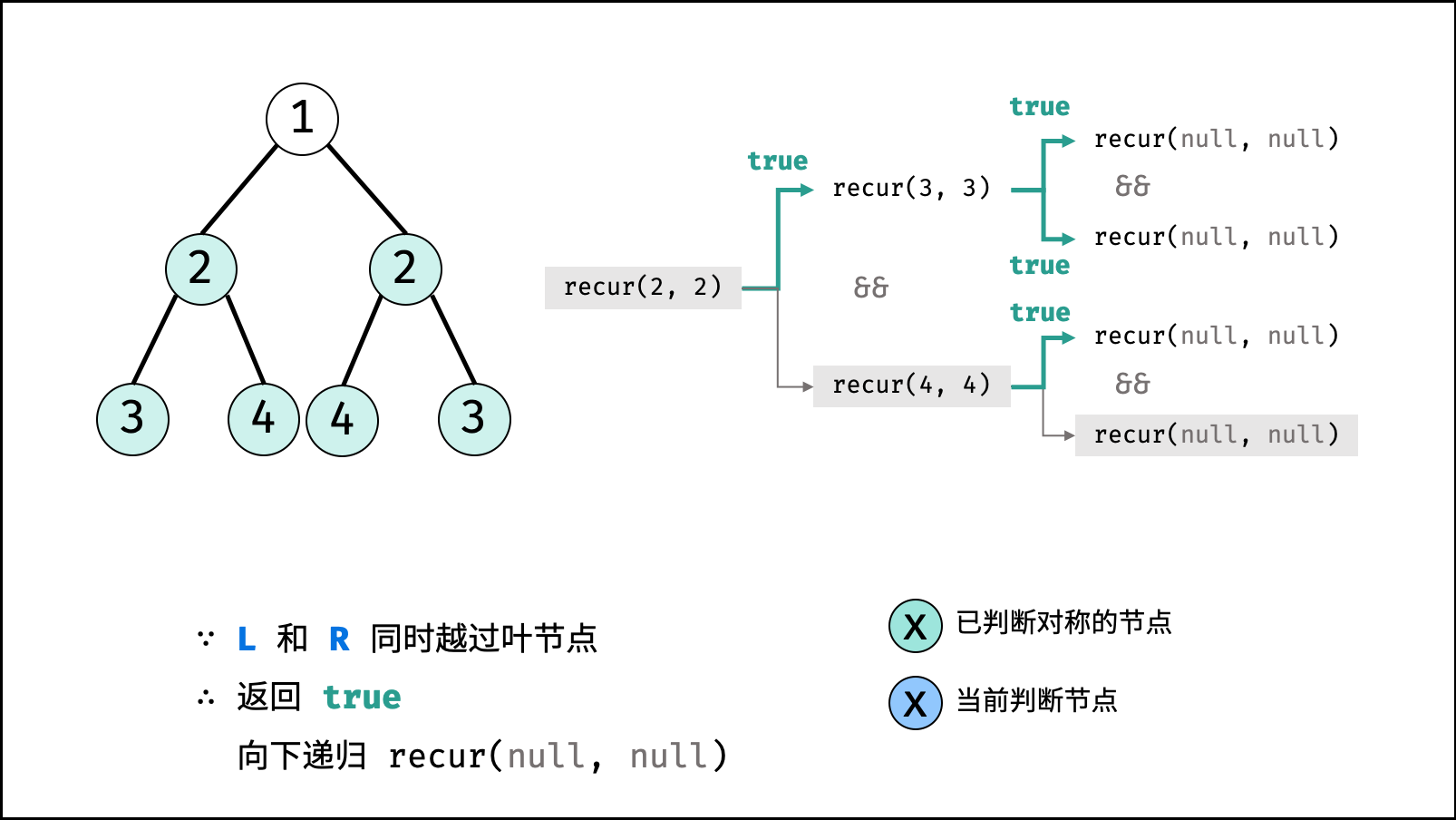Picture9.png](https://pic.leetcode-cn.com/1599398062-hqfyyY-Picture9.png),![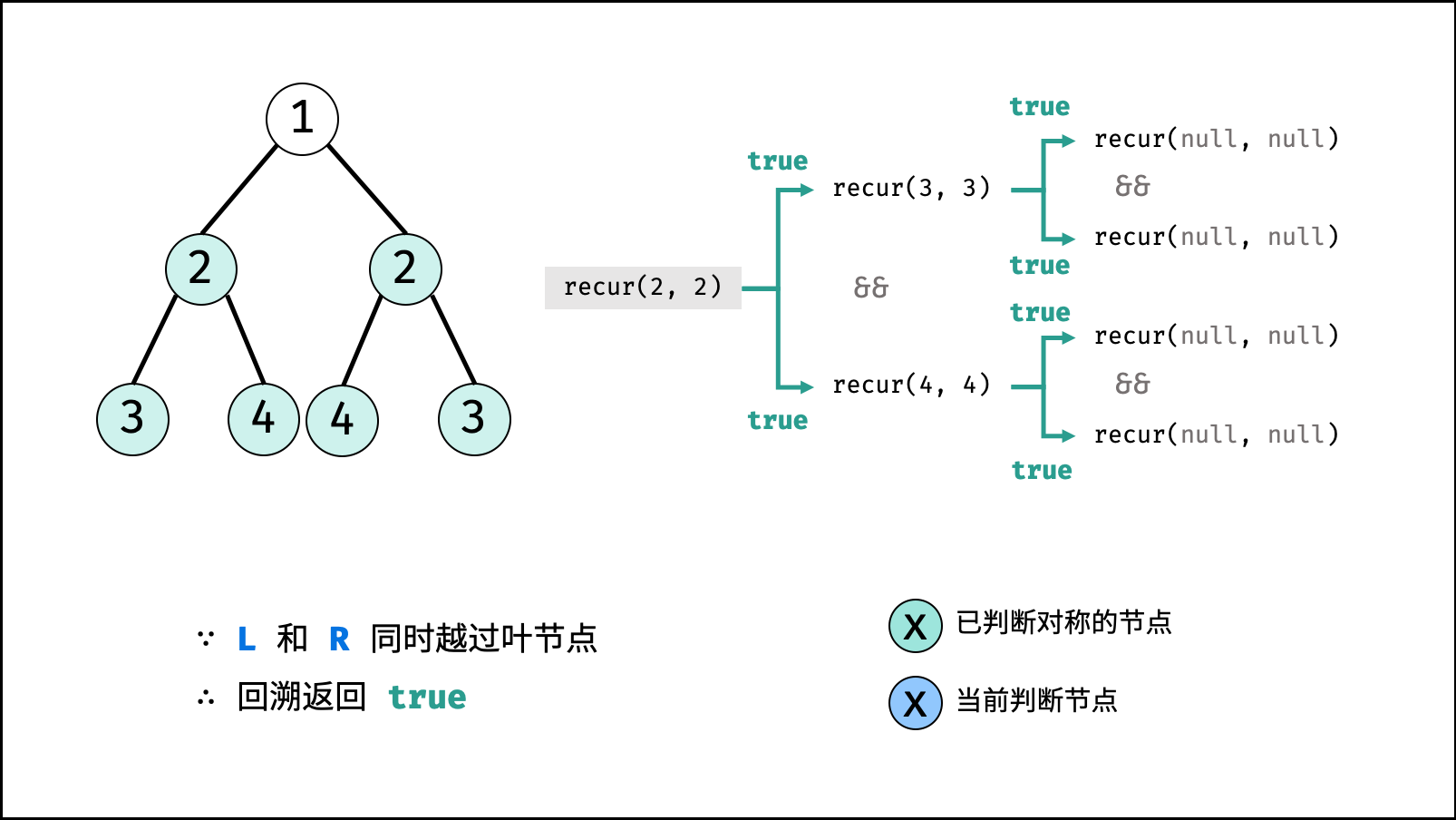Picture10.png](https://pic.leetcode-cn.com/1599400509-JkxjsM-Picture10.png),![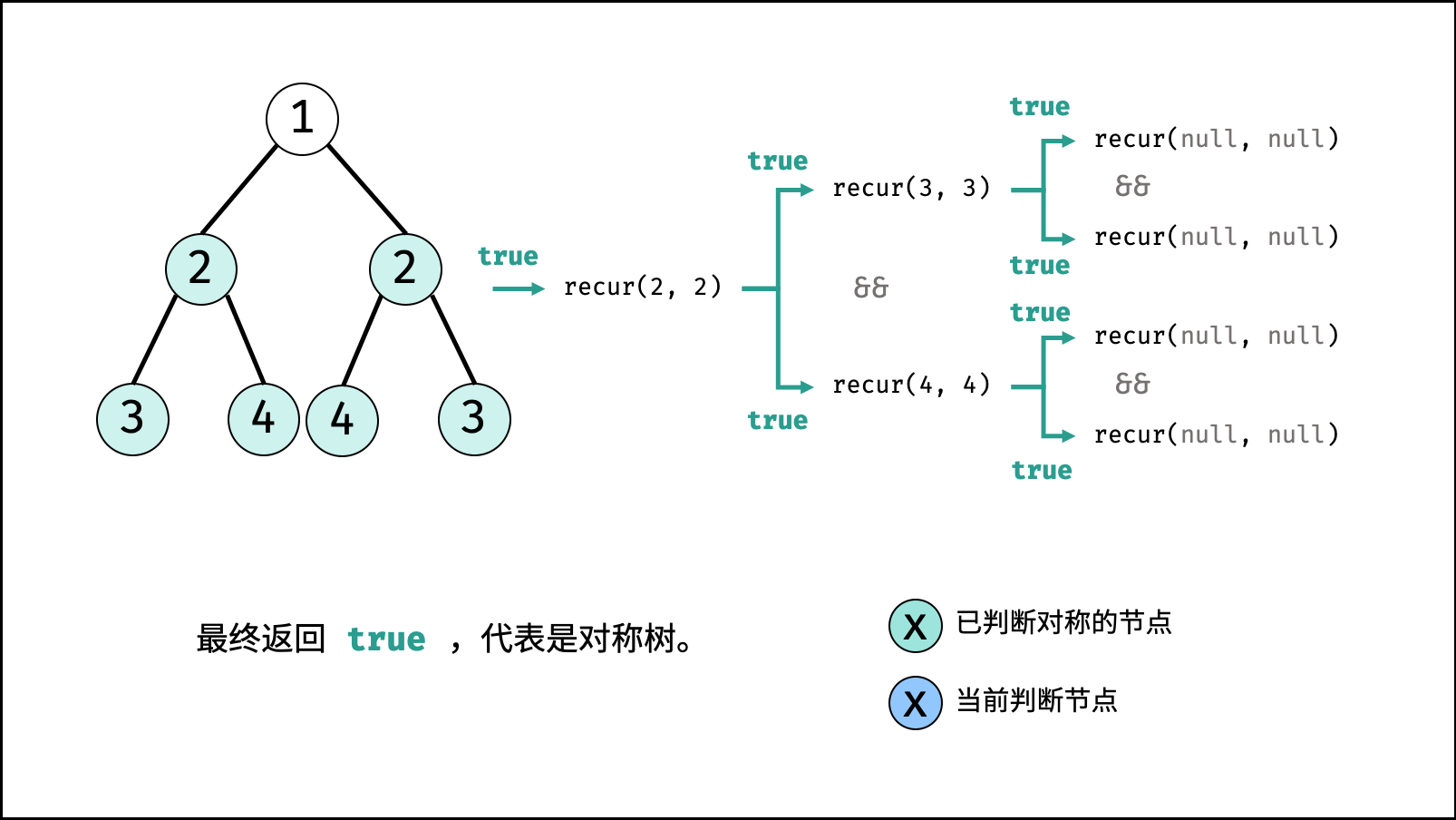Picture11.png](https://pic.leetcode-cn.com/1599398062-DIXRnB-Picture11.png)>
## 代码：
```Python []
class Solution:
def checkSymmetricTree(self, root: TreeNode) -> bool:
def recur(L, R):
if not L and not R: return True
if not L or not R or L.val != R.val: return False
return recur(L.left, R.right) and recur(L.right, R.left)
return not root or recur(root.left, root.right)
```
```Java []
class Solution {
public boolean checkSymmetricTree(TreeNode root) {
return root == null || recur(root.left, root.right);
}
boolean recur(TreeNode L, TreeNode R) {
if(L == null && R == null) return true;
if(L == null || R == null || L.val != R.val) return false;
return recur(L.left, R.right) && recur(L.right, R.left);
}
}
```
```C++ []
class Solution {
public:
bool checkSymmetricTree(TreeNode* root) {
return root == nullptr || recur(root->left, root->right);
}
private:
bool recur(TreeNode* L, TreeNode* R) {
if(L == nullptr && R == nullptr) return true;
if(L == nullptr || R == nullptr || L->val != R->val) return false;
return recur(L->left, R->right) && recur(L->right, R->left);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为二叉树的节点数量，每次执行 `recur()` 可以判断一对节点是否对称，因此最多调用 $N/2$ 次 `recur()` 方法。
- **空间复杂度 $O(N)$ ：** 如下图所示，最差情况下（二叉树退化为链表），系统使用 $O(N)$ 大小的空间。
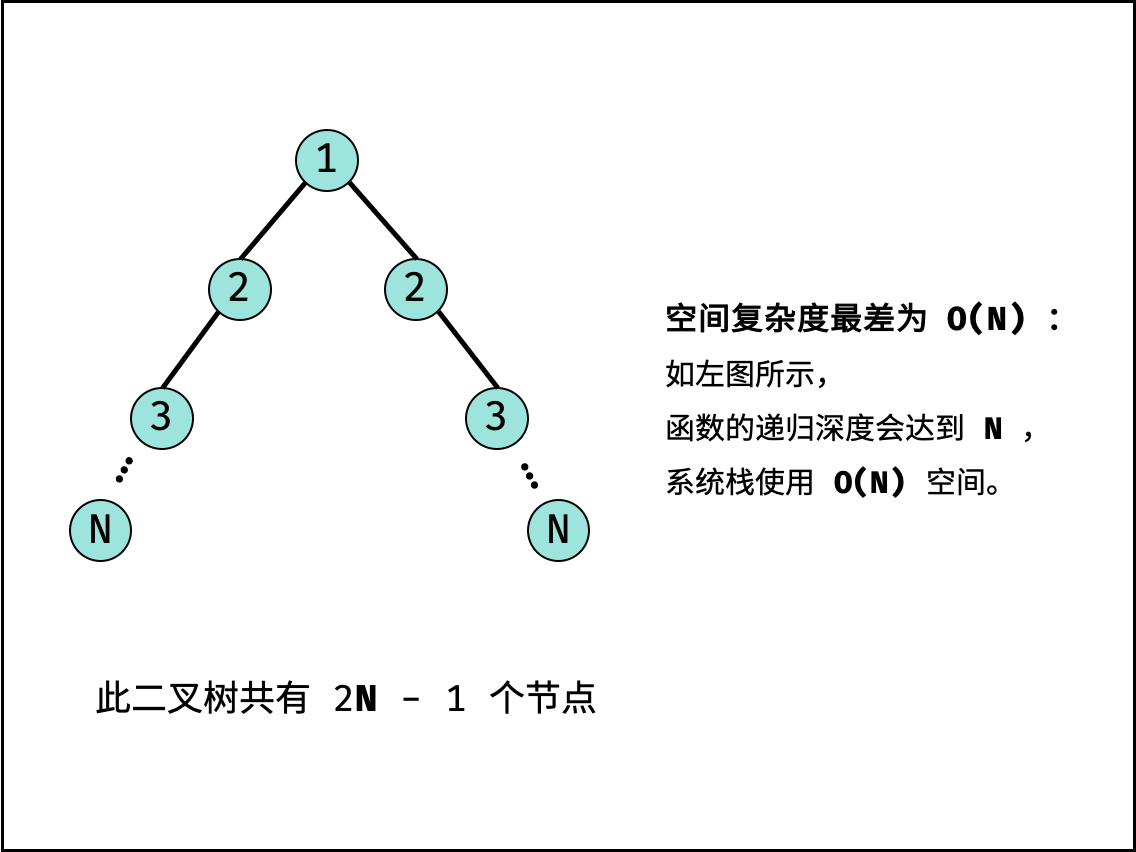![Picture2.png](https://pic.leetcode-cn.com/1599398062-LmPbix-Picture2.png){:align=center width=450}

106
leetbook_ioa/docs/LCR 146. 螺旋遍历二维数组.md Executable file
View File

@@ -0,0 +1,106 @@
## 解题思路：
根据题目示例 `array = [[1,2,3],[4,5,6],[7,8,9]]` 的对应输出 `[1,2,3,6,9,8,7,4,5]` 可以发现，顺时针打印矩阵的顺序是 **“从左向右、从上向下、从右向左、从下向上”** 循环。
因此，考虑设定矩阵的 “左、上、右、下” 四个边界，模拟以上矩阵遍历顺序。
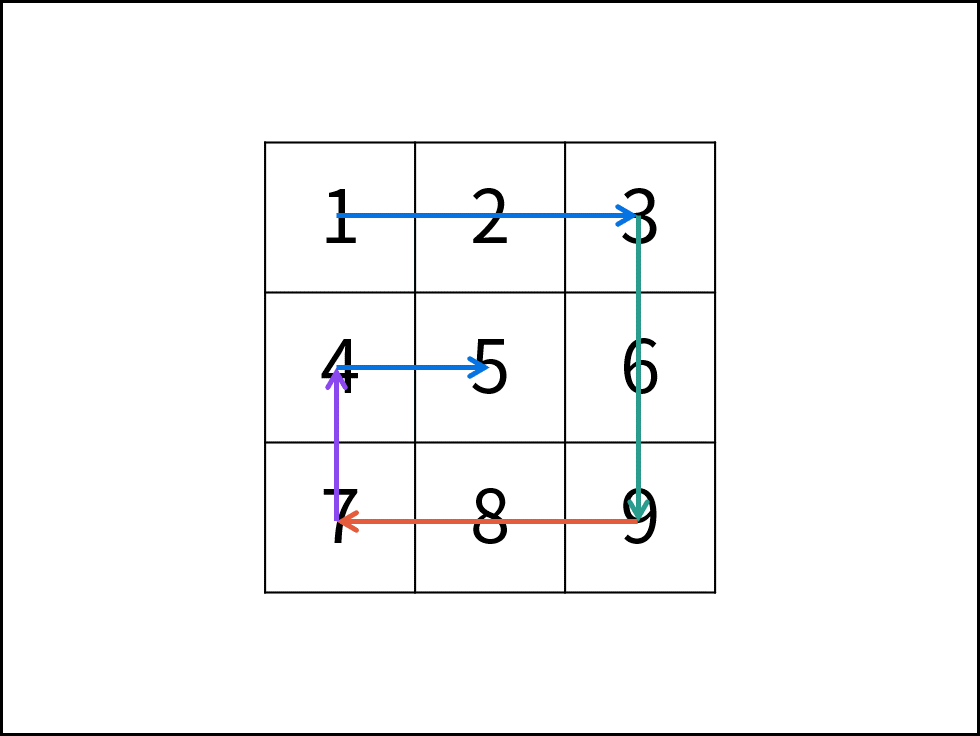![Picture1.png](https://pic.leetcode-cn.com/7605d807782923e4ad3c7995dc2485f538f202ac326bb330fe997f449123a548-Picture1.png){:align=center width=450}
### 算法流程：
1. **空值处理：** 当 `array` 为空时，直接返回空列表 `[]` 即可。
2. **初始化：** 矩阵 左、右、上、下 四个边界 `l` , `r` , `t` , `b` ，用于打印的结果列表 `res` 。
3. **循环打印：** “从左向右、从上向下、从右向左、从下向上” 四个方向循环打印；
1. 根据边界打印，即将元素按顺序添加至列表 `res` 尾部；
2. 边界向内收缩 1 （代表已被打印）；
3. 判断边界是否相遇（是否打印完毕），若打印完毕则跳出。
4. **返回值：** 返回 `res` 即可。
| 打印方向 | 1. 根据边界打印 | 2. 边界向内收缩 | 3. 是否打印完毕 |
| -------- | ---------------------- | ----------------- | --------------- |
| 从左向右 | 左边界`l` ，右边界 `r` | 上边界 `t` 加 $1$ | 是否 `t > b` |
| 从上向下 | 上边界 `t` ，下边界`b` | 右边界 `r` 减 $1$ | 是否 `l > r` |
| 从右向左 | 右边界 `r` ，左边界`l` | 下边界 `b` 减 $1$ | 是否 `t > b` |
| 从下向上 | 下边界 `b` ，上边界`t` | 左边界 `l` 加 $1$ | 是否 `l > r` |
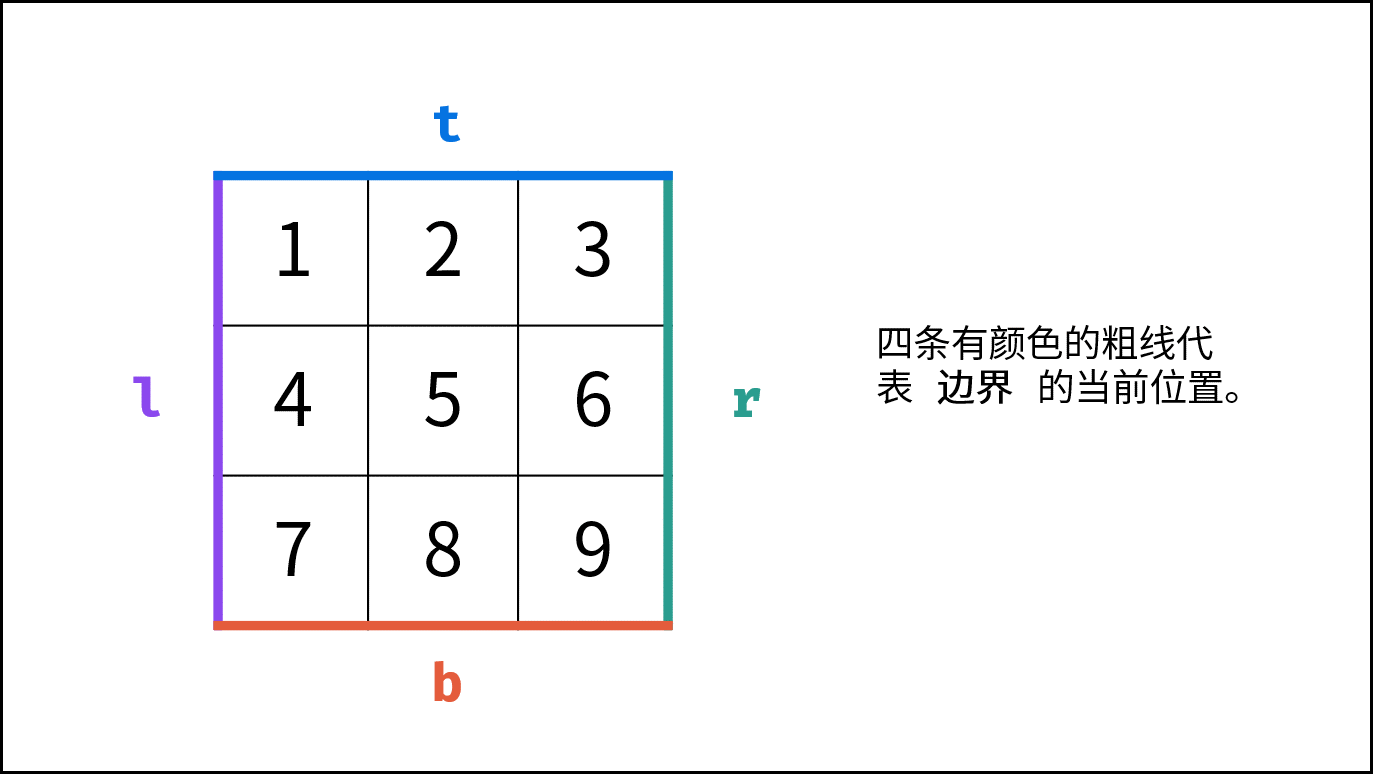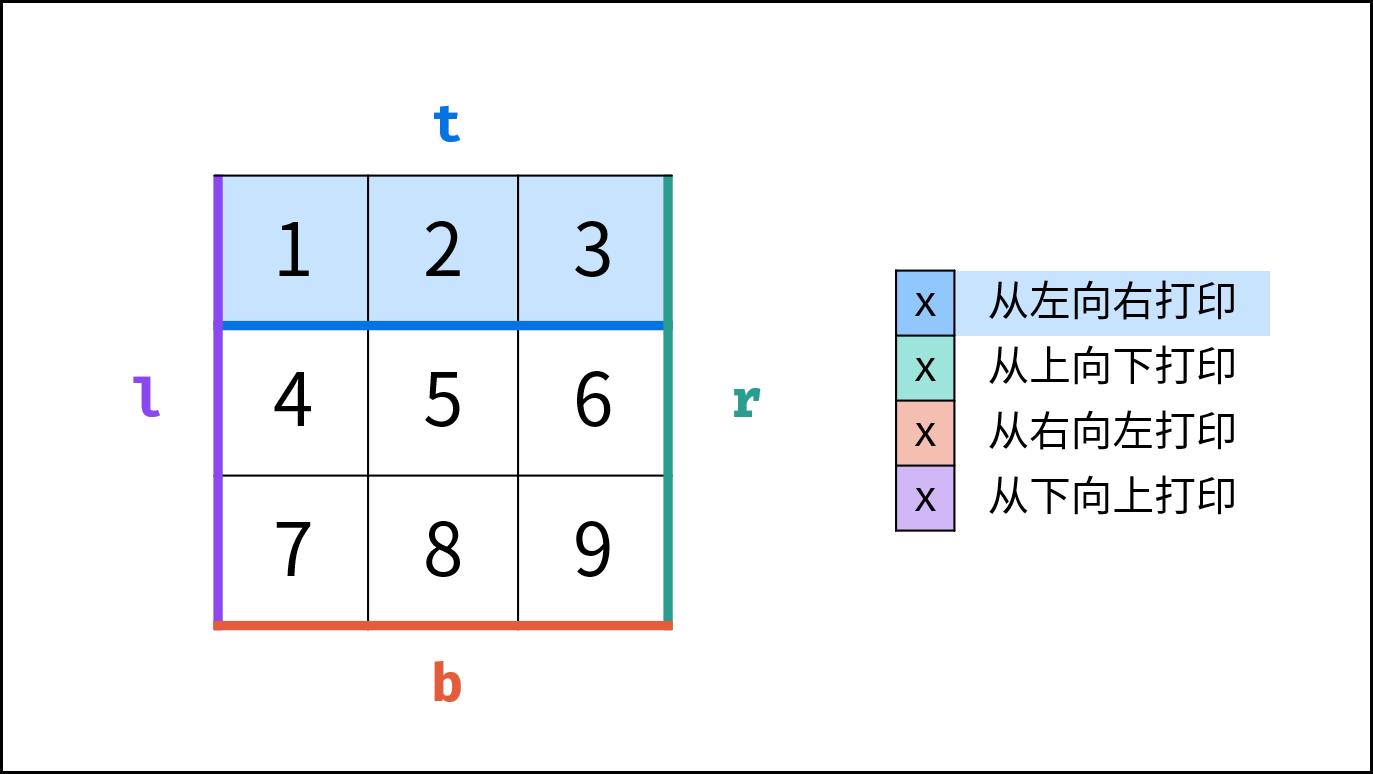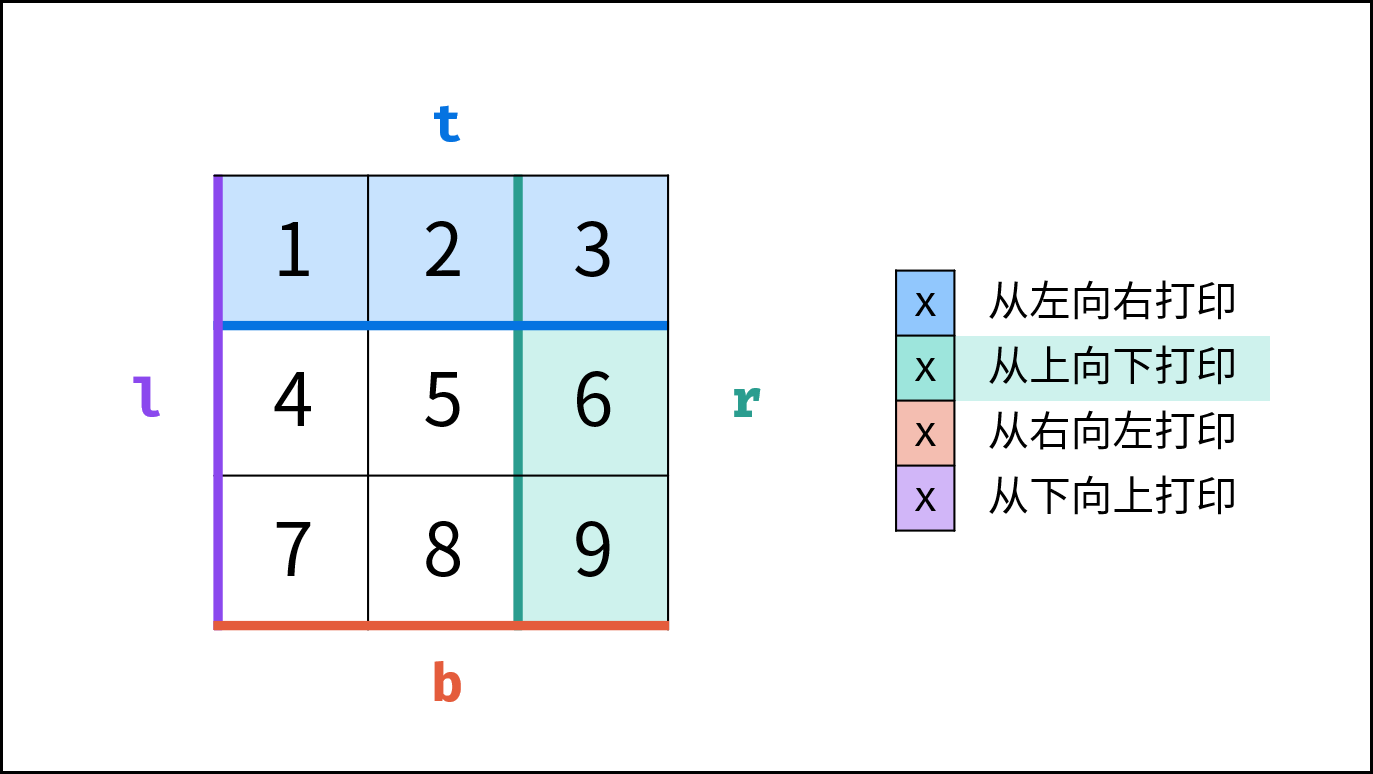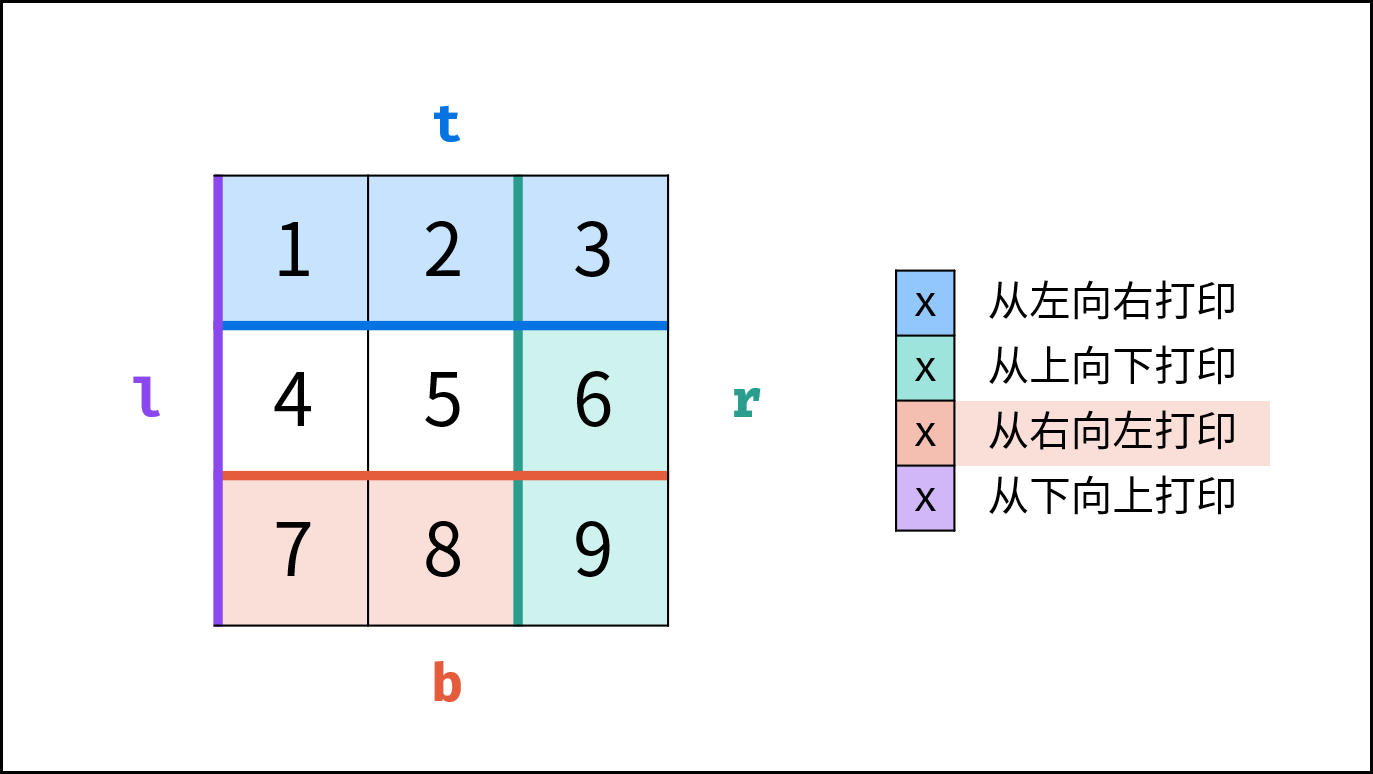<![Picture2.png](https://pic.leetcode-cn.com/1ad0fe88d15dc87643435eb7a17b368191725a44da4596722977e5798ace5b62-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/193444cbca5529fcd1bafec33ef576fe1309690be2c0110de05868f4415a8723-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/bca38a428306cb2aacc00513821e74150947ba241d9b7199bcad6c7e843a0105-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/e5de1e07957417f13d9fae22e6fb18dd5331b50258f0297f00ba57d25651df4a-Picture5.png),![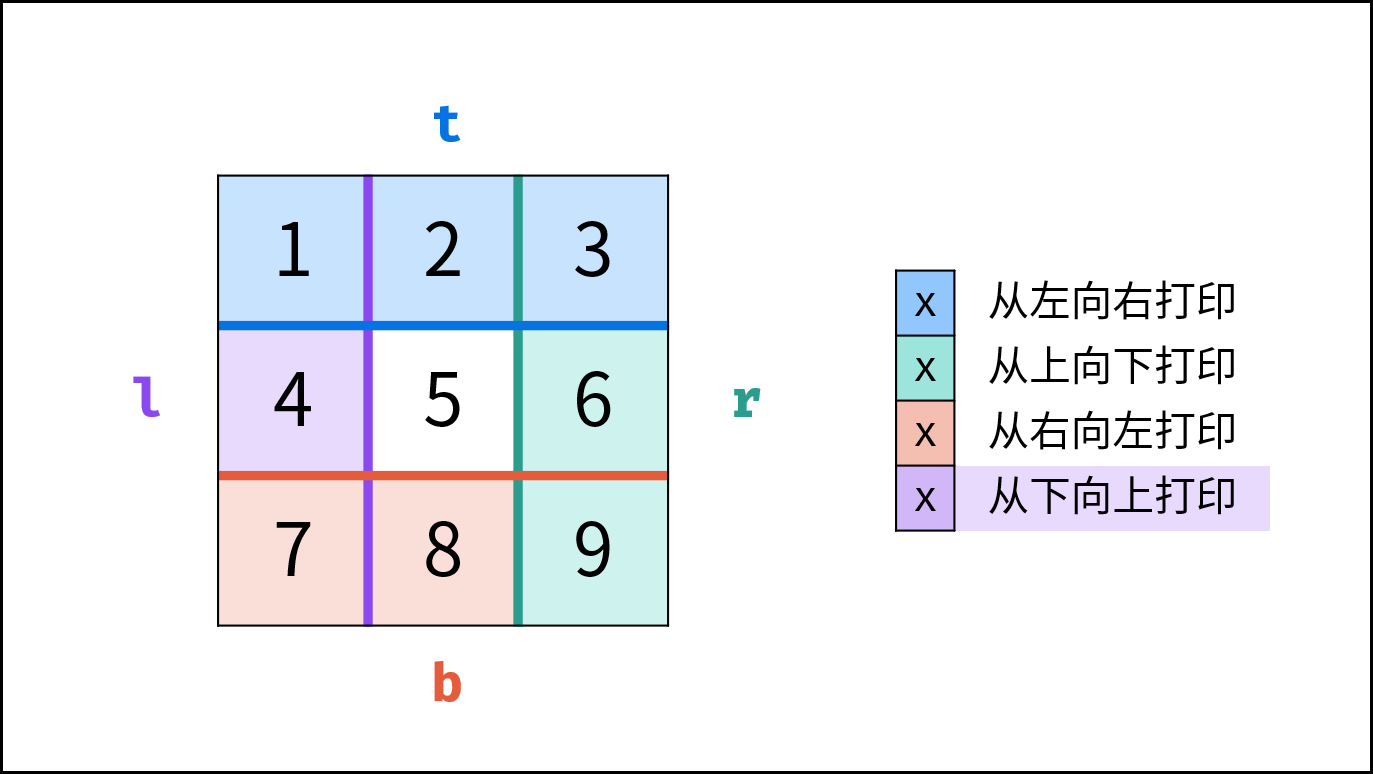Picture6.png](https://pic.leetcode-cn.com/2fde8dcd1481e390532995c02d3575ec9675a27390513c1540f40431dad7997a-Picture6.png),![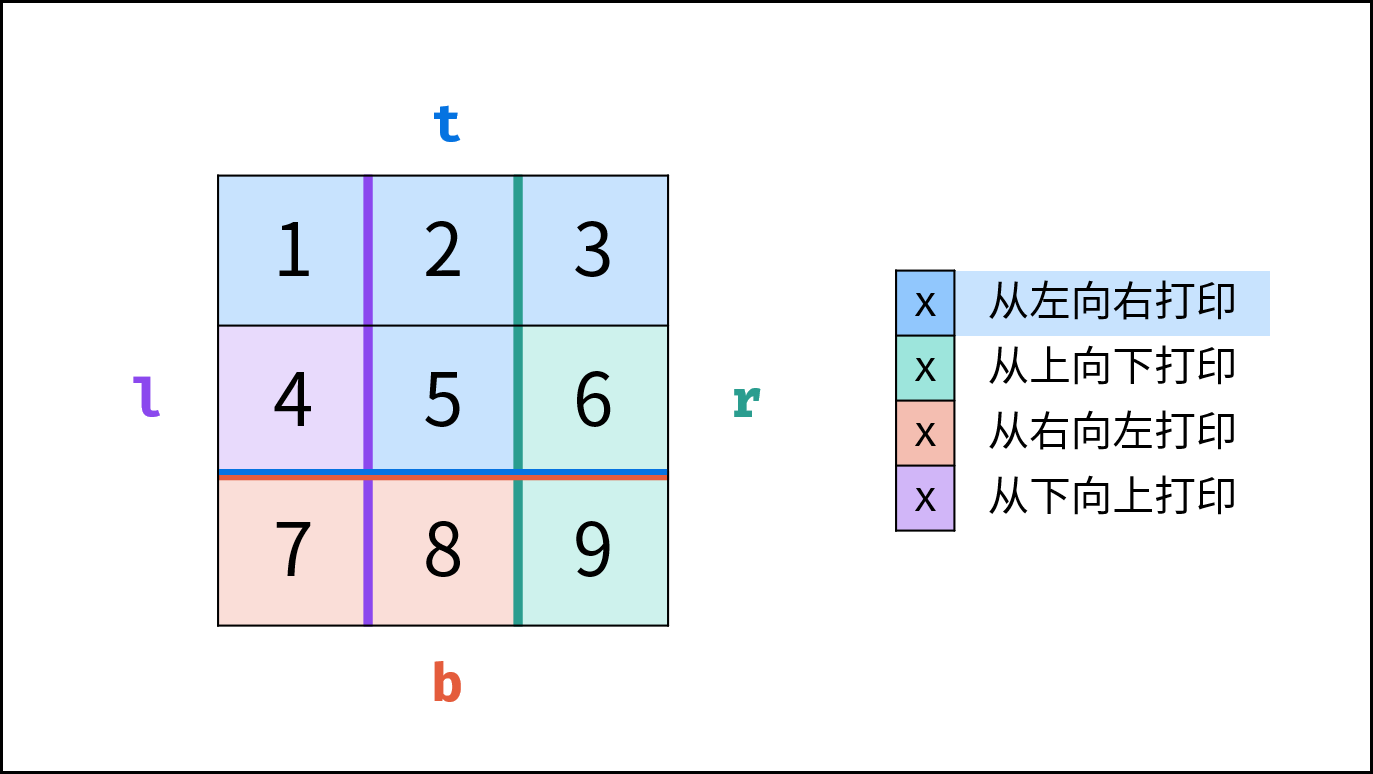Picture7.png](https://pic.leetcode-cn.com/1950d4c8ab6b09b62b7d5900ece4d8d4be882abebd2417a3030d172aedbc304e-Picture7.png)>
## 代码：
Java/C++ 代码利用了 `++` 操作的便利性，详情可见 [++i 和 i++ 的区别](https://www.jianshu.com/p/b62eac216499) ；
- `res[x++]` 等价于先给 `res[x]` 赋值，再给 `x` 自增 $1$ ；
- `++t > b` 等价于先给 `t` 自增 $1$ ，再判断 `t > b` 逻辑表达式。
> TIPS： 请注意区分数字 `1` 和变量 `l` 。
```Python []
class Solution:
def spiralArray(self, array: List[List[int]]) -> List[int]:
if not array: return []
l, r, t, b, res = 0, len(array[0]) - 1, 0, len(array) - 1, []
while True:
for i in range(l, r + 1): res.append(array[t][i]) # left to right
t += 1
if t > b: break
for i in range(t, b + 1): res.append(array[i][r]) # top to bottom
r -= 1
if l > r: break
for i in range(r, l - 1, -1): res.append(array[b][i]) # right to left
b -= 1
if t > b: break
for i in range(b, t - 1, -1): res.append(array[i][l]) # bottom to top
l += 1
if l > r: break
return res
```
```Java []
class Solution {
public int[] spiralArray(int[][] array) {
if(array.length == 0) return new int[0];
int l = 0, r = array[0].length - 1, t = 0, b = array.length - 1, x = 0;
int[] res = new int[(r + 1) * (b + 1)];
while(true) {
for(int i = l; i <= r; i++) res[x++] = array[t][i]; // left to right
if(++t > b) break;
for(int i = t; i <= b; i++) res[x++] = array[i][r]; // top to bottom
if(l > --r) break;
for(int i = r; i >= l; i--) res[x++] = array[b][i]; // right to left
if(t > --b) break;
for(int i = b; i >= t; i--) res[x++] = array[i][l]; // bottom to top
if(++l > r) break;
}
return res;
}
}
```
```C++ []
class Solution {
public:
vector<int> spiralArray(vector<vector<int>>& array)
{
if (array.empty()) return {};
int l = 0, r = array[0].size() - 1, t = 0, b = array.size() - 1;
vector<int> res;
while(true)
{
for (int i = l; i <= r; i++) res.push_back(array[t][i]); // left to right
if (++t > b) break;
for (int i = t; i <= b; i++) res.push_back(array[i][r]); // top to bottom
if (l > --r) break;
for (int i = r; i >= l; i--) res.push_back(array[b][i]); // right to left
if (t > --b) break;
for (int i = b; i >= t; i--) res.push_back(array[i][l]); // bottom to top
if (++l > r) break;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(MN)$ ：** $M, N$ 分别为矩阵行数和列数。
- **空间复杂度 $O(1)$ ：** 四个边界 `l` , `r` , `t` , `b` 使用常数大小的额外空间。

117
leetbook_ioa/docs/LCR 147. 最小栈.md Executable file
View File

@@ -0,0 +1,117 @@
## 解题思路：
普通栈的 `push()` 和 `pop()` 函数的复杂度为 $O(1)$ ；而获取栈最小值 `getMin()` 函数需要遍历整个栈，复杂度为 $O(N)$ 。
**本题难点：** 将 `getMin()` 函数复杂度降为 $O(1)$ 。可借助辅助栈实现：
- **数据栈 `A` ：** 栈 `A` 用于存储所有元素，保证入栈 `push()` 函数、出栈 `pop()` 函数、获取栈顶 `top()` 函数的正常逻辑。
- **辅助栈 `B` ：** 栈 `B` 中存储栈 `A` 中所有 **非严格降序** 元素的子序列，则栈 `A` 中的最小元素始终对应栈 `B` 的栈顶元素。此时，`getMin()` 函数只需返回栈 `B` 的栈顶元素即可。
因此，只需设法维护好 栈 `B` 的元素，使其保持是栈 `A` 的非严格降序元素的子序列，即可实现 `getMin()` 函数的 $O(1)$ 复杂度。
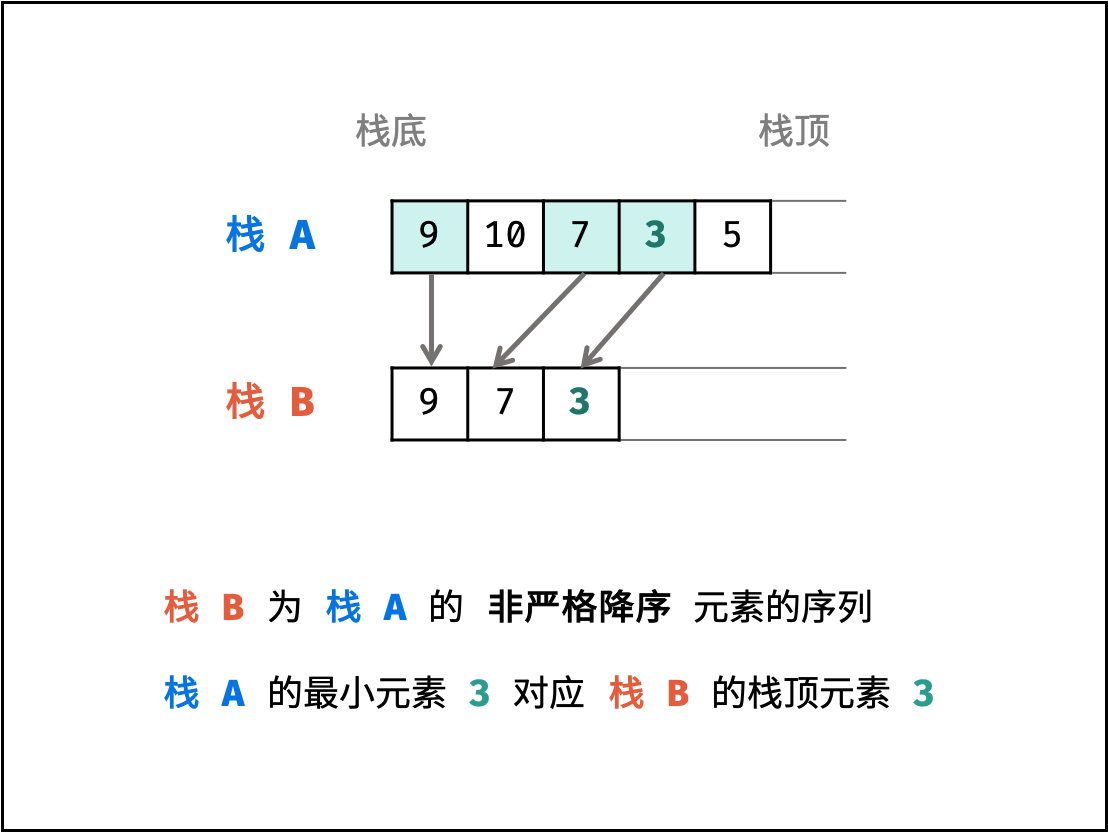![Picture1.png](https://pic.leetcode-cn.com/1599880866-aLaPYz-Picture1.png){:align=center width=450}
### 函数设计：
**`push(x)` 函数：** 重点为保持栈 `B` 的元素是 **非严格降序** 的；
1. 执行「元素 `x` 压入栈 `A`」 ；
2. 若「栈 `B` 为空」**或**「`x` $\leq$ 栈 `B` 的栈顶元素」，则执行「元素 `x` 压入栈 `B`」 ；
**`pop()` 函数：** 重点为保持栈 `A` , `B` 的 **元素一致性** ；
1. 执行「栈 `A` 元素出栈」，将出栈元素记为 `y` ；
2. 若 「`y` 等于栈 `B` 的栈顶元素」，则执行「栈 `B` 元素出栈」；
**`top()` 函数：** 直接返回栈 `A` 的栈顶元素，即返回 `A.peek()` ；
**`getMin()` 函数：** 直接返回栈 `B` 的栈顶元素，即返回 `B.peek()` ；
> 下图中的 `min()` 对应本题的 `getMin()` 。
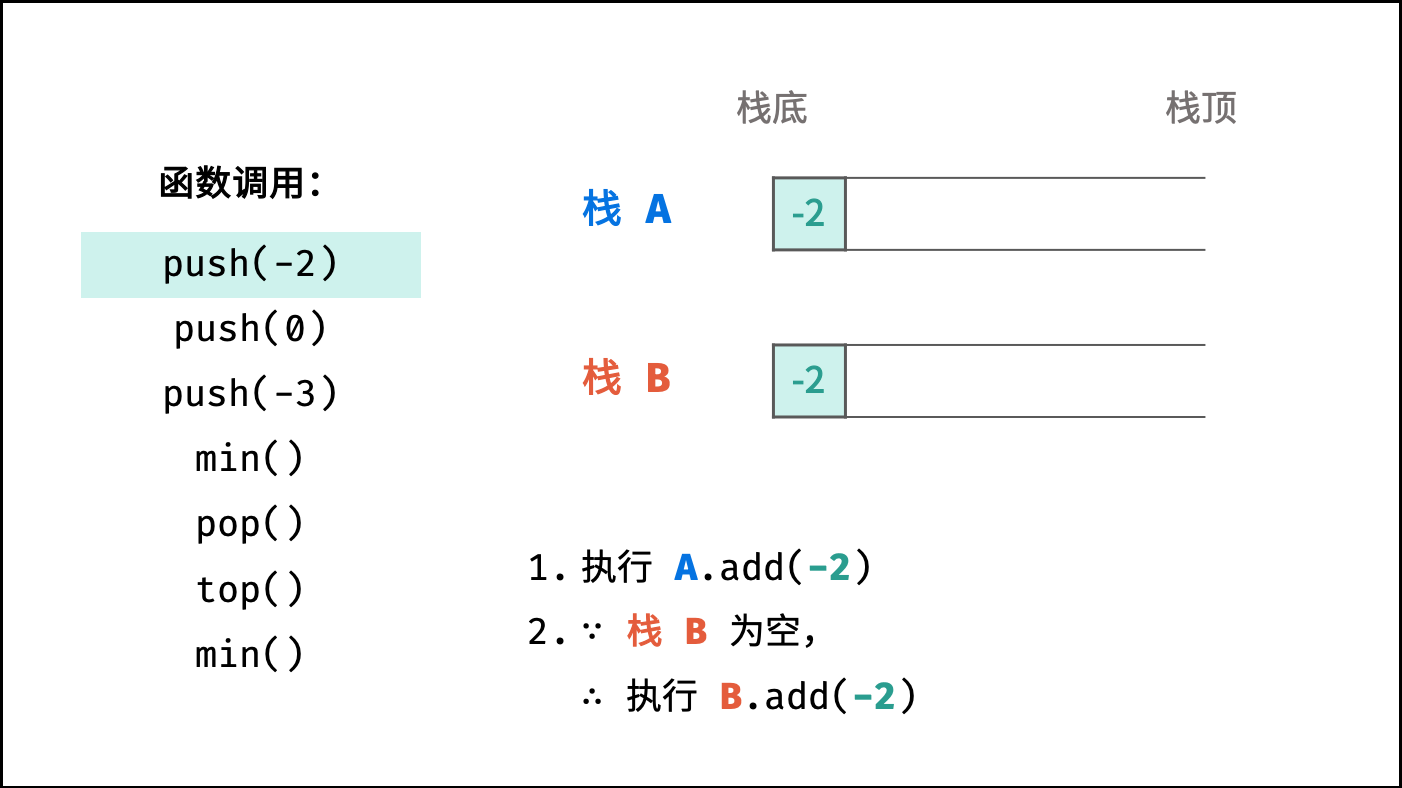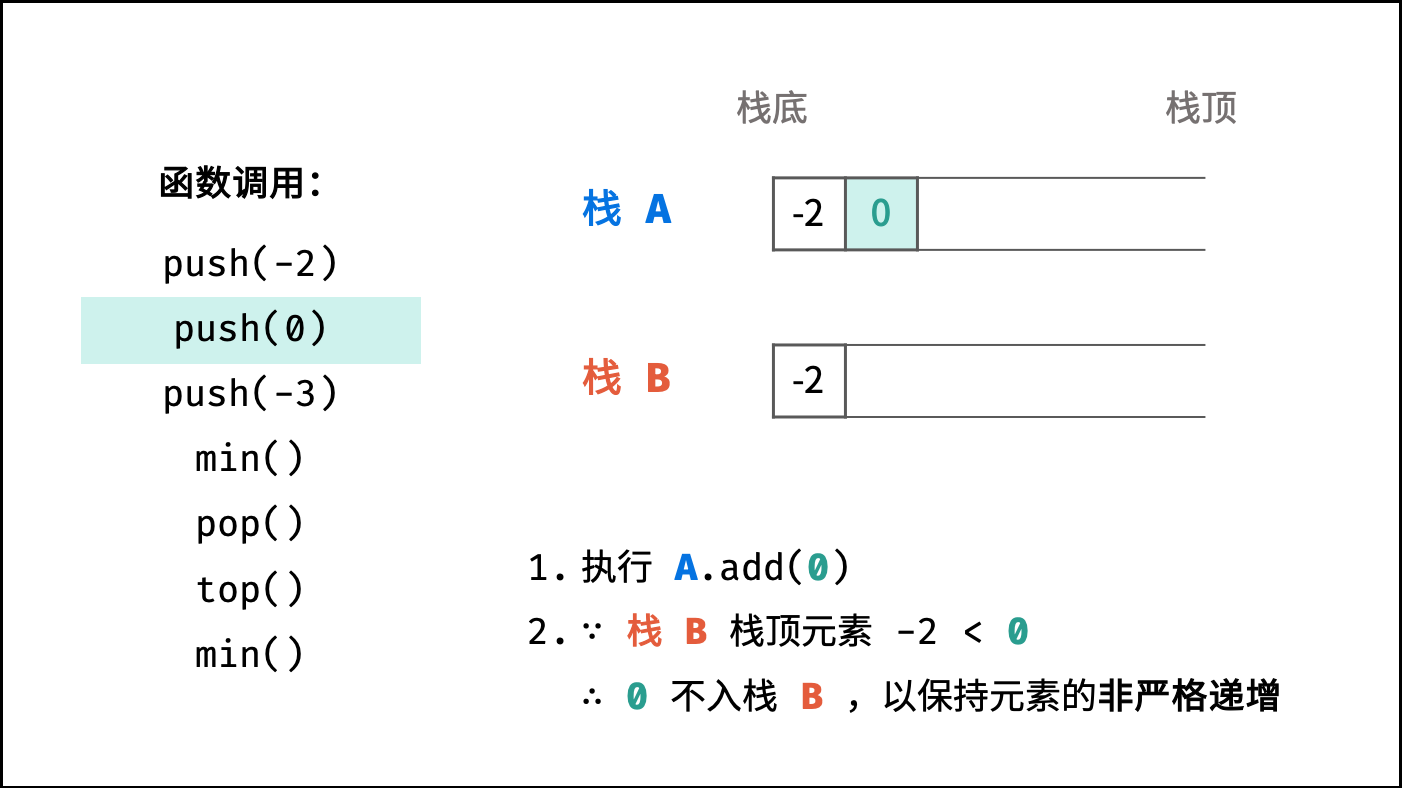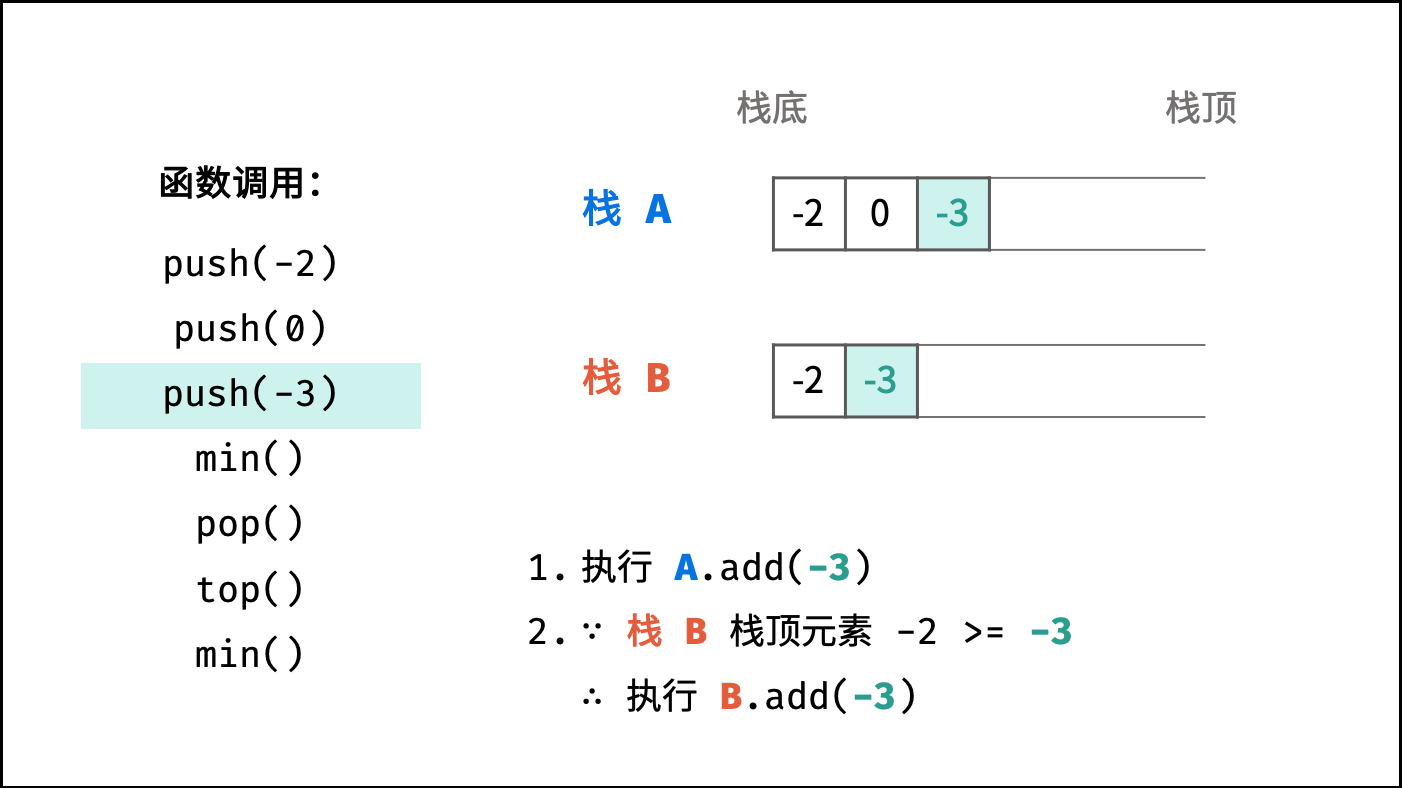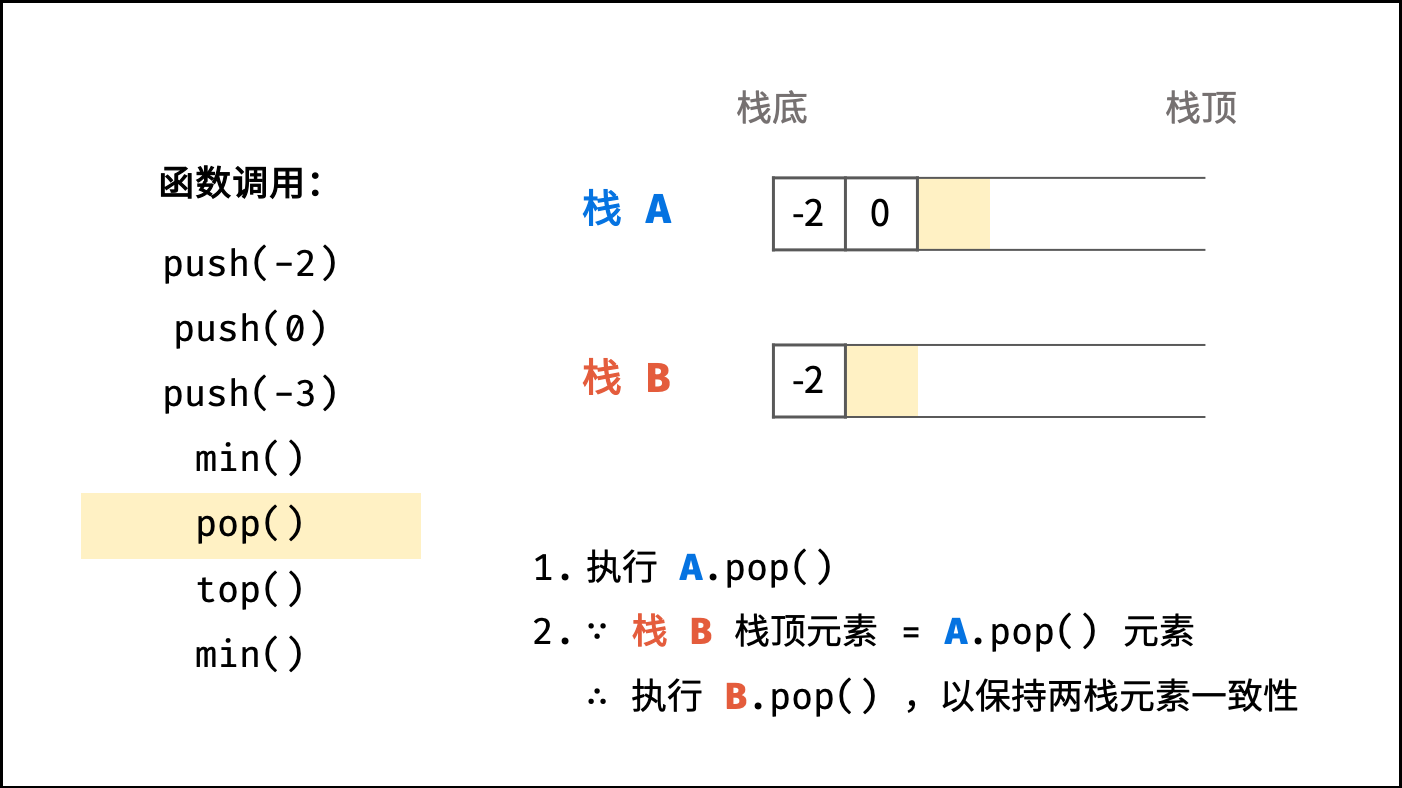<![Picture3.png](https://pic.leetcode-cn.com/1599880866-bYSlQk-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599880866-sQSkFc-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599880866-mcXiyv-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599880866-GrbVAi-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599880866-CJnETD-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599880866-wqhJmV-Picture8.png),![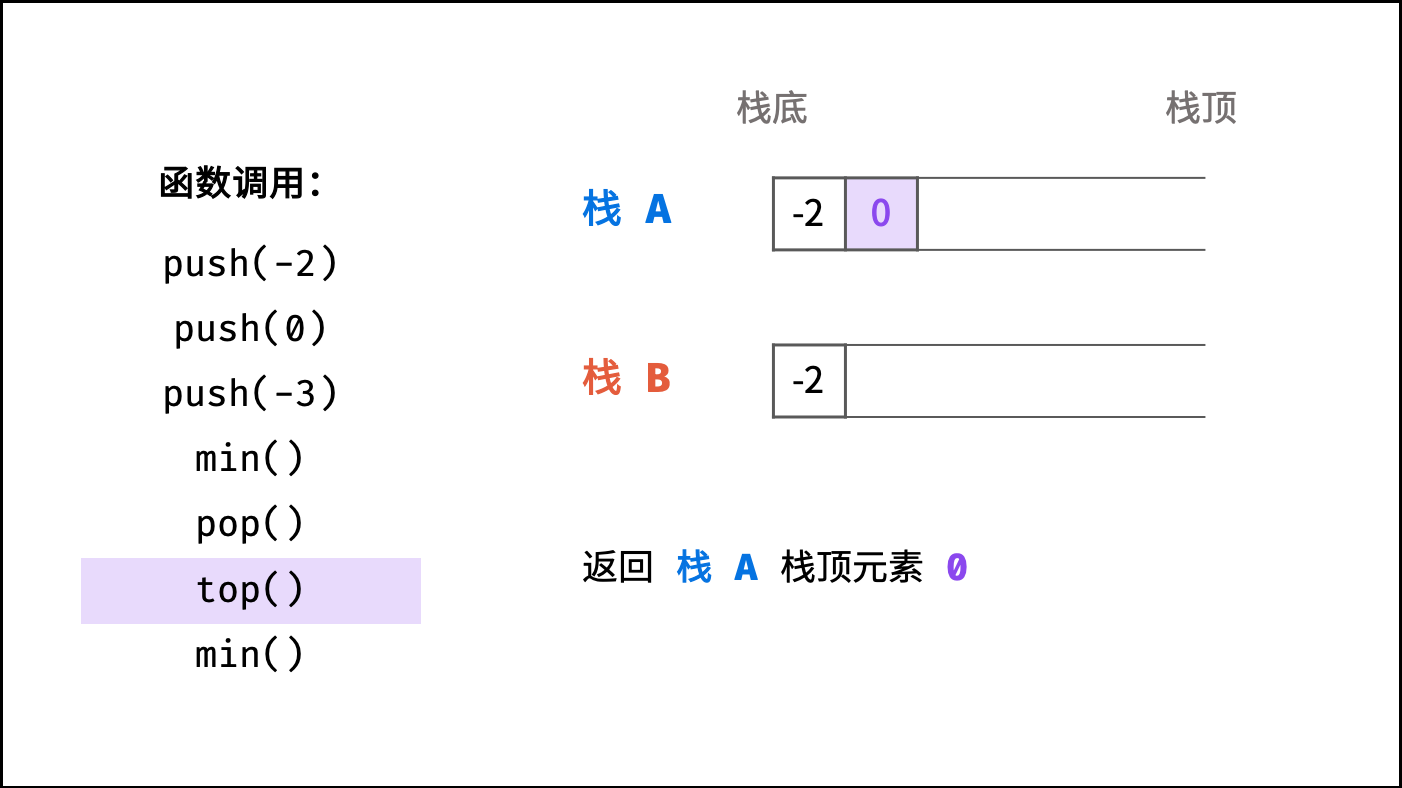Picture9.png](https://pic.leetcode-cn.com/1599880866-hBNKsi-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599880866-OQhXhy-Picture10.png)>
### 采用 “非严格” 降序原因：
在栈 `A` 具有 **重复** 最小值元素时，非严格降序可防止栈 `B` 提前弹出最小值元素，示例如下：
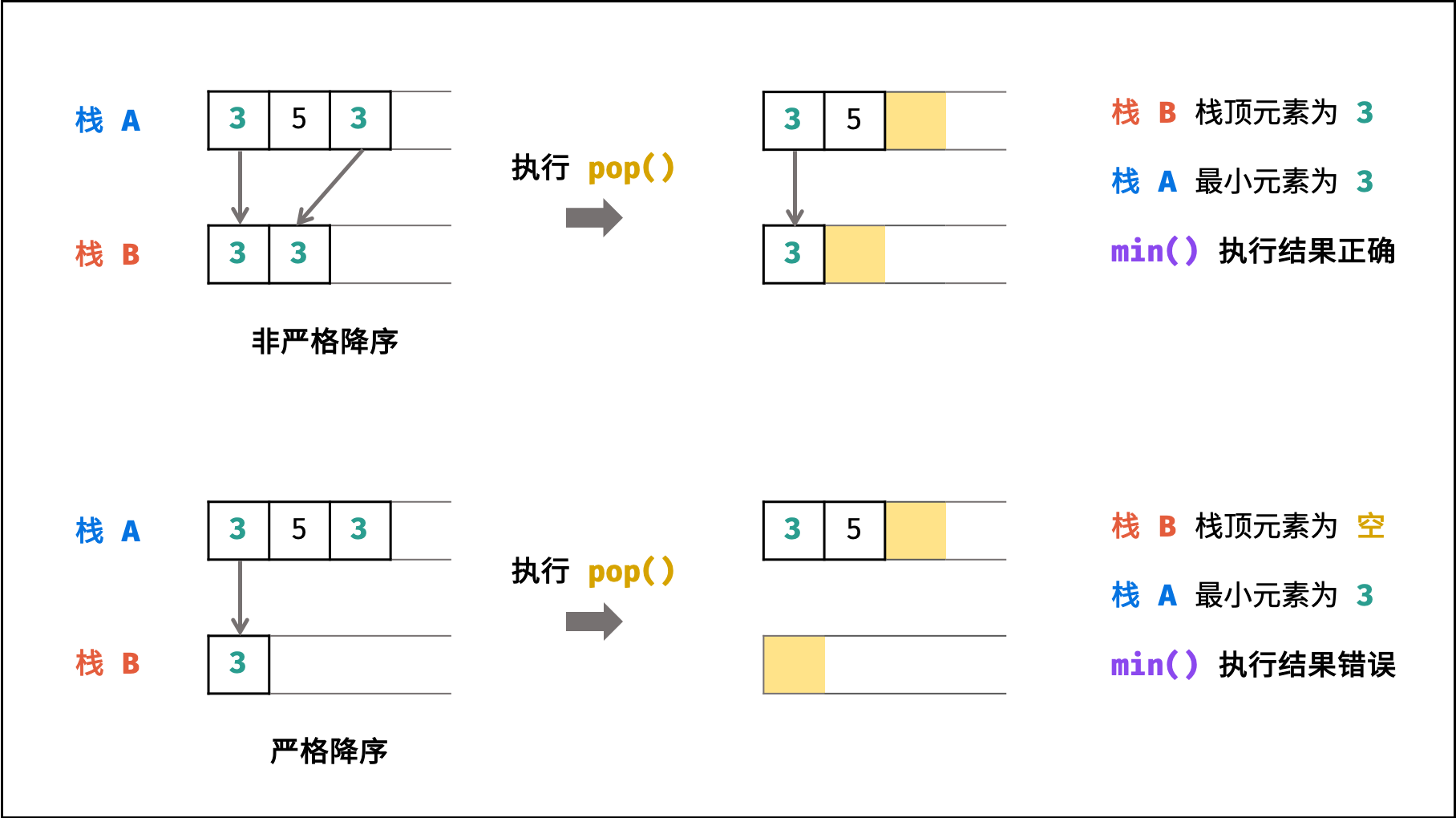![Picture2.png](https://pic.leetcode-cn.com/1600086305-BSfBJu-Picture2.png){:align=center width=550}
## 代码：
Java 代码中，由于 Stack 中存储的是 int 的包装类 Integer ，因此需要使用 `equals()` 代替 `==` ，以比较对象的值。
```Python []
class MinStack:
def __init__(self):
self.A, self.B = [], []
def push(self, x: int) -> None:
self.A.append(x)
if not self.B or self.B[-1] >= x:
self.B.append(x)
def pop(self) -> None:
if self.A.pop() == self.B[-1]:
self.B.pop()
def top(self) -> int:
return self.A[-1]
def getMin(self) -> int:
return self.B[-1]
```
```Java []
class MinStack {
Stack<Integer> A, B;
public MinStack() {
A = new Stack<>();
B = new Stack<>();
}
public void push(int x) {
A.add(x);
if(B.empty() || B.peek() >= x)
B.add(x);
}
public void pop() {
if(A.pop().equals(B.peek()))
B.pop();
}
public int top() {
return A.peek();
}
public int getMin() {
return B.peek();
}
}
```
```C++ []
class MinStack {
public:
stack<int> A, B;
MinStack() {}
void push(int x) {
A.push(x);
if(B.empty() || B.top() >= x)
B.push(x);
}
void pop() {
if(A.top() == B.top())
B.pop();
A.pop();
}
int top() {
return A.top();
}
int getMin() {
return B.top();
}
};
```
### 复杂度分析：
- **时间复杂度 $O(1)$ ：** `push()`, `pop()`, `top()`, `getMin()` 四个函数的时间复杂度均为常数级别。
- **空间复杂度 $O(N)$ ：** 当共有 $N$ 个待入栈元素时，辅助栈 `B` 最差情况下存储 $N$ 个元素，使用 $O(N)$ 额外空间。

84
leetbook_ioa/docs/LCR 148. 验证图书取出顺序.md Executable file
View File

@@ -0,0 +1,84 @@
## 解题思路：
如下图所示，给定一个放入序列 `putIn` 和拿取序列 `takeOut` ，则放入（压栈）和拿取（弹出）操作的顺序是 **唯一确定** 的。
> 下图中 `pushed` 和 `popped` 分别对应本题的 `putIn` 和 `takeOut` 。
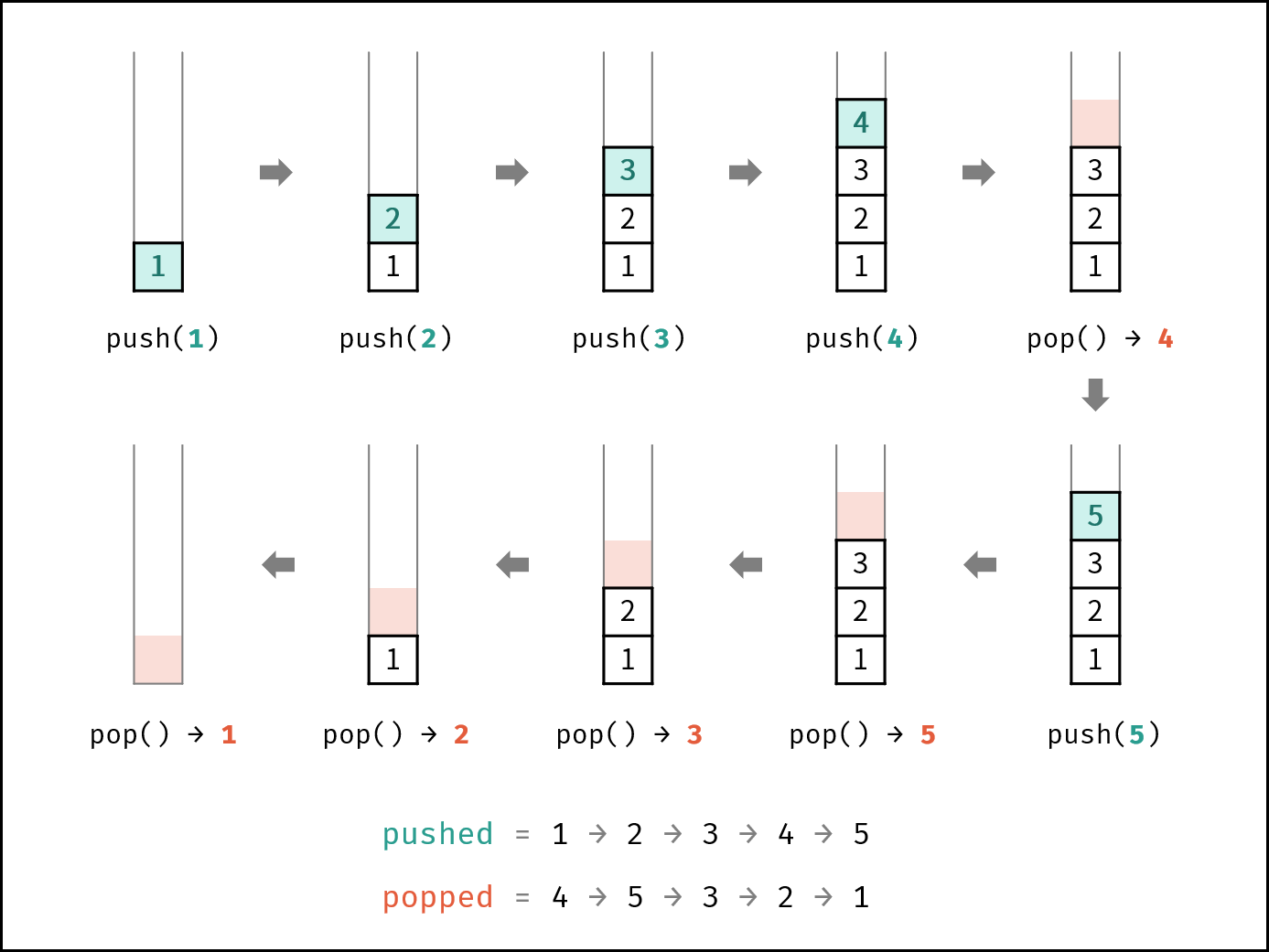![Picture1.png](https://pic.leetcode-cn.com/1188474dc6a377fc258004bca84e5a130b663eeb24bf22c4fa4eb998a0249f97-Picture1.png){:align=center width=500}
如下图所示，栈的数据操作具有 **先入后出** 的特性，因此某些拿取序列是无法实现的。
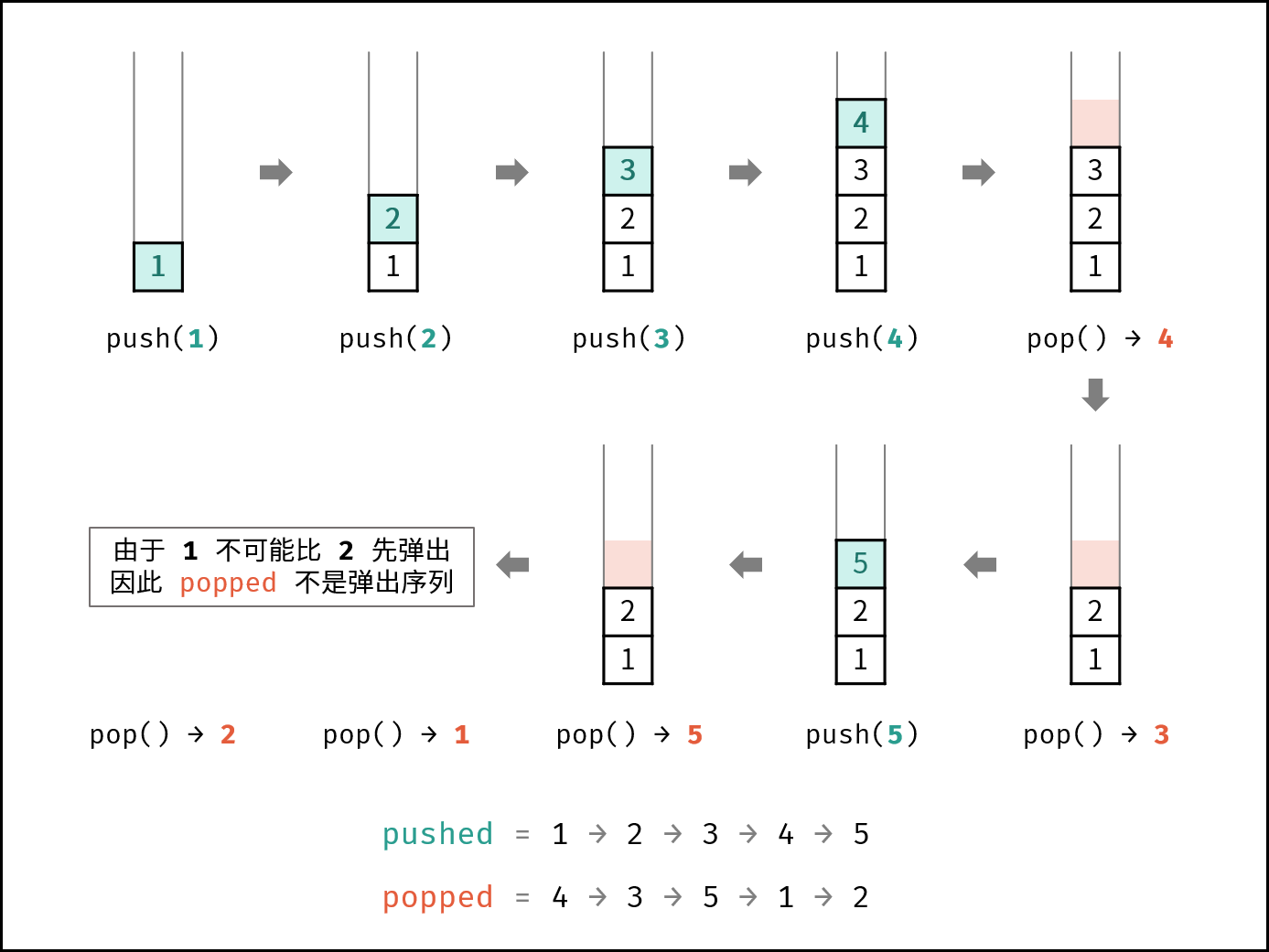![Picture2.png](https://pic.leetcode-cn.com/3f43b224553bf3a37f9758dbb41655e547795e293524a148380c6f335af315e4-Picture2.png){:align=center width=500}
考虑借用一个辅助栈 `stack` ，**模拟** 放入 / 拿取操作的排列。根据是否模拟成功，即可得到结果。
- **入栈操作：** 按照压栈序列的顺序执行。
- **出栈操作：** 每次入栈后，循环判断 “栈顶元素 $=$ 拿取序列的当前元素” 是否成立，将符合拿取序列顺序的栈顶元素全部拿取。
> 由于题目规定 “栈的所有数字均不相等” ，因此在循环入栈中，每个元素出栈的位置的可能性是唯一的（若有重复数字，则具有多个可出栈的位置）。因而，在遇到 “栈顶元素 $=$ 拿取序列的当前元素” 就应立即执行出栈。
### 算法流程：
1. **初始化：** 辅助栈 `stack` ，拿取序列的索引 `i` ；
2. **遍历压栈序列：** 各元素记为 `num` ；
1. 元素 `num` 入栈；
2. 循环出栈：若 `stack` 的栈顶元素 $=$ 拿取序列元素 `takeOut[i]` ，则执行出栈与 `i++` ；
3. **返回值：** 若 `stack` 为空，则此拿取序列合法。
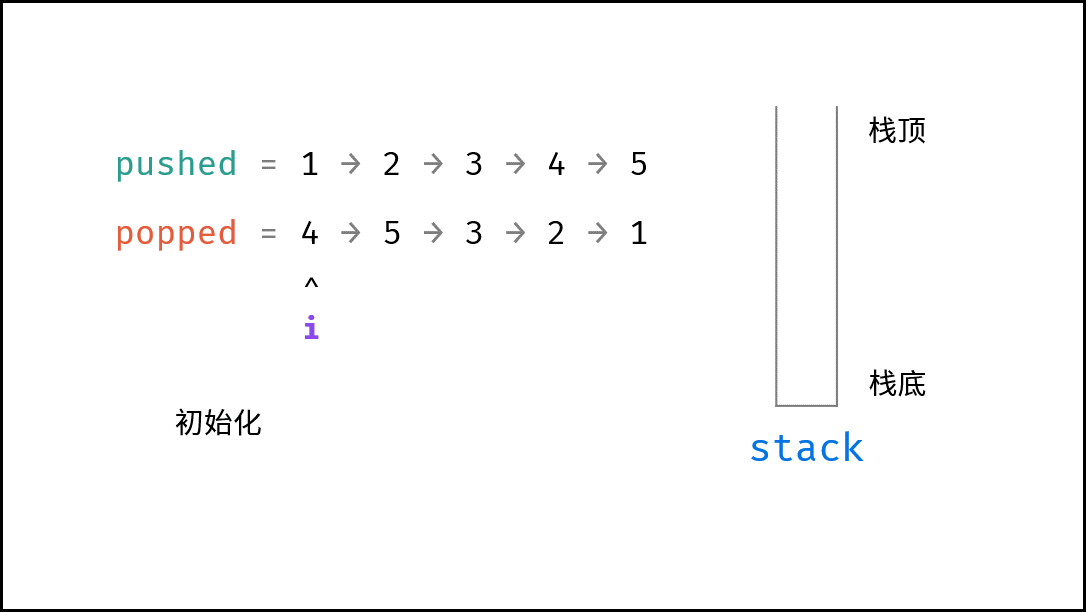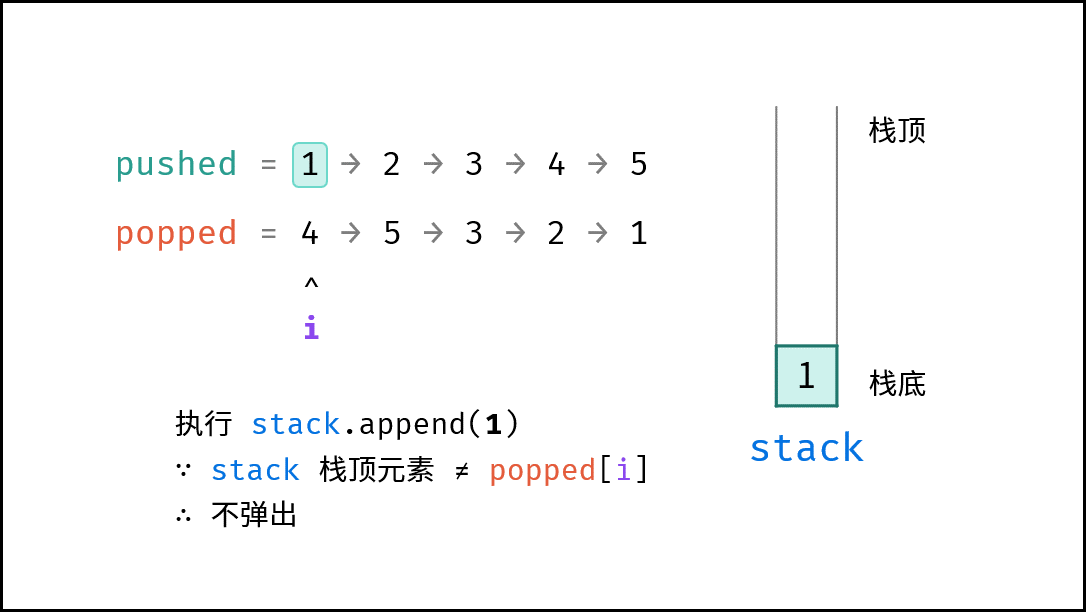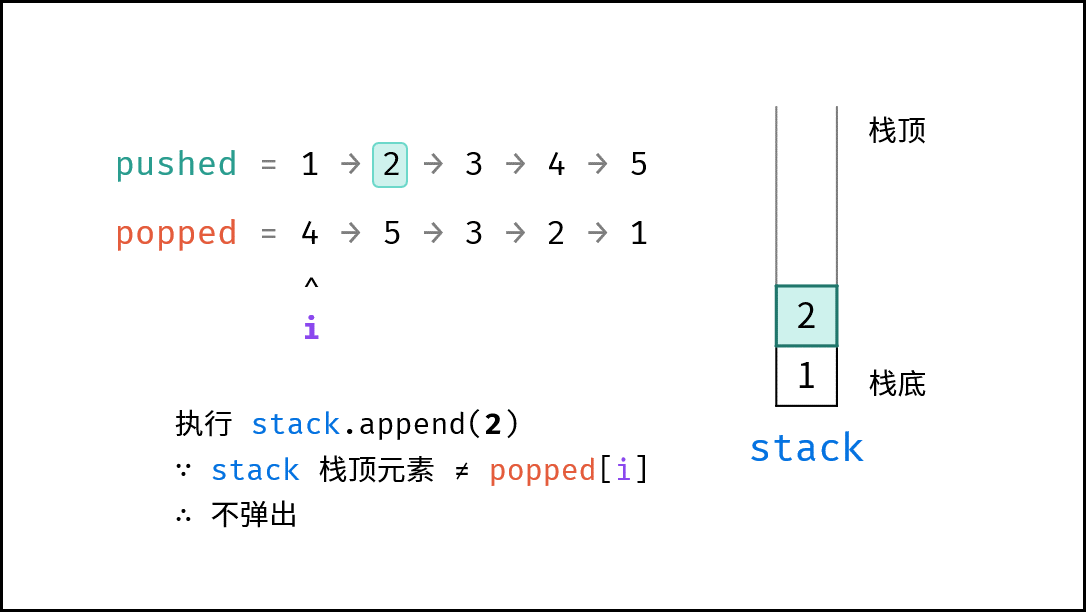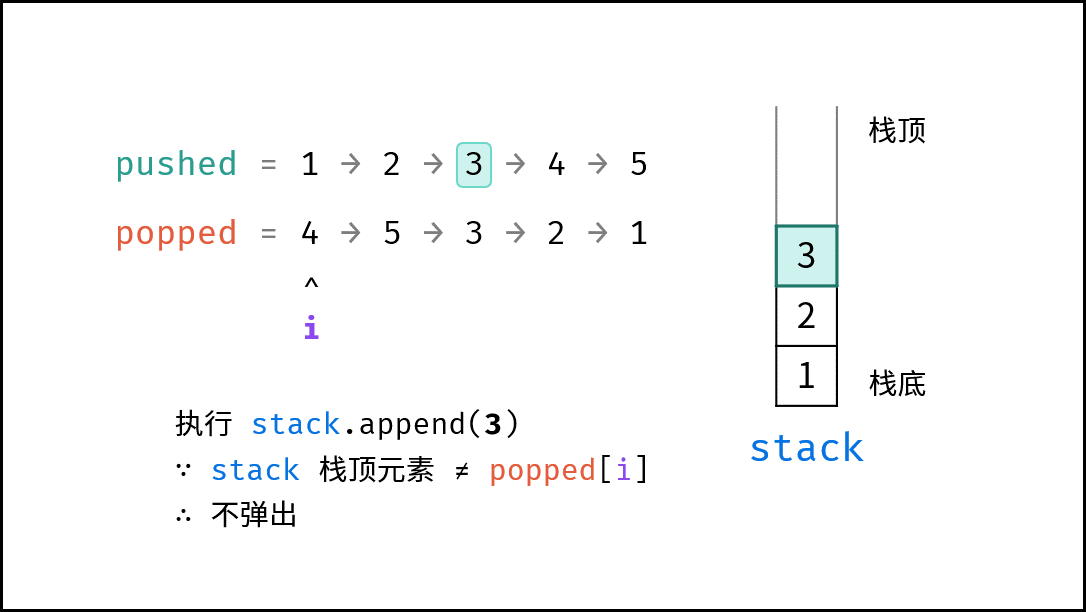<![Picture3.png](https://pic.leetcode-cn.com/33835fb3df651d93d659895384988371e50d1f2fc6773fb4e4f1539ade09ba33-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/92c7af00dfef949480599e229883c03ec7283f6f5206d8414d98771ebdc69115-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/ca8300ed98b8e03433661bb08a50b114d0364e7504f5705c18d12117de2a6b0b-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/fa133ea2602a09c88779b2ddfc7d4fdda6b3896efdb9e58a6565ad346cf46278-Picture6.png),![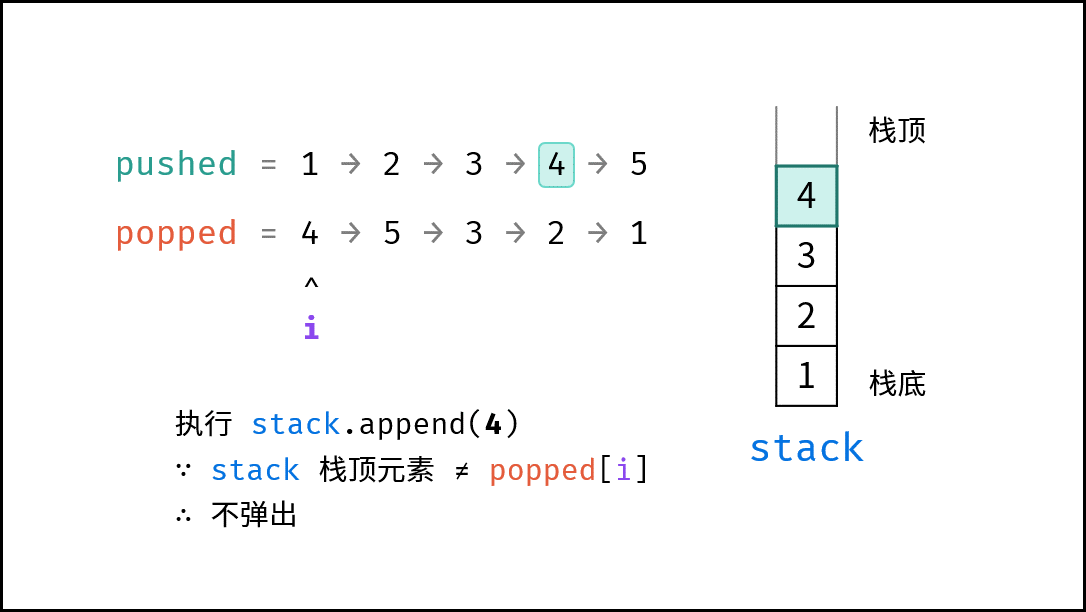Picture7.png](https://pic.leetcode-cn.com/ac7d8c2bebee22110298c6977e62546014b8692f244ba1921904304b130e8e9e-Picture7.png),![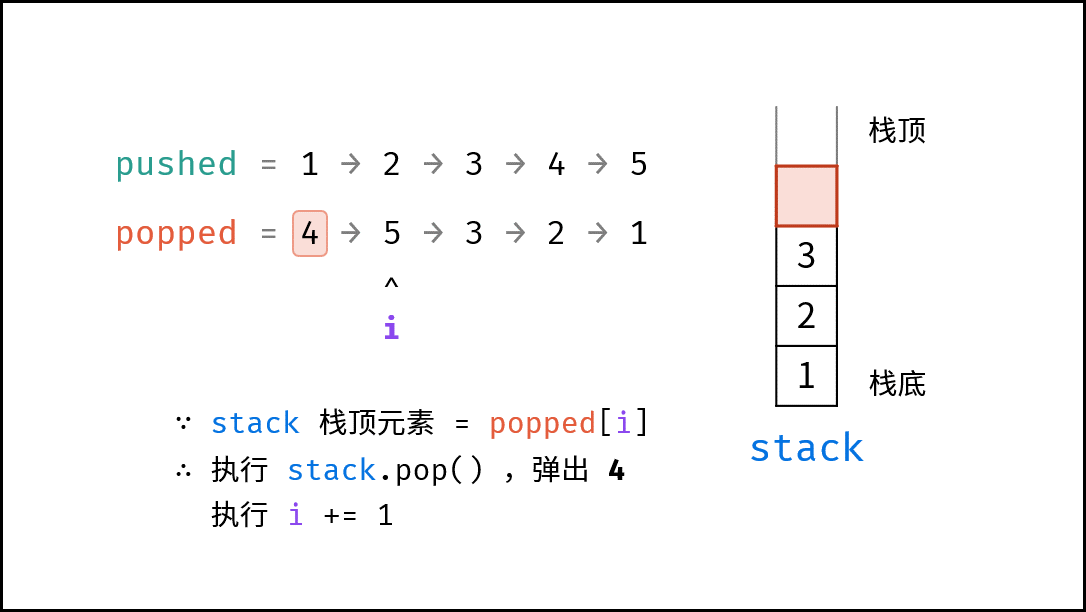Picture8.png](https://pic.leetcode-cn.com/75d2d318a1f6a2f4e4638a9bd5711ea1b9ab849fbfc2a442be898d499eed926d-Picture8.png),![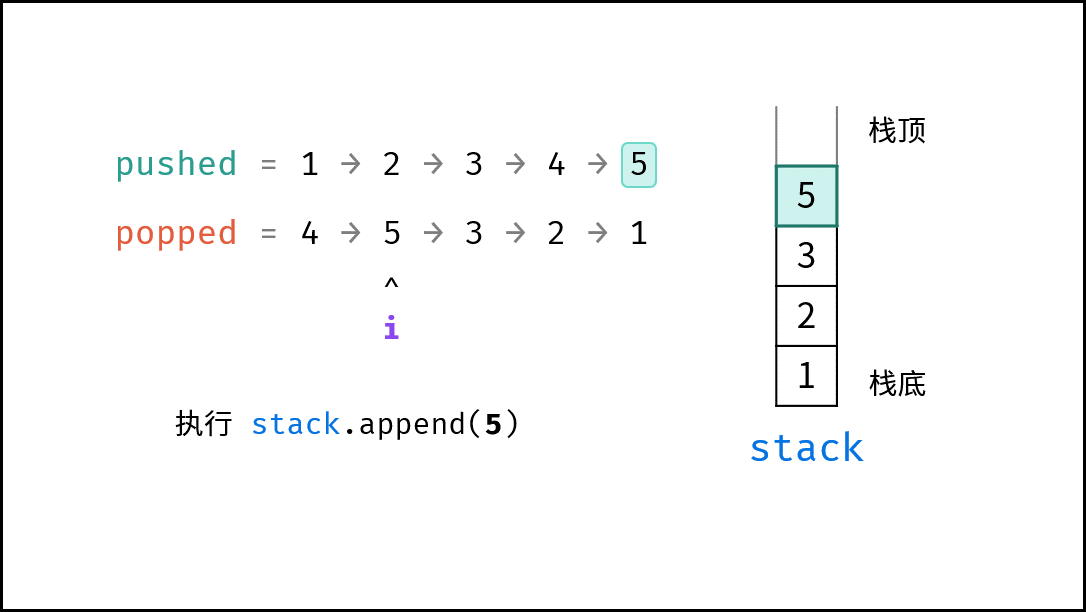Picture9.png](https://pic.leetcode-cn.com/d905d5e62029bdef4c31bf63c3bde4f7accf49f300558fd30569474b61989234-Picture9.png),![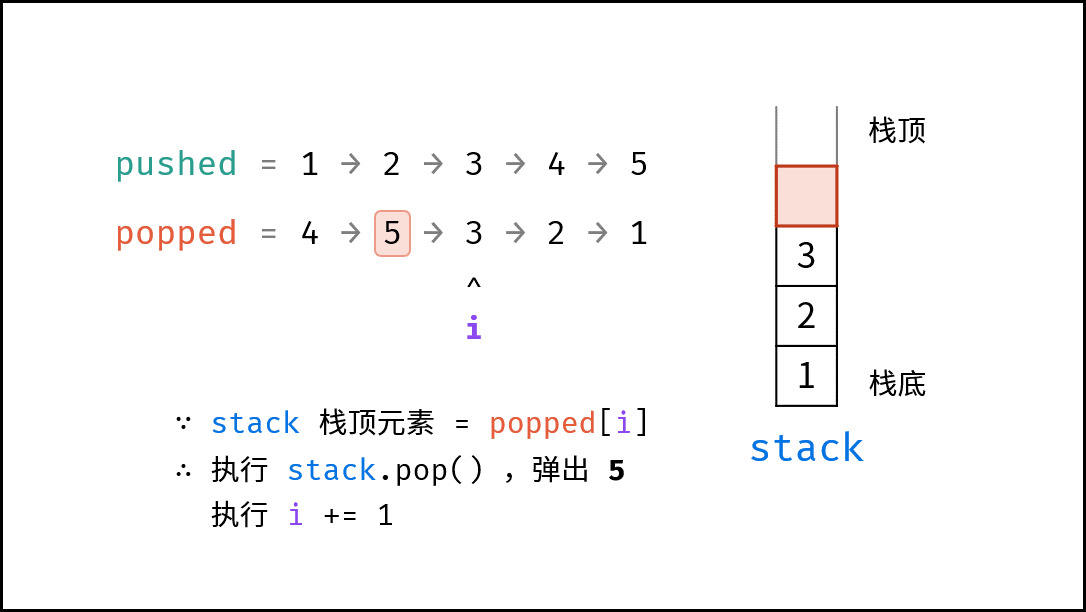Picture10.png](https://pic.leetcode-cn.com/5329e3532d0e9f4dae3aa10ef029e03e27c465adc7768a545acc2a3724fa6a41-Picture10.png),![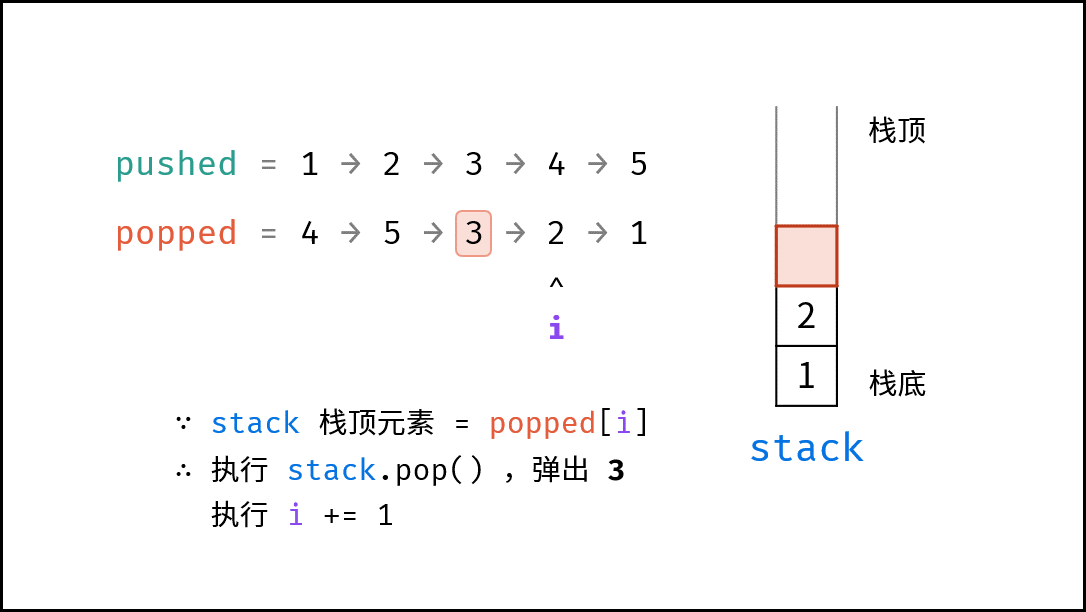Picture11.png](https://pic.leetcode-cn.com/e861009affb8c7b36911193ab4b317352f97a25d340f9cb3b01f457d49bd0ee7-Picture11.png),![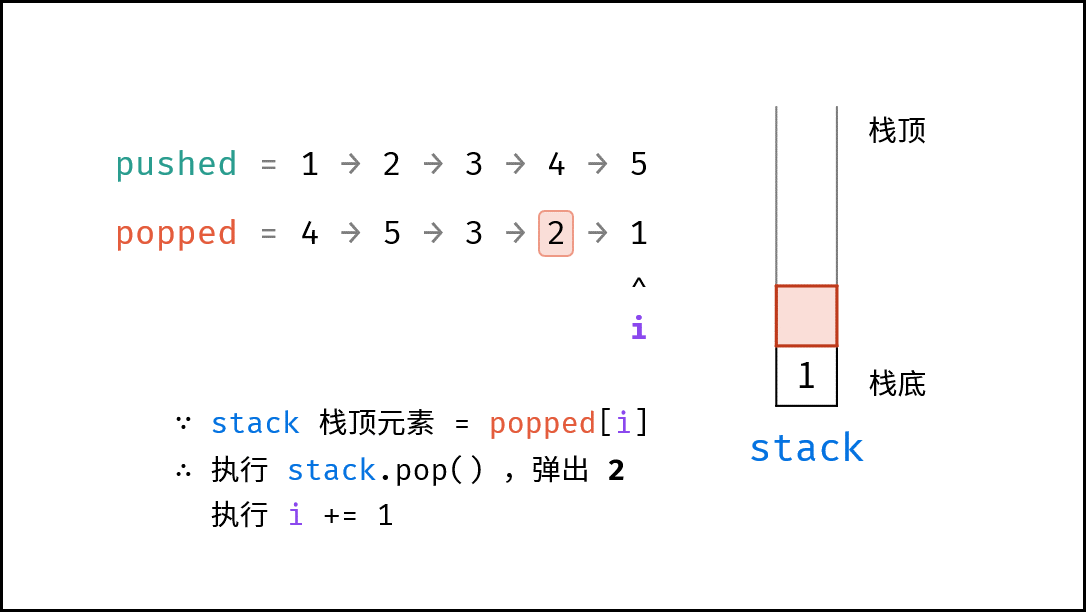Picture12.png](https://pic.leetcode-cn.com/d42823ece52a7c105010480eb4a8cdb130637949f18f0be9443a5dd6fbb95764-Picture12.png),![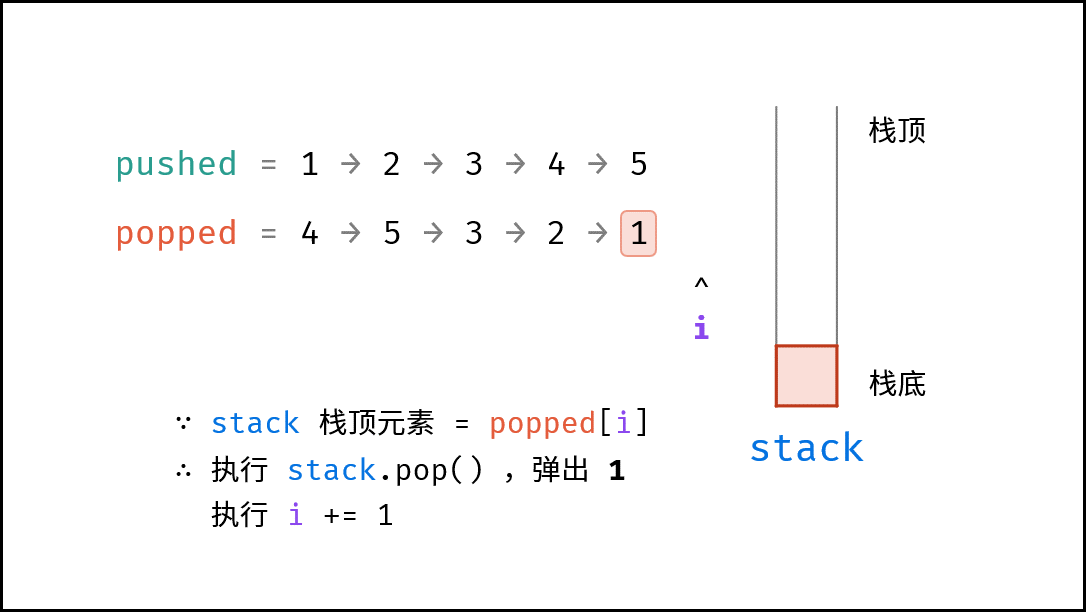Picture13.png](https://pic.leetcode-cn.com/d5e5da64bc2f62ad94e3a3dc65cf049ffa4268a8a4ab44bf9337d9d8378ccde2-Picture13.png),![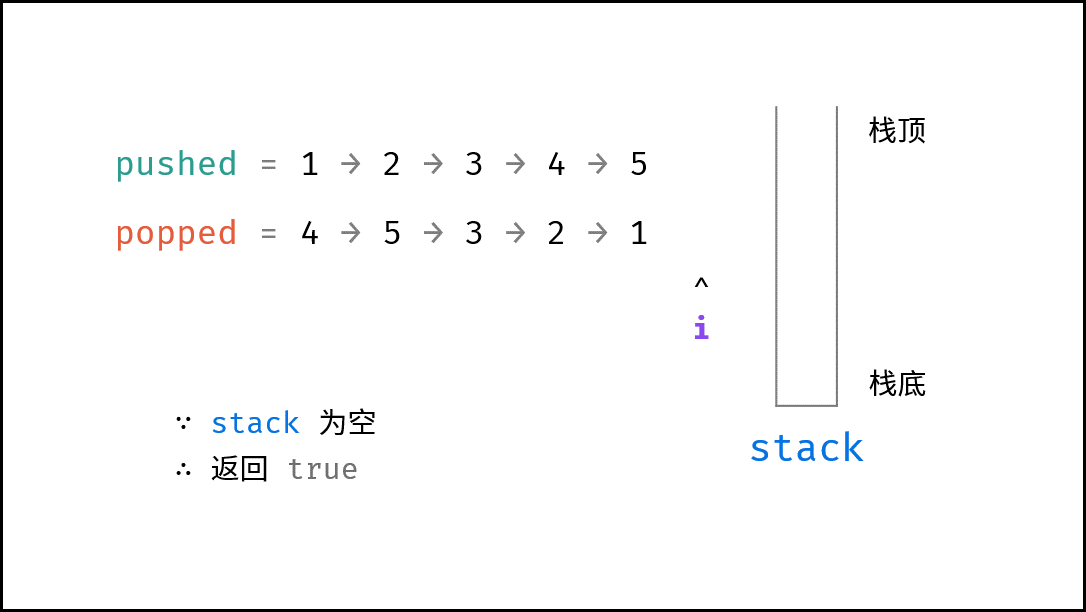Picture14.png](https://pic.leetcode-cn.com/b30701ab475dd8a4f8f8ee45abf086367e8cad82d3f8475555a828fdb57ea992-Picture14.png)>
## 代码：
题目指出 “putIn 是 takeOut 的排列” 。因此，无需考虑 `putIn` 和 `takeOut` **长度不同** 或 **包含元素不同** 的情况。
```Python []
class Solution:
def validateBookSequences(self, putIn: List[int], takeOut: List[int]) -> bool:
stack, i = [], 0
for num in putIn:
stack.append(num) # num 入栈
while stack and stack[-1] == takeOut[i]: # 循环判断与出栈
stack.pop()
i += 1
return not stack
```
```Java []
class Solution {
public boolean validateBookSequences(int[] putIn, int[] takeOut) {
Stack<Integer> stack = new Stack<>();
int i = 0;
for(int num : putIn) {
stack.push(num); // num 入栈
while(!stack.isEmpty() && stack.peek() == takeOut[i]) { // 循环判断与出栈
stack.pop();
i++;
}
}
return stack.isEmpty();
}
}
```
```C++ []
class Solution {
public:
bool validateBookSequences(vector<int>& putIn, vector<int>& takeOut) {
stack<int> stk;
int i = 0;
for(int num : putIn) {
stk.push(num); // num 入栈
while(!stk.empty() && stk.top() == takeOut[i]) { // 循环判断与出栈
stk.pop();
i++;
}
}
return stk.empty();
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为列表 `putIn` 的长度；每个元素最多入栈与出栈一次，即最多共 $2N$ 次出入栈操作。
- **空间复杂度 $O(N)$ ：** 辅助栈 `stack` 最多同时存储 $N$ 个元素。

80
leetbook_ioa/docs/LCR 149. 彩灯装饰记录 I.md Executable file
View File

@@ -0,0 +1,80 @@
## 解题思路：
题目要求按层打印二叉树，即二叉树的 **广度优先遍历** ，其通常借助 **队列** 的先入先出特性来实现。
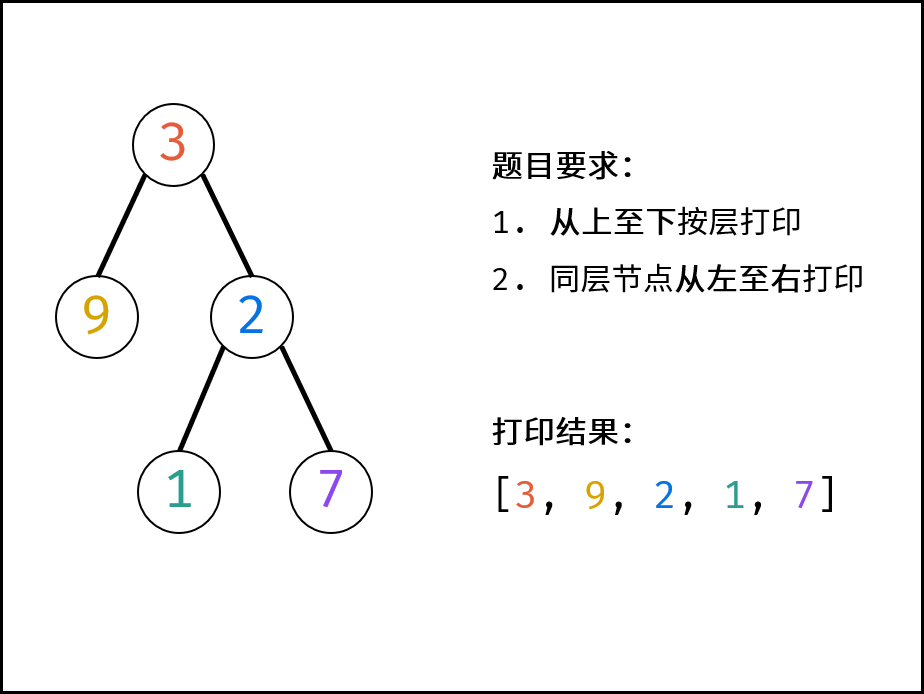![Picture1.png](https://pic.leetcode-cn.com/a872b50fa42011748437ec9123d8f77a104b3d528880efca8b212f91d115f835-Picture1.png){:align=center width=450}
### 算法流程：
1. **特例处理：** 当树的根节点为空，则直接返回空列表 `[]` ；
2. **初始化：** 打印结果列表 `res = []` ，包含根节点的队列 `queue = [root]` ；
3. **BFS 循环：** 当队列 `queue` 为空时跳出；
1. **出队：** 队首元素出队，记为 `node`；
2. **打印：** 将 `node.val` 添加至列表 `tmp` 尾部；
3. **添加子节点：** 若 `node` 的左（右）子节点不为空，则将左（右）子节点加入队列 `queue` ；
4. **返回值：** 返回打印结果列表 `res` 即可。
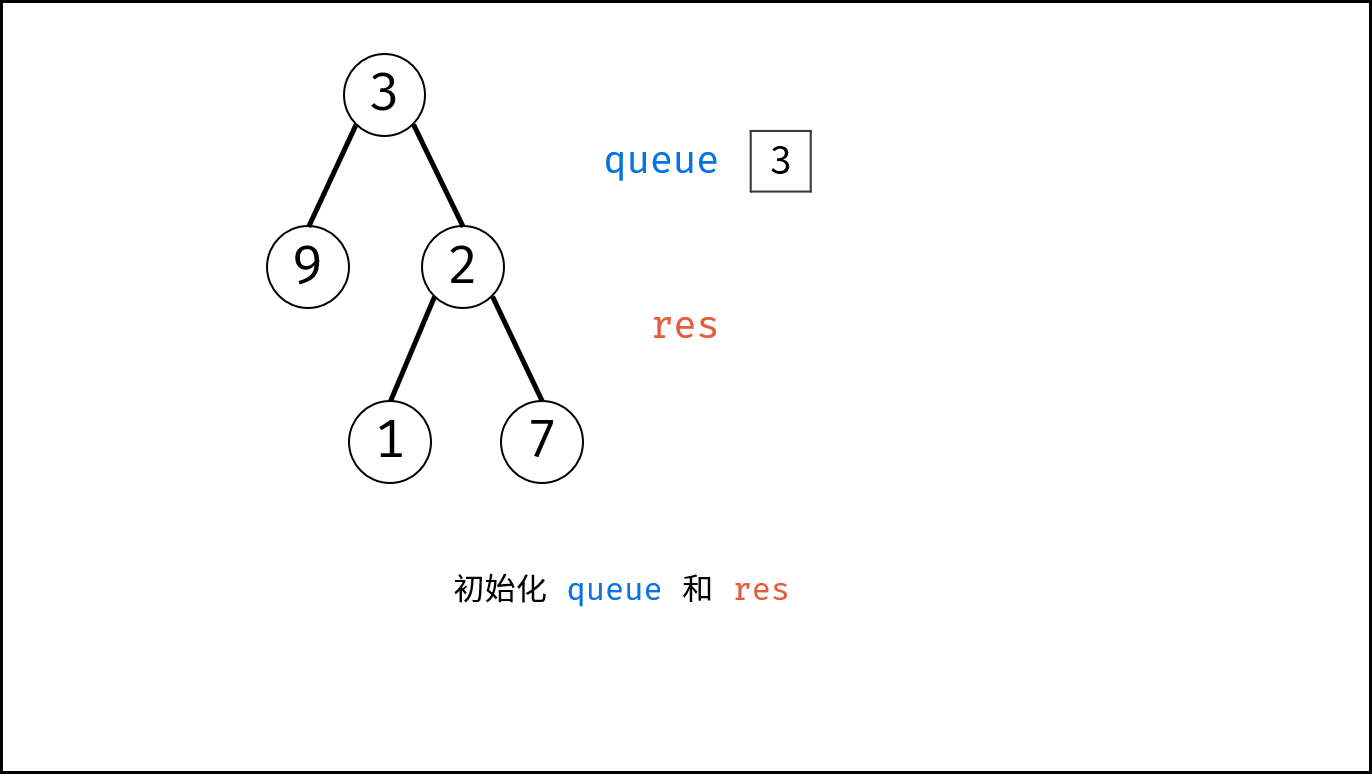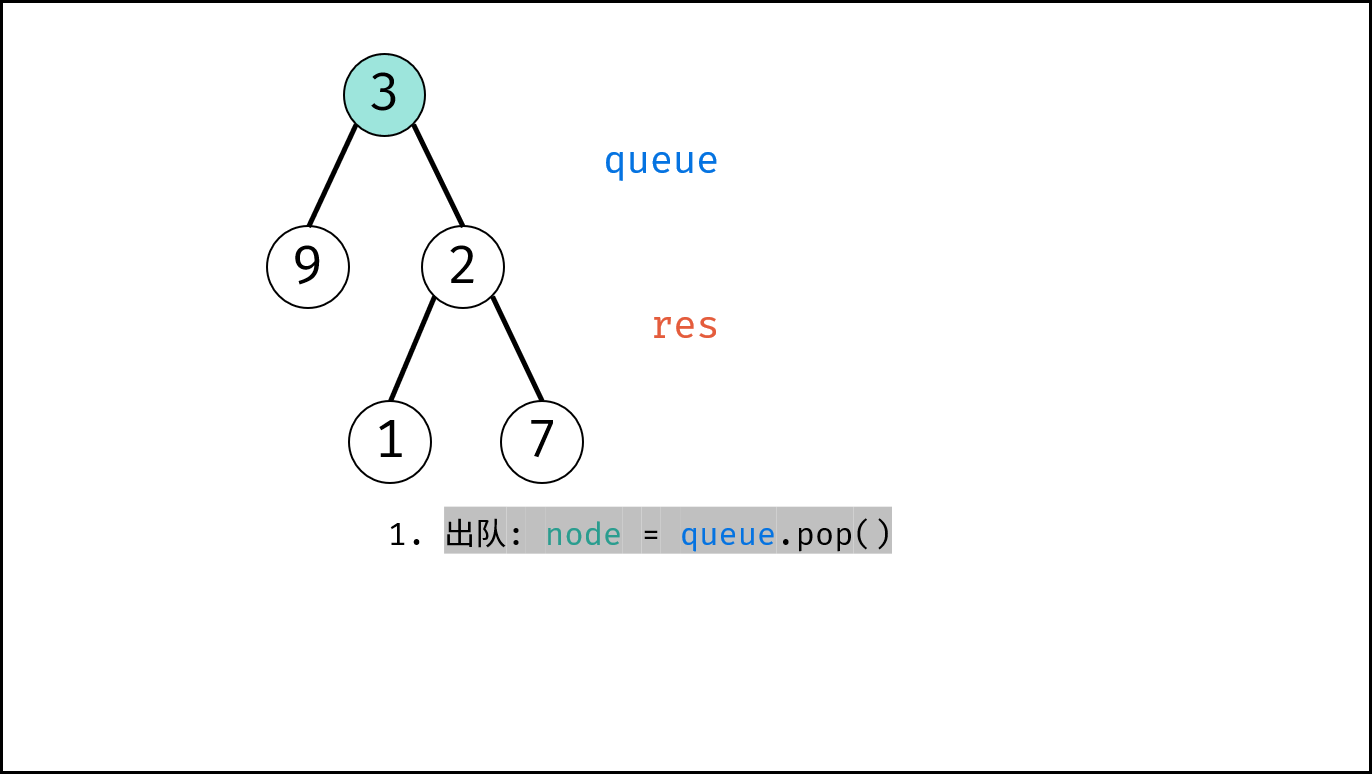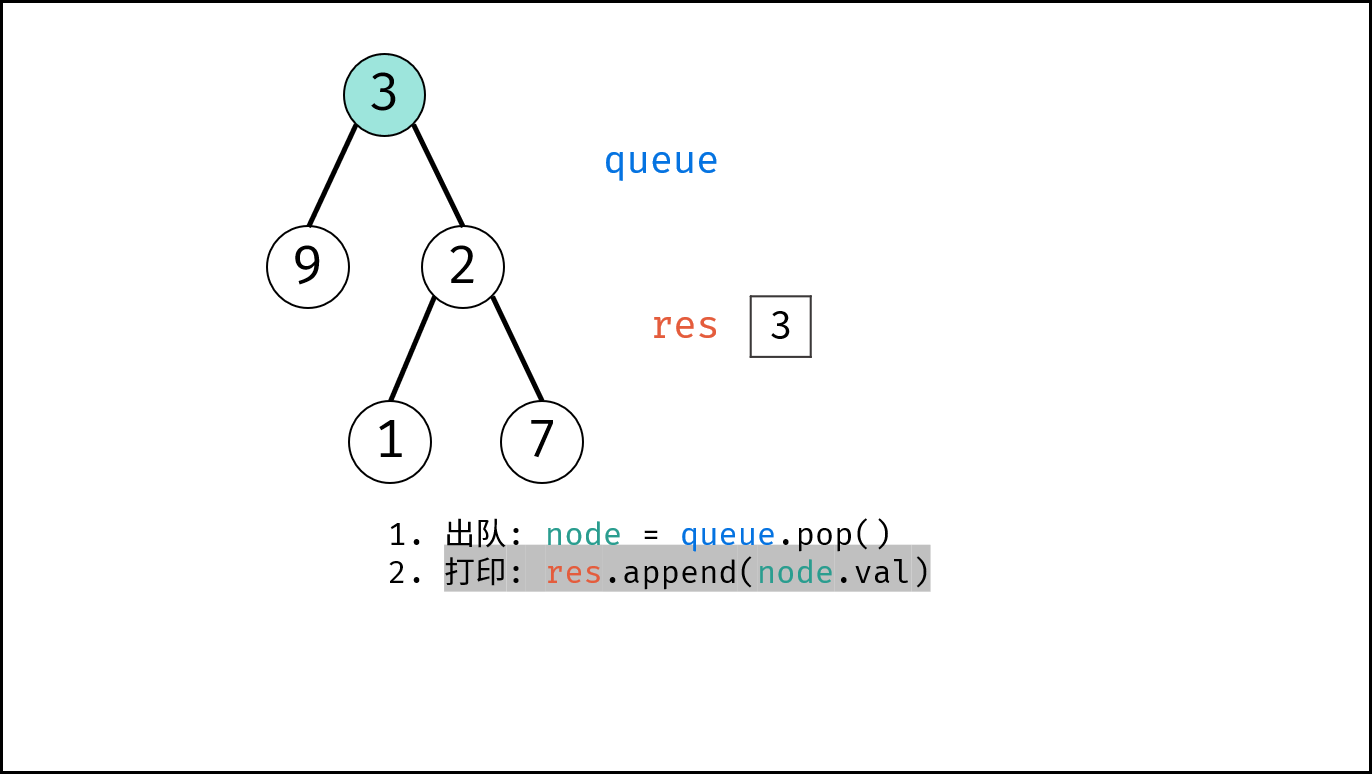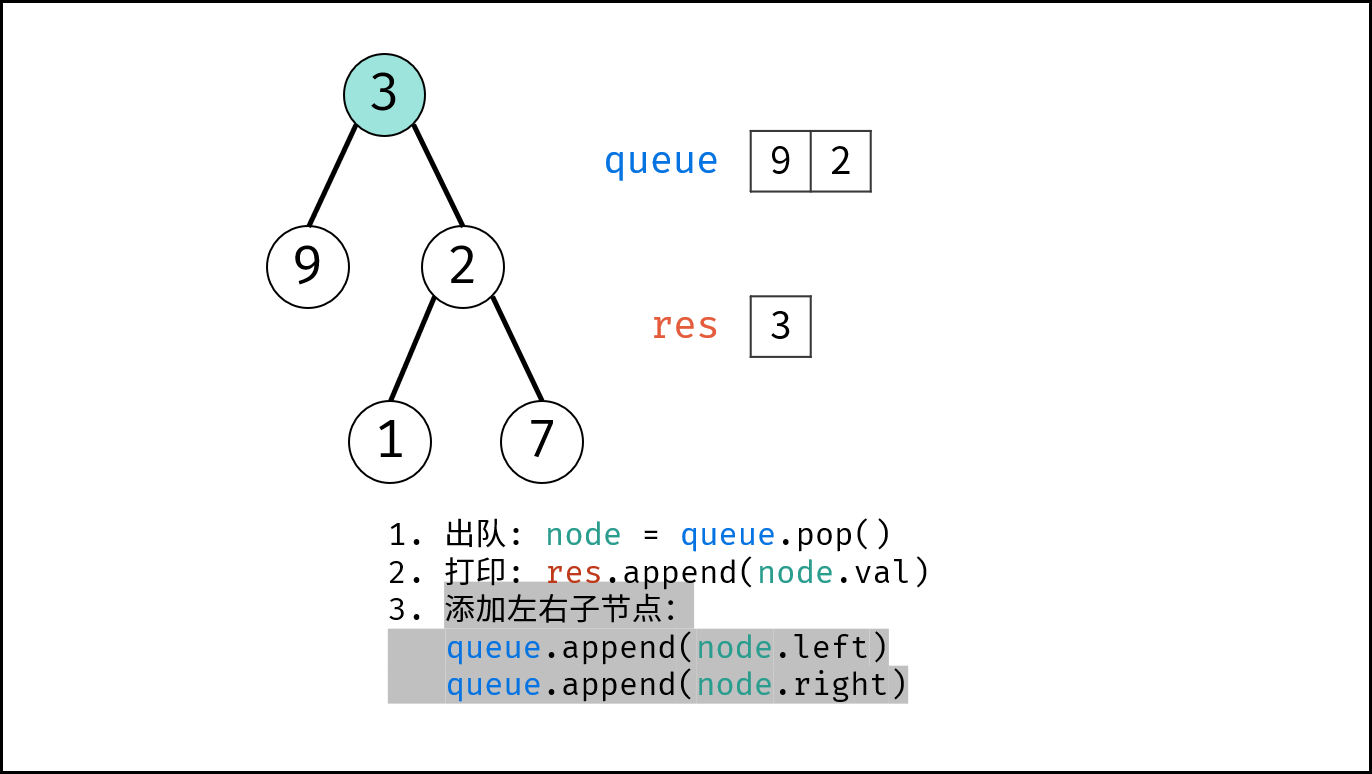<![Picture2.png](https://pic.leetcode-cn.com/1943050c7d48251cadc2c52545ce067a8fbec1c6b1960ef287c51a18fec55dd7-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1605540168-GqnDPn-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/ec82e40de2bfb211f8195545ee1b72d5fb4c9c5518c49e61874182ff142c359f-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/3e0bf6c4209905c972ae73a3793323b59352f4cb219d218ce238baeb7a4f815b-Picture5.png),![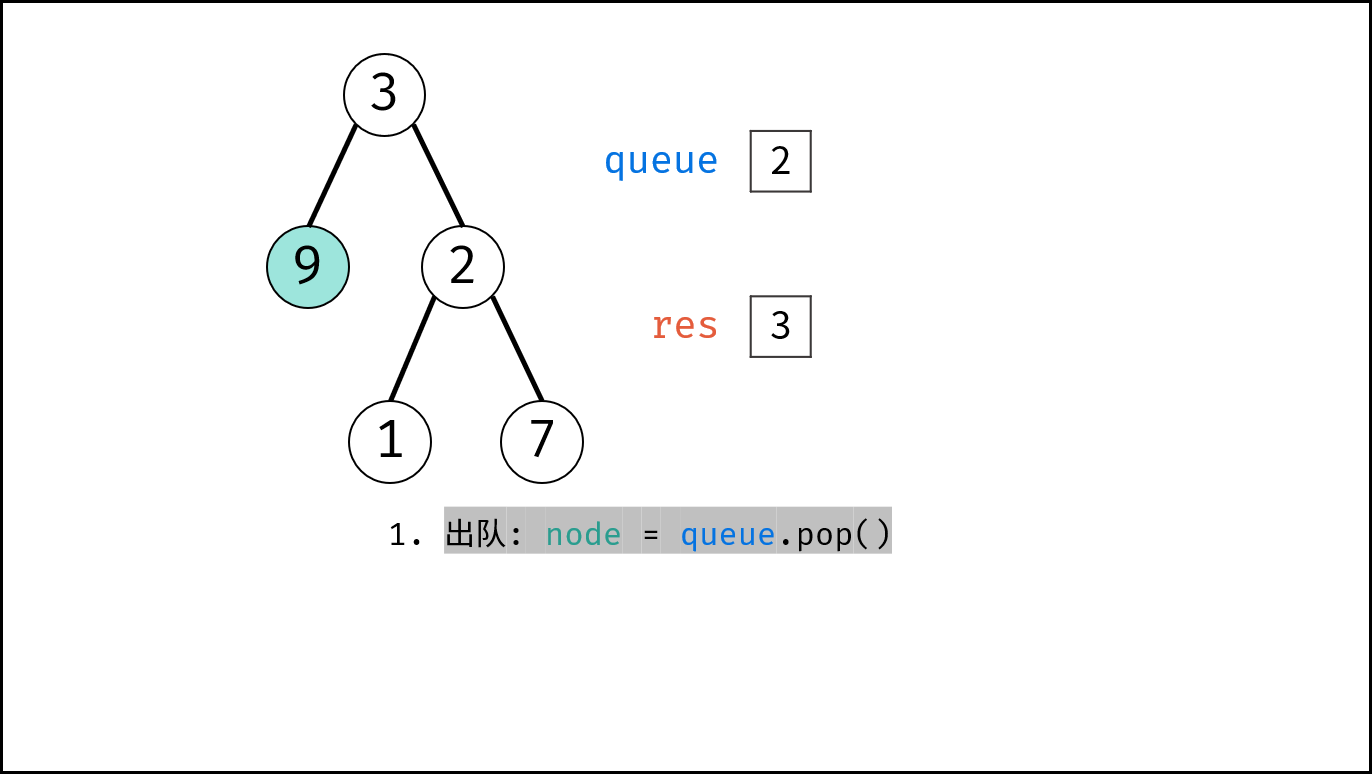Picture6.png](https://pic.leetcode-cn.com/352c729f306dd3c6d3a8ea04c90eb5fbfb1607ae8b5dcf1e57a4124d77bb4a17-Picture6.png),![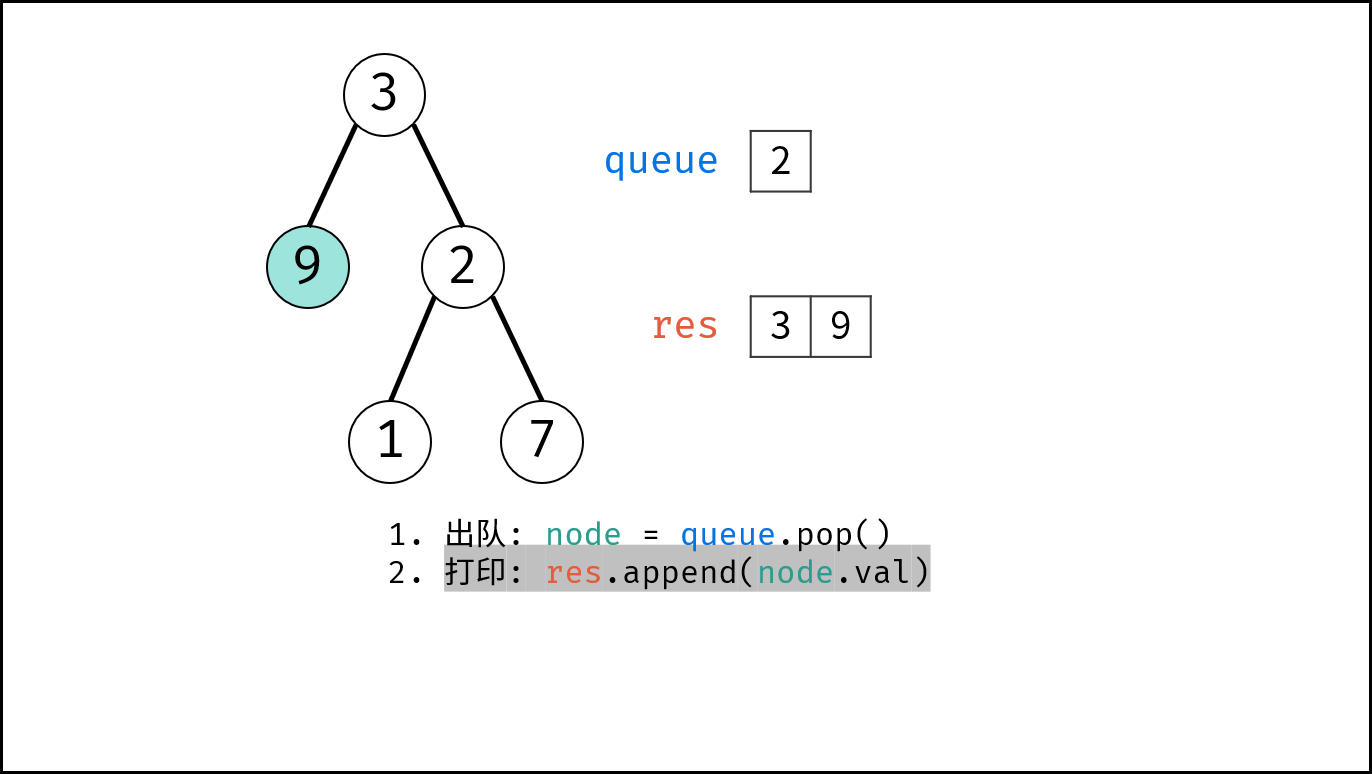Picture7.png](https://pic.leetcode-cn.com/bdbad0817bdf85ba5f4d01e8d06f6dc82b295f15f27498ed8e314344707c9cd2-Picture7.png),![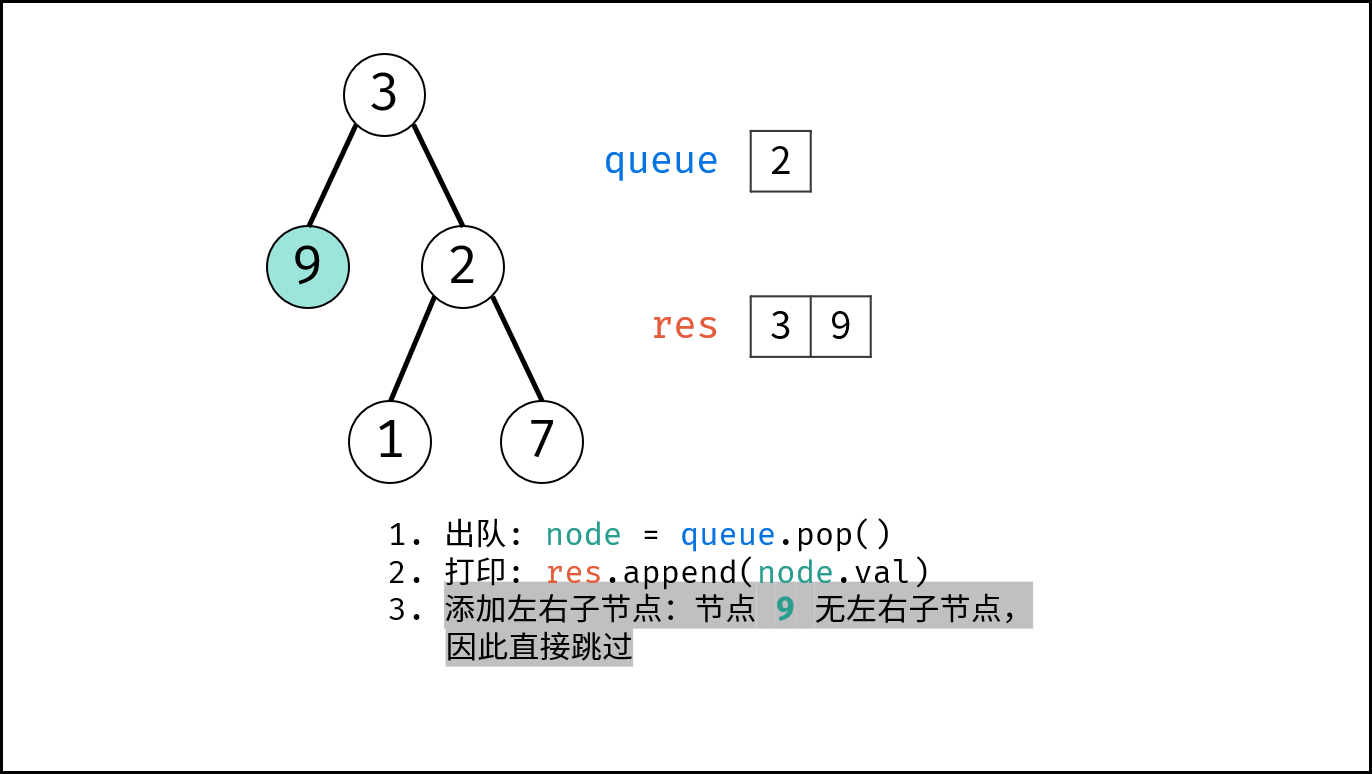Picture8.png](https://pic.leetcode-cn.com/5e54460c69fcef7fb86277da6b8d132dbe652bdf540558ae0a5c8b22ae94a49e-Picture8.png),![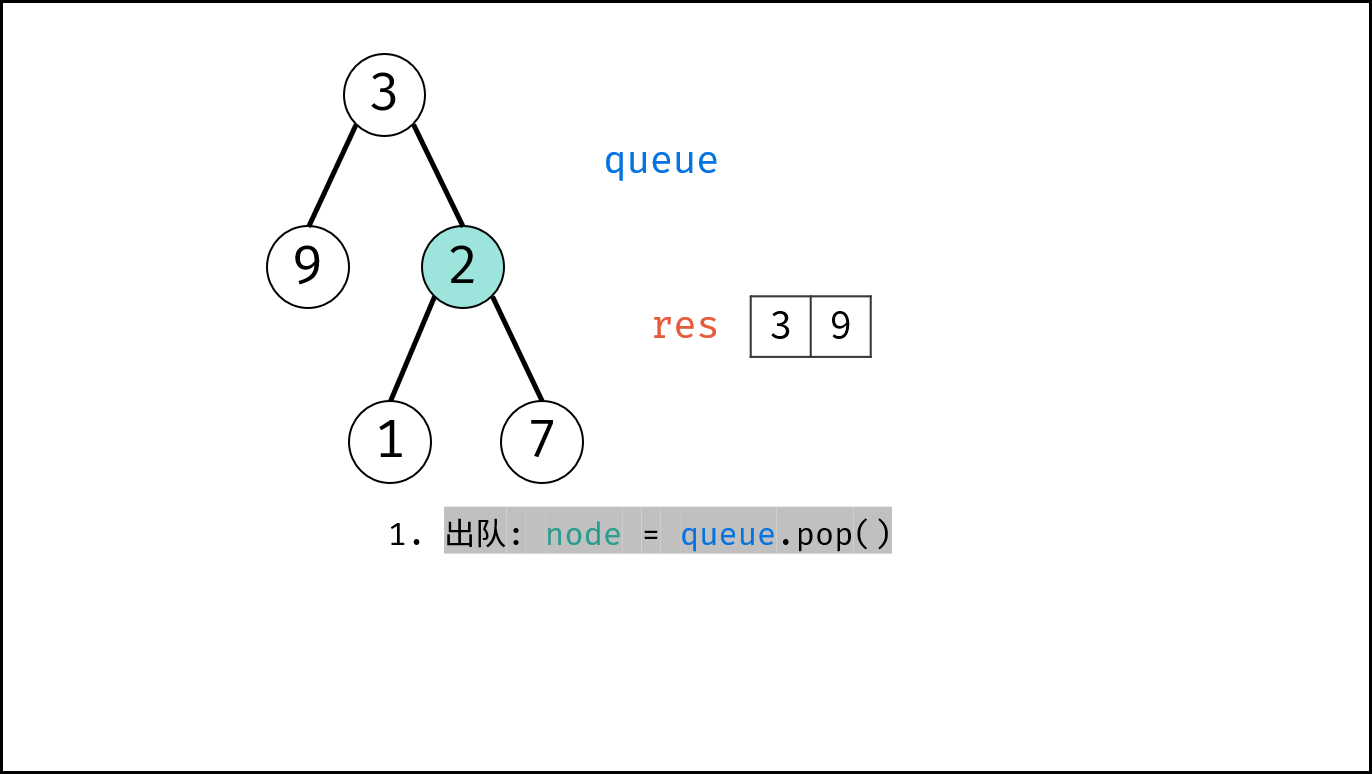Picture9.png](https://pic.leetcode-cn.com/49c7a62abdd0e1a5af2ada6fd1f0e5f10e7304fe60c321e9e674bf3814db5ad8-Picture9.png),![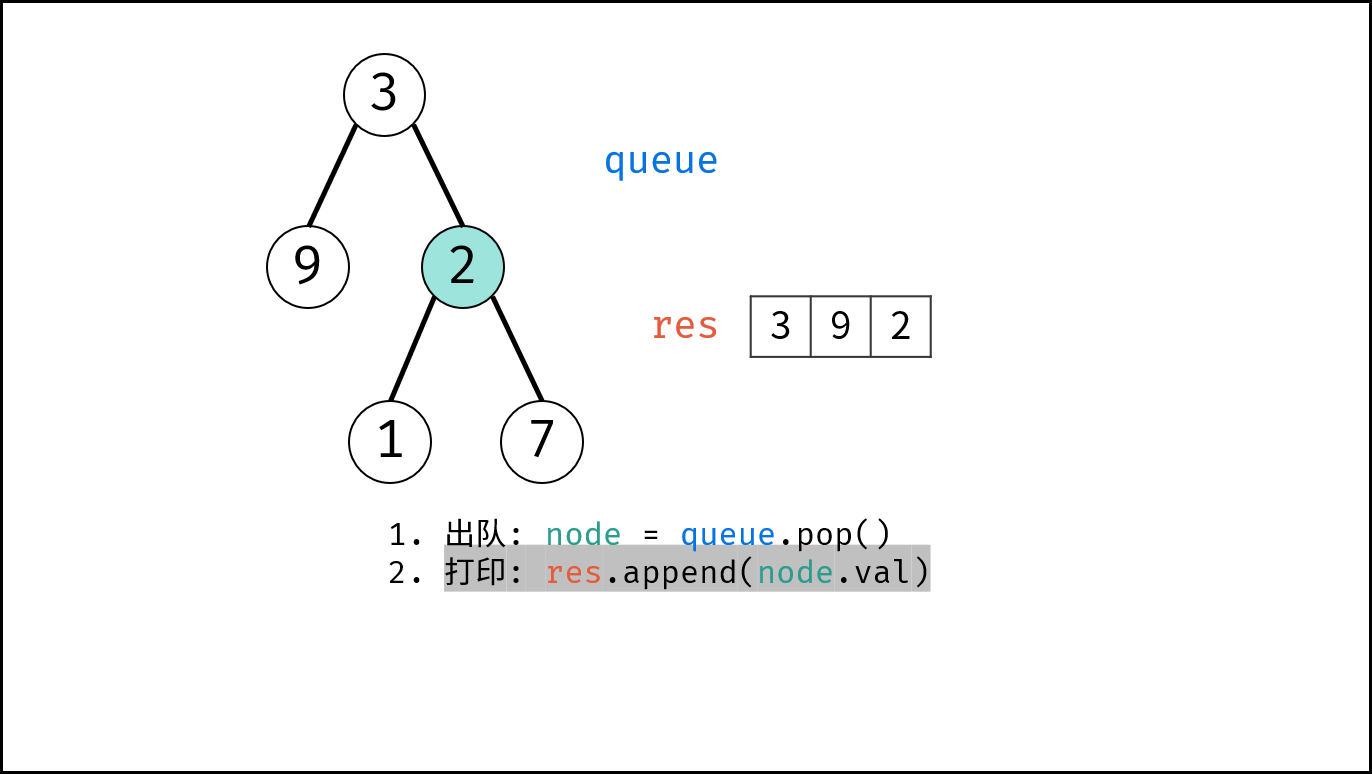Picture10.png](https://pic.leetcode-cn.com/8eea301df52d3e40e95cd42b871b560859a9fcb867507338dd98ff5d5a5fb5be-Picture10.png),![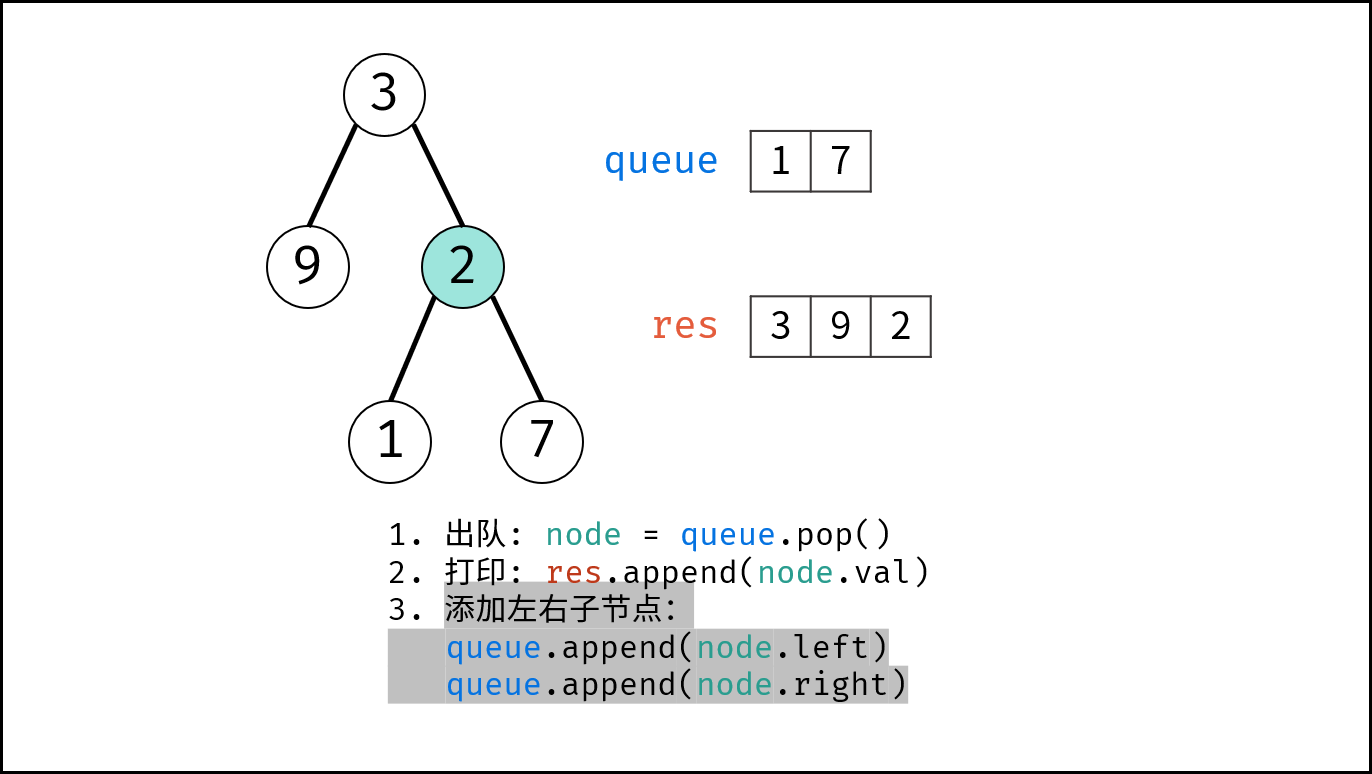Picture11.png](https://pic.leetcode-cn.com/782e1e35a19754d4ab9d19e1c44504ec364c13007b5d12ecf5598e7af7149758-Picture11.png),![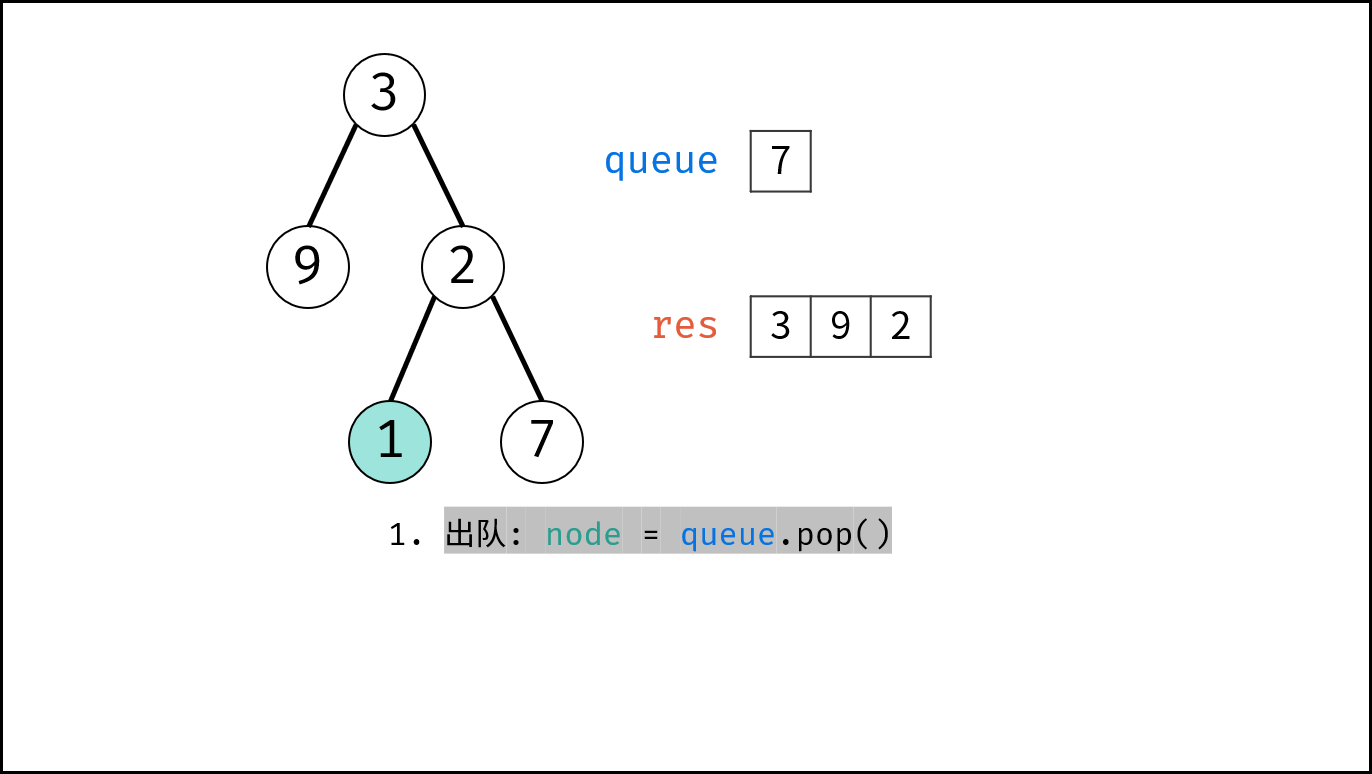Picture12.png](https://pic.leetcode-cn.com/fcfeb4448d3123c19122d18babb93ef110ea693fb809427d8eb63cef59d03888-Picture12.png),![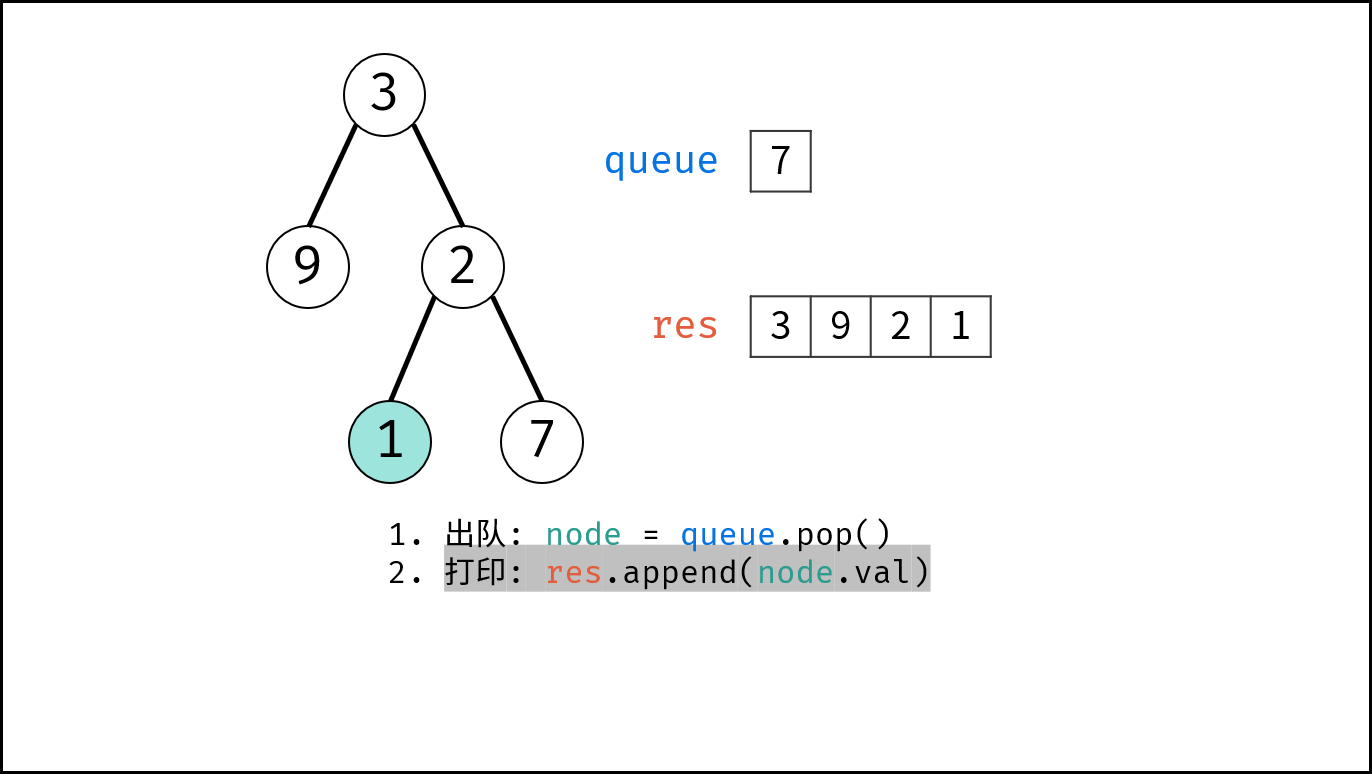Picture13.png](https://pic.leetcode-cn.com/b9a578c85d3bb8c08170809f0f61f18db52e1cb74c7f5439d313f7aaba1eaa6c-Picture13.png),![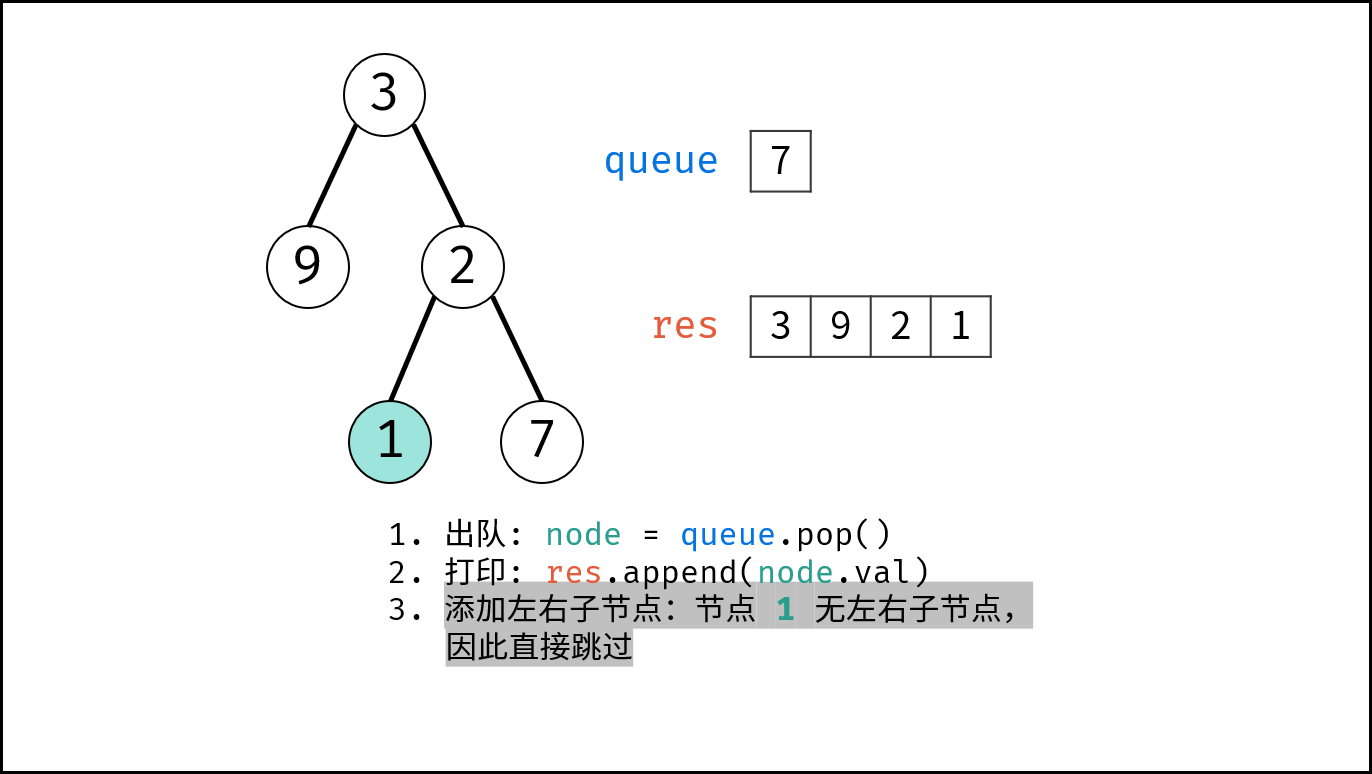Picture14.png](https://pic.leetcode-cn.com/d6cc7b71c747140178c5096b489ae4dbf246121dac61dfe24c253ba28c0402b1-Picture14.png),![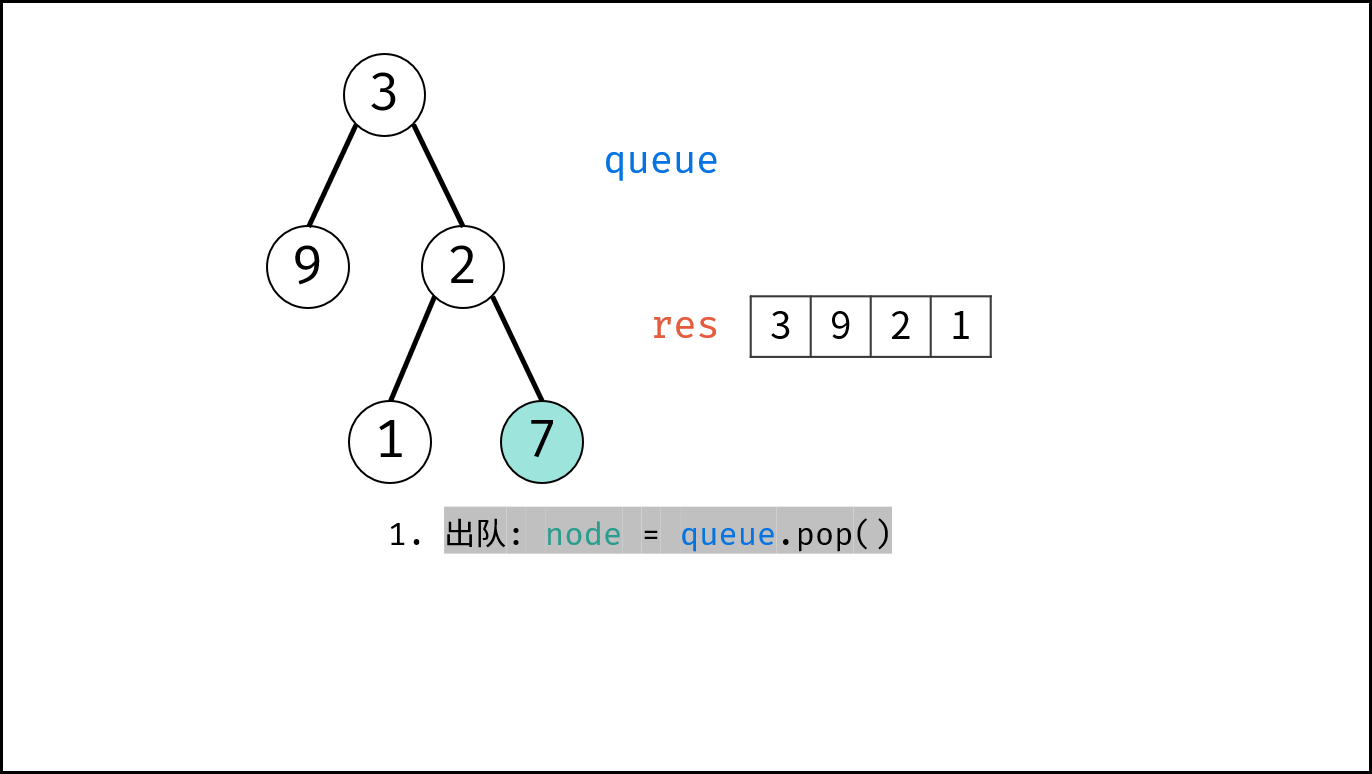Picture15.png](https://pic.leetcode-cn.com/ee5d52b5bdc79d5ec04d82a6249e7e03aaa4707be4384aa29cc960d48066e290-Picture15.png),![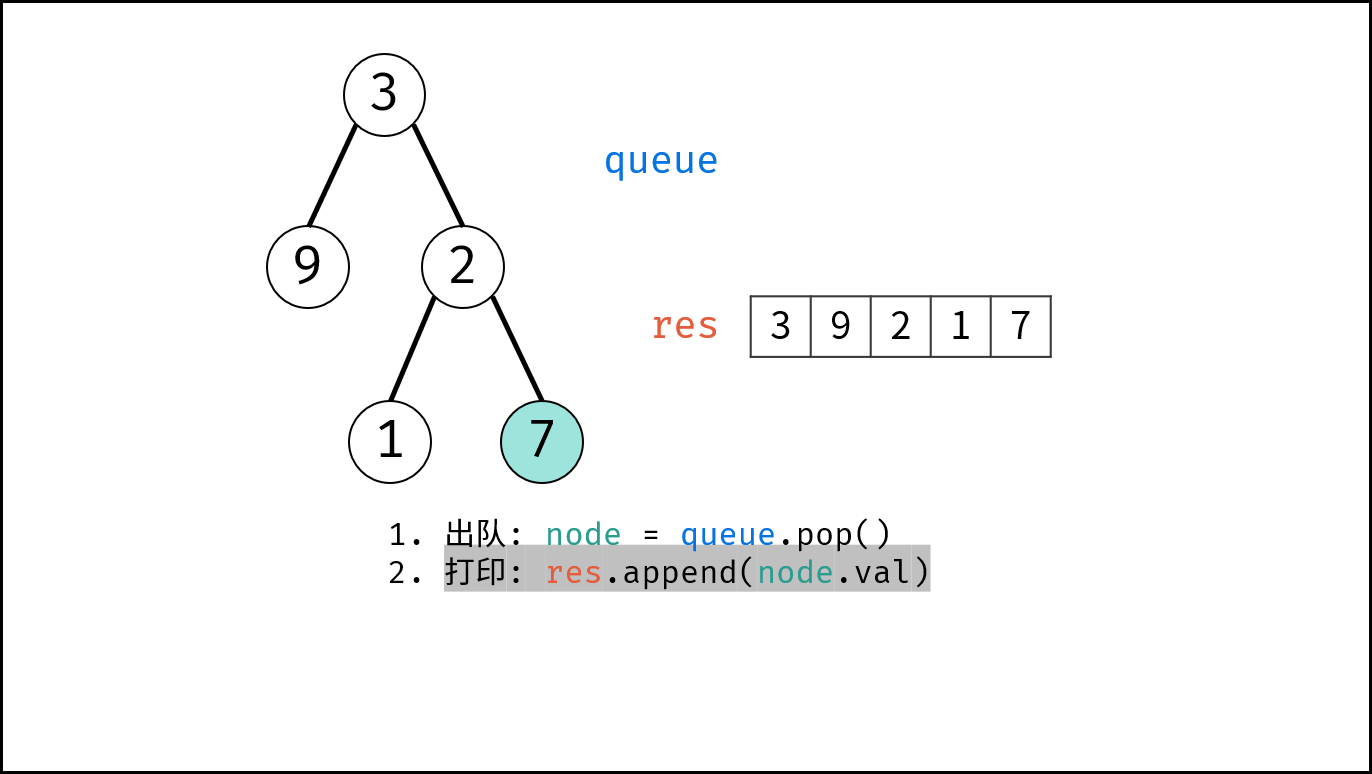Picture16.png](https://pic.leetcode-cn.com/8ffed118931f0c49efcd1acd637a832e7e885083d6f40fc7f6b0fc6b42099a57-Picture16.png),![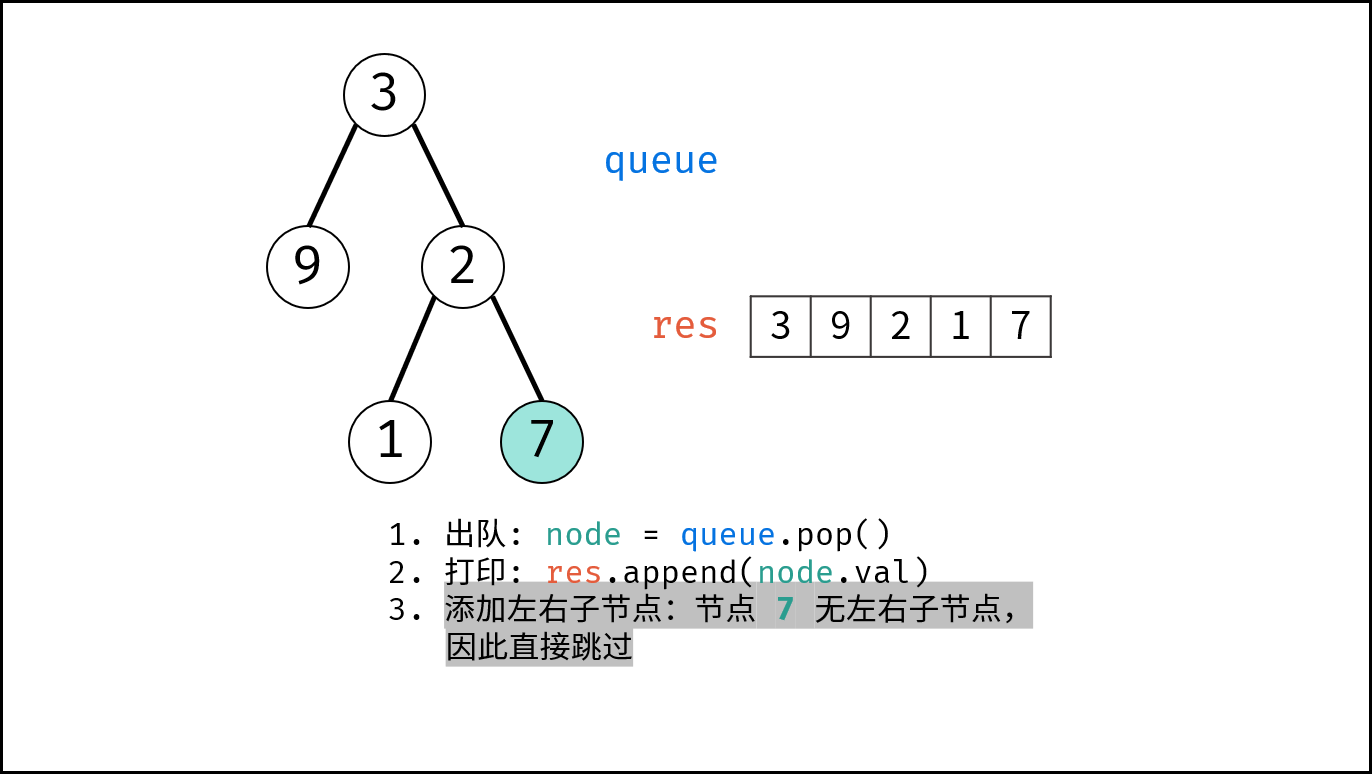Picture17.png](https://pic.leetcode-cn.com/0626f28e8c1aff530808ce78863f6dcca4ffda747acfaeb831572f5fff90f597-Picture17.png),![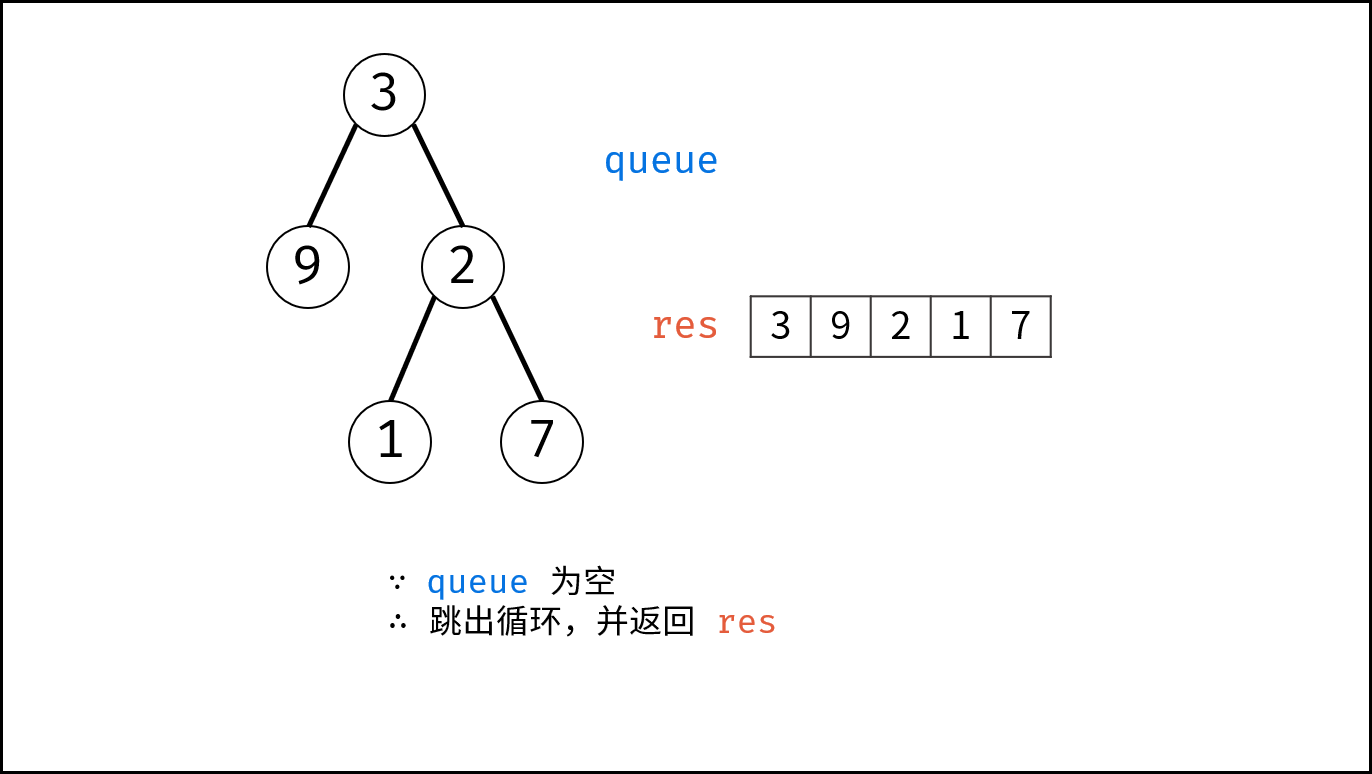Picture18.png](https://pic.leetcode-cn.com/d7a1a57e60db621c5213a170ff8bb8ad2545ea4cfd07ca98b12525aea38ad38a-Picture18.png)>
## 代码：
Python 中使用 collections 中的双端队列 `deque()` ，其 `popleft()` 方法可达到 $O(1)$ 时间复杂度；列表 list 的 `pop(0)` 方法时间复杂度为 $O(N)$ 。
```Python []
class Solution:
def decorateRecord(self, root: TreeNode) -> List[int]:
if not root: return []
res, queue = [], collections.deque()
queue.append(root)
while queue:
node = queue.popleft()
res.append(node.val)
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
return res
```
```Java []
class Solution {
public int[] decorateRecord(TreeNode root) {
if(root == null) return new int[0];
Queue<TreeNode> queue = new LinkedList<>(){{ add(root); }};
ArrayList<Integer> ans = new ArrayList<>();
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
ans.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
int[] res = new int[ans.size()];
for(int i = 0; i < ans.size(); i++)
res[i] = ans.get(i);
return res;
}
}
```
```C++ []
class Solution {
public:
vector<int> decorateRecord(TreeNode* root) {
vector<int> res;
if(!root) return res;
queue<TreeNode *> que;
que.push(root);
while(!que.empty()){
TreeNode* node = que.front();
que.pop();
res.push_back(node->val);
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数量，即 BFS 需循环 $N$ 次。
- **空间复杂度 $O(N)$ ：** 最差情况下，即当树为平衡二叉树时，最多有 $N/2$ 个树节点**同时**在 `queue` 中，使用 $O(N)$ 大小的额外空间。

90
leetbook_ioa/docs/LCR 150. 彩灯装饰记录 II.md Executable file
View File

@@ -0,0 +1,90 @@
## 解题思路：
在上一题层序遍历的基础上，本题要求将 **每层打印到一行**。考虑将当前全部节点打印到一行，并将下一层全部节点加入队列，以此类推，即可分为多行打印。
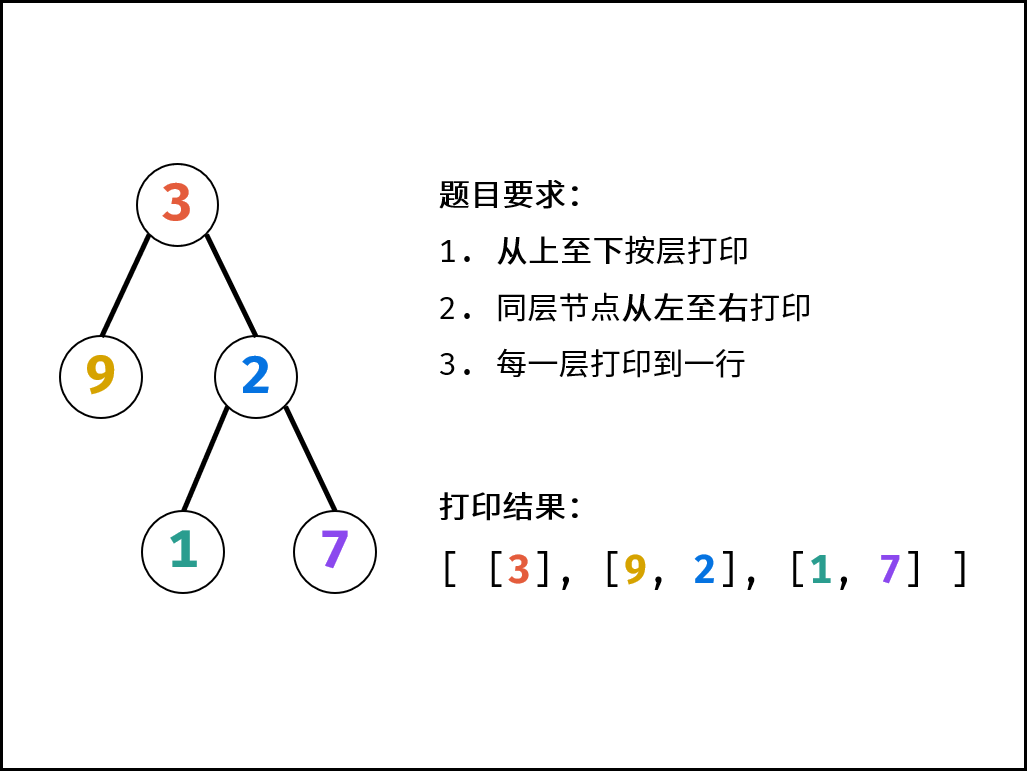![Picture1.png](https://pic.leetcode-cn.com/a58477c74c96779c265ce3028def7625d16042895d2c21f7fb0293df7b213276-Picture1.png){:align=center width=450}
### 算法流程：
1. **特例处理：** 当根节点为空，则返回空列表 `[]` ；
2. **初始化：** 打印结果列表 `res = []` ，包含根节点的队列 `queue = [root]` ；
3. **BFS 循环：** 当队列 `queue` 为空时跳出；
1. 新建一个临时列表 `tmp` ，用于存储当前层打印结果；
2. **当前层打印循环：** 循环次数为当前层节点数（即队列 `queue` 长度）；
1. **出队：** 队首元素出队，记为 `node`；
2. **打印：** 将 `node.val` 添加至 `tmp` 尾部；
3. **添加子节点：** 若 `node` 的左（右）子节点不为空，则将左（右）子节点加入队列 `queue` ；
3. 将当前层结果 `tmp` 添加入 `res` 。
4. **返回值：** 返回打印结果列表 `res` 即可。
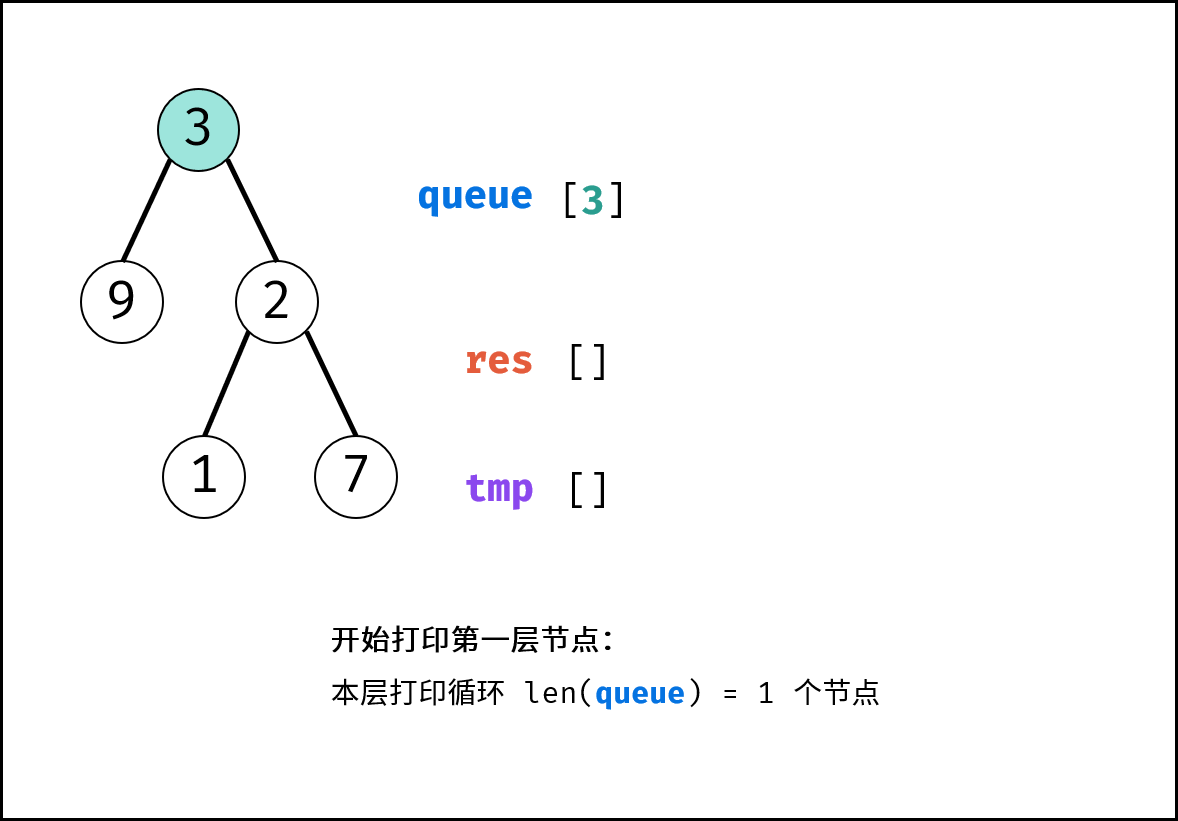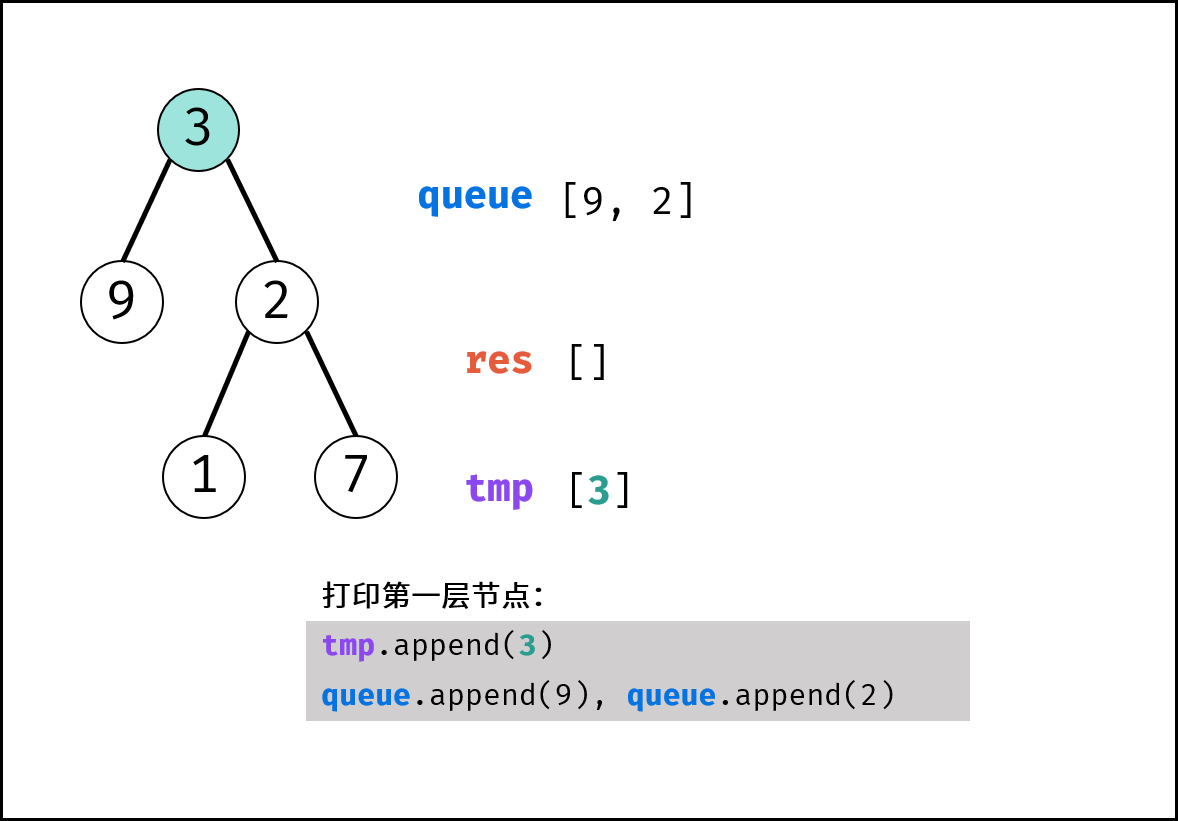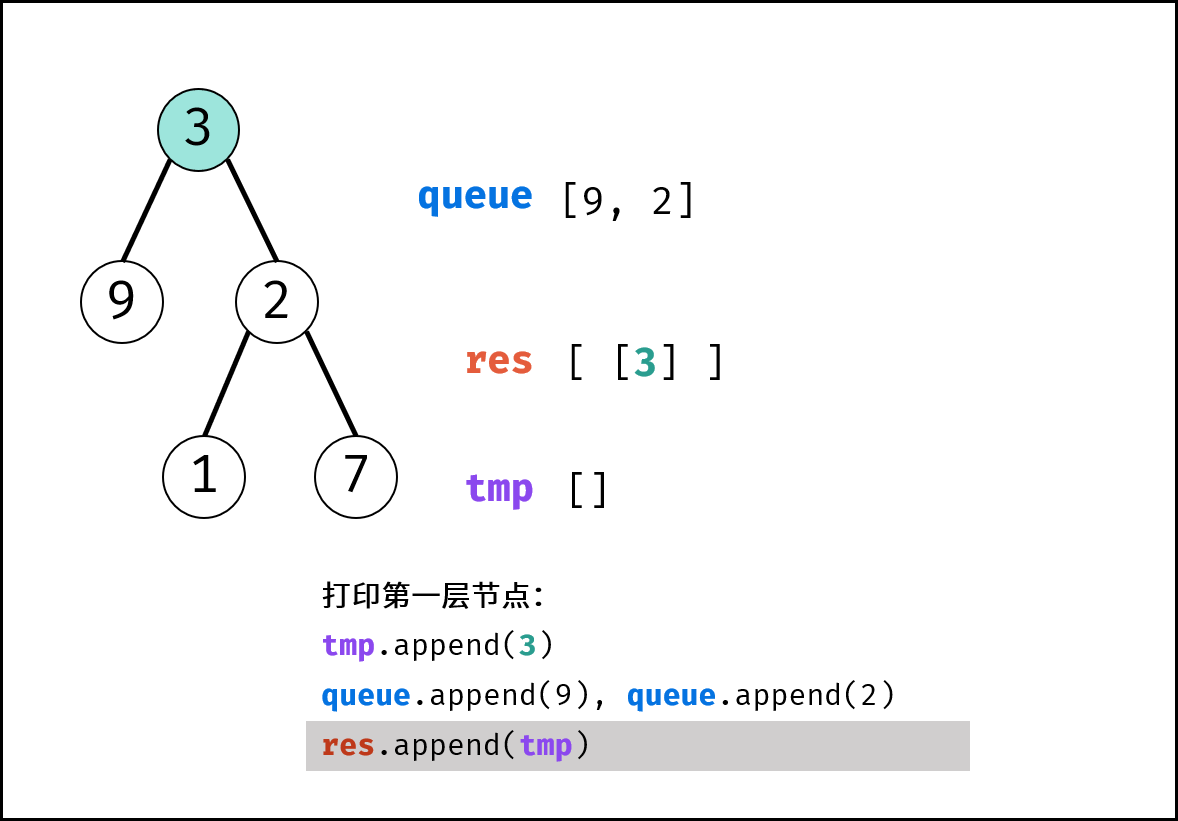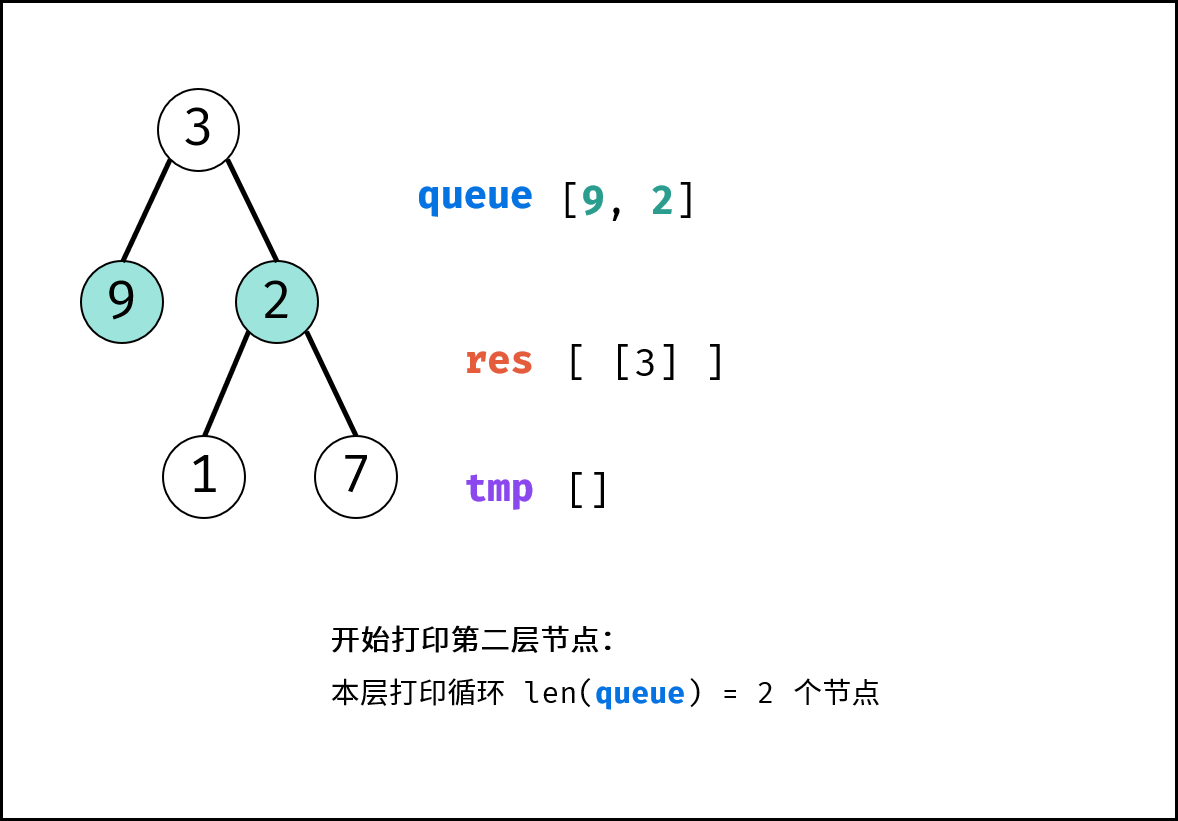<![Picture2.png](https://pic.leetcode-cn.com/2aaa6b8a29c2cc3b5bf90cafc2a2d26c3fa0691ea9ad3d2139826c9fa20e5325-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/af416e73f4c3ee15a92e895697f1e8da09a225958db3697ae68083dfd835a5b0-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/435a8f39b8365bf7fdbdac6ad3f952d3d86552703cf6c6d8986811d23cef41ee-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/5bb17b9bdbe2b6f2cc82adfa80beb09a269ee1988c87e0301f8104e0e3ea72fb-Picture5.png),![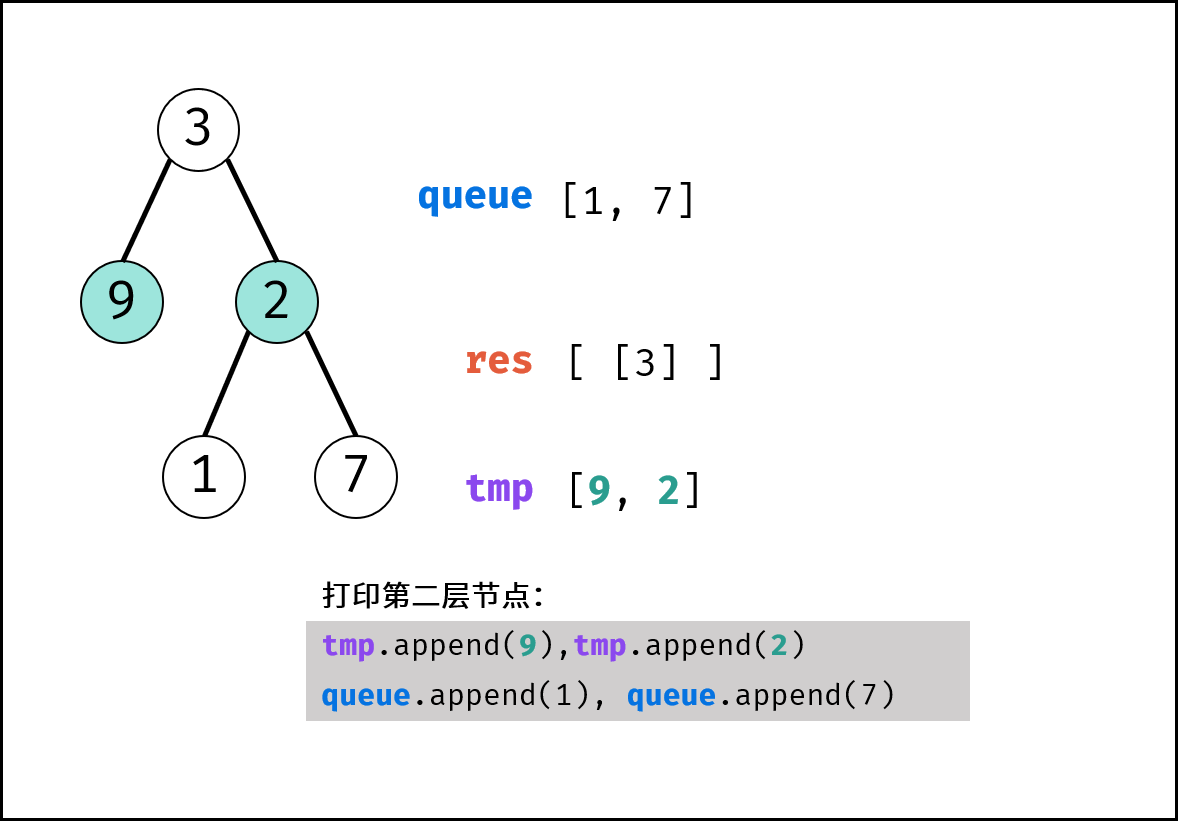Picture6.png](https://pic.leetcode-cn.com/5ecd431e77936c8cfdfe67ce18592ba3b1bd786818fed8728dc4c1303de5029e-Picture6.png),![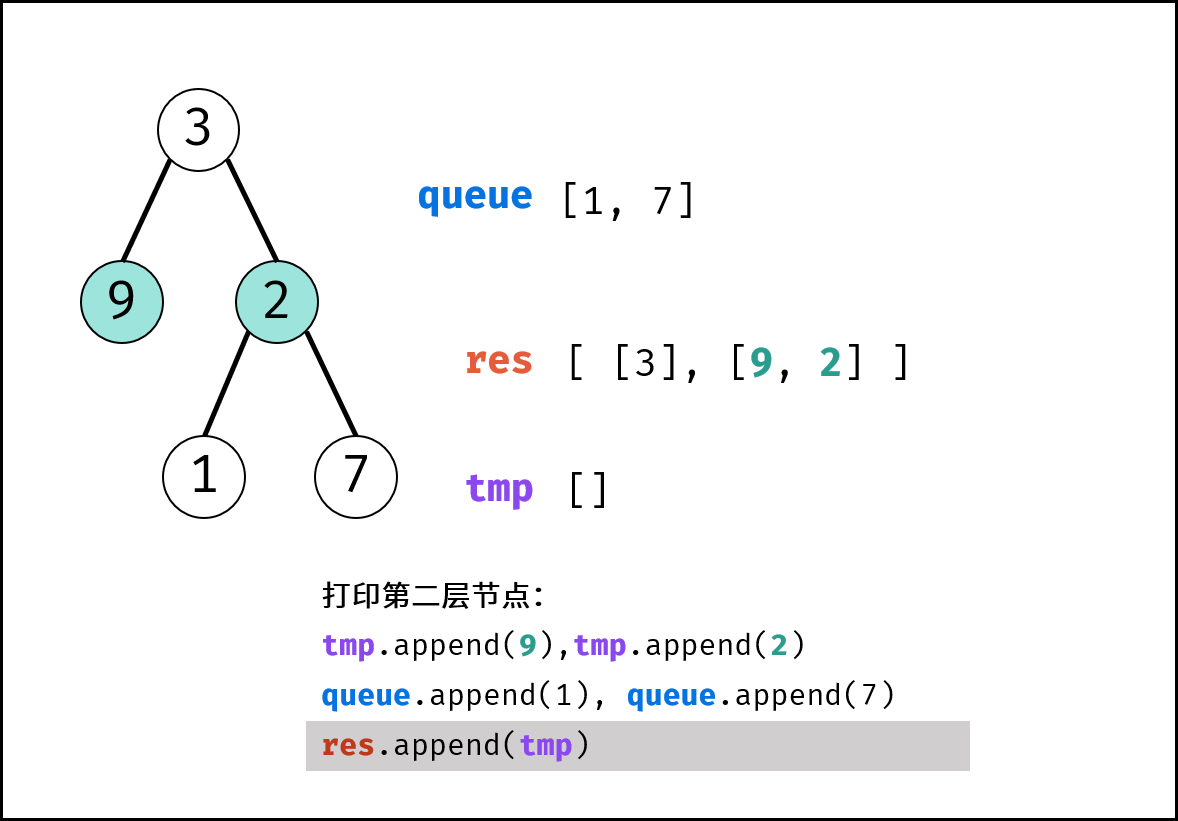Picture7.png](https://pic.leetcode-cn.com/aaa30c224754d66181d906fca0989e4e3c78b4359659a9e5627339993642fc47-Picture7.png),![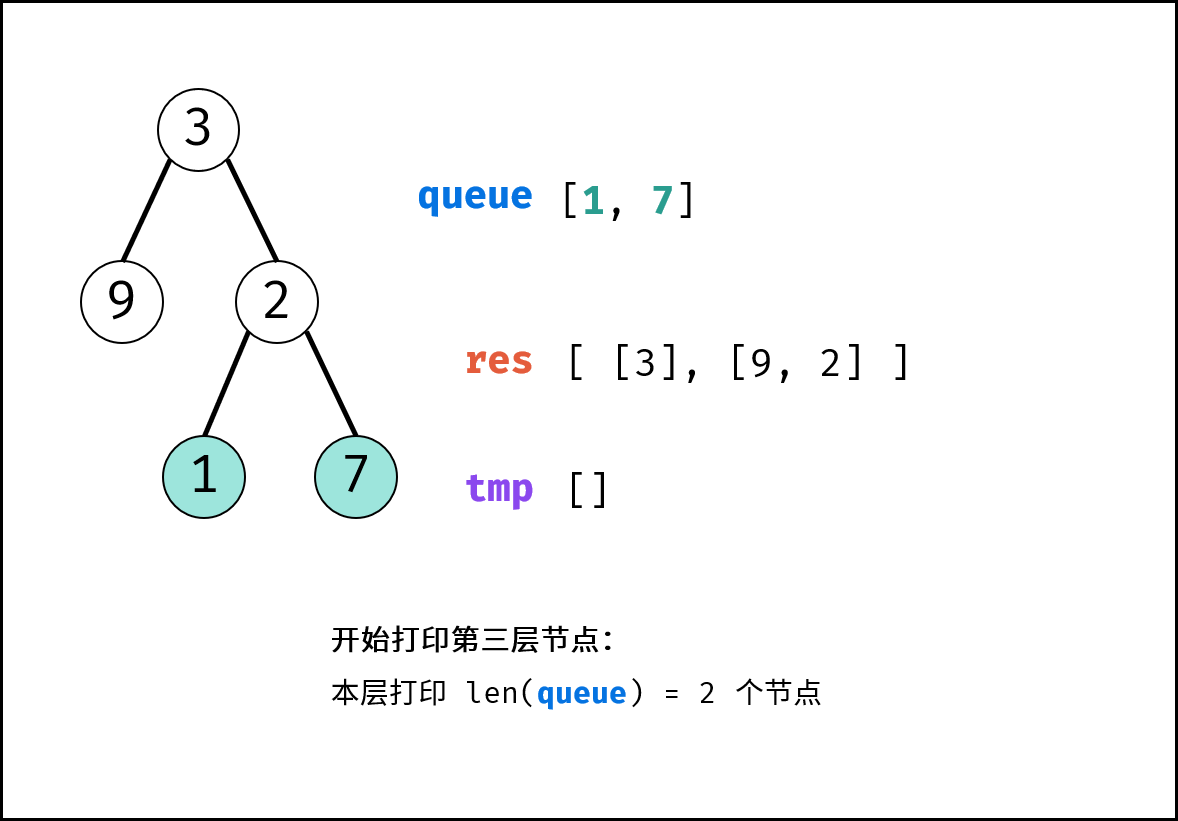Picture8.png](https://pic.leetcode-cn.com/8bd6149dc6b5245b652e55aa86f311fceed164058b70a56eb859a0e94f1e5884-Picture8.png),![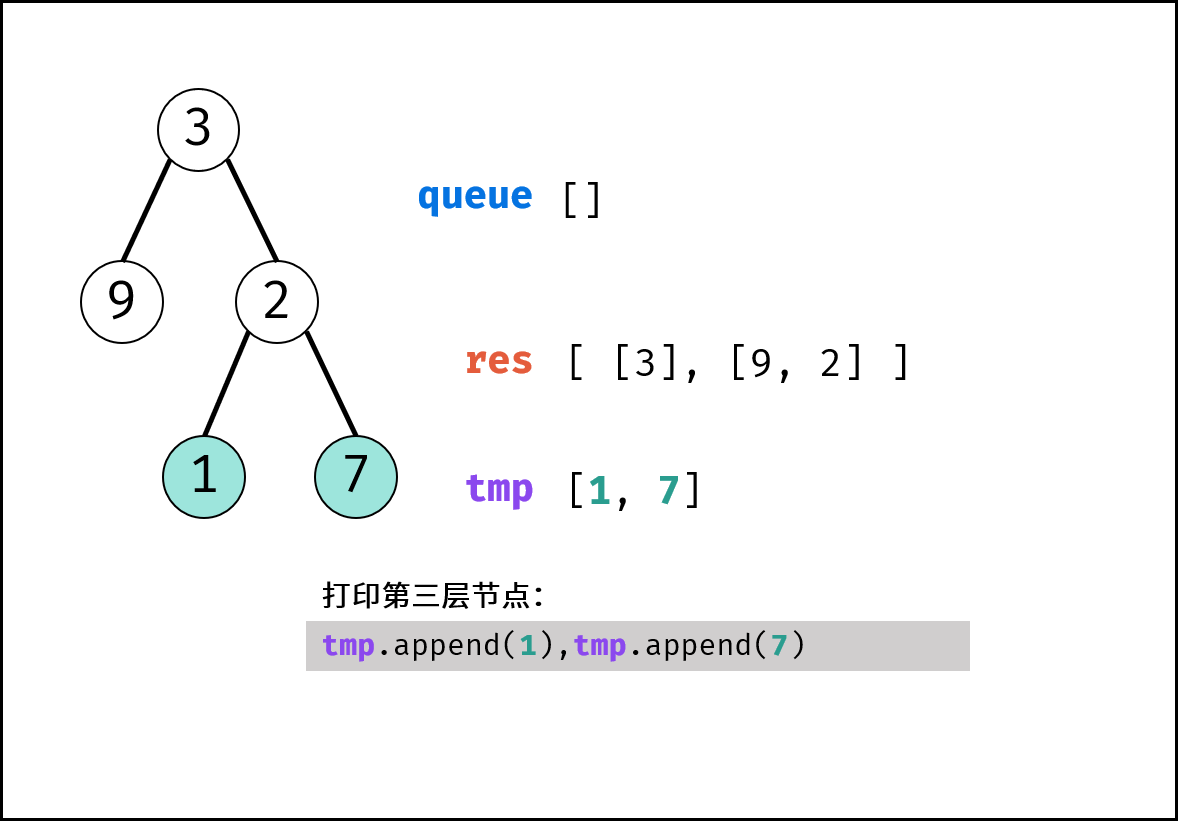Picture9.png](https://pic.leetcode-cn.com/9dc9b25624dc3a2e34498df7e0ad62fb4d4f1344b8a357000316d30da66ea1d2-Picture9.png),![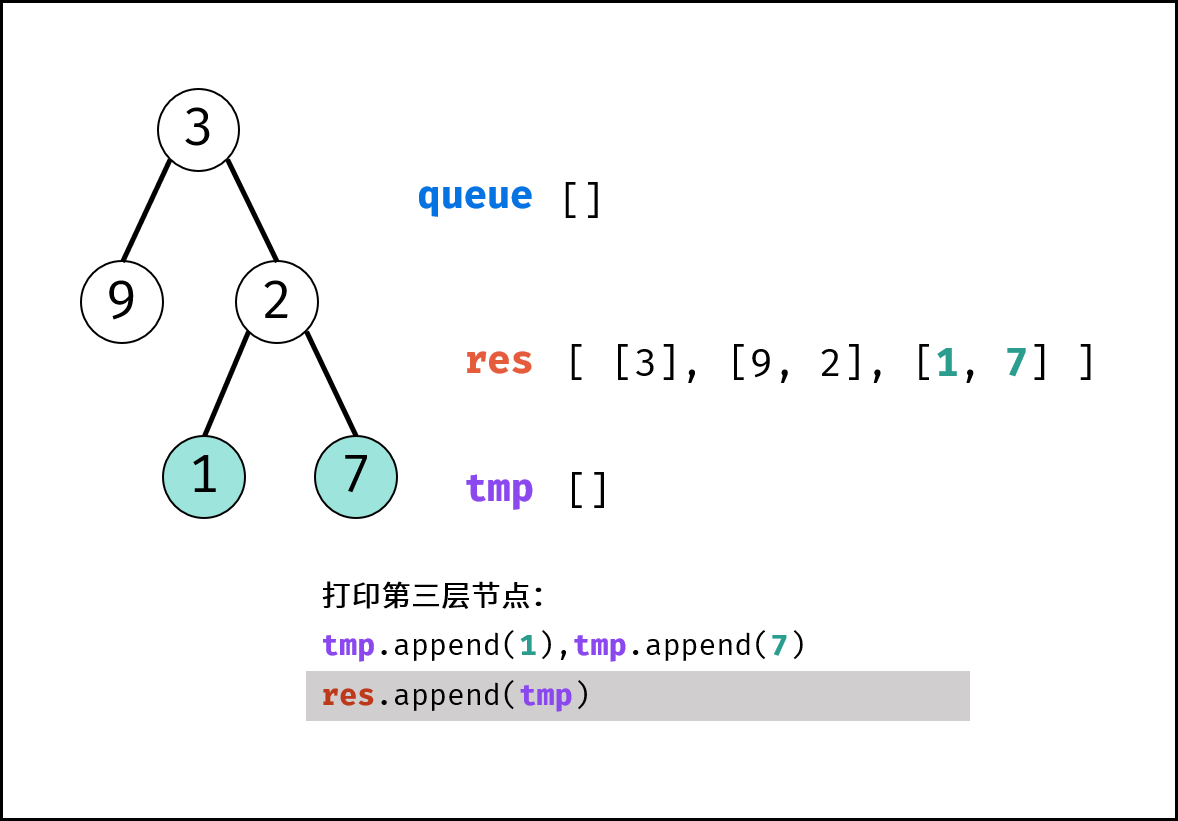Picture10.png](https://pic.leetcode-cn.com/12083cf216791dc6dbe6261feb1677dc9548215f6739a4465fd0aa042faa1284-Picture10.png),![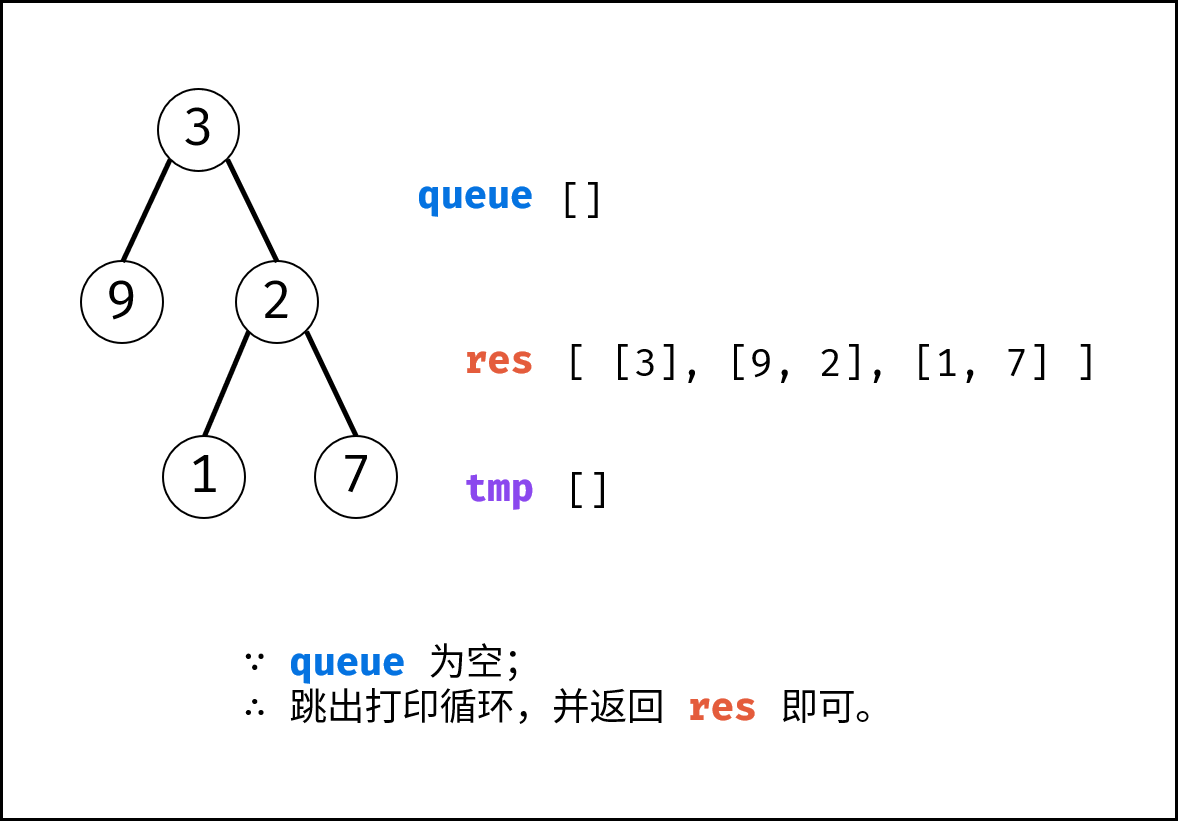Picture11.png](https://pic.leetcode-cn.com/87e1cd8e79655516f5881421153b16d8dbb3f4aea59d925b0aa89016cfc690b0-Picture11.png)>
## 代码：
Python 中使用 collections 中的双端队列 `deque()` ，其 `popleft()` 方法可达到 $O(1)$ 时间复杂度；列表 list 的 `pop(0)` 方法时间复杂度为 $O(N)$ 。
```Python []
class Solution:
def decorateRecord(self, root: TreeNode) -> List[List[int]]:
if not root: return []
res, queue = [], collections.deque()
queue.append(root)
while queue:
tmp = []
for _ in range(len(queue)):
node = queue.popleft()
tmp.append(node.val)
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
res.append(tmp)
return res
```
```Java []
class Solution {
public List<List<Integer>> decorateRecord(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
```
```C++ []
class Solution {
public:
vector<vector<int>> decorateRecord(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if(root != NULL) que.push(root);
while(!que.empty()) {
vector<int> tmp;
for(int i = que.size(); i > 0; --i) {
root = que.front();
que.pop();
tmp.push_back(root->val);
if(root->left != NULL) que.push(root->left);
if(root->right != NULL) que.push(root->right);
}
res.push_back(tmp);
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数量，即 BFS 需循环 $N$ 次。
- **空间复杂度 $O(N)$ ：** 最差情况下，即当树为平衡二叉树时，最多有 $N/2$ 个树节点**同时**在 `queue` 中，使用 $O(N)$ 大小的额外空间。

277
leetbook_ioa/docs/LCR 151. 彩灯装饰记录 III.md Executable file
View File

@@ -0,0 +1,277 @@
## 方法一：层序遍历 + 双端队列
利用双端队列的两端皆可添加元素的特性，设打印列表（双端队列） `tmp` ，并规定：
- 奇数层 则添加至 `tmp` **尾部** 。
- 偶数层 则添加至 `tmp` **头部** 。
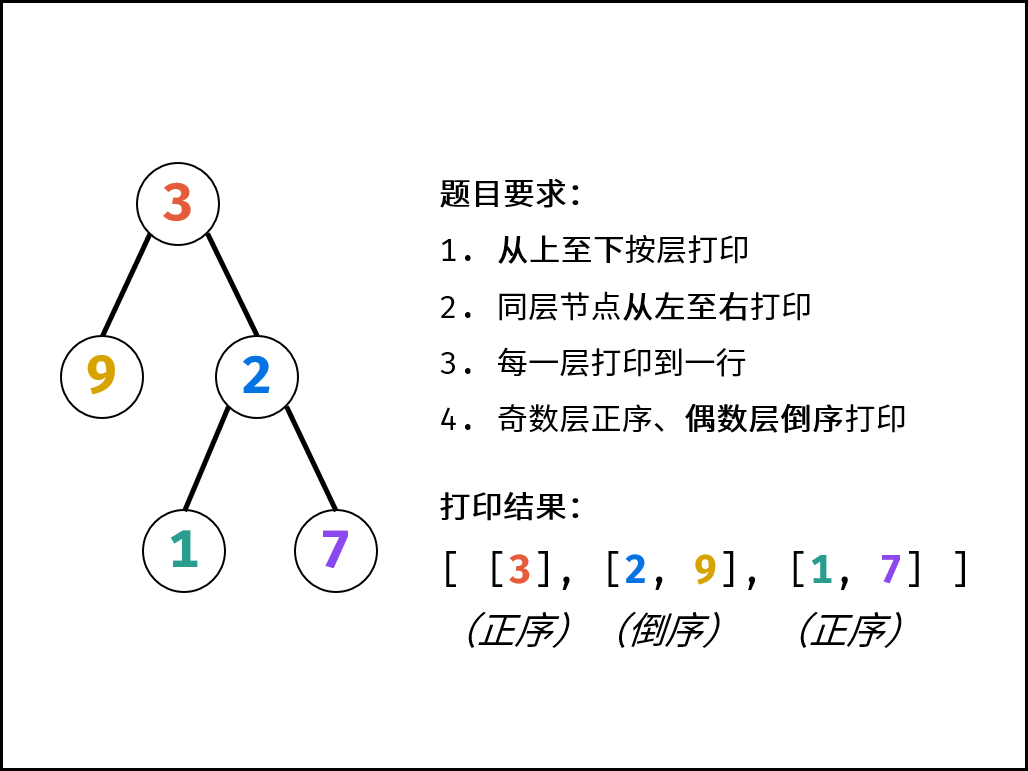![Picture1.png](https://pic.leetcode-cn.com/9513dcb034f5dcdea947a2f667b3d380df4f8732da6397778e00718b77584010-Picture1.png){:align=center width=450}
### 算法流程：
1. **特例处理：** 当树的根节点为空，则直接返回空列表 `[]` ；
2. **初始化：** 打印结果空列表 `res` ，包含根节点的双端队列 `deque` ；
3. **BFS 循环：** 当 `deque` 为空时跳出；
1. 新建列表 `tmp` ，用于临时存储当前层打印结果；
2. **当前层打印循环：** 循环次数为当前层节点数（即 `deque` 长度）；
1. **出队：** 队首元素出队，记为 `node`；
2. **打印：** 若为奇数层，将 `node.val` 添加至 `tmp` 尾部；否则，添加至 `tmp` 头部；
3. **添加子节点：** 若 `node` 的左（右）子节点不为空，则加入 `deque` ；
3. 将当前层结果 `tmp` 转化为 list 并添加入 `res` ；
4. **返回值：** 返回打印结果列表 `res` 即可；
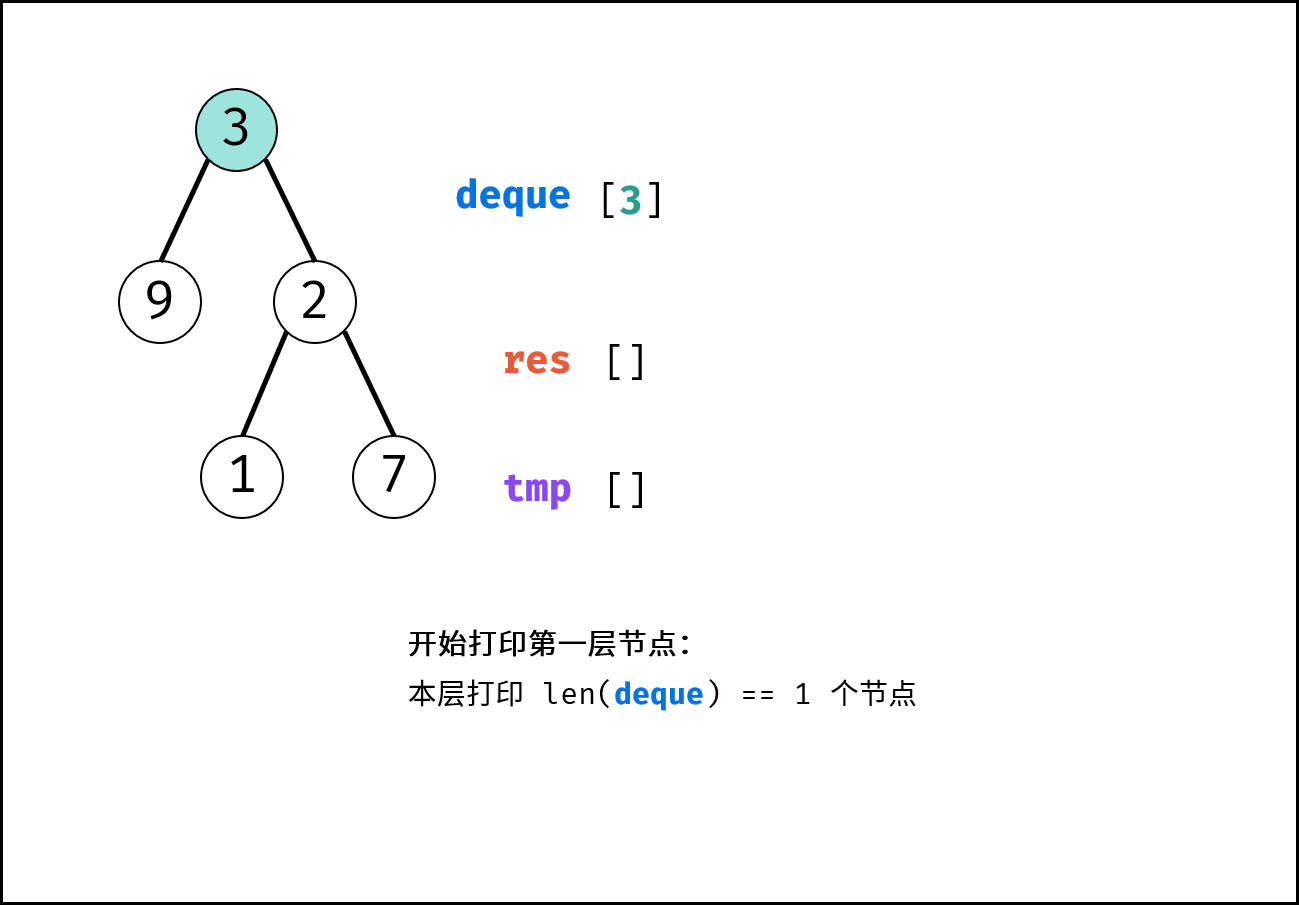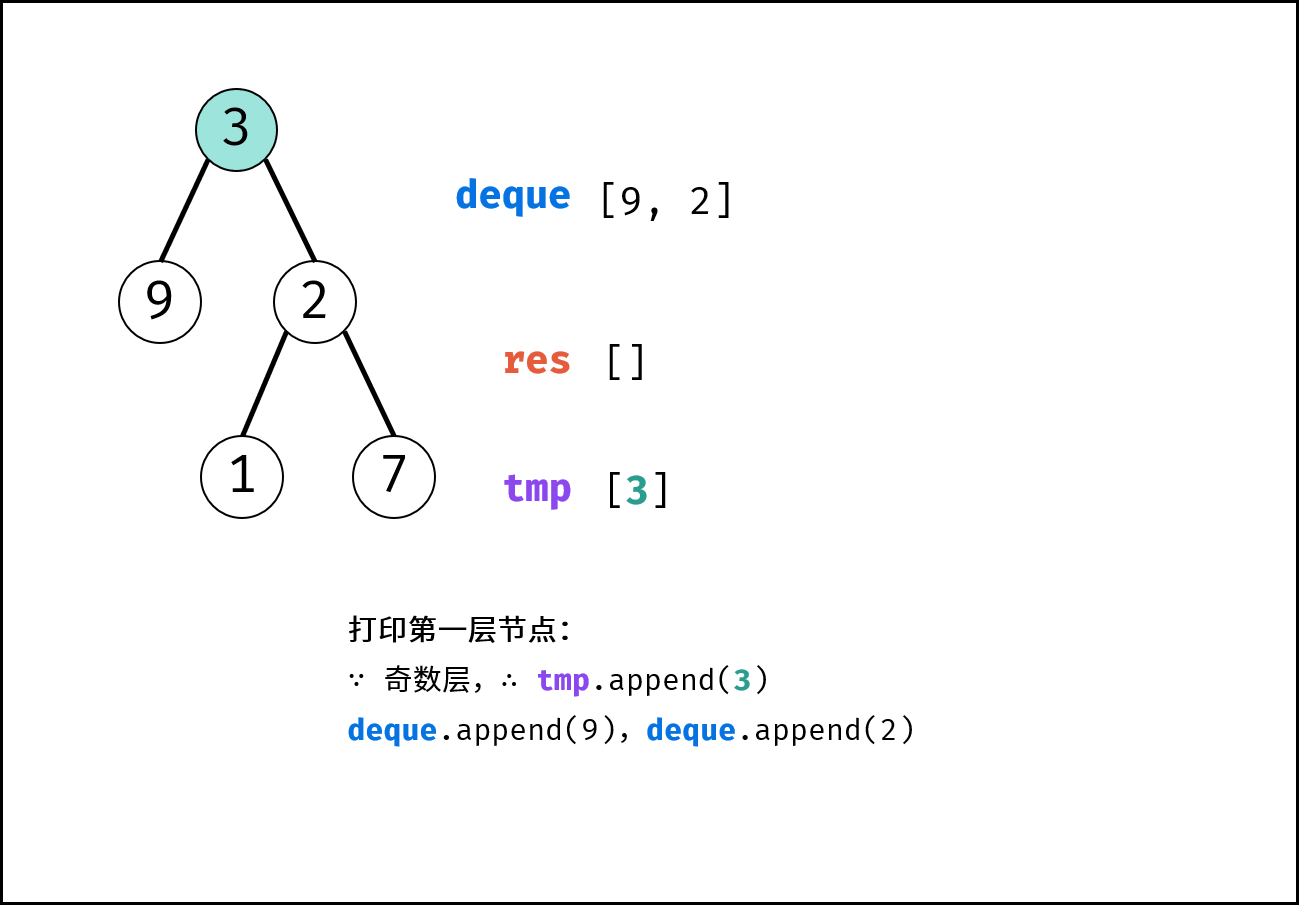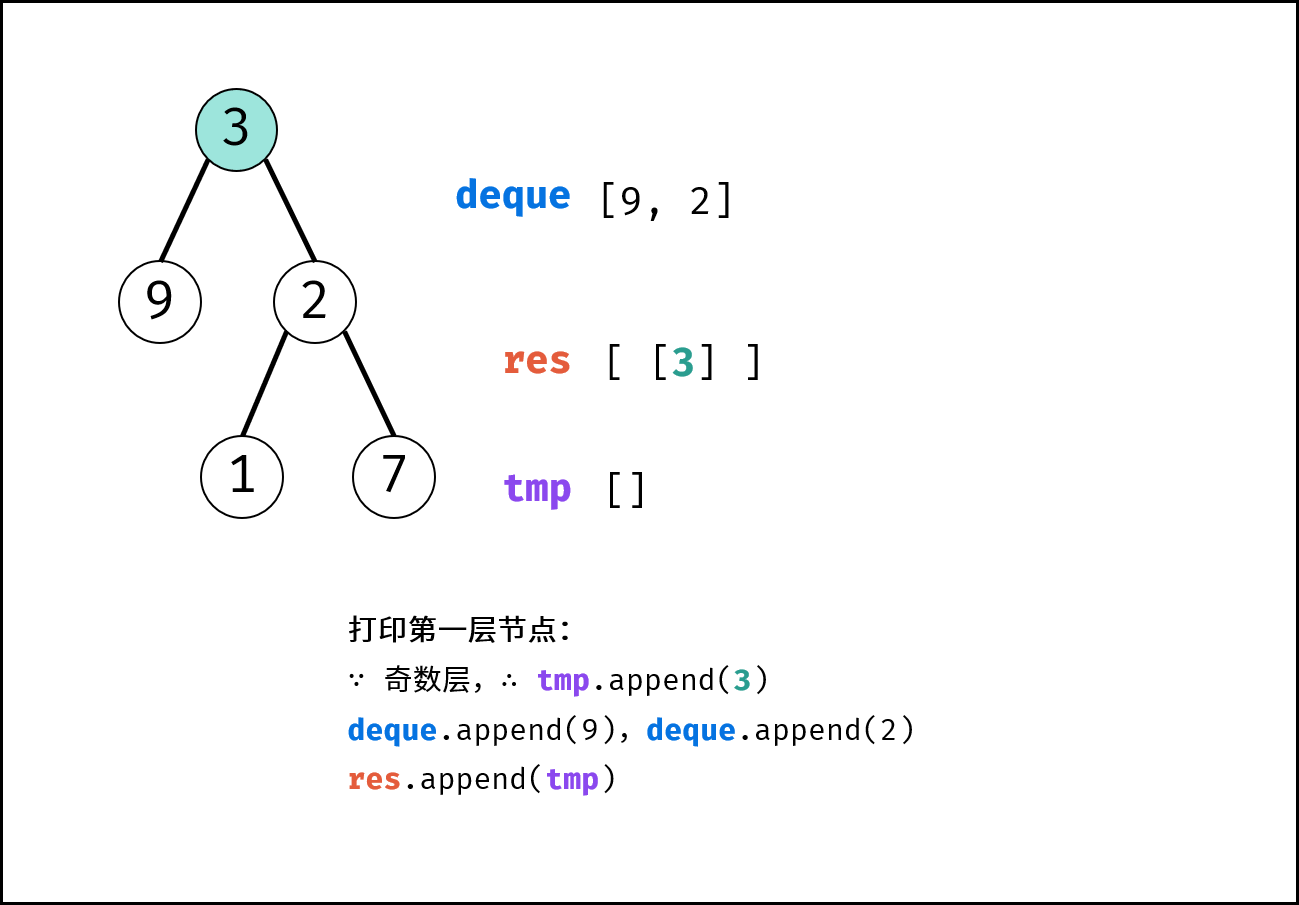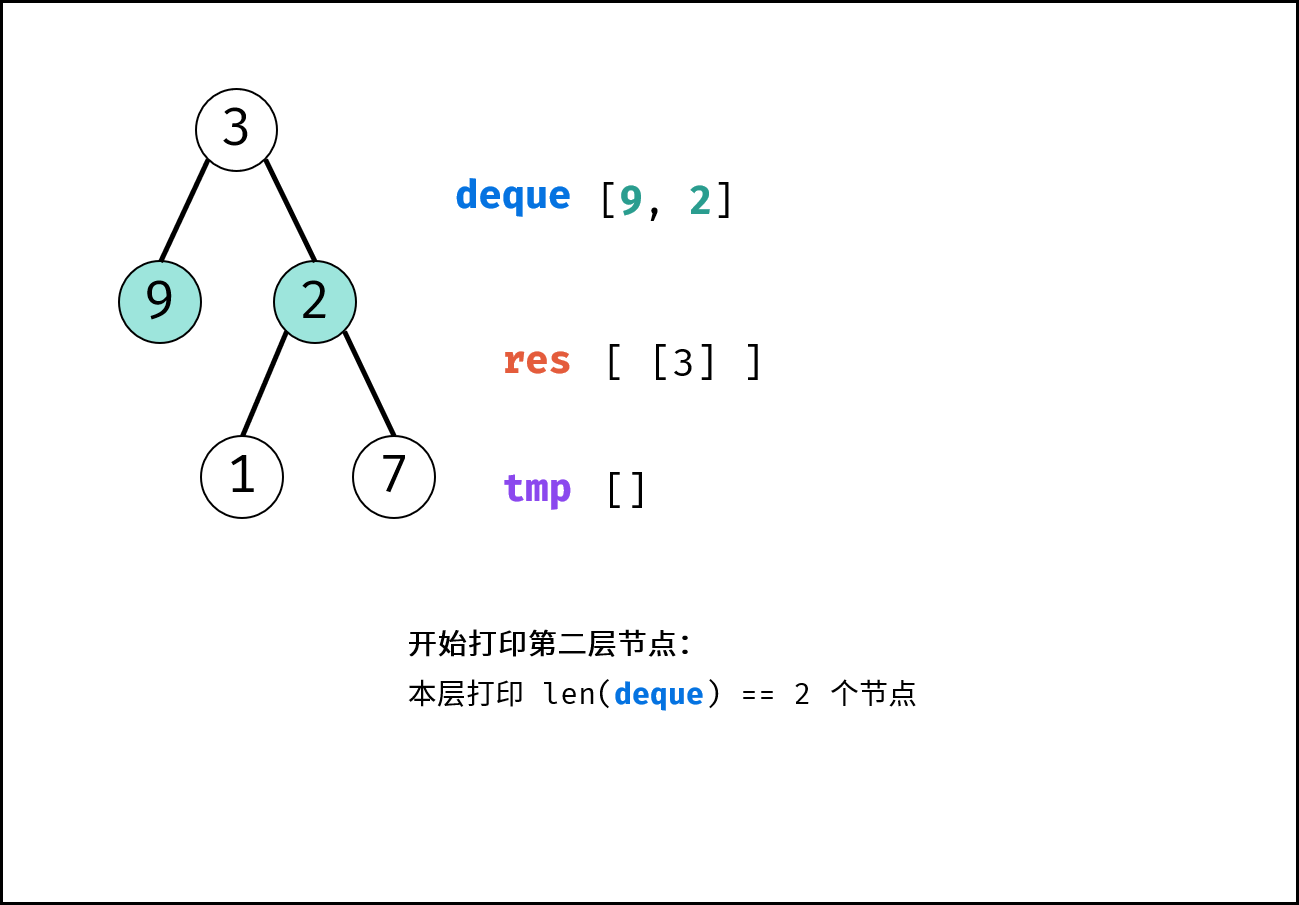<![Picture2.png](https://pic.leetcode-cn.com/f558b222e3ba3662d3582f114736a3a73e4ac49d3d7673b86be408479bdef524-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/a499d6c3fe9bef6be1ea4ae665e307b29eb608bb7d63dd7c143e9d91f4be76ac-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/568358dbc58b54a710c8f698250fe23519c2ccd0ceb3c098530b6aca67c3344c-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/598a4e9ace5854c0114130b349101add2b18e10120c57375fd69365892d57e17-Picture5.png),![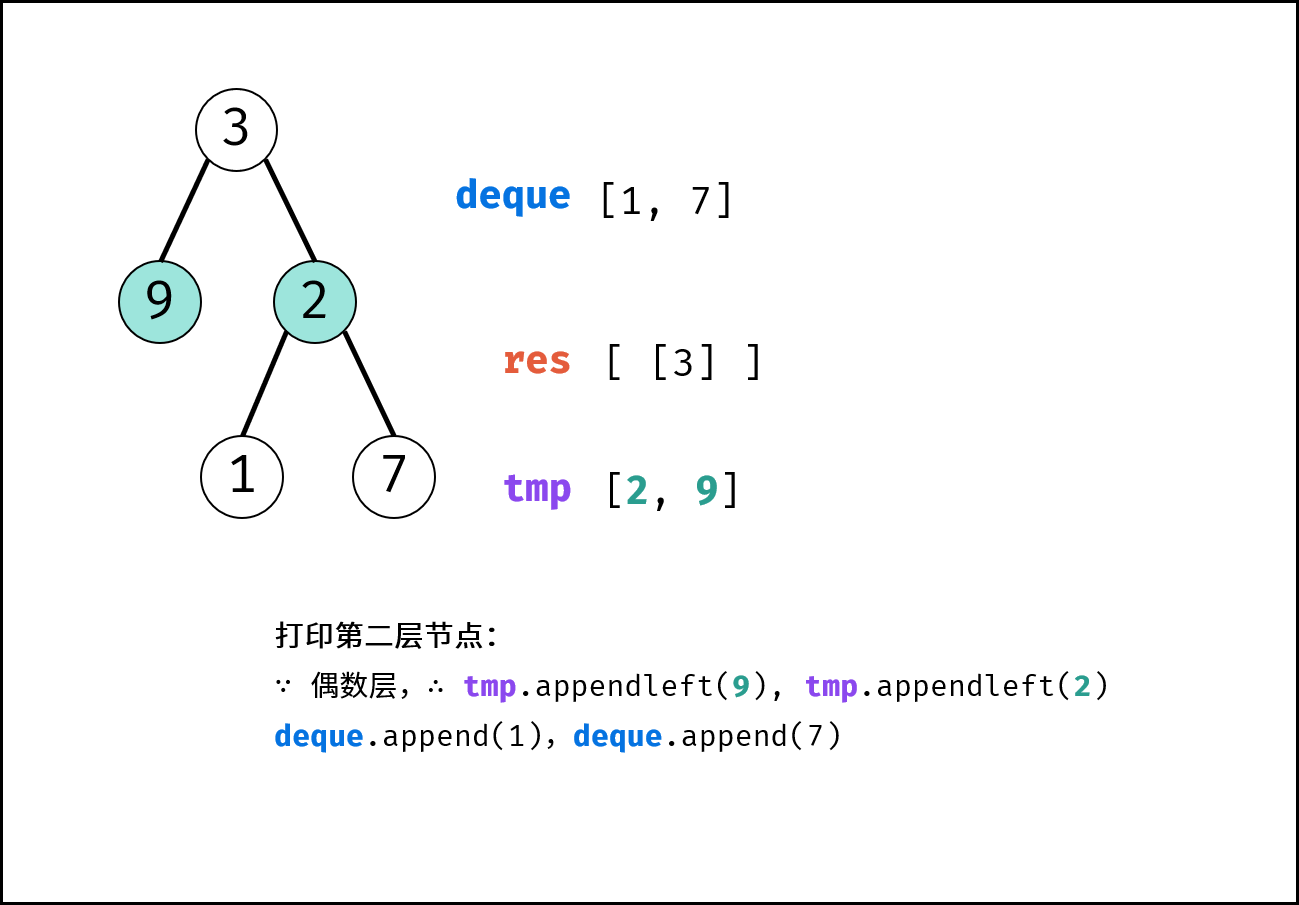Picture6.png](https://pic.leetcode-cn.com/60aacb8f27c26c46929f1ccd0ba56f340389eb4c370bf3669712fcf4117558e1-Picture6.png),![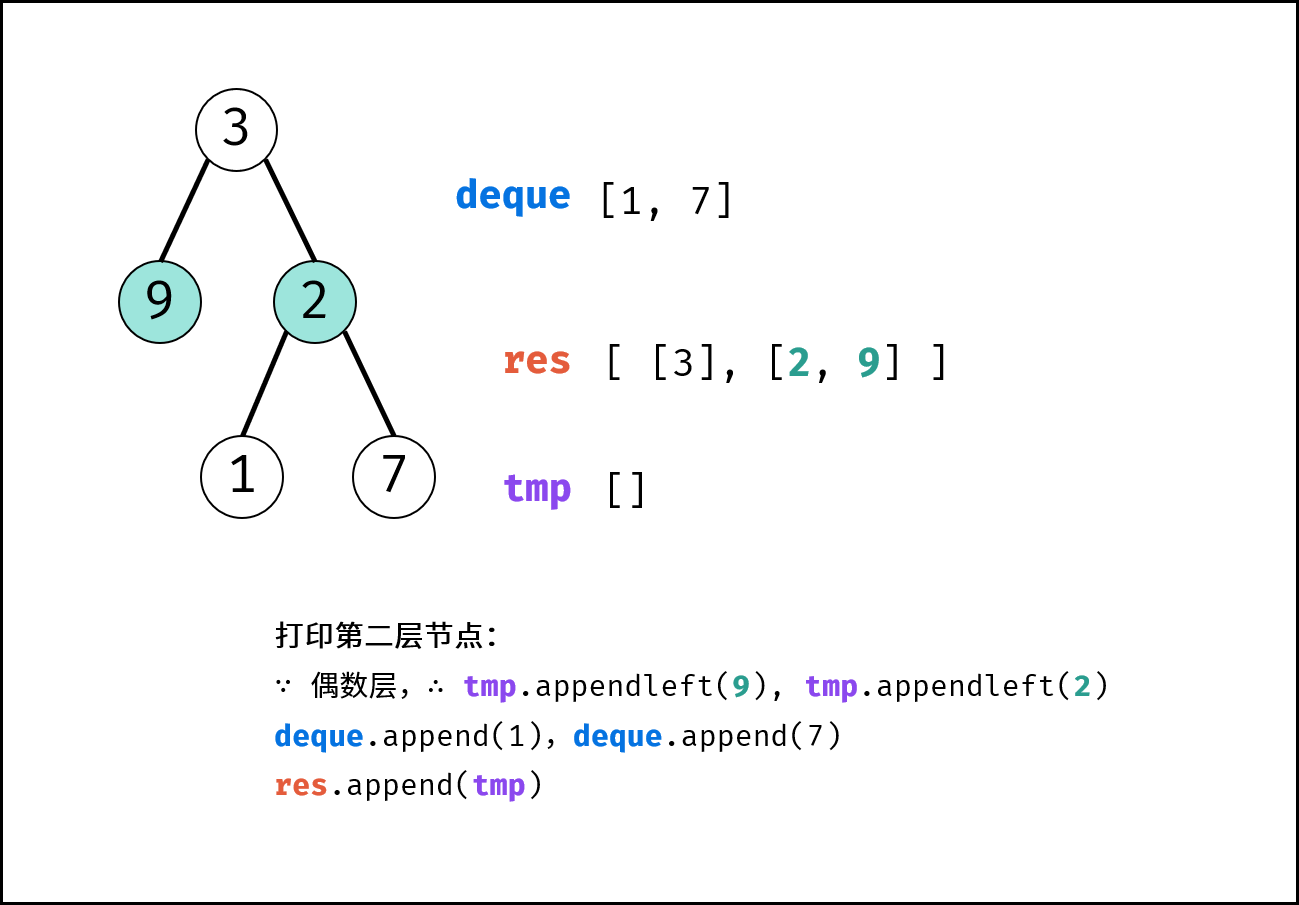Picture7.png](https://pic.leetcode-cn.com/6c1cf508aa660f2fbb1bf724e8a1cab24eadf2889b83b7cfead07152c285a941-Picture7.png),![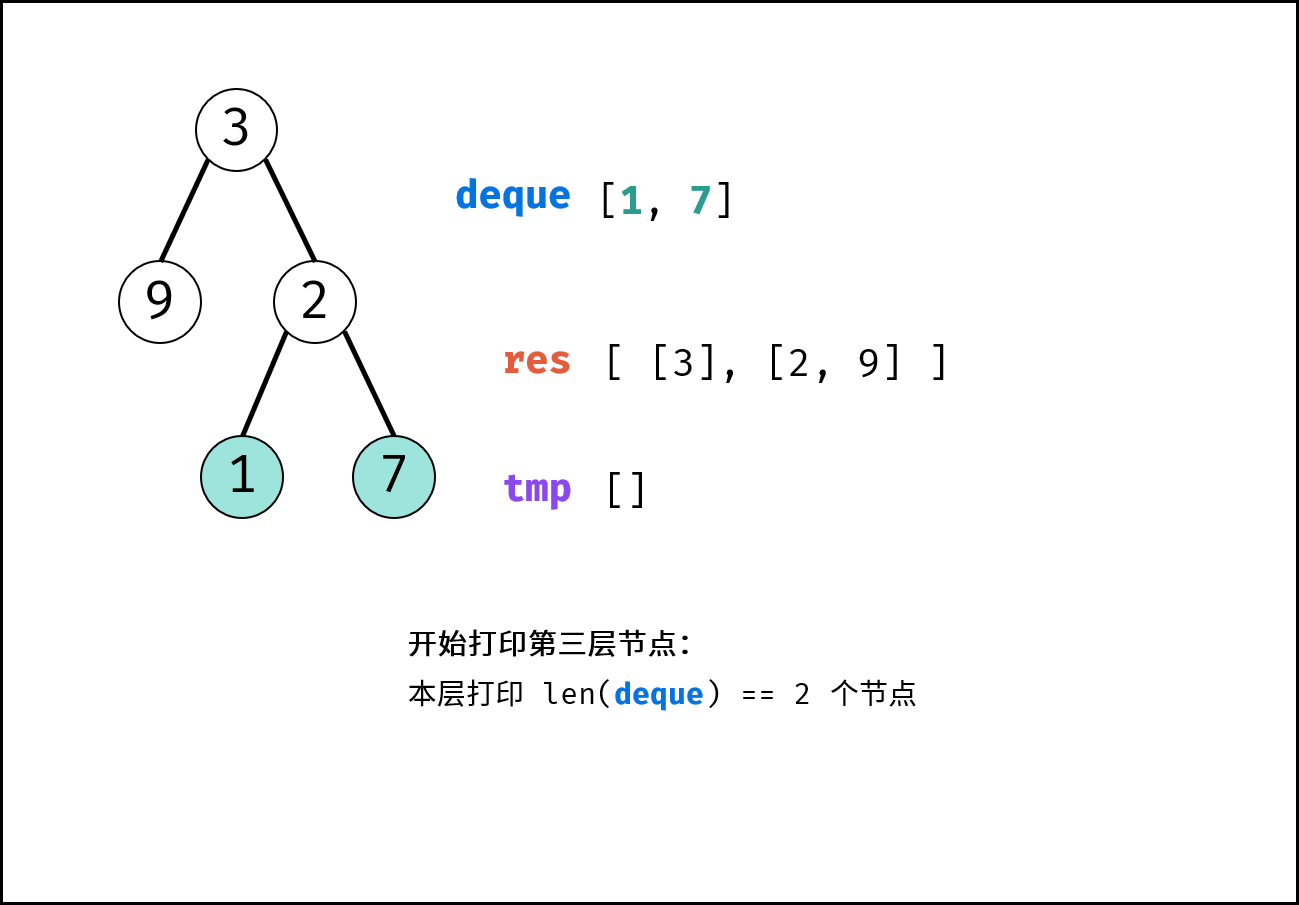Picture8.png](https://pic.leetcode-cn.com/335f1930d37da63c1cedd0798a0c37d0b0b2901493c7fc476fc9ed2144c76b24-Picture8.png),![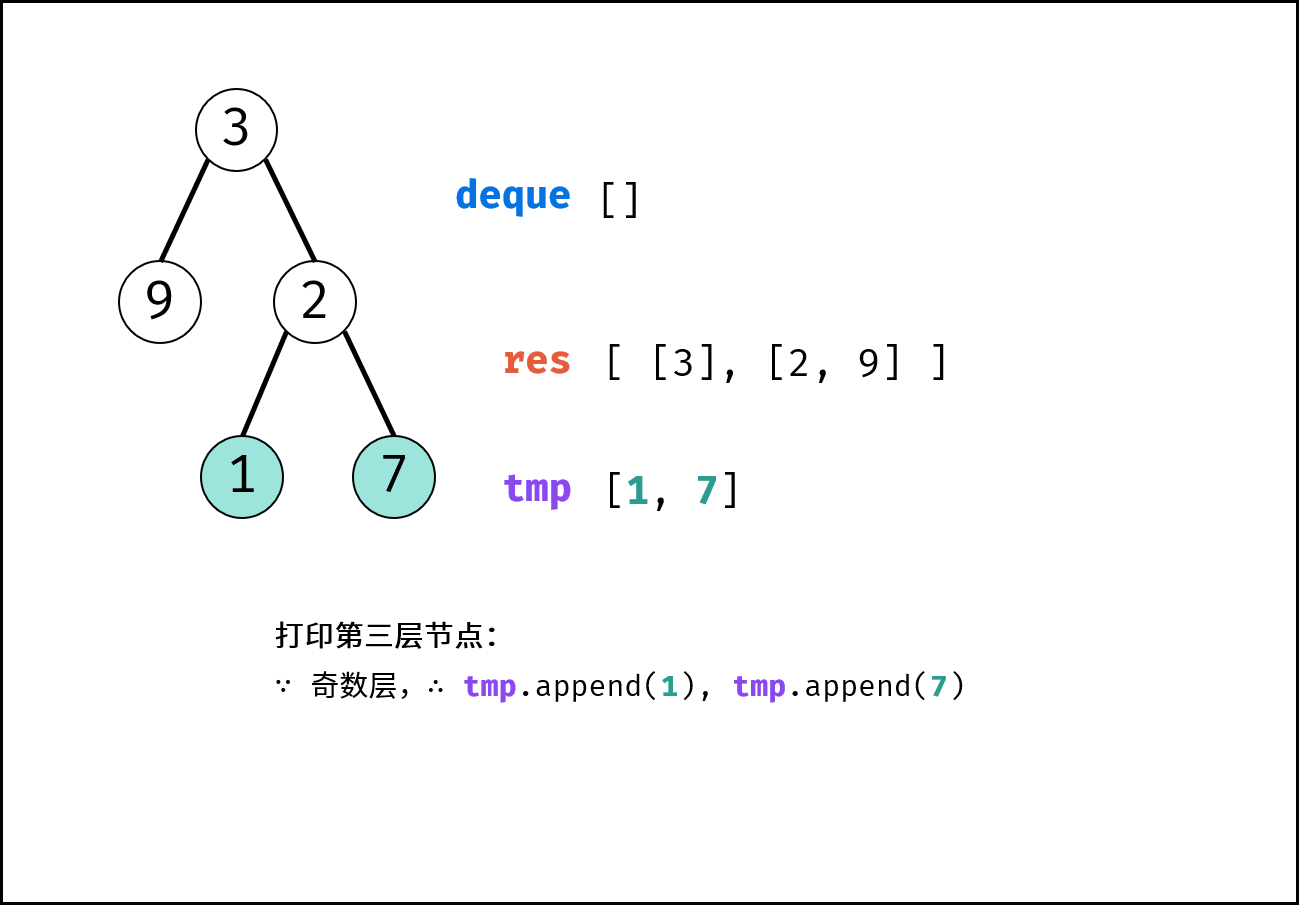Picture9.png](https://pic.leetcode-cn.com/bec5d57e0a349ea209c22bb1cf9bb4ffc6a5b1bcfae79caa97fb9a87546f95c5-Picture9.png),![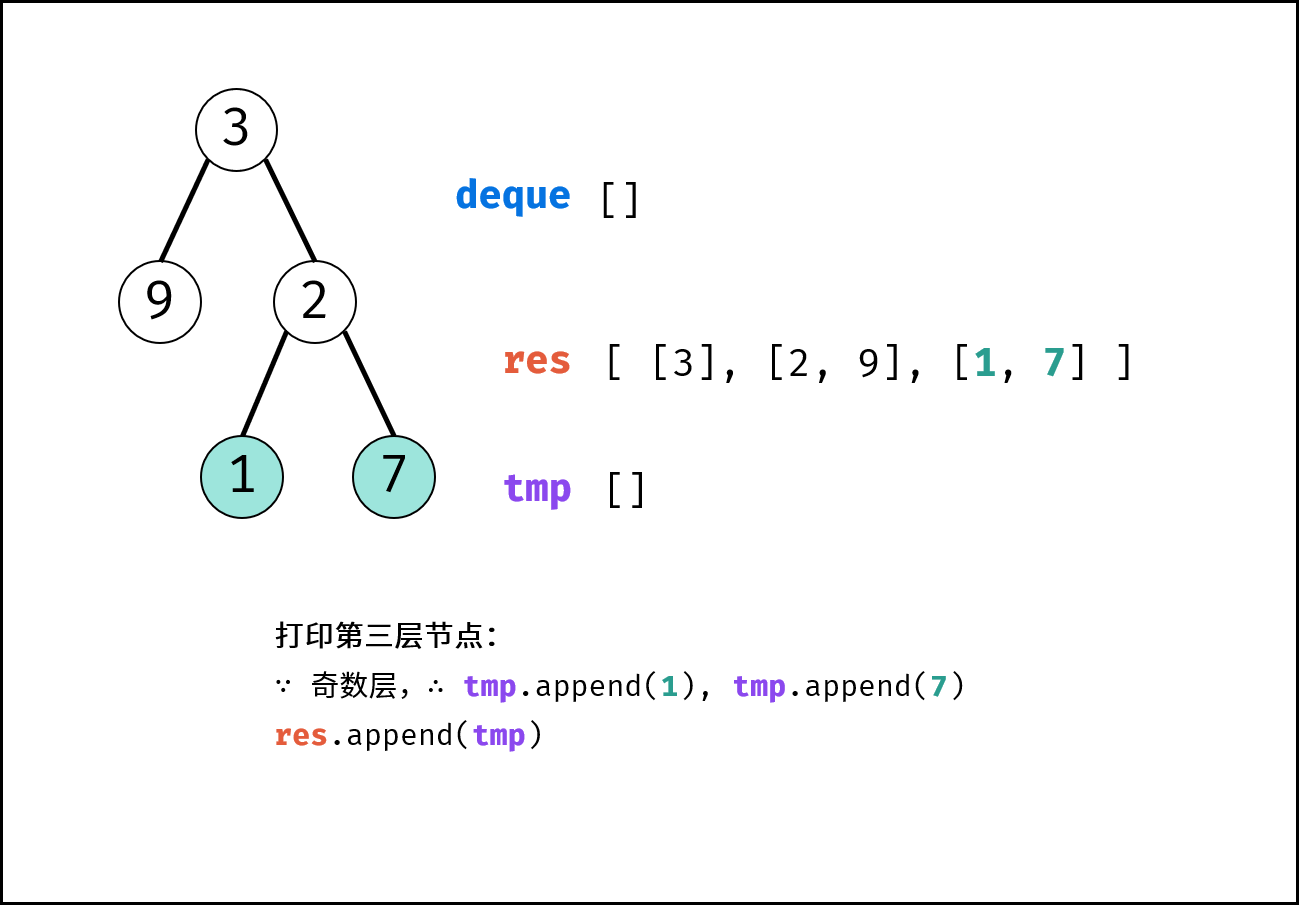Picture10.png](https://pic.leetcode-cn.com/387355a0b771c69610119c4da142a1252baba3aab5a99e43ca387cedac162560-Picture10.png),![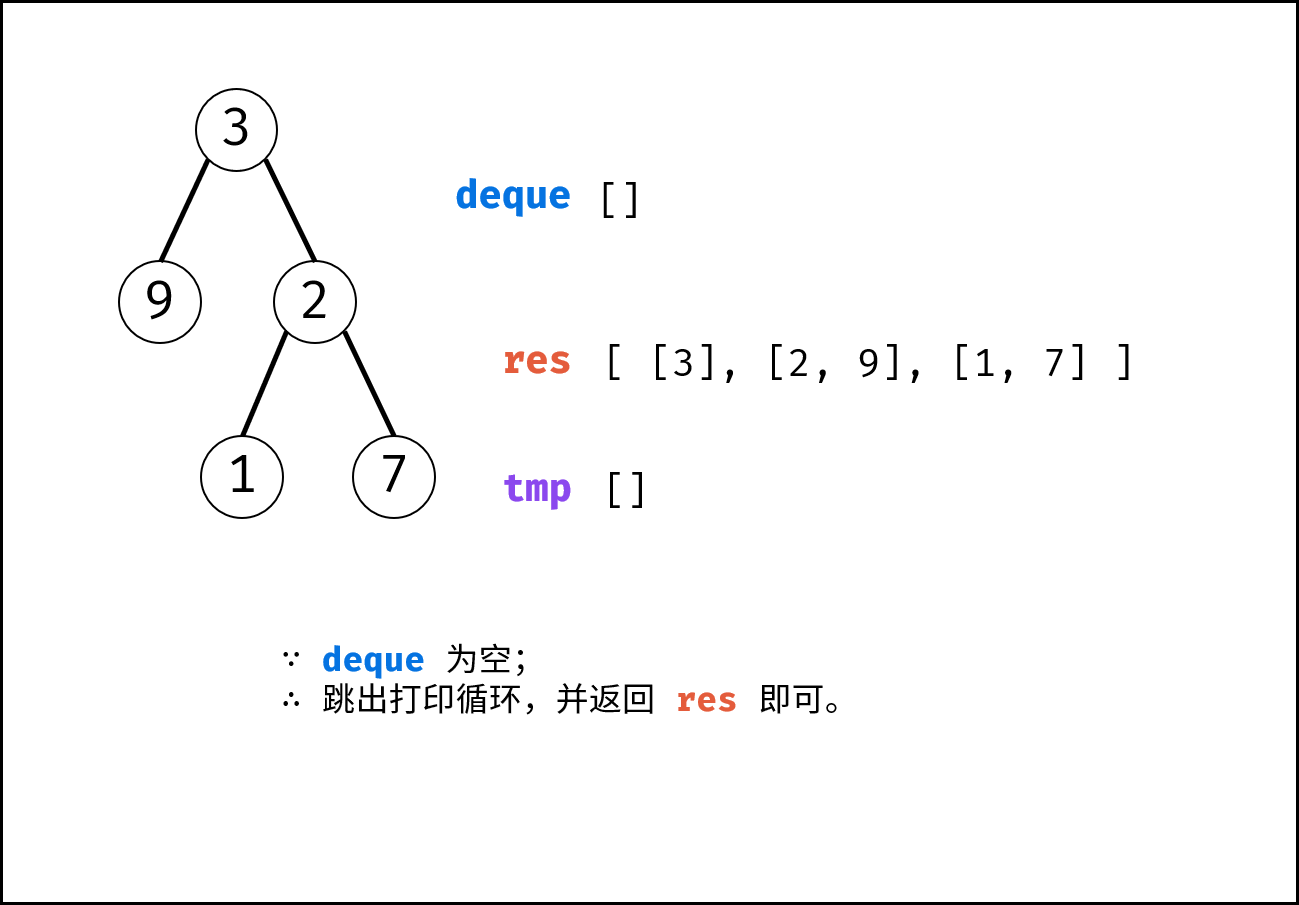Picture11.png](https://pic.leetcode-cn.com/c9bbd82ee2727d3387cda111ea47146599acc5e984ad73a8260f56cb7deb11e4-Picture11.png)>
### 代码：
- Python 中使用 collections 中的双端队列 `deque()` ，其 `popleft()` 方法可达到 $O(1)$ 时间复杂度；列表 list 的 `pop(0)` 方法时间复杂度为 $O(N)$ 。
- Java 中将链表 LinkedList 作为双端队列使用。
```Python []
class Solution:
def decorateRecord(self, root: TreeNode) -> List[List[int]]:
if not root: return []
res, deque = [], collections.deque([root])
while deque:
tmp = collections.deque()
for _ in range(len(deque)):
node = deque.popleft()
if len(res) % 2 == 0: tmp.append(node.val) # 奇数层 -> 插入队列尾部
else: tmp.appendleft(node.val) # 偶数层 -> 插入队列头部
if node.left: deque.append(node.left)
if node.right: deque.append(node.right)
res.append(list(tmp))
return res
```
```Java []
class Solution {
public List<List<Integer>> decorateRecord(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
LinkedList<Integer> tmp = new LinkedList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
if(res.size() % 2 == 0) tmp.addLast(node.val);
else tmp.addFirst(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数量，即 BFS 需循环 $N$ 次，占用 $O(N)$ ；双端队列的队首和队尾的添加和删除操作的时间复杂度均为 $O(1)$ 。
- **空间复杂度 $O(N)$ ：** 最差情况下，即当树为满二叉树时，最多有 $N/2$ 个树节点 **同时** 在 `deque` 中，使用 $O(N)$ 大小的额外空间。
## 方法二：层序遍历 + 双端队列（奇偶层逻辑分离）
- 方法一代码简短、容易实现；但需要判断每个节点的所在层奇偶性，即冗余了 $N$ 次判断。
- 通过将奇偶层逻辑拆分，可以消除冗余的判断。
### 算法流程：
> 与方法一对比，仅 BFS 循环不同。
**BFS 循环：** 循环打印奇 / 偶数层，当 `deque` 为空时跳出；
1. **打印奇数层：** **从左向右** 打印，**先左后右** 加入下层节点；
2. 若 `deque` 为空，说明向下无偶数层，则跳出；
3. **打印偶数层：** **从右向左** 打印，**先右后左** 加入下层节点；
### 代码：
```Python []
class Solution:
def decorateRecord(self, root: TreeNode) -> List[List[int]]:
if not root: return []
res, deque = [], collections.deque()
deque.append(root)
while deque:
tmp = []
# 打印奇数层
for _ in range(len(deque)):
# 从左向右打印
node = deque.popleft()
tmp.append(node.val)
# 先左后右加入下层节点
if node.left: deque.append(node.left)
if node.right: deque.append(node.right)
res.append(tmp)
if not deque: break # 若为空则提前跳出
# 打印偶数层
tmp = []
for _ in range(len(deque)):
# 从右向左打印
node = deque.pop()
tmp.append(node.val)
# 先右后左加入下层节点
if node.right: deque.appendleft(node.right)
if node.left: deque.appendleft(node.left)
res.append(tmp)
return res
```
```Java []
class Solution {
public List<List<Integer>> decorateRecord(TreeNode root) {
Deque<TreeNode> deque = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) deque.add(root);
while(!deque.isEmpty()) {
// 打印奇数层
List<Integer> tmp = new ArrayList<>();
for(int i = deque.size(); i > 0; i--) {
// 从左向右打印
TreeNode node = deque.removeFirst();
tmp.add(node.val);
// 先左后右加入下层节点
if(node.left != null) deque.addLast(node.left);
if(node.right != null) deque.addLast(node.right);
}
res.add(tmp);
if(deque.isEmpty()) break; // 若为空则提前跳出
// 打印偶数层
tmp = new ArrayList<>();
for(int i = deque.size(); i > 0; i--) {
// 从右向左打印
TreeNode node = deque.removeLast();
tmp.add(node.val);
// 先右后左加入下层节点
if(node.right != null) deque.addFirst(node.right);
if(node.left != null) deque.addFirst(node.left);
}
res.add(tmp);
}
return res;
}
}
```
```C++ []
class Solution {
public:
vector<vector<int>> decorateRecord(TreeNode* root) {
deque<TreeNode*> deque;
vector<vector<int>> res;
if(root != NULL) deque.push_back(root);
while(!deque.empty()) {
// 打印奇数层
vector<int> tmp;
for(int i = deque.size(); i > 0; i--) {
// 从左向右打印
TreeNode* node = deque.front();
deque.pop_front();
tmp.push_back(node->val);
// 先左后右加入下层节点
if(node->left != NULL) deque.push_back(node->left);
if(node->right != NULL) deque.push_back(node->right);
}
res.push_back(tmp);
if(deque.empty()) break; // 若为空则提前跳出
// 打印偶数层
tmp.clear();
for(int i = deque.size(); i > 0; i--) {
// 从右向左打印
TreeNode* node = deque.back();
deque.pop_back();
tmp.push_back(node->val);
// 先右后左加入下层节点
if(node->right != NULL) deque.push_front(node->right);
if(node->left != NULL) deque.push_front(node->left);
}
res.push_back(tmp);
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 同方法一。
- **空间复杂度 $O(N)$ ：** 同方法一。
## 方法三：层序遍历 + 倒序
- 此方法的优点是只用列表即可，无需其他数据结构。
- **偶数层倒序：** 若 `res` 的长度为 **奇数** ，说明当前是偶数层，则对 `tmp` 执行 **倒序** 操作。
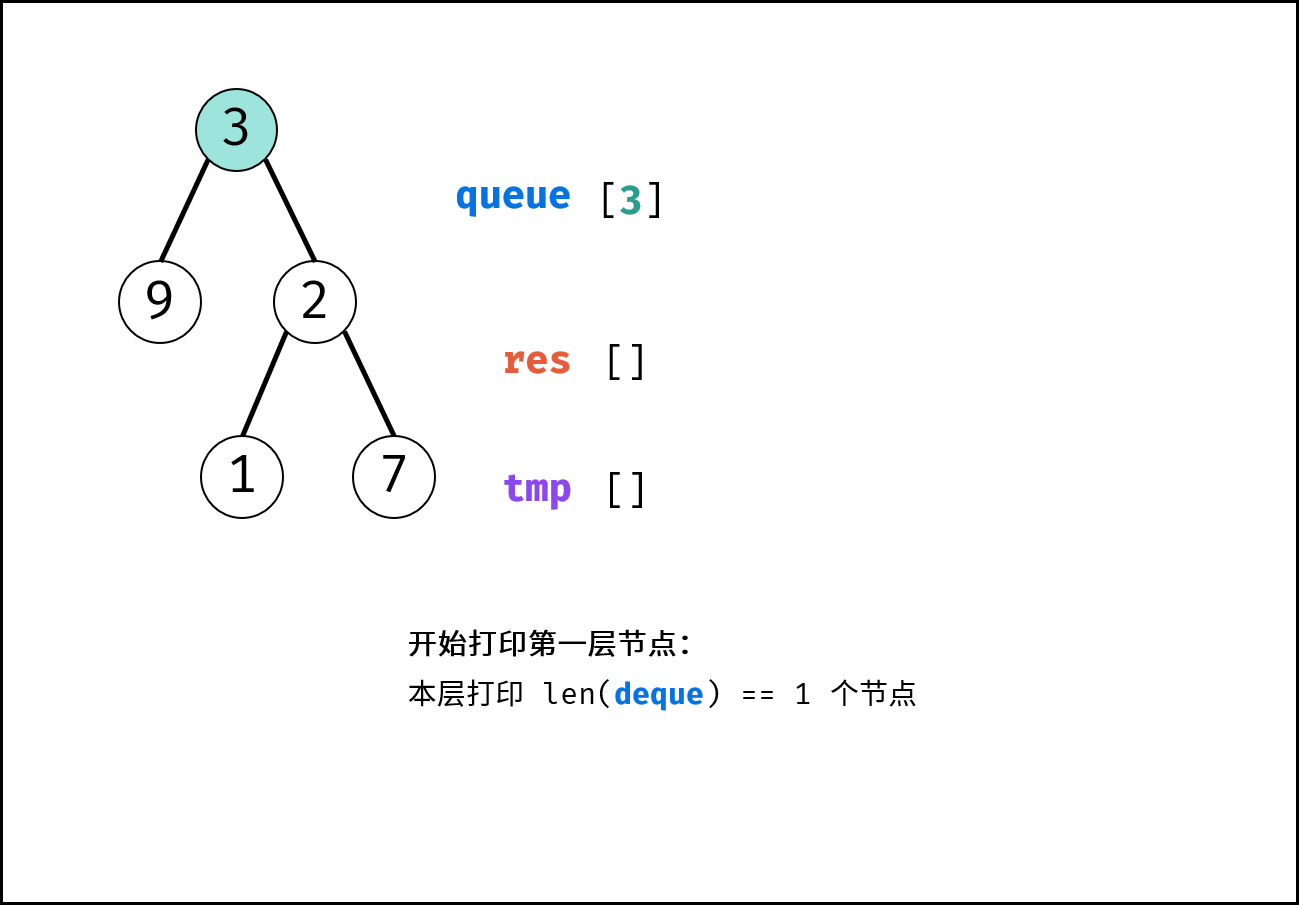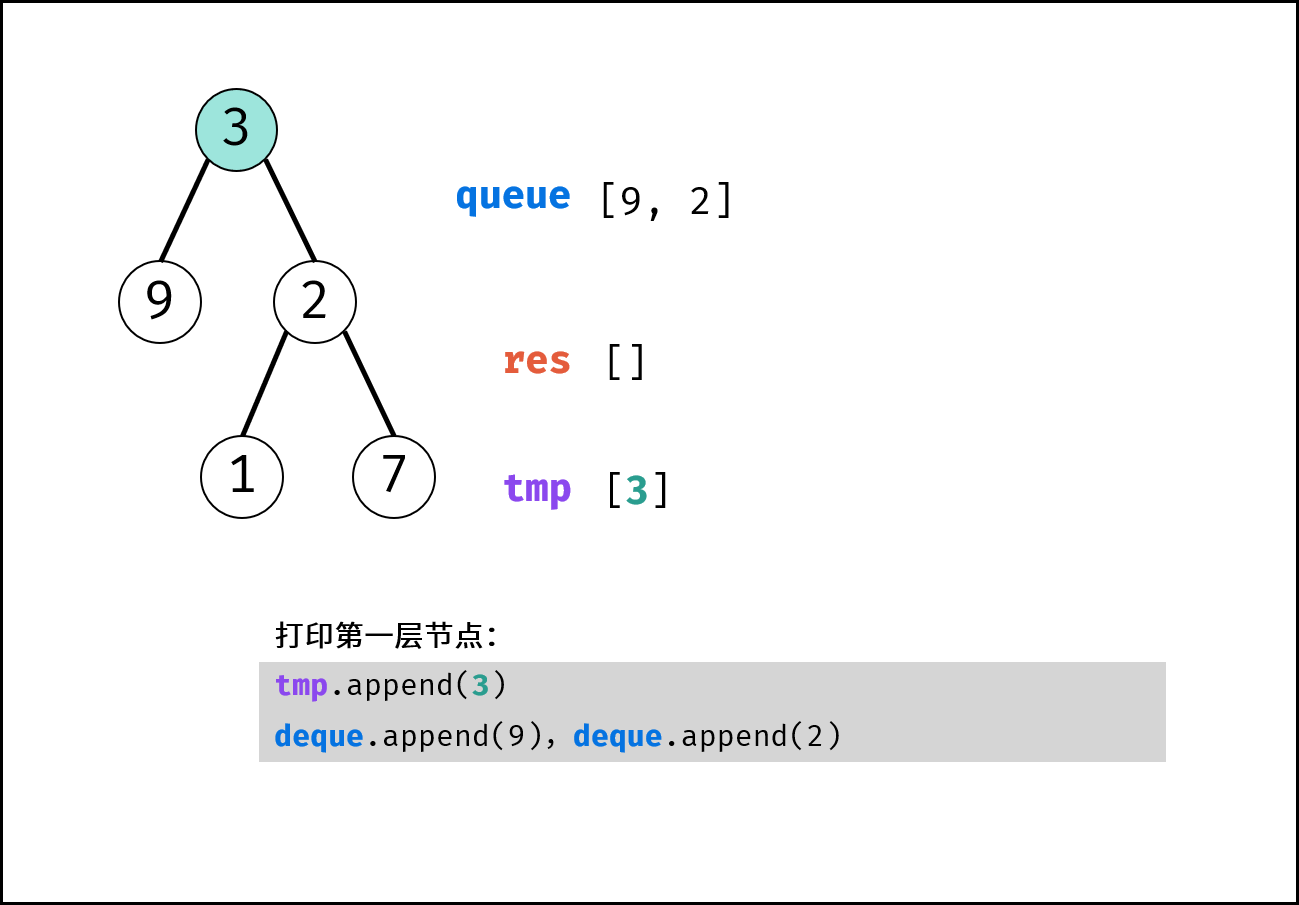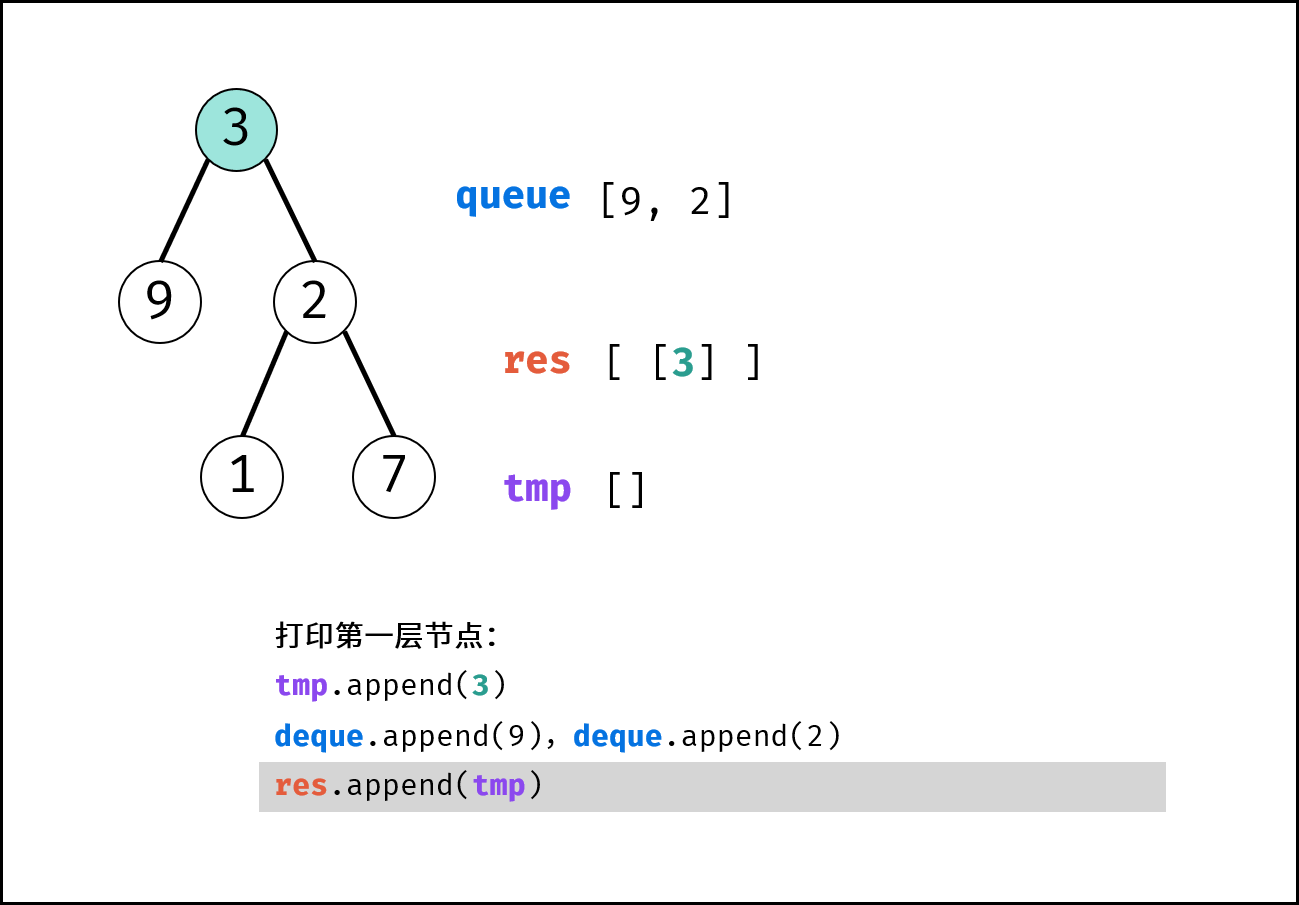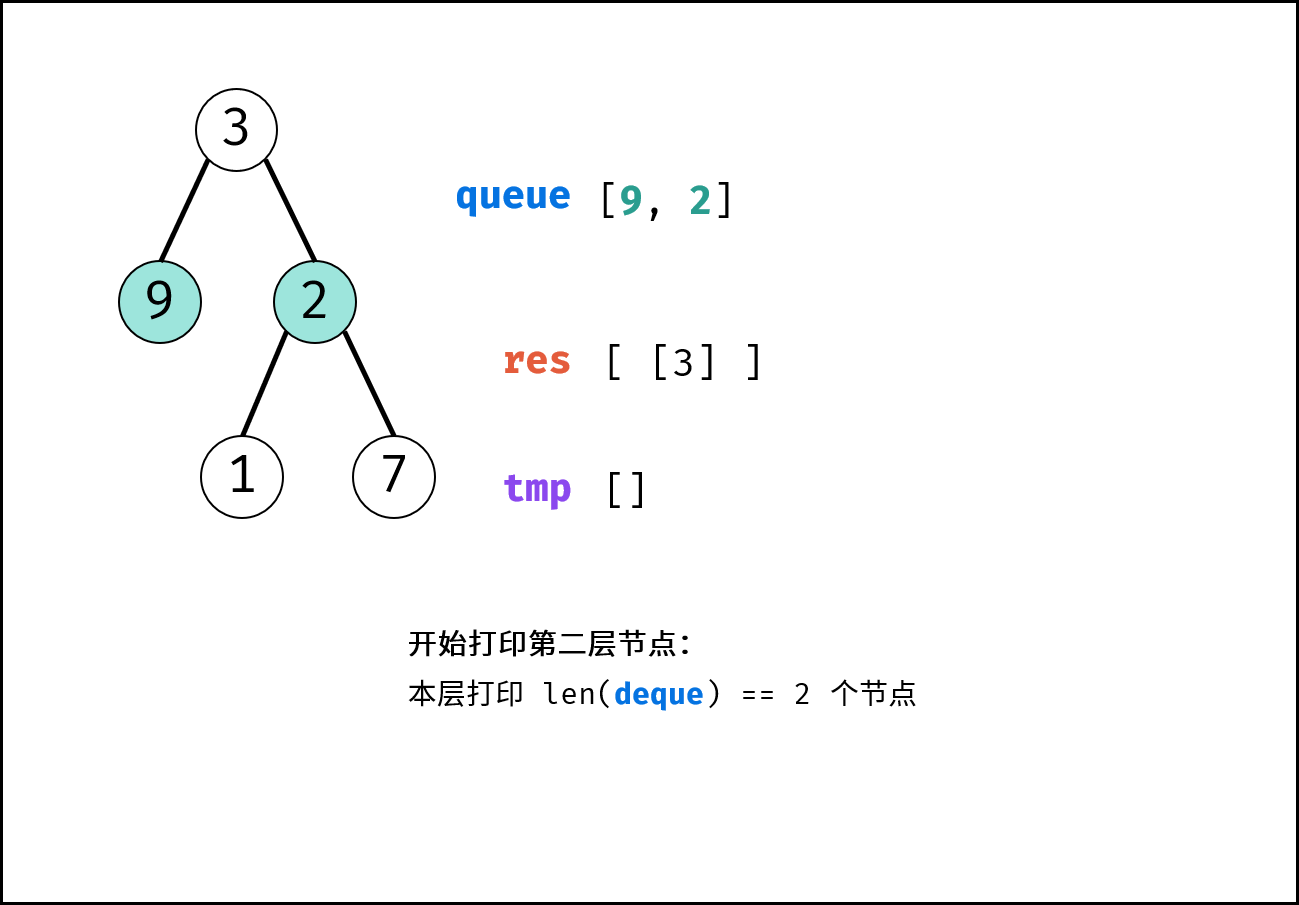<![Picture12.png](https://pic.leetcode-cn.com/8e05160224f36ce5acb4ac9b96eaa141779b6b6d6153ae794082206ad5481f77-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/5bf8f63845dbbbe6a56e17a2dadf1b87d3f97e99702bdce1ad8eddfeadeeaa89-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/4d610a5b6b7375eaba712e73e96c8e29e5d041378332ca2e00e0a6415bfd3890-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/34d3a083c42f8eaa21eacb98f7f3d731b7264a1e424908788abe8edd3387228e-Picture15.png),![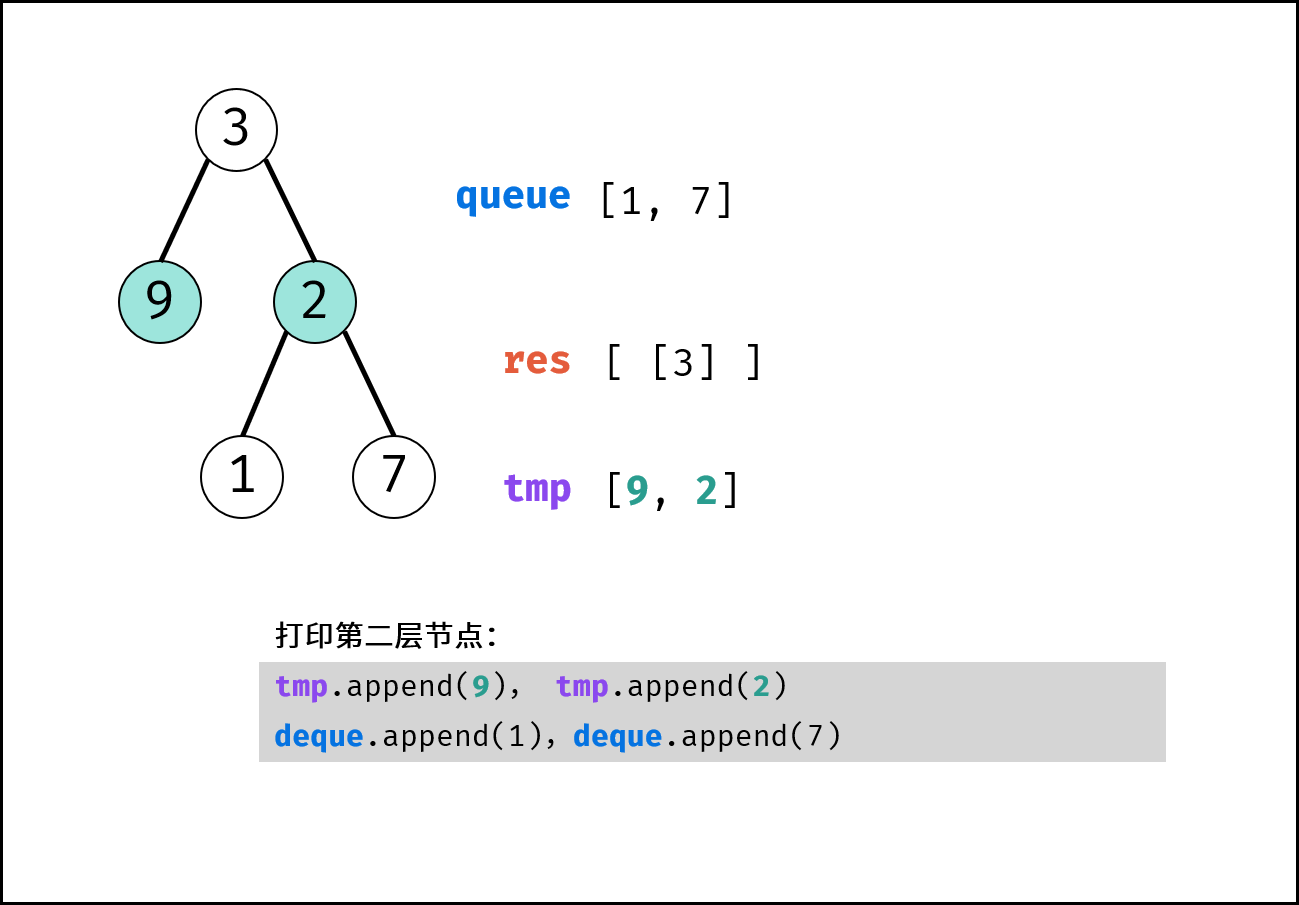Picture16.png](https://pic.leetcode-cn.com/a61fcdeb1dacd14b2849898f8c6506394586debf3e67550aa5ad8e2f9e8dcac4-Picture16.png),![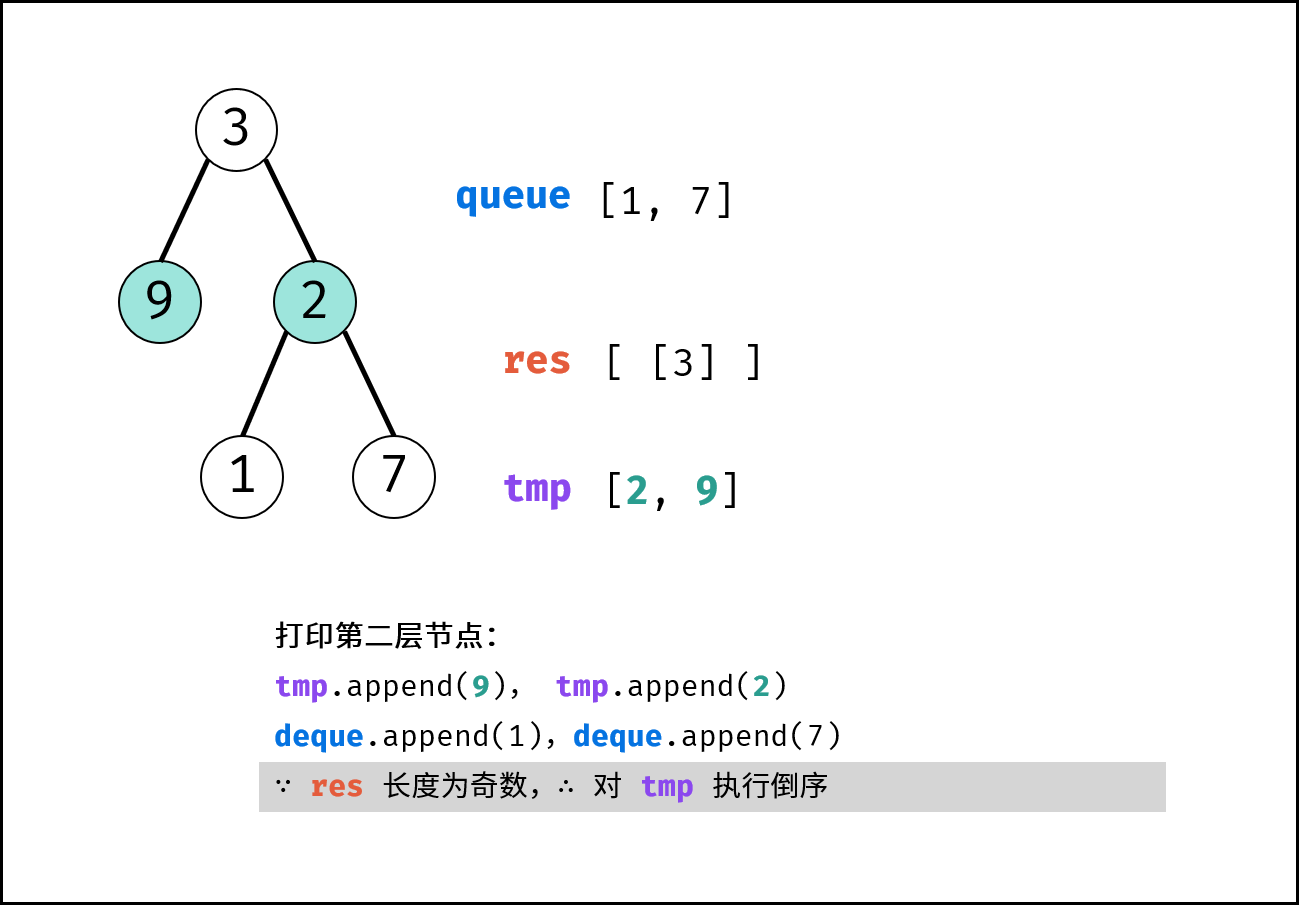Picture17.png](https://pic.leetcode-cn.com/6897ae8b2dcc14f6cf012df34bfed98a2ea4d831b6515de9bd2db363968e217a-Picture17.png),![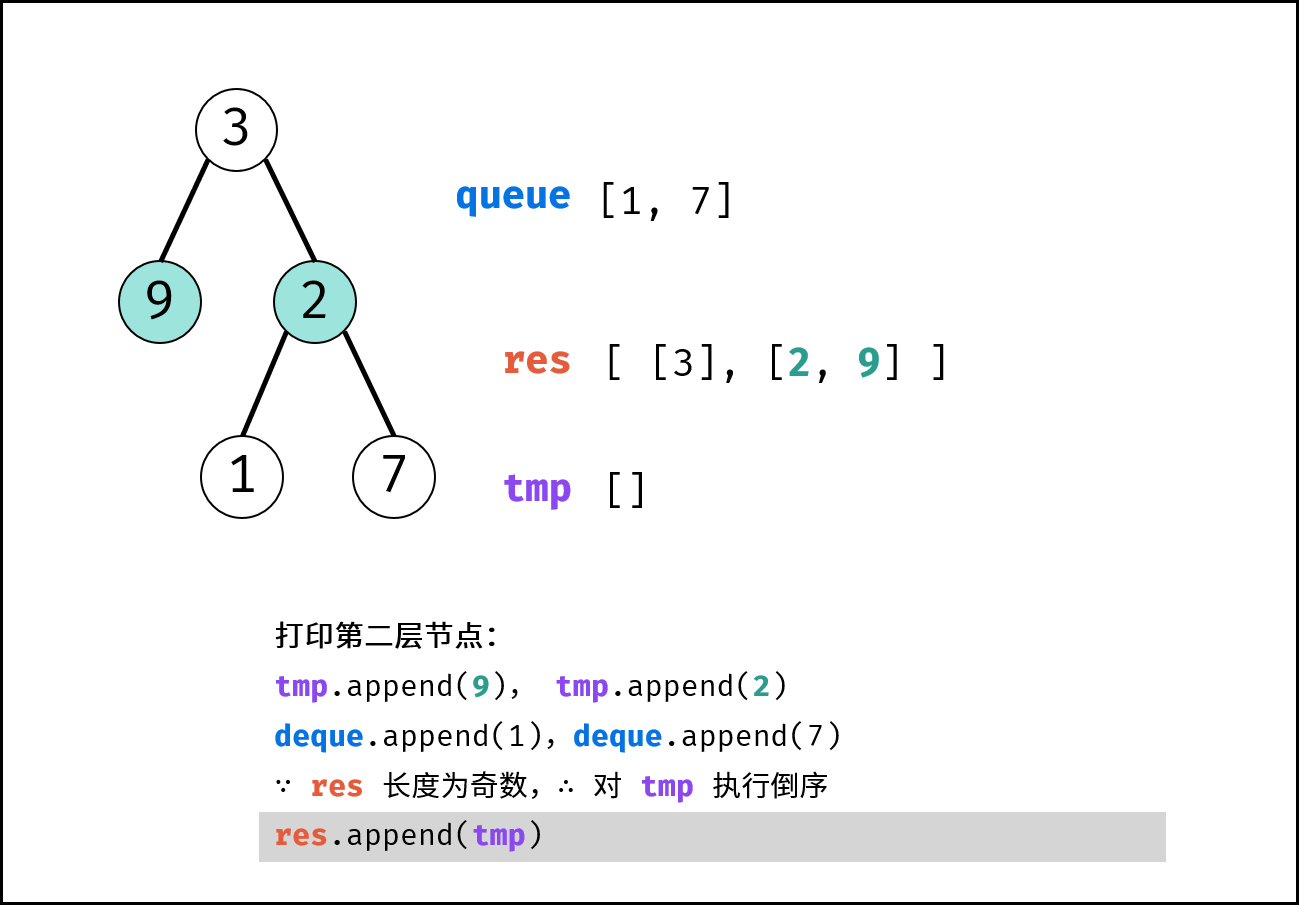Picture18.png](https://pic.leetcode-cn.com/0fe9e90477e1a3762ad0c3f7877d6acfdc5b7090466a26dca2ef03242192209f-Picture18.png),![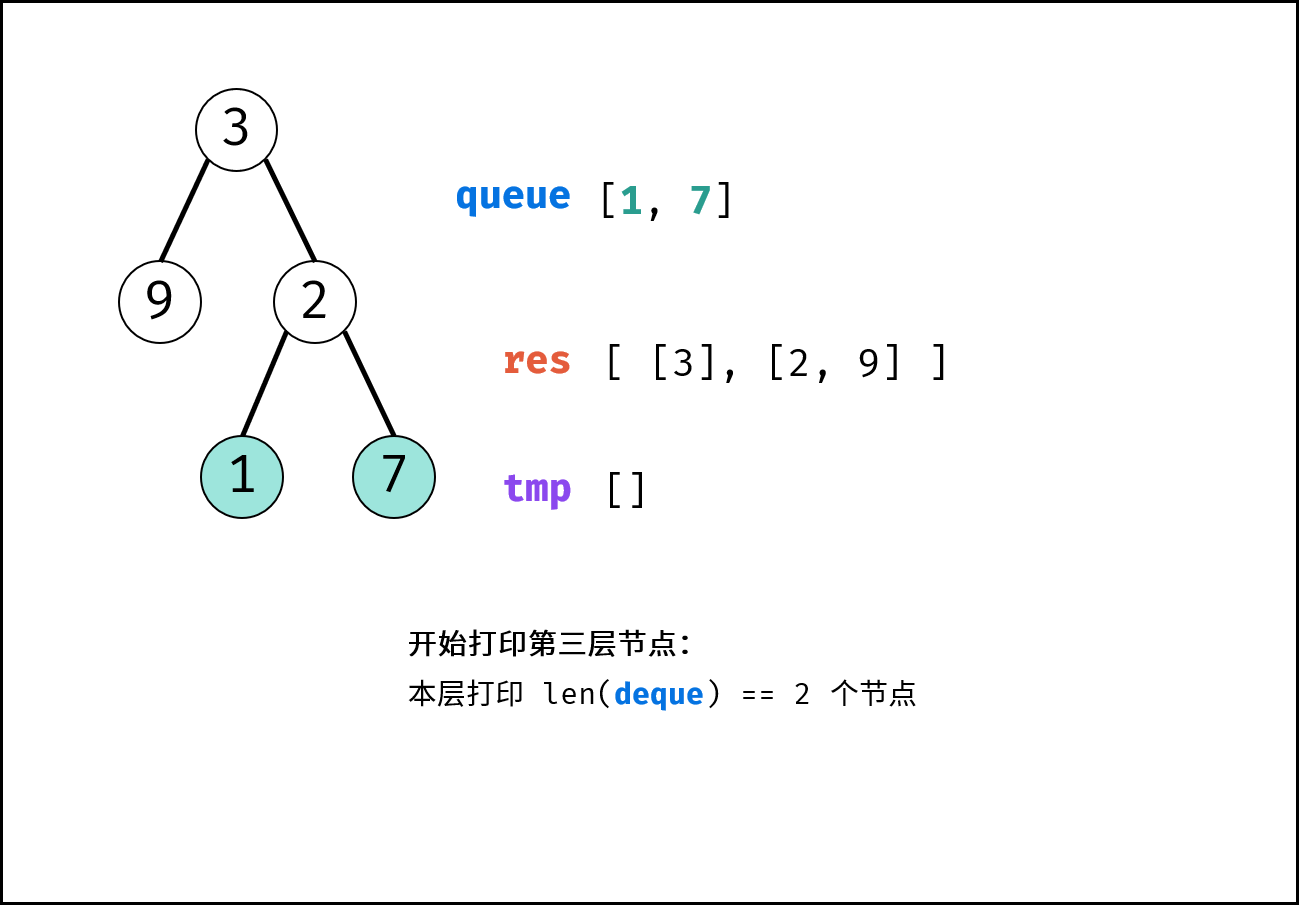Picture19.png](https://pic.leetcode-cn.com/f24f424fe5d1799694db1128d7d8ed1b91a7d2c4920f1a2704a03aad14afec38-Picture19.png),![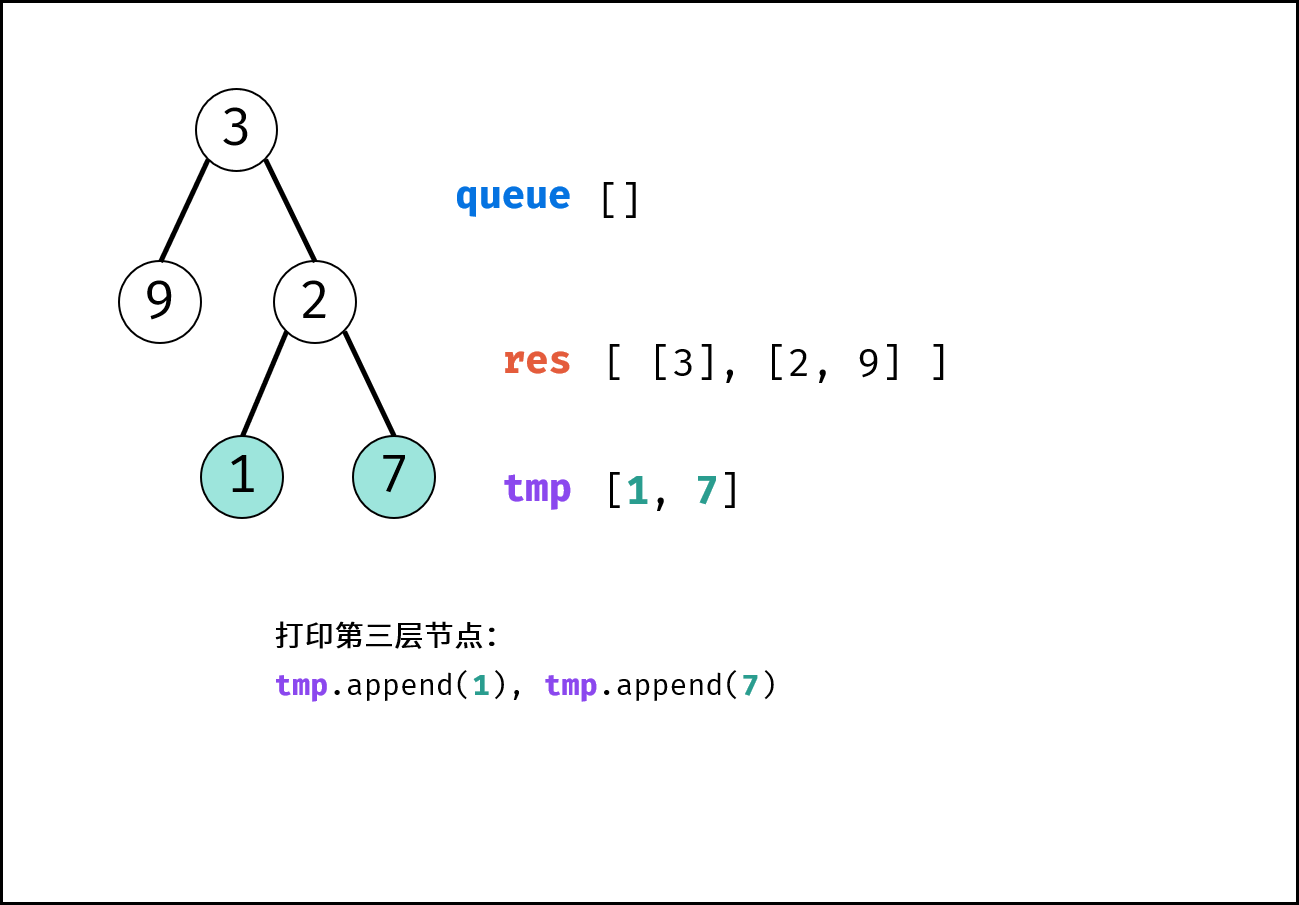Picture20.png](https://pic.leetcode-cn.com/b31f1ce86db66b141430c693085273e241676a3071ee6fa2b374509361b14012-Picture20.png),![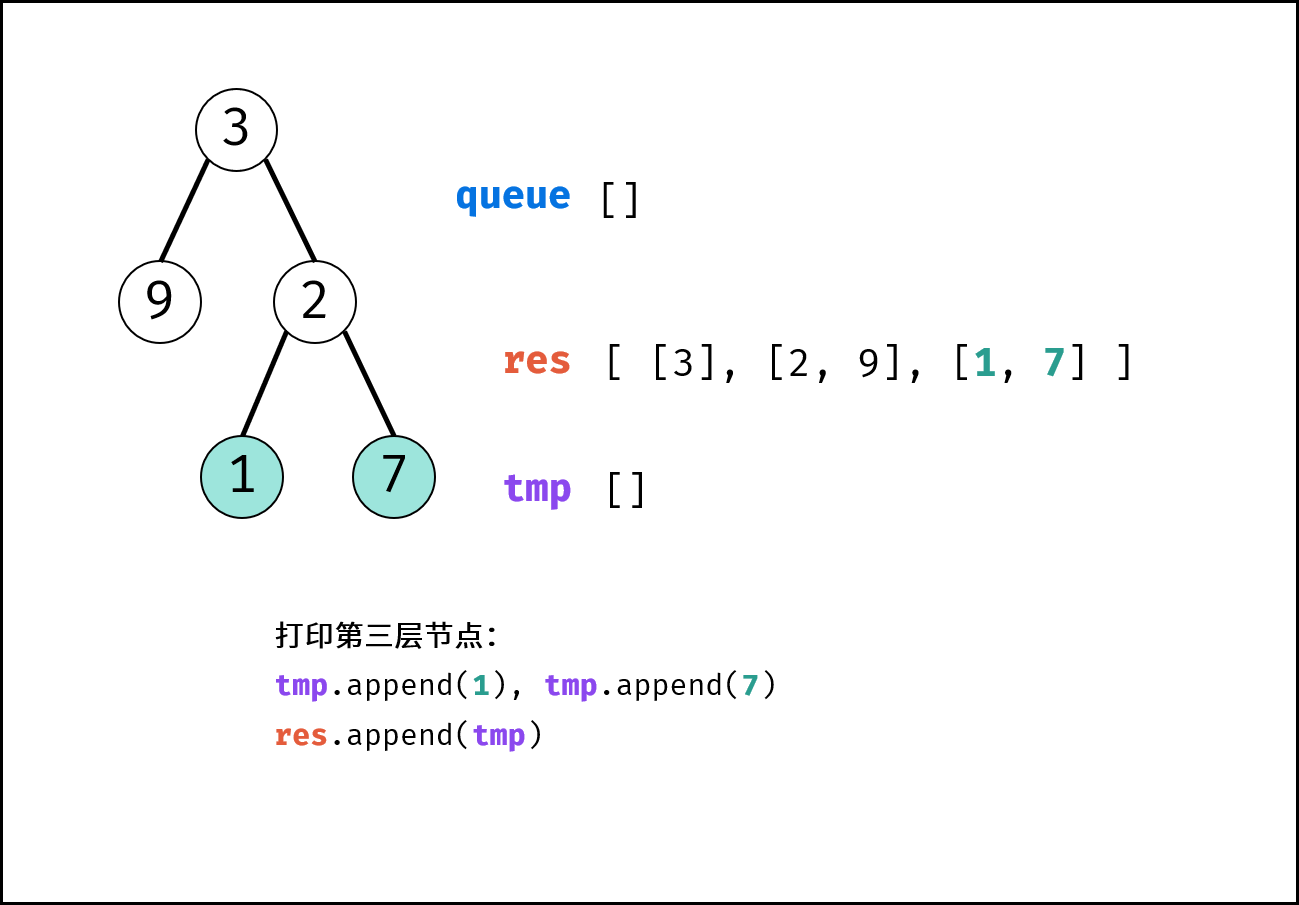Picture21.png](https://pic.leetcode-cn.com/422986f0e798f155b2cf94e95d3febf5739d6a22e5ddfb1fc10dec0289f7b543-Picture21.png),![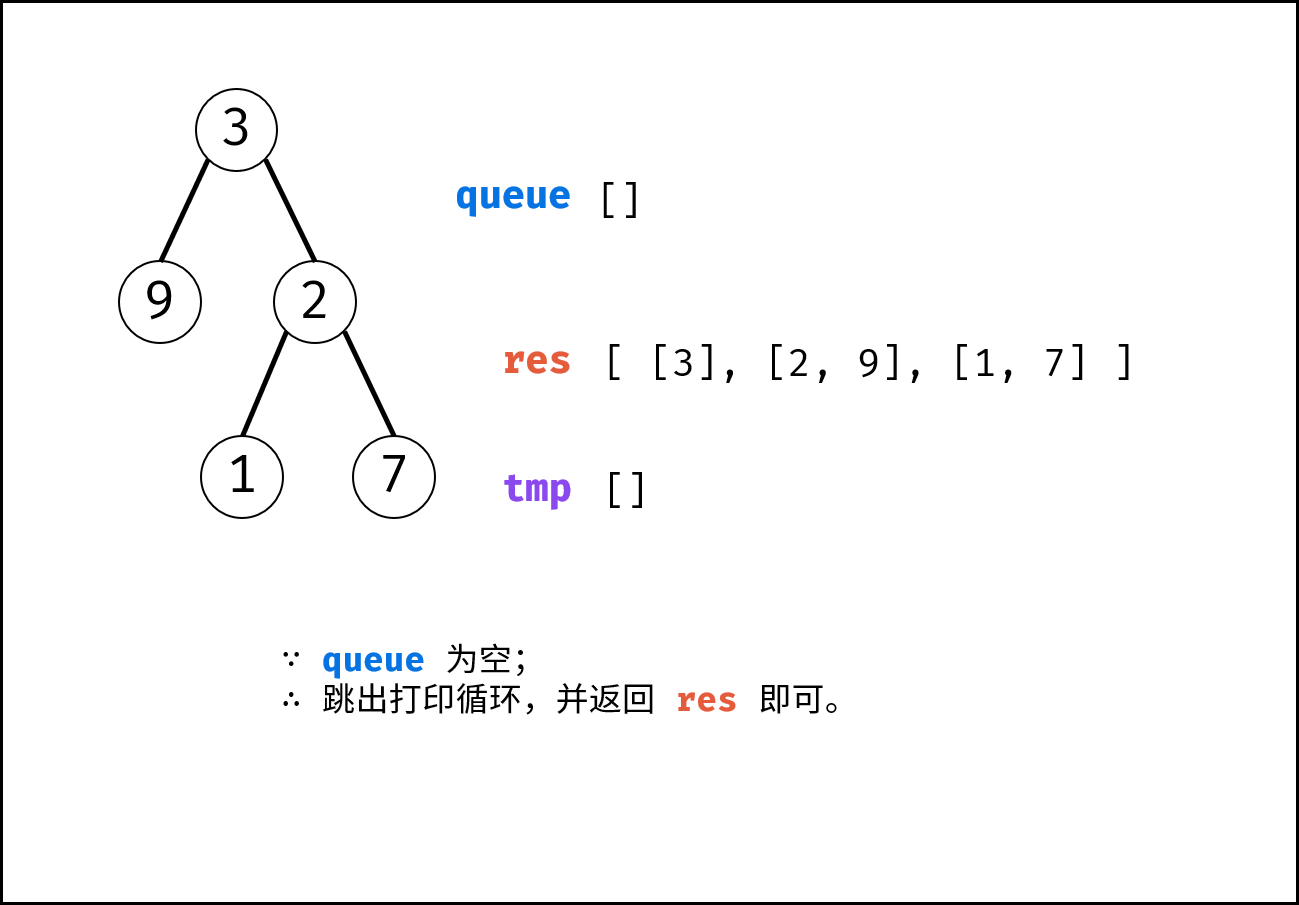Picture22.png](https://pic.leetcode-cn.com/0301e32e08f8b2d25a9806bc986b7d5507ec681df3bf386d5c12c37c9dcf6036-Picture22.png)>
### 代码：
```Python []
class Solution:
def decorateRecord(self, root: TreeNode) -> List[List[int]]:
if not root: return []
res, queue = [], collections.deque()
queue.append(root)
while queue:
tmp = []
for _ in range(len(queue)):
node = queue.popleft()
tmp.append(node.val)
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
res.append(tmp[::-1] if len(res) % 2 else tmp)
return res
```
```Java []
class Solution {
public List<List<Integer>> decorateRecord(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
if(res.size() % 2 == 1) Collections.reverse(tmp);
res.add(tmp);
}
return res;
}
}
```
```C++ []
class Solution {
public:
vector<vector<int>> decorateRecord(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if(root != NULL) que.push(root);
while(!que.empty()) {
vector<int> tmp;
for(int i = que.size(); i > 0; i--) {
TreeNode* node = que.front();
que.pop();
tmp.push_back(node->val);
if(node->left != NULL) que.push(node->left);
if(node->right != NULL) que.push(node->right);
}
if(res.size() % 2 == 1) reverse(tmp.begin(),tmp.end());
res.push_back(tmp);
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数量，即 BFS 需循环 $N$ 次，占用 $O(N)$ 。**共完成** 少于 $N$ 个节点的倒序操作，占用 $O(N)$ 。
- **空间复杂度 $O(N)$ ：** 最差情况下，即当树为满二叉树时，最多有 $N/2$ 个树节点**同时**在 `queue` 中，使用 $O(N)$ 大小的额外空间。

175
leetbook_ioa/docs/LCR 152. 验证二叉搜索树的后序遍历序列.md Executable file
View File

@@ -0,0 +1,175 @@
## 解题思路：
**后序遍历定义：** `[ 左子树 | 右子树 | 根节点 ]` ，即遍历顺序为 “左、右、根” 。
**二叉搜索树定义：** 左子树中所有节点的值 $<$ 根节点的值；右子树中所有节点的值 $>$ 根节点的值；其左、右子树也分别为二叉搜索树。
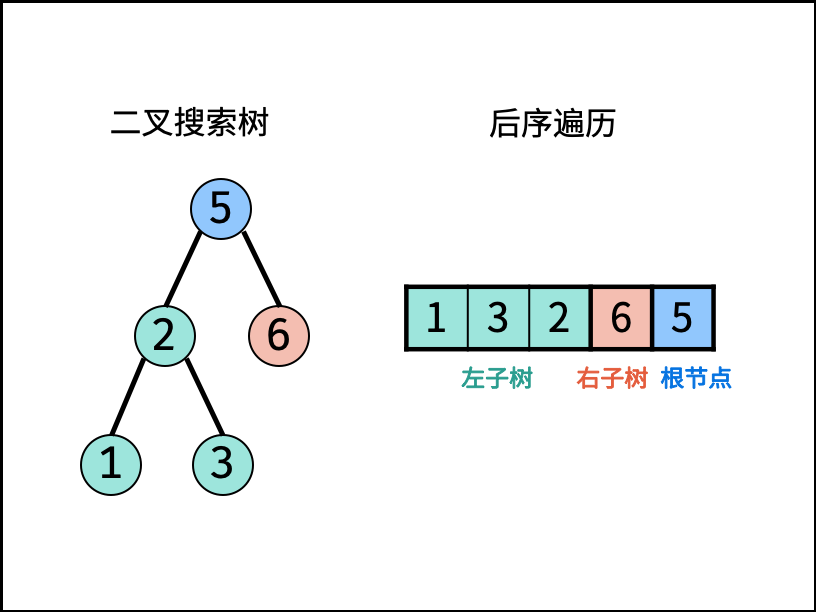![Picture1.png](https://pic.leetcode-cn.com/1599753507-JrFBjm-Picture1.png){:align=center width=500}
## 方法一：递归分治
根据二叉搜索树的定义，可以通过递归，判断所有子树的 **正确性** （即其后序遍历是否满足二叉搜索树的定义） ，若所有子树都正确，则此序列为二叉搜索树的后序遍历。
### 递归解析：
**终止条件：** 当 $i \geq j$ ，说明此子树节点数量 $\leq 1$ ，无需判别正确性，因此直接返回 $\text{true}$ ；
**递推工作：**
1. **划分左右子树：** 遍历后序遍历的 $[i, j]$ 区间元素，寻找 **第一个大于根节点** 的节点，索引记为 $m$ 。此时，可划分出左子树区间 $[i,m-1]$ 、右子树区间 $[m, j - 1]$ 、根节点索引 $j$ 。
2. **判断是否为二叉搜索树：**
- **左子树区间** $[i, m - 1]$ 内的所有节点都应 $<$ $postorder[j]$ 。而第 `1.划分左右子树` 步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
- **右子树区间** $[m, j-1]$ 内的所有节点都应 $>$ $postorder[j]$ 。实现方式为遍历，当遇到 $\leq postorder[j]$ 的节点则跳出；则可通过 $p = j$ 判断是否为二叉搜索树。
**返回值：** 所有子树都需正确才可判定正确，因此使用 **与逻辑符** $\&\&$ 连接。
1. **$p = j$ ：** 判断 **此树** 是否正确。
2. **$recur(i, m - 1)$ ：** 判断 **此树的左子树** 是否正确。
3. **$recur(m, j - 1)$ ：** 判断 **此树的右子树** 是否正确。
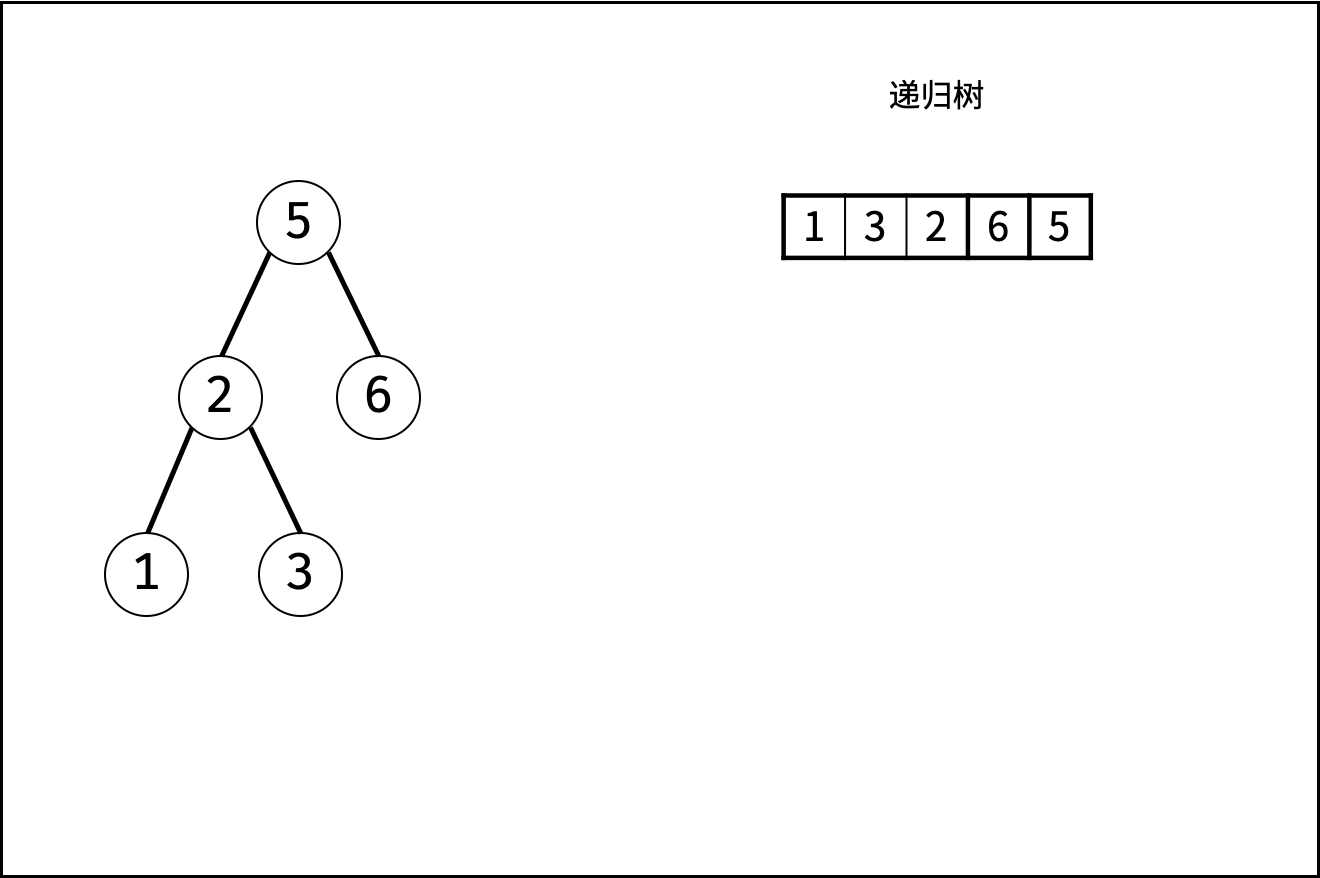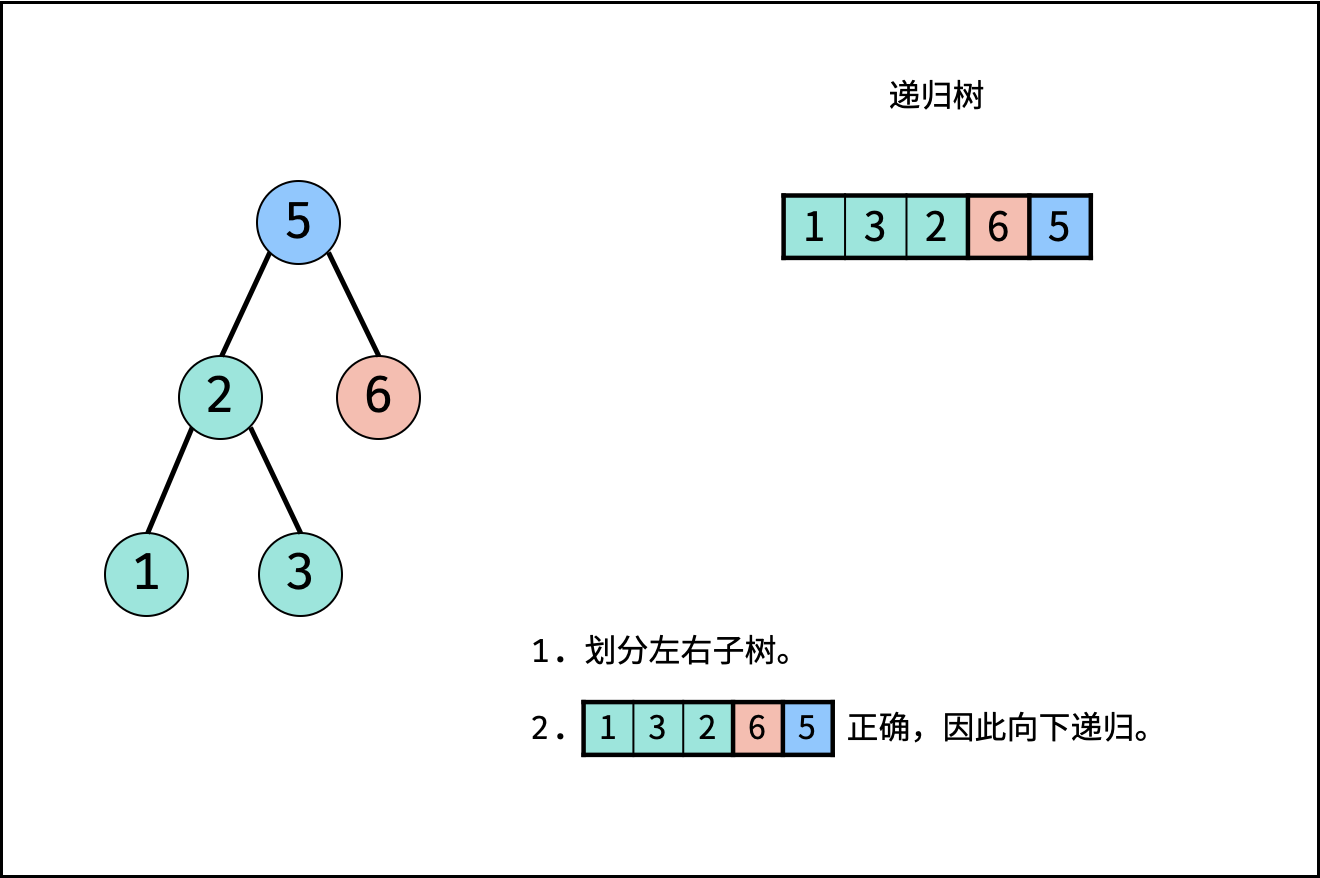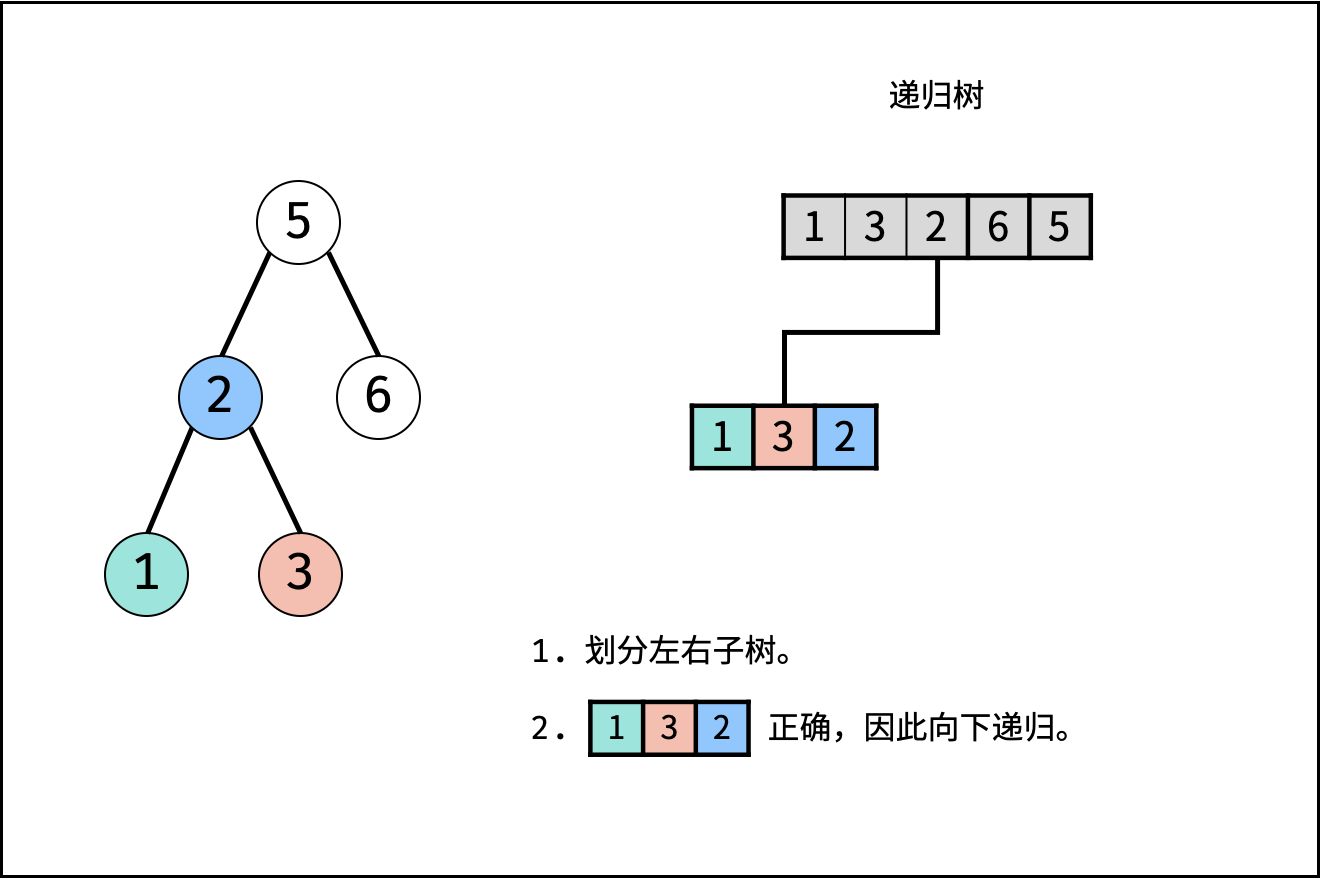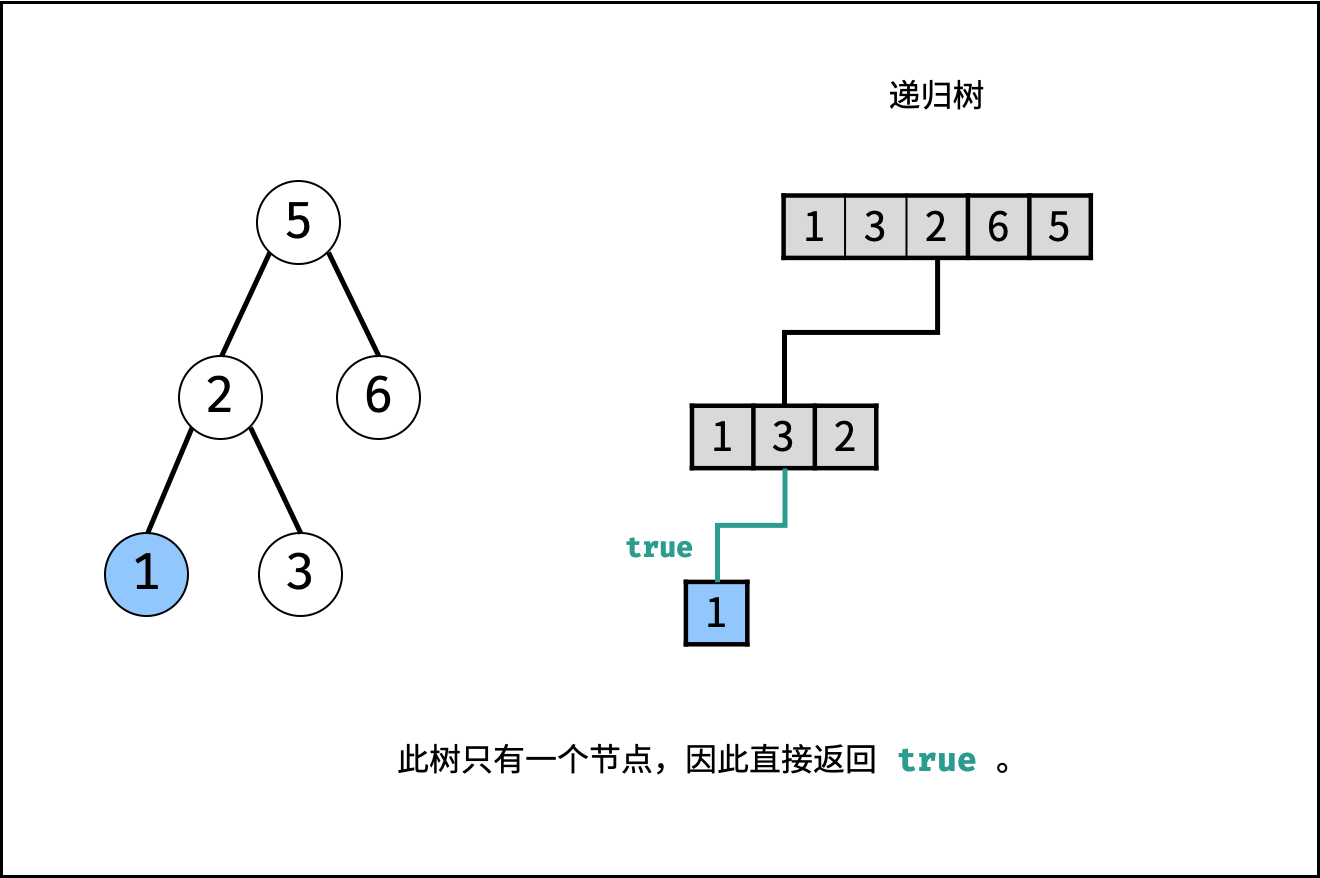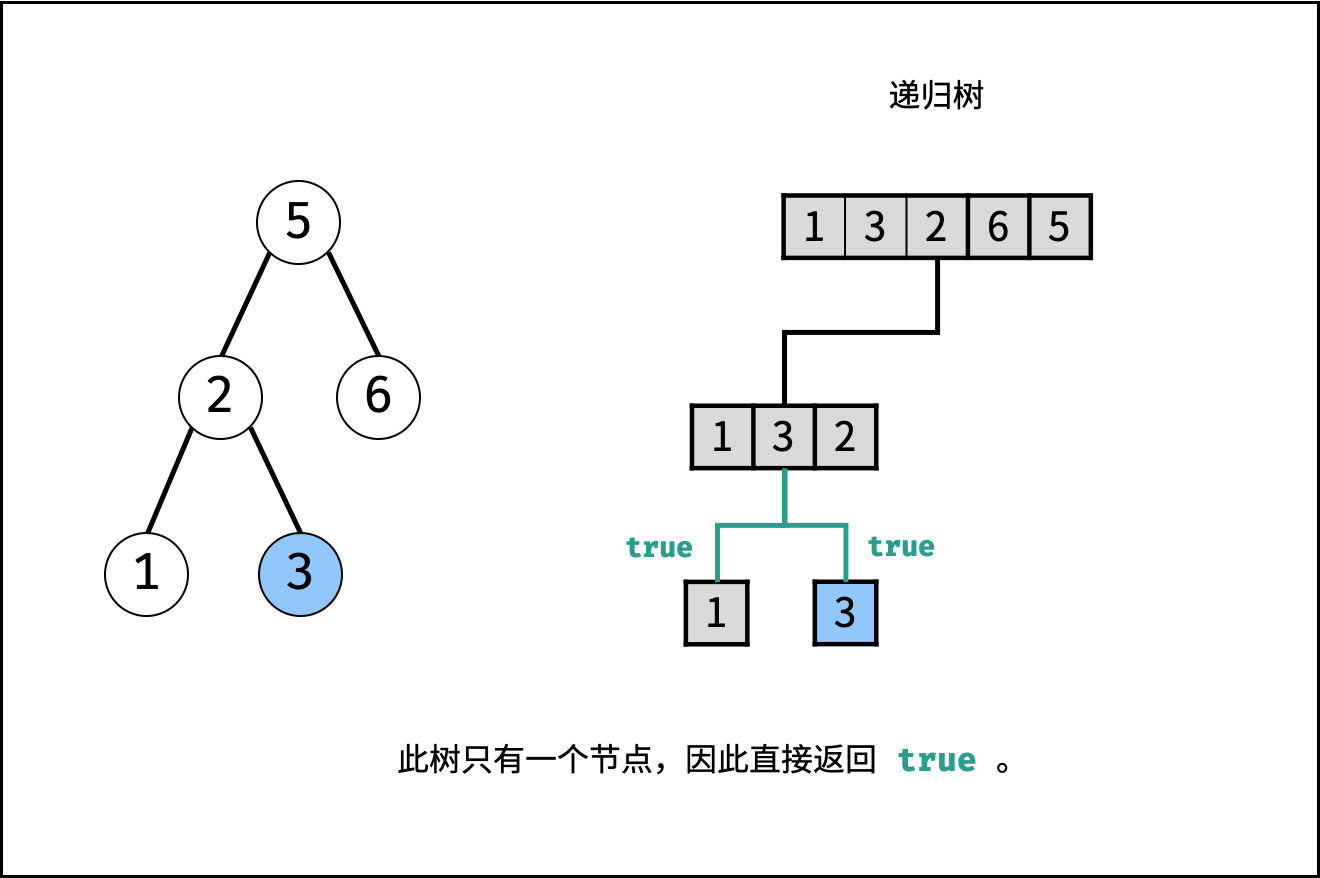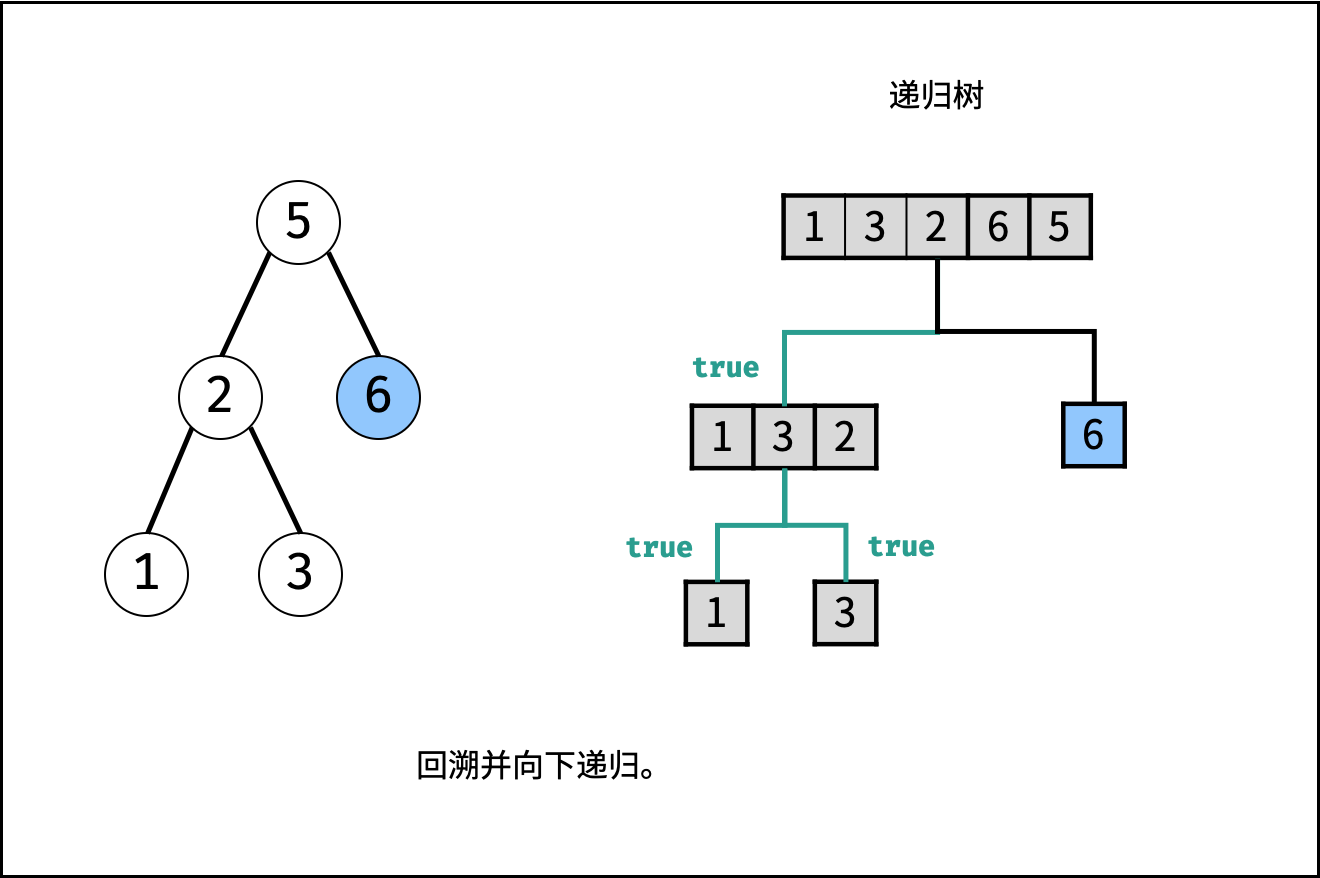<![Picture2.png](https://pic.leetcode-cn.com/1599753507-XspWrm-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599753507-zCqwnA-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599753507-YNXiie-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599753507-uRRdpj-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599753507-wTKbiX-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599753507-MTcDOX-Picture7.png),![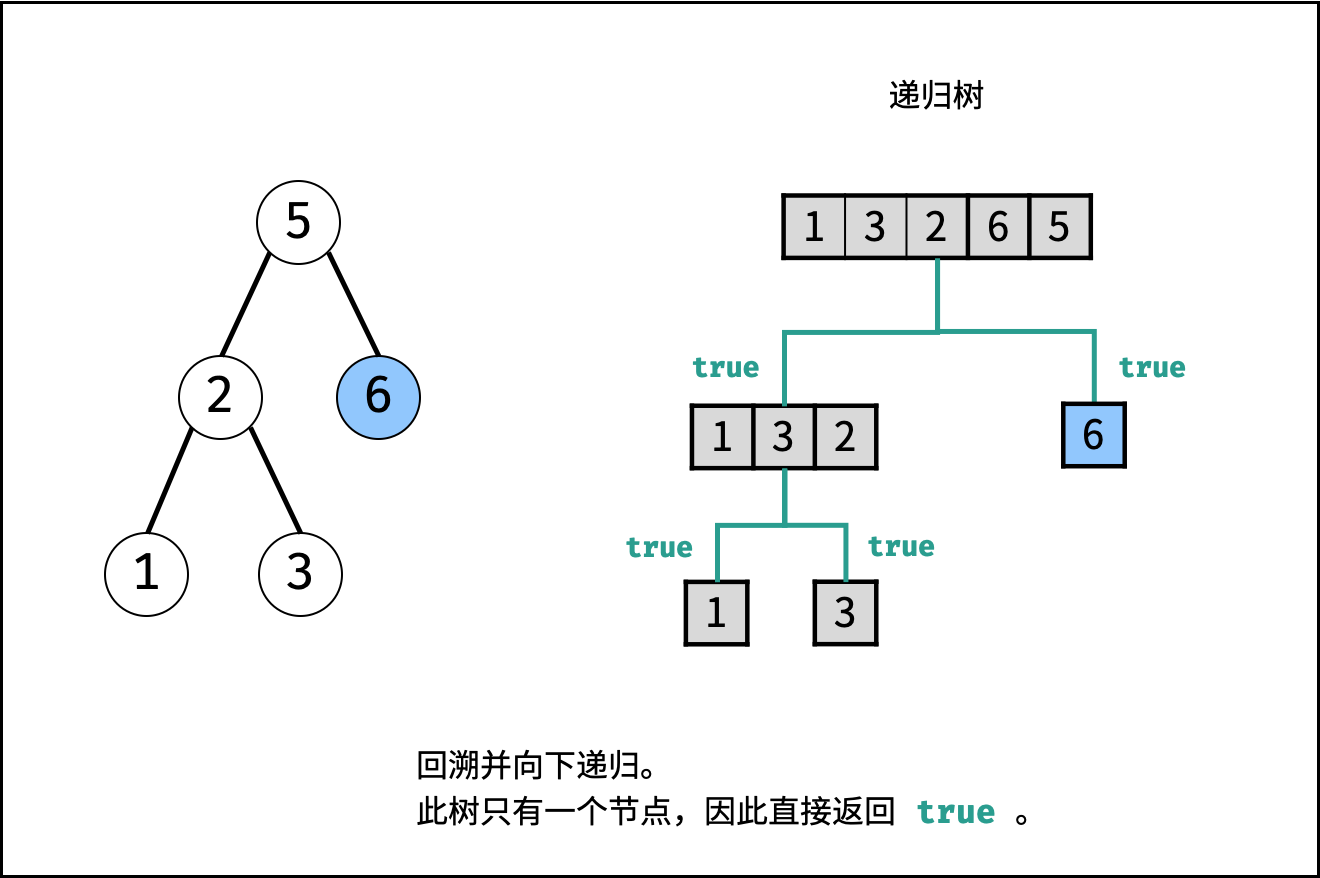Picture8.png](https://pic.leetcode-cn.com/1599753507-DHkXTP-Picture8.png),![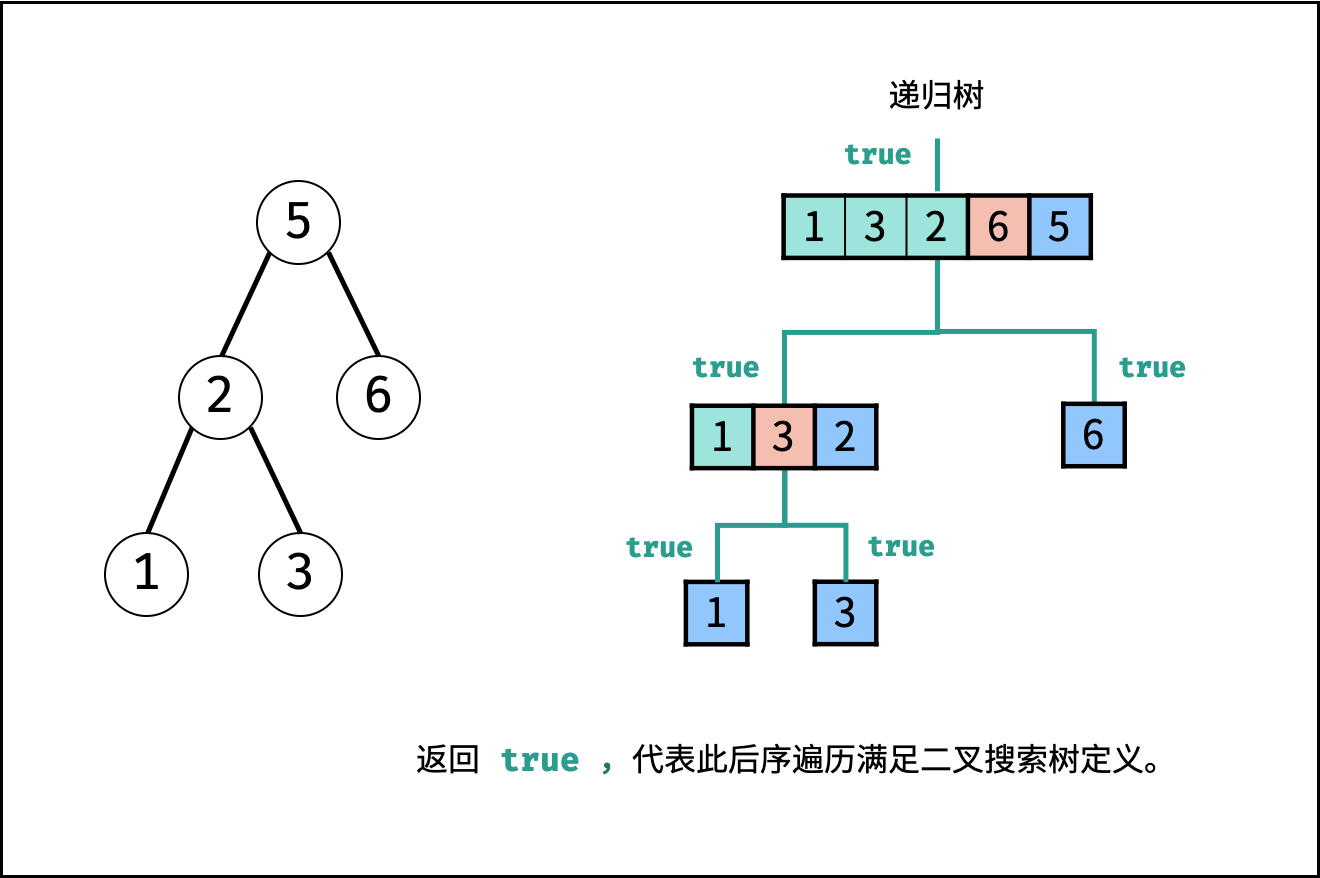Picture9.png](https://pic.leetcode-cn.com/1599753507-TyHQkm-Picture9.png)>
### 代码：
```Python []
class Solution:
def verifyTreeOrder(self, postorder: List[int]) -> bool:
def recur(i, j):
if i >= j: return True
p = i
while postorder[p] < postorder[j]: p += 1
m = p
while postorder[p] > postorder[j]: p += 1
return p == j and recur(i, m - 1) and recur(m, j - 1)
return recur(0, len(postorder) - 1)
```
```Java []
class Solution {
public boolean verifyTreeOrder(int[] postorder) {
return recur(postorder, 0, postorder.length - 1);
}
boolean recur(int[] postorder, int i, int j) {
if(i >= j) return true;
int p = i;
while(postorder[p] < postorder[j]) p++;
int m = p;
while(postorder[p] > postorder[j]) p++;
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
}
}
```
```C++ []
class Solution {
public:
bool verifyTreeOrder(vector<int>& postorder) {
return recur(postorder, 0, postorder.size() - 1);
}
private:
bool recur(vector<int>& postorder, int i, int j) {
if(i >= j) return true;
int p = i;
while(postorder[p] < postorder[j]) p++;
int m = p;
while(postorder[p] > postorder[j]) p++;
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N^2)$ ：** 每次调用 $recur(i,j)$ 减去一个根节点，因此递归占用 $O(N)$ ；最差情况下（即当树退化为链表），每轮递归都需遍历树所有节点，占用 $O(N)$ 。
- **空间复杂度 $O(N)$ ：** 最差情况下（即当树退化为链表），递归深度将达到 $N$ 。
## 方法二：辅助单调栈
**后序遍历倒序：** `[ 根节点 | 右子树 | 左子树 ]` 。类似 **先序遍历的镜像** ，即先序遍历为 “根、左、右” 的顺序，而后序遍历的倒序为 “根、右、左” 顺序。
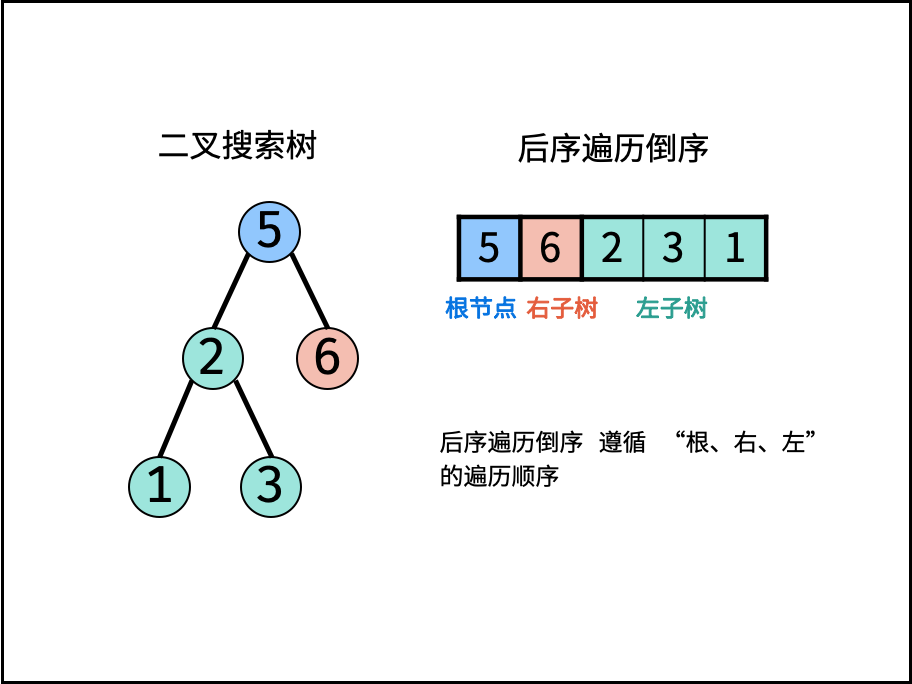![Picture10.png](https://pic.leetcode-cn.com/1599753507-KaeaWl-Picture10.png){:align=center width=500}
设后序遍历倒序列表为 $[r_{n}, r_{n-1},...,r_1]$，遍历此列表，设索引为 $i$ ，若为 **二叉搜索树** ，则有：
- **当节点值 $r_i > r_{i+1}$ 时：** 节点 $r_i$ 一定是节点 $r_{i+1}$ 的右子节点。
- **当节点值 $r_i < r_{i+1}$ 时：** 节点 $r_i$ 一定是某节点 $root$ 的左子节点，且 $root$ 为节点 $r_{i+1}, r_{i+2},..., r_{n}$ 中值大于且最接近 $r_i$ 的节点（∵ $root$ **直接连接** 左子节点 $r_i$ ）。
当遍历时遇到递减节点 $r_i < r_{i+1}$ ，若为二叉搜索树，则对于后序遍历中节点 $r_i$ 右边的任意节点 $r_x \in [r_{i-1}, r_{i-2}, ..., r_1]$ ，必有节点值 $r_x < root$ 。
> 节点 $r_x$ 只可能为以下两种情况：(1) $r_x$ 为 $r_i$ 的左、右子树的各节点；(2) $r_x$ 为 $root$ 的父节点或更高层父节点的左子树的各节点。在二叉搜索树中，以上节点都应小于 $root$ 。
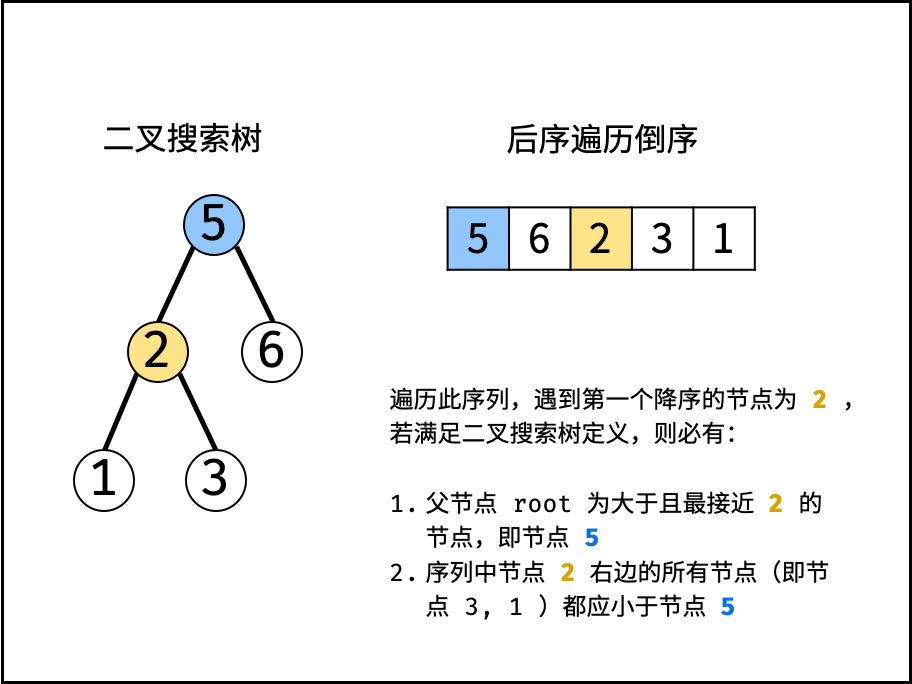![Picture11.png](https://pic.leetcode-cn.com/1599753507-mgqkoF-Picture11.png){:align=center width=500}
遍历 “后序遍历的倒序” 会多次遇到递减节点 $r_i$ ，若所有的递减节点 $r_i$ 对应的父节点 $root$ 都满足以上条件，则可判定为二叉搜索树。根据以上特点，考虑借助 **单调栈** 实现：
1. 借助一个单调栈 $stack$ 存储值递增的节点；
2. 每当遇到值递减的节点 $r_i$ ，则通过出栈来更新节点 $r_i$ 的父节点 $root$ ；
3. 每轮判断 $r_i$ 和 $root$ 的值关系：
1. 若 $r_i > root$ 则说明不满足二叉搜索树定义，直接返回 $\text{false}$ 。
2. 若 $r_i < root$ 则说明满足二叉搜索树定义，则继续遍历。
### 算法流程：
1. **初始化：** 单调栈 $stack$ ，父节点值 $root = +\infin$ （初始值为正无穷大，可把树的根节点看为此无穷大节点的左孩子）；
2. **倒序遍历 $postorder$** ：记每个节点为 $r_i$；
1. **判断：** 若 $r_i>root$ ，说明此后序遍历序列不满足二叉搜索树定义，直接返回 $\text{false}$ ；
2. **更新父节点 $root$ ：** 当栈不为空 **且** $r_i<stack.peek()$ 时，循环执行出栈，并将出栈节点赋给 $root$ 。
3. **入栈：** 将当前节点 $r_i$ 入栈；
3. 若遍历完成，则说明后序遍历满足二叉搜索树定义，返回 $\text{true}$ 。
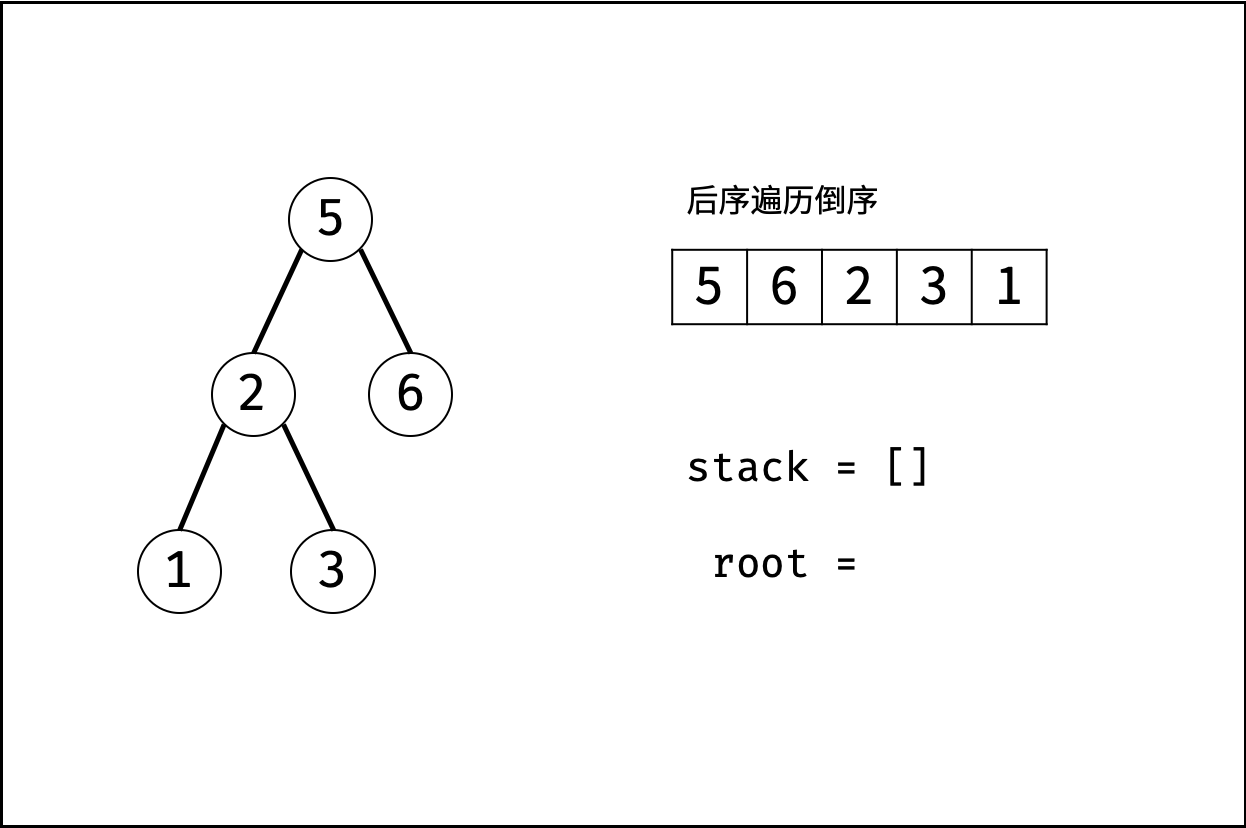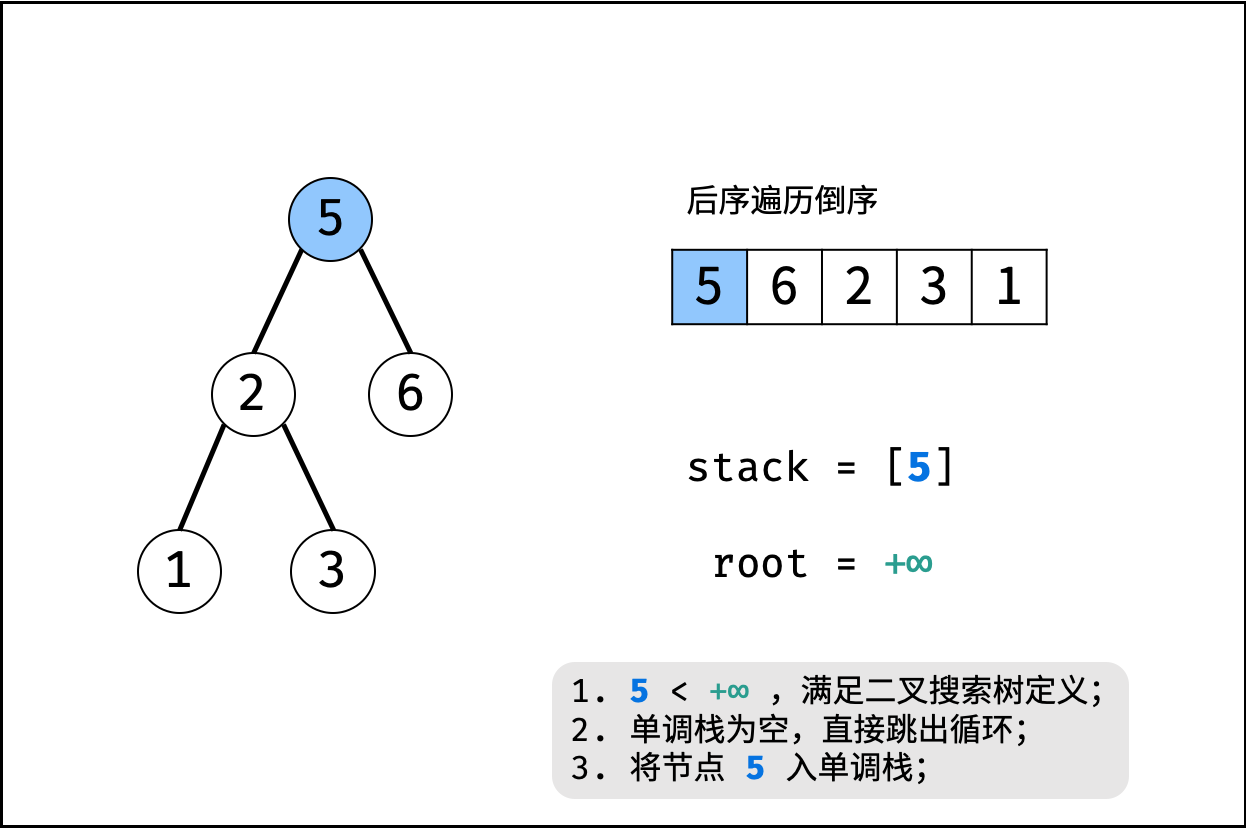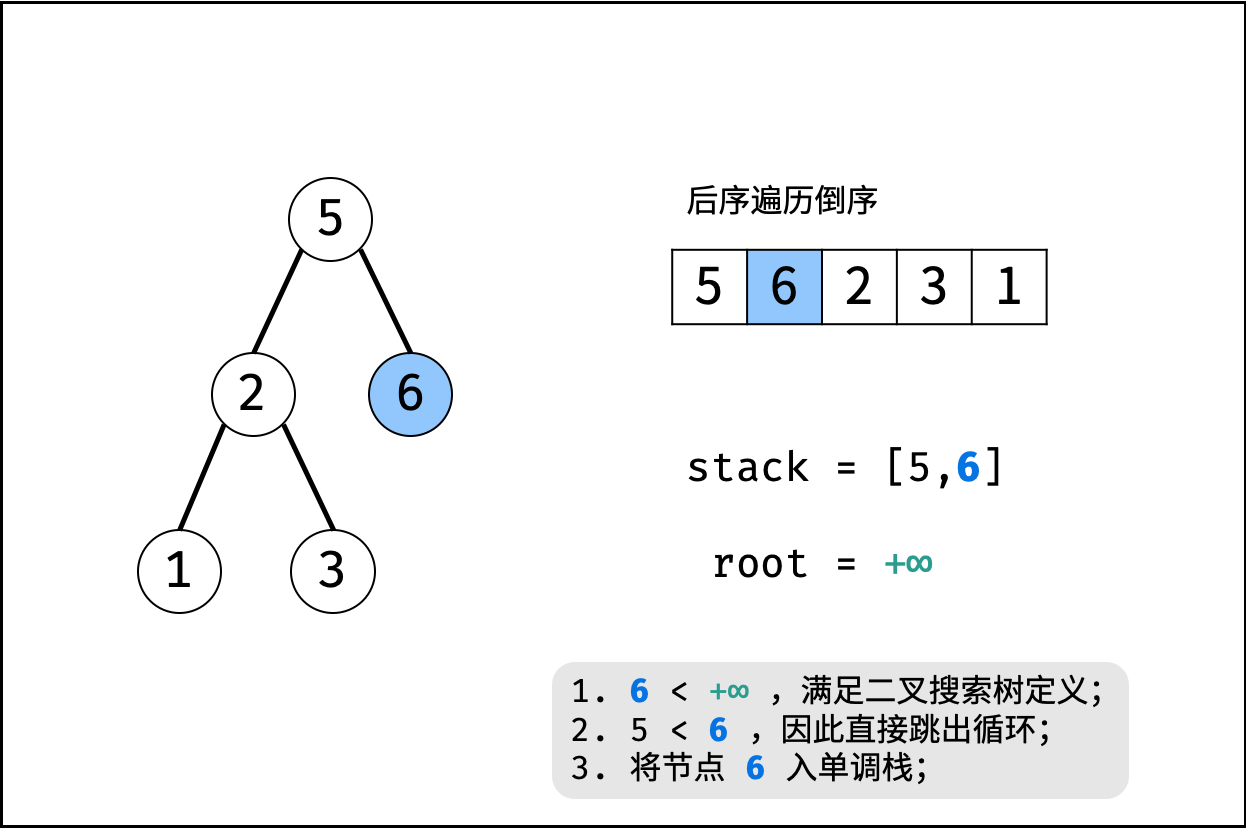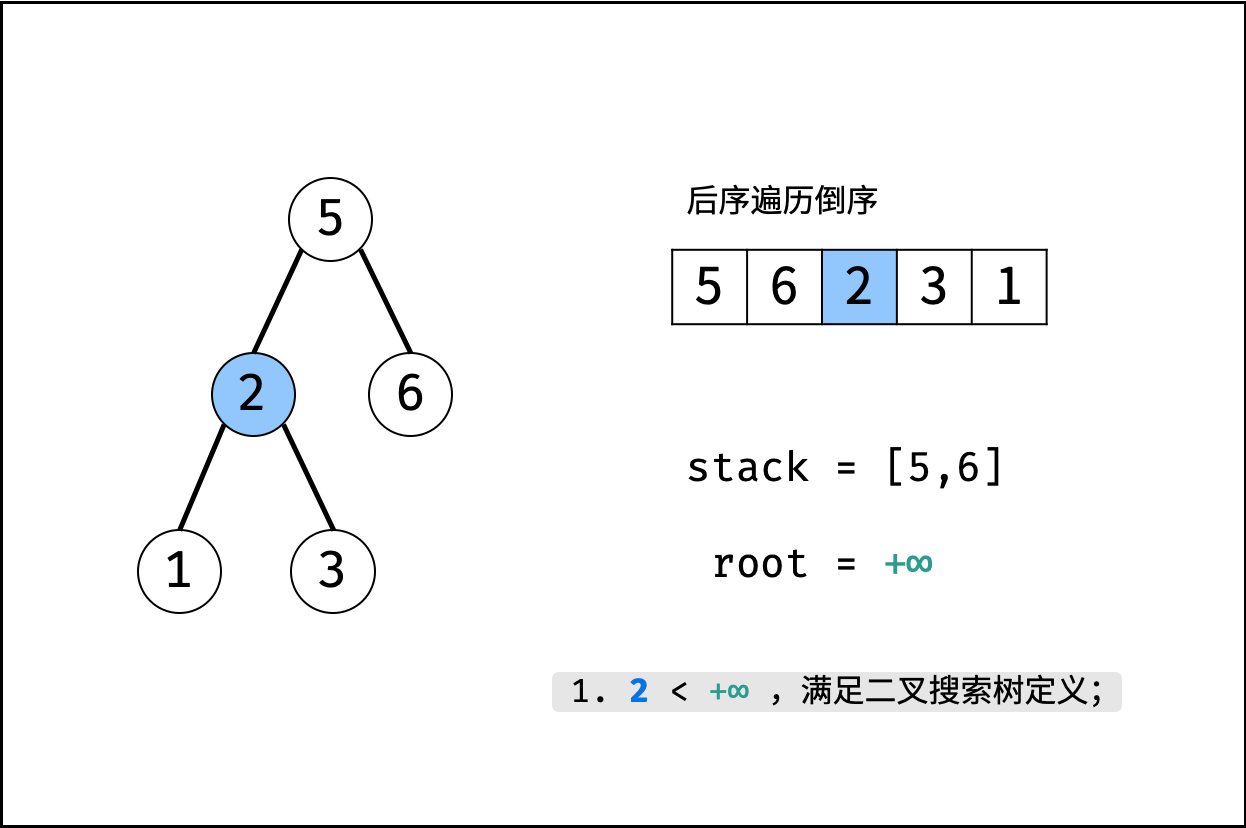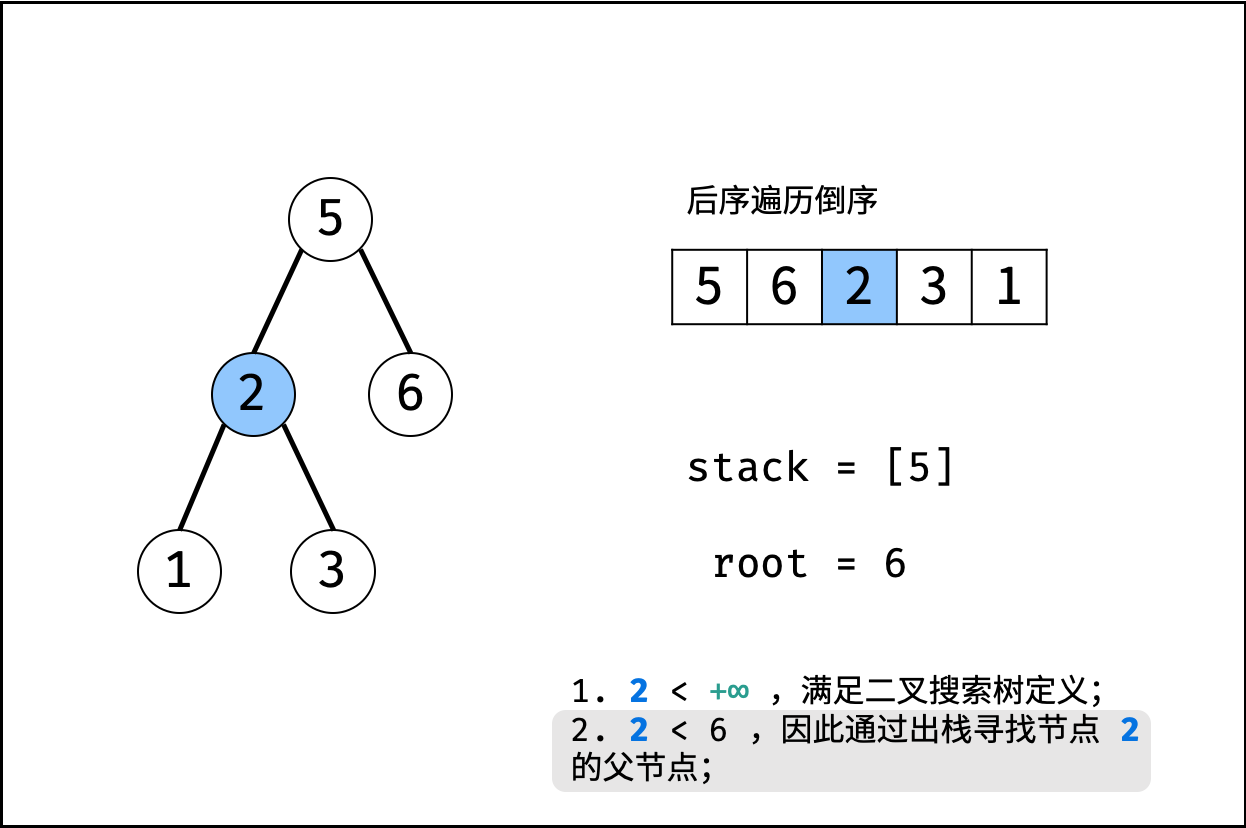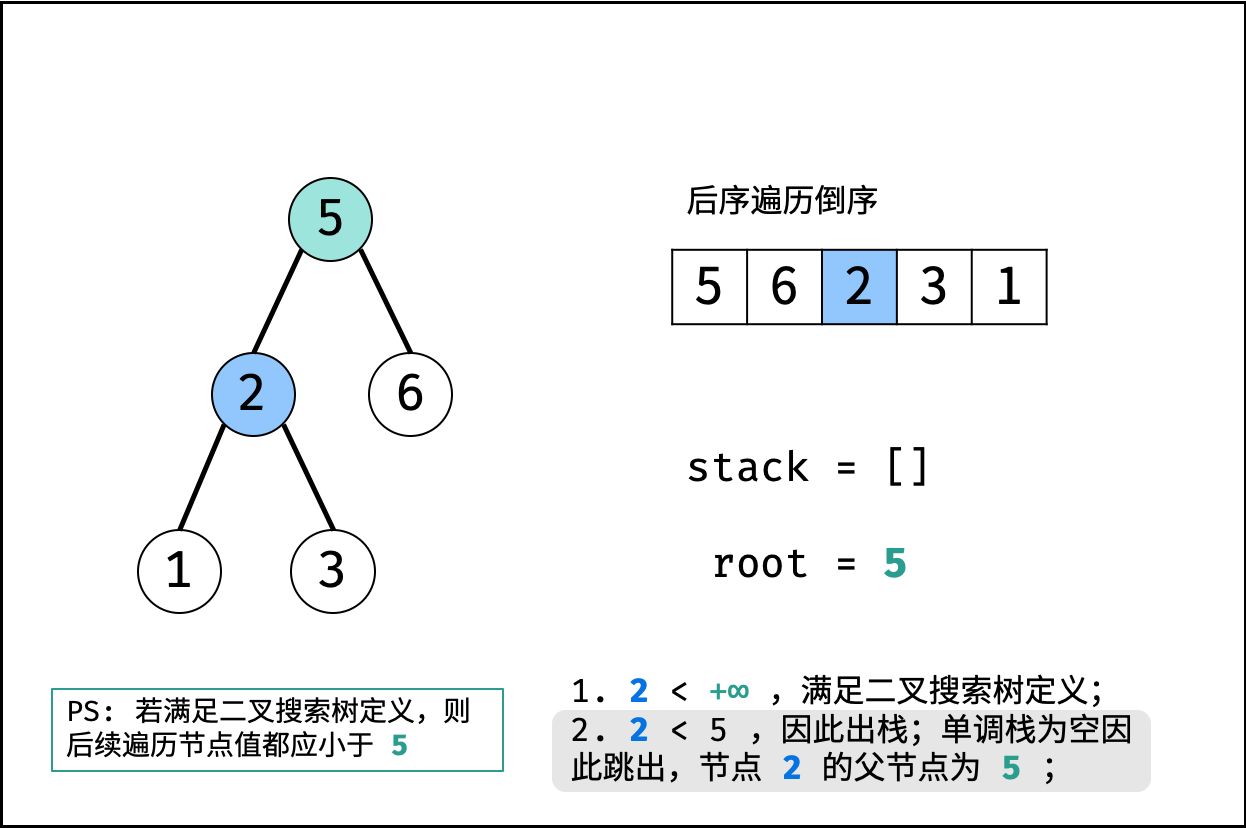<![Picture12.png](https://pic.leetcode-cn.com/1599753507-RNJMua-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1599753507-vEzTsr-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1599753507-bKuQFg-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1599753507-teTCOf-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1599753507-dMUcJm-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1599753507-LmdXnR-Picture17.png),![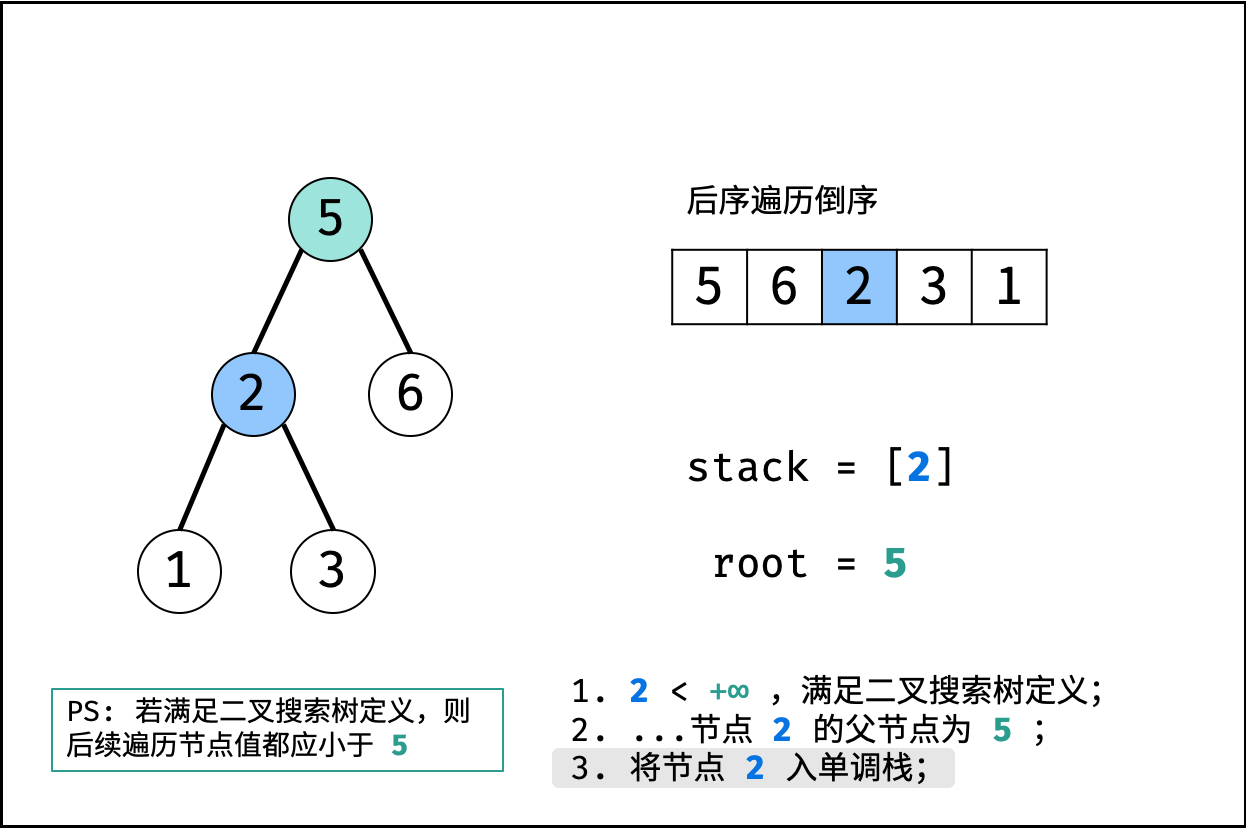Picture18.png](https://pic.leetcode-cn.com/1599753507-xxTcgK-Picture18.png),![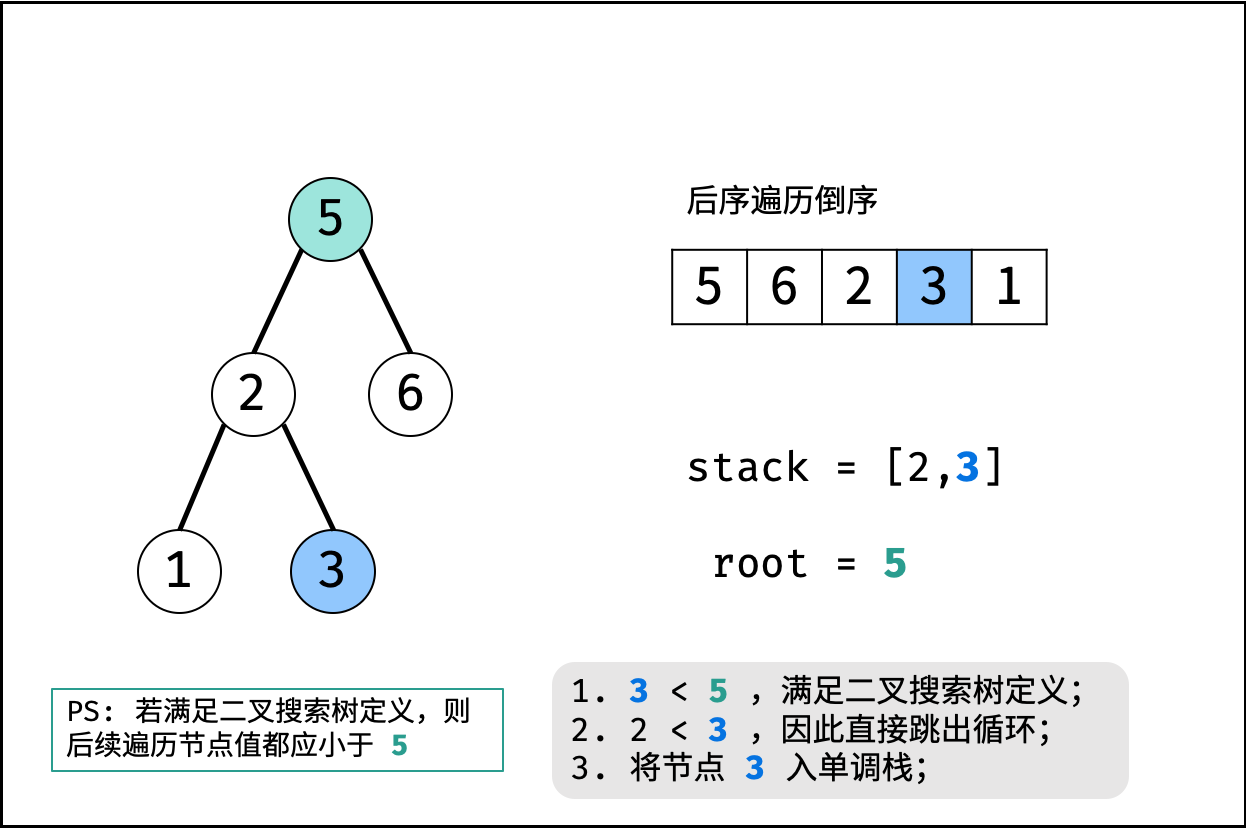Picture19.png](https://pic.leetcode-cn.com/1599753507-yhkHOi-Picture19.png),![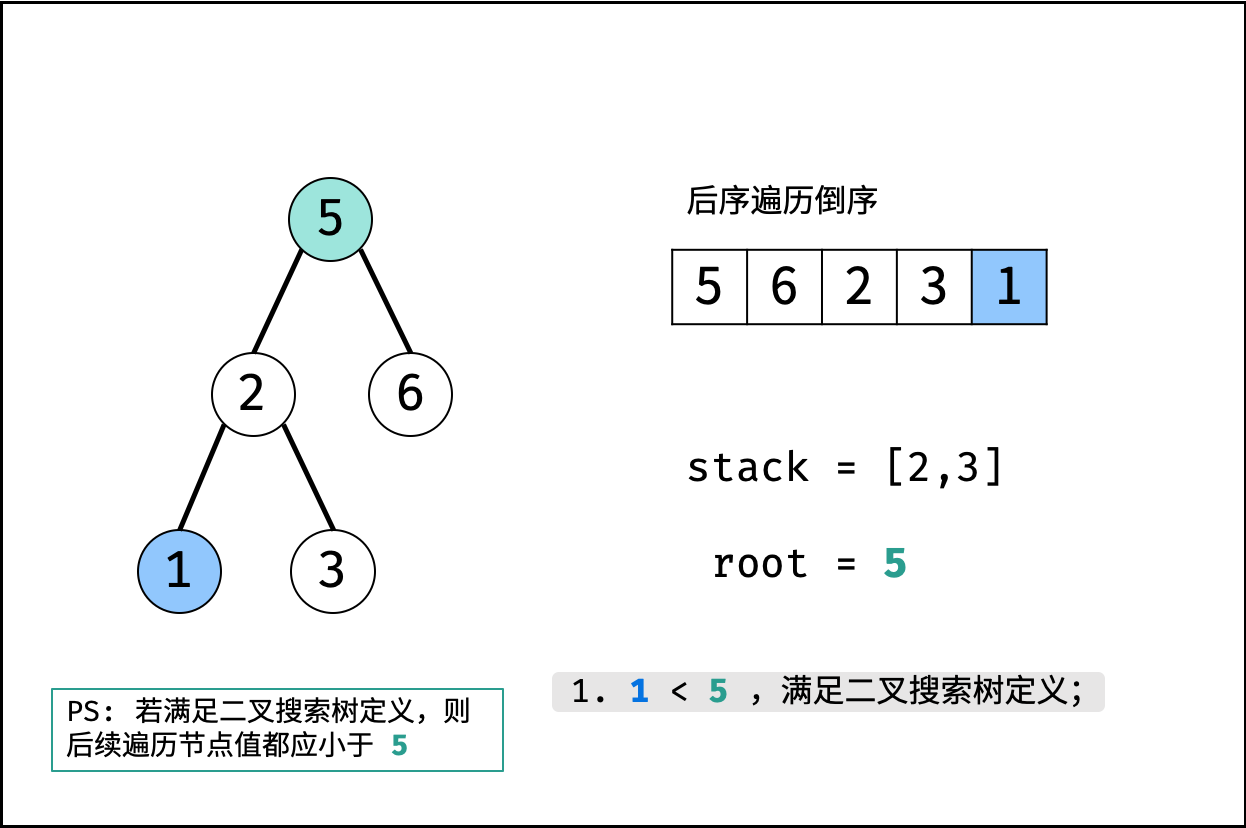Picture20.png](https://pic.leetcode-cn.com/1599753507-wDSNSr-Picture20.png),![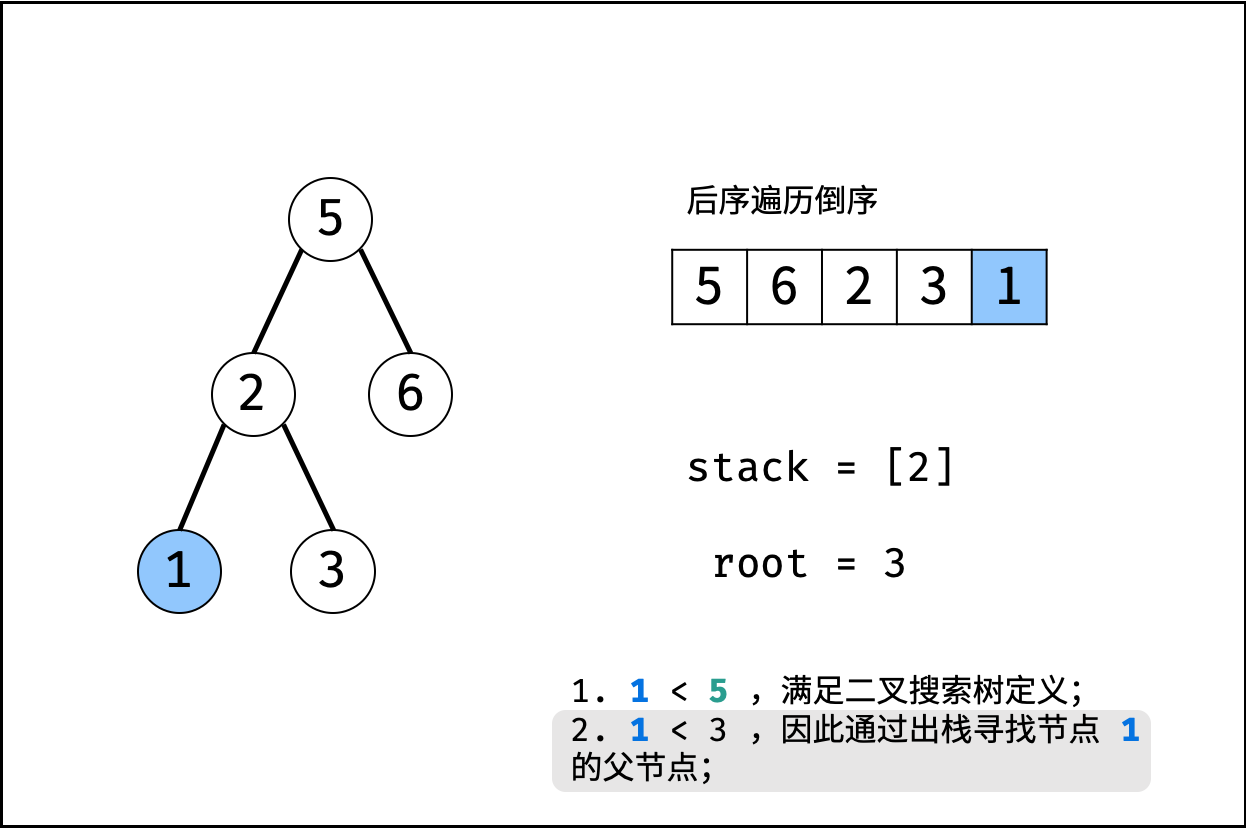Picture21.png](https://pic.leetcode-cn.com/1599753507-ZQXapk-Picture21.png),![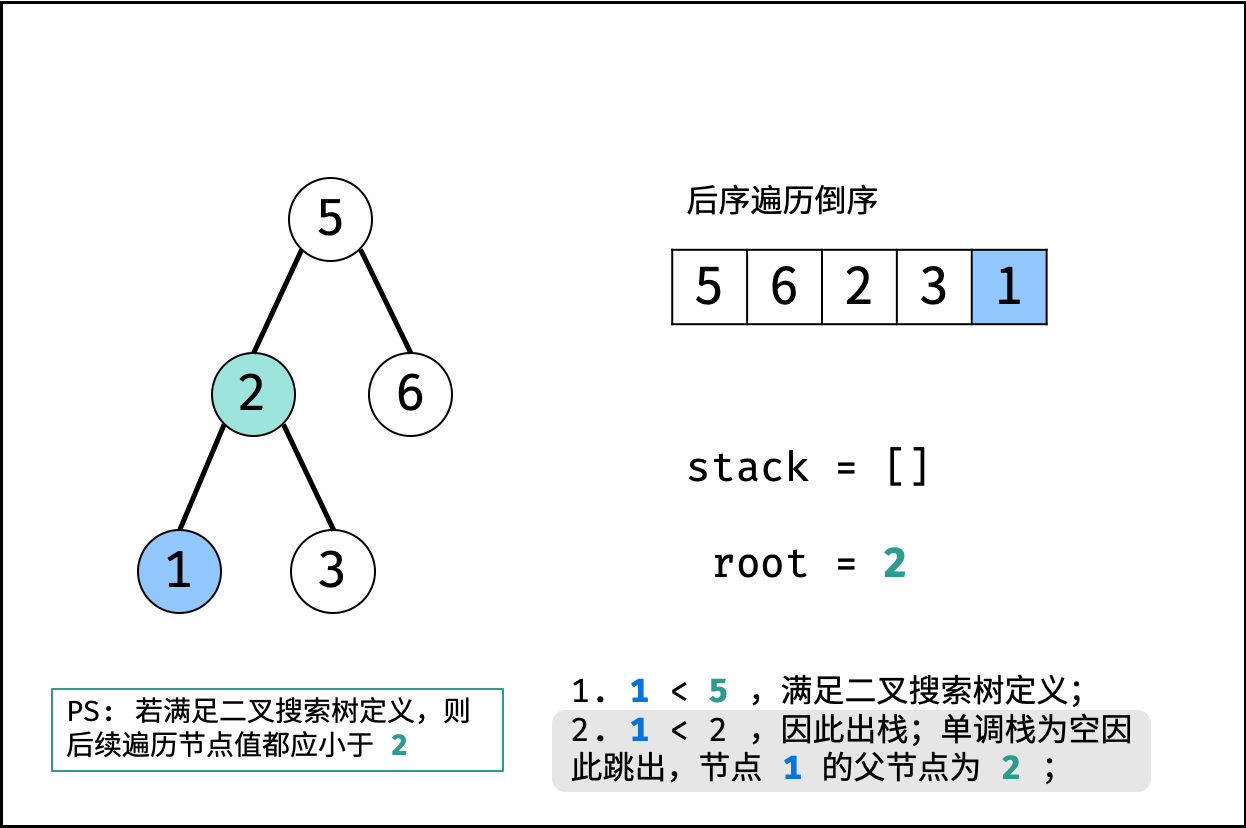Picture22.png](https://pic.leetcode-cn.com/1599753507-rNdjQT-Picture22.png),![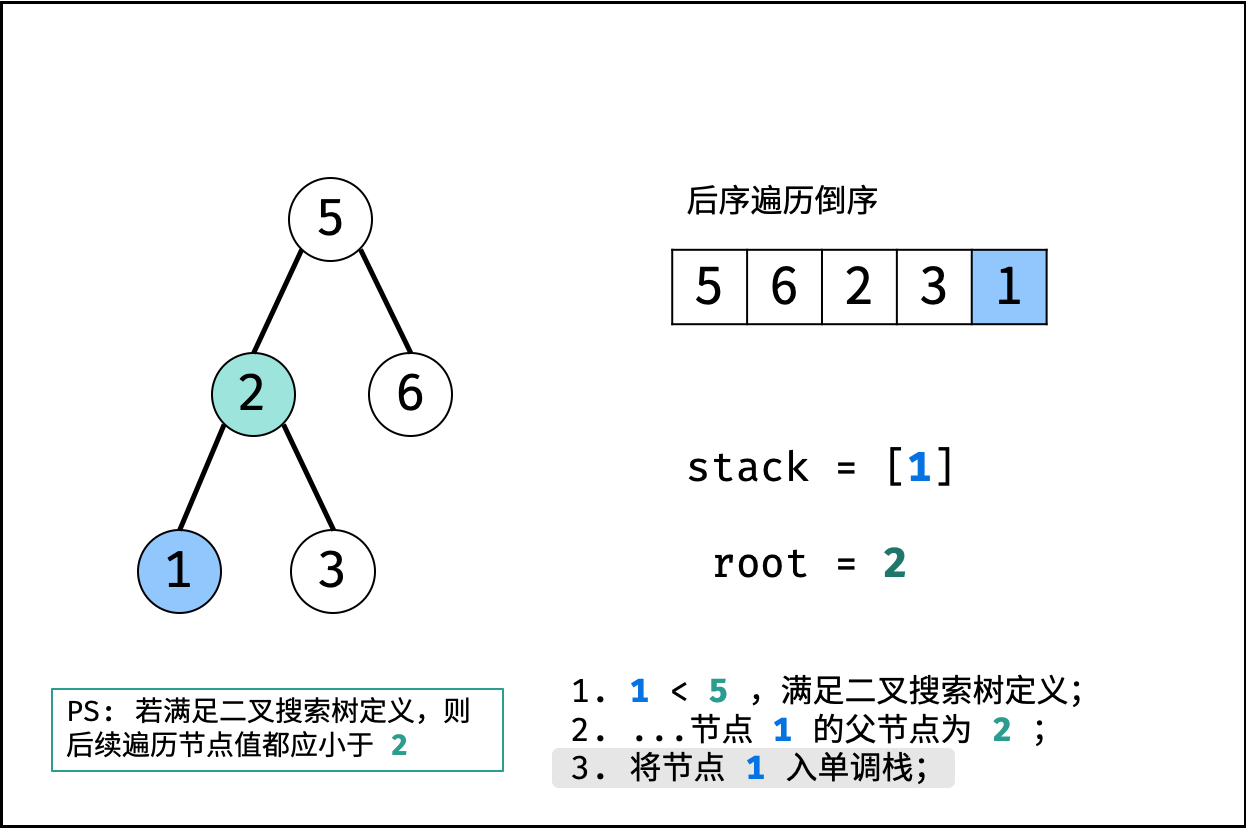Picture23.png](https://pic.leetcode-cn.com/1599753507-VDeZeK-Picture23.png),![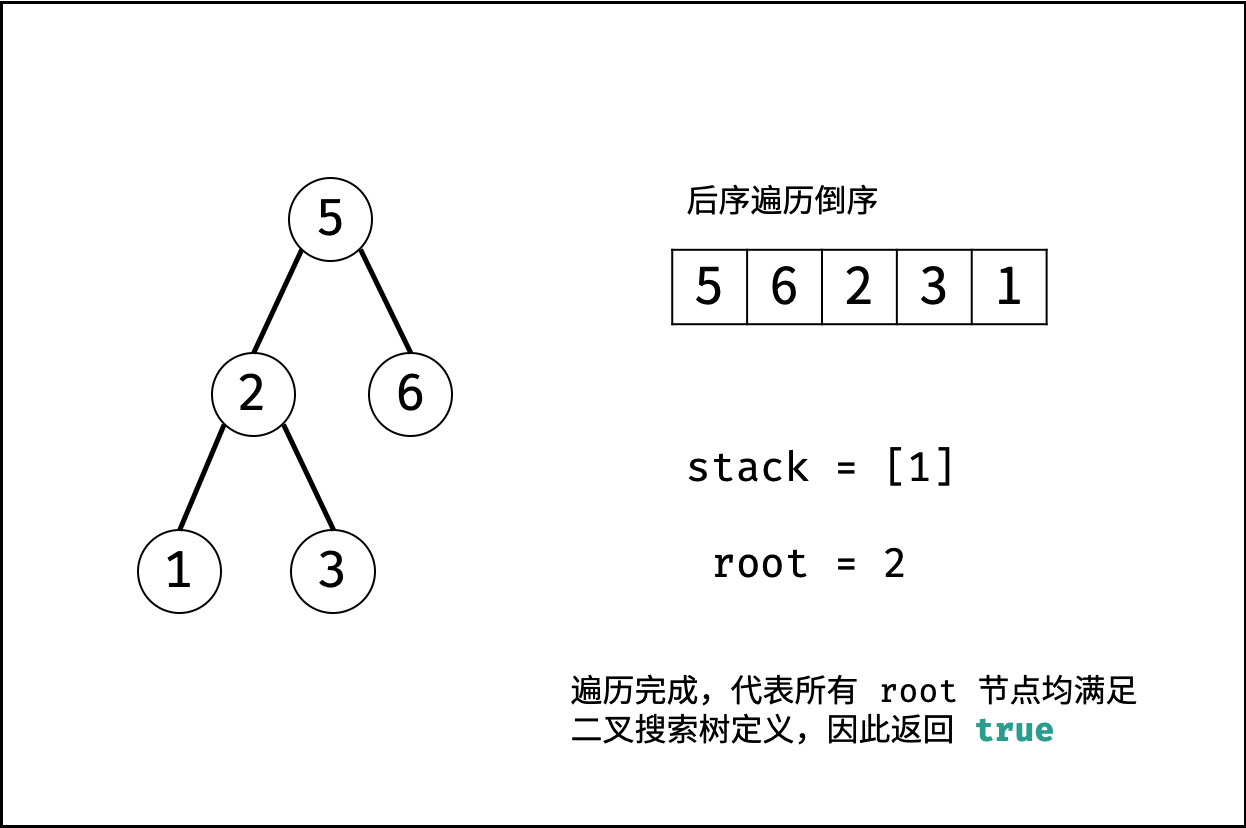Picture24.png](https://pic.leetcode-cn.com/1599753507-QfiHaw-Picture24.png)>
### 代码：
```Python []
class Solution:
def verifyTreeOrder(self, postorder: List[int]) -> bool:
stack, root = [], float("+inf")
for i in range(len(postorder) - 1, -1, -1):
if postorder[i] > root: return False
while(stack and postorder[i] < stack[-1]):
root = stack.pop()
stack.append(postorder[i])
return True
```
```Java []
class Solution {
public boolean verifyTreeOrder(int[] postorder) {
Stack<Integer> stack = new Stack<>();
int root = Integer.MAX_VALUE;
for(int i = postorder.length - 1; i >= 0; i--) {
if(postorder[i] > root) return false;
while(!stack.isEmpty() && stack.peek() > postorder[i])
root = stack.pop();
stack.add(postorder[i]);
}
return true;
}
}
```
```C++ []
class Solution {
public:
bool verifyTreeOrder(vector<int>& postorder) {
stack<int> stk;
int root = INT_MAX;
for(int i = postorder.size() - 1; i >= 0; i--) {
if(postorder[i] > root) return false;
while(!stk.empty() && stk.top() > postorder[i]) {
root = stk.top();
stk.pop();
}
stk.push(postorder[i]);
}
return true;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 遍历 $postorder$ 所有节点，各节点均入栈 / 出栈一次，使用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** 最差情况下，单调栈 $stack$ 存储所有节点，使用 $O(N)$ 额外空间。

105
leetbook_ioa/docs/LCR 153. 二叉树中和为目标值的路径.md Executable file
View File

@@ -0,0 +1,105 @@
## 解题思路：
本题是典型的二叉树方案搜索问题，使用回溯法解决，其包含 **先序遍历 + 路径记录** 两部分。
- **先序遍历：** 按照 “根、左、右” 的顺序，遍历树的所有节点。
- **路径记录：** 在先序遍历中，记录从根节点到当前节点的路径。当路径满足 (1) 根节点到叶节点形成的路径 **且** (2) 各节点值的和等于目标值 `target` 时，将此路径加入结果列表。
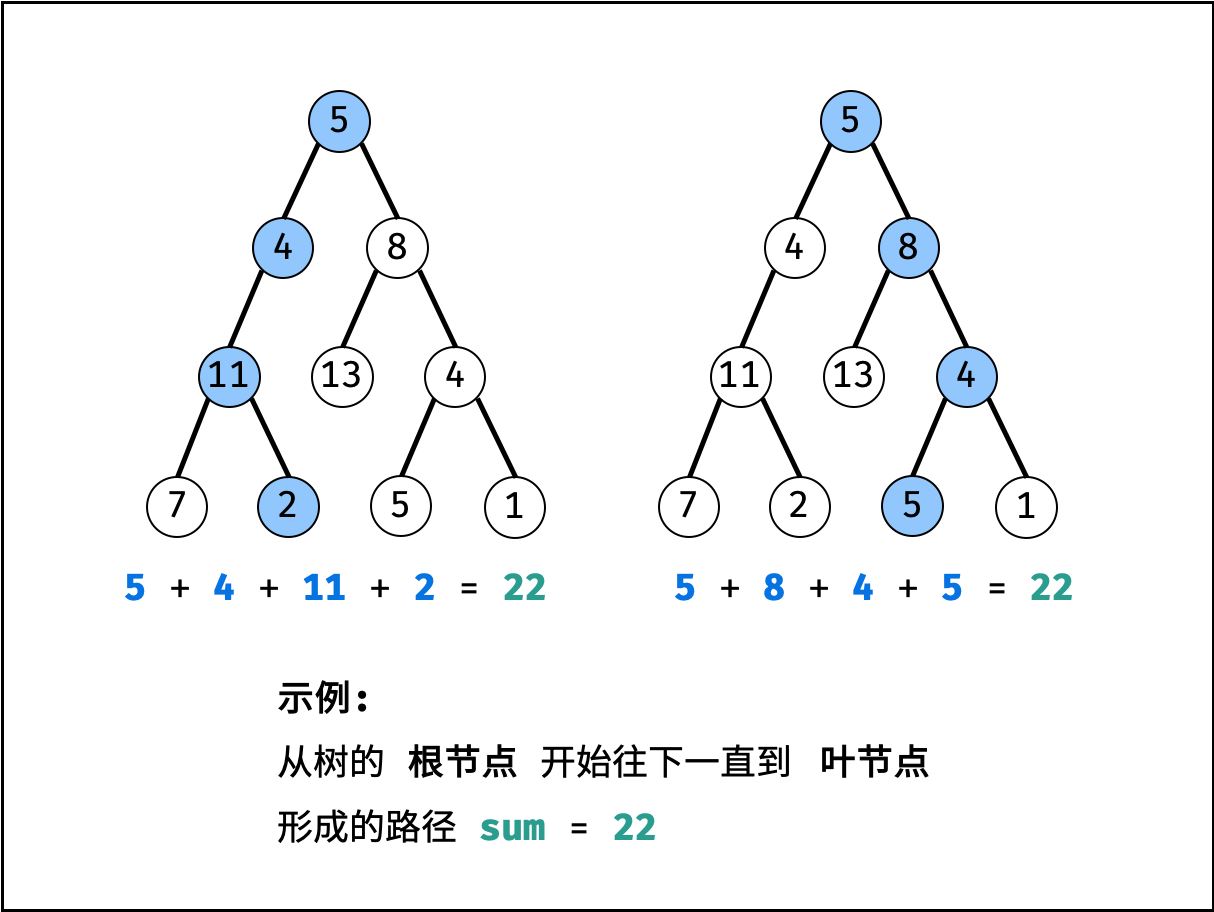![Picture1.png](https://pic.leetcode-cn.com/1599400747-BuGhCT-Picture1.png){:align=center width=500}
### 算法流程：
**`pathTarget(root, target)` 函数：**
- **初始化：** 结果列表 `res` ，路径列表 `path` 。
- **返回值：** 返回 `res` 即可。
**`recur(root, tar) 函数：`**
- **递推参数：** 当前节点 `root` ，当前目标值 `tar` 。
- **终止条件：** 若节点 `root` 为空，则直接返回。
- **递推工作：**
1. 路径更新： 将当前节点值 `root.val` 加入路径 `path` 。
2. 目标值更新： `tar = tar - root.val`（即目标值 `tar` 从 `target` 减至 $0$ ）。
3. 路径记录： 当 “`root` 为叶节点” **且** “路径和等于目标值” ，则将此路径 `path` 加入 `res` 。
4. 先序遍历： 递归左 / 右子节点。
5. 路径恢复： 向上回溯前，需要将当前节点从路径 `path` 中删除，即执行 `path.pop()` 。
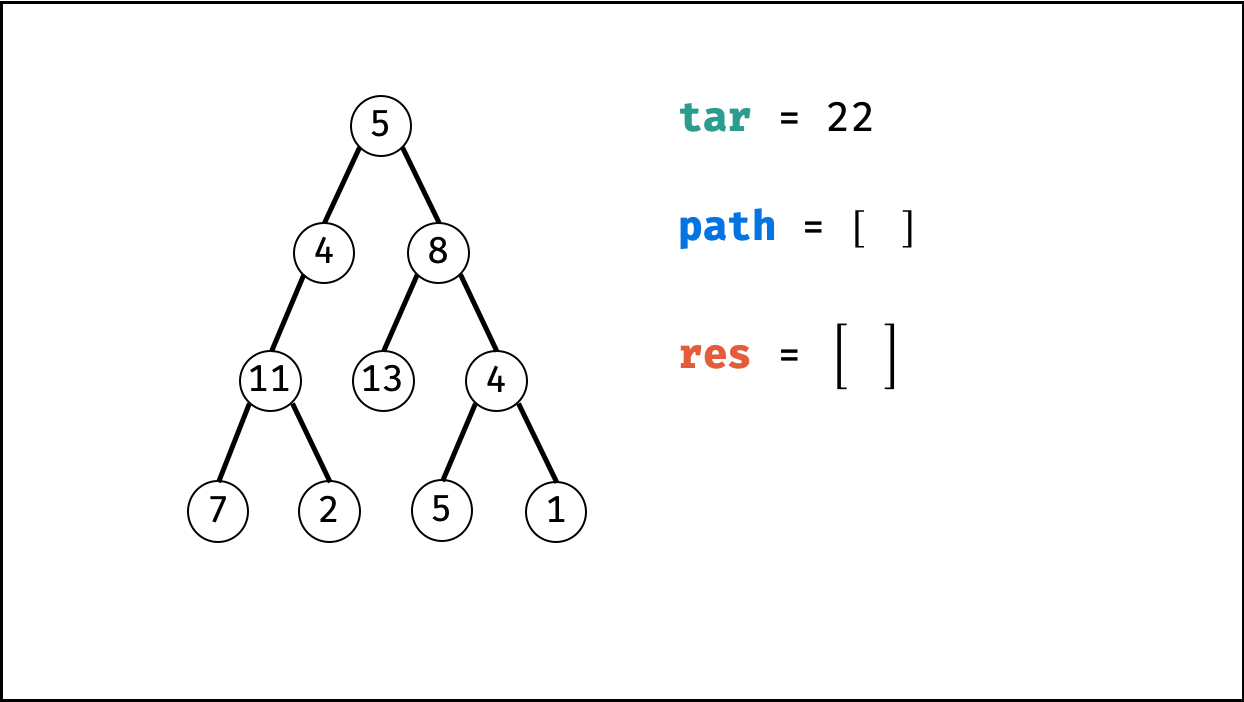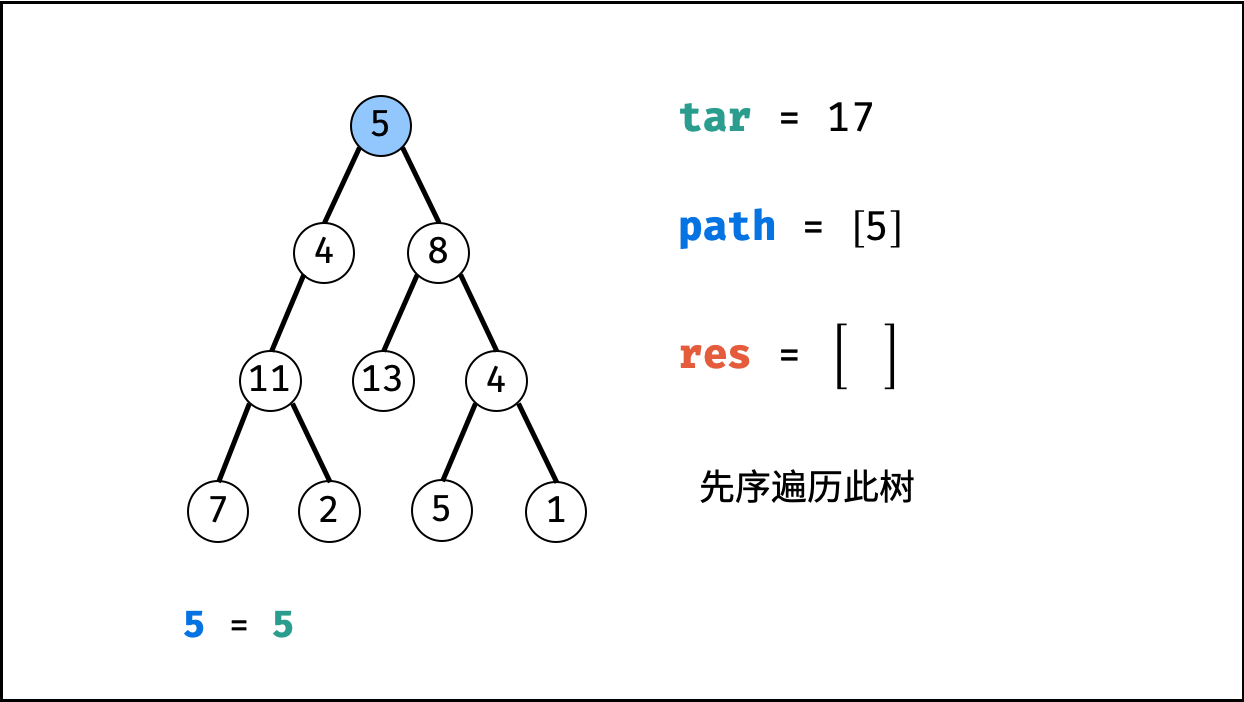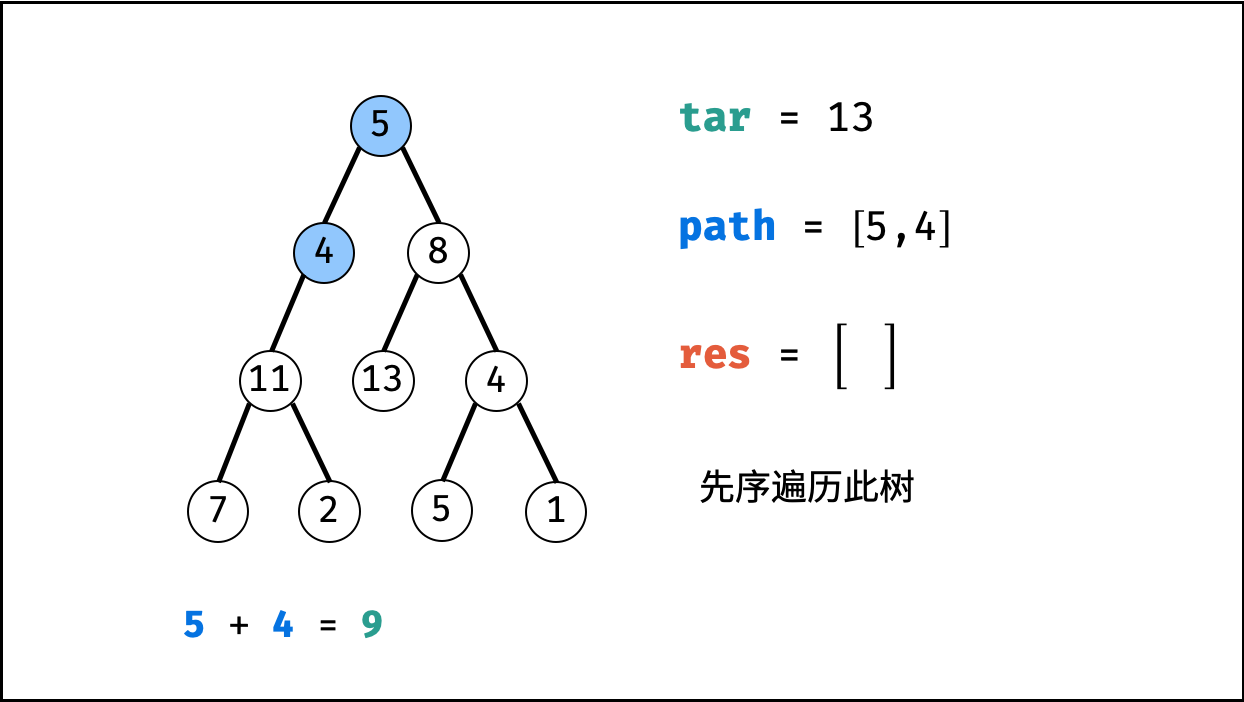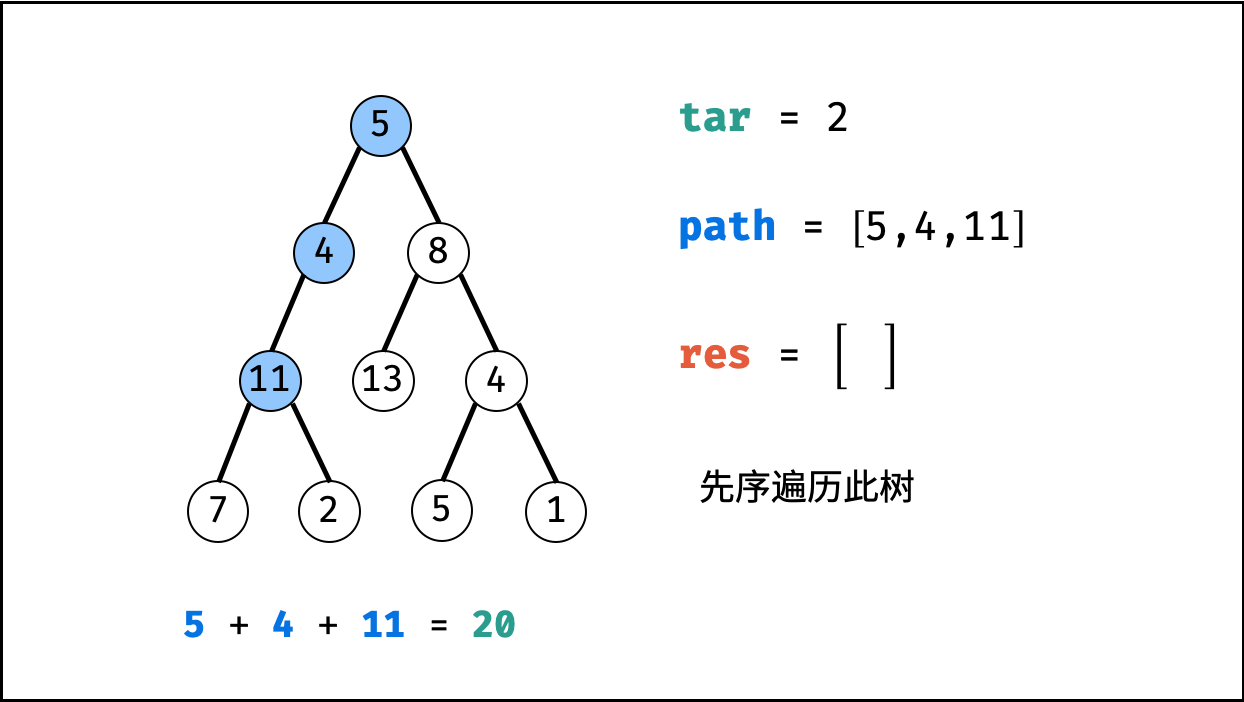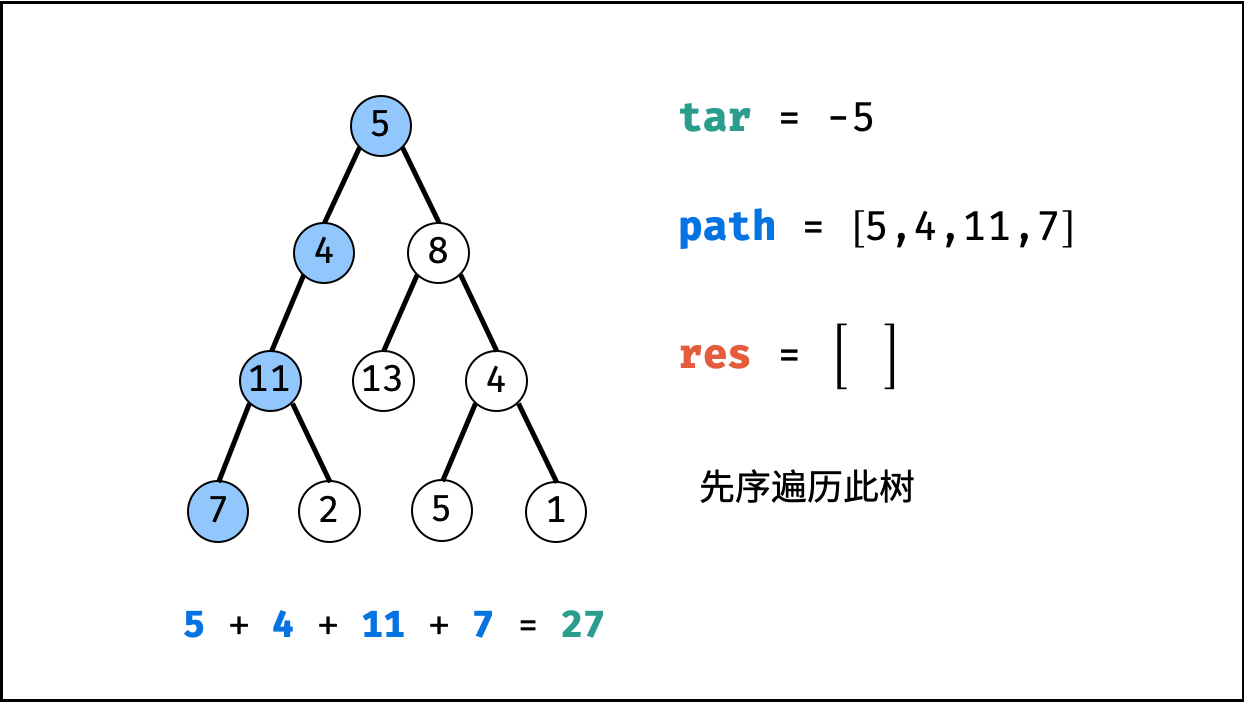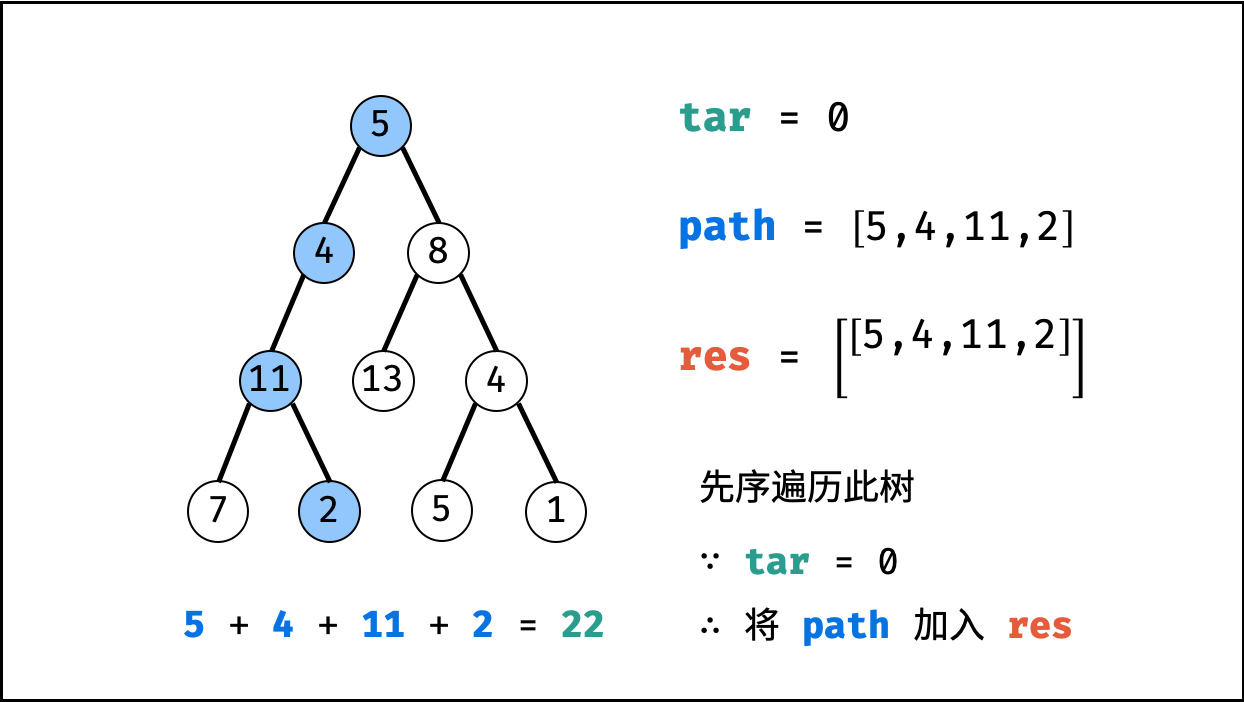<![Picture2.png](https://pic.leetcode-cn.com/1599400747-FhiySZ-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599400747-SAVFMR-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599400747-HsbajF-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599400747-FGhOvI-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599400747-ZIBiod-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599400747-IplqhE-Picture7.png),![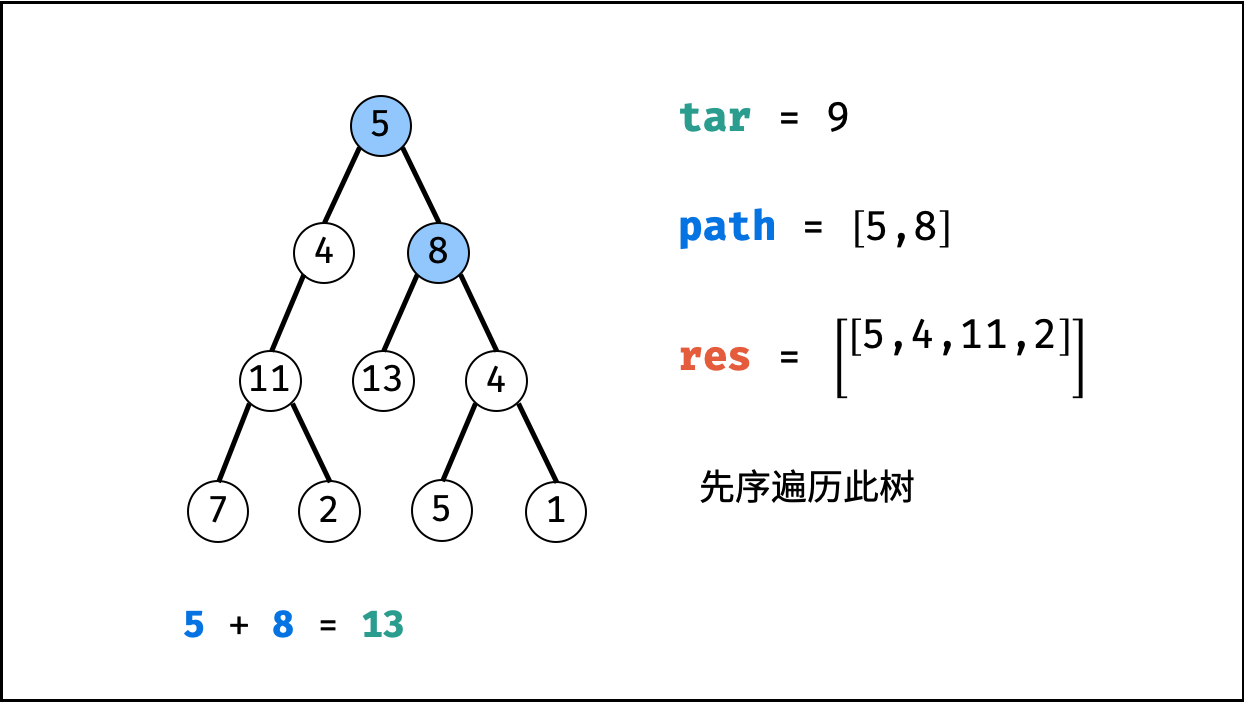Picture8.png](https://pic.leetcode-cn.com/1599400747-bDmOoi-Picture8.png),![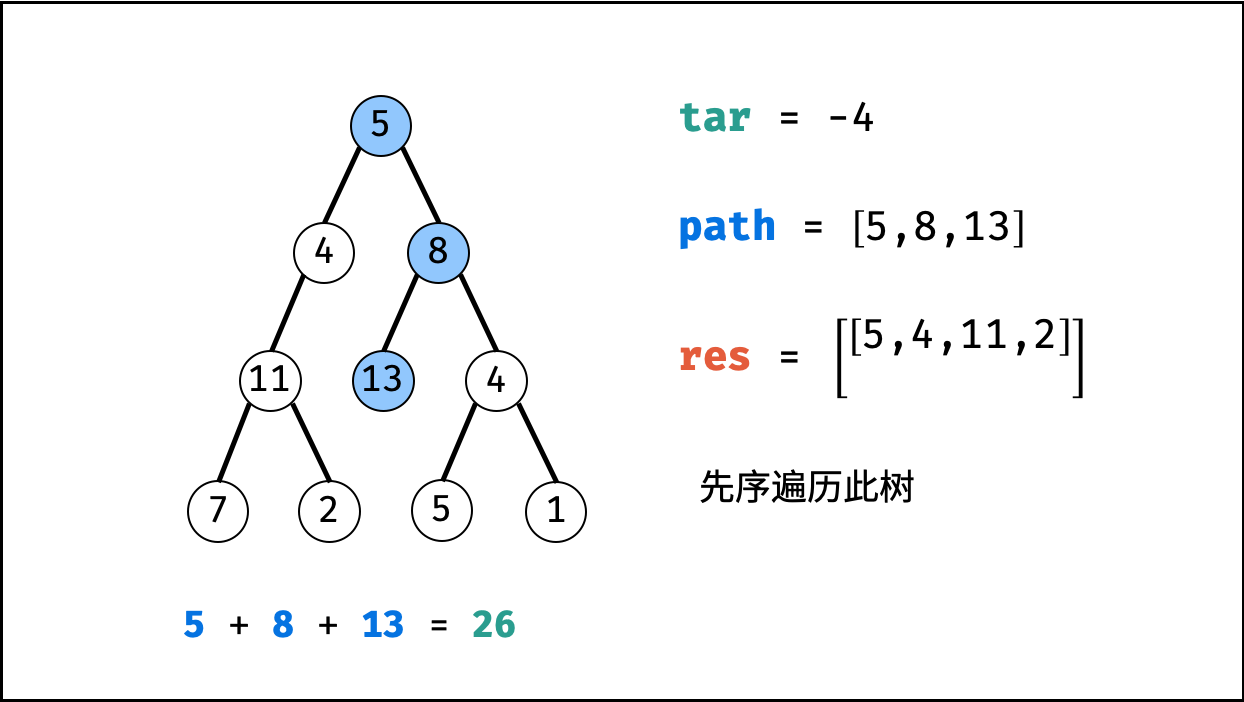Picture9.png](https://pic.leetcode-cn.com/1599400747-QWjiJz-Picture9.png),![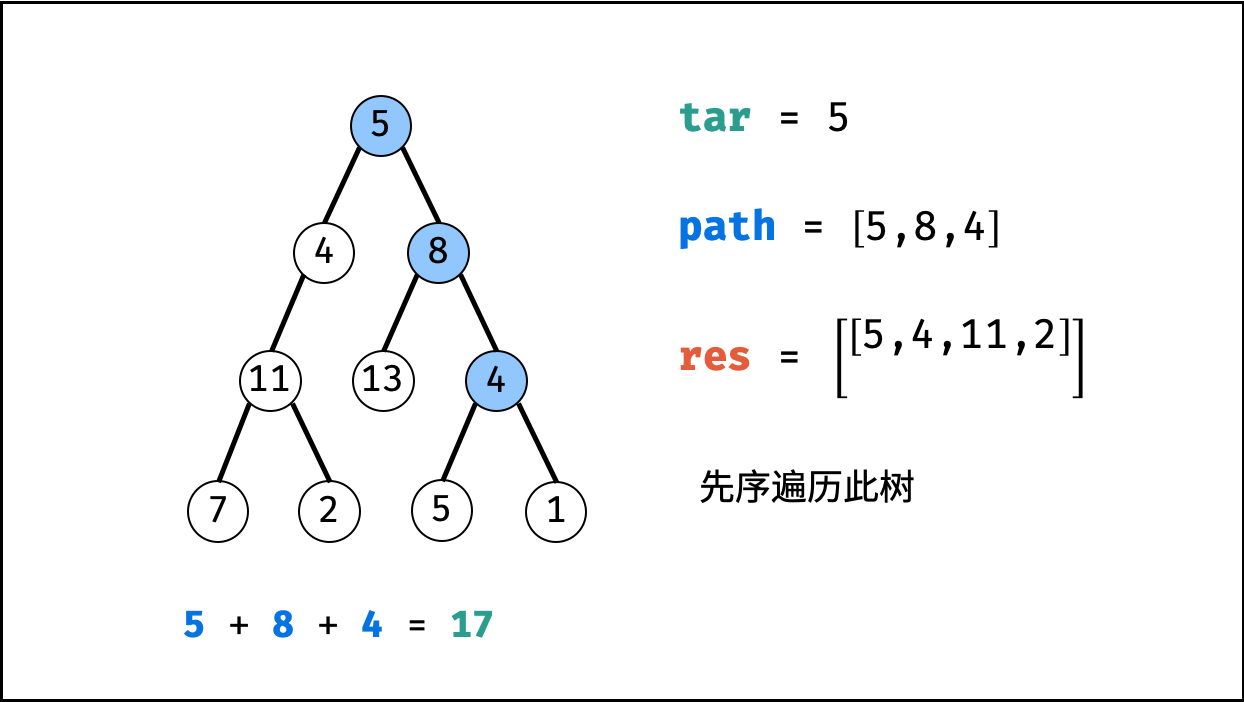Picture10.png](https://pic.leetcode-cn.com/1599400747-PWOXkh-Picture10.png),![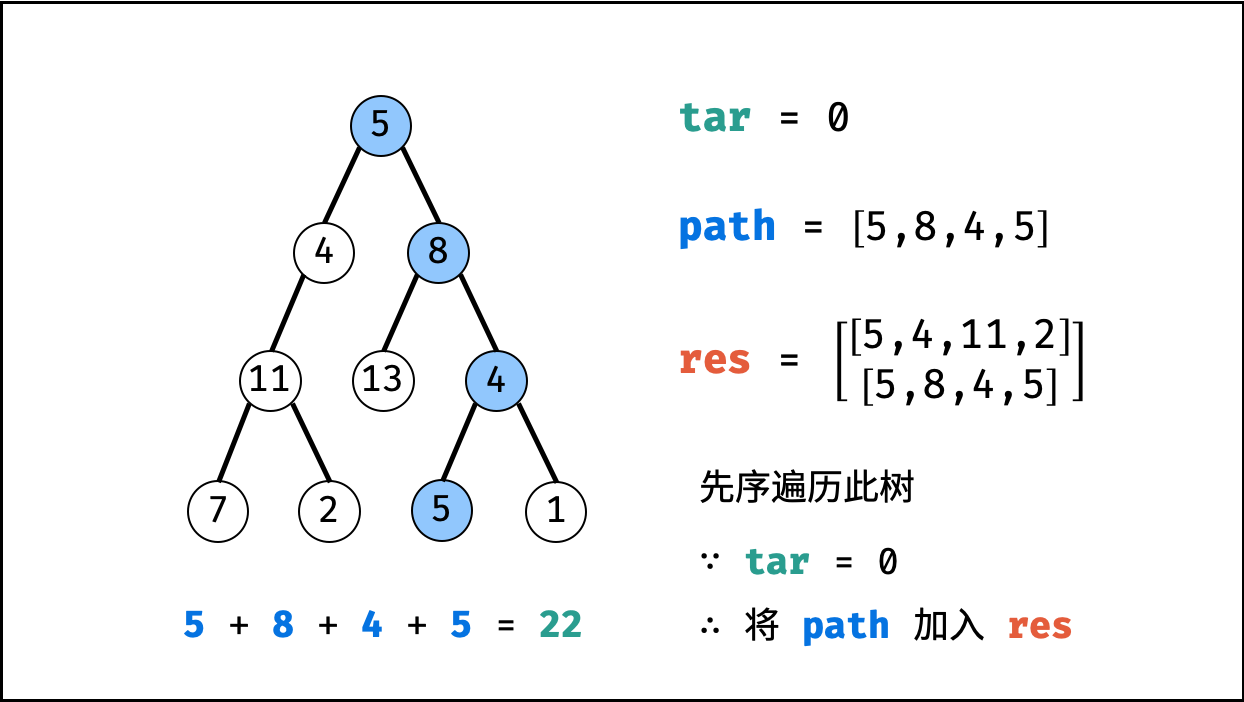Picture11.png](https://pic.leetcode-cn.com/1599400747-zLGIme-Picture11.png),![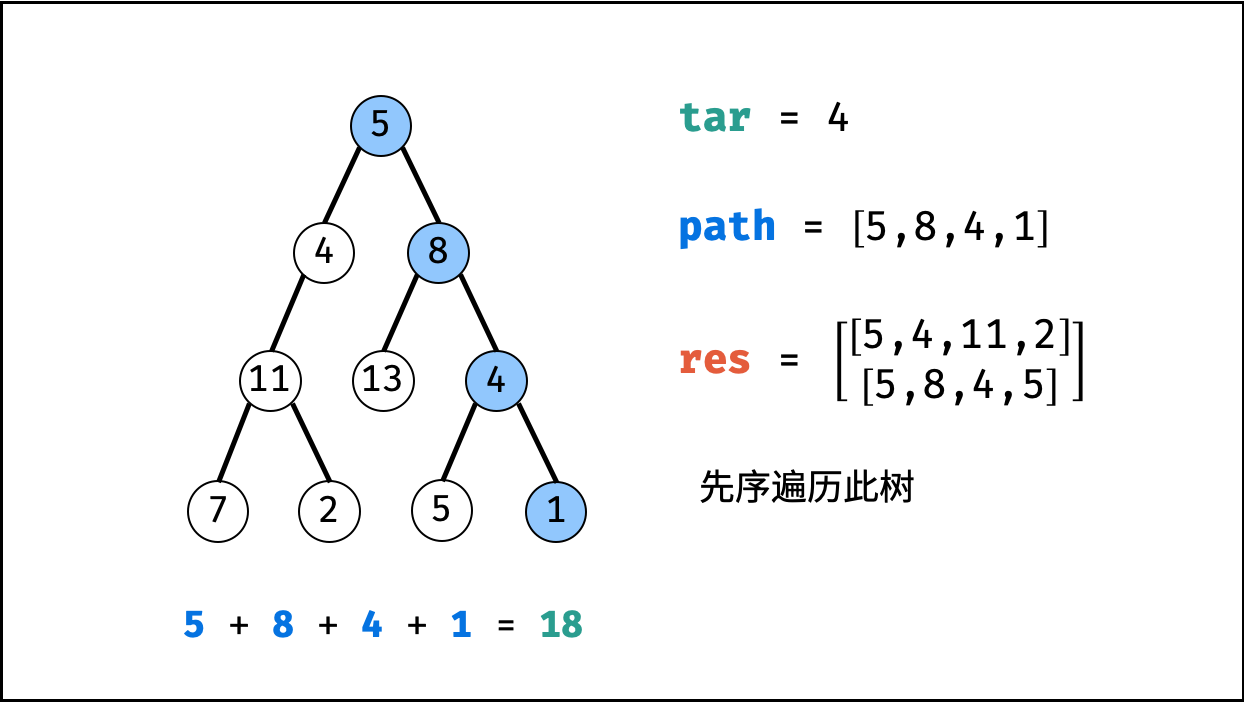Picture12.png](https://pic.leetcode-cn.com/1599400747-qtezAS-Picture12.png),![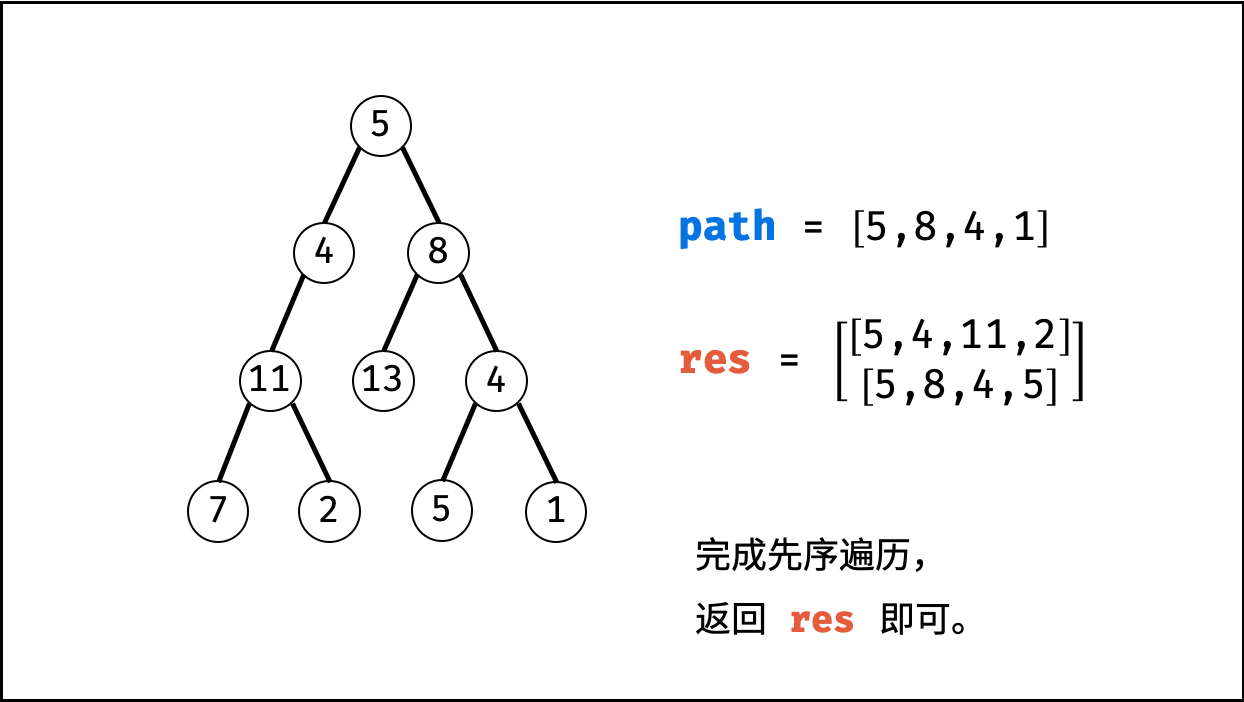Picture13.png](https://pic.leetcode-cn.com/1599400747-ppbdOa-Picture13.png)>
## 代码：
以 Python 语言为例，记录路径时若直接执行 `res.append(path)` ，则是将此 `path` 对象加入了 `res` ；后续 `path` 改变时，`res` 中的 `path` 对象也会随之改变，因此无法实现结果记录。正确做法为：
- Python: `res.append(list(path))` ；
- Java: `res.add(new LinkedList(path))` ；
- C++: `res.push_back(path)` ；
> 三者的原理都是避免直接添加 `path` 对象，而是 **拷贝** 了一个 `path` 对象并加入到 `res` 。
```Python []
class Solution:
def pathTarget(self, root: TreeNode, target: int) -> List[List[int]]:
res, path = [], []
def recur(root, tar):
if not root: return
path.append(root.val)
tar -= root.val
if tar == 0 and not root.left and not root.right:
res.append(list(path))
recur(root.left, tar)
recur(root.right, tar)
path.pop()
recur(root, target)
return res
```
```Java []
class Solution {
LinkedList<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> pathTarget(TreeNode root, int target) {
recur(root, target);
return res;
}
void recur(TreeNode root, int tar) {
if(root == null) return;
path.add(root.val);
tar -= root.val;
if(tar == 0 && root.left == null && root.right == null)
res.add(new LinkedList(path));
recur(root.left, tar);
recur(root.right, tar);
path.removeLast();
}
}
```
```C++ []
class Solution {
public:
vector<vector<int>> pathTarget(TreeNode* root, int target) {
recur(root, target);
return res;
}
private:
vector<vector<int>> res;
vector<int> path;
void recur(TreeNode* root, int tar) {
if(root == nullptr) return;
path.push_back(root->val);
tar -= root->val;
if(tar == 0 && root->left == nullptr && root->right == nullptr)
res.push_back(path);
recur(root->left, tar);
recur(root->right, tar);
path.pop_back();
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数，先序遍历需要遍历所有节点。
- **空间复杂度 $O(N)$ ：** 最差情况下，即树退化为链表时，`path` 存储所有树节点，使用 $O(N)$ 额外空间。

359
leetbook_ioa/docs/LCR 154. 随机链表的复制.md Executable file
View File

@@ -0,0 +1,359 @@
## 解题思路：
普通链表的节点定义如下：
```Python []
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None):
self.val = int(x)
self.next = next
```
```Java []
// Definition for a Node.
class Node {
int val;
Node next;
public Node(int val) {
this.val = val;
this.next = null;
}
}
```
```C++ []
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node(int _val) {
val = _val;
next = NULL;
}
};
```
本题链表的节点定义如下：
```Python []
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
```
```Java []
// Definition for a Node.
class Node {
int val;
Node next, random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
```
```C++ []
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
```
给定链表的头节点 `head` ，复制普通链表很简单，只需遍历链表，每轮建立新节点 + 构建前驱节点 `pre` 和当前节点 `node` 的引用指向即可。
本题链表的节点新增了 `random` 指针，指向链表中的 **任意节点** 或者 $\text{null}$ 。这个 `random` 指针意味着在复制过程中，除了构建前驱节点和当前节点的引用指向 `pre.next` ，还要构建前驱节点和其随机节点的引用指向 `pre.random` 。
**本题难点：** 在复制链表的过程中构建新链表各节点的 `random` 引用指向。
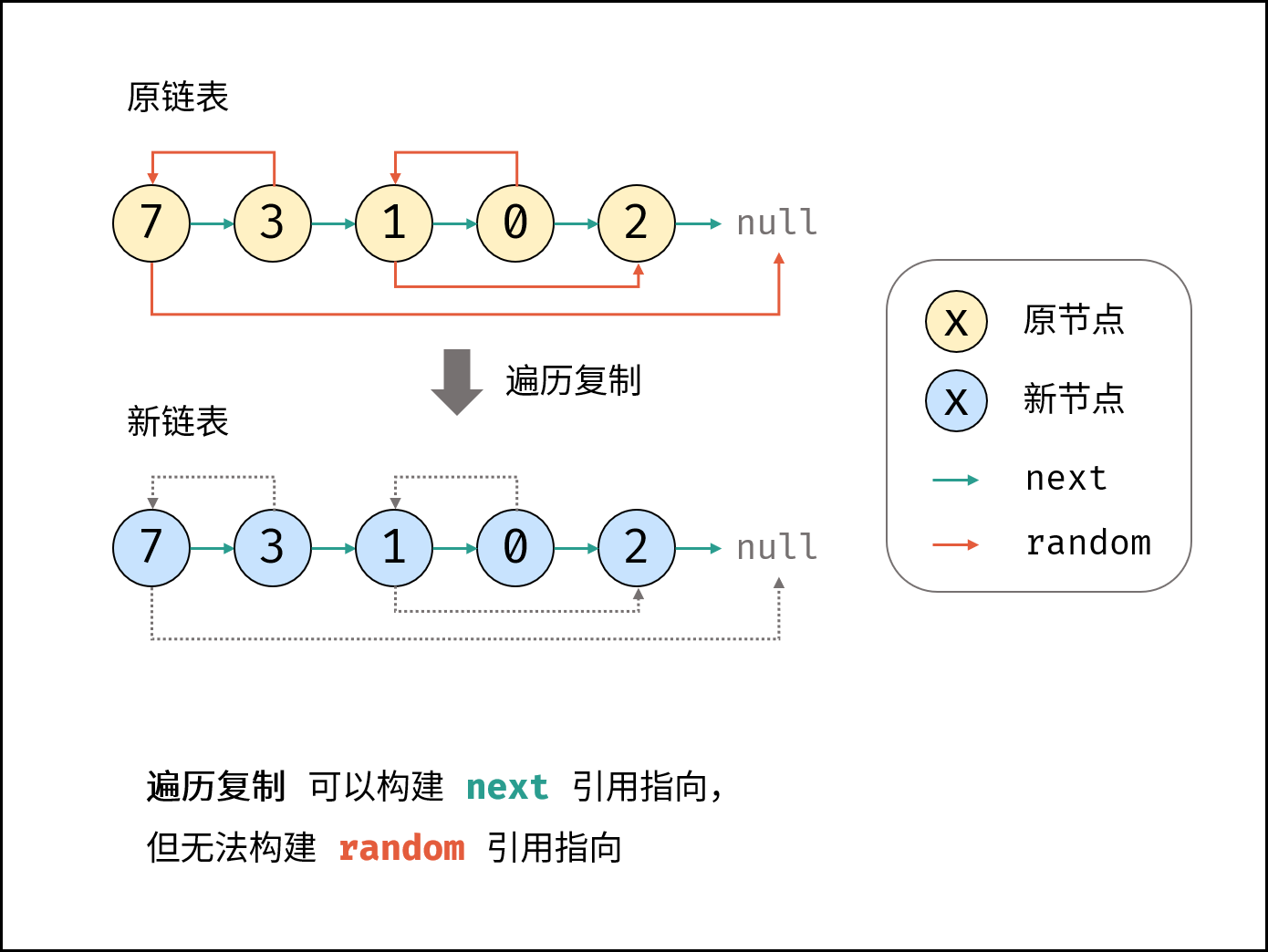![Picture1.png](https://pic.leetcode-cn.com/1604747285-ELUgCd-Picture1.png){:align=center width=450}
```Python []
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
cur = head
dum = pre = Node(0)
while cur:
node = Node(cur.val) # 复制节点 cur
pre.next = node # 新链表的 前驱节点 -> 当前节点
# pre.random = '???' # 新链表的 「 前驱节点 -> 当前节点 」 无法确定
cur = cur.next # 遍历下一节点
pre = node # 保存当前新节点
return dum.next
```
```Java []
class Solution {
public Node copyRandomList(Node head) {
Node cur = head;
Node dum = new Node(0), pre = dum;
while(cur != null) {
Node node = new Node(cur.val); // 复制节点 cur
pre.next = node; // 新链表的 前驱节点 -> 当前节点
// pre.random = "???"; // 新链表的 「 前驱节点 -> 当前节点 」 无法确定
cur = cur.next; // 遍历下一节点
pre = node; // 保存当前新节点
}
return dum.next;
}
}
```
```C++ []
class Solution {
public:
Node* copyRandomList(Node* head) {
Node* cur = head;
Node* dum = new Node(0), *pre = dum;
while(cur != nullptr) {
Node* node = new Node(cur->val); // 复制节点 cur
pre->next = node; // 新链表的 前驱节点 -> 当前节点
// pre->random = "???"; // 新链表的 「 前驱节点 -> 当前节点 」 无法确定
cur = cur->next; // 遍历下一节点
pre = node; // 保存当前新节点
}
return dum->next;
}
};
```
> 本文介绍「哈希表」和「拼接 + 拆分」两种方法。哈希表方法比较直观；拼接 + 拆分方法的空间复杂度更低。
## 方法一：哈希表
利用哈希表的查询特点，考虑构建 **原链表节点** 和 **新链表对应节点** 的键值对映射关系，再遍历构建新链表各节点的 `next` 和 `random` 引用指向即可。
### 算法流程：
1. 若头节点 `head` 为空节点，直接返回 $\text{null}$ ；
2. **初始化：** 哈希表 `hmap` ， 节点 `cur` 指向头节点；
3. **复制链表：**
1. 建立新节点，并向 `hmap` 添加键值对 `(原 cur 节点, 新 cur 节点）` ；
2. `cur` 遍历至原链表下一节点；
4. **构建新链表的引用指向：**
1. 构建新节点的 `next` 和 `random` 引用指向；
2. `cur` 遍历至原链表下一节点；
5. **返回值：** 新链表的头节点 `hmap[cur]` ；
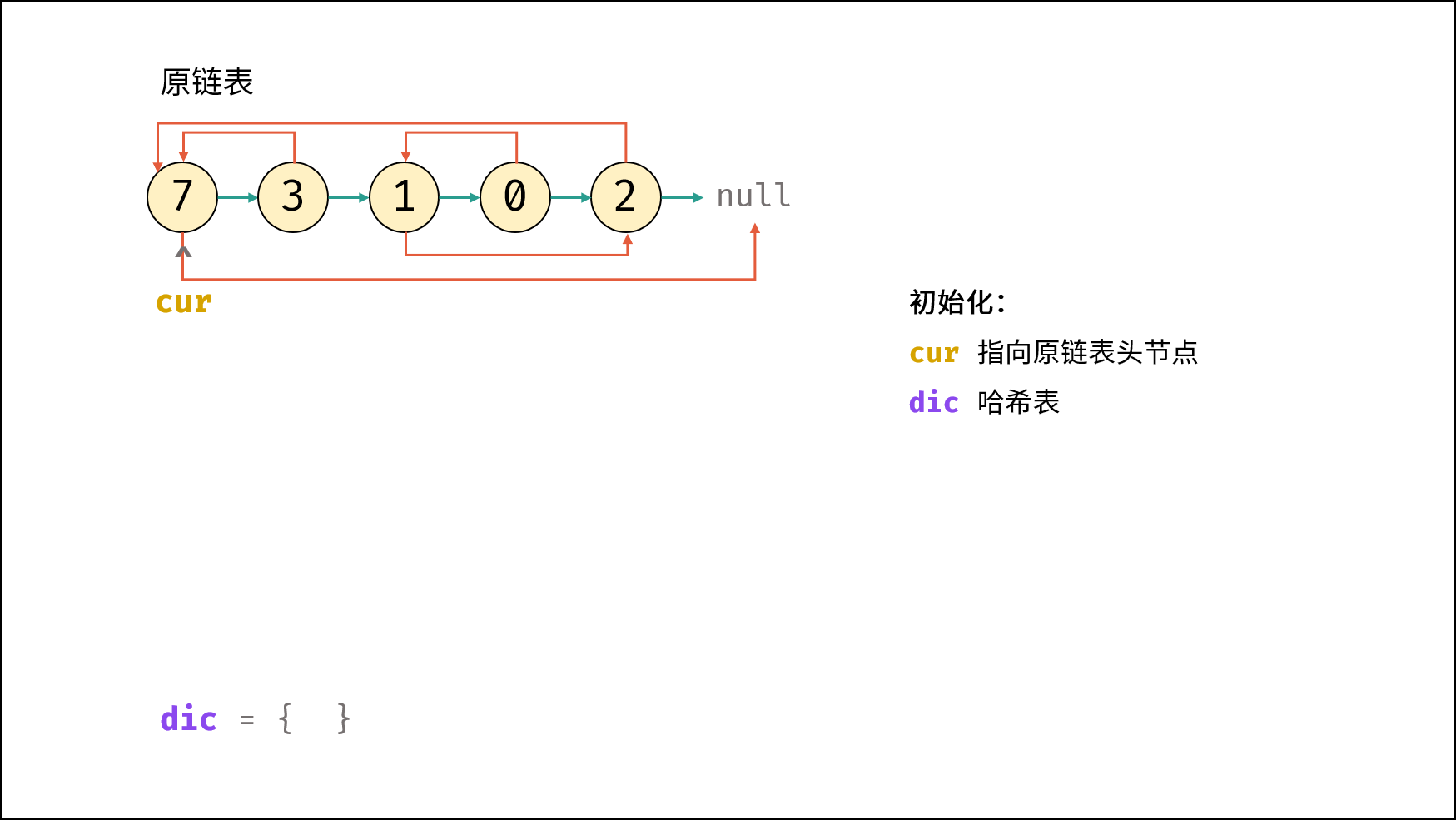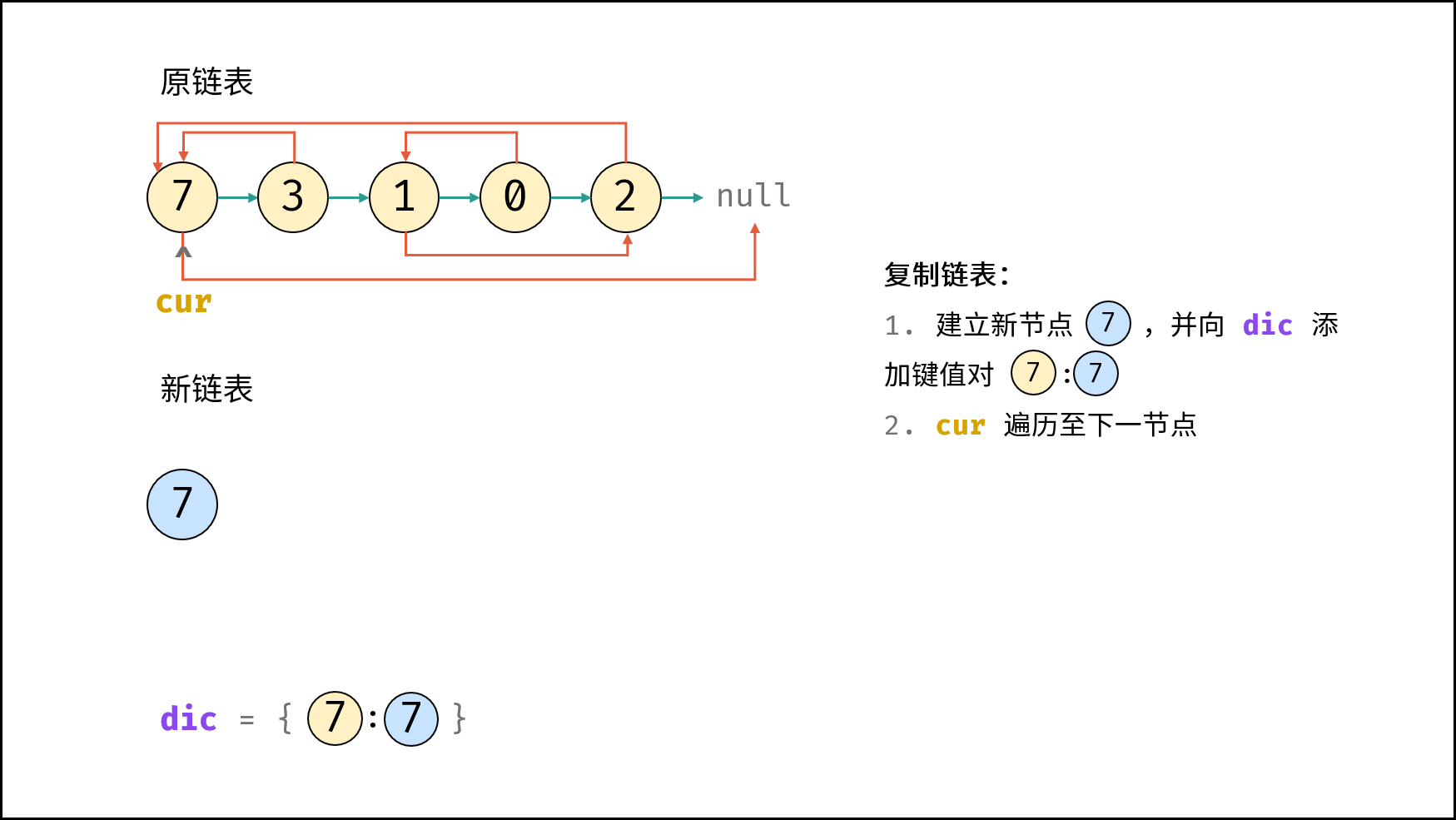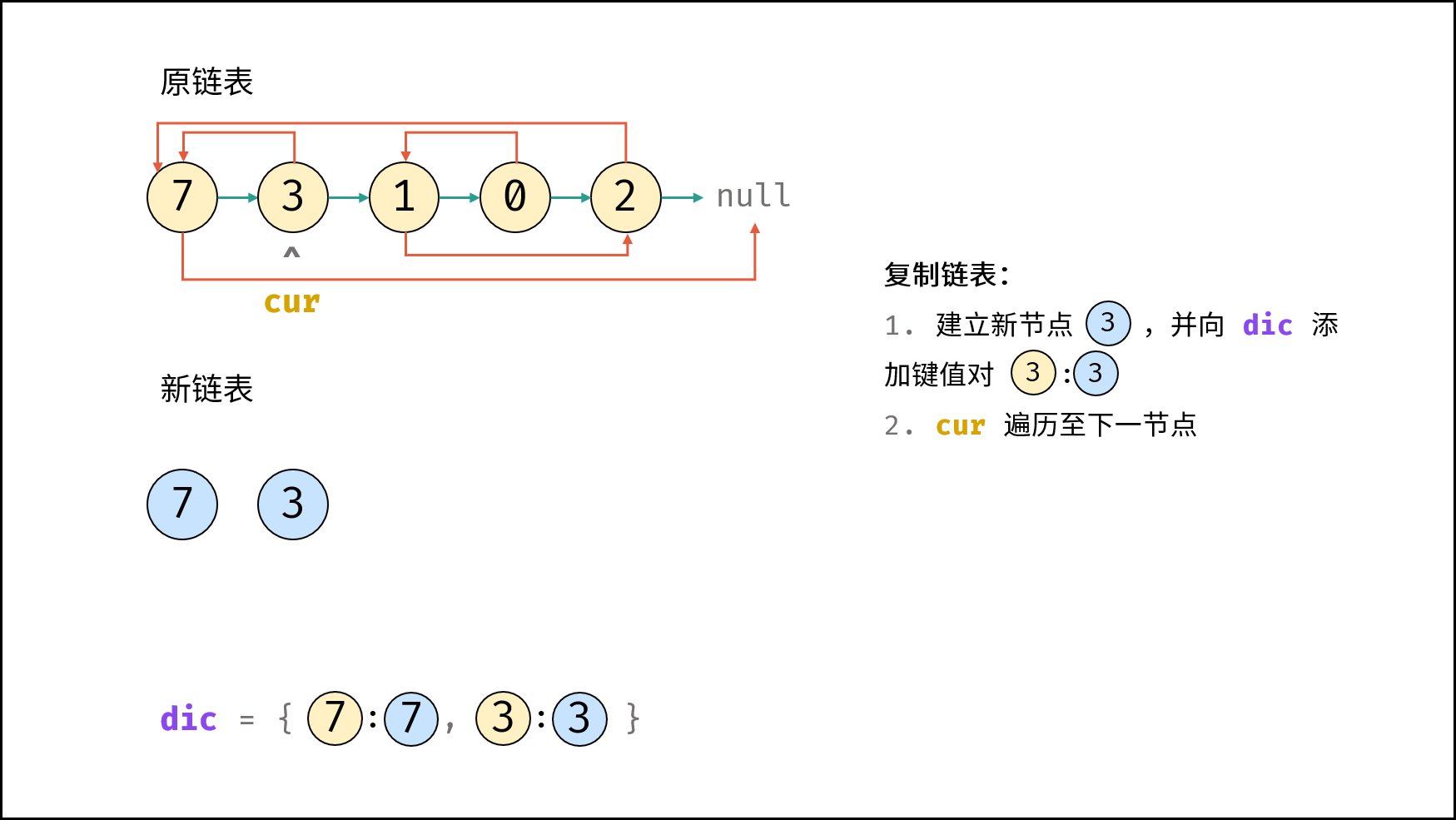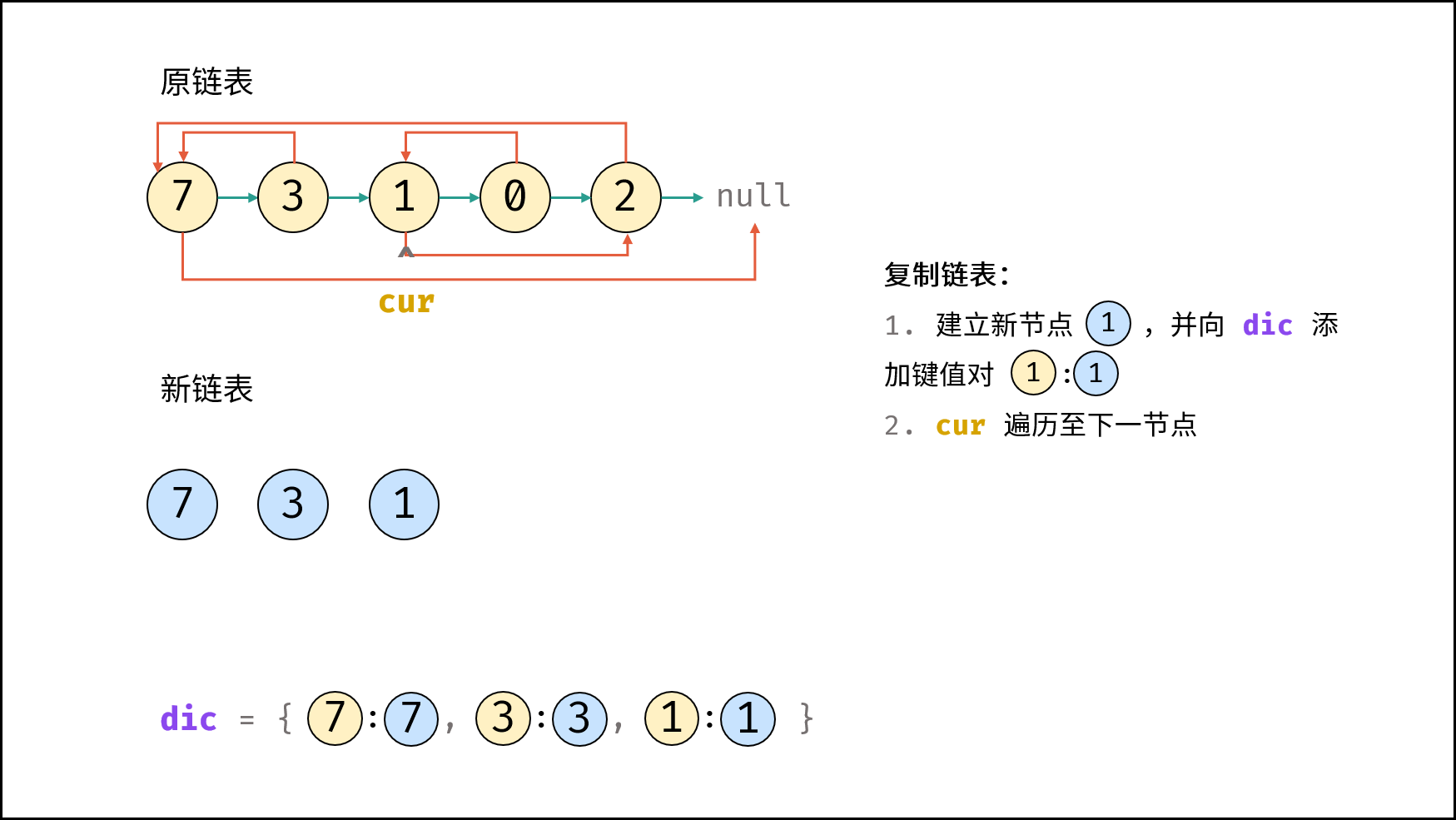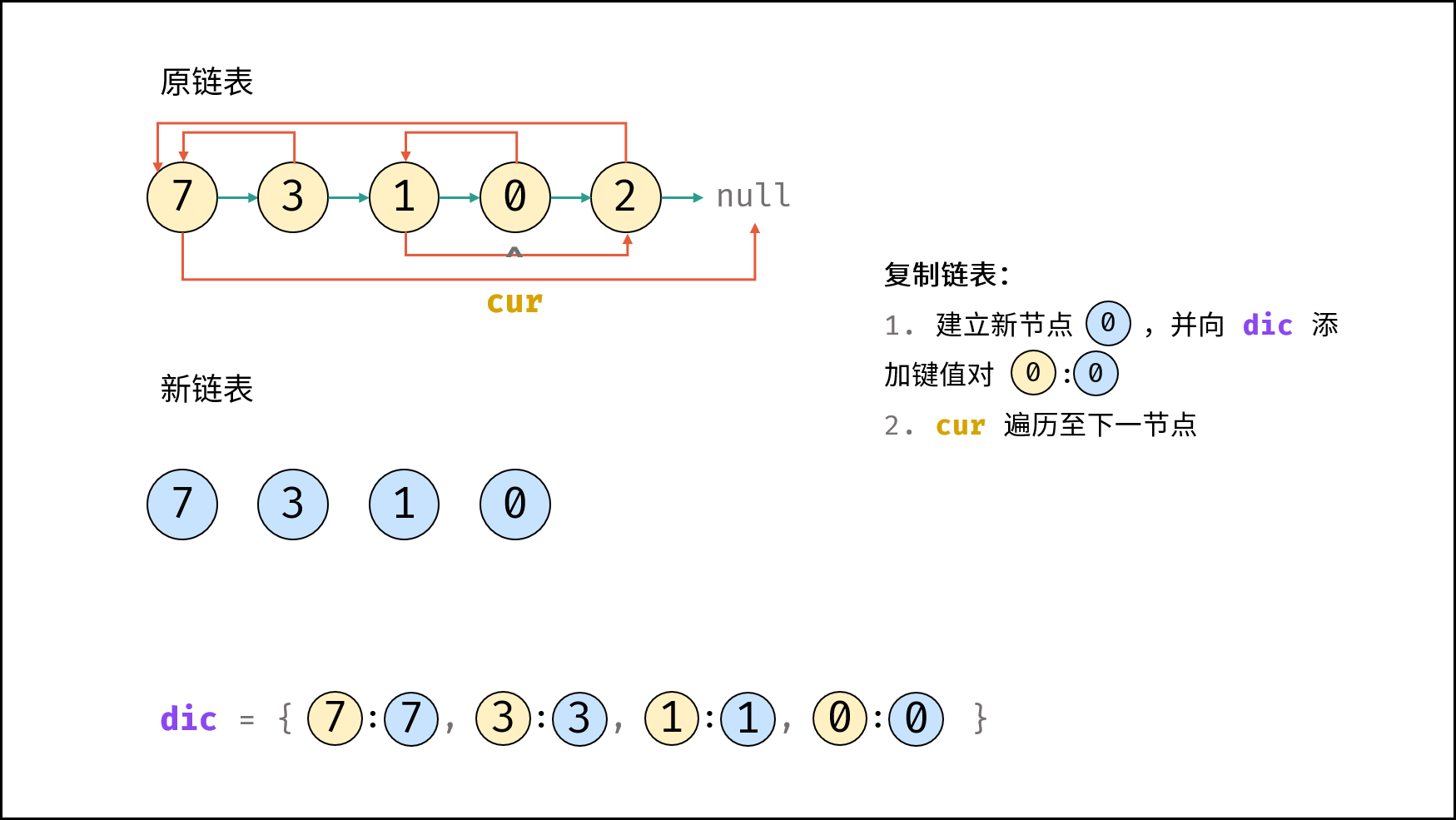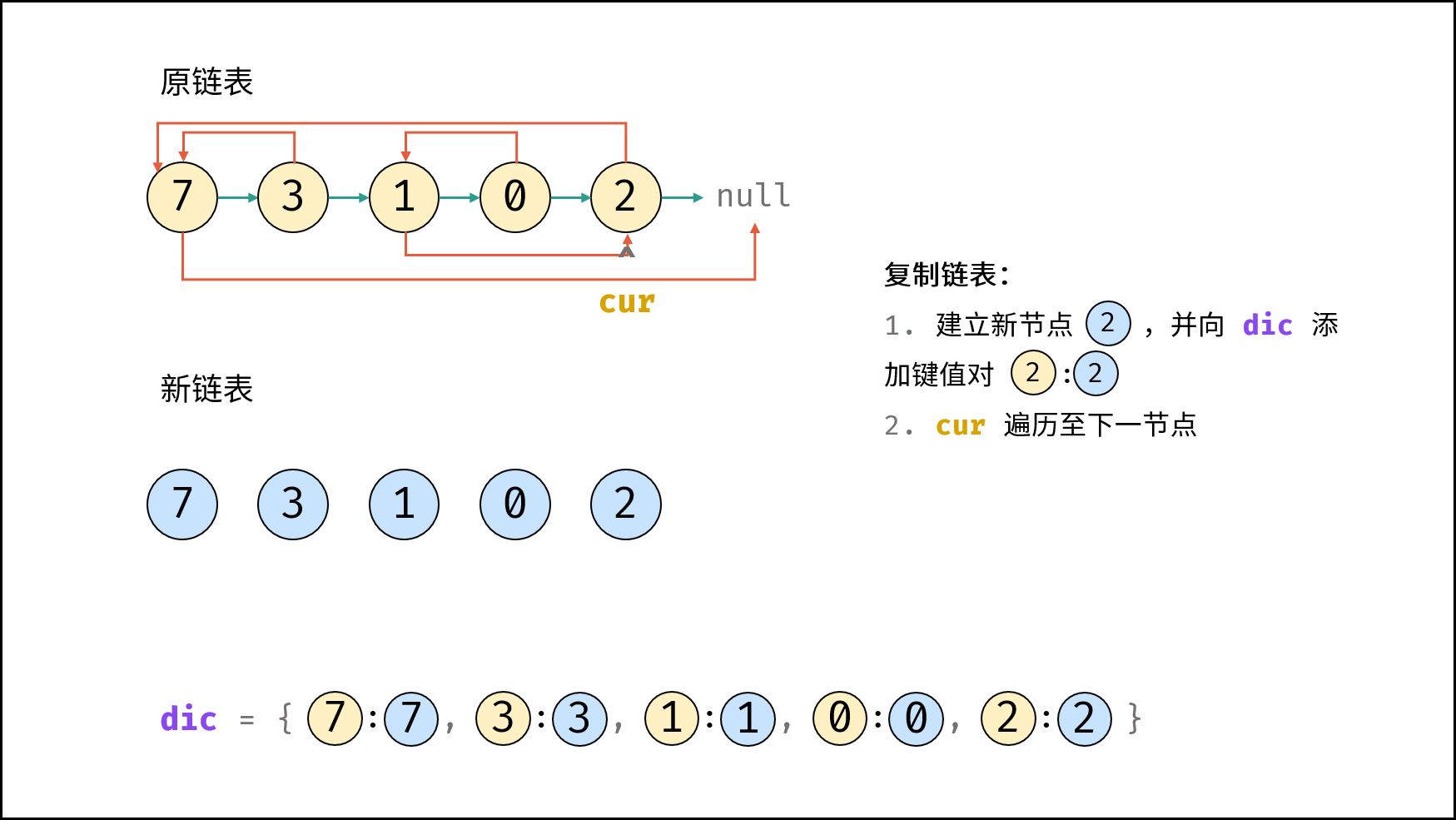<![Picture2.png](https://pic.leetcode-cn.com/1604747285-ZidetZ-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1604747285-JWRWlw-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1604747285-NlKOBP-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1604747285-bohuRC-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1604747285-YjPYai-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1604747285-gKnCSl-Picture7.png),![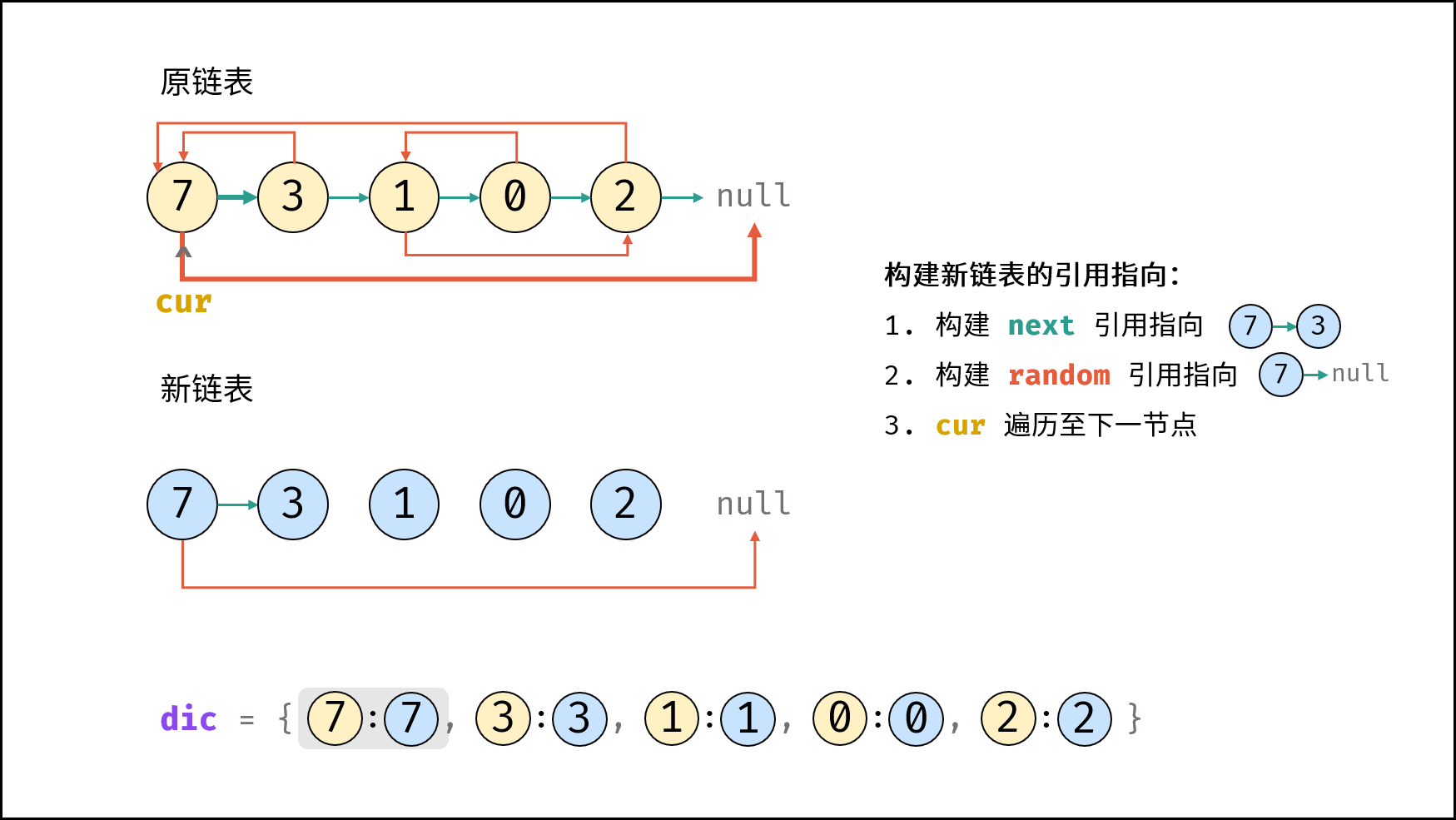Picture8.png](https://pic.leetcode-cn.com/1604747285-lmVIhC-Picture8.png),![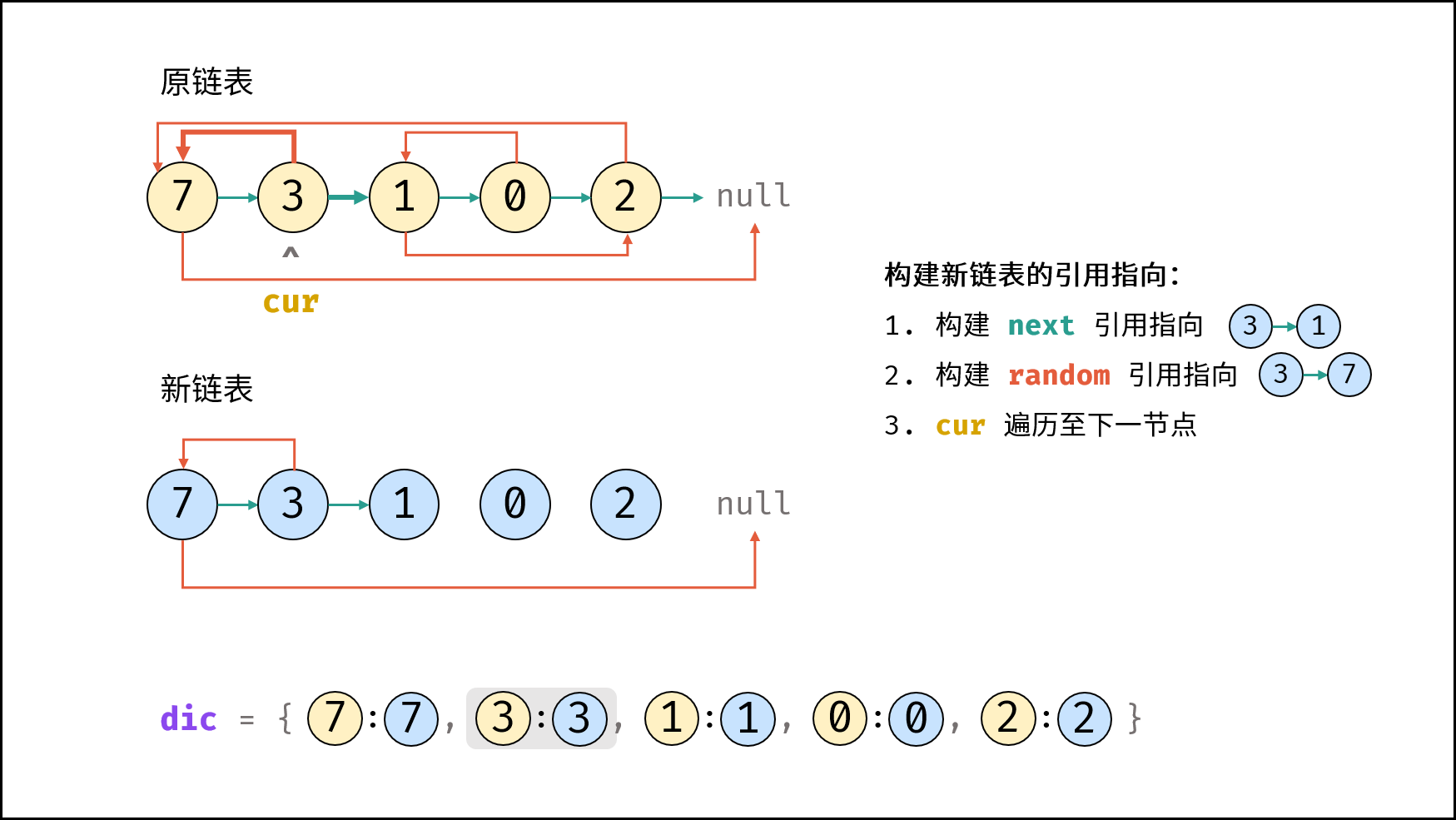Picture9.png](https://pic.leetcode-cn.com/1604747285-mitGOO-Picture9.png),![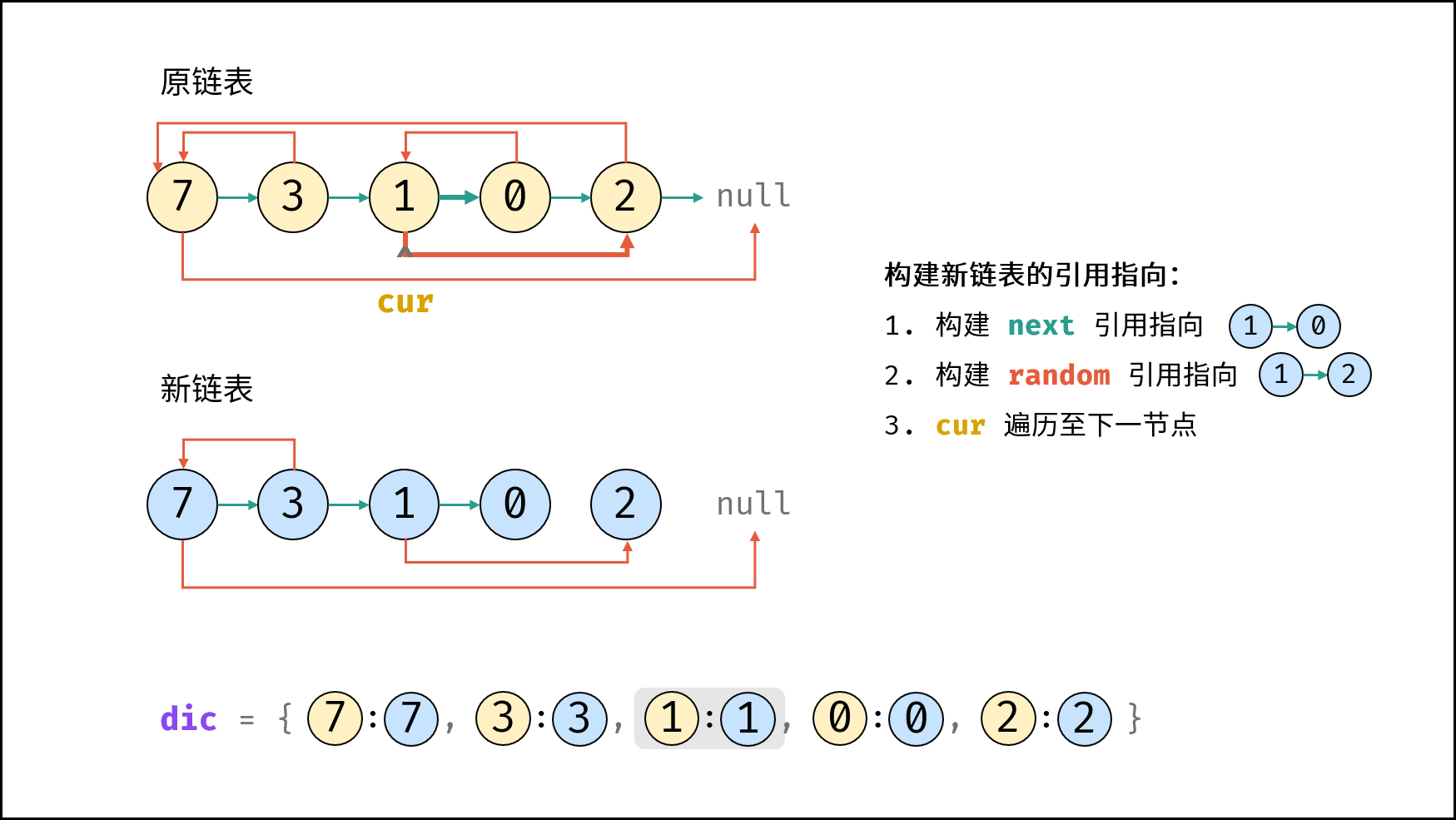Picture10.png](https://pic.leetcode-cn.com/1604747285-fecewt-Picture10.png),![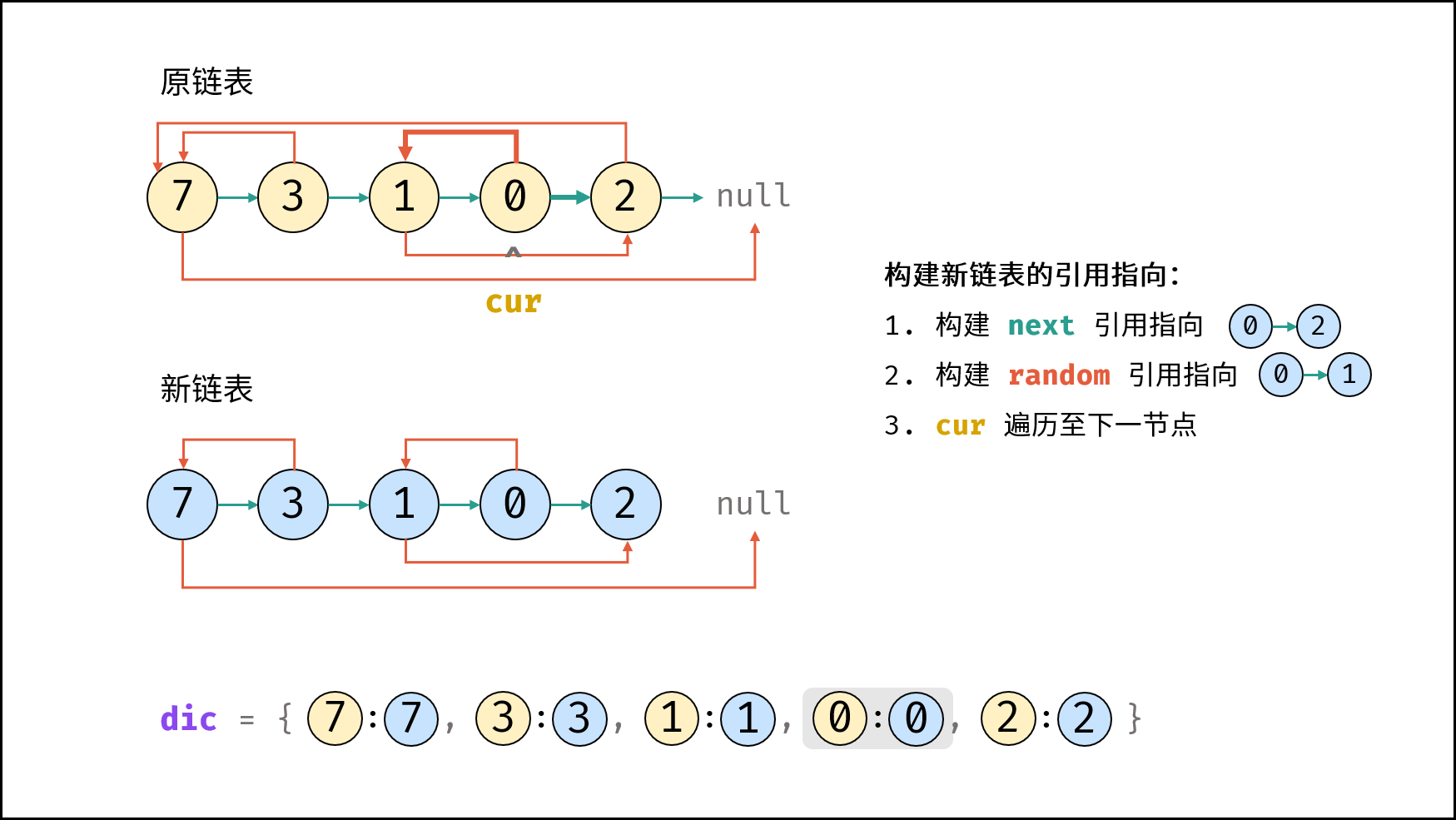Picture11.png](https://pic.leetcode-cn.com/1604747285-RuvuGW-Picture11.png),![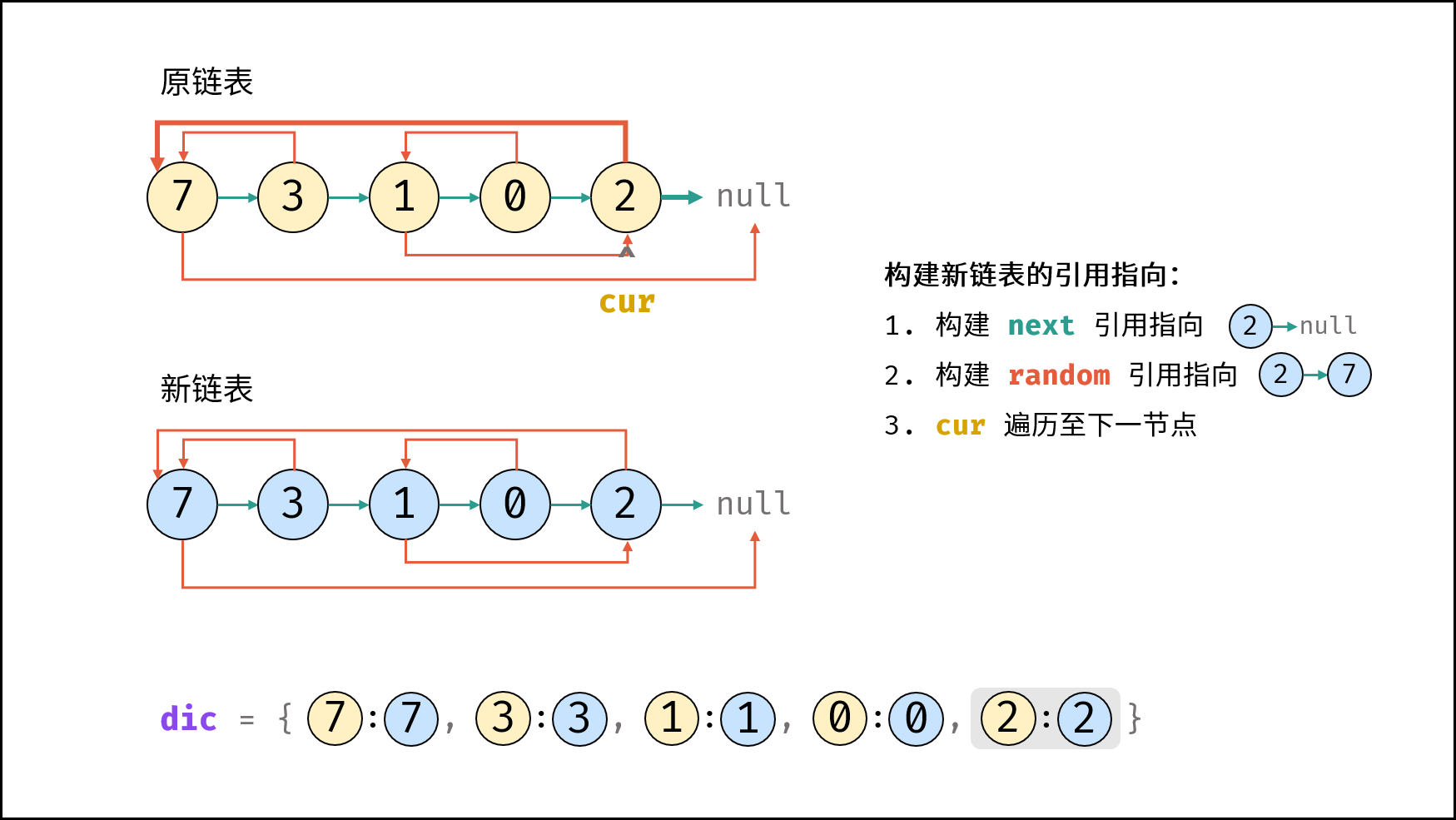Picture12.png](https://pic.leetcode-cn.com/1604747285-vDhdiA-Picture12.png),![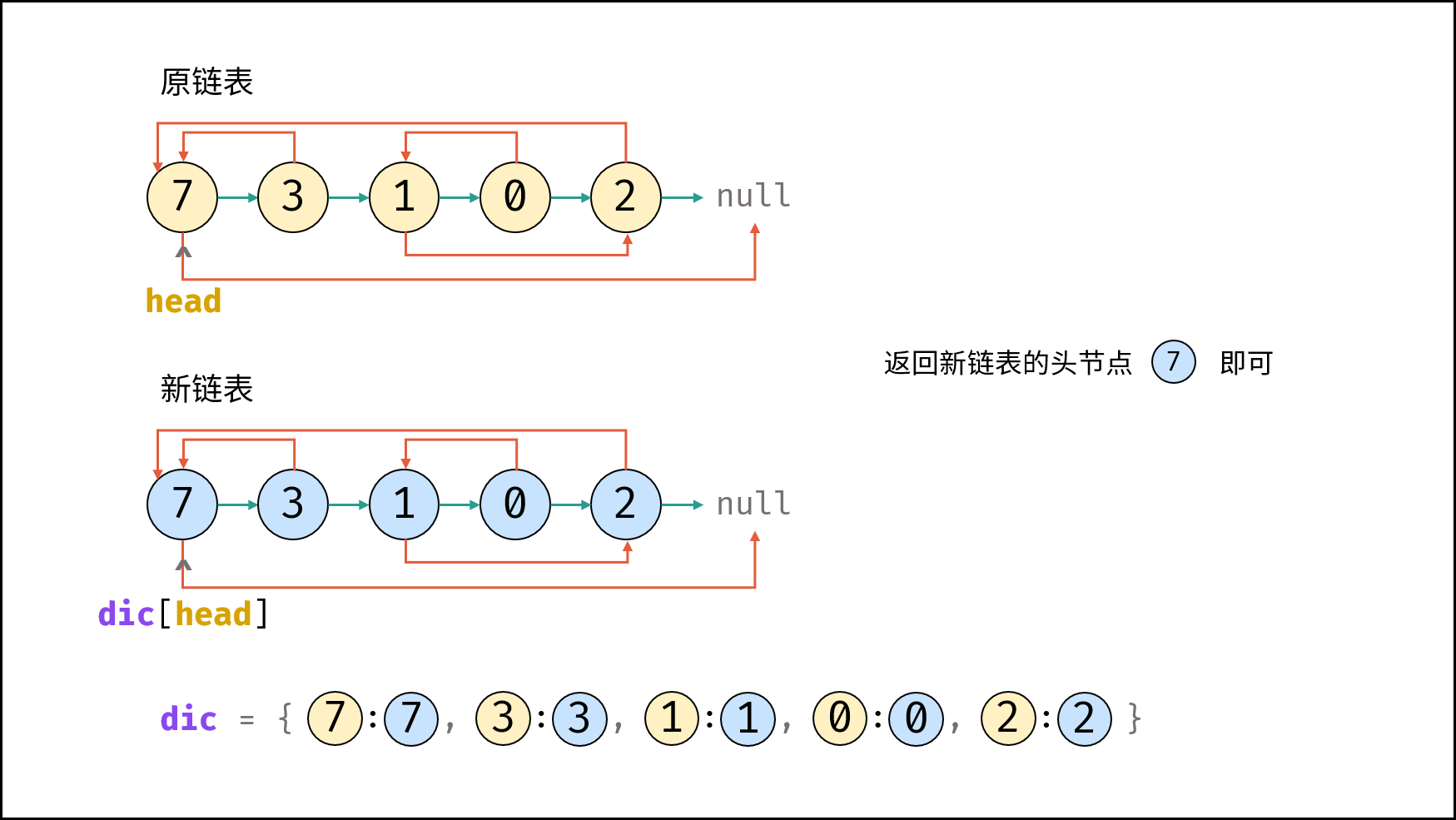Picture13.png](https://pic.leetcode-cn.com/1604747285-bhLYzn-Picture13.png)>
### 代码：
```Python []
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
if not head: return
hmap = {}
# 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
cur = head
while cur:
hmap[cur] = Node(cur.val)
cur = cur.next
cur = head
# 4. 构建新节点的 next 和 random 指向
while cur:
hmap[cur].next = hmap.get(cur.next)
hmap[cur].random = hmap.get(cur.random)
cur = cur.next
# 5. 返回新链表的头节点
return hmap[head]
```
```Java []
class Solution {
public Node copyRandomList(Node head) {
if(head == null) return null;
Node cur = head;
Map<Node, Node> map = new HashMap<>();
// 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
while(cur != null) {
map.put(cur, new Node(cur.val));
cur = cur.next;
}
cur = head;
// 4. 构建新链表的 next 和 random 指向
while(cur != null) {
map.get(cur).next = map.get(cur.next);
map.get(cur).random = map.get(cur.random);
cur = cur.next;
}
// 5. 返回新链表的头节点
return map.get(head);
}
}
```
```C++ []
class Solution {
public:
Node* copyRandomList(Node* head) {
if(head == nullptr) return nullptr;
Node* cur = head;
unordered_map<Node*, Node*> map;
// 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
while(cur != nullptr) {
map[cur] = new Node(cur->val);
cur = cur->next;
}
cur = head;
// 4. 构建新链表的 next 和 random 指向
while(cur != nullptr) {
map[cur]->next = map[cur->next];
map[cur]->random = map[cur->random];
cur = cur->next;
}
// 5. 返回新链表的头节点
return map[head];
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 两轮遍历链表，使用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** 哈希表 `hmap` 使用线性大小的额外空间。
## 方法二：拼接 + 拆分
考虑构建 `原节点 1 -> 新节点 1 -> 原节点 2 -> 新节点 2 -> ……` 的拼接链表，如此便可在访问原节点的 `random` 指向节点的同时找到新对应新节点的 `random` 指向节点。
### 算法流程：
1. **复制各节点，构建拼接链表:**
- 设原链表为 $node1 \rightarrow node2 \rightarrow \cdots$ ，构建的拼接链表如下所示：
$$
node1 \rightarrow node1_{new} \rightarrow node2 \rightarrow node2_{new} \rightarrow \cdots
$$
2. **构建新链表各节点的 `random` 指向：**
- 当访问原节点 `cur` 的随机指向节点 `cur.random` 时，对应新节点 `cur.next` 的随机指向节点为 `cur.random.next` 。
3. **拆分原 / 新链表：**
- 设置 `pre` / `cur` 分别指向原 / 新链表头节点，遍历执行 `pre.next = pre.next.next` 和 `cur.next = cur.next.next` 将两链表拆分开。
4. 返回新链表的头节点 `res` 即可。
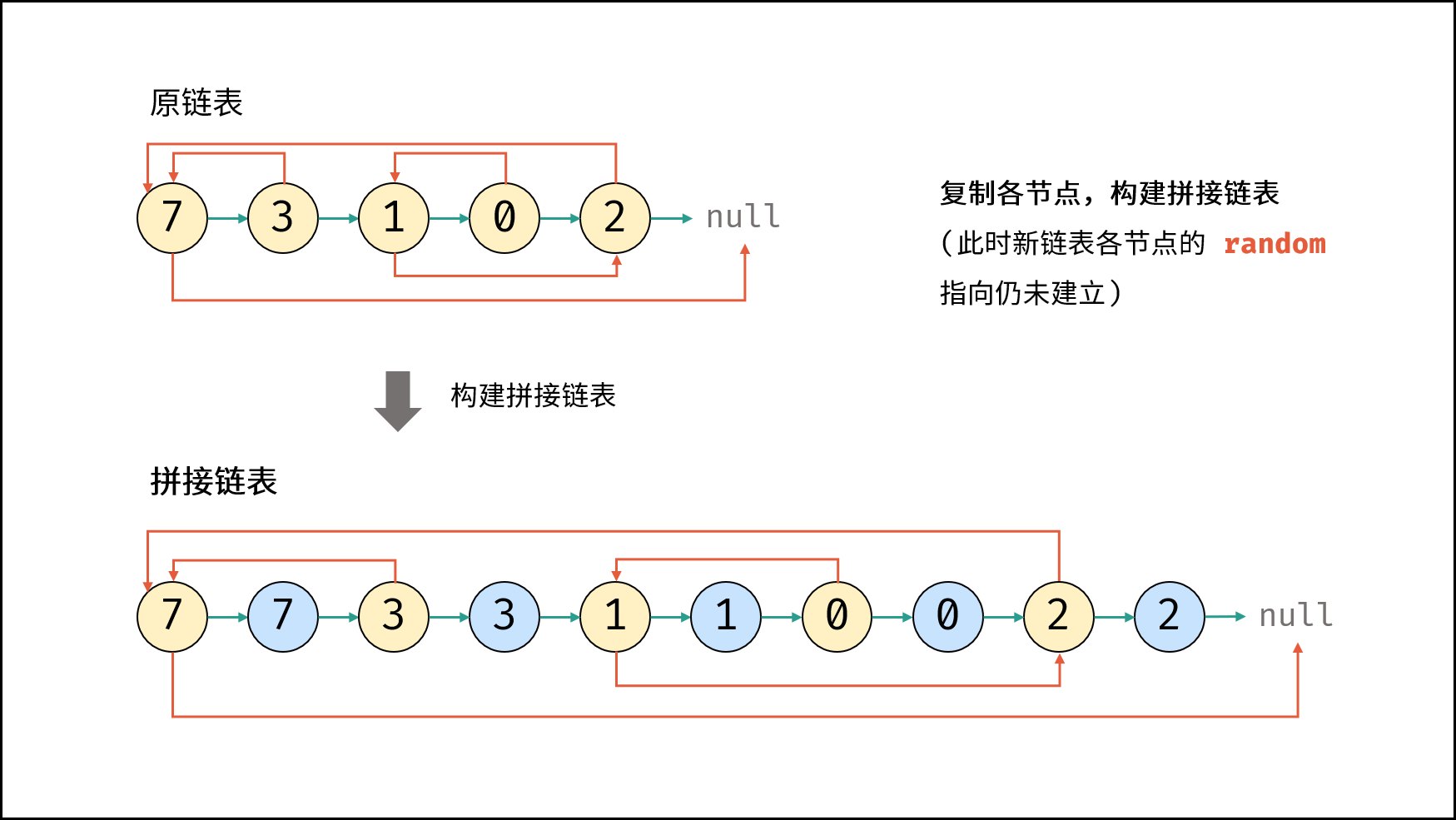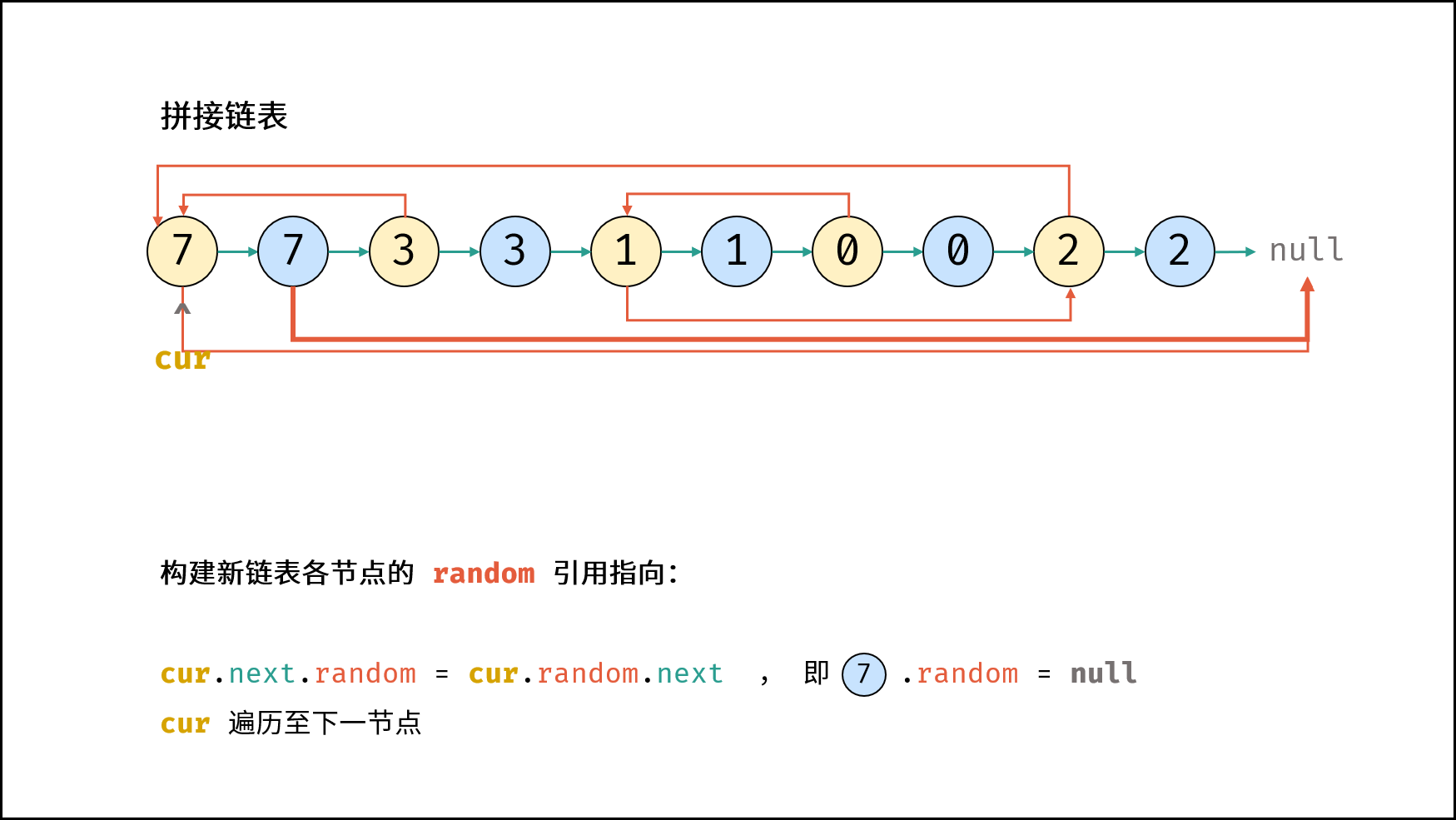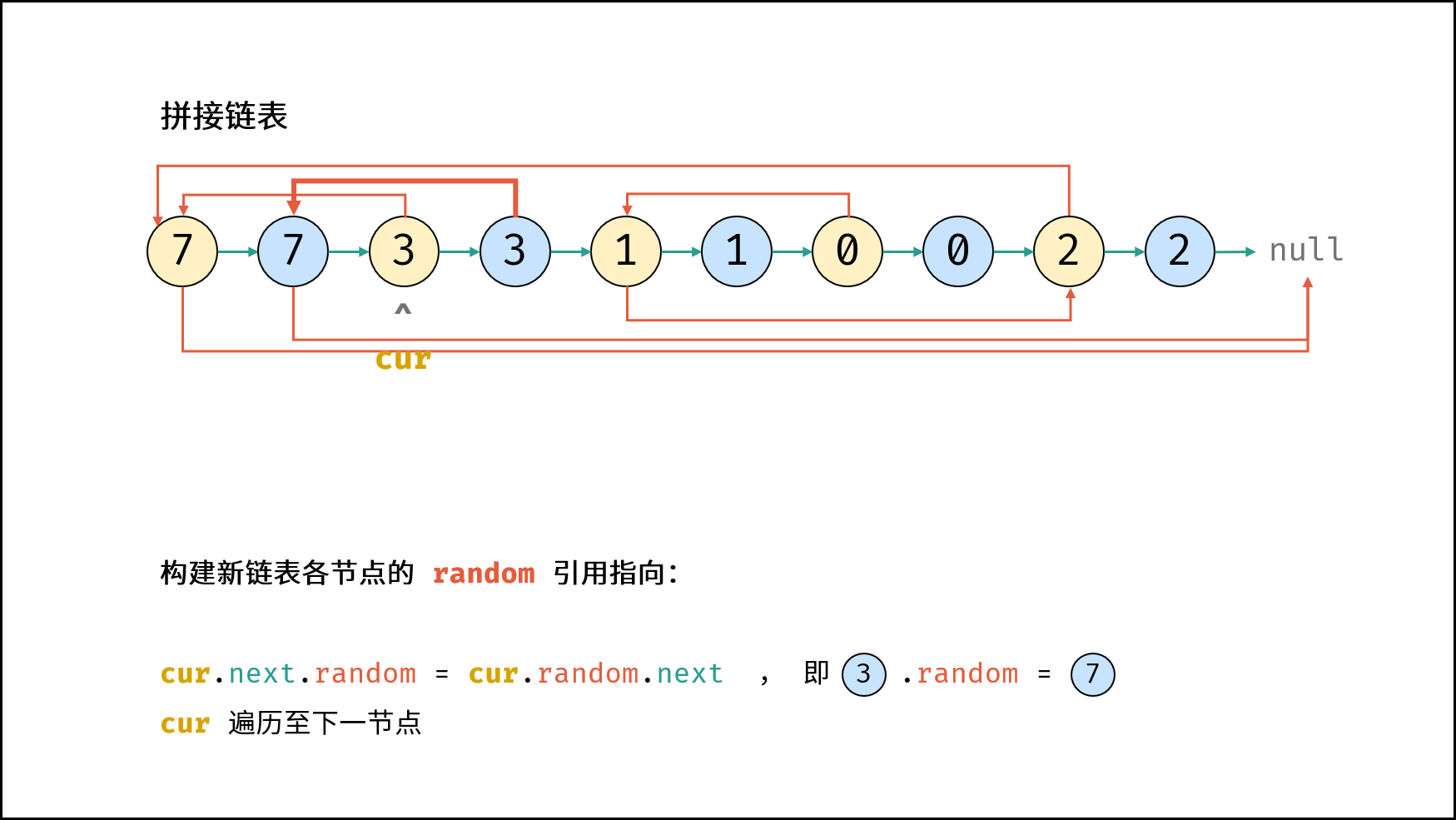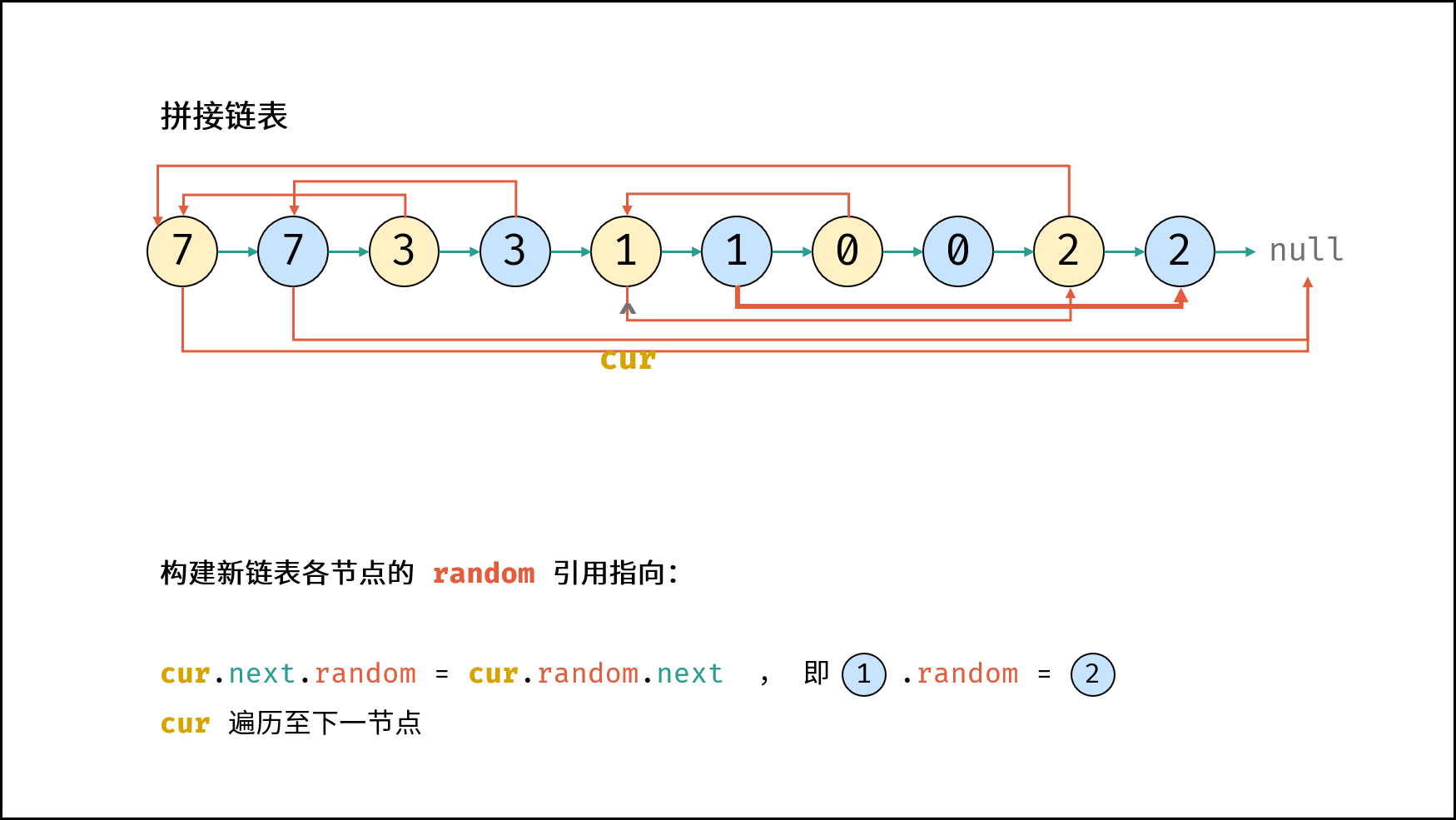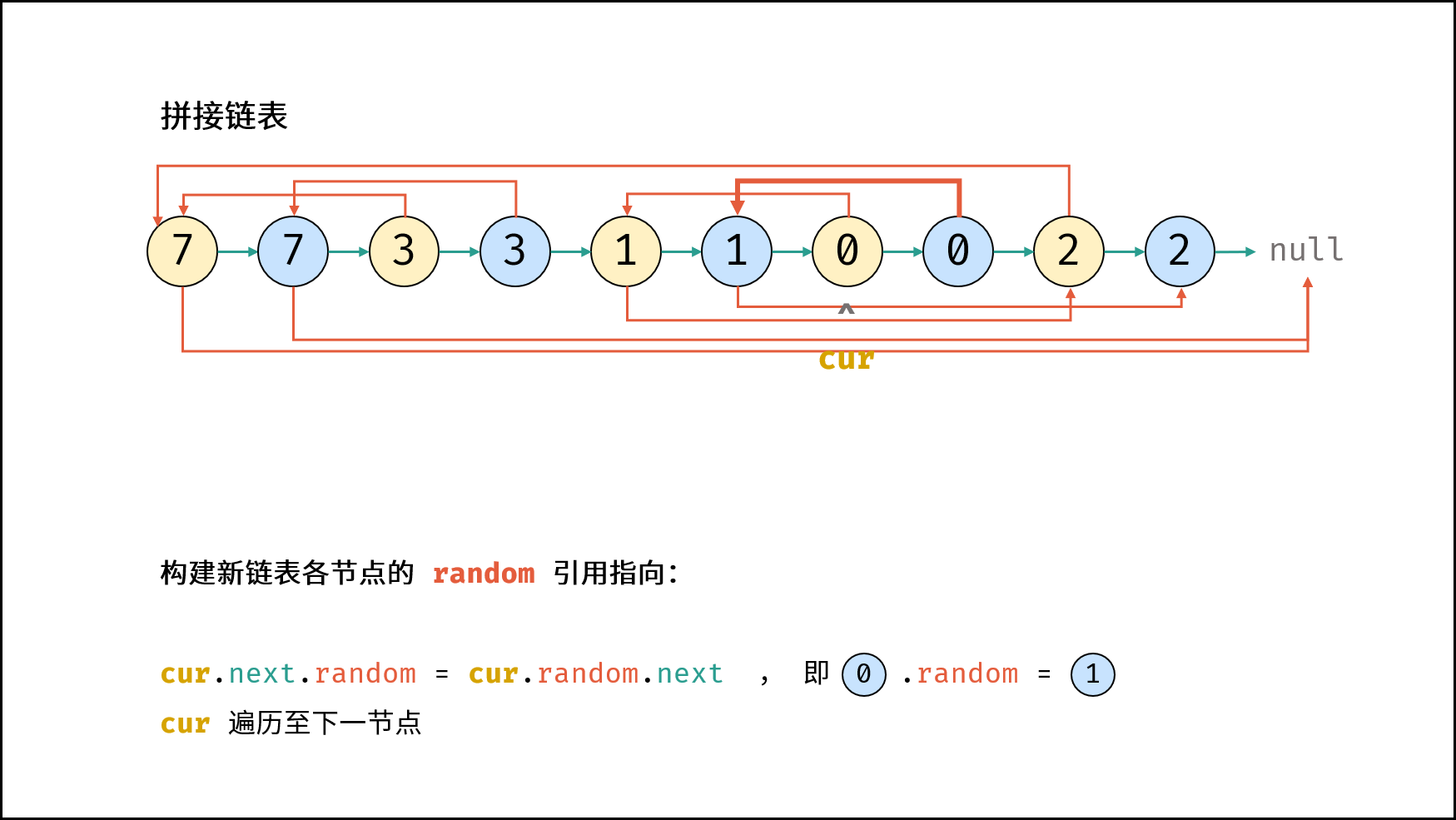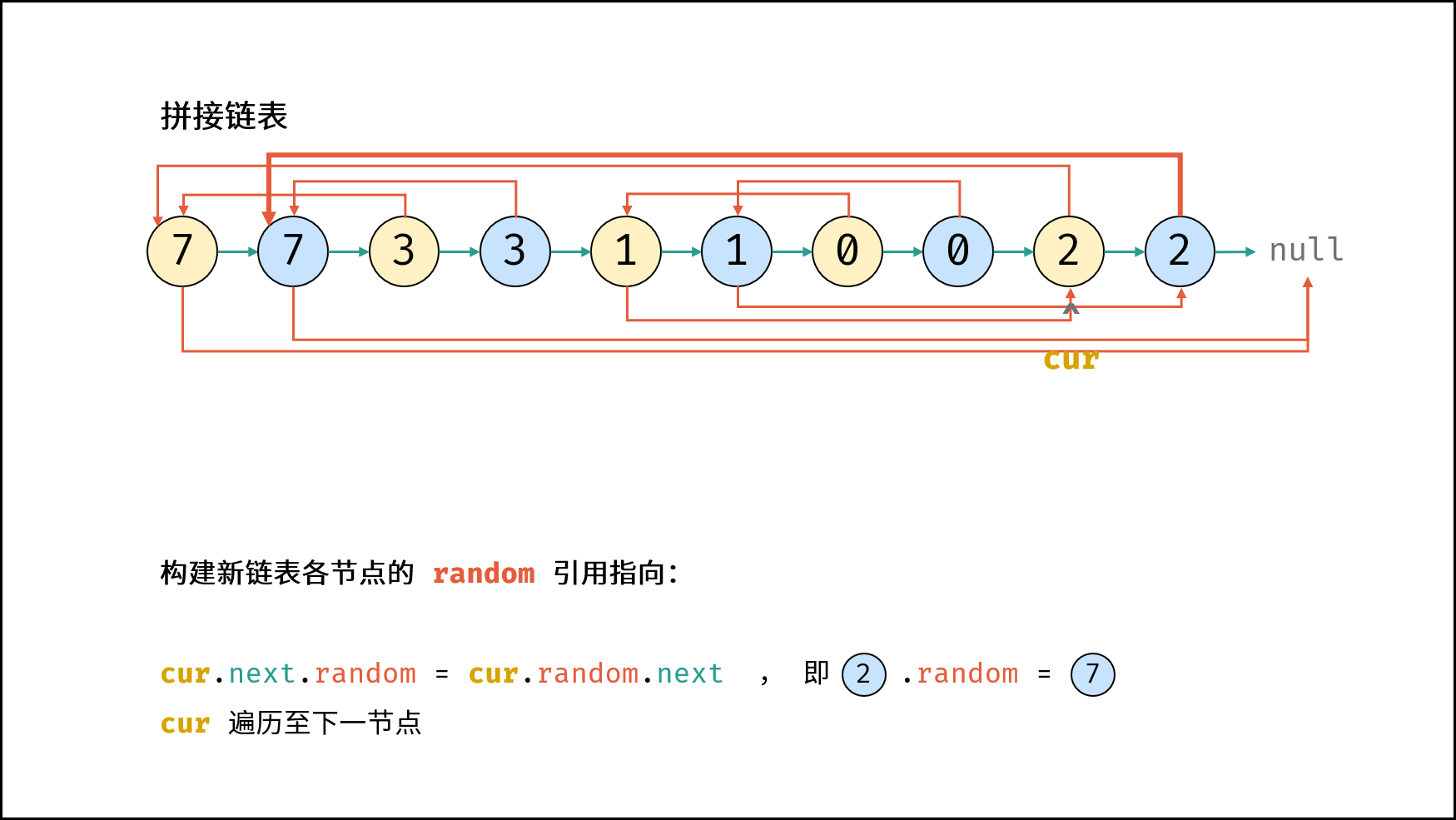<![Picture14.png](https://pic.leetcode-cn.com/1604747742-aMDdkM-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1604747285-ADzCgN-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1604747285-LidbfG-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1604747285-mxOiHF-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1604747285-PYYwDy-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1604747285-TJdMjI-Picture19.png),![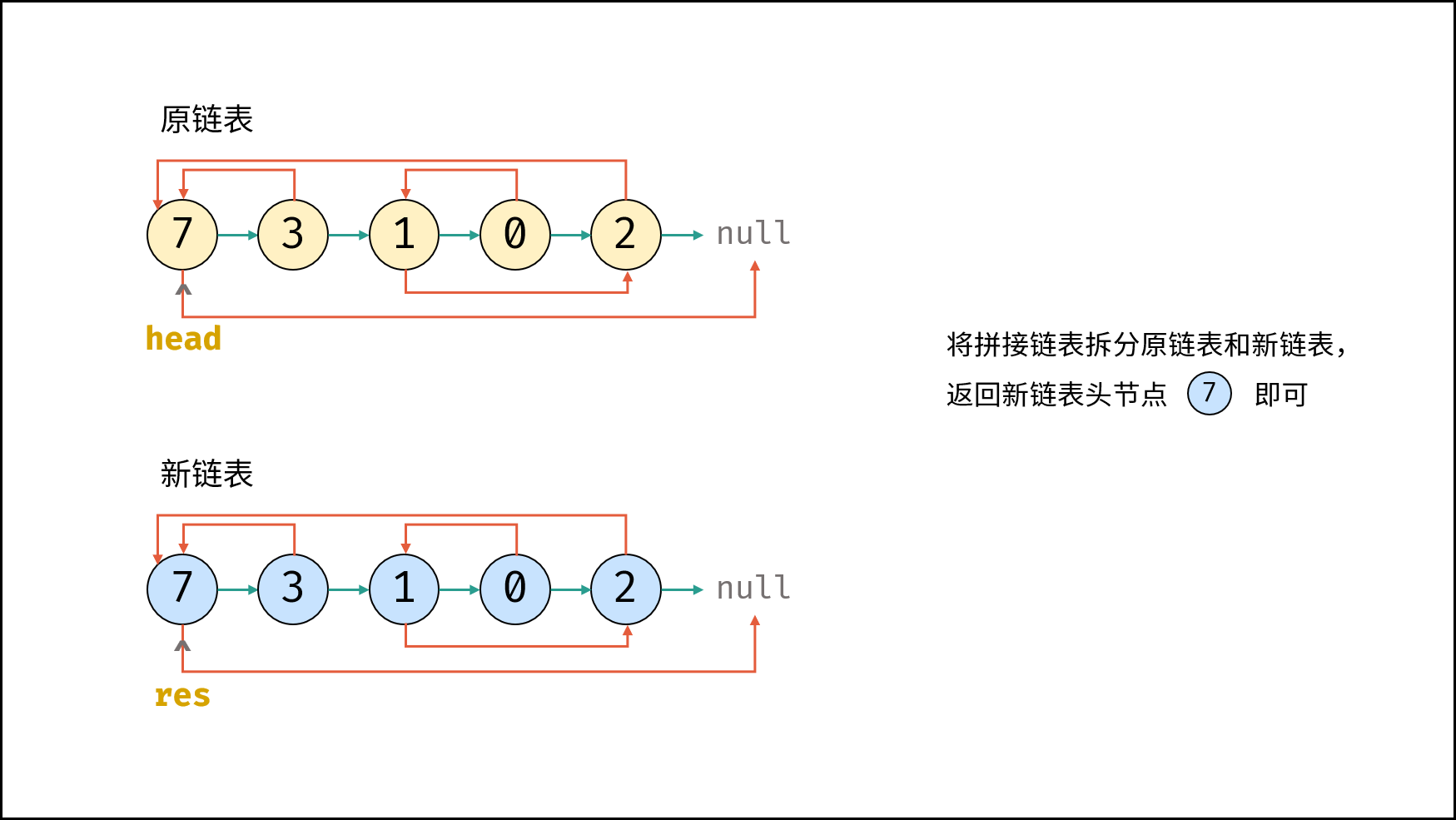Picture20.png](https://pic.leetcode-cn.com/1604747285-EMCcno-Picture20.png)>
## 代码：
```Python []
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
if not head: return
cur = head
# 1. 复制各节点，并构建拼接链表
while cur:
tmp = Node(cur.val)
tmp.next = cur.next
cur.next = tmp
cur = tmp.next
# 2. 构建各新节点的 random 指向
cur = head
while cur:
if cur.random:
cur.next.random = cur.random.next
cur = cur.next.next
# 3. 拆分两链表
cur = res = head.next
pre = head
while cur.next:
pre.next = pre.next.next
cur.next = cur.next.next
pre = pre.next
cur = cur.next
pre.next = None # 单独处理原链表尾节点
return res # 返回新链表头节点
```
```Java []
class Solution {
public Node copyRandomList(Node head) {
if(head == null) return null;
Node cur = head;
// 1. 复制各节点，并构建拼接链表
while(cur != null) {
Node tmp = new Node(cur.val);
tmp.next = cur.next;
cur.next = tmp;
cur = tmp.next;
}
// 2. 构建各新节点的 random 指向
cur = head;
while(cur != null) {
if(cur.random != null)
cur.next.random = cur.random.next;
cur = cur.next.next;
}
// 3. 拆分两链表
cur = head.next;
Node pre = head, res = head.next;
while(cur.next != null) {
pre.next = pre.next.next;
cur.next = cur.next.next;
pre = pre.next;
cur = cur.next;
}
pre.next = null; // 单独处理原链表尾节点
return res; // 返回新链表头节点
}
}
```
```C++ []
class Solution {
public:
Node* copyRandomList(Node* head) {
if(head == nullptr) return nullptr;
Node* cur = head;
// 1. 复制各节点，并构建拼接链表
while(cur != nullptr) {
Node* tmp = new Node(cur->val);
tmp->next = cur->next;
cur->next = tmp;
cur = tmp->next;
}
// 2. 构建各新节点的 random 指向
cur = head;
while(cur != nullptr) {
if(cur->random != nullptr)
cur->next->random = cur->random->next;
cur = cur->next->next;
}
// 3. 拆分两链表
cur = head->next;
Node* pre = head, *res = head->next;
while(cur->next != nullptr) {
pre->next = pre->next->next;
cur->next = cur->next->next;
pre = pre->next;
cur = cur->next;
}
pre->next = nullptr; // 单独处理原链表尾节点
return res; // 返回新链表头节点
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 三轮遍历链表，使用 $O(N)$ 时间。
- **空间复杂度 $O(1)$ ：** 节点引用变量使用常数大小的额外空间。

138
leetbook_ioa/docs/LCR 155. 将二叉搜索树转化为排序的双向链表.md Executable file
View File

@@ -0,0 +1,138 @@
## 解题思路：
本文解法基于性质：二叉搜索树的中序遍历为 **递增序列** 。
将 二叉搜索树 转换成一个 “排序的循环双向链表” ，其中包含三个要素：
1. **排序链表：** 节点应从小到大排序，因此应使用 **中序遍历** “从小到大”访问树的节点。
2. **双向链表：** 在构建相邻节点的引用关系时，设前驱节点 `pre` 和当前节点 `cur` ，不仅应构建 `pre.right = cur` ，也应构建 `cur.left = pre` 。
3. **循环链表：** 设链表头节点 `head` 和尾节点 `tail` ，则应构建 `head.left = tail` 和 `tail.right = head` 。
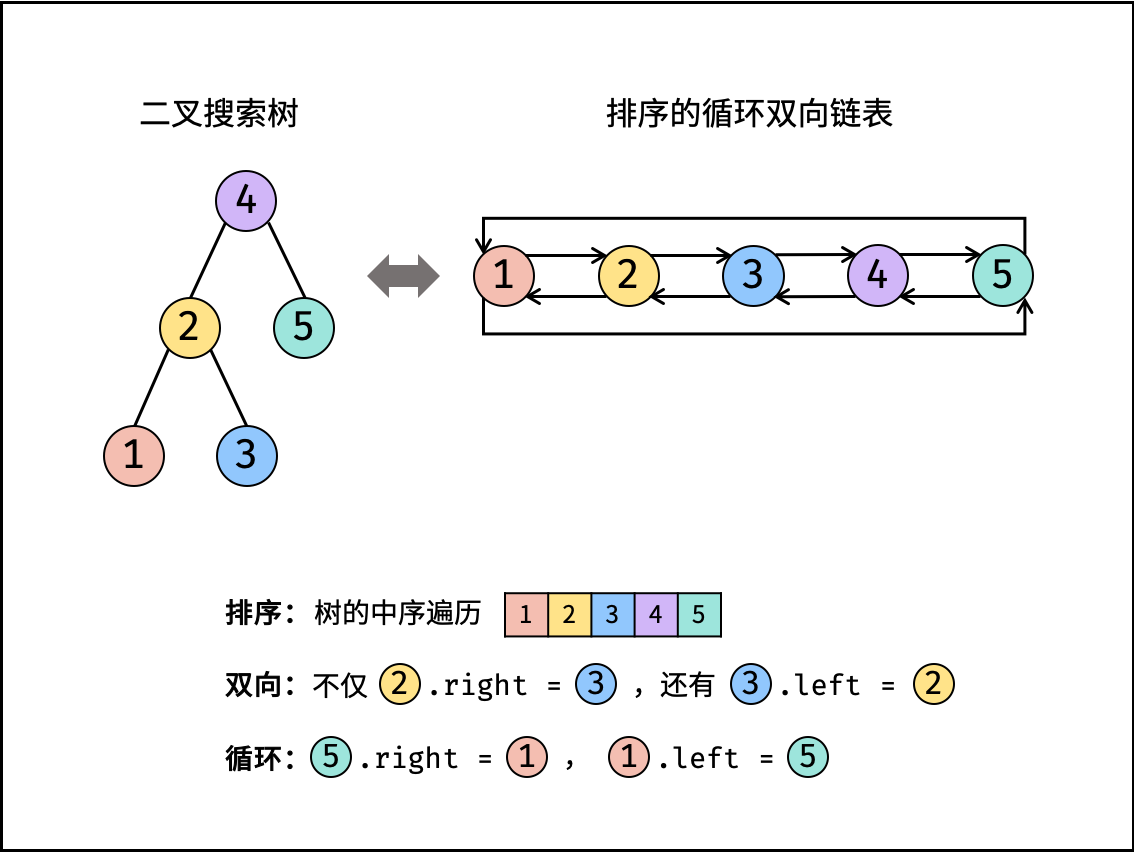![Picture1.png](https://pic.leetcode-cn.com/1599401091-PKIjds-Picture1.png){:align=center width=500}
**中序遍历** 为对二叉树作 “左、根、右” 顺序遍历，递归实现如下：
```Python []
# 打印中序遍历
def dfs(root):
if not root: return
dfs(root.left) # 左
print(root.val) # 根
dfs(root.right) # 右
```
```Java []
// 打印中序遍历
void dfs(Node root) {
if(root == null) return;
dfs(root.left); // 左
System.out.println(root.val); // 根
dfs(root.right); // 右
}
```
```C++ []
// 打印中序遍历
void dfs(Node* root) {
if(root == nullptr) return;
dfs(root->left); // 左
cout << root->val << endl; // 根
dfs(root->right); // 右
}
```
根据以上分析，考虑使用中序遍历访问树的各节点 `cur` ；并在访问每个节点时构建 `cur` 和前驱节点 `pre` 的引用指向；中序遍历完成后，最后构建头节点和尾节点的引用指向即可。
### 算法流程：
**`dfs(cur):`** 递归中序遍历；
1. **终止条件：** 当节点 `cur` 为空，代表越过叶节点，直接返回；
2. 递归左子树，即 `dfs(cur.left)` ；
3. **构建链表：**
1. **当 `pre` 为空时：** 代表正在访问链表头节点，记为 `head` ；
2. **当 `pre` 不为空时：** 修改双向节点引用，即 `pre.right = cur` ，`cur.left = pre` ；
3. **保存 `cur` ：** 更新 `pre = cur` ，即节点 `cur` 是后继节点的 `pre` ；
4. 递归右子树，即 `dfs(cur.right)` ；
**`treeToDoublyList(root)：`**
1. **特例处理：** 若节点 `root` 为空，则直接返回；
2. **初始化：** 空节点 `pre` ；
3. **转化为双向链表：** 调用 `dfs(root)` ；
4. **构建循环链表：** 中序遍历完成后，`head` 指向头节点，`pre` 指向尾节点，因此修改 `head` 和 `pre` 的双向节点引用即可；
5. **返回值：** 返回链表的头节点 `head` 即可；
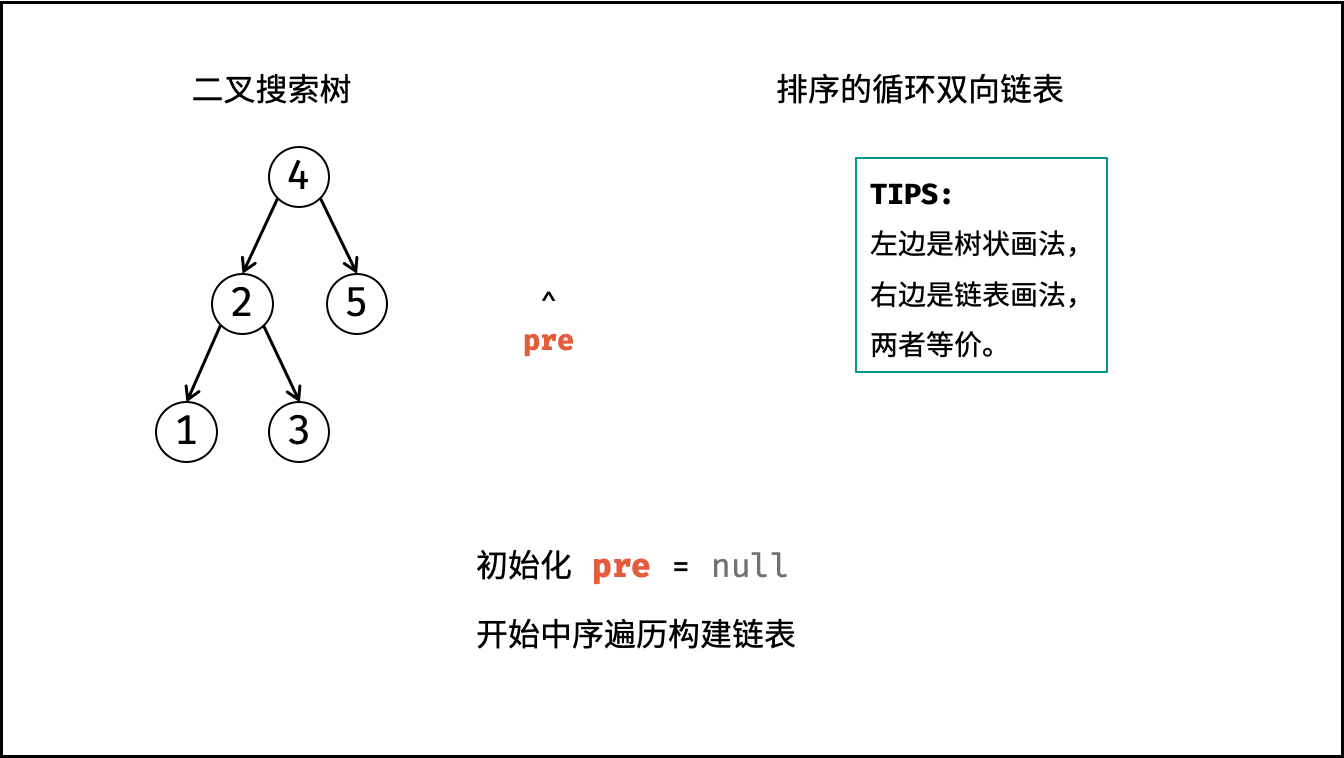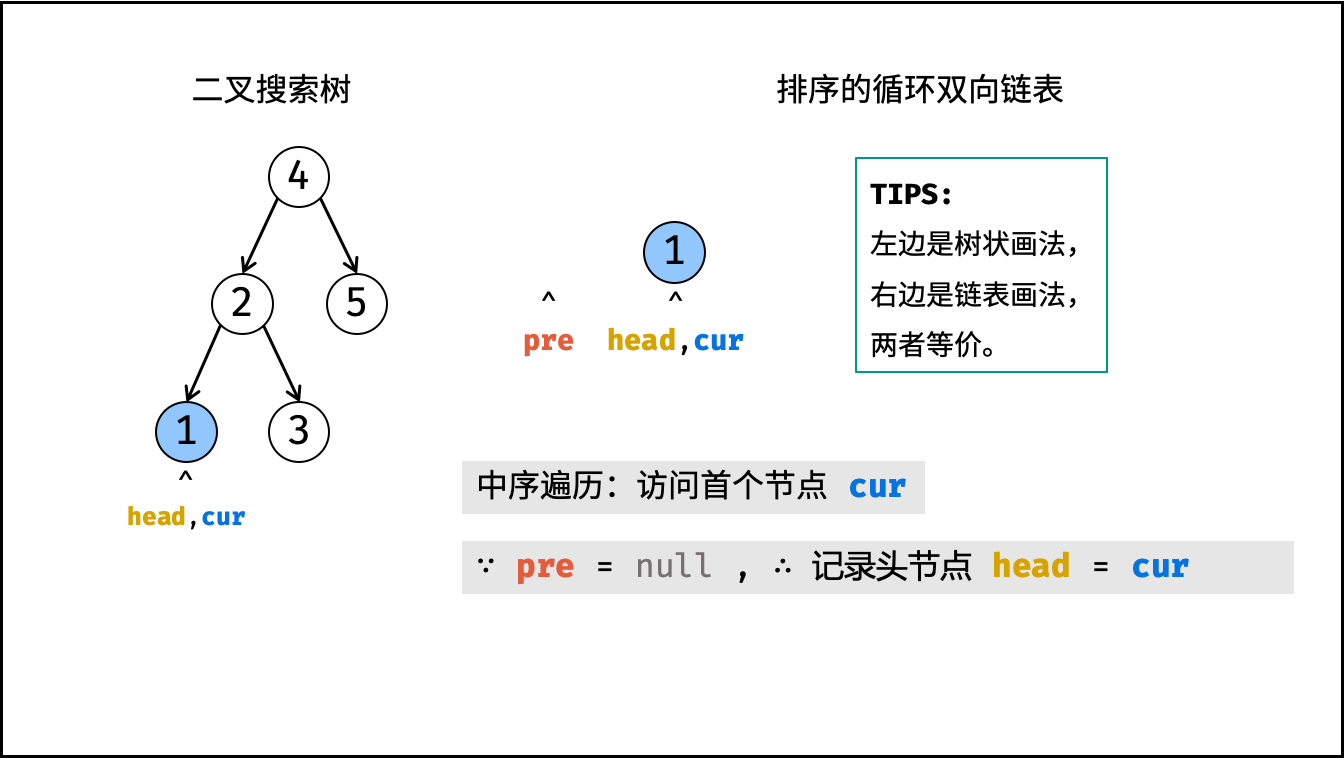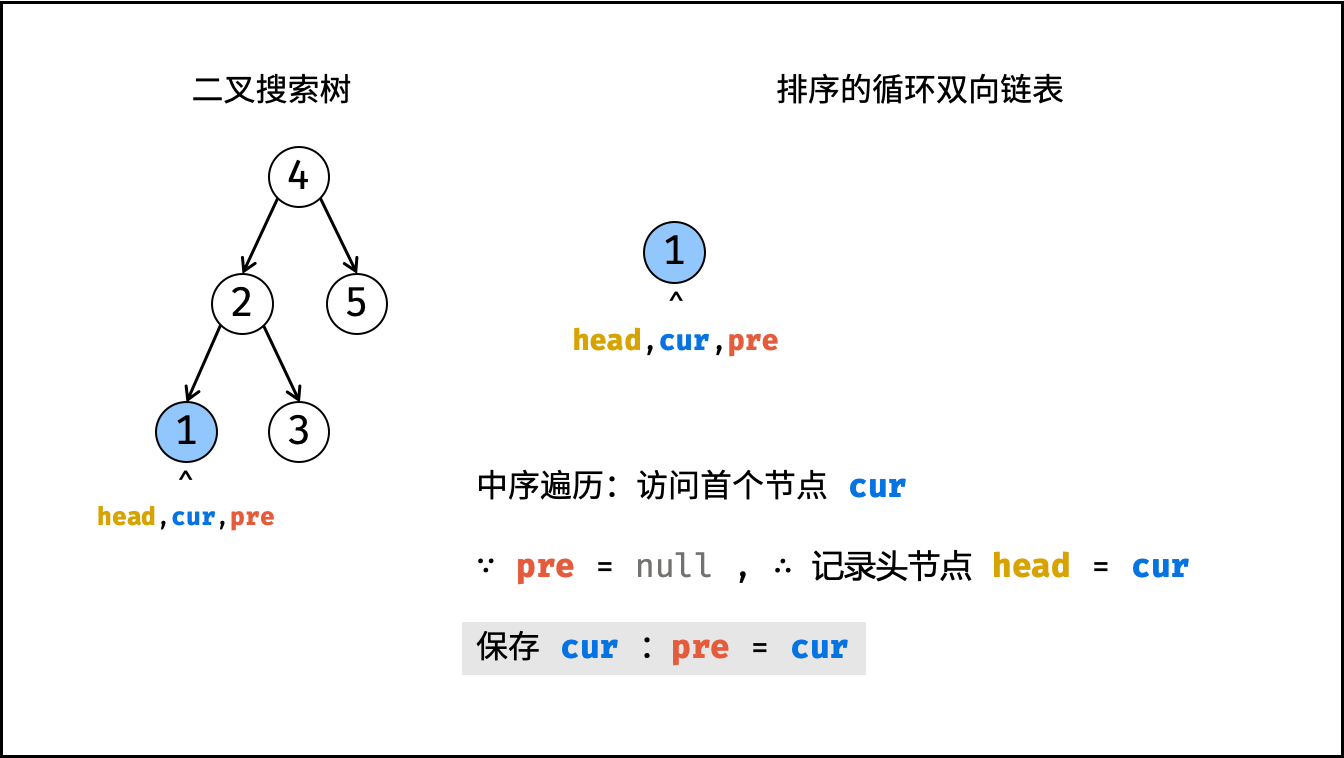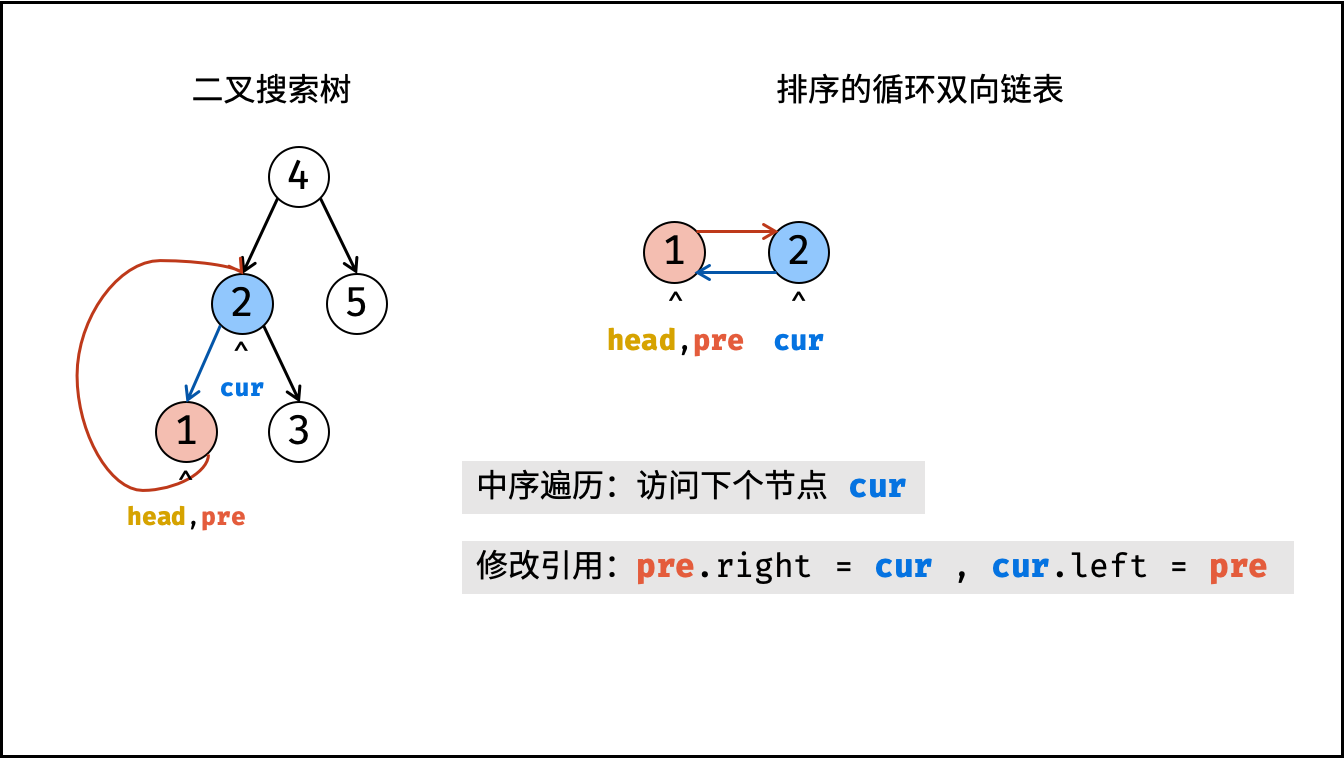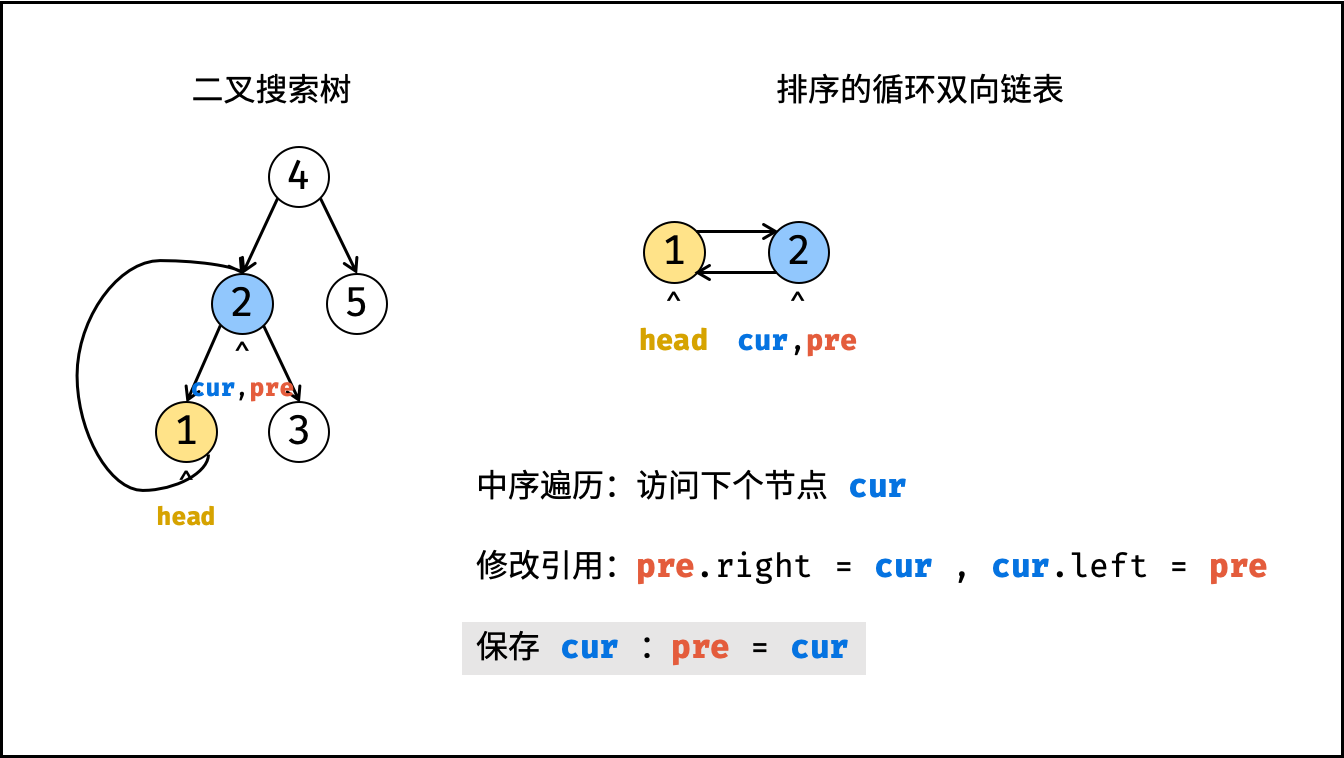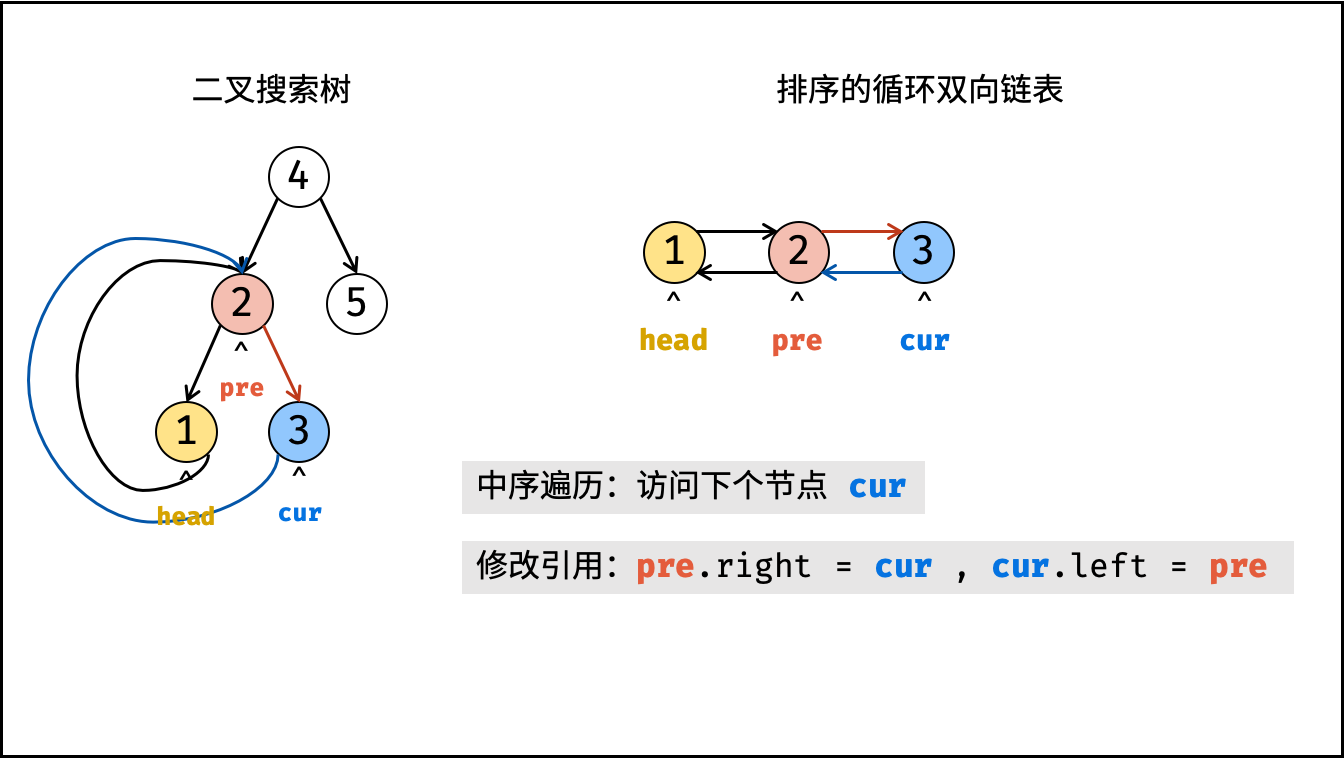<![Picture2.png](https://pic.leetcode-cn.com/1599402776-vPeoHZ-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599402776-ZUbEpW-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599402776-BeGvpX-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599402776-qstaql-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599402776-NNnLfI-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599402776-WMHCrE-Picture7.png),![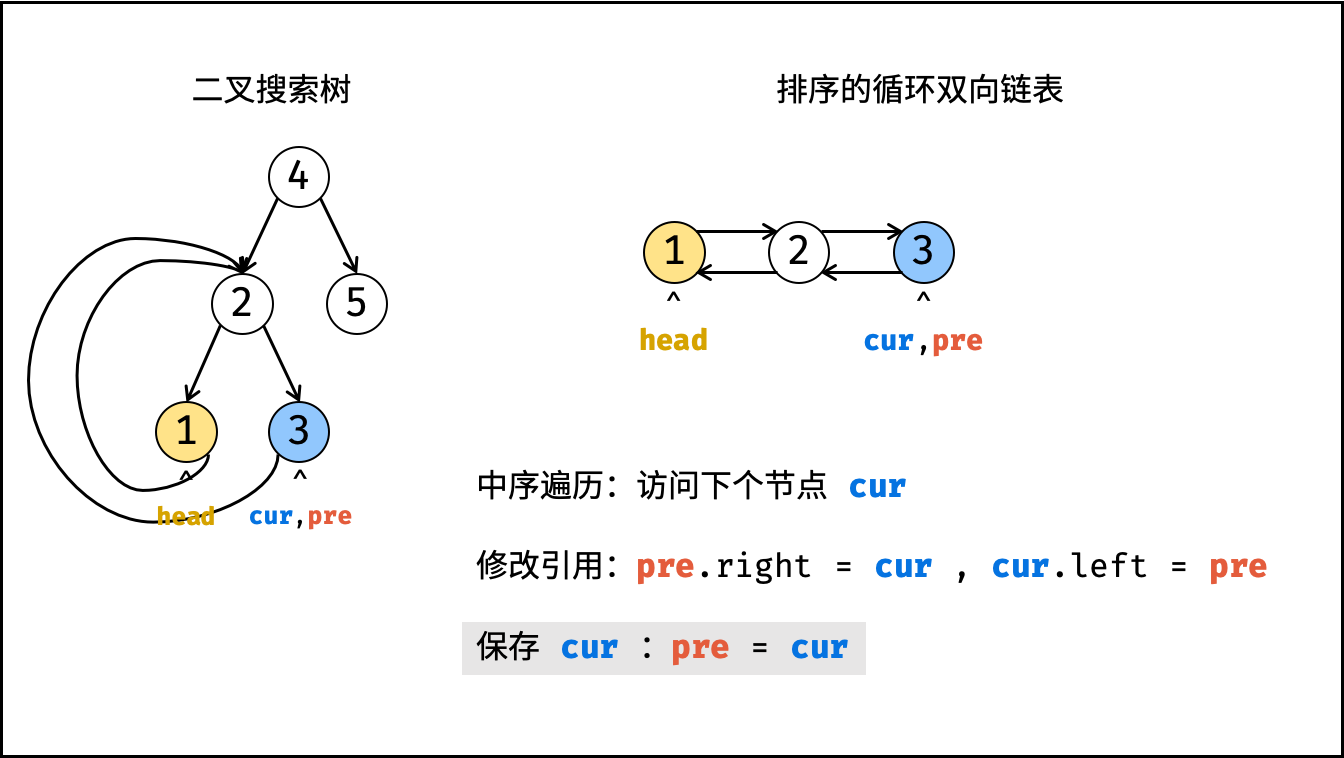Picture8.png](https://pic.leetcode-cn.com/1599402776-GVXFzi-Picture8.png),![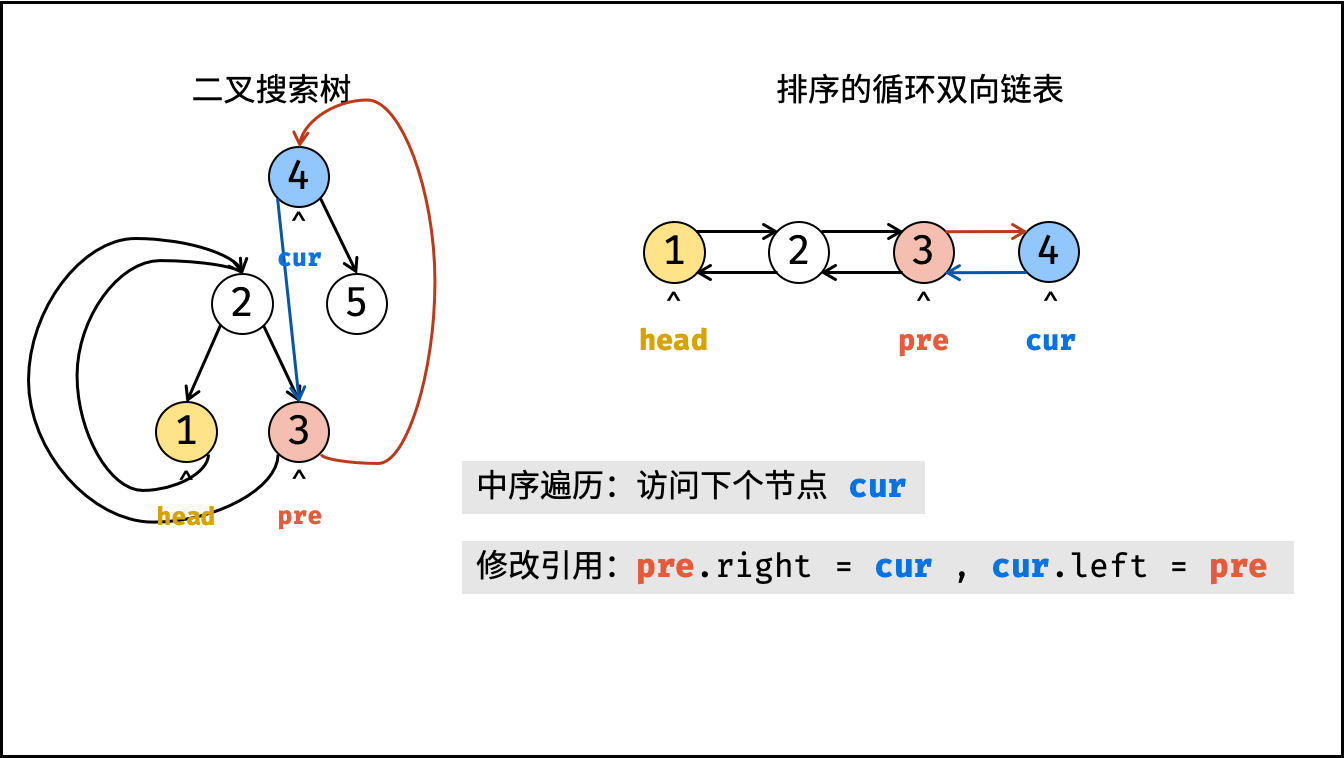Picture9.png](https://pic.leetcode-cn.com/1599402776-VCkREF-Picture9.png),![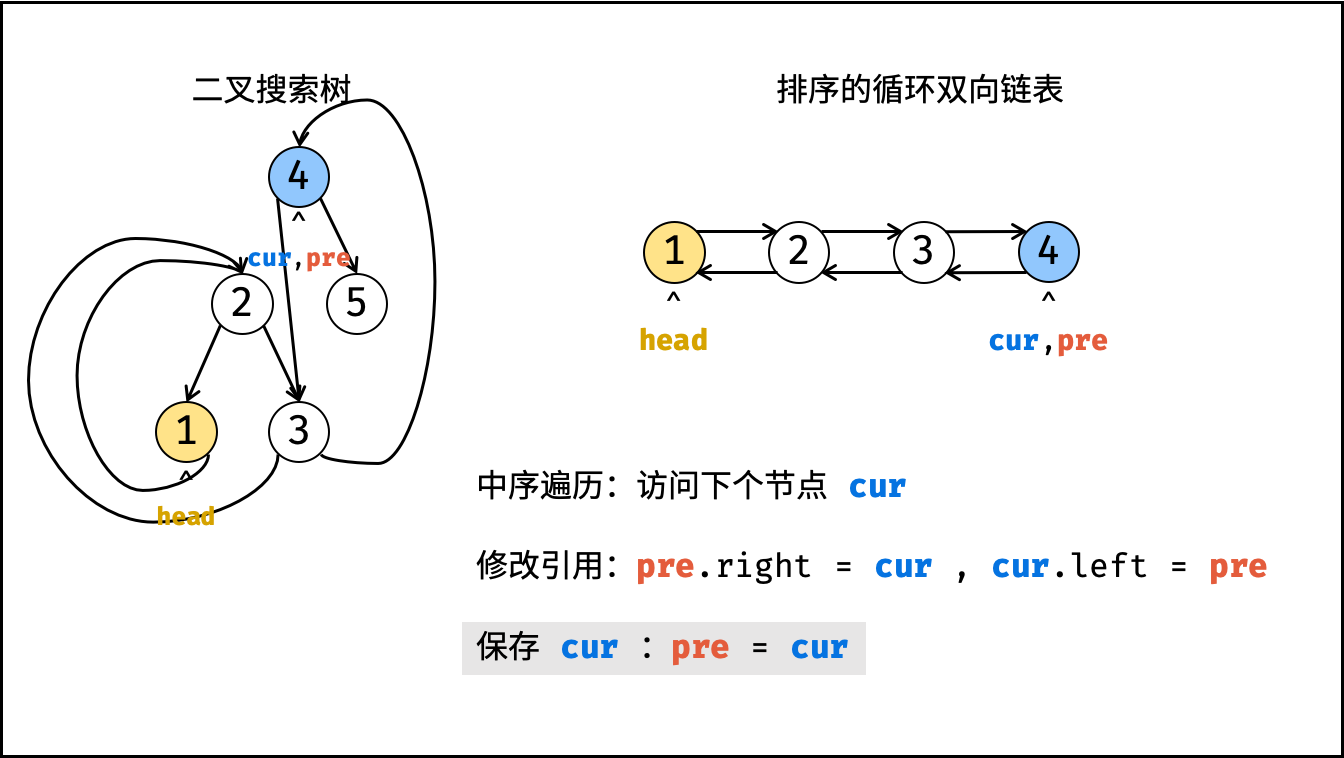Picture10.png](https://pic.leetcode-cn.com/1599402776-VIUGkY-Picture10.png),![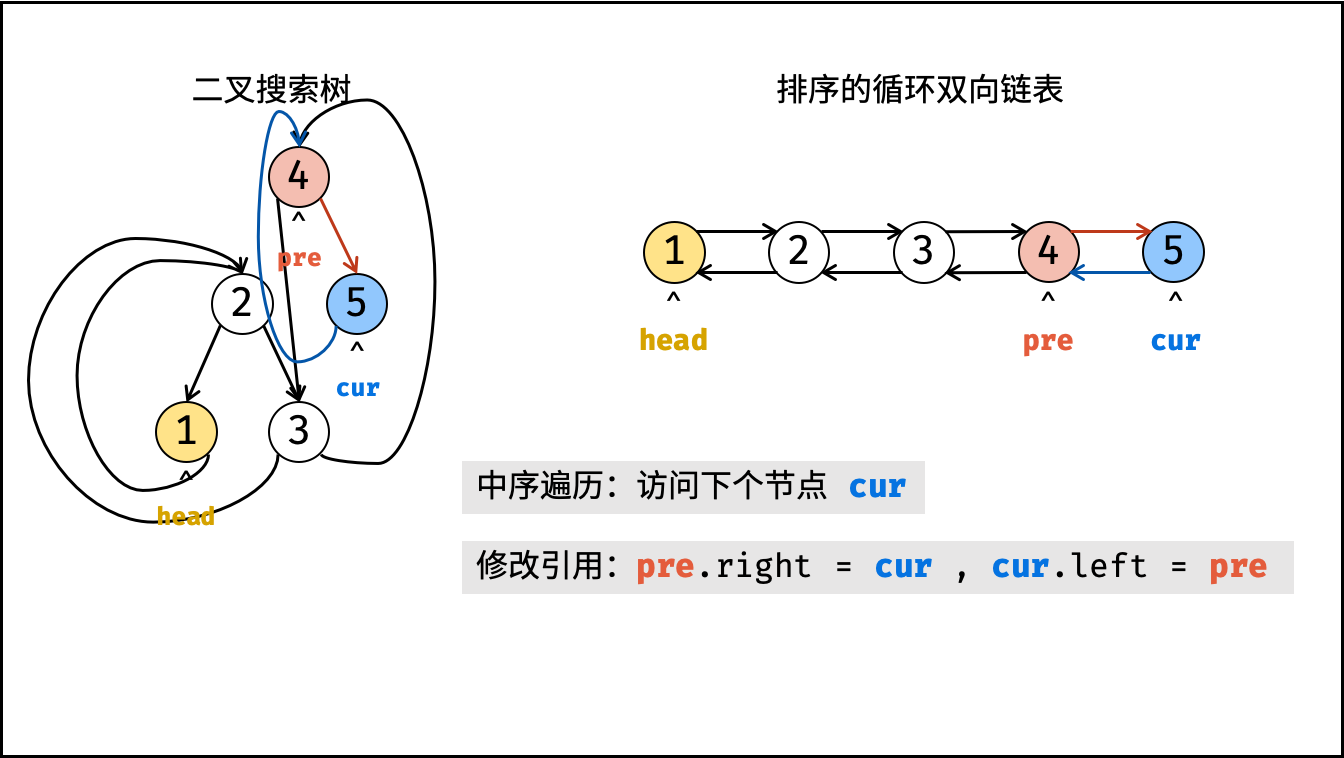Picture11.png](https://pic.leetcode-cn.com/1599402776-tmZvCu-Picture11.png),![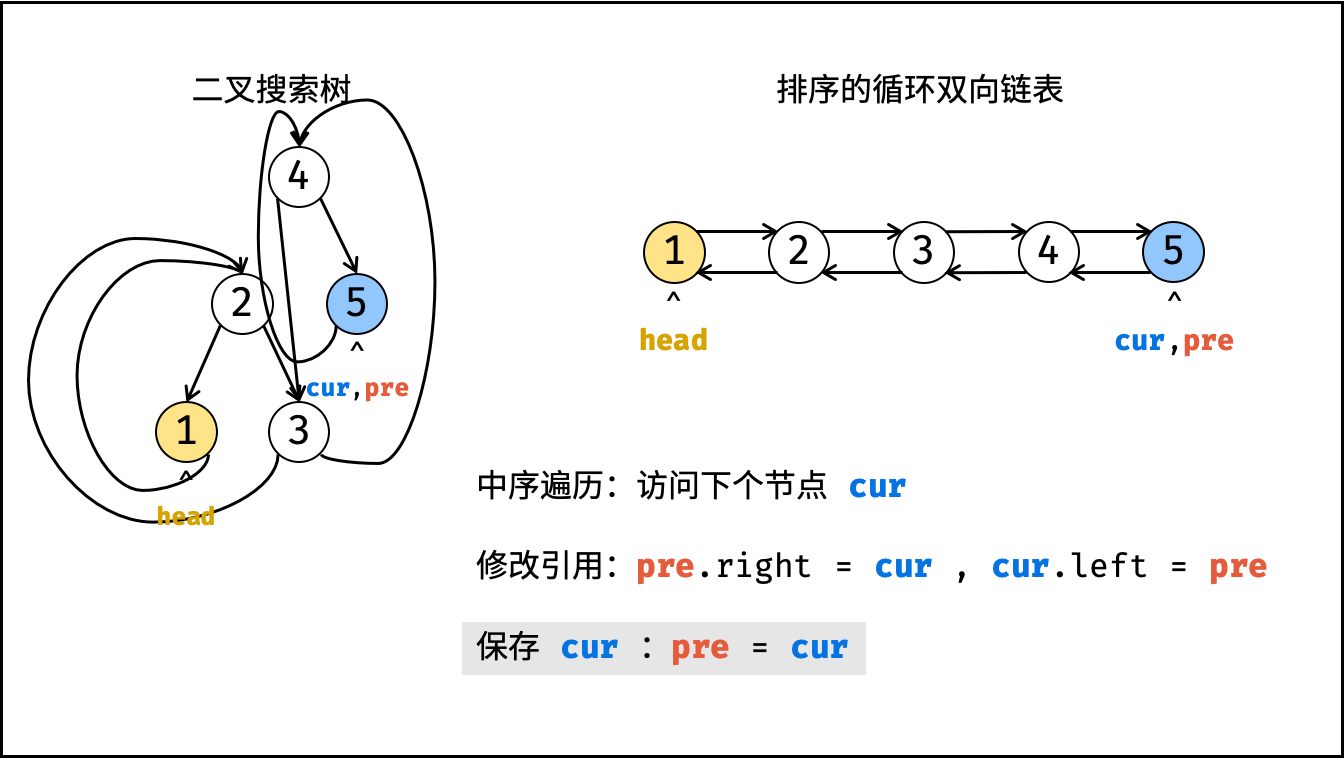Picture12.png](https://pic.leetcode-cn.com/1599402776-MhDqlj-Picture12.png),![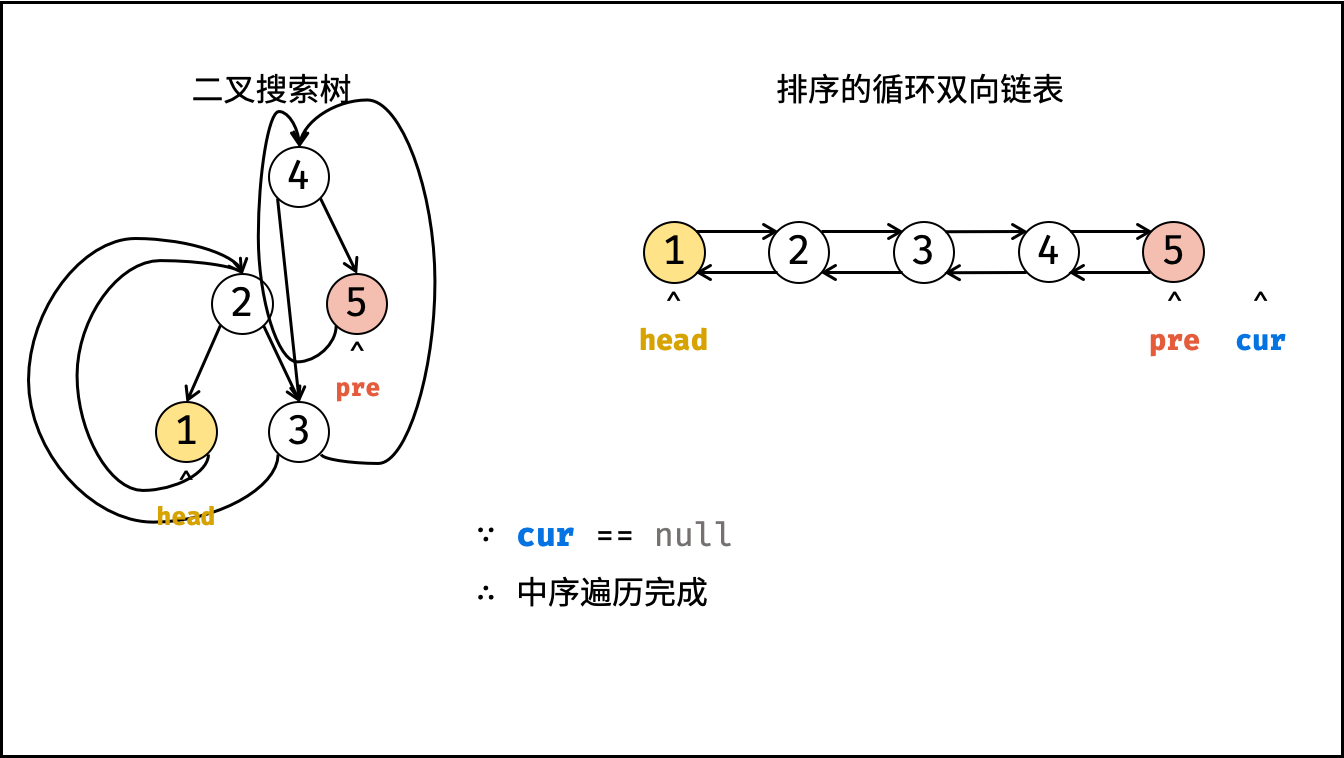Picture13.png](https://pic.leetcode-cn.com/1599402776-BHNrPD-Picture13.png),![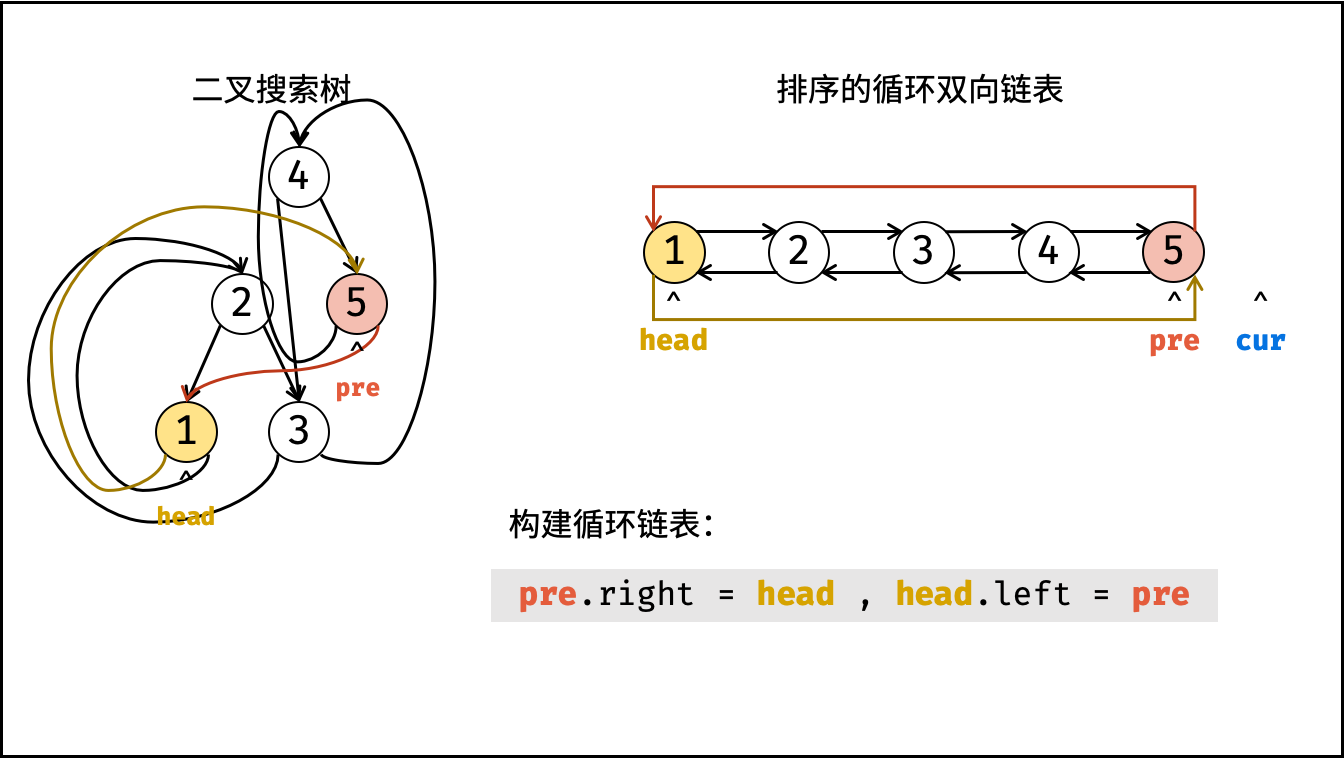Picture14.png](https://pic.leetcode-cn.com/1599402776-WrwMzD-Picture14.png),![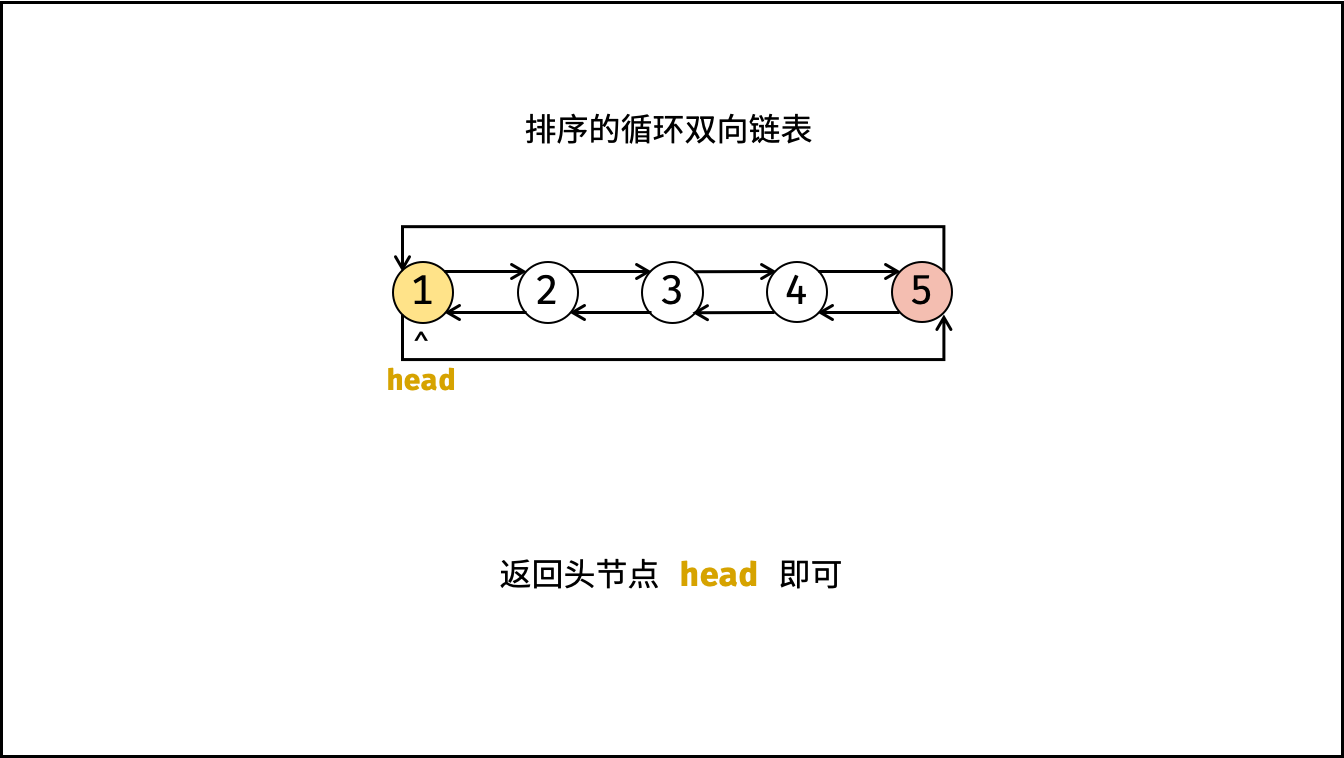Picture15.png](https://pic.leetcode-cn.com/1599402776-aUyeTI-Picture15.png)>
## 代码：
```Python []
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
def dfs(cur):
if not cur: return
dfs(cur.left) # 递归左子树
if self.pre: # 修改节点引用
self.pre.right, cur.left = cur, self.pre
else: # 记录头节点
self.head = cur
self.pre = cur # 保存 cur
dfs(cur.right) # 递归右子树
if not root: return
self.pre = None
dfs(root)
self.head.left, self.pre.right = self.pre, self.head
return self.head
```
```Java []
class Solution {
Node pre, head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
dfs(root);
head.left = pre;
pre.right = head;
return head;
}
void dfs(Node cur) {
if(cur == null) return;
dfs(cur.left);
if(pre != null) pre.right = cur;
else head = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}
```
```C++ []
class Solution {
public:
Node* treeToDoublyList(Node* root) {
if(root == nullptr) return nullptr;
dfs(root);
head->left = pre;
pre->right = head;
return head;
}
private:
Node *pre, *head;
void dfs(Node* cur) {
if(cur == nullptr) return;
dfs(cur->left);
if(pre != nullptr) pre->right = cur;
else head = cur;
cur->left = pre;
pre = cur;
dfs(cur->right);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数，中序遍历需要访问所有节点。
- **空间复杂度 $O(N)$ ：** 最差情况下，即树退化为链表时，递归深度达到 $N$，系统使用 $O(N)$ 栈空间。

155
leetbook_ioa/docs/LCR 156. 序列化与反序列化二叉树.md Executable file
View File

@@ -0,0 +1,155 @@
## 解题思路：
通常使用的前序、中序、后序、层序遍历记录的二叉树的信息不完整，即唯一的输出序列可能对应着多种二叉树可能性。题目要求的 序列化 和 反序列化 是 **可逆操作** 。因此，序列化的字符串应携带 **完整的二叉树信息** 。
> 观察题目示例，序列化的字符串实际上是二叉树的 “层序遍历”（BFS）结果，本文也采用层序遍历。
为完整表示二叉树，考虑将叶节点下的 $\text{null}$ 也记录。在此基础上，对于列表中任意某节点 `node` ，其左子节点 `node.left` 和右子节点 `node.right` 在序列中的位置都是 **唯一确定** 的。如下图所示：
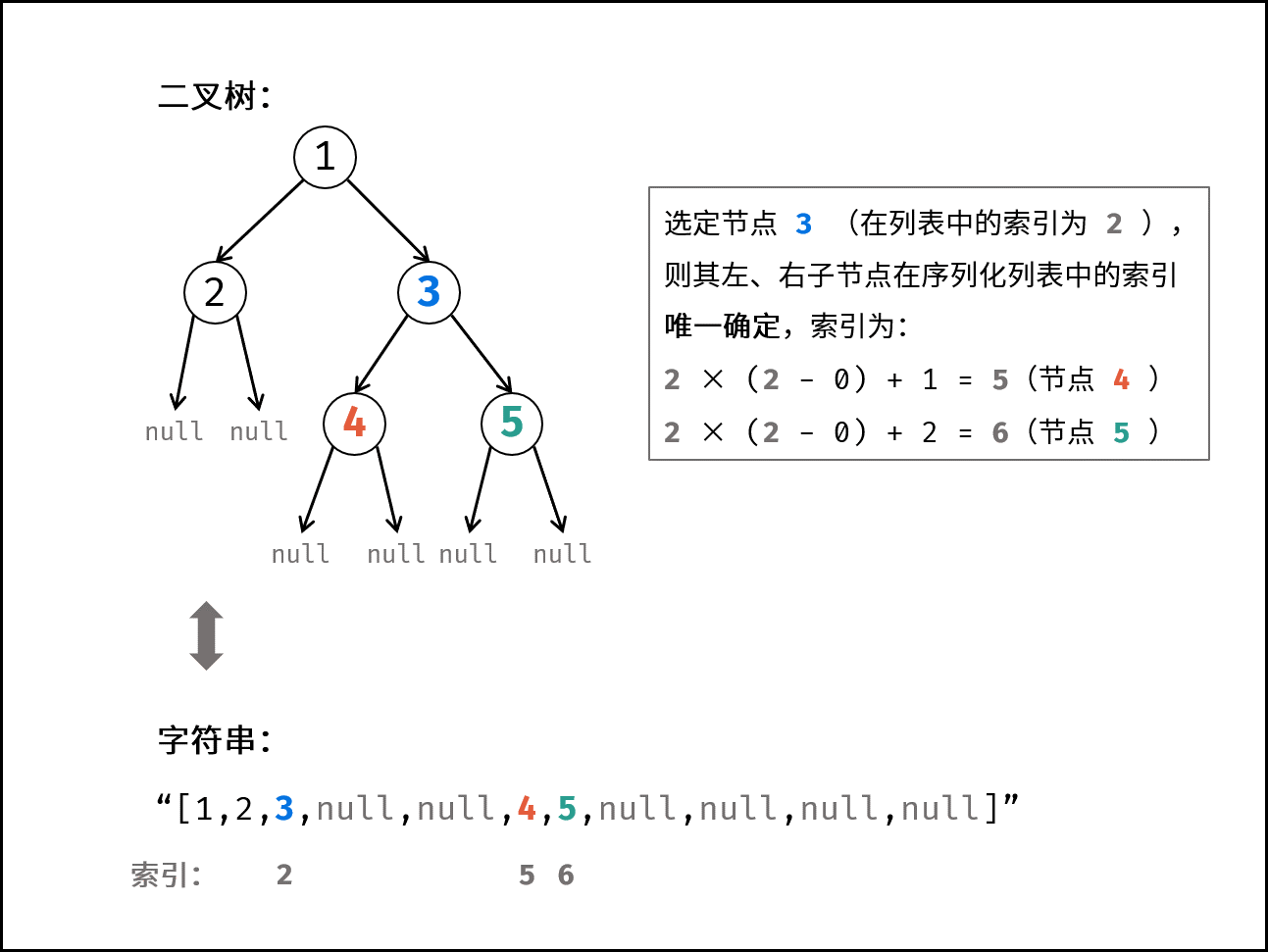![Picture1.png](https://pic.leetcode-cn.com/1603117385-ehAGsP-Picture1.png){:align=center width=550}
上图规律可总结为下表：
| `node.val` | `node` 的索引 | `node.left` 的索引 | `node.right` 的索引 |
| :--------: | :-----------: | :----------------: | :-----------------: |
| $1$ | $0$ | $1$ | $2$ |
| $2$ | $1$ | $3$ | $4$ |
| $3$ | $2$ | $5$ | $6$ |
| $4$ | $5$ | $7$ | $8$ |
| $5$ | $6$ | $9$ | $10$ |
设 $m$ 为列表区间 $[0, n]$ 中的 $\text{null}$ 节点个数，则可总结出根节点、左子节点、右子节点的列表索引的递推公式：
| `node.val` | `node` 的列表索引 | `node.left` 的列表索引 | `node.right` 的列表索引 |
| :-----------------: | :---------------: | :--------------------: | :---------------------: |
| $\ne$ $\text{null}$ | $n$ | $2(n-m) + 1$ | $2(n-m) + 2$ |
| $=$ $\text{null}$ | $n$ | 无 | 无 |
**序列化** 使用层序遍历实现。**反序列化** 通过以上递推公式反推各节点在序列中的索引，进而实现。
## 序列化 Serialize ：
借助队列，对二叉树做层序遍历，并将越过叶节点的 $\text{null}$ 也打印出来。
### 算法流程：
1. **特例处理：** 若 `root` 为空，则直接返回空列表 `"[]"` ；
2. **初始化：** 队列 `queue` （包含根节点 `root` ）；序列化列表 `res` ；
3. **层序遍历：** 当 `queue` 为空时跳出；
1. 节点出队，记为 `node` ；
2. 若 `node` 不为空：(1) 打印字符串 `node.val` ，(2) 将左、右子节点加入 `queue` ；
3. 否则（若 `node` 为空）：打印字符串 `"null"` ；
4. **返回值：** 拼接列表，用 `','` 隔开，首尾添加中括号；
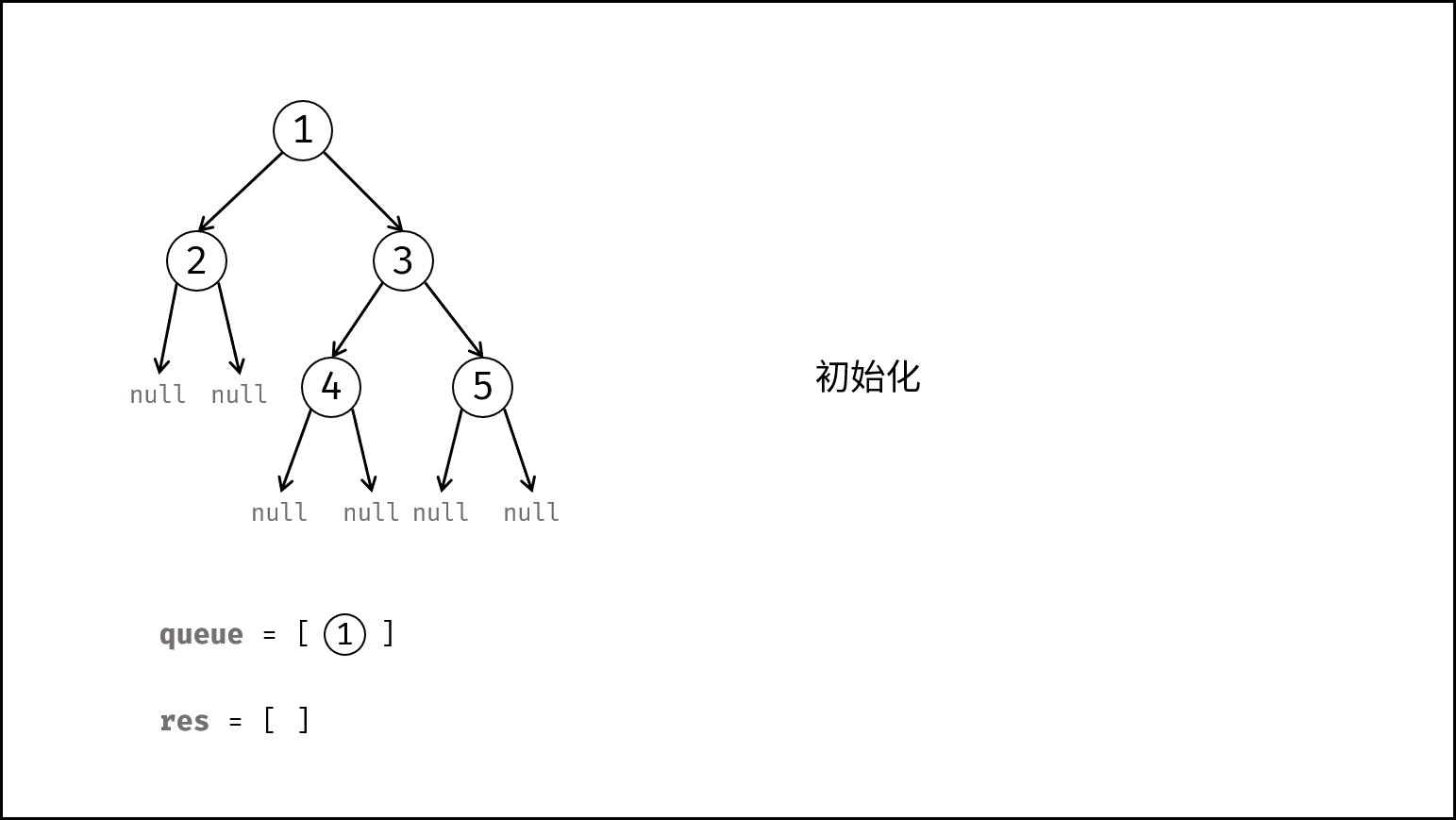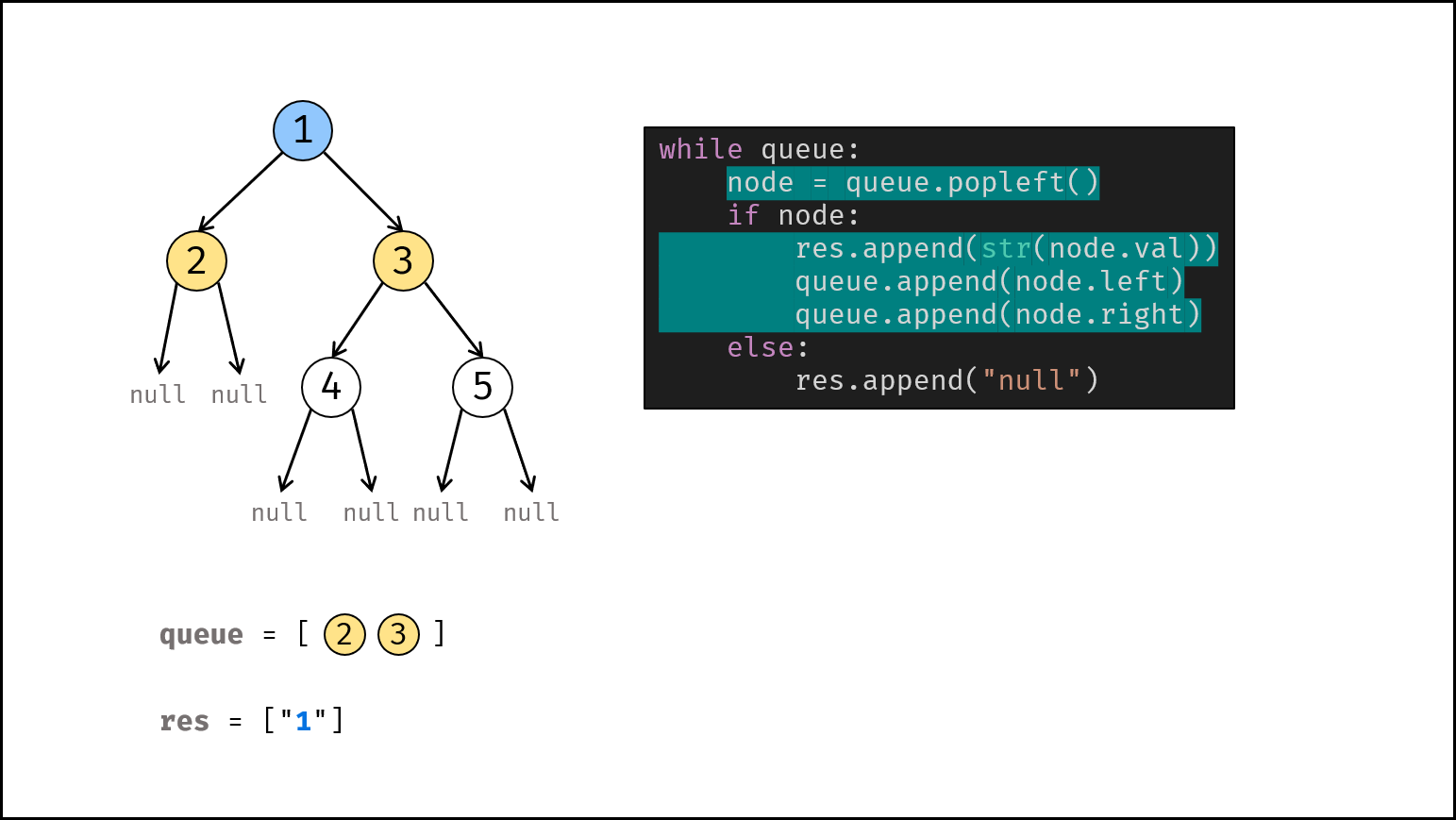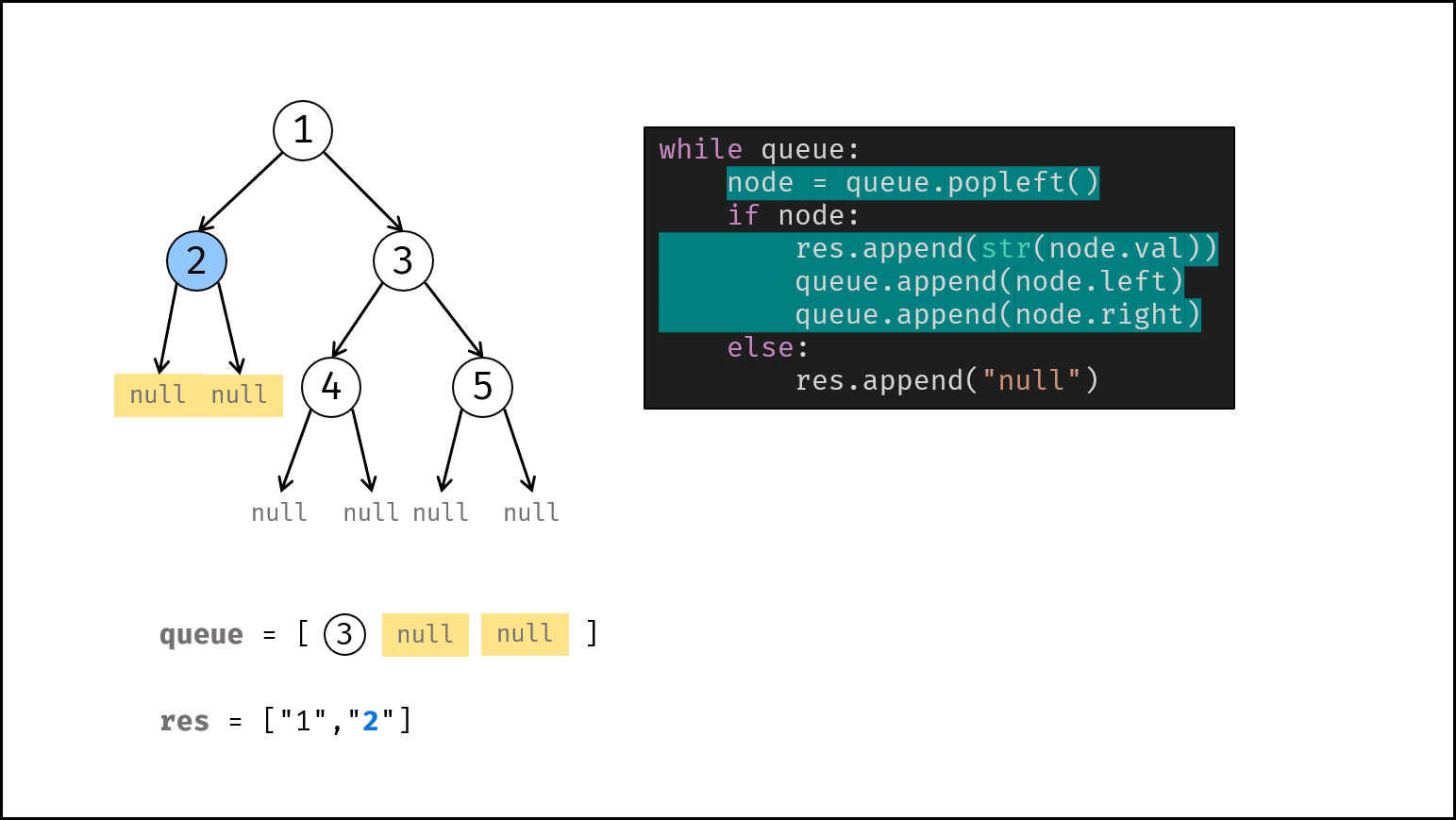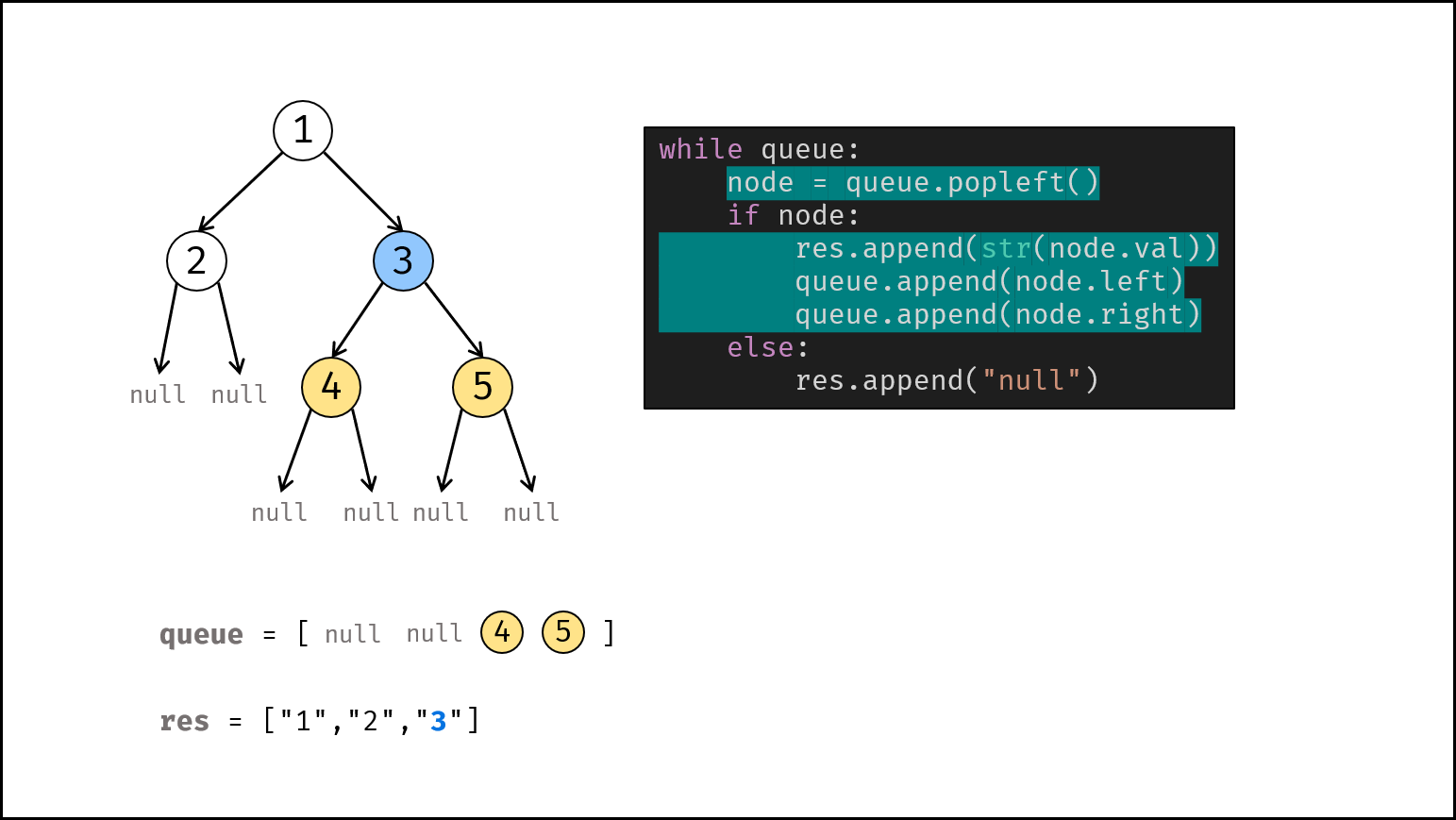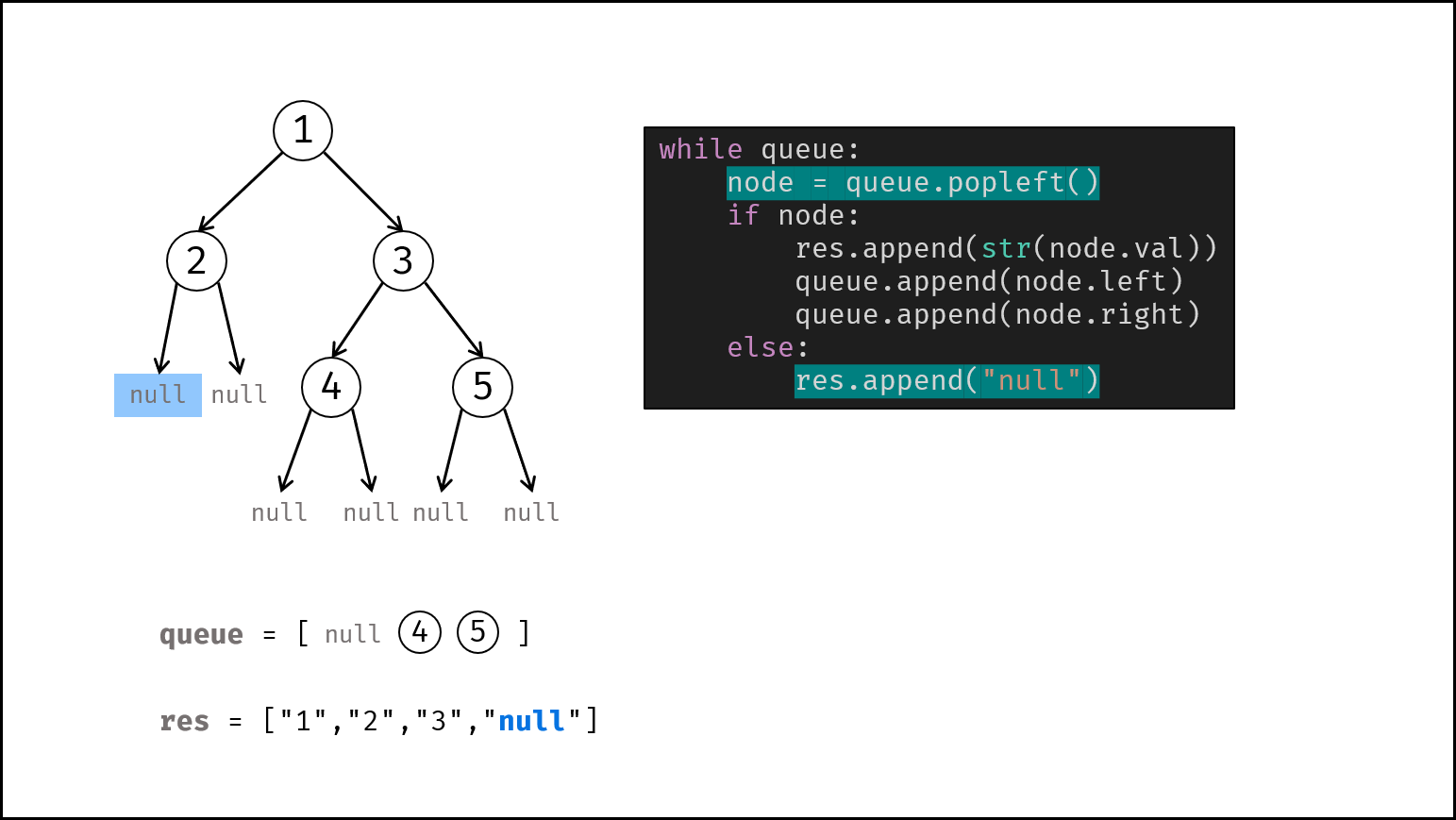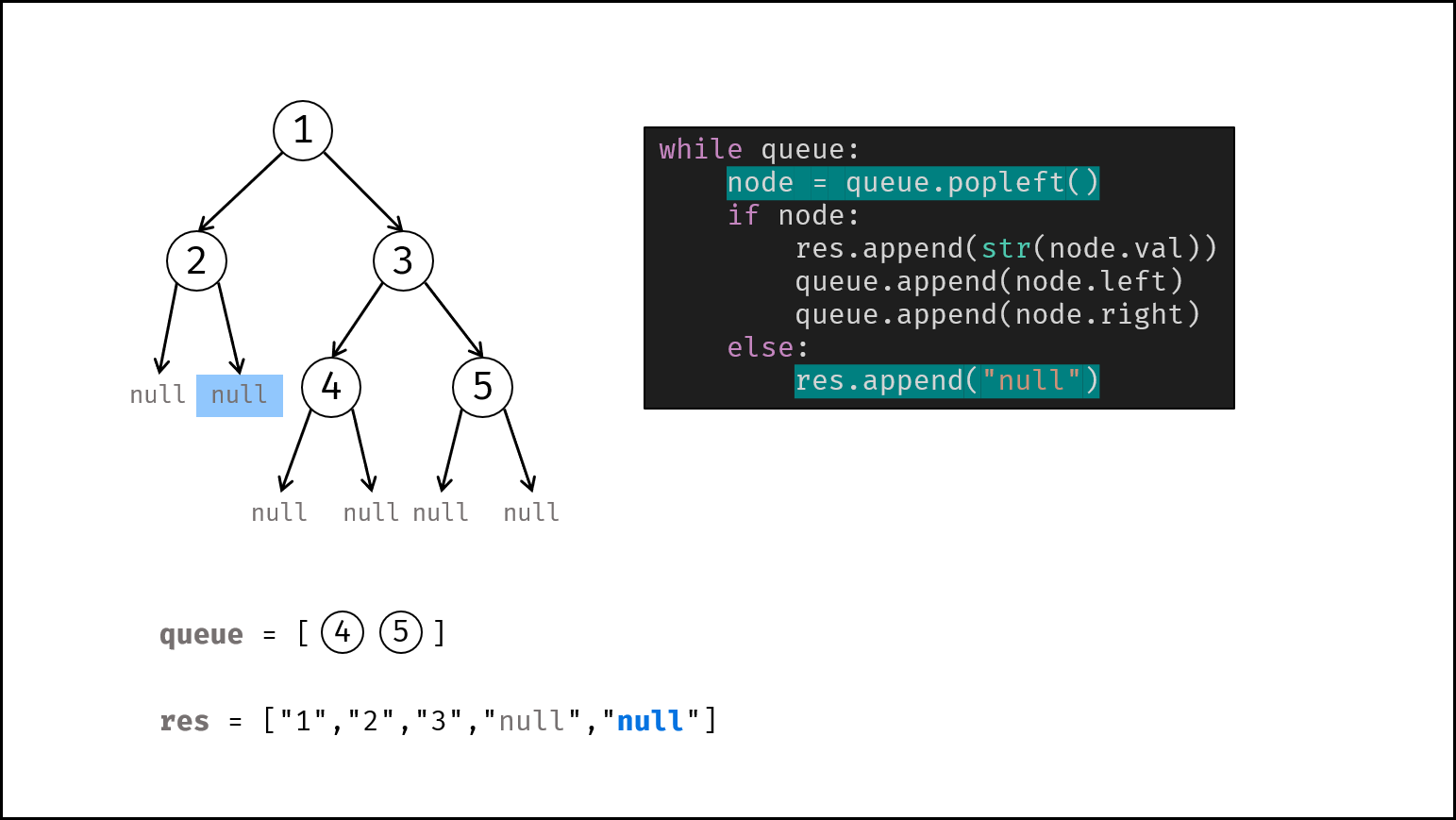<![Picture2.png](https://pic.leetcode-cn.com/1603117385-wmoUSQ-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603117385-UEgpOH-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603117385-yFlBIF-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603117385-ZrhoFK-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603117385-xJrjxc-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603117385-uaYOCC-Picture7.png),![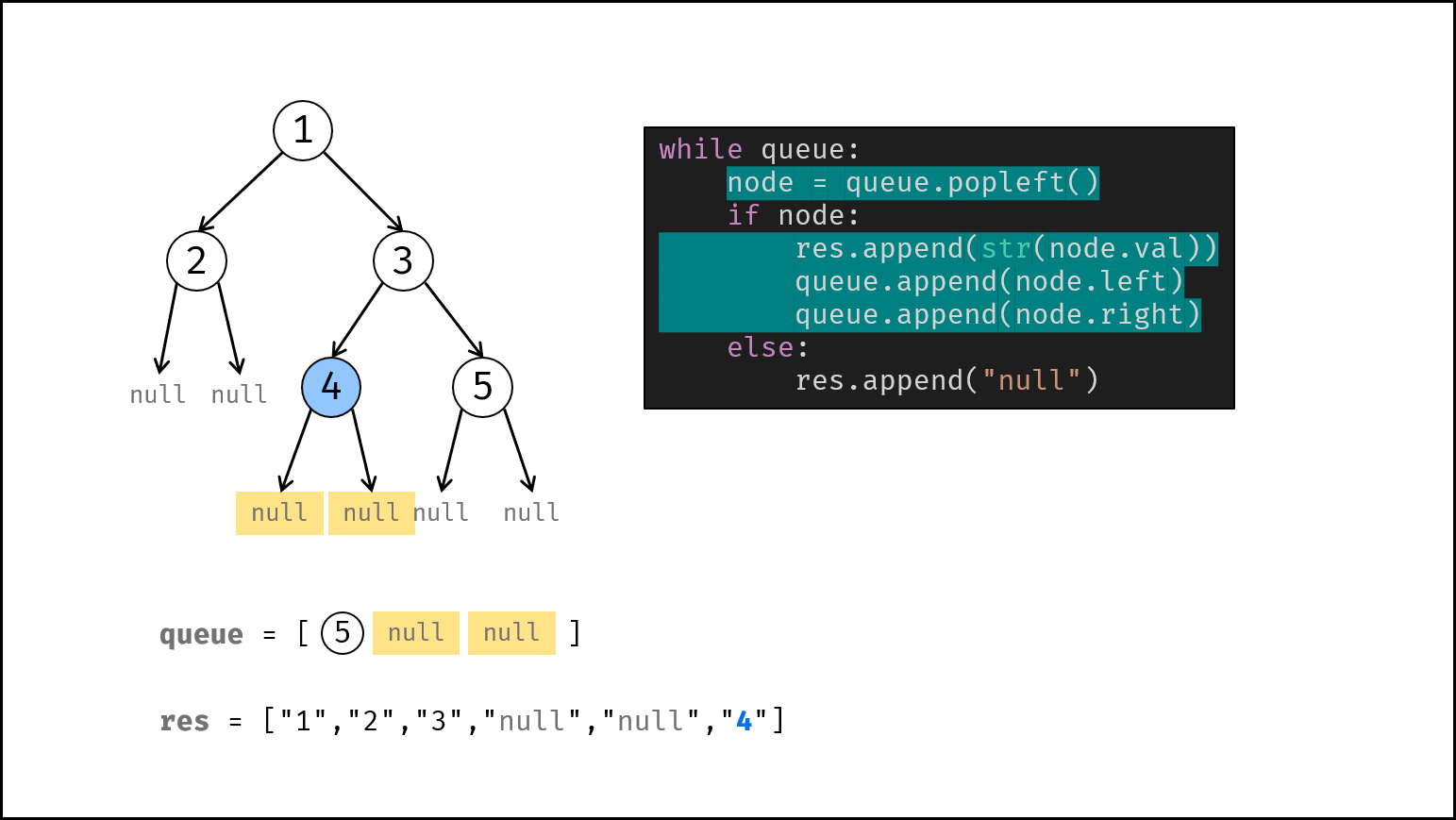Picture8.png](https://pic.leetcode-cn.com/1603117385-KJezRV-Picture8.png),![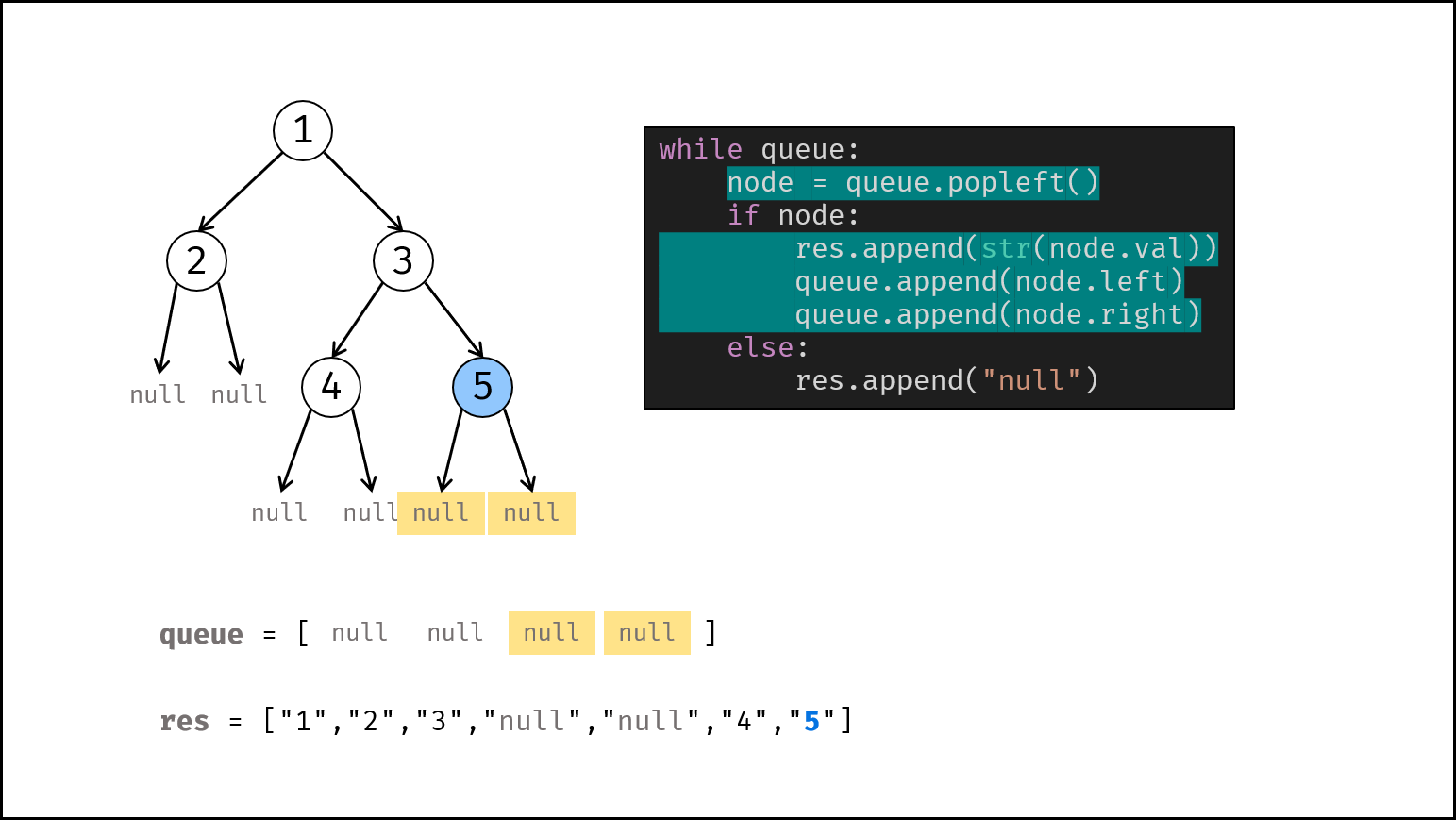Picture9.png](https://pic.leetcode-cn.com/1603117385-GWylSS-Picture9.png),![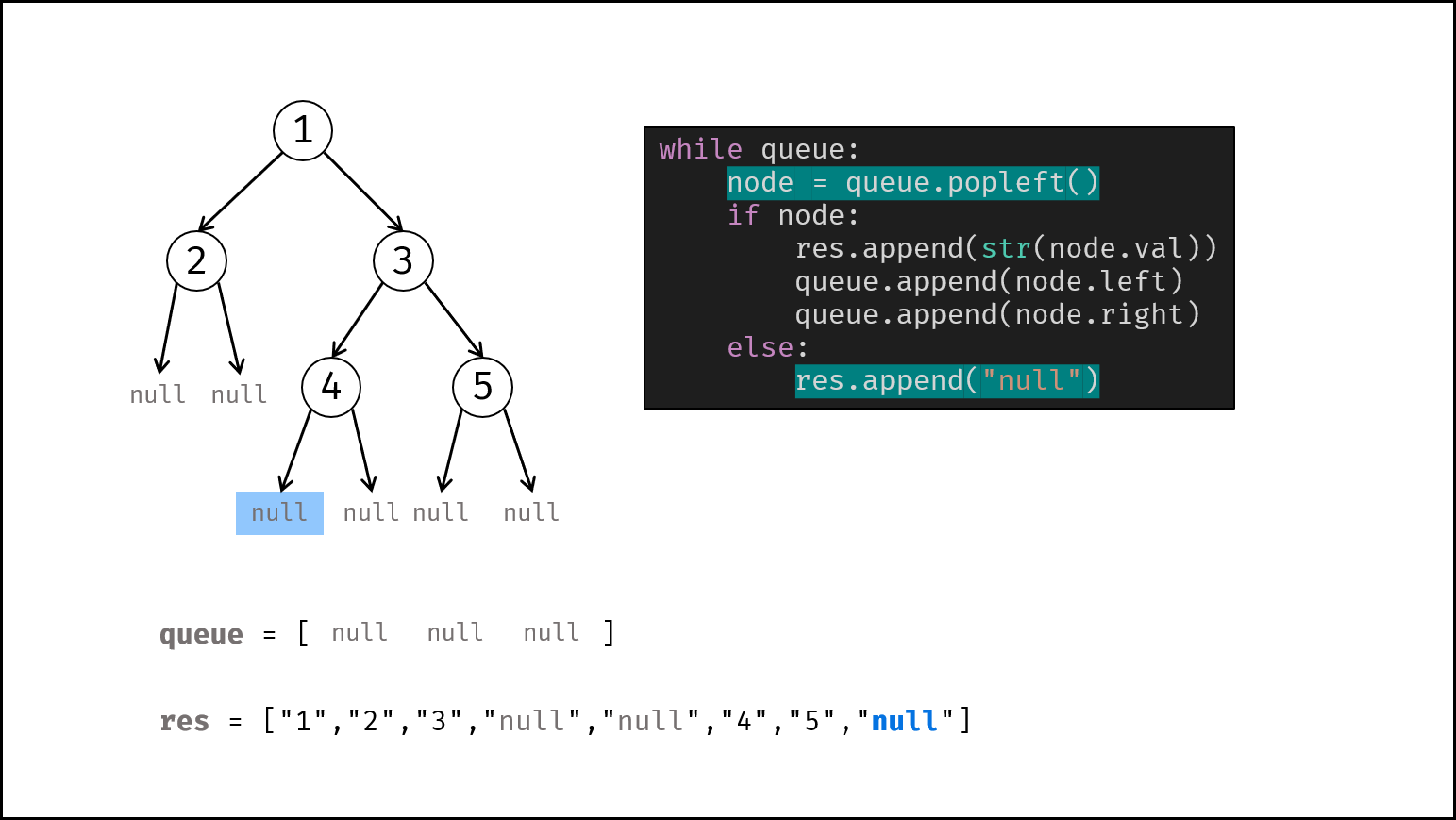Picture10.png](https://pic.leetcode-cn.com/1603117385-TjmJwG-Picture10.png),![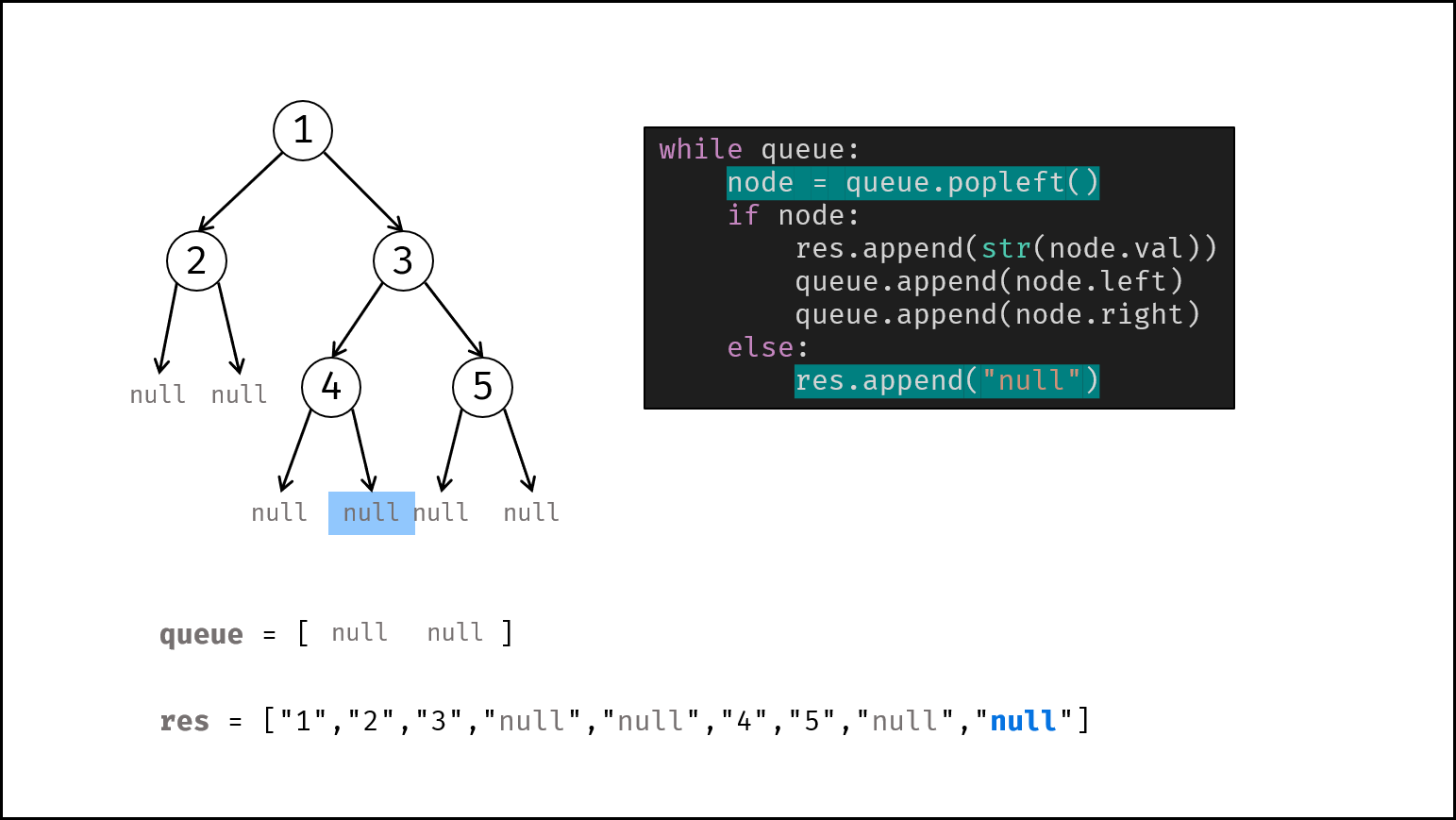Picture11.png](https://pic.leetcode-cn.com/1603117385-dSelCu-Picture11.png),![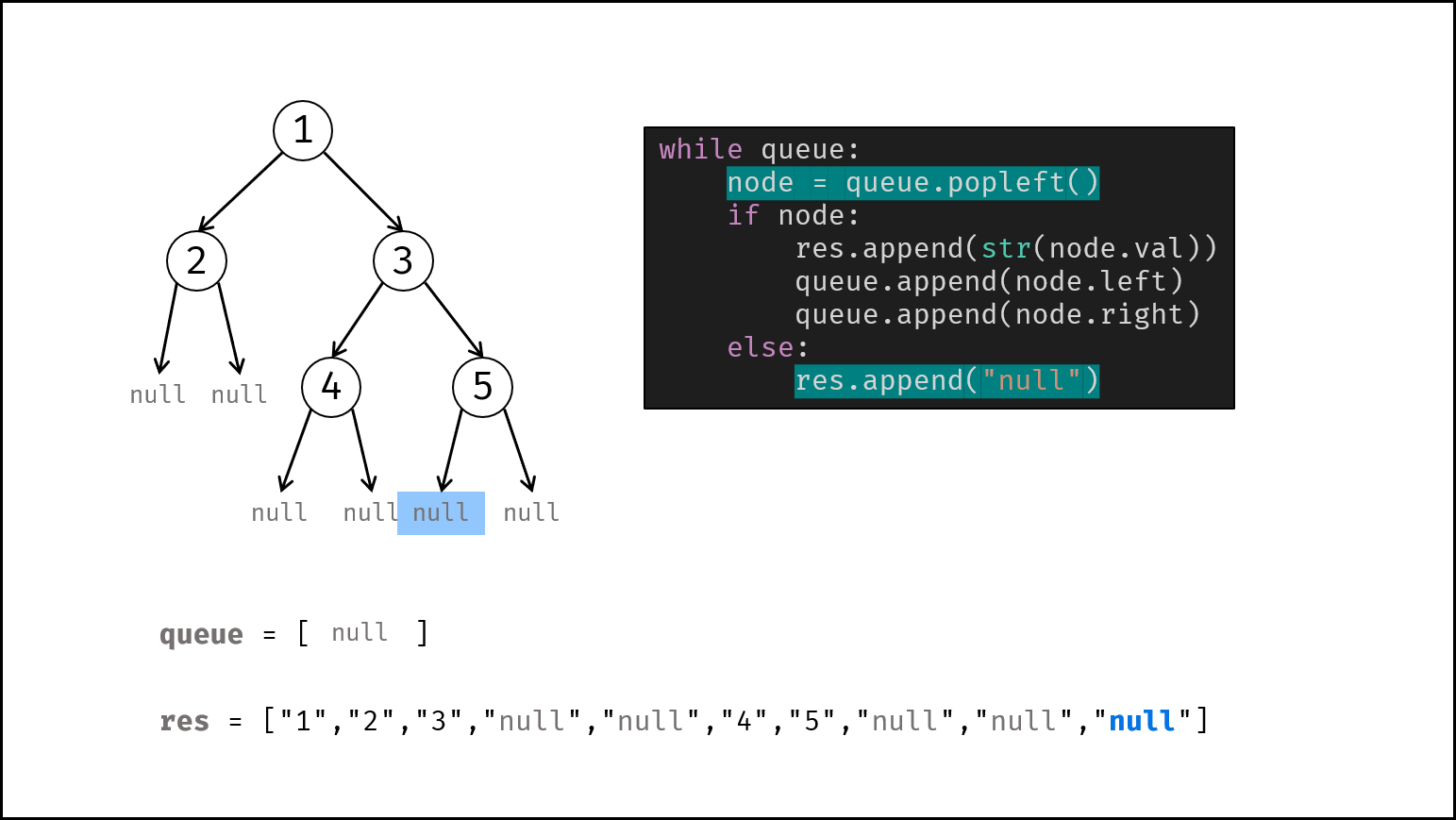Picture12.png](https://pic.leetcode-cn.com/1603117385-ZCwlAy-Picture12.png),![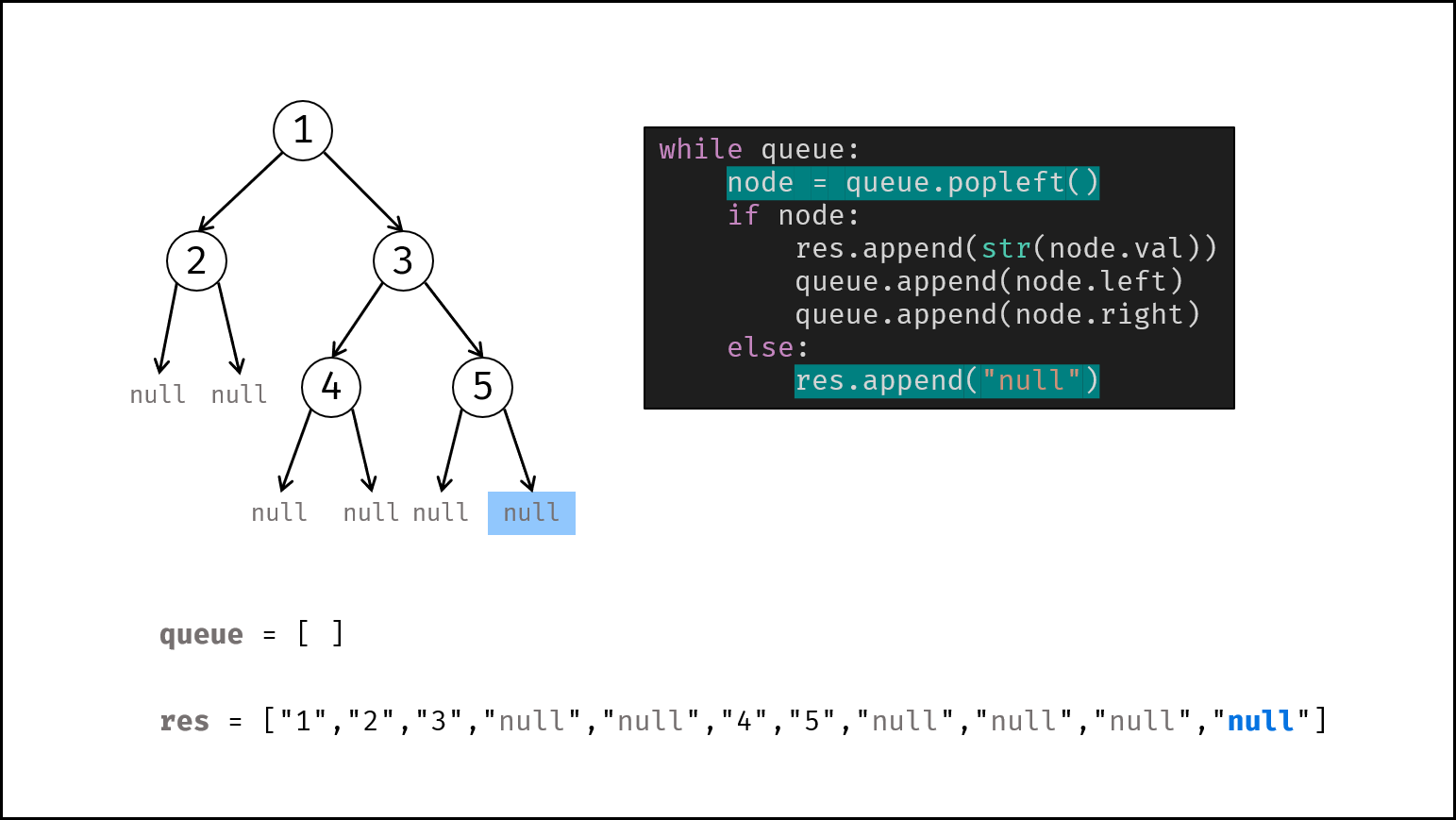Picture13.png](https://pic.leetcode-cn.com/1603117385-oMjbol-Picture13.png),![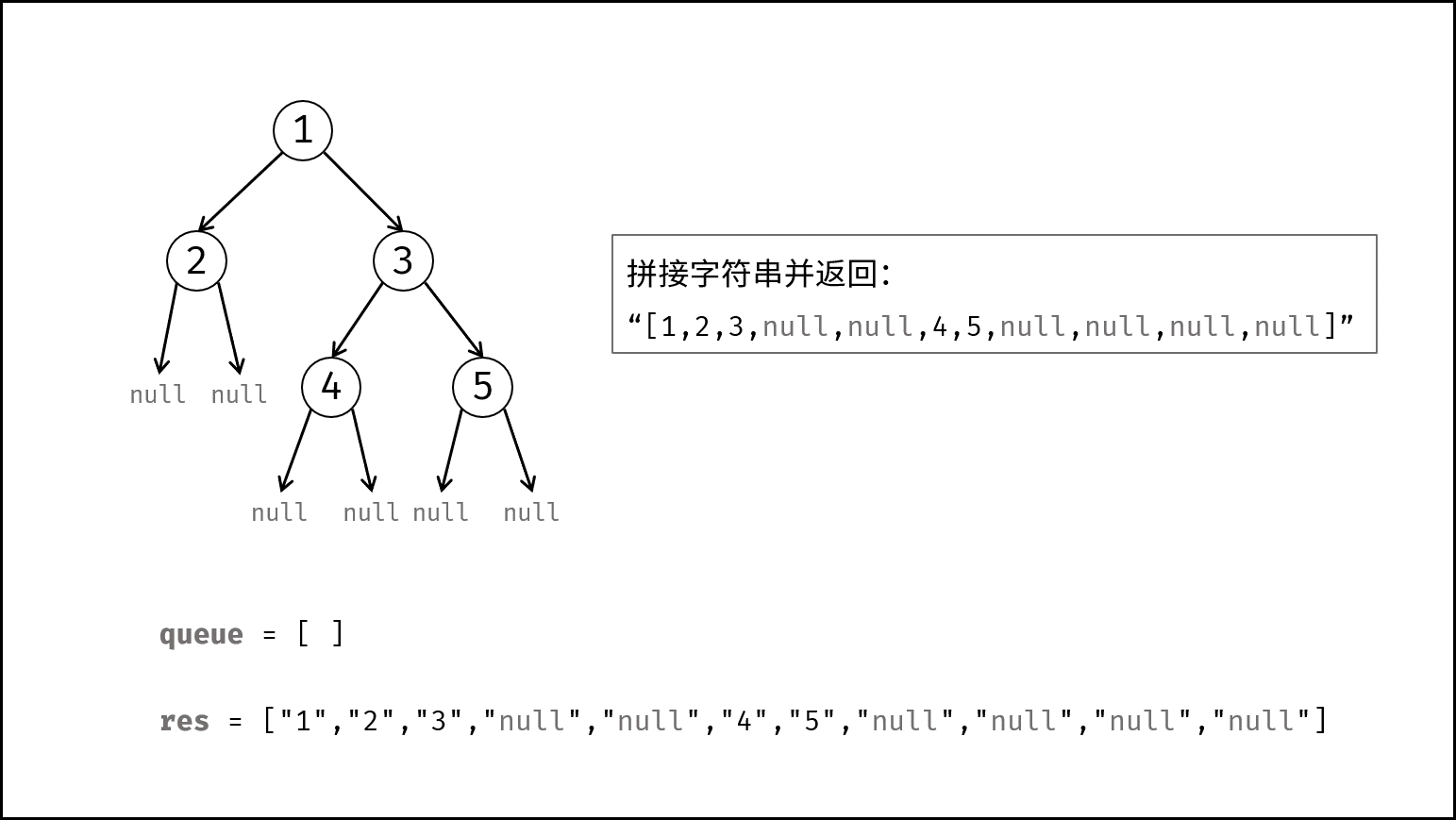Picture14.png](https://pic.leetcode-cn.com/1603117385-fRWVBK-Picture14.png)>
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数，层序遍历需要访问所有节点，最差情况下需要访问 $N + 1$ 个 $\text{null}$ ，总体复杂度为 $O(2N + 1) = O(N)$ 。
- **空间复杂度 $O(N)$ ：** 最差情况下，队列 `queue` 同时存储 $\frac{N + 1}{2}$ 个节点（或 $N+1$ 个 $\text{null}$ ），使用 $O(N)$ ；列表 `res` 使用 $O(N)$ 。
## 反序列化 Deserialize ：
基于本文开始推出的 `node` , `node.left` , `node.right` 在序列化列表中的位置关系，可实现反序列化。
利用队列按层构建二叉树，借助一个指针 `i` 指向节点 `node` 的左、右子节点，每构建一个 `node` 的左、右子节点，指针 `i` 就向右移动 $1$ 位。
### 算法流程：
1. **特例处理：** 若 `data` 为空，直接返回 $\text{null}$ ；
2. **初始化：** 序列化列表 `vals` （先去掉首尾中括号，再用逗号隔开），指针 `i = 1` ，根节点 `root` （值为 `vals[0]` ），队列 `queue`（包含 `root` ）；
3. **按层构建：** 当 `queue` 为空时跳出；
1. 节点出队，记为 `node` ；
2. 构建 `node` 的左子节点：`node.left` 的值为 `vals[i]` ，并将 `node.left` 入队；
3. 执行 `i += 1` ；
4. 构建 `node` 的右子节点：`node.right` 的值为 `vals[i]` ，并将 `node.right` 入队；
5. 执行 `i += 1` ；
4. **返回值：** 返回根节点 `root` 即可；
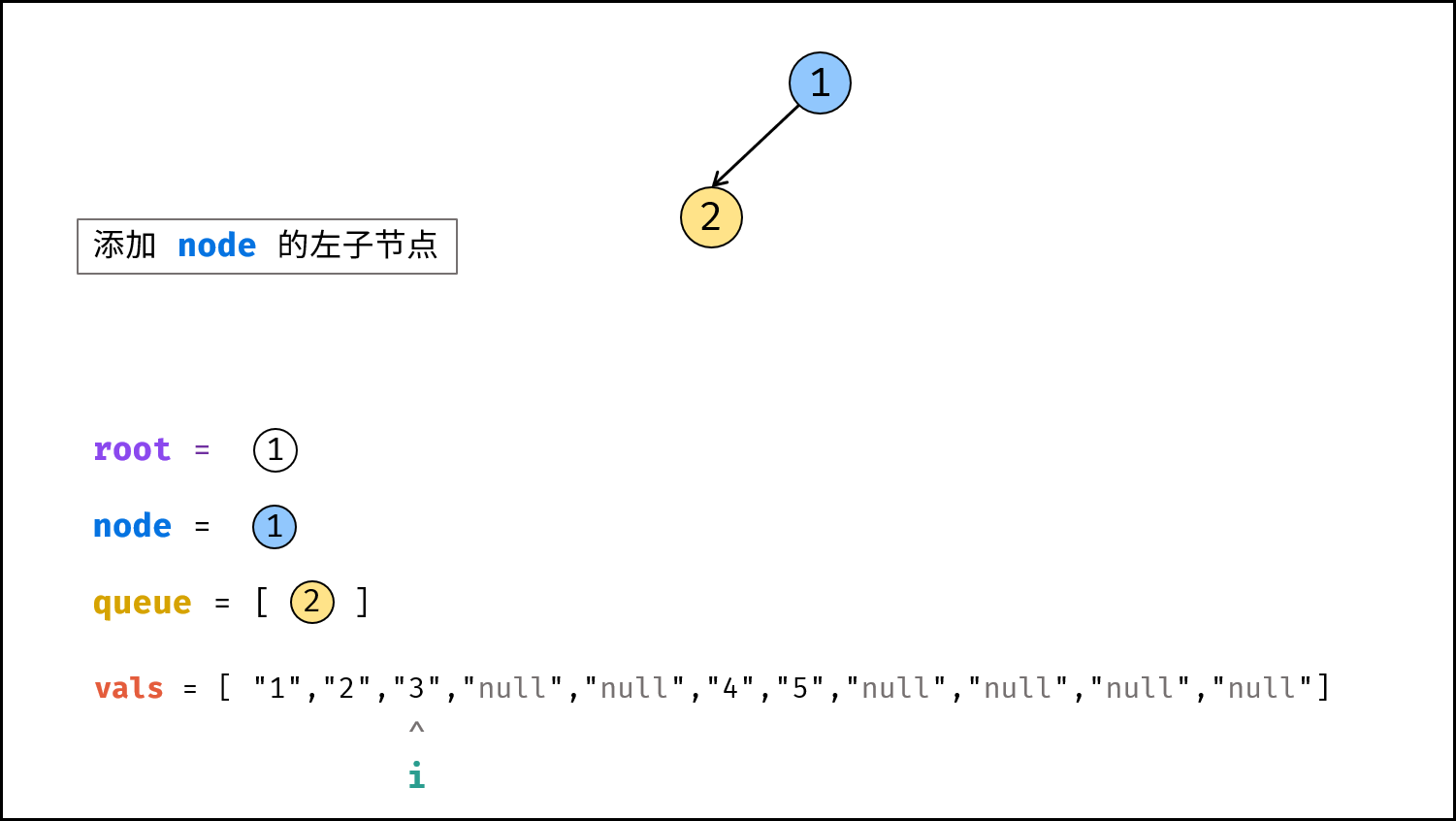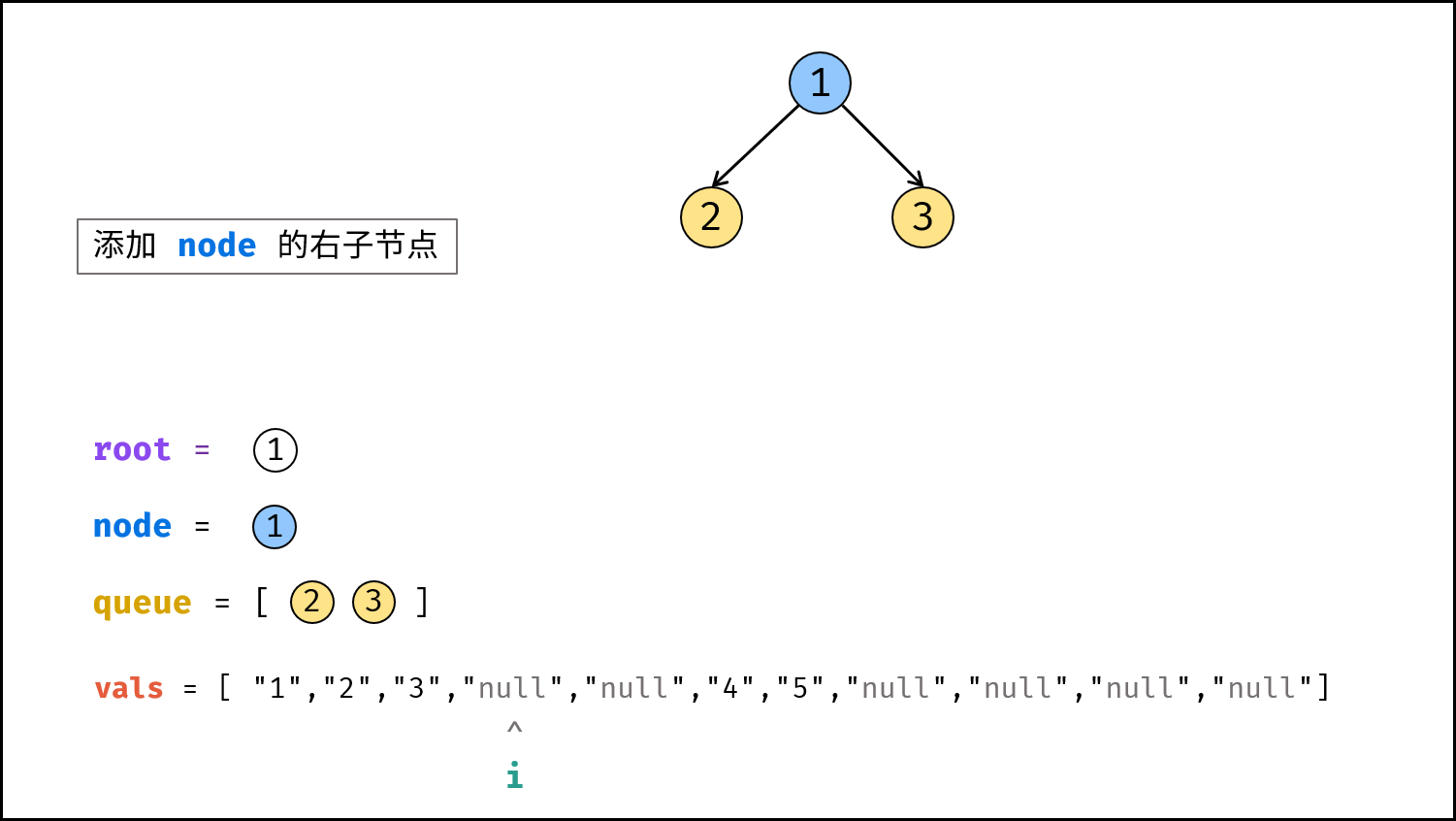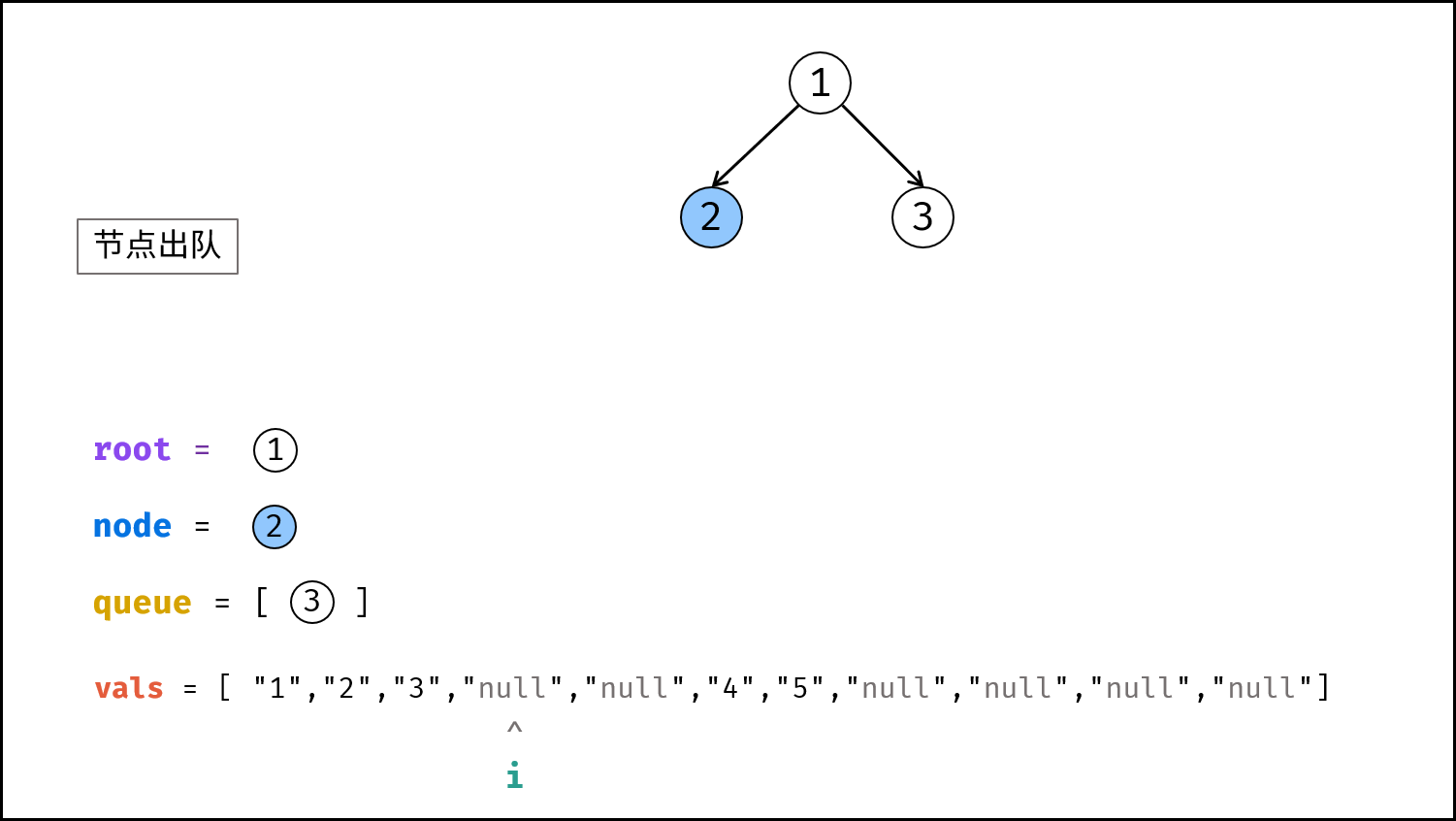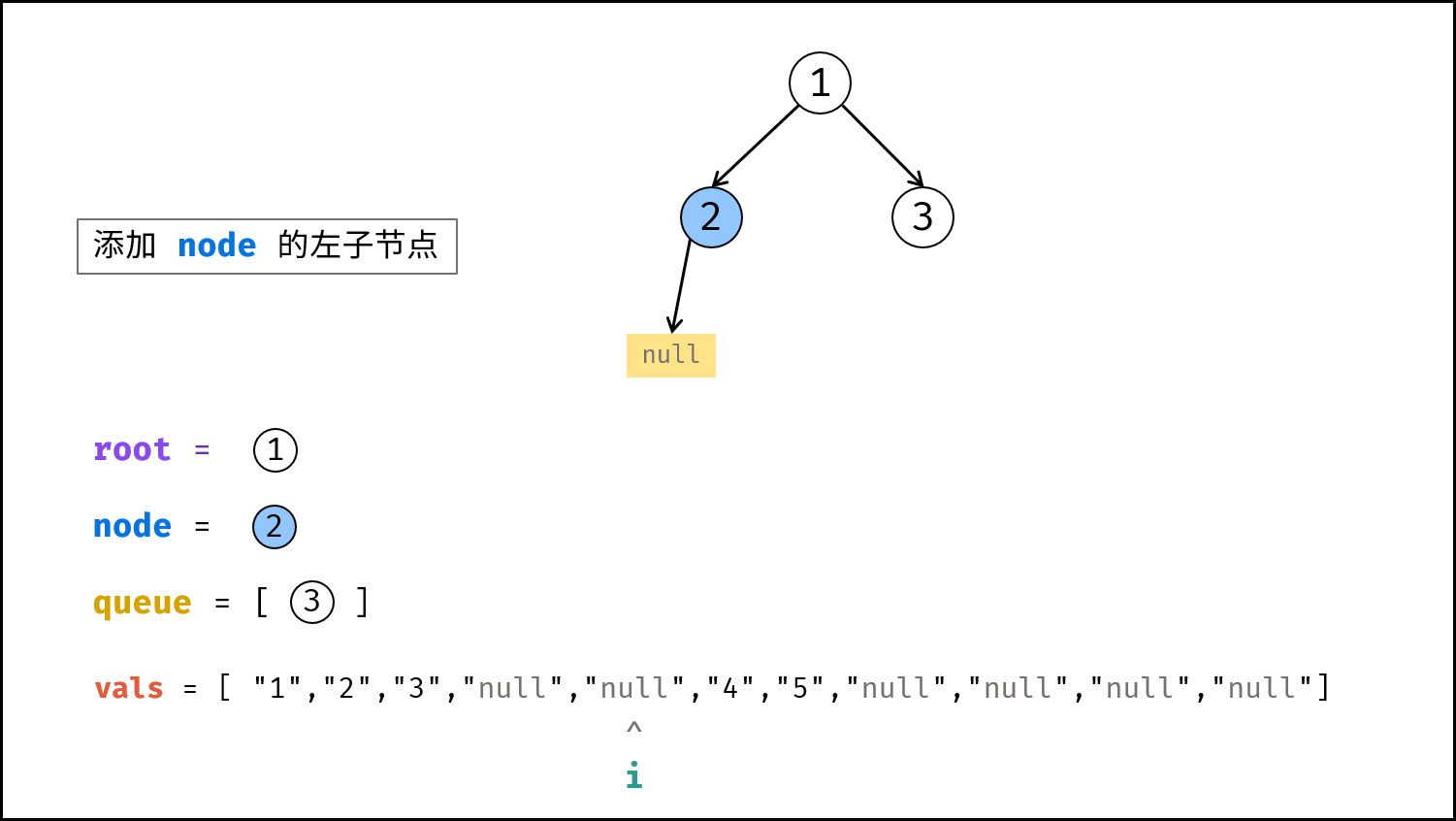<![Picture15.png](https://pic.leetcode-cn.com/1603117385-uvKOBl-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1603117385-TRsTKE-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1603117385-gHPLUg-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1603117385-GVUBJX-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1603117385-ivwlHv-Picture19.png),![Picture20.png](https://pic.leetcode-cn.com/1603117385-pIPjom-Picture20.png),![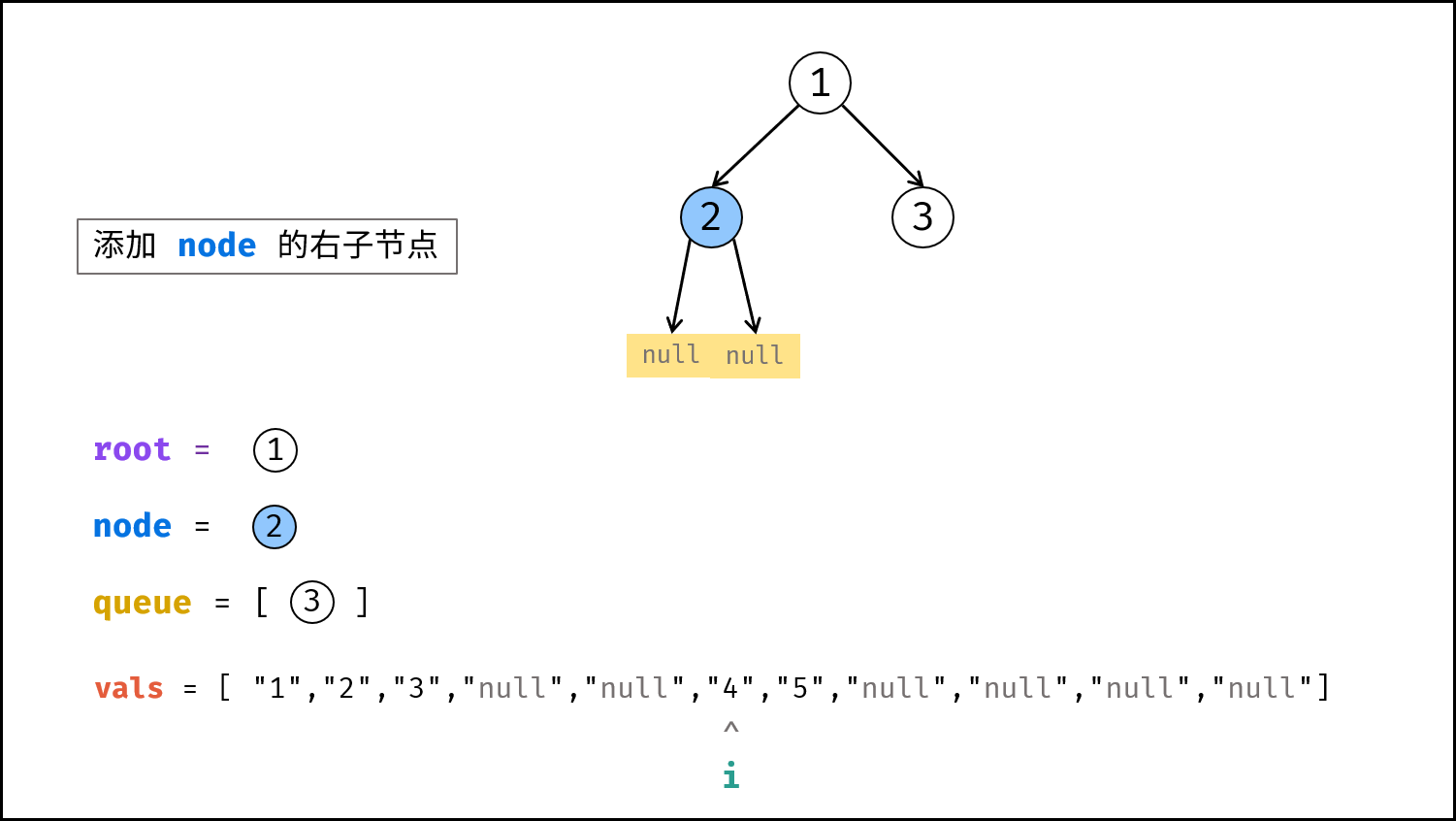Picture21.png](https://pic.leetcode-cn.com/1603117385-NyaOkB-Picture21.png),![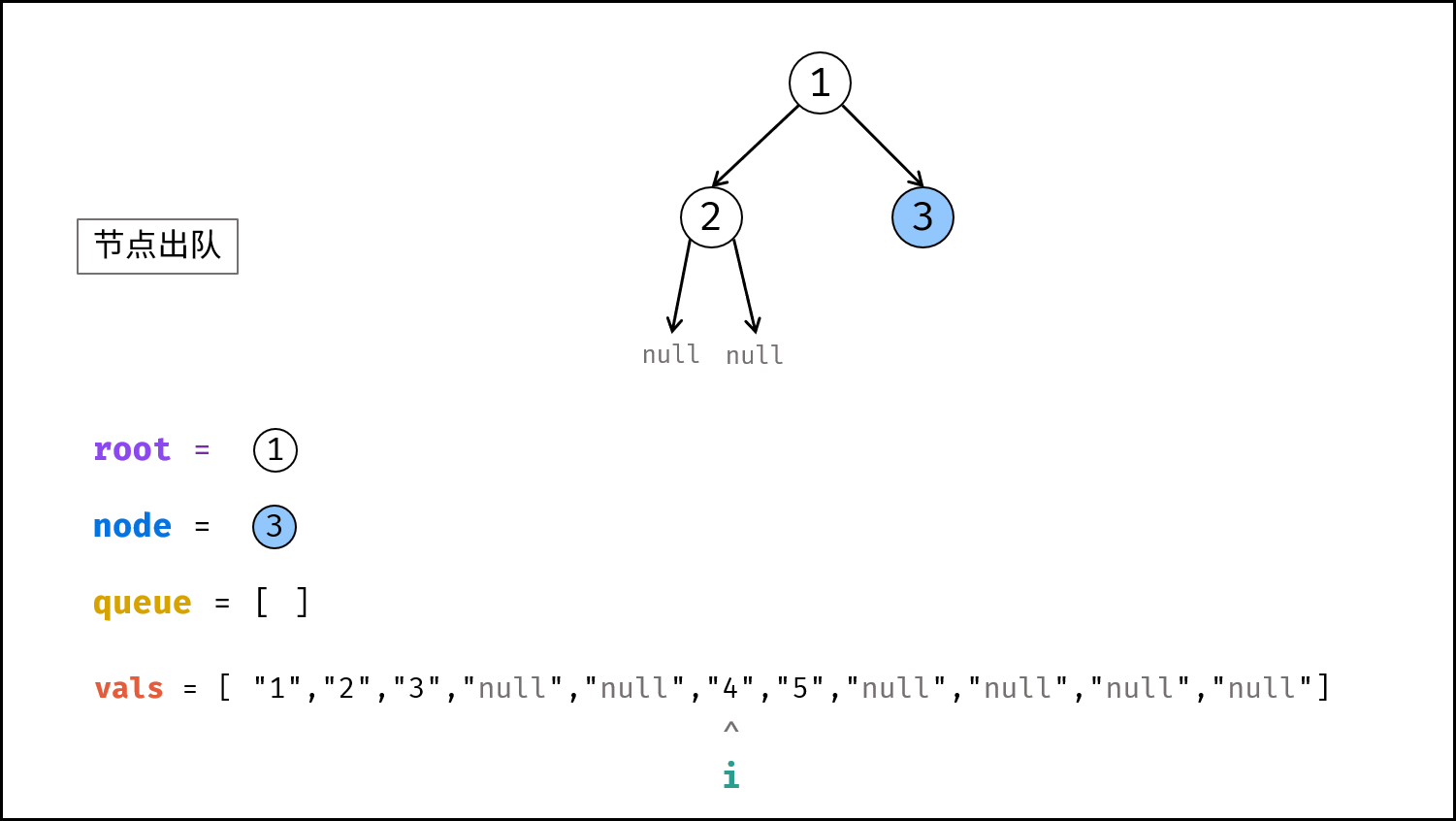Picture22.png](https://pic.leetcode-cn.com/1603117385-dKntBu-Picture22.png),![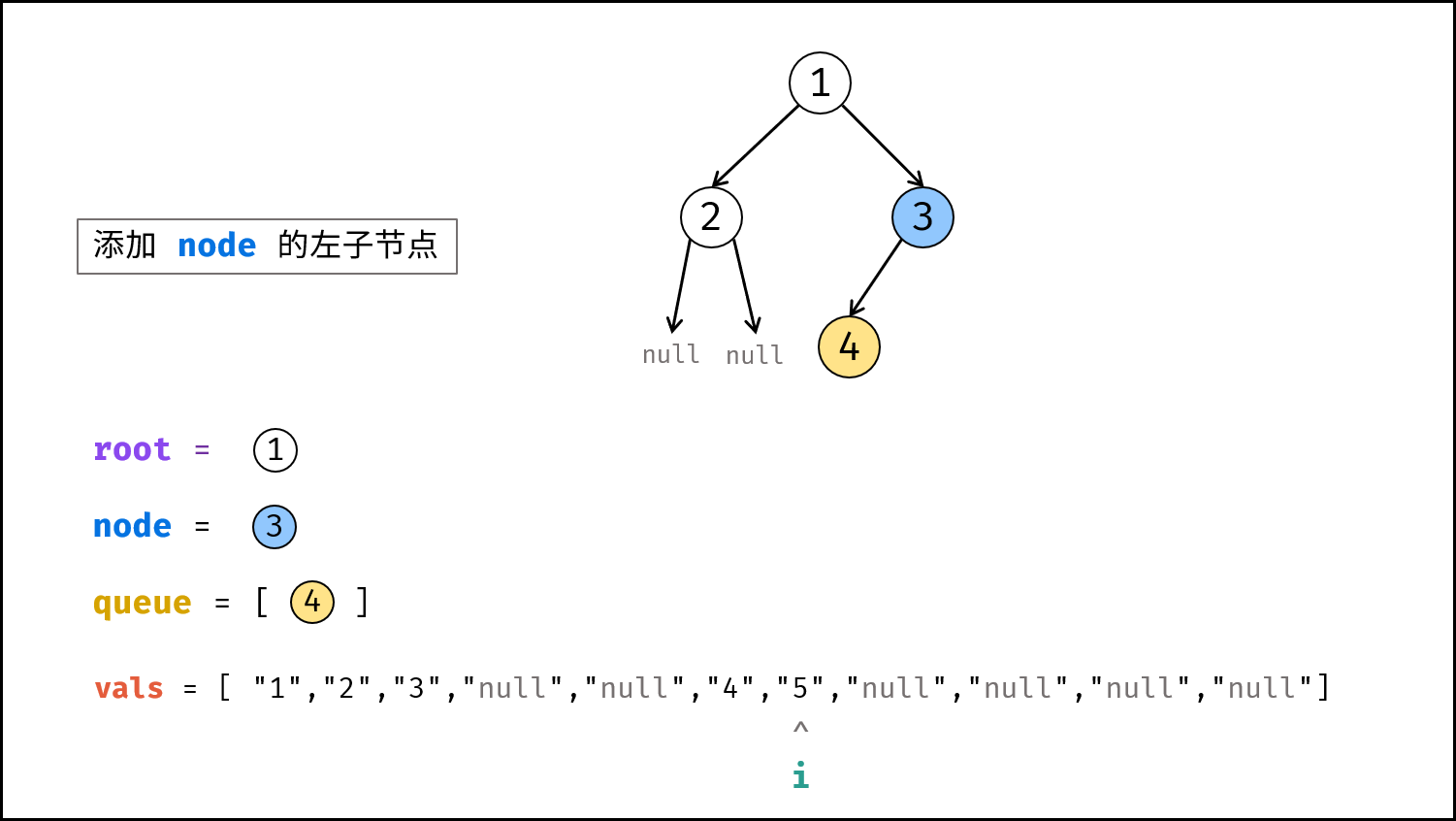Picture23.png](https://pic.leetcode-cn.com/1603117385-QbdFOw-Picture23.png),![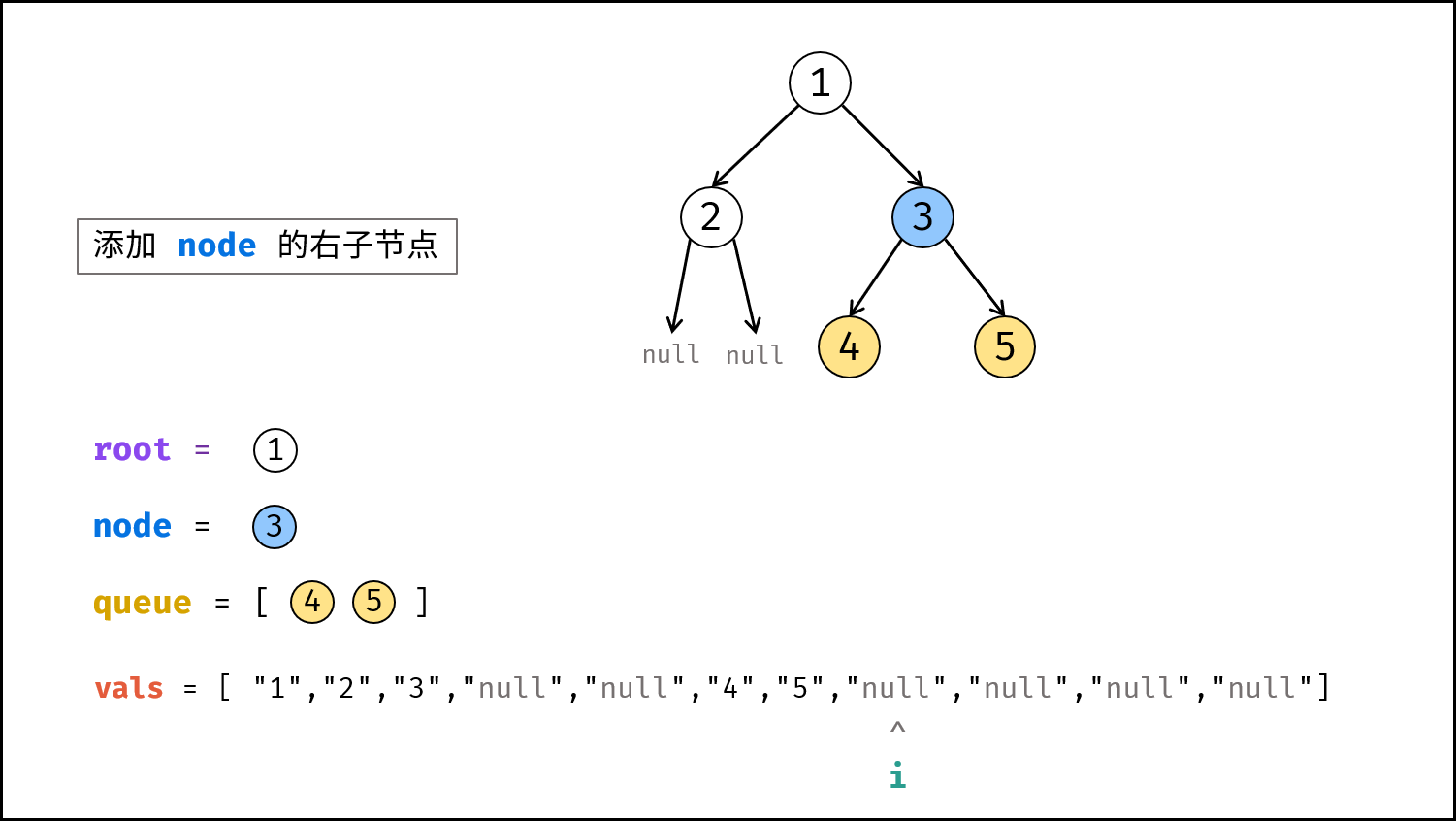Picture24.png](https://pic.leetcode-cn.com/1603117385-vctarq-Picture24.png),![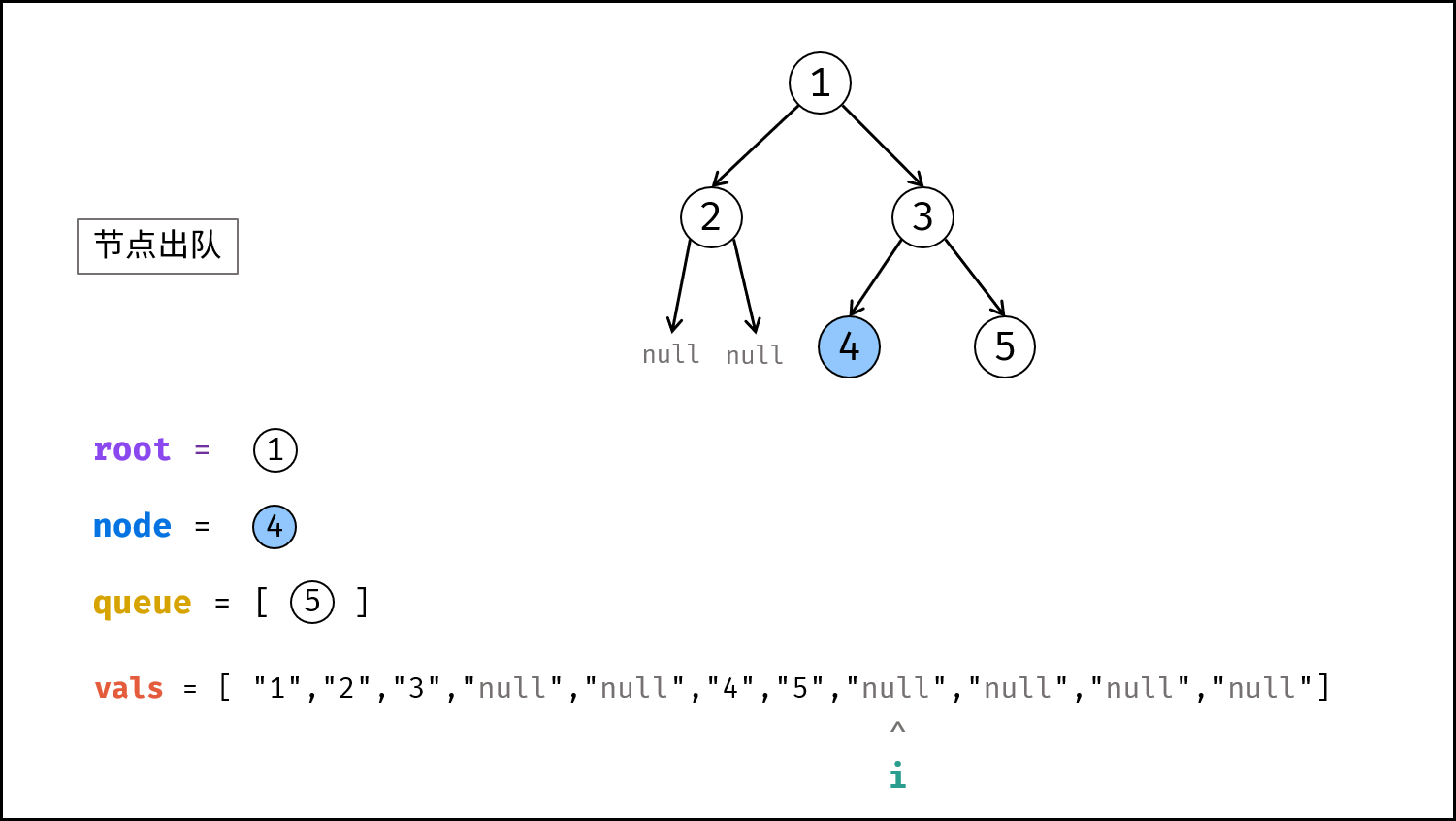Picture25.png](https://pic.leetcode-cn.com/1603117385-uGbitX-Picture25.png),![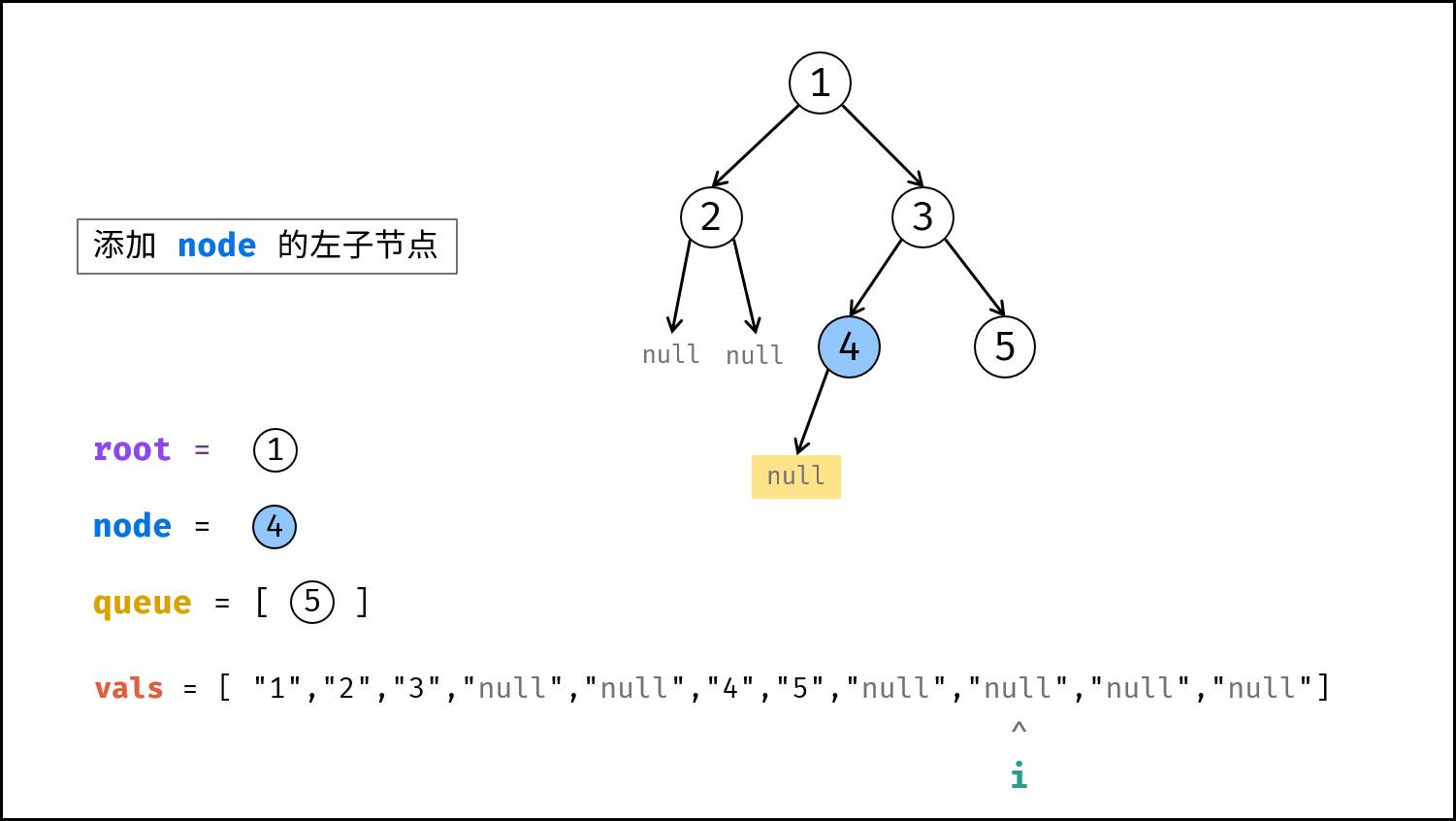Picture26.png](https://pic.leetcode-cn.com/1603117385-hLRmwd-Picture26.png),![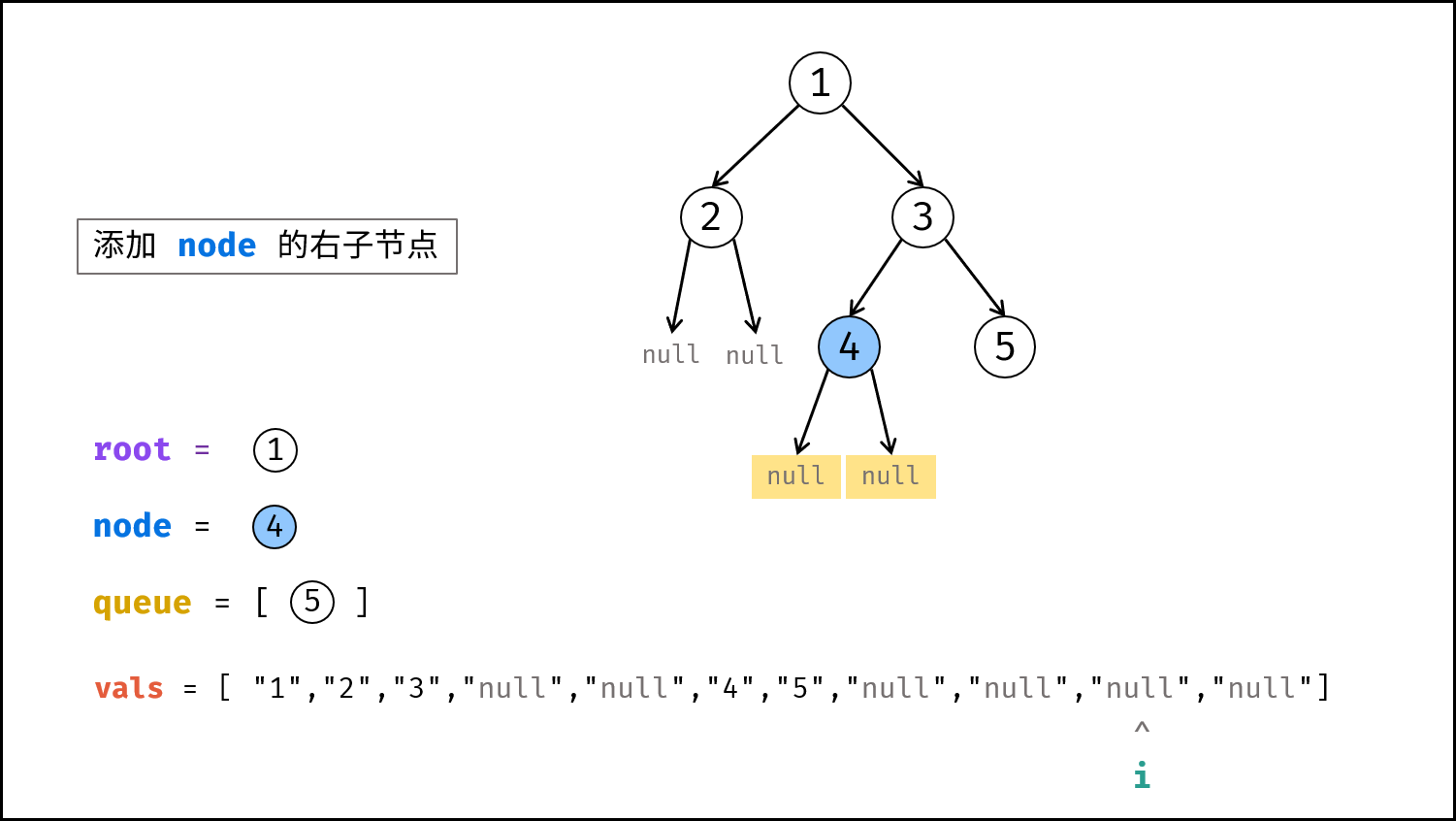Picture27.png](https://pic.leetcode-cn.com/1603117385-Hfyuyj-Picture27.png),![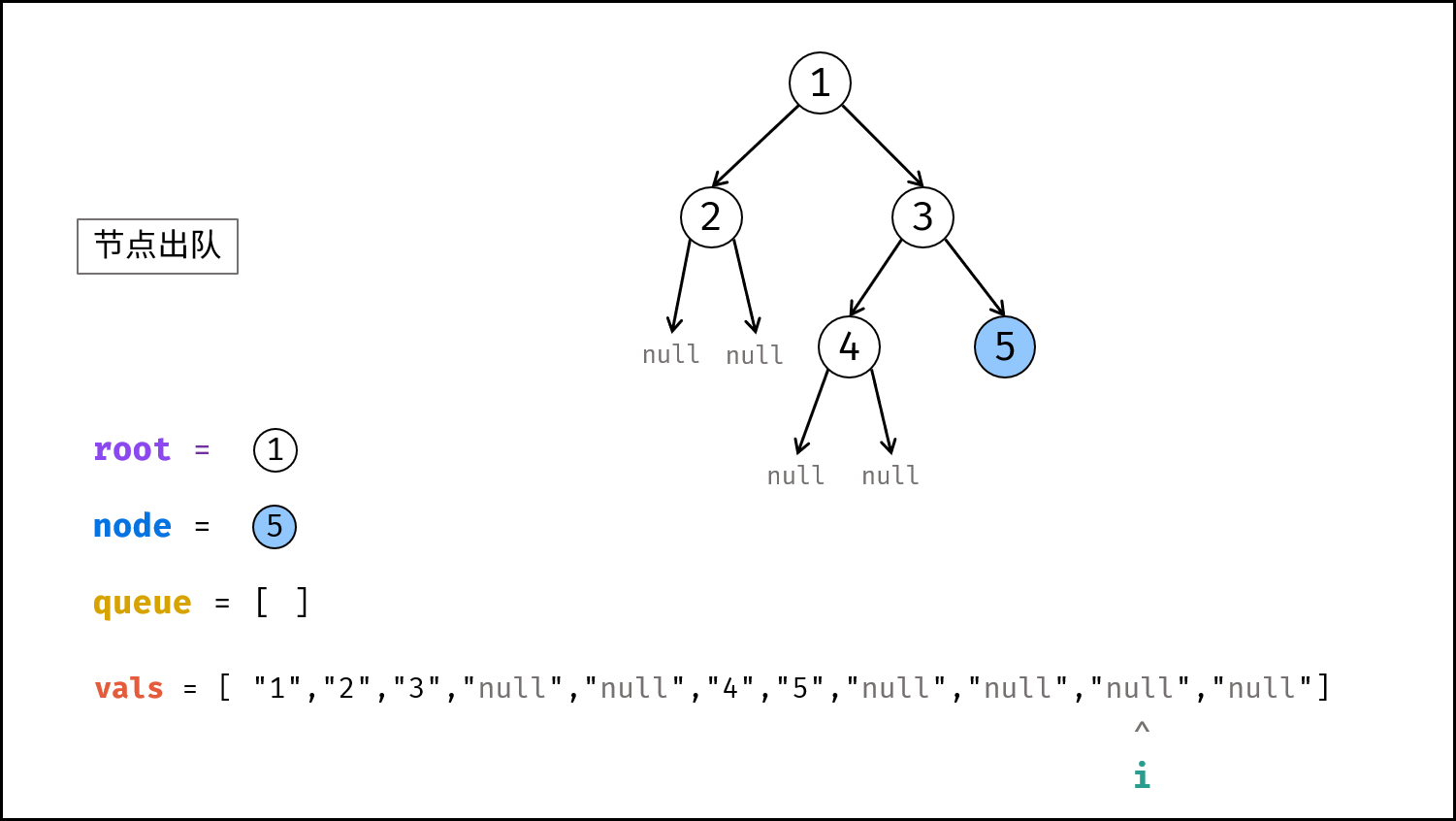Picture28.png](https://pic.leetcode-cn.com/1603117385-jKTBKw-Picture28.png),![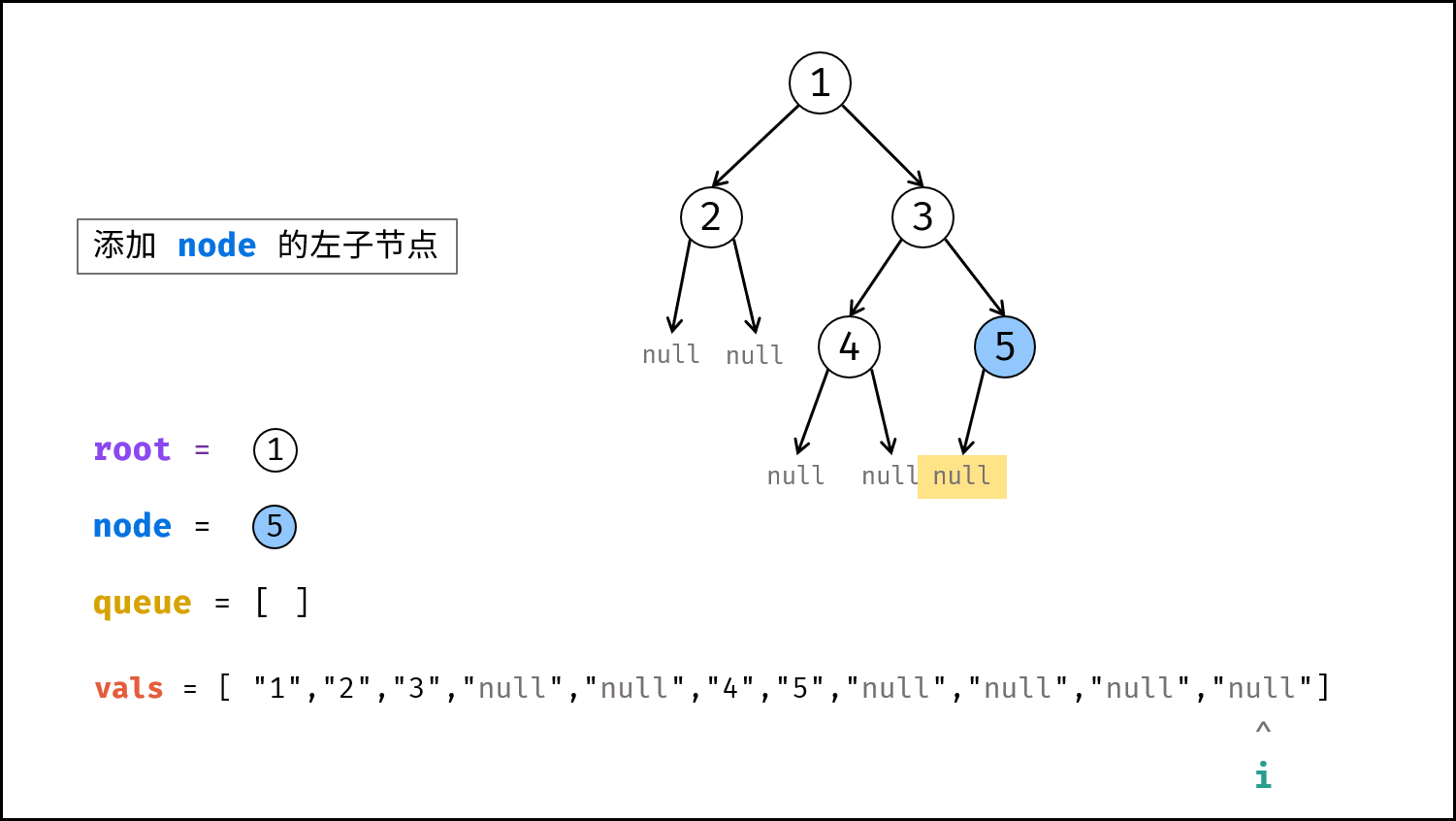Picture29.png](https://pic.leetcode-cn.com/1603117385-uvlvyV-Picture29.png),![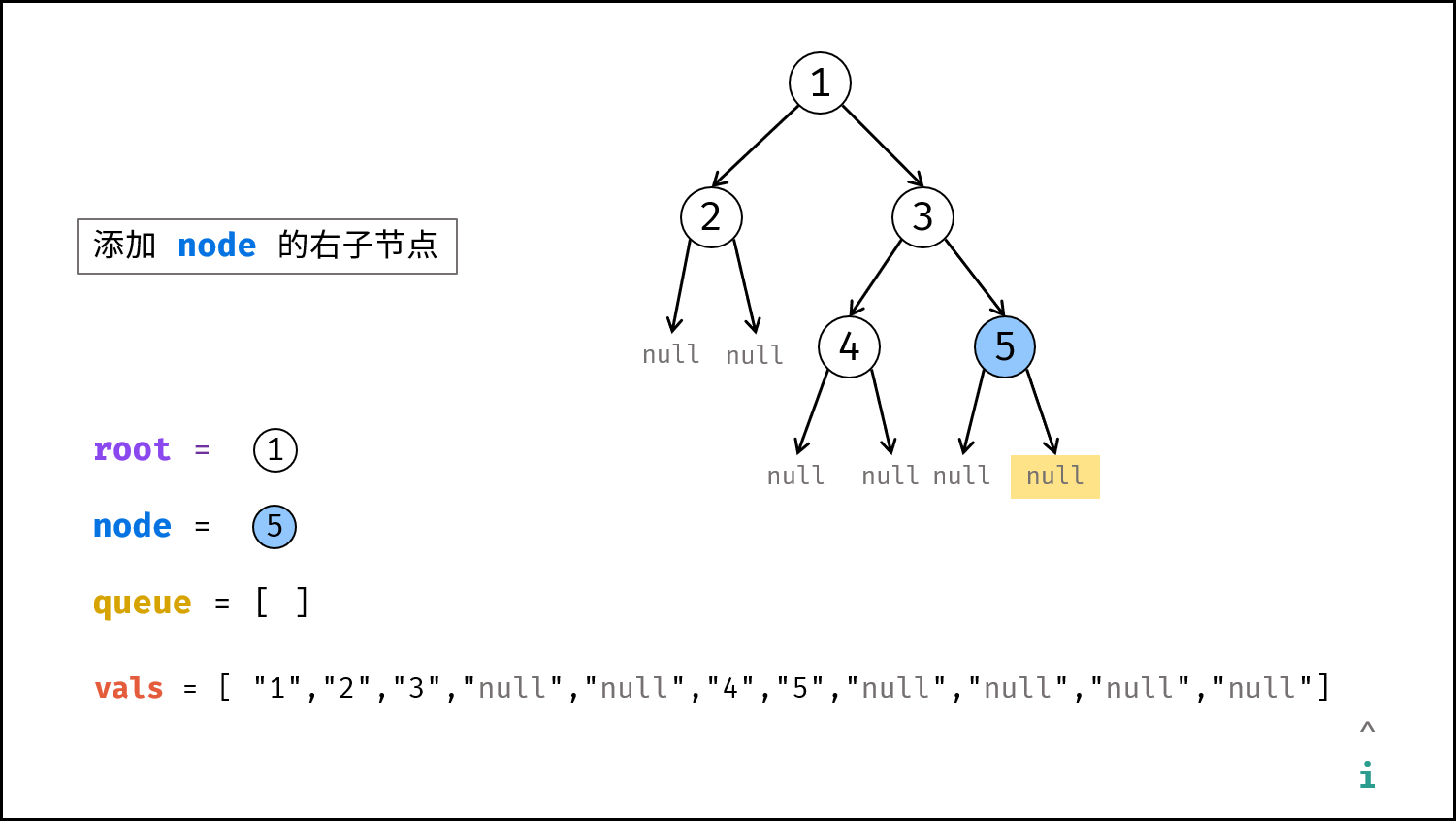Picture30.png](https://pic.leetcode-cn.com/1603117385-OKajxr-Picture30.png),![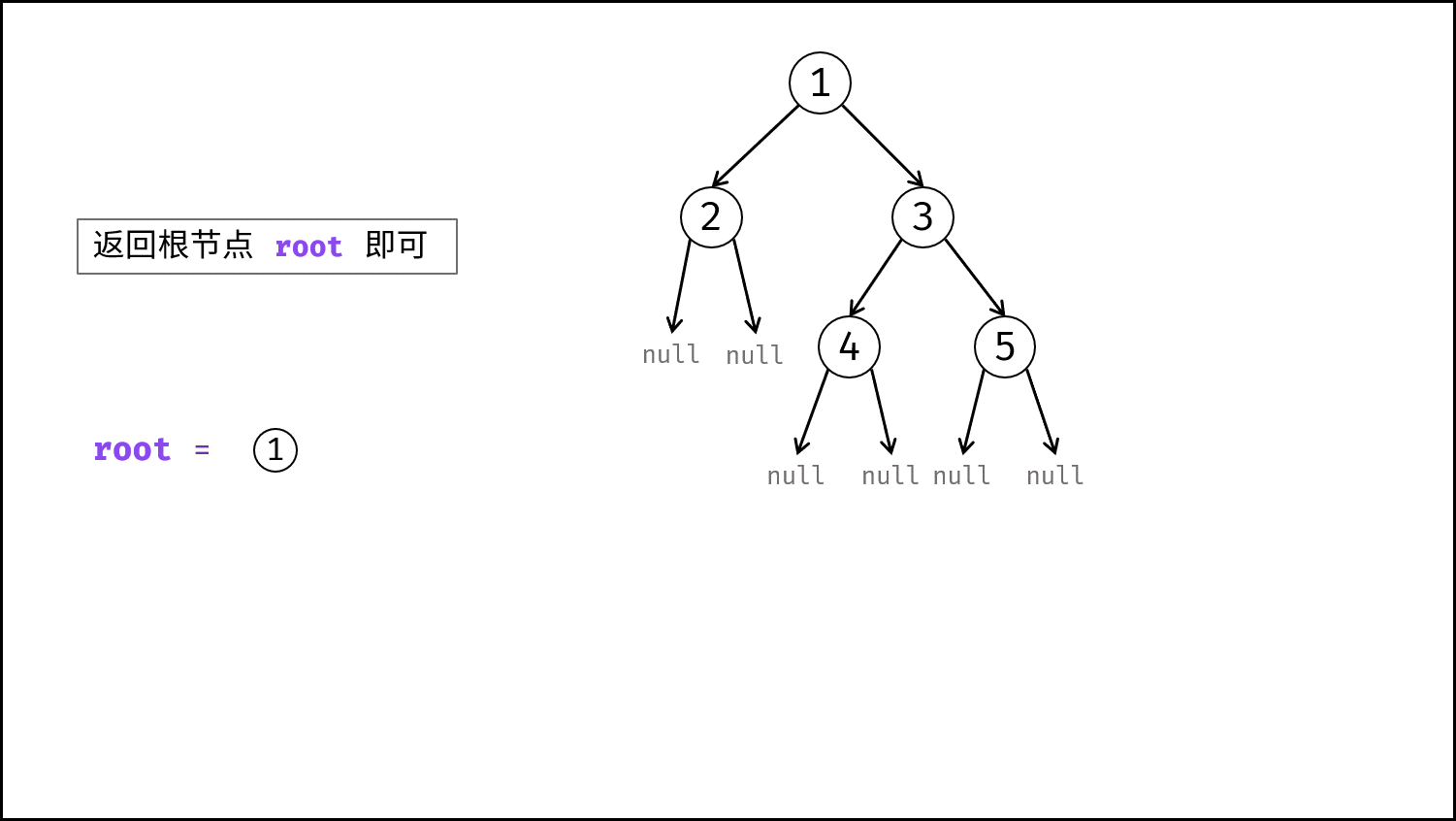Picture31.png](https://pic.leetcode-cn.com/1603117385-wkwBBw-Picture31.png)>
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为二叉树的节点数，按层构建二叉树需要遍历整个 $vals$ ，其长度最大为 $2N+1$ 。
- **空间复杂度 $O(N)$ ：** 最差情况下，队列 `queue` 同时存储 $\frac{N + 1}{2}$ 个节点，因此使用 $O(N)$ 额外空间。
## 代码：
```Python []
class Codec:
def serialize(self, root):
if not root: return "[]"
queue = collections.deque()
queue.append(root)
res = []
while queue:
node = queue.popleft()
if node:
res.append(str(node.val))
queue.append(node.left)
queue.append(node.right)
else: res.append("null")
return '[' + ','.join(res) + ']'
def deserialize(self, data):
if data == "[]": return
vals, i = data[1:-1].split(','), 1
root = TreeNode(int(vals[0]))
queue = collections.deque()
queue.append(root)
while queue:
node = queue.popleft()
if vals[i] != "null":
node.left = TreeNode(int(vals[i]))
queue.append(node.left)
i += 1
if vals[i] != "null":
node.right = TreeNode(int(vals[i]))
queue.append(node.right)
i += 1
return root
```
```Java []
public class Codec {
public String serialize(TreeNode root) {
if(root == null) return "[]";
StringBuilder res = new StringBuilder("[");
Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
if(node != null) {
res.append(node.val + ",");
queue.add(node.left);
queue.add(node.right);
}
else res.append("null,");
}
res.deleteCharAt(res.length() - 1);
res.append("]");
return res.toString();
}
public TreeNode deserialize(String data) {
if(data.equals("[]")) return null;
String[] vals = data.substring(1, data.length() - 1).split(",");
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
int i = 1;
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
if(!vals[i].equals("null")) {
node.left = new TreeNode(Integer.parseInt(vals[i]));
queue.add(node.left);
}
i++;
if(!vals[i].equals("null")) {
node.right = new TreeNode(Integer.parseInt(vals[i]));
queue.add(node.right);
}
i++;
}
return root;
}
}
```

117
leetbook_ioa/docs/LCR 157. 套餐内商品的排列顺序.md Executable file
View File

@@ -0,0 +1,117 @@
## 解题思路：
对于一个长度为 $n$ 的字符串（假设字符互不重复），其排列方案数共有：
$$
n \times (n-1) \times (n-2) … \times 2 \times 1
$$
**排列方案的生成：**
根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第 $1$ 位字符（ $n$ 种情况）、再固定第 $2$ 位字符（ $n-1$ 种情况）、... 、最后固定第 $n$ 位字符（ $1$ 种情况）。
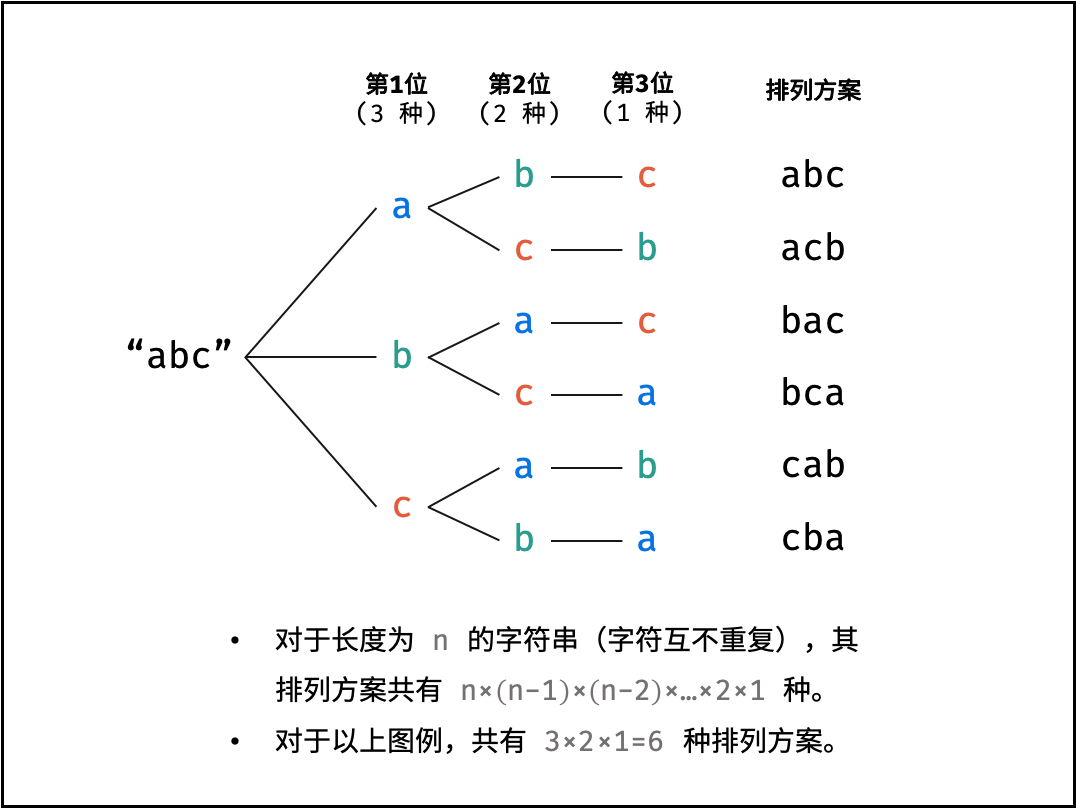![Picture1.png](https://pic.leetcode-cn.com/1599403497-KXKQcp-Picture1.png){:align=center width=500}
**重复排列方案与剪枝：**
当字符串存在重复字符时，排列方案中也存在重复的排列方案。为排除重复方案，需在固定某位字符时，保证 “每种字符只在此位固定一次” ，即遇到重复字符时不交换，直接跳过。从 DFS 角度看，此操作称为 “剪枝” 。
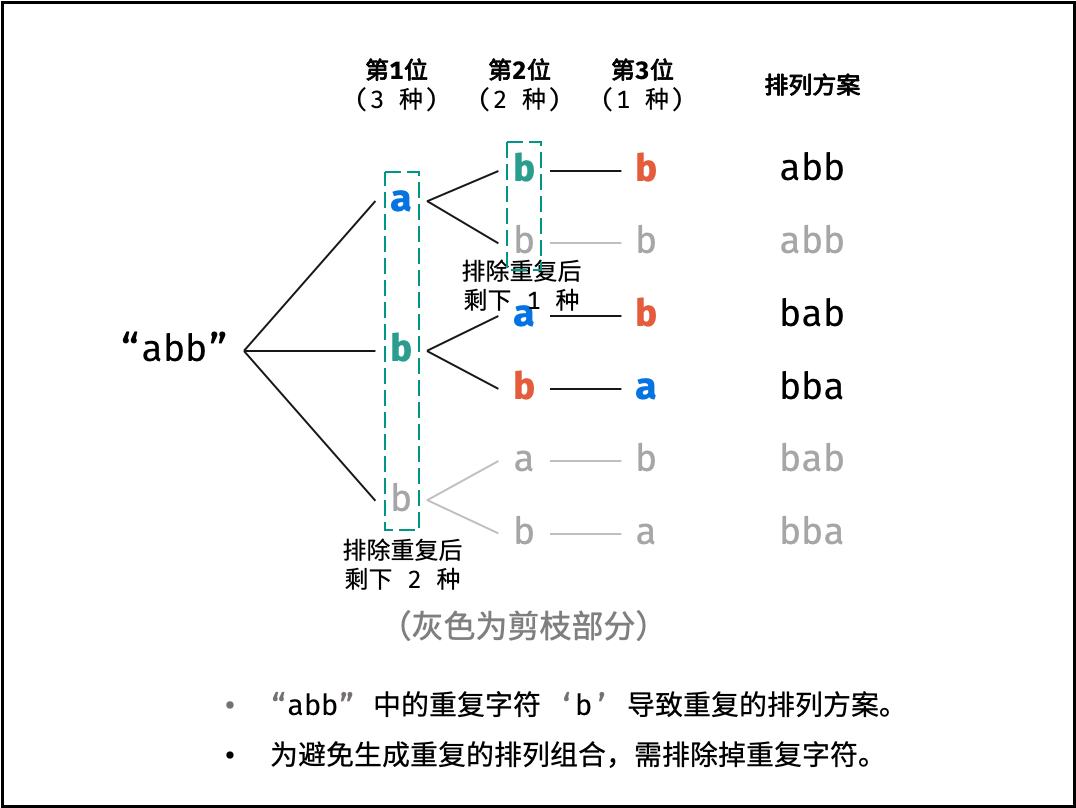![Picture2.png](https://pic.leetcode-cn.com/1599403497-GATdFr-Picture2.png){:align=center width=500}
### 递归解析：
1. **终止条件：** 当 `x = len(arr) - 1` 时，代表所有位已固定（最后一位只有 $1$ 种情况），则将当前组合 `arr` 转化为字符串并加入 `res` ，并返回；
2. **递推参数：** 当前固定位 `x` ；
3. **递推工作：** 初始化一个 Set ，用于排除重复的字符；将第 `x` 位字符与 `i` $\in$ `[x, len(arr)]` 字符分别交换，并进入下层递归；
1. **剪枝：** 若 `arr[i]` 在 Set​ 中，代表其是重复字符，因此 “剪枝” ；
2. 将 `arr[i]` 加入 Set​ ，以便之后遇到重复字符时剪枝；
3. **固定字符：** 将字符 `arr[i]` 和 `arr[x]` 交换，即固定 `arr[i]` 为当前位字符；
4. **开启下层递归：** 调用 `dfs(x + 1)` ，即开始固定第 `x + 1` 个字符；
5. **还原交换：** 将字符 `arr[i]` 和 `arr[x]` 交换（还原之前的交换）；
> 下图的测试样例为 `goods = "abc"` 。
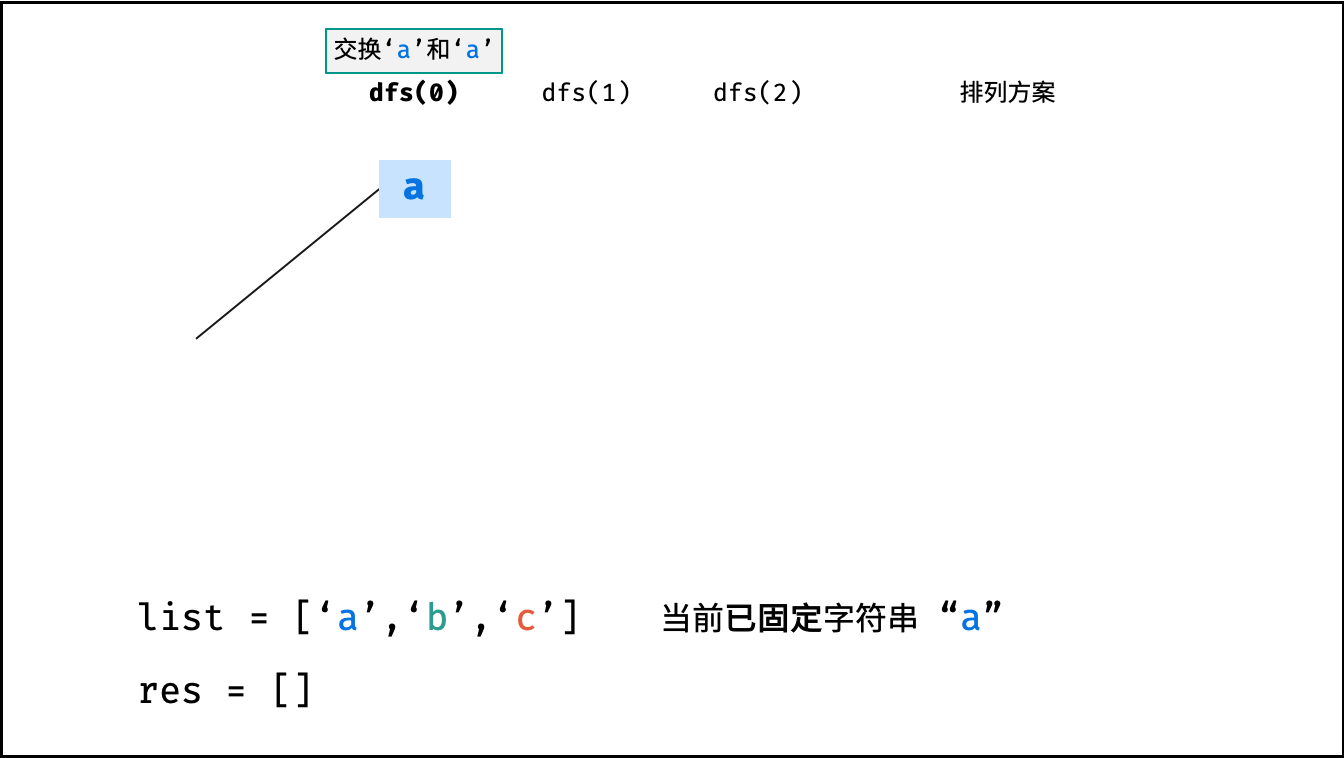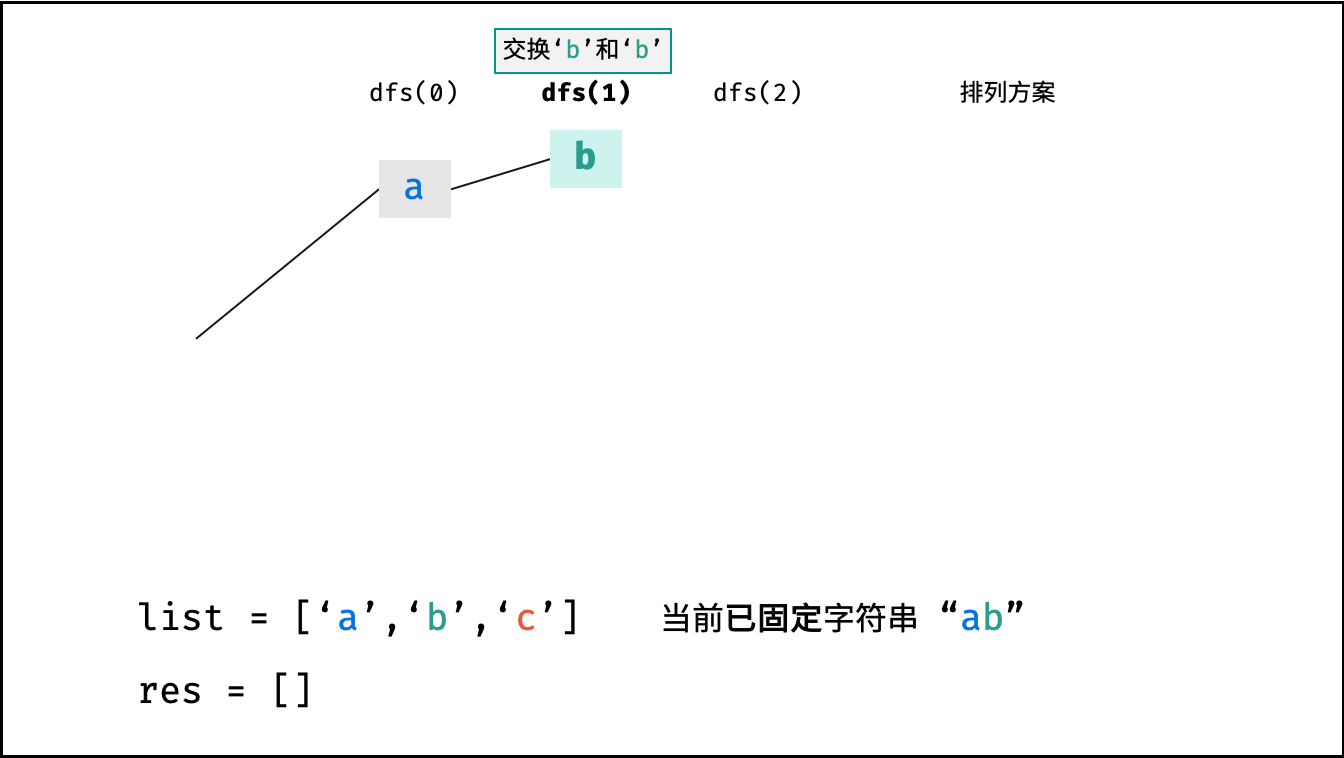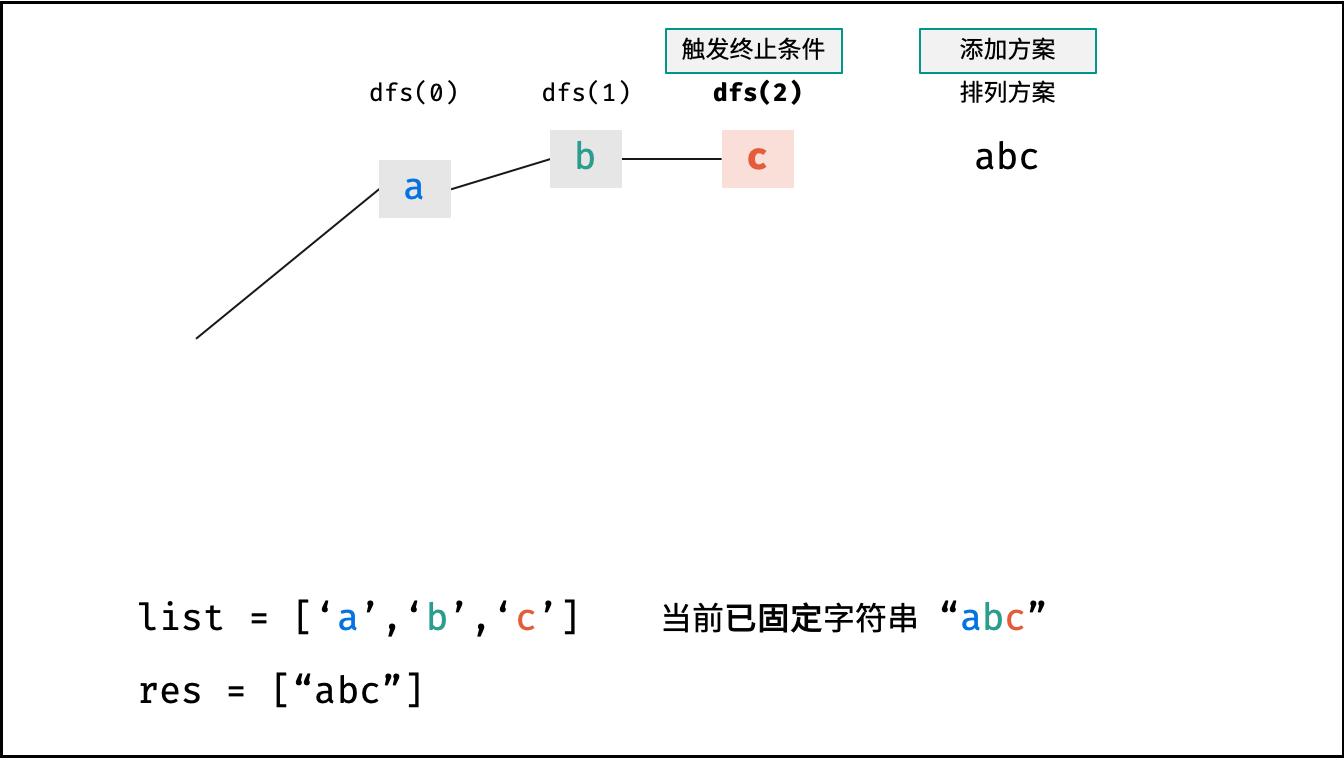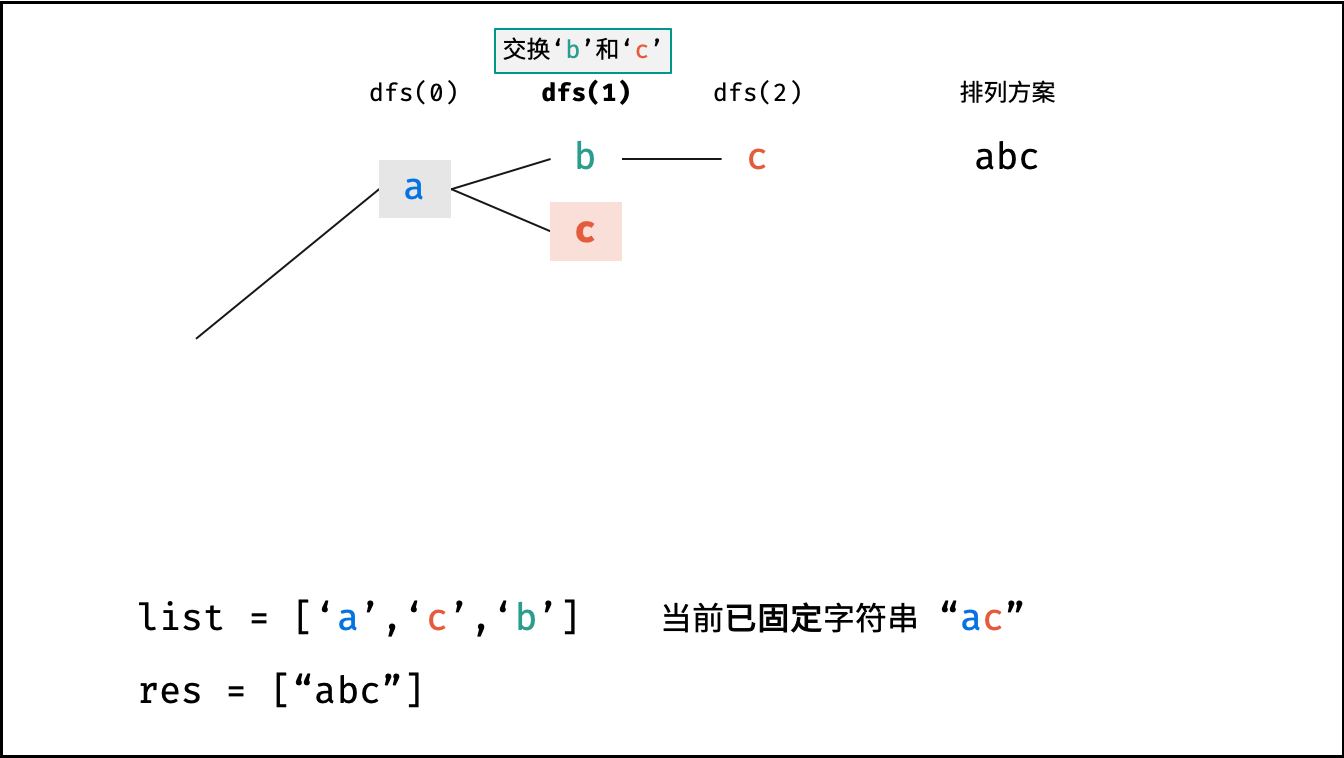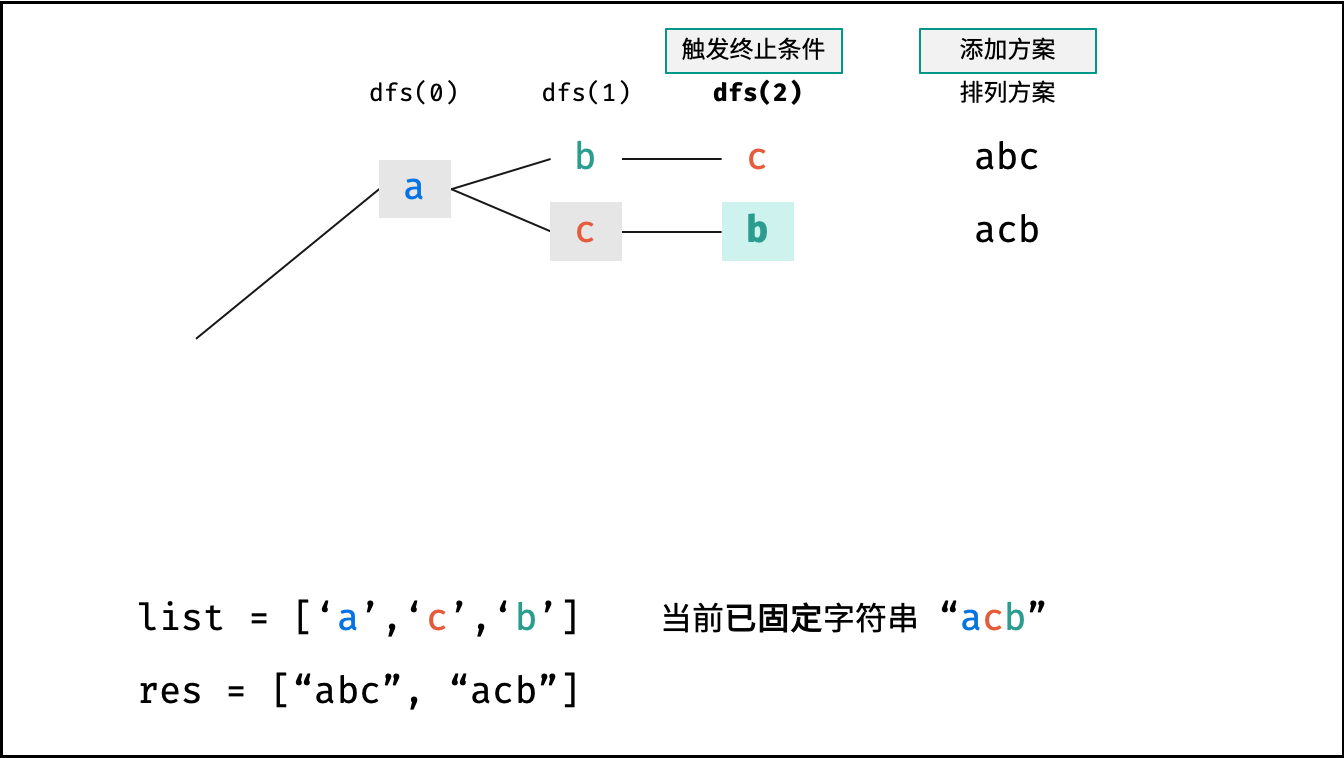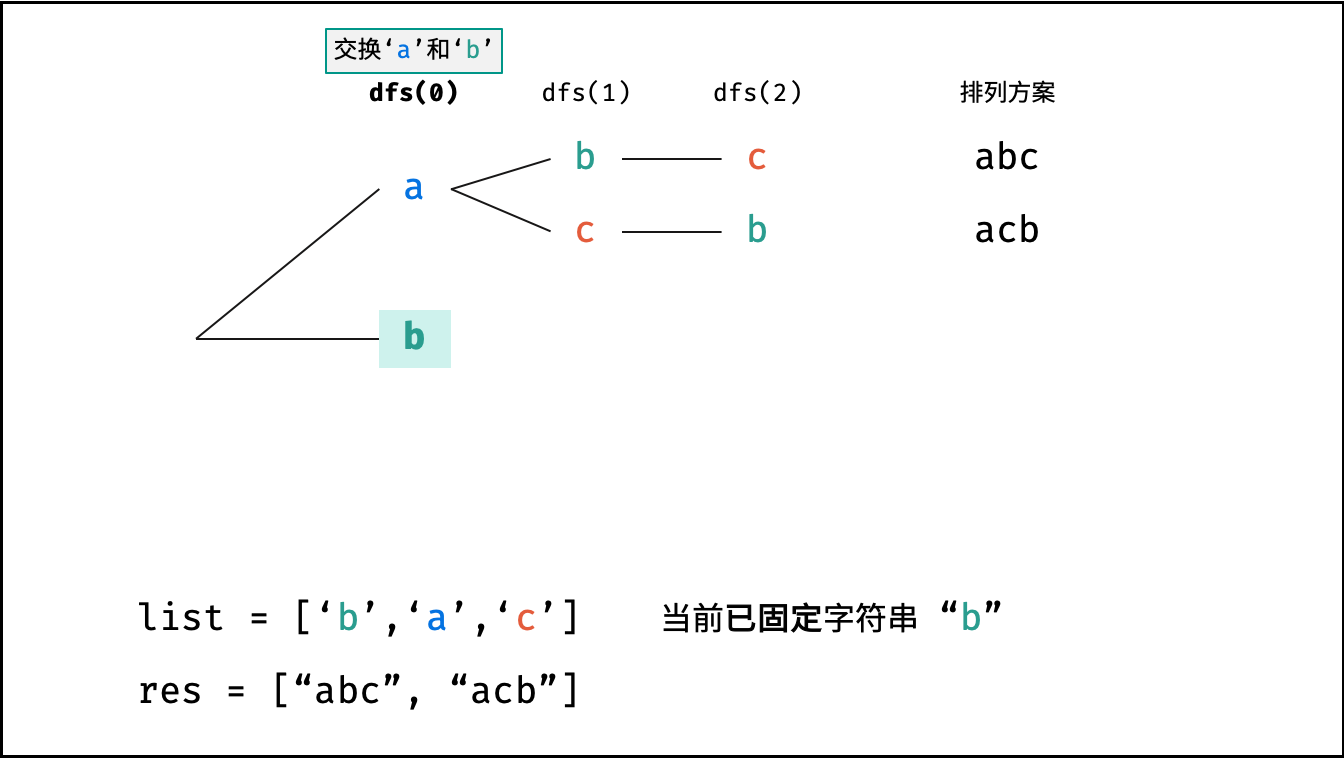<![Picture3.png](https://pic.leetcode-cn.com/1599403497-OCDfsB-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599403497-wEILvT-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599403497-eBHuvg-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599403497-hCtrpl-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599403497-BvuqQX-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599403497-QPjcfe-Picture8.png),![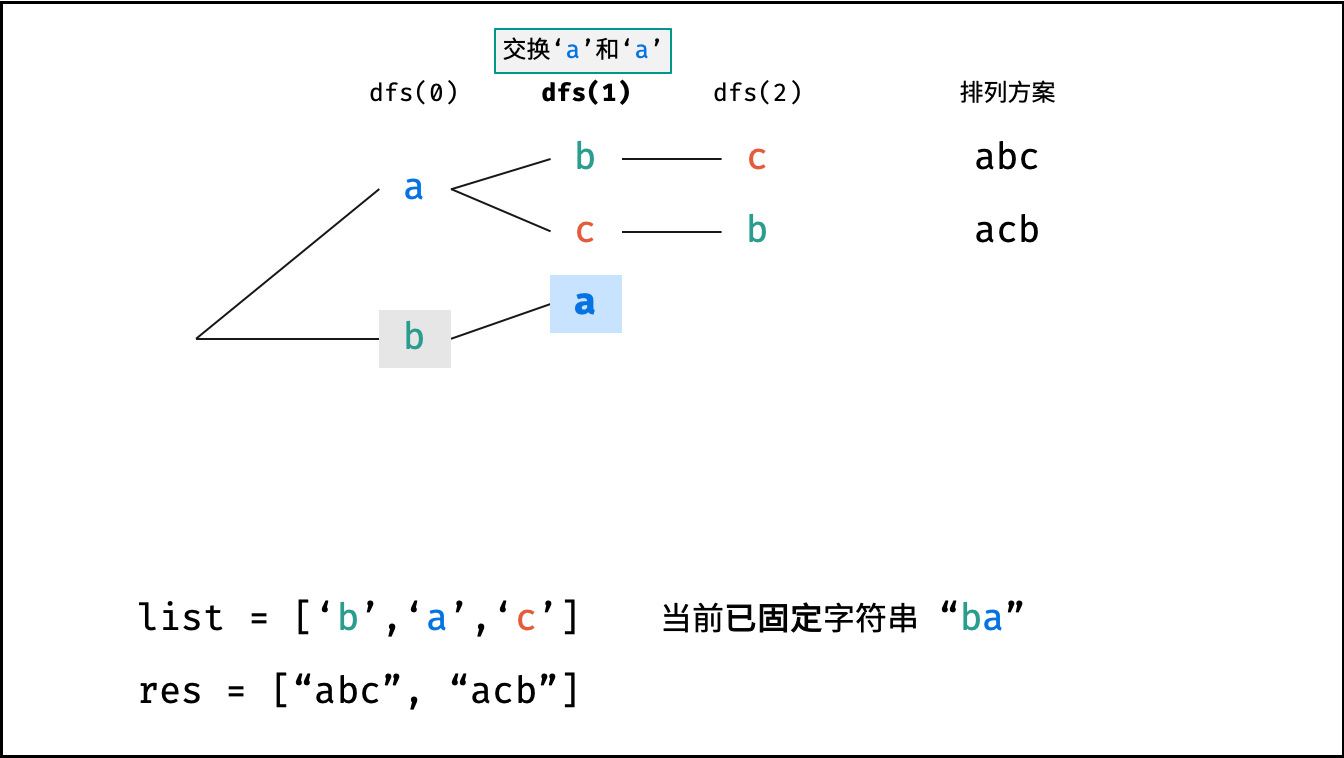Picture9.png](https://pic.leetcode-cn.com/1599403497-crBxOP-Picture9.png),![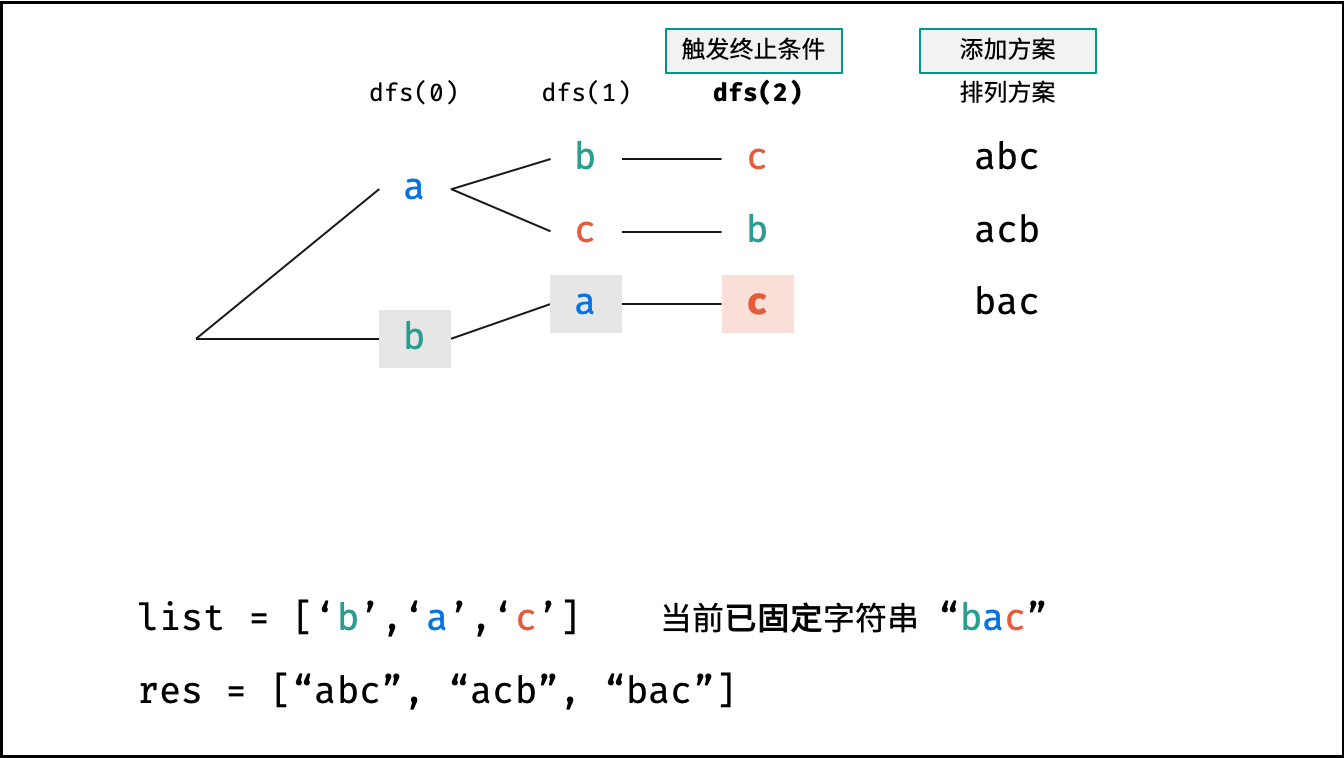Picture10.png](https://pic.leetcode-cn.com/1599403497-lwELHl-Picture10.png),![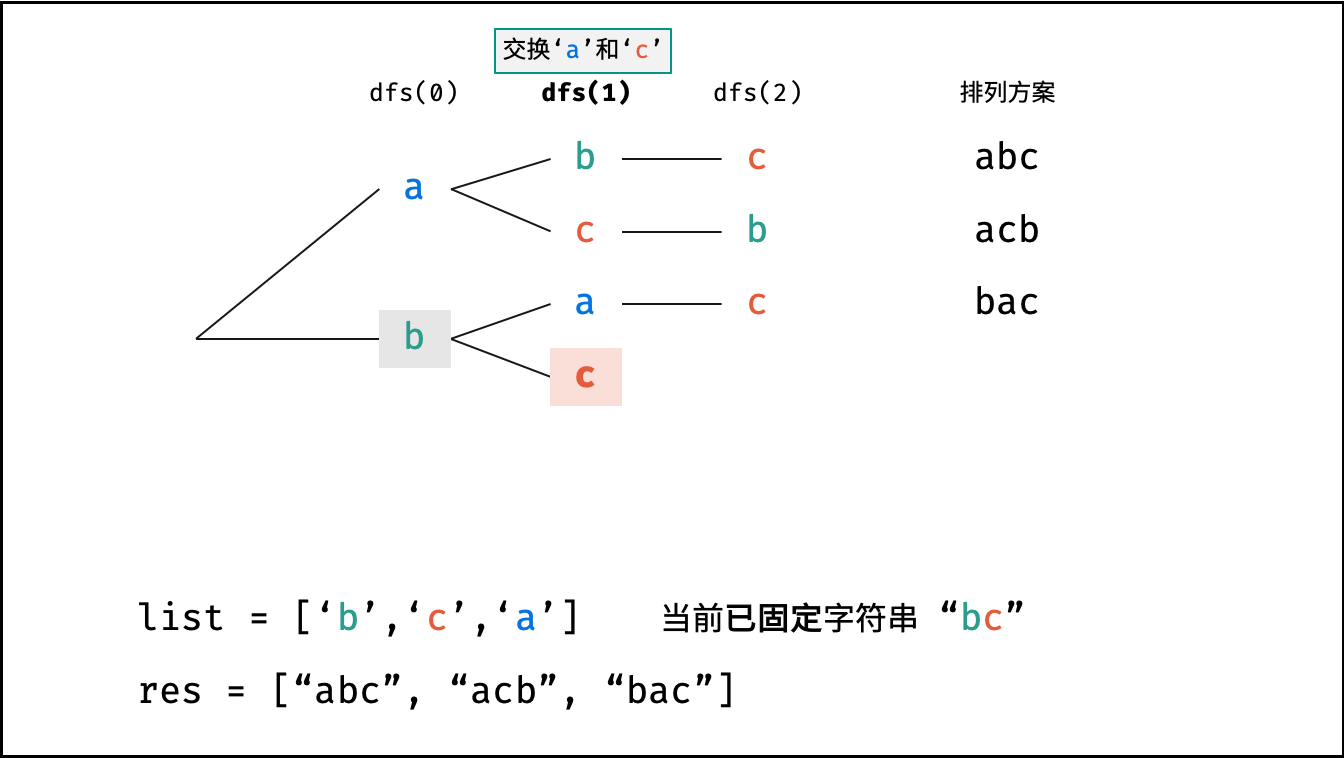Picture11.png](https://pic.leetcode-cn.com/1599403497-yjHsYa-Picture11.png),![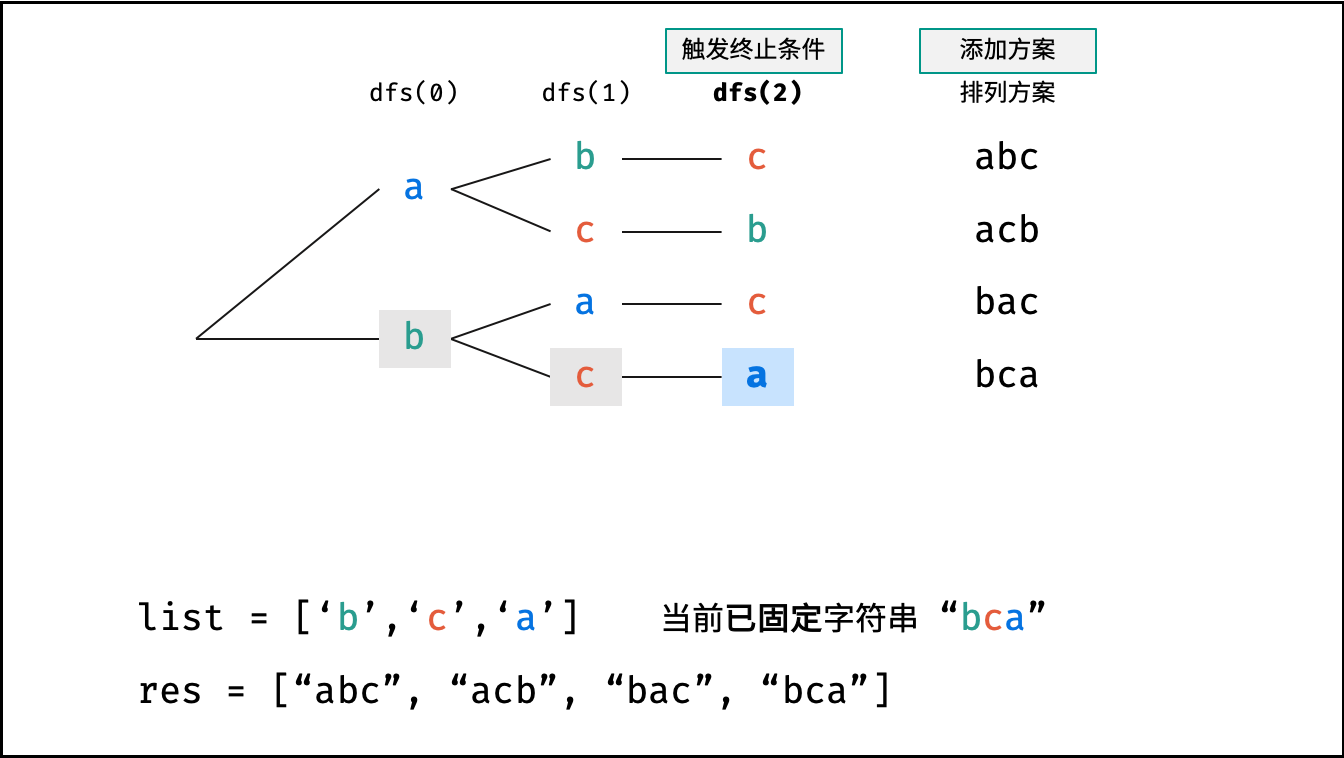Picture12.png](https://pic.leetcode-cn.com/1599403497-oYRpaR-Picture12.png),![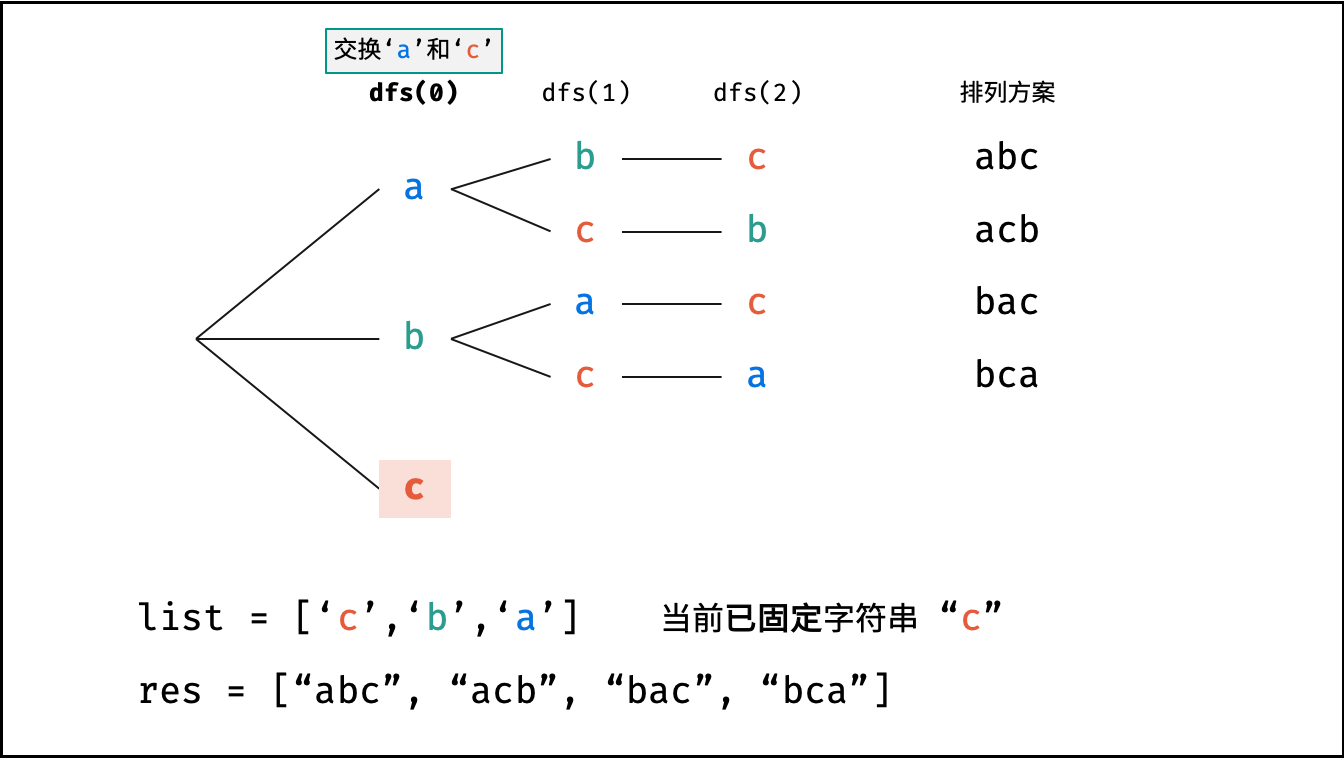Picture13.png](https://pic.leetcode-cn.com/1599403497-CadkyC-Picture13.png),![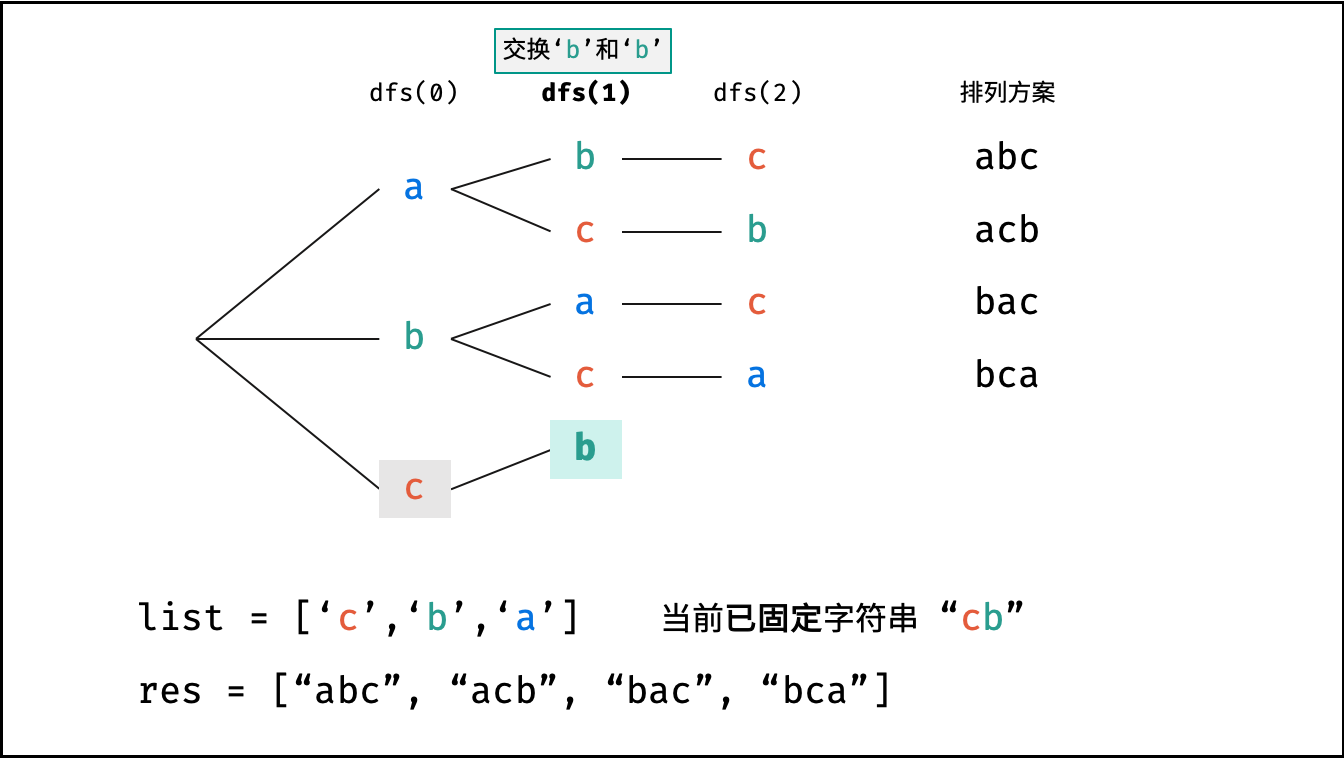Picture14.png](https://pic.leetcode-cn.com/1599403497-Sbywbs-Picture14.png),![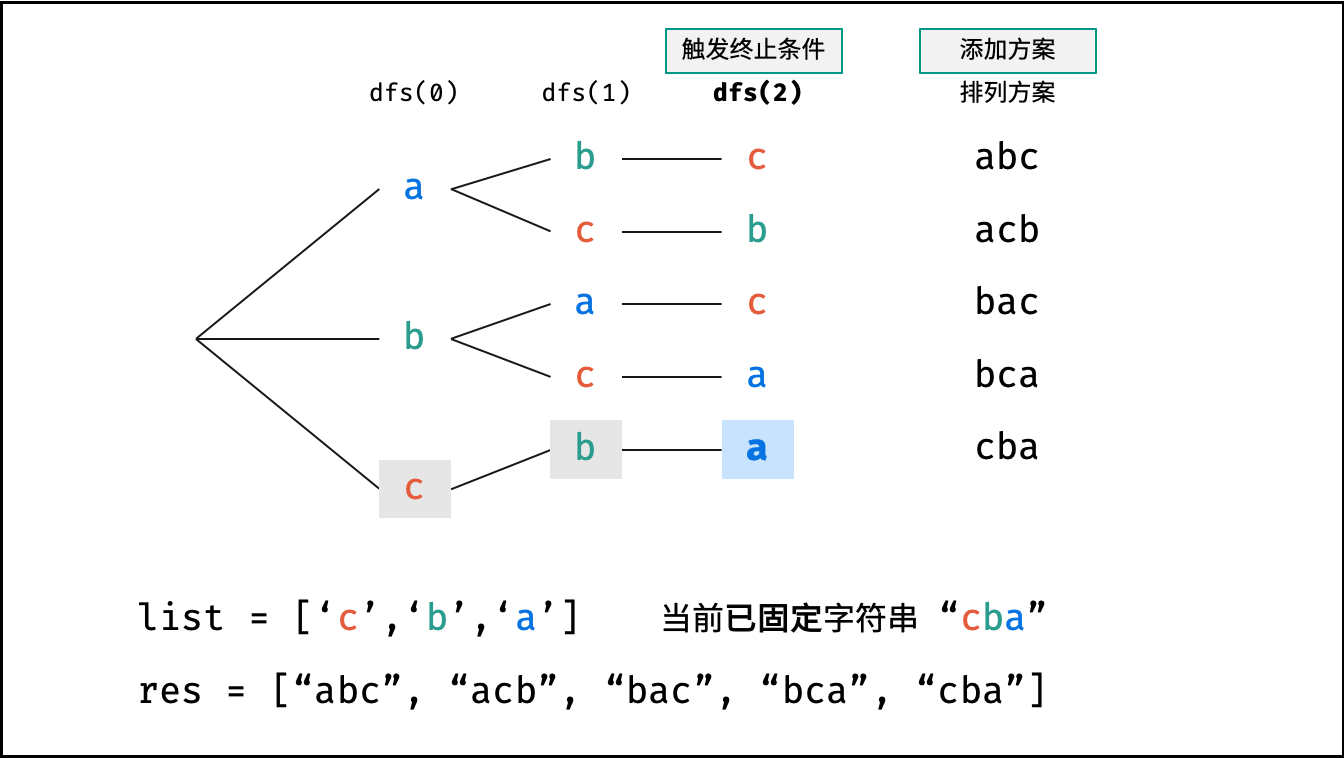Picture15.png](https://pic.leetcode-cn.com/1599403497-RNgwPK-Picture15.png),![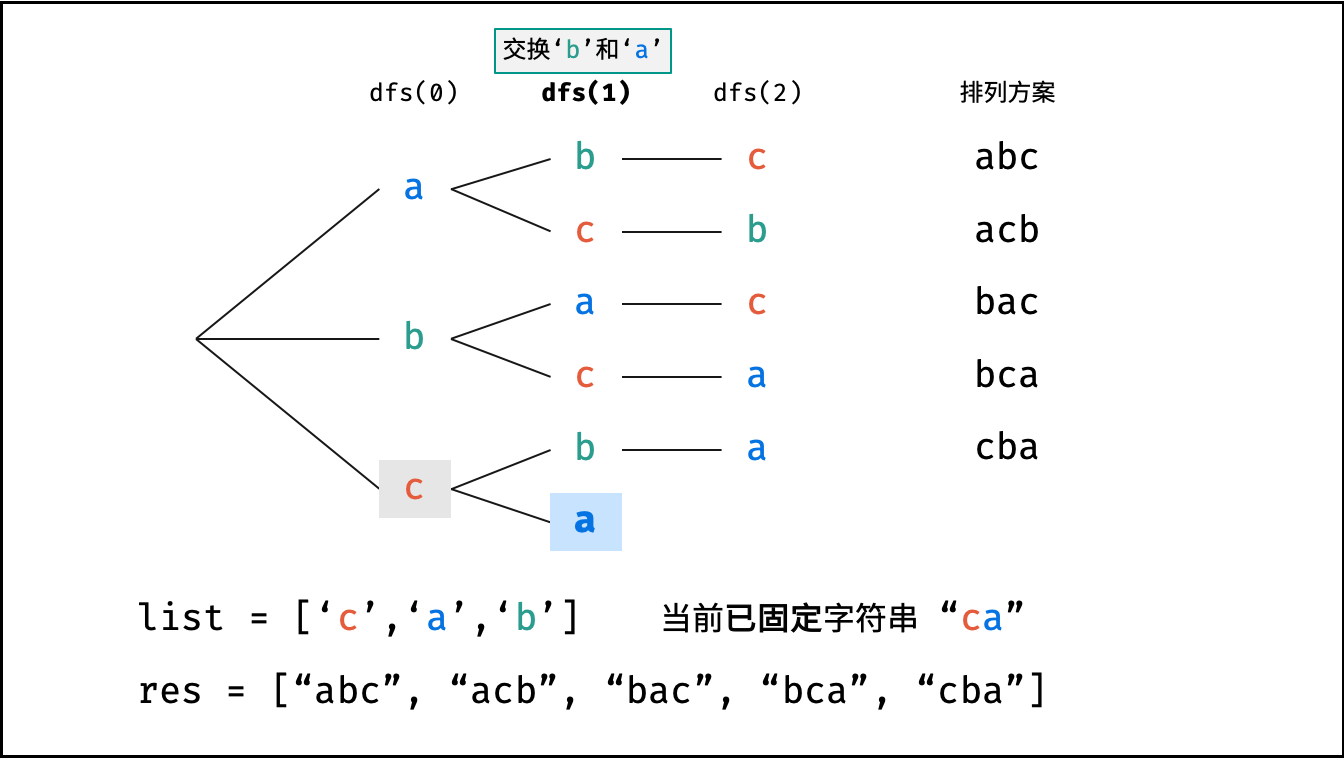Picture16.png](https://pic.leetcode-cn.com/1599403497-nOToNd-Picture16.png),![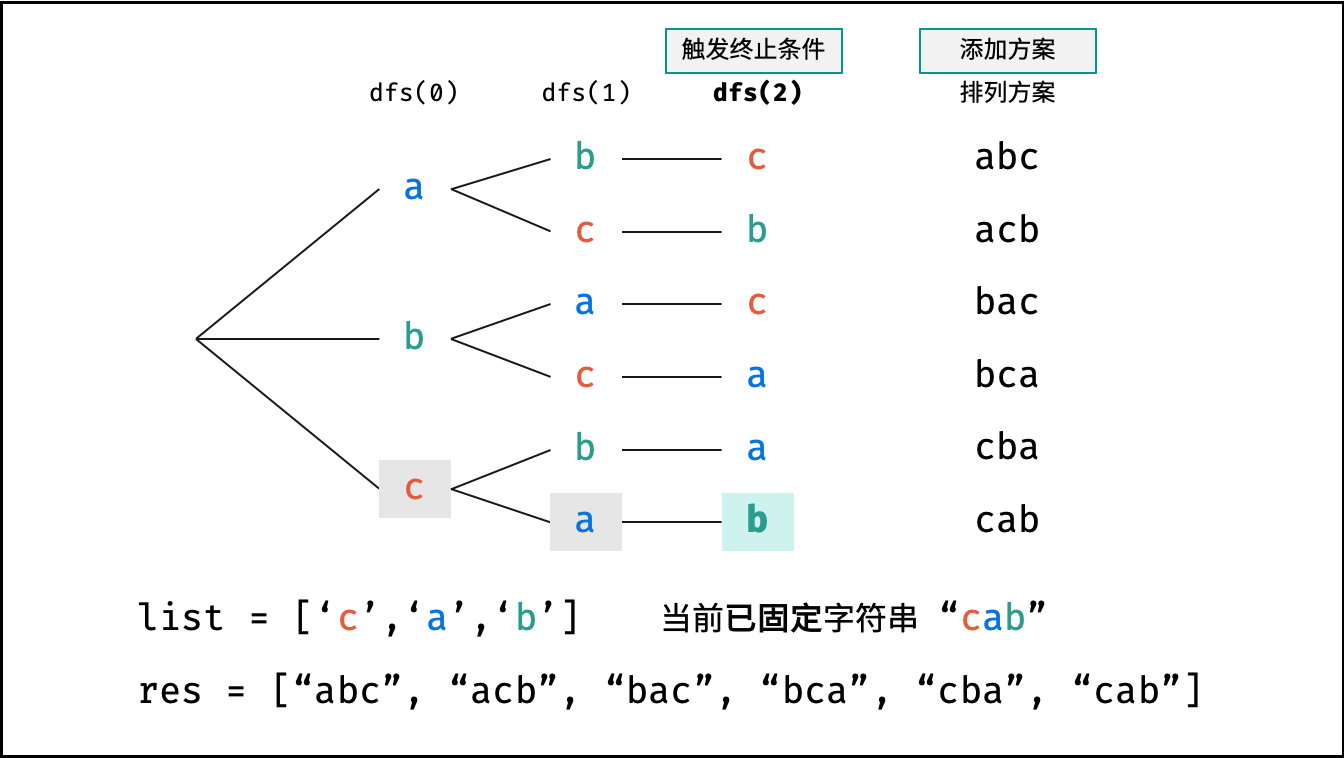Picture17.png](https://pic.leetcode-cn.com/1599403497-ddKpYy-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1599403497-xvTQhj-Picture18.png)>
## 代码：
```Python []
class Solution:
def goodsOrder(self, goods: str) -> List[str]:
arr, res = list(goods), []
def dfs(x):
if x == len(arr) - 1:
res.append(''.join(arr)) # 添加排列方案
return
hmap = set()
for i in range(x, len(arr)):
if arr[i] in hmap: continue # 重复，因此剪枝
hmap.add(arr[i])
arr[i], arr[x] = arr[x], arr[i] # 交换，将 arr[i] 固定在第 x 位
dfs(x + 1) # 开启固定第 x + 1 位字符
arr[i], arr[x] = arr[x], arr[i] # 恢复交换
dfs(0)
return res
```
```Java []
class Solution {
List<String> res = new LinkedList<>();
char[] arr;
public String[] goodsOrder(String goods) {
arr = goods.toCharArray();
dfs(0);
return res.toArray(new String[res.size()]);
}
void dfs(int x) {
if(x == arr.length - 1) {
res.add(String.valueOf(arr)); // 添加排列方案
return;
}
HashSet<Character> set = new HashSet<>();
for(int i = x; i < arr.length; i++) {
if(set.contains(arr[i])) continue; // 重复，因此剪枝
set.add(arr[i]);
swap(i, x); // 交换，将 arr[i] 固定在第 x 位
dfs(x + 1); // 开启固定第 x + 1 位字符
swap(i, x); // 恢复交换
}
}
void swap(int a, int b) {
char tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
}
```
```C++ []
class Solution {
public:
vector<string> goodsOrder(string goods) {
dfs(goods, 0);
return res;
}
private:
vector<string> res;
void dfs(string goods, int x) {
if(x == goods.size() - 1) {
res.push_back(goods); // 添加排列方案
return;
}
set<int> st;
for(int i = x; i < goods.size(); i++) {
if(st.find(goods[i]) != st.end()) continue; // 重复，因此剪枝
st.insert(goods[i]);
swap(goods[i], goods[x]); // 交换，将 goods[i] 固定在第 x 位
dfs(goods, x + 1); // 开启固定第 x + 1 位字符
swap(goods[i], goods[x]); // 恢复交换
}
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N!N)$ ：** $N$ 为字符串 `goods` 的长度；时间复杂度和字符串排列的方案数成线性关系，方案数为 $N \times (N-1) \times (N-2) … \times 2 \times 1$ ，即复杂度为 $O(N!)$ ；字符串拼接操作 `join()` 使用 $O(N)$ ；因此总体时间复杂度为 $O(N!N)$ 。
- **空间复杂度 $O(N^2)$ ：** 全排列的递归深度为 $N$ ，系统累计使用栈空间大小为 $O(N)$ ；递归中辅助 Set 累计存储的字符数量最多为 $N + (N-1) + ... + 2 + 1 = (N+1)N/2$ ，即占用 $O(N^2)$ 的额外空间。

135
leetbook_ioa/docs/LCR 158. 库存管理 II.md Executable file
View File

@@ -0,0 +1,135 @@
## 解题思路：
> 请注意，数学中众数的定义为 “数组中出现次数最多的数字” ，与本文定义不同。本文将 “数组中出现次数超过一半的数字” 称为 **“众数”**。
本题常见的三种解法：
1. **哈希表统计法：** 遍历数组 `stock` ，用 HashMap 统计各数字的数量，即可找出 众数 。此方法时间和空间复杂度均为 $O(N)$ 。
2. **数组排序法：** 将数组 `stock` 排序，**数组中点的元素** 一定为众数。
3. **摩尔投票法：** 核心理念为 **票数正负抵消** 。此方法时间和空间复杂度分别为 $O(N)$ 和 $O(1)$ ，为本题的最佳解法。
### 摩尔投票法：
> 设输入数组 `stock` 的众数为 $x$ ，数组长度为 $n$ 。
**推论一：** 若记 **众数** 的票数为 $+1$ ，**非众数** 的票数为 $-1$ ，则一定有所有数字的 **票数和 $> 0$** 。
**推论二：** 若数组的前 $a$ 个数字的 **票数和 $= 0$** ，则 数组剩余 $(n-a)$ 个数字的 **票数和一定仍 $>0$** ，即后 $(n-a)$ 个数字的 **众数仍为 $x$** 。
> 下图中的 `nums` 对应本题的 `stock` 。
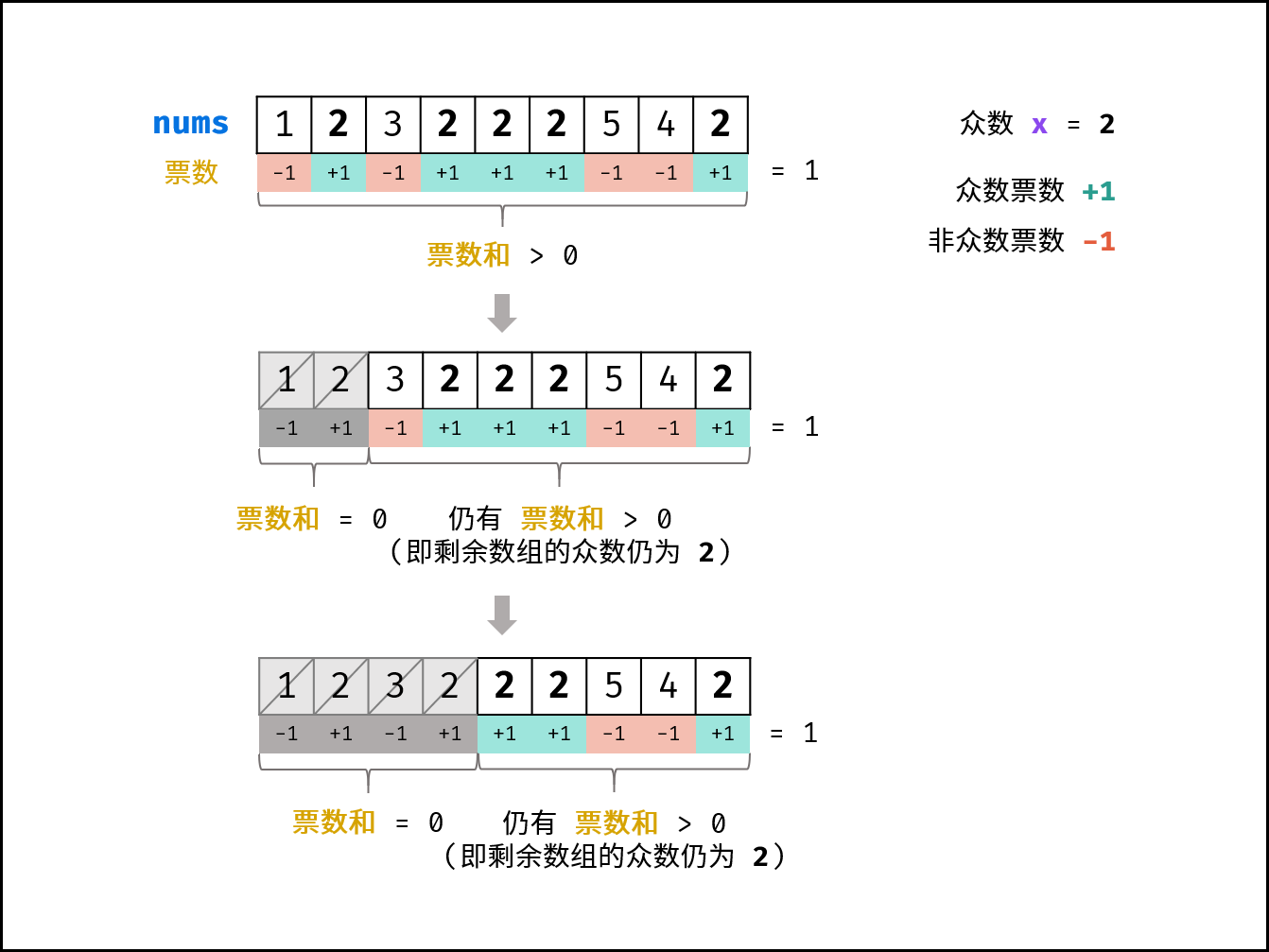![Picture1.png](https://pic.leetcode-cn.com/1603612327-bOQxzq-Picture1.png){:align=center width=500}
根据以上推论，记数组首个元素为 $n_1$ ，众数为 $x$ ，遍历并统计票数。当发生 **票数和 $= 0$** 时，**剩余数组的众数一定不变** ，这是由于：
- **当 $n_1 = x$ ：** 抵消的所有数字中，有一半是众数 $x$ 。
- **当 $n_1 \neq x$ ：** 抵消的所有数字中，众数 $x$ 的数量最少为 0 个，最多为一半。
利用此特性，每轮假设发生 **票数和 $= 0$** 都可以 **缩小剩余数组区间** 。当遍历完成时，最后一轮假设的数字即为众数。
### 算法流程:
1. **初始化：** 票数统计 `votes = 0` ， 众数 `x`；
2. **循环：** 遍历数组 `stock` 中的每个数字 `num` ；
1. 当 票数 `votes` 等于 0 ，则假设当前数字 `num` 是众数；
2. 当 `num = x` 时，票数 `votes` 自增 1 ；当 `num != x` 时，票数 `votes` 自减 1 ；
3. **返回值：** 返回 `x` 即可；
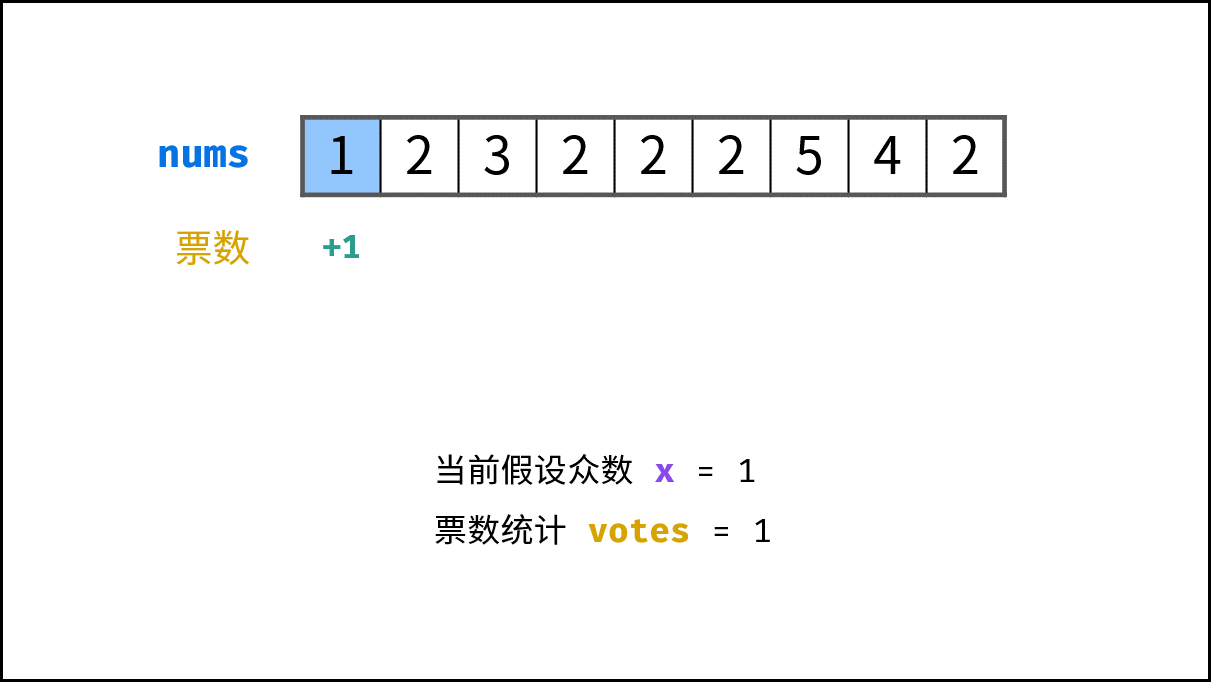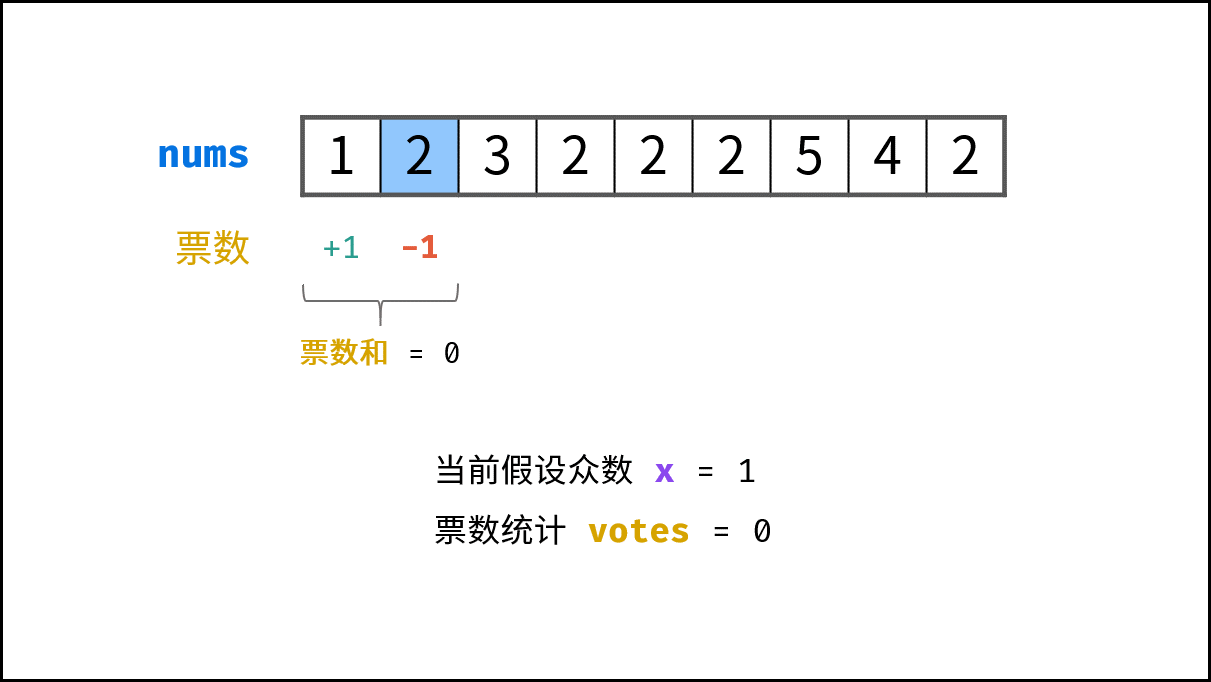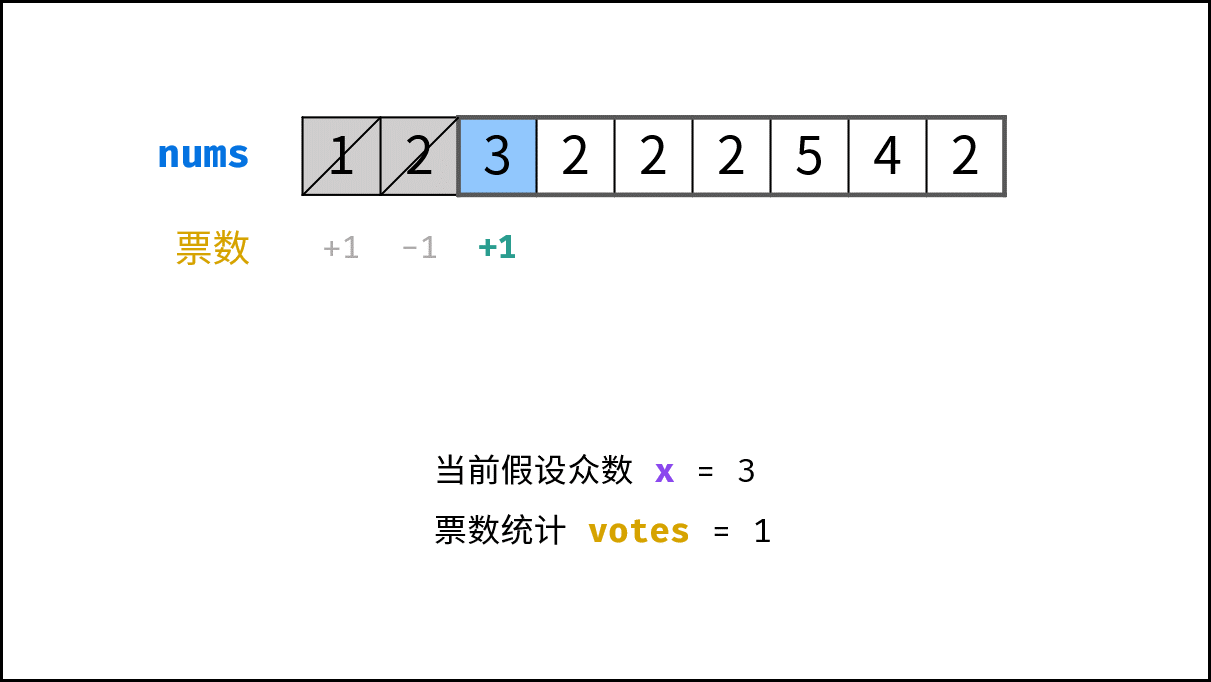<![Picture2.png](https://pic.leetcode-cn.com/1603612327-mqrUIY-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603612327-MfsWQB-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603612327-dhVmEY-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603612327-QdHZir-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603612327-WWGfIa-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603612327-WvtbDg-Picture7.png),![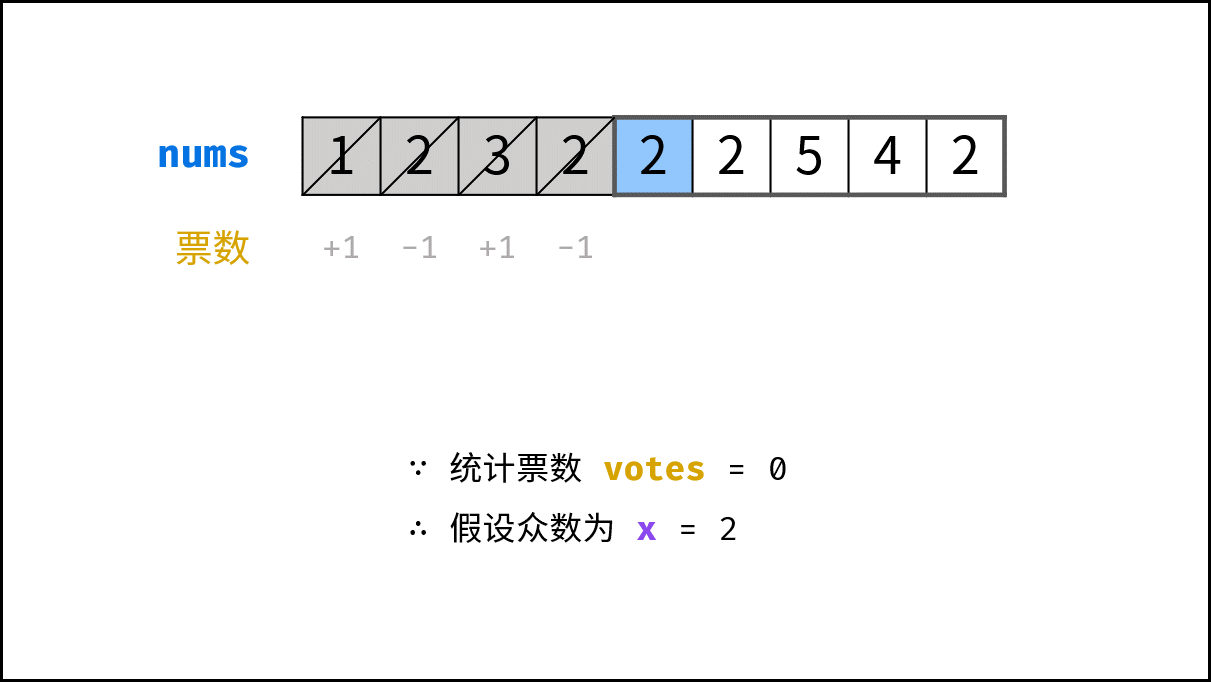Picture8.png](https://pic.leetcode-cn.com/1603612327-qbANWt-Picture8.png),![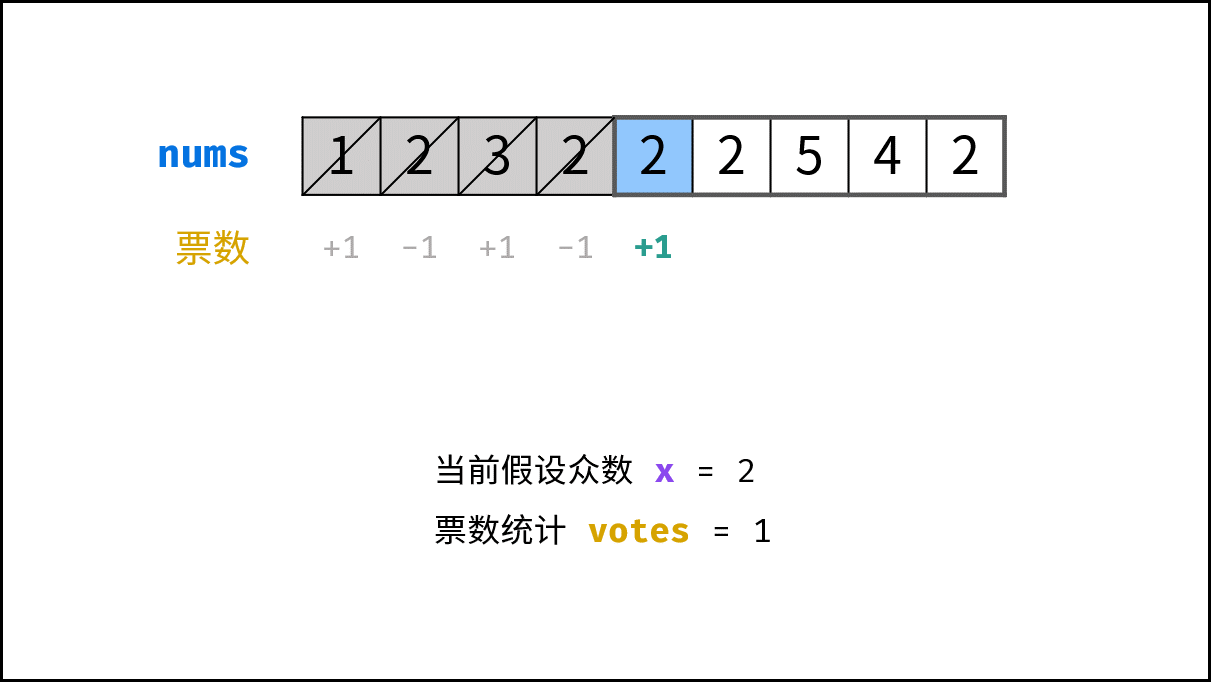Picture9.png](https://pic.leetcode-cn.com/1603612327-FyPKfT-Picture9.png),![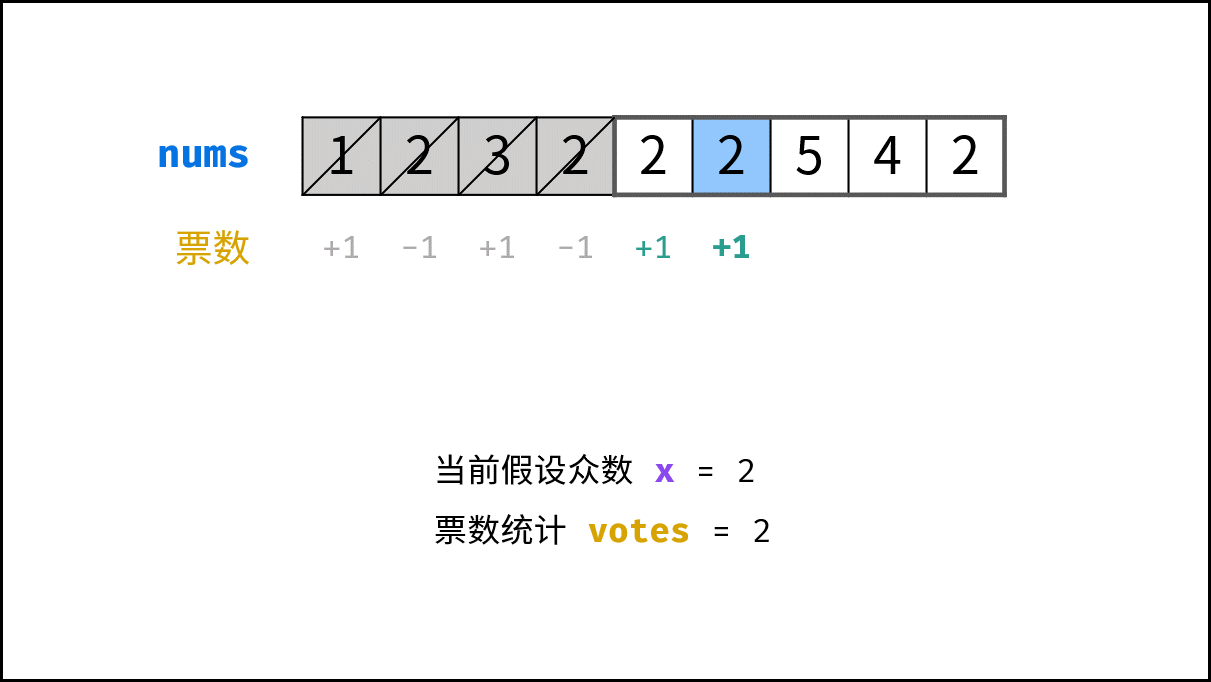Picture10.png](https://pic.leetcode-cn.com/1603612327-wbGYtp-Picture10.png),![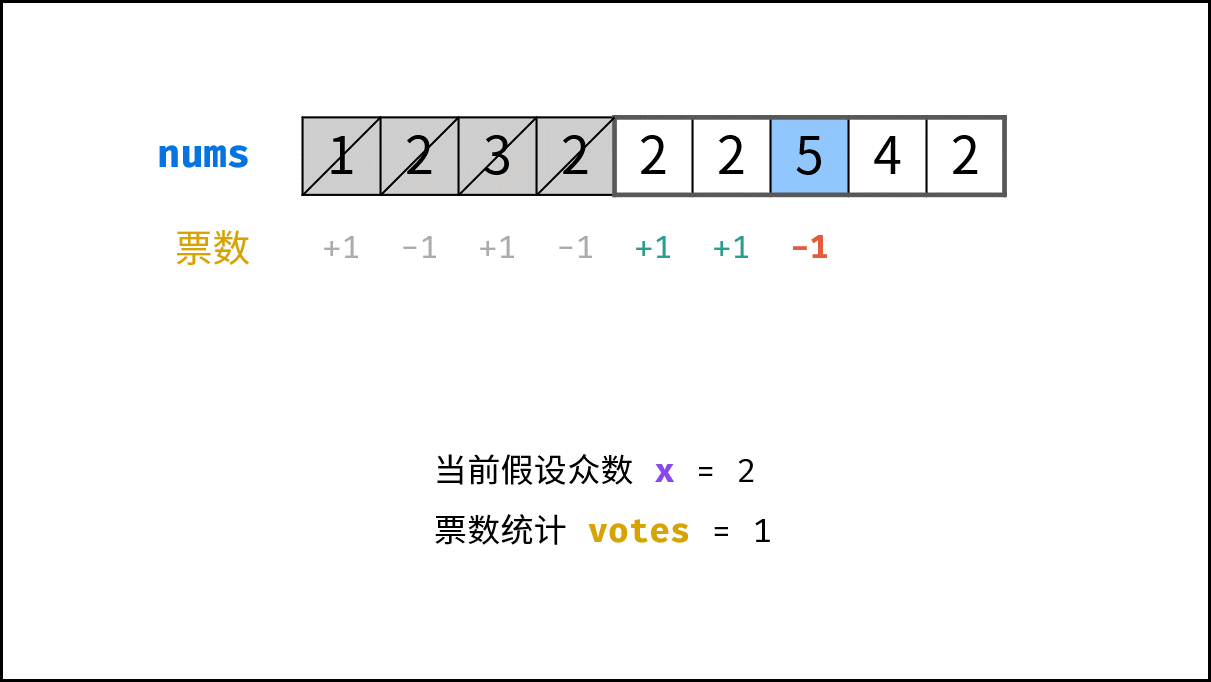Picture11.png](https://pic.leetcode-cn.com/1603612327-sLvIAG-Picture11.png),![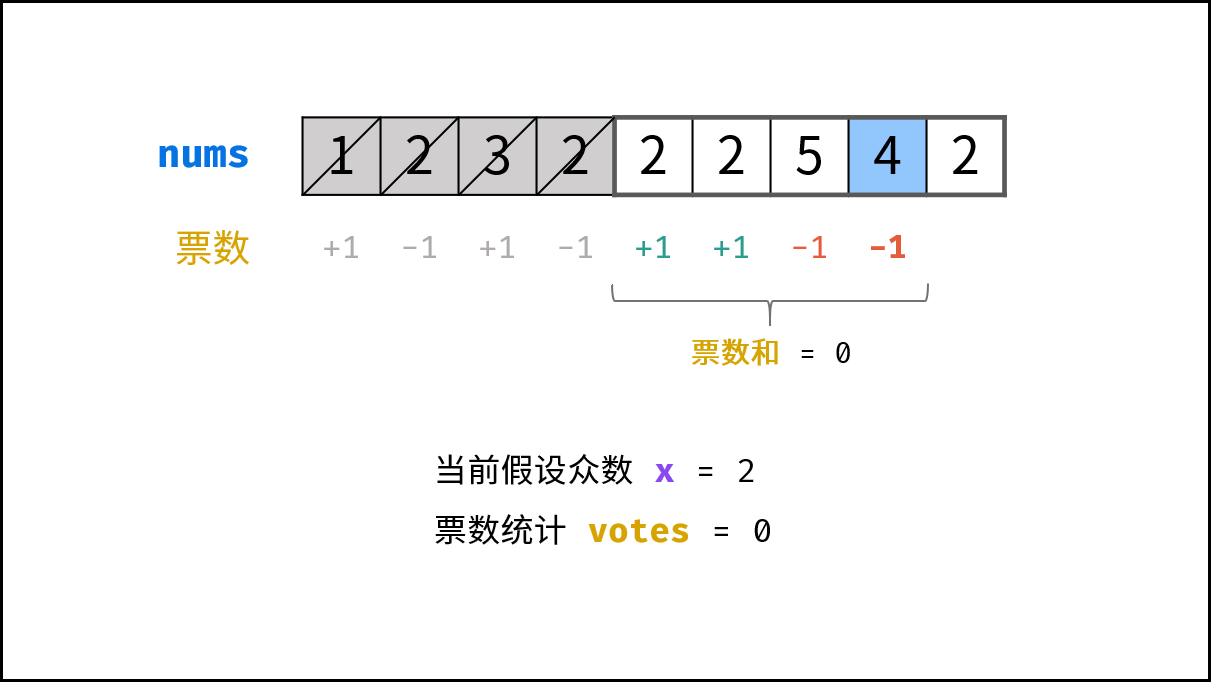Picture12.png](https://pic.leetcode-cn.com/1603612327-wYupjD-Picture12.png),![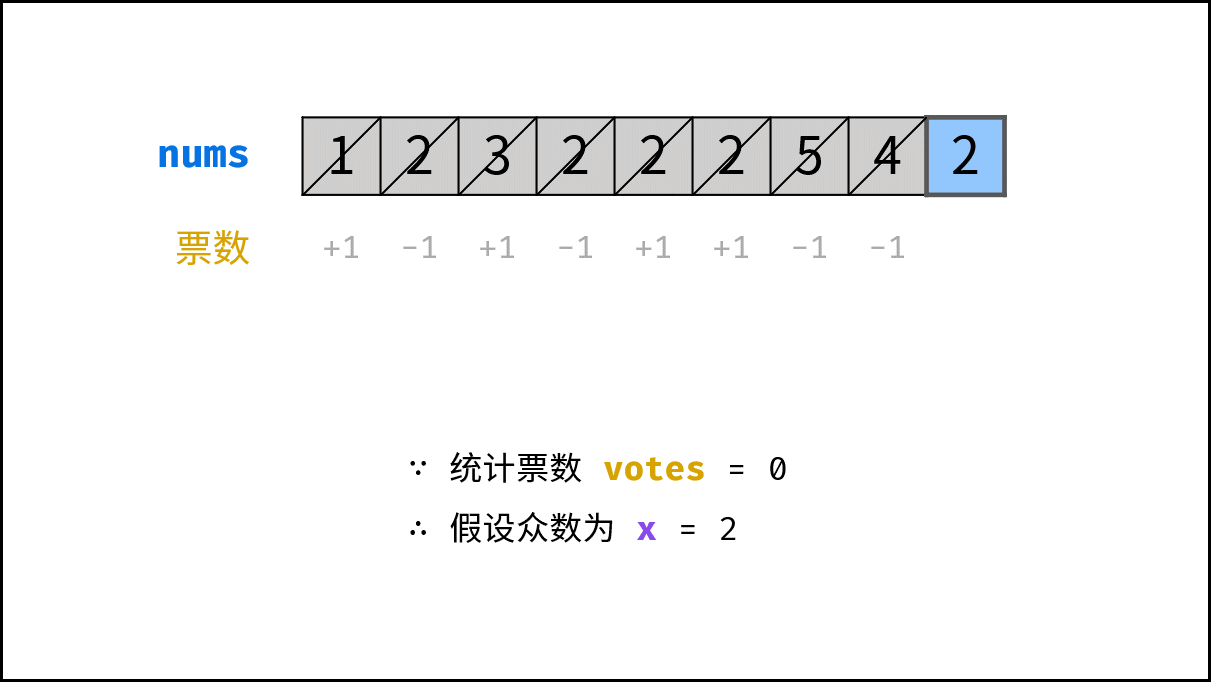Picture13.png](https://pic.leetcode-cn.com/1603612327-fSpbfK-Picture13.png),![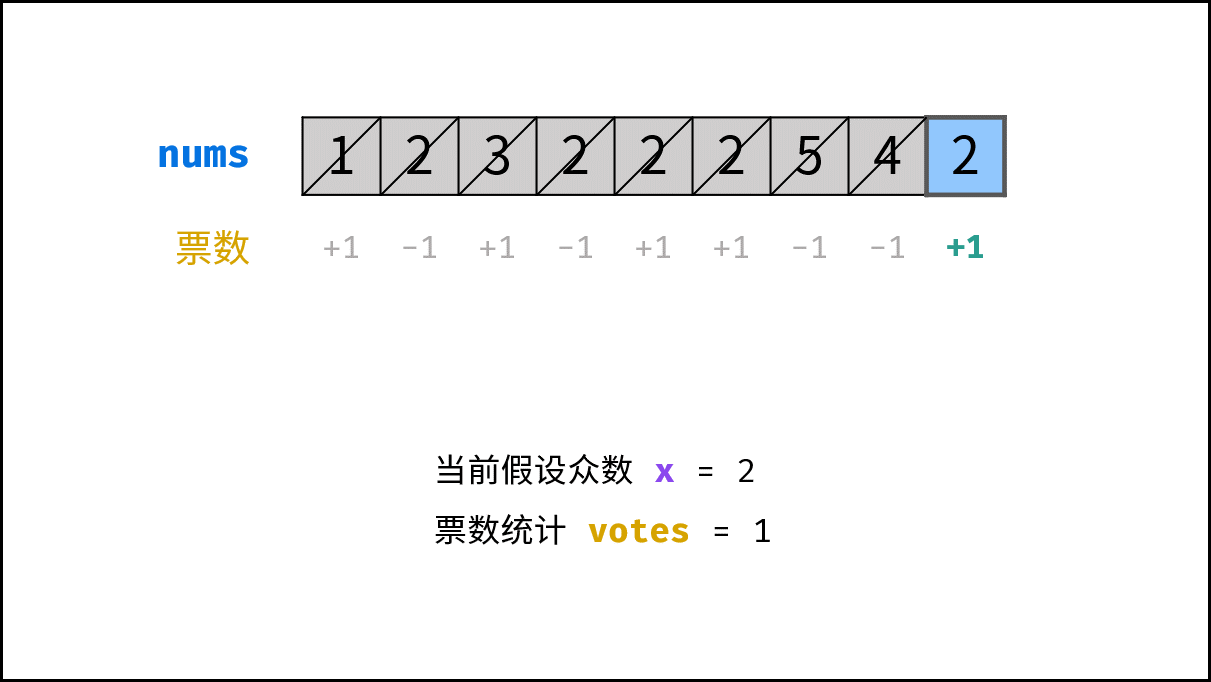Picture14.png](https://pic.leetcode-cn.com/1603612327-ccBkhy-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1603612327-yArPBb-Picture15.png)>
## 代码：
```Python []
class Solution:
def inventoryManagement(self, stock: List[int]) -> int:
votes = 0
for num in stock:
if votes == 0: x = num
votes += 1 if num == x else -1
return x
```
```Java []
class Solution {
public int inventoryManagement(int[] stock) {
int x = 0, votes = 0;
for(int num : stock){
if(votes == 0) x = num;
votes += num == x ? 1 : -1;
}
return x;
}
}
```
```C++ []
class Solution {
public:
int inventoryManagement(vector<int>& stock) {
int x = 0, votes = 0;
for(int num : stock){
if(votes == 0) x = num;
votes += num == x ? 1 : -1;
}
return x;
}
};
```
**拓展：** 由于题目说明 “给定的数组总是存在多数元素” ，因此本题不用考虑 **数组不存在众数** 的情况。若考虑，需要加入一个 “验证环节” ，遍历数组 `stock` 统计 `x` 的数量。
- 若 `x` 的数量超过数组长度一半，则返回 `x` ；
- 否则，返回未找到众数；
时间和空间复杂度不变，仍为 $O(N)$ 和 $O(1)$ 。
```Python []
class Solution:
def inventoryManagement(self, stock: List[int]) -> int:
votes, count = 0, 0
for num in stock:
if votes == 0: x = num
votes += 1 if num == x else -1
# 验证 x 是否为众数
for num in stock:
if num == x: count += 1
return x if count > len(stock) // 2 else 0 # 当无众数时返回 0
```
```Java []
class Solution {
public int inventoryManagement(int[] stock) {
int x = 0, votes = 0, count = 0;
for(int num : stock){
if(votes == 0) x = num;
votes += num == x ? 1 : -1;
}
// 验证 x 是否为众数
for(int num : stock)
if(num == x) count++;
return count > stock.length / 2 ? x : 0; // 当无众数时返回 0
}
}
```
```C++ []
class Solution {
public:
int inventoryManagement(vector<int>& stock) {
int x = 0, votes = 0, count = 0;
for(int num : stock){
if(votes == 0) x = num;
votes += num == x ? 1 : -1;
}
// 验证 x 是否为众数
for(int num : stock)
if(num == x) count++;
return count > stock.size() / 2 ? x : 0; // 当无众数时返回 0
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为数组 `stock` 长度。
- **空间复杂度 $O(1)$ ：** `votes` 变量使用常数大小的额外空间。

213
leetbook_ioa/docs/LCR 159. 库存管理 III.md Executable file
View File

@@ -0,0 +1,213 @@
## 方法一：快速排序
本题使用排序算法解决最直观，对数组 `stock` 执行排序，再返回前 $cnt$ 个元素即可。使用任意排序算法皆可，本文采用并介绍 **快速排序** ，为下文 **方法二** 做铺垫。
### 快速排序原理：
快速排序算法有两个核心点，分别为 “哨兵划分” 和 “递归” 。
**哨兵划分操作：** 以数组某个元素（一般选取首元素）为 **基准数** ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。
> 如下图所示，为哨兵划分操作流程。通过一轮 **哨兵划分** ，可将数组排序问题拆分为 **两个较短数组的排序问题** （本文称之为左（右）子数组）。
<![Picture2.png](https://pic.leetcode-cn.com/1612615167-etrYaH-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1612615167-PHsLgY-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1612615167-aMCCrd-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1612615167-smzuGu-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1612615167-WXDRIU-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1612615167-lWmBlA-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1612615167-ghPekO-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1612615167-azMHYj-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1623073951-BKkDwO-Picture10.png)>
**递归：** 对 **左子数组** 和 **右子数组** 递归执行 **哨兵划分**，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。
> 如下图所示，为示例数组 `[2,4,1,0,3,5]` 的快速排序流程。观察发现，快速排序和 **二分法** 的原理类似，都是以 $\log$ 时间复杂度实现搜索区间缩小。
![Picture1.png](https://pic.leetcode-cn.com/1612615552-rifQwI-Picture1.png){:width=550}
### 代码：
```Python []
class Solution:
def inventoryManagement(self, stock: List[int], cnt: int) -> List[int]:
def quick_sort(stock, l, r):
# 子数组长度为 1 时终止递归
if l >= r: return
# 哨兵划分操作（以 stock[l] 作为基准数）
i, j = l, r
while i < j:
while i < j and stock[j] >= stock[l]: j -= 1
while i < j and stock[i] <= stock[l]: i += 1
stock[i], stock[j] = stock[j], stock[i]
stock[l], stock[i] = stock[i], stock[l]
# 递归左（右）子数组执行哨兵划分
quick_sort(stock, l, i - 1)
quick_sort(stock, i + 1, r)
quick_sort(stock, 0, len(stock) - 1)
return stock[:cnt]
```
```Java []
class Solution {
public int[] inventoryManagement(int[] stock, int cnt) {
quickSort(stock, 0, stock.length - 1);
return Arrays.copyOf(stock, cnt);
}
private void quickSort(int[] stock, int l, int r) {
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作（以 stock[l] 作为基准数）
int i = l, j = r;
while (i < j) {
while (i < j && stock[j] >= stock[l]) j--;
while (i < j && stock[i] <= stock[l]) i++;
swap(stock, i, j);
}
swap(stock, i, l);
// 递归左（右）子数组执行哨兵划分
quickSort(stock, l, i - 1);
quickSort(stock, i + 1, r);
}
private void swap(int[] stock, int i, int j) {
int tmp = stock[i];
stock[i] = stock[j];
stock[j] = tmp;
}
}
```
```C++ []
class Solution {
public:
vector<int> inventoryManagement(vector<int>& stock, int cnt) {
quickSort(stock, 0, stock.size() - 1);
vector<int> res;
res.assign(stock.begin(), stock.begin() + cnt);
return res;
}
private:
void quickSort(vector<int>& stock, int l, int r) {
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作（以 stock[l] 作为基准数）
int i = l, j = r;
while (i < j) {
while (i < j && stock[j] >= stock[l]) j--;
while (i < j && stock[i] <= stock[l]) i++;
swap(stock[i], stock[j]);
}
swap(stock[i], stock[l]);
// 递归左（右）子数组执行哨兵划分
quickSort(stock, l, i - 1);
quickSort(stock, i + 1, r);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N \log N)$ ：** 库函数、快排等排序算法的平均时间复杂度为 $O(N \log N)$ 。
- **空间复杂度 $O(N)$ ：** 快速排序的递归深度最好（平均）为 $O(\log N)$ ，最差情况（即输入数组完全倒序）为 $O(N)$。
## 方法二：快速选择
题目只要求返回最小的 cnt 个数，对这 cnt 个数的顺序并没有要求。因此，只需要将数组划分为 **最小的 $cnt$ 个数** 和 **其他数字** 两部分即可，而快速排序的哨兵划分可完成此目标。
根据快速排序原理，如果某次哨兵划分后 **基准数正好是第 $cnt+1$ 小的数字** ，那么此时基准数左边的所有数字便是题目所求的 **最小的 cnt 个数** 。
根据此思路，考虑在每次哨兵划分后，判断基准数在数组中的索引是否等于 $cnt$ ，若 $\text{true}$ 则直接返回此时数组的前 $cnt$ 个数字即可。
### 算法流程：
**`inventoryManagement() 函数：`**
1. 若 $cnt$ 大于数组长度，则直接返回整个数组；
2. 执行并返回 `quick_sort()` 即可；
**`quick_sort() 函数：`**
> 注意，此时 `quick_sort()` 的功能不是排序整个数组，而是搜索并返回最小的 $cnt$ 个数。
1. **哨兵划分**：
- 划分完毕后，基准数为 `stock[i]` ，左 / 右子数组区间分别为 $[l, i - 1]$ , $[i + 1, r]$ ；
2. **递归或返回：**
- 若 $cnt < i$ ，代表第 $cnt + 1$ 小的数字在 **左子数组** 中，则递归左子数组；
- 若 $cnt > i$ ，代表第 $cnt + 1$ 小的数字在 **右子数组** 中，则递归右子数组；
- 若 $cnt = i$ ，代表此时 `stock[cnt]` 即为第 $cnt + 1$ 小的数字，则直接返回数组前 $cnt$ 个数字即可；
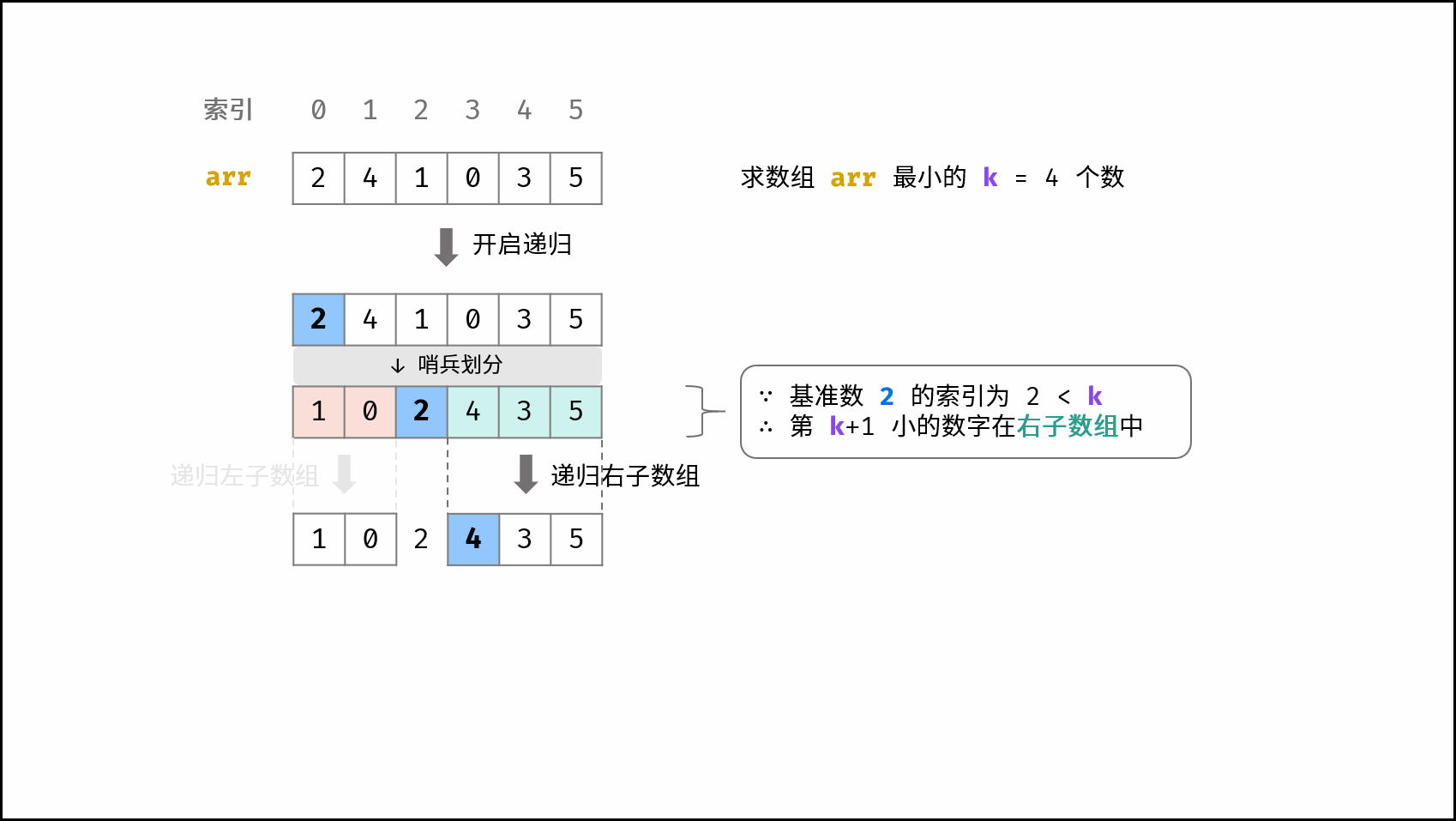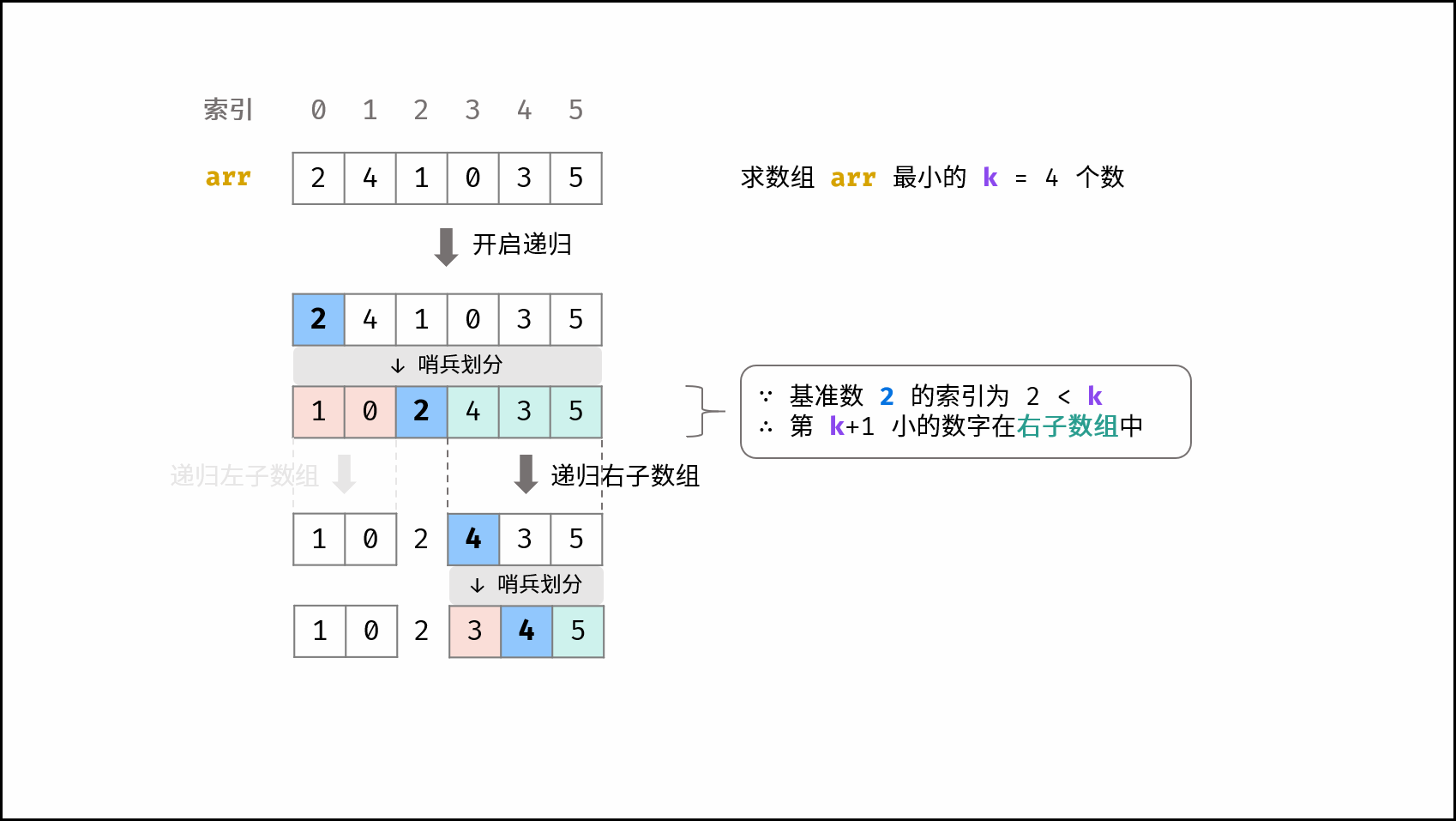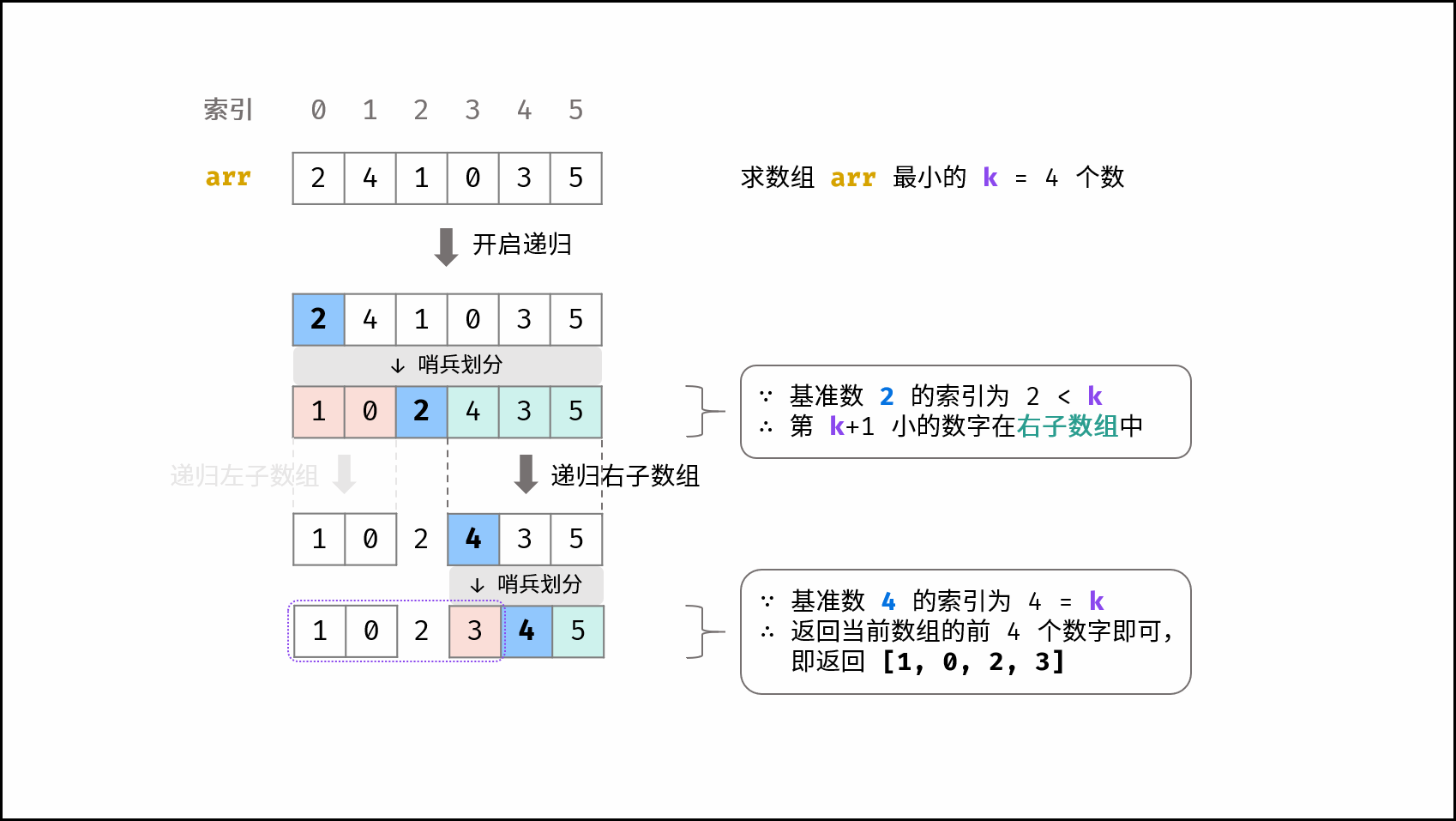<![Picture12.png](https://pic.leetcode-cn.com/1612615167-DELAJU-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1612615167-XApQqA-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1612615167-AjiQZD-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1612615167-HWPotV-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1612615167-TPvFMZ-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1612615167-sJXJwS-Picture17.png)>
## 代码：
```Python []
class Solution:
def inventoryManagement(self, stock: List[int], cnt: int) -> List[int]:
if cnt >= len(stock): return stock
def quick_sort(l, r):
i, j = l, r
while i < j:
while i < j and stock[j] >= stock[l]: j -= 1
while i < j and stock[i] <= stock[l]: i += 1
stock[i], stock[j] = stock[j], stock[i]
stock[l], stock[i] = stock[i], stock[l]
if cnt < i: return quick_sort(l, i - 1)
if cnt > i: return quick_sort(i + 1, r)
return stock[:cnt]
return quick_sort(0, len(stock) - 1)
```
```Java []
class Solution {
public int[] inventoryManagement(int[] stock, int cnt) {
if (cnt >= stock.length) return stock;
return quickSort(stock, cnt, 0, stock.length - 1);
}
private int[] quickSort(int[] stock, int cnt, int l, int r) {
int i = l, j = r;
while (i < j) {
while (i < j && stock[j] >= stock[l]) j--;
while (i < j && stock[i] <= stock[l]) i++;
swap(stock, i, j);
}
swap(stock, i, l);
if (i > cnt) return quickSort(stock, cnt, l, i - 1);
if (i < cnt) return quickSort(stock, cnt, i + 1, r);
return Arrays.copyOf(stock, cnt);
}
private void swap(int[] stock, int i, int j) {
int tmp = stock[i];
stock[i] = stock[j];
stock[j] = tmp;
}
}
```
```C++ []
class Solution {
public:
vector<int> inventoryManagement(vector<int>& stock, int cnt) {
if (cnt >= stock.size()) return stock;
return quickSort(stock, cnt, 0, stock.size() - 1);
}
private:
vector<int> quickSort(vector<int>& stock, int cnt, int l, int r) {
int i = l, j = r;
while (i < j) {
while (i < j && stock[j] >= stock[l]) j--;
while (i < j && stock[i] <= stock[l]) i++;
swap(stock[i], stock[j]);
}
swap(stock[i], stock[l]);
if (i > cnt) return quickSort(stock, cnt, l, i - 1);
if (i < cnt) return quickSort(stock, cnt, i + 1, r);
vector<int> res;
res.assign(stock.begin(), stock.begin() + cnt);
return res;
}
};
```
### 复杂度分析：
本方法优化时间复杂度的本质是通过判断舍去了不必要的递归（哨兵划分）。
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为数组元素数量；对于长度为 $N$ 的数组执行哨兵划分操作的时间复杂度为 $O(N)$ ；每轮哨兵划分后根据 $cnt$ 和 $i$ 的大小关系选择递归，由于 $i$ 分布的随机性，则向下递归子数组的平均长度为 $\frac{N}{2}$ ；因此平均情况下，哨兵划分操作一共有 $N + \frac{N}{2} + \frac{N}{4} + ... + \frac{N}{N} = \frac{N - \frac{1}{2}}{1 - \frac{1}{2}} = 2N - 1$ （等比数列求和），即总体时间复杂度为 $O(N)$ 。
- **空间复杂度 $O(\log N)$ ：** 划分函数的平均递归深度为 $O(\log N)$ 。

134
leetbook_ioa/docs/LCR 160. 数据流中的中位数.md Executable file
View File

@@ -0,0 +1,134 @@
## 解题思路：
> 给定一长度为 $N$ 的无序数组，其中位数的计算方法：首先对数组执行排序（使用 $O(N \log N)$ 时间），然后返回中间元素即可（使用 $O(1)$ 时间）。
针对本题，根据以上思路，可以将数据流保存在一个列表中，并在添加元素时 **保持数组有序** 。此方法的时间复杂度为 $O(N)$ ，其中包括： 查找元素插入位置 $O(\log N)$ （二分查找）、向数组某位置插入元素 $O(N)$ （插入位置之后的元素都需要向后移动一位）。
> 借助 **堆** 可进一步优化时间复杂度。
建立一个 **小顶堆** $A$ 和 **大顶堆** $B$ ，各保存列表的一半元素，且规定：
- $A$ 保存 **较大** 的一半，长度为 $\frac{N}{2}$（ $N$ 为偶数）或 $\frac{N+1}{2}$（ $N$ 为奇数）；
- $B$ 保存 **较小** 的一半，长度为 $\frac{N}{2}$（ $N$ 为偶数）或 $\frac{N-1}{2}$（ $N$ 为奇数）；
随后，中位数可仅根据 $A, B$ 的堆顶元素计算得到。
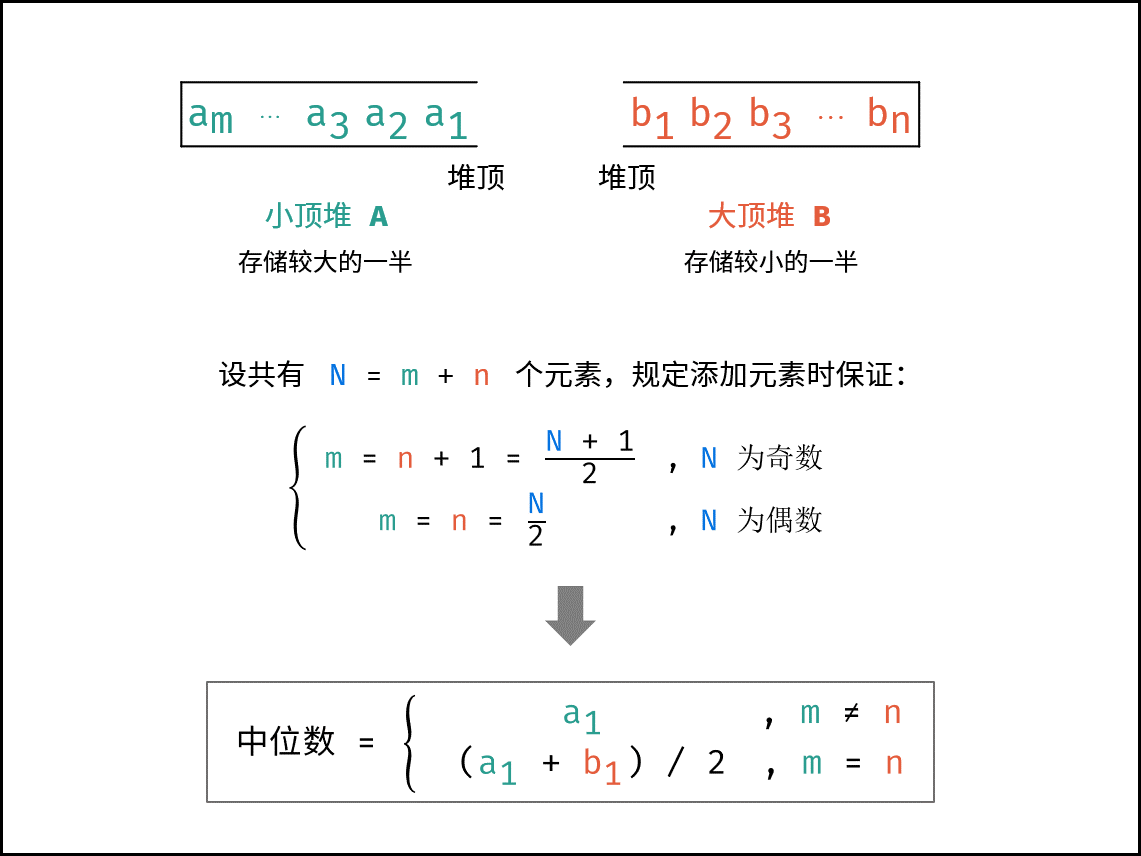![Picture1.png](https://pic.leetcode-cn.com/bcfaca2b1920d2dd6bbb01aeff990698eb36d53830c38ed499ea3239a15296b3-Picture1.png){:align=center width=500}
### 算法流程：
> 设元素总数为 $N = m + n$ ，其中 $m$ 和 $n$ 分别为 $A$ 和 $B$ 中的元素个数。
**`addNum(num)` 函数：**
1. 当 $m = n$（即 $N$ 为 **偶数**）：需向 $A$ 添加一个元素。实现方法：将新元素 $num$ 插入至 $B$ ，再将 $B$ 堆顶元素插入至 $A$ ；
2. 当 $m \ne n$（即 $N$ 为 **奇数**）：需向 $B$ 添加一个元素。实现方法：将新元素 $num$ 插入至 $A$ ，再将 $A$ 堆顶元素插入至 $B$ ；
> 假设插入数字 $num$ 遇到情况 `1.` 。由于 $num$ 可能属于 “较小的一半” （即属于 $B$ ），因此不能将 $nums$ 直接插入至 $A$ 。而应先将 $num$ 插入至 $B$ ，再将 $B$ 堆顶元素插入至 $A$ 。这样就可以始终保持 $A$ 保存较大一半、 $B$ 保存较小一半。
**`findMedian()` 函数：**
1. 当 $m = n$（ $N$ 为 **偶数**）：则中位数为 $($ $A$ 的堆顶元素 + $B$ 的堆顶元素 $)/2$。
2. 当 $m \ne n$（ $N$ 为 **奇数**）：则中位数为 $A$ 的堆顶元素。
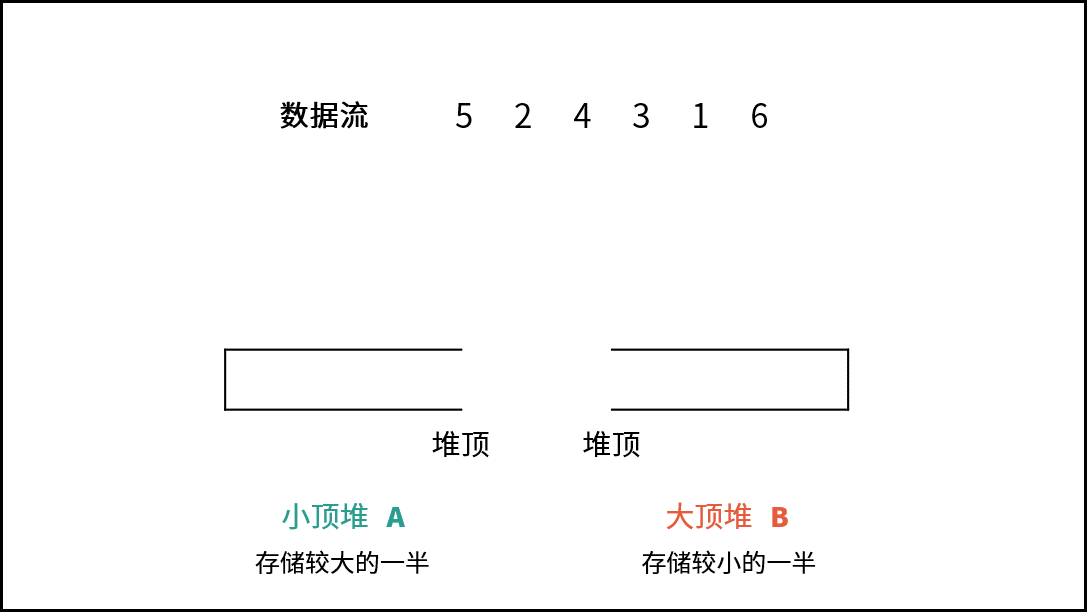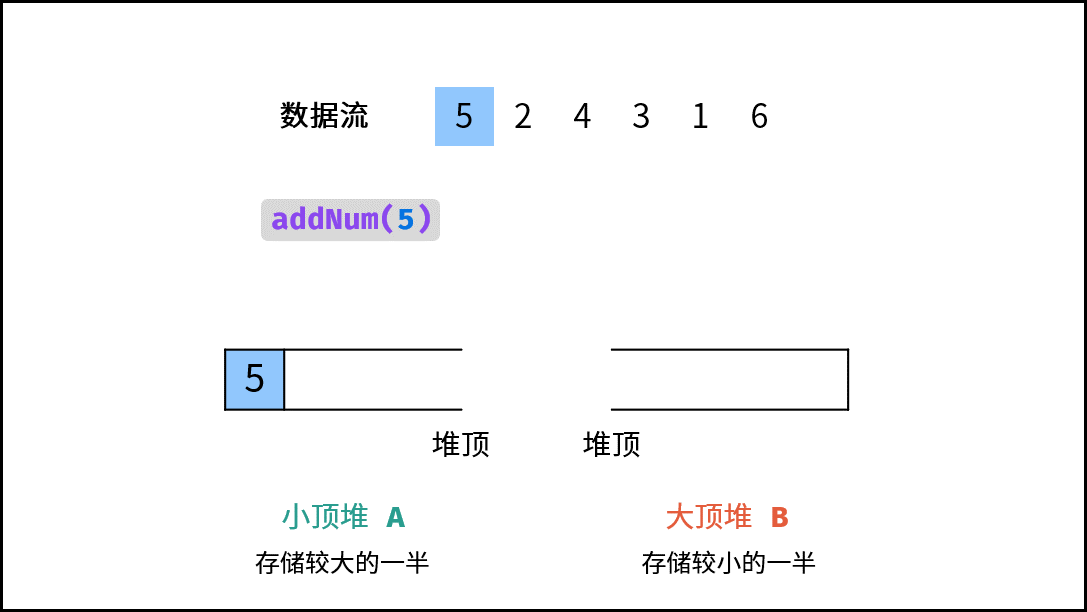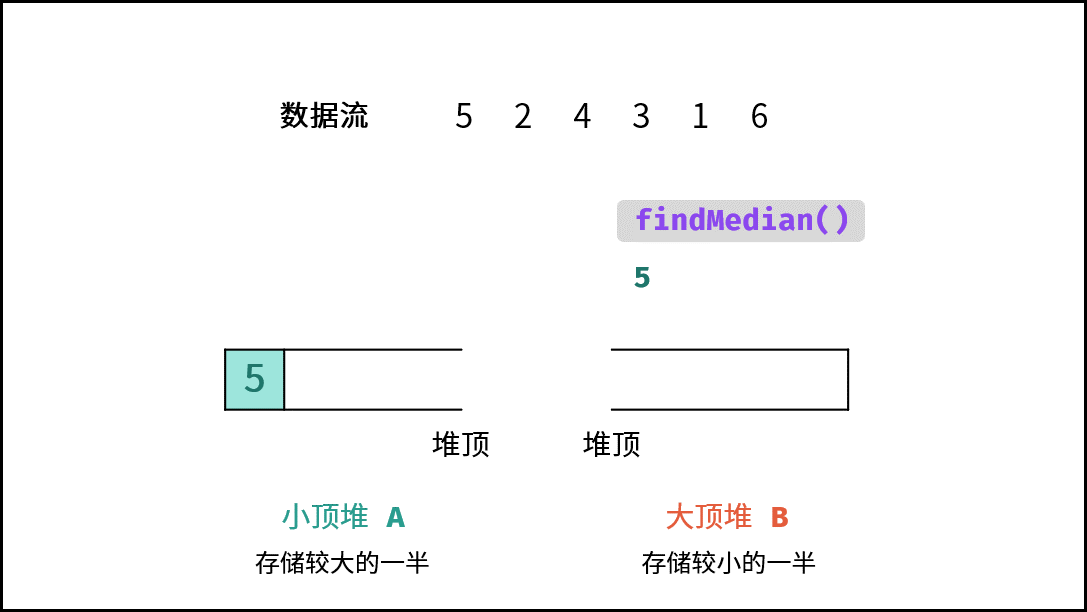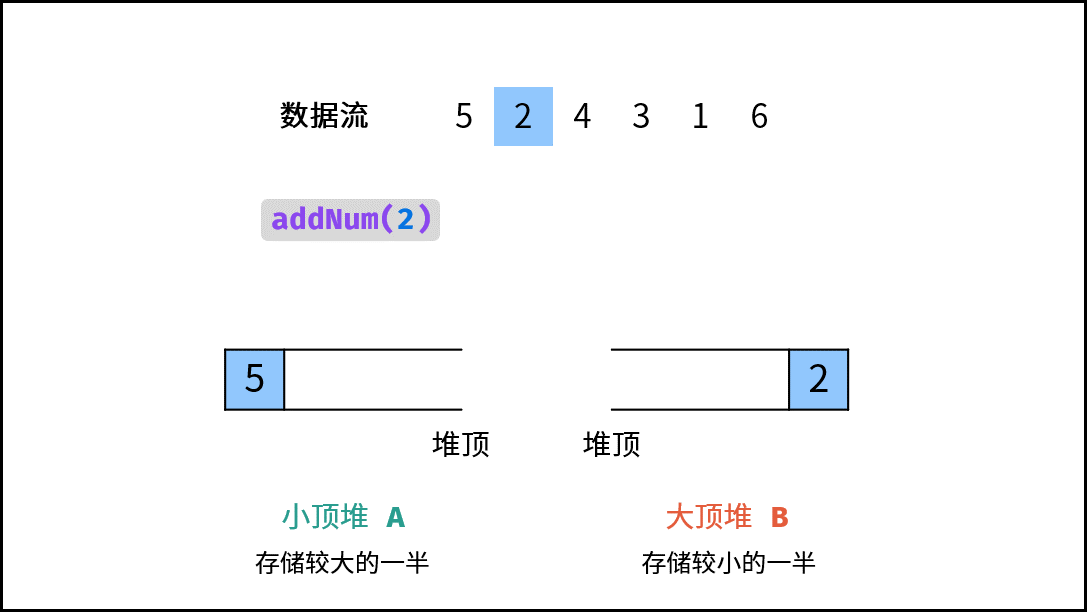<![Picture2.png](https://pic.leetcode-cn.com/d2592f943c0fd1eaa4e8a2c16480914907f1e9d2ba1f995e8f942d856178ed97-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/e9d88312332faa583069420df1e74a891f767d0bd2460c87b2ebe235b166e72f-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/afef056087d60ecc5c492c4c1443117ad6836cbf87fef3c619cfec876239a65e-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/74d154aa3bd575617860af2e90efb34cfe010ba375a94777859ae18944c49668-Picture5.png),![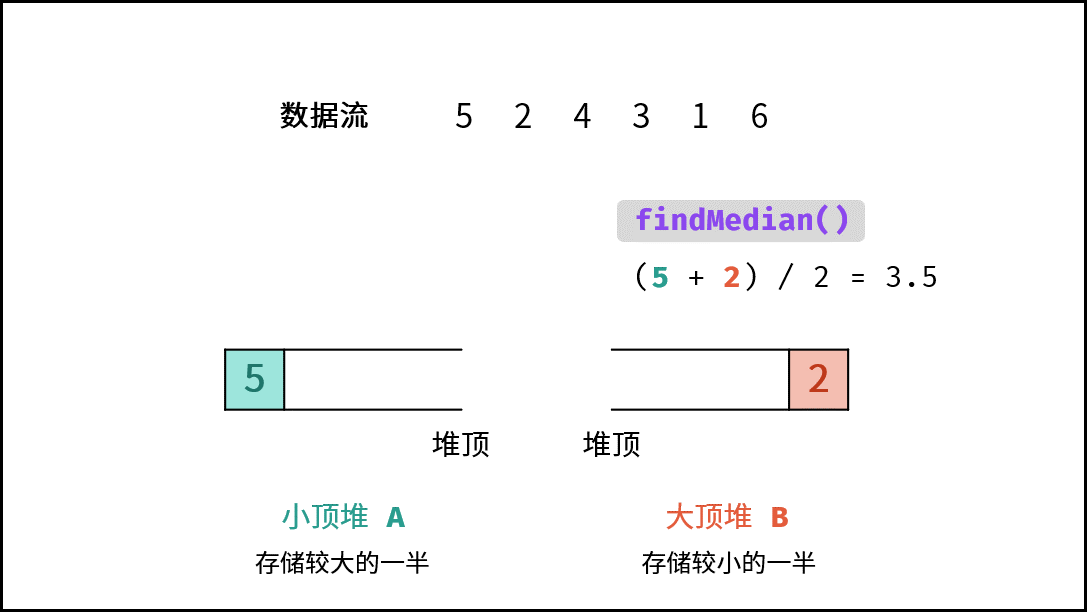Picture6.png](https://pic.leetcode-cn.com/4ed9e5c760dd0d2a72cc64a3ee68c4b6809260a4fc1f6044be9c69ee726e8c84-Picture6.png),![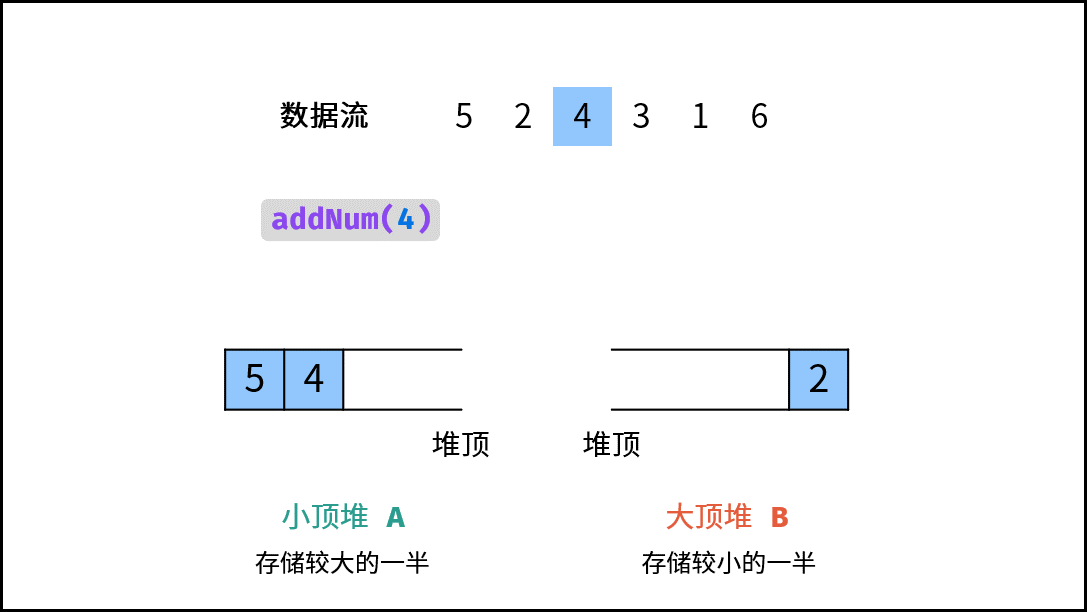Picture7.png](https://pic.leetcode-cn.com/88665d76d519800fb73c6bfca1ce4a5fb8b610ad2bb8098f482281b0c1aab6b4-Picture7.png),![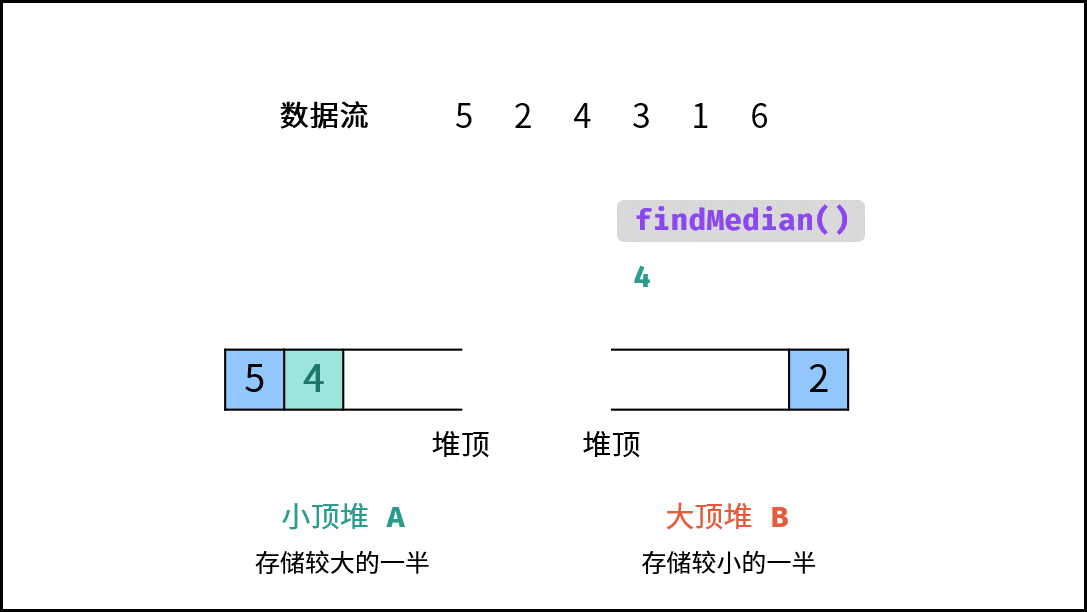Picture8.png](https://pic.leetcode-cn.com/6b0f054825e3a9cb2e311dc151cd98fbe18b0a5593845e3a31d8b72bcd49f48d-Picture8.png),![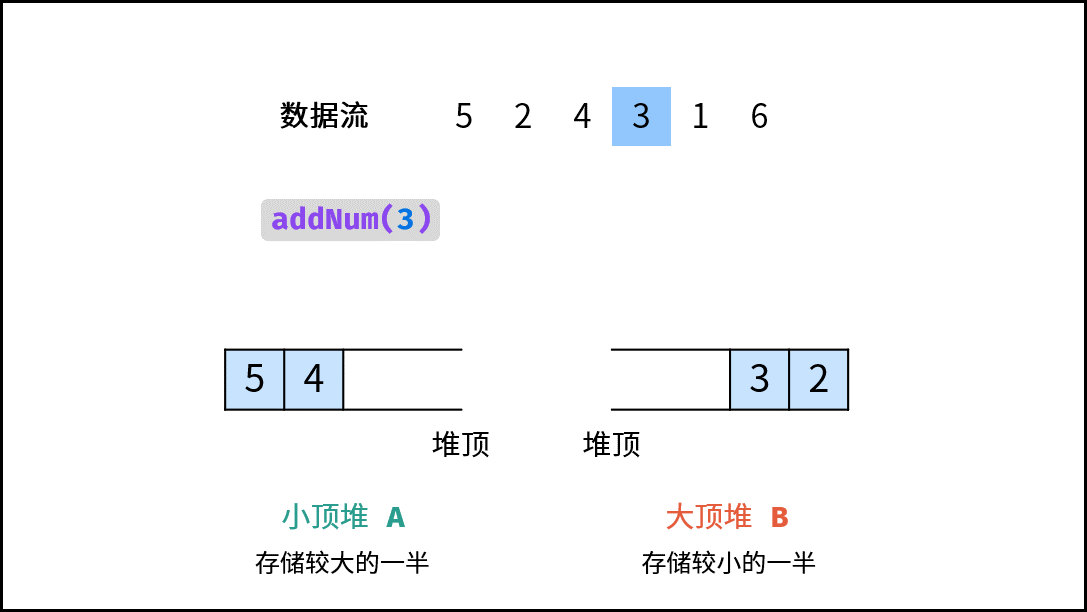Picture9.png](https://pic.leetcode-cn.com/2cccae18c6e7c3ce1ebd07740ff95495ffbf27023895cac1ee00d7cdc45700c6-Picture9.png),![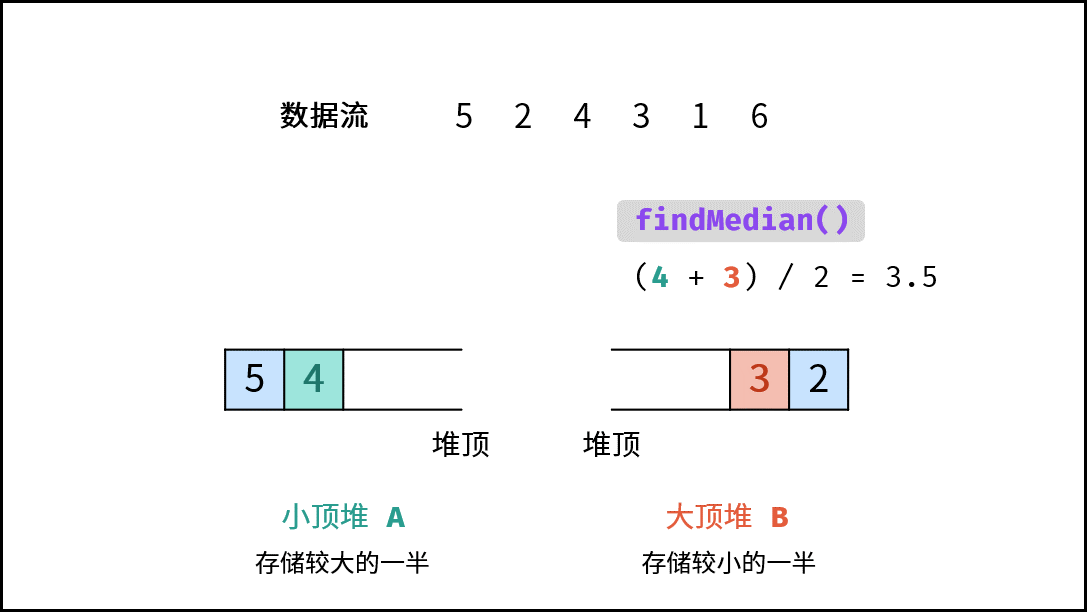Picture10.png](https://pic.leetcode-cn.com/30da0e3c05ce2f6d191e638de344ef42f2b83eb69fc073ab1536c4f0abf1d2b3-Picture10.png),![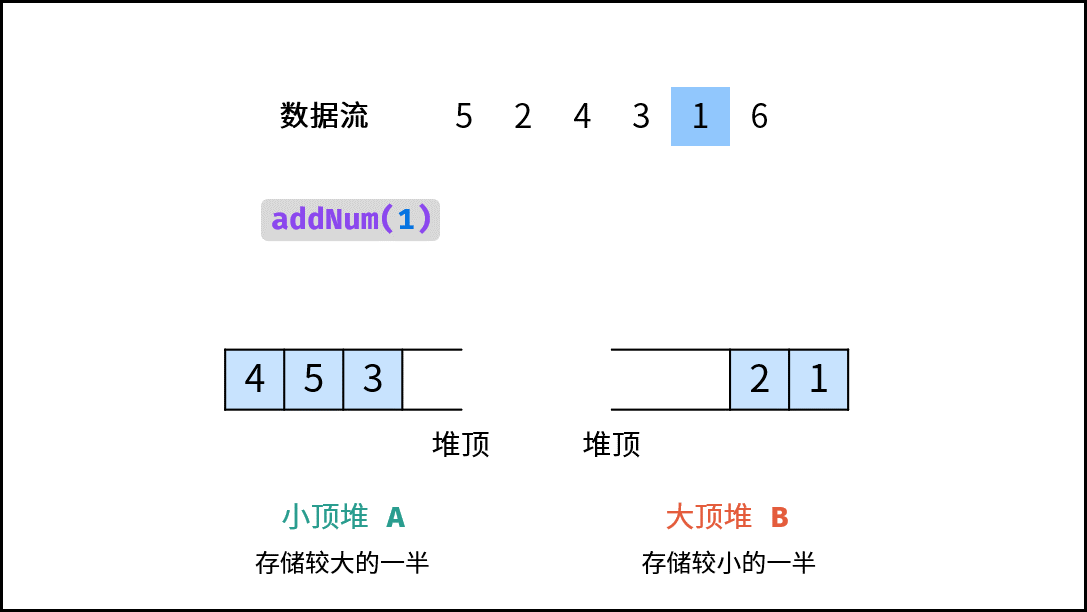Picture11.png](https://pic.leetcode-cn.com/68a1972bd8f51f8b042717a82f2984787729d8daec41f965e9a26f0adccd3a29-Picture11.png),![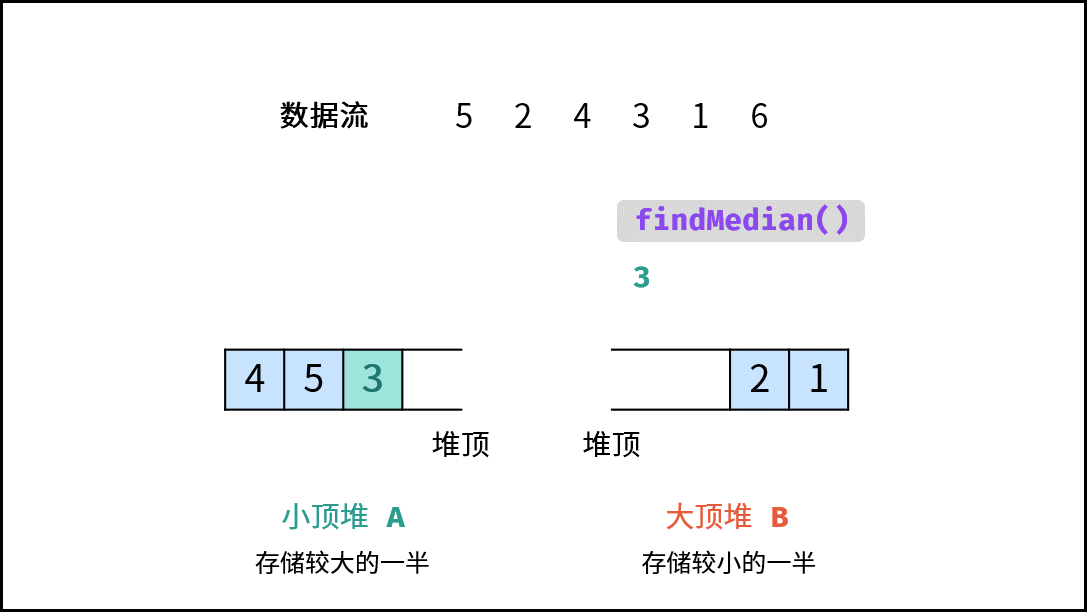Picture12.png](https://pic.leetcode-cn.com/2a7e10fc49d6bd0a19f9cc4c8bb793eee8a8382fa0ef004de40fed3df96b4304-Picture12.png),![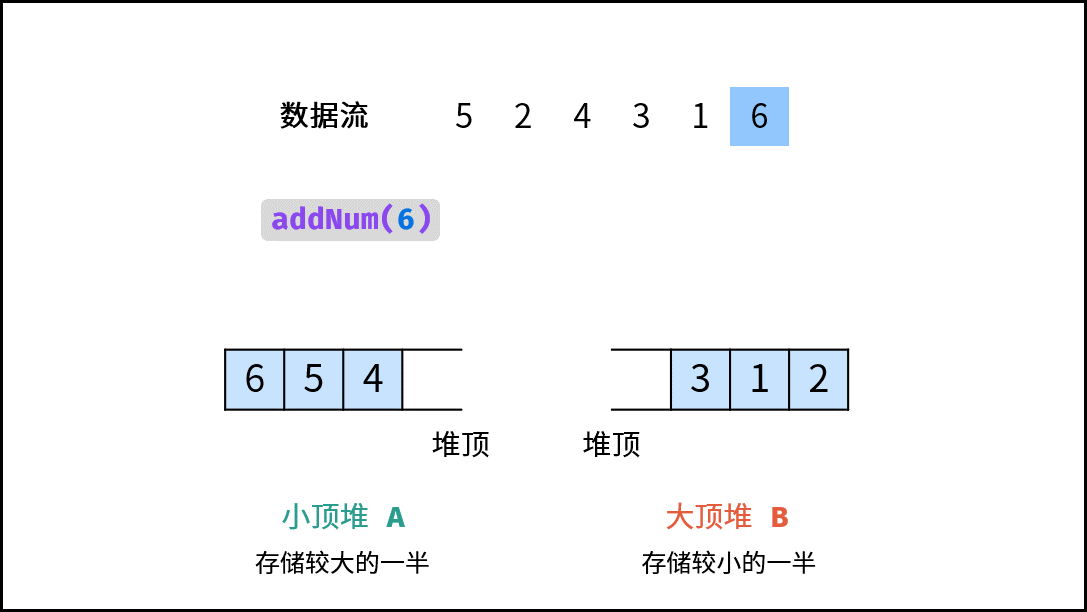Picture13.png](https://pic.leetcode-cn.com/15969490140ba0d730443c13c019bbbf396478691a711cb5e59854ac9f06e5fc-Picture13.png),![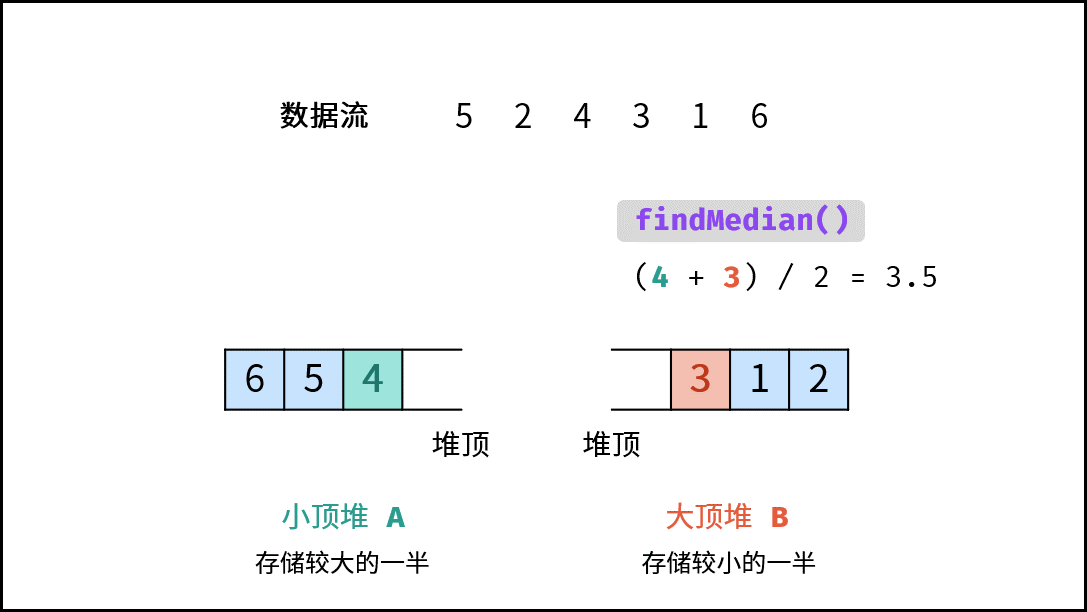Picture14.png](https://pic.leetcode-cn.com/d8d22df91c39ce03cdd43a814ebe5146c35087db9487afb2f45ed3a667ecbd98-Picture14.png)>
## 代码：
Python 中 heapq 模块是小顶堆。实现 **大顶堆** 方法： 小顶堆的插入和弹出操作均将元素 **取反** 即可。
Java 使用 `PriorityQueue<>((x, y) -> (y - x))` 可方便实现大顶堆。
C++ 中 `greater` 为小顶堆，`less` 为大顶堆。
```Python []
from heapq import *
class MedianFinder:
def __init__(self):
self.A = [] # 小顶堆，保存较大的一半
self.B = [] # 大顶堆，保存较小的一半
def addNum(self, num: int) -> None:
if len(self.A) != len(self.B):
heappush(self.A, num)
heappush(self.B, -heappop(self.A))
else:
heappush(self.B, -num)
heappush(self.A, -heappop(self.B))
def findMedian(self) -> float:
return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0
```
```Java []
class MedianFinder {
Queue<Integer> A, B;
public MedianFinder() {
A = new PriorityQueue<>(); // 小顶堆，保存较大的一半
B = new PriorityQueue<>((x, y) -> (y - x)); // 大顶堆，保存较小的一半
}
public void addNum(int num) {
if(A.size() != B.size()) {
A.add(num);
B.add(A.poll());
} else {
B.add(num);
A.add(B.poll());
}
}
public double findMedian() {
return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;
}
}
```
```C++ []
class MedianFinder {
public:
priority_queue<int, vector<int>, greater<int>> A; // 小顶堆，保存较大的一半
priority_queue<int, vector<int>, less<int>> B; // 大顶堆，保存较小的一半
MedianFinder() { }
void addNum(int num) {
if(A.size() != B.size()) {
A.push(num);
B.push(A.top());
A.pop();
} else {
B.push(num);
A.push(B.top());
B.pop();
}
}
double findMedian() {
return A.size() != B.size() ? A.top() : (A.top() + B.top()) / 2.0;
}
};
```
> Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop().
根据以上文档说明，可将 Python 代码优化为：
```Python []
from heapq import *
class MedianFinder:
def __init__(self):
self.A = [] # 小顶堆，保存较大的一半
self.B = [] # 大顶堆，保存较小的一半
def addNum(self, num: int) -> None:
if len(self.A) != len(self.B):
heappush(self.B, -heappushpop(self.A, num))
else:
heappush(self.A, -heappushpop(self.B, -num))
def findMedian(self) -> float:
return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0
```
### 复杂度分析：
- **时间复杂度：**
- **查找中位数 $O(1)$ ：** 获取堆顶元素使用 $O(1)$ 时间；
- **添加数字 $O(\log N)$ ：** 堆的插入和弹出操作使用 $O(\log N)$ 时间。
- **空间复杂度 $O(N)$ ：** 其中 $N$ 为数据流中的元素数量，小顶堆 $A$ 和大顶堆 $B$ 最多同时保存 $N$ 个元素。

81
leetbook_ioa/docs/LCR 161. 连续天数的最高销售额.md Executable file
View File

@@ -0,0 +1,81 @@
## 解题思路：
观察不同解法的复杂度，可知动态规划是本题的最优解法。
| 常见解法 | 时间复杂度 | 空间复杂度 |
| -------- | ------------- | ----------- |
| 暴力搜索 | $O(N^2)$ | $O(1)$ |
| 分治思想 | $O(N \log N)$ | $O(\log N)$ |
| 动态规划 | $O(N)$ | $O(1)$ |
### 动态规划解析：
**状态定义：** 设动态规划列表 $dp$ ，$dp[i]$ 代表以元素 $sales[i]$ 为结尾的连续子数组最大和。
**转移方程：** 若 $dp[i-1] \leq 0$ ，说明 $dp[i - 1]$ 对 $dp[i]$ 产生负贡献，即 $dp[i-1] + sales[i]$ 还不如 $sales[i]$ 本身大。
$$
dp[i] =
\begin{cases}
dp[i-1] + sales[i] & , dp[i - 1] > 0 \\
sales[i] & , dp[i - 1] \leq 0 \\
\end{cases}
$$
**初始状态：** $dp[0] = sales[0]$，即以 $sales[0]$ 结尾的连续子数组最大和为 $sales[0]$ 。
**返回值：** 返回 $dp$ 列表中的最大值，代表全局最大值。
> 下图中的 `nums` 对应本题的 `sales` 。
![Picture1.png](https://pic.leetcode-cn.com/77d1aa6a444743d3c8606ac951cd7fc38faf68a62064fd2639df517cd666a4d0-Picture1.png){:align=center width=500}
### 空间优化：
由于 $dp[i]$ 只与 $dp[i-1]$ 和 $sales[i]$ 有关系，因此可以将原数组 $sales$ 用作 $dp$ 列表，即直接在 $sales$ 上修改即可。
由于省去 $dp$ 列表使用的额外空间，因此空间复杂度从 $O(N)$ 降至 $O(1)$ 。
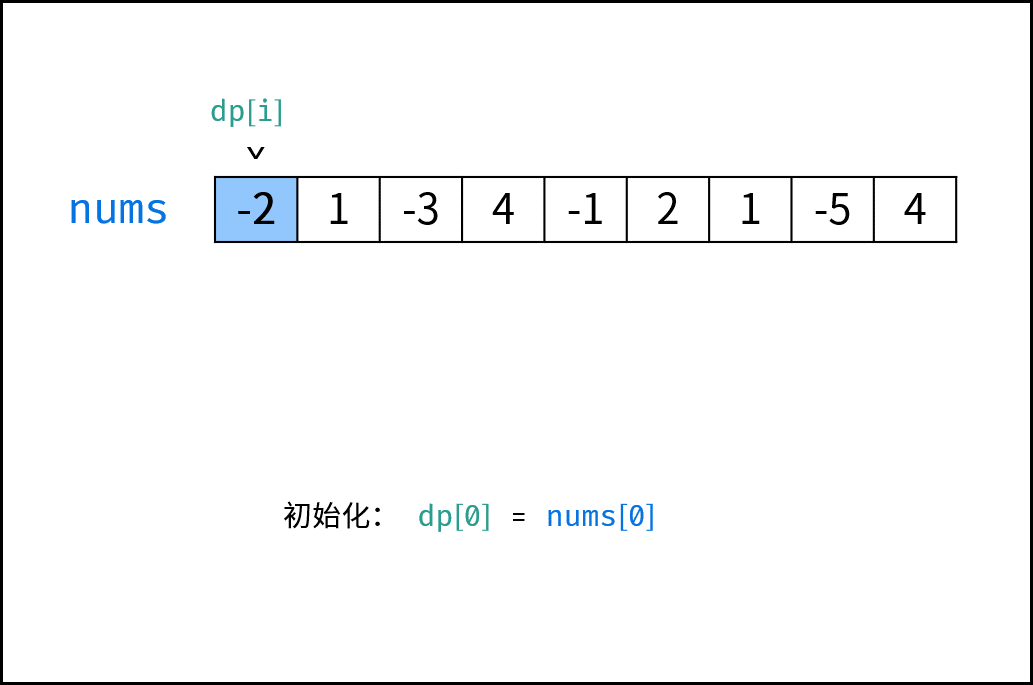<![Picture2.png](https://pic.leetcode-cn.com/c05fcc23f37290d4445ea7ee0ff4e0217fa9d7a0d0fdada765672900590d7ecd-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/384a20d1538b3fecda3e64f36e6a1cffb2e90aa3def9a06457c0ab5495202f64-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/79596dec42eedd88012ce0b06ede6fcd76fdb61140551503deda234005f22f5c-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/0ad8500b80f4705ab0458d46cf4e9228177373fed84187948352df11a133cc18-Picture5.png),![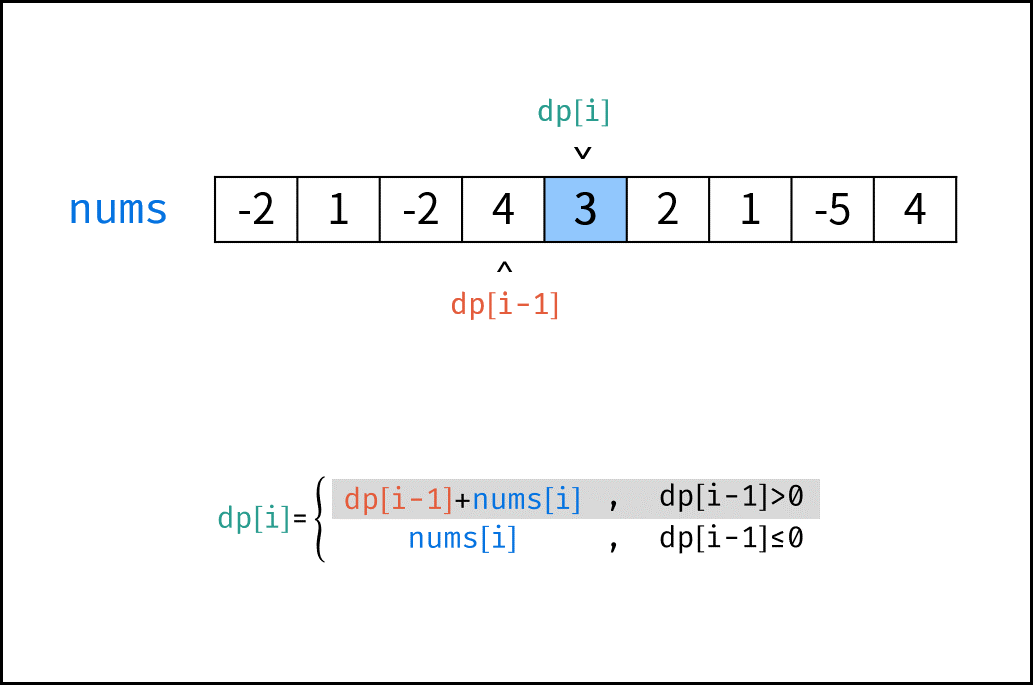Picture6.png](https://pic.leetcode-cn.com/e1cad157f82a37d6960a660e7e648e81da6875e912edd613b10ab639f87674c2-Picture6.png),![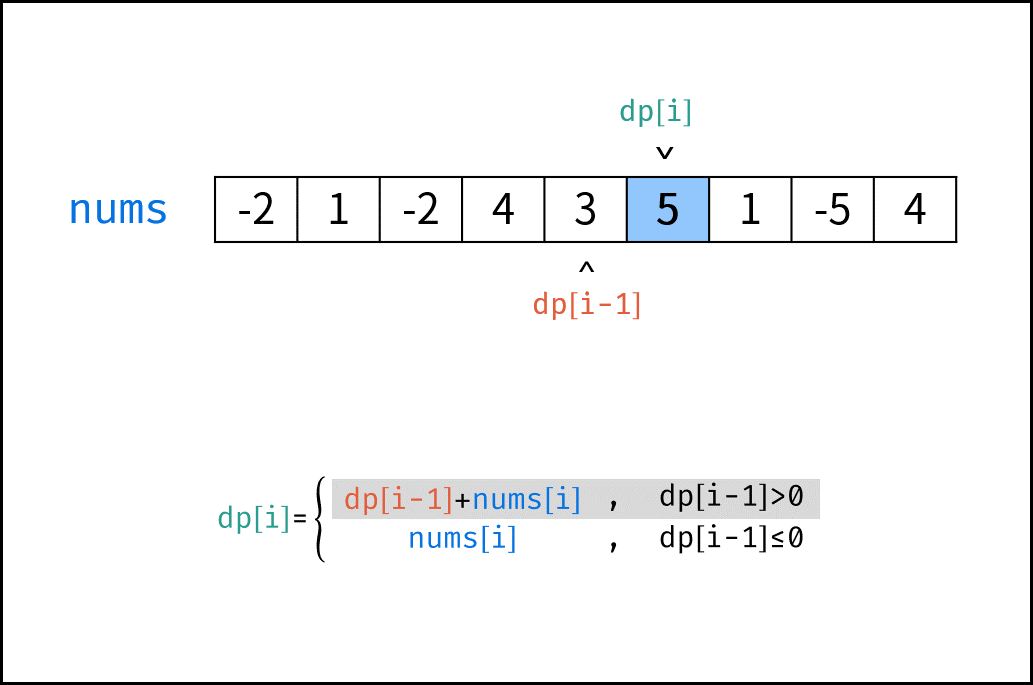Picture7.png](https://pic.leetcode-cn.com/269dbec6c7e0c7580cd74d60d151c651a7cee9a6a0feb4229a3a8a5f2062afca-Picture7.png),![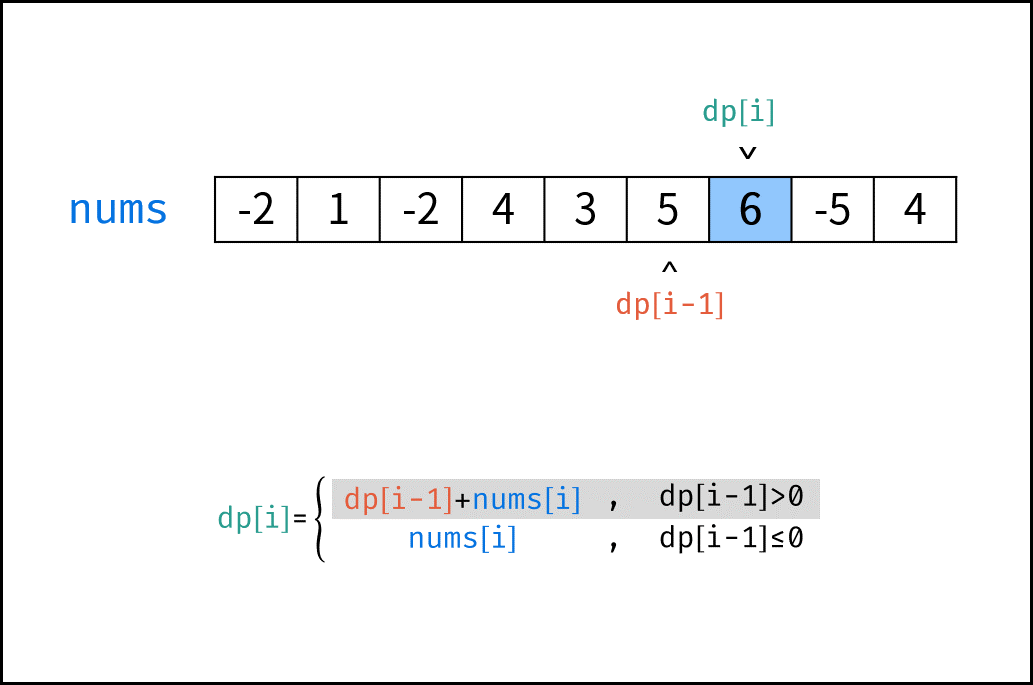Picture8.png](https://pic.leetcode-cn.com/b1218b8594854c40f048db7bce3bb163d41163fc1eef03d8aa4135c8c23ec911-Picture8.png),![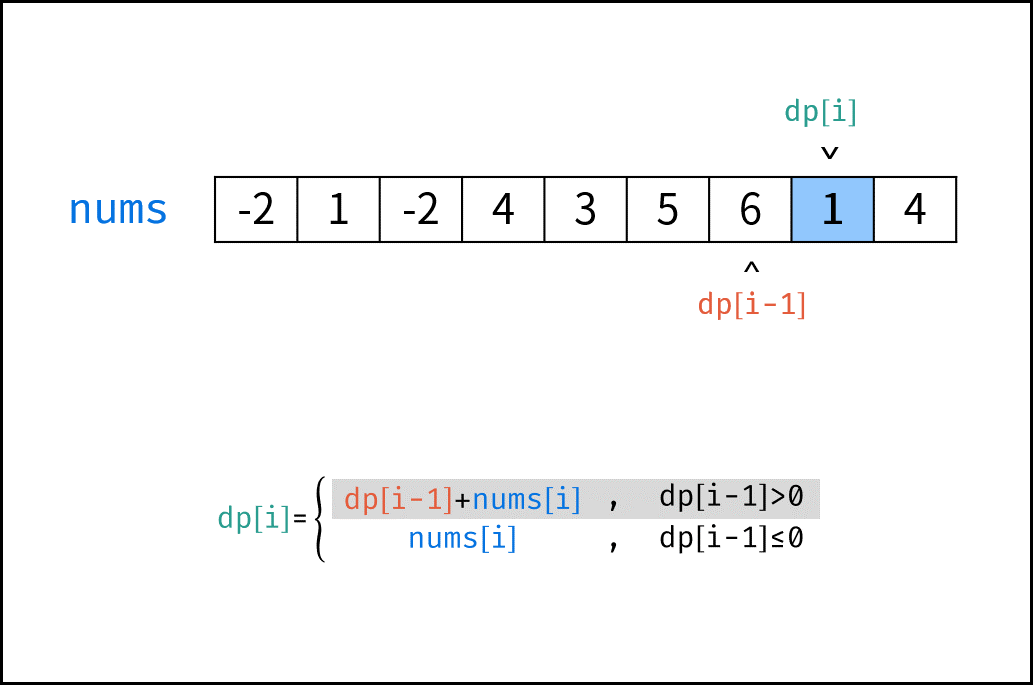Picture9.png](https://pic.leetcode-cn.com/ff0d403e4de402ec0a4122cdb66a9262f93a4986442b18dbb1655fe367052a25-Picture9.png),![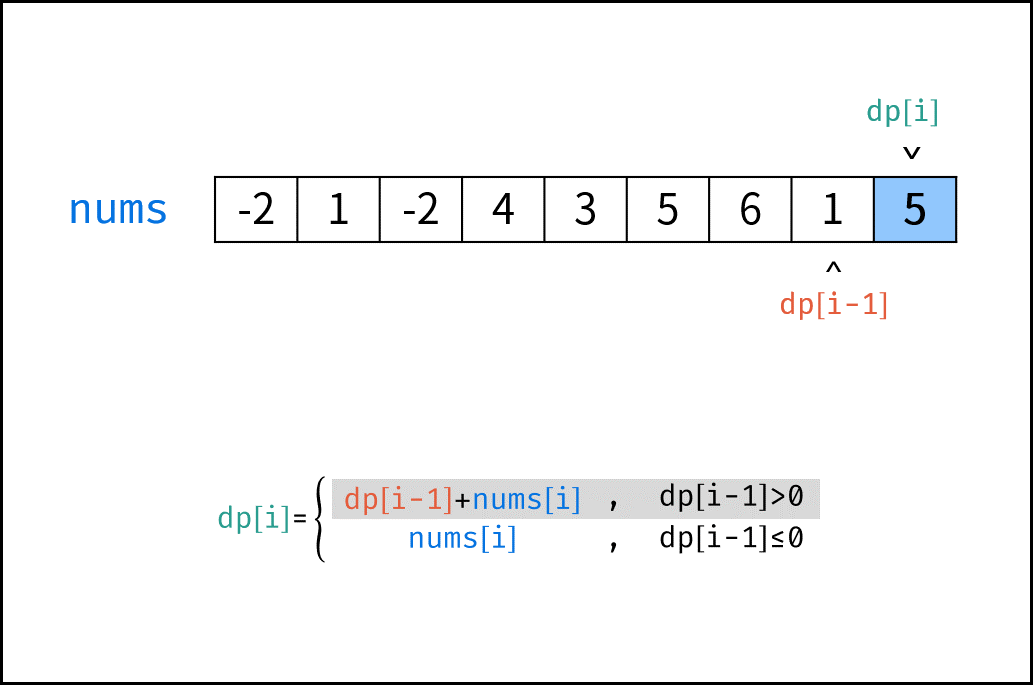Picture10.png](https://pic.leetcode-cn.com/1fde43a35e65c800a274e2dd46fe9641ce38e215ff85a73a8d7e5d26163fe17e-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/86e7af90fbef1c11702fb72132df9b5fb2b33e13585d7ef67268fdf74d8611d4-Picture11.png)>
## 代码：
```Python []
class Solution:
def maxSales(self, sales: List[int]) -> int:
for i in range(1, len(sales)):
sales[i] += max(sales[i - 1], 0)
return max(sales)
```
```Java []
class Solution {
public int maxSales(int[] sales) {
int res = sales[0];
for(int i = 1; i < sales.length; i++) {
sales[i] += Math.max(sales[i - 1], 0);
res = Math.max(res, sales[i]);
}
return res;
}
}
```
```C++ []
class Solution {
public:
int maxSales(vector<int>& sales) {
int res = sales[0];
for(int i = 1; i < sales.size(); i++) {
if(sales[i - 1] > 0) sales[i] += sales[i - 1];
if(sales[i] > res) res = sales[i];
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 线性遍历数组 $sales$ 即可获得结果，使用 $O(N)$ 时间。
- **空间复杂度 $O(1)$ ：** 使用常数大小的额外空间。

163
leetbook_ioa/docs/LCR 162. 数字 1 的个数.md Executable file
View File

@@ -0,0 +1,163 @@
## 解题思路：
> 为简化篇幅，本文将 $num$ 记为 $n$ 。
将 $1$ ~ $n$ 的个位、十位、百位、...的 $1$ 出现次数相加，即为 $1$ 出现的总次数。
设数字 $n$ 是个 $x$ 位数，记 $n$ 的第 $i$ 位为 $n_i$ ，则可将 $n$ 写为 $n_{x} n_{x-1} \cdots n_{2} n_{1}$ ；本文名词规定如下：
- 称 「 $n_i$ 」称为 **当前位** ，记为 $cur$ ；
- 将 「 $n_{i-1} n_{i-2} \cdots n_{2} n_{1}$ 」称为 **低位** ，记为 $low$ ；
- 将 「 $n_{x} n_{x-1} \cdots n_{i+2} n_{i+1}$ 」称为 **高位** ，记为 $high$ ；
- 将 「 $10^i$ 」称为 **位因子** ，记为 $digit$ ；
### 某位中 $1$ 出现次数的计算方法：
根据当前位 $cur$ 值的不同，分为以下三种情况：
1. 当 **$cur = 0$ 时：** 此位 $1$ 的出现次数只由高位 $high$ 决定，计算公式为：
$$
high \times digit
$$
> 如下图所示，以 $n = 2304$ 为例，求 $digit = 10$ （即十位）的 $1$ 出现次数。
![Picture1.png](https://pic.leetcode-cn.com/1599887431-cVmcVA-Picture1.png){:align=center width=450}
2. 当 **$cur = 1$ 时：** 此位 $1$ 的出现次数由高位 $high$ 和低位 $low$ 决定，计算公式为：
$$
high \times digit + low + 1
$$
> 如下图所示，以 $n = 2314$ 为例，求 $digit = 10$ （即十位）的 $1$ 出现次数。
![Picture2.png](https://pic.leetcode-cn.com/1599887431-HAAvVp-Picture2.png){:align=center width=450}
3. 当 **$cur = 2, 3, \cdots, 9$ 时：** 此位 $1$ 的出现次数只由高位 $high$ 决定，计算公式为：
$$
(high + 1) \times digit
$$
> 如下图所示，以 $n = 2324$ 为例，求 $digit = 10$ （即十位）的 $1$ 出现次数。
![Picture3.png](https://pic.leetcode-cn.com/1599887431-djUZTe-Picture3.png){:align=center width=450}
### 变量递推公式：
设计按照 “个位、十位、...” 的顺序计算，则 $high / cur / low / digit$ 应初始化为：
```Python []
high = n // 10
cur = n % 10
low = 0
digit = 1 # 个位
```
```Java []
int high = n / 10;
int cur = n % 10;
int low = 0;
int digit = 1; // 个位
```
```C++ []
int high = n / 10;
int cur = n % 10;
int low = 0;
int digit = 1; // 个位
```
因此，从个位到最高位的变量递推公式为：
```Python []
while high != 0 or cur != 0: # 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
low += cur * digit # 将 cur 加入 low ，组成下轮 low
cur = high % 10 # 下轮 cur 是本轮 high 的最低位
high //= 10 # 将本轮 high 最低位删除，得到下轮 high
digit *= 10 # 位因子每轮 × 10
```
```Java []
while(high != 0 || cur != 0) { // 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
low += cur * digit; // 将 cur 加入 low ，组成下轮 low
cur = high % 10; // 下轮 cur 是本轮 high 的最低位
high /= 10; // 将本轮 high 最低位删除，得到下轮 high
digit *= 10; // 位因子每轮 × 10
}
```
```C++ []
while(high != 0 || cur != 0) { // 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
low += cur * digit; // 将 cur 加入 low ，组成下轮 low
cur = high % 10; // 下轮 cur 是本轮 high 的最低位
high /= 10; // 将本轮 high 最低位删除，得到下轮 high
digit *= 10; // 位因子每轮 × 10
}
```
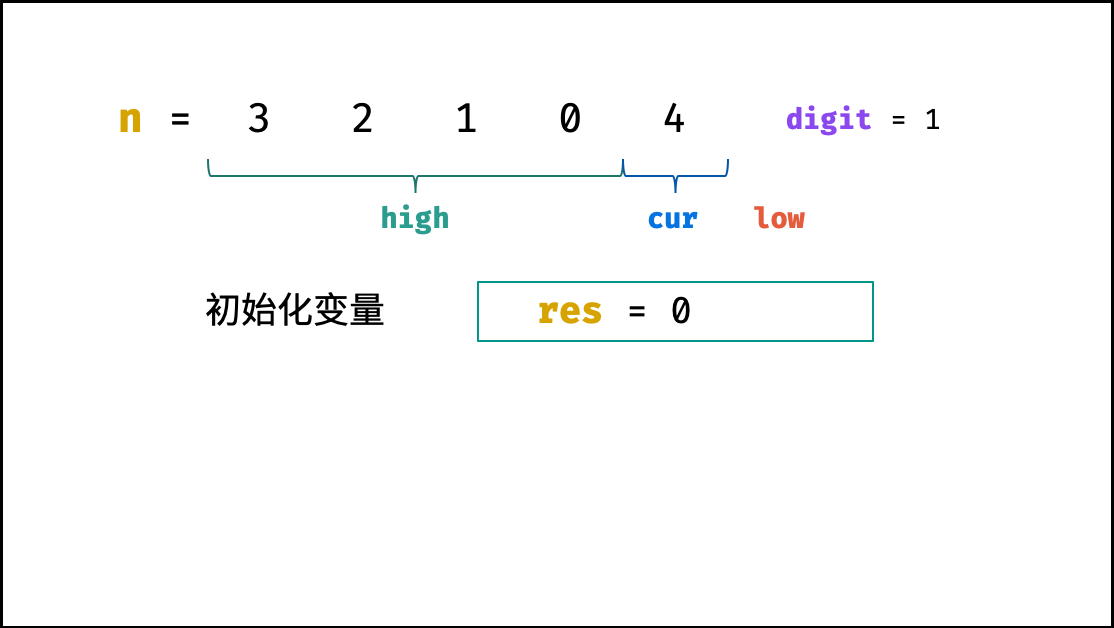<![Picture4.png](https://pic.leetcode-cn.com/1599886793-UnGSFA-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599886793-XAkJaS-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599886793-FFgjAB-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599886793-yhuxHN-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599886793-BBSKuG-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1599886793-osrlME-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599886793-XTSnxb-Picture10.png)>
## 代码：
```Python []
class Solution:
def digitOneInNumber(self, n: int) -> int:
digit, res = 1, 0
high, cur, low = n // 10, n % 10, 0
while high != 0 or cur != 0:
if cur == 0: res += high * digit
elif cur == 1: res += high * digit + low + 1
else: res += (high + 1) * digit
low += cur * digit
cur = high % 10
high //= 10
digit *= 10
return res
```
```Java []
class Solution {
public int digitOneInNumber(int n) {
int digit = 1, res = 0;
int high = n / 10, cur = n % 10, low = 0;
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
}
```
```C++ []
class Solution {
public:
int digitOneInNumber(int n) {
long digit = 1;
int high = n / 10, cur = n % 10, low = 0, res = 0;
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(\log n)$ ：** 循环内的计算操作使用 $O(1)$ 时间；循环次数为数字 $n$ 的位数，即 $\log_{10}{n}$ ，因此循环使用 $O(\log n)$ 时间。
- **空间复杂度 $O(1)$ ：** 几个变量使用常数大小的额外空间。

169
leetbook_ioa/docs/LCR 163. 找到第 k 位数字.md Executable file
View File

@@ -0,0 +1,169 @@
## 解题思路：
文名词规定如下：
1. 将 $101112 \cdots$ 中的每一位称为 **数位** ，记为 $k$ ；
2. 将 $10, 11, 12, \cdots$ 称为 **数字** ，记为 $num$ ；
3. 数字 $10$ 是一个两位数，称此数字的 **位数** 为 $2$ ，记为 $digit$ ；
4. 每 $digit$ 位数的起始数字（即：$1, 10, 100, \cdots$），记为 $start$ ；
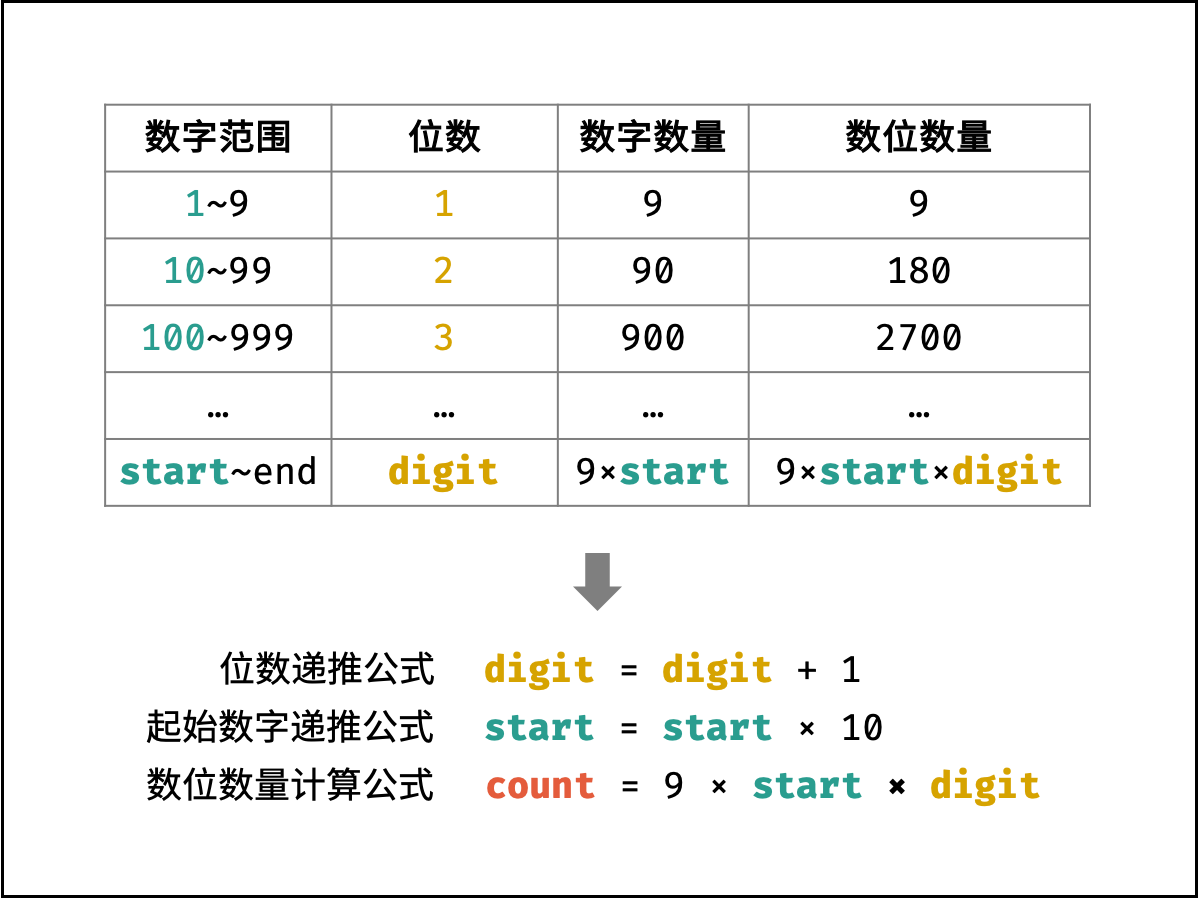![Picture1.png](https://pic.leetcode-cn.com/1599888213-CYhLfm-Picture1.png){:align=center width=450}
观察上表，可推出各 $digit$ 下的数位数量 $count$ 的计算公式：
$$
count = 9 \times start \times digit
$$
根据以上分析，可将求解分为三步：
1. 确定 $k$ 所在 **数字** 的 **位数** ，记为 $digit$ ；
2. 确定 $k$ 所在的 **数字** ，记为 $num$ ；
3. 确定 $k$ 是 $num$ 中的哪一数位，并返回结果；
### 1. 确定所求数位的所在数字的位数
如下图所示，循环执行 $k$ 减去 一位数、两位数、... 的数位数量 $count$ ，直至 $k \leq count$ 时跳出。
由于 $k$ 已经减去了一位数、两位数、...、$(digit-1)$ 位数的 **数位数量** $count$ ，因而此时的 $k$ 是从起始数字 $start$ 开始计数的。
```Python []
digit, start, count = 1, 1, 9
while k > count:
k -= count
start *= 10 # 1, 10, 100, ...
digit += 1 # 1, 2, 3, ...
count = 9 * start * digit # 9, 180, 2700, ...
```
```Java []
int digit = 1;
long start = 1;
long count = 9;
while (k > count) {
k -= count;
start *= 10; // 1, 10, 100, ...
digit += 1; // 1, 2, 3, ...
count = digit * start * 9; // 9, 180, 2700, ...
}
```
```C++ []
int digit = 1;
long start = 1;
long count = 9;
while (k > count) { // 1.
k -= count;
start *= 10; // 1, 10, 100, ...
digit += 1; // 1, 2, 3, ...
count = digit * start * 9; // 9, 180, 2700, ...
}
```
**结论：** 所求数位 (1) 在某个 $digit$ 位数中； (2) 为从数字 $start$ 开始的第 $k$ 个数位。
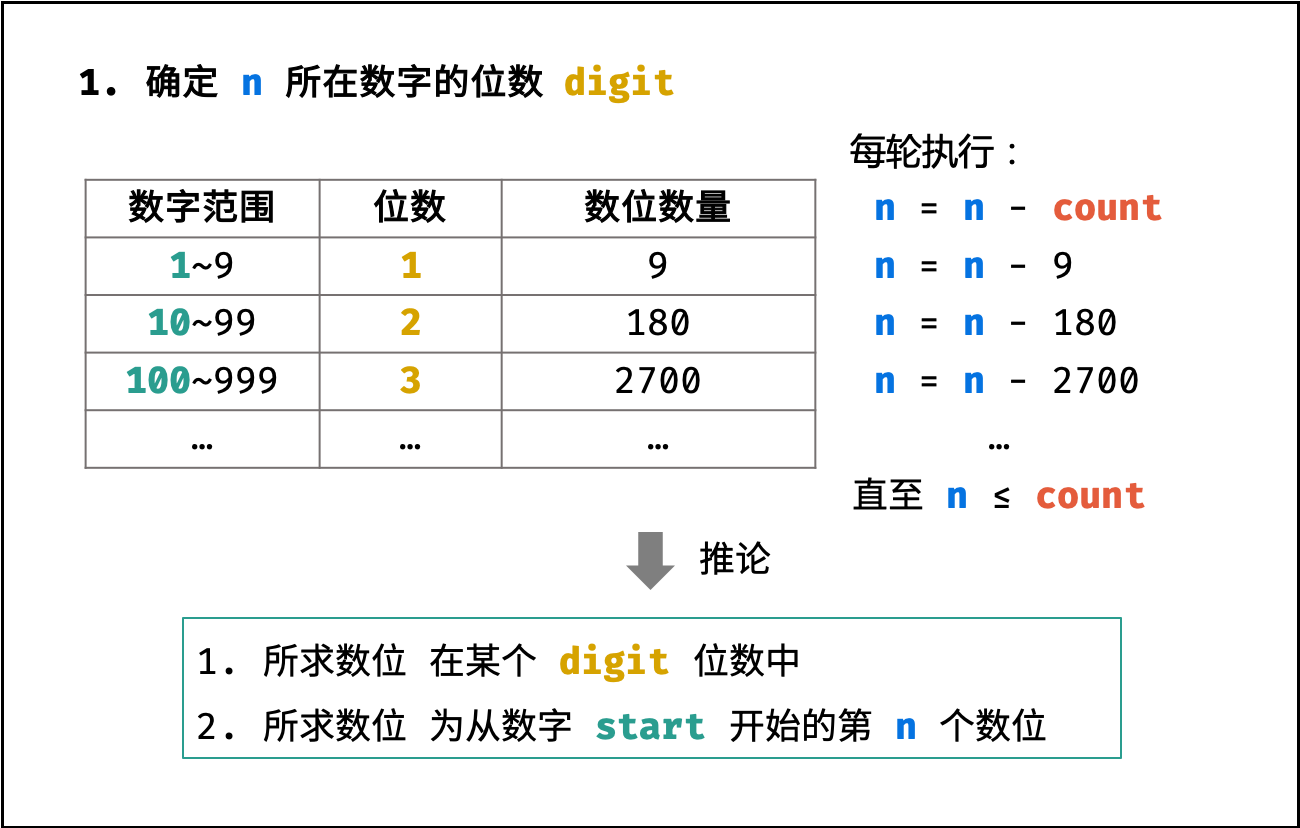![Picture2.png](https://pic.leetcode-cn.com/1599888496-HivJvS-Picture2.png){:align=center width=500}
### 2. 确定所求数位所在的数字
如下图所示，所求数位 在从数字 $start$ 开始的第 $[(k - 1) / digit]$ 个 **数字** 中（ $start$ 为第 0 个数字）。
```Python []
num = start + (k - 1) // digit
```
```Java []
long num = start + (k - 1) / digit;
```
```C++ []
long num = start + (k - 1) / digit;
```
**结论：** 所求数位在数字 $num$ 中。
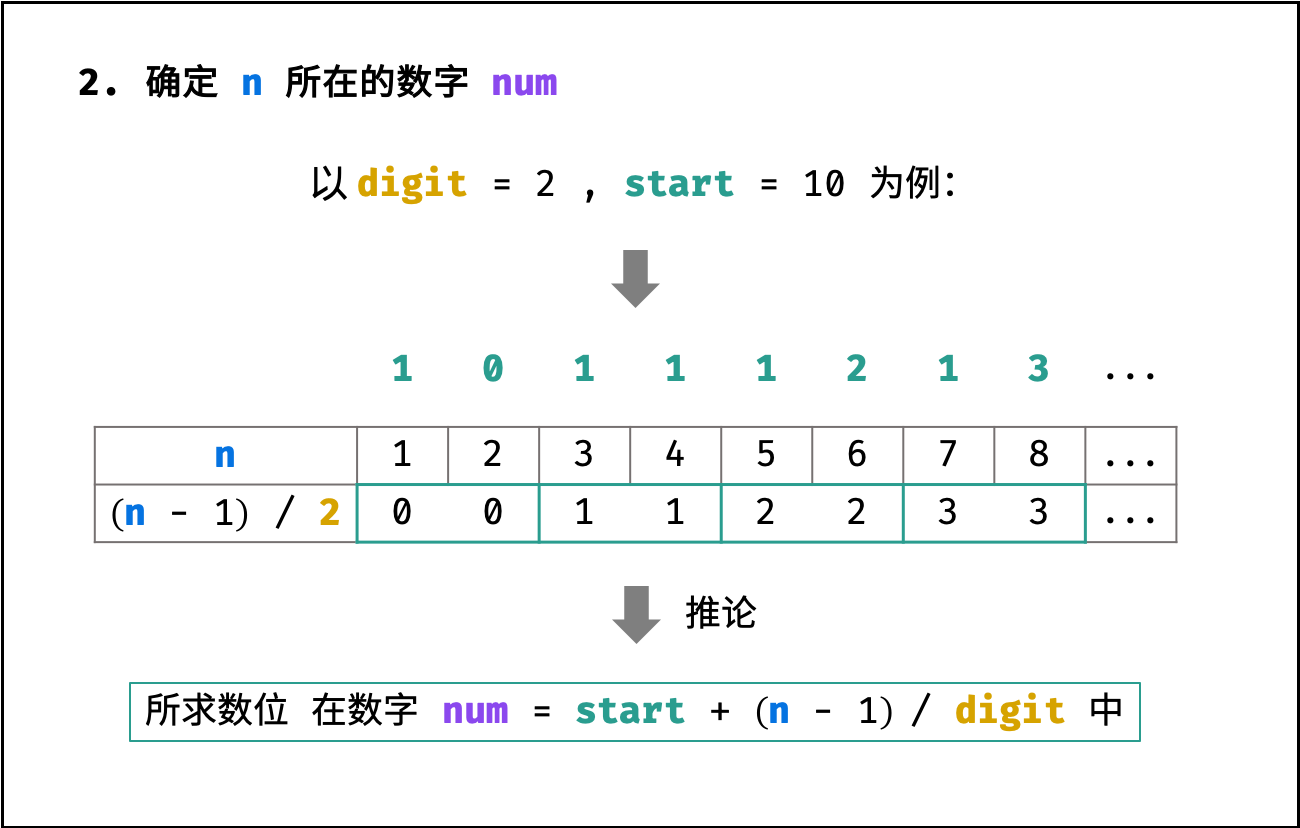![Picture3.png](https://pic.leetcode-cn.com/1599888213-gCcnEA-Picture3.png){:align=center width=500}
### 3. 确定所求数位在 $num$ 的哪一数位
如下图所示，所求数位为数字 $num$ 的第 $(k - 1) \mod digit$ 位（ 数字的首个数位为第 0 位）。
```Python []
s = str(num) # 转化为 string
res = int(s[(k - 1) % digit]) # 获得 num 的 第 (k - 1) % digit 个数位，并转化为 int
```
```Java []
String s = Long.toString(num); // 转化为 string
int res = s.charAt((k - 1) % digit) - '0'; // 获得 num 的 第 (k - 1) % digit 个数位，并转化为 int
```
```C++ []
string s = to_string(num); // 转化为 string
int res = s[(k - 1) % digit] - '0'; // 获得 num 的 第 (k - 1) % digit 个数位，并转化为 int
```
**结论：** 所求数位是 $res$ 。
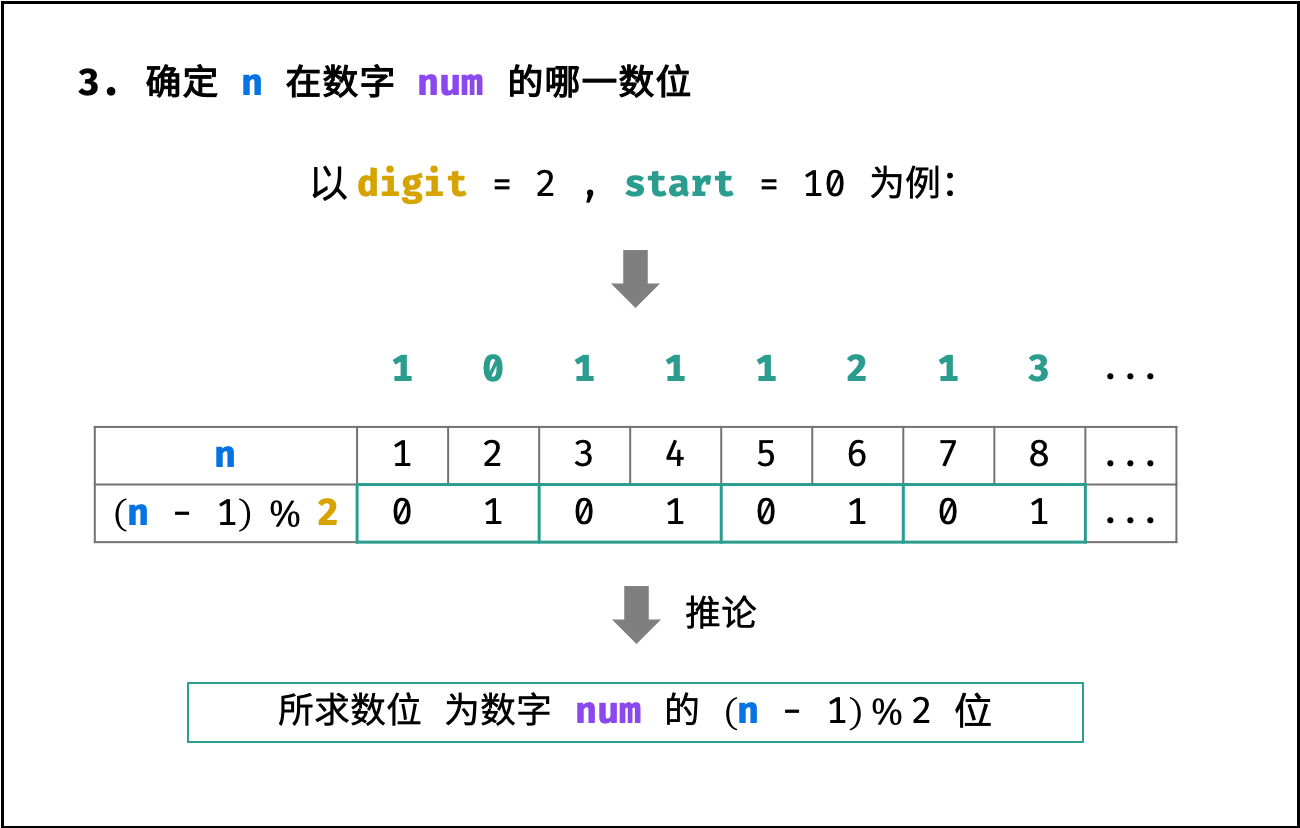![Picture4.png](https://pic.leetcode-cn.com/1599888395-oeWGAH-Picture4.png){:align=center width=500}
整体流程如下图所示。
<![Picture5.png](https://pic.leetcode-cn.com/1599888213-wmVktF-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599888213-vPFqup-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599888796-IlfLEc-Picture7.png)>
## 代码：
```Python []
class Solution:
def findKthNumber(self, k: int) -> int:
digit, start, count = 1, 1, 9
while k > count: # 1.
k -= count
start *= 10
digit += 1
count = 9 * start * digit
num = start + (k - 1) // digit # 2.
return int(str(num)[(k - 1) % digit]) # 3.
```
```Java []
class Solution {
public int findKthNumber(int k) {
int digit = 1;
long start = 1;
long count = 9;
while (k > count) { // 1.
k -= count;
start *= 10;
digit += 1;
count = digit * start * 9;
}
long num = start + (k - 1) / digit; // 2.
return Long.toString(num).charAt((k - 1) % digit) - '0'; // 3.
}
}
```
```C++ []
class Solution {
public:
int findKthNumber(int k) {
int digit = 1;
long start = 1;
long count = 9;
while (k > count) { // 1.
k -= count;
start *= 10;
digit += 1;
count = digit * start * 9;
}
long num = start + (k - 1) / digit; // 2.
return to_string(num)[(k - 1) % digit] - '0'; // 3.
}
};
```
### 复杂度分析：
- **时间复杂度 $O(\log k)$ ：** 所求数位 $k$ 对应数字 $num$ 的位数 $digit$ 最大为 $O(\log k)$ ；第一步最多循环 $O(\log k)$ 次；第三步中将 $num$ 转化为字符串使用 $O(\log k)$ 时间；因此总体为 $O(\log k)$ 。
- **空间复杂度 $O(\log k)$ ：** 将数字 $num$ 转化为字符串 `str(num)` ，占用 $O(\log k)$ 的额外空间。

170
leetbook_ioa/docs/LCR 164. 破解闯关密码.md Executable file
View File

@@ -0,0 +1,170 @@
## 解题思路：
此题求拼接起来的最小数字，本质上是一个排序问题。设数组 $password$ 中任意两数字的字符串为 $x$ 和 $y$ ，则规定 **排序判断规则** 为：
- 若拼接字符串 $x + y > y + x$ ，则 $x$ “大于” $y$ ；
- 反之，若 $x + y < y + x$ ，则 $x$ “小于” $y$ ；
> $x$ “小于” $y$ 代表：排序完成后，数组中 $x$ 应在 $y$ 左边；“大于” 则反之。
根据以上规则，套用任何排序方法对 $password$ 执行排序即可。
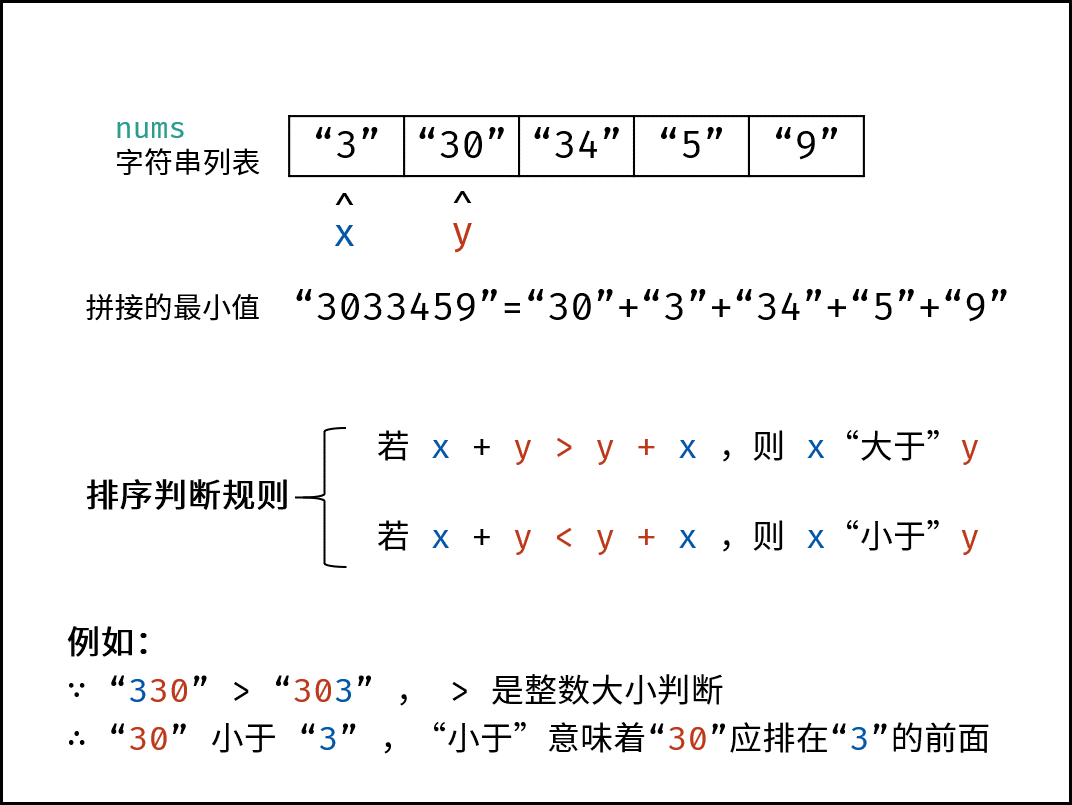![Picture1.png](https://pic.leetcode-cn.com/95e81dbccc44f26292d88c509afd68204a86b37d342f83d109fa7aa0cd4a6049-Picture1.png){:align=center width=450}
### 算法流程：
1. **初始化：** 字符串列表 $strs$ ，保存各数字的字符串格式；
2. **列表排序：** 应用以上 “排序判断规则” ，对 $strs$ 执行排序；
3. **返回值：** 拼接 $strs$ 中的所有字符串，并返回。
> 下图中 `nums` 对应本题的 `password` 。
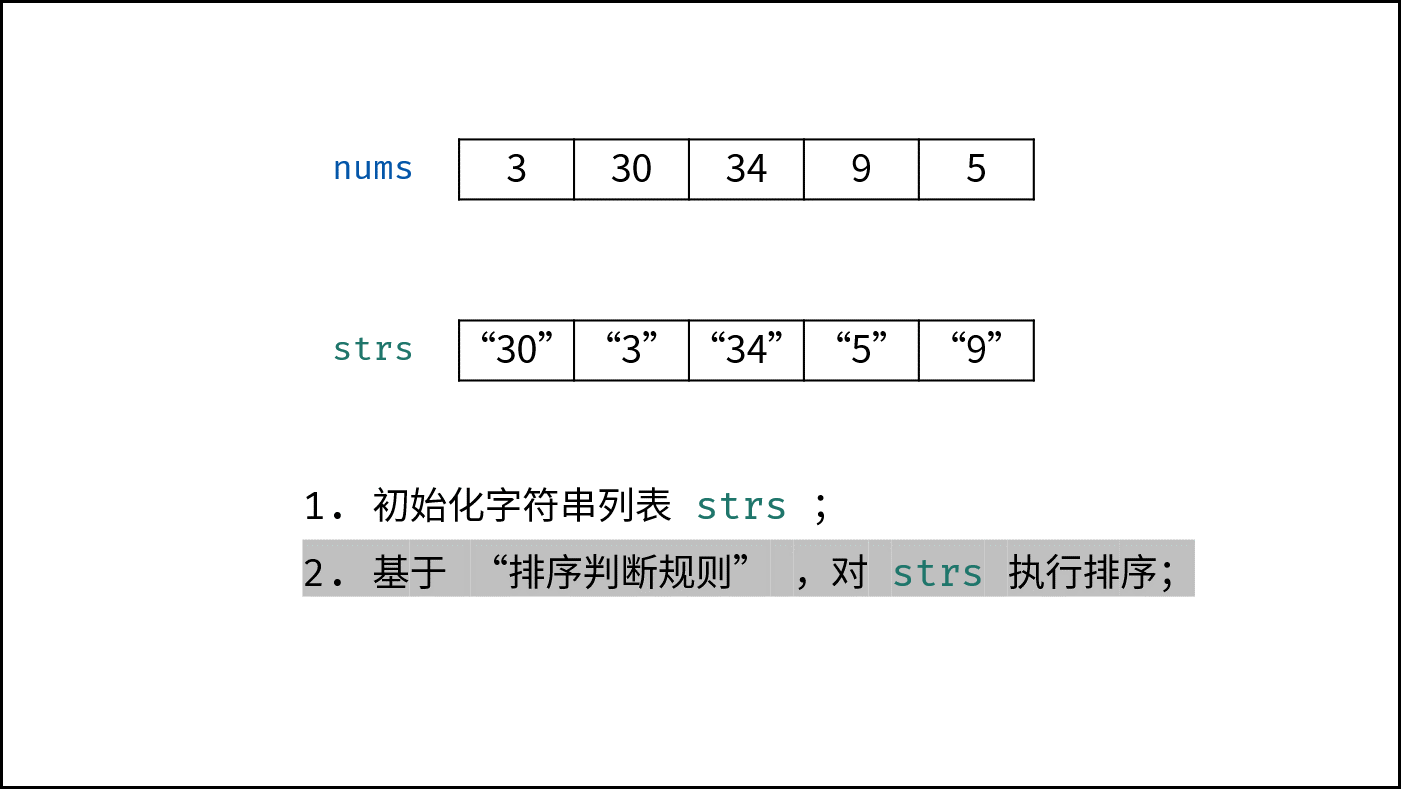<![Picture2.png](https://pic.leetcode-cn.com/069f69477b88178c40054505fb178352ca84d74031238167f47b97cb93a99d86-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/18ef32b109f995e67051632b0c78947eb3660687b803ab6c968efa0887e44958-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/14e3e6b5a28486fc4b0e7c614d75eb239aafca71b4ac5a6907d7e4154b27784a-Picture4.png)>
## 代码：
本文列举 **快速排序** 和 **内置函数** 两种排序方法，其他排序方法也可实现。
### 快速排序：
需修改快速排序函数中的排序判断规则。字符串大小（字典序）对比的实现方法：
- Python/C++ 中可直接用 `<` , `>`；
- Java 中使用函数 `A.compareTo(B)`；
```Python []
class Solution:
def crackPassword(self, password: List[int]) -> str:
def quick_sort(l , r):
if l >= r: return
i, j = l, r
while i < j:
while strs[j] + strs[l] >= strs[l] + strs[j] and i < j: j -= 1
while strs[i] + strs[l] <= strs[l] + strs[i] and i < j: i += 1
strs[i], strs[j] = strs[j], strs[i]
strs[i], strs[l] = strs[l], strs[i]
quick_sort(l, i - 1)
quick_sort(i + 1, r)
strs = [str(num) for num in password]
quick_sort(0, len(strs) - 1)
return ''.join(strs)
```
```Java []
class Solution {
public String crackPassword(int[] password) {
String[] strs = new String[password.length];
for(int i = 0; i < password.length; i++)
strs[i] = String.valueOf(password[i]);
quickSort(strs, 0, strs.length - 1);
StringBuilder res = new StringBuilder();
for(String s : strs)
res.append(s);
return res.toString();
}
void quickSort(String[] strs, int l, int r) {
if(l >= r) return;
int i = l, j = r;
String tmp = strs[i];
while(i < j) {
while((strs[j] + strs[l]).compareTo(strs[l] + strs[j]) >= 0 && i < j) j--;
while((strs[i] + strs[l]).compareTo(strs[l] + strs[i]) <= 0 && i < j) i++;
tmp = strs[i];
strs[i] = strs[j];
strs[j] = tmp;
}
strs[i] = strs[l];
strs[l] = tmp;
quickSort(strs, l, i - 1);
quickSort(strs, i + 1, r);
}
}
```
```C++ []
class Solution {
public:
string crackPassword(vector<int>& password) {
vector<string> strs;
for(int i = 0; i < password.size(); i++)
strs.push_back(to_string(password[i]));
quickSort(strs, 0, strs.size() - 1);
string res;
for(string s : strs)
res.append(s);
return res;
}
private:
void quickSort(vector<string>& strs, int l, int r) {
if(l >= r) return;
int i = l, j = r;
while(i < j) {
while(strs[j] + strs[l] >= strs[l] + strs[j] && i < j) j--;
while(strs[i] + strs[l] <= strs[l] + strs[i] && i < j) i++;
swap(strs[i], strs[j]);
}
swap(strs[i], strs[l]);
quickSort(strs, l, i - 1);
quickSort(strs, i + 1, r);
}
};
```
### 内置函数：
需定义排序规则：
- Python 定义在函数 `sort_rule(x, y)` 中；
- Java 定义为 `(x, y) -> (x + y).compareTo(y + x)` ；
- C++ 定义为 `(string& x, string& y){ return x + y < y + x; }` ；
```Python []
class Solution:
def crackPassword(self, password: List[int]) -> str:
def sort_rule(x, y):
a, b = x + y, y + x
if a > b: return 1
elif a < b: return -1
else: return 0
strs = [str(num) for num in password]
strs.sort(key = functools.cmp_to_key(sort_rule))
return ''.join(strs)
```
```Java []
class Solution {
public String crackPassword(int[] password) {
String[] strs = new String[password.length];
for(int i = 0; i < password.length; i++)
strs[i] = String.valueOf(password[i]);
Arrays.sort(strs, (x, y) -> (x + y).compareTo(y + x));
StringBuilder res = new StringBuilder();
for(String s : strs)
res.append(s);
return res.toString();
}
}
```
```C++ []
class Solution {
public:
string crackPassword(vector<int>& password) {
vector<string> strs;
string res;
for(int i = 0; i < password.size(); i++)
strs.push_back(to_string(password[i]));
sort(strs.begin(), strs.end(), [](string& x, string& y){ return x + y < y + x; });
for(int i = 0; i < strs.size(); i++)
res.append(strs[i]);
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N \log N)$ ：** $N$ 为最终返回值的字符数量（ $strs$ 列表的长度 $\leq N$ ）；使用快排或内置函数的平均时间复杂度为 $O(N \log N)$ ，最差为 $O(N^2)$ 。
- **空间复杂度 $O(N)$ ：** 字符串列表 $strs$ 占用线性大小的额外空间。

212
leetbook_ioa/docs/LCR 165. 解密数字.md Executable file
View File

@@ -0,0 +1,212 @@
## 解题思路：
根据题意，可按照下图的思路，总结出 “递推公式” （即转移方程）。
> 下图中的 `num` 对应本题的 `ciphertext` 。
![Picture1.png](https://pic.leetcode-cn.com/1603462412-iUcKzA-Picture1.png){:align=center width=600}
因此，此题可用动态规划解决，以下按照流程解题。
### 动态规划解析：
> 记数字 $ciphertext$ 第 $i$ 位数字为 $x_i$ ，数字 $ciphertext$ 的位数为 $n$ ；
> 例如： $ciphertext = 12258$ 的 $n = 5$ , $x_1 = 1$ 。
- **状态定义：** 设动态规划列表 $dp$ ，$dp[i]$ 代表以 $x_i$ 为结尾的数字的翻译方案数量。
- **转移方程：** 若 $x_i$ 和 $x_{i-1}$ 组成的两位数字可被整体翻译，则 $dp[i] = dp[i - 1] + dp[i - 2]$ ，否则 $dp[i] = dp[i - 1]$ 。
$$
dp[i] =
\begin{cases}
dp[i - 1] + dp[i - 2] & {, (10 x_{i-1} + x_i) \in [10,25]} \\
dp[i - 1] & {, (10 x_{i-1} + x_i) \in [0, 10) \cup (25, 99]}
\end{cases}
$$
> **可被整体翻译的两位数区间分析：** 当 $x_{i-1} = 0$ 时，组成的两位数无法被整体翻译（例如 $00, 01, 02, \cdots$ ），大于 $25$ 的两位数也无法被整体翻译（例如 $26, 27, \cdots$ ），因此区间为 $[10, 25]$ 。
- **初始状态：** $dp[0] = dp[1] = 1$ ，即 “无数字” 和 “第 $1$ 位数字” 的翻译方法数量均为 $1$ ；
- **返回值：** $dp[n]$ ，即此数字的翻译方案数量；
> **Q：** 无数字情况 $dp[0] = 1$ 从何而来？
> **A：** 当 $ciphertext$ 第 $1, 2$ 位的组成的数字 $\in [10,25]$ 时，显然应有 $2$ 种翻译方法，即 $dp[2] = dp[1] + dp[0] = 2$ ，而显然 $dp[1] = 1$ ，因此推出 $dp[0] = 1$ 。
## 方法一：字符串遍历
- 为方便获取数字的各位 $x_i$ ，考虑先将数字 $ciphertext$ 转化为字符串 $s$ ，通过遍历 $s$ 实现动态规划。
- 通过字符串切片 $s[i - 2:i]$ 获取数字组合 $10 x_{i-1} + x_i$ ，通过对比字符串 ASCII 码判断字符串对应的数字区间。
- **空间使用优化：** 由于 $dp[i]$ 只与 $dp[i - 1]$ 有关，因此可使用两个变量 $a, b$ 分别记录 $dp[i]$ , $dp[i - 1]$ ，两变量交替前进即可。此方法可省去 $dp$ 列表使用的 $O(N)$ 的额外空间。
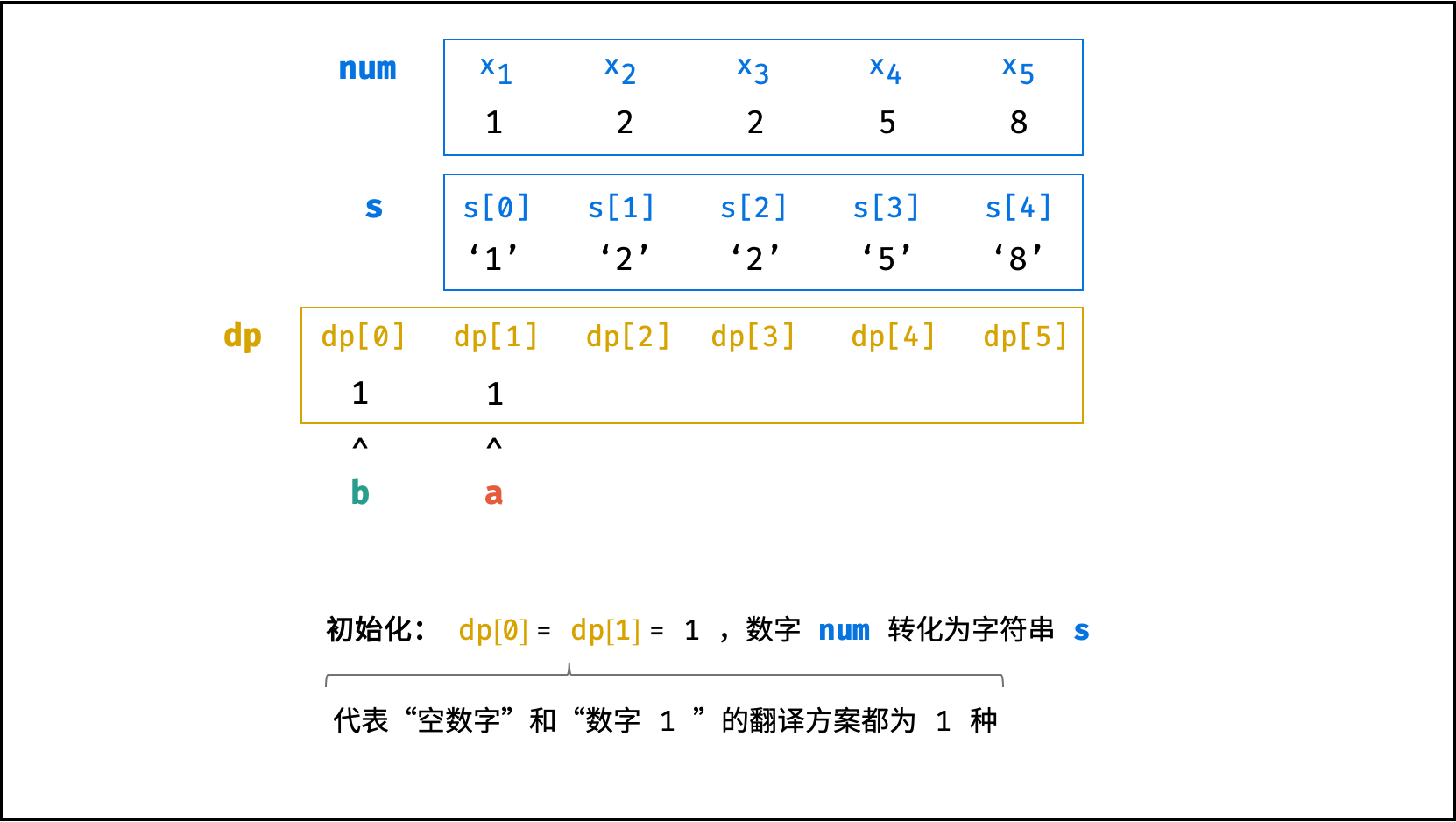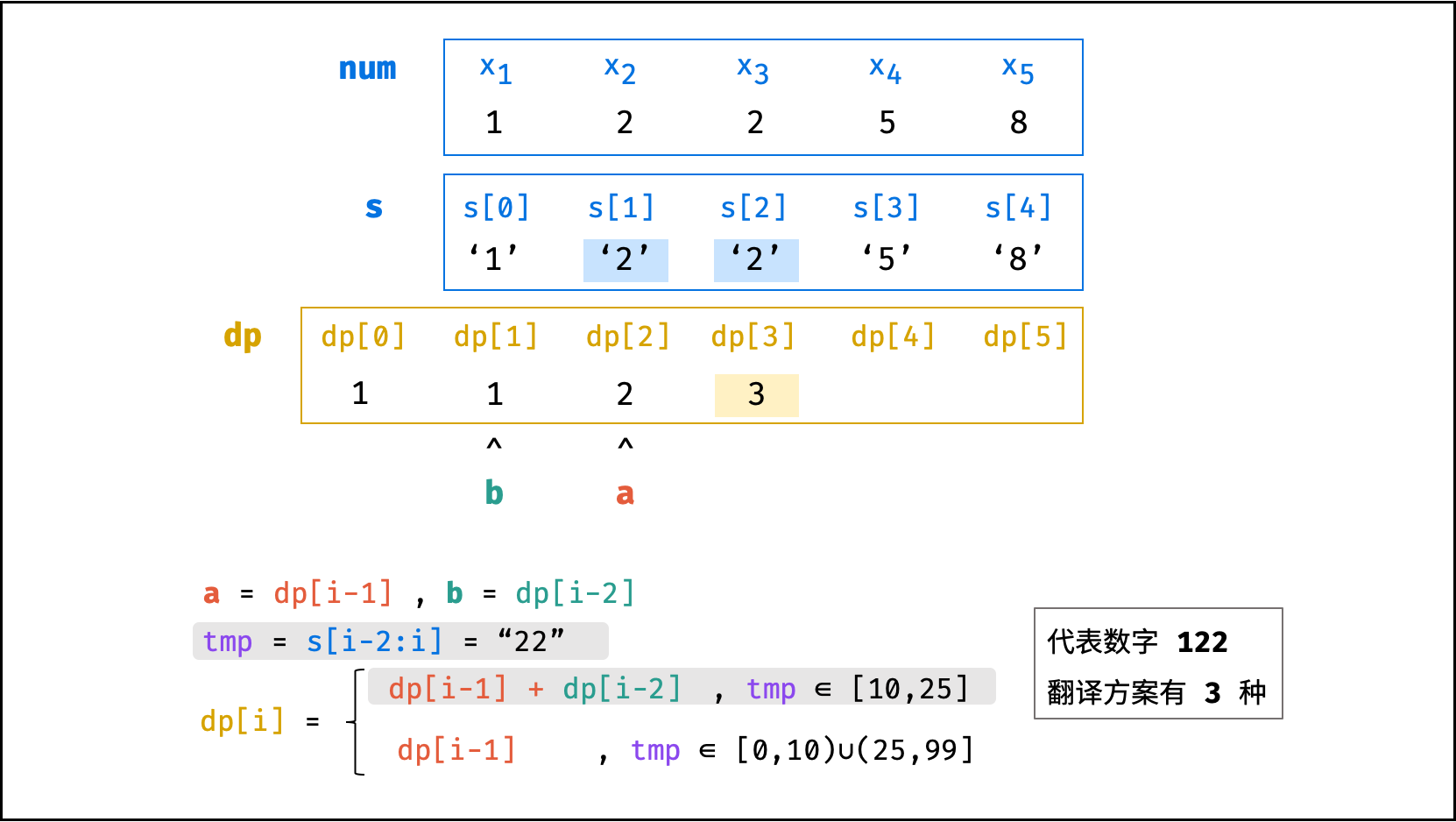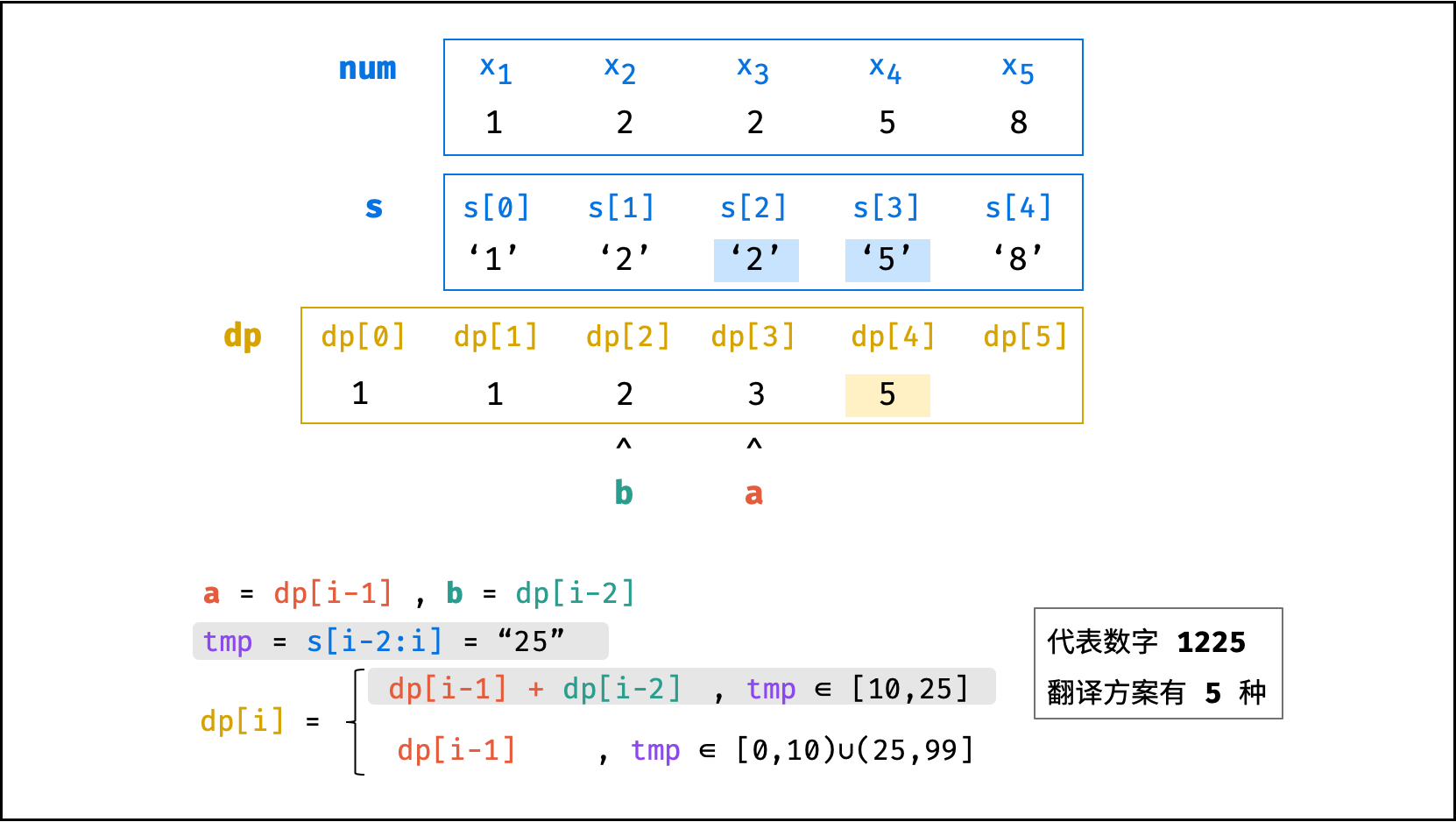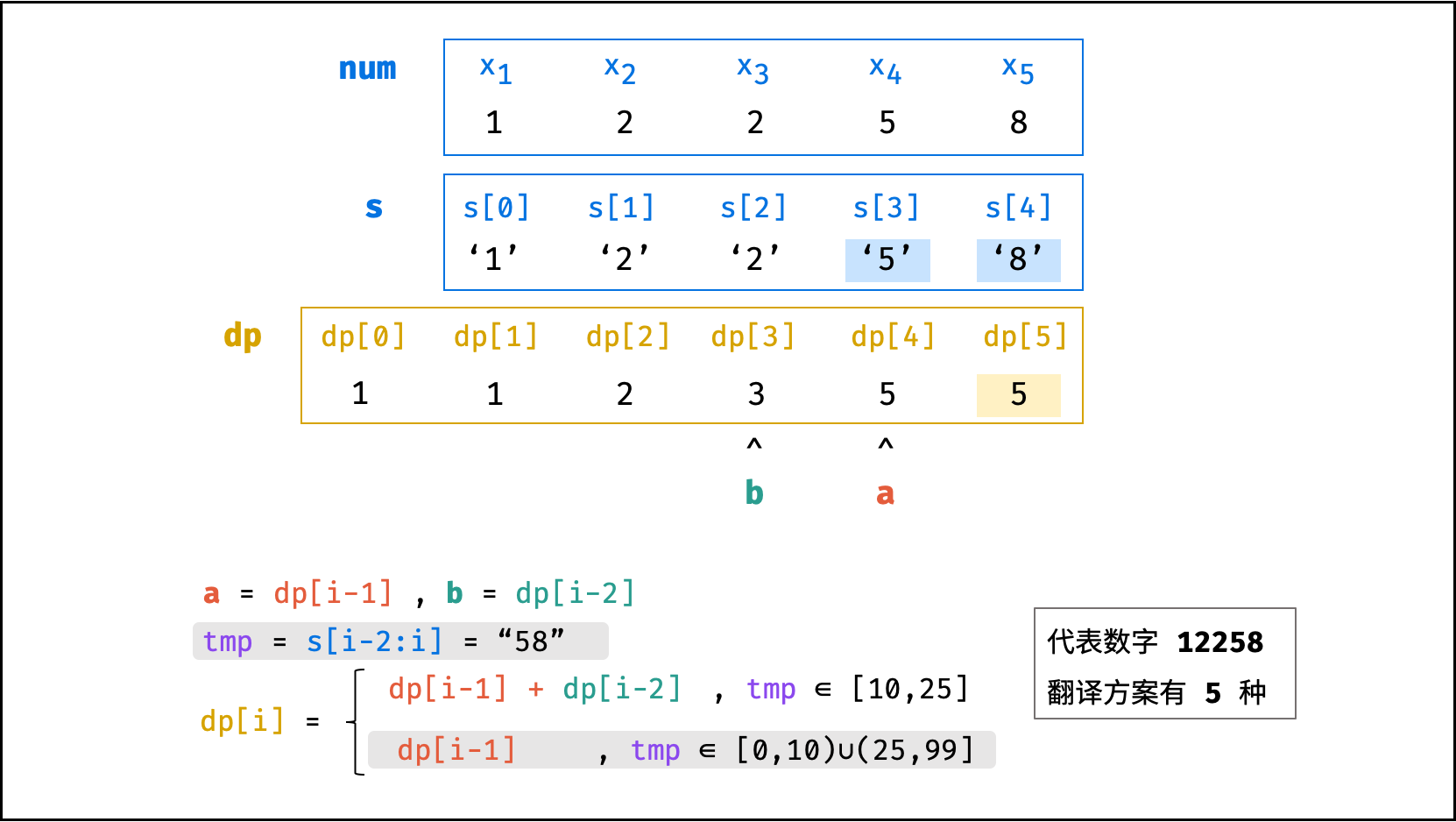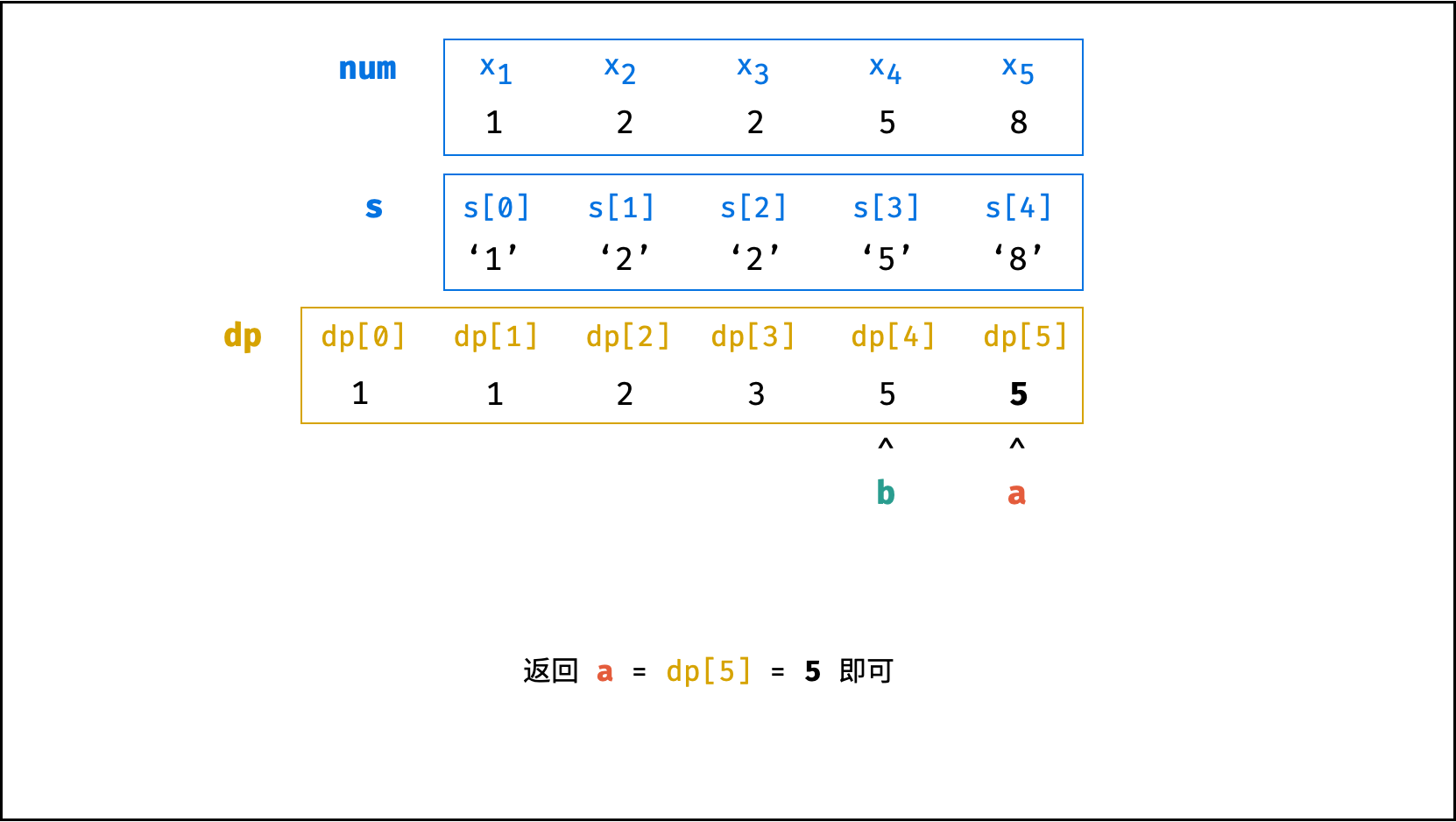<![Picture2.png](https://pic.leetcode-cn.com/1603461843-IWieLl-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603461843-RdXlrc-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603461843-htTNGs-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603461843-HapPbm-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603462672-yBdpkD-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603461843-aRyHmo-Picture7.png)>
### 代码：
```Python []
class Solution:
def crackNumber(self, ciphertext: int) -> int:
s = str(ciphertext)
a = b = 1
for i in range(2, len(s) + 1):
tmp = s[i - 2:i]
c = a + b if "10" <= tmp <= "25" else a
b = a
a = c
return a
```
```Java []
class Solution {
public int crackNumber(int ciphertext) {
String s = String.valueOf(ciphertext);
int a = 1, b = 1;
for(int i = 2; i <= s.length(); i++) {
String tmp = s.substring(i - 2, i);
int c = tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0 ? a + b : a;
b = a;
a = c;
}
return a;
}
}
```
```C++ []
class Solution {
public:
int crackNumber(int ciphertext) {
string s = to_string(ciphertext);
int a = 1, b = 1, len = s.size();
for(int i = 2; i <= len; i++) {
string tmp = s.substr(i - 2, 2);
int c = tmp.compare("10") >= 0 && tmp.compare("25") <= 0 ? a + b : a;
b = a;
a = c;
}
return a;
}
};
```
此题的动态规划计算是 **对称的** ，即 **从左向右** 遍历（从第 $dp[2]$ 计算至 $dp[n]$ ）和 **从右向左** 遍历（从第 $dp[n - 2]$ 计算至 $dp[0]$ ）所得方案数一致。从右向左遍历的代码如下所示。
```Python []
class Solution:
def crackNumber(self, ciphertext: int) -> int:
s = str(ciphertext)
a = b = 1
for i in range(len(s) - 2, -1, -1):
a, b = (a + b if "10" <= s[i:i + 2] <= "25" else a), a
return a
```
```Java []
class Solution {
public int crackNumber(int ciphertext) {
String s = String.valueOf(ciphertext);
int a = 1, b = 1;
for(int i = s.length() - 2; i > -1; i--) {
String tmp = s.substring(i, i + 2);
int c = tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0 ? a + b : a;
b = a;
a = c;
}
return a;
}
}
```
```C++ []
class Solution {
public:
int crackNumber(int ciphertext) {
string s = to_string(ciphertext);
int a = 1, b = 1, len = s.size();
for(int i = len - 2; i > -1; i--) {
string tmp = s.substr(i, 2);
int c = tmp.compare("10") >= 0 && tmp.compare("25") <= 0 ? a + b : a;
b = a;
a = c;
}
return a;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为字符串 $s$ 的长度（即数字 $ciphertext$ 的位数 $\log(ciphertext)$ ），其决定了循环次数。
- **空间复杂度 $O(N)$ ：** 字符串 $s$ 使用 $O(N)$ 大小的额外空间。
## 方法二：数字求余
上述方法虽然已经节省了 $dp$ 列表的空间占用，但字符串 $s$ 仍使用了 $O(N)$ 大小的额外空间。
### 空间优化：
- 利用求余运算 $ciphertext \mod 10$ 和求整运算 $ciphertext // 10$ ，可获取数字 $ciphertext$ 的各位数字（获取顺序为个位、十位、百位…）。
- 运用 **求余** 和 **求整** 运算实现，可实现 **从右向左** 的动态规划计算。而根据上述动态规划 “对称性” ，可知从右向左计算是正确的。
- 自此，字符串 $s$ 的空间占用也被省去，空间复杂度从 $O(N)$ 降至 $O(1)$ 。
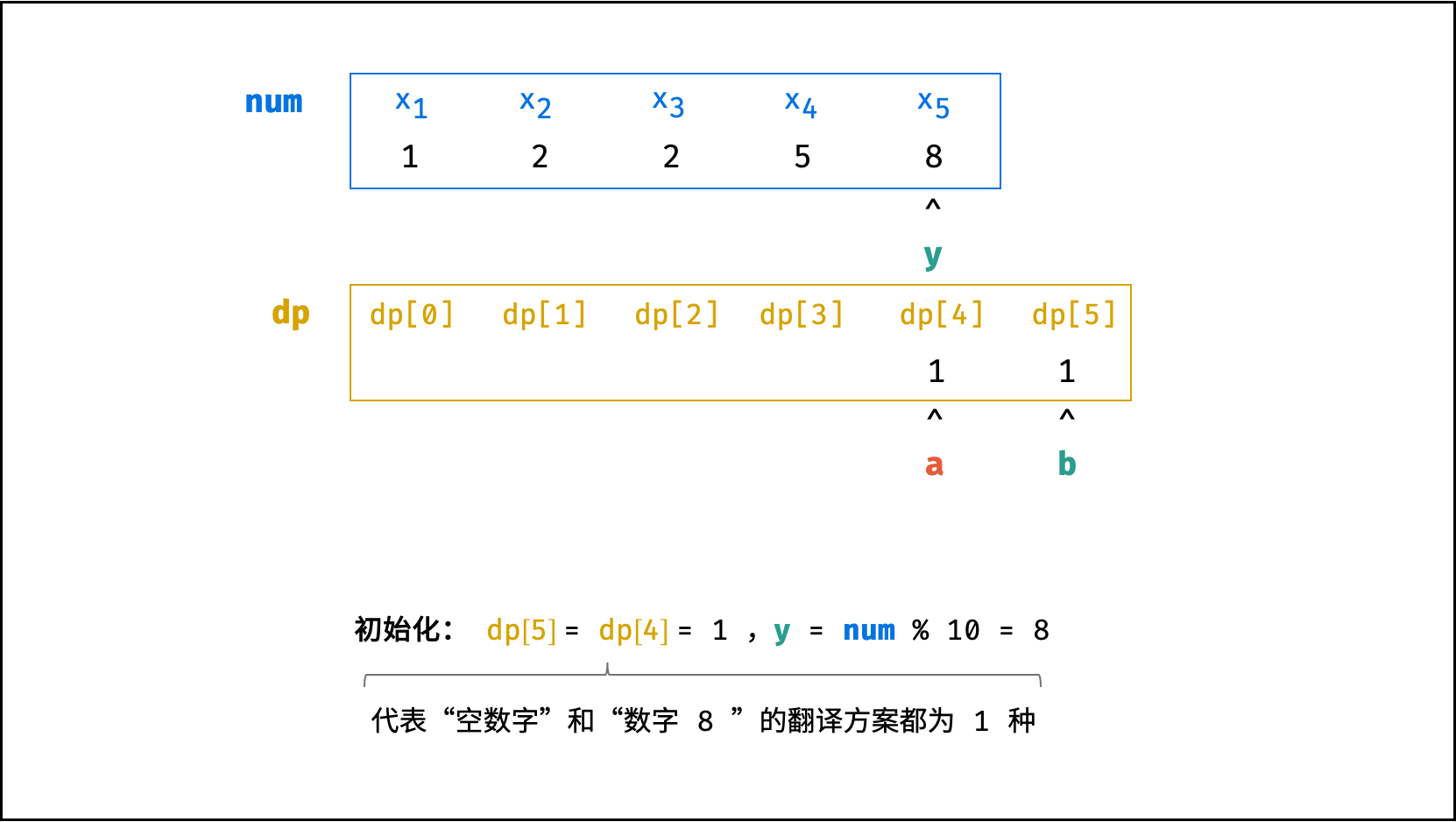<![Picture8.png](https://pic.leetcode-cn.com/1603461843-qyOiIi-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1603461843-pzuECB-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1603461843-RopRil-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1603461843-qKJgMt-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1603461843-tEOtkx-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1603461843-mhJyfP-Picture13.png),![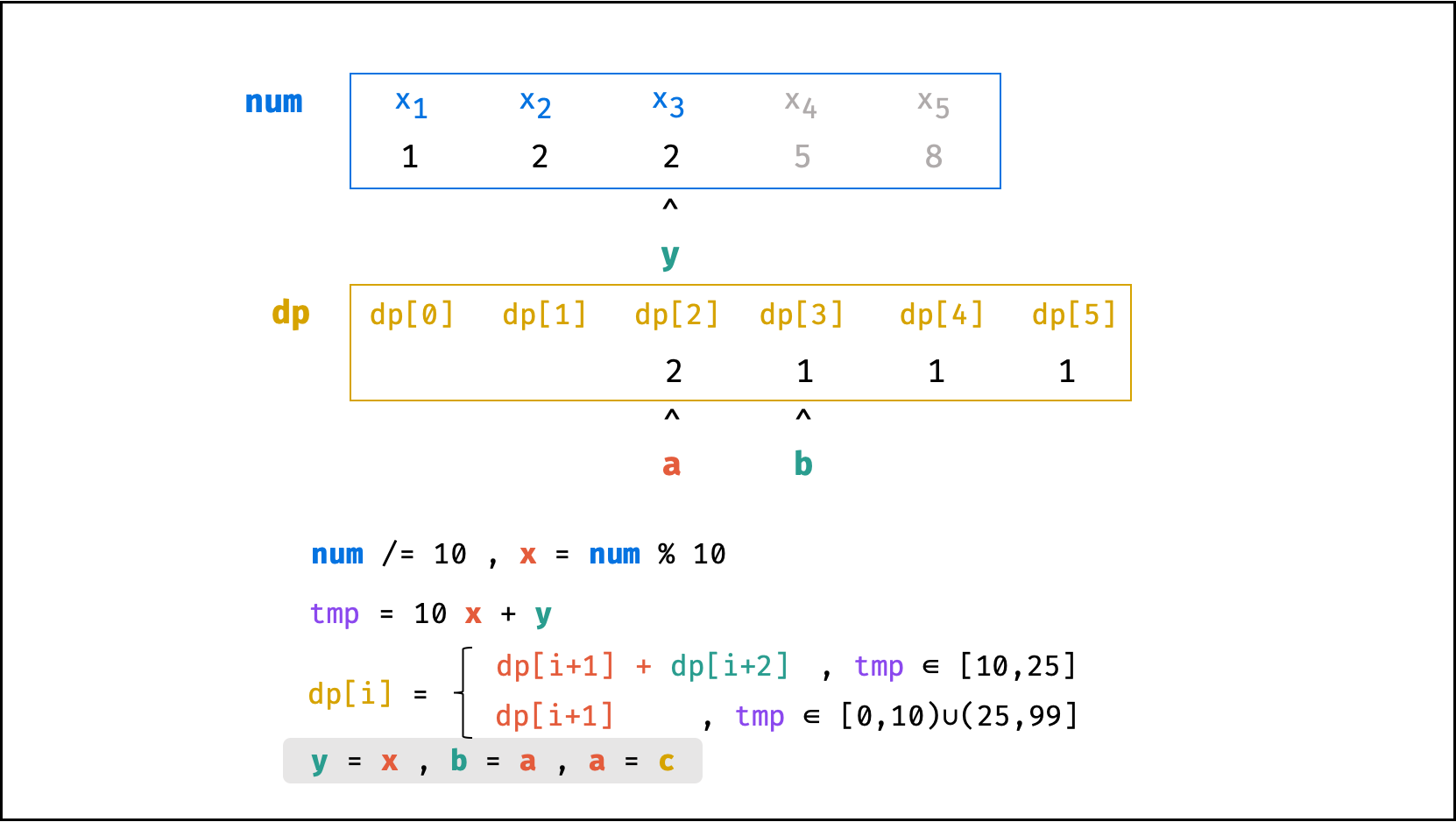Picture14.png](https://pic.leetcode-cn.com/1603461843-FwNzWa-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1603461844-iEZRGi-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1603461844-uoytcS-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1603461844-PTdlYK-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1603461844-cbADSp-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1603461844-NMDwLM-Picture19.png),![Picture20.png](https://pic.leetcode-cn.com/1603461844-lCjoMd-Picture20.png),![Picture21.png](https://pic.leetcode-cn.com/1603461844-FPdyqr-Picture21.png)>
### 代码：
```Python []
class Solution:
def crackNumber(self, ciphertext: int) -> int:
a = b = 1
y = ciphertext % 10
while ciphertext > 9:
ciphertext //= 10
x = ciphertext % 10
tmp = 10 * x + y
c = a + b if 10 <= tmp <= 25 else a
a, b = c, a
y = x
return a
```
```Java []
class Solution {
public int crackNumber(int ciphertext) {
int a = 1, b = 1, x, y = ciphertext % 10;
while(ciphertext > 9) {
ciphertext /= 10;
x = ciphertext % 10;
int tmp = 10 * x + y;
int c = (tmp >= 10 && tmp <= 25) ? a + b : a;
b = a;
a = c;
y = x;
}
return a;
}
}
```
```C++ []
class Solution {
public:
int crackNumber(int ciphertext) {
int a = 1, b = 1, x, y = ciphertext % 10;
while(ciphertext > 9) {
ciphertext /= 10;
x = ciphertext % 10;
int tmp = 10 * x + y;
int c = (tmp >= 10 && tmp <= 25) ? a + b : a;
b = a;
a = c;
y = x;
}
return a;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为字符串 $s$ 的长度，即数字 $ciphertext$ 的位数 $\log(ciphertext)$ ，其决定了循环次数。
- **空间复杂度 $O(1)$ ：** 几个变量使用常数大小的额外空间。

152
leetbook_ioa/docs/LCR 166. 珠宝的最高价值.md Executable file
View File

@@ -0,0 +1,152 @@
## 解题思路：
题目说明：从棋盘的左上角开始拿格子里的珠宝，并每次 **向右** 或者 **向下** 移动一格、直到到达棋盘的右下角。
根据题目说明，易得某单元格只可能从上边单元格或左边单元格到达。
设 $f(i, j)$ 为从棋盘左上角走至单元格 $(i ,j)$ 的珠宝最大累计价值，易得到以下递推关系：$f(i,j)$ 等于 $f(i,j-1)$ 和 $f(i-1,j)$ 中的较大值加上当前单元格珠宝价值 $frame(i,j)$ 。
$$
f(i,j) = \max[f(i,j-1), f(i-1,j)] + frame(i,j)
$$
因此，可用动态规划解决此问题，以上公式便为转移方程。
> 下图中的 `grid` 对应本题的 `frame` 。
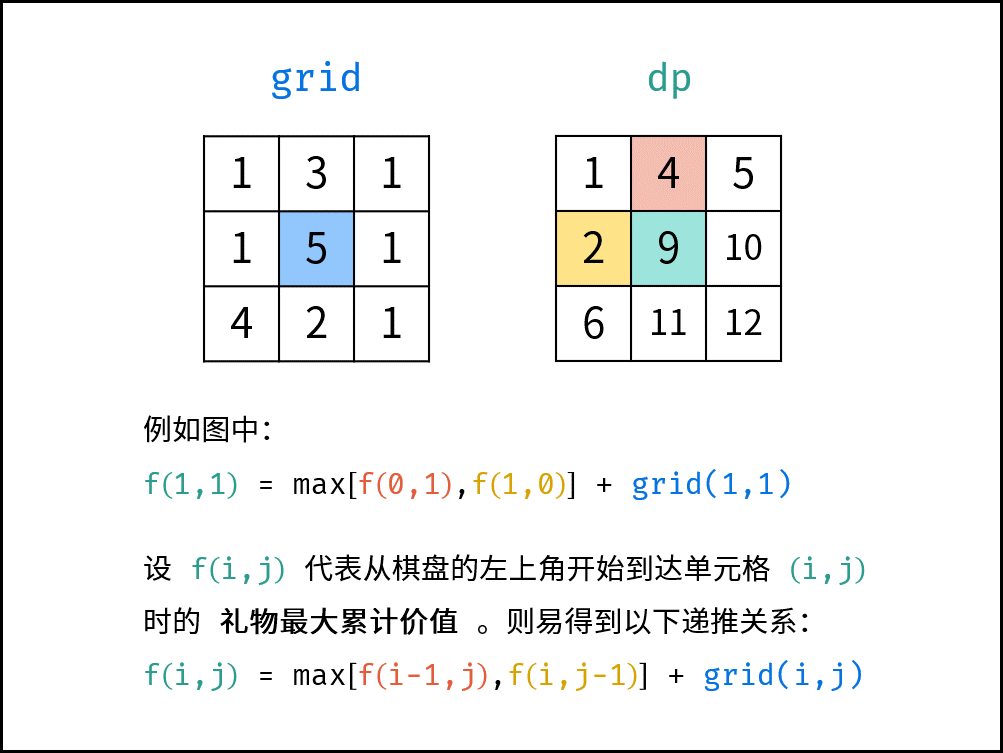![Picture1.png](https://pic.leetcode-cn.com/1662cdf7aafd8c9ed6e1eadc41bfc9adf58ea808e11f1a3dd2e8ba4632b9d1ac-Picture1.png){:align=center width=450}
### 动态规划解析：
**状态定义：** 设动态规划矩阵 $dp$ ，$dp(i,j)$ 代表从棋盘的左上角开始，到达单元格 $(i,j)$ 时能拿到珠宝的最大累计价值。
**转移方程：**
1. 当 $i = 0$ 且 $j = 0$ 时，为起始元素；
2. 当 $i = 0$ 且 $j \ne 0$ 时，为矩阵第一行元素，只可从左边到达；
3. 当 $i \ne 0$ 且 $j = 0$ 时，为矩阵第一列元素，只可从上边到达；
4. 当 $i \ne 0$ 且 $j \ne 0$ 时，可从左边或上边到达；
$$
dp(i,j)=
\begin{cases}
frame(i,j) & {,i=0, j=0}\\
frame(i,j) + dp(i,j-1) & {,i=0, j \ne 0}\\
frame(i,j) + dp(i-1,j) & {,i \ne 0, j=0}\\
frame(i,j) + \max[dp(i-1,j),dp(i,j-1)]& ,{i \ne 0, j \ne 0}
\end{cases}
$$
**初始状态：** $dp[0][0] = frame[0][0]$ ，即到达单元格 $(0,0)$ 时能拿到珠宝的最大累计价值为 $frame[0][0]$ ；
**返回值：** $dp[m-1][n-1]$ ，$m, n$ 分别为矩阵的行高和列宽，即返回 $dp$ 矩阵右下角元素。
### 空间优化：
由于 $dp[i][j]$ 只与 $dp[i-1][j]$ , $dp[i][j-1]$ , $frame[i][j]$ 有关系，因此可以将原矩阵 $frame$ 用作 $dp$ 矩阵，即直接在 $frame$ 上修改即可。
应用此方法可省去 $dp$ 矩阵使用的额外空间，因此空间复杂度从 $O(MN)$ 降至 $O(1)$ 。
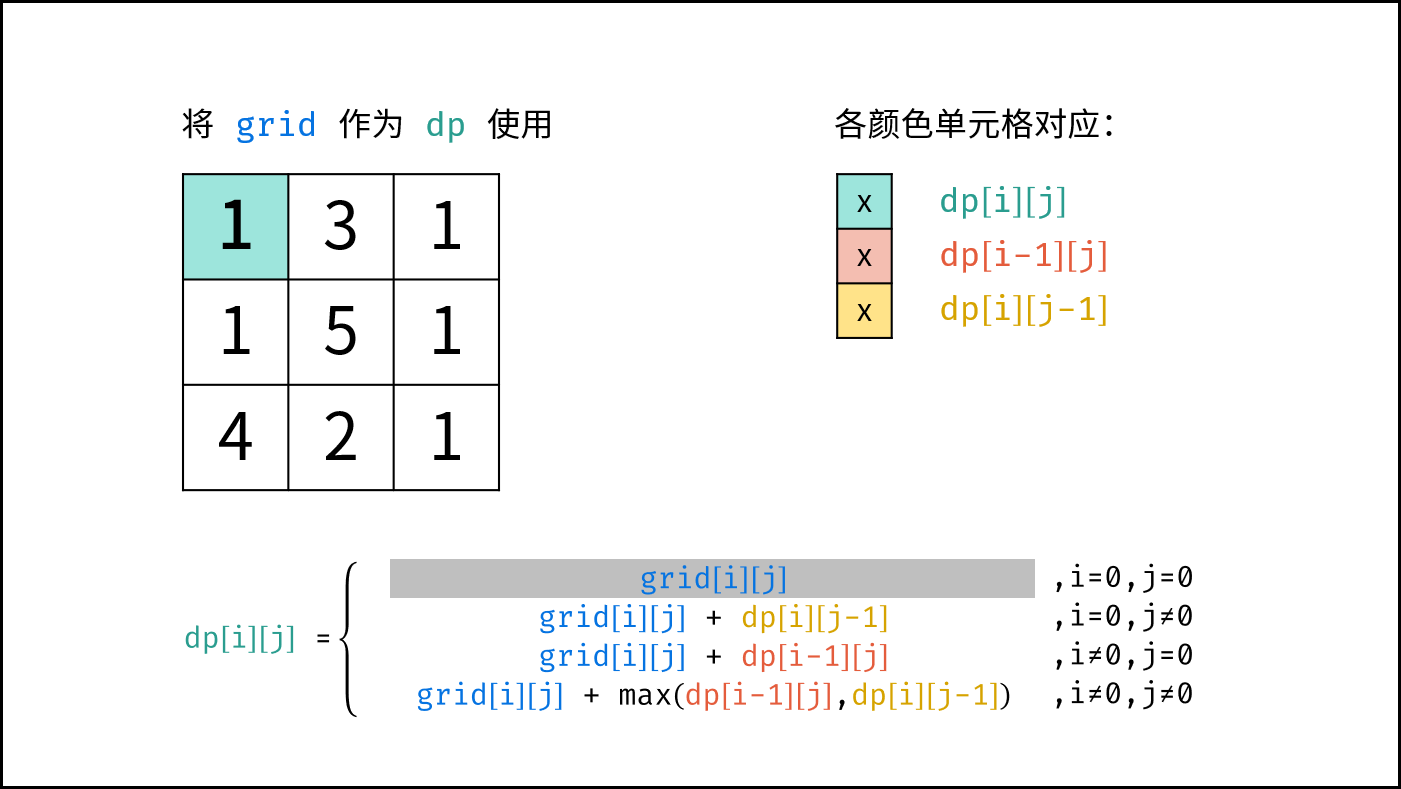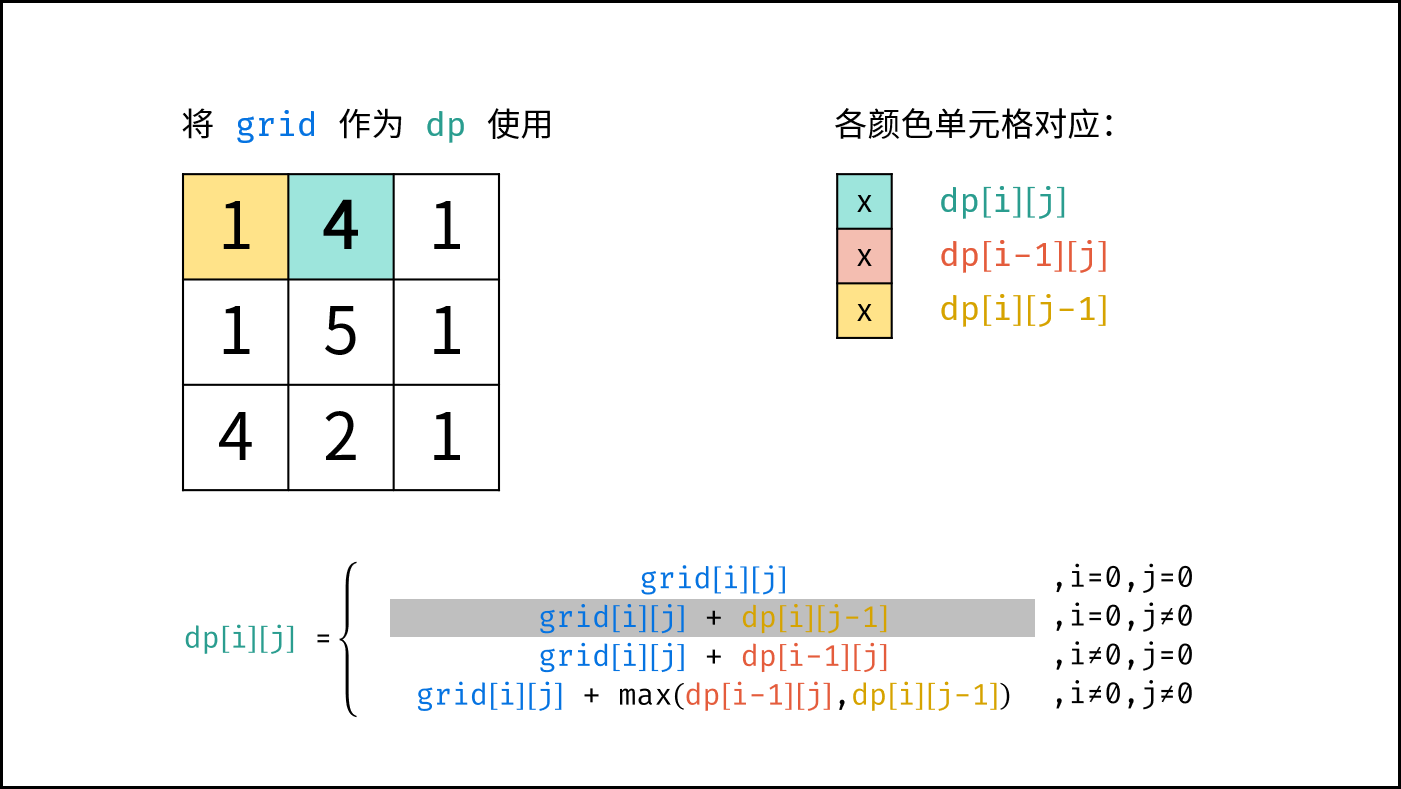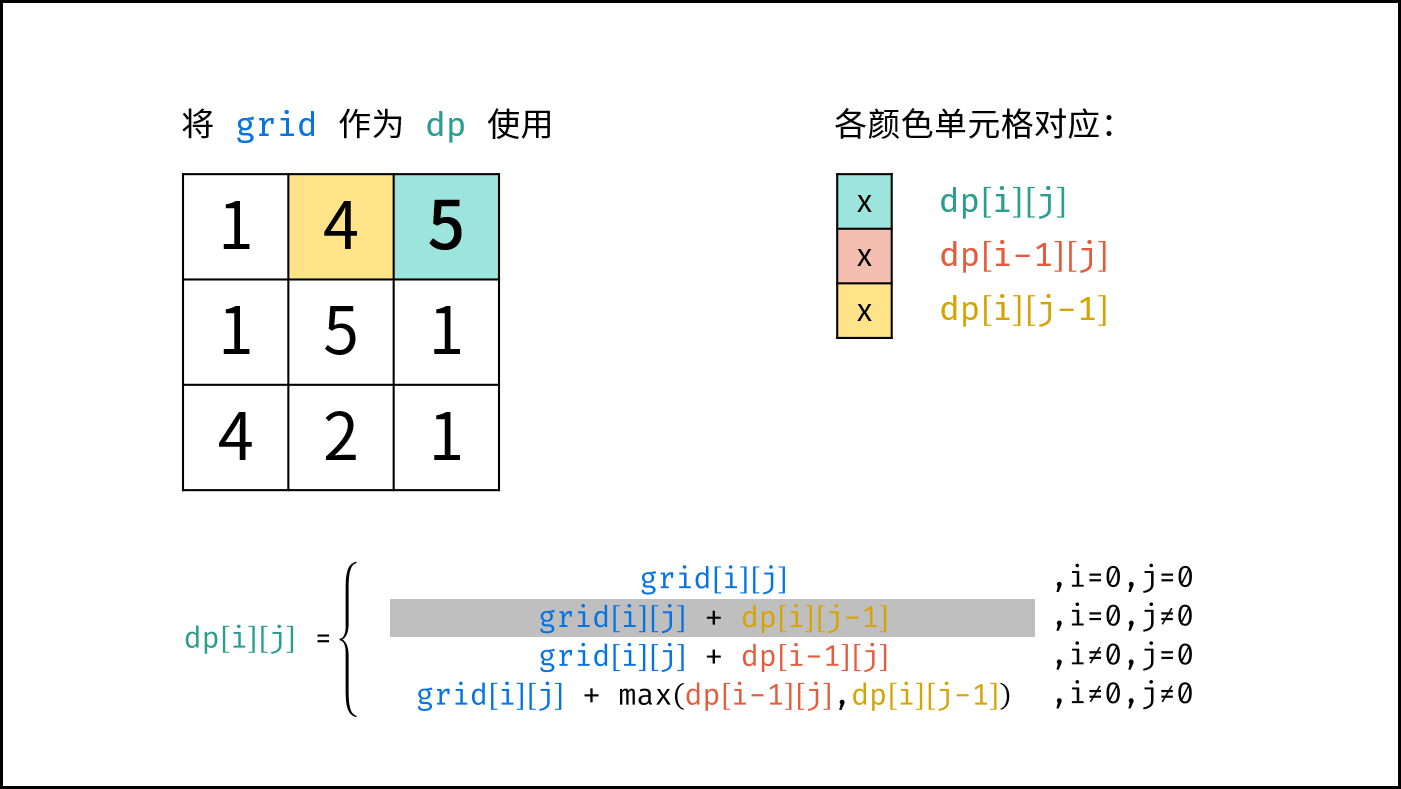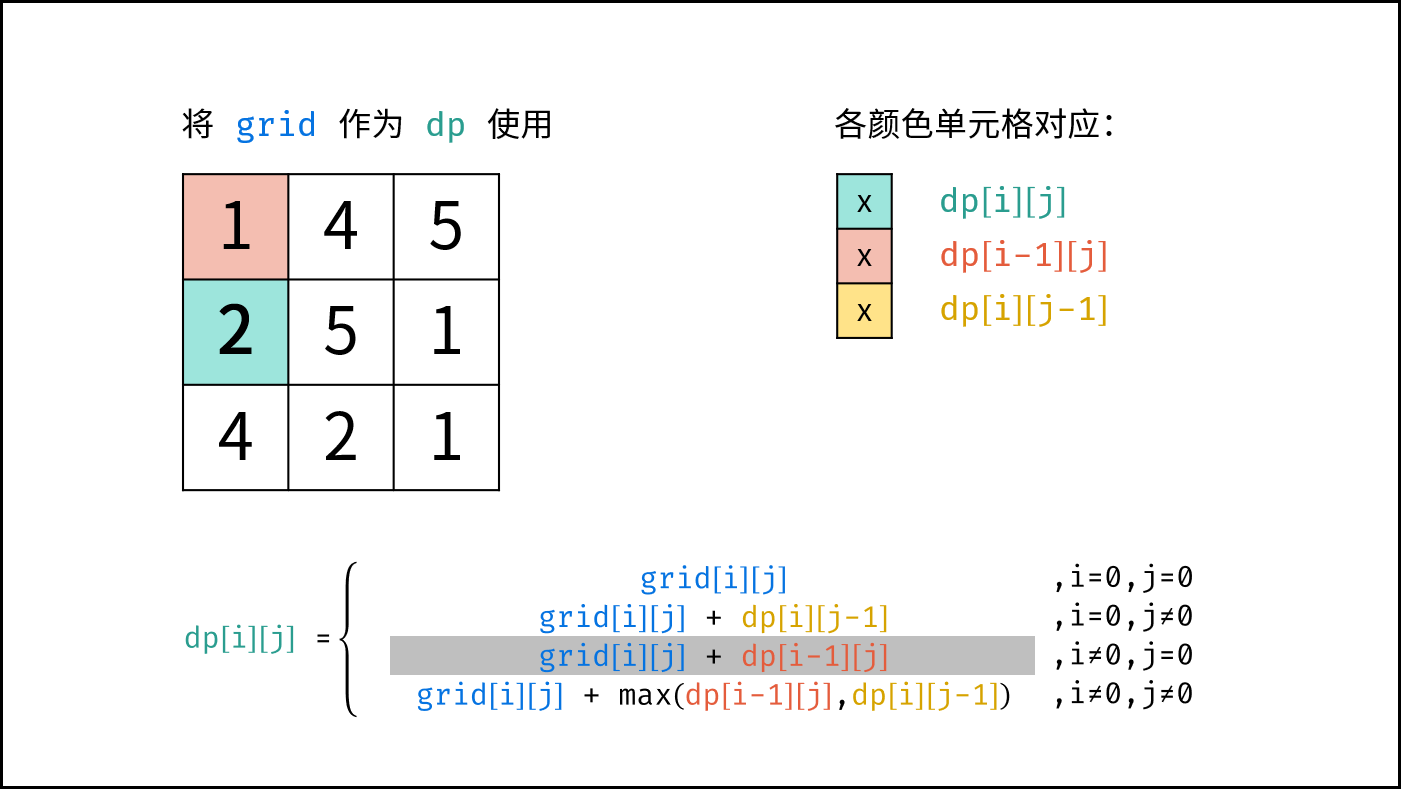<![Picture2.png](https://pic.leetcode-cn.com/6189bf2953793ba132441027f38017ccf42c6a86d8d578b0d5848bc9f0247d00-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/af90f0122772097f0e2bb15dccc46357b5eddaa20b5d16923146cfece3f9305d-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/fada524d36bf8a11d7ea4eab2f84f5adf07dd7be4881a6fa93dc1bdce05bca1d-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/ef0653b42f1008d2fd1735e21987255a179094ce0774071bff7b74415bd8624a-Picture5.png),![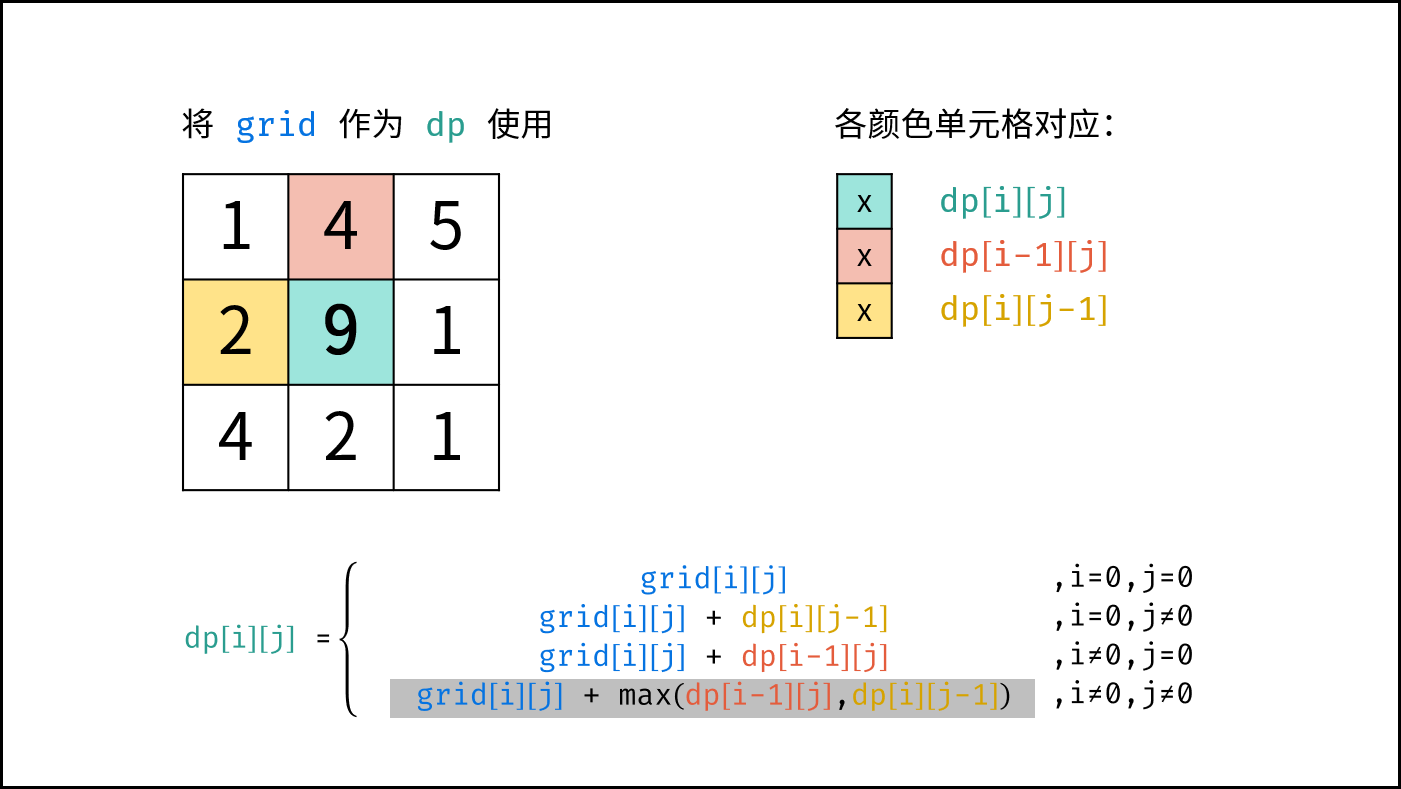Picture6.png](https://pic.leetcode-cn.com/3784679f83f195ffdf82f15ed0506f4f06f25202c7c2ad6d587e6fdd7bf32e35-Picture6.png),![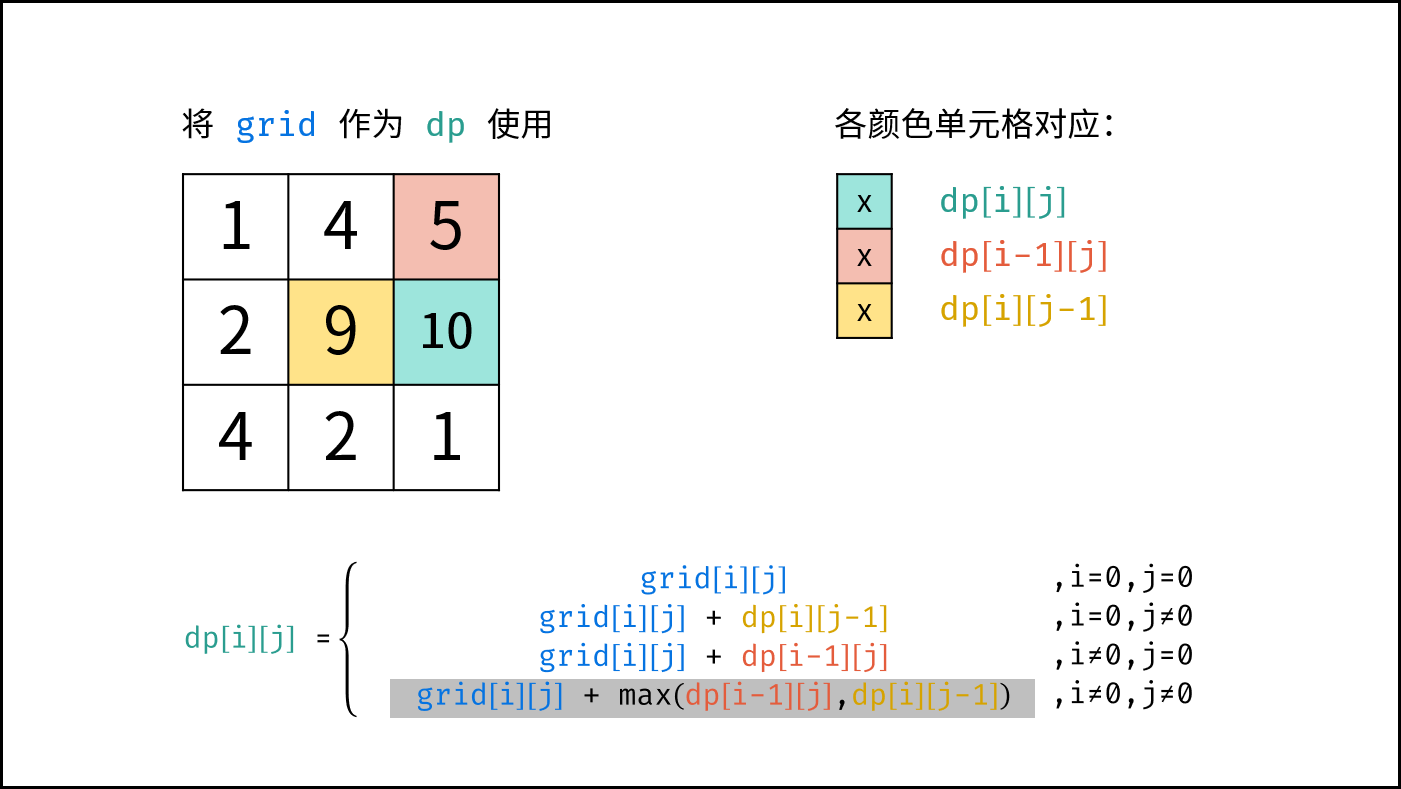Picture7.png](https://pic.leetcode-cn.com/6aeb93075d0213260552af7b8f1f97a5c470ff6d6d6d6a8cdc775aef79d8572b-Picture7.png),![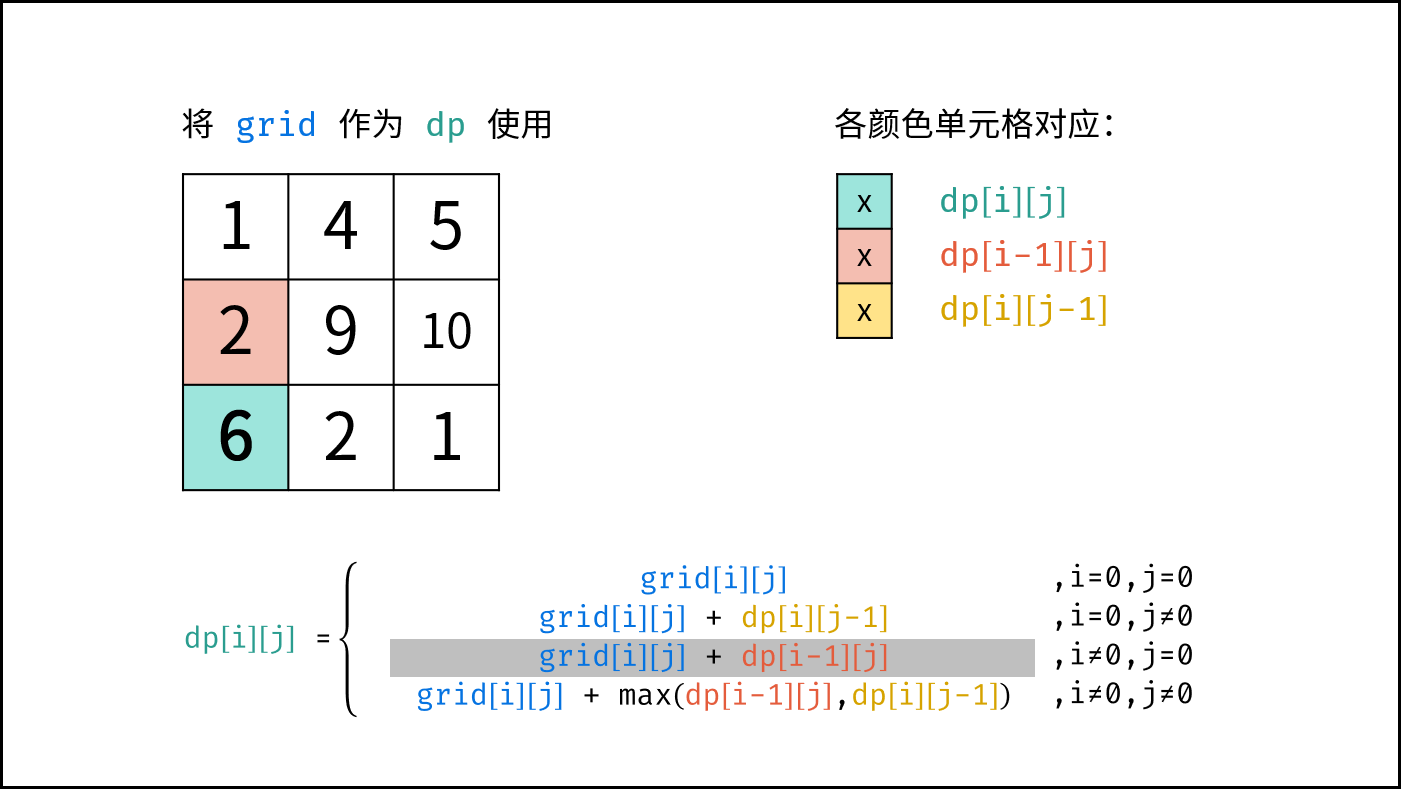Picture8.png](https://pic.leetcode-cn.com/be92ca4e4735866de0675b0014bdd937b5c2270c531b7efb28335191378db066-Picture8.png),![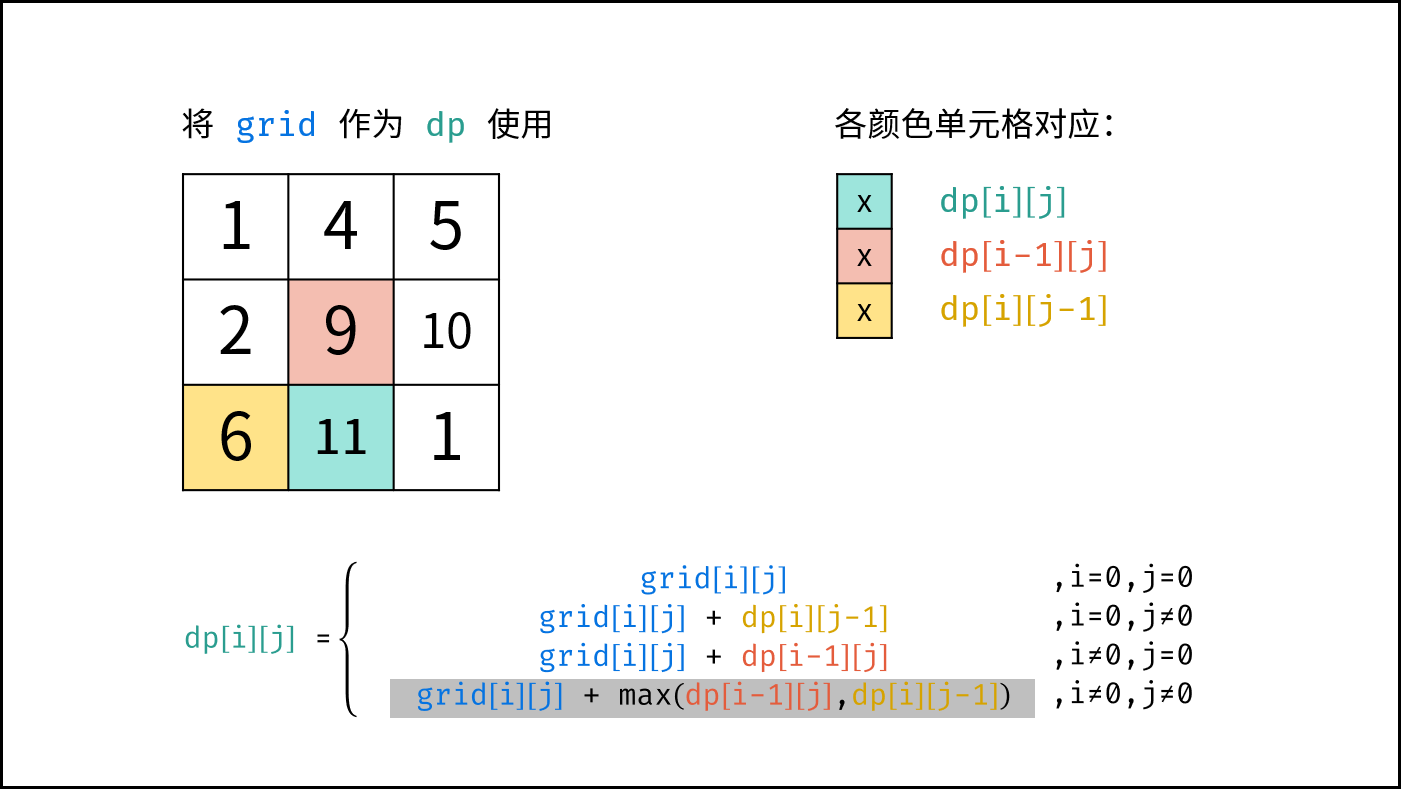Picture9.png](https://pic.leetcode-cn.com/af9da50dde707d7be49d3764b482942fda28867f2624024c64c29fc0137131cc-Picture9.png),![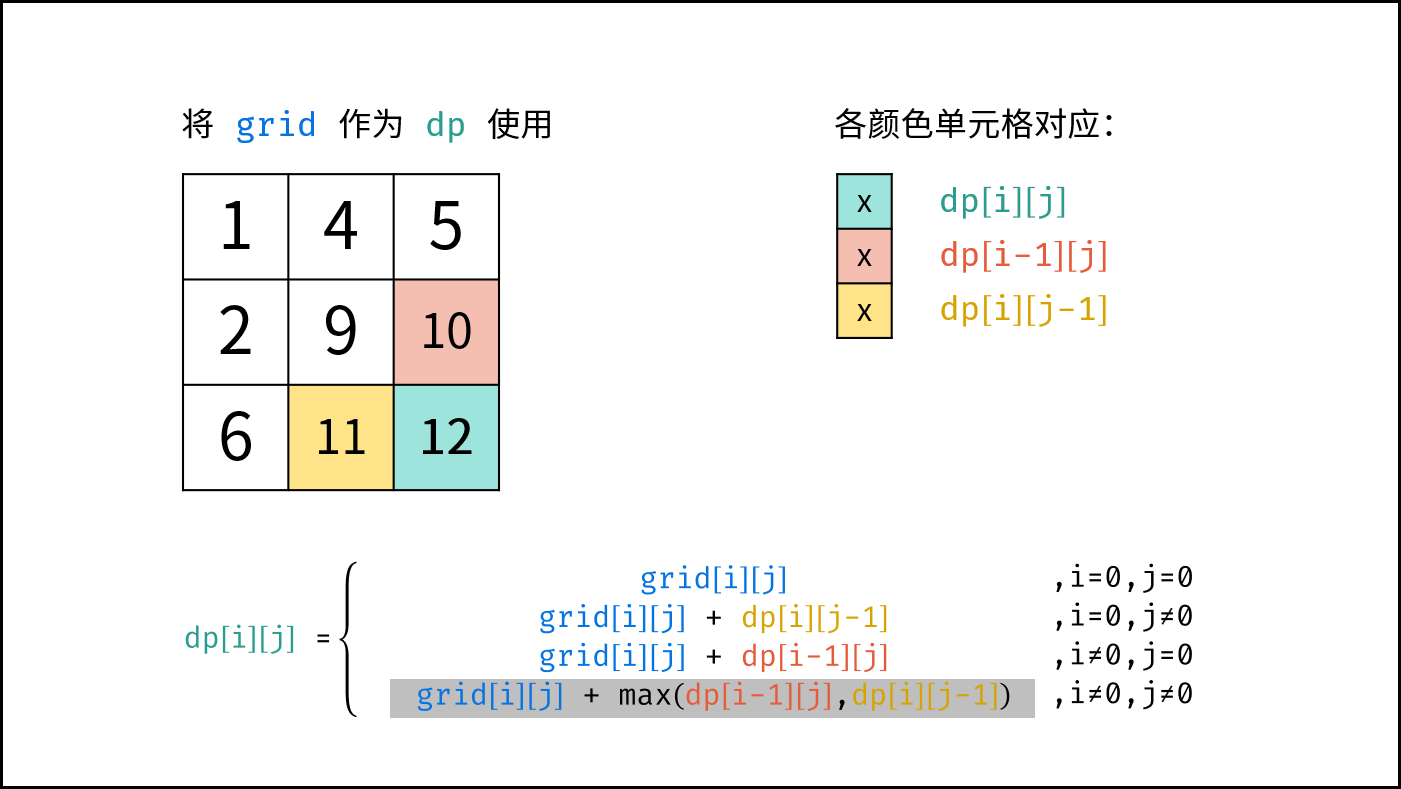Picture10.png](https://pic.leetcode-cn.com/f86f34be835f15f86c6a52ffde0d1af5e8030f514960631e324660445bddecd0-Picture10.png),![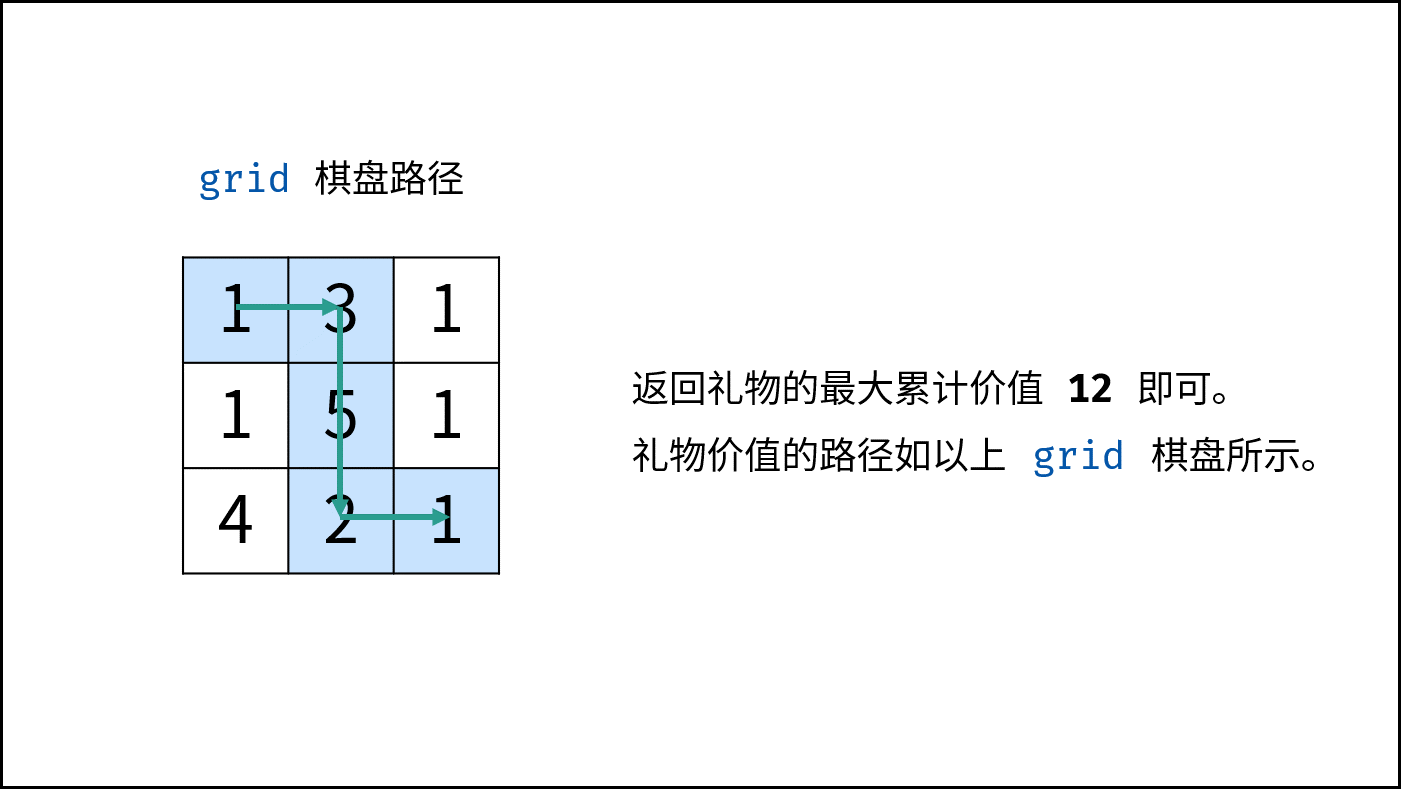Picture11.png](https://pic.leetcode-cn.com/effdeef2927144b88f1a7f7601f6d7491f4f618f5ff506ce471336445dfccc31-Picture11.png)>
## 代码：
```Python []
class Solution:
def jewelleryValue(self, frame: List[List[int]]) -> int:
for i in range(len(frame)):
for j in range(len(frame[0])):
if i == 0 and j == 0: continue
if i == 0: frame[i][j] += frame[i][j - 1]
elif j == 0: frame[i][j] += frame[i - 1][j]
else: frame[i][j] += max(frame[i][j - 1], frame[i - 1][j])
return frame[-1][-1]
```
```Java []
class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length, n = frame[0].length;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(i == 0 && j == 0) continue;
if(i == 0) frame[i][j] += frame[i][j - 1] ;
else if(j == 0) frame[i][j] += frame[i - 1][j];
else frame[i][j] += Math.max(frame[i][j - 1], frame[i - 1][j]);
}
}
return frame[m - 1][n - 1];
}
}
```
```C++ []
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size(), n = frame[0].size();
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(i == 0 && j == 0) continue;
if(i == 0) frame[i][j] += frame[i][j - 1] ;
else if(j == 0) frame[i][j] += frame[i - 1][j];
else frame[i][j] += max(frame[i][j - 1], frame[i - 1][j]);
}
}
return frame[m - 1][n - 1];
}
};
```
以上代码逻辑清晰，和转移方程直接对应，但仍可提升效率，这是因为：当 $frame$ 矩阵很大时，$i = 0$ 或 $j = 0$ 的情况仅占极少数，相当循环每轮都冗余了一次判断。因此，可先初始化矩阵第一行和第一列，再开始遍历递推。
```Python []
class Solution:
def jewelleryValue(self, frame: List[List[int]]) -> int:
m, n = len(frame), len(frame[0])
for j in range(1, n): # 初始化第一行
frame[0][j] += frame[0][j - 1]
for i in range(1, m): # 初始化第一列
frame[i][0] += frame[i - 1][0]
for i in range(1, m):
for j in range(1, n):
frame[i][j] += max(frame[i][j - 1], frame[i - 1][j])
return frame[-1][-1]
```
```Java []
class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length, n = frame[0].length;
for(int j = 1; j < n; j++) // 初始化第一行
frame[0][j] += frame[0][j - 1];
for(int i = 1; i < m; i++) // 初始化第一列
frame[i][0] += frame[i - 1][0];
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
frame[i][j] += Math.max(frame[i][j - 1], frame[i - 1][j]);
return frame[m - 1][n - 1];
}
}
```
```C++ []
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size(), n = frame[0].size();
for(int j = 1; j < n; j++) // 初始化第一行
frame[0][j] += frame[0][j - 1];
for(int i = 1; i < m; i++) // 初始化第一列
frame[i][0] += frame[i - 1][0];
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
frame[i][j] += max(frame[i][j - 1], frame[i - 1][j]);
return frame[m - 1][n - 1];
}
};
```
### 复杂度分析：
- **时间复杂度 $O(MN)$ ：** $M, N$ 分别为矩阵行高、列宽；动态规划需遍历整个 $frame$ 矩阵，使用 $O(MN)$ 时间。
- **空间复杂度 $O(1)$ ：** 原地修改使用常数大小的额外空间。

169
leetbook_ioa/docs/LCR 167. 招式拆解 I.md Executable file
View File

@@ -0,0 +1,169 @@
## 解题思路：
长度为 $N$ 的字符串共有 $\frac{(1 + N)N}{2}$ 个子字符串（复杂度为 $O(N^2)$ ），判断长度为 $N$ 的字符串是否有重复字符的复杂度为 $O(N)$ ，因此本题使用暴力法解决的复杂度为 $O(N^3)$ 。
本题有滑动窗口和动态规划两种解法。
## 方法一：滑动窗口 + 哈希表
**哈希表 $dic$ 统计：** 指针 $j$ 遍历字符 $arr$ ，哈希表统计字符 $arr[j]$ **最后一次出现的索引** 。
**更新左指针 $i$ ：** 根据上轮左指针 $i$ 和 $dic[arr[j]]$ ，每轮更新左边界 $i$ ，保证区间 $[i + 1, j]$ 内无重复字符且最大。
$$
i = \max(dic[arr[j]], i)
$$
**更新结果 $res$ ：** 取上轮 $res$ 和本轮双指针区间 $[i + 1,j]$ 的宽度（即 $j - i$ ）中的最大值。
$$
res = \max(res, j - i)
$$
> 下图中的 `s` 对应本题中的 `arr` 。
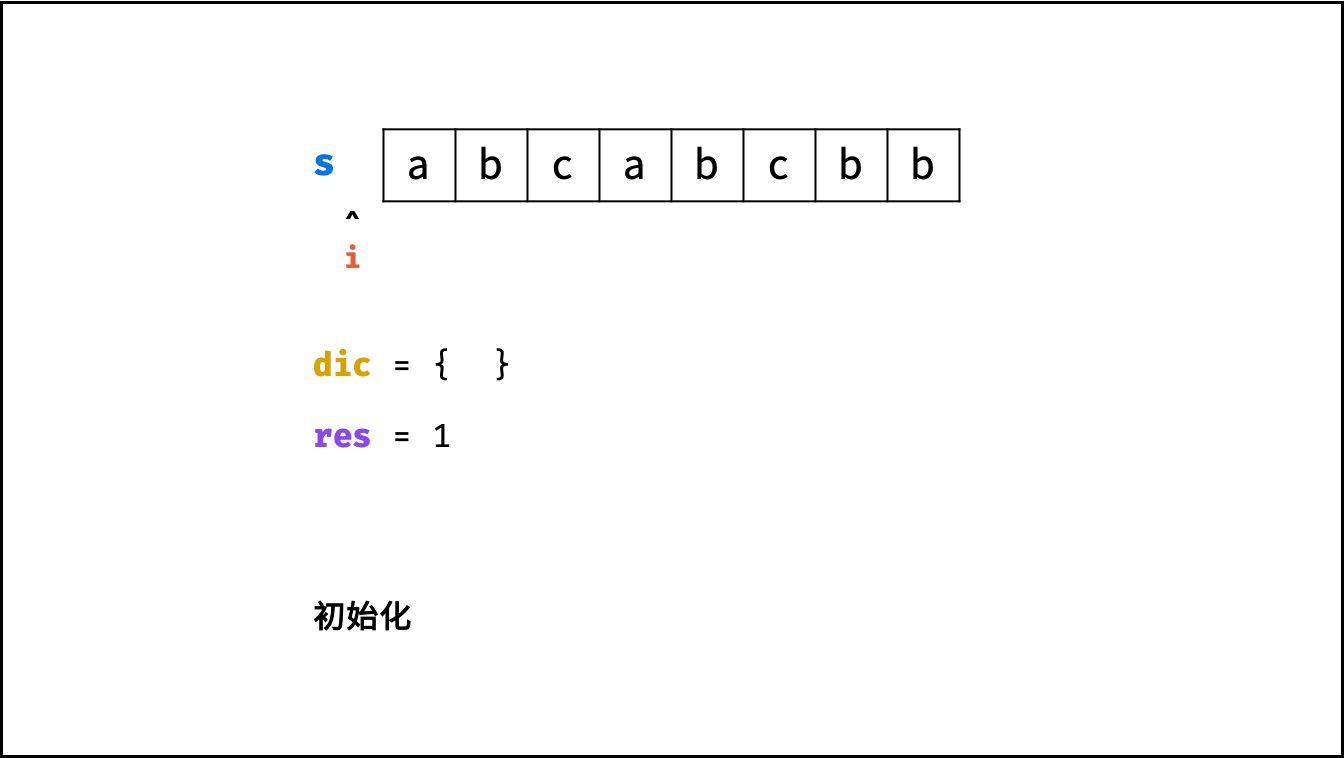<![Picture12.png](https://pic.leetcode-cn.com/1599287290-kSAvhB-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1599287290-gMAGHB-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1599287290-EUtrGG-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1599287290-krFnDj-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1599287290-gXKABp-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1599287290-NulcED-Picture17.png),![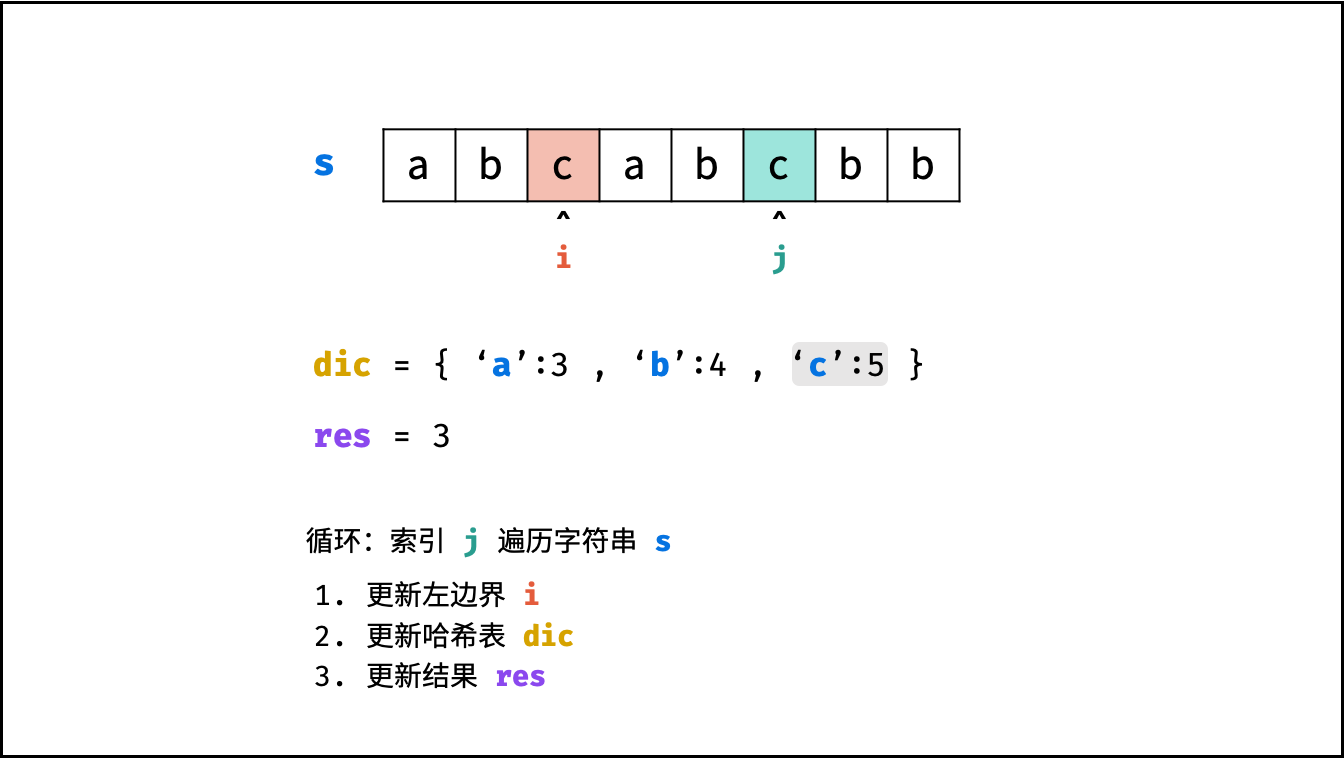Picture18.png](https://pic.leetcode-cn.com/1599287290-EsTtWj-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1599287290-KCXIDC-Picture19.png),![Picture20.png](https://pic.leetcode-cn.com/1599287290-otyVYl-Picture20.png),![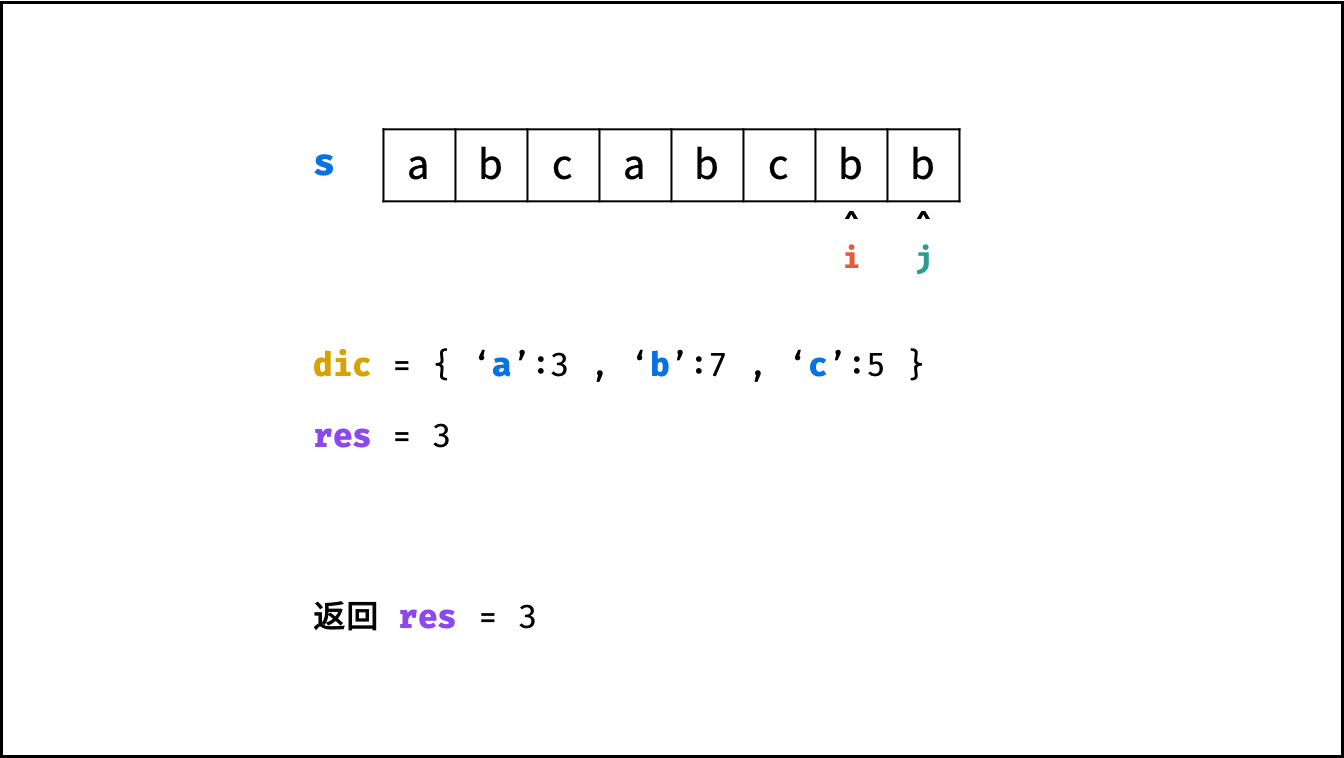Picture21.png](https://pic.leetcode-cn.com/1599287290-bqGnkn-Picture21.png)>
### 代码：
```Python []
class Solution:
def dismantlingAction(self, arr: str) -> int:
dic, res, i = {}, 0, -1
for j in range(len(arr)):
if arr[j] in dic:
i = max(dic[arr[j]], i) # 更新左指针 i
dic[arr[j]] = j # 哈希表记录
res = max(res, j - i) # 更新结果
return res
```
```Java []
class Solution {
public int dismantlingAction(String arr) {
Map<Character, Integer> dic = new HashMap<>();
int i = -1, res = 0, len = arr.length();
for(int j = 0; j < len; j++) {
if (dic.containsKey(arr.charAt(j)))
i = Math.max(i, dic.get(arr.charAt(j))); // 更新左指针 i
dic.put(arr.charAt(j), j); // 哈希表记录
res = Math.max(res, j - i); // 更新结果
}
return res;
}
}
```
```C++ []
class Solution {
public:
int dismantlingAction(string arr) {
unordered_map<char, int> dic;
int i = -1, res = 0, len = arr.size();
for(int j = 0; j < len; j++) {
if (dic.find(arr[j]) != dic.end())
i = max(i, dic.find(arr[j])->second); // 更新左指针
dic[arr[j]] = j; // 哈希表记录
res = max(res, j - i); // 更新结果
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为字符串长度，动态规划需遍历计算 $dp$ 列表。
- **空间复杂度 $O(1)$ ：** 字符的 ASCII 码范围为 $0$ ~ $127$ ，哈希表 $dic$ 最多使用 $O(128) = O(1)$ 大小的额外空间。
## 方法二：动态规划 + 哈希表
- **状态定义：** 设动态规划列表 $dp$ ，$dp[j]$ 代表以字符 $arr[j]$ 为结尾的 “最长不重复子字符串” 的长度。
- **转移方程：** 固定右边界 $j$ ，设字符 $arr[j]$ 左边距离最近的相同字符为 $arr[i]$ ，即 $arr[i] = arr[j]$ 。
1. 当 $i < 0$ ，即 $arr[j]$ 左边无相同字符，则 $dp[j] = dp[j-1] + 1$ 。
2. 当 $dp[j - 1] < j - i$ ，说明字符 $arr[i]$ 在子字符串 $dp[j-1]$ **区间之外** ，则 $dp[j] = dp[j - 1] + 1$ 。
3. 当 $dp[j - 1] \geq j - i$ ，说明字符 $arr[i]$ 在子字符串 $dp[j-1]$ **区间之中** ，则 $dp[j]$ 的左边界由 $arr[i]$ 决定，即 $dp[j] = j - i$ 。
> 当 $i < 0$ 时，由于 $dp[j - 1] \leq j$ 恒成立，因而 $dp[j - 1] < j - i$ 恒成立，因此分支 `1.` 和 `2.` 可被合并。
$$
dp[j] =
\begin{cases}
dp[j - 1] + 1 & , dp[j-1] < j - i \\
j - i & , dp[j-1] \geq j - i
\end{cases}
$$
- **返回值：** $\max(dp)$ ，即全局的 “最长不重复子字符串” 的长度。
![Picture1.png](https://pic.leetcode-cn.com/1599287290-mTdFye-Picture1.png){:align=center width=500}
### 状态压缩：
- 由于返回值是取 $dp$ 列表最大值，因此可借助变量 $tmp$ 存储 $dp[j]$ ，变量 $res$ 每轮更新最大值即可。
- 此优化可节省 $dp$ 列表使用的 $O(N)$ 大小的额外空间。
### 哈希表记录：
观察转移方程，可知关键问题：每轮遍历字符 $arr[j]$ 时，如何计算索引 $i$ ？
- **哈希表统计：** 遍历字符串 $arr$ 时，使用哈希表（记为 $dic$ ）统计 **各字符最后一次出现的索引位置** 。
- **左边界 $i$ 获取方式：** 遍历到 $arr[j]$ 时，可通过访问哈希表 $dic[arr[j]]$ 获取最近的相同字符的索引 $i$ 。
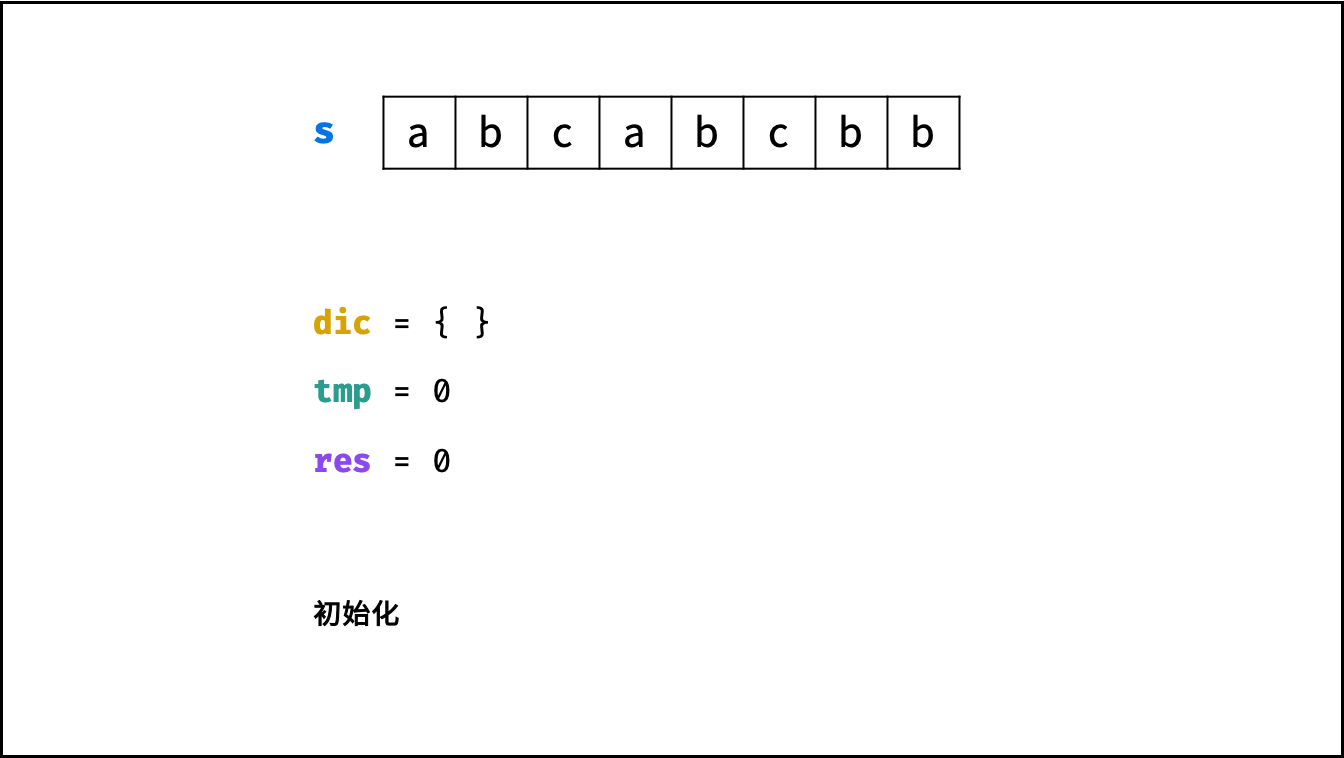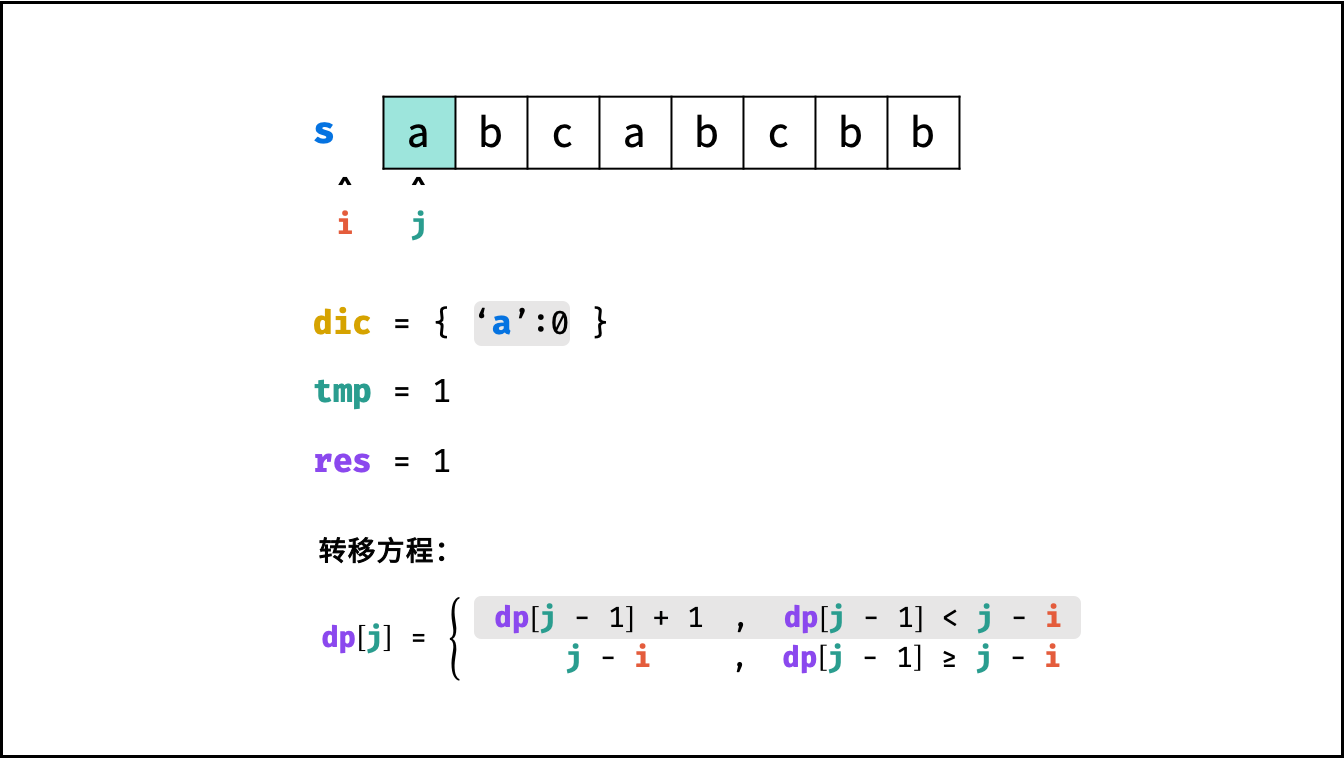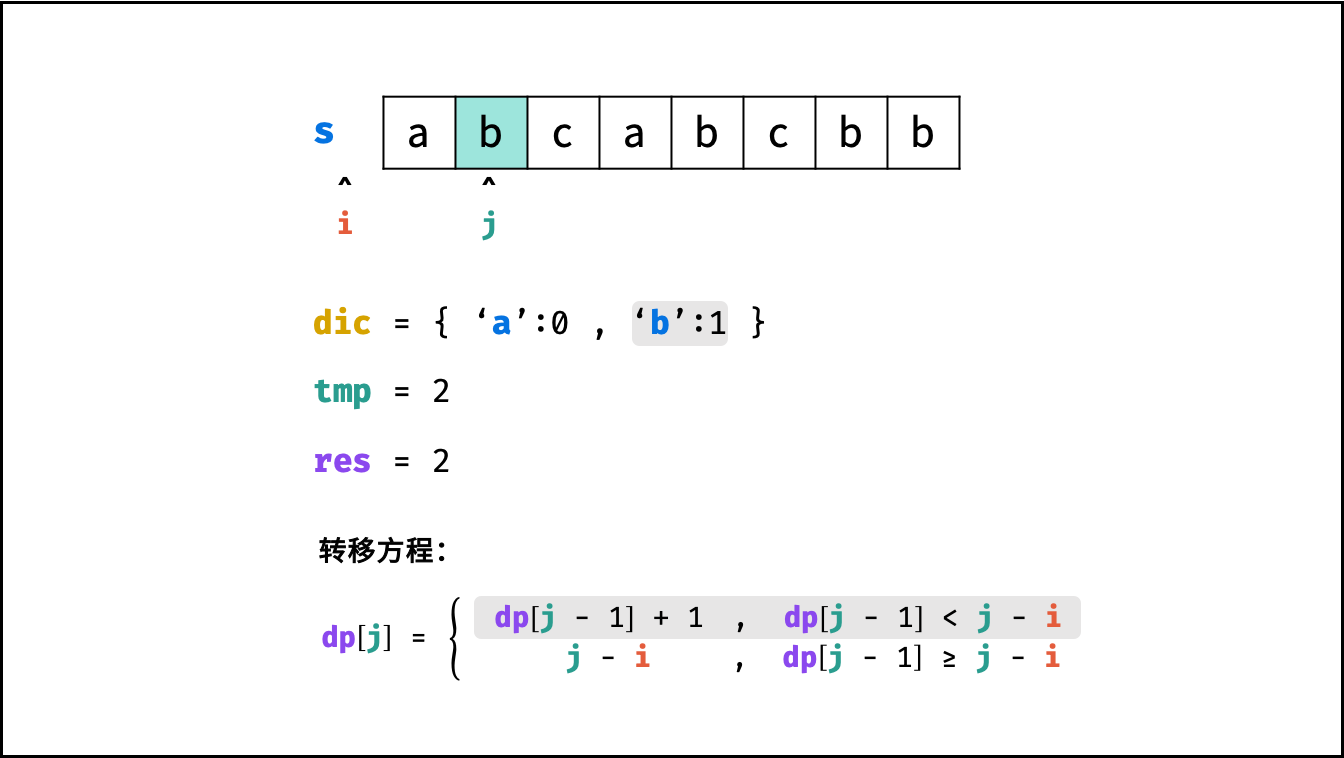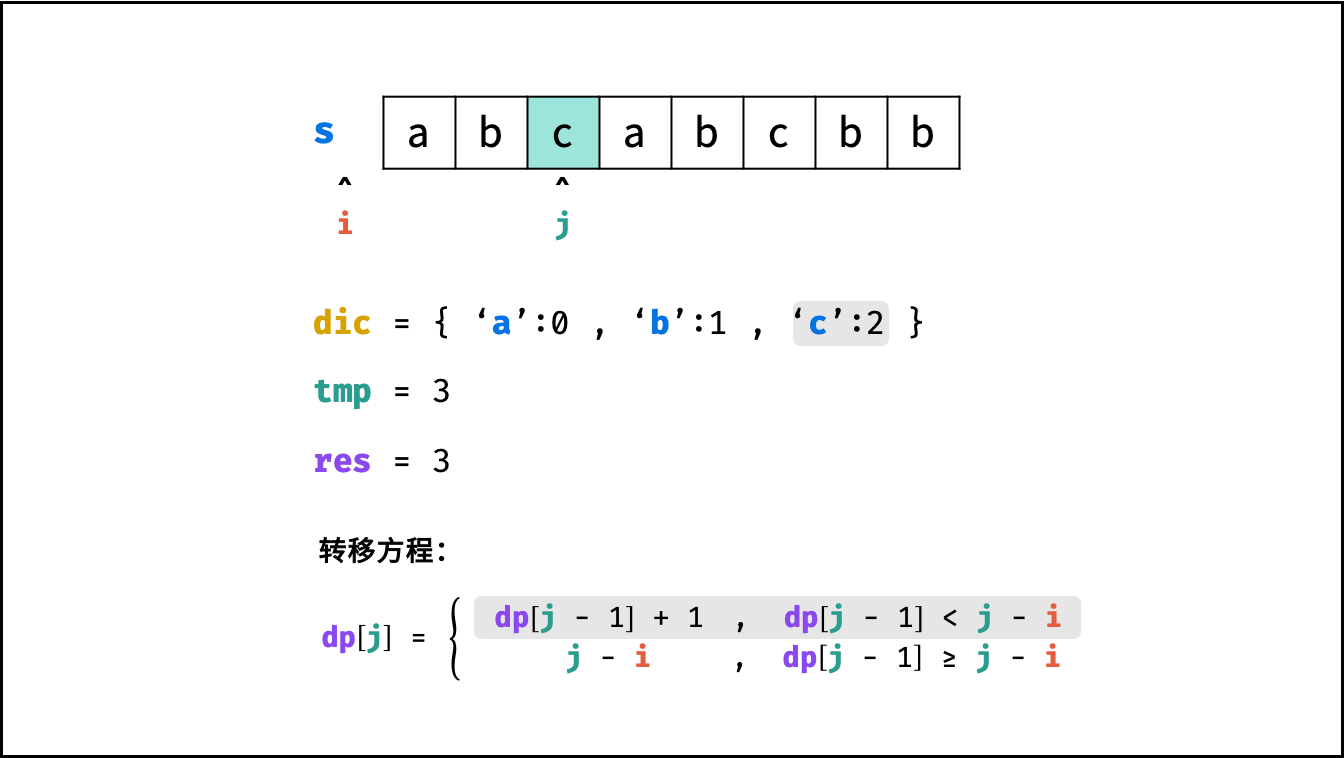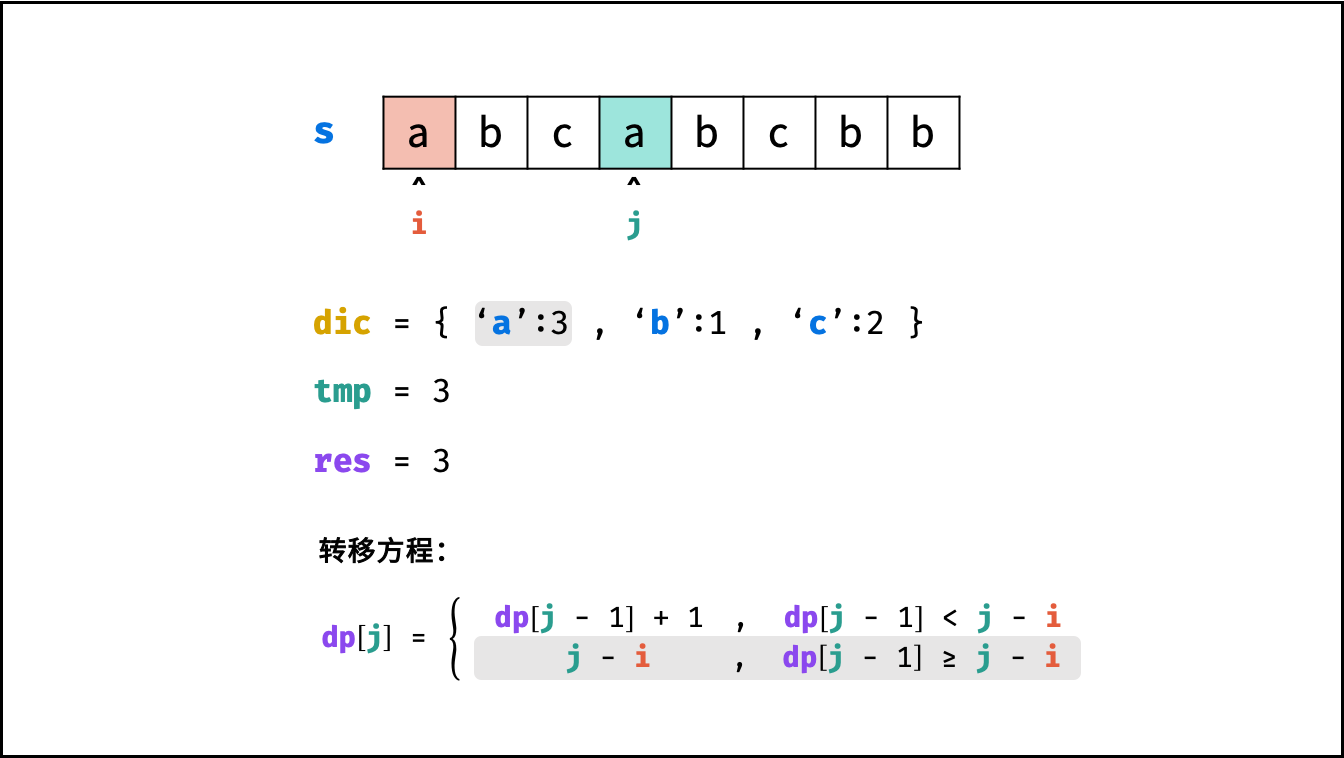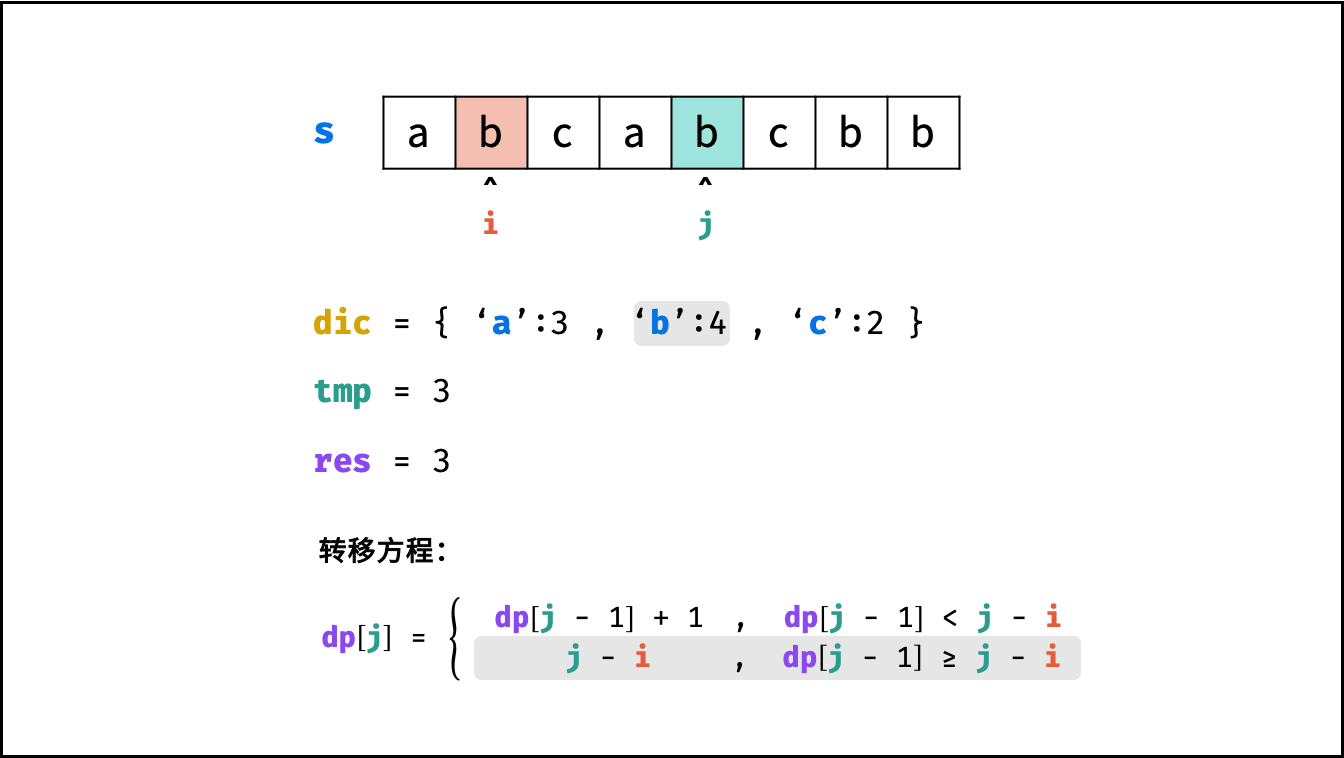<![Picture2.png](https://pic.leetcode-cn.com/1599287290-YYoGEq-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599288203-AgXaMi-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599288203-BMgZPS-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599288203-XNbdBL-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599288203-xqFtNq-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599288203-UfNUNP-Picture7.png),![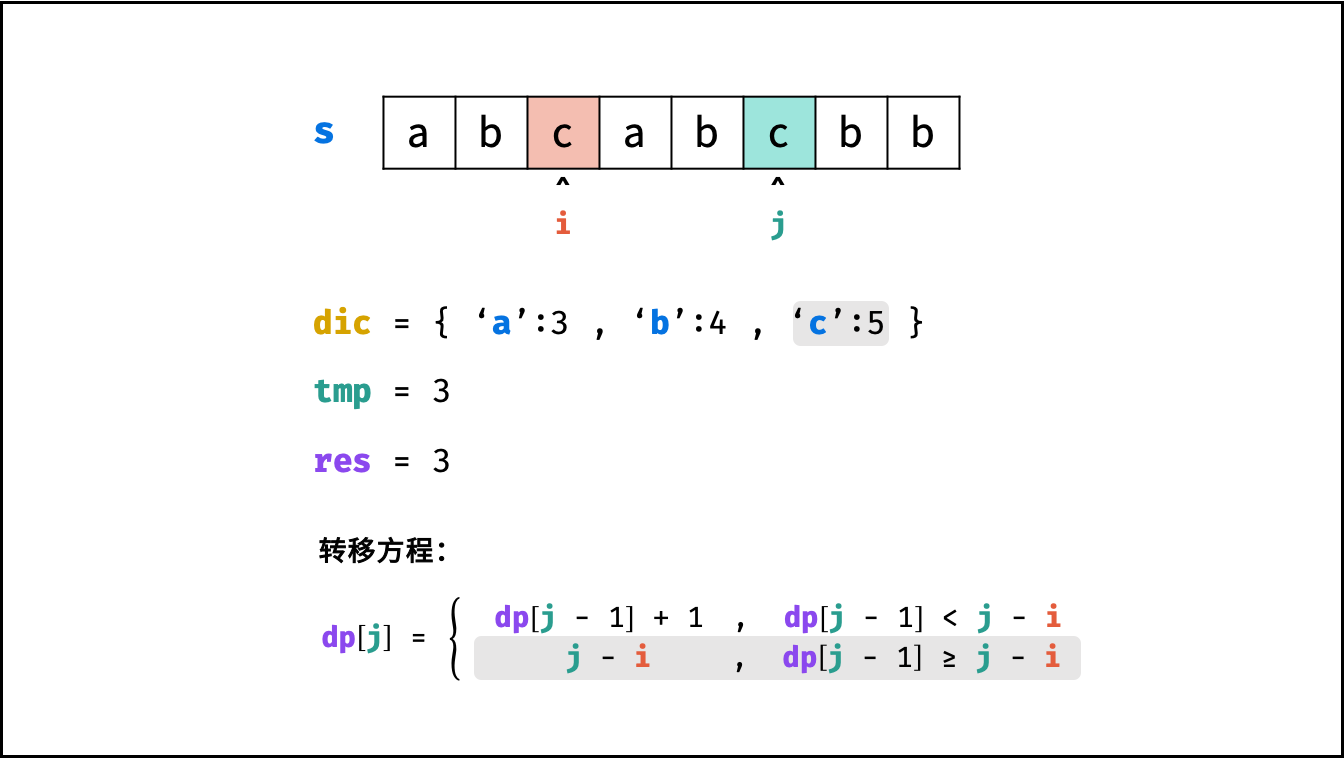Picture8.png](https://pic.leetcode-cn.com/1599288203-phuRqz-Picture8.png),![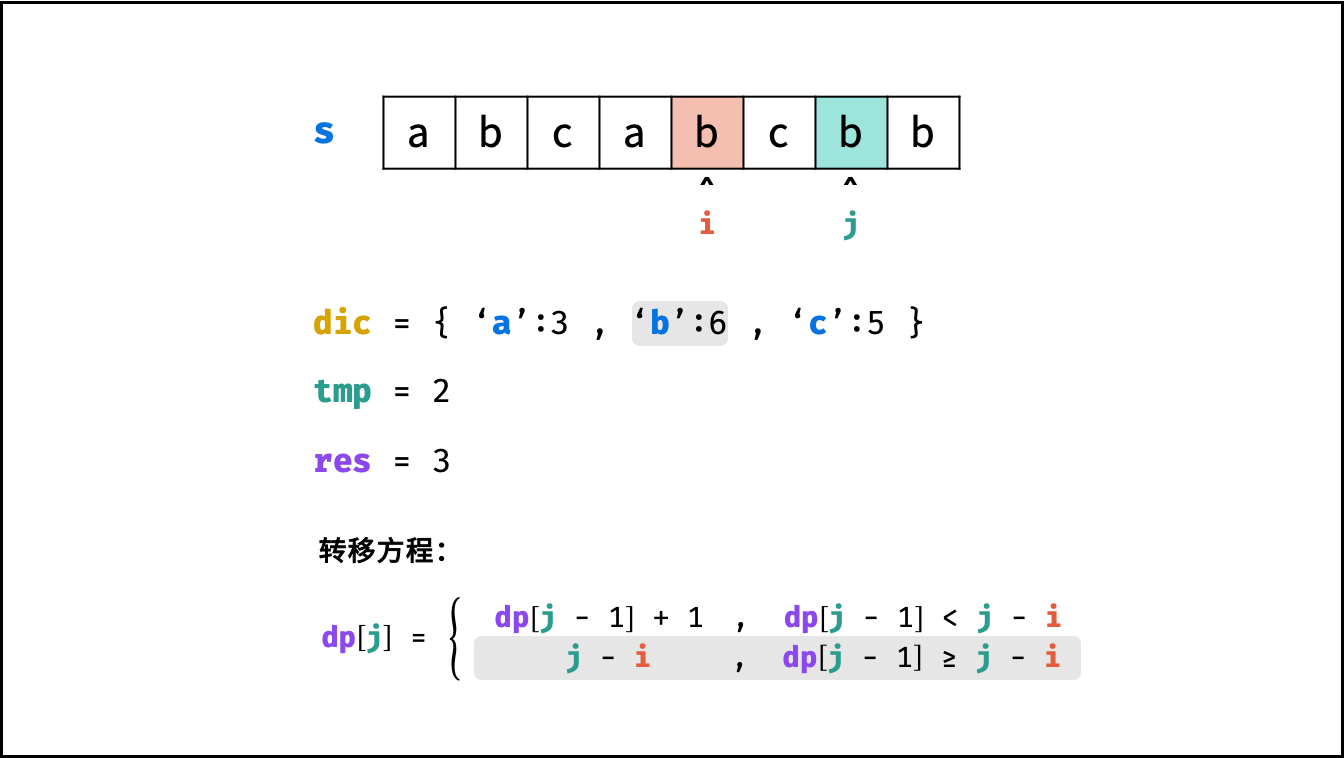Picture9.png](https://pic.leetcode-cn.com/1599288203-iXmXyN-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599288203-CVwEdK-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1599287290-OSCdZT-Picture11.png)>
### 代码：
Python 的 `get(key, default)` 方法和 Java 的 `getOrDefault(key, default)` ，代表当哈希表包含键 `key` 时返回对应 `value` ，不包含时返回默认值 `default` 。
```Python []
class Solution:
def dismantlingAction(self, arr: str) -> int:
dic = {}
res = tmp = 0
for j in range(len(arr)):
i = dic.get(arr[j], -1) # 获取索引 i
dic[arr[j]] = j # 更新哈希表
tmp = tmp + 1 if tmp < j - i else j - i # dp[j - 1] -> dp[j]
res = max(res, tmp) # max(dp[j - 1], dp[j])
return res
```
```Java []
class Solution {
public int dismantlingAction(String arr) {
Map<Character, Integer> dic = new HashMap<>();
int res = 0, tmp = 0, len = arr.length();
for(int j = 0; j < len; j++) {
int i = dic.getOrDefault(arr.charAt(j), -1); // 获取索引 i
dic.put(arr.charAt(j), j); // 更新哈希表
tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
}
return res;
}
}
```
```C++ []
class Solution {
public:
int dismantlingAction(string arr) {
unordered_map<char, int> dic;
int res = 0, tmp = 0, len = arr.size(), i;
for(int j = 0; j < len; j++) {
if (dic.find(arr[j]) == dic.end()) i = - 1;
else i = dic.find(arr[j])->second; // 获取索引 i
dic[arr[j]] = j; // 更新哈希表
tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
res = max(res, tmp); // max(dp[j - 1], dp[j])
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为字符串长度，动态规划需遍历计算 $dp$ 列表。
- **空间复杂度 $O(1)$ ：** 字符的 ASCII 码范围为 $0$ ~ $127$ ，哈希表 $dic$ 最多使用 $O(128) = O(1)$ 大小的额外空间。

82
leetbook_ioa/docs/LCR 168. 丑数.md Executable file
View File

@@ -0,0 +1,82 @@
## 解题思路：
根据题意，每个丑数都可以由其他较小的丑数通过乘以 $2$ 或 $3$ 或 $5$ 得到。
所以，可以考虑使用一个优先队列保存所有的丑数，每次取出最小的那个，然后乘以 $2$ , $3$ , $5$ 后放回队列。然而，**这样做会出现重复的丑数**。例如：
```shell
初始化丑数列表 [1]
第一轮： 1 -> 2, 3, 5 ，丑数列表变为 [1, 2, 3, 5]
第二轮： 2 -> 4, 6, 10 ，丑数列表变为 [1, 2, 3, 4, 6, 10]
第三轮： 3 -> 6, 9, 15 ，出现重复的丑数 6
```
为了避免重复，我们可以用三个指针 $a$ , $b$, $c$ ，分别表示下一个丑数是当前指针指向的丑数乘以 $2$ , $3$ , $5$ 。
利用三个指针生成丑数的算法流程：
1. 初始化丑数列表 $res$ ，首个丑数为 $1$ ，三个指针 $a$ , $b$, $c$ 都指向首个丑数。
2. 开启循环生成丑数：
1. 计算下一个丑数的候选集 $res[a] \cdot 2$ , $res[b] \cdot 3$ , $res[c] \cdot 5$ 。
2. 选择丑数候选集中最小的那个作为下一个丑数，填入 $res$ 。
3. 将被选中的丑数对应的指针向右移动一格。
3. 返回 $res$ 的最后一个元素即可。
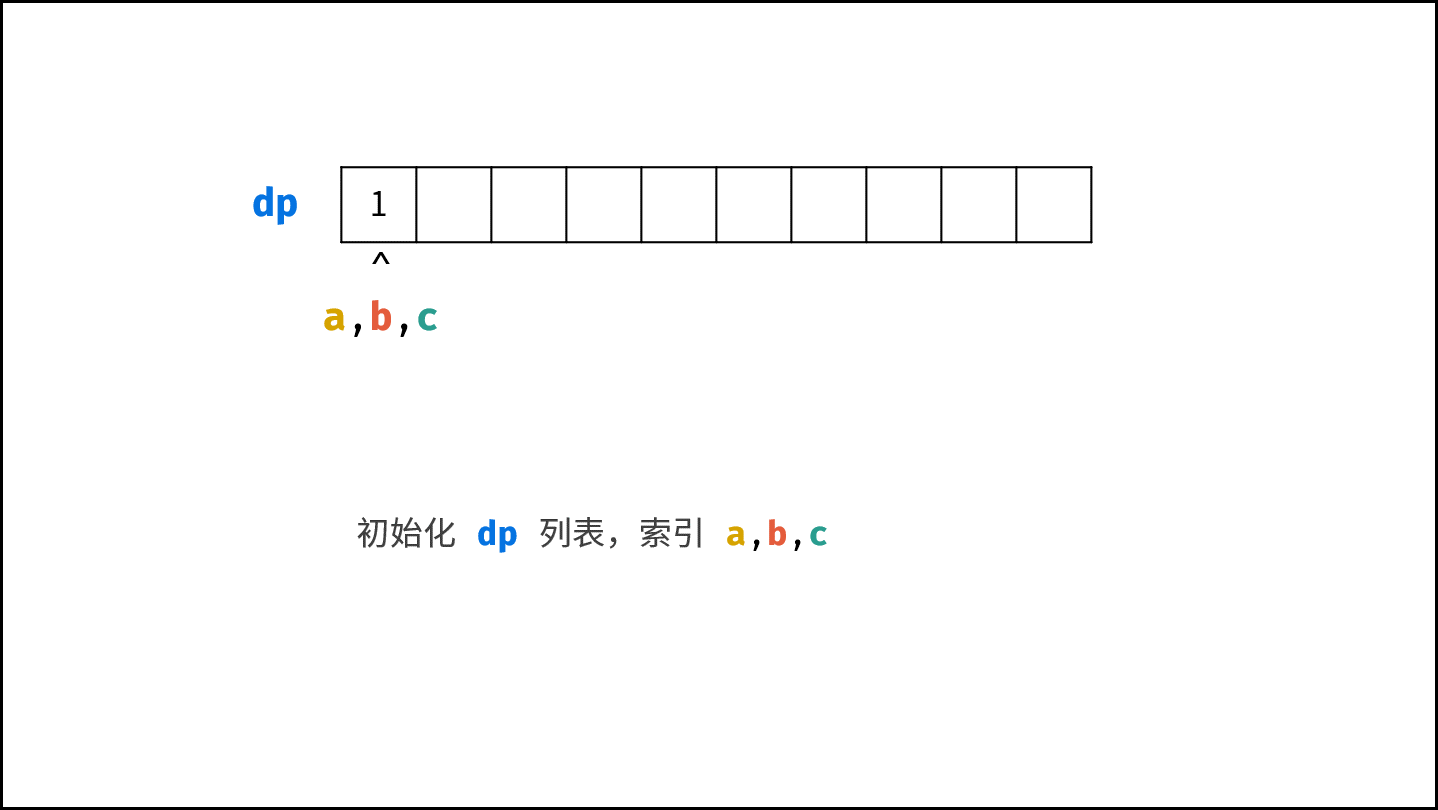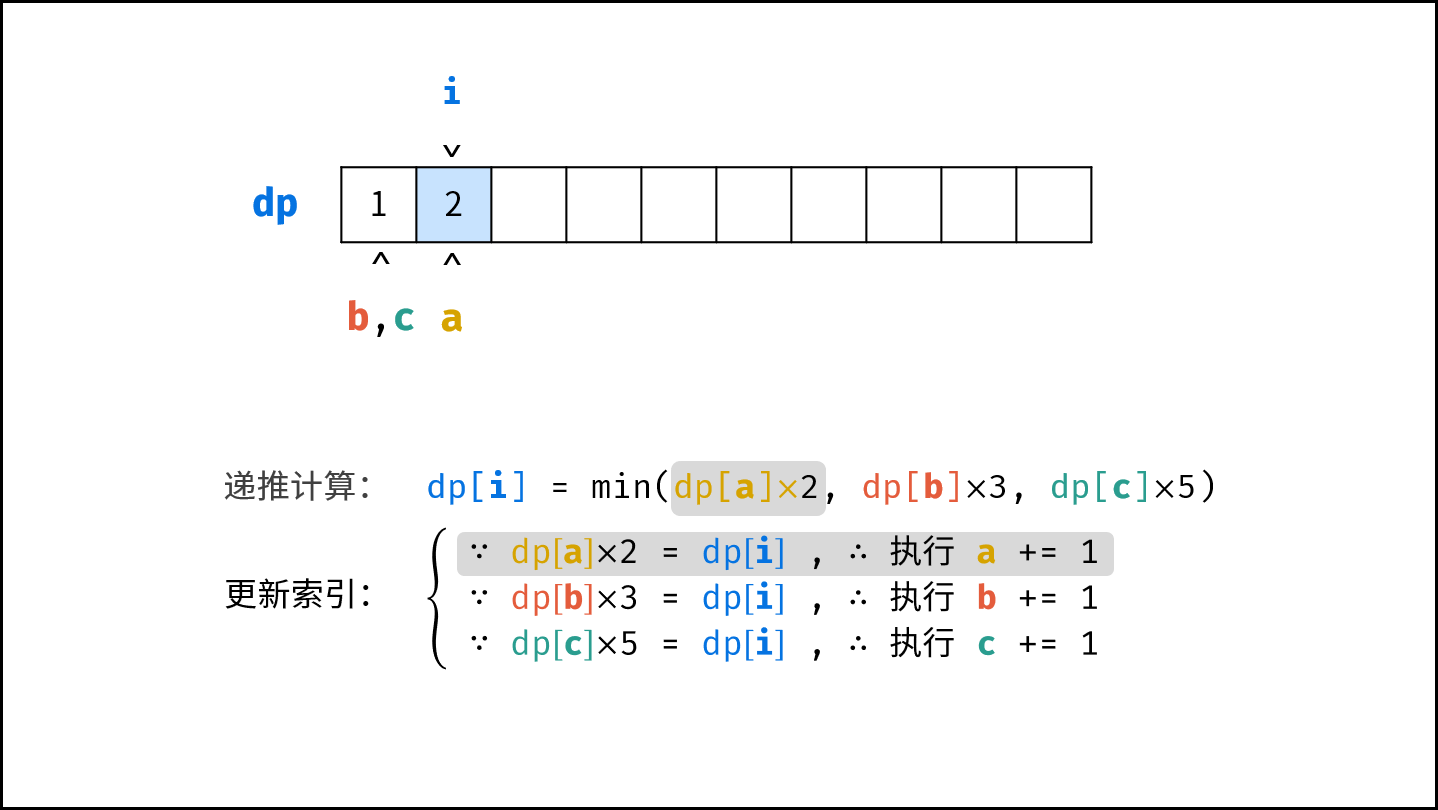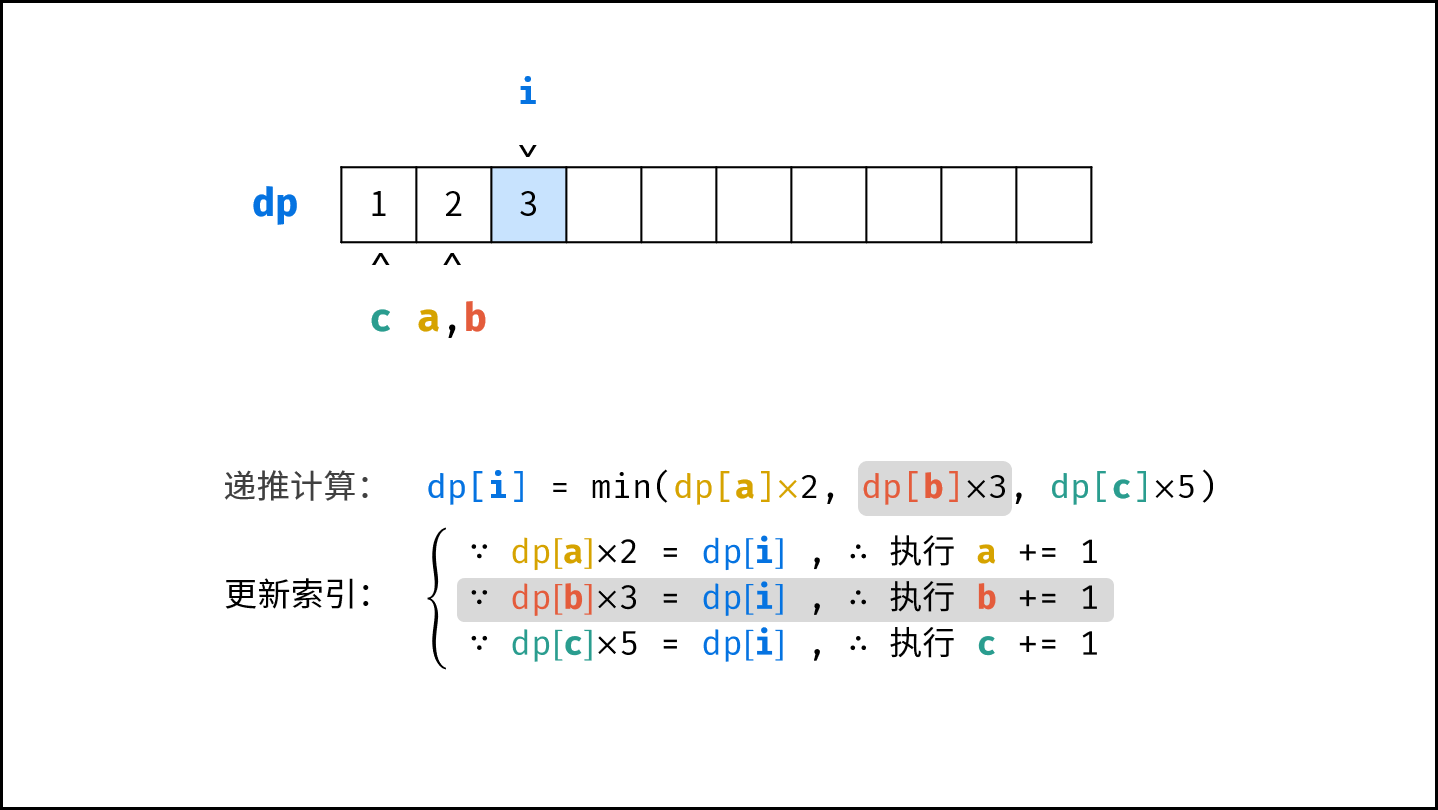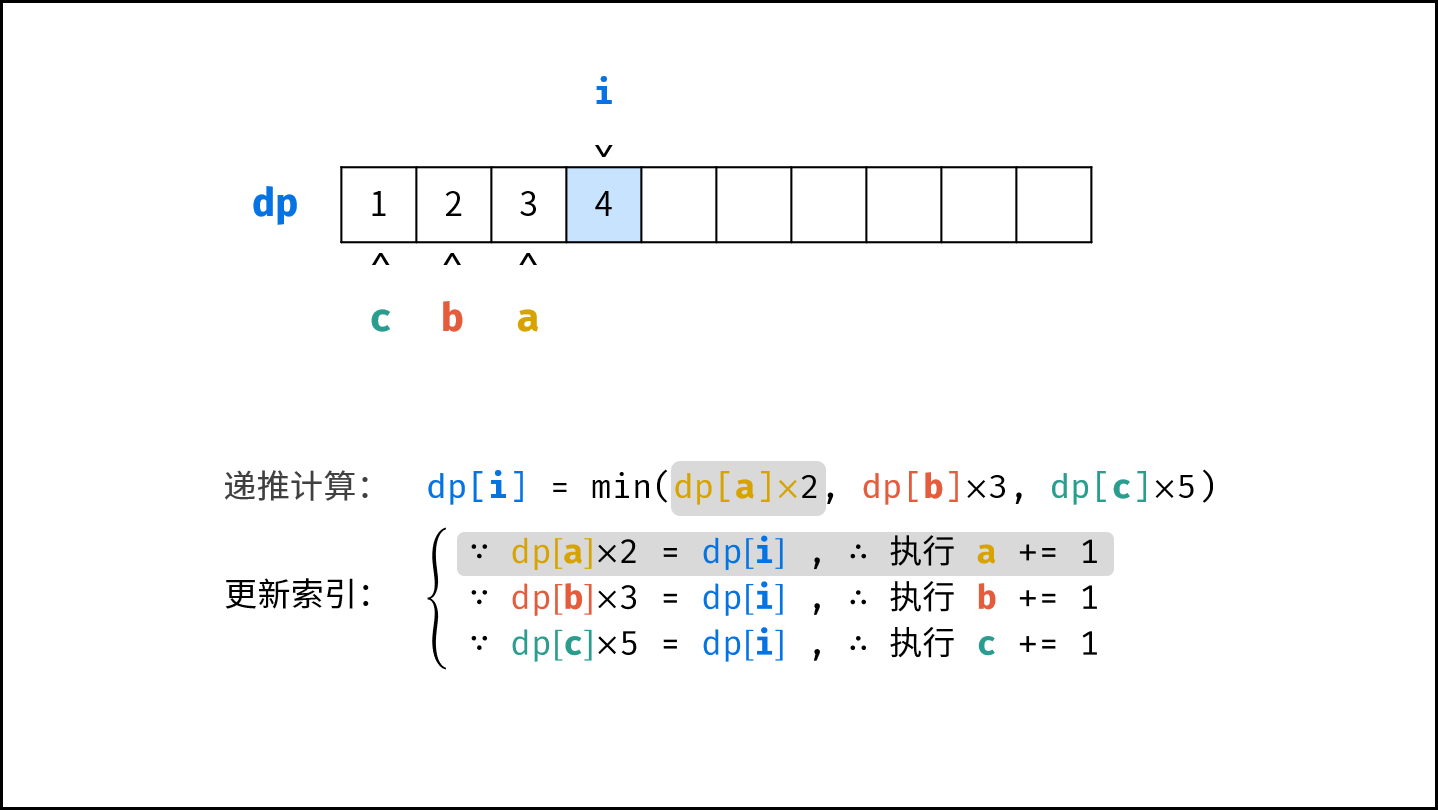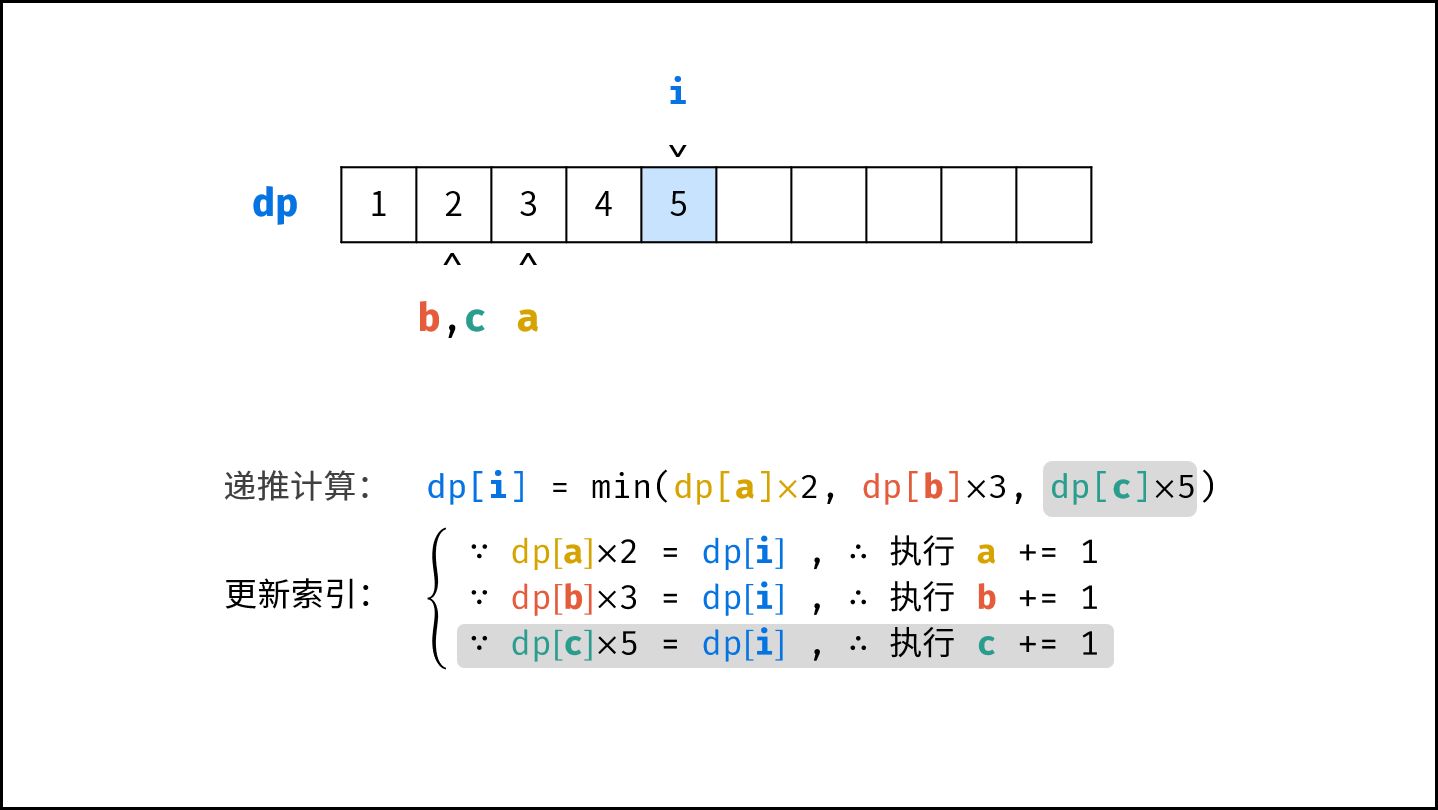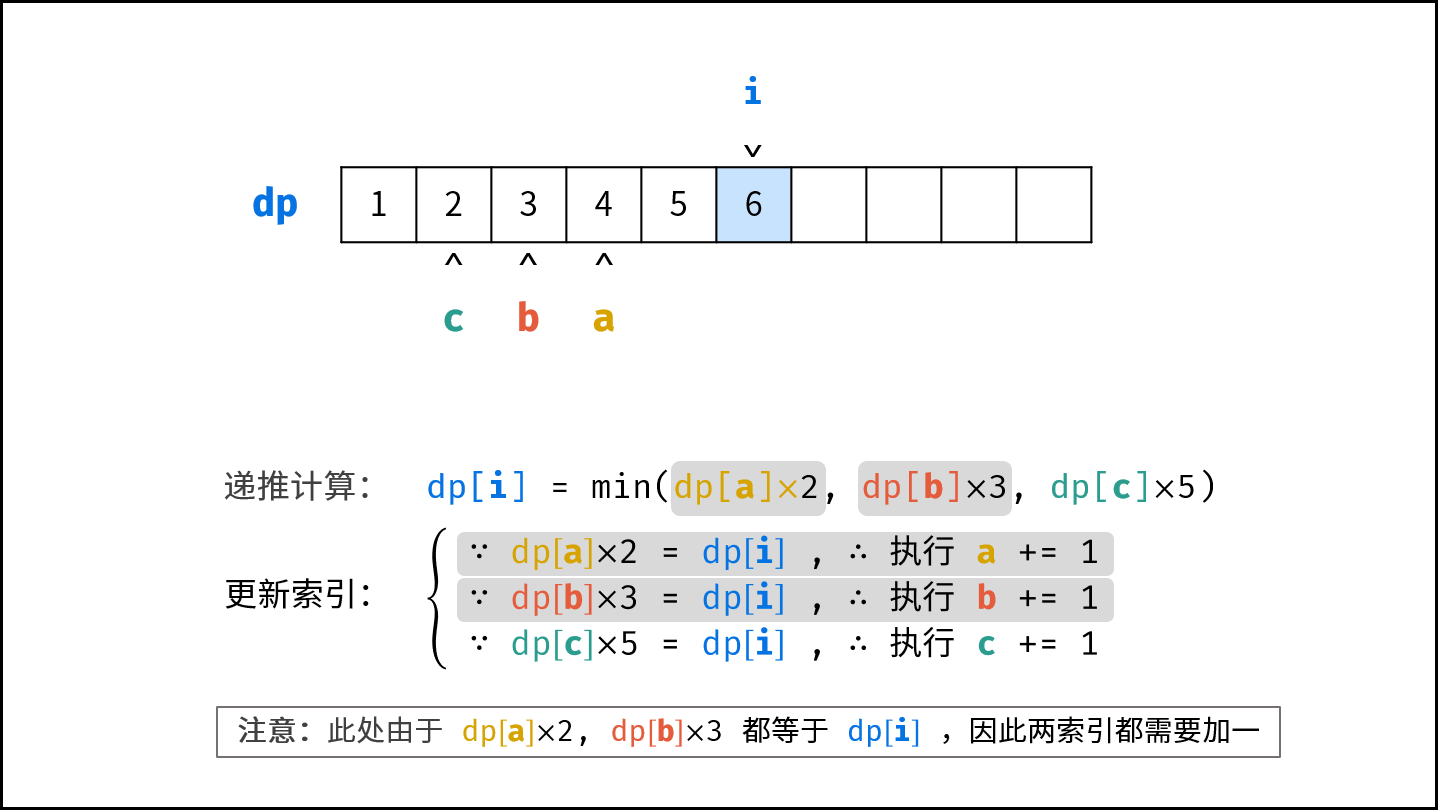<![Picture2.png](https://pic.leetcode-cn.com/1603023853-bcETWT-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603023853-BOsikd-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603023853-HrvzLL-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603023853-CzbMnV-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603023853-MoDFOM-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603023853-sjhztx-Picture7.png),![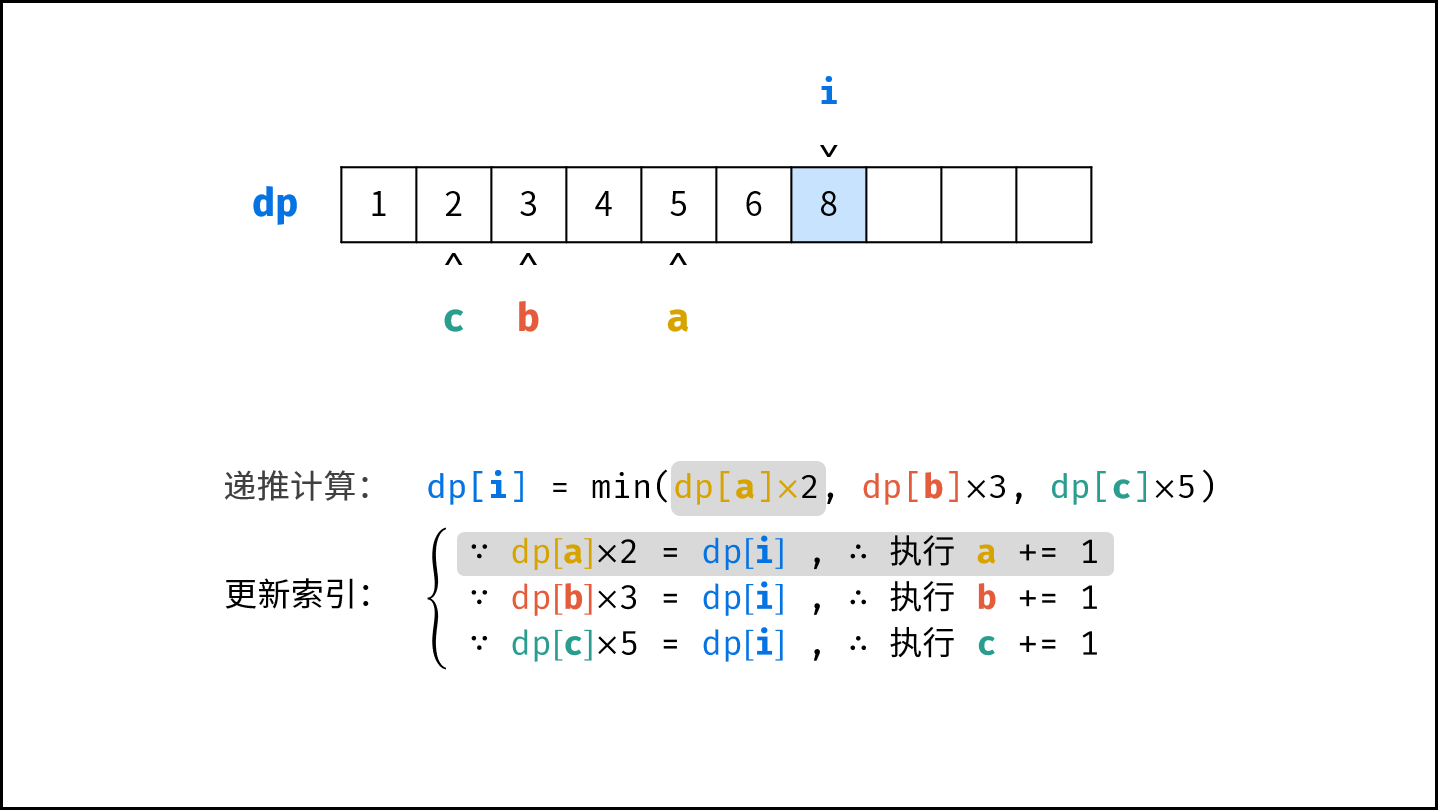Picture8.png](https://pic.leetcode-cn.com/1603023853-NYylSy-Picture8.png),![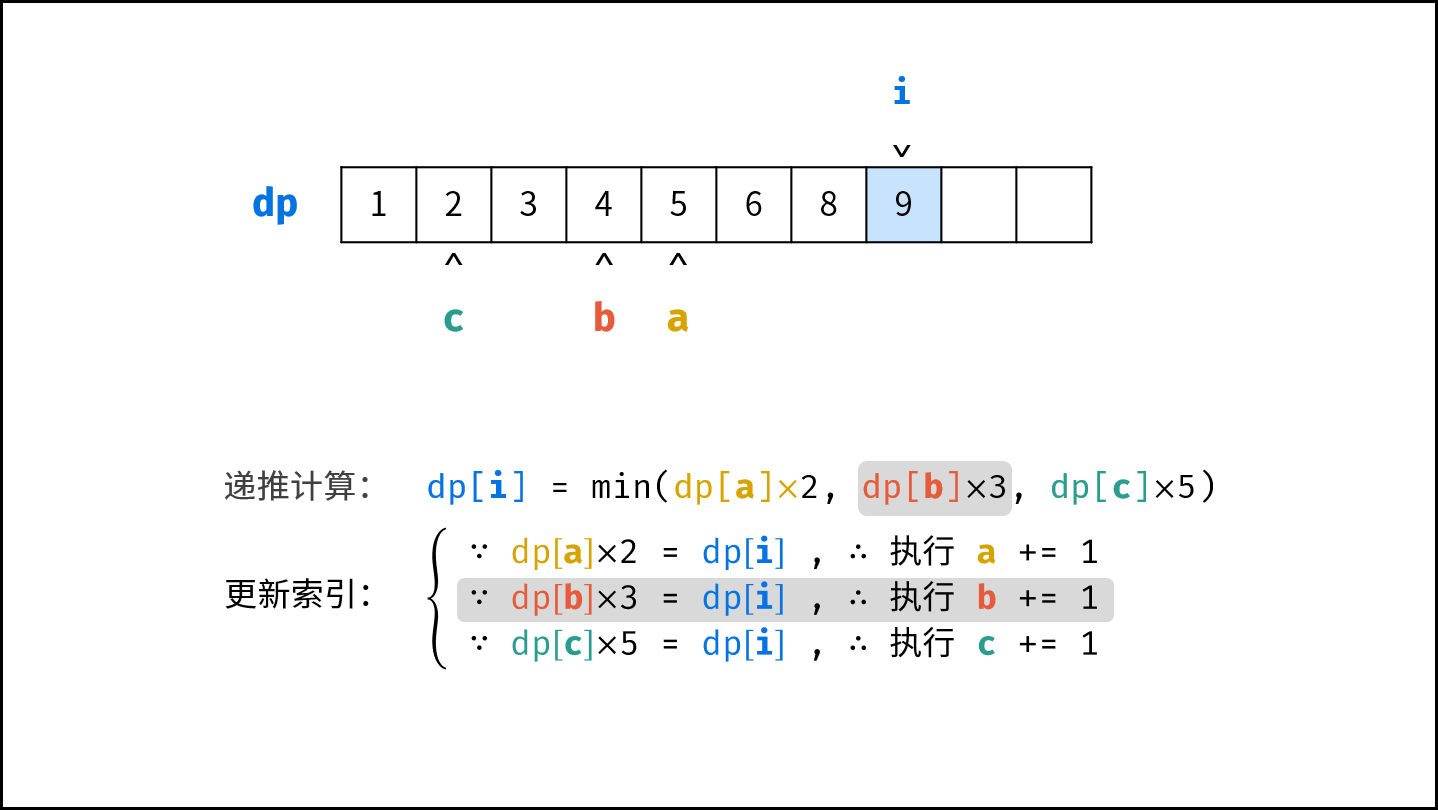Picture9.png](https://pic.leetcode-cn.com/1603023853-saAyFf-Picture9.png),![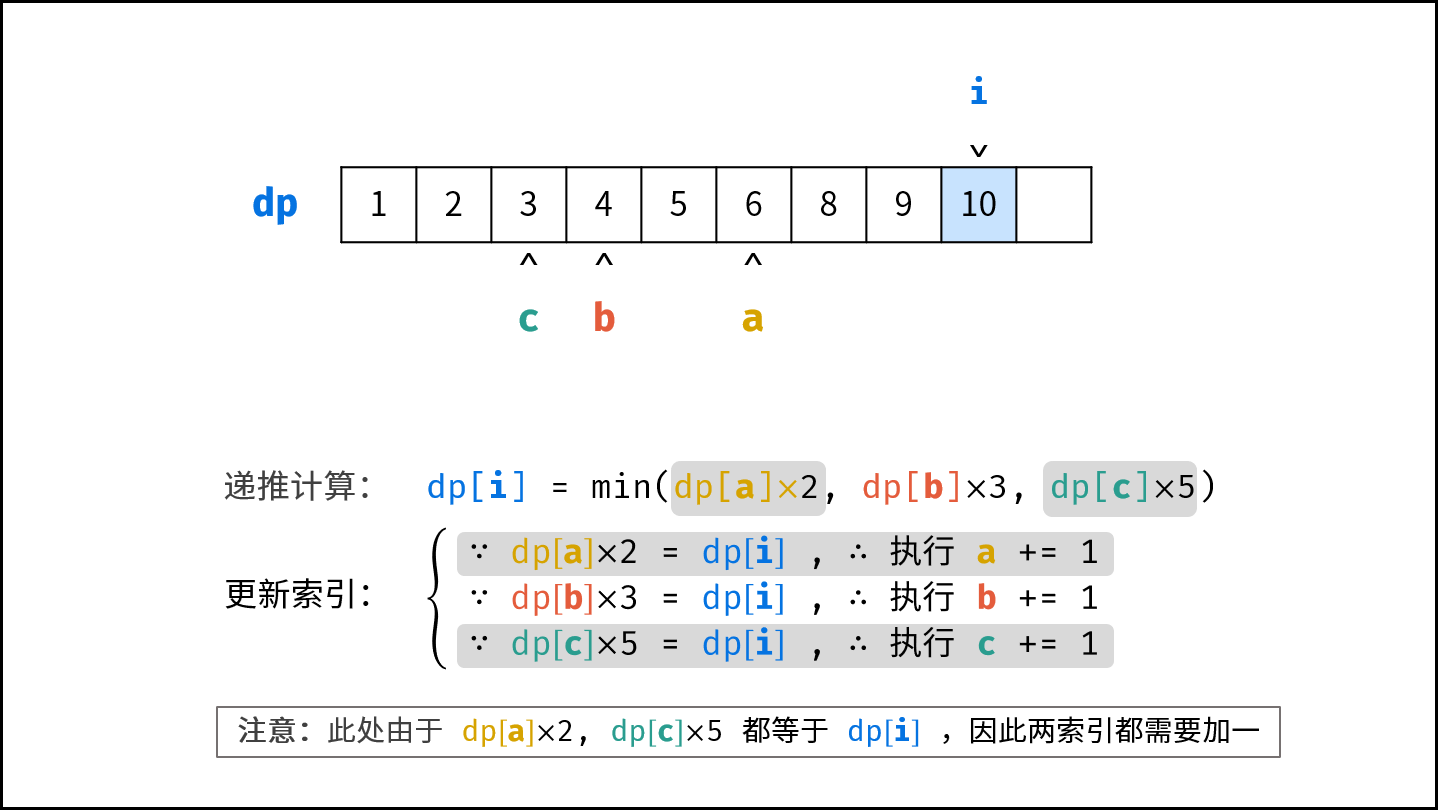Picture10.png](https://pic.leetcode-cn.com/1603023853-IALBSE-Picture10.png),![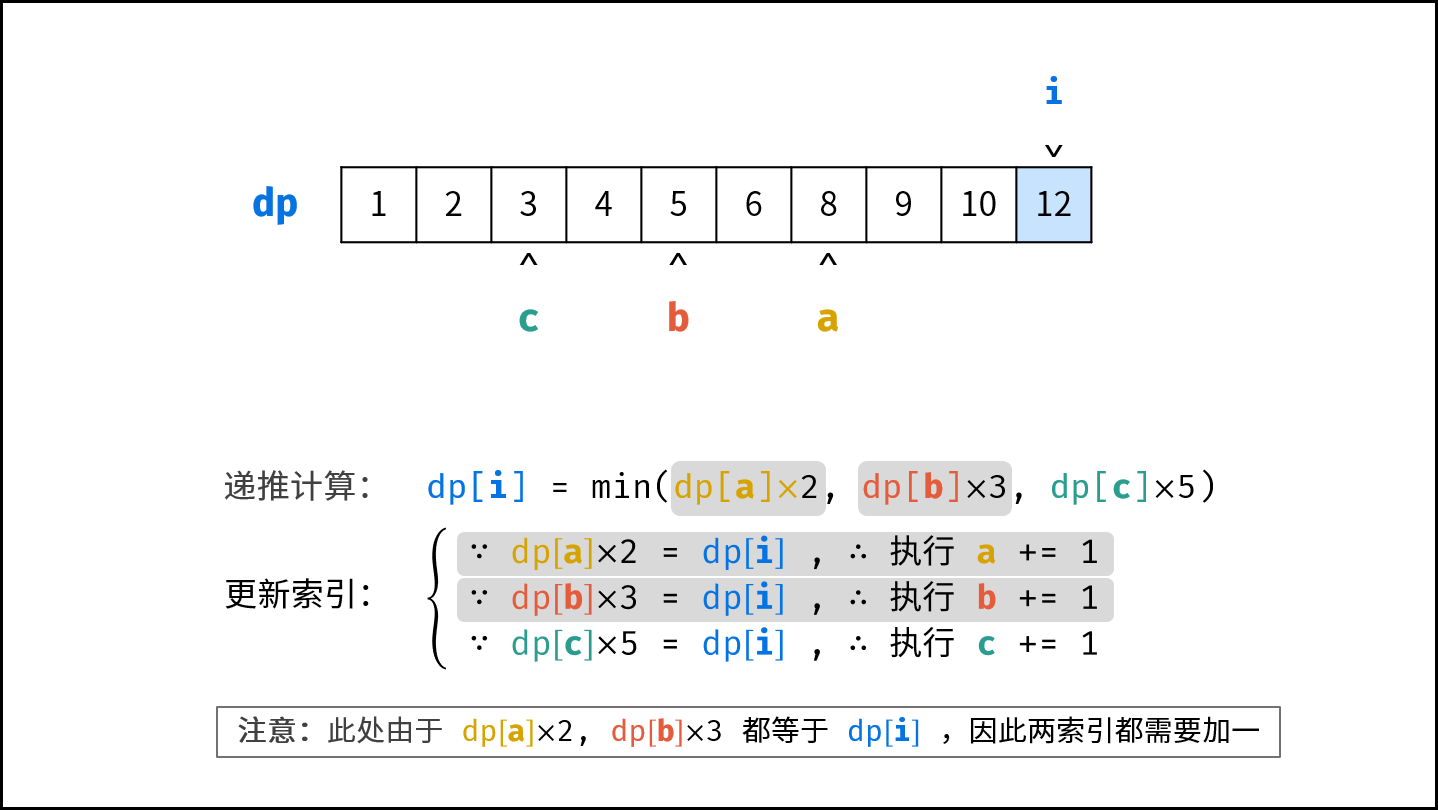Picture11.png](https://pic.leetcode-cn.com/1603023853-kMoqKL-Picture11.png),![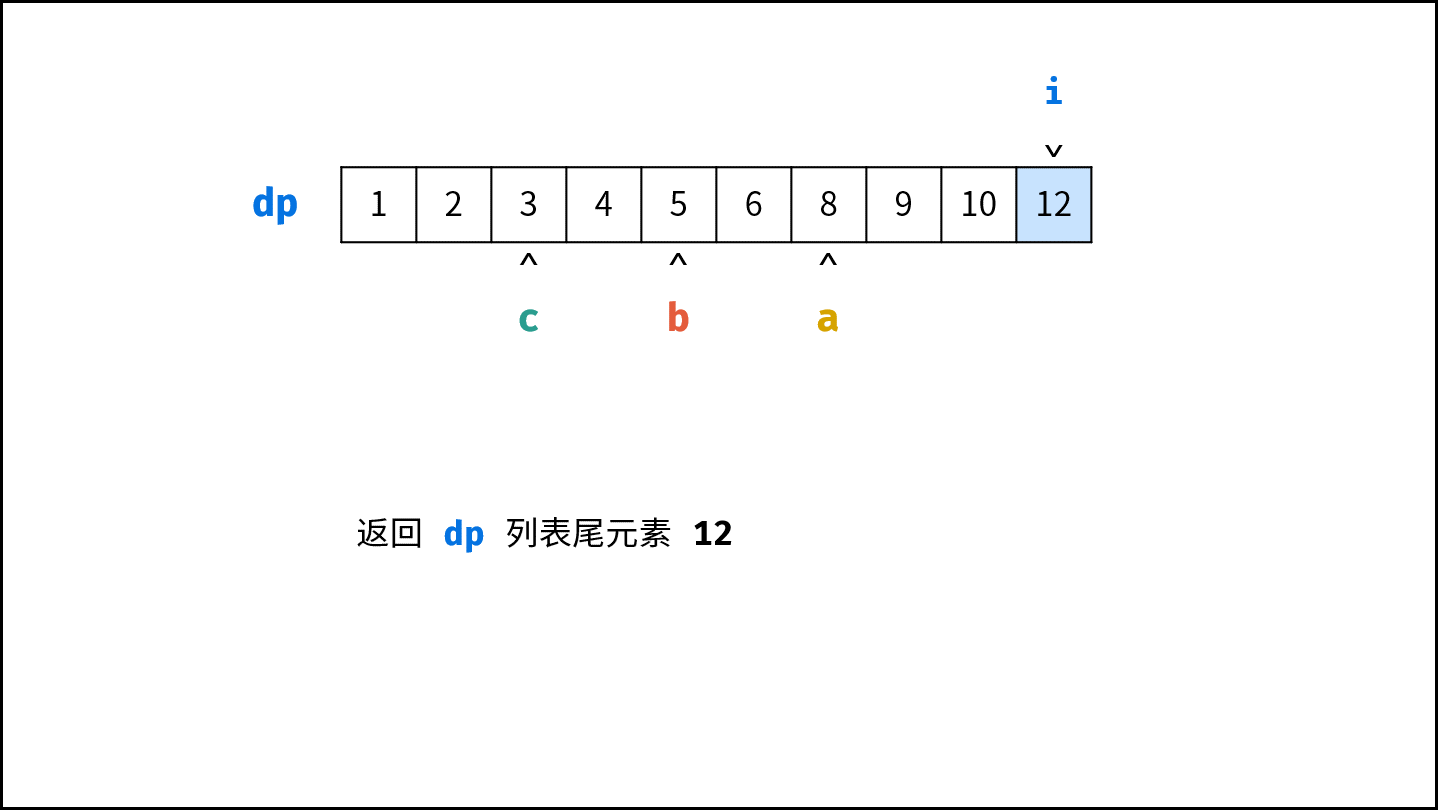Picture12.png](https://pic.leetcode-cn.com/1603023853-tsYuXg-Picture12.png)>
## 代码：
```Python []
class Solution:
def nthUglyNumber(self, n: int) -> int:
res, a, b, c = [1] * n, 0, 0, 0
for i in range(1, n):
n2, n3, n5 = res[a] * 2, res[b] * 3, res[c] * 5
res[i] = min(n2, n3, n5)
if res[i] == n2: a += 1
if res[i] == n3: b += 1
if res[i] == n5: c += 1
return res[-1]
```
```Java []
class Solution {
public int nthUglyNumber(int n) {
int a = 0, b = 0, c = 0;
int[] res = new int[n];
res[0] = 1;
for(int i = 1; i < n; i++) {
int n2 = res[a] * 2, n3 = res[b] * 3, n5 = res[c] * 5;
res[i] = Math.min(Math.min(n2, n3), n5);
if (res[i] == n2) a++;
if (res[i] == n3) b++;
if (res[i] == n5) c++;
}
return res[n - 1];
}
}
```
```C++ []
class Solution {
public:
int nthUglyNumber(int n) {
int a = 0, b = 0, c = 0;
int res[n];
res[0] = 1;
for(int i = 1; i < n; i++) {
int n2 = res[a] * 2, n3 = res[b] * 3, n5 = res[c] * 5;
res[i] = min(min(n2, n3), n5);
if (res[i] == n2) a++;
if (res[i] == n3) b++;
if (res[i] == n5) c++;
}
return res[n - 1];
}
};
```
### 复杂度分析：
- **时间复杂度 $O(n)$ ：** 计算 $res$ 列表需遍历 $n-1$ 轮。
- **空间复杂度 $O(n)$ ：** 长度为 $n$ 的 $res$ 列表使用 $O(n)$ 的额外空间。

146
leetbook_ioa/docs/LCR 169. 招式拆解 II.md Executable file
View File

@@ -0,0 +1,146 @@
## 解题思路：
本题考察 **哈希表** 的使用，本文介绍 **哈希表** 和 **有序哈希表** 两种解法。其中，在字符串长度较大、重复字符很多时，“有序哈希表” 解法理论上效率更高。
## 方法一：哈希表
1. 遍历字符串 `arr` ，使用哈希表统计 “各字符数量是否 $> 1$ ”。
2. 再遍历字符串 `arr` ，在哈希表中找到首个 “数量为 $1$ 的字符”，并返回。
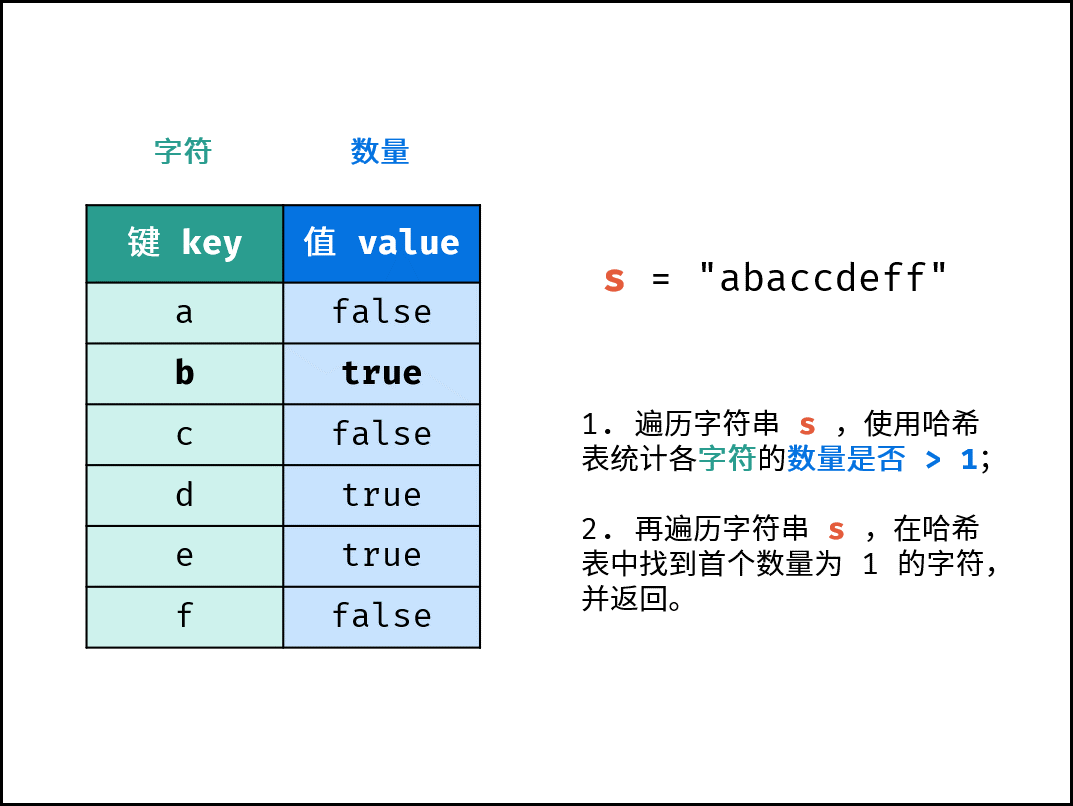![Picture1.png](https://pic.leetcode-cn.com/ed093aabc9195caff6d088454eaebe3cad875e8ca4a643c004ef25e4e5e9e174-Picture1.png){:align=center width=450}
### 算法流程：
1. **初始化：** 字典 (Python)、HashMap(Java)、map(C++)，记为 `hmap` ；
2. **字符统计：** 遍历字符串 `arr` 中的每个字符 `c` ；
1. 若 `hmap` 中 **不包含** 键(key) `c` ：则向 `hmap` 中添加键值对 `(c, True)` ，代表字符 `c` 的数量为 $1$ ；
2. 若 `hmap` 中 **包含** 键(key) `c` ：则修改键 `c` 的键值对为 `(c, False)` ，代表字符 `c` 的数量 $> 1$ 。
3. **查找数量为 $1$ 的字符：** 遍历字符串 `arr` 中的每个字符 `c` ；
1. 若 `hmap`中键 `c` 对应的值为 `True` ：，则返回 `c` 。
4. 返回 `' '` ，代表字符串无数量为 $1$ 的字符。
> 下图中的 `s` 对应本题的 `arr` 。
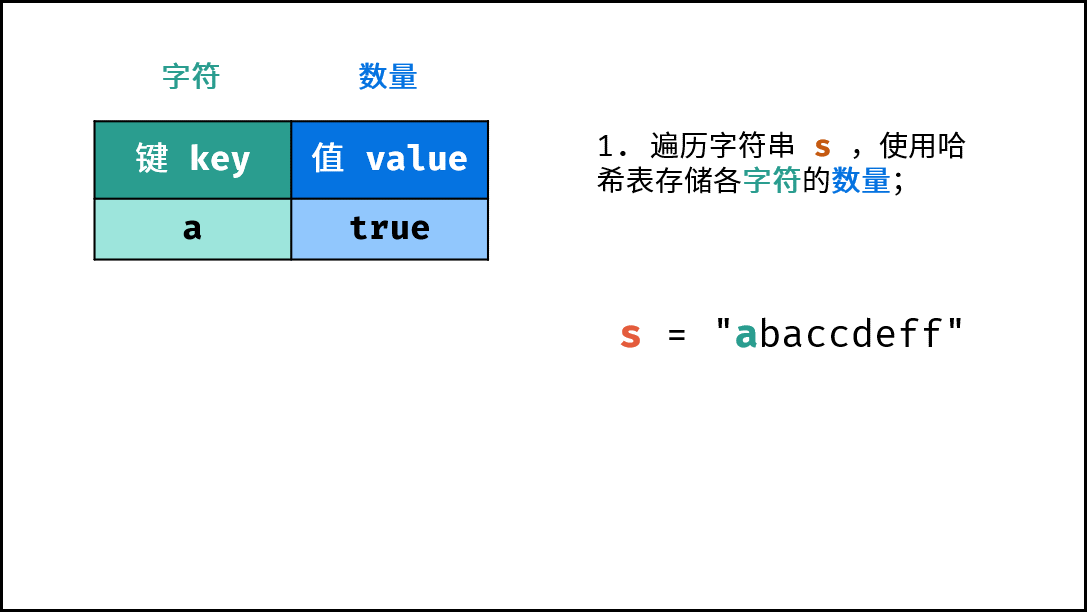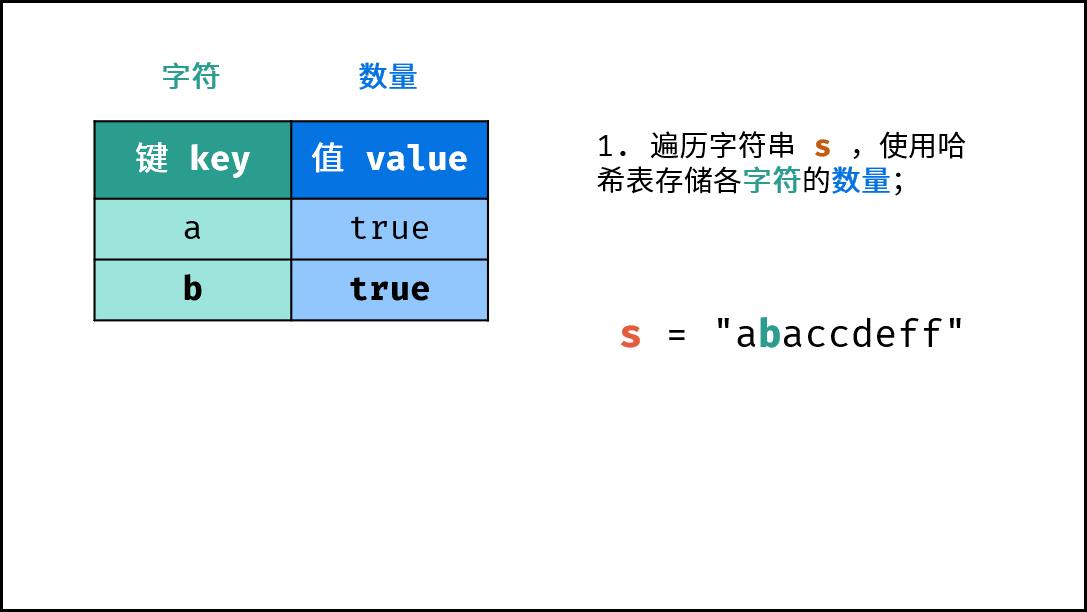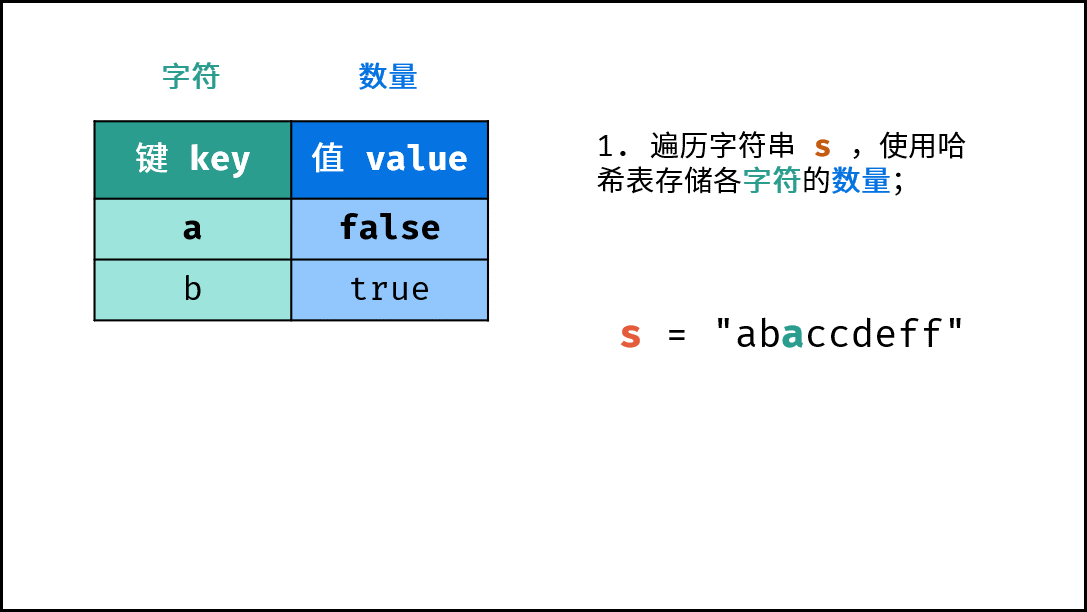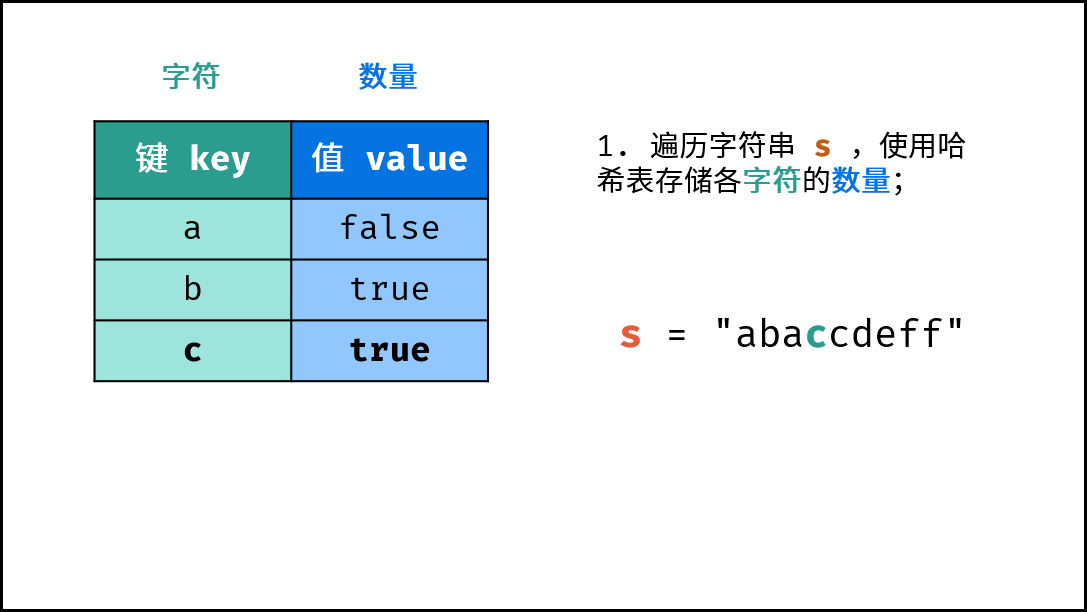<![Picture2.png](https://pic.leetcode-cn.com/776cae7063c810e0f86031d44099b199c5f55f81f4d58ffbad19f1d798d31550-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/5b6324b396d06abe0511f81fa67a1eb795bad6a37e94e9ef6bde8557967ab8bc-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/240c928b3110664fbdd9c86aa44e4a6a34e29ceb55531b2640a802a00bf4a46f-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/7cb3b93272e8e7f770a32ce0c39271dc4b50804cc6e4dbe9541d2b9d64e96db8-Picture5.png),![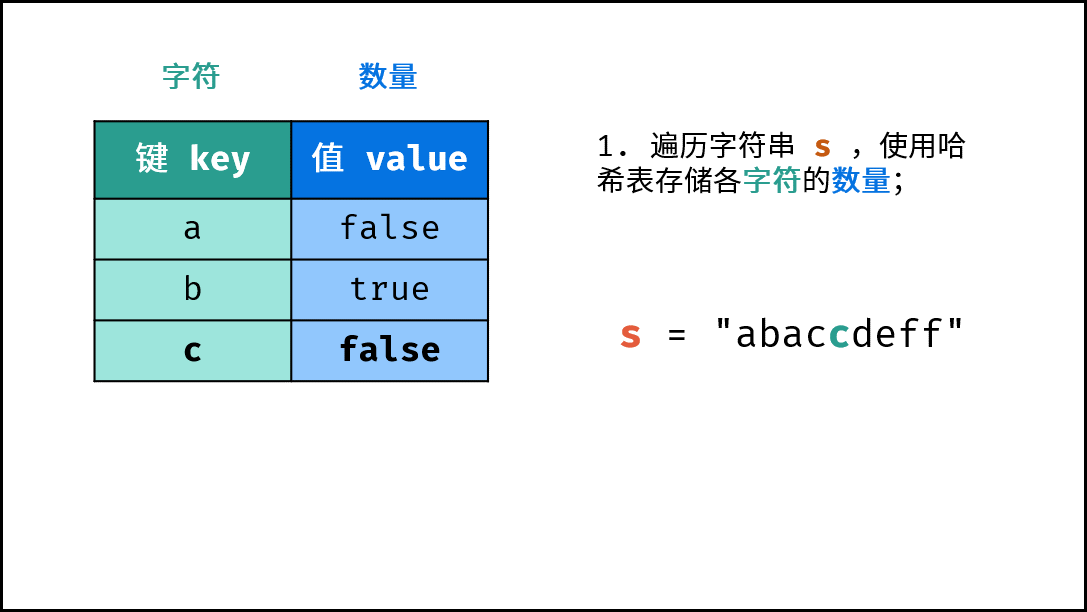Picture6.png](https://pic.leetcode-cn.com/5c68b55d5a5abae9223db9f380bcd199b5da5c8f9248e4809298b685f218d29a-Picture6.png),![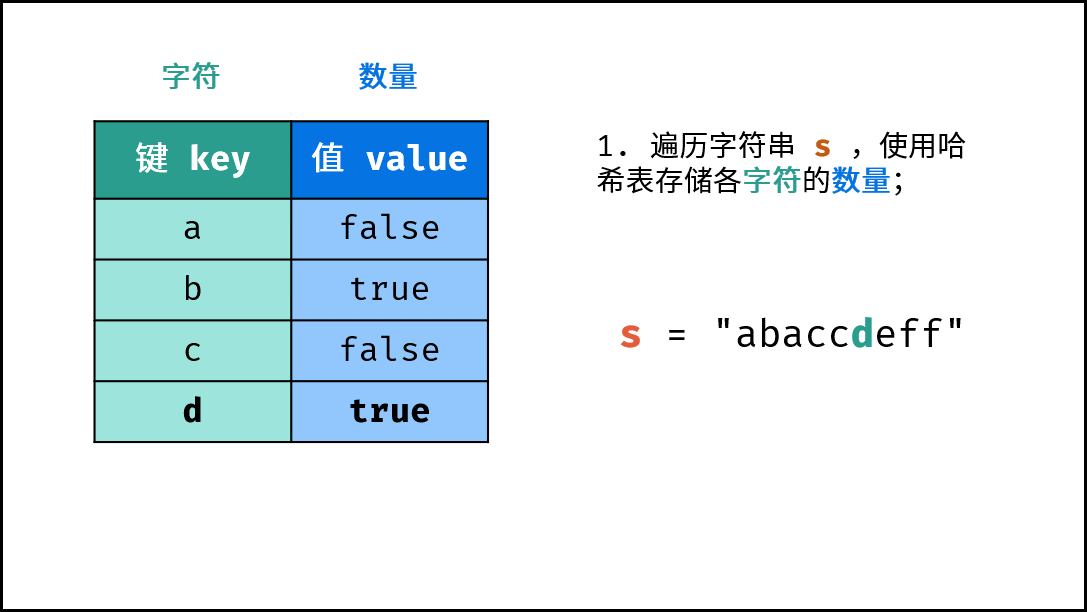Picture7.png](https://pic.leetcode-cn.com/aea83f7d093a5662867d34a8fc8da26ada4bbe7b64868d697645848167f6f3eb-Picture7.png),![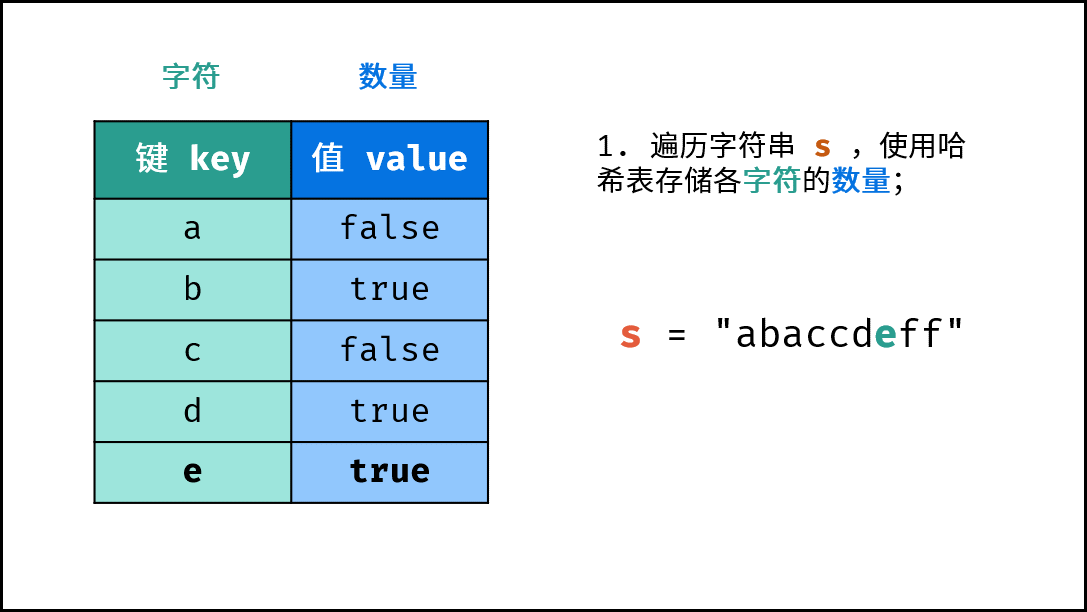Picture8.png](https://pic.leetcode-cn.com/32cf6ba91b799bf1f625fa39796f73a60dfad041589e82d0ed3545d08393f3bb-Picture8.png),![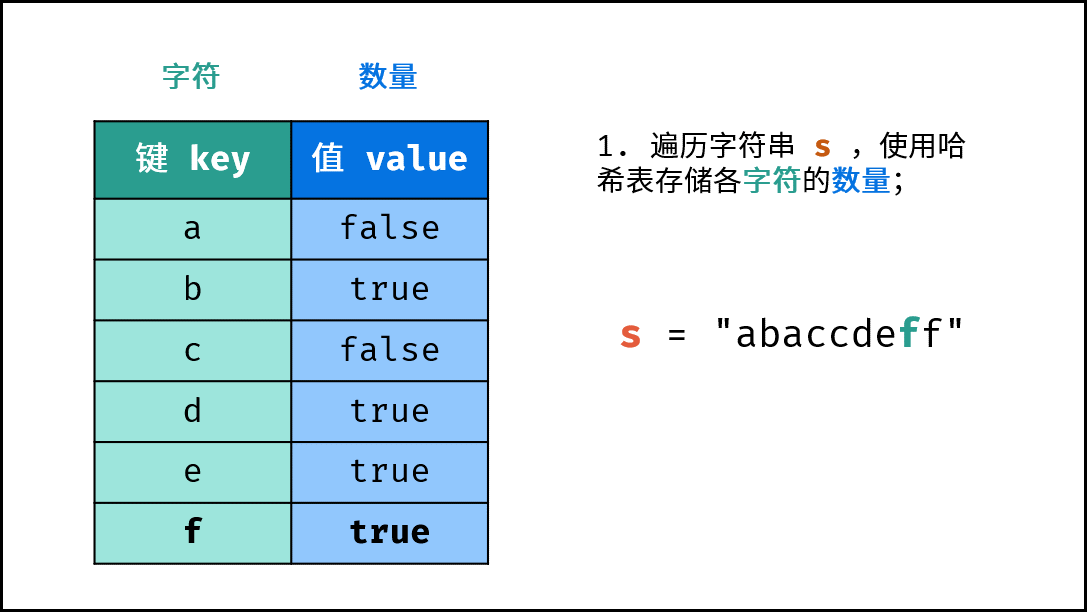Picture9.png](https://pic.leetcode-cn.com/10bc69cab88ba6f5071b8b67c370d1e1dfa0db2e341268191c41e1e9c9820d52-Picture9.png),![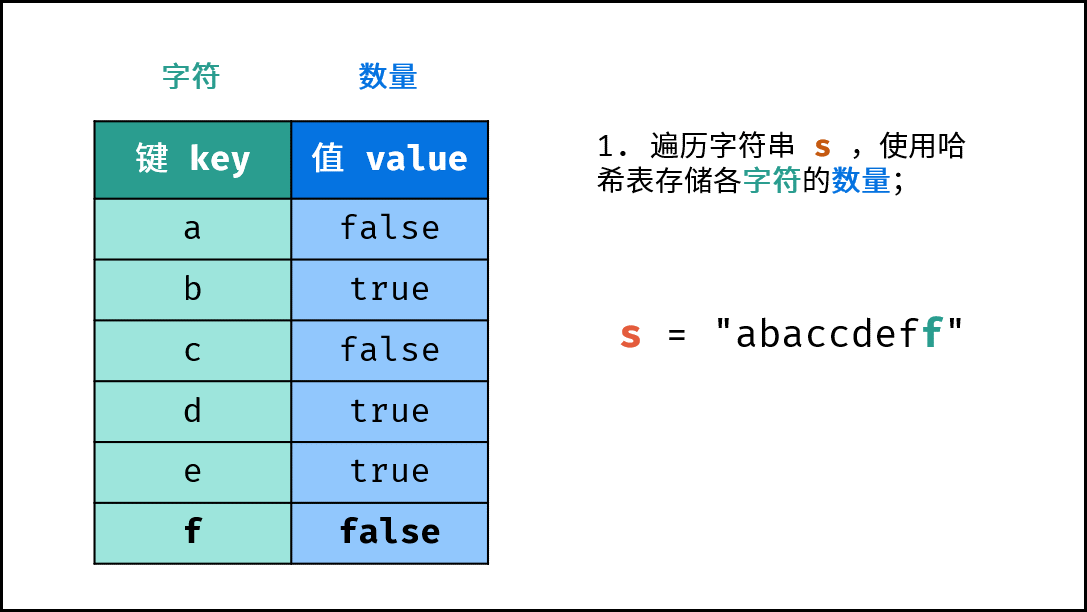Picture10.png](https://pic.leetcode-cn.com/4b44c787abeed308cbfc5c92cb72922d63cd7806b4524c961e025aac8bf59fbf-Picture10.png),![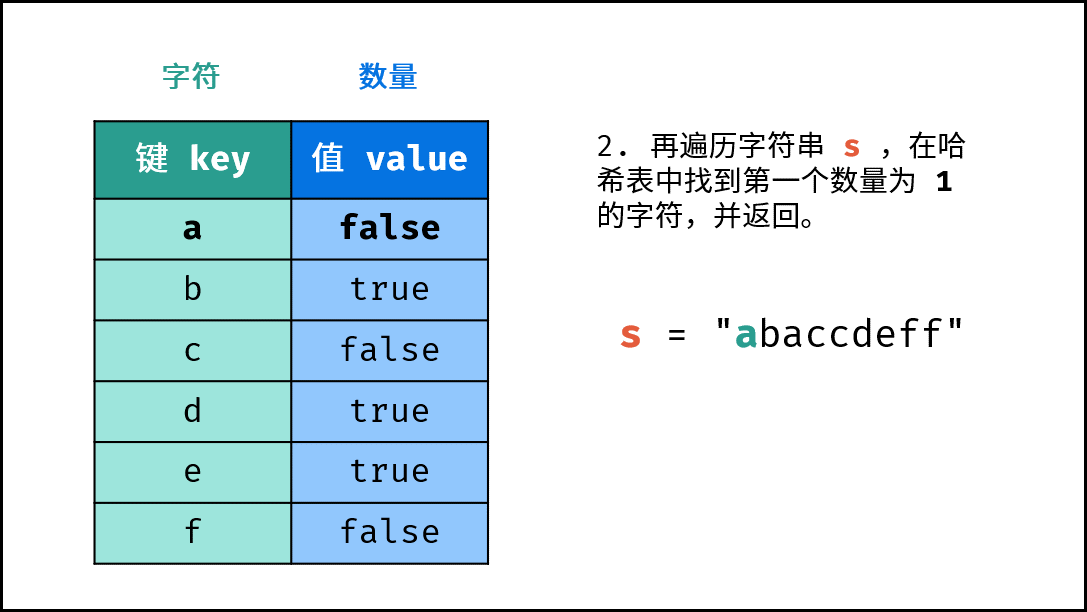Picture11.png](https://pic.leetcode-cn.com/f0e078920fee1d2486d489fbaa10c75a3da3c2f3703d810509cfc8581b118274-Picture11.png),![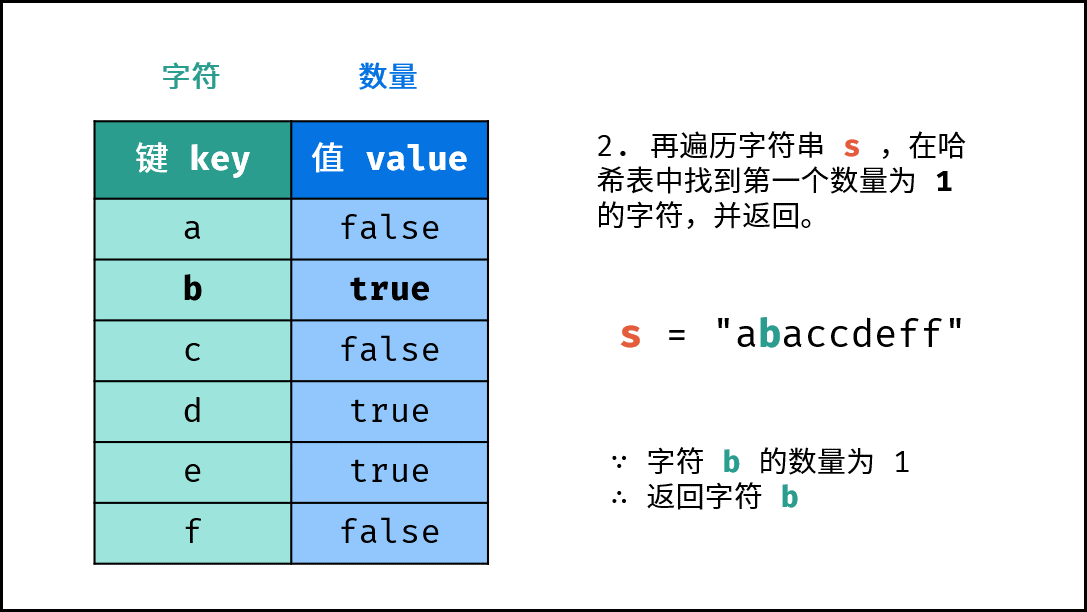Picture12.png](https://pic.leetcode-cn.com/98825f51afdf7c59df3bbb9a9370406d82cd1425eb5eaa508335cd727a82983d-Picture12.png)>
### 代码：
Python 代码中的 `not c in hmap` 整体为一个布尔值；`c in hmap` 为判断字典中是否含有键 `c` 。
```Python []
class Solution:
def dismantlingAction(self, arr: str) -> str:
hmap = {}
for c in arr:
hmap[c] = not c in hmap
for c in arr:
if hmap[c]: return c
return ' '
```
```Java []
class Solution {
public char dismantlingAction(String arr) {
HashMap<Character, Boolean> hmap = new HashMap<>();
char[] sc = arr.toCharArray();
for(char c : sc)
hmap.put(c, !hmap.containsKey(c));
for(char c : sc)
if(hmap.get(c)) return c;
return ' ';
}
}
```
```C++ []
class Solution {
public:
char dismantlingAction(string arr) {
unordered_map<char, bool> hmap;
for(char c : arr)
hmap[c] = hmap.find(c) == hmap.end();
for(char c : arr)
if(hmap[c]) return c;
return ' ';
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为字符串 `arr` 的长度；需遍历 `arr` 两轮，使用 $O(N)$ ；HashMap 查找操作的复杂度为 $O(1)$ ；
- **空间复杂度 $O(1)$ ：** 由于题目指出 `arr` 只包含小写字母，因此最多有 26 个不同字符，HashMap 存储需占用 $O(26) = O(1)$ 的额外空间。
## 方法二：有序哈希表
在哈希表的基础上，有序哈希表中的键值对是 **按照插入顺序排序** 的。基于此，可通过遍历有序哈希表，实现搜索首个 “数量为 $1$ 的字符”。
哈希表是 **去重** 的，即哈希表中键值对数量 $\leq$ 字符串 `arr` 的长度。因此，相比于方法一，方法二减少了第二轮遍历的循环次数。当字符串很长（重复字符很多）时，方法二则效率更高。
### 代码：
Python 3.6 后，默认字典就是有序的，因此无需使用 `OrderedDict()` ，详情可见：[为什么Python 3.6以后字典有序并且效率更高？](https://www.cnblogs.com/xieqiankun/p/python_dict.html)
Java 使用 `LinkedHashMap` 实现有序哈希表。
由于 C++ 未提供自带的链式哈希表，因此借助一个 vector 按序存储哈希表 hmap 中的 key ，第二轮遍历此 vector 即可。
```Python []
class Solution:
def dismantlingAction(self, arr: str) -> str:
hmap = collections.OrderedDict()
for c in arr:
hmap[c] = not c in hmap
for k, v in hmap.items():
if v: return k
return ' '
```
```Python []
class Solution:
def dismantlingAction(self, arr: str) -> str:
hmap = {}
for c in arr:
hmap[c] = not c in hmap
for k, v in hmap.items():
if v: return k
return ' '
```
```Java []
class Solution {
public char dismantlingAction(String arr) {
Map<Character, Boolean> hmap = new LinkedHashMap<>();
char[] sc = arr.toCharArray();
for(char c : sc)
hmap.put(c, !hmap.containsKey(c));
for(Map.Entry<Character, Boolean> d : hmap.entrySet()){
if(d.getValue()) return d.getKey();
}
return ' ';
}
}
```
```C++ []
class Solution {
public:
char dismantlingAction(string arr) {
vector<char> keys;
unordered_map<char, bool> hmap;
for(char c : arr) {
if(hmap.find(c) == hmap.end())
keys.push_back(c);
hmap[c] = hmap.find(c) == hmap.end();
}
for(char c : keys) {
if(hmap[c]) return c;
}
return ' ';
}
};
```
### 复杂度分析：
时间和空间复杂度均与 “方法一” 相同，而具体分析：方法一 需遍历 `arr` 两轮；方法二 遍历 `arr` 一轮，遍历 `hmap` 一轮（ `hmap` 的长度不大于 26 ）。

148
leetbook_ioa/docs/LCR 170. 交易逆序对的总数.md Executable file
View File

@@ -0,0 +1,148 @@
## 解题思路：
直观来看，使用暴力统计法即可，即遍历数组的所有数字对并统计逆序对数量。此方法时间复杂度为 $O(N^2)$ ，观察题目给定的数组长度范围 $0 \leq N \leq 50000$ ，可知此复杂度是不能接受的。
「归并排序」与「逆序对」是息息相关的。归并排序体现了 “分而治之” 的算法思想，具体为：
- **分：** 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
- **治：** 划分到子数组长度为 1 时，开始向上合并，不断将 **较短排序数组** 合并为 **较长排序数组**，直至合并至原数组时完成排序；
> 如下图所示，为数组 $[7, 3, 2, 6, 0, 1, 5, 4]$ 的归并排序过程。
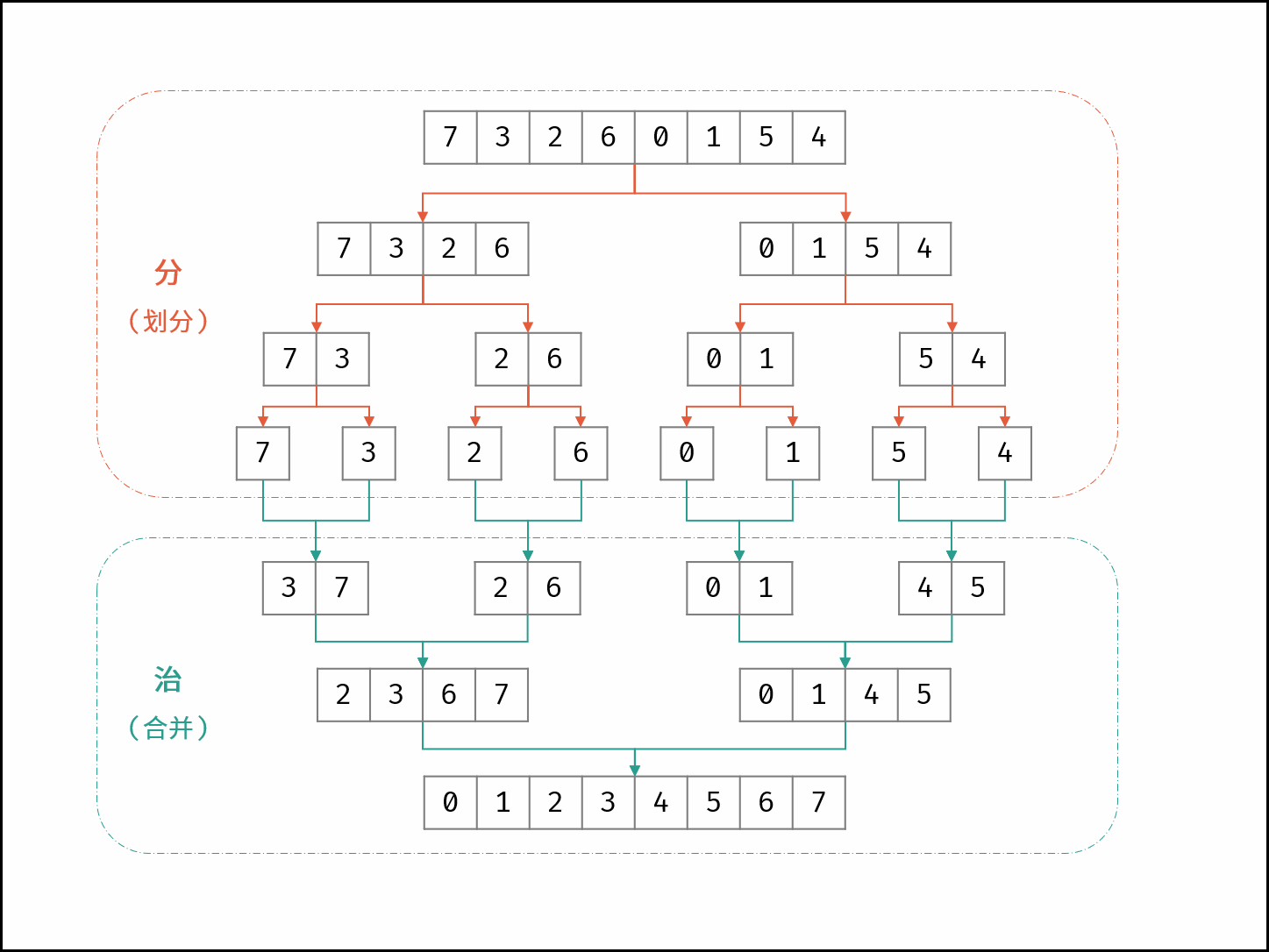![Picture1.png](https://pic.leetcode-cn.com/1614274007-nBQbZZ-Picture1.png){:align=center width=500}
**合并阶段** 本质上是 **合并两个排序数组** 的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。
> 如下图所示，为左子数组 $[2, 3, 6, 7]$ 与 右子数组 $[0, 1, 4, 5]$ 的合并与逆序对统计过程。
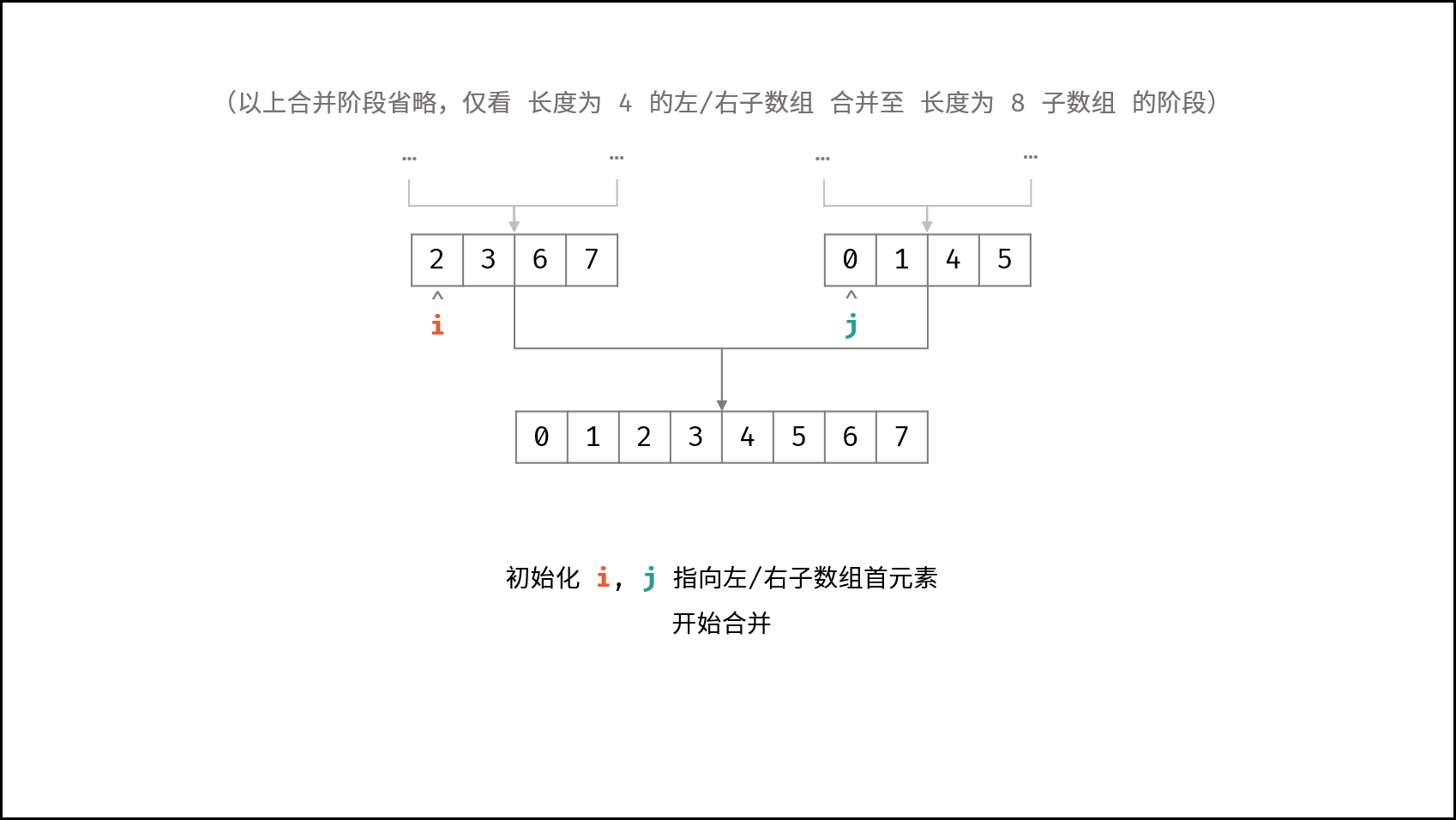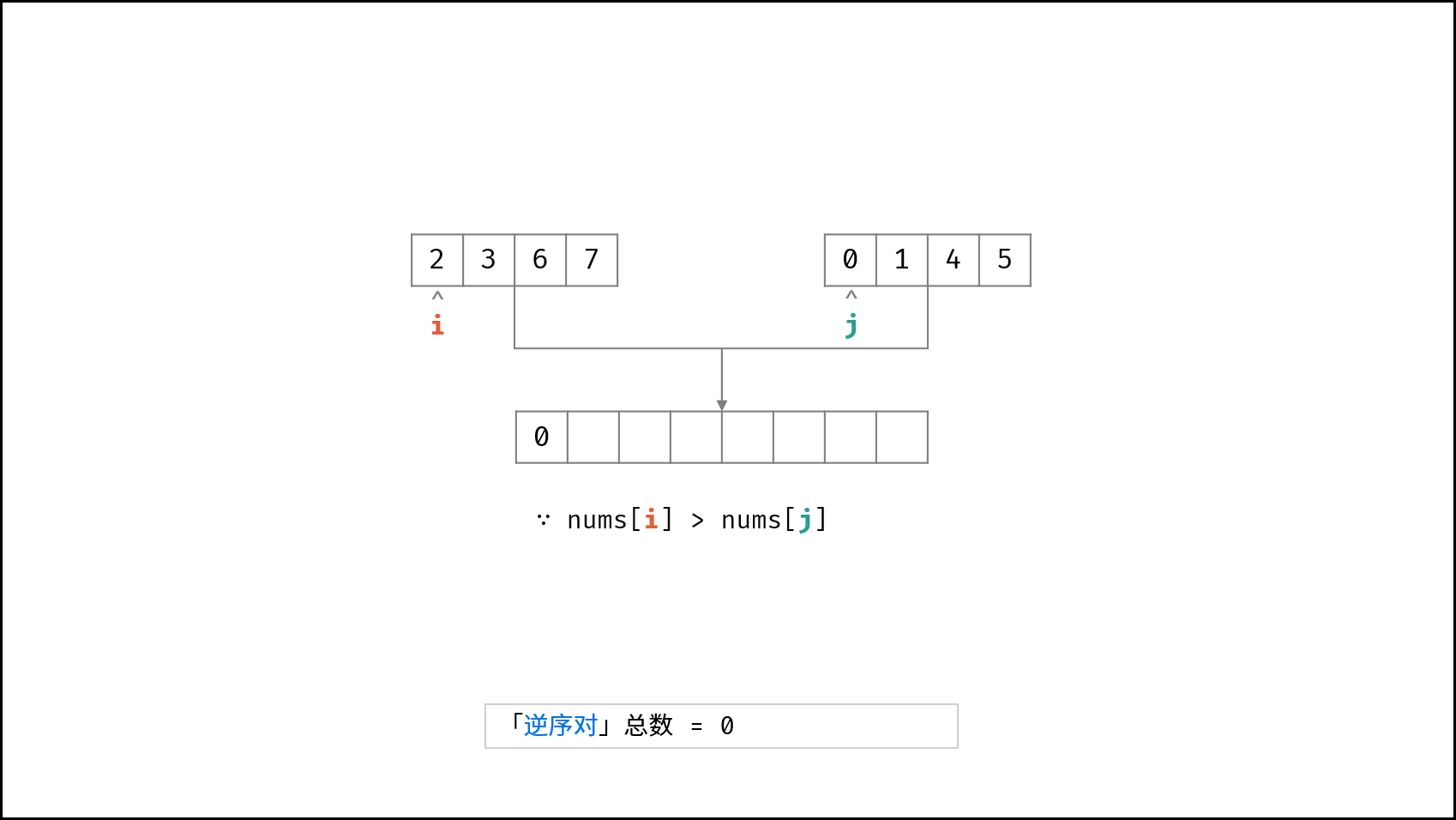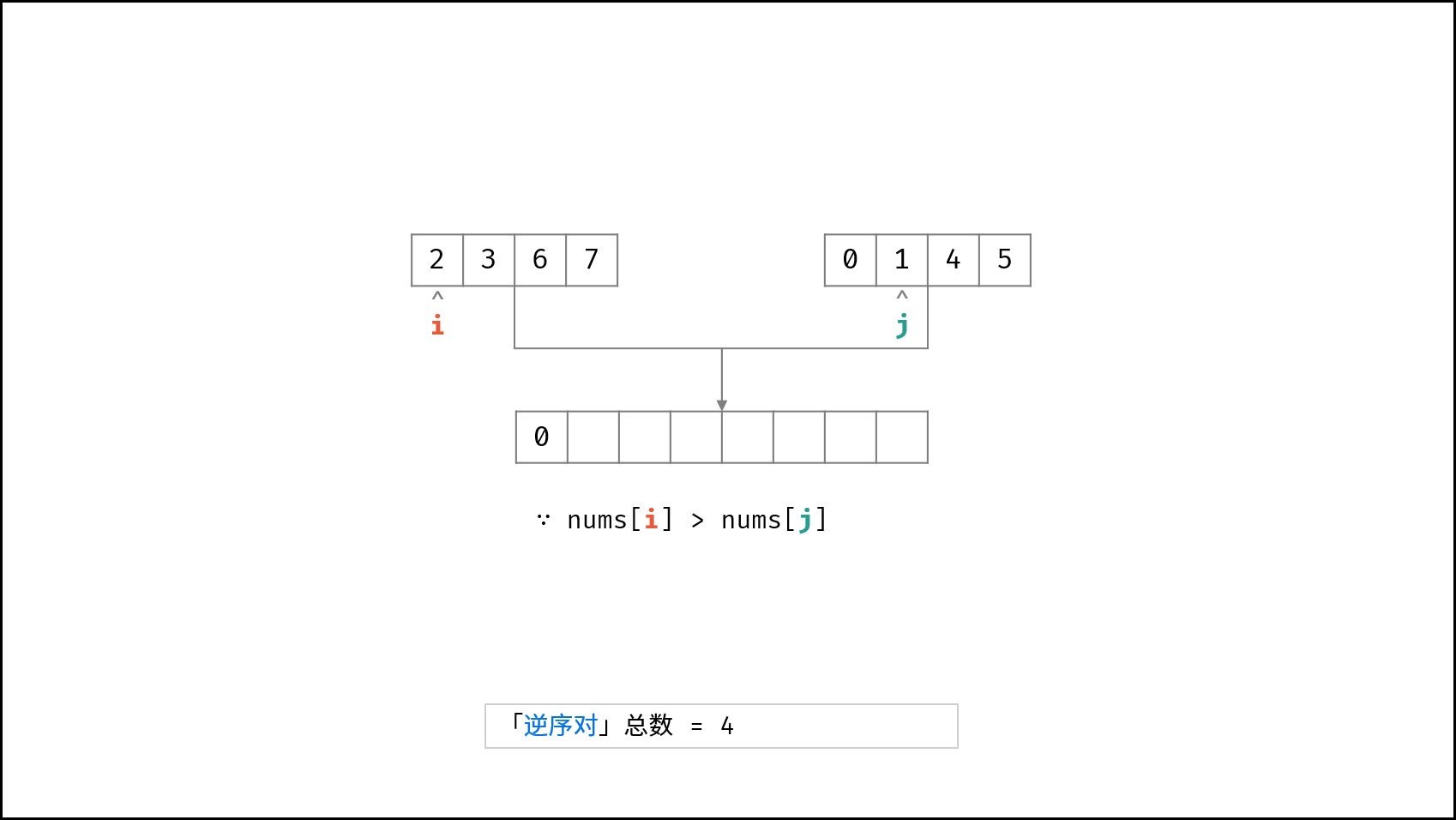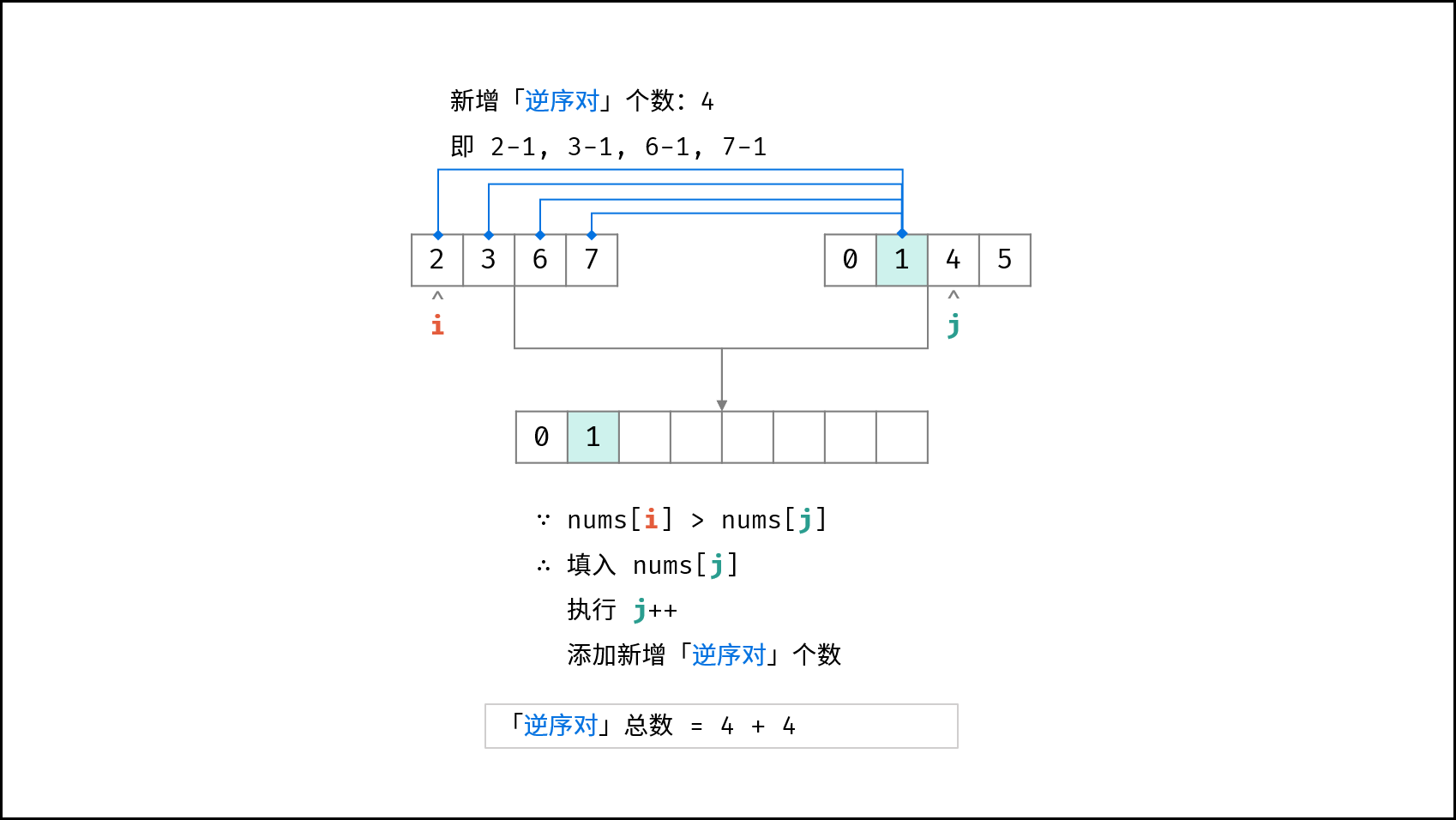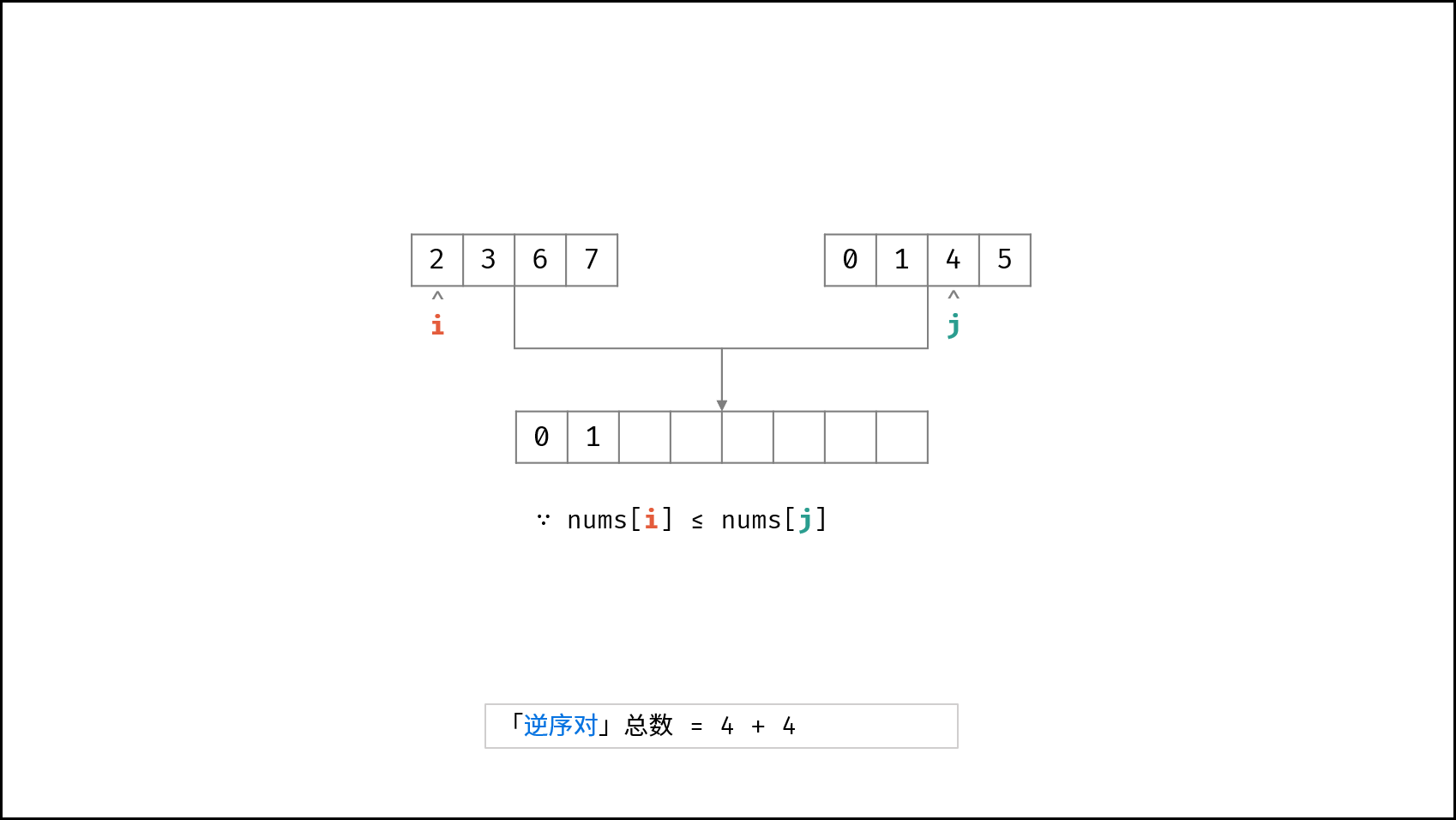<![Picture3.png](https://pic.leetcode-cn.com/1614274007-YkCQOz-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1614274007-pnkccs-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1614274007-nIGXwT-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1614274007-CiIXuc-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1614274007-oEmevZ-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1614274007-lQuslJ-Picture8.png),![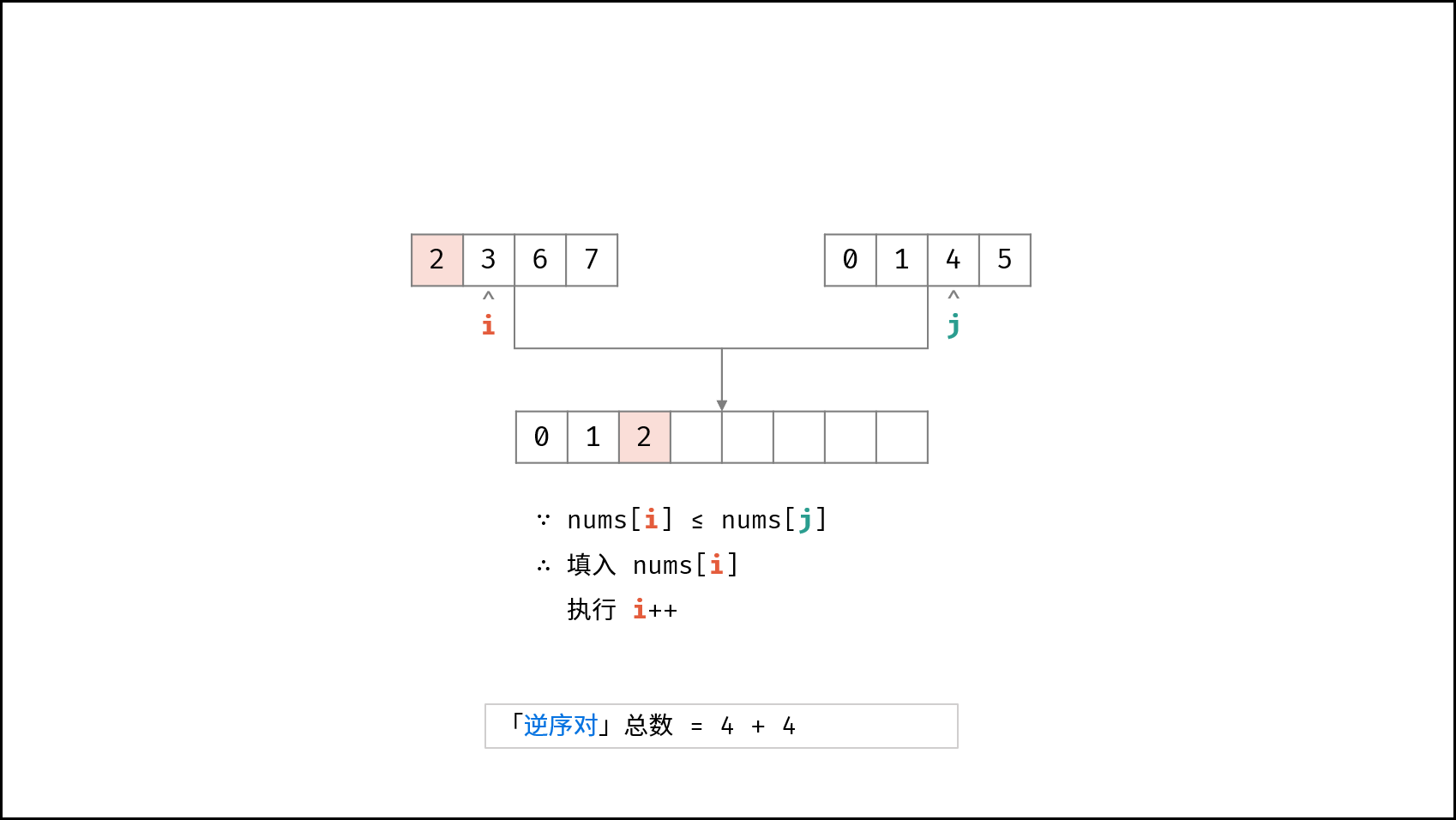Picture9.png](https://pic.leetcode-cn.com/1614274007-SaPJHu-Picture9.png),![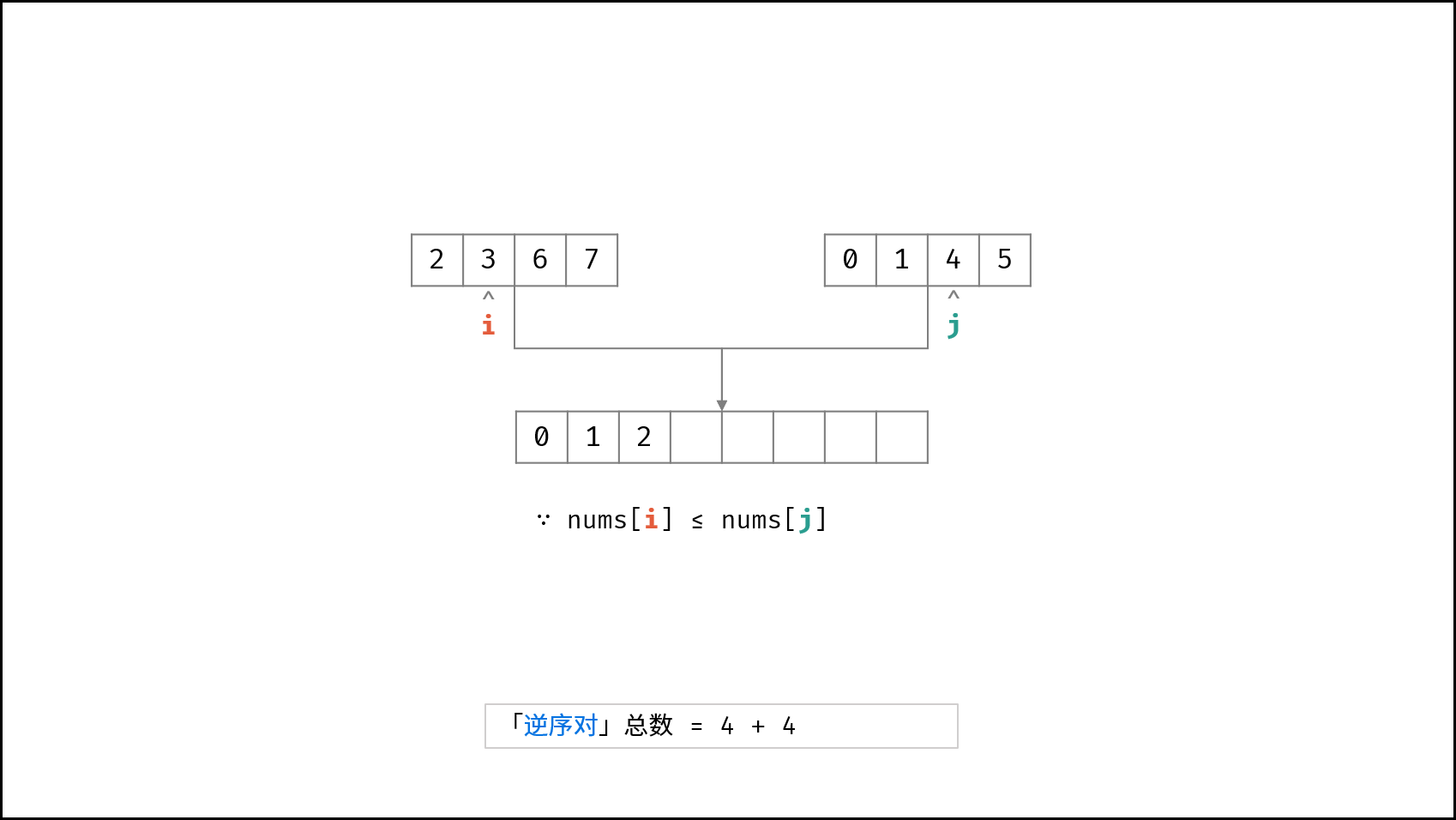Picture10.png](https://pic.leetcode-cn.com/1614274007-OiRvkv-Picture10.png),![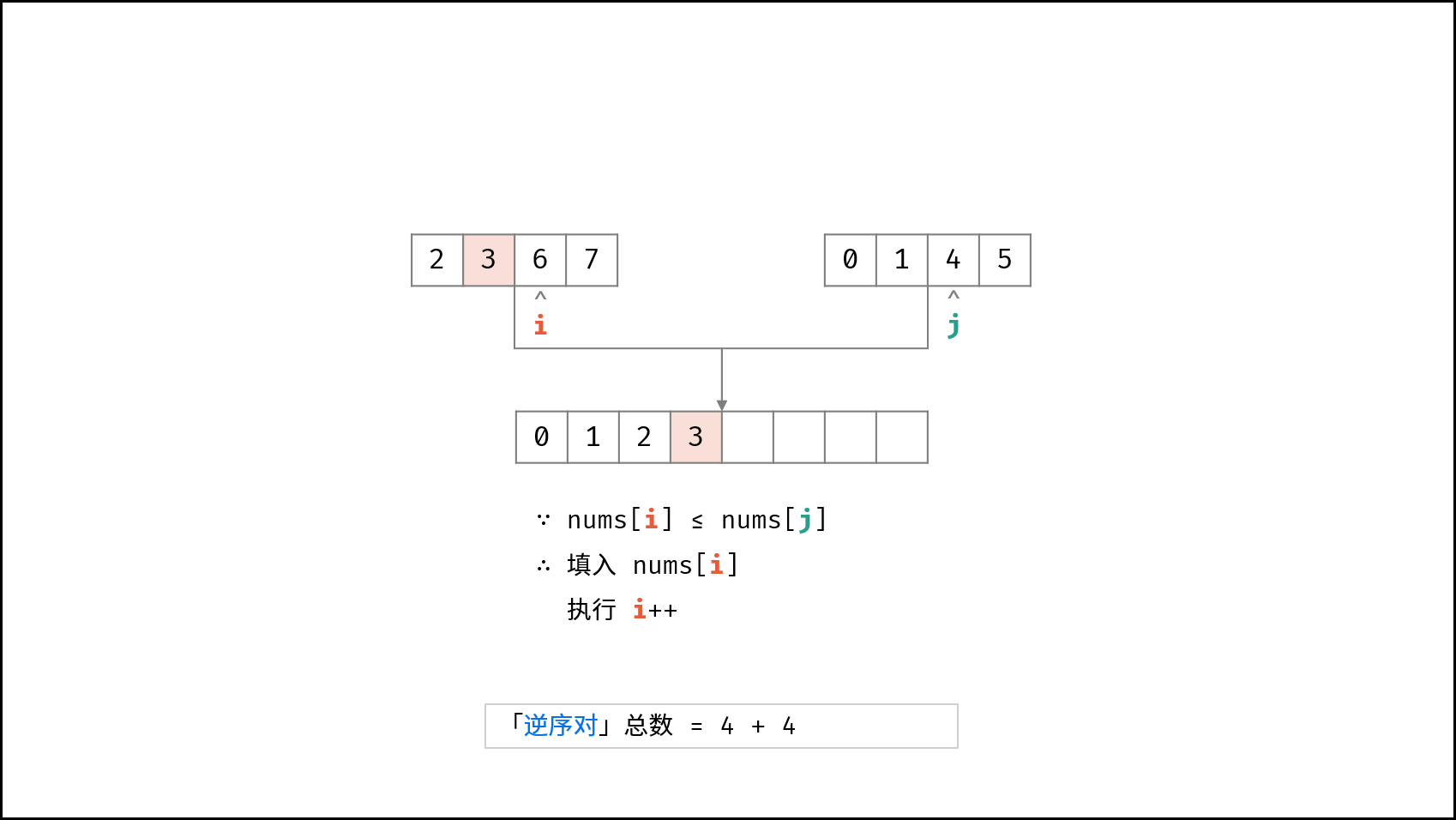Picture11.png](https://pic.leetcode-cn.com/1614274007-SaTkTO-Picture11.png),![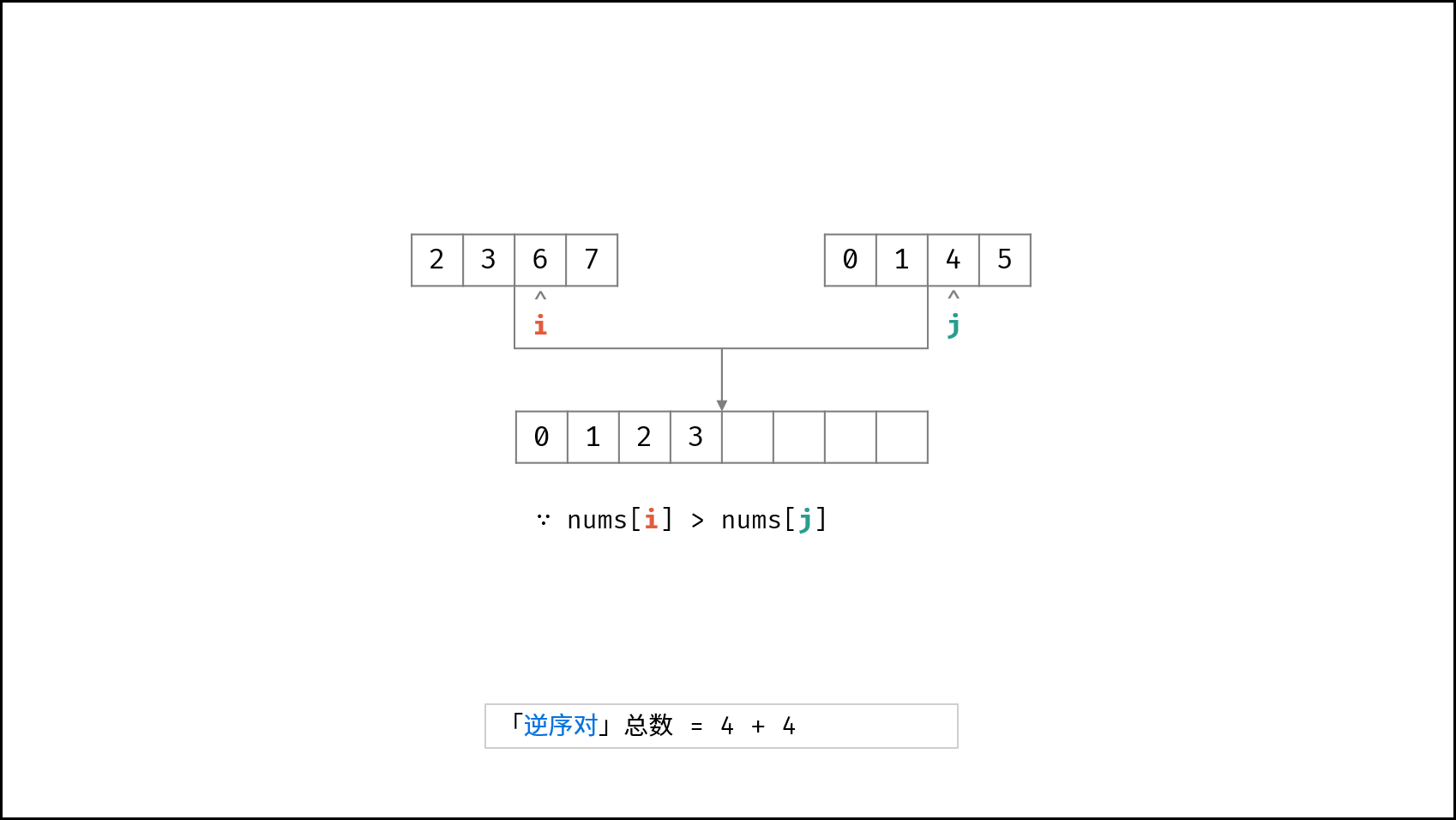Picture12.png](https://pic.leetcode-cn.com/1614274007-vRSdQI-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1614274007-ounrkz-Picture13.png),![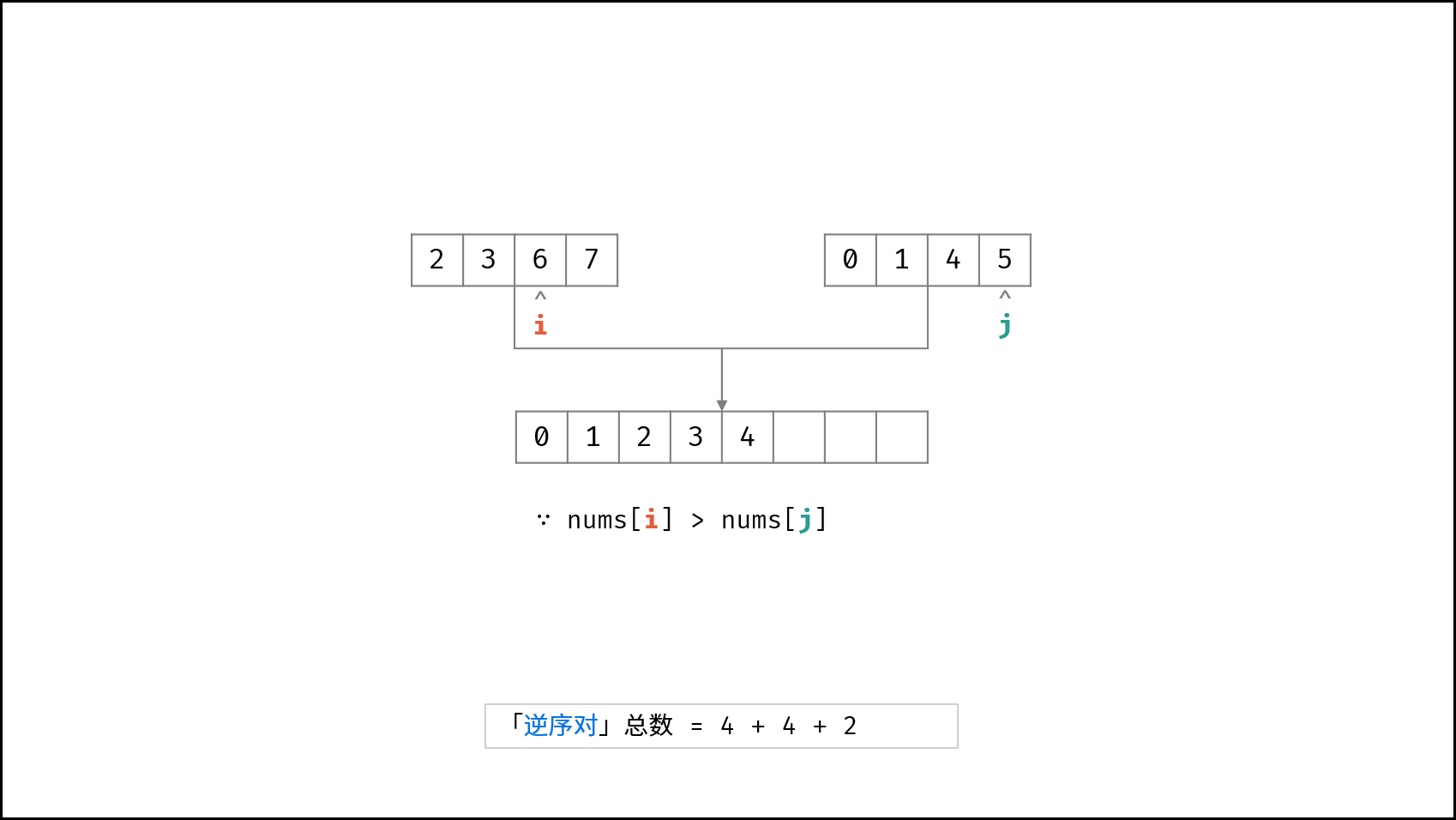Picture14.png](https://pic.leetcode-cn.com/1614274007-UZQbes-Picture14.png),![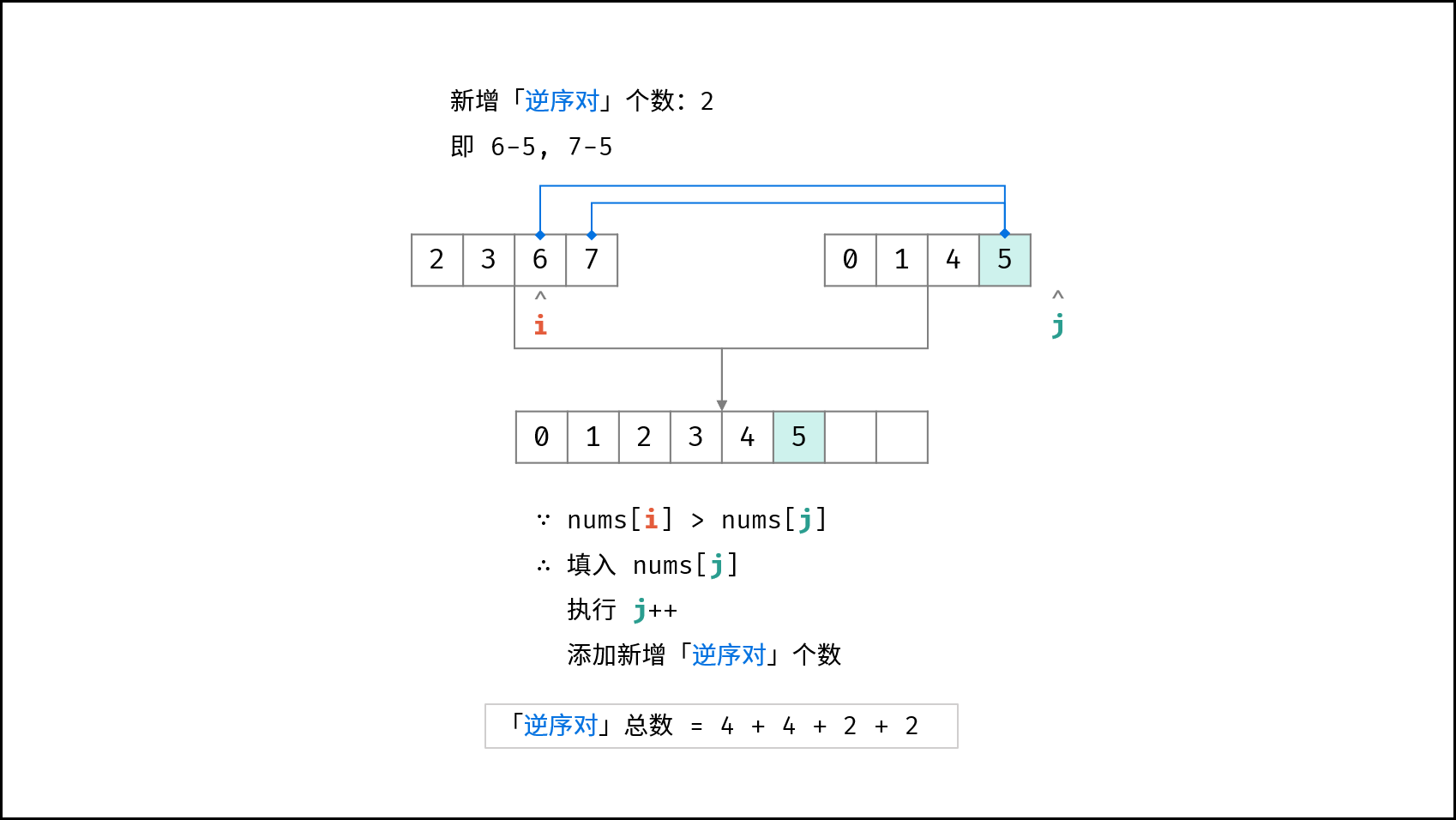Picture15.png](https://pic.leetcode-cn.com/1614274007-YlPdBQ-Picture15.png),![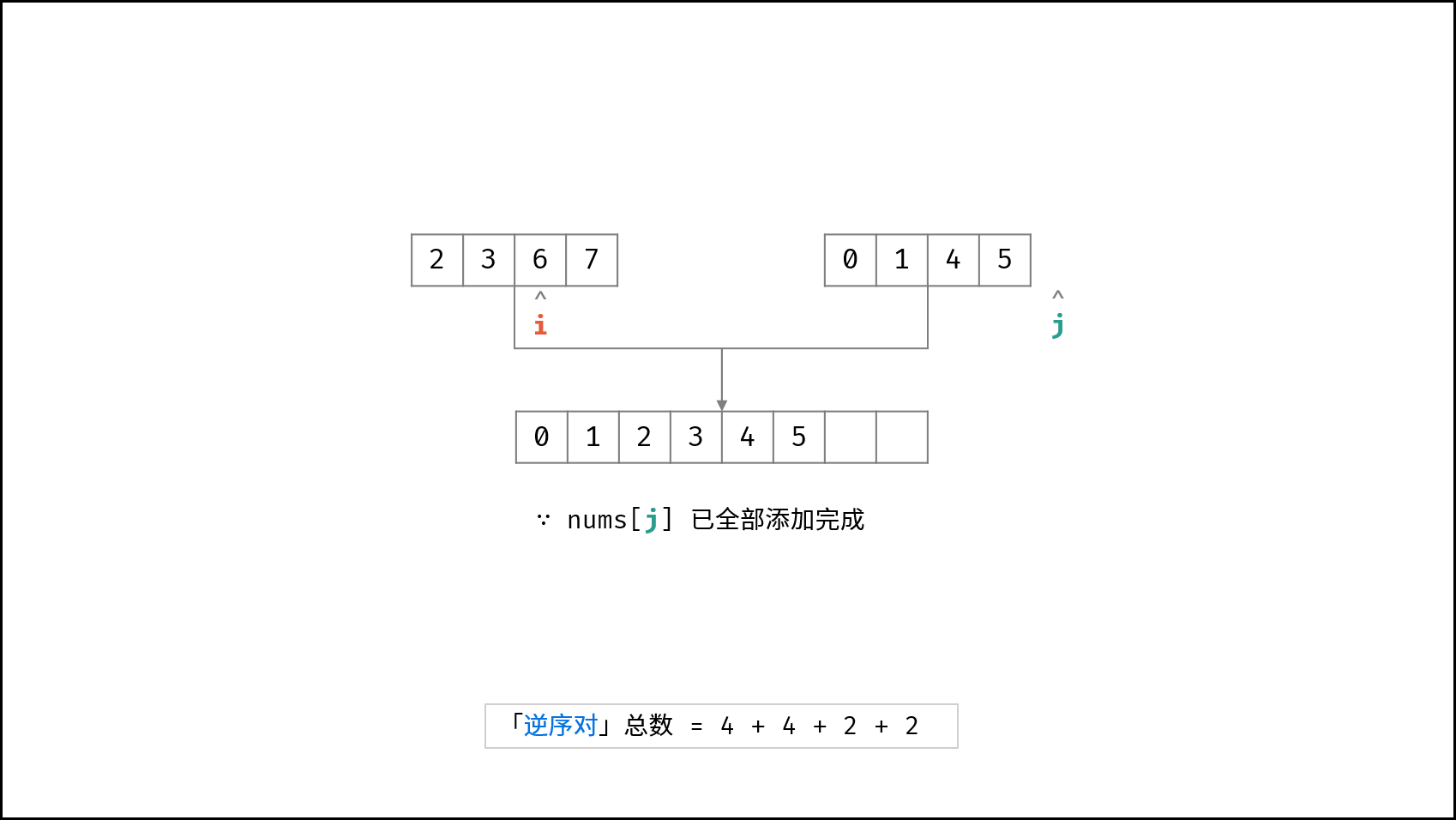Picture16.png](https://pic.leetcode-cn.com/1614274007-cCdAyU-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1614274007-TnzixB-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1614274007-rowvTK-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1614274007-srjZbc-Picture19.png)>
因此，考虑在归并排序的合并阶段统计「逆序对」数量，完成归并排序时，也随之完成所有逆序对的统计。
### 算法流程：
**`merge_sort()` 归并排序与逆序对统计：**
1. **终止条件：** 当 $l \geq r$ 时，代表子数组长度为 1 ，此时终止划分；
2. **递归划分：** 计算数组中点 $m$ ，递归划分左子数组 `merge_sort(l, m)` 和右子数组 `merge_sort(m + 1, r)` ；
3. **合并与逆序对统计：**
1. 暂存数组 $record$ 闭区间 $[l, r]$ 内的元素至辅助数组 $tmp$ ；
2. **循环合并：** 设置双指针 $i$ , $j$ 分别指向左 / 右子数组的首元素；
- **当 $i = m + 1$ 时：** 代表左子数组已合并完，因此添加右子数组当前元素 $tmp[j]$ ，并执行 $j = j + 1$ ；
- **否则，当 $j = r + 1$ 时：** 代表右子数组已合并完，因此添加左子数组当前元素 $tmp[i]$ ，并执行 $i = i + 1$ ；
- **否则，当 $tmp[i] \leq tmp[j]$ 时：** 添加左子数组当前元素 $tmp[i]$ ，并执行 $i = i + 1$；
- **否则（即 $tmp[i] > tmp[j]$）时：** 添加右子数组当前元素 $tmp[j]$ ，并执行 $j = j + 1$ ；此时构成 $m - i + 1$ 个「逆序对」，统计添加至 $res$ ；
4. **返回值：** 返回直至目前的逆序对总数 $res$ ；
**`reversePairs()` 主函数：**
1. **初始化：** 辅助数组 $tmp$ ，用于合并阶段暂存元素；
2. **返回值：** 执行归并排序 `merge_sort()` ，并返回逆序对总数即可；
> 如下图所示，为数组 $[7, 3, 2, 6, 0, 1, 5, 4]$ 的归并排序与逆序对统计过程。
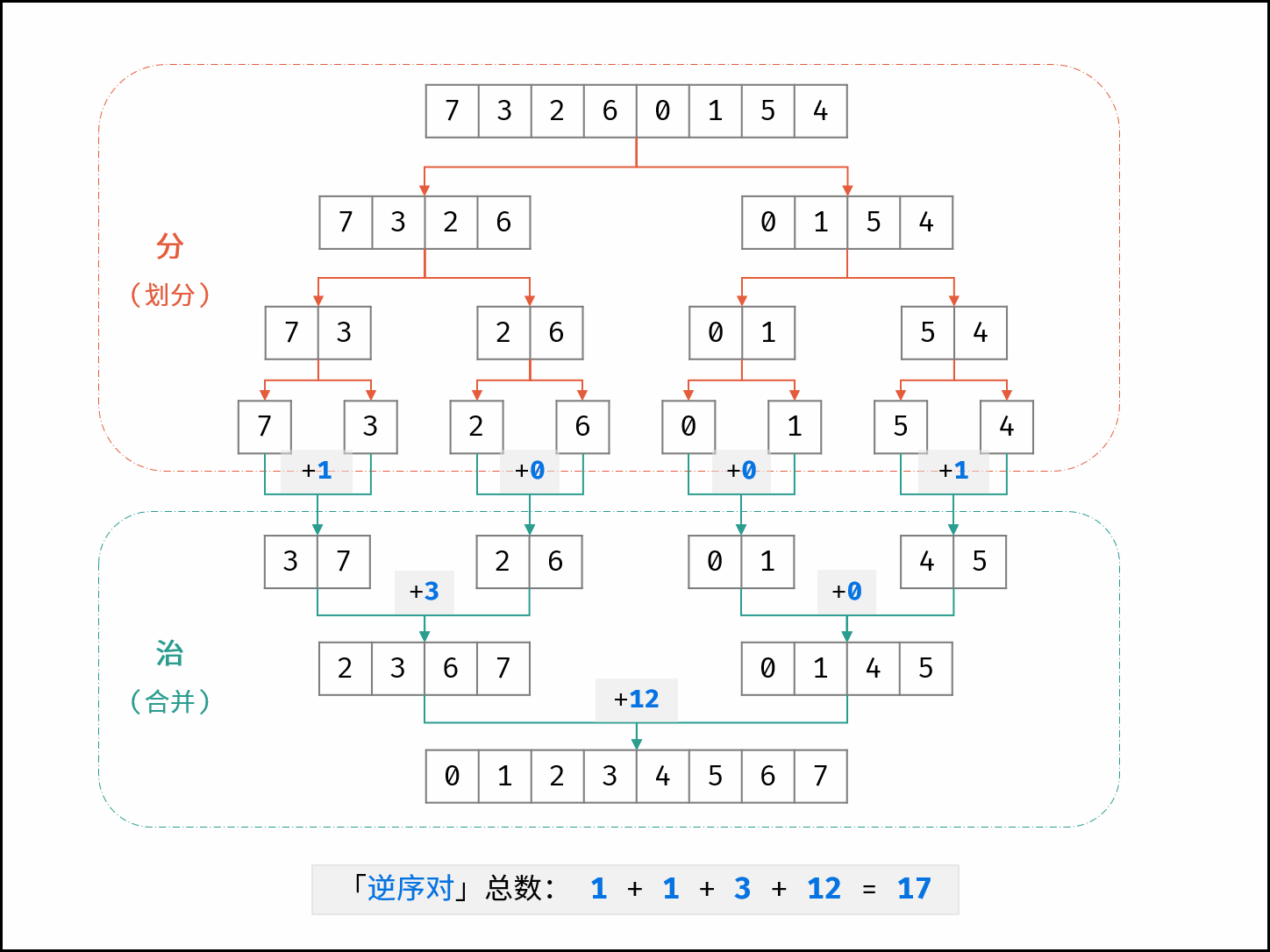![Picture2.png](https://pic.leetcode-cn.com/1614274007-rtFHbG-Picture2.png){:align=center width=500}
## 代码：
为简化代码，可将“当 $j = r + 1$ 时”与“当 $tmp[i] \leq tmp[j]$ 时”两判断项合并。
```Python []
class Solution:
def reversePairs(self, record: List[int]) -> int:
def merge_sort(l, r):
# 终止条件
if l >= r: return 0
# 递归划分
m = (l + r) // 2
res = merge_sort(l, m) + merge_sort(m + 1, r)
# 合并阶段
i, j = l, m + 1
tmp[l:r + 1] = record[l:r + 1]
for k in range(l, r + 1):
if i == m + 1:
record[k] = tmp[j]
j += 1
elif j == r + 1 or tmp[i] <= tmp[j]:
record[k] = tmp[i]
i += 1
else:
record[k] = tmp[j]
j += 1
res += m - i + 1 # 统计逆序对
return res
tmp = [0] * len(record)
return merge_sort(0, len(record) - 1)
```
```Java []
class Solution {
int[] record, tmp;
public int reversePairs(int[] record) {
this.record = record;
tmp = new int[record.length];
return mergeSort(0, record.length - 1);
}
private int mergeSort(int l, int r) {
// 终止条件
if (l >= r) return 0;
// 递归划分
int m = (l + r) / 2;
int res = mergeSort(l, m) + mergeSort(m + 1, r);
// 合并阶段
int i = l, j = m + 1;
for (int k = l; k <= r; k++)
tmp[k] = record[k];
for (int k = l; k <= r; k++) {
if (i == m + 1)
record[k] = tmp[j++];
else if (j == r + 1 || tmp[i] <= tmp[j])
record[k] = tmp[i++];
else {
record[k] = tmp[j++];
res += m - i + 1; // 统计逆序对
}
}
return res;
}
}
```
```C++ []
class Solution {
public:
int reversePairs(vector<int>& record) {
vector<int> tmp(record.size());
return mergeSort(0, record.size() - 1, record, tmp);
}
private:
int mergeSort(int l, int r, vector<int>& record, vector<int>& tmp) {
// 终止条件
if (l >= r) return 0;
// 递归划分
int m = (l + r) / 2;
int res = mergeSort(l, m, record, tmp) + mergeSort(m + 1, r, record, tmp);
// 合并阶段
int i = l, j = m + 1;
for (int k = l; k <= r; k++)
tmp[k] = record[k];
for (int k = l; k <= r; k++) {
if (i == m + 1)
record[k] = tmp[j++];
else if (j == r + 1 || tmp[i] <= tmp[j])
record[k] = tmp[i++];
else {
record[k] = tmp[j++];
res += m - i + 1; // 统计逆序对
}
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N \log N)$ ：** 其中 $N$ 为数组长度；归并排序使用 $O(N \log N)$ 时间；
- **空间复杂度 $O(N)$ ：** 辅助数组 $tmp$ 占用 $O(N)$ 大小的额外空间；

81
leetbook_ioa/docs/LCR 171. 训练计划 V.md Executable file
View File

@@ -0,0 +1,81 @@
## 解题思路：
设第一个公共节点为 `node` ，链表 `headA` 的节点数量为 $a$ ，链表 `headB` 的节点数量为 $b$ ，两链表的公共尾部的节点数量为 $c$ ，则有：
- 头节点 `headA` 到 `node` 前，共有 $a - c$ 个节点；
- 头节点 `headB` 到 `node` 前，共有 $b - c$ 个节点；
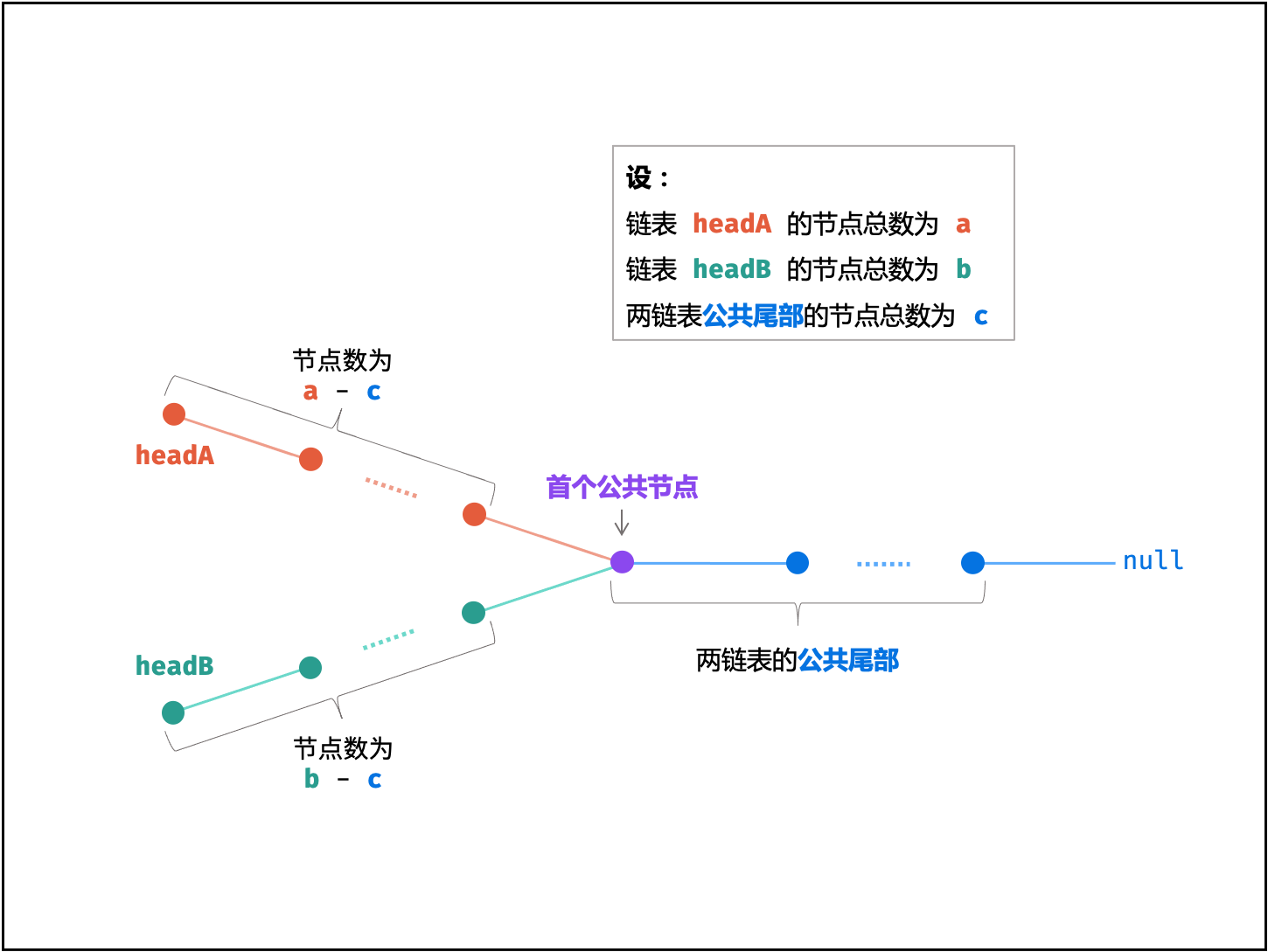![Picture1.png](https://pic.leetcode-cn.com/1615224578-EBRtwv-Picture1.png){:align=center width=500}
考虑构建两个节点指针 `A​` , `B` 分别指向两链表头节点 `headA` , `headB` ，做如下操作：
- 指针 `A` 先遍历完链表 `headA` ，再开始遍历链表 `headB` ，当走到 `node` 时，共走步数为：
$$
a + (b - c)
$$
- 指针 `B` 先遍历完链表 `headB` ，再开始遍历链表 `headA` ，当走到 `node` 时，共走步数为：
$$
b + (a - c)
$$
如下式所示，此时指针 `A` , `B` 重合，并有两种情况：
$$
a + (b - c) = b + (a - c)
$$
1. 若两链表 **有** 公共尾部 (即 $c > 0$ ) ：指针 `A` , `B` 同时指向「第一个公共节点」`node` 。
2. 若两链表 **无** 公共尾部 (即 $c = 0$ ) ：指针 `A` , `B` 同时指向 $\text{null}$ 。
因此返回 `A` 即可。
> 下图展示了 $a = 5$ , $b = 3$ , $c = 2$ 示例的算法执行过程。
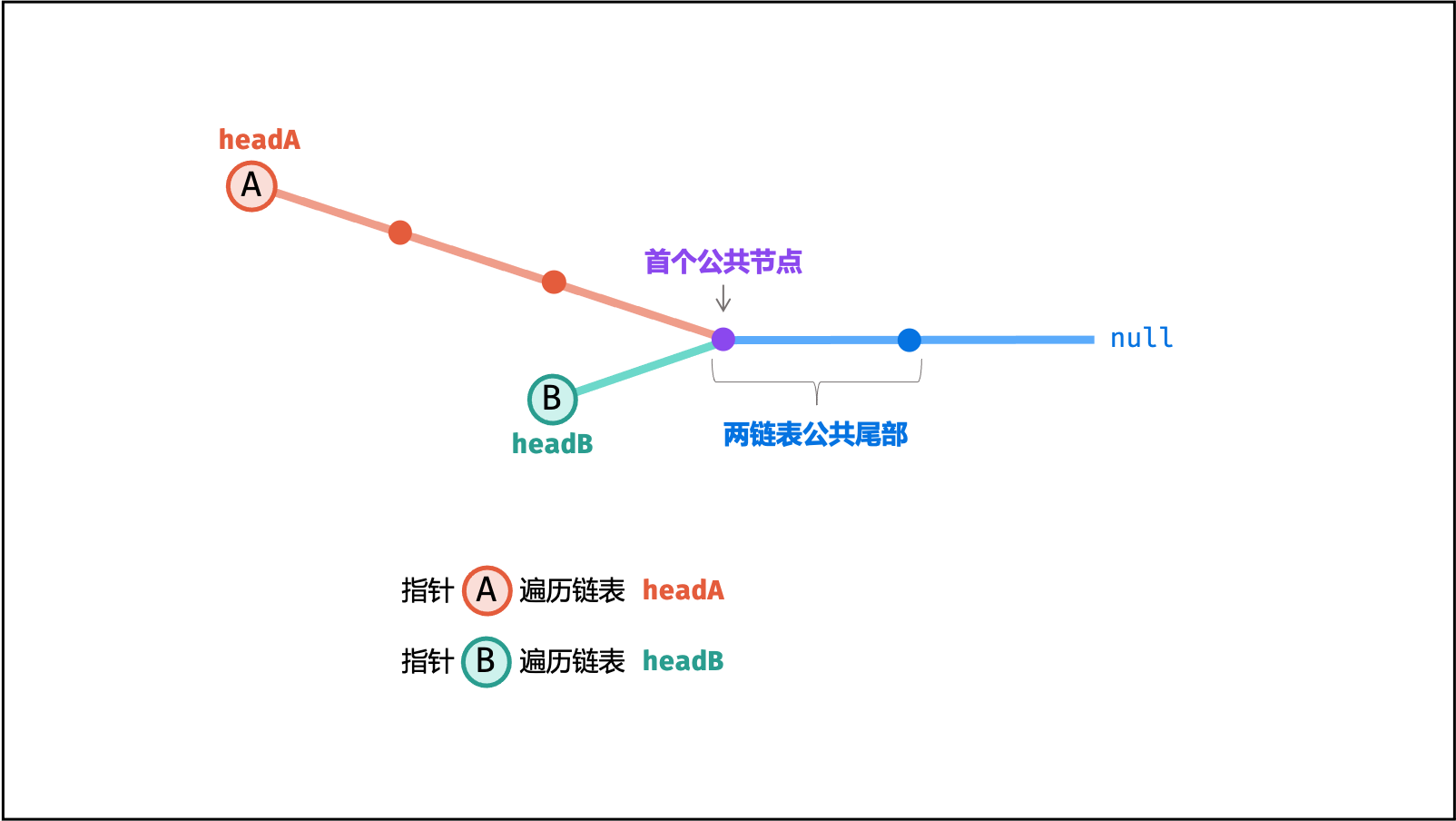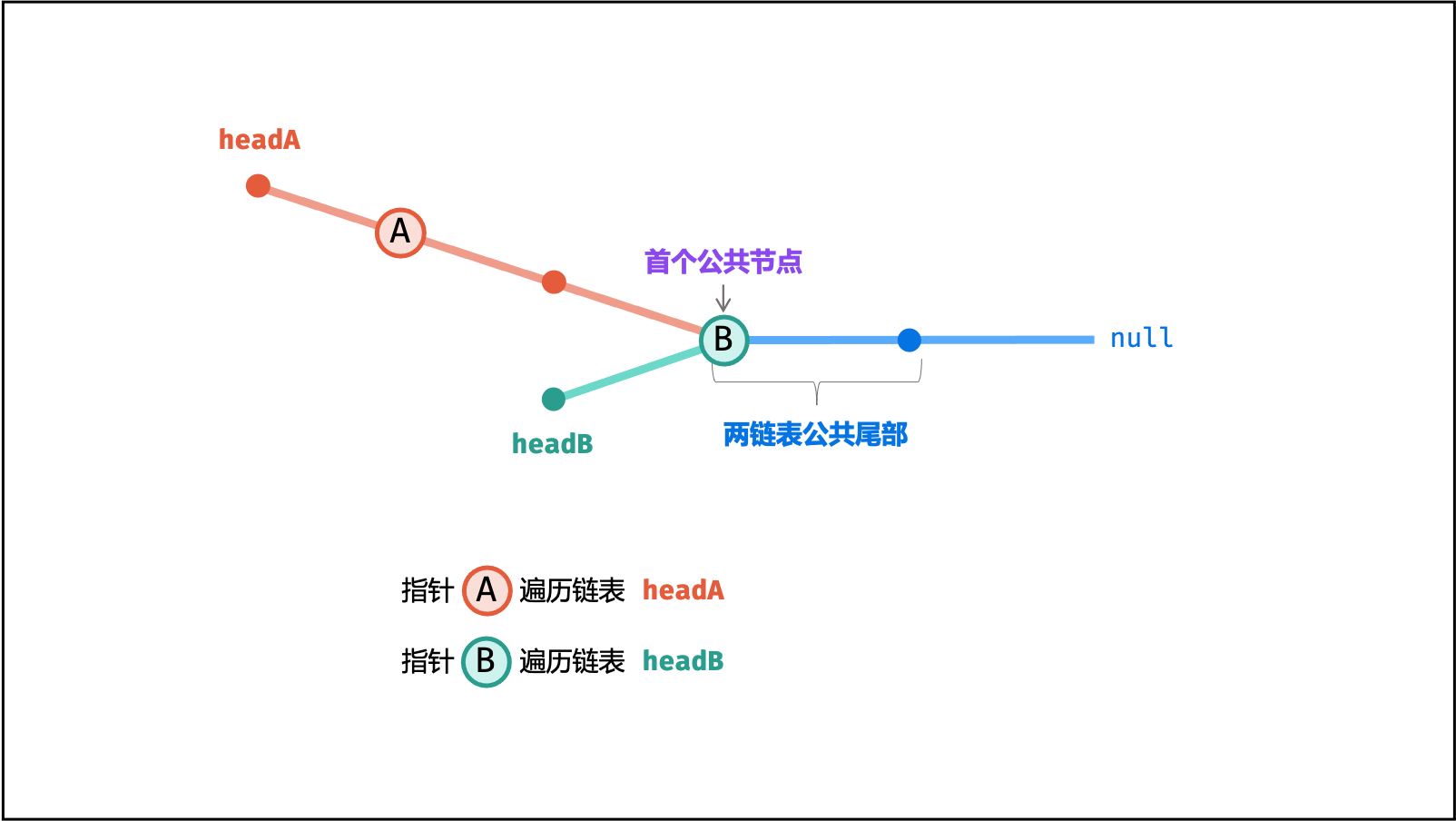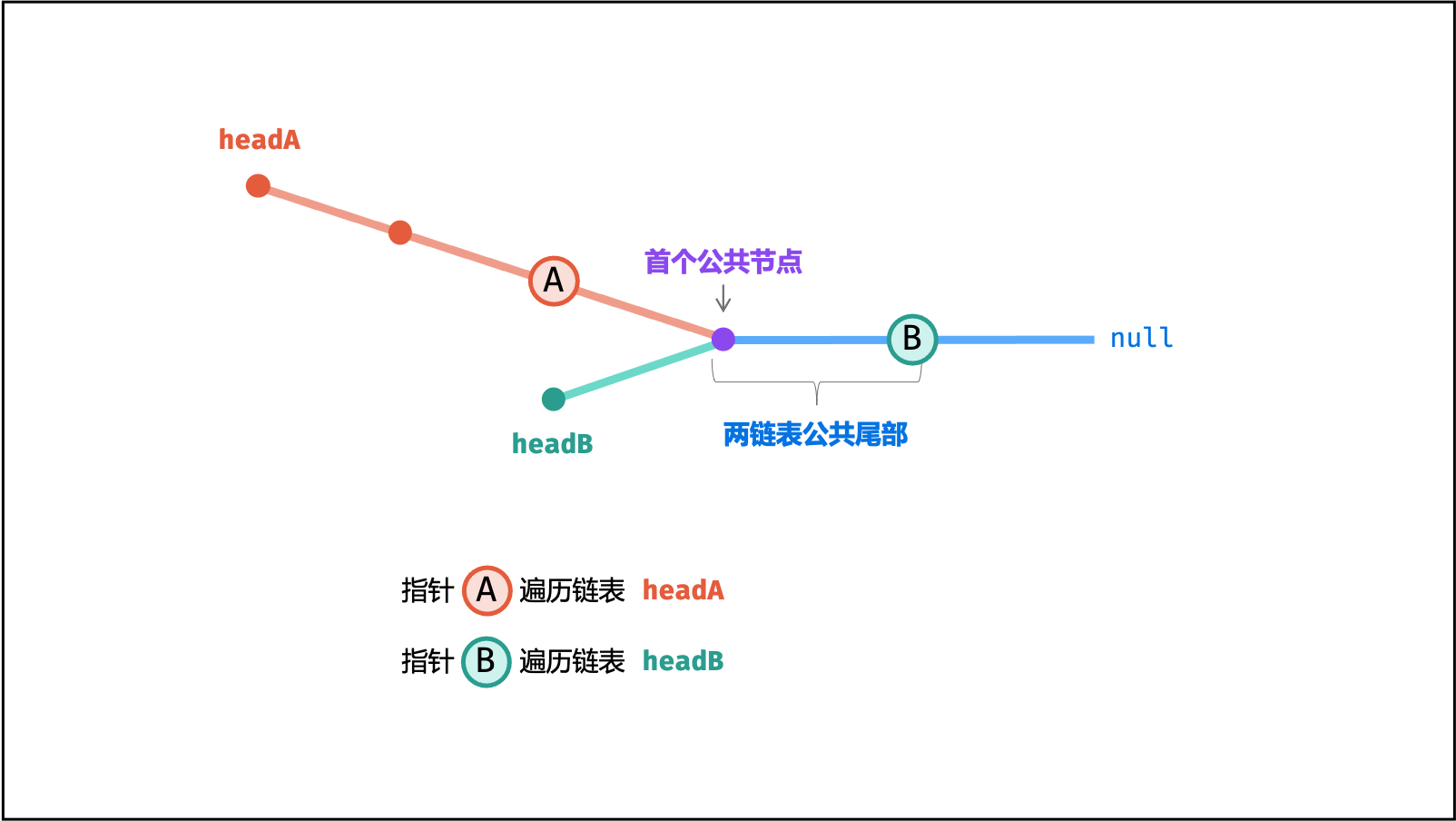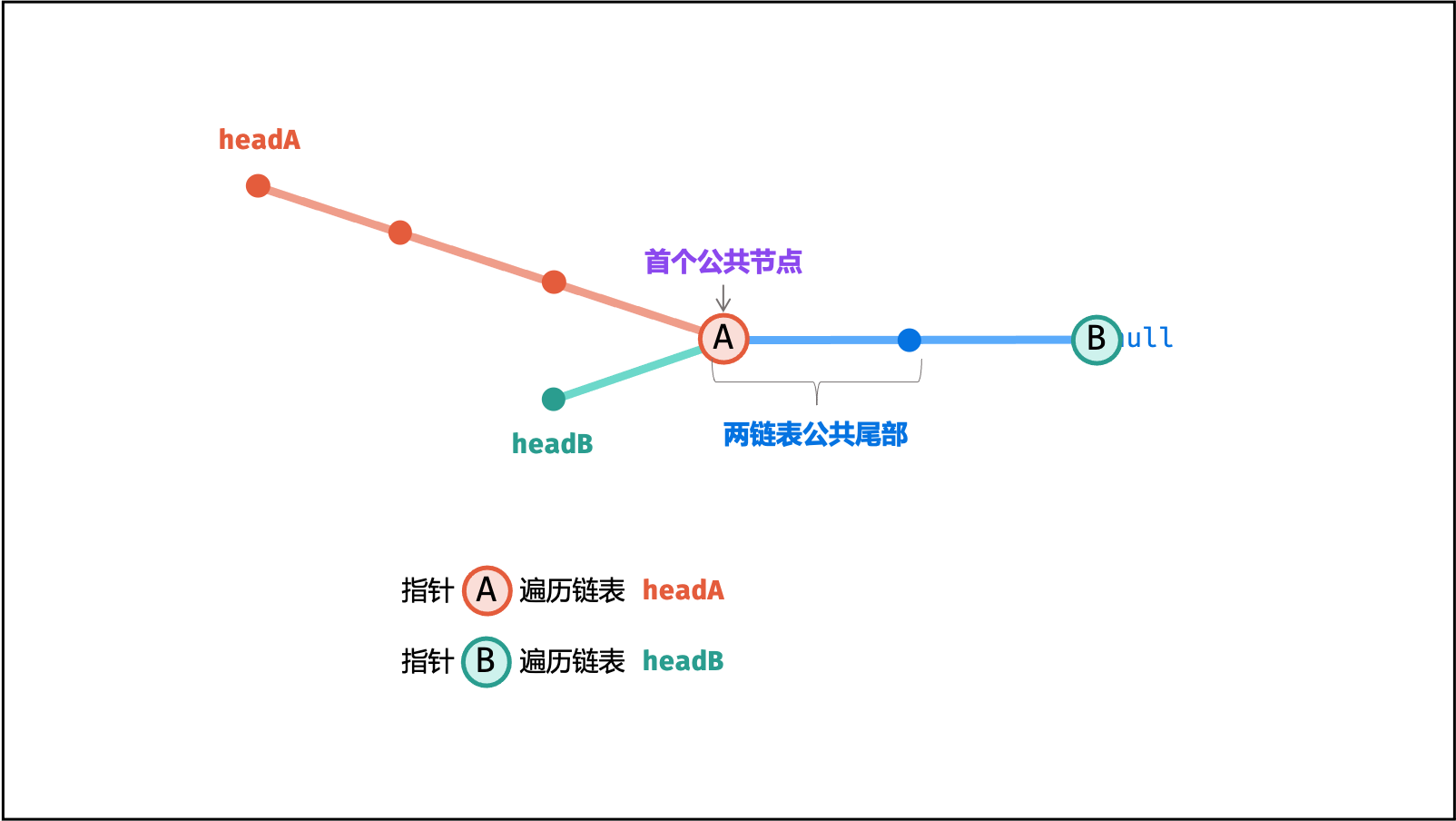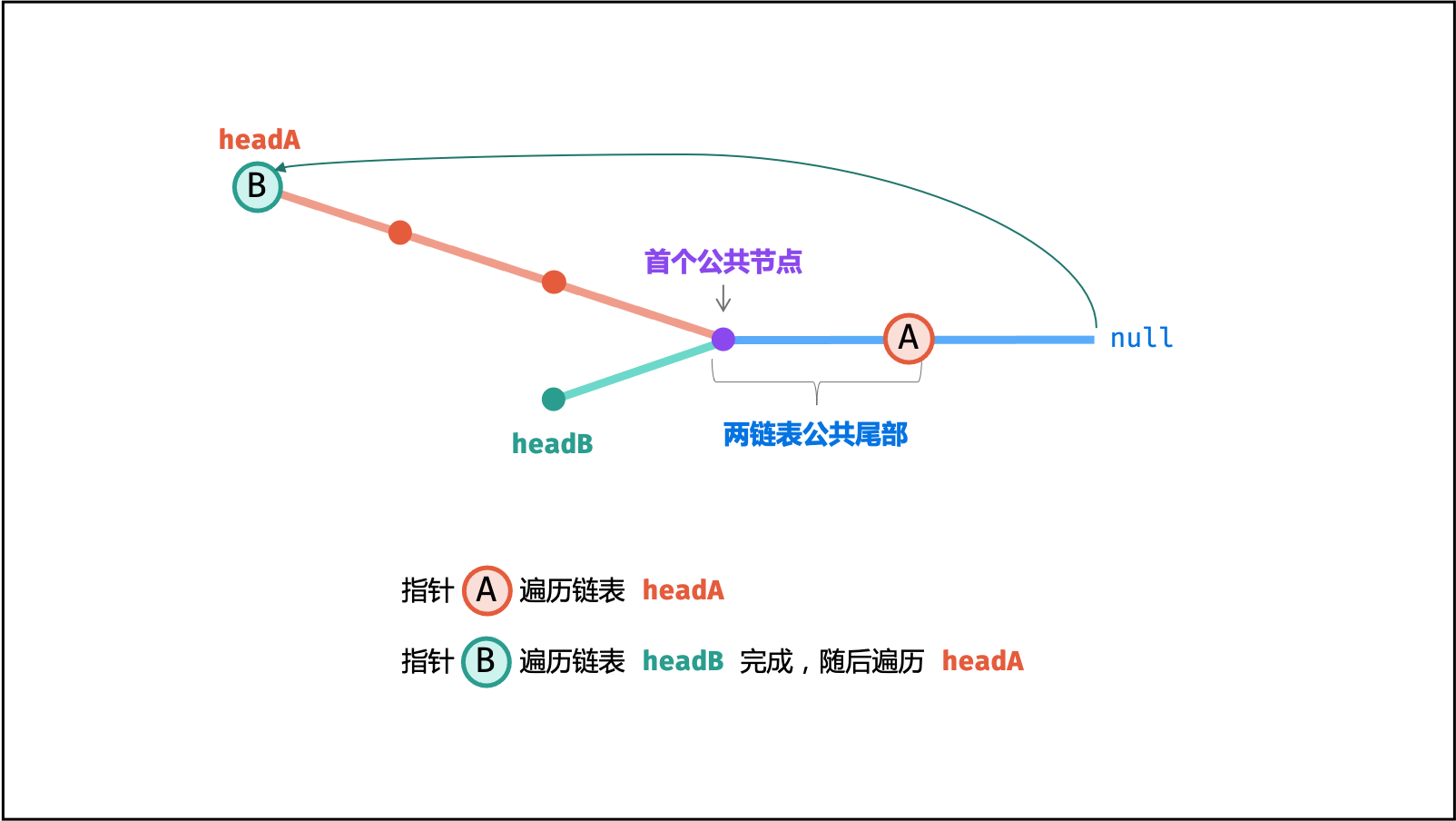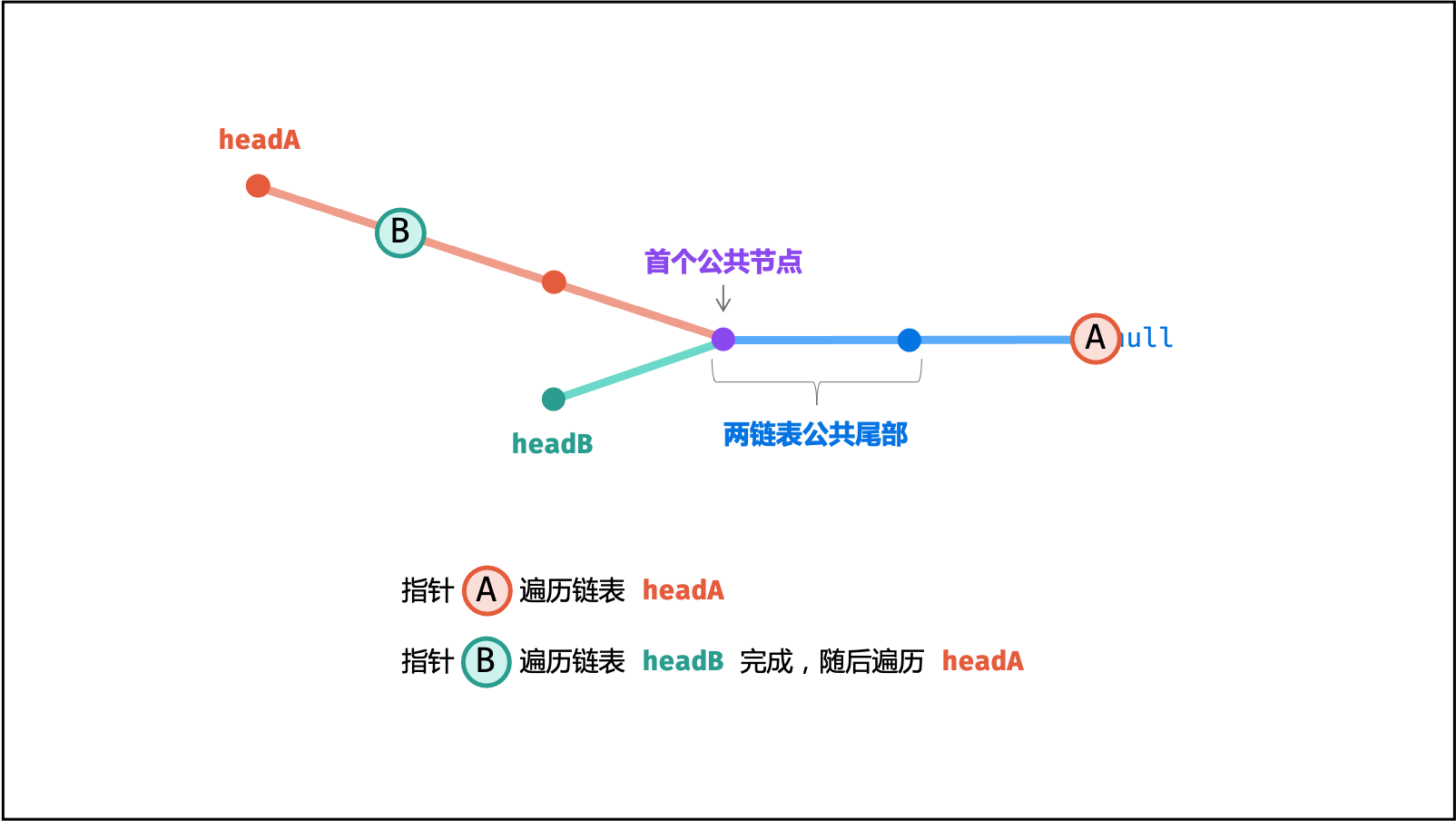<![Picture2.png](https://pic.leetcode-cn.com/1615224578-lFxRVR-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1615224578-atzfoi-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1615224578-QvNyxe-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1615224578-zPMkyB-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1615224578-MRfzKN-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1615224578-UIHyvx-Picture7.png),![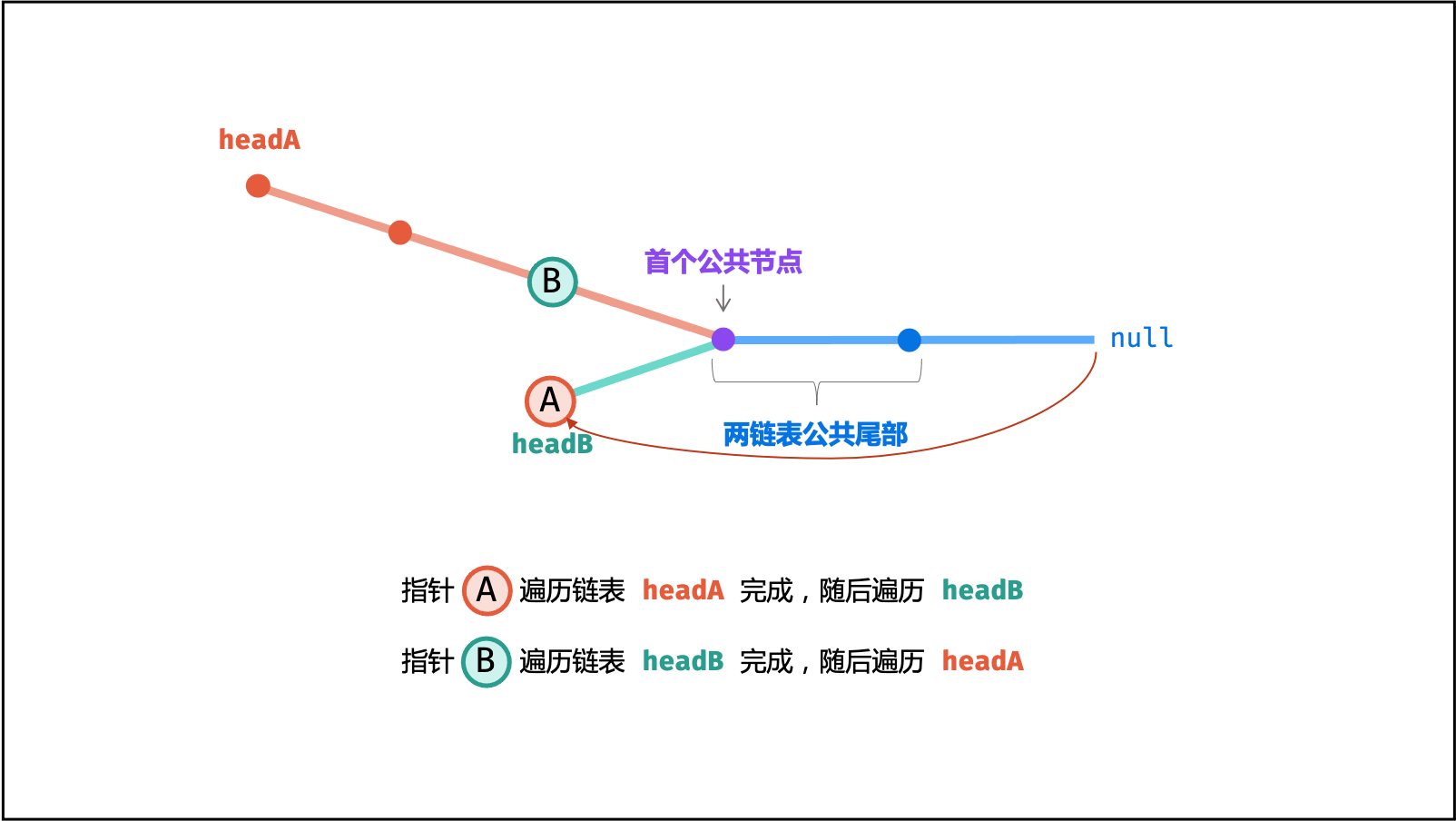Picture8.png](https://pic.leetcode-cn.com/1615224578-fyOdzW-Picture8.png),![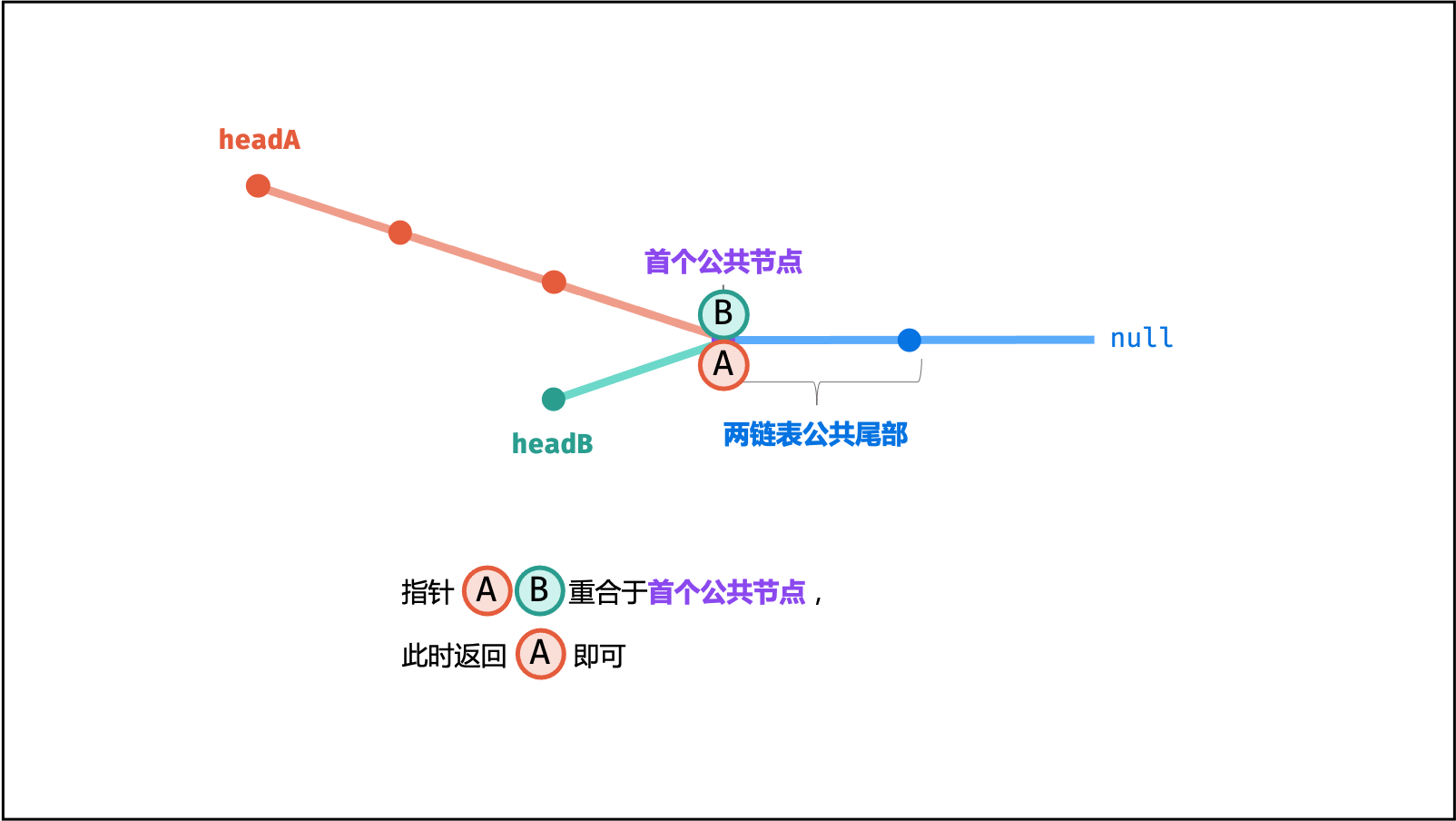Picture9.png](https://pic.leetcode-cn.com/1615224578-LcVJxI-Picture9.png)>
## 代码：
```Python []
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
A, B = headA, headB
while A != B:
A = A.next if A else headB
B = B.next if B else headA
return A
```
```Java []
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode A = headA, B = headB;
while (A != B) {
A = A != null ? A.next : headB;
B = B != null ? B.next : headA;
}
return A;
}
}
```
```C++ []
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *A = headA, *B = headB;
while (A != B) {
A = A != nullptr ? A->next : headB;
B = B != nullptr ? B->next : headA;
}
return A;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(a + b)$ ：** 最差情况下（即 $|a - b| = 1$ , $c = 0$ ），此时需遍历 $a + b$ 个节点。
- **空间复杂度 $O(1)$ ：** 节点指针 `A` , `B` 使用常数大小的额外空间。

172
leetbook_ioa/docs/LCR 172. 统计目标成绩的出现次数.md Executable file
View File

@@ -0,0 +1,172 @@
## 解题思路：
> 排序数组中的搜索问题，首先想到 **二分法** 解决。
排序数组 $scores$ 中的所有数字 $target$ 形成一个窗口，记窗口的 **左 / 右边界** 索引分别为 $left$ 和 $right$ ，分别对应窗口左边 / 右边的首个元素。
本题要求统计数字 $target$ 的出现次数，可转化为：使用二分法分别找到 **左边界 $left$** 和 **右边界 $right$** ，易得数字 $target$ 的数量为 $right - left - 1$ 。
> 下图中的 `nums` 对应本题的 `scores` 。
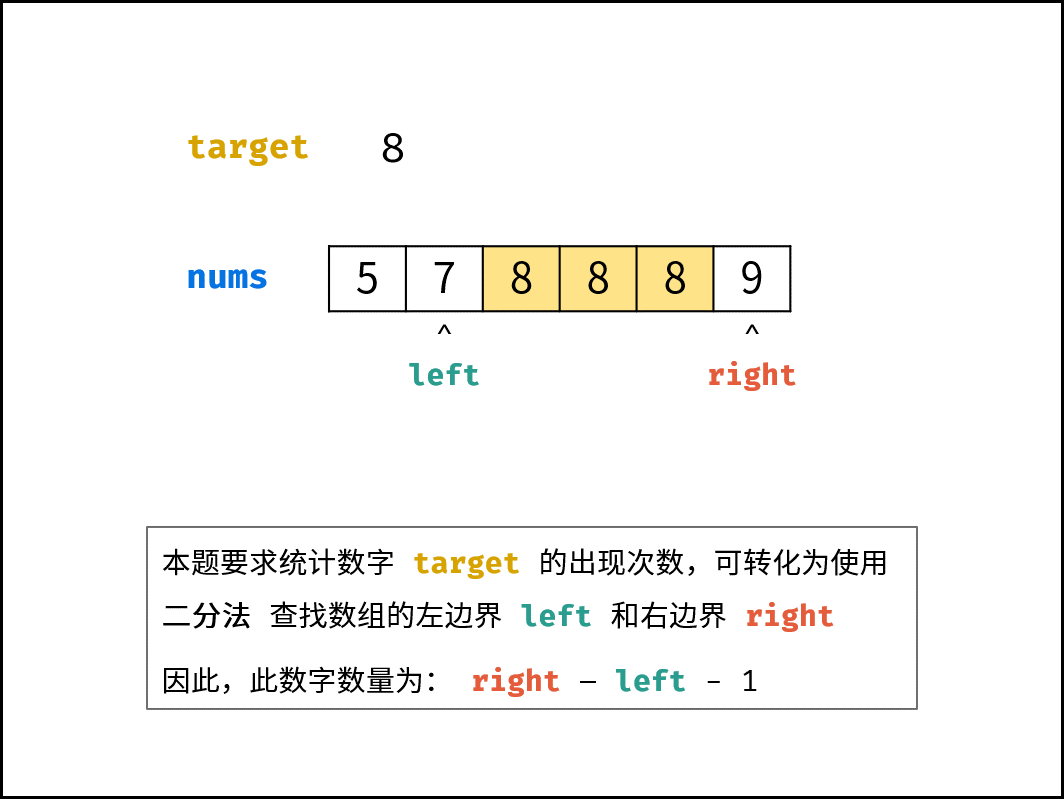![Picture1.png](https://pic.leetcode-cn.com/1600793982-pWqZGf-Picture1.png){:align=center width=500}
### 算法解析：
1. **初始化：** 左边界 $i = 0$ ，右边界 $j = len(scores) - 1$ 。
2. **循环二分：** 当闭区间 $[i, j]$ 无元素时跳出；
1. 计算中点 $m = (i + j) / 2$ （向下取整）；
2. 若 $scores[m] < target$ ，则 $target$ 在闭区间 $[m + 1, j]$ 中，因此执行 $i = m + 1$；
3. 若 $scores[m] > target$ ，则 $target$ 在闭区间 $[i, m - 1]$ 中，因此执行 $j = m - 1$；
4. 若 $scores[m] = target$ ，则右边界 $right$ 在闭区间 $[m+1, j]$ 中；左边界 $left$ 在闭区间 $[i, m-1]$ 中。因此分为以下两种情况：
1. 若查找 **右边界 $right$** ，则执行 $i = m + 1$ ；（跳出时 $i$ 指向右边界）
2. 若查找 **左边界 $left$** ，则执行 $j = m - 1$ ；（跳出时 $j$ 指向左边界）
3. **返回值：** 应用两次二分，分别查找 $right$ 和 $left$ ，最终返回 $right - left - 1$ 即可。
### 效率优化：
> 以下优化基于：查找完右边界 $right = i$ 后，则 $scores[j]$ 指向最右边的 $target$ （若存在）。
1. 查找完右边界后，可用 $scores[j] = target$ 判断数组中是否包含 $target$ ，若不包含则直接提前返回 $0$ ，无需后续查找左边界。
2. 查找完右边界后，左边界 $left$ 一定在闭区间 $[0, j]$ 中，因此直接从此区间开始二分查找即可。
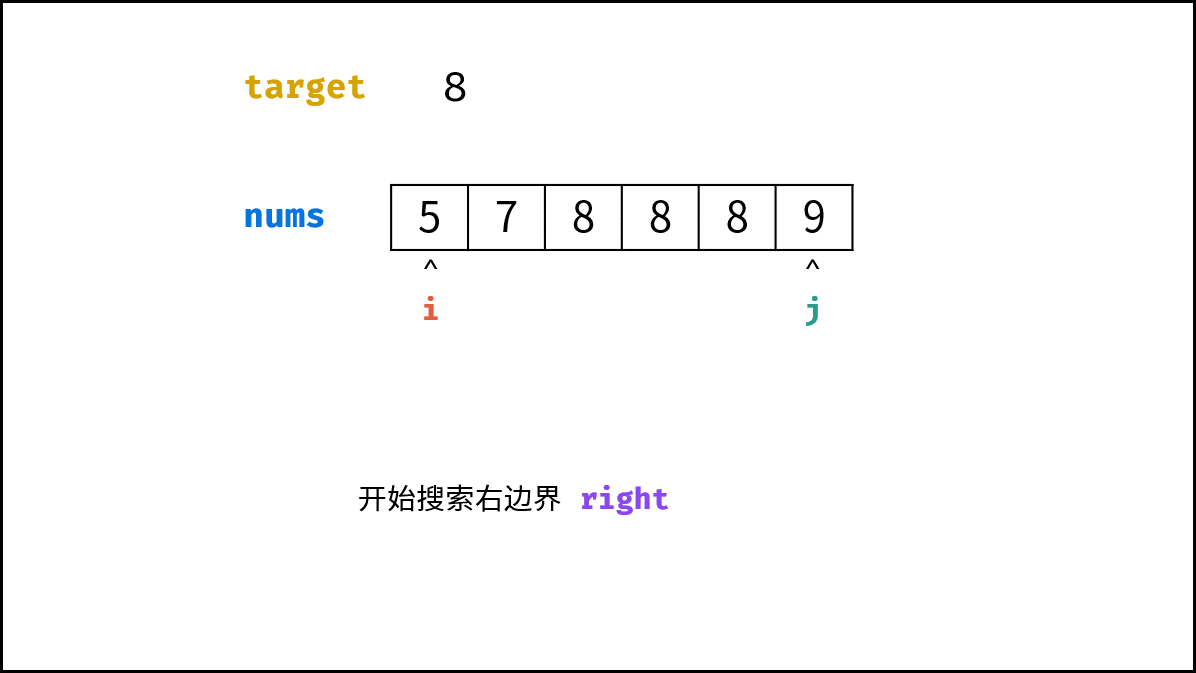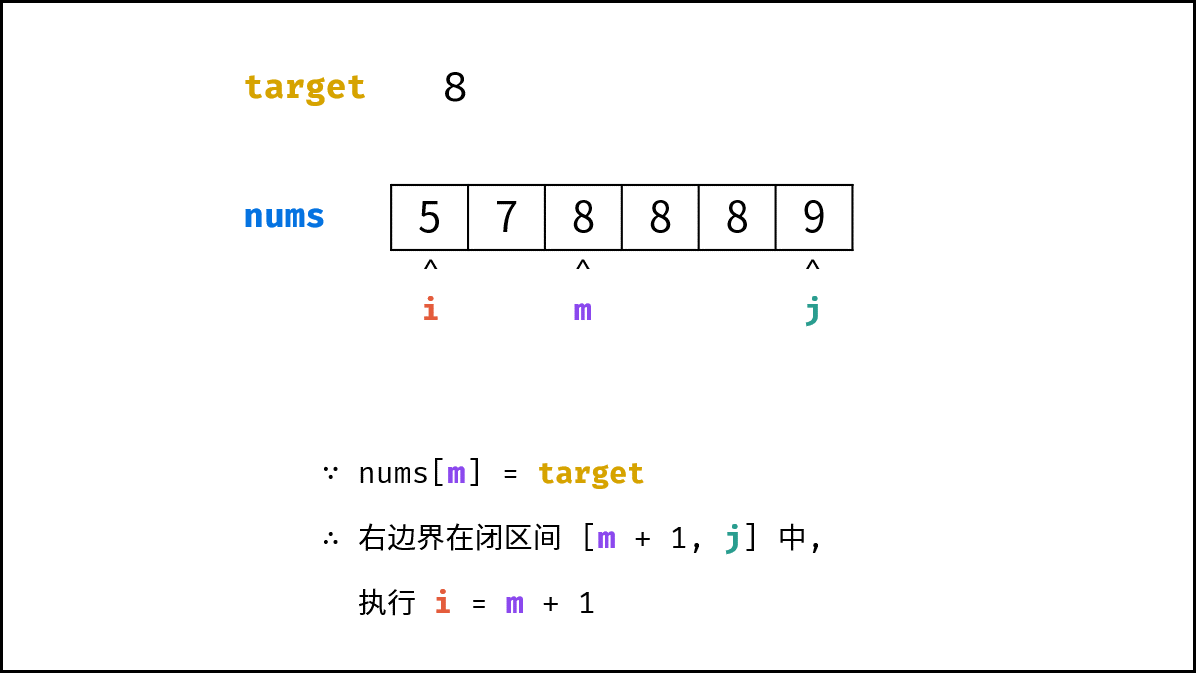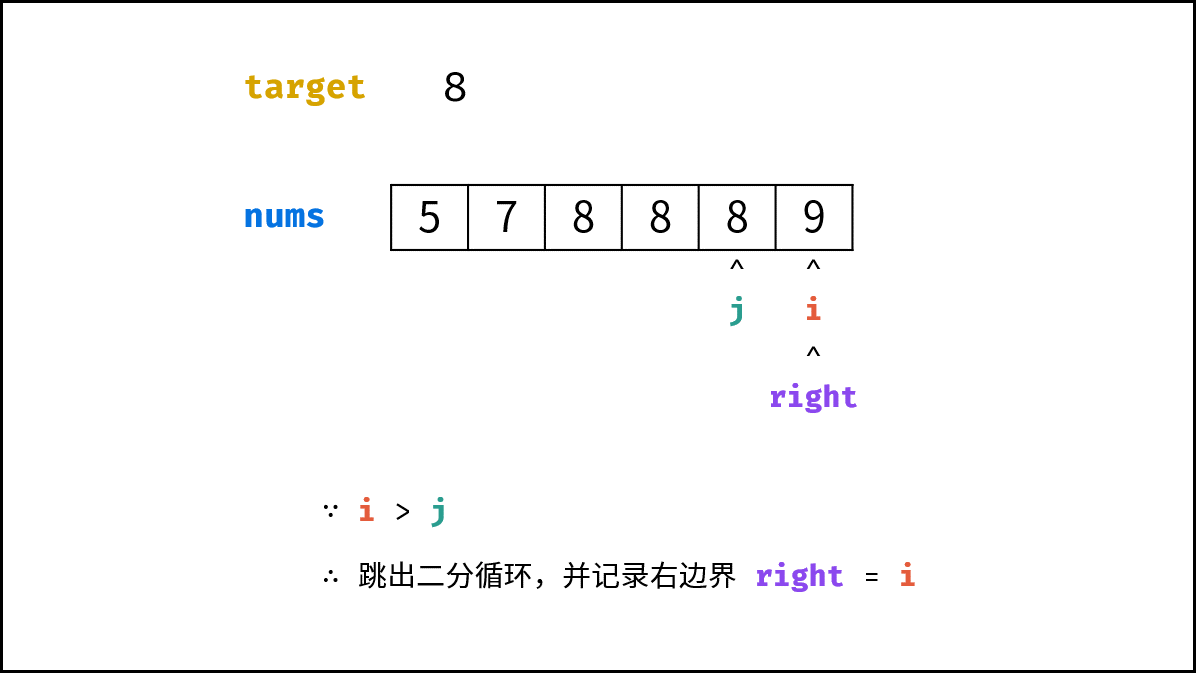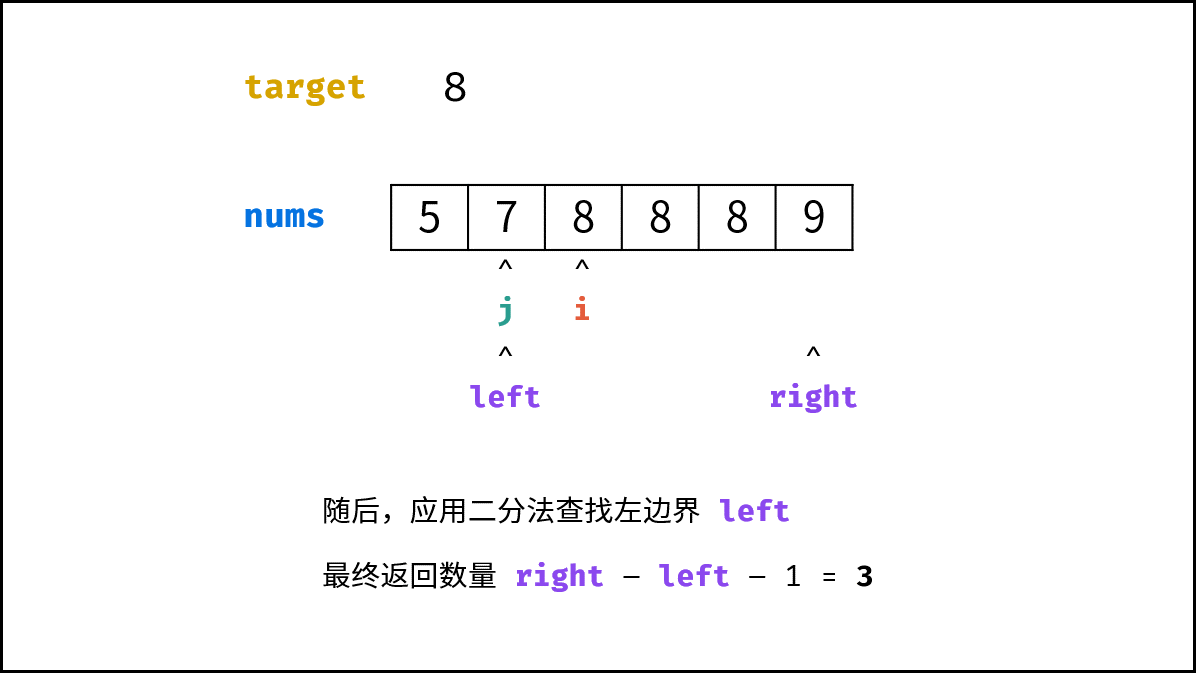<![Picture3.png](https://pic.leetcode-cn.com/1600793982-omMfDH-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600793982-bUXLGC-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600794190-pDMqjT-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600793982-Uvhvcw-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600793982-CGLgjg-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1600793982-WNaiRL-Picture8.png)>
## 代码：
可将 $scores[m] = target$ 情况合并至其他两种情况中。
```Python []
class Solution:
def countTarget(self, scores: List[int], target: int) -> int:
# 搜索右边界 right
i, j = 0, len(scores) - 1
while i <= j:
m = (i + j) // 2
if scores[m] <= target: i = m + 1
else: j = m - 1
right = i
# 若数组中无 target ，则提前返回
if j >= 0 and scores[j] != target: return 0
# 搜索左边界 left
i = 0
while i <= j:
m = (i + j) // 2
if scores[m] < target: i = m + 1
else: j = m - 1
left = j
return right - left - 1
```
```Java []
class Solution {
public int countTarget(int[] scores, int target) {
// 搜索右边界 right
int i = 0, j = scores.length - 1;
while(i <= j) {
int m = (i + j) / 2;
if(scores[m] <= target) i = m + 1;
else j = m - 1;
}
int right = i;
// 若数组中无 target ，则提前返回
if(j >= 0 && scores[j] != target) return 0;
// 搜索左边界 right
i = 0; j = scores.length - 1;
while(i <= j) {
int m = (i + j) / 2;
if(scores[m] < target) i = m + 1;
else j = m - 1;
}
int left = j;
return right - left - 1;
}
}
```
```C++ []
class Solution {
public:
int countTarget(vector<int>& scores, int target) {
// 搜索右边界 right
int i = 0, j = scores.size() - 1;
while(i <= j) {
int m = (i + j) / 2;
if(scores[m] <= target) i = m + 1;
else j = m - 1;
}
int right = i;
// 若数组中无 target ，则提前返回
if(j >= 0 && scores[j] != target) return 0;
// 搜索左边界 right
i = 0; j = scores.size() - 1;
while(i <= j) {
int m = (i + j) / 2;
if(scores[m] < target) i = m + 1;
else j = m - 1;
}
int left = j;
return right - left - 1;
}
};
```
以上代码显得比较臃肿（两轮二分查找代码冗余）。为简化代码，可将**二分查找右边界 $right$ 的代码** 封装至函数 `helper()` 。
如下图所示，由于数组 $scores$ 中元素都为整数，因此可以分别二分查找 $target$ 和 $target - 1$ 的右边界，将两结果相减并返回即可。
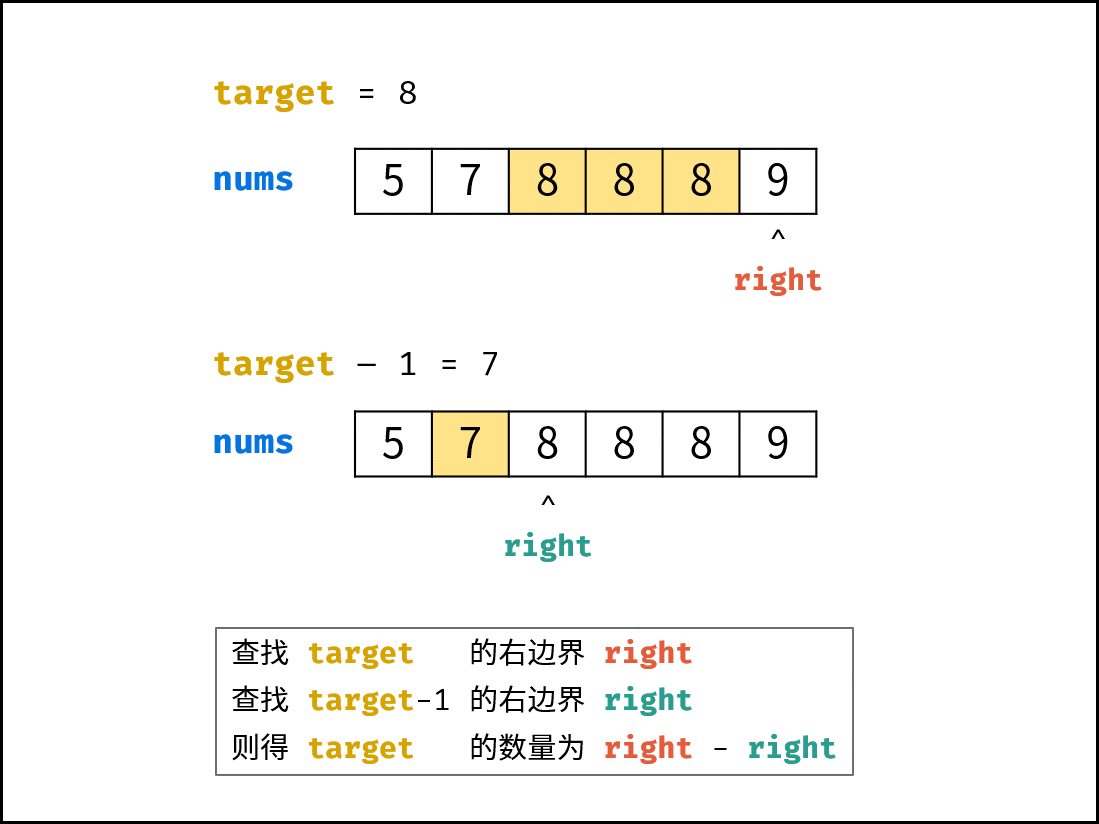![Picture2.png](https://pic.leetcode-cn.com/1600793982-ikEYZs-Picture2.png){:align=center width=450}
本质上看，`helper()` 函数旨在查找数字 $tar$ 在数组 $scores$ 中的 **插入点** ，且若数组中存在值相同的元素，则插入到这些元素的右边。
```Python []
class Solution:
def countTarget(self, scores: List[int], target: int) -> int:
def helper(tar):
i, j = 0, len(scores) - 1
while i <= j:
m = (i + j) // 2
if scores[m] <= tar: i = m + 1
else: j = m - 1
return i
return helper(target) - helper(target - 1)
```
```Java []
class Solution {
public int countTarget(int[] scores, int target) {
return helper(scores, target) - helper(scores, target - 1);
}
int helper(int[] scores, int tar) {
int i = 0, j = scores.length - 1;
while(i <= j) {
int m = (i + j) / 2;
if(scores[m] <= tar) i = m + 1;
else j = m - 1;
}
return i;
}
}
```
```C++ []
class Solution {
public:
int countTarget(vector<int>& scores, int target) {
return helper(scores, target) - helper(scores, target - 1);
}
private:
int helper(vector<int>& scores, int tar) {
int i = 0, j = scores.size() - 1;
while(i <= j) {
int m = (i + j) / 2;
if(scores[m] <= tar) i = m + 1;
else j = m - 1;
}
return i;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(\log N)$ ：** 二分法为对数级别复杂度。
- **空间复杂度 $O(1)$ ：** 几个变量使用常数大小的额外空间。

70
leetbook_ioa/docs/LCR 173. 点名.md Executable file
View File

@@ -0,0 +1,70 @@
## 解题思路：
排序数组中的搜索问题，首先想到 **二分法** 解决。根据题意，数组可以按照以下规则划分为两部分。
- **左子数组：** $records[i] = i$ ；
- **右子数组：** $records[i] \ne i$ ；
缺失的数字等于 **“右子数组的首位元素”** 对应的索引；因此考虑使用二分法查找 “右子数组的首位元素” 。
> 下图中的 `nums` 对应本题的 `records` 。
![Picture1.png](https://pic.leetcode-cn.com/1600794300-lLZwAz-Picture1.png){:align=center width=500}
### 算法解析：
1. **初始化：** 左边界 $i = 0$ ，右边界 $j = len(records) - 1$ ；代表闭区间 $[i, j]$ 。
2. **循环二分：** 当 $i \leq j$ 时循环 *（即当闭区间 $[i, j]$ 为空时跳出）* ；
1. 计算中点 $m = (i + j) // 2$ ，其中 "$//$" 为向下取整除法；
2. 若 $records[m] = m$ ，则 “右子数组的首位元素” 一定在闭区间 $[m + 1, j]$ 中，因此执行 $i = m + 1$；
3. 若 $records[m] \ne m$ ，则 “左子数组的末位元素” 一定在闭区间 $[i, m - 1]$ 中，因此执行 $j = m - 1$；
3. **返回值：** 跳出时，变量 $i$ 和 $j$ 分别指向 “右子数组的首位元素” 和 “左子数组的末位元素” 。因此返回 $i$ 即可。
<![Picture2.png](https://pic.leetcode-cn.com/1600794300-qbJfal-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600794300-VjhSkK-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600794300-FMaRIx-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600794300-GXuUPk-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600794300-FmuzzQ-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600794300-KnWTTf-Picture7.png)>
## 代码：
```Python []
class Solution:
def takeAttendance(self, records: List[int]) -> int:
i, j = 0, len(records) - 1
while i <= j:
m = (i + j) // 2
if records[m] == m: i = m + 1
else: j = m - 1
return i
```
```Java []
class Solution {
public int takeAttendance(int[] records) {
int i = 0, j = records.length - 1;
while(i <= j) {
int m = (i + j) / 2;
if(records[m] == m) i = m + 1;
else j = m - 1;
}
return i;
}
}
```
```C++ []
class Solution {
public:
int takeAttendance(vector<int>& records) {
int i = 0, j = records.size() - 1;
while(i <= j) {
int m = (i + j) / 2;
if(records[m] == m) i = m + 1;
else j = m - 1;
}
return i;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(\log N)$：** 二分法为对数级别复杂度。
- **空间复杂度 $O(1)$：** 几个变量使用常数大小的额外空间。

151
leetbook_ioa/docs/LCR 174. 寻找二叉搜索树中的目标节点.md Executable file
View File

@@ -0,0 +1,151 @@
## 解题思路：
本文解法基于性质：二叉搜索树的中序遍历为递增序列。根据此性质，易得二叉搜索树的 **中序遍历倒序** 为 **递减序列** 。
因此，我们可将求 “二叉搜索树第 $cnt$ 大的节点” 可转化为求 “此树的中序遍历倒序的第 $cnt$ 个节点”。
> 下图中的 `k` 对应本题的 `cnt` 。
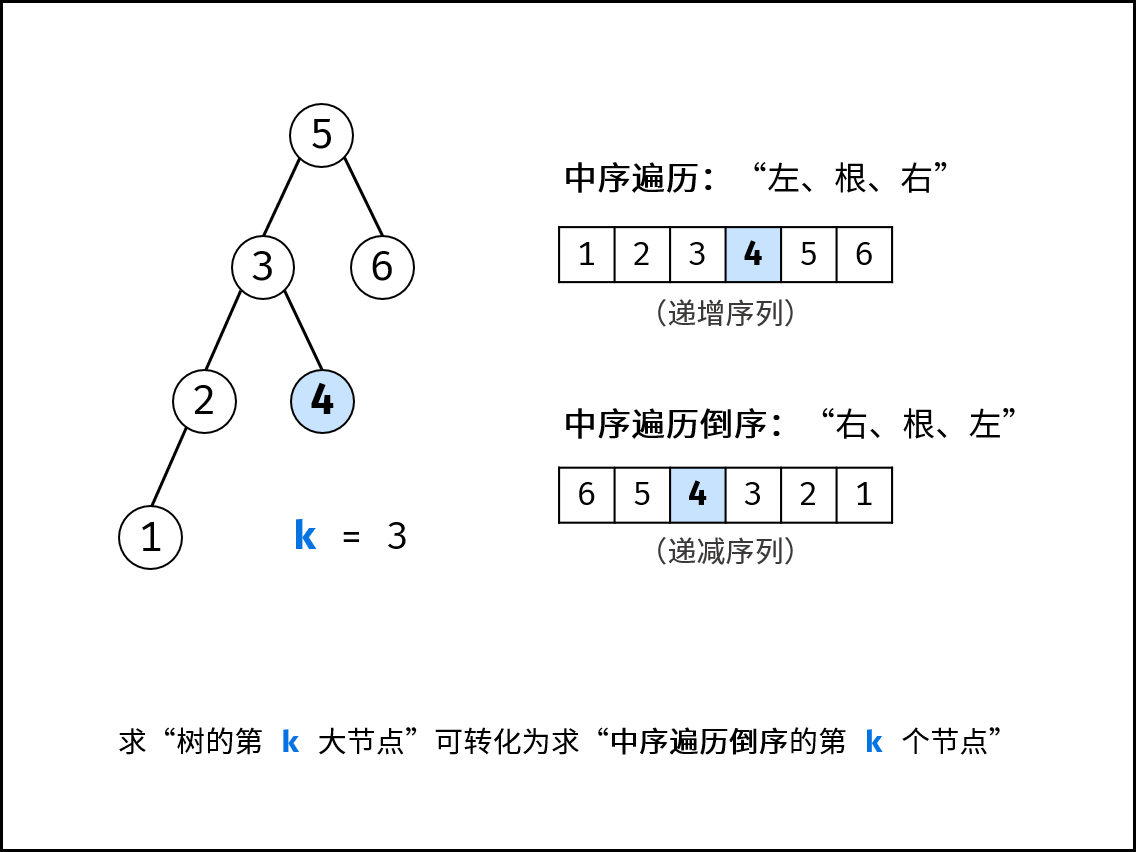![Picture1.png](https://pic.leetcode-cn.com/1600793852-IaPwtP-Picture1.png){:align=center width=450}
**中序遍历** 为 “左、根、右” 顺序，递归代码如下：
```Python []
# 打印中序遍历
def dfs(root):
if not root: return
dfs(root.left) # 左
print(root.val) # 根
dfs(root.right) # 右
```
```Java []
// 打印中序遍历
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.left); // 左
System.out.println(root.val); // 根
dfs(root.right); // 右
}
```
```C++ []
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->left);
cout << root->val;
dfs(root->right);
}
```
**中序遍历的倒序** 为 “右、根、左” 顺序，递归法代码如下：
```Python []
# 打印中序遍历倒序
def dfs(root):
if not root: return
dfs(root.right) # 右
print(root.val) # 根
dfs(root.left) # 左
```
```Java []
// 打印中序遍历倒序
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.right); // 右
System.out.println(root.val); // 根
dfs(root.left); // 左
}
```
```C++ []
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->right);
cout << root->val;
dfs(root->left);
}
```
为求第 $cnt$ 个节点，需要实现以下三项工作：
1. 递归遍历时计数，统计当前节点的序号；
2. 递归到第 $cnt$ 个节点时，应记录结果 $res$ ；
3. 记录结果后，后续的遍历即失去意义，应提前终止（即返回）；
### 递归解析：
1. **终止条件：** 当节点 $root$ 为空（越过叶节点），则直接返回；
2. **递归右子树：** 即 $dfs(root.right)$ ；
3. **递推工作：**
1. 提前返回： 若 $cnt = 0$ ，代表已找到目标节点，无需继续遍历，因此直接返回；
2. 统计序号： 执行 $cnt = cnt - 1$ （即从 $cnt$ 减至 $0$ ）；
3. 记录结果： 若 $cnt = 0$ ，代表当前节点为第 $cnt$ 大的节点，因此记录 $res = root.val$ ；
4. **递归左子树：** 即 $dfs(root.left)$ ；
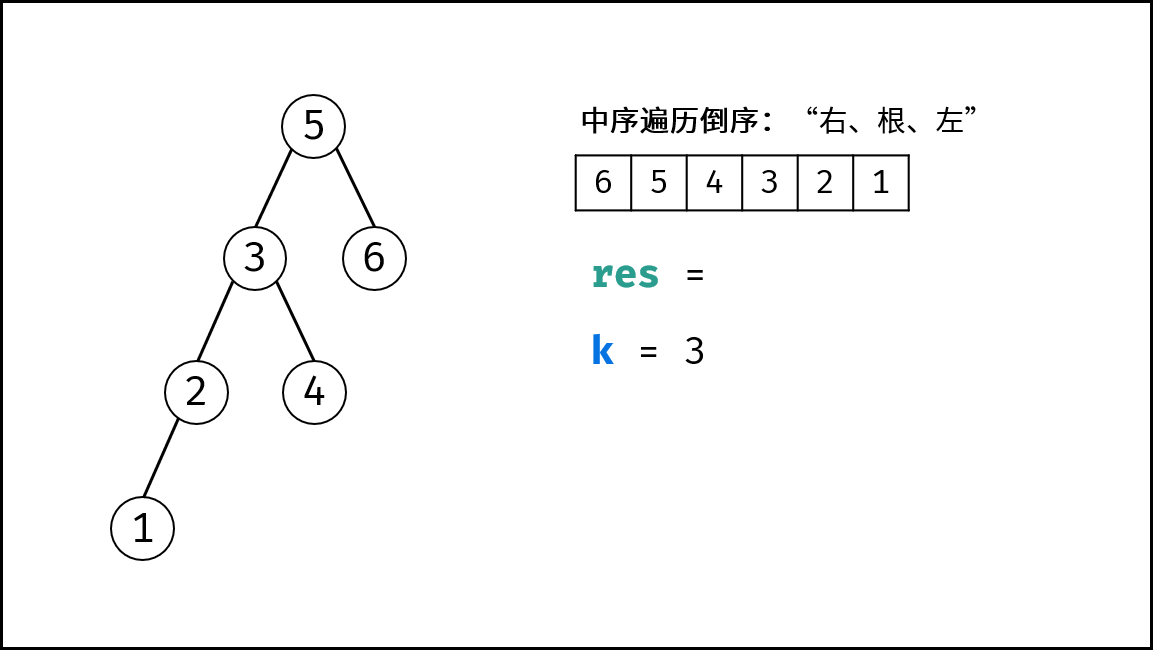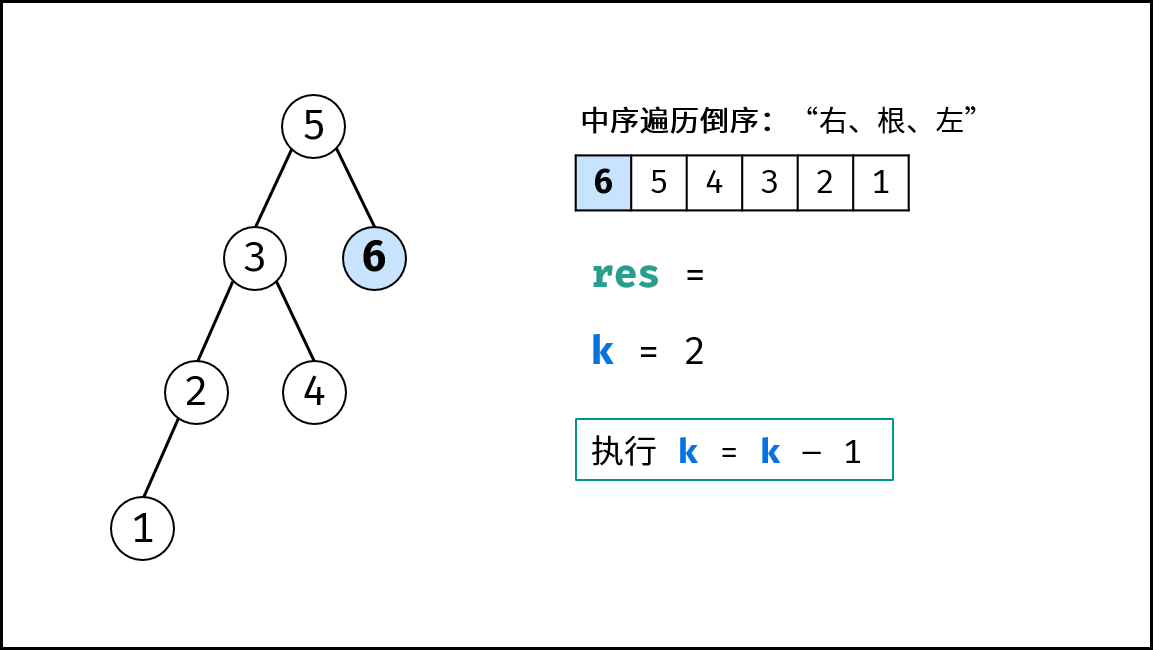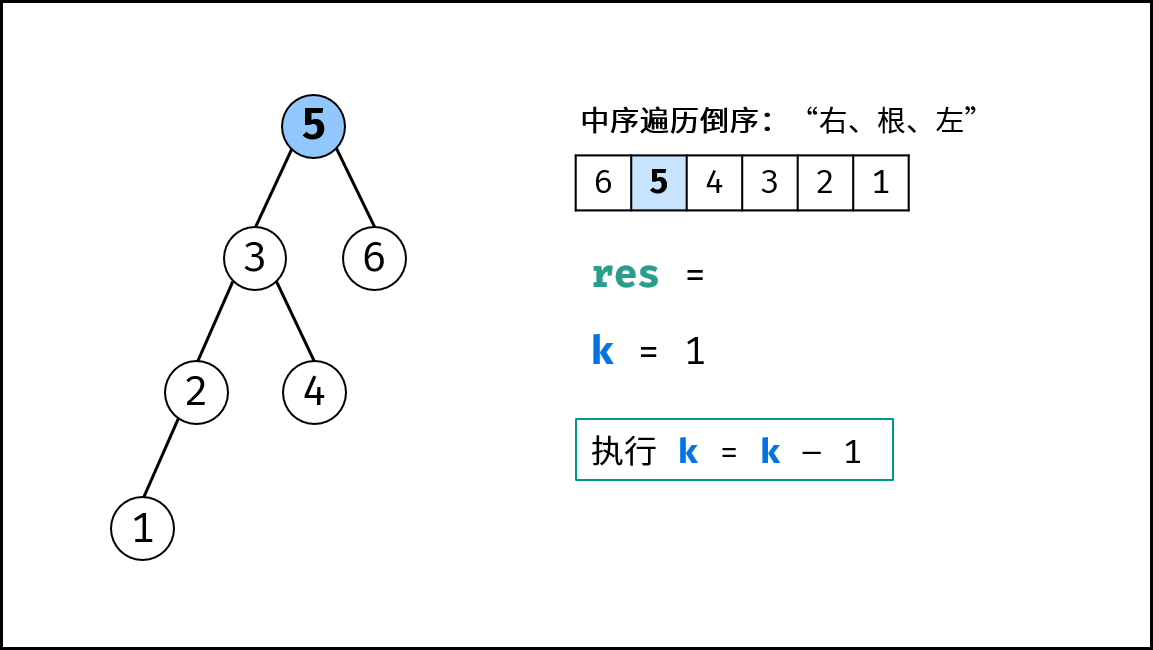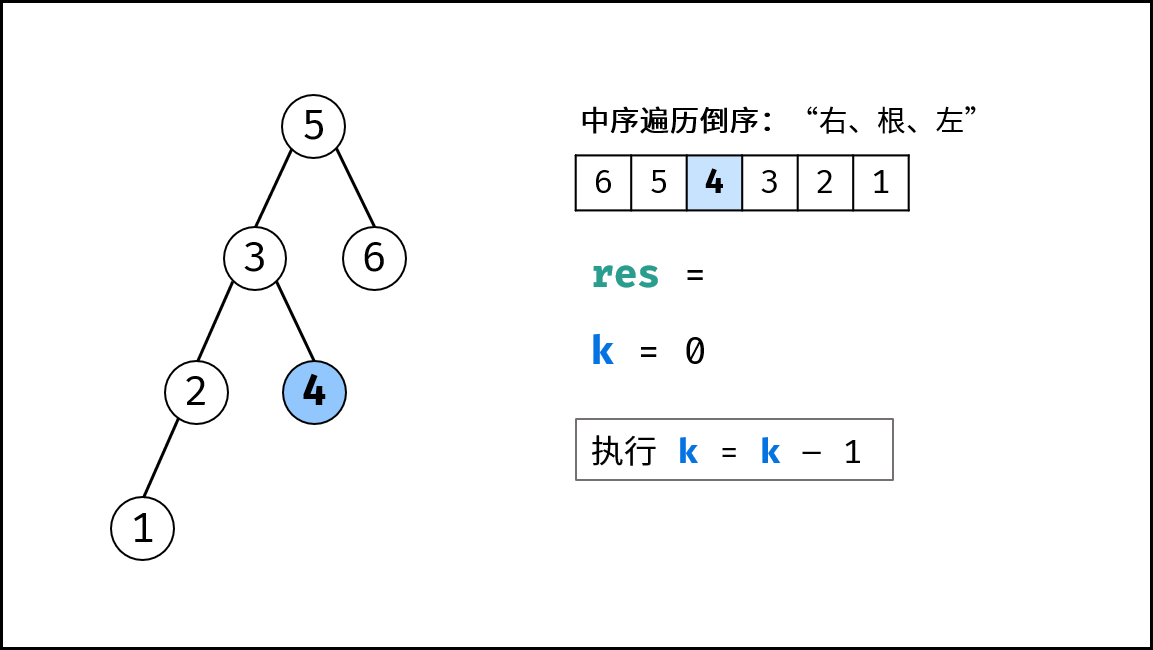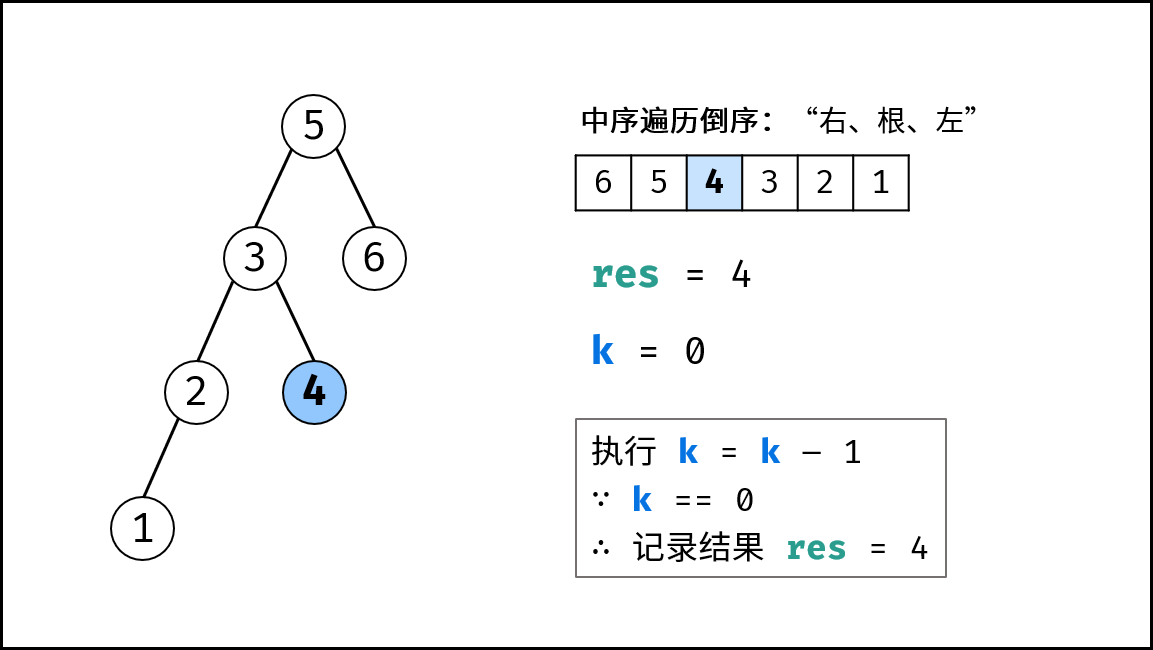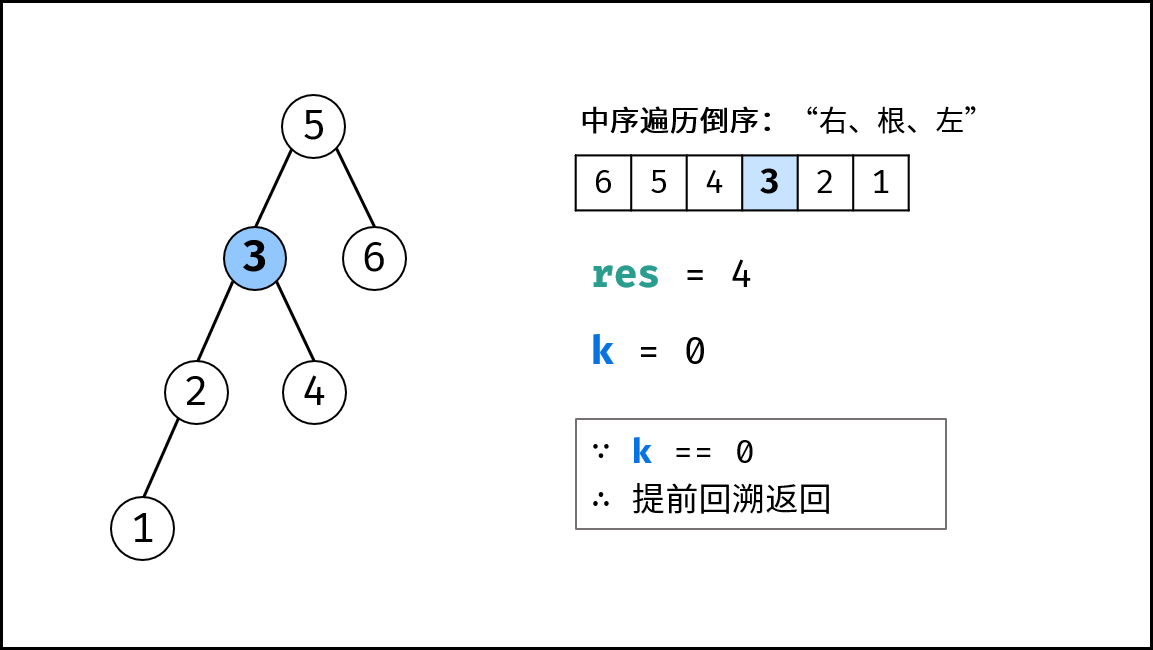<![Picture2.png](https://pic.leetcode-cn.com/1600793852-tpKrIb-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600793852-wPEuqr-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600793852-GnlyUZ-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600793852-LTtEdQ-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600793852-bmFayB-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600793852-RYrsrM-Picture7.png),![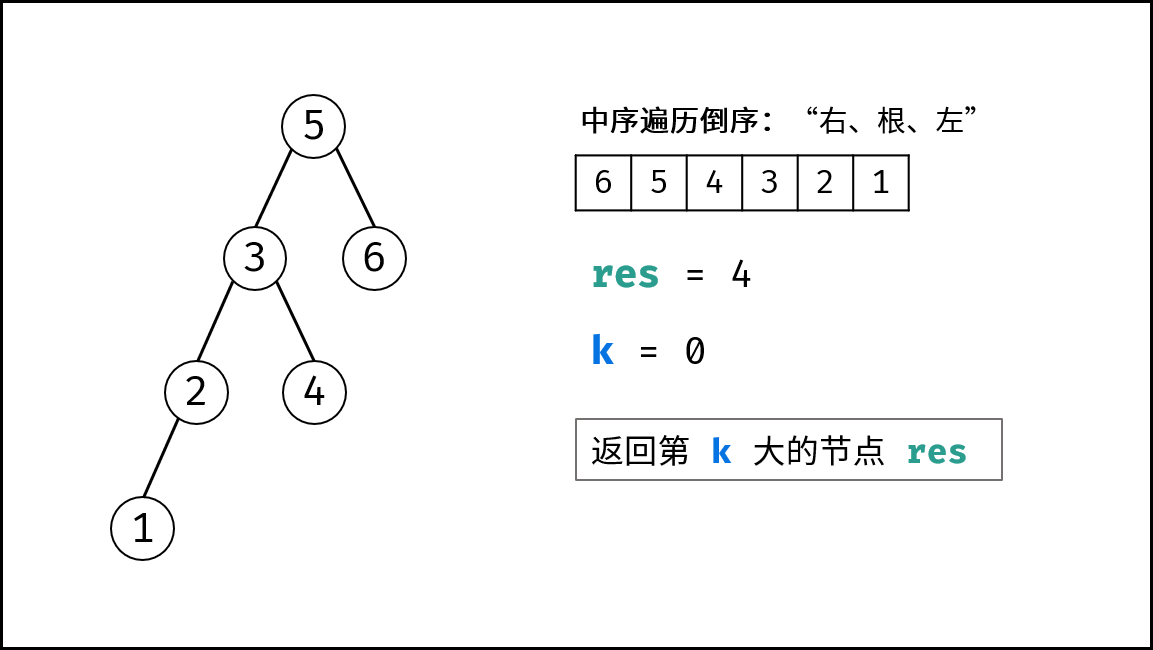Picture8.png](https://pic.leetcode-cn.com/1600793852-ebmUlX-Picture8.png)>
## 代码：
题目指出：$1 \leq cnt \leq N$ （二叉搜索树节点个数）；因此无需考虑 $cnt > N$ 的情况。
若考虑，可以在中序遍历完成后判断 $cnt > 0$ 是否成立，若成立则说明 $cnt > N$ 。
```Python []
class Solution:
def findTargetNode(self, root: TreeNode, cnt: int) -> int:
def dfs(root):
if not root: return
dfs(root.right)
if self.cnt == 0: return
self.cnt -= 1
if self.cnt == 0: self.res = root.val
dfs(root.left)
self.cnt = cnt
dfs(root)
return self.res
```
```Java []
class Solution {
int res, cnt;
public int findTargetNode(TreeNode root, int cnt) {
this.cnt = cnt;
dfs(root);
return res;
}
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.right);
if(cnt == 0) return;
if(--cnt == 0) res = root.val;
dfs(root.left);
}
}
```
```C++ []
class Solution {
public:
int findTargetNode(TreeNode* root, int cnt) {
this->cnt = cnt;
dfs(root);
return res;
}
private:
int res, cnt;
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->right);
if(cnt == 0) return;
if(--cnt == 0) res = root->val;
dfs(root->left);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 当树退化为链表时（全部为右子节点），无论 $cnt$ 的值大小，递归深度都为 $N$ ，占用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** 当树退化为链表时（全部为右子节点），系统使用 $O(N)$ 大小的栈空间。

142
leetbook_ioa/docs/LCR 175. 计算二叉树的深度.md Executable file
View File

@@ -0,0 +1,142 @@
## 解题思路：
树的遍历方式总体分为两类：
- **深度优先搜索（DFS）：** 先序遍历、中序遍历、后序遍历；
- **广度优先搜索（BFS）：** 层序遍历；
求树的深度需要遍历树的所有节点，本文将介绍基于 **后序遍历（DFS）** 和 **层序遍历（BFS）** 的两种解法。
## 方法一：后序遍历（DFS）
树的后序遍历 / 深度优先搜索往往利用 **递归** 或 **栈** 实现，本文使用递归实现。
**关键点：** 此树的深度和其左（右）子树的深度之间的关系。显然，**此树的深度** 等于 **左子树的深度** 与 **右子树的深度** 中的 **最大值** $+1$ 。
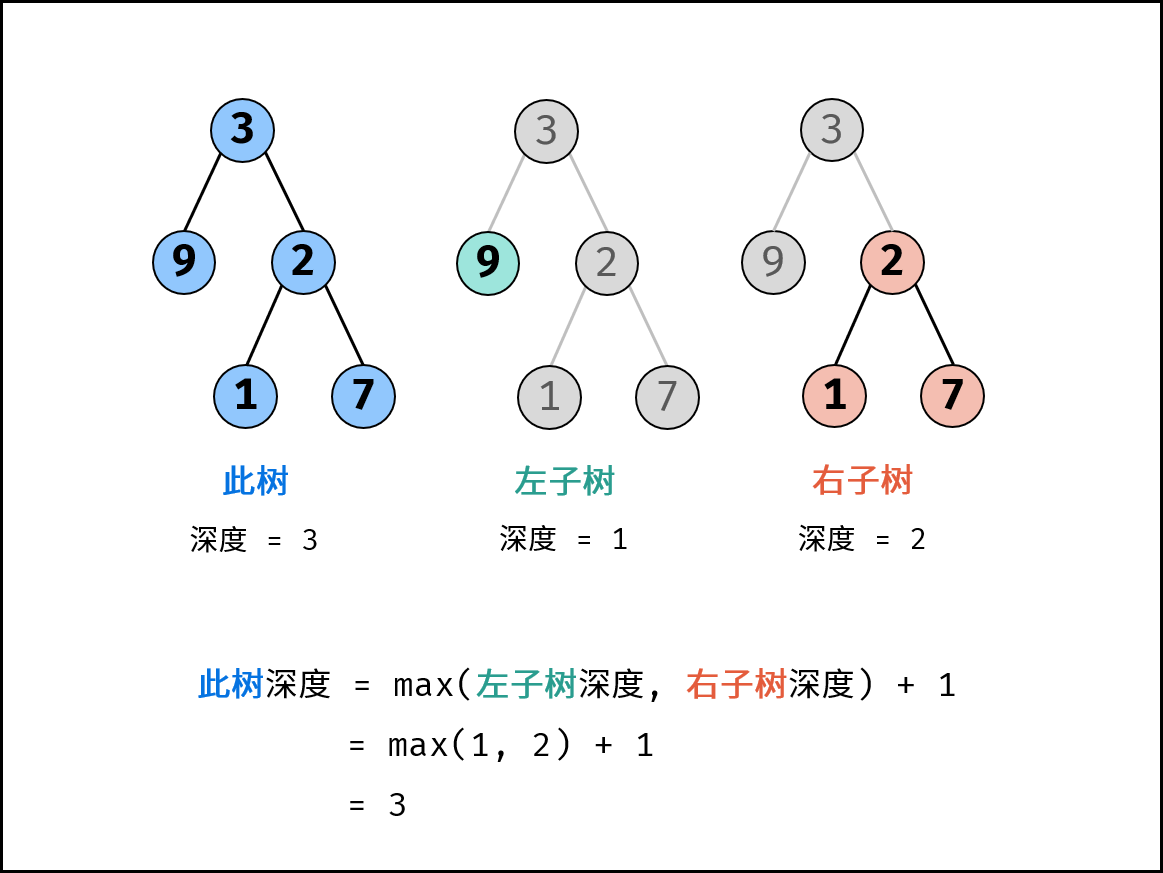![Picture1.png](https://pic.leetcode-cn.com/1603024336-lXVRDd-Picture1.png){:align=center width=450}
### 算法解析：
1. **终止条件：** 当 `root​` 为空，说明已越过叶节点，因此返回 深度 $0$ 。
2. **递推工作：** 本质上是对树做后序遍历。
1. 计算节点 `root​` 的 **左子树的深度** ，即调用 `calculateDepth(root.left)`；
2. 计算节点 `root​` 的 **右子树的深度** ，即调用 `calculateDepth(root.right)`；
3. **返回值：** 返回 **此树的深度** ，即 `max(calculateDepth(root.left), calculateDepth(root.right)) + 1`。
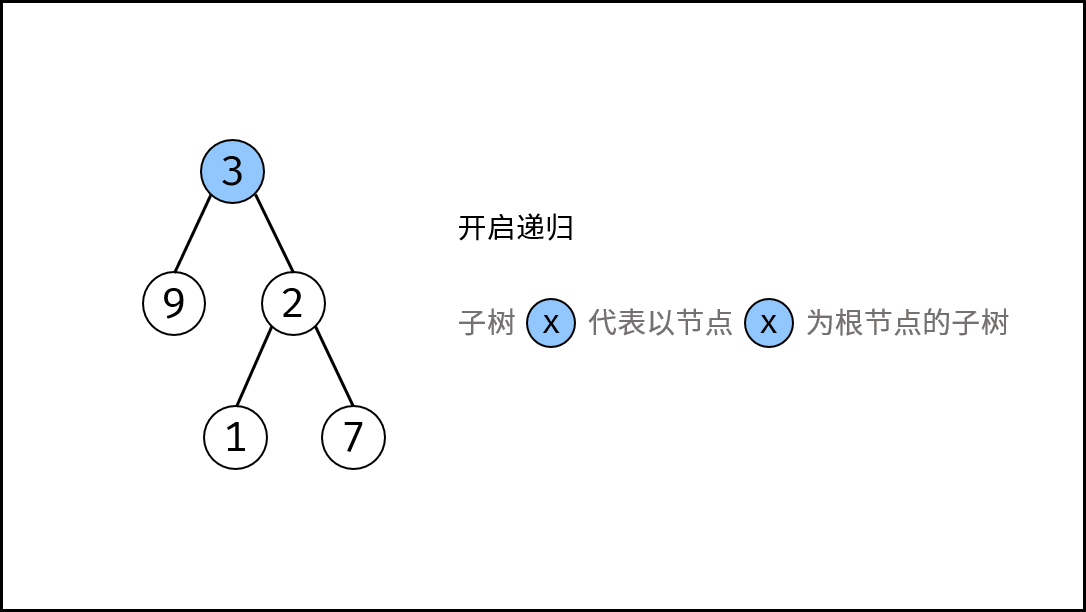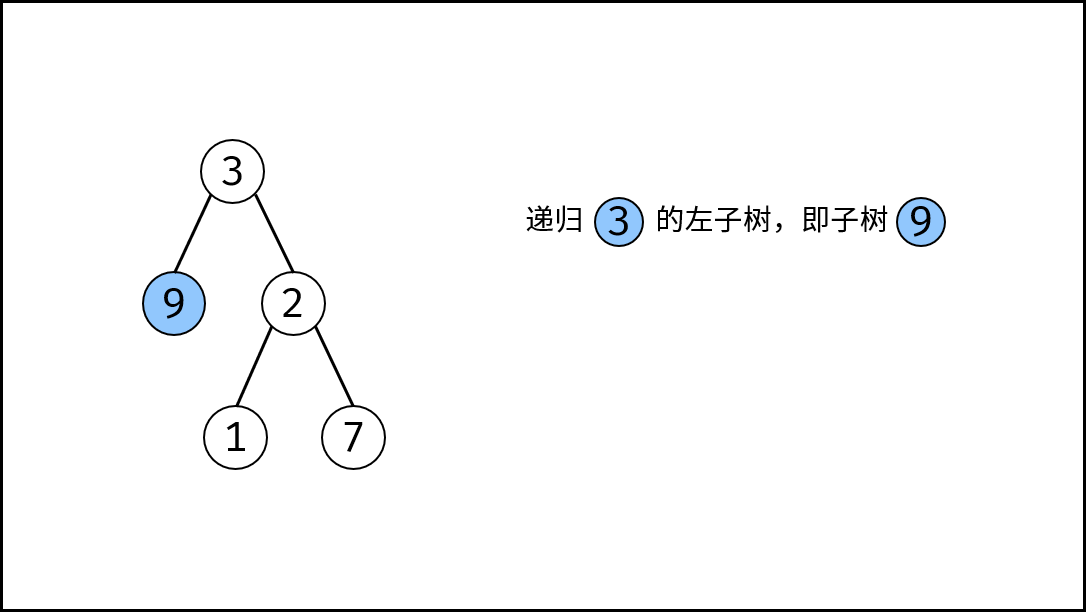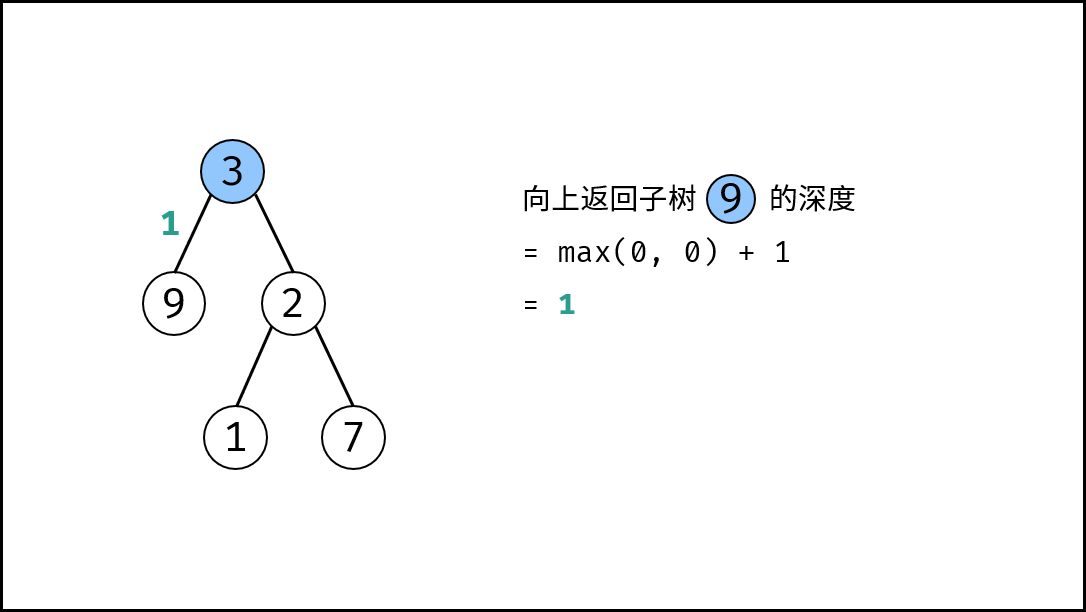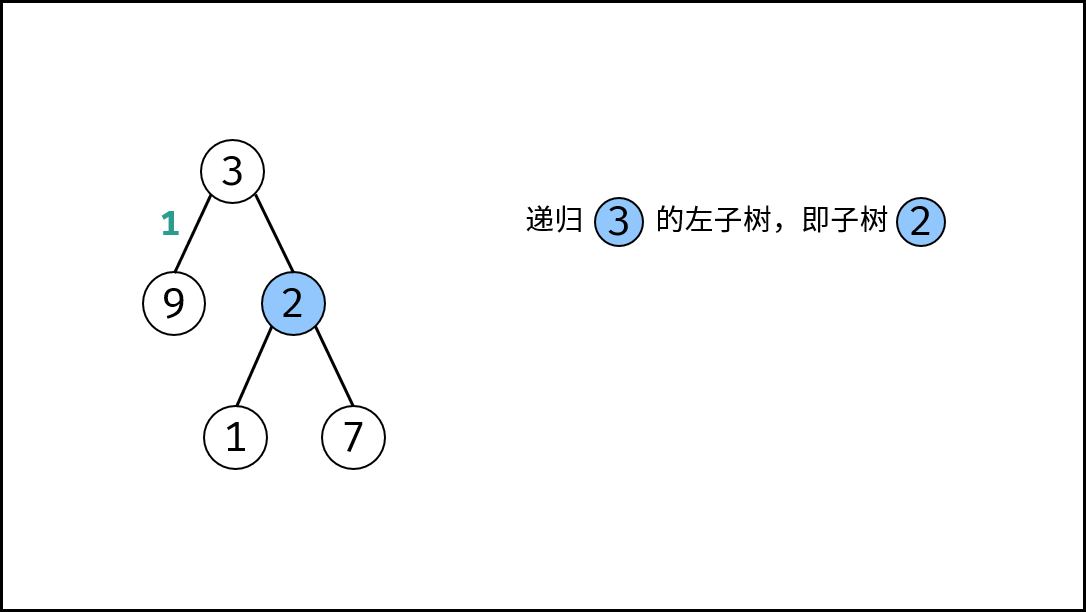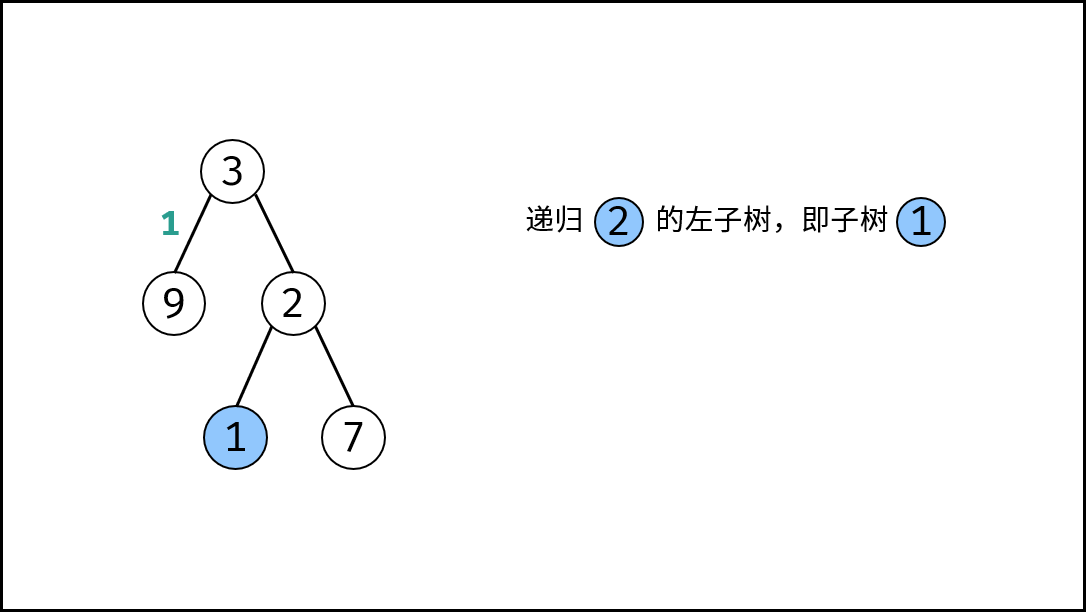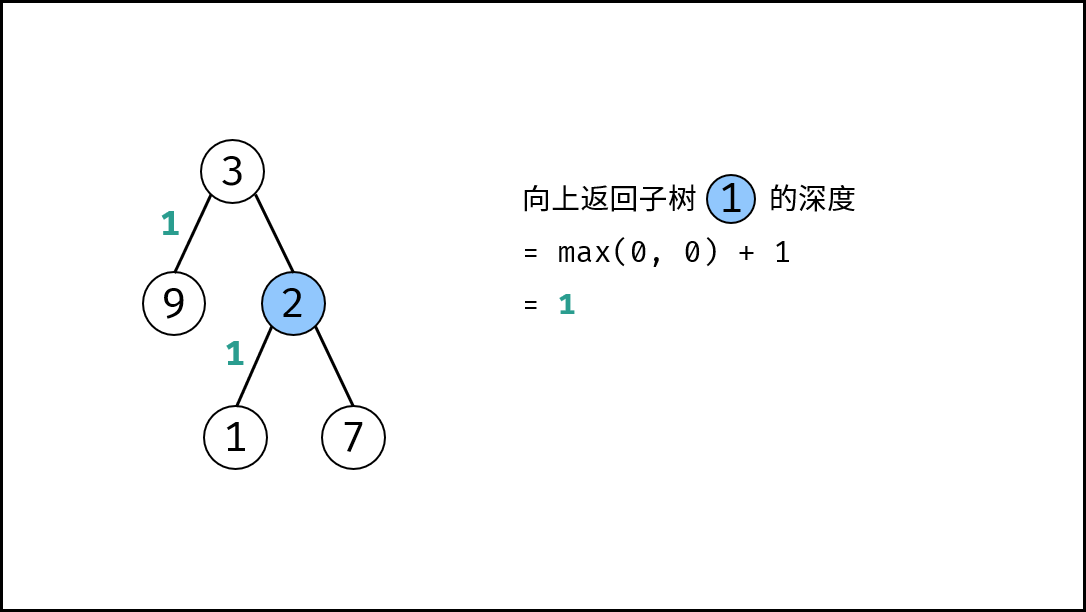<![Picture2.png](https://pic.leetcode-cn.com/1603024336-bRXFKg-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603024336-xohQQM-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603024336-LXqphi-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603024336-kHinqB-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603024336-hltgwg-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603024336-tcizEe-Picture7.png),![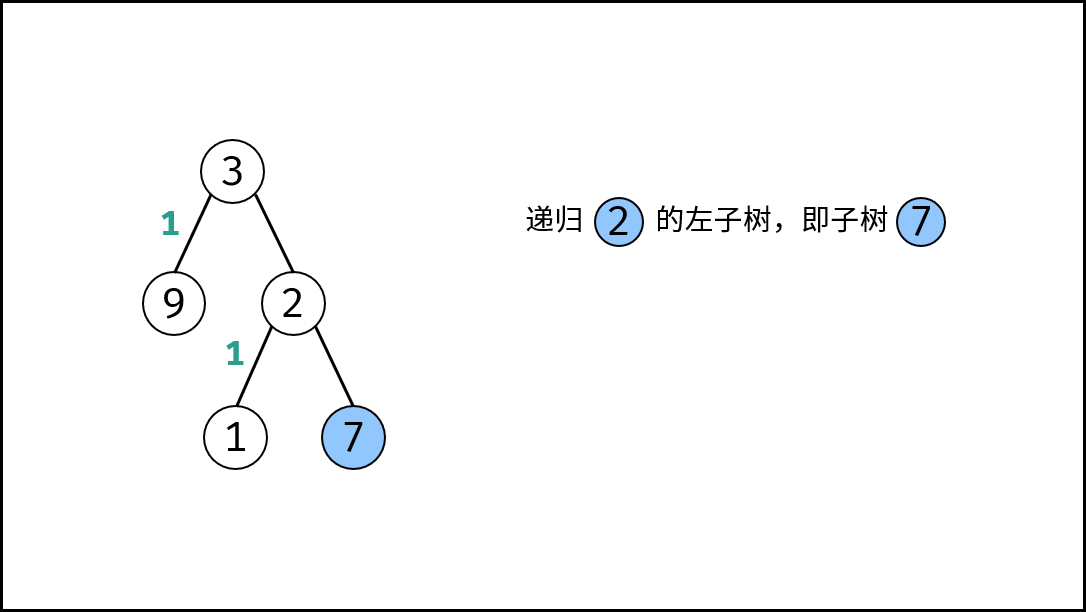Picture8.png](https://pic.leetcode-cn.com/1603024336-mbVGBM-Picture8.png),![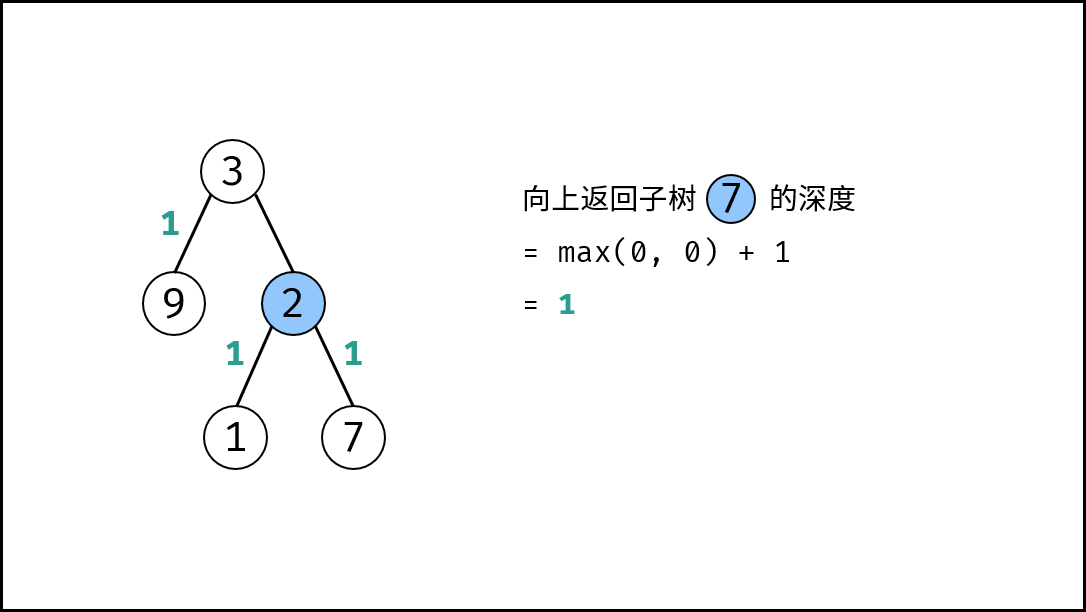Picture9.png](https://pic.leetcode-cn.com/1603024336-KGNMeX-Picture9.png),![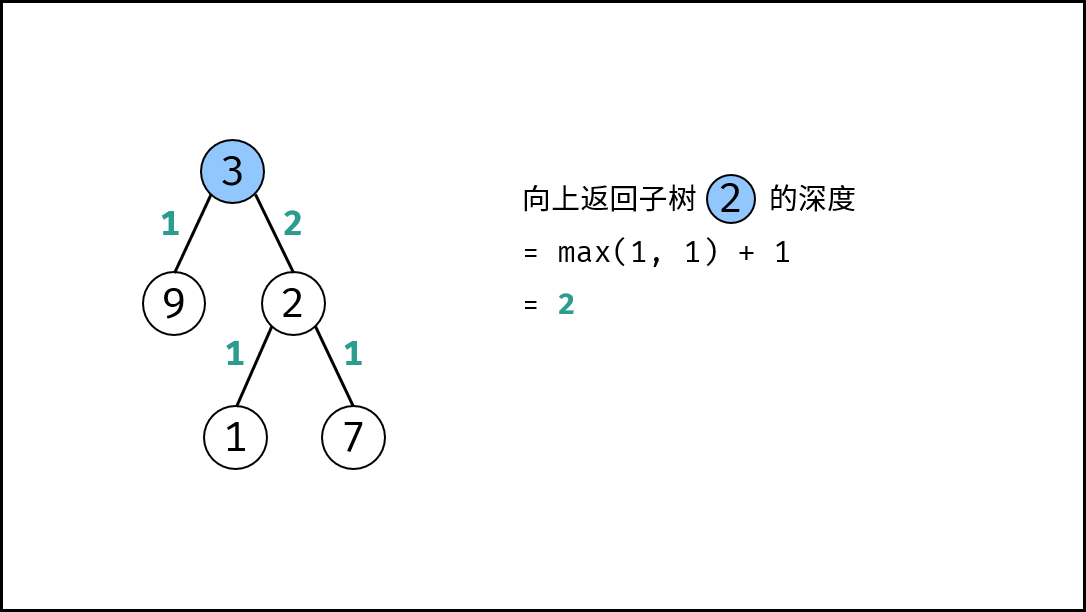Picture10.png](https://pic.leetcode-cn.com/1603024336-AlgMZC-Picture10.png),![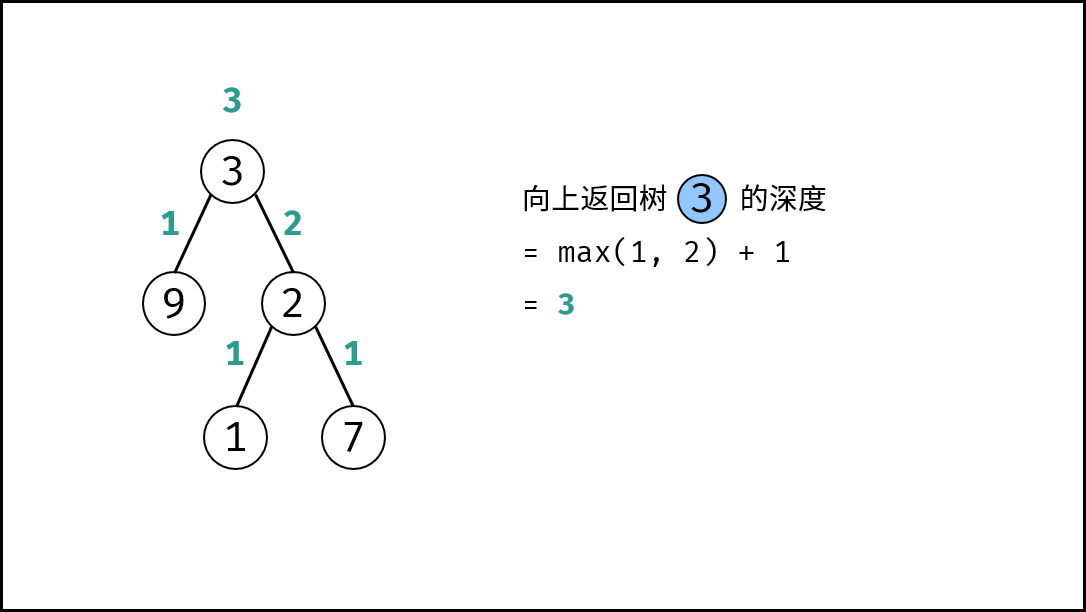Picture11.png](https://pic.leetcode-cn.com/1603024336-YjXKMf-Picture11.png)>
### 代码：
```Python []
class Solution:
def calculateDepth(self, root: TreeNode) -> int:
if not root: return 0
return max(self.calculateDepth(root.left), self.calculateDepth(root.right)) + 1
```
```Java []
class Solution {
public int calculateDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(calculateDepth(root.left), calculateDepth(root.right)) + 1;
}
}
```
```C++ []
class Solution {
public:
int calculateDepth(TreeNode* root) {
if(root == nullptr) return 0;
return max(calculateDepth(root->left), calculateDepth(root->right)) + 1;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为树的节点数量，计算树的深度需要遍历所有节点。
- **空间复杂度 $O(N)$ ：** 最差情况下（当树退化为链表时），递归深度可达到 $N$ 。
## 方法二：层序遍历（BFS）
树的层序遍历 / 广度优先搜索往往利用 **队列** 实现。
**关键点：** 每遍历一层，则计数器 $+1$ ，直到遍历完成，则可得到树的深度。
### 算法解析：
1. **特例处理：** 当 `root​` 为空，直接返回 深度 $0$ 。
2. **初始化：** 队列 `queue` （加入根节点 `root` ），计数器 `res = 0`。
3. **循环遍历：** 当 `queue` 为空时跳出。
1. 初始化一个空列表 `tmp` ，用于临时存储下一层节点；
2. 遍历队列： 遍历 `queue` 中的各节点 `node` ，并将其左子节点和右子节点加入 `tmp`；
3. 更新队列： 执行 `queue = tmp` ，将下一层节点赋值给 `queue`；
4. 统计层数： 执行 `res += 1` ，代表层数加 $1$；
4. **返回值：** 返回 `res` 即可。
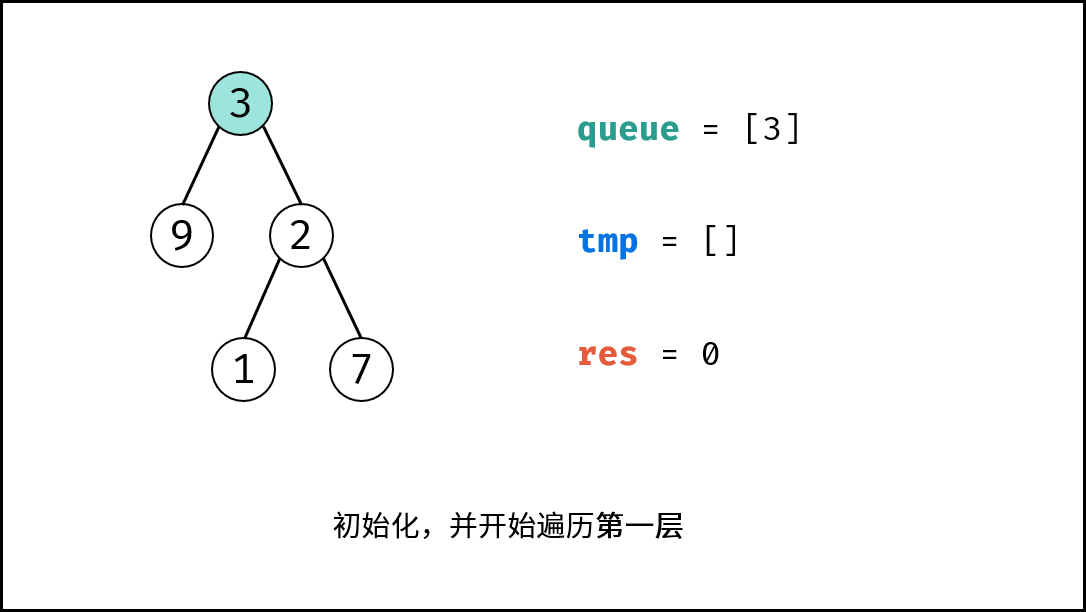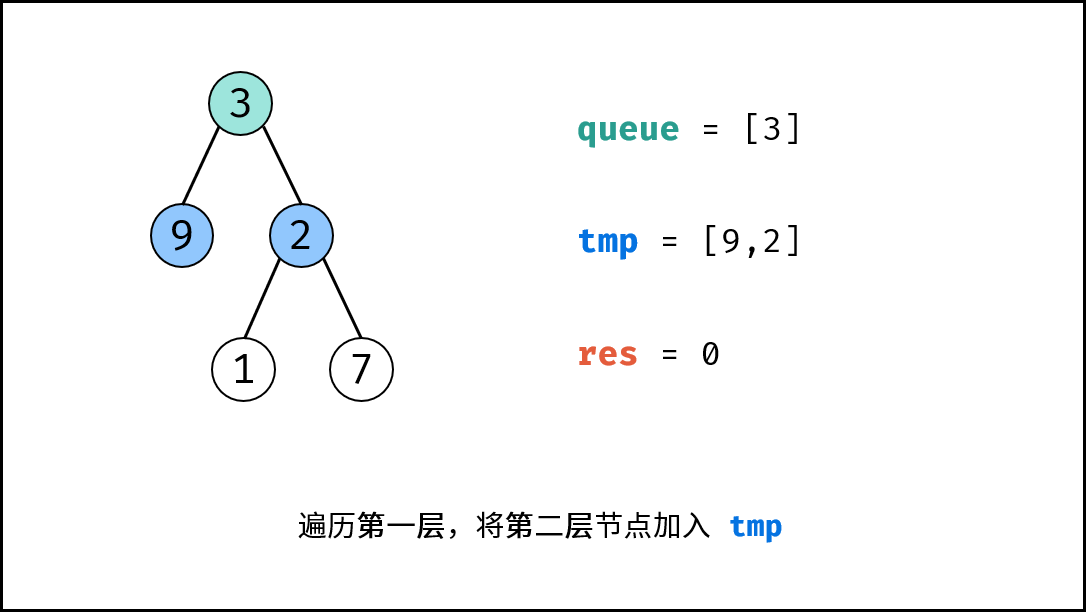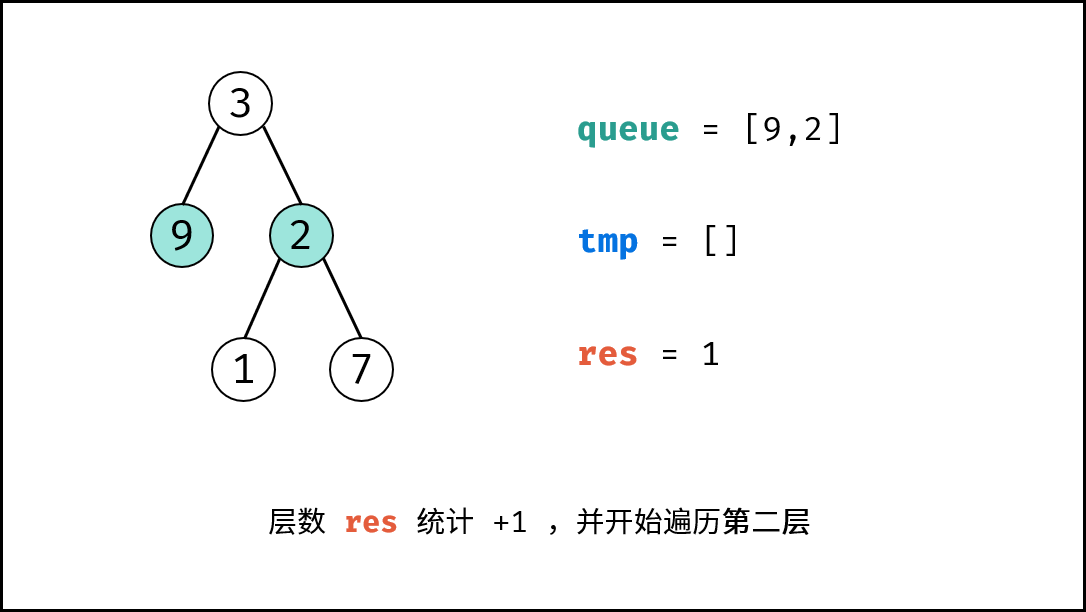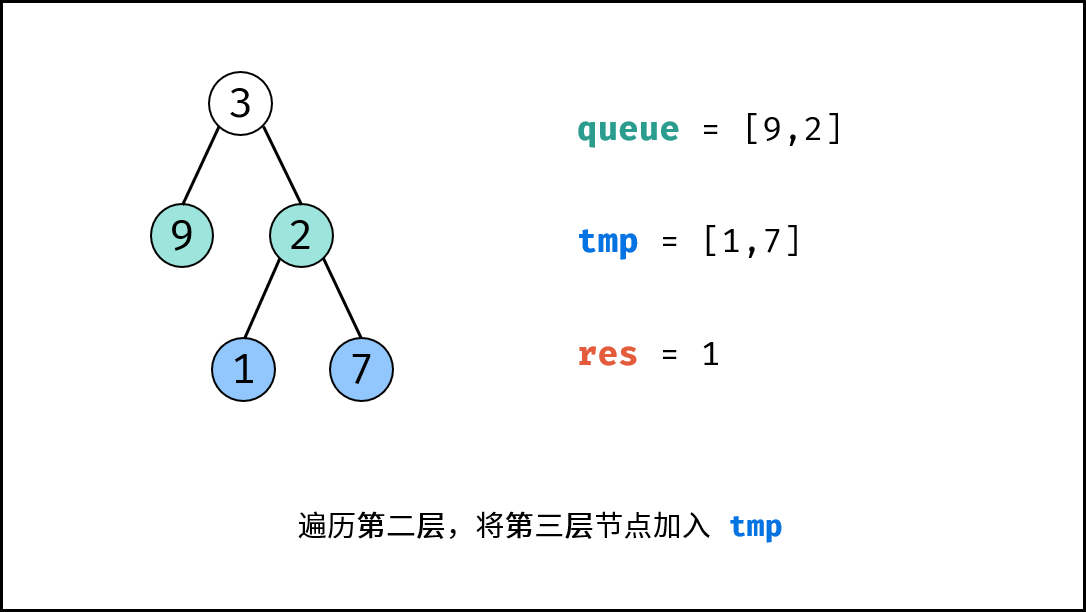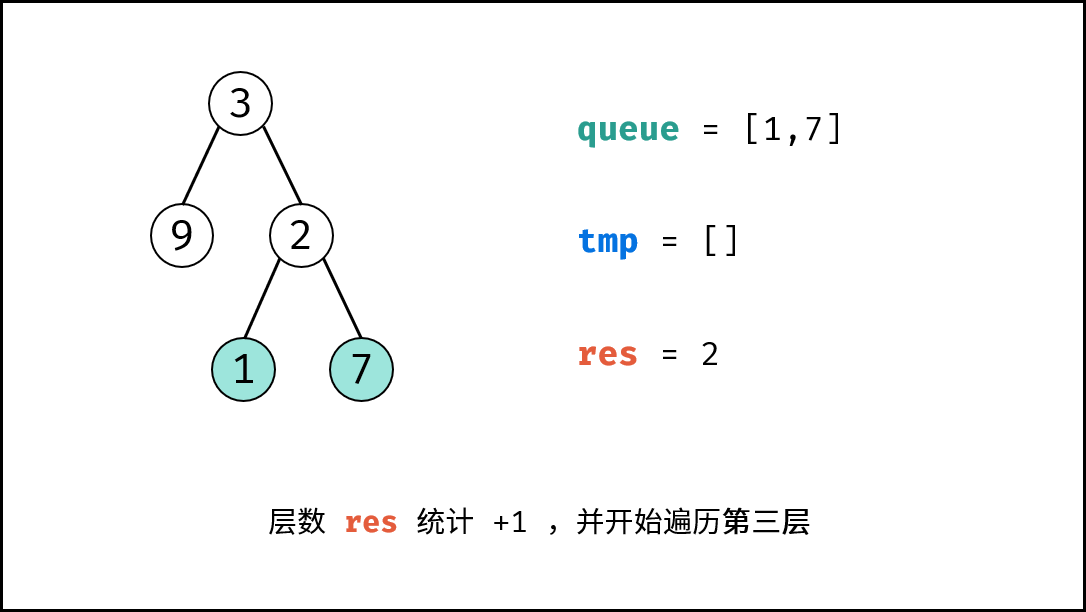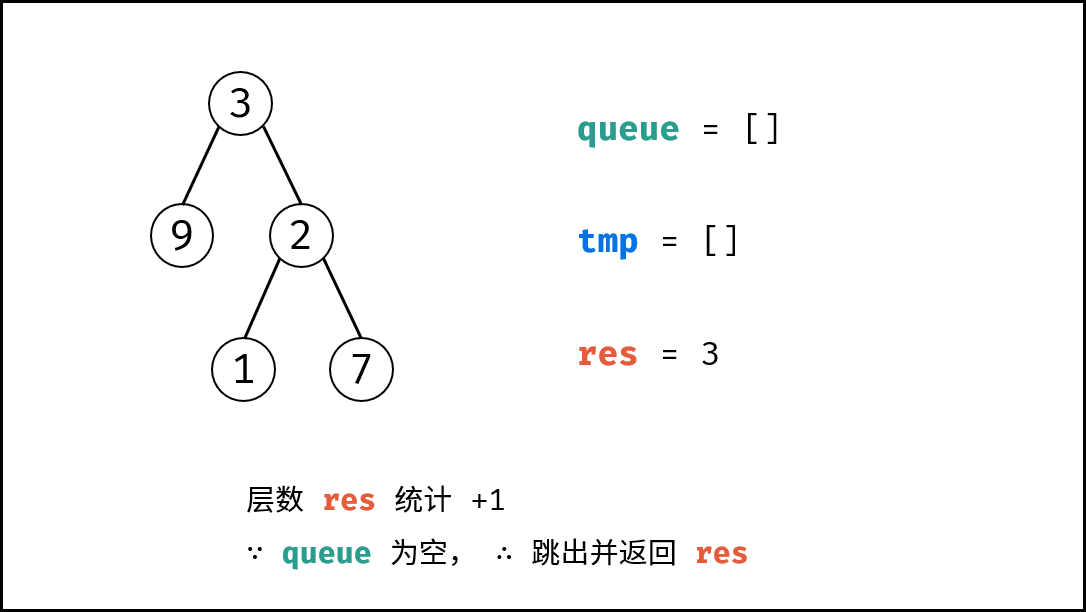<![Picture12.png](https://pic.leetcode-cn.com/1603024336-ZojeTj-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1603024336-fMIPed-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1603024336-ANiQQj-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1603024336-EXcbJg-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1603024336-dSOwtz-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1603024336-byqvuK-Picture17.png)>
### 代码：
```Python []
class Solution:
def calculateDepth(self, root: TreeNode) -> int:
if not root: return 0
queue, res = [root], 0
while queue:
tmp = []
for node in queue:
if node.left: tmp.append(node.left)
if node.right: tmp.append(node.right)
queue = tmp
res += 1
return res
```
```Java []
class Solution {
public int calculateDepth(TreeNode root) {
if(root == null) return 0;
List<TreeNode> queue = new LinkedList<>() {{ add(root); }}, tmp;
int res = 0;
while(!queue.isEmpty()) {
tmp = new LinkedList<>();
for(TreeNode node : queue) {
if(node.left != null) tmp.add(node.left);
if(node.right != null) tmp.add(node.right);
}
queue = tmp;
res++;
}
return res;
}
}
```
```C++ []
class Solution {
public:
int calculateDepth(TreeNode* root) {
if(root == nullptr) return 0;
vector<TreeNode*> que;
que.push_back(root);
int res = 0;
while(!que.empty()) {
vector<TreeNode*> tmp;
for(TreeNode* node : que) {
if(node->left != nullptr) tmp.push_back(node->left);
if(node->right != nullptr) tmp.push_back(node->right);
}
que = tmp;
res++;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为树的节点数量，计算树的深度需要遍历所有节点。
- **空间复杂度 $O(N)$ ：** 最差情况下（当树平衡时），队列 `queue` 同时存储 $N/2$ 个节点。

162
leetbook_ioa/docs/LCR 176. 判断是否为平衡二叉树.md Executable file
View File

@@ -0,0 +1,162 @@
## 解题思路：
以下两种方法均基于以下性质推出： **此树的深度** 等于 **左子树的深度** 与 **右子树的深度** 中的 **最大值** $+1$ 。
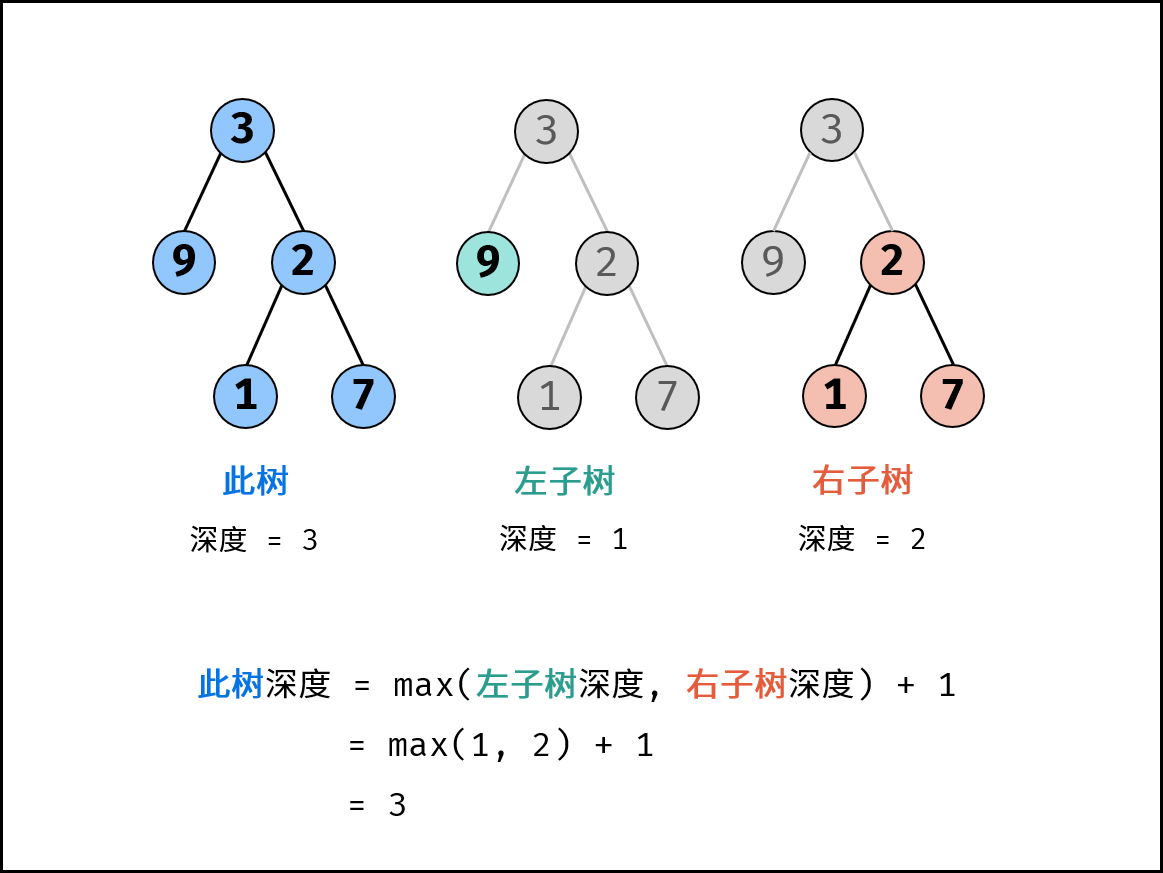![Picture1.png](https://pic.leetcode-cn.com/1603024695-GYNvjf-Picture1.png){:align=center width=450}
## 方法一：后序遍历 + 剪枝 （从底至顶）
> 此方法为本题的最优解法，但剪枝的方法不易第一时间想到。
思路是对二叉树做后序遍历，从底至顶返回子树深度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。
### 算法流程：
**`recur(root)` 函数：**
- **返回值：**
1. 当节点`root` 左 / 右子树的深度差 $\leq 1$ ：则返回当前子树的深度，即节点 `root` 的左 / 右子树的深度最大值 $+1$ （ `max(left, right) + 1` ）；
2. 当节点`root` 左 / 右子树的深度差 $> 1$ ：则返回 $-1$ ，代表 **此子树不是平衡树** 。
- **终止条件：**
1. 当 `root` 为空：说明越过叶节点，因此返回高度 $0$ ；
2. 当左（右）子树深度为 $-1$ ：代表此树的 **左（右）子树** 不是平衡树，因此剪枝，直接返回 $-1$ ；
**`isBalanced(root)` 函数：**
- **返回值：** 若 `recur(root) != -1` ，则说明此树平衡，返回 $\text{true}$ ； 否则返回 $\text{false}$ 。
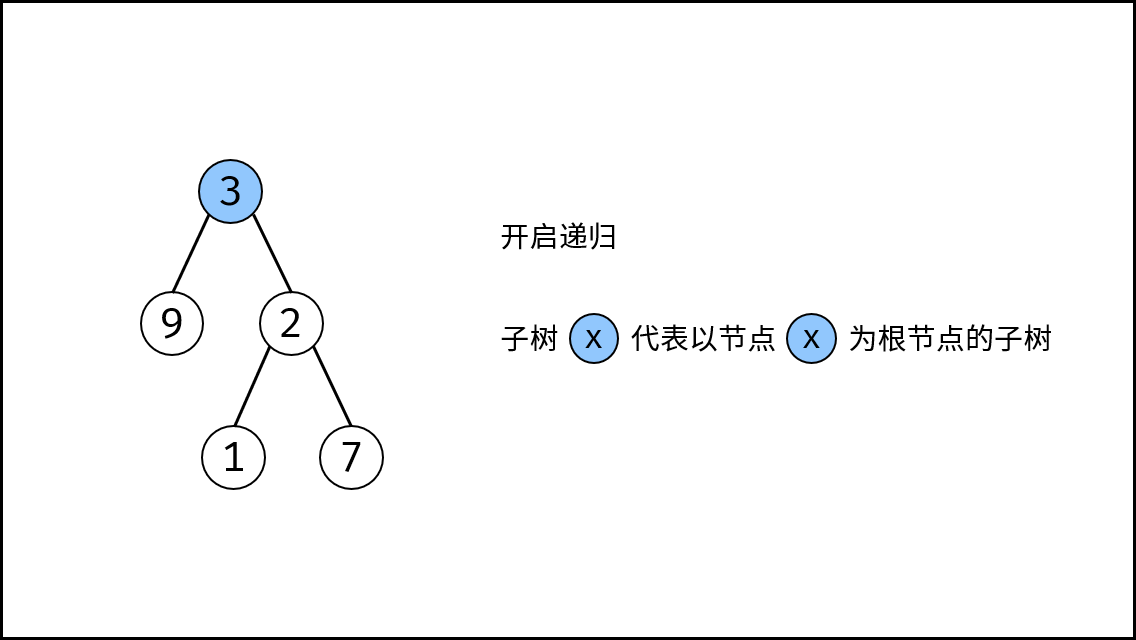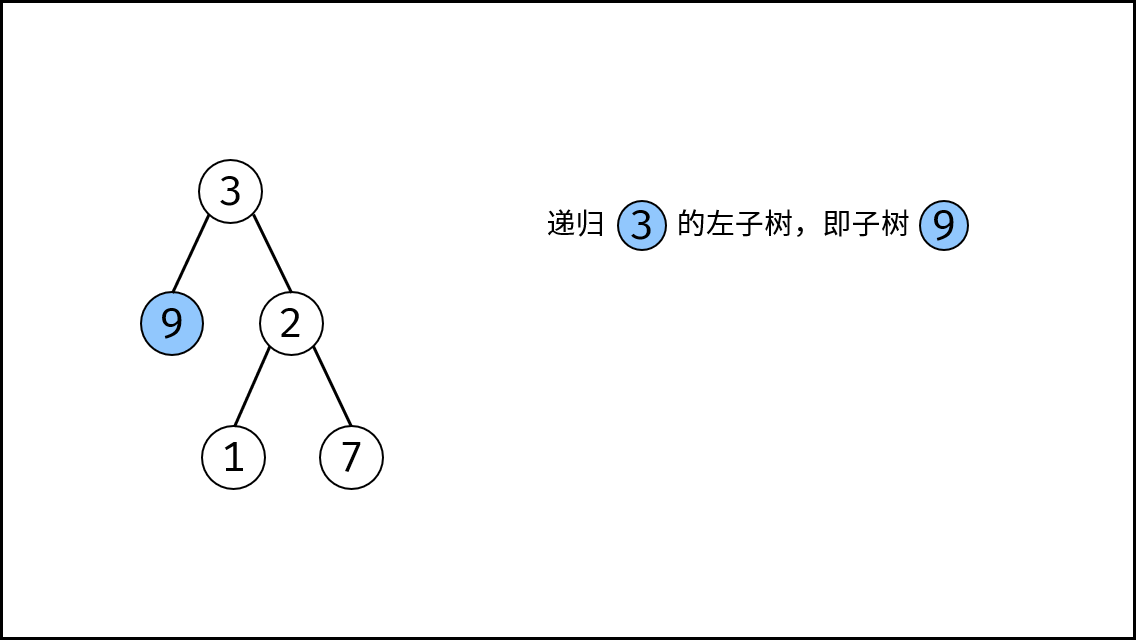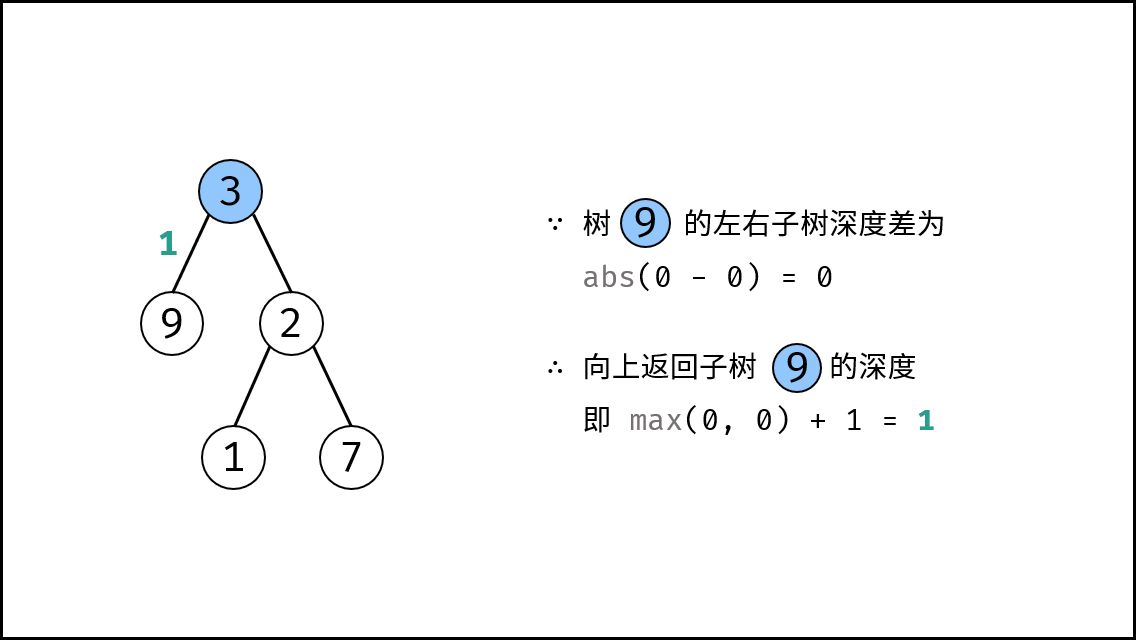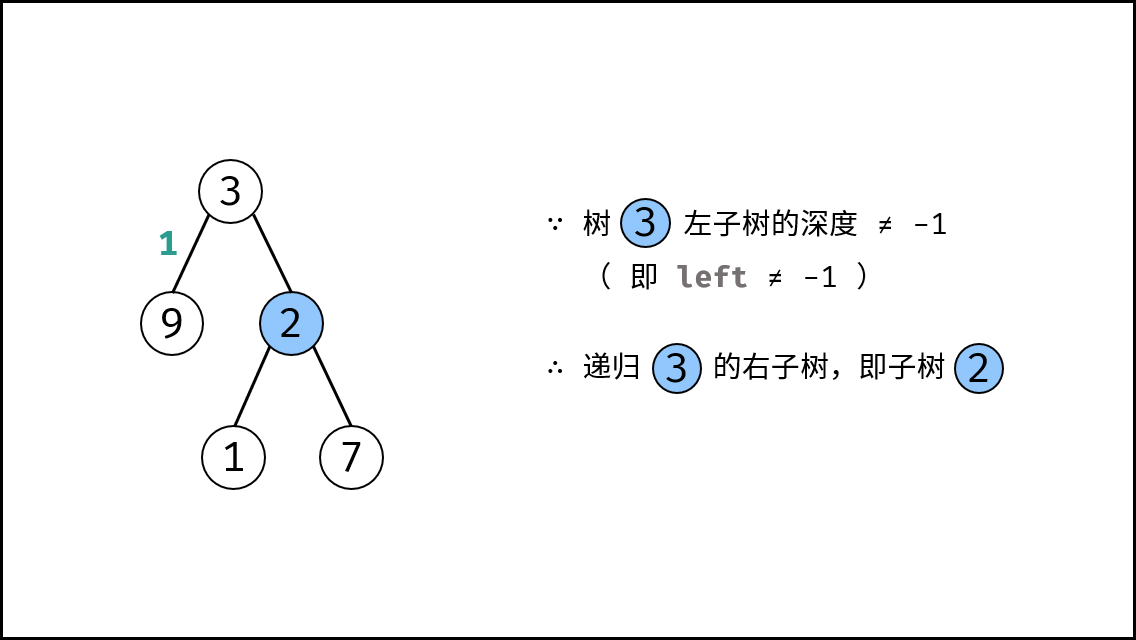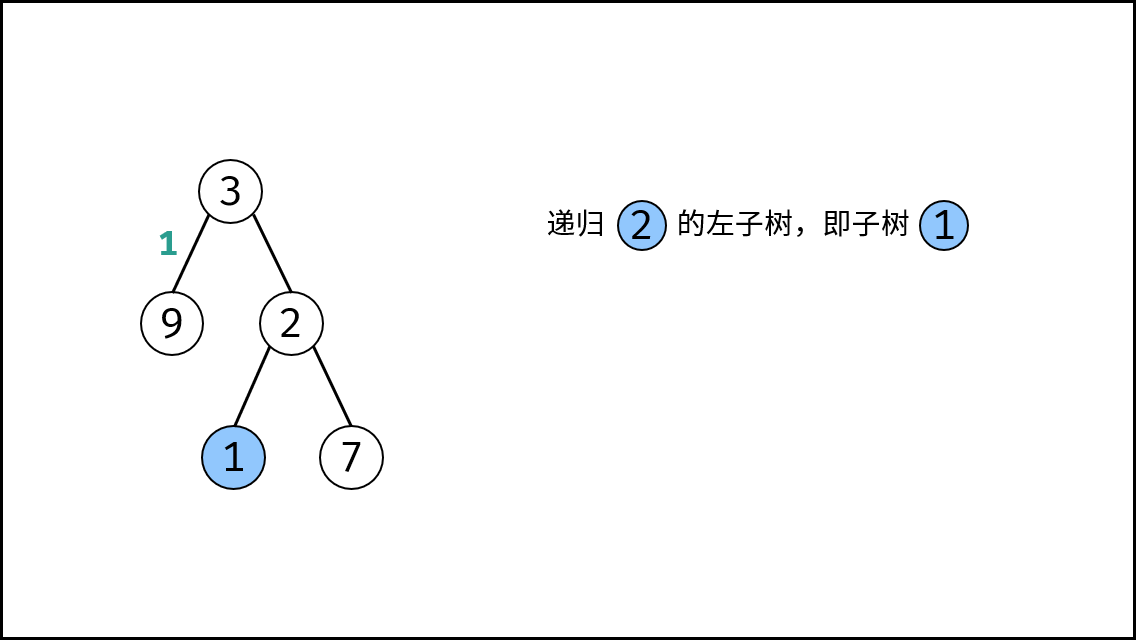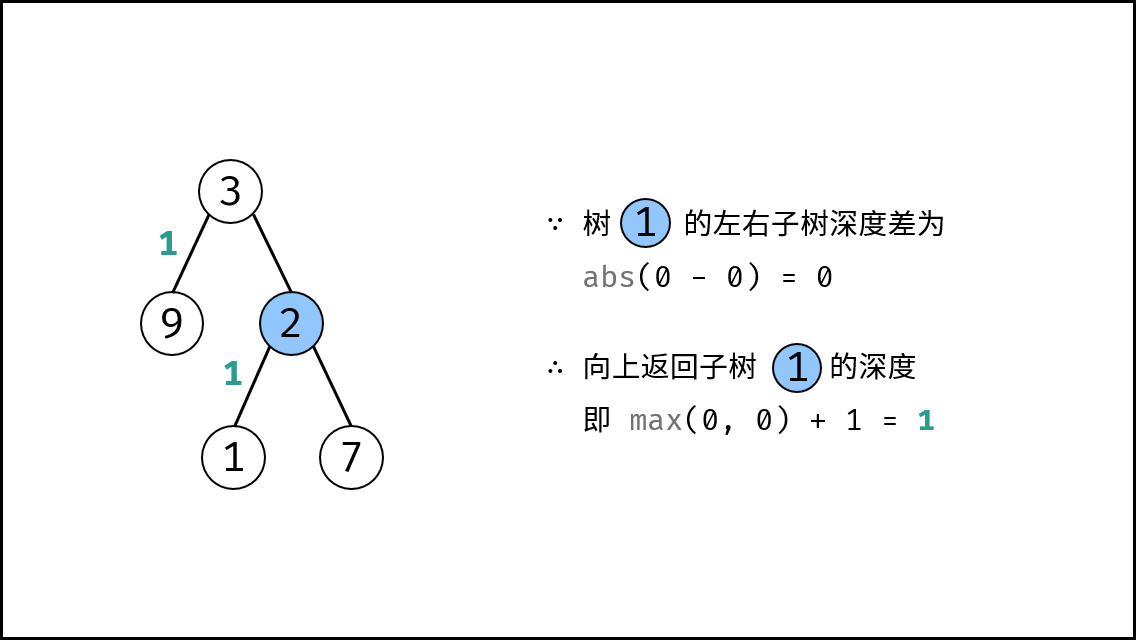<![Picture3.png](https://pic.leetcode-cn.com/1603024695-bBzthj-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603024695-YnYrml-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603024695-oleXkN-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603024695-ntCzMn-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603024695-htsJbo-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1603024695-nQlcgg-Picture8.png),![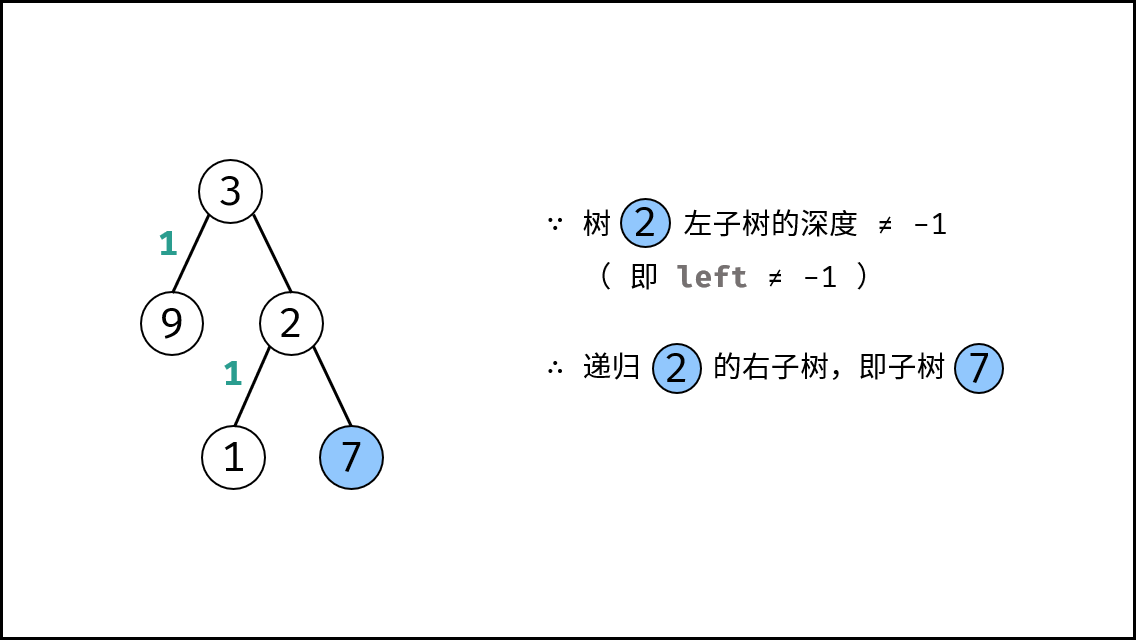Picture9.png](https://pic.leetcode-cn.com/1603024695-uRsaMq-Picture9.png),![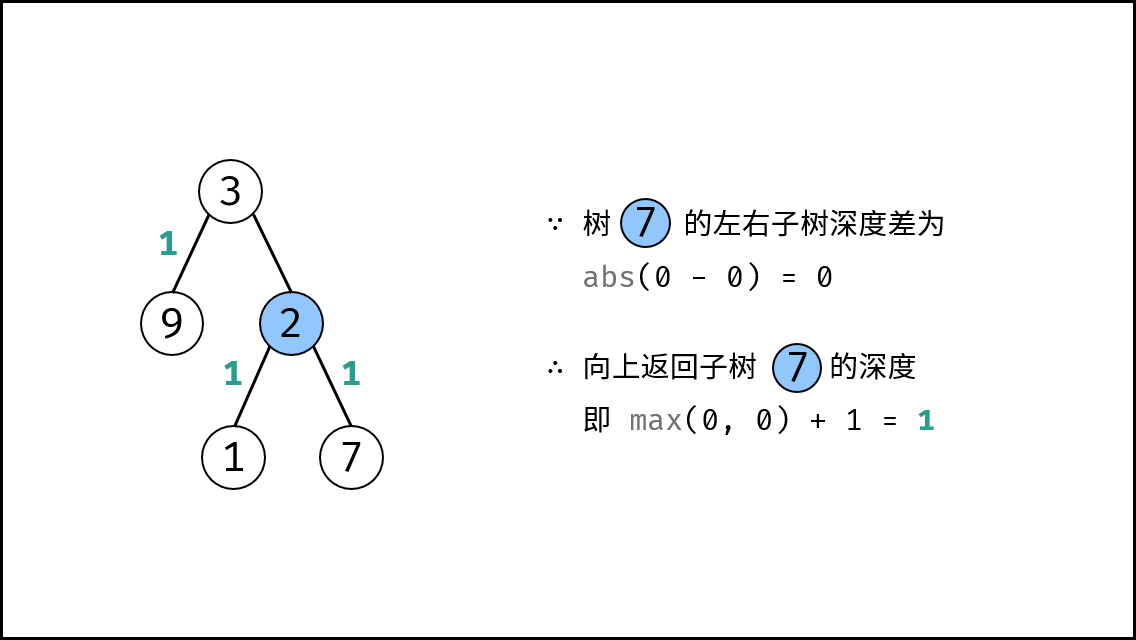Picture10.png](https://pic.leetcode-cn.com/1603024695-uuYLyq-Picture10.png),![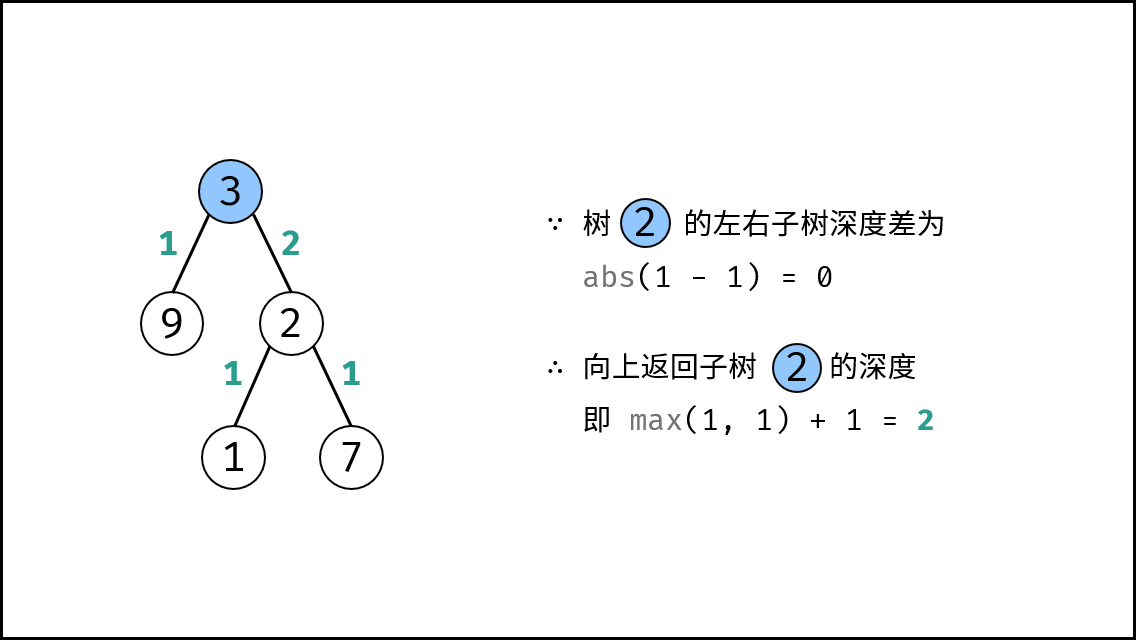Picture11.png](https://pic.leetcode-cn.com/1603024695-TRJhDI-Picture11.png),![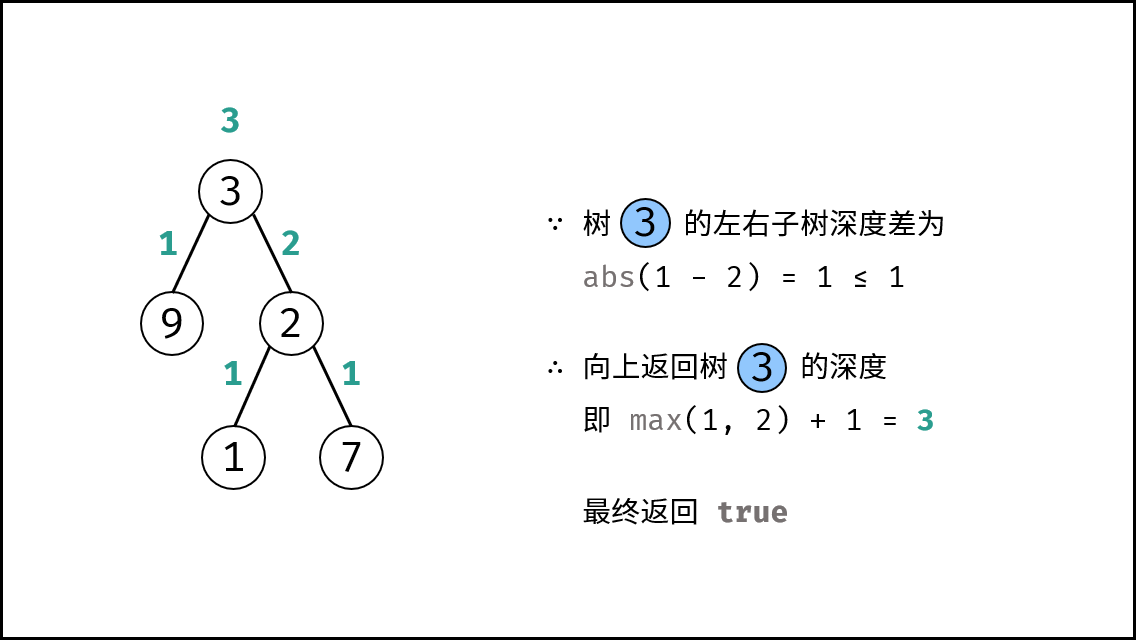Picture12.png](https://pic.leetcode-cn.com/1603024695-Jqbiev-Picture12.png)>
### 代码：
```Python []
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def recur(root):
if not root: return 0
left = recur(root.left)
if left == -1: return -1
right = recur(root.right)
if right == -1: return -1
return max(left, right) + 1 if abs(left - right) <= 1 else -1
return recur(root) != -1
```
```Java []
class Solution {
public boolean isBalanced(TreeNode root) {
return recur(root) != -1;
}
private int recur(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
if(left == -1) return -1;
int right = recur(root.right);
if(right == -1) return -1;
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
```
```C++ []
class Solution {
public:
bool isBalanced(TreeNode* root) {
return recur(root) != -1;
}
private:
int recur(TreeNode* root) {
if (root == nullptr) return 0;
int left = recur(root->left);
if(left == -1) return -1;
int right = recur(root->right);
if(right == -1) return -1;
return abs(left - right) < 2 ? max(left, right) + 1 : -1;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$：** $N$ 为树的节点数；最差情况下，需要递归遍历树的所有节点。
- **空间复杂度 $O(N)$：** 最差情况下（树退化为链表时），系统递归需要使用 $O(N)$ 的栈空间。
## 方法二：先序遍历 + 判断深度 （从顶至底）
> 此方法容易想到，但会产生大量重复计算，时间复杂度较高。
思路是构造一个获取当前子树的深度的函数 `depth(root)` （即 [面试题55 - I. 二叉树的深度](https://leetcode-cn.com/problems/er-cha-shu-de-shen-du-lcof/solution/mian-shi-ti-55-i-er-cha-shu-de-shen-du-xian-xu-bia/) ），通过比较某子树的左右子树的深度差 `abs(depth(root.left) - depth(root.right)) <= 1` 是否成立，来判断某子树是否是二叉平衡树。若所有子树都平衡，则此树平衡。
### 算法流程：
**`isBalanced(root)` 函数：** 判断树 `root` 是否平衡
- **特例处理：** 若树根节点 `root` 为空，则直接返回 $\text{true}$ ；
- **返回值：** 所有子树都需要满足平衡树性质，因此以下三者使用与逻辑 $\&\&$ 连接；
1. `abs(self.depth(root.left) - self.depth(root.right)) <= 1` ：判断 **当前子树** 是否是平衡树；
2. `self.isBalanced(root.left)` ： 先序遍历递归，判断 **当前子树的左子树** 是否是平衡树；
3. `self.isBalanced(root.right)` ： 先序遍历递归，判断 **当前子树的右子树** 是否是平衡树；
**`depth(root)` 函数：** 计算树 `root` 的深度
- **终止条件：** 当 `root` 为空，即越过叶子节点，则返回高度 $0$ ；
- **返回值：** 返回左 / 右子树的深度的最大值 $+1$ 。
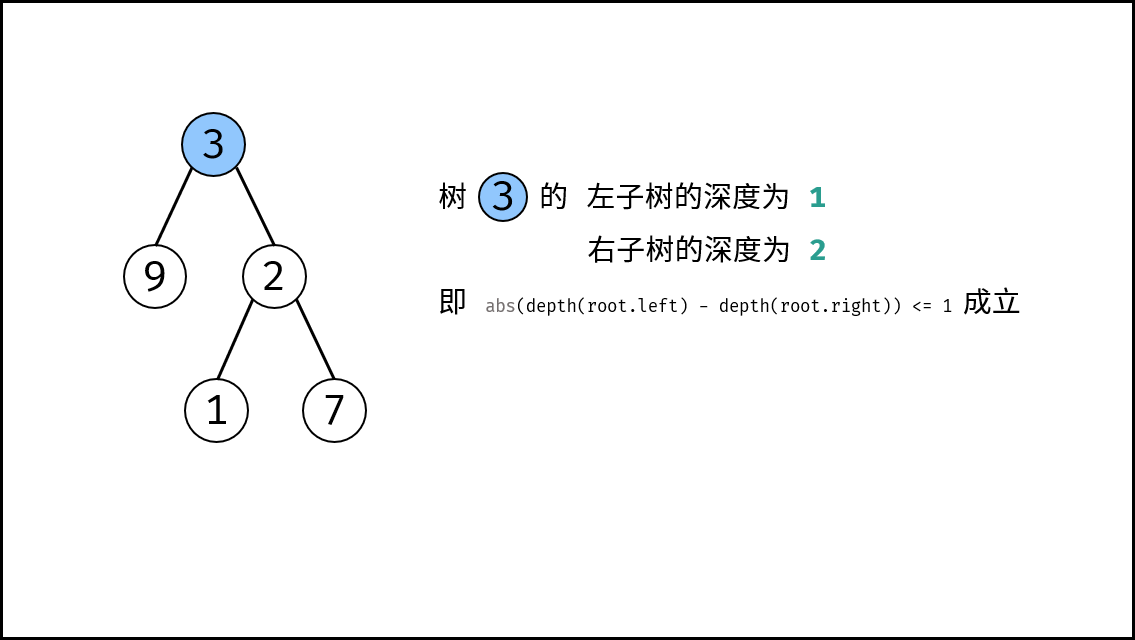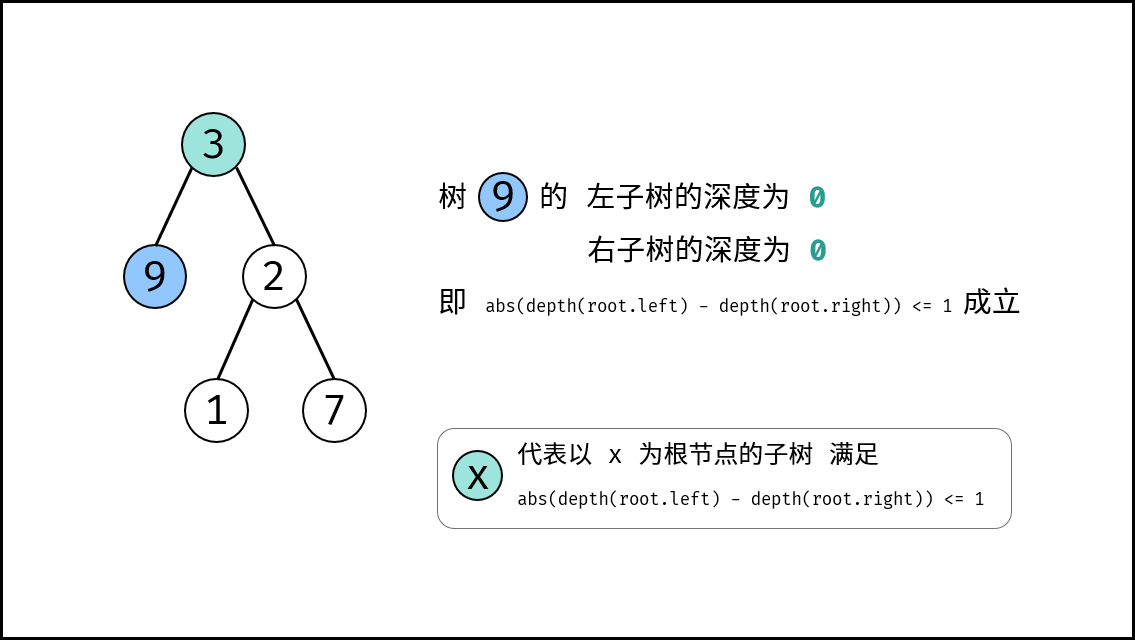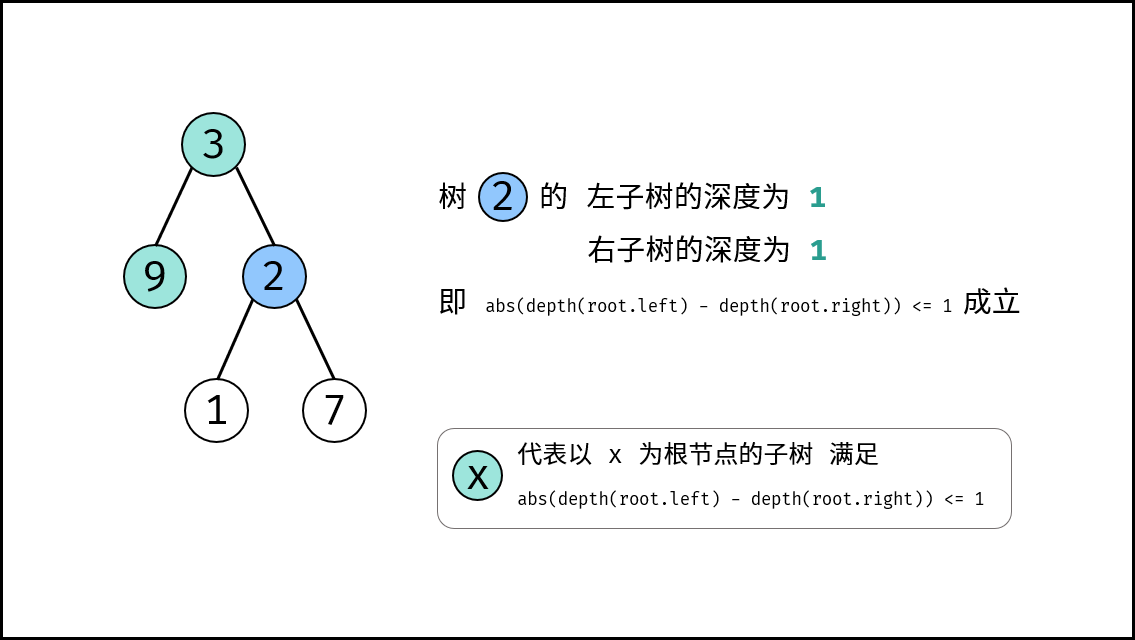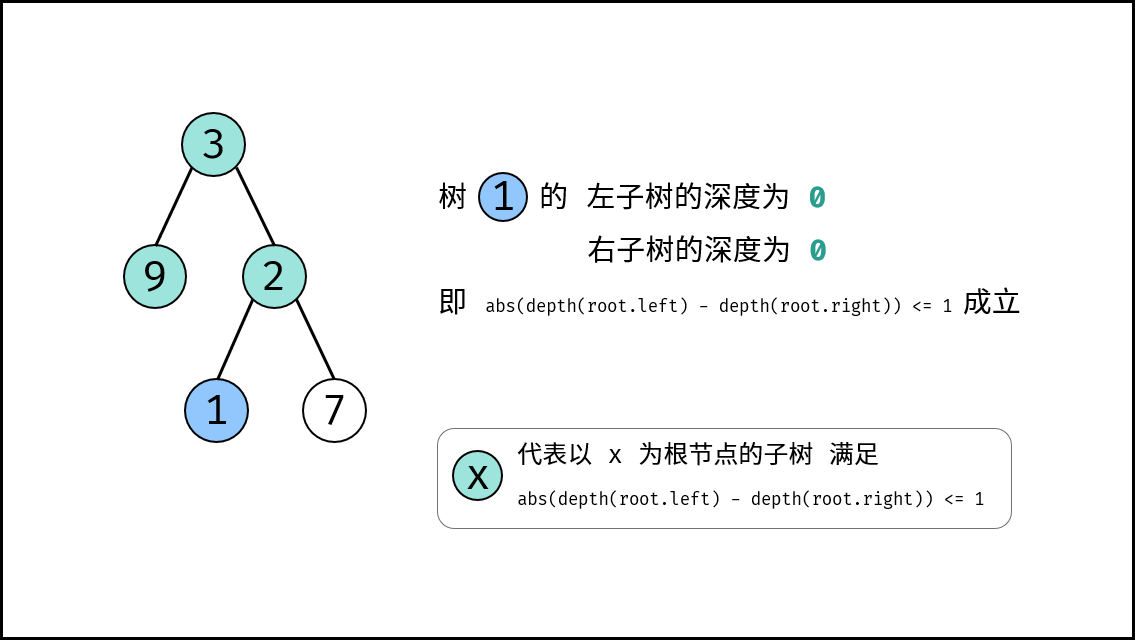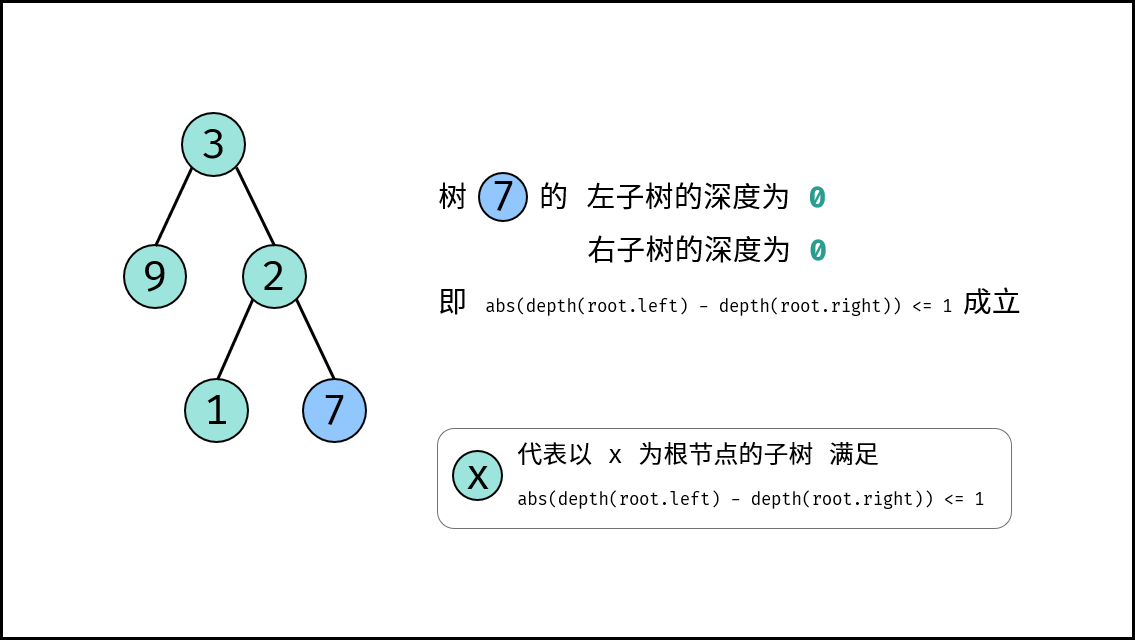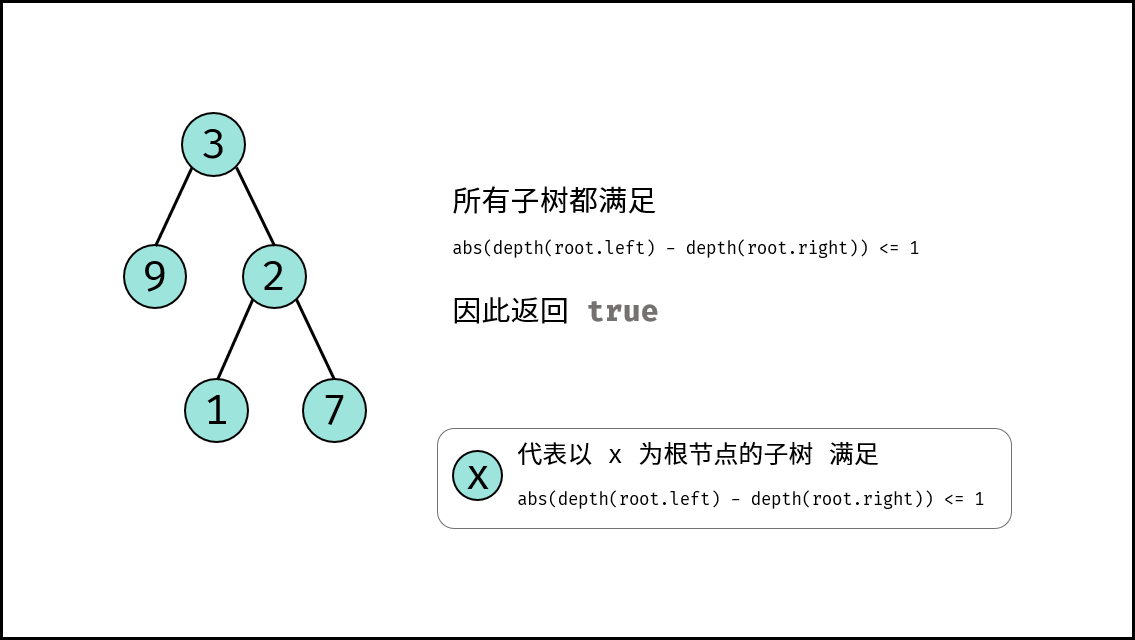<![Picture13.png](https://pic.leetcode-cn.com/1603024695-arQZak-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1603024695-ROWicj-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1603024695-pJrxlo-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1603024695-RfTiKq-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1603024695-uuegMD-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1603024695-cHrqSg-Picture18.png)>
### 代码：
```Python []
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root: return True
return abs(self.depth(root.left) - self.depth(root.right)) <= 1 and \
self.isBalanced(root.left) and self.isBalanced(root.right)
def depth(self, root):
if not root: return 0
return max(self.depth(root.left), self.depth(root.right)) + 1
```
```Java []
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
private int depth(TreeNode root) {
if (root == null) return 0;
return Math.max(depth(root.left), depth(root.right)) + 1;
}
}
```
```C++ []
class Solution {
public:
bool isBalanced(TreeNode* root) {
if (root == nullptr) return true;
return abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}
private:
int depth(TreeNode* root) {
if (root == nullptr) return 0;
return max(depth(root->left), depth(root->right)) + 1;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N \log N)$：** 最差情况下（为 “满二叉树” 时），`isBalanced(root)` 遍历树所有节点，判断每个节点的深度 `depth(root)` 需要遍历 **各子树的所有节点** 。
- 满二叉树高度的复杂度 $O(log N)$ ，将满二叉树按层分为 $log (N+1)$ 层；
- 通过调用 `depth(root)` ，判断二叉树各层的节点的对应子树的深度，需遍历节点数量为 $N \times 1, \frac{N-1}{2} \times 2, \frac{N-3}{4} \times 4, \frac{N-7}{8} \times 8, ..., 1 \times \frac{N+1}{2}$ 。因此各层执行 `depth(root)` 的时间复杂度为 $O(N)$ （每层开始，最多遍历 $N$ 个节点，最少遍历 $\frac{N+1}{2}$ 个节点）。
> 其中，$\frac{N-3}{4} \times 4$ 代表从此层开始总共需遍历 $N-3$ 个节点，此层共有 $4$ 个节点，因此每个子树需遍历 $\frac{N-3}{4}$ 个节点。
- 因此，总体时间复杂度 $=$ 每层执行复杂度 $\times$ 层数复杂度 = $O(N \times \log N)$ 。
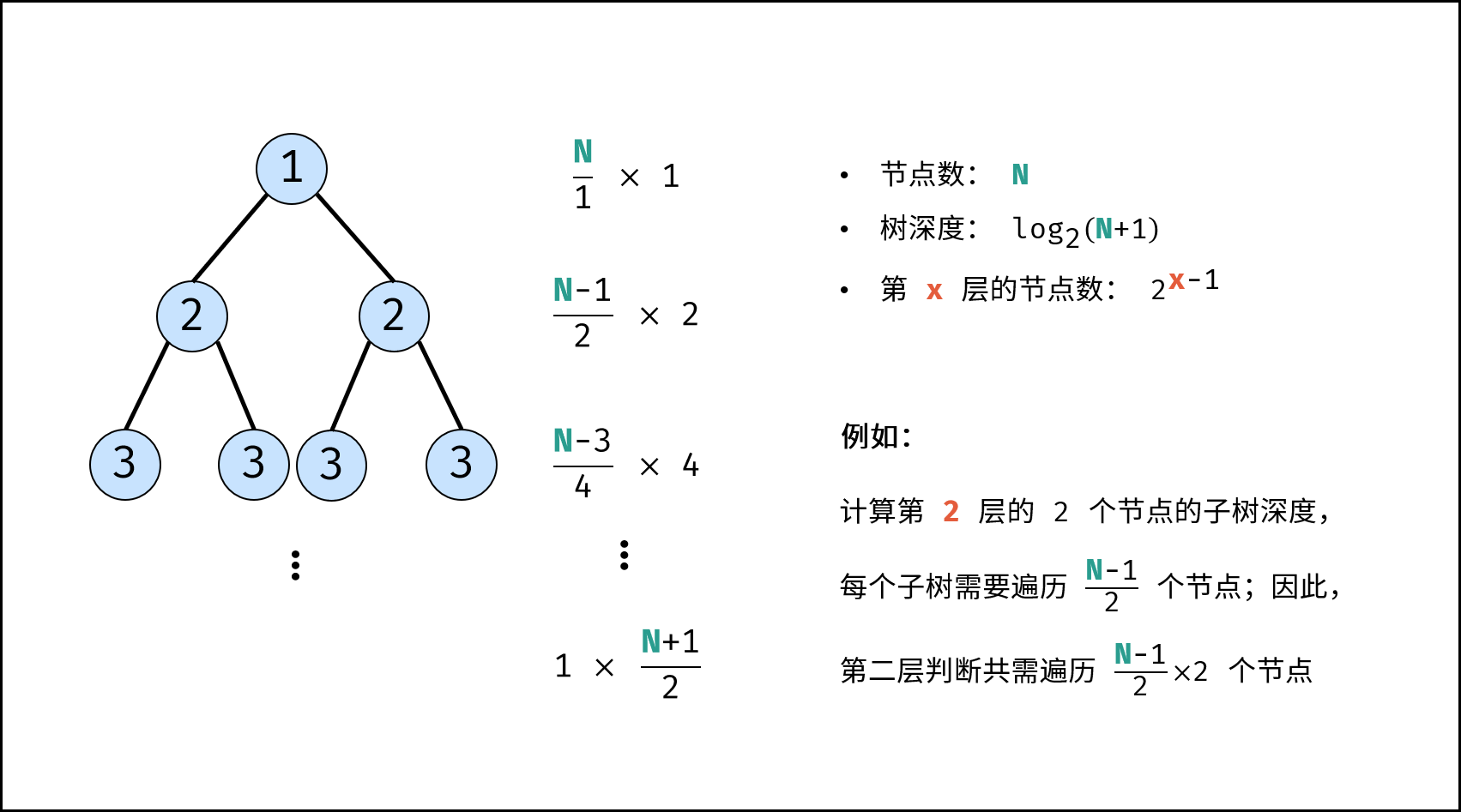![Picture2.png](https://pic.leetcode-cn.com/1603024695-yyFsRH-Picture2.png){:align=center width=550}
- **空间复杂度 $O(N)$：** 最差情况下（树退化为链表时），系统递归需要使用 $O(N)$ 的栈空间。

190
leetbook_ioa/docs/LCR 177. 撞色搭配.md Executable file
View File

@@ -0,0 +1,190 @@
## 解题思路：
题目要求时间复杂度 $O(N)$ ，空间复杂度 $O(1)$ ，因此首先排除 **暴力法** 和 **哈希表统计法** 。
> **简化问题：** 一个整型数组 `sockets` 里除 **一个** 数字之外，其他数字都出现了两次。
设整型数组 $sockets$ 中出现一次的数字为 $x$ ，出现两次的数字为 $a, a, b, b, ...$ ，即：
$$
sockets = [a, a, b, b, ..., x]
$$
异或运算有个重要的性质，两个相同数字异或为 $0$ ，即对于任意整数 $a$ 有 $a \oplus a = 0$ 。因此，若将 $sockets$ 中所有数字执行异或运算，留下的结果则为 **出现一次的数字 $x$** ，即：
$$
\begin{aligned}
& \ \ a \oplus a \oplus b \oplus b \oplus ... \oplus x \\
= & \ \ 0 \oplus 0 \oplus ... \oplus x \\
= & \ \ x
\end{aligned}
$$
异或运算满足交换律 $a \oplus b = b \oplus a$ ，即以上运算结果与 $sockets$ 的元素顺序无关。代码如下：
```Python []
def singleNumber(self, sockets: List[int]) -> List[int]:
x = 0
for num in sockets: # 1. 遍历 sockets 执行异或运算
x ^= num
return x; # 2. 返回出现一次的数字 x
```
```Java []
public int[] singleNumber(int[] sockets) {
int x = 0;
for(int num : sockets) // 1. 遍历 sockets 执行异或运算
x ^= num;
return x; // 2. 返回出现一次的数字 x
}
```
```C++ []
vector<int> singleNumber(vector<int>& sockets) {
int x = 0;
for(int num : sockets) // 1. 遍历 sockets 执行异或运算
x ^= num;
return x; // 2. 返回出现一次的数字 x
}
```
> 下图中的 `nums` 对应本题的 `sockets` 。
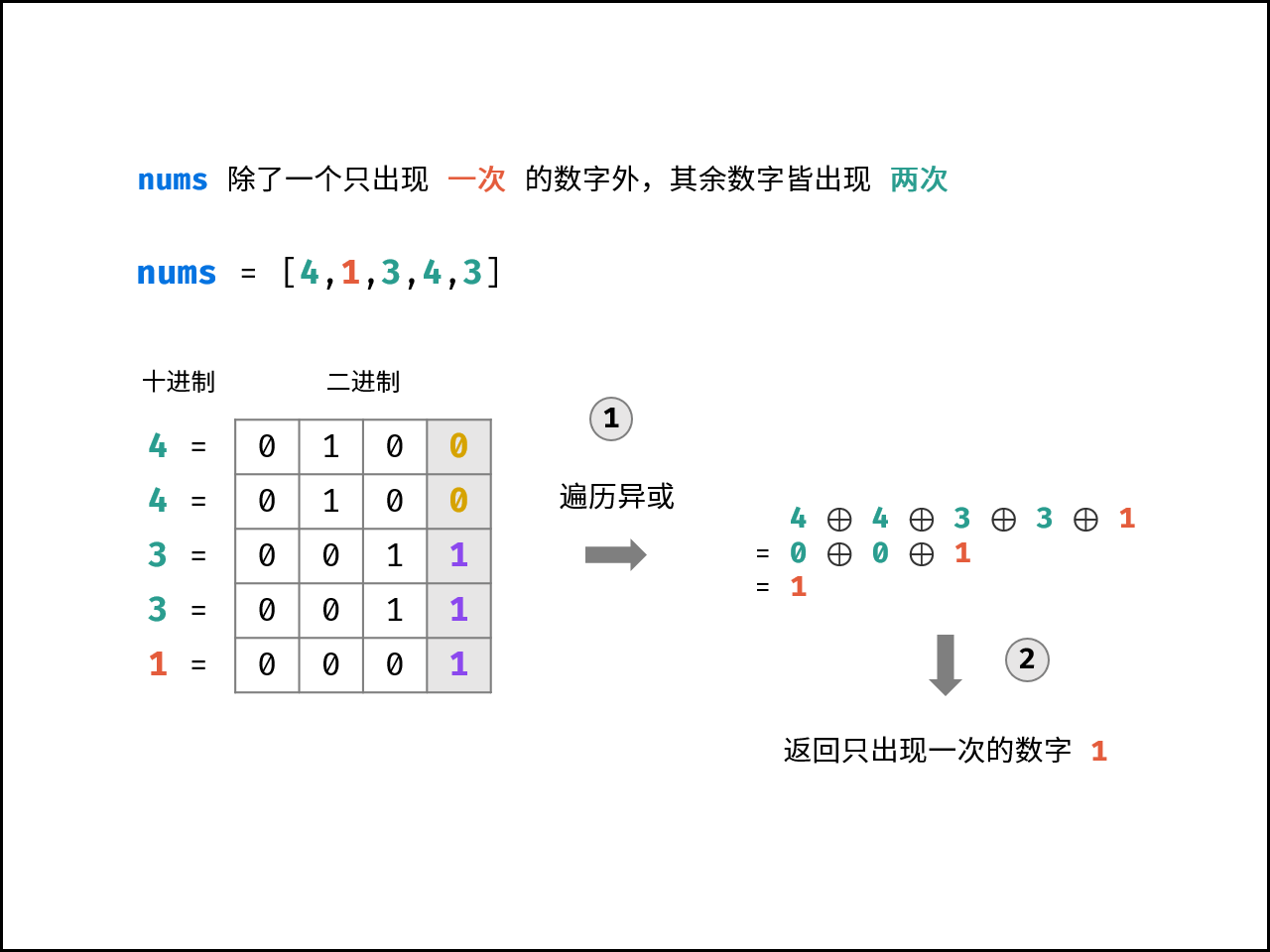![Picture1.png](https://pic.leetcode-cn.com/1611393960-EnUIaQ-Picture1.png){:align=center width=500}
> **本题难点：** 数组 $sockets$ 有 **两个** 只出现一次的数字，因此无法通过异或直接得到这两个数字。
设两个只出现一次的数字为 $x$ , $y$ ，由于 $x \ne y$ ，则 $x$ 和 $y$ 二进制至少有一位不同（即分别为 $0$ 和 $1$ ），根据此位可以将 $sockets$ 拆分为分别包含 $x$ 和 $y$ 的两个子数组。
易知两子数组都满足 「除一个数字之外，其他数字都出现了两次」。因此，仿照以上简化问题的思路，分别对两子数组遍历执行异或操作，即可得到两个只出现一次的数字 $x$, $y$ 。
### 算法流程：
1. **遍历 $sockets$ 执行异或：**
- 设整型数组 $sockets = [a, a, b, b, ..., x, y]$ ，对 $sockets$ 中所有数字执行异或，得到的结果为 $x \oplus y$ ，即：
$$
\begin{aligned}
& \ \ a \oplus a \oplus b \oplus b \oplus ... \oplus x \oplus y \\
= & \ \ 0 \oplus 0 \oplus ... \oplus x \oplus y \\
= & \ \ x \oplus y
\end{aligned}
$$
2. **循环左移计算 $m$ ：**
- 根据异或运算定义，若整数 $x \oplus y$ 某二进制位为 $1$ ，则 $x$ 和 $y$ 的此二进制位一定不同。换言之，找到 $x \oplus y$ 某为 $1$ 的二进制位，即可将数组 $sockets$ 拆分为上述的两个子数组。根据与运算特点，可知对于任意整数 $a$ 有：
- 若 $a \& 0001 \ne 0$ ，则 $a$ 的第一位为 $1$ ；
- 若 $a \& 0010 \ne 0$ ，则 $a$ 的第二位为 $1$ ；
- 以此类推……
- 因此，初始化一个辅助变量 $m = 1$ ，通过与运算从右向左循环判断，可 **获取整数 $x \oplus y$ 首位 $1$** ，记录于 $m$ 中，代码如下：
```Python []
while z & m == 0: # m 循环左移一位，直到 z & m ！= 0
m <<= 1
```
```Java []
while(z & m == 0) // m 循环左移一位，直到 z & m ！= 0
m <<= 1
```
```C++ []
while(z & m == 0) // m 循环左移一位，直到 z & m ！= 0
m <<= 1
```
3. **拆分 $sockets$ 为两个子数组：**
4. **分别遍历两个子数组执行异或：**
- 通过遍历判断 $sockets$ 中各数字和 $m$ 做与运算的结果，可将数组拆分为两个子数组，并分别对两个子数组遍历求异或，则可得到两个只出现一次的数字，代码如下：
```Python []
for num in sockets:
if num & m: x ^= num # 若 num & m != 0 , 划分至子数组 1 ，执行遍历异或
else: y ^= num # 若 num & m == 0 , 划分至子数组 2 ，执行遍历异或
return x, y # 遍历异或完毕，返回只出现一次的数字 x 和 y
```
```Java []
for(int num: sockets) {
if((num & m) != 0) x ^= num; // 若 num & m != 0 , 划分至子数组 1 ，执行遍历异或
else y ^= num; // 若 num & m == 0 , 划分至子数组 2 ，执行遍历异或
}
return new int[] {x, y}; // 遍历异或完毕，返回只出现一次的数字 x 和 y
```
```C++ []
for(int num : sockets) {
if(num & m) x ^= num; // 若 num & m != 0 , 划分至子数组 1 ，执行遍历异或
else y ^= num; // 若 num & m == 0 , 划分至子数组 2 ，执行遍历异或
}
return vector<int> {x, y}; // 遍历异或完毕，返回只出现一次的数字 x 和 y
```
5. **返回值**：
- 返回只出现一次的数字 x, y 即可。
> 下图中的 `nums` 对应本题的 `sockets` 。
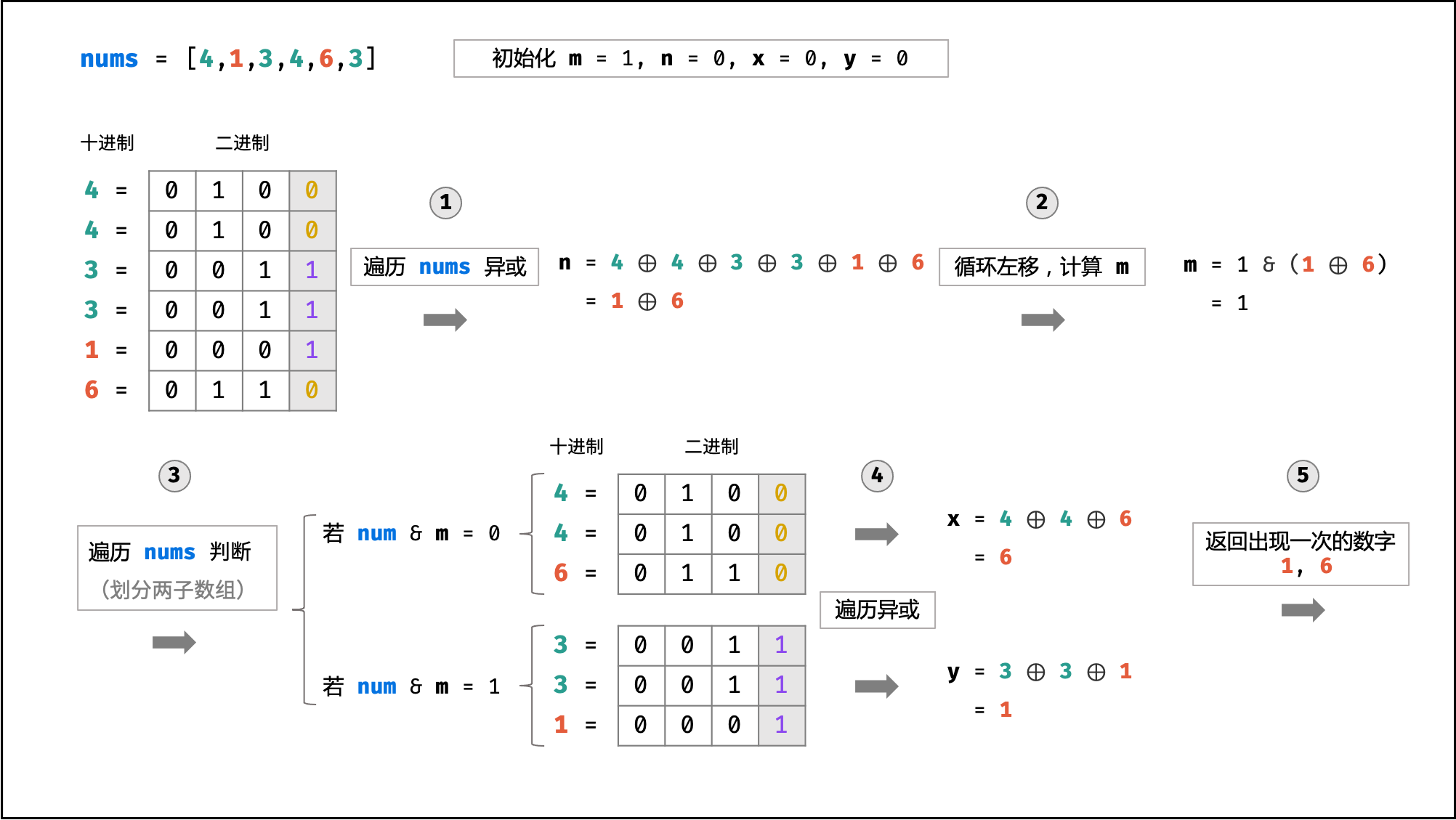
![Picture2.png](https://pic.leetcode-cn.com/1614836837-oygHyk-Picture2.png)
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 线性遍历 $sockets$ 使用 $O(N)$ 时间，遍历 $x \oplus y$ 二进制位使用 $O(32) = O(1)$ 时间。
- **空间复杂度 $O(1)$ ：** 辅助变量 $a$ , $b$ , $x$ , $y$ 使用常数大小额外空间。
## 代码：
```Python []
class Solution:
def sockCollocation(self, sockets: List[int]) -> List[int]:
x, y, n, m = 0, 0, 0, 1
for num in sockets: # 1. 遍历异或
n ^= num
while n & m == 0: # 2. 循环左移，计算 m
m <<= 1
for num in sockets: # 3. 遍历 sockets 分组
if num & m: x ^= num # 4. 当 num & m != 0
else: y ^= num # 4. 当 num & m == 0
return x, y # 5. 返回出现一次的数字
```
```Java []
class Solution {
public int[] sockCollocation(int[] sockets) {
int x = 0, y = 0, n = 0, m = 1;
for(int num : sockets) // 1. 遍历异或
n ^= num;
while((n & m) == 0) // 2. 循环左移，计算 m
m <<= 1;
for(int num: sockets) { // 3. 遍历 sockets 分组
if((num & m) != 0) x ^= num; // 4. 当 num & m != 0
else y ^= num; // 4. 当 num & m == 0
}
return new int[] {x, y}; // 5. 返回出现一次的数字
}
}
```
```C++ []
class Solution {
public:
vector<int> sockCollocation(vector<int>& sockets) {
int x = 0, y = 0, n = 0, m = 1;
for(int num : sockets) // 1. 遍历异或
n ^= num;
while((n & m) == 0) // 2. 循环左移，计算 m
m <<= 1;
for(int num : sockets) { // 3. 遍历 sockets 分组
if(num & m) x ^= num; // 4. 当 num & m != 0
else y ^= num; // 4. 当 num & m == 0
}
return vector<int> {x, y}; // 5. 返回出现一次的数字
}
};
```

287
leetbook_ioa/docs/LCR 178. 训练计划 VI.md Executable file
View File

@@ -0,0 +1,287 @@
## 解题思路：
如下图所示，考虑数字的二进制形式，对于出现三次的数字，各 **二进制位** 出现的次数都是 $3$ 的倍数。
因此，统计所有数字的各二进制位中 $1$ 的出现次数，并对 $3$ 求余，结果则为只出现一次的数字。
> 下图中的 `nums` 对应本题的 `actions` 。
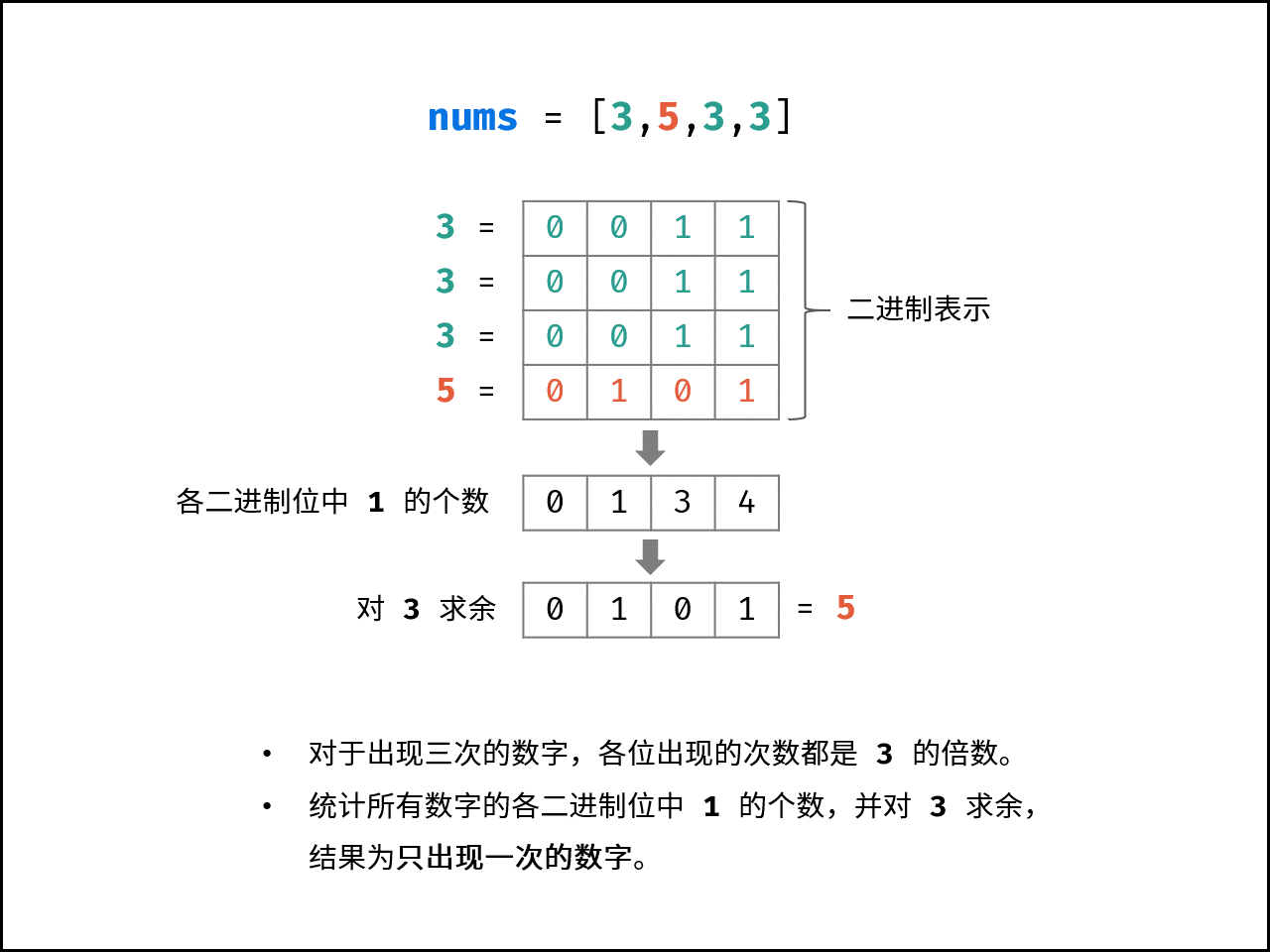![Picture1.png](https://pic.leetcode-cn.com/1603022900-quEtJr-Picture1.png){:align=center width=450}
## 方法一：有限状态自动机
各二进制位的 **位运算规则相同** ，因此只需考虑一位即可。如下图所示，对于所有数字中的某二进制位 $1$ 的个数，存在 3 种状态，即对 3 余数为 $0, 1, 2$ 。
- 若输入二进制位 $1$ ，则状态按照以下顺序转换；
- 若输入二进制位 $0$ ，则状态不变。
$$
0 \rightarrow 1 \rightarrow 2 \rightarrow 0 \rightarrow \cdots
$$
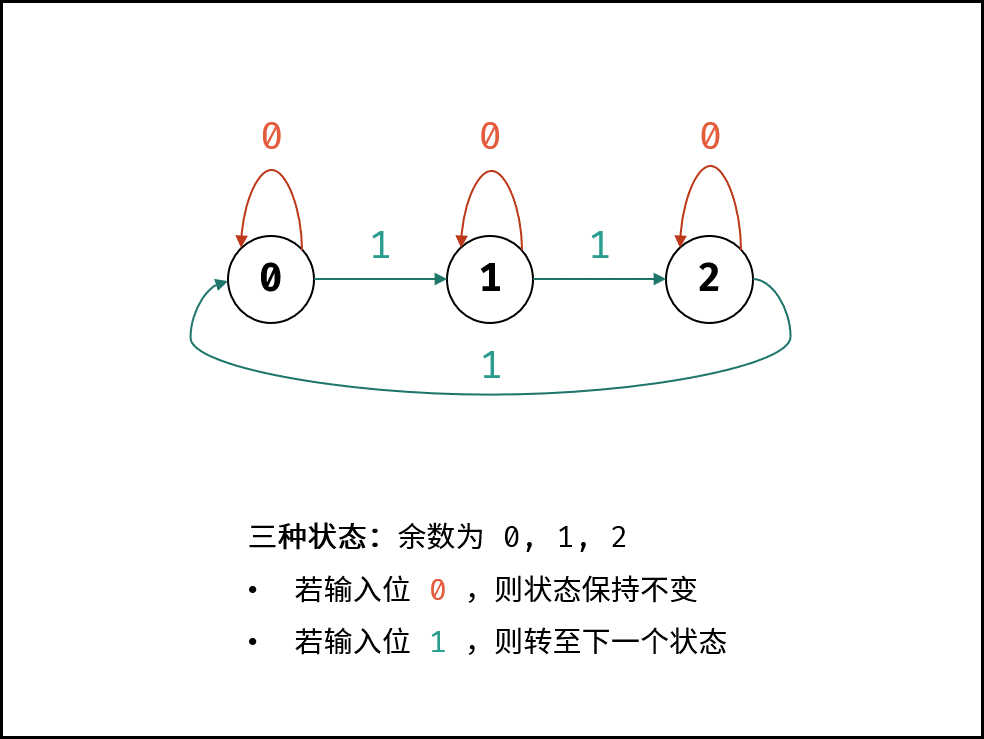![Picture2.png](https://pic.leetcode-cn.com/1603022900-GNKGMP-Picture2.png){:align=center width=450}
如下图所示，由于二进制只能表示 $0, 1$ ，因此需要使用两个二进制位来表示 $3$ 个状态。设此两位分别为 $two$ , $one$ ，则状态转换变为：
$$
00 \rightarrow 01 \rightarrow 10 \rightarrow 00 \rightarrow \cdots
$$
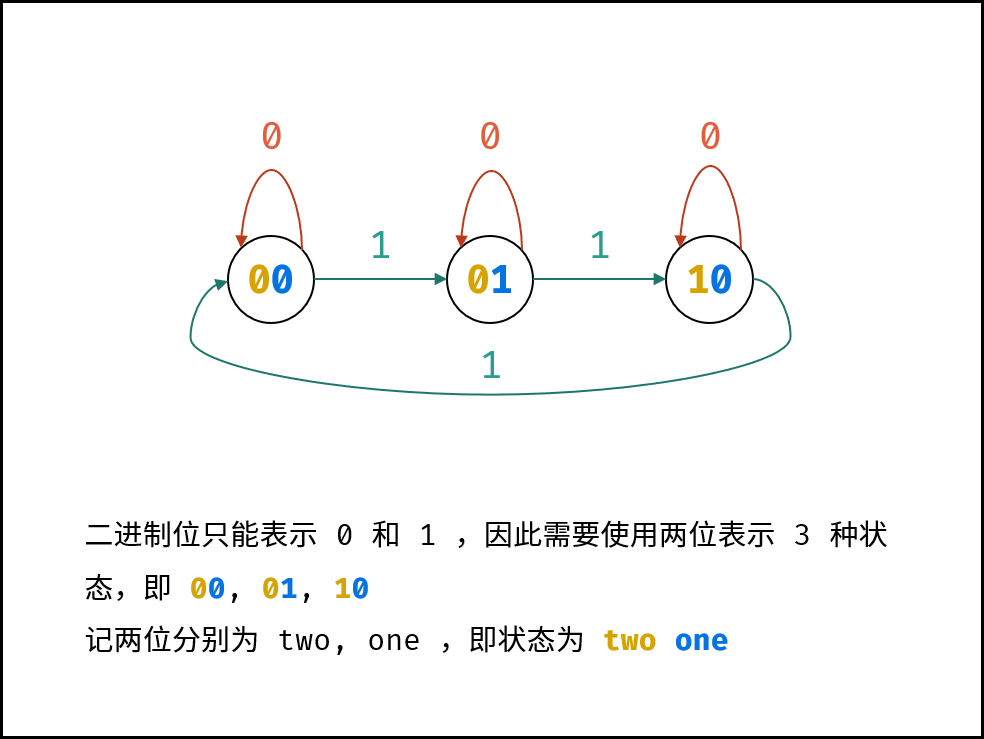![Picture3.png](https://pic.leetcode-cn.com/1603022900-nPXQLk-Picture3.png){:align=center width=450}
接下来，需要通过 **状态转换表** 导出 **状态转换的计算公式** 。首先回忆一下位运算特点，对于任意二进制位 $x$ ，有：
- 异或运算：`x ^ 0 = x`​ ，`x ^ 1 = ~x`
- 与运算：`x & 0 = 0` ，`x & 1 = x`
**计算 $one$ 方法：**
设当前状态为 $two$ $one$ ，此时输入二进制位 $n$ 。如下图所示，通过对状态表的情况拆分，可推出 $one$ 的计算方法为：
```Python
if two == 0:
if n == 0:
one = one
if n == 1:
one = ~one
if two == 1:
one = 0
```
引入 **异或运算** ，可将以上拆分简化为：
```Python
if two == 0:
one = one ^ n
if two == 1:
one = 0
```
引入 **与运算** ，可继续简化为：
```Python
one = one ^ n & ~two
```
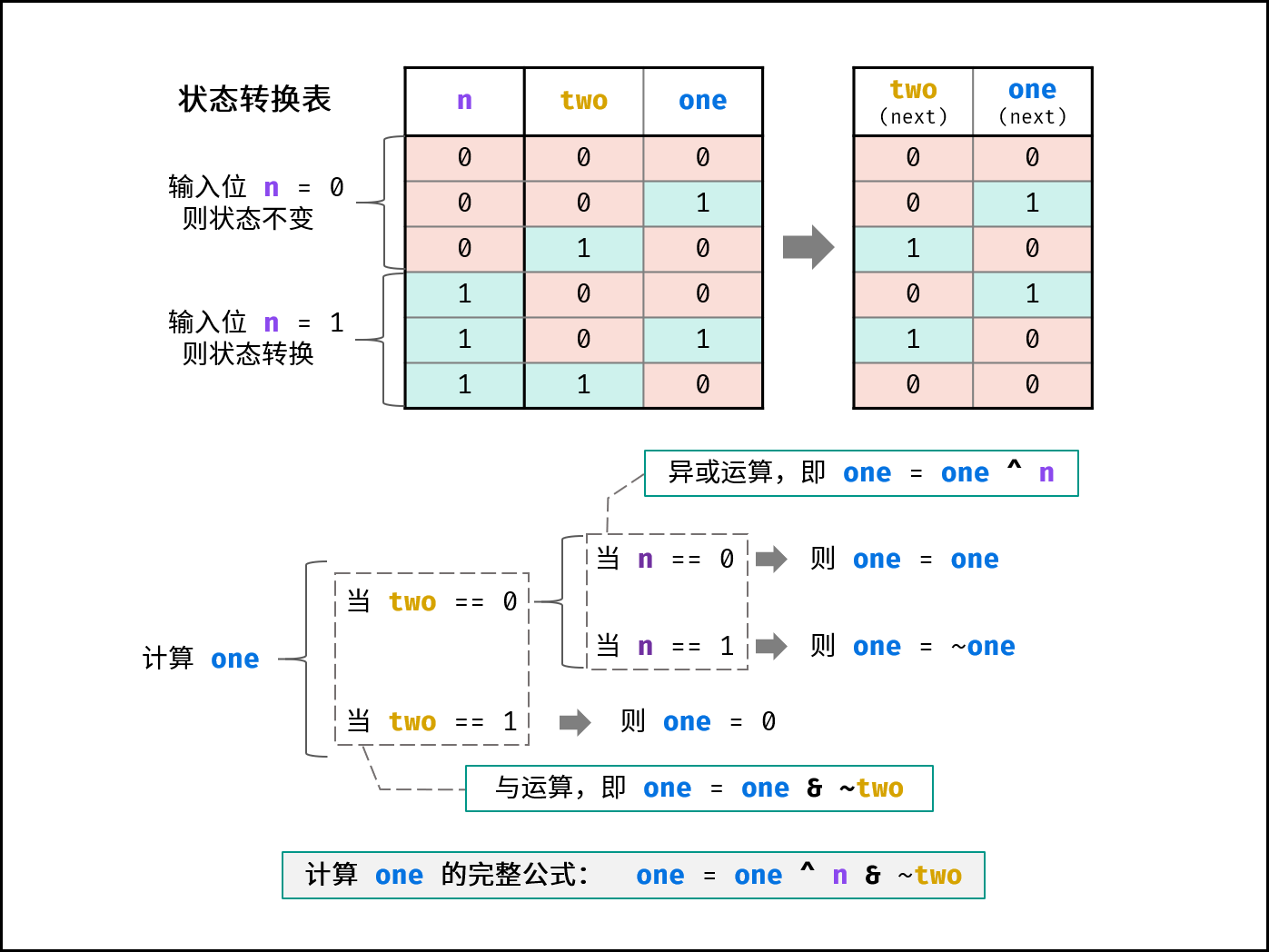![Picture4.png](https://pic.leetcode-cn.com/1603022900-qIFpAR-Picture4.png){:align=center width=550}
**计算 $two$ 方法：**
由于是先计算 $one$ ，因此应在新 $one$ 的基础上计算 $two$ 。
如下图所示，修改为新 $one$ 后，得到了新的状态图。观察发现，可以使用同样的方法计算 $two$ ，即：
```Python
two = two ^ n & ~one
```
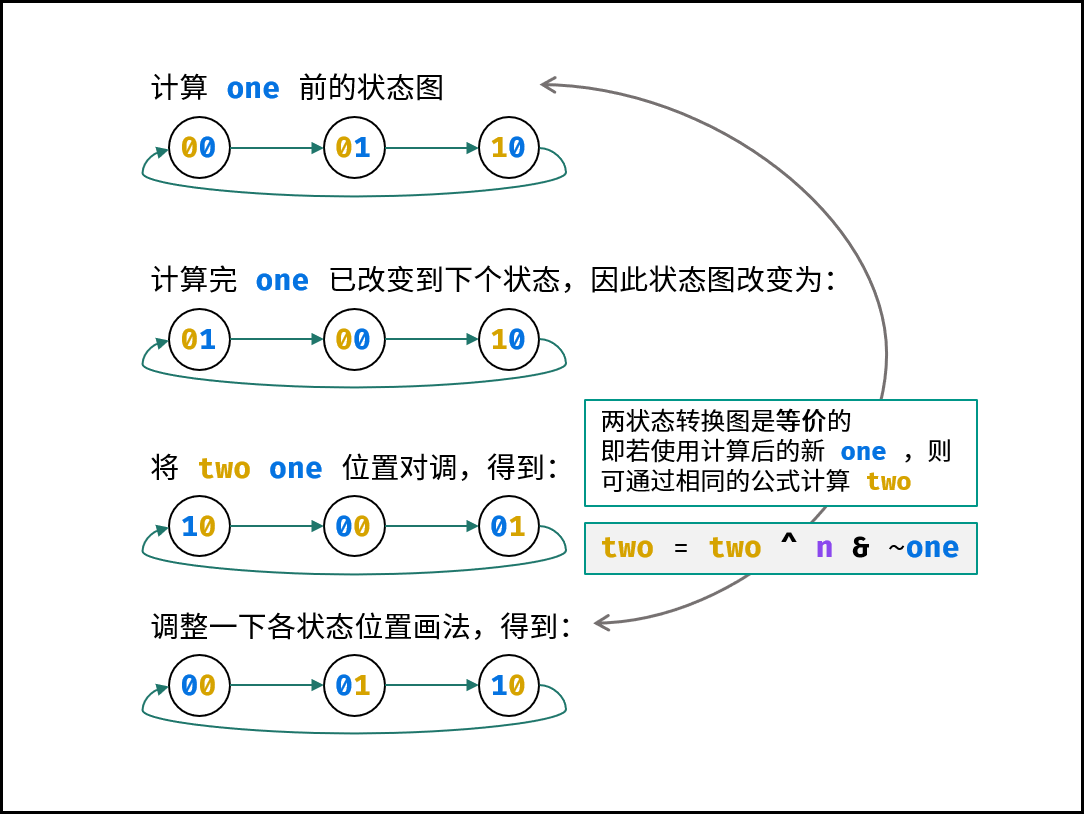![Picture5.png](https://pic.leetcode-cn.com/1603022900-hnUxBz-Picture5.png){:align=center width=450}
**返回值：**
以上是对数字的二进制中 “一位” 的分析，而 `int` 类型的其他 31 位具有相同的运算规则，因此可将以上公式直接套用在 32 位数上。
遍历完所有数字后，各二进制位都处于状态 $00$ 和状态 $01$ （取决于 “只出现一次的数字” 的各二进制位是 $1$ 还是 $0$ ），而此两状态是由 $one$ 来记录的（此两状态下 $twos$ 恒为 $0$ ），因此返回 $ones$ 即可。
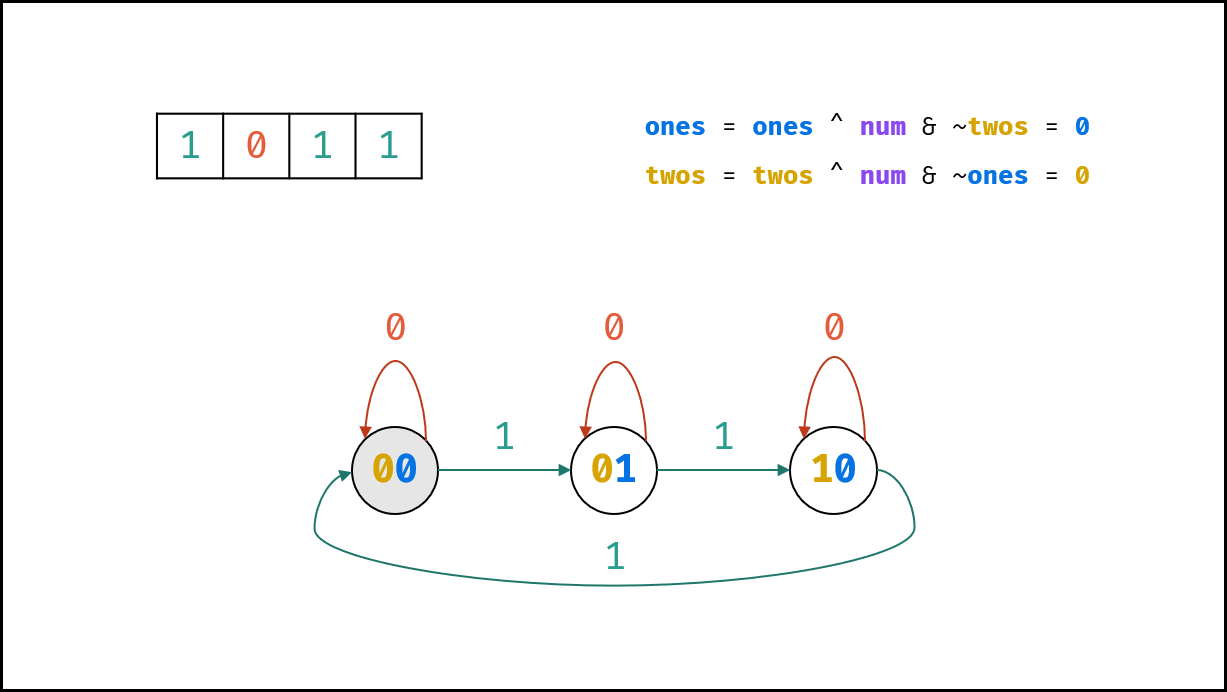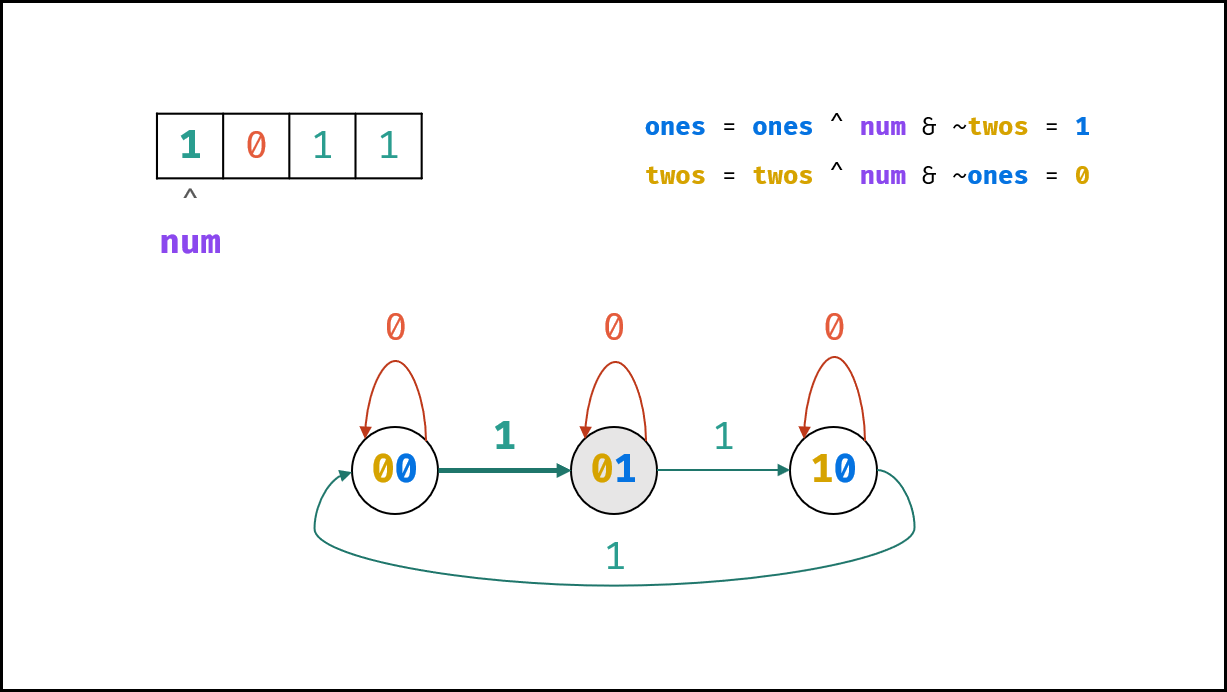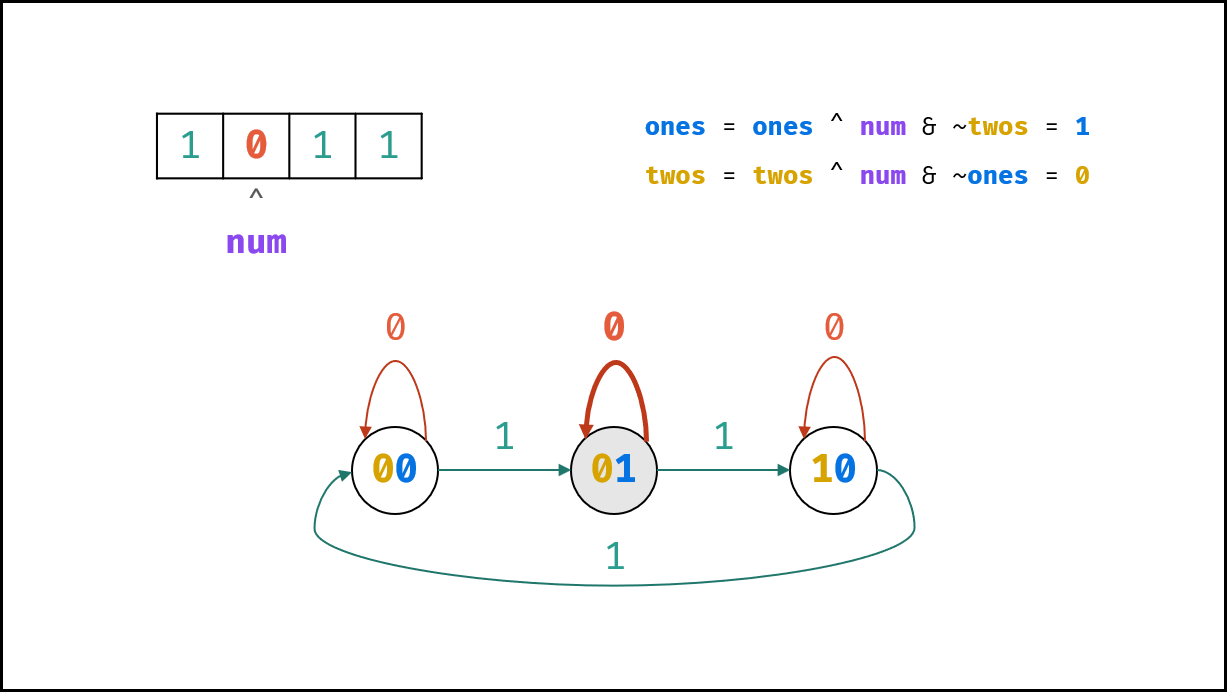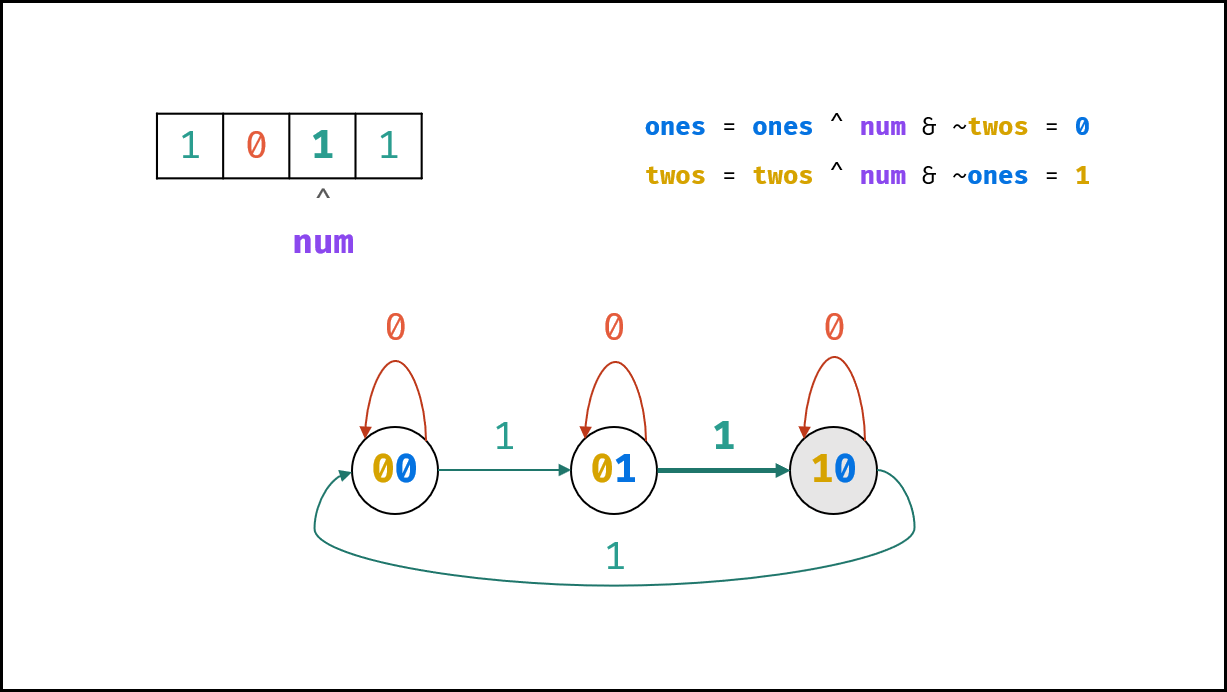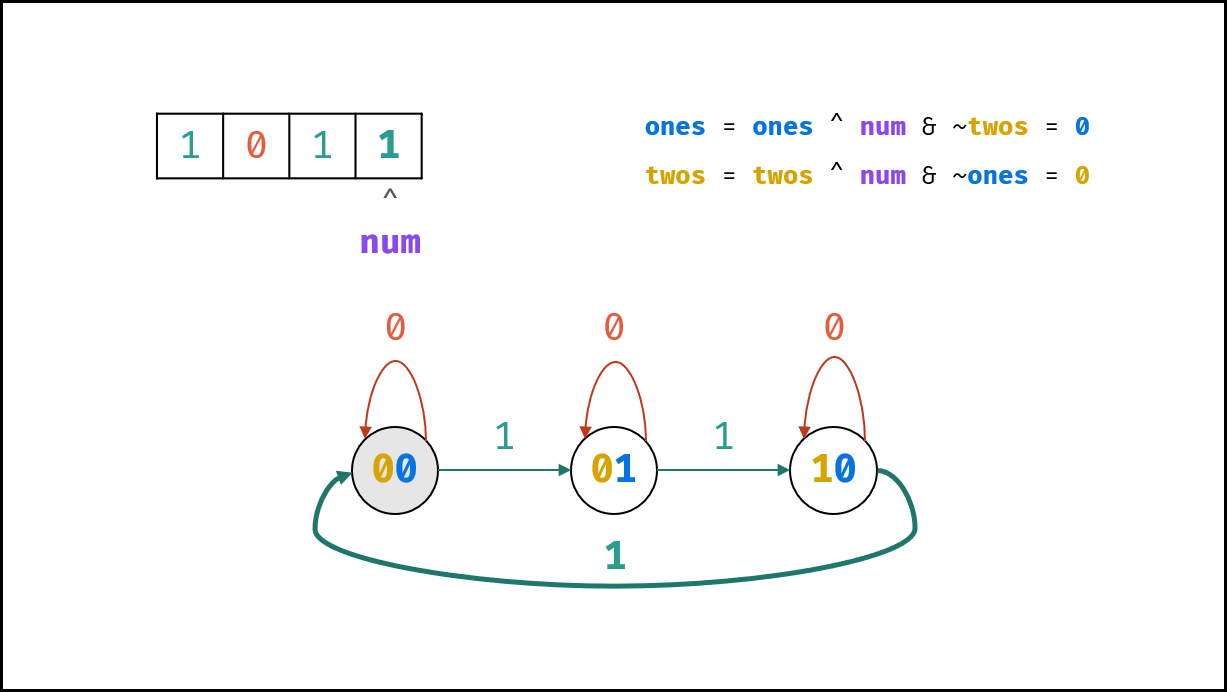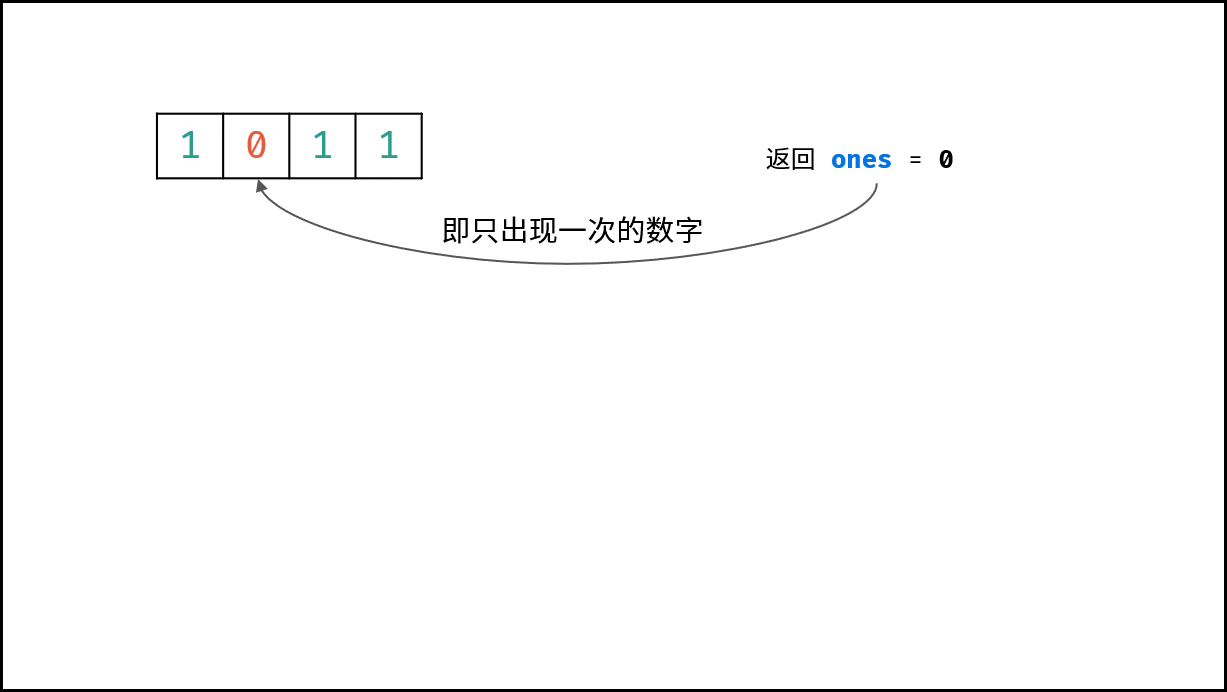<![Picture6.png](https://pic.leetcode-cn.com/1603022900-SczbmE-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603022900-JmEYqX-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1603022900-NjZXDu-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1603022900-aBFKZQ-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1603022900-CdTJxx-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1603022900-xotbQY-Picture11.png)>
### 代码：
```Python []
class Solution:
def trainingPlan(self, actions: List[int]) -> int:
ones, twos = 0, 0
for action in actions:
ones = ones ^ action & ~twos
twos = twos ^ action & ~ones
return ones
```
```Java []
class Solution {
public int trainingPlan(int[] actions) {
int ones = 0, twos = 0;
for(int action : actions){
ones = ones ^ action & ~twos;
twos = twos ^ action & ~ones;
}
return ones;
}
}
```
```C++ []
class Solution {
public:
int trainingPlan(vector<int>& actions) {
int ones = 0, twos = 0;
for(int action : actions){
ones = ones ^ action & ~twos;
twos = twos ^ action & ~ones;
}
return ones;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 位数组 $actions$ 的长度；遍历数组占用 $O(N)$ ，每轮中的常数个位运算操作占用 $O(32 \times3 \times 2) = O(1)$ 。
- **空间复杂度 $O(1)$ ：** 变量 $ones$ , $twos$ 使用常数大小的额外空间。
## 方法二：遍历统计
> 此方法相对容易理解，但效率较低，总体推荐方法一。
使用 **与运算** ，可获取二进制数字 $action$ 的最右一位 $n_1$ ：
$$
n_1 = action \& i
$$
配合 **右移操作** ，可从低位至高位，获取 $action$ 所有位的值（设 int 类型从低至高的位数为第 0 位 至第 31 位，即 $n_0$ ~ $n_{31}$ ）：
$$
action = action >> 1
$$
建立一个长度为 32 的数组 $counts$ ，通过以上方法可记录所有数字的各二进制位的 $1$ 的出现次数之和。
```Python []
counts = [0] * 32
for action in actions:
for i in range(32):
counts[i] += action & 1 # 更新第 i 位 1 的个数之和
action >>= 1 # 第 i 位 --> 第 i + 1 位
```
```Java []
int[] counts = new int[32];
for(int action : actions) {
for(int i = 0; i < 32; i++) {
counts[i] += action & 1; // 更新第 i 位 1 的个数之和
action >>= 1; // 第 i 位 --> 第 i + 1 位
}
}
```
```C++ []
int counts[32] = {0}; // C++ 初始化数组需要写明初始值 0
for(int action : actions) {
for(int i = 0; i < 32; i++) {
counts[i] += action & 1; // 更新第 i 位 1 的个数之和
action >>= 1; // 第 i 位 --> 第 i + 1 位
}
}
```
将 $counts$ 各元素对 $3$ 求余，则结果为 “只出现一次的数字” 的各二进制位。
```Python []
for i in range(31, -1, -1):
x = counts[i] %= 3 # 得到 “只出现一次的数字” 的第 i 位
```
```Java []
for(int i = 31; i >= 0; i--) {
int x = counts[i] %= 3; // 得到 “只出现一次的数字” 的第 i 位
}
```
```C++ []
for(int i = 31; i >= 0; i--) {
int x = counts[i] % 3; // 得到 “只出现一次的数字” 的第 i 位
}
```
利用 **左移操作** 和 **或运算** ，可将 $counts$ 数组中各二进位的值恢复到数字 $res$ 上。
```Python []
for i in range(31, -1, -1):
res <<= 1
res |= counts[i] % 3 # 恢复第 i 位
```
```Java []
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= counts[i] % 3; // 恢复第 i 位
}
```
```C++ []
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= counts[i] % 3; // 恢复第 i 位
}
```
最终返回 $res$ 即可。
> 由于 Python 的存储负数的特殊性，需要先将 $0$ - $31$ 位取反（即 `res ^ 0xffffffff` ），再将所有位取反（即 `~` ）。
> **此组合操作含义：** 将数字 $31$ 以上位取反，$0$ - $31$ 位不变。
### 代码：
实际上，只需要修改求余数值 $m$ ，即可实现解决 **除了一个数字以外，其余数字都出现 $m$ 次** 的通用问题。
> 设 int 类型从低至高的位数为第 0 位 至第 31 位。
```Python []
class Solution:
def trainingPlan(self, actions: List[int]) -> int:
counts = [0] * 32
for action in actions:
for i in range(32):
counts[i] += action & 1 # 更新第 i 位 1 的个数之和
action >>= 1 # 第 i 位 --> 第 i 位
res, m = 0, 3
for i in range(31, -1, -1):
res <<= 1
res |= counts[i] % m # 恢复第 i 位
return res if counts[31] % m == 0 else ~(res ^ 0xffffffff)
```
```Java []
class Solution {
public int trainingPlan(int[] actions) {
int[] counts = new int[32];
for(int action : actions) {
for(int i = 0; i < 32; i++) {
counts[i] += action & 1; // 更新第 i 位 1 的个数之和
action >>= 1; // 第 i 位 --> 第 i 位
}
}
int res = 0, m = 3;
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= counts[i] % m; // 恢复第 i 位
}
return res;
}
}
```
```C++ []
class Solution {
public:
int trainingPlan(vector<int>& actions) {
int counts[32] = {0}; // C++ 初始化数组需要写明初始值 0
for(int action : actions) {
for(int i = 0; i < 32; i++) {
counts[i] += action & 1; // 更新第 i 位 1 的个数之和
action >>= 1; // 第 i 位 --> 第 i 位
}
}
int res = 0, m = 3;
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= counts[i] % m; // 恢复第 i 位
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 位数组 $actions$ 的长度；遍历数组占用 $O(N)$ ，每轮中的常数个位运算操作占用 $O(1)$ 。
- **空间复杂度 $O(1)$ ：** 数组 $counts$ 长度恒为 $32$ ，占用常数大小的额外空间。

80
leetbook_ioa/docs/LCR 179. 查找总价格为目标值的两个商品.md Executable file
View File

@@ -0,0 +1,80 @@
## 解题思路：
利用 HashMap 可以通过遍历数组找到数字组合，时间和空间复杂度均为 $O(N)$ 。
注意本题的 $price$ 是 **排序数组** ，因此可使用 **双指针法** 将空间优化至 $O(1)$ 。
### 算法流程：
1. **初始化：** 双指针 $i$ , $j$ 分别指向数组 $price$ 的左右两端。
2. **循环搜索：** 当双指针相遇时跳出；
1. 计算和 $s = price[i] + price[j]$ ；
2. 若 $s > target$ ，则指针 $j$ 向左移动，即执行 $j = j - 1$ ；
3. 若 $s < target$ ，则指针 $i$ 向右移动，即执行 $i = i + 1$ ；
4. 若 $s = target$ ，立即返回数组 $[price[i], price[j]]$ ；
3. 若循环结束，则返回空数组，代表无和为 $target$ 的数字组合。
> 下图中的 `nums` 对应本题的 `price` 。
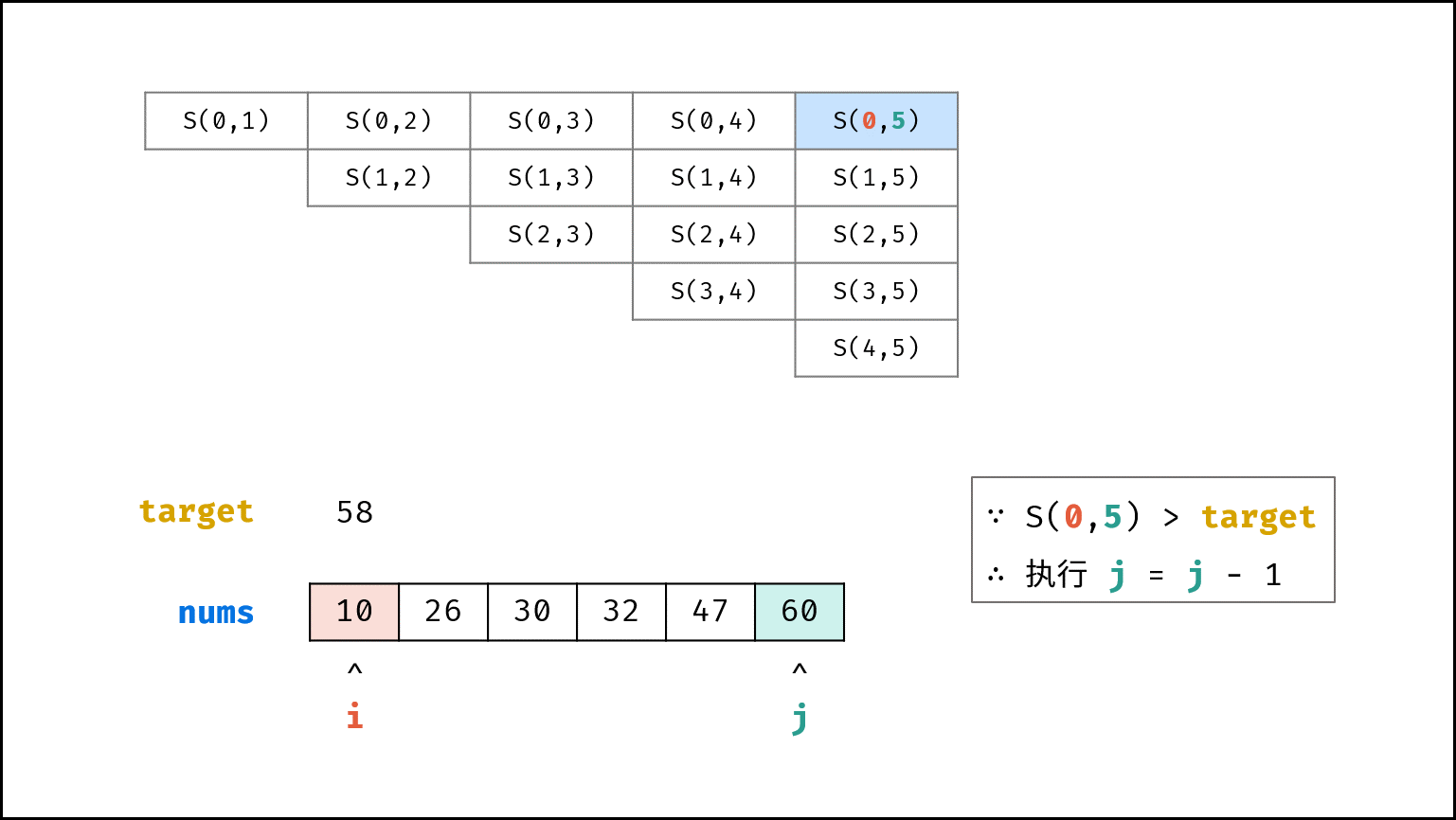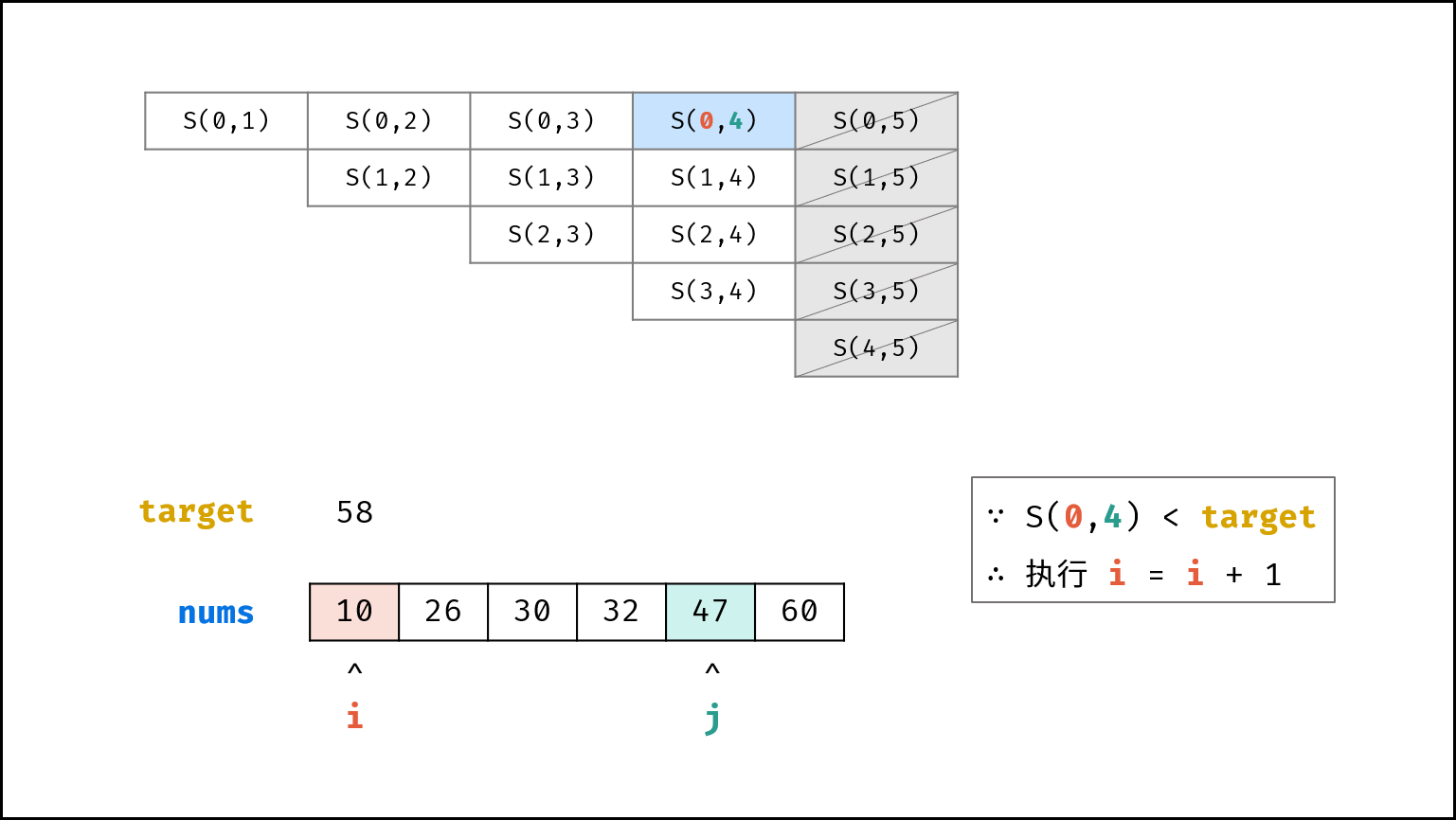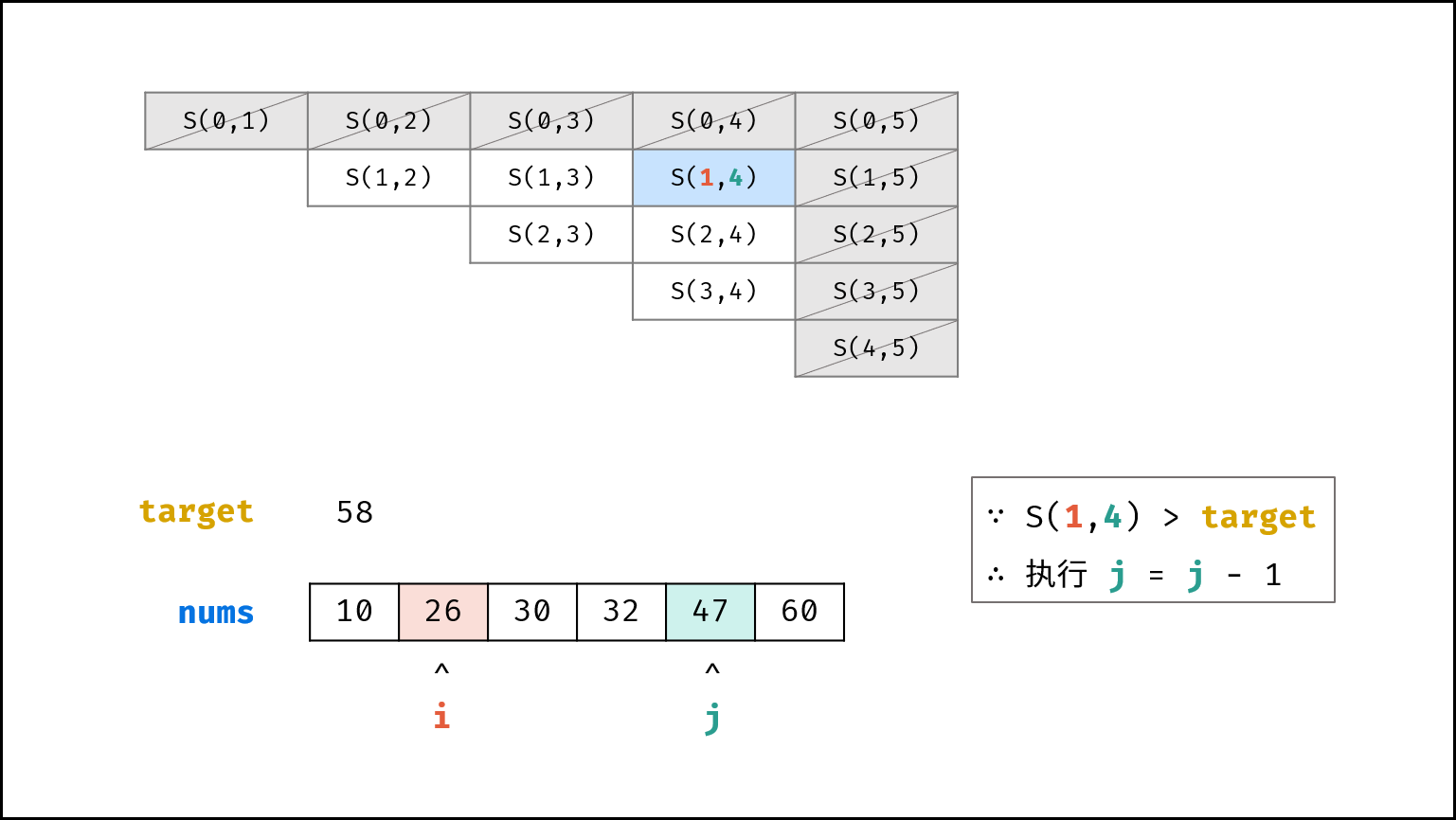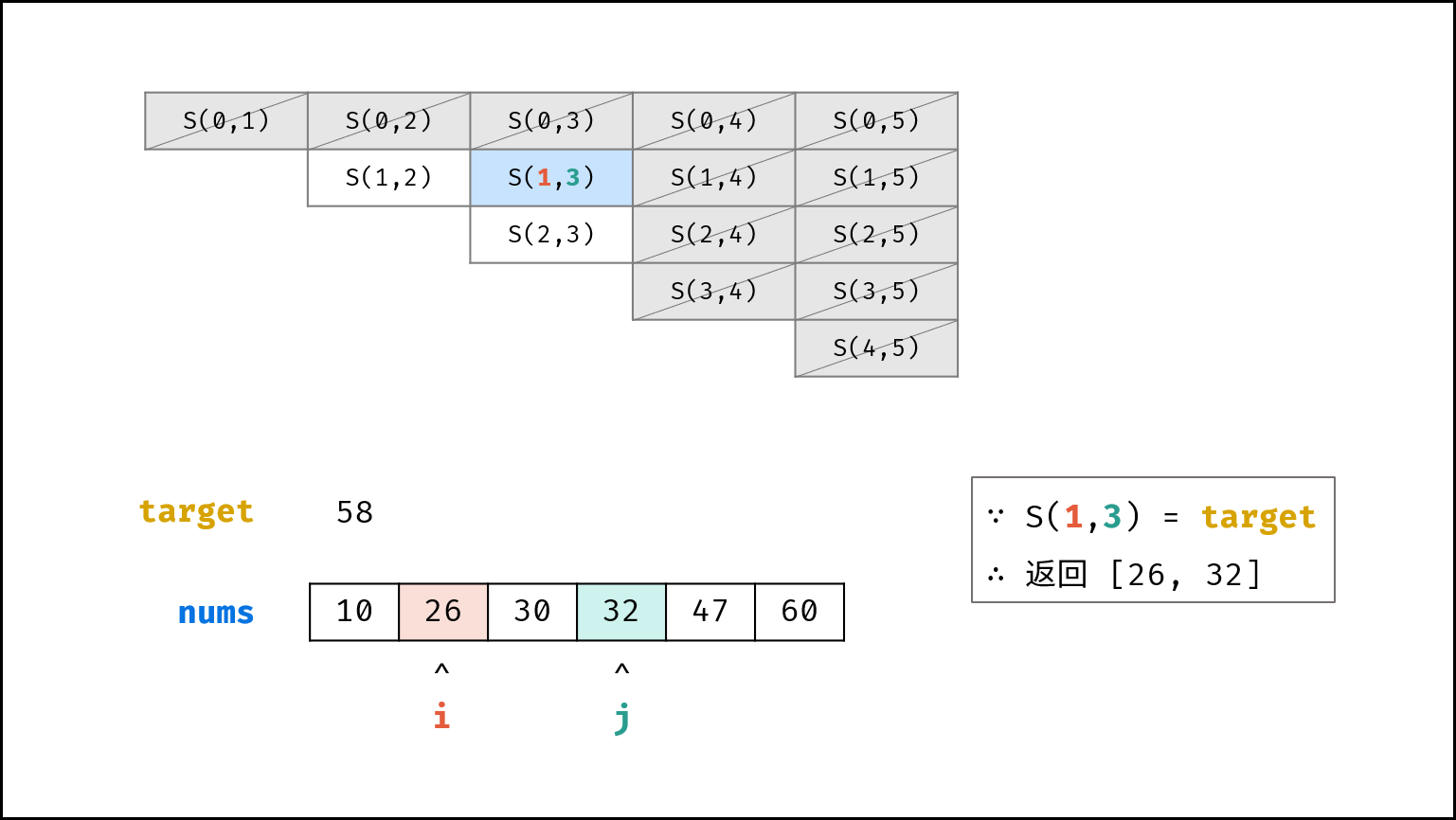<![Picture2.png](https://pic.leetcode-cn.com/1600794717-cWKhsr-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600794717-tWeYBB-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600794717-aaNviv-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600794717-MdyQXK-Picture5.png)>
### 正确性证明：
> 记每个状态为 $S(i, j)$ ，即 $S(i, j) = price[i] + price[j]$ 。假设 $S(i, j) < target$ ，则执行 $i = i + 1$ ，即状态切换至 $S(i + 1, j)$ 。
状态 $S(i, j)$ 切换至 $S(i + 1, j)$ ，则会消去一行元素，相当于 **消去了状态集合** {$S(i, i + 1), S(i, i + 2), ..., S(i, j - 2), S(i, j - 1), S(i, j)$ } 。（由于双指针都是向中间收缩，因此这些状态之后不可能再遇到）。
由于 $price$ 是排序数组，因此这些 **消去的状态** 都一定满足 $S(i, j) < target$ ，即这些状态都 **不是解** 。
**结论：** 以上分析已证明 “每次指针 $i$ 的移动操作，都不会导致解的丢失” ，即指针 $i$ 的移动操作是安全的；同理，对于指针 $j$ 可得出同样推论；因此，此双指针法是正确的。
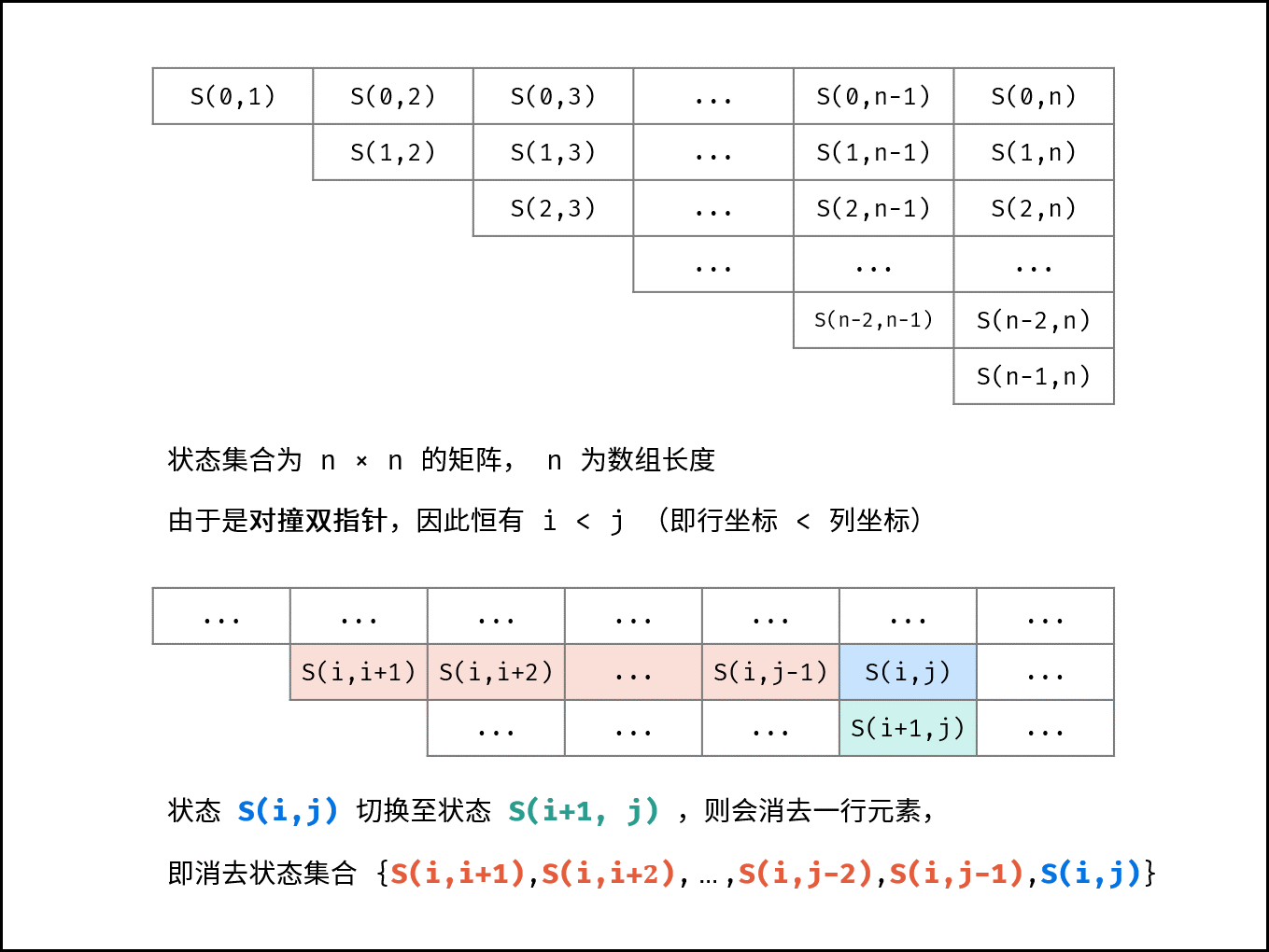![Picture1.png](https://pic.leetcode-cn.com/1600794717-VSmNyQ-Picture1.png){:align=center width=550}
## 代码：
```Python []
class Solution:
def twoSum(self, price: List[int], target: int) -> List[int]:
i, j = 0, len(price) - 1
while i < j:
s = price[i] + price[j]
if s > target: j -= 1
elif s < target: i += 1
else: return price[i], price[j]
return []
```
```Java []
class Solution {
public int[] twoSum(int[] price, int target) {
int i = 0, j = price.length - 1;
while(i < j) {
int s = price[i] + price[j];
if(s < target) i++;
else if(s > target) j--;
else return new int[] { price[i], price[j] };
}
return new int[0];
}
}
```
```C++ []
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int i = 0, j = price.size() - 1;
while(i < j) {
int s = price[i] + price[j];
if(s < target) i++;
else if(s > target) j--;
else return { price[i], price[j] };
}
return {};
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** $N$ 为数组 $price$ 的长度；双指针共同线性遍历整个数组。
- **空间复杂度 $O(1)$ ：** 变量 $i$, $j$ 使用常数大小的额外空间。

205
leetbook_ioa/docs/LCR 180. 文件组合.md Executable file
View File

@@ -0,0 +1,205 @@
## 方法一：求和公式
设连续正整数序列的左边界 $i$ 和右边界 $j$ ，则此序列的 **元素和** $target$ 等于 **元素平均值 $\frac{i + j}{2}$** 乘以 **元素数量 $(j - i + 1)$** ，即：
$$
target = \frac{(i + j) \times (j - i + 1)}{2}
$$
观察发现，当确定 元素和 $target$ 与 左边界 $i$ 时，可通过 **解一元二次方程** ，直接计算出右边界 $j$ ，公式推导如下：
$$
\begin{aligned}
target & = \frac{(i + j) \times (j - i + 1)}{2} \\
& = \frac{j^2 + j - i^2 + i}{2} \\
\end{aligned}
$$
整理上式得：
$$
0 = j^2 + j - (2 \times target + i^2 - i)
$$
根据一元二次方程求根公式得：
$$
j = \frac{-1 \pm \sqrt{1 + 4(2 \times target + i^2 - i)}}{2}
$$
由于 $j > i$ 恒成立，因此直接 **舍去必为负数的解** ，即 $j$ 的唯一解求取公式为：
$$
\begin{aligned}
j & = \frac{-1 + \sqrt{1 + 4(2 \times target + i^2 - i)}}{2}
\end{aligned}
$$
因此，通过从小到大遍历左边界 $i$ 来计算 **以 $i$ 为起始数字的连续正整数序列** 。每轮中，由以上公式计算得到右边界 $j$ ，当 $j$ 满足以下两个条件时记录结果：
1. $j$ 为 **整数** ：符合题目所求「连续正整数序列」；
2. $i < j$ ：满足题目要求「至少含有两个数」；
> 当 $target = 9$ 时，以上求解流程如下图所示。
![Picture1.png](https://pic.leetcode-cn.com/1611494538-VUzxtS-Picture1.png){:align=center width=550xl}
### 代码：
计算公式中 $i^2$ 项可能超过 int 类型取值范围，因此在 Java, C++ 中需要转化成 long 类型。
```Python []
class Solution:
def fileCombination(self, target: int):
i, j, res = 1, 2, []
while i < j:
j = (-1 + (1 + 4 * (2 * target + i * i - i)) ** 0.5) / 2
if i < j and j == int(j):
res.append(list(range(i, int(j) + 1)))
i += 1
return res
```
```Java []
class Solution {
public int[][] fileCombination(int target) {
int i = 1;
double j = 2.0;
List<int[]> res = new ArrayList<>();
while(i < j) {
j = (-1 + Math.sqrt(1 + 4 * (2 * target + (long) i * i - i))) / 2;
if(i < j && j == (int)j) {
int[] ans = new int[(int)j - i + 1];
for(int k = i; k <= (int)j; k++)
ans[k - i] = k;
res.add(ans);
}
i++;
}
return res.toArray(new int[0][]);
}
}
```
```C++ []
class Solution {
public:
vector<vector<int>> fileCombination(int target) {
int i = 1;
double j = 2.0;
vector<vector<int>> res;
while(i < j) {
j = (-1 + sqrt(1 + 4 * (2 * target + (long) i * i - i))) / 2;
if(i < j && j == (int)j) {
vector<int> ans;
for(int k = i; k <= (int)j; k++)
ans.push_back(k);
res.push_back(ans);
}
i++;
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N = target$ ；连续整数序列至少有两个数字，而 $i < j$ 恒成立，因此至多循环 $\frac{target}{2}$ 次，使用 $O(N)$ 时间；循环内，计算 $j$ 使用 $O(1)$ 时间；当 $i = 1$ 时，达到最大序列长度 $\frac{-1 + \sqrt{1 + 8s}}{2}$ ，考虑到解的稀疏性，将列表构建时间简化考虑为 $O(1)$ ；
- **空间复杂度 $O(1)$ ：** 变量 $i$ , $j$ 使用常数大小的额外空间。
## 方法二：滑动窗口
设连续正整数序列的左边界 $i$ 和右边界 $j$ ，则可构建滑动窗口从左向右滑动。循环中，每轮判断滑动窗口内元素和与目标值 $target$ 的大小关系，若相等则记录结果，若大于 $target$ 则移动左边界 $i$ （以减小窗口内的元素和），若小于 $target$ 则移动右边界 $j$ （以增大窗口内的元素和）。
### 算法流程：
1. **初始化：** 左边界 $i = 1$ ，右边界 $j = 2$ ，元素和 $s = 3$ ，结果列表 $res$ ；
2. **循环：** 当 $i \geq j$ 时跳出；
- 当 $s > target$ 时： 向右移动左边界 $i = i + 1$ ，并更新元素和 $s$ ；
- 当 $s < target$ 时： 向右移动右边界 $j = j + 1$ ，并更新元素和 $s$ ；
- 当 $s = target$ 时： 记录连续整数序列，并向右移动左边界 $i = i + 1$ ；
3. **返回值：** 返回结果列表 $res$ ；
> 当 $target = 9$ 时，以上求解流程如下图所示：
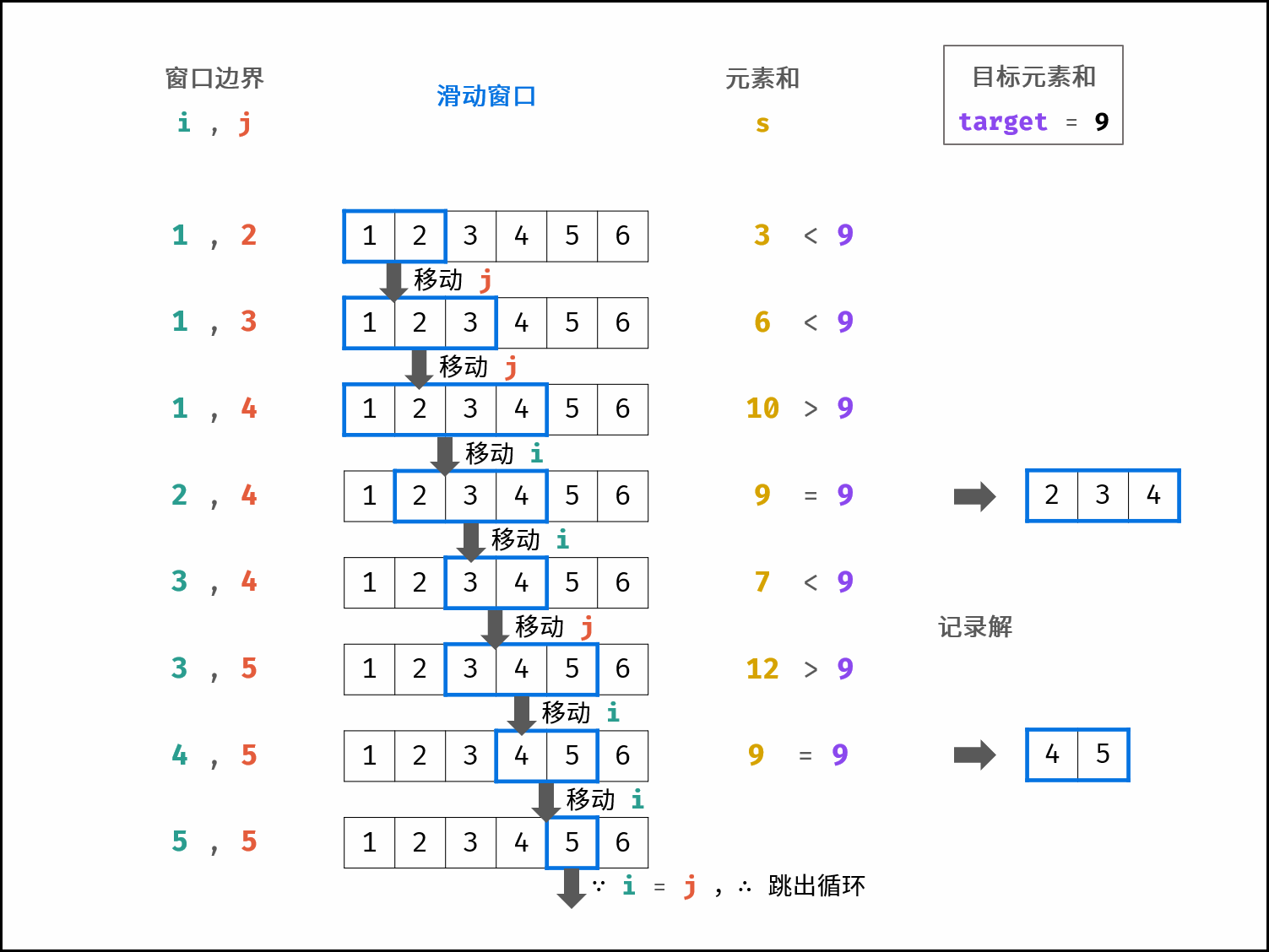![Picture2.png](https://pic.leetcode-cn.com/1611495306-LsrxgS-Picture2.png){:align=center width=600}
### 代码：
观察本文的算法流程发现，当 $s = target$ 和 $s > target$ 的移动边界操作相同，因此可以合并，代码如下所示。
```Python []
class Solution:
def fileCombination(self, target: int) -> List[List[int]]:
i, j, s, res = 1, 2, 3, []
while i < j:
if s == target:
res.append(list(range(i, j + 1)))
if s >= target:
s -= i
i += 1
else:
j += 1
s += j
return res
```
```Java []
class Solution {
public int[][] fileCombination(int target) {
int i = 1, j = 2, s = 3;
List<int[]> res = new ArrayList<>();
while(i < j) {
if(s == target) {
int[] ans = new int[j - i + 1];
for(int k = i; k <= j; k++)
ans[k - i] = k;
res.add(ans);
}
if(s >= target) {
s -= i;
i++;
} else {
j++;
s += j;
}
}
return res.toArray(new int[0][]);
}
}
```
```C++ []
class Solution {
public:
vector<vector<int>> fileCombination(int target) {
int i = 1, j = 2, s = 3;
vector<vector<int>> res;
while(i < j) {
if(s == target) {
vector<int> ans;
for(int k = i; k <= j; k++)
ans.push_back(k);
res.push_back(ans);
}
if(s >= target) {
s -= i;
i++;
} else {
j++;
s += j;
}
}
return res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N = target$ ；连续整数序列至少有两个数字，而 $i < j$ 恒成立，因此至多循环 $target$ 次（ $i$ , $j$ 都移动到 $\frac{target}{2}$ ），使用 $O(N)$ 时间；当 $i = 1$ 时，达到最大序列长度 $\frac{-1 + \sqrt{1 + 8s}}{2}$ ，考虑到解的稀疏性，将列表构建时间简化考虑为 $O(1)$ ；
- **空间复杂度 $O(1)$ ：** 变量 $i$ , $j$ , $s$ 使用常数大小的额外空间。

105
leetbook_ioa/docs/LCR 181. 字符串中的单词反转.md Executable file
View File

@@ -0,0 +1,105 @@
## 方法一：双指针
### 算法解析：
- 倒序遍历字符串 $message$ ，记录单词左右索引边界 $i$ , $j$ ；
- 每确定一个单词的边界，则将其添加至单词列表 $res$ ；
- 最终，将单词列表拼接为字符串，并返回即可。
> 下图中的 `s` 对应本题的 `message` 。
<![Picture3.png](https://pic.leetcode-cn.com/1600795186-ODVGAC-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600795186-KByGhl-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600795186-pMSOXg-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600795186-EllOEO-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600795186-QrOavH-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1600795186-YlpmuP-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1600795186-PITxbA-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1600795186-fVKJYO-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1600795186-fMtNcl-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1600795186-GmppFo-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1600795186-PXYpnz-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1600795186-GezFXt-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1600795186-XiNAjG-Picture15.png),![Picture16.png](https://pic.leetcode-cn.com/1600795186-ySOfTy-Picture16.png),![Picture17.png](https://pic.leetcode-cn.com/1600795186-DGmFEv-Picture17.png),![Picture18.png](https://pic.leetcode-cn.com/1600795186-rjhJhL-Picture18.png),![Picture19.png](https://pic.leetcode-cn.com/1600795186-CeiDKq-Picture19.png),![Picture20.png](https://pic.leetcode-cn.com/1600795251-iKyEDa-Picture20.png)>
### 代码：
```Python []
class Solution:
def reverseMessage(self, message: str) -> str:
message = message.strip() # 删除首尾空格
i = j = len(message) - 1
res = []
while i >= 0:
while i >= 0 and message[i] != ' ': i -= 1 # 搜索首个空格
res.append(message[i + 1: j + 1]) # 添加单词
while i >= 0 and message[i] == ' ': i -= 1 # 跳过单词间空格
j = i # j 指向下个单词的尾字符
return ' '.join(res) # 拼接并返回
```
```Java []
class Solution {
public String reverseMessage(String message) {
message = message.trim(); // 删除首尾空格
int j = message.length() - 1, i = j;
StringBuilder res = new StringBuilder();
while (i >= 0) {
while (i >= 0 && message.charAt(i) != ' ') i--; // 搜索首个空格
res.append(message.substring(i + 1, j + 1) + " "); // 添加单词
while (i >= 0 && message.charAt(i) == ' ') i--; // 跳过单词间空格
j = i; // j 指向下个单词的尾字符
}
return res.toString().trim(); // 转化为字符串并返回
}
}
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为字符串 $message$ 的长度，线性遍历字符串。
- **空间复杂度 $O(N)$ ：** 新建的 list(Python) 或 StringBuilder(Java) 中的字符串总长度 $\leq N$ ，占用 $O(N)$ 大小的额外空间。
## 方法二：分割 + 倒序
利用 “字符串分割”、“列表倒序” 的内置函数 *（面试时不建议使用）* ，可简便地实现本题的字符串翻转要求。
### 算法解析：
- **Python ：** 由于 $split()$ 方法将单词间的 “多个空格看作一个空格” （参考自 [split()和split(' ')的区别](https://www.cnblogs.com/python-coder/p/10073329.html) ），因此不会出现多余的 “空单词” 。因此，直接利用 $reverse()$ 方法翻转单词列表 $strs$ ，拼接为字符串并返回即可。
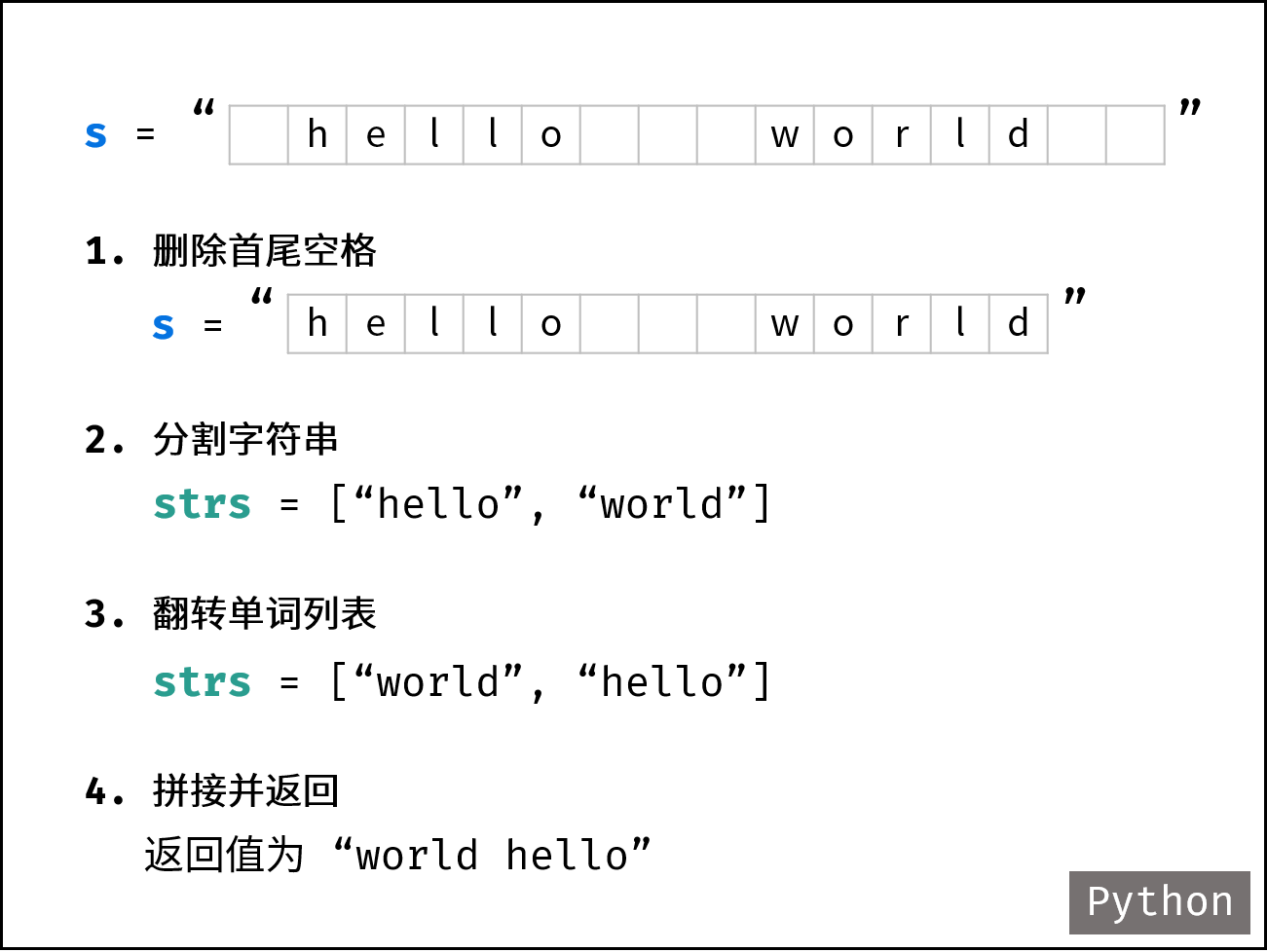![Picture1.png](https://pic.leetcode-cn.com/1600795186-pzCvCm-Picture1.png){:align=center width=500}
- **Java ：** 以空格为分割符完成字符串分割后，若两单词间有 $x > 1$ 个空格，则在单词列表 $strs$ 中，此两单词间会多出 $x - 1$ 个 “空单词” （即 `""` ）。解决方法：倒序遍历单词列表，并将单词逐个添加至 StringBuilder ，遇到空单词时跳过。
![Picture2.png](https://pic.leetcode-cn.com/1600795186-RmKJXL-Picture2.png){:align=center width=500}
### 代码：
```Python []
class Solution:
def reverseMessage(self, message: str) -> str:
message = message.strip() # 删除首尾空格
strs = message.split() # 分割字符串
strs.reverse() # 翻转单词列表
return ' '.join(strs) # 拼接为字符串并返回
```
```Java []
class Solution {
public String reverseMessage(String message) {
String[] strs = message.trim().split(" "); // 删除首尾空格，分割字符串
StringBuilder res = new StringBuilder();
for (int i = strs.length - 1; i >= 0; i--) { // 倒序遍历单词列表
if(strs[i].equals("")) continue; // 遇到空单词则跳过
res.append(strs[i] + " "); // 将单词拼接至 StringBuilder
}
return res.toString().trim(); // 转化为字符串，删除尾部空格，并返回
}
}
```
Python 可一行实现：
```Python []
class Solution:
def reverseMessage(self, message: str) -> str:
return ' '.join(message.strip().split()[::-1])
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 总体为线性时间复杂度，各函数时间复杂度和参考资料链接如下。
- [`split()` 方法：](https://softwareengineering.stackexchange.com/questions/331909/whats-the-complexity-of-javas-string-split-function) 为 $O(N)$ ；
- [`trim()` 和 `strip()` 方法：](https://stackoverflow.com/questions/51110114/is-string-trim-faster-than-string-replace) 最差情况下（当字符串全为空格时），为 $O(N)$ ；
- [`join()` 方法：](https://stackoverflow.com/questions/37133547/time-complexity-of-string-concatenation-in-python) 为 $O(N)$ ；
- [`reverse()` 方法：](https://stackoverflow.com/questions/37606159/what-is-the-time-complexity-of-python-list-reverse) 为 $O(N)$ ；
- **空间复杂度 $O(N)$ ：** 单词列表 $strs$ 占用线性大小的额外空间。

278
leetbook_ioa/docs/LCR 182. 动态口令.md Executable file
View File

@@ -0,0 +1,278 @@
## 解题思路：
本题解法较多，本文主要介绍 **字符串切片** ， **列表遍历拼接** ， **字符串遍历拼接** 三种方法，适用于 Python 和 Java 语言。同时，介绍了 **三次翻转法** ，适用于 C++ 语言。
## 方法一：字符串切片
获取字符串 `password[target:]` 切片和 `password[:target]` 切片，使用 "$+$" 运算符拼接并返回即可。
> 下图中的 `s` 对应本题的 `password` 。
![Picture1.png](https://pic.leetcode-cn.com/1600793170-eyvDTJ-Picture1.png){:align=center width=500}
### 代码：
```Python []
class Solution:
def dynamicPassword(self, password: str, target: int) -> str:
return password[target:] + password[:target]
```
```Java []
class Solution {
public String dynamicPassword(String password, int target) {
return password.substring(target, password.length()) + password.substring(0, target);
}
}
```
```C++ []
class Solution {
public:
string dynamicPassword(string password, int target) {
return password.substr(target, password.size()) + password.substr(0, target);
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为字符串 `password` 的长度，字符串切片函数为线性时间复杂度（[参考资料](https://stackoverflow.com/questions/4679746/time-complexity-of-javas-substring)）。
- **空间复杂度 $O(N)$ ：** 两个字符串切片的总长度为 $N$ 。
## 方法二：列表遍历拼接
> 若面试规定不允许使用 **切片函数** ，则使用此方法。
### 算法流程：
1. 新建一个 list (Python) 、StringBuilder (Java) ，记为 `res` ；
2. 先向 `res` 添加 “第 $target + 1$ 位至末位的字符” ；
3. 再向 `res` 添加 “首位至第 $target$ 位的字符” ；
4. 将 `res` 转化为字符串并返回；
![Picture2.png](https://pic.leetcode-cn.com/1600793170-ViWBNV-Picture2.png){:align=center width=550}
### 代码：
```Python []
class Solution:
def dynamicPassword(self, password: str, target: int) -> str:
res = []
for i in range(target, len(password)):
res.append(password[i])
for i in range(target):
res.append(password[i])
return ''.join(res)
```
```Java []
class Solution {
public String dynamicPassword(String password, int target) {
StringBuilder res = new StringBuilder();
for(int i = target; i < password.length(); i++)
res.append(password.charAt(i));
for(int i = 0; i < target; i++)
res.append(password.charAt(i));
return res.toString();
}
}
```
利用求余运算，可以简化代码。
```Python []
class Solution:
def dynamicPassword(self, password: str, target: int) -> str:
res = []
for i in range(target, target + len(password)):
res.append(password[i % len(password)])
return ''.join(res)
```
```Java []
class Solution {
public String dynamicPassword(String password, int target) {
StringBuilder res = new StringBuilder();
for(int i = target; i < target + password.length(); i++)
res.append(password.charAt(i % password.length()));
return res.toString();
}
}
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 线性遍历 `password` 并添加，使用线性时间。
- **空间复杂度 $O(N)$ ：** 新建的辅助 `res` 使用 $O(N)$ 大小的额外空间。
## 方法三：字符串遍历拼接
> 若规定 Python 不能使用 `join()` 函数，或规定 Java 只能用 String ，则使用此方法。
此方法与 **方法二** 思路一致，区别是使用字符串代替列表。
![Picture3.png](https://pic.leetcode-cn.com/1600793170-uasqXO-Picture3.png){:align=center width=550}
```Python []
class Solution:
def dynamicPassword(self, password: str, target: int) -> str:
res = ""
for i in range(target, len(password)):
res += password[i]
for i in range(target):
res += password[i]
return res
```
```Java []
class Solution {
public String dynamicPassword(String password, int target) {
String res = "";
for(int i = target; i < password.length(); i++)
res += password.charAt(i);
for(int i = 0; i < target; i++)
res += password.charAt(i);
return res;
}
}
```
同理，利用求余运算，可以简化代码。
```Python []
class Solution:
def dynamicPassword(self, password: str, target: int) -> str:
res = ""
for i in range(target, target + len(password)):
res += password[i % len(password)]
return res
```
```Java []
class Solution {
public String dynamicPassword(String password, int target) {
String res = "";
for(int i = target; i < target + password.length(); i++)
res += password.charAt(i % password.length());
return res;
}
}
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 线性遍历 `password` 并添加，使用线性时间。
- **空间复杂度 $O(N)$ ：** 假设循环过程中内存会被及时回收，内存中至少同时存在长度为 $N$ 和 $N-1$ 的两个字符串（新建长度为 $N$ 的 `res` 需要使用前一个长度 $N-1$ 的 `res` ），因此至少使用 $O(N)$ 的额外空间。
## 效率对比：
由于本题的多解法涉及到了 **字符串为不可变对象** 的相关概念，导致效率区别较大。以上三种方法的空间使用如下图所示。
> 详细分析请参考 [Efficient String Concatenation in Python](https://waymoot.org/home/python_string/) 。
以 Python 为例开展三种方法的效率测试，结论同样适用于 Java 语言。
![Picture4.png](https://pic.leetcode-cn.com/1600793170-xExsDE-Picture4.png){:align=center width=650}
### 测试数据：
长度为 $10000000$ 的全为 `'1'` 的字符串。
```Python
password = "1" * 10000000
```
**方法一测试：**
新建两切片字符串，并将两切片拼接为结果字符串，无冗余操作，效率最高。
```Python []
# 运行时间: 0.01 秒
def func1(password):
cut = len(password) // 3
return password[:cut] + password[cut:]
```
**方法二测试：**
列表(Python) 和 StringBuilder(Java) 都是可变对象，每轮遍历拼接字符时，只是向列表尾部添加一个新的字符元素。最终拼接转化为字符串时，系统 **仅申请一次内存** 。
```Python []
# 运行时间: 1.86 秒
def func2(password):
res = []
for i in range(len(password)):
res.append(password[i]) # 仅需在列表尾部添加元素
return ''.join(res)
```
**方法三测试：**
在 Python 和 Java 中，字符串是 “不可变对象” 。因此，每轮遍历拼接字符时，都需要新建一个字符串；因此，系统 **需申请 $N$ 次内存** ，数据量较大时效率低下。
```Python []
# 运行时间: 6.31 秒
def func3(password):
res = ""
for i in range(len(password)):
res += password[i] # 每次拼接都需要新建一个字符串
return res
```
## 方法四：三次翻转（C++）
由于 C++ 中的字符串是 **可变类型** ，因此可在原字符串上直接操作实现字符串旋转，实现 $O(1)$ 的空间复杂度。
设字符串 $password = s_1 s_2$ ，字符串 $password$ 的反转字符串为 $\hat password$ ，则左旋转字符串 $s_2 s_1$ 计算方法为：
$$
s_2 s_1 = \hat{\hat{s_1} \hat{s_2}}
$$
> 例如，$password = "abcdefg"$ , $s_1 = "ab"$ , $s_2 = "cdefg"$ ，则有：
> $$
> \hat{s_1} = "ba" \\
> \hat{s_2} = "gfedc" \\
> \hat{\hat{s_1} \hat{s_2}} = \hat{"bagfedc"} = "cdefgba"
> $$
> 即 $"cdefgba"$ 为所求字符串 $password$ 的左旋转结果。
### 代码：
自行实现字符串翻转函数 `reverseString()` ，代码如下：
```C++ []
class Solution {
public:
string dynamicPassword(string password, int target) {
reverseString(password, 0, target - 1);
reverseString(password, target, password.size() - 1);
reverseString(password, 0, password.size() - 1);
return password;
}
private:
void reverseString(string& password, int i, int j) {
while(i < j) swap(password[i++], password[j--]);
}
};
```
也可使用库函数实现，代码如下：
```C++ []
class Solution {
public:
string dynamicPassword(string password, int target) {
reverse(password.begin(), password.begin() + target);
reverse(password.begin() + target, password.end());
reverse(password.begin(), password.end());
return password;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 共线性遍历两轮 `password` 。
- **空间复杂度 $O(1)$ ：** C++ 原地字符串操作，使用常数大小额外空间。

147
leetbook_ioa/docs/LCR 183. 望远镜中最高的海拔.md Executable file
View File

@@ -0,0 +1,147 @@
## 解题思路：
设窗口区间为 $[i, j]$ ，最大值为 $x_j$ 。当窗口向前移动一格，则区间变为 $[i+1,j+1]$ ，即添加了 $heights[j + 1]$ ，删除了 $heights[i]$ 。
若只向窗口 $[i, j]$ 右边添加数字 $heights[j + 1]$ ，则新窗口最大值可以 **通过一次对比** 使用 $O(1)$ 时间得到，即：
$$
x_{j+1} = \max(x_{j}, heights[j + 1])
$$
而由于删除的 $heights[i]$ 可能恰好是窗口内唯一的最大值 $x_j$ ，因此不能通过以上方法计算 $x_{j+1}$ ，而必须使用 $O(j-i)$ 时间， **遍历整个窗口区间** 获取最大值，即：
$$
x_{j+1} = \max(heights(i+1), \cdots , heights(j+1))
$$
根据以上分析，可得 **暴力法** 的时间复杂度为 $O((n-limit+1)limit) \approx O(nk)$ 。
- 设数组 $heights$ 的长度为 $n$ ，则共有 $(n-limit+1)$ 个窗口；
- 获取每个窗口最大值需线性遍历，时间复杂度为 $O(limit)$ 。
> 下图中的 `nums` 对应本题的 `heights` 。
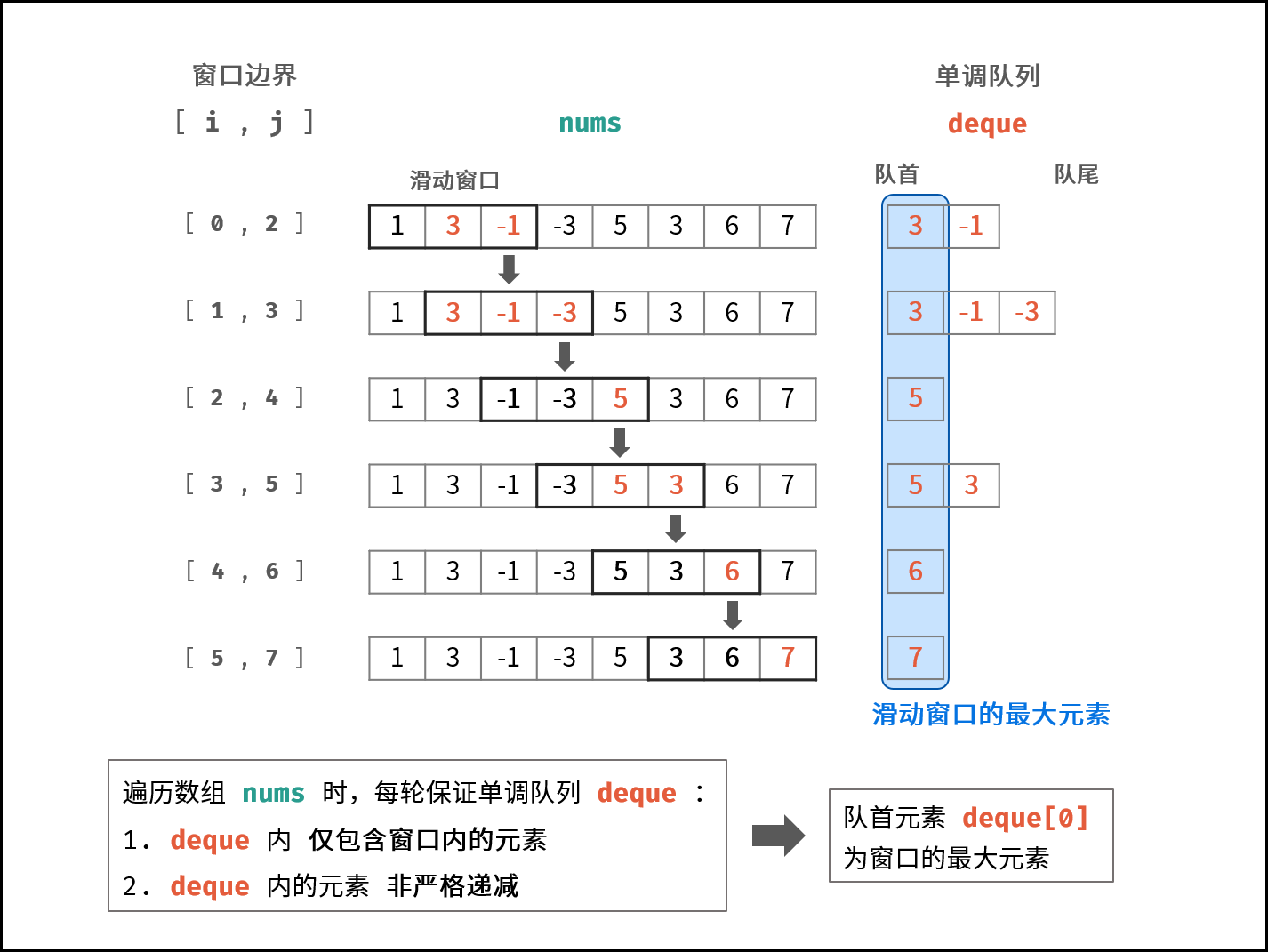![Picture1.png](https://pic.leetcode-cn.com/1600878237-pBiBdf-Picture1.png){:align=center width=650}
> **本题难点：** 如何在每次窗口滑动后，将 “获取窗口内最大值” 的时间复杂度从 $O(limit)$ 降低至 $O(1)$ 。
回忆“最小栈”问题，其使用 **单调栈** 实现了随意入栈、出栈情况下的 $O(1)$ 时间获取 “栈内最小值” 。本题同理，不同点在于 “出栈操作” 删除的是 “列表尾部元素” ，而 “窗口滑动” 删除的是 “列表首部元素” 。
窗口对应的数据结构为 **双端队列** ，本题使用 **单调队列** 即可解决以上问题。遍历数组时，每轮保证单调队列 $deque$ ：
1. $deque$ 内 **仅包含窗口内的元素** $\Rightarrow$ 每轮窗口滑动移除了元素 $heights[i - 1]$ ，需将 $deque$ 内的对应元素一起删除。
2. $deque$ 内的元素 **非严格递减** $\Rightarrow$ 每轮窗口滑动添加了元素 $heights[j + 1]$ ，需将 $deque$ 内所有 $< heights[j + 1]$ 的元素删除。
### 算法流程：
1. **初始化：** 双端队列 $deque$ ，结果列表 $res$ ，数组长度 $n$ ；
2. **滑动窗口：** 左边界范围 $i \in [1 - limit, n - limit]$ ，右边界范围 $j \in [0, n - 1]$ ；
1. 若 $i > 0$ 且 队首元素 $deque[0]$ $=$ 被删除元素 $heights[i - 1]$ ：则队首元素出队；
2. 删除 $deque$ 内所有 $< heights[j]$ 的元素，以保持 $deque$ 递减；
3. 将 $heights[j]$ 添加至 $deque$ 尾部；
4. 若已形成窗口（即 $i \geq 0$ ）：将窗口最大值（即队首元素 $deque[0]$ ）添加至列表 $res$ ；
3. **返回值：** 返回结果列表 $res$ ；
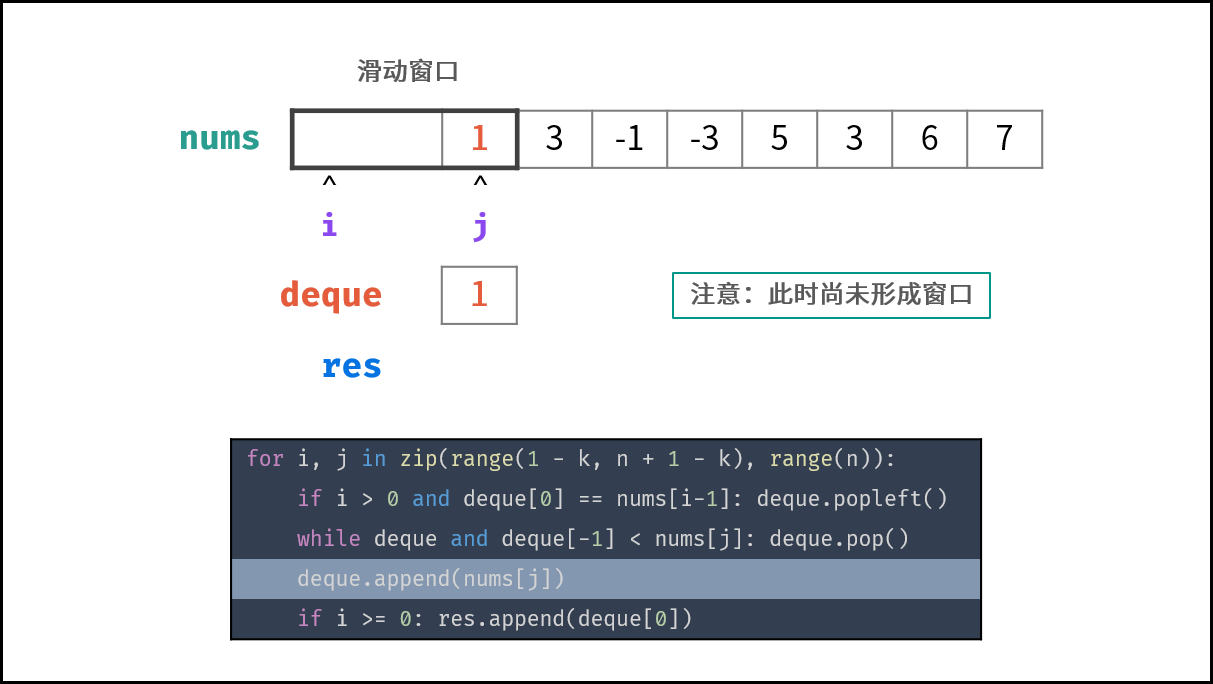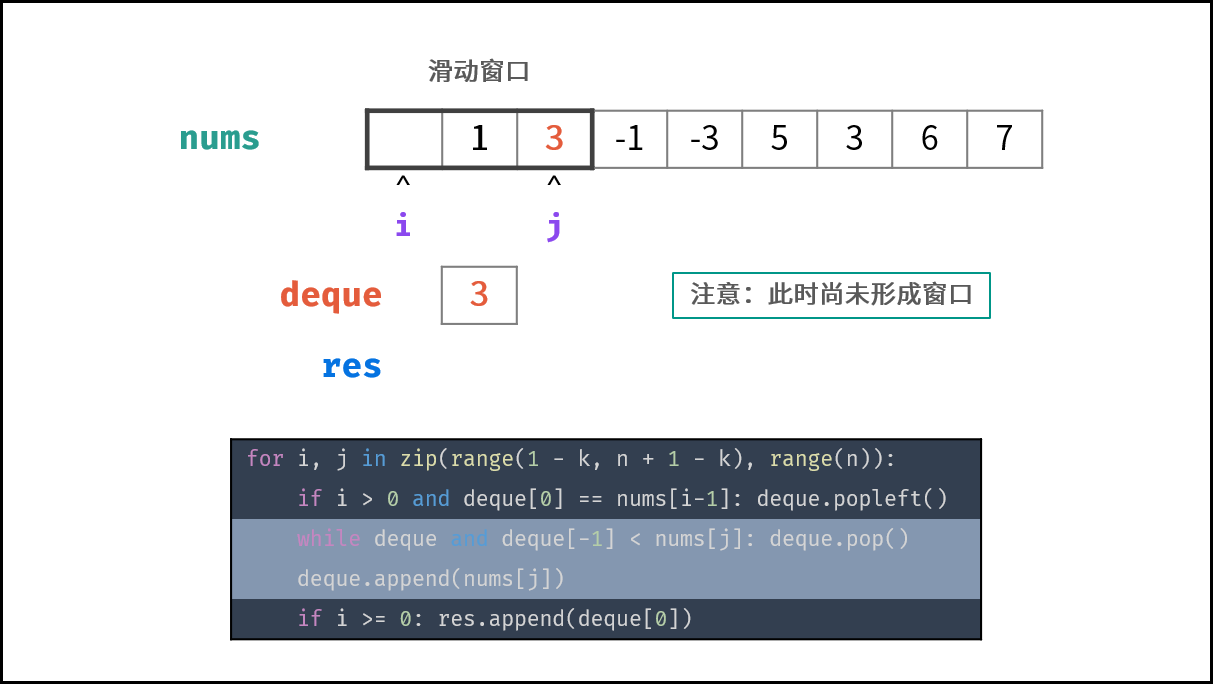<![Picture2.png](https://pic.leetcode-cn.com/1600878237-EsFWhx-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600878237-EYkUHE-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600878237-YoQeRX-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600878237-cFWnrv-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600878237-jrguEx-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600878237-NCrTNi-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1600878237-KPnHbt-Picture8.png),![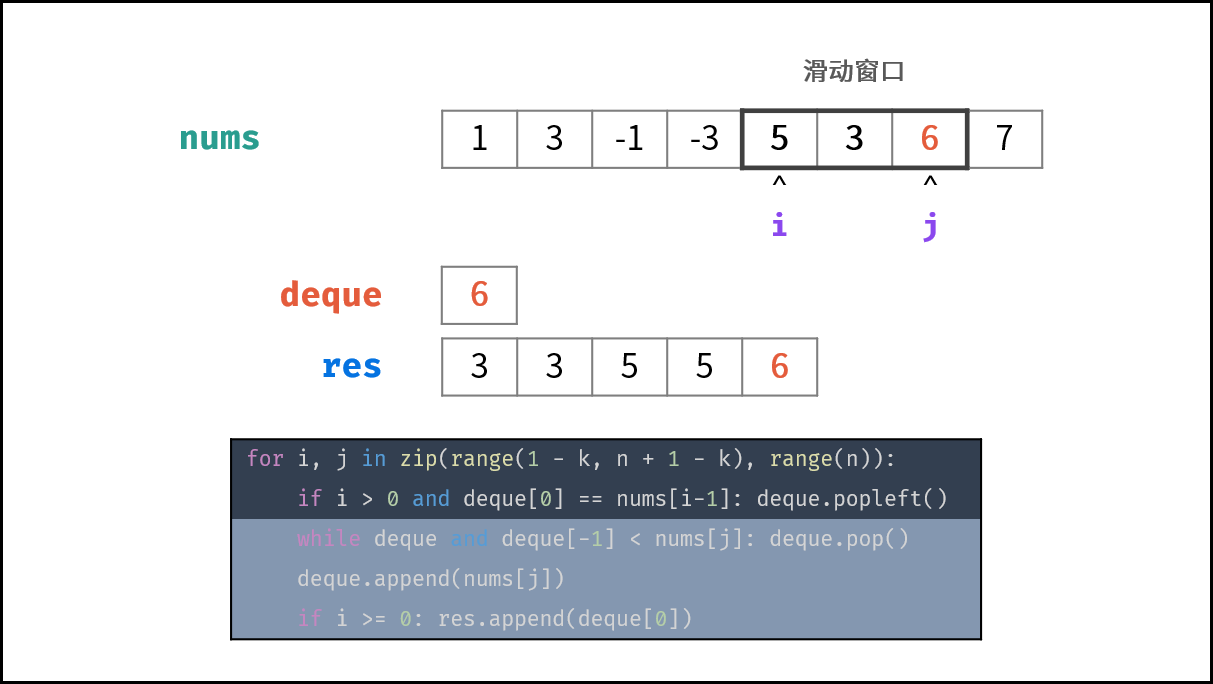Picture9.png](https://pic.leetcode-cn.com/1600878237-ndEtNd-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1600878237-WnULJt-Picture10.png),![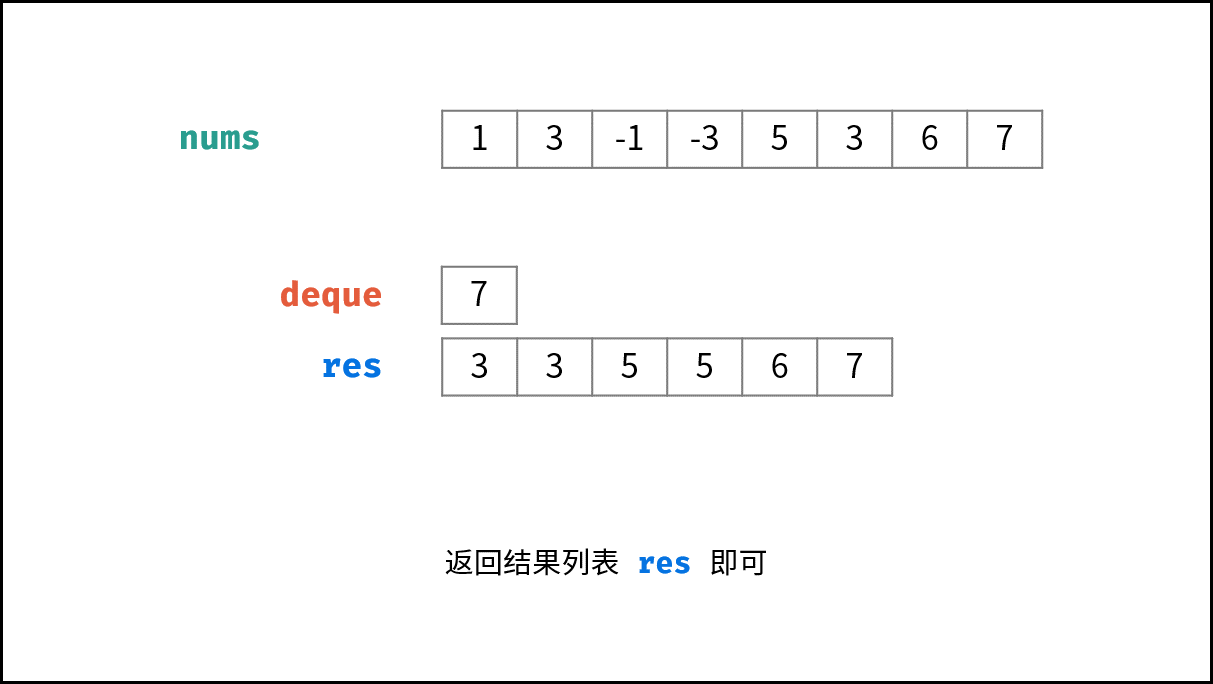Picture11.png](https://pic.leetcode-cn.com/1600878237-omRkXY-Picture11.png)>
## 代码：
Python 通过 `zip(range(), range())` 可实现滑动窗口的左右边界 `i, j` 同时遍历。
```Python []
class Solution:
def maxAltitude(self, heights: List[int], limit: int) -> List[int]:
deque = collections.deque()
res, n = [], len(heights)
for i, j in zip(range(1 - limit, n + 1 - limit), range(n)):
# 删除 deque 中对应的 heights[i-1]
if i > 0 and deque[0] == heights[i - 1]:
deque.popleft()
# 保持 deque 递减
while deque and deque[-1] < heights[j]:
deque.pop()
deque.append(heights[j])
# 记录窗口最大值
if i >= 0:
res.append(deque[0])
return res
```
```Java []
class Solution {
public int[] maxAltitude(int[] heights, int limit) {
if(heights.length == 0 || limit == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[heights.length - limit + 1];
for(int j = 0, i = 1 - limit; j < heights.length; i++, j++) {
// 删除 deque 中对应的 heights[i-1]
if(i > 0 && deque.peekFirst() == heights[i - 1])
deque.removeFirst();
// 保持 deque 递减
while(!deque.isEmpty() && deque.peekLast() < heights[j])
deque.removeLast();
deque.addLast(heights[j]);
// 记录窗口最大值
if(i >= 0)
res[i] = deque.peekFirst();
}
return res;
}
}
```
可以将 “未形成窗口” 和 “形成窗口后” 两个阶段拆分到两个循环里实现。代码虽变长，但减少了冗余的判断操作。
```Python []
class Solution:
def maxAltitude(self, heights: List[int], limit: int) -> List[int]:
if not heights or limit == 0: return []
deque = collections.deque()
# 未形成窗口
for i in range(limit):
while deque and deque[-1] < heights[i]:
deque.pop()
deque.append(heights[i])
res = [deque[0]]
# 形成窗口后
for i in range(limit, len(heights)):
if deque[0] == heights[i - limit]:
deque.popleft()
while deque and deque[-1] < heights[i]:
deque.pop()
deque.append(heights[i])
res.append(deque[0])
return res
```
```Java []
class Solution {
public int[] maxAltitude(int[] heights, int limit) {
if(heights.length == 0 || limit == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[heights.length - limit + 1];
// 未形成窗口
for(int i = 0; i < limit; i++) {
while(!deque.isEmpty() && deque.peekLast() < heights[i])
deque.removeLast();
deque.addLast(heights[i]);
}
res[0] = deque.peekFirst();
// 形成窗口后
for(int i = limit; i < heights.length; i++) {
if(deque.peekFirst() == heights[i - limit])
deque.removeFirst();
while(!deque.isEmpty() && deque.peekLast() < heights[i])
deque.removeLast();
deque.addLast(heights[i]);
res[i - limit + 1] = deque.peekFirst();
}
return res;
}
}
```
### 复杂度分析：
- **时间复杂度 $O(n)$ ：** 其中 $n$ 为数组 $heights$ 长度；线性遍历 $heights$ 占用 $O(n)$ ；每个元素最多仅入队和出队一次，因此单调队列 $deque$ 占用 $O(2n)$ 。
- **空间复杂度 $O(limit)$ ：** 双端队列 $deque$ 中最多同时存储 $limit$ 个元素（即窗口大小）。

129
leetbook_ioa/docs/LCR 184. 设计自助结算系统.md Executable file
View File

@@ -0,0 +1,129 @@
## 解题思路：
> 对于普通队列，入队 `add()` 和出队 `remove()` 的时间复杂度均为 $O(1)$ ；本题难点为实现查找最大值 `get_max()` 的 $O(1)$ 时间复杂度。
> 假设队列中存储 $N$ 个元素，从中获取最大值需要遍历队列，时间复杂度为 $O(N)$ ，单从算法上无优化空间。
如下图所示，最直观的想法是 **维护一个最大值变量** ，在元素入队时更新此变量即可；但当最大值出队后，并无法确定下一个 **次最大值** ，因此不可行。
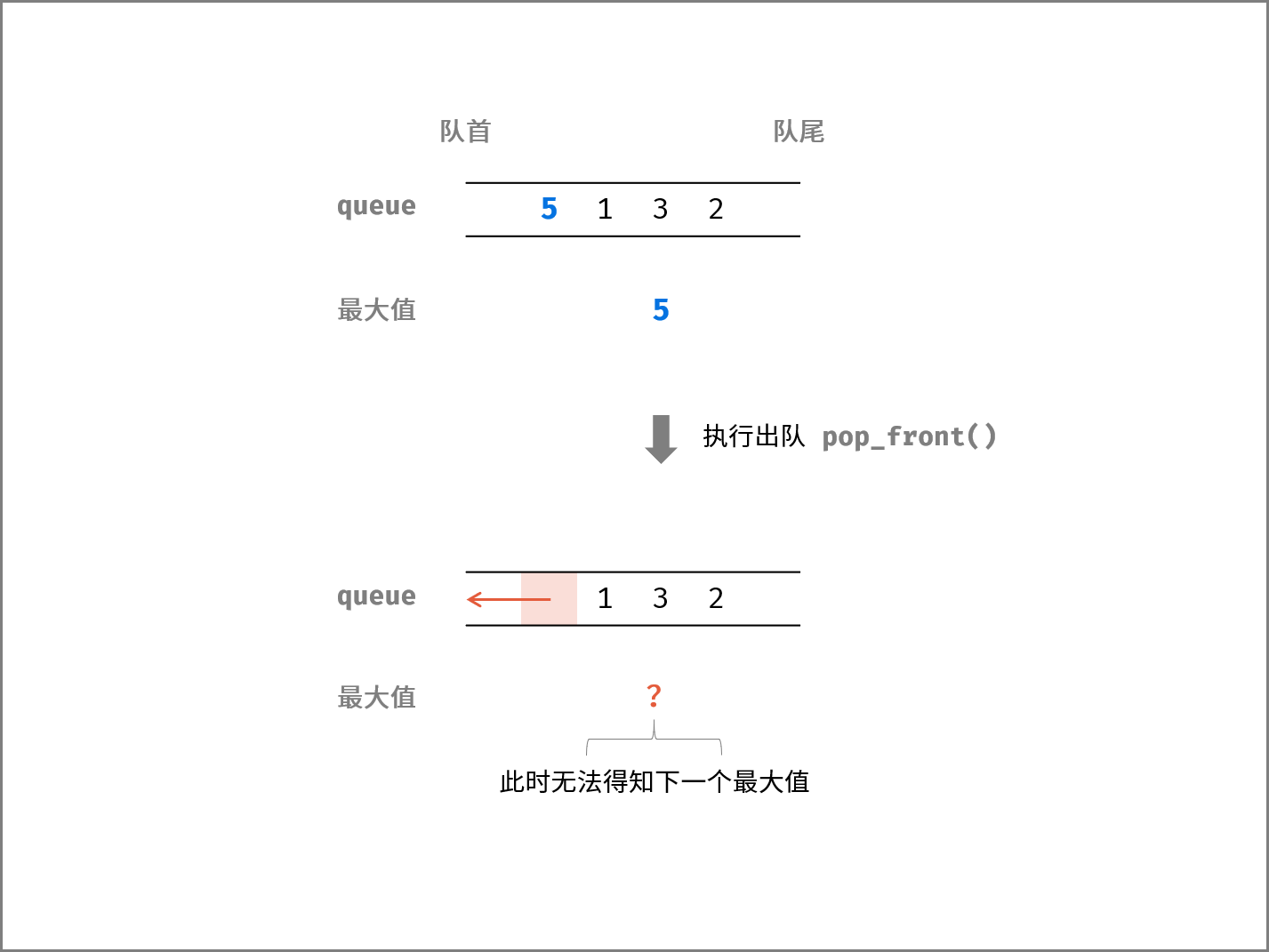![Picture1.png](https://pic.leetcode-cn.com/1609261470-WanZuG-Picture1.png){:align=center width=500}
考虑利用 **数据结构** 来实现，即经常使用的 “空间换时间” 。如下图所示，考虑构建一个递减列表来保存队列 **所有递减的元素** ，递减链表随着入队和出队操作实时更新，这样队列最大元素就始终对应递减列表的首元素，实现了获取最大值 $O(1)$ 时间复杂度。
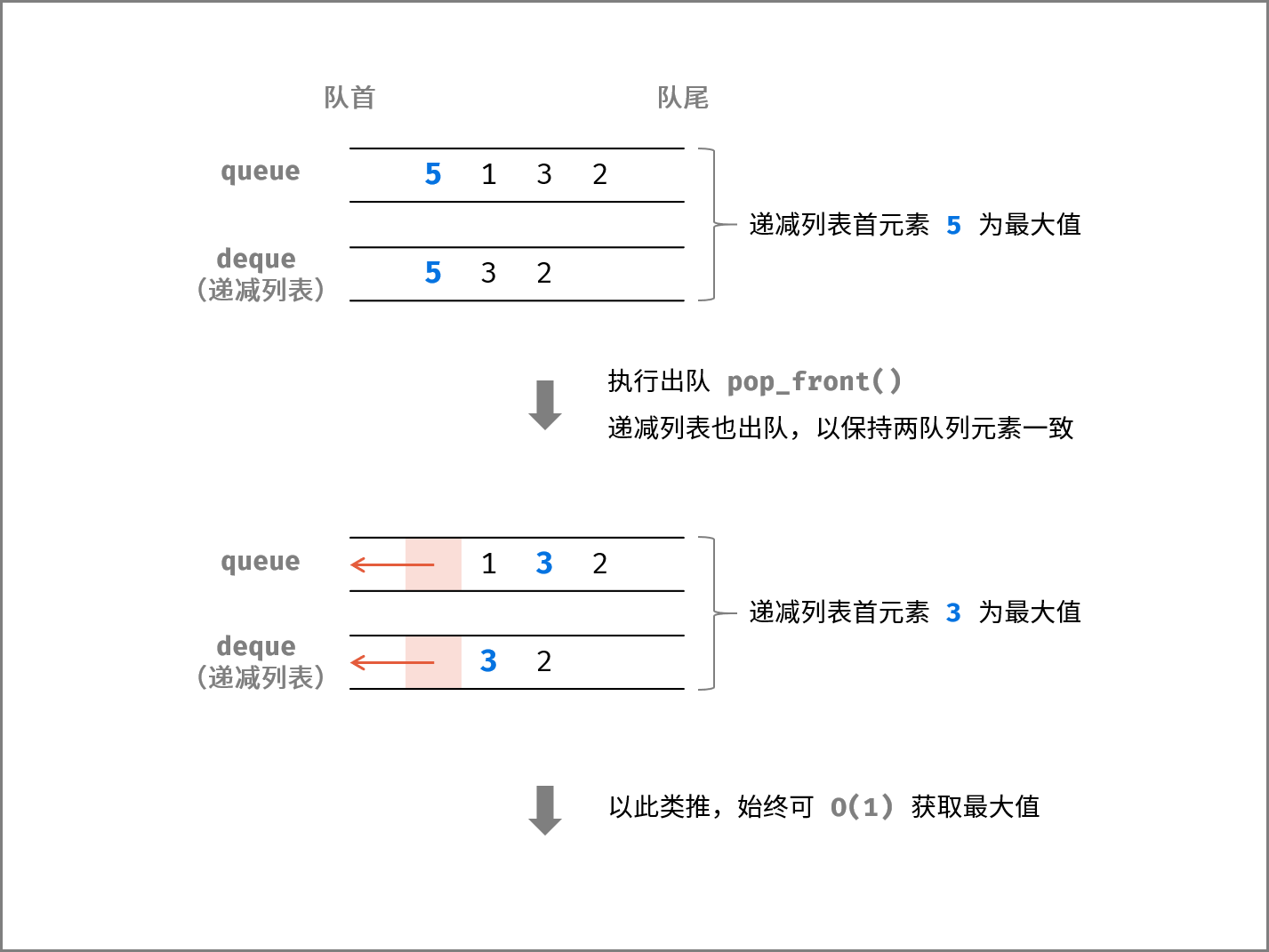![Picture2.png](https://pic.leetcode-cn.com/1609261470-gMTEAf-Picture2.png){:align=center width=500}
为了实现此递减列表，需要使用 **双向队列** ，假设队列已经有若干元素：
1. 当执行入队 `add()` 时： 若入队一个比队列某些元素更大的数字 $x$ ，则为了保持此列表递减，需要将双向队列 **尾部所有小于 $x$ 的元素** 弹出。
2. 当执行出队 `remove()` 时： 若出队的元素是最大元素，则 双向队列 需要同时 **将首元素出队** ，以保持队列和双向队列的元素一致性。
> 使用双向队列原因：维护递减列表需要元素队首弹出、队尾插入、队尾弹出操作皆为 $O(1)$ 时间复杂度。
### 函数设计：
初始化队列 `queue` ，双向队列 `deque` ；
**最大值 `get_max()` ：**
- 当双向队列 `deque` 为空，则返回 $-1$ ；
- 否则，返回 `deque` 首元素；
**入队 `add()` ：**
1. 将元素 `value` 入队 `queue` ；
2. 将双向队列中队尾 **所有** 小于 `value` 的元素弹出（以保持 `deque` 非单调递减），并将元素 `value` 入队 `deque` ；
**出队 `remove()` ：**
1. 若队列 `queue` 为空，则直接返回 $-1$ ；
2. 否则，将 `queue` 首元素出队；
3. 若 `deque` 首元素和 `queue` 首元素 **相等** ，则将 `deque` 首元素出队（以保持两队列 **元素一致** ） ；
> 设计双向队列为 **单调不增** 的原因：若队列 `queue` 中存在两个 **值相同的最大元素** ，此时 `queue` 和 `deque` 同时弹出一个最大元素，而 `queue` 中还有一个此最大元素；即采用单调递减将导致两队列中的元素不一致。
> 下图中的 `push_back()` , `pop_front()` , `max_value()` 分别对应本题的 `add()` , `remove()` , `get_max()` 。
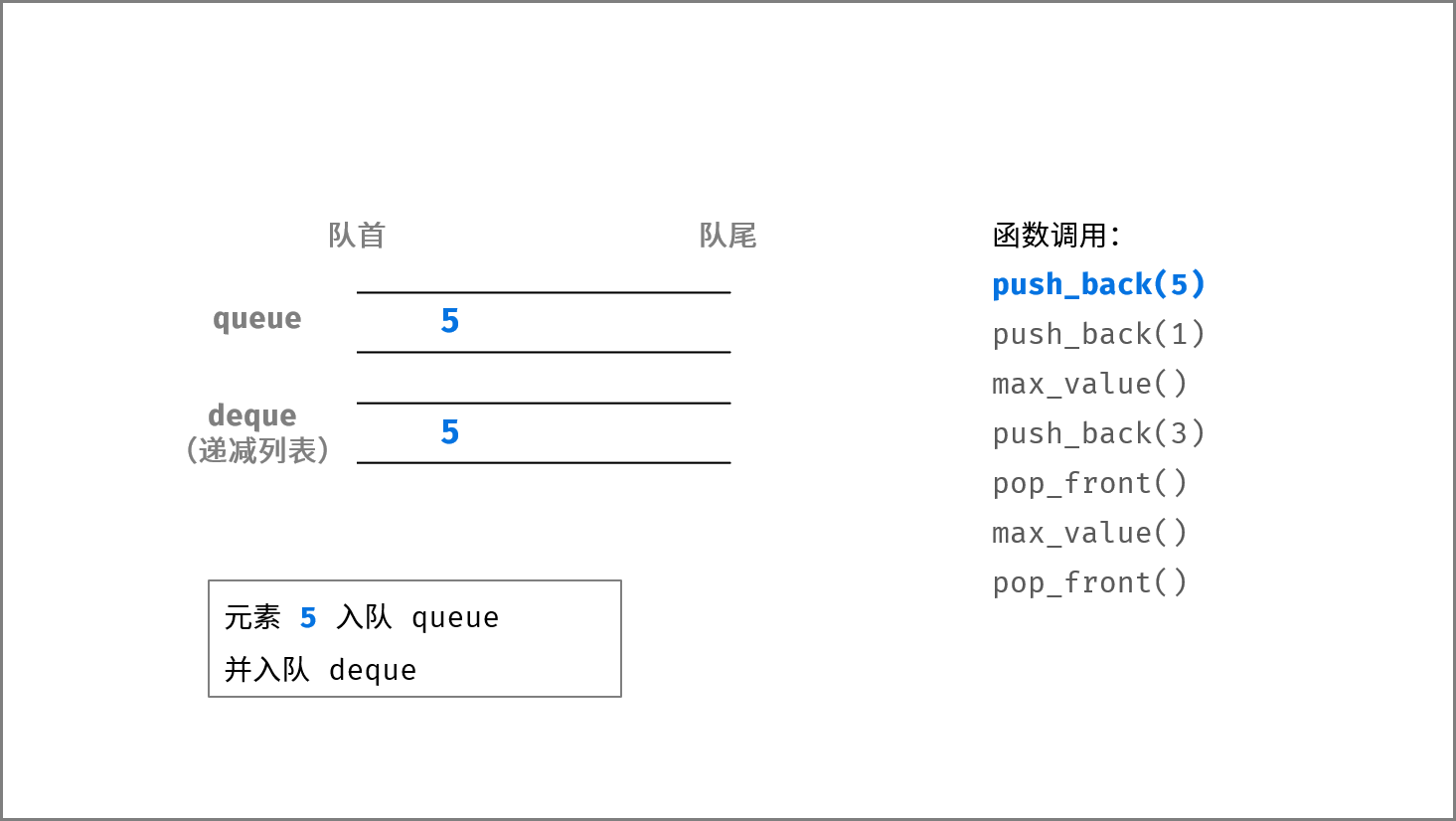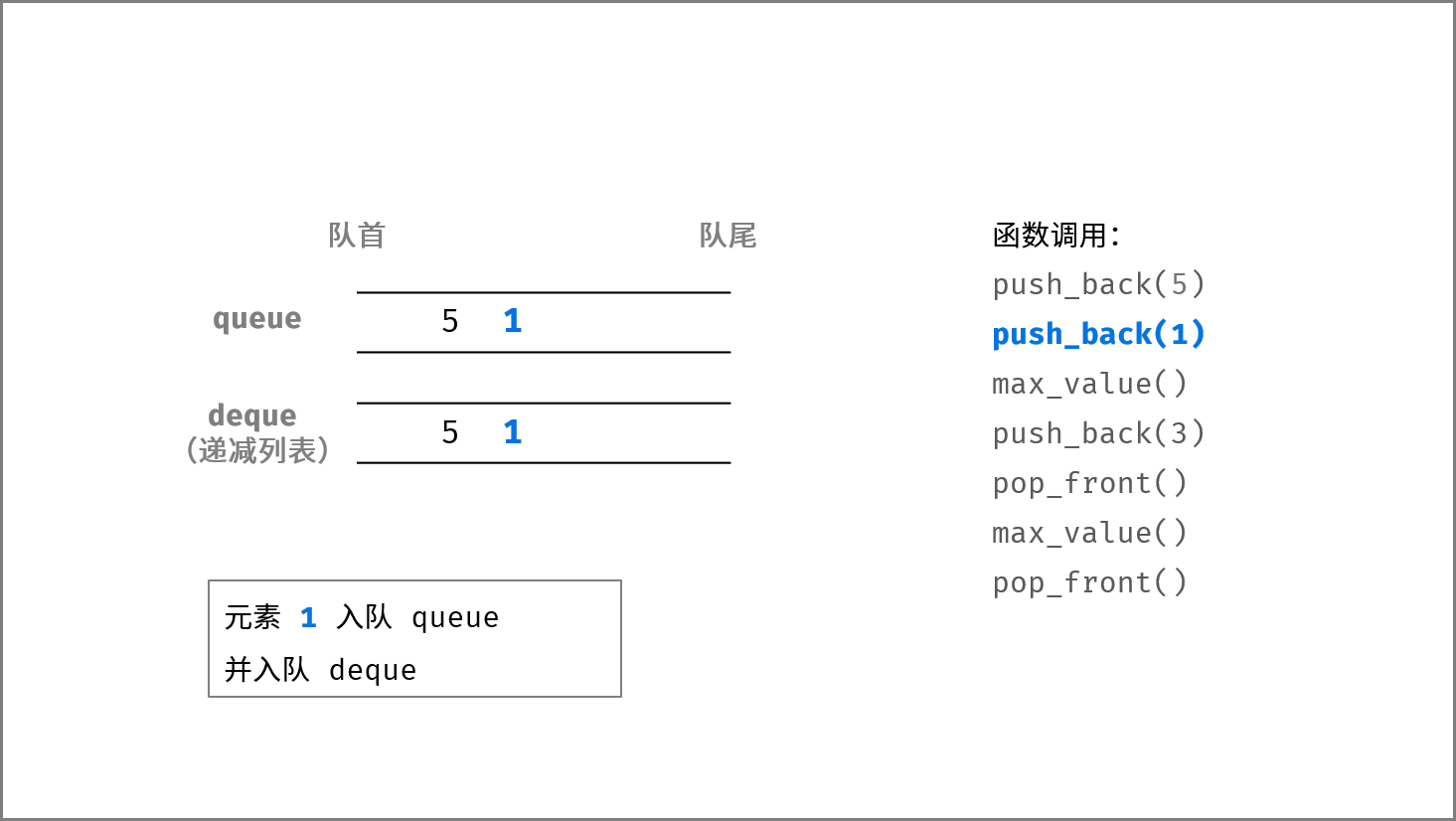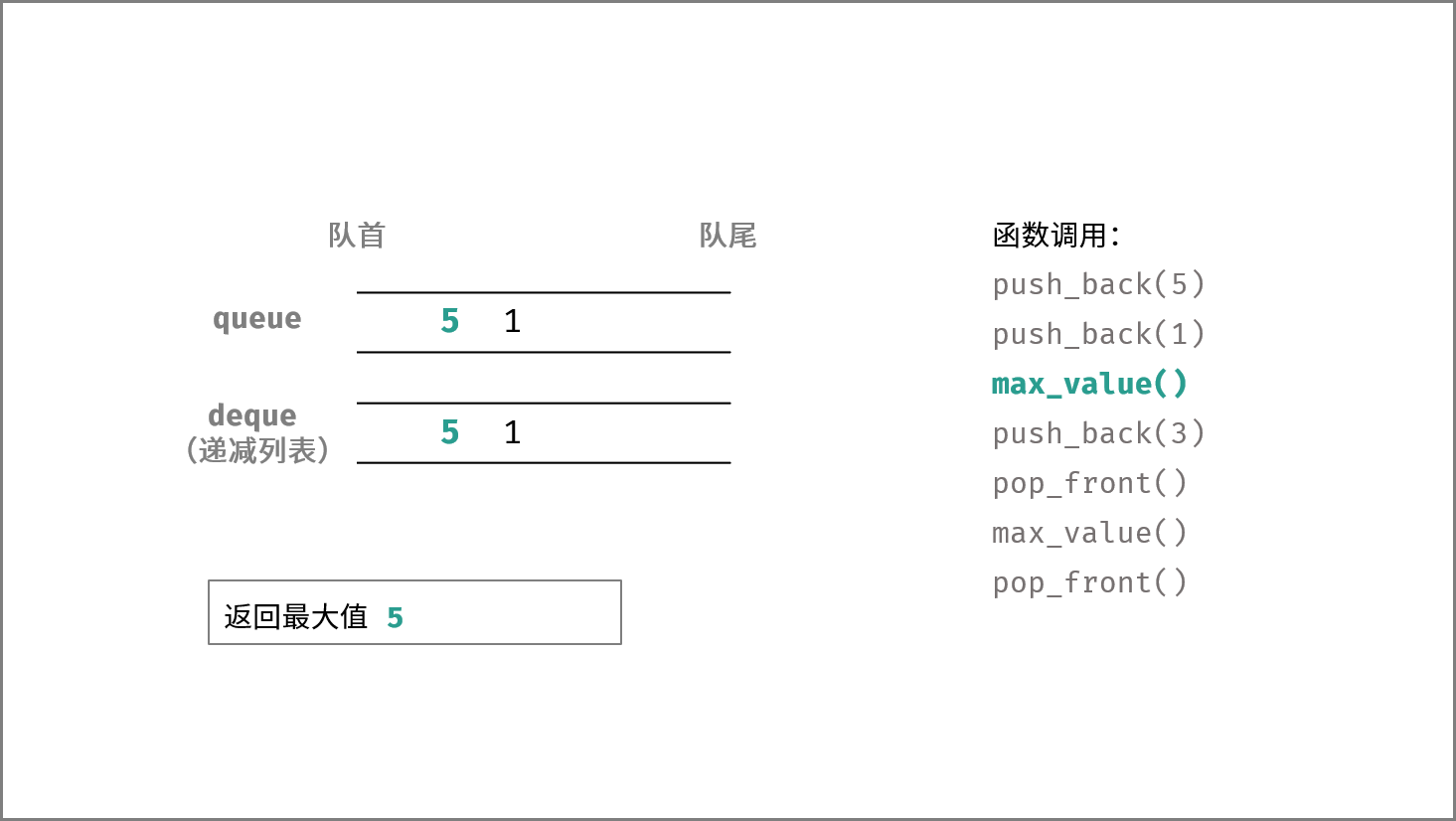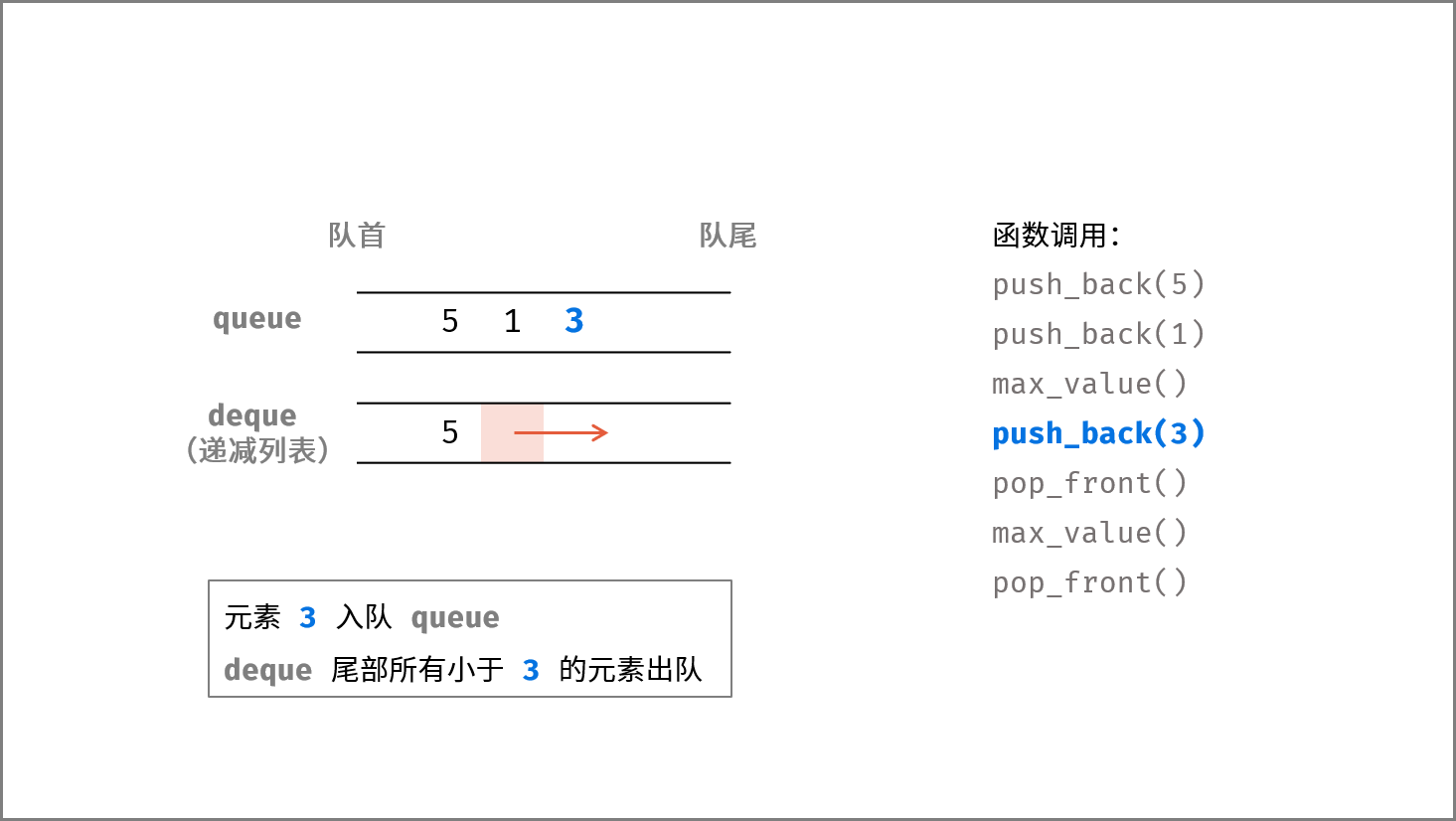<![Picture3.png](https://pic.leetcode-cn.com/1609261619-jyPPLT-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1609261619-bCHZki-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1609261619-VJHbWU-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1609261757-CwSwSi-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1609261619-TeDGxf-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1609261619-xvlryq-Picture8.png),![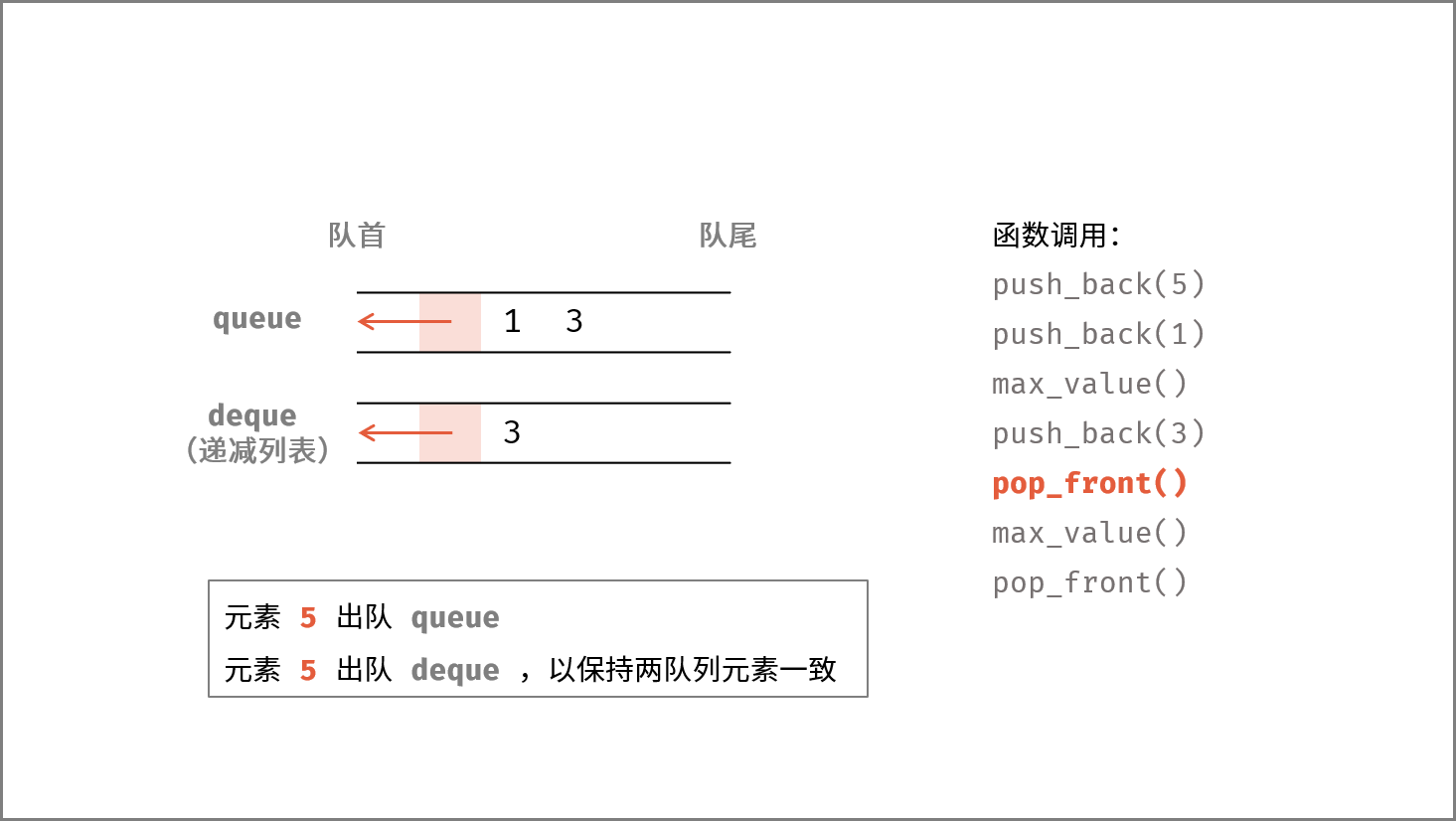Picture9.png](https://pic.leetcode-cn.com/1609261619-ARzNSA-Picture9.png),![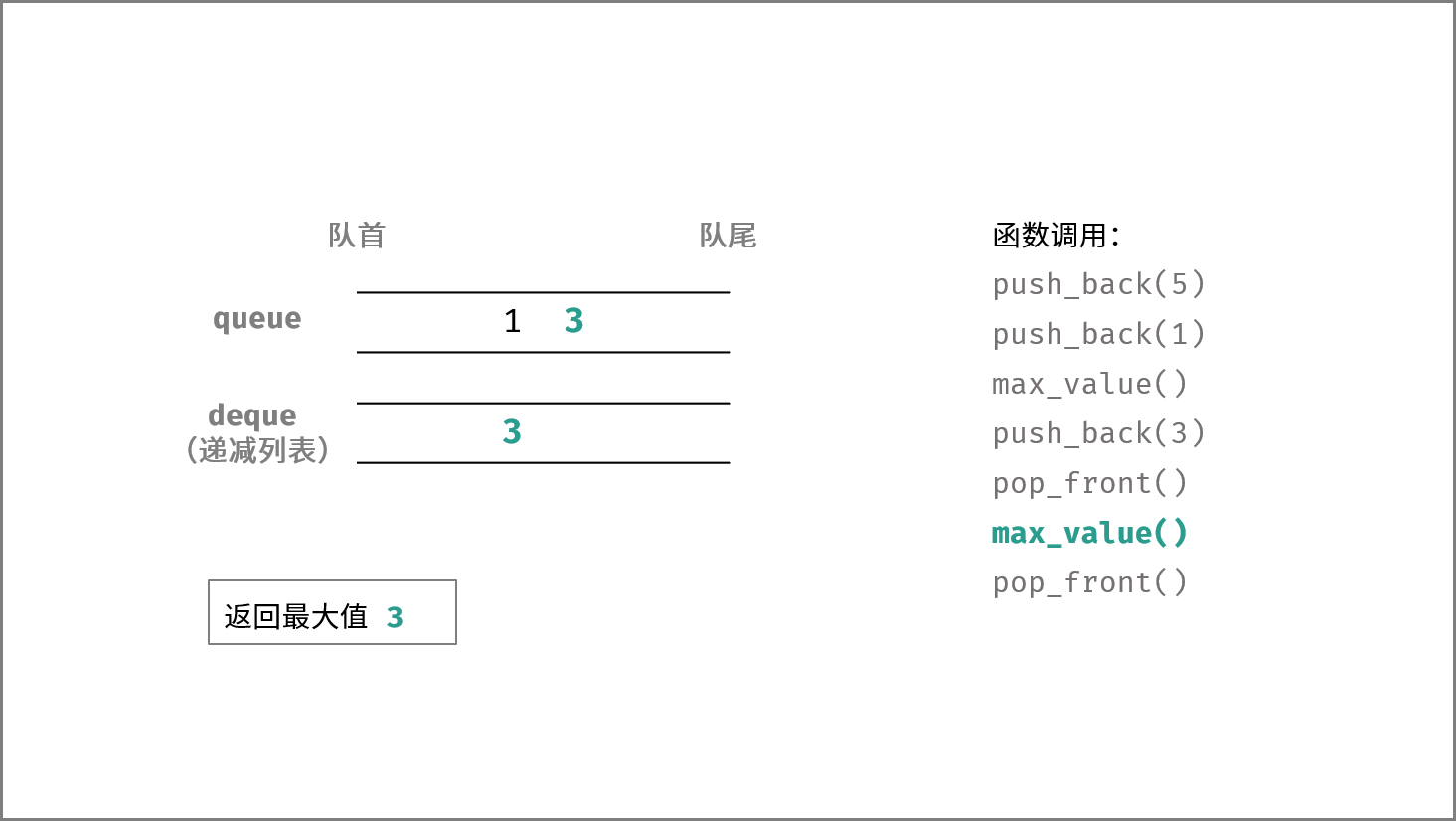Picture10.png](https://pic.leetcode-cn.com/1609261619-UZBWSp-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1609261619-CiZXVu-Picture11.png)>
## 代码：
```Python []
import queue
class Checkout:
def __init__(self):
self.queue = queue.Queue()
self.deque = queue.deque()
def get_max(self) -> int:
return self.deque[0] if self.deque else -1
def add(self, value: int) -> None:
self.queue.put(value)
while self.deque and self.deque[-1] < value:
self.deque.pop()
self.deque.append(value)
def remove(self) -> int:
if self.queue.empty(): return -1
val = self.queue.get()
if val == self.deque[0]:
self.deque.popleft()
return val
```
```Java []
class Checkout {
Queue<Integer> queue;
Deque<Integer> deque;
public Checkout() {
queue = new LinkedList<>();
deque = new LinkedList<>();
}
public int get_max() {
return deque.isEmpty() ? -1 : deque.peekFirst();
}
public void add(int value) {
queue.offer(value);
while(!deque.isEmpty() && deque.peekLast() < value)
deque.pollLast();
deque.offerLast(value);
}
public int remove() {
if(queue.isEmpty()) return -1;
if(queue.peek().equals(deque.peekFirst()))
deque.pollFirst();
return queue.poll();
}
}
```
```C++ []
class Checkout {
queue<int> que;
deque<int> deq;
public:
Checkout() { }
int get_max() {
return deq.empty() ? -1 : deq.front();
}
void add(int value) {
que.push(value);
while(!deq.empty() && deq.back() < value)
deq.pop_back();
deq.push_back(value);
}
int remove() {
if(que.empty()) return -1;
int val = que.front();
if(val == deq.front())
deq.pop_front();
que.pop();
return val;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(1)$ ：** `get_max()`, `add()`, `remove()` 方法的均摊时间复杂度均为 $O(1)$ ；
- **空间复杂度 $O(N)$ ：** 当元素个数为 $N$ 时，最差情况下`deque` 中保存 $N$ 个元素，使用 $O(N)$ 的额外空间；

113
leetbook_ioa/docs/LCR 185. 统计结果概率.md Executable file
View File

@@ -0,0 +1,113 @@
## 方法一：暴力法
> 此方法超时，但为便于理解「方法二」，建议先理解此方法。
>
> 为简化篇幅，本文使用 $n$ 代替题目中的 $num$ 。
给定 $n$ 个骰子，可得：
- 每个骰子摇到 $1$ 至 $6$ 的概率相等，都为 $\frac{1}{6}$ 。
- 将每个骰子的点数看作独立情况，共有 $6^n$ 种「**点数组合**」。例如 $n = 2$ 时的点数组合为：
$$
(1,1), (1,2), \cdots, (2, 1), (2, 2), \cdots, (6,1), \cdots, (6, 6)
$$
- $n$ 个骰子「**点数和**」的范围为 $[n, 6n]$ ，数量为 $6n - n + 1 = 5n + 1$ 种。
**暴力统计：** 每个「点数组合」都对应一个「点数和」，考虑遍历所有点数组合，统计每个点数和的出现次数，最后除以点数组合的总数（即除以 $6^n$ ），即可得到每个点数和的出现概率。
> 如下图所示，为输入 $n = 2$ 时，点数组合、点数和、各点数概率的计算过程。
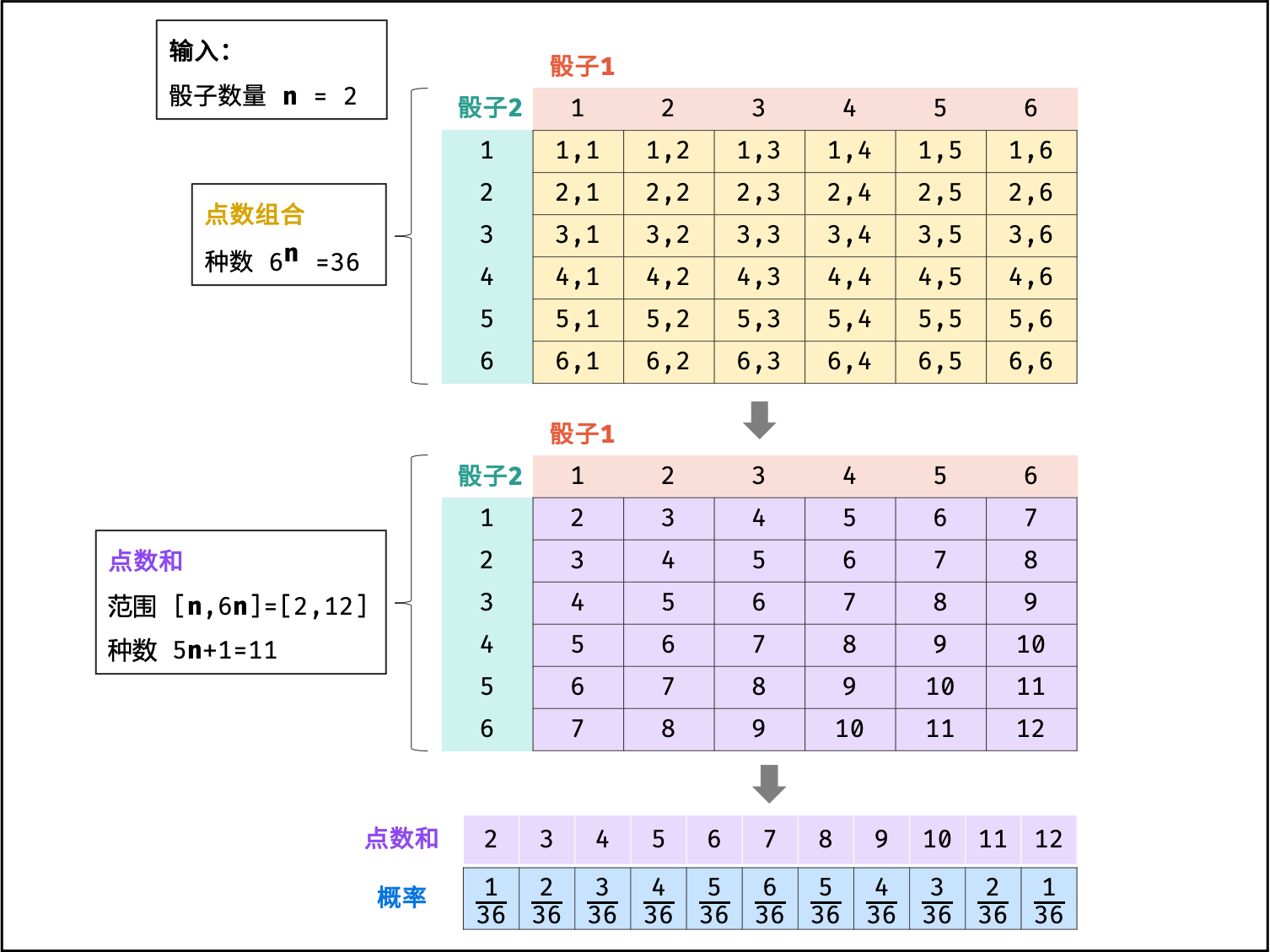![Picture1.png](https://pic.leetcode-cn.com/1615223242-EMOnIR-Picture1.png){:align=center width=550}
暴力法需要遍历所有点数组合，因此时间复杂度为 $O(6^n)$ ，观察本题输入取值范围 $1 \leq n \leq 11$ ，可知此复杂度是无法接受的。
## 方法二：动态规划
> 设输入 $n$ 个骰子的解（即概率列表）为 $f(n)$ ，其中「点数和」 $x$ 的概率为 $f(n, x)$ 。
假设已知 $n - 1$ 个骰子的解 $f(n - 1)$ ，此时**添加**一枚骰子，求 $n$ 个骰子的点数和为 $x$ 的概率 $f(n, x)$ 。
当添加骰子的点数为 $1$ 时，前 $n - 1$ 个骰子的点数和应为 $x - 1$ ，方可组成点数和 $x$ ；同理，当此骰子为 $2$ 时，前 $n - 1$ 个骰子应为 $x - 2$ ；以此类推，直至此骰子点数为 $6$ 。将这 $6$ 种情况的概率相加，即可得到概率 $f(n, x)$ 。递推公式如下所示：
$$
f(n, x) = \sum_{i=1}^6 f(n - 1, x - i) \times \frac{1}{6}
$$
根据以上分析，得知通过子问题的解 $f(n - 1)$ 可递推计算出 $f(n)$ ，而输入一个骰子的解 $f(1)$ 已知，因此可通过解 $f(1)$ 依次递推出任意解 $f(n)$ 。
> 如下图所示，为 $n = 2$ , $x = 7$ 的递推计算示例。
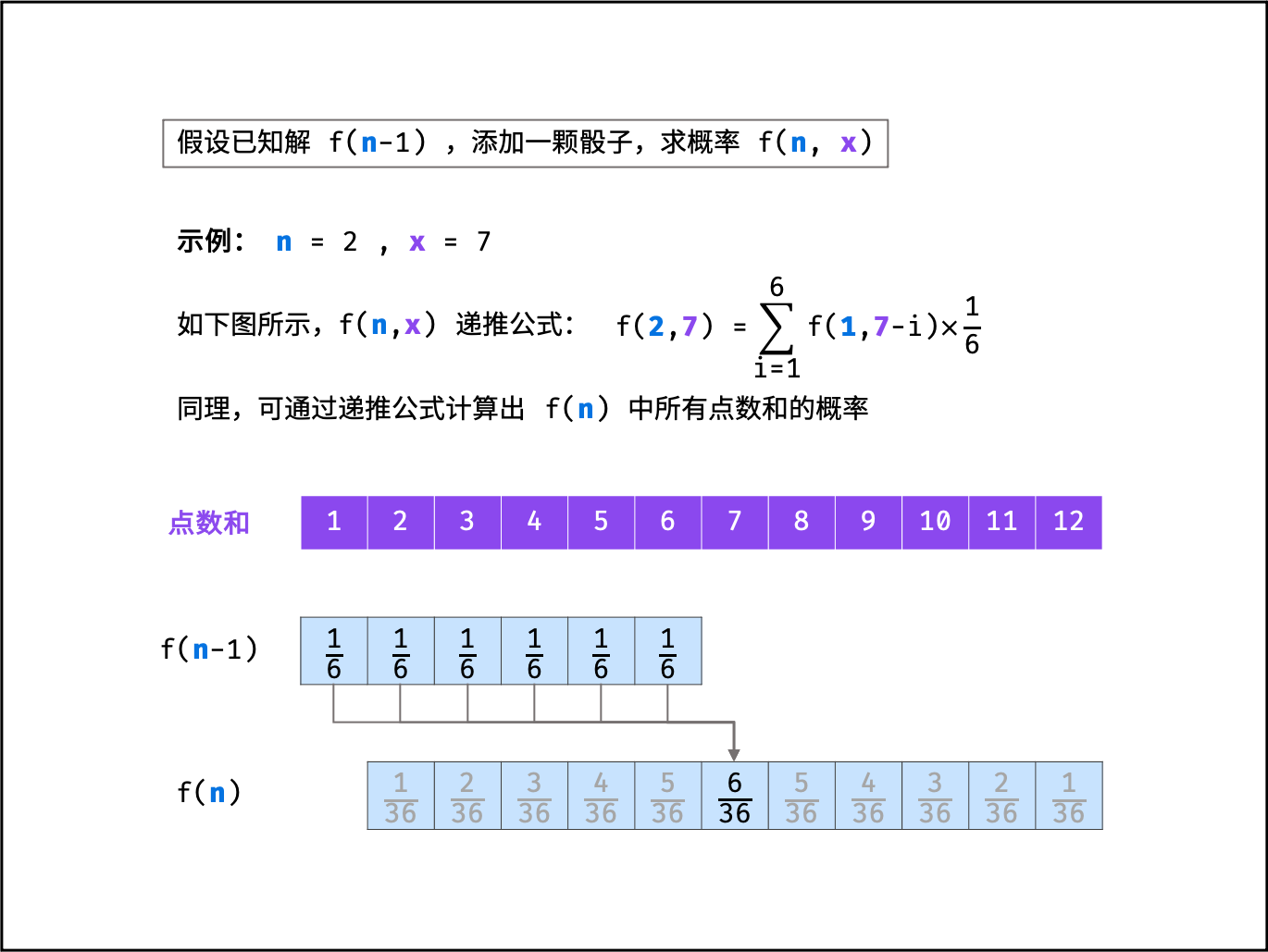![Picture2.png](https://pic.leetcode-cn.com/1614960989-tpJNRQ-Picture2.png){:align=center width=550}
观察发现，以上递推公式虽然可行，但 $f(n - 1, x - i)$ 中的 $x - i$ 会有越界问题。例如，若希望递推计算 $f(2, 2)$ ，由于一个骰子的点数和范围为 $[1, 6]$ ，因此只应求和 $f(1, 1)$ ，即 $f(1, 0)$ , $f(1, -1)$ , ... , $f(1, -4)$ 皆无意义。此越界问题导致代码编写的难度提升。
> 如下图所示，以上递推公式是 “逆向” 的，即为了计算 $f(n, x)$ ，将所有与之有关的情况求和；而倘若改换为 “正向” 的递推公式，便可解决越界问题。
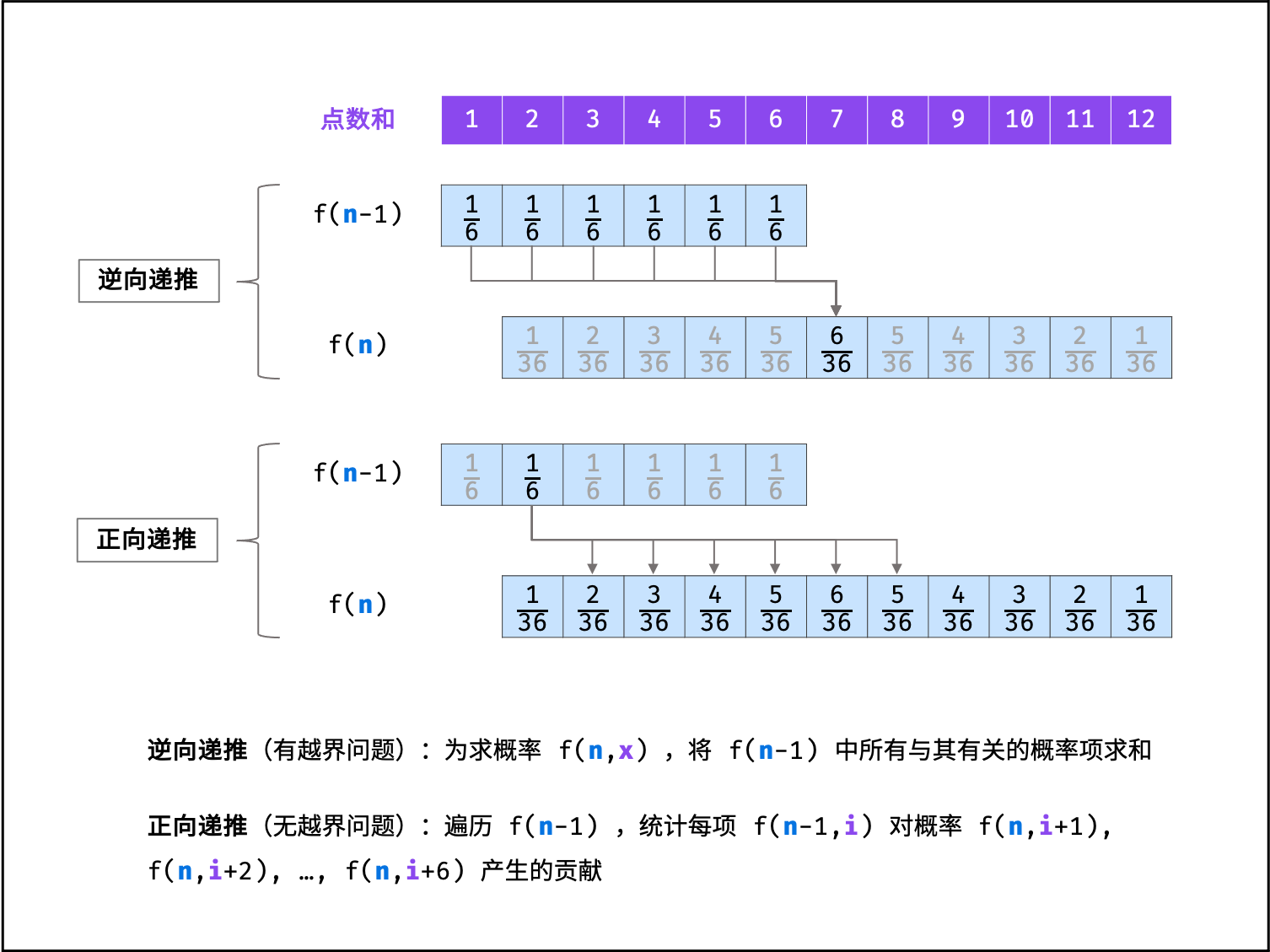![Picture3.png](https://pic.leetcode-cn.com/1614960989-mMonMs-Picture3.png){:align=center width=550}
具体来看，由于新增骰子的点数只可能为 $1$ 至 $6$ ，因此概率 $f(n - 1, x)$ 仅与 $f(n, x + 1)$ , $f(n, x + 2)$, ... , $f(n, x + 6)$ 相关。因而，遍历 $f(n - 1)$ 中各点数和的概率，并将其相加至 $f(n)$ 中所有相关项，即可完成 $f(n - 1)$ 至 $f(n)$ 的递推。
> 将 $f(i)$ 记为动态规划列表形式 $dp[i]$ ，则 $i = 1, 2, ..., n$ 的状态转移过程如下图所示。
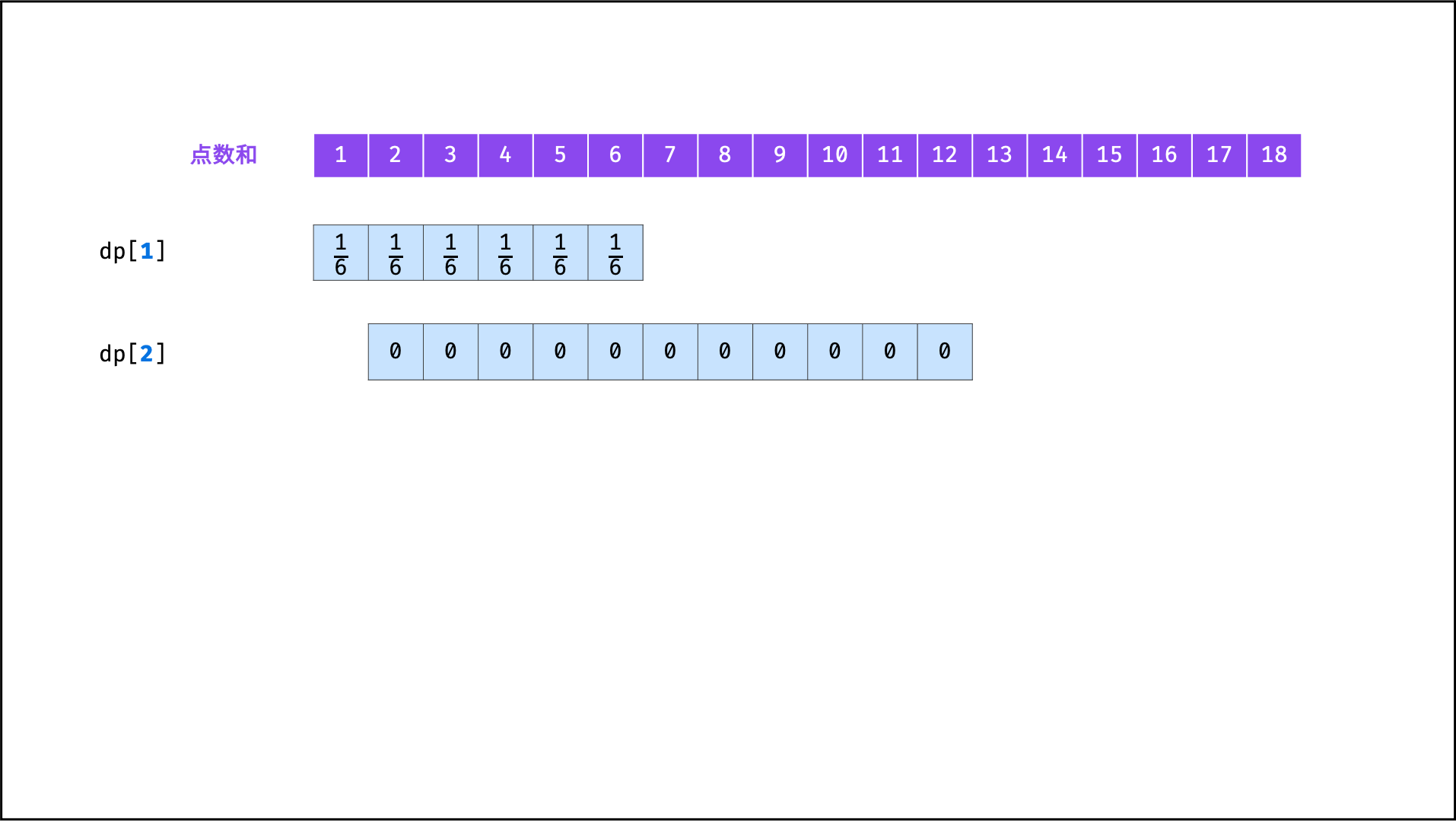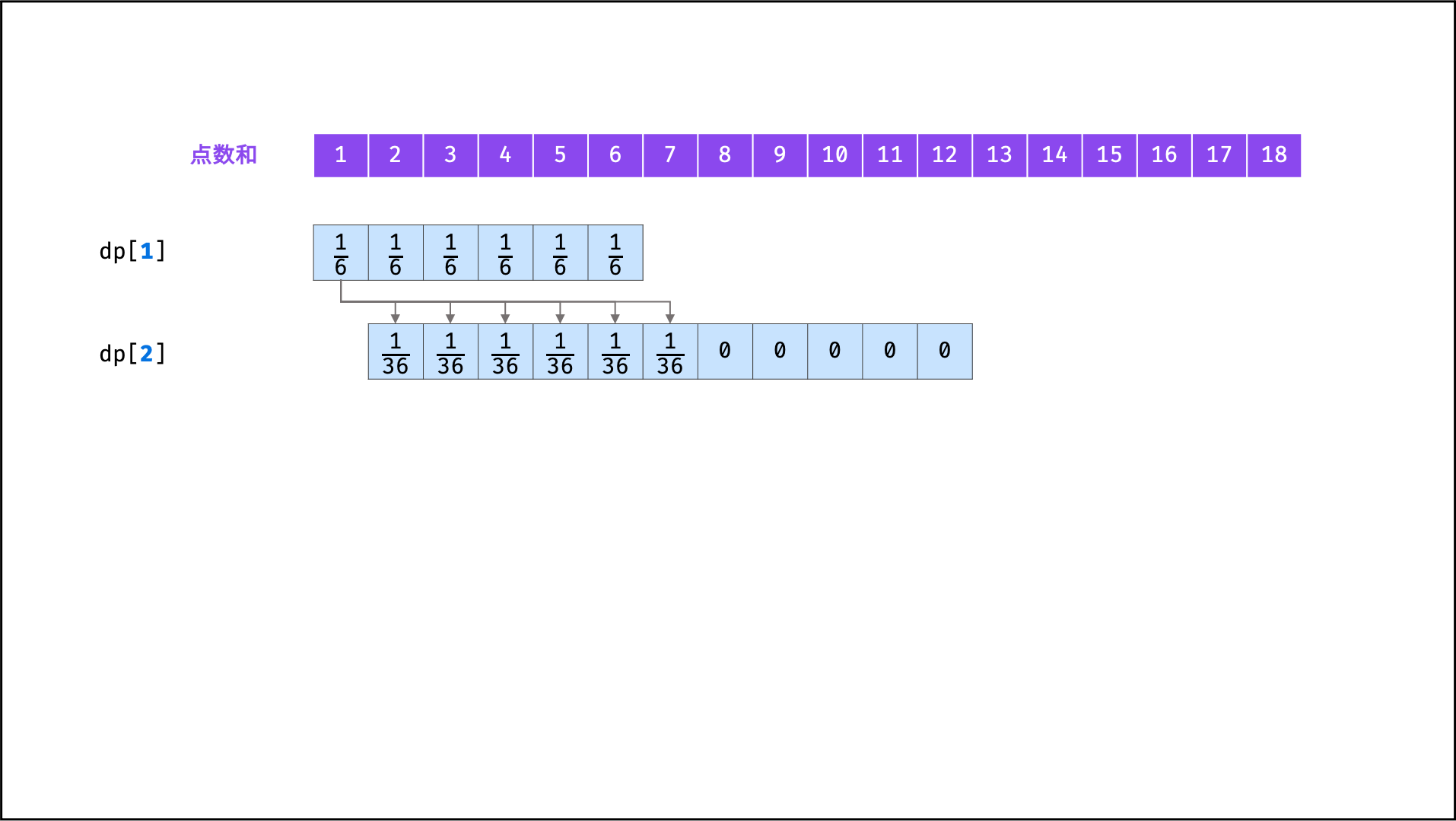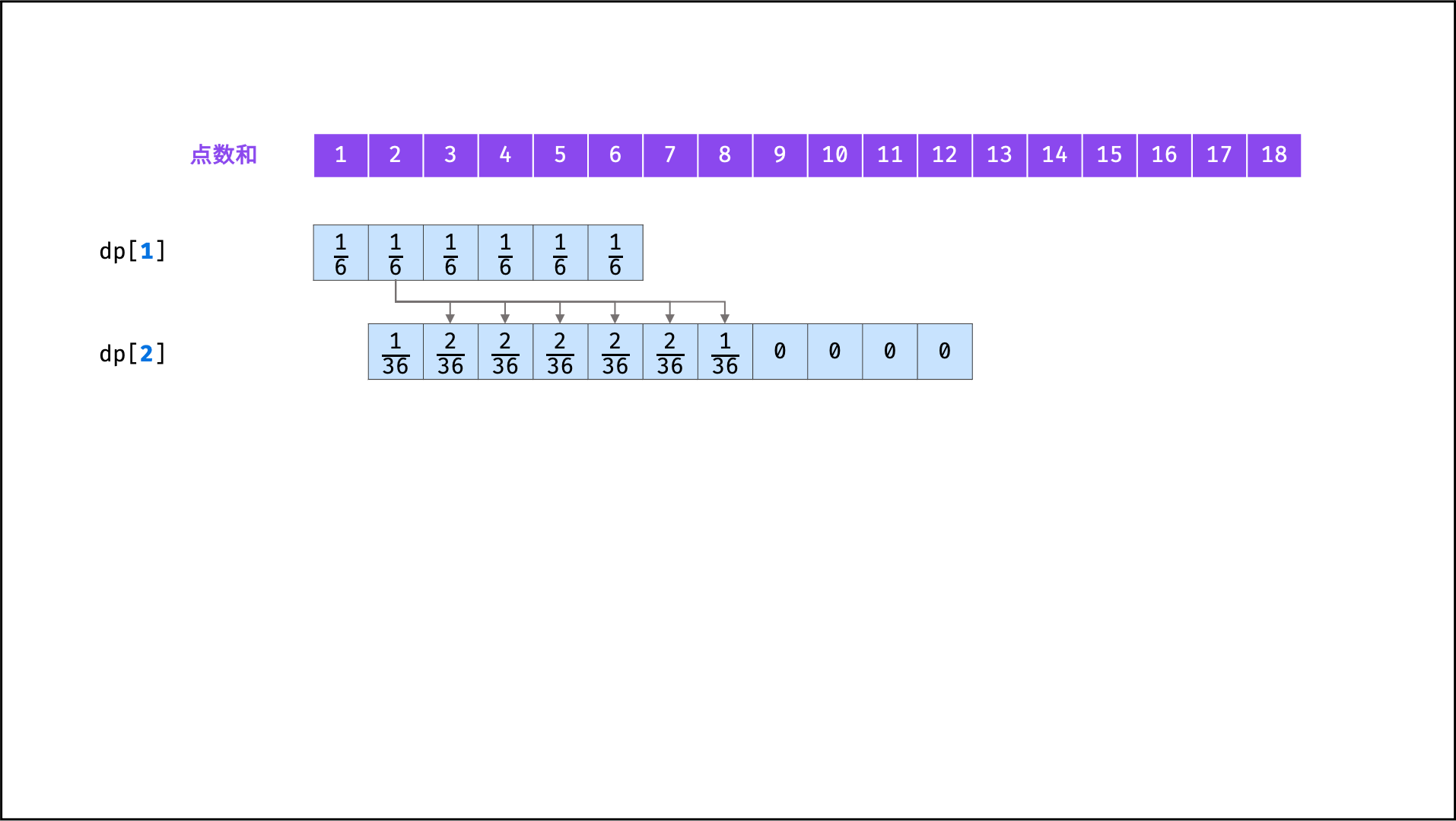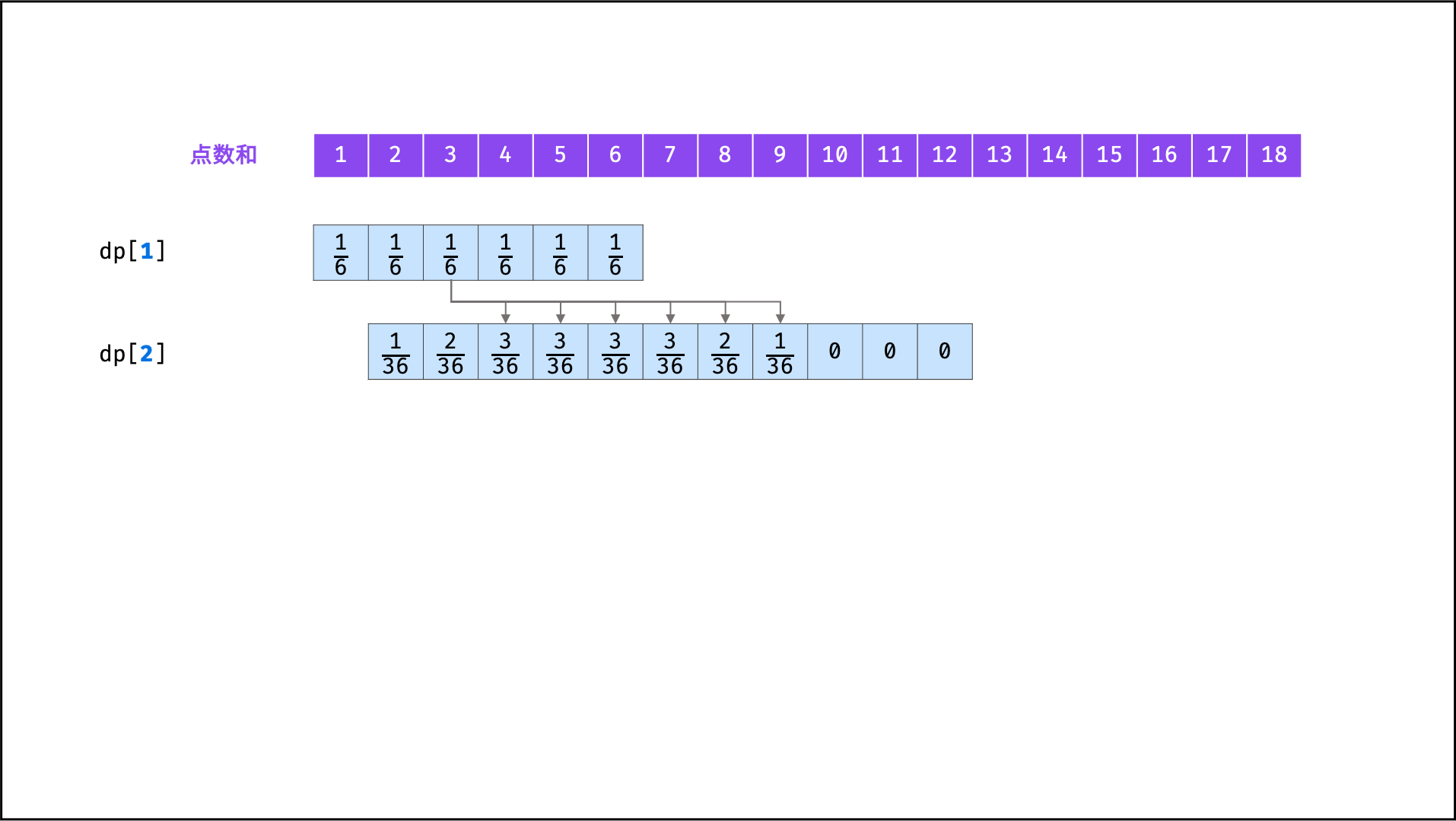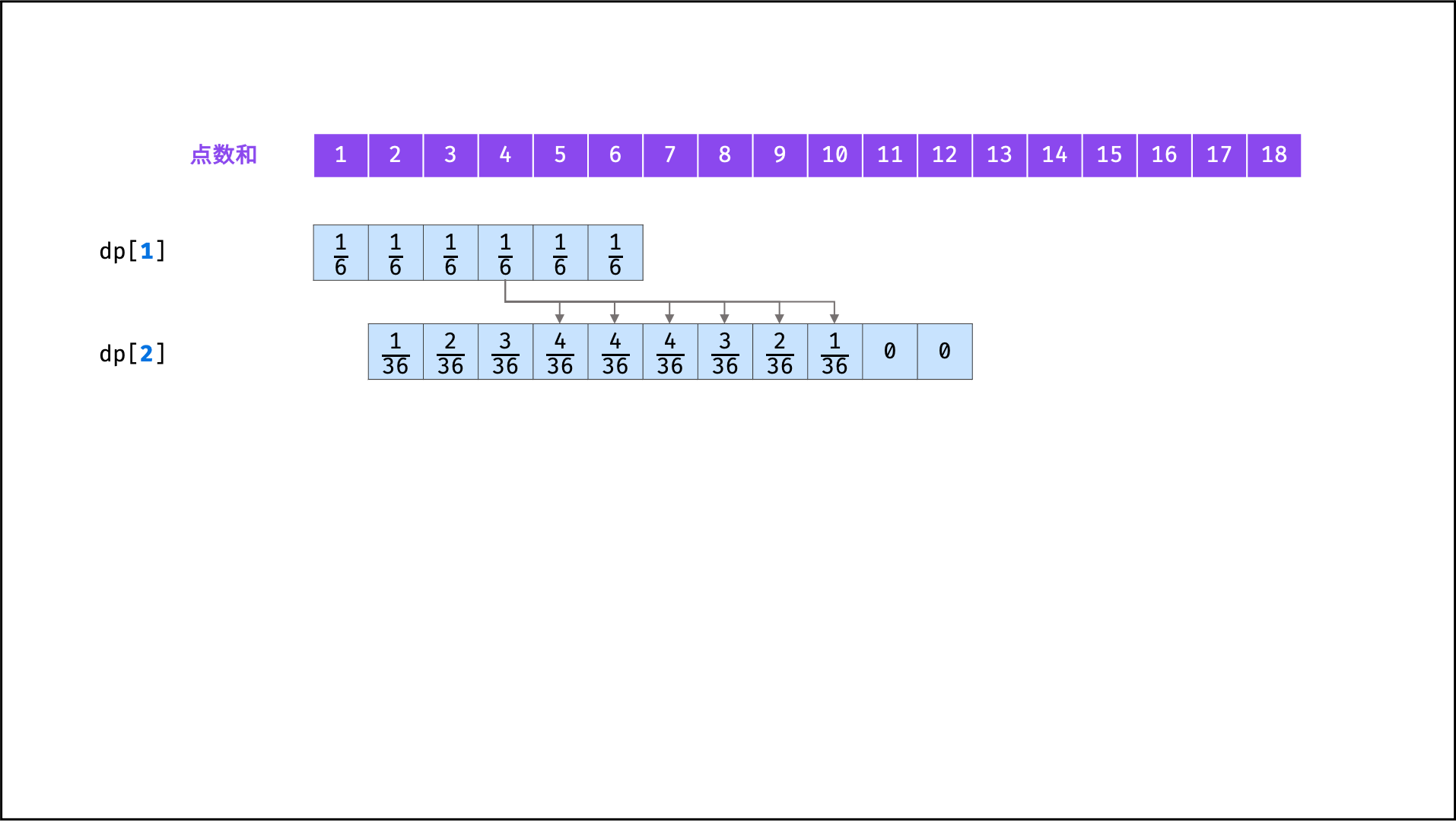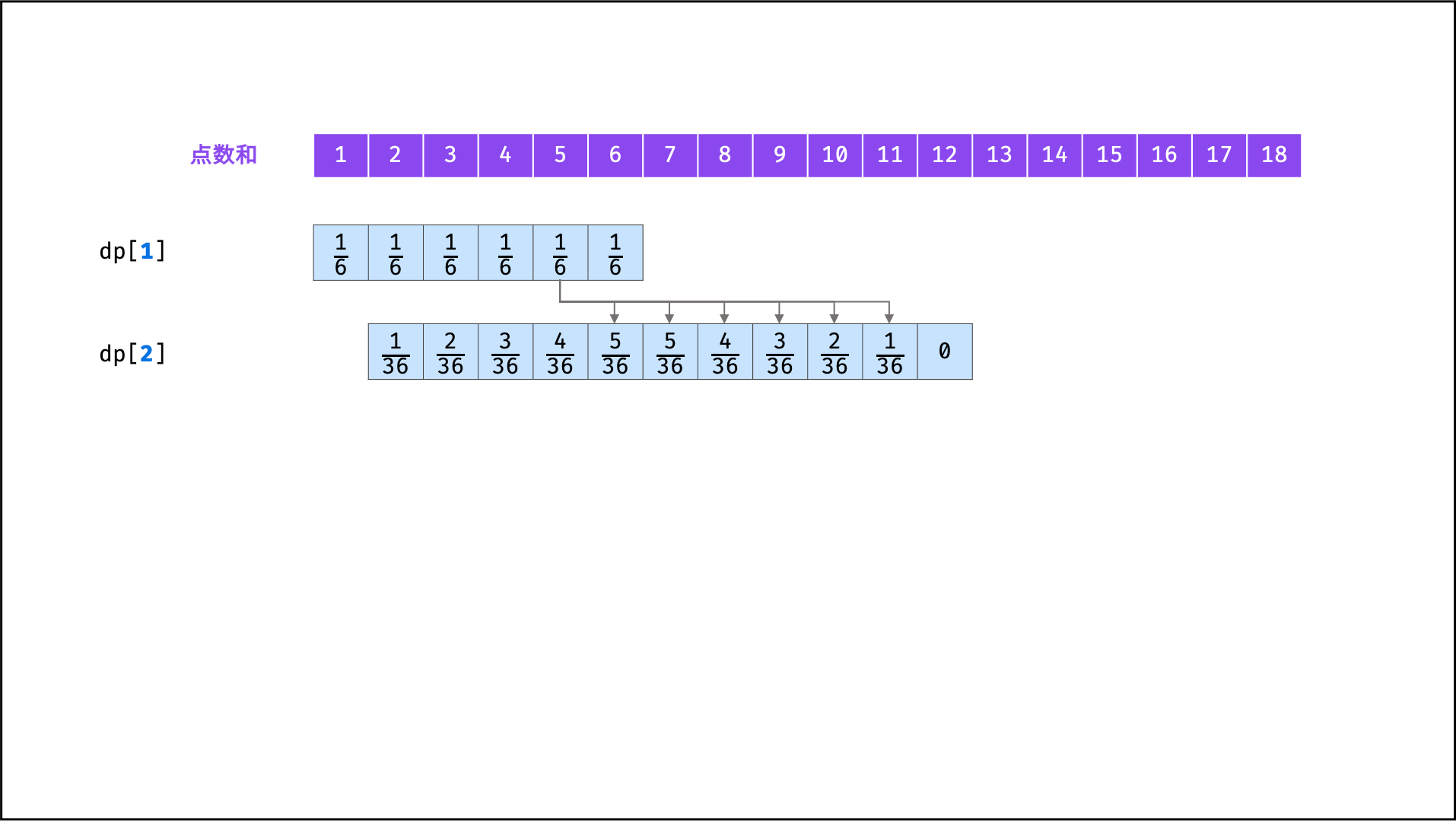<![Picture4.png](https://pic.leetcode-cn.com/1614960989-vkPMks-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1614960989-lzbHYA-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1614960989-pNSQec-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1614960989-oRLcts-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1614960989-foAgUF-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1614960989-hYgICF-Picture9.png),![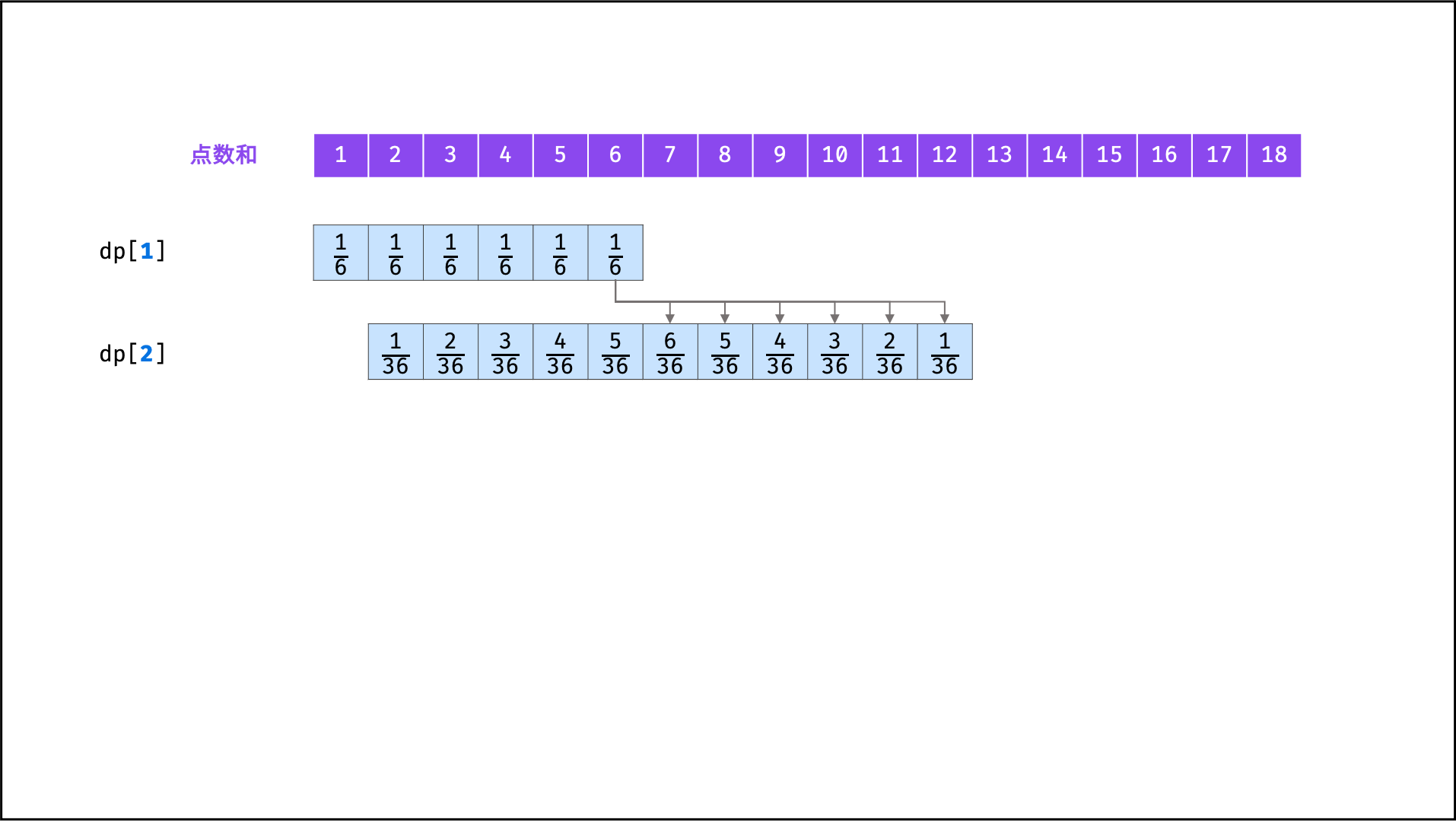Picture10.png](https://pic.leetcode-cn.com/1614960989-SlimYn-Picture10.png),![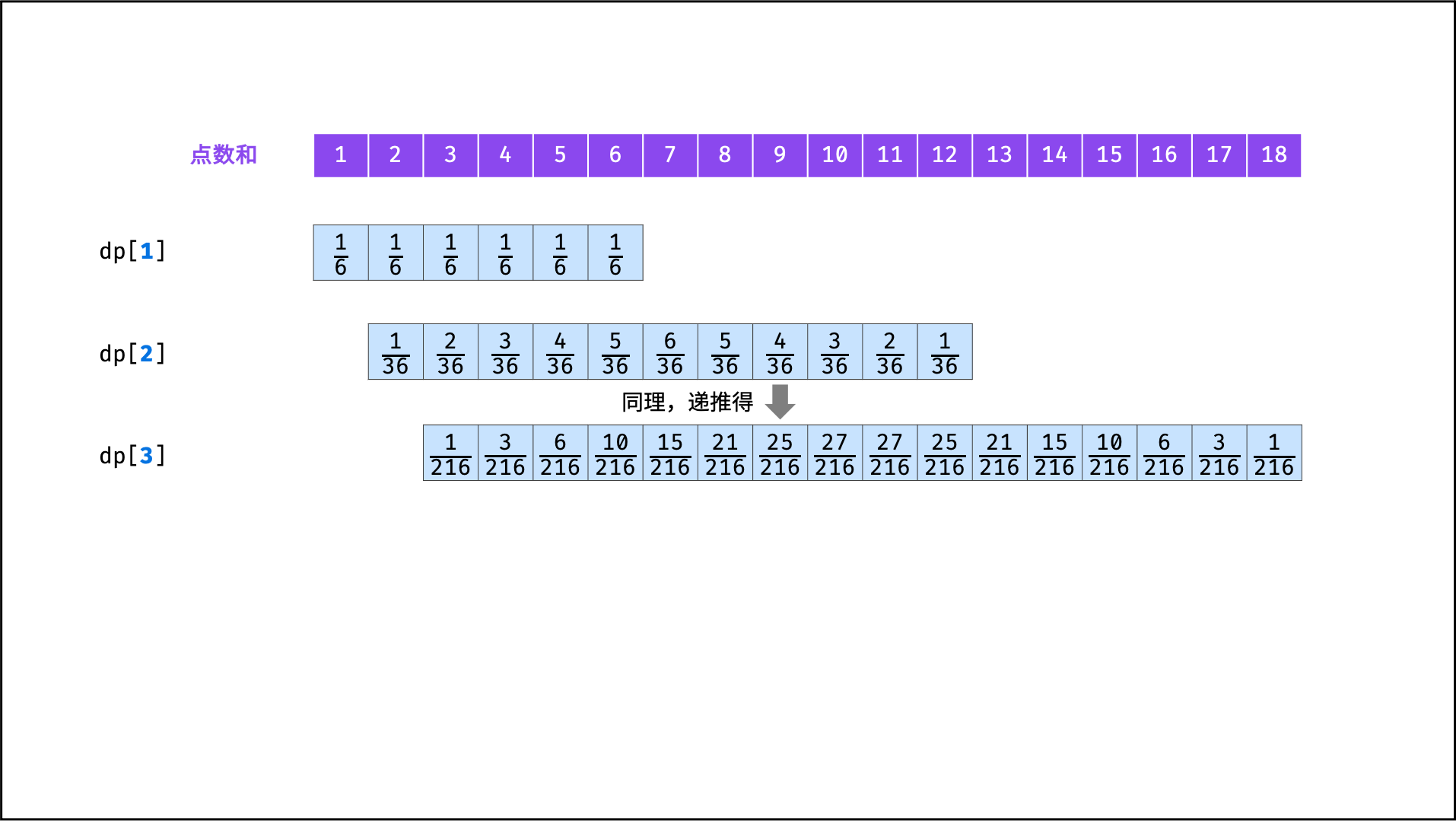Picture11.png](https://pic.leetcode-cn.com/1614960989-AnyWXD-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1614960989-WyeOfz-Picture12.png)>
## 代码：
通常做法是声明一个二维数组 $dp$ ，$dp[i][j]$ 代表前 $i$ 个骰子的点数和 $j$ 的概率，并执行状态转移。而由于 $dp[i]$ 仅由 $dp[i-1]$ 递推得出，为降低空间复杂度，只建立两个一维数组 $dp$ , $tmp$ 交替前进即可。
```Python []
class Solution:
def statisticsProbability(self, n: int) -> List[float]:
dp = [1 / 6] * 6
for i in range(2, n + 1):
tmp = [0] * (5 * i + 1)
for j in range(len(dp)):
for k in range(6):
tmp[j + k] += dp[j] / 6
dp = tmp
return dp
```
```Java []
class Solution {
public double[] statisticsProbability(int n) {
double[] dp = new double[6];
Arrays.fill(dp, 1.0 / 6.0);
for (int i = 2; i <= n; i++) {
double[] tmp = new double[5 * i + 1];
for (int j = 0; j < dp.length; j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += dp[j] / 6.0;
}
}
dp = tmp;
}
return dp;
}
}
```
```C++ []
class Solution {
public:
vector<double> statisticsProbability(int n) {
vector<double> dp(6, 1.0 / 6.0);
for (int i = 2; i <= n; i++) {
vector<double> tmp(5 * i + 1, 0);
for (int j = 0; j < dp.size(); j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += dp[j] / 6.0;
}
}
dp = tmp;
}
return dp;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(n ^ 2)$ ：** 状态转移循环 $n - 1$ 轮；每轮中，当 $i = 2, 3, ..., n$ 时，对应循环数量分别为 $6 \times 6, 11 \times 6, ..., [5(n - 1) + 1] \times 6$ ；因此总体复杂度为 $O((n - 1) \times \frac{6 + [5(n - 1) + 1]}{2} \times 6)$ ，即等价于 $O(n^2)$ 。
- **空间复杂度 $O(n)$ ：** 状态转移过程中，辅助数组 `tmp` 最大长度为 $6(n-1) - [(n-1) - 1] = 5n - 4$ ，因此使用 $O(5n - 4) = O(n)$ 大小的额外空间。

135
leetbook_ioa/docs/LCR 186. 文物朝代判断.md Executable file
View File

@@ -0,0 +1,135 @@
## 解题思路：
根据题意，此 $5$ 个朝代连续的 **充分条件** 如下：
1. 除未知朝代外，所有朝代 **无重复** ；
2. 设此 $5$ 个朝代中最大的朝代为 $ma$ ，最小的朝代为 $mi$ （未知朝代除外），则需满足：
$$
ma - mi < 5
$$
因此可将问题转化为：此 $5$ 个朝代是否满足以上两个条件？
> 下图中的“牌”对应本题的“朝代”。
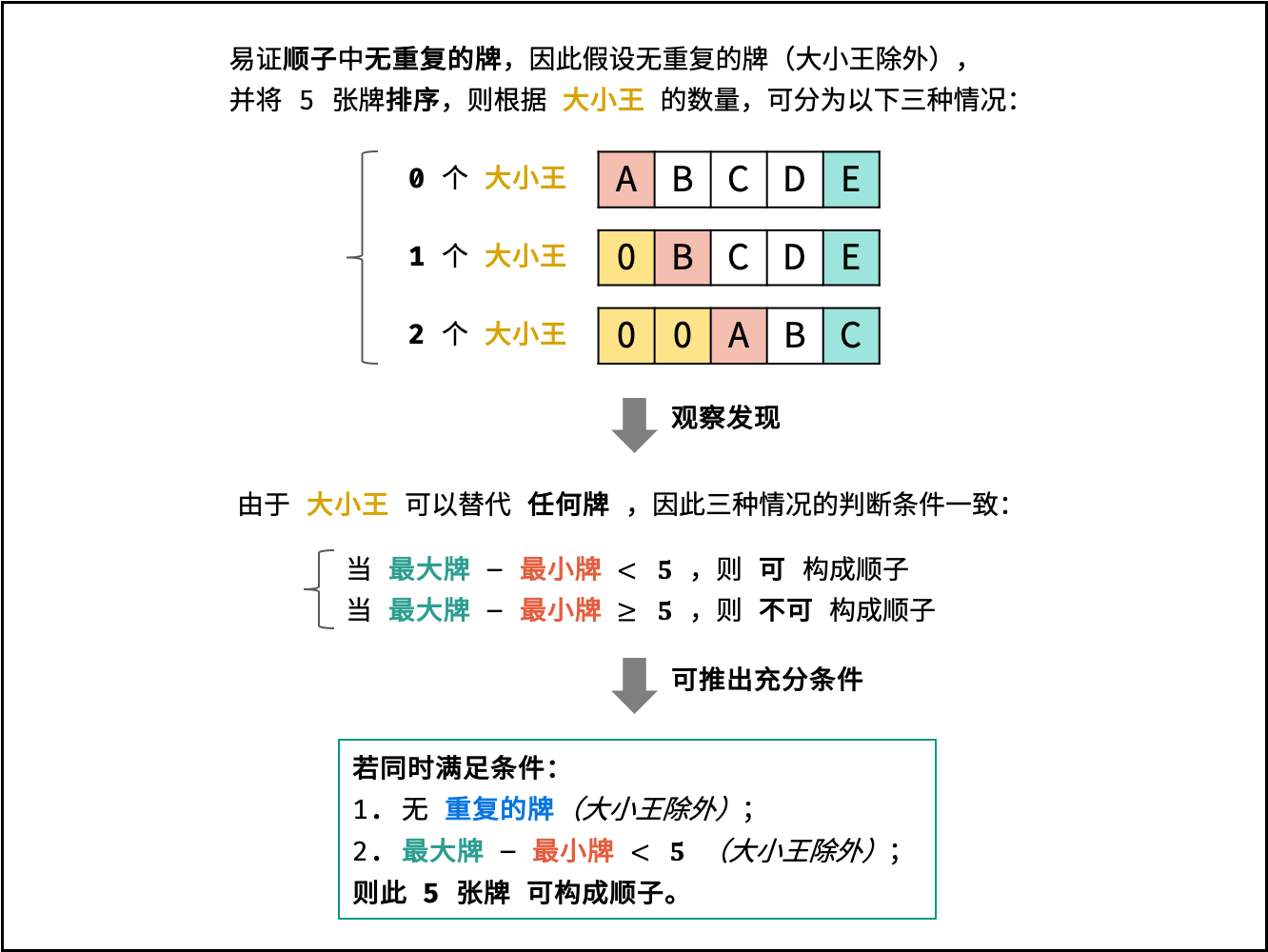![Picture1.png](https://pic.leetcode-cn.com/1599885716-MGMODX-Picture1.png){:align=center width=650}
## 方法一： 辅助哈希表
- 遍历五个朝代，遇到未知朝代（即 $0$ ）直接跳过。
- **判别重复：** 利用 Set 实现遍历判重， Set 的查找方法的时间复杂度为 $O(1)$ ；
- **获取最大 / 最小的朝代：** 借助辅助变量 $ma$ 和 $mi$ ，遍历统计即可。
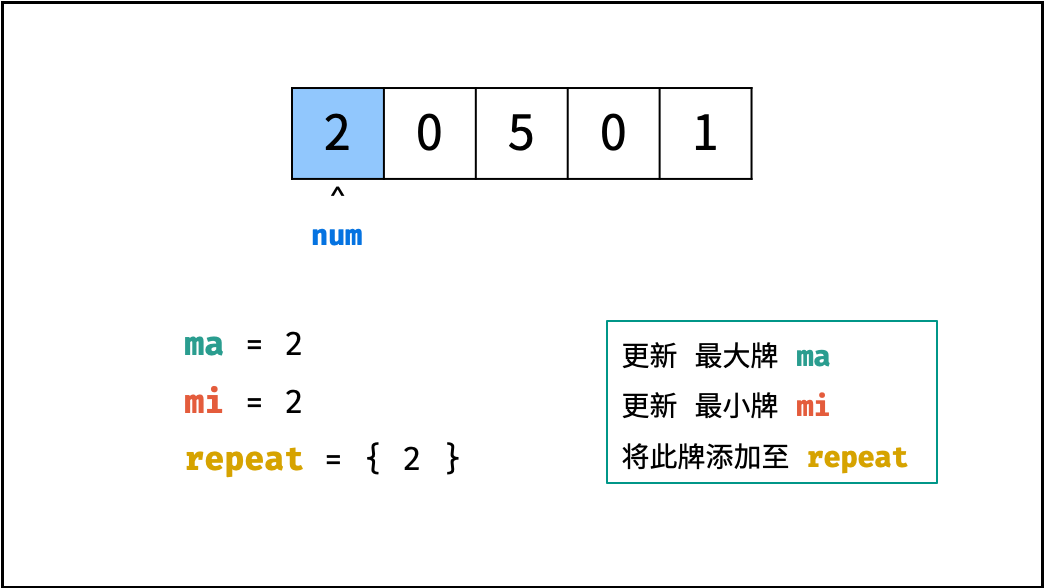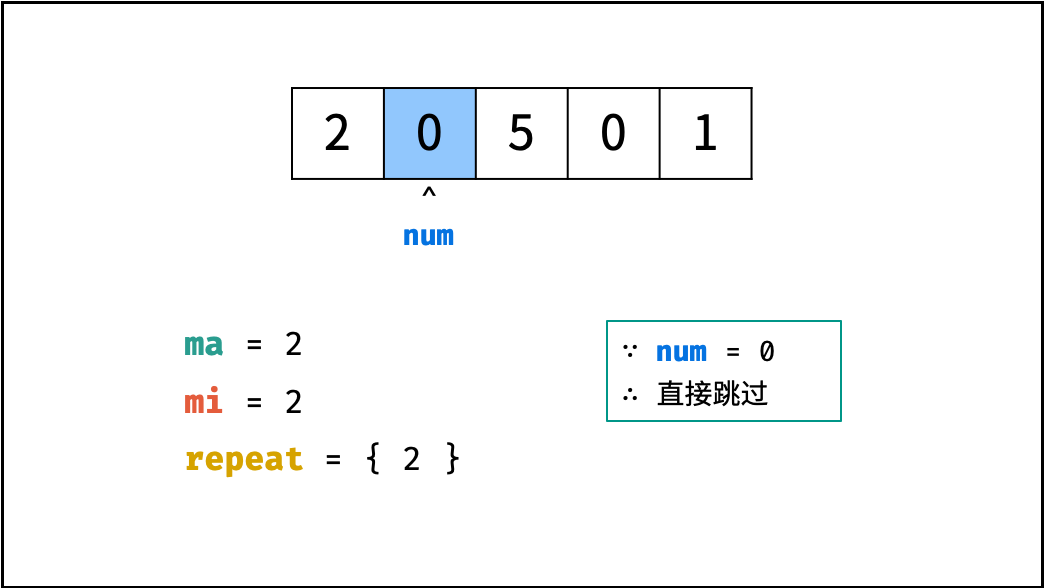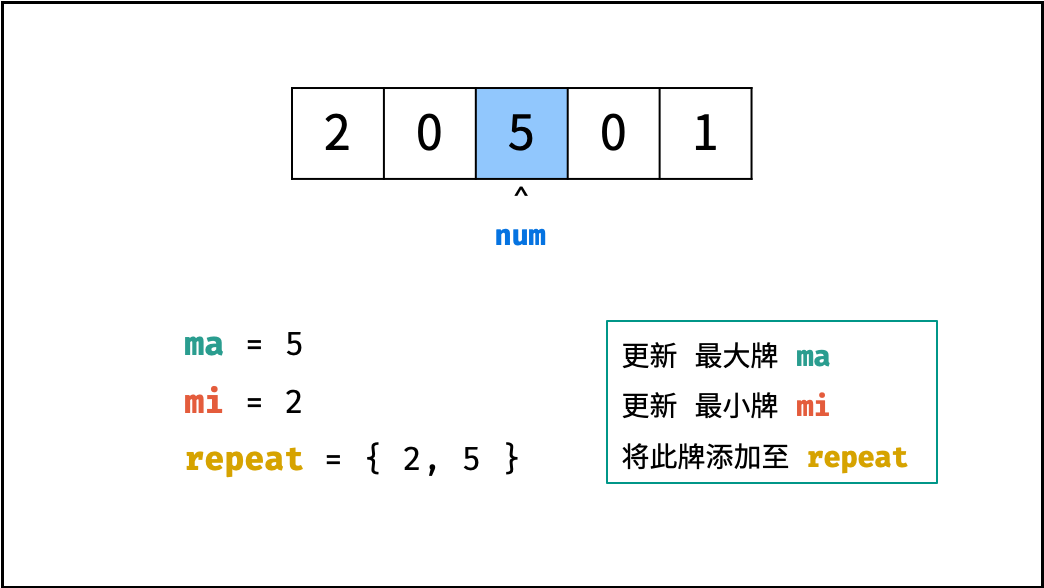<![Picture2.png](https://pic.leetcode-cn.com/1599885716-wApHky-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599885716-DYlnGL-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599885716-rZVTio-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599885716-wurjNA-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599885716-xyjhRQ-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599885716-JgkdBO-Picture7.png),![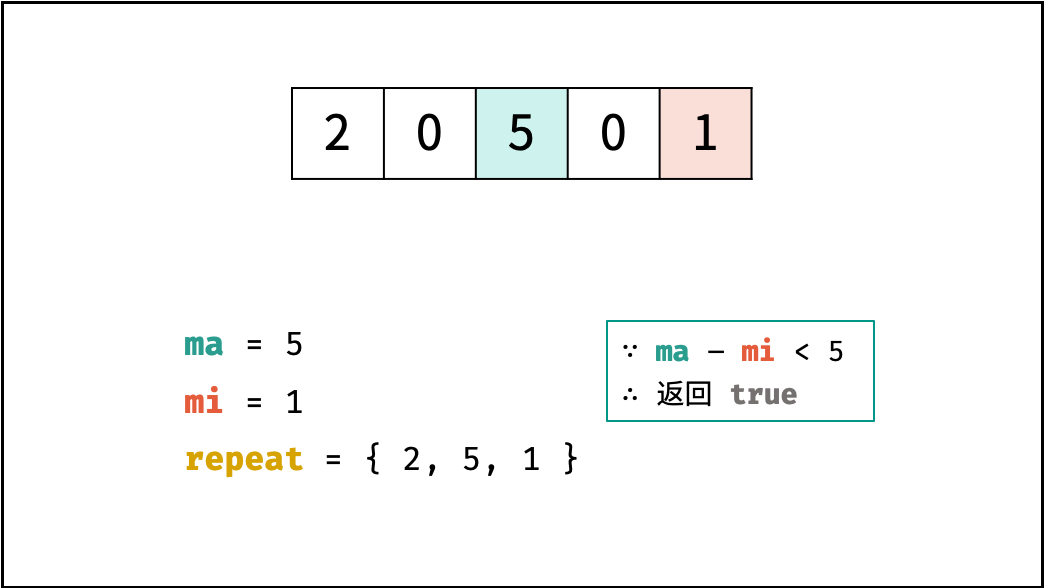Picture8.png](https://pic.leetcode-cn.com/1599885716-DUzUKd-Picture8.png)>
### 代码：
```Python []
class Solution:
def checkDynasty(self, places: List[int]) -> bool:
repeat = set()
ma, mi = 0, 14
for place in places:
if place == 0: continue # 跳过未知朝代
ma = max(ma, place) # 最大编号朝代
mi = min(mi, place) # 最小编号朝代
if place in repeat: return False # 若有重复，提前返回 false
repeat.add(place) # 添加朝代至 Set
return ma - mi < 5 # 最大编号朝代 - 最小编号朝代 < 5 则连续
```
```Java []
class Solution {
public boolean checkDynasty(int[] places) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for(int place : places) {
if(place == 0) continue; // 跳过未知朝代
max = Math.max(max, place); // 最大编号朝代
min = Math.min(min, place); // 最小编号朝代
if(repeat.contains(place)) return false; // 若有重复，提前返回 false
repeat.add(place); // 添加此朝代至 Set
}
return max - min < 5; // 最大编号朝代 - 最小编号朝代 < 5 则连续
}
}
```
```C++ []
class Solution {
public:
bool checkDynasty(vector<int>& places) {
unordered_set<int> repeat;
int ma = 0, mi = 14;
for(int place : places) {
if(place == 0) continue; // 跳过未知朝代
ma = max(ma, place); // 最大编号朝代
mi = min(mi, place); // 最小编号朝代
if(repeat.find(place) != repeat.end()) return false; // 若有重复，提前返回 false
repeat.insert(place); // 添加此朝代至 Set
}
return ma - mi < 5; // 最大编号朝代 - 最小编号朝代 < 5 则连续
}
};
```
### 复杂度分析：
- **时间复杂度 $O(1)$ ：** 本题中给定朝代数量 $N \equiv 5$ ；遍历数组使用 $O(N) = O(5) = O(1)$ 时间。
- **空间复杂度 $O(1)$ ：** 用于判重的辅助 Set 使用 $O(N) = O(1)$ 额外空间。
## 方法二：排序 + 遍历
- 先对数组执行排序。
- **判别重复：** 排序数组中的相同元素位置相邻，因此可通过遍历数组，判断 $places[i] = places[i + 1]$ 是否成立来判重。
- **获取最大 / 最小的朝代：** 排序后，数组末位元素 $places[4]$ 为最大编号朝代；元素 $places[unknown]$ 为最小编号朝代，其中 $unknown$ 为未知朝代的数量。
<![Picture9.png](https://pic.leetcode-cn.com/1599885716-kfnHqU-Picture9.png),![Picture10.png](https://pic.leetcode-cn.com/1599885716-tfWCOX-Picture10.png),![Picture11.png](https://pic.leetcode-cn.com/1599885716-NkLqOa-Picture11.png),![Picture12.png](https://pic.leetcode-cn.com/1599885716-kEsven-Picture12.png),![Picture13.png](https://pic.leetcode-cn.com/1599885716-BXvbwz-Picture13.png),![Picture14.png](https://pic.leetcode-cn.com/1599885716-BtPEYq-Picture14.png),![Picture15.png](https://pic.leetcode-cn.com/1599885716-Lqyuwk-Picture15.png)>
### 代码：
```Python []
class Solution:
def checkDynasty(self, places: List[int]) -> bool:
unknown = 0
places.sort() # 数组排序
for i in range(4):
if places[i] == 0: unknown += 1 # 统计未知朝代数量
elif places[i] == places[i + 1]: return False # 若有重复，提前返回 false
return places[4] - places[unknown] < 5 # 最大编号朝代 - 最小编号朝代 < 5 则连续
```
```Java []
class Solution {
public boolean checkDynasty(int[] places) {
int unknown = 0;
Arrays.sort(places); // 数组排序
for(int i = 0; i < 4; i++) {
if(places[i] == 0) unknown++; // 统计未知朝代数量
else if(places[i] == places[i + 1]) return false; // 若有重复，提前返回 false
}
return places[4] - places[unknown] < 5; // 最大编号朝代 - 最小编号朝代 < 5 则连续
}
}
```
```C++ []
class Solution {
public:
bool checkDynasty(vector<int>& places) {
int unknown = 0;
sort(places.begin(), places.end()); // 数组排序
for(int i = 0; i < 4; i++) {
if(places[i] == 0) unknown++; // 统计未知朝代数量
else if(places[i] == places[i + 1]) return false; // 若有重复，提前返回 false
}
return places[4] - places[unknown] < 5; // 最大编号朝代 - 最小编号朝代 < 5 则连续
}
};
```
### 复杂度分析：
- **时间复杂度 $O(1)$ ：** 本题中给定朝代数量 $N \equiv 5$ ；数组排序使用 $O(N \log N) = O(5 \log 5) = O(1)$ 时间。
- **空间复杂度 $O(1)$ ：** 变量 $unknown$ 使用 $O(1)$ 大小的额外空间。

123
leetbook_ioa/docs/LCR 187. 破冰游戏.md Executable file
View File

@@ -0,0 +1,123 @@
## 解题思路：
> 为简化篇幅，本文将 $num$ 和 $target$ 分别记为 $n$ 和 $m$ 。
模拟整个删除过程最直观，即构建一个长度为 $n$ 的链表，各节点值为对应的顺序索引；每轮删除第 $m$ 个节点，直至链表长度为 1 时结束，返回最后剩余节点的值即可。
模拟法需要循环删除 $n - 1$ 轮，每轮在链表中寻找删除节点需要 $m$ 次访问操作（链表线性遍历），因此总体时间复杂度为 $O(nm)$ 。题目给定的 $m, n$ 取值范围如下所示，观察可知此时间复杂度是不可接受的。
$$
1 \leq n \leq 10^5 \\
1 \leq m \leq 10^6
$$
> 实际上，本题是著名的 “约瑟夫环” 问题，可使用 **动态规划** 解决。
输入 $n, m$ ，记此约瑟夫环问题为 「$n, m$ 问题」 ，设解（即最后留下的数字）为 $f(n)$ ，则有：
- 「$n, m$ 问题」：数字环为 $0, 1, 2, ..., n - 1$ ，解为 $f(n)$ ；
- 「$n-1, m$ 问题」：数字环为 $0, 1, 2, ..., n - 2$ ，解为 $f(n-1)$ ；
- 以此类推……
> 请注意，数字环是 **首尾相接** 的，为方便行文，本文使用列表形式表示。
对于「$n, m$ 问题」，首轮删除环中第 $m$ 个数字后，得到一个长度为 $n - 1$ 的数字环。由于有可能 $m > n$ ，因此删除的数字为 $(m - 1) \mod n$ ，删除后的数字环从下个数字（即 $m \mod n$ ）开始，设 $t = m \mod n$ ，可得数字环：
$$
t, t + 1, t + 2, ..., 0, 1, ..., t - 3, t - 2
$$
删除一轮后的数字环也变为一个「$n-1, m$ 问题」，观察以下数字编号对应关系：
$$
\begin{aligned}
「n-1, m 问题」 && \rightarrow && 「n, m 问题」删除后 \\
0 && \rightarrow && t + 0 \\
1 && \rightarrow && t + 1 \\
... && \rightarrow && ... \\
n - 2 && \rightarrow && t - 2 \\
\end{aligned}
$$
设「$n-1, m$ 问题」某数字为 $x$ ，则可得递推关系：
$$
x \rightarrow (x + t) \mod n \\
$$
换而言之，若已知「$n-1, m$ 问题」的解 $f(n - 1)$ ，则可通过以上公式计算得到「$n, m$ 问题」的解 $f(n)$ ，即：
$$
\begin{aligned}
f(n) & = (f(n - 1) + t) \mod n \\
& = (f(n - 1) + m \mod n) \mod n \\
& = (f(n - 1) + m) \mod n
\end{aligned}
$$
> 下图中 `n` , `m` 分别对应本题的 `n` , `m` 。
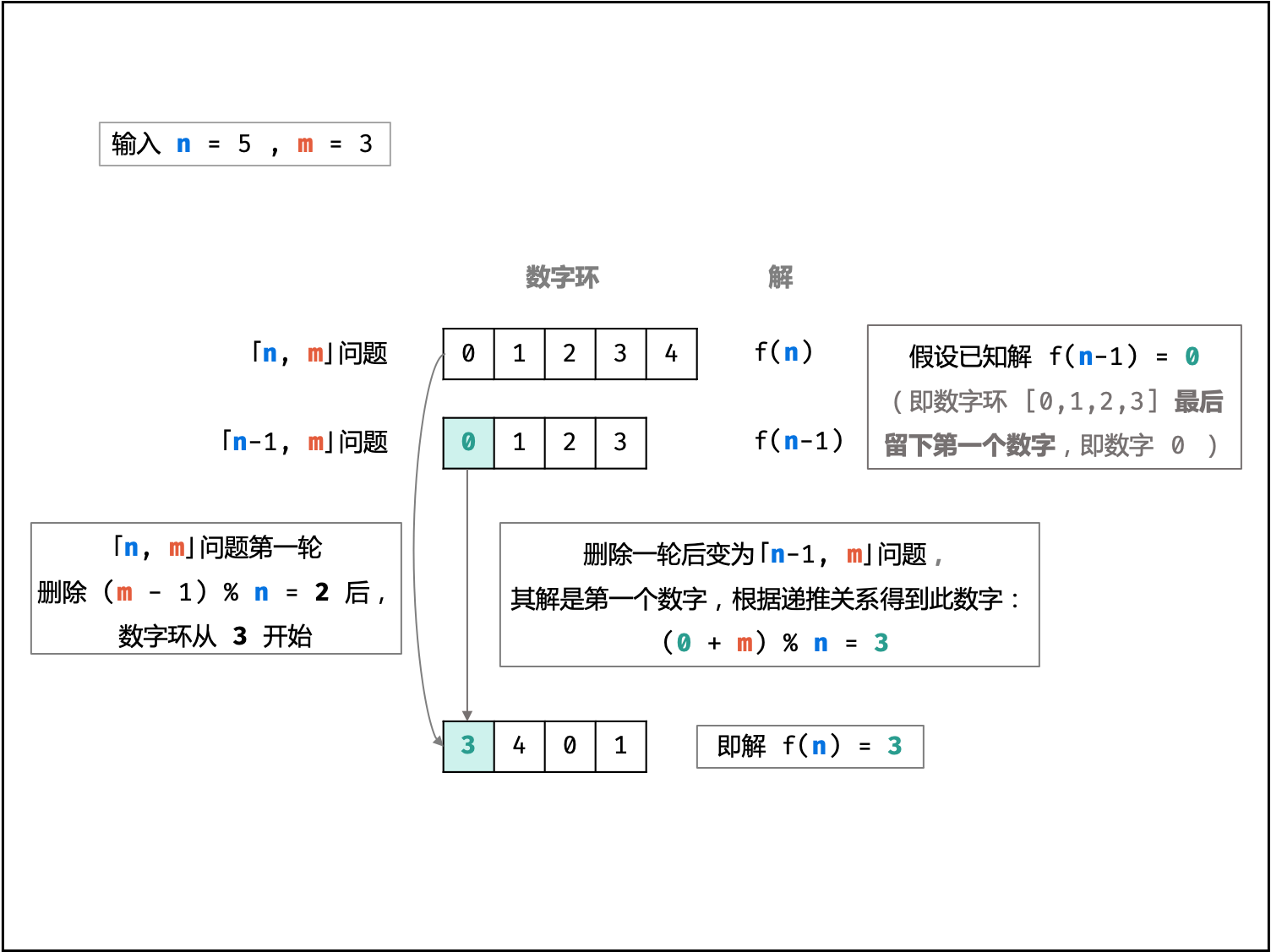![Picture1.png](https://pic.leetcode-cn.com/1615096532-kUoKUe-Picture1.png){:align=center width=550}
$f(n)$ 可由 $f(n - 1)$ 得到，$f(n - 1)$ 可由 $f(n - 2)$ 得到，……，$f(2)$ 可由 $f(1)$ 得到；因此，若给定 $f(1)$ 的值，就可以递推至任意 $f(n)$ 。而「$1, m$ 问题」的解 $f(1) = 0$ 恒成立，即无论 $m$ 为何值，长度为 1 的数字环留下的是一定是数字 $0$ 。
> 以上数学推导本质是得出动态规划的 转移方程 和 初始状态 。
### 动态规划解析：
1. **状态定义：** 设「$i, m$ 问题」的解为 $dp[i]$ ；
2. **转移方程：** 通过以下公式可从 $dp[i - 1]$ 递推得到 $dp[i]$ ；
$$
dp[i] = (dp[i - 1] + m) \mod i
$$
3. **初始状态：**「$1, m$ 问题」的解恒为 $0$ ，即 $dp[1] = 0$ ；
4. **返回值：** 返回「$n, m$ 问题」的解 $dp[n]$ ；
> 如下图所示，为 $n = 5$ , $m = 3$ 时的状态转移和对应的模拟删除过程。
![Picture2.png](https://pic.leetcode-cn.com/1613584667-AQpTlK-Picture2.png)
## 代码：
根据状态转移方程的递推特性，无需建立状态列表 $dp$ ，而使用一个变量 $x$ 执行状态转移即可。
```Python []
class Solution:
def iceBreakingGame(self, num: int, target: int) -> int:
x = 0
for i in range(2, num + 1):
x = (x + target) % i
return x
```
```Java []
class Solution {
public int iceBreakingGame(int num, int target) {
int x = 0;
for (int i = 2; i <= num; i++) {
x = (x + target) % i;
}
return x;
}
}
```
```C++ []
class Solution {
public:
int iceBreakingGame(int num, int target) {
int x = 0;
for (int i = 2; i <= num; i++) {
x = (x + target) % i;
}
return x;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(n)$ ：** 状态转移循环 $n - 1$ 次使用 $O(n)$ 时间，状态转移方程计算使用 $O(1)$ 时间；
- **空间复杂度 $O(1)$ ：** 使用常数大小的额外空间；

87
leetbook_ioa/docs/LCR 188. 买卖芯片的最佳时机.md Executable file
View File

@@ -0,0 +1,87 @@
## 解题思路：
设共有 $n$ 天，第 $a$ 天买，第 $b$ 天卖，则需保证 $a < b$ ；可推出交易方案数共有：
$$
(n - 1) + (n - 2) + \cdots + 2 + 1 = n(n - 1) / 2
$$
因此，暴力法的时间复杂度为 $O(n^2)$ 。考虑使用动态规划降低时间复杂度。
### 动态规划解析：
- **状态定义：** 设动态规划列表 $dp$ ，$dp[i]$ 代表以 $prices[i]$ 为结尾的子数组的最大利润（以下简称为 **前 $i$ 日的最大利润** ）。
- **转移方程：** 由于题目限定 “买卖该芯片一次” ，因此前 $i$ 日最大利润 $dp[i]$ 等于前 $i - 1$ 日最大利润 $dp[i-1]$ 和第 $i$ 日卖出的最大利润中的最大值。
$$
dp[i] = \max(dp[i - 1], prices[i] - \min(prices[0:i])) \\
\uparrow \\
前 i 日最大利润 = \max(前 (i-1) 日最大利润, 第 i 日价格 - 前 i 日最低价格)
$$
- **初始状态：** $dp[0] = 0$ ，即首日利润为 $0$ ；
- **返回值：** $dp[n - 1]$ ，其中 $n$ 为 $dp$ 列表长度。
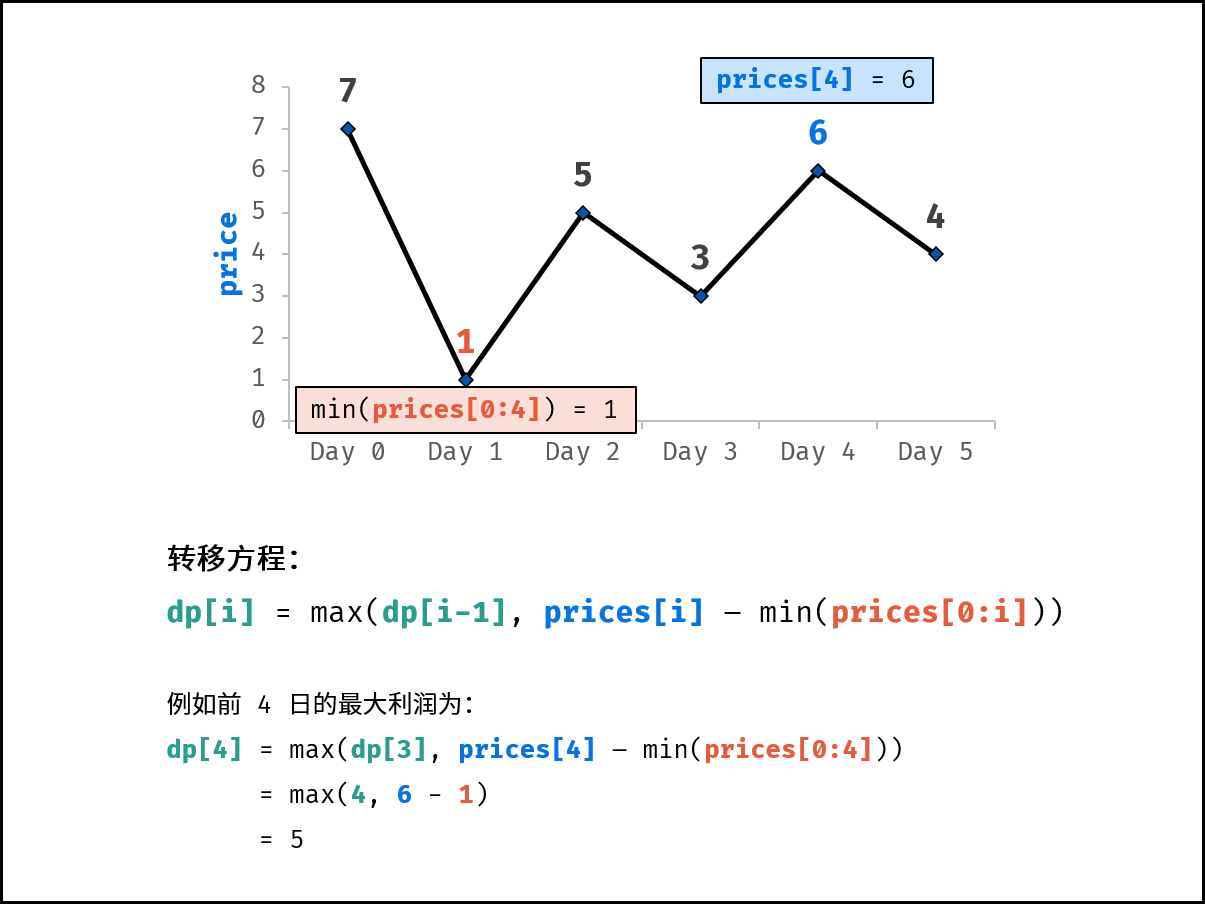![Picture1.png](https://pic.leetcode-cn.com/1600880605-QGgqZW-Picture1.png){:align=center width=550}
### 时间优化：
前 $i$ 日的最低价格 $\min(prices[0:i])$ 时间复杂度为 $O(i)$ 。而在遍历 $prices$ 时，可以借助一个变量（记为成本 $cost$ ）每日更新最低价格。优化后的转移方程为：
$$
dp[i] = \max(dp[i - 1], prices[i] - \min(cost, prices[i])
$$
### 空间优化：
由于 $dp[i]$ 只与 $dp[i - 1]$ , $prices[i]$ , $cost$ 相关，因此可使用一个变量（记为利润 $profit$ ）代替 $dp$ 列表。优化后的转移方程为：
$$
profit = \max(profit, prices[i] - \min(cost, prices[i])
$$
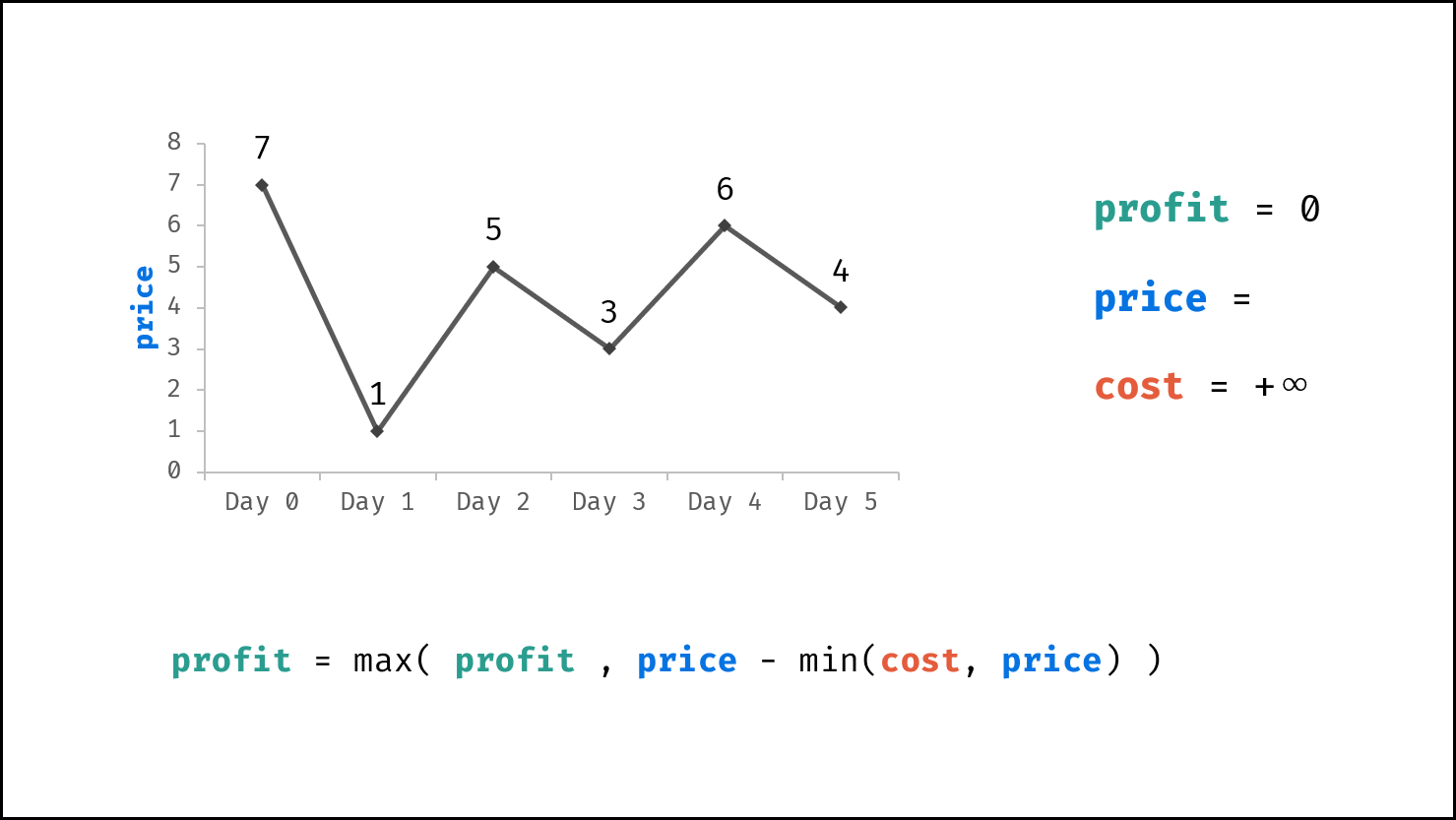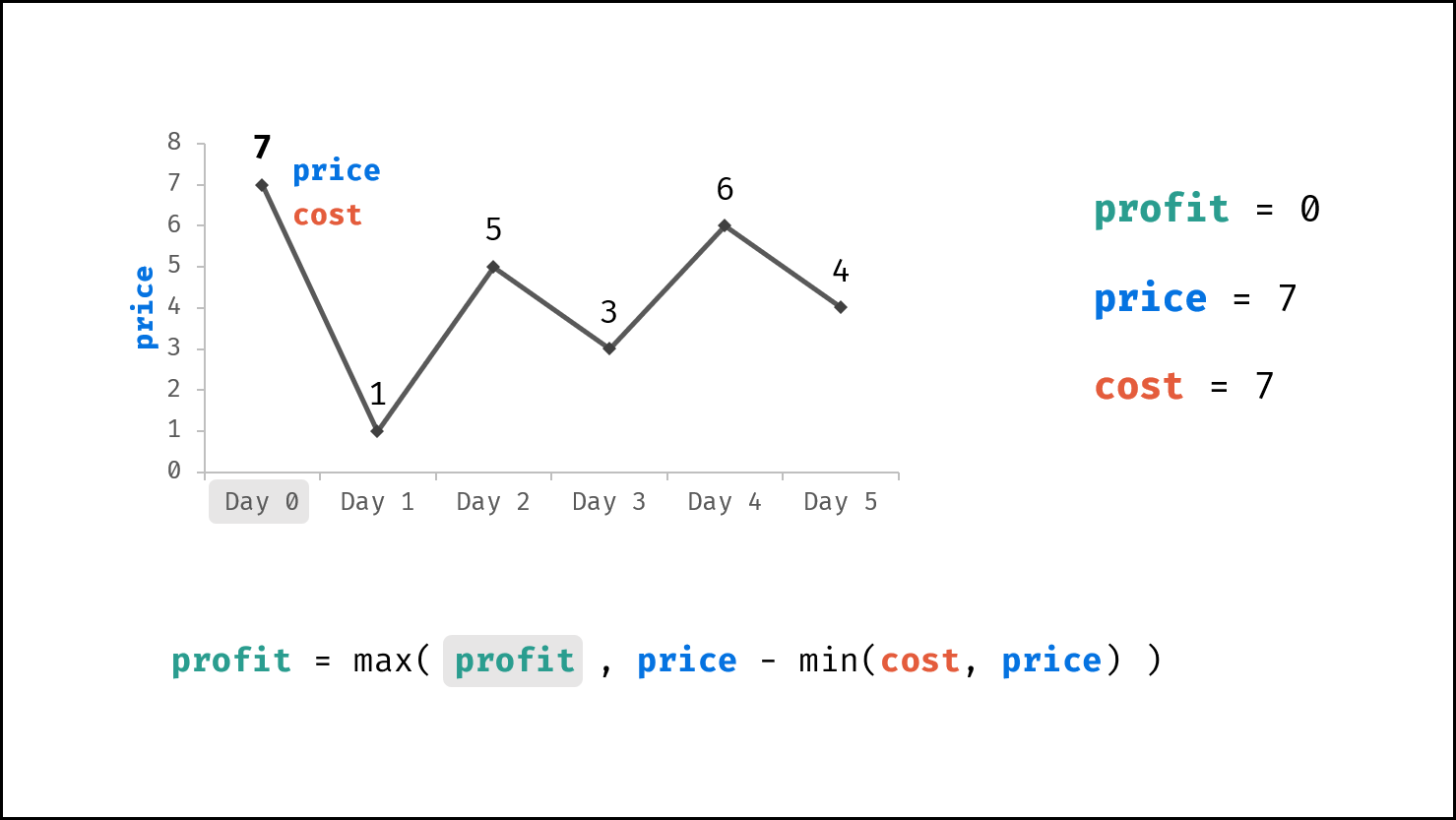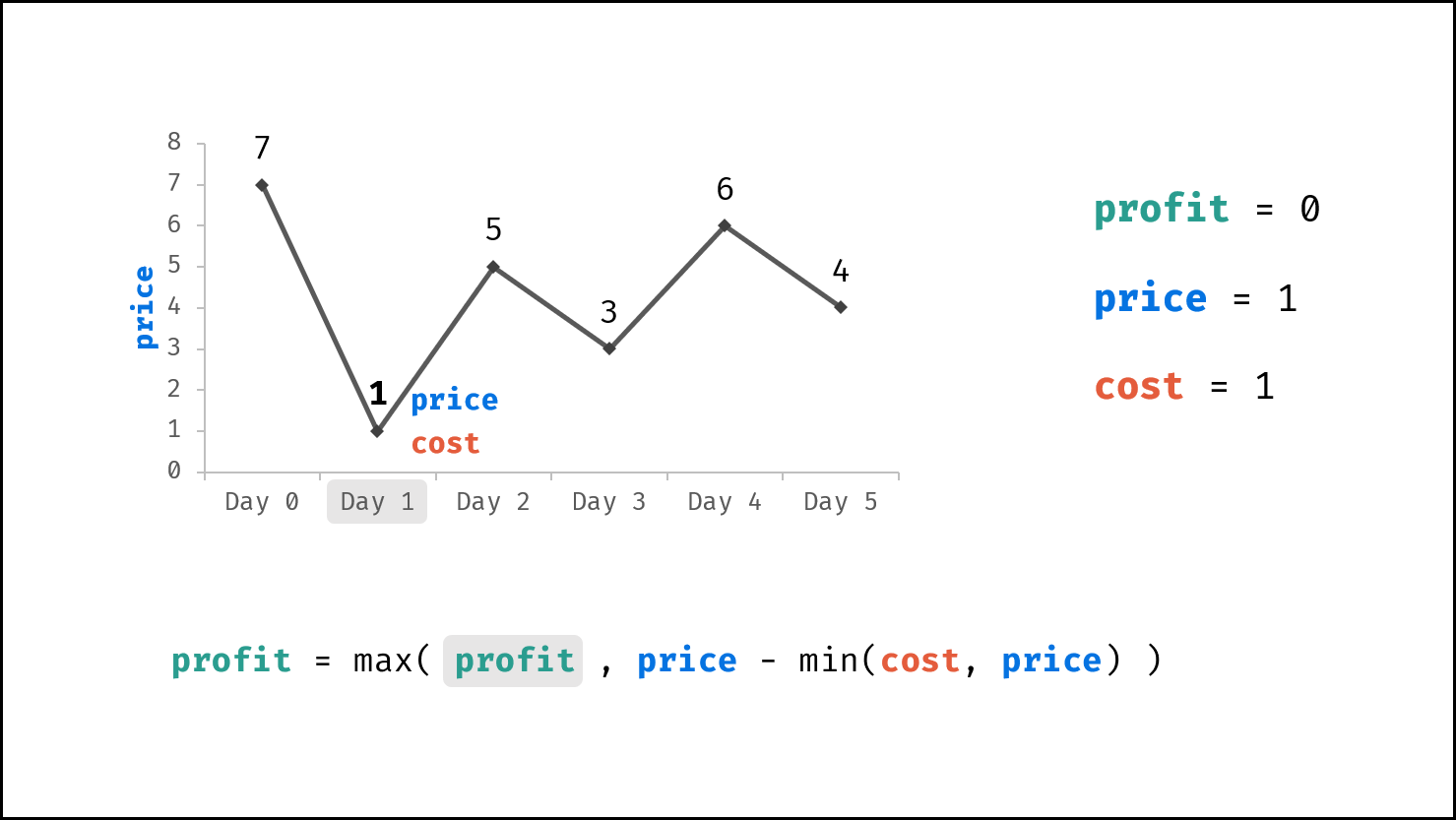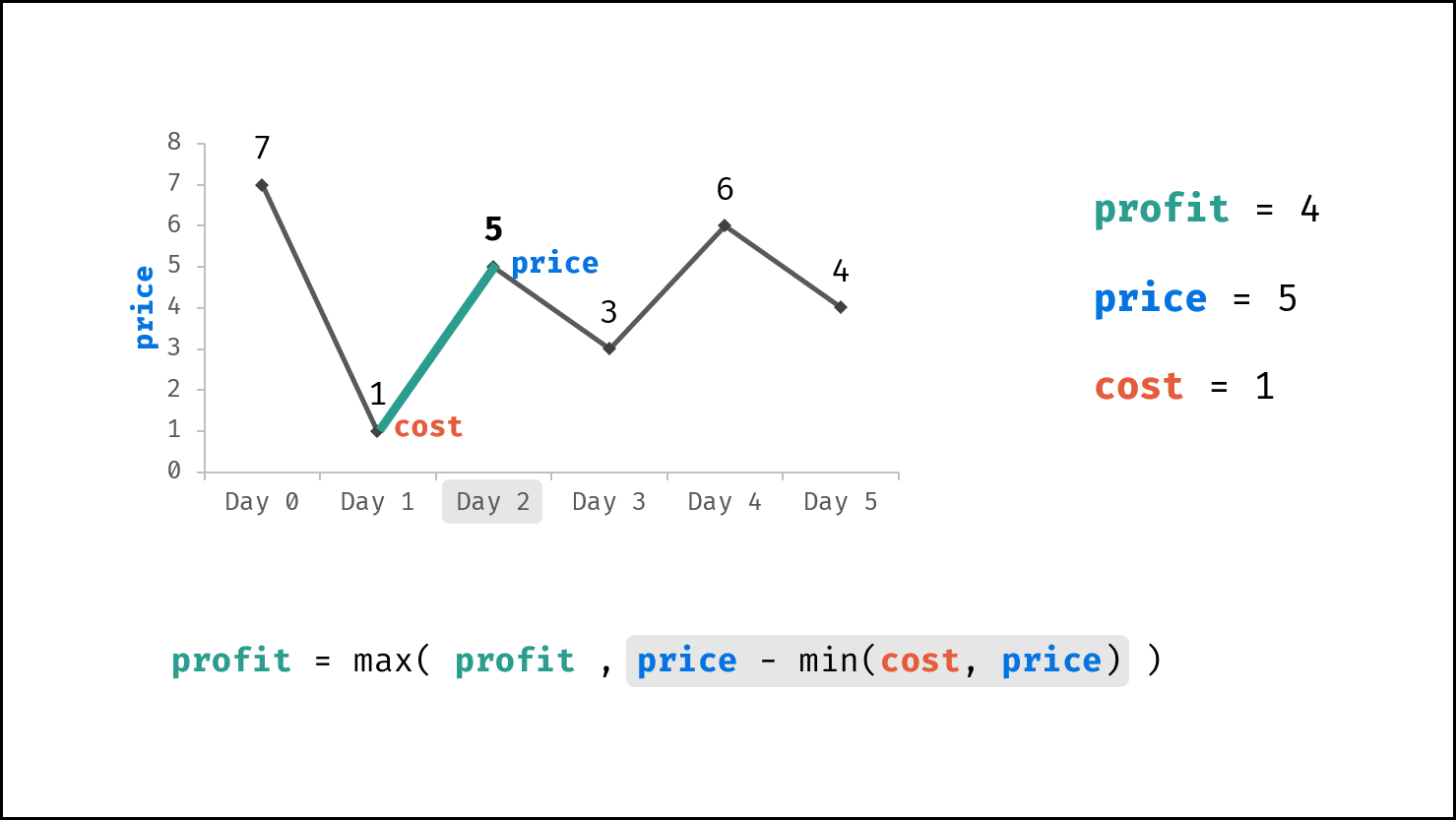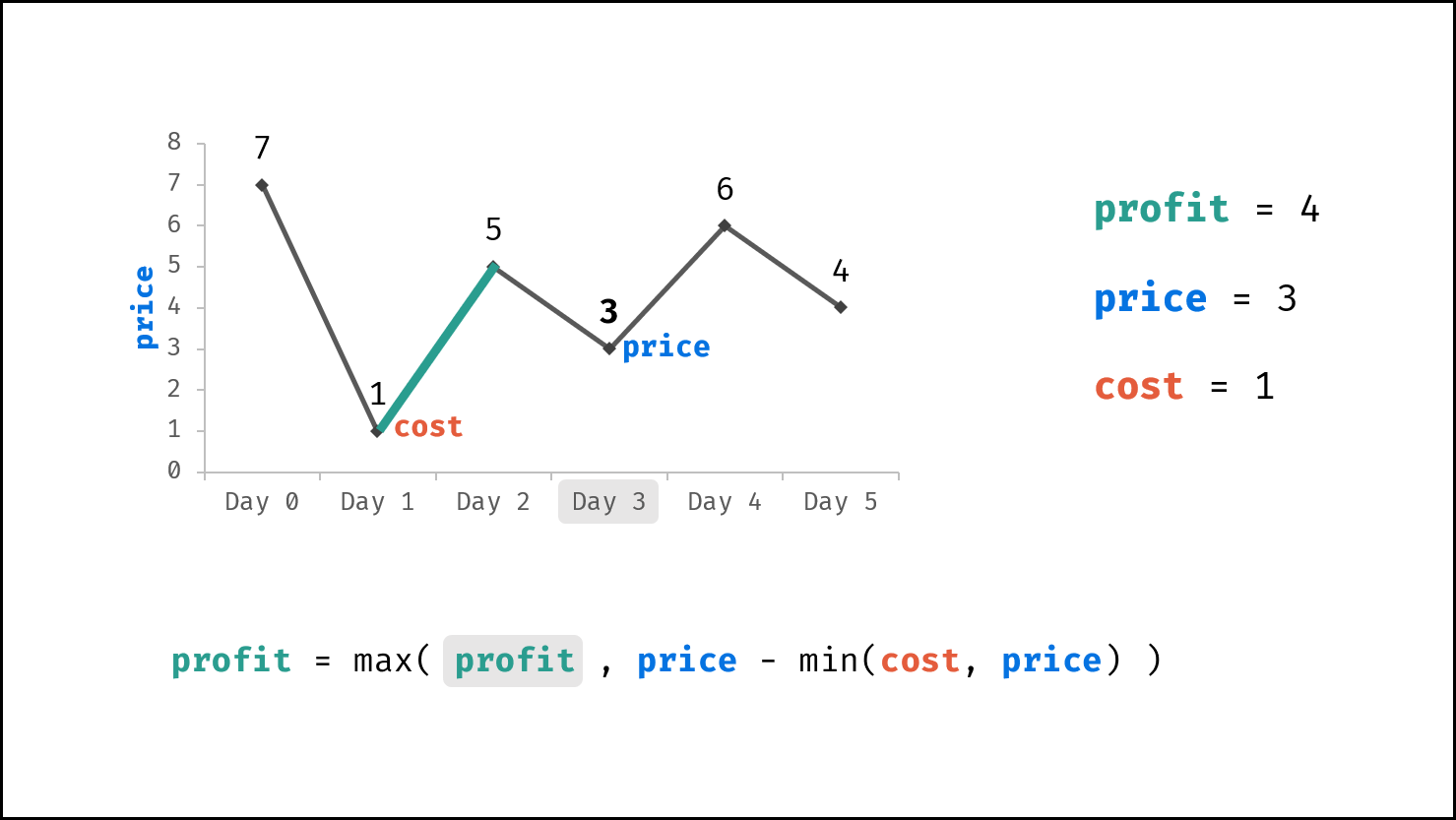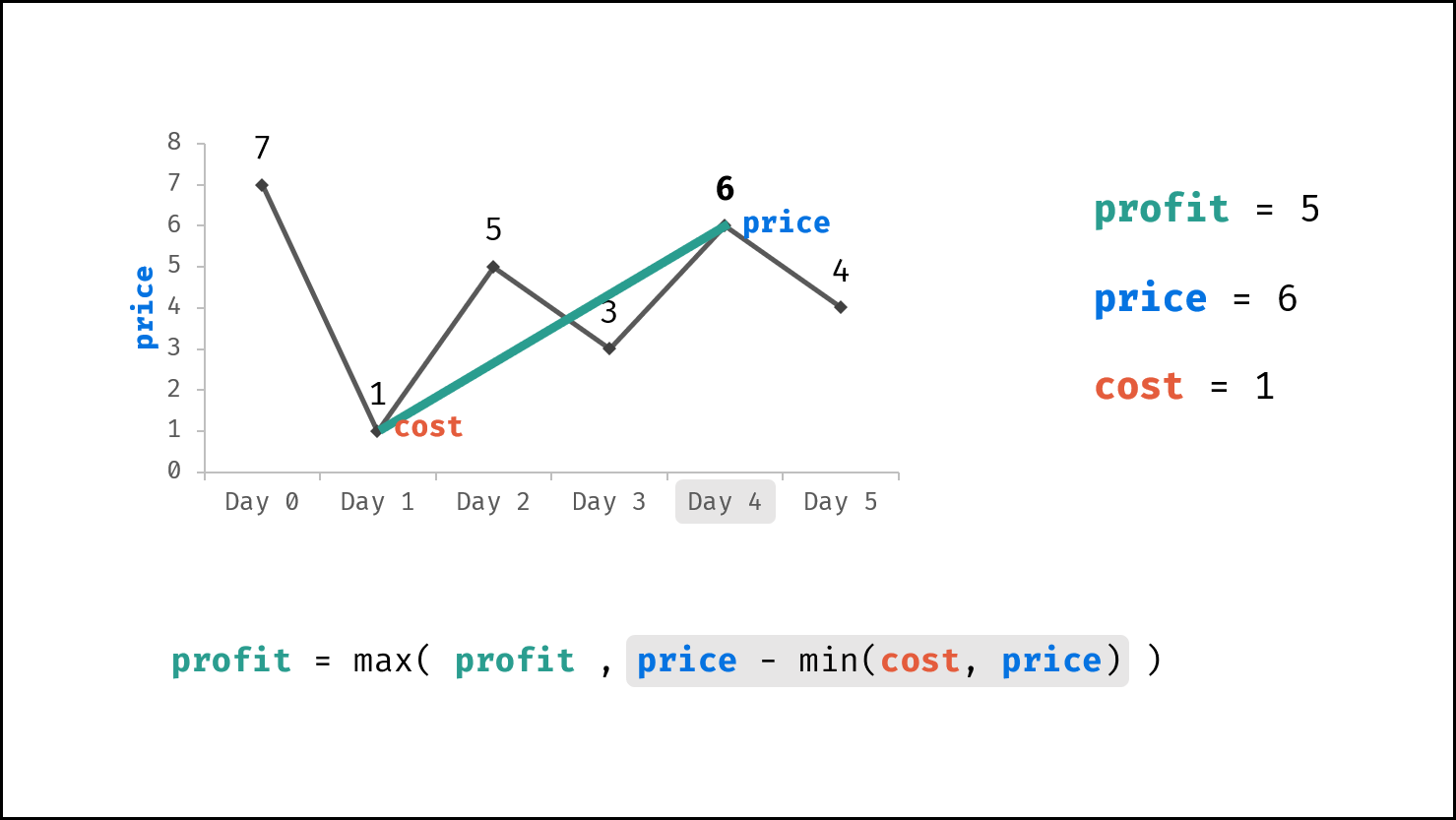<![Picture2.png](https://pic.leetcode-cn.com/1600880423-rEnBje-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1600880423-GLrbjp-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600880423-PONxGf-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600880423-kuJwjX-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600880423-vQxDNV-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600880423-mcBVmr-Picture7.png),![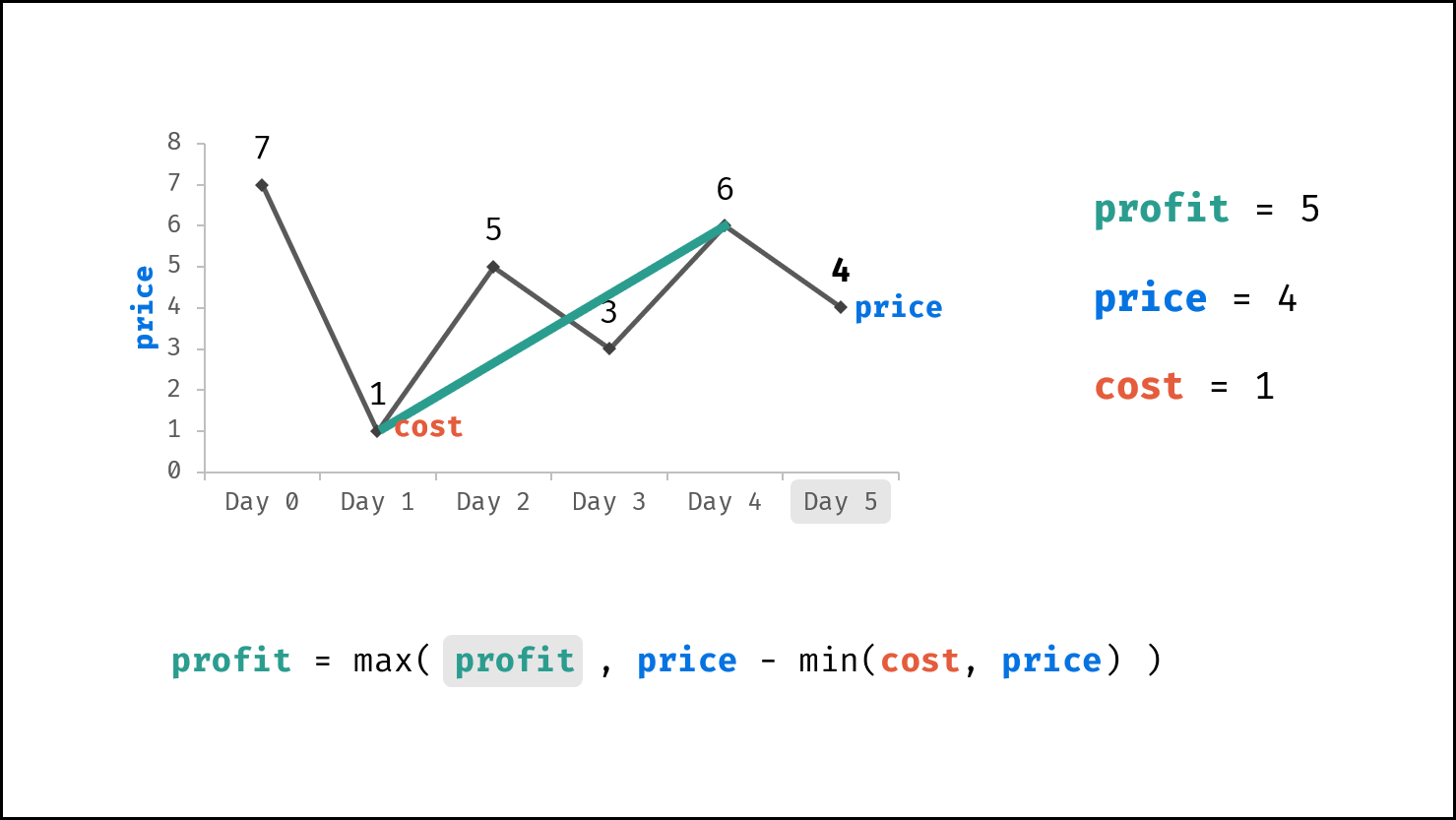Picture8.png](https://pic.leetcode-cn.com/1600880423-NIjPdB-Picture8.png),![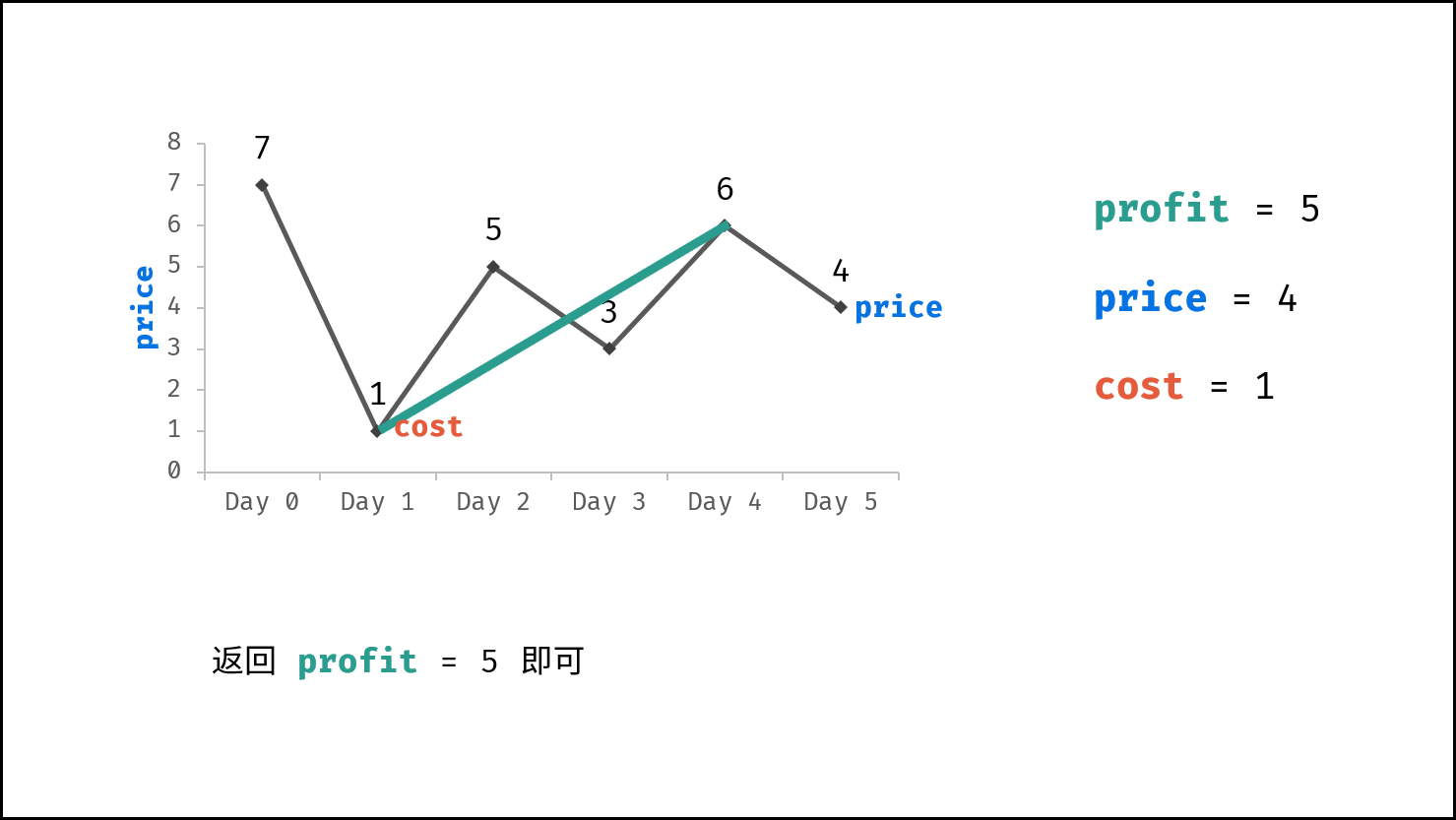Picture9.png](https://pic.leetcode-cn.com/1600880423-sNOhNp-Picture9.png)>
## 代码：
```Python []
class Solution:
def bestTiming(self, prices: List[int]) -> int:
cost, profit = float("+inf"), 0
for price in prices:
cost = min(cost, price)
profit = max(profit, price - cost)
return profit
```
```Java []
class Solution {
public int bestTiming(int[] prices) {
int cost = Integer.MAX_VALUE, profit = 0;
for(int price : prices) {
cost = Math.min(cost, price);
profit = Math.max(profit, price - cost);
}
return profit;
}
}
```
```C++ []
class Solution {
public:
int bestTiming(vector<int>& prices) {
int cost = INT_MAX, profit = 0;
for(int price : prices) {
cost = min(cost, price);
profit = max(profit, price - cost);
}
return profit;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为 $prices$ 列表长度，动态规划需遍历 $prices$ 。
- **空间复杂度 $O(1)$ ：** 变量 $cost$ 和 $profit$ 使用常数大小的额外空间。

153
leetbook_ioa/docs/LCR 189. 设计机械累加器.md Executable file
View File

@@ -0,0 +1,153 @@
## 解题思路：
本题在简单问题上做了许多限制，需要使用排除法一步步导向答案。
$1+2+...+(target-1)+target$ 的计算方法主要有三种：平均计算、迭代、递归。
**方法一：** 平均计算
**问题：** 此计算必须使用 **乘除法** ，因此本方法不可取，直接排除。
```Java []
public int mechanicalAccumulator(int target) {
return (1 + target) * target / 2;
}
```
```Python []
def mechanicalAccumulator(target):
return (1 + target) * target // 2
```
```C++ []
int mechanicalAccumulator(int target) {
return (1 + target) * target / 2;
}
```
**方法二：** 迭代
**问题：** 循环必须使用 $while$ 或 $for$ ，因此本方法不可取，直接排除。
```Java []
public int mechanicalAccumulator(int target) {
int res = 0;
for(int i = 1; i <= target; i++)
res += i;
return res;
}
```
```Python []
def mechanicalAccumulator(target):
res = 0
for i in range(1, target + 1):
res += i
return res
```
```C++ []
int mechanicalAccumulator(int target) {
int res = 0;
for(int i = 1; i <= target; i++)
res += i;
return res;
}
```
**方法三：** 递归
**问题：** 终止条件需要使用 $if$ ，因此本方法不可取。
**思考：** 除了 $if$ 和 $switch$ 等判断语句外，是否有其他方法可用来终止递归？
```Java []
public int mechanicalAccumulator(int target) {
if(target == 1) return 1;
target += mechanicalAccumulator(target - 1);
return target;
}
```
```Python []
def mechanicalAccumulator(target):
if target == 1: return 1
target += mechanicalAccumulator(target - 1)
return target
```
```C++ []
int mechanicalAccumulator(int target) {
if(target == 1) return 1;
target += mechanicalAccumulator(target - 1);
return target;
}
```
> 下图中的 `sumNums()` 对应本题的 `mechanicalAccumulator` 。
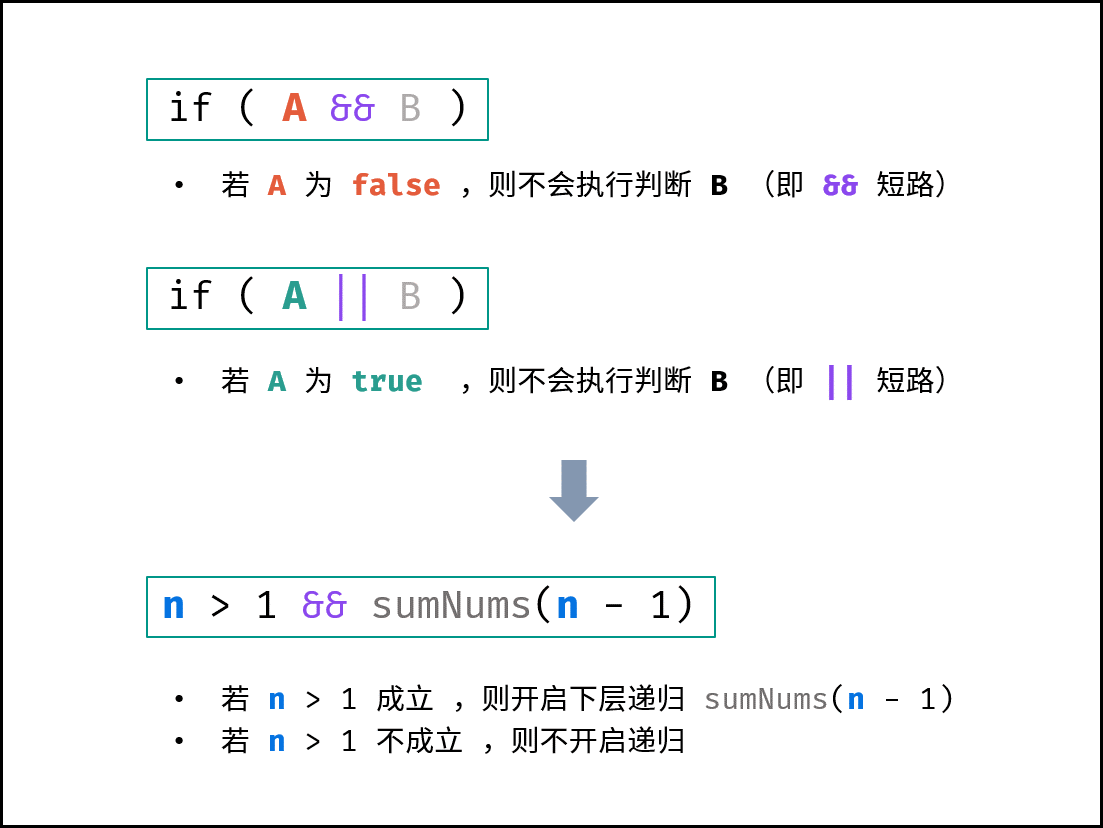![Picture1.png](https://pic.leetcode-cn.com/1603023621-WFZwzS-Picture1.png){:align=center width=500}
### 逻辑运算符的短路效应：
常见的逻辑运算符有三种，即 “与 $\&\&$ ”，“或 $||$ ”，“非 $!$ ” ；而其有重要的短路效应，如下所示：
```Java
if(A && B) // 若 A 为 false ，则 B 的判断不会执行（即短路），直接判定 A && B 为 false
if(A || B) // 若 A 为 true ，则 B 的判断不会执行（即短路），直接判定 A || B 为 true
```
本题需要实现 “当 $target = 1$ 时终止递归” 的需求，可通过短路效应实现。
```Java
target > 1 && mechanicalAccumulator(target - 1) // 当 target = 1 时 target > 1 不成立 ，此时 “短路” ，终止后续递归
```
<![Picture2.png](https://pic.leetcode-cn.com/1603023621-vtSwPG-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1603023621-cPevuH-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1603023621-AvmvCE-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1603023621-ODBDJu-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1603023621-wBgrFm-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1603023621-pFQtHw-Picture7.png),![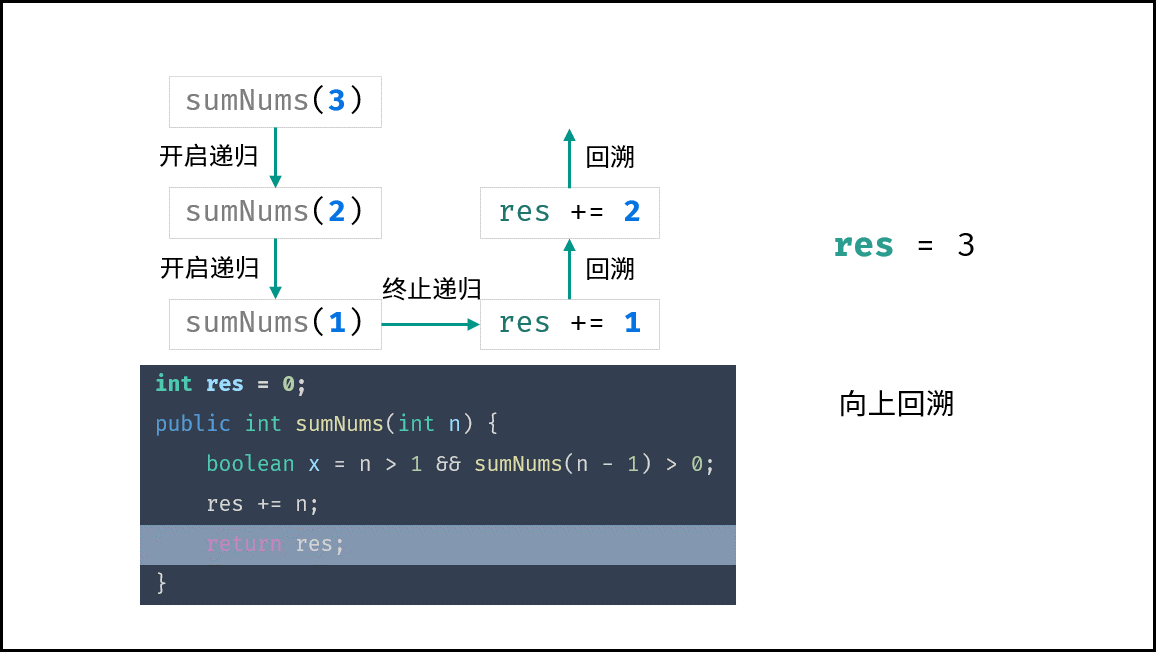Picture8.png](https://pic.leetcode-cn.com/1603023621-vIzkcI-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1603023621-rrafGq-Picture9.png),![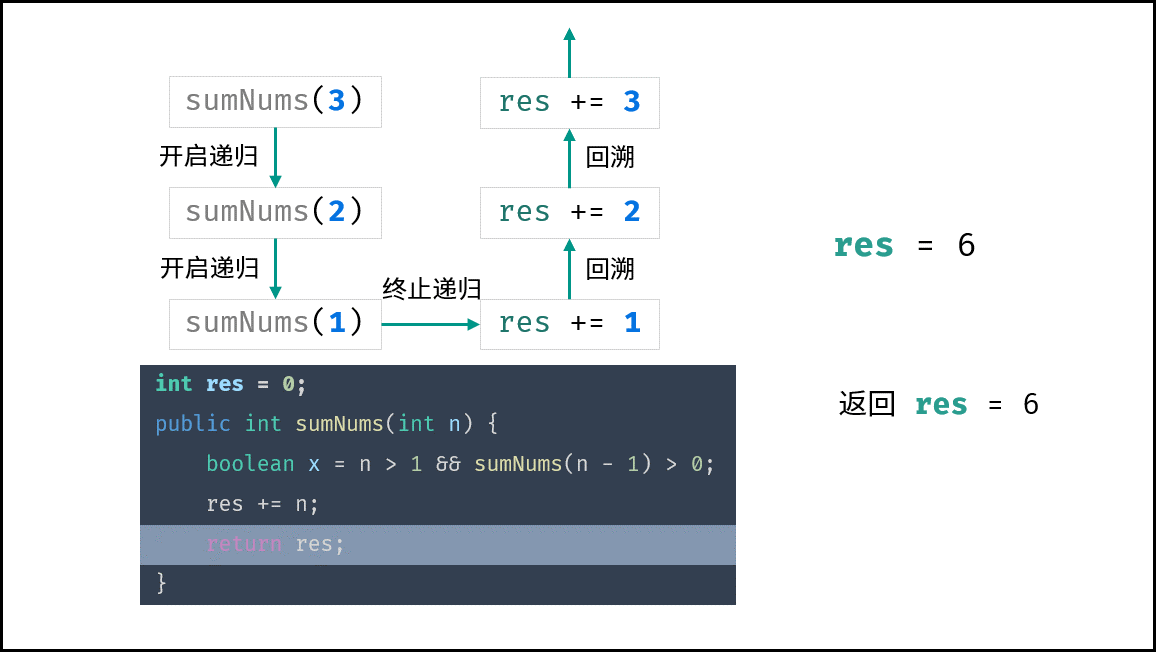Picture10.png](https://pic.leetcode-cn.com/1603023621-nIAzSV-Picture10.png)>
## 代码：
1. Java 中，为构成语句，需加一个辅助布尔量 $x$ ，否则会报错；
2. Java 中，开启递归函数需改写为 `mechanicalAccumulator(target - 1) > 0` ，此整体作为一个布尔量输出，否则会报错；
3. 初始化变量 $res$ 记录结果。（ Java 可使用第二栏的简洁写法，不用借助变量 $res$ ）。
```Java []
class Solution {
int res = 0;
public int mechanicalAccumulator(int target) {
boolean x = target > 1 && mechanicalAccumulator(target - 1) > 0;
res += target;
return res;
}
}
```
```Java []
class Solution {
public int mechanicalAccumulator(int target) {
boolean x = target > 1 && (target += mechanicalAccumulator(target - 1)) > 0;
return target;
}
}
```
```Python []
class Solution:
def __init__(self):
self.res = 0
def mechanicalAccumulator(self, target: int) -> int:
target > 1 and self.mechanicalAccumulator(target - 1)
self.res += target
return self.res
```
```C++ []
class Solution {
public:
int mechanicalAccumulator(int target) {
target > 1 && (target += mechanicalAccumulator(target - 1));
return target;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(target)$ ：** 计算 $target + (target-1) + ... + 2 + 1$ 需要开启 $target$ 个递归函数。
- **空间复杂度 $O(target)$ ：** 递归深度达到 $target$ ，系统使用 $O(target)$ 大小的额外空间。

101
leetbook_ioa/docs/LCR 190. 加密运算.md Executable file
View File

@@ -0,0 +1,101 @@
## 解题思路：
本题考察对位运算的灵活使用，即使用位运算实现加法。
设两数字的二进制形式 $dataA, dataB$ ，其求和 $s = dataA + dataB$ ，$dataA(i)$ 代表 $dataA$ 的二进制第 $i$ 位，则分为以下四种情况：
| $dataA(i)$ | $dataB(i)$ | 无进位和 $n(i)$ | 进位 $c(i+1)$ |
| :--------: | :--------: | :-------------: | :-----------: |
| $0$ | $0$ | $0$ | $0$ |
| $0$ | $1$ | $1$ | $0$ |
| $1$ | $0$ | $1$ | $0$ |
| $1$ | $1$ | $0$ | $1$ |
观察发现，**无进位和** 与 **异或运算** 规律相同，**进位** 和 **与运算** 规律相同（并需左移一位）。因此，无进位和 $n$ 与进位 $c$ 的计算公式如下；
$$
\begin{cases}
n = dataA \oplus dataB & 非进位和：异或运算 \\
c = dataA \space \& \space dataB << 1 & 进位：与运算 + 左移一位
\end{cases}
$$
（和 $s$ ）$=$（非进位和 $n$ ）$+$（进位 $c$ ）。即可将 $s = dataA + dataB$ 转化为：
$$
s = dataA + dataB \Rightarrow s = n + c
$$
循环求 $n$ 和 $c$ ，直至进位 $c = 0$ ；此时 $s = n$ ，返回 $n$ 即可。
> 下图中的 `a` 和 `b` 对应本题的 `dataA` 和 `dataB` 。
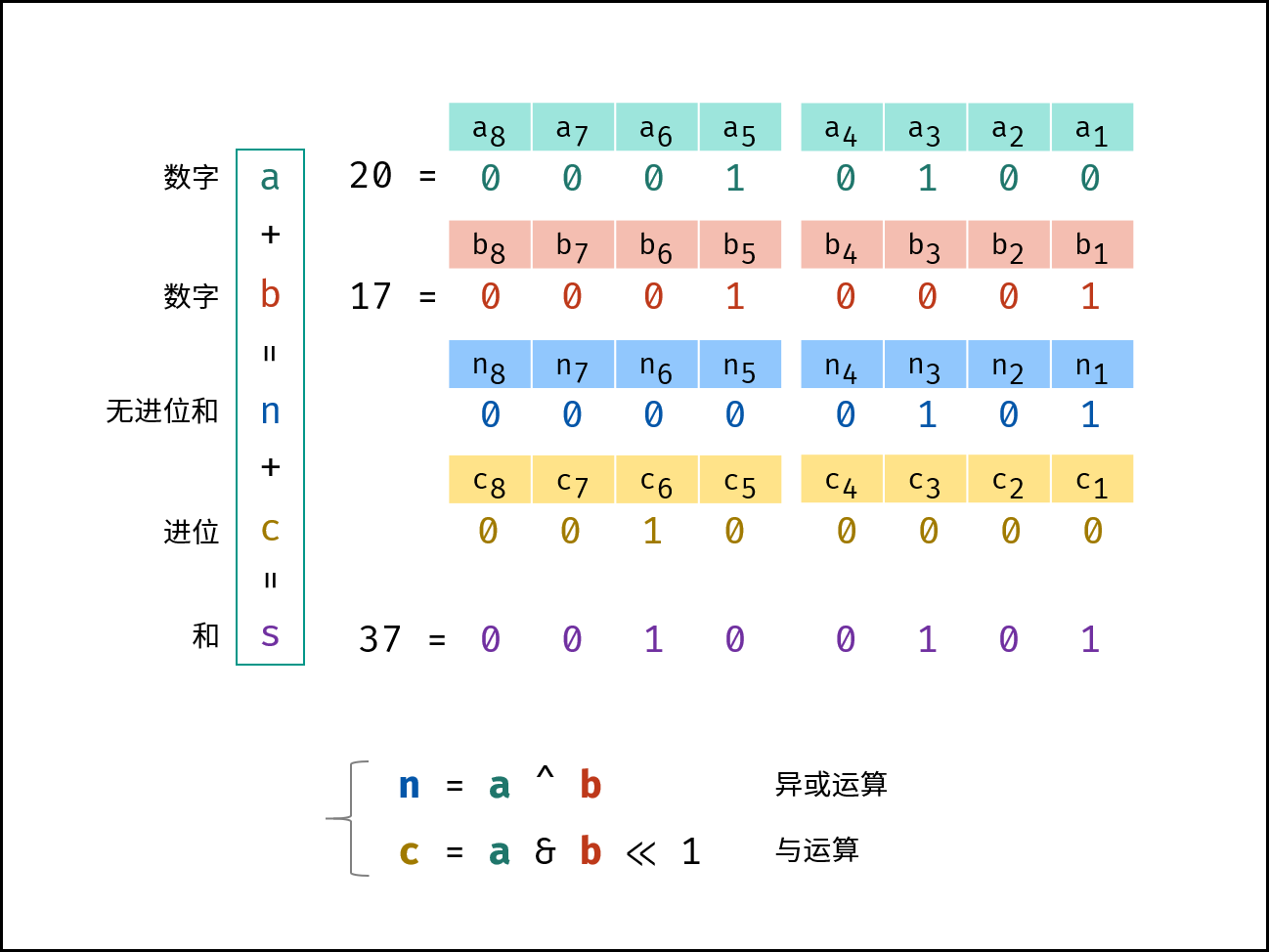![Picture1.png](https://pic.leetcode-cn.com/9716b1a1ead21824b8216c7d54910bee4d838c011581f4e3d82a14f71cb392a1-Picture1.png){:align=center width=500}
> **Q ：** 若数字 $dataA$ 和 $dataB$ 中有负数，则变成了减法，如何处理？
> **A ：** 在计算机系统中，数值一律用 **补码** 来表示和存储。**补码的优势：** 加法、减法可以统一处理（CPU只有加法器）。因此，以上方法 **同时适用于正数和负数的加法** 。
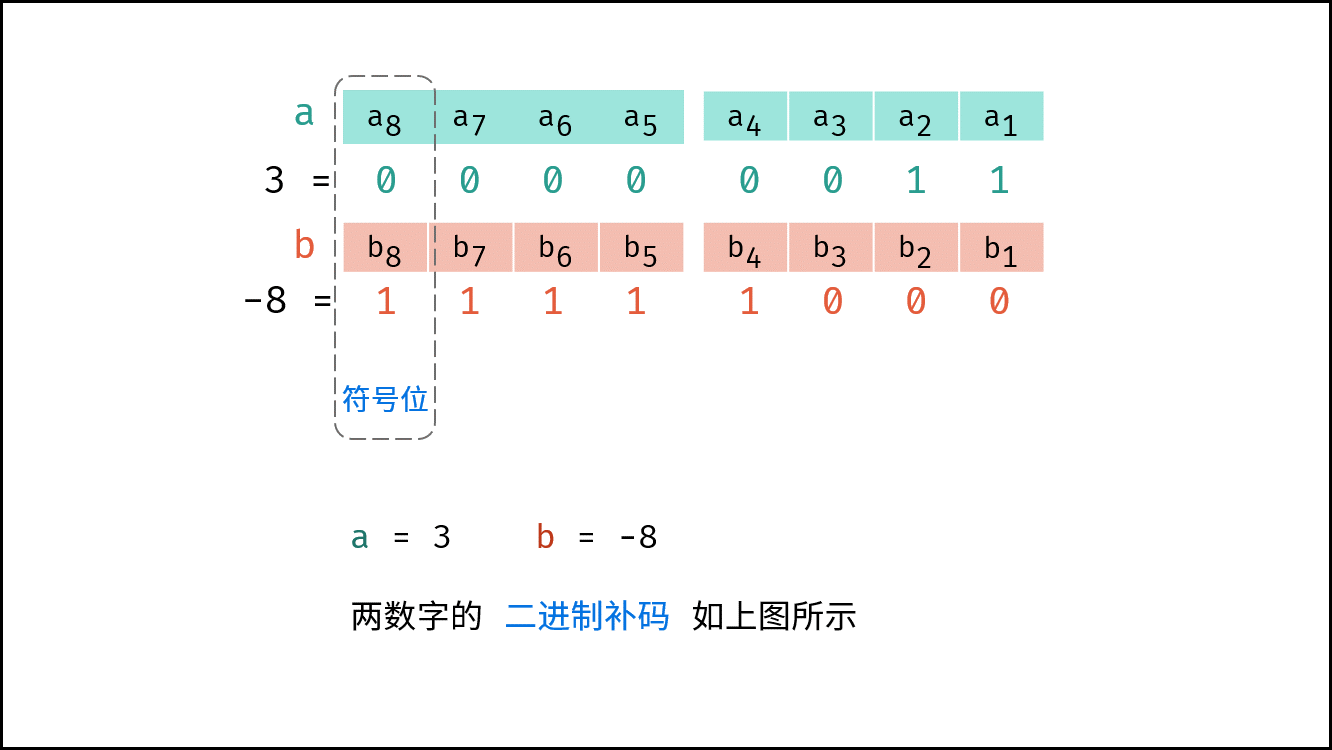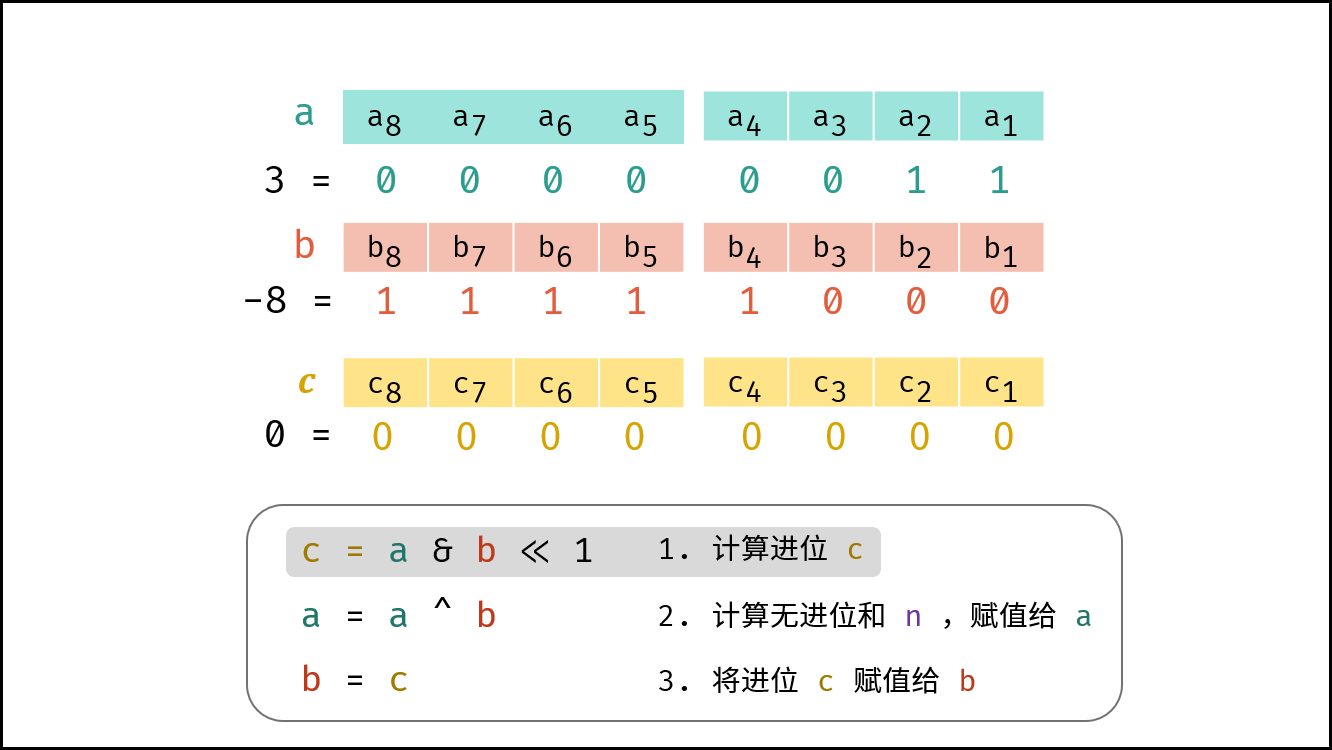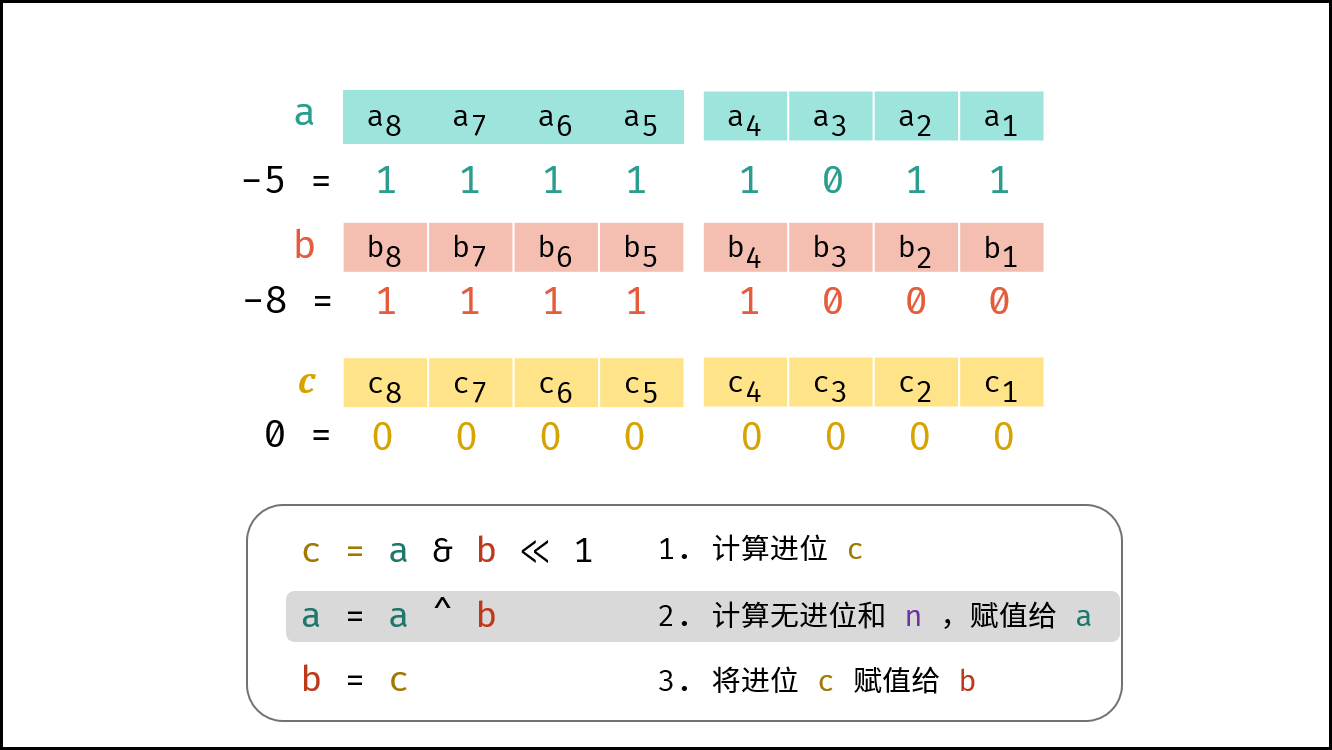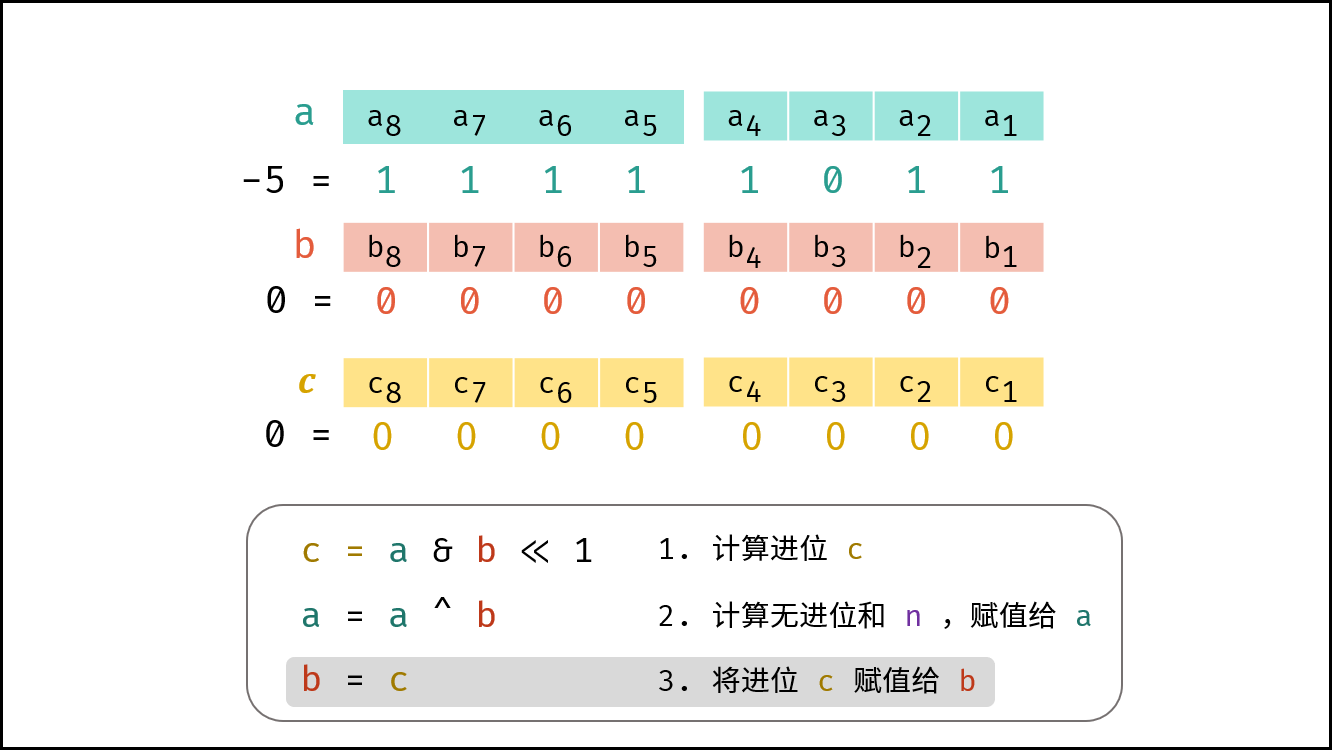<![Picture2.png](https://pic.leetcode-cn.com/d0039bd73623aafd56741a1aed9d52ca00451f434d5c8b33b04da9173e460f8b-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/42ea80334f0aff1d2d6e772390759850f7ccd501805158fb72f5a83cb6eebc24-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/dbf420b8ae88071e0a176162bb2b2f44ce5368644408ca25eda8e72c1f102ac3-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/87f697a25ee42e382c5d5dcd38dd7890a0e7216ac5d254facec14892d0e48dc1-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/3067c3007ad93318be3b08834a674288d4aed011b95d302a83206e88a5302252-Picture6.png)>
## 代码：
```Java []
class Solution {
public int encryptionCalculate(int dataA, int dataB) {
while(dataB != 0) { // 当进位为 0 时跳出
int c = (dataA & dataB) << 1; // c = 进位
dataA ^= dataB; // dataA = 非进位和
dataB = c; // dataB = 进位
}
return dataA;
}
}
```
```C++ []
class Solution {
public:
int encryptionCalculate(int dataA, int dataB) {
while(dataB != 0)
{
int c = (unsigned int)(dataA & dataB) << 1;
dataA ^= dataB;
dataB = c;
}
return dataA;
}
};
```
```Python []
class Solution:
def encryptionCalculate(self, dataA: int, dataB: int) -> int:
x = 0xffffffff
dataA, dataB = dataA & x, dataB & x
while dataB != 0:
dataA, dataB = (dataA ^ dataB), (dataA & dataB) << 1 & x
return dataA if dataA <= 0x7fffffff else ~(dataA ^ x)
```
### 复杂度分析：
- **时间复杂度 $O(1)$ ：** 最差情况下（例如 $dataA =$ $\text{0x7fffffff}$ , $dataB = 1$ 时），需循环 32 次，使用 $O(1)$ 时间；每轮中的常数次位操作使用 $O(1)$ 时间。
- **空间复杂度 $O(1)$ ：** 使用常数大小的额外空间。
### Python 负数的存储：
Python，Java, C++ 等语言中的数字都是以 **补码** 形式存储的。但 Python 没有 `int` , `long` 等不同长度变量，即在编程时无变量位数的概念。
**获取负数的补码：** 需要将数字与十六进制数 `0xffffffff` 相与。可理解为舍去此数字 32 位以上的数字（将 32 位以上都变为 $0$ ），从无限长度变为一个 32 位整数。
**返回前数字还原：** 若补码 $dataA$ 为负数（ `0x7fffffff` 是最大的正数的补码 ），需执行 `~(dataA ^ x)` 操作，将补码还原至 Python 的存储格式。`dataA ^ x` 运算将 1 至 32 位按位取反；`~` 运算是将整个数字取反；因此，`~(dataA ^ x)` 是将 32 位以上的位取反，1 至 32 位不变。
```Python
print(hex(1)) # = 0x1 补码
print(hex(-1)) # = -0x1 负号 + 原码 （ Python 特色，Java 会直接输出补码）
print(hex(1 & 0xffffffff)) # = 0x1 正数补码
print(hex(-1 & 0xffffffff)) # = 0xffffffff 负数补码
print(-1 & 0xffffffff) # = 4294967295 （ Python 将其认为正数）
```

78
leetbook_ioa/docs/LCR 191. 按规则计算统计结果.md Executable file
View File

@@ -0,0 +1,78 @@
## 解题思路：
> 本文将 `arrayA` , `arrayB` 简写为 `A` , `B` 。
本题的难点在于 **不能使用除法** ，即需要 **只用乘法** 生成数组 $B$ 。根据题目对 $B[i]$ 的定义，可列如下图所示的表格。
根据表格的主对角线（全为 $1$ ），可将表格分为 **上三角** 和 **下三角** 两部分。分别迭代计算下三角和上三角两部分的乘积，即可 **不使用除法** 就获得结果。
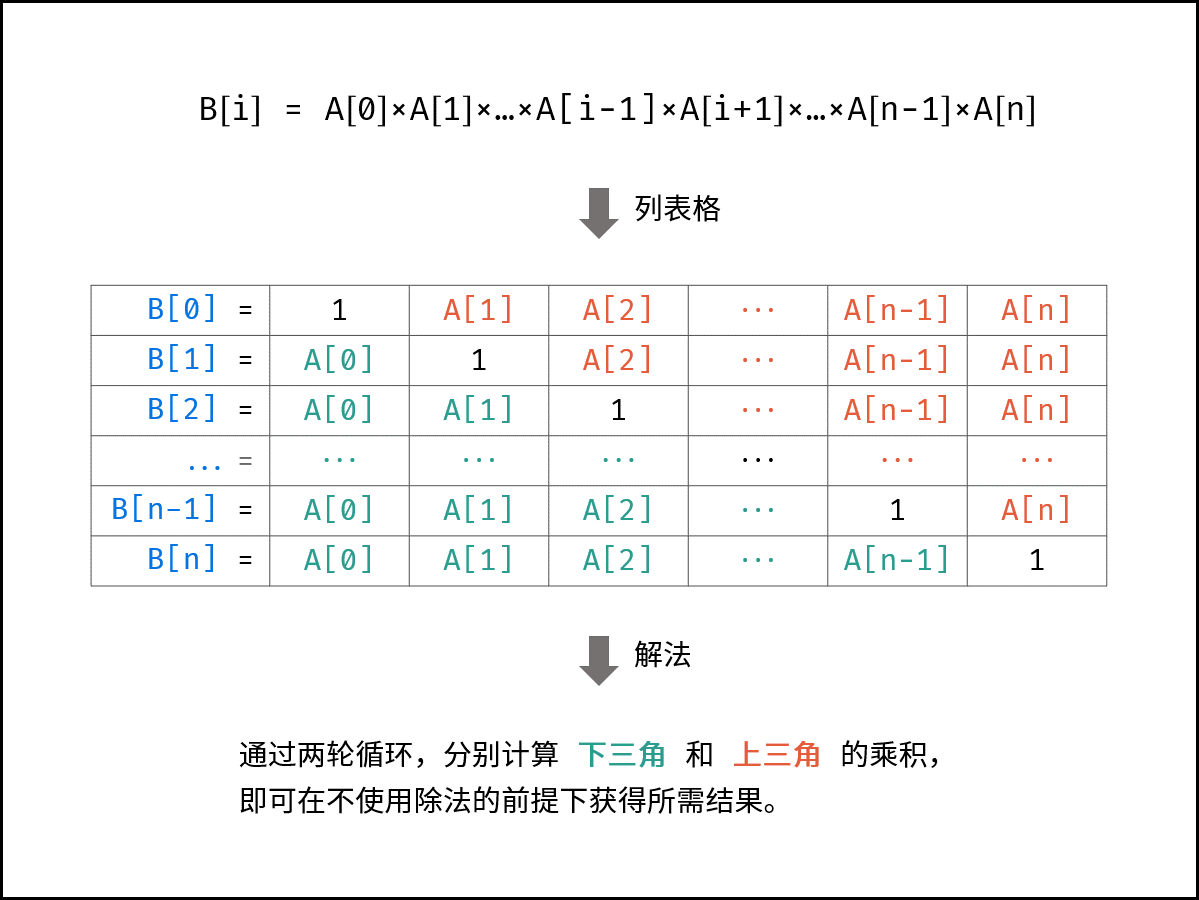![Picture1.png](https://pic.leetcode-cn.com/1624619180-vpyyqh-Picture1.png){:align=center width=500}
### 算法流程：
1. 初始化：数组 $B$ ，其中 $B[0] = 1$ ；辅助变量 $tmp = 1$ ；
2. 计算 $B[i]$ 的 **下三角** 各元素的乘积，直接乘入 $B[i]$ ；
3. 计算 $B[i]$ 的 **上三角** 各元素的乘积，记为 $tmp$ ，并乘入 $B[i]$ ；
4. 返回 $B$ 。
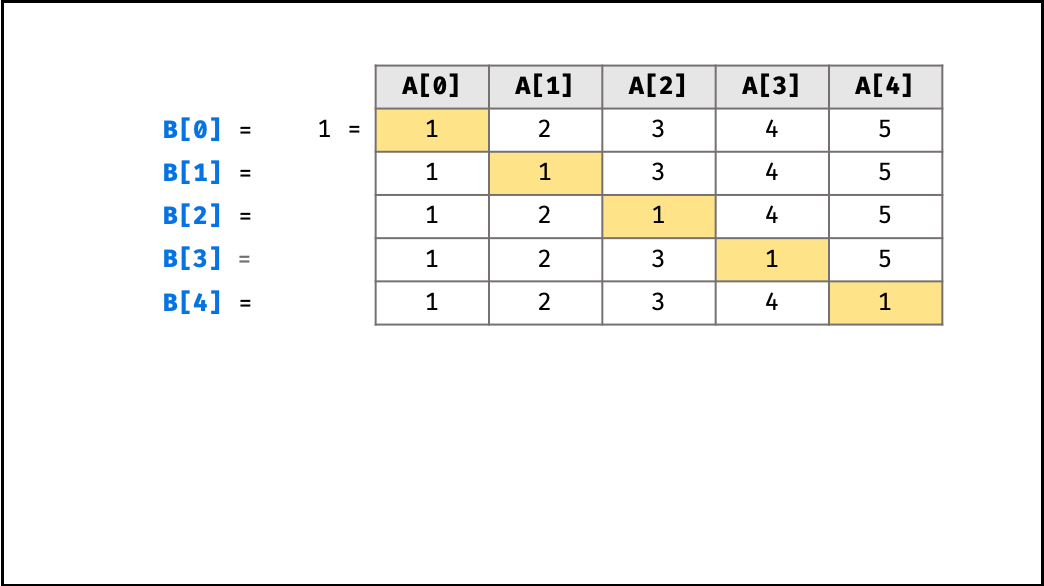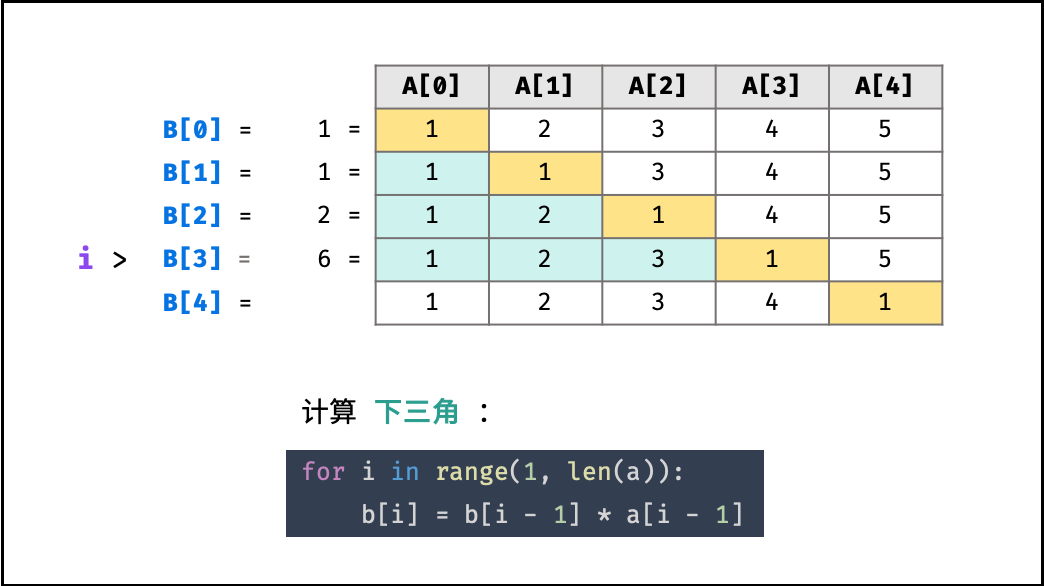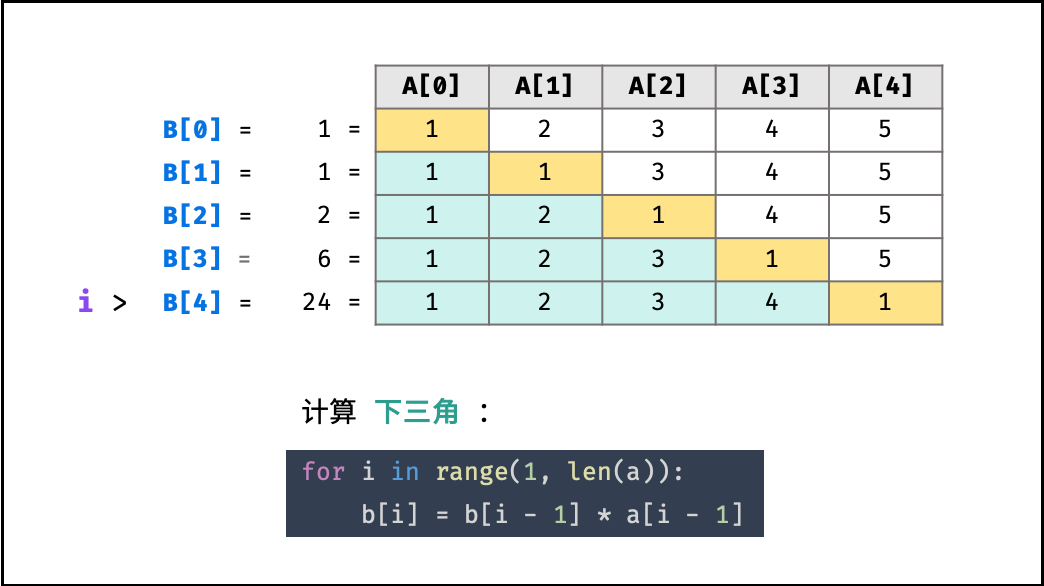<![Picture2.png](https://pic.leetcode-cn.com/1599920669-VflJdy-Picture2.png),![Picture3.png](https://pic.leetcode-cn.com/1599920669-hLhpTV-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599920669-atltNE-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599920669-qHySih-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599920669-qmJFXC-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599920669-zaVZDZ-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599920669-ufmhnT-Picture8.png),![Picture9.png](https://pic.leetcode-cn.com/1599920669-JBtgsZ-Picture9.png),![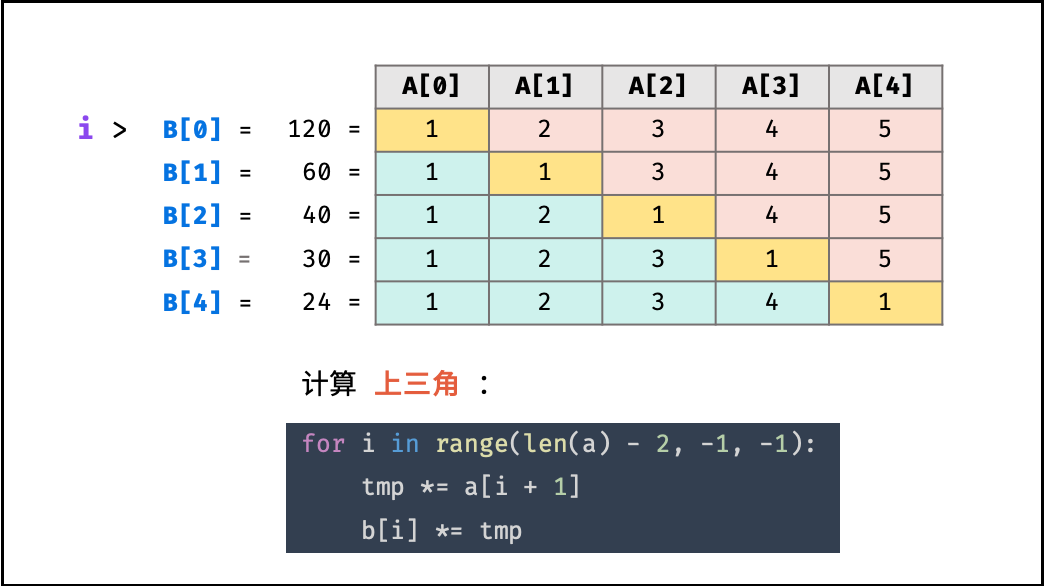Picture10.png](https://pic.leetcode-cn.com/1599920669-thDqmQ-Picture10.png),![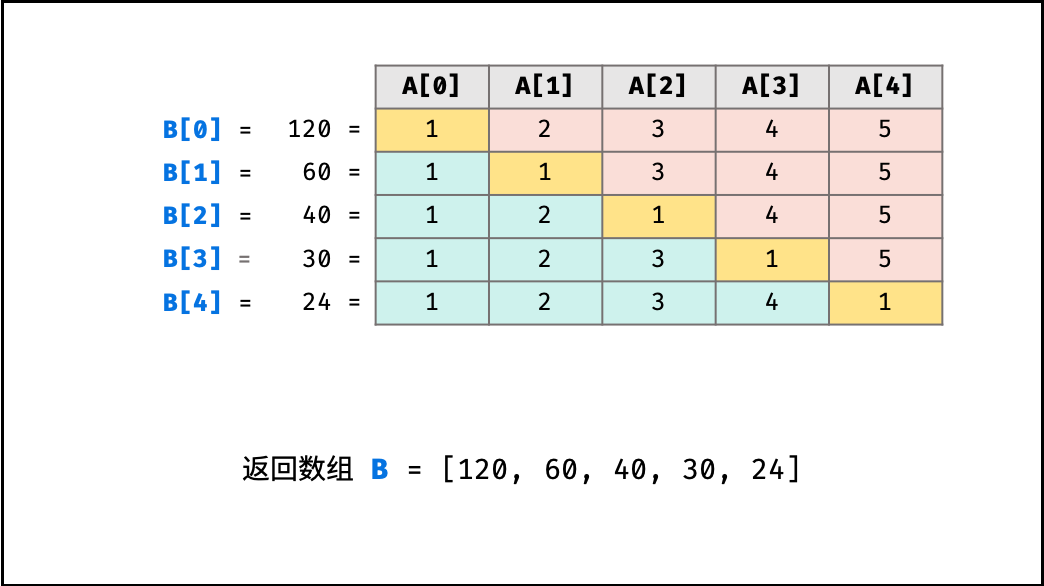Picture11.png](https://pic.leetcode-cn.com/1599920669-QvVjSS-Picture11.png)>
## 代码：
```Python []
class Solution:
def statisticalResult(self, arrayA: List[int]) -> List[int]:
arrayB, tmp = [1] * len(arrayA), 1
for i in range(1, len(arrayA)):
arrayB[i] = arrayB[i - 1] * arrayA[i - 1]
for i in range(len(arrayA) - 2, -1, -1):
tmp *= arrayA[i + 1]
arrayB[i] *= tmp
return arrayB
```
```Java []
class Solution {
public int[] statisticalResult(int[] arrayA) {
int len = arrayA.length;
if(len == 0) return new int[0];
int[] arrayB = new int[len];
arrayB[0] = 1;
int tmp = 1;
for(int i = 1; i < len; i++) {
arrayB[i] = arrayB[i - 1] * arrayA[i - 1];
}
for(int i = len - 2; i >= 0; i--) {
tmp *= arrayA[i + 1];
arrayB[i] *= tmp;
}
return arrayB;
}
}
```
```C++ []
class Solution {
public:
vector<int> statisticalResult(vector<int>& arrayA) {
int len = arrayA.size();
if(len == 0) return {};
vector<int> arrayB(len, 1);
arrayB[0] = 1;
int tmp = 1;
for(int i = 1; i < len; i++) {
arrayB[i] = arrayB[i - 1] * arrayA[i - 1];
}
for(int i = len - 2; i >= 0; i--) {
tmp *= arrayA[i + 1];
arrayB[i] *= tmp;
}
return arrayB;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为数组长度，两轮遍历数组 $A$ ，使用 $O(N)$ 时间。
- **空间复杂度 $O(1)$ ：** 变量 $tmp$ 使用常数大小额外空间（数组 $B$ 作为返回值，不计入复杂度考虑）。

143
leetbook_ioa/docs/LCR 192. 把字符串转换成整数 (atoi).md Executable file
View File

@@ -0,0 +1,143 @@
## 解题思路：
根据题意，有以下四种字符需要考虑：
1. **首部空格：** 删除之即可；
2. **符号位：** 三种情况，即 ''$+$'' , ''$-$'' , ''无符号" ；新建一个变量保存符号位，返回前判断正负即可；
3. **非数字字符：** 遇到首个非数字的字符时，应立即返回；
4. **数字字符：**
1. **字符转数字：** “此数字的 ASCII 码” 与 “ $0$ 的 ASCII 码” 相减即可；
2. **数字拼接：** 若从左向右遍历数字，设当前位字符为 $c$ ，当前位数字为 $x$ ，数字结果为 $res$ ，则数字拼接公式为：
$$
res = 10 \times res + x \\
x = ascii(c) - ascii('0')
$$
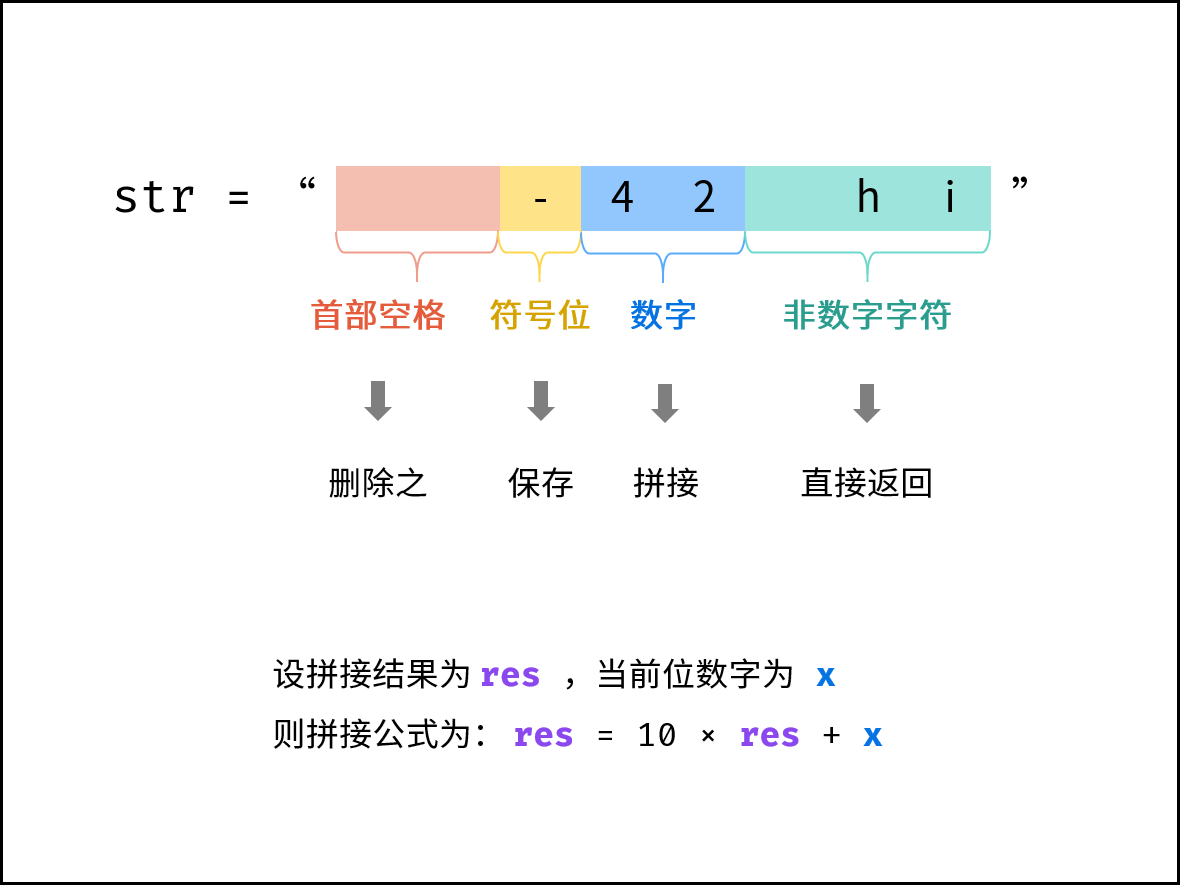![Picture1.png](https://pic.leetcode-cn.com/1600793383-jCgsGU-Picture1.png){:align=center width=450}
**数字越界处理：**
> 题目要求返回的数值范围应在 $[-2^{31}, 2^{31} - 1]$ ，因此需要考虑数字越界问题。而由于题目指出 `环境只能存储 32 位大小的有符号整数` ，因此判断数字越界时，要始终保持 $res$ 在 int 类型的取值范围内。
在每轮数字拼接前，判断 $res$ **在此轮拼接后是否超过 $2147483647$** ，若超过则加上符号位直接返回。
设数字拼接边界 $bndry = 2147483647 // 10 = 214748364$ ，则以下两种情况越界：
$$
\begin{cases}
res > bndry & 情况一：执行拼接 10 \times res \geq 2147483650 越界 \\
res = bndry, x > 7 & 情况二：拼接后是 2147483648 或 2147483649 越界 \\
\end{cases}
$$
![Picture2.png](https://pic.leetcode-cn.com/1600793383-JZRYip-Picture2.png){:align=center width=450}
解题的整体流程为：
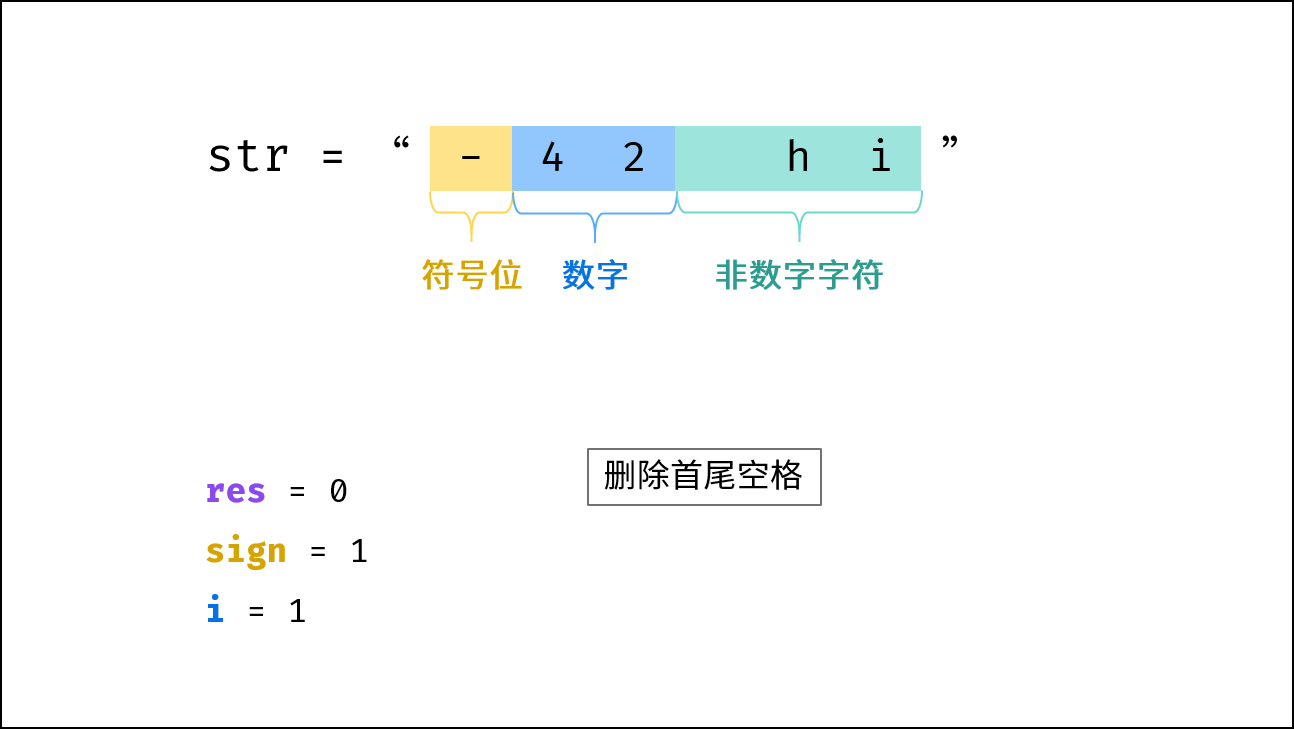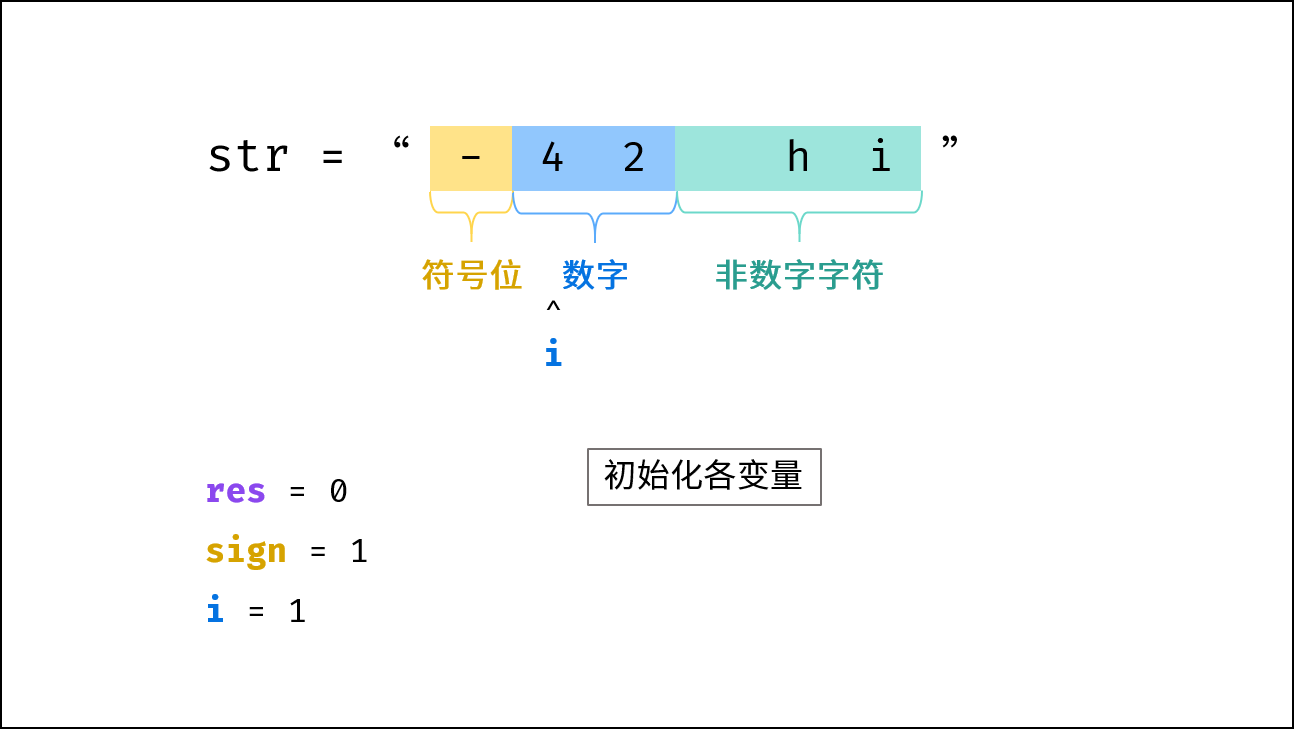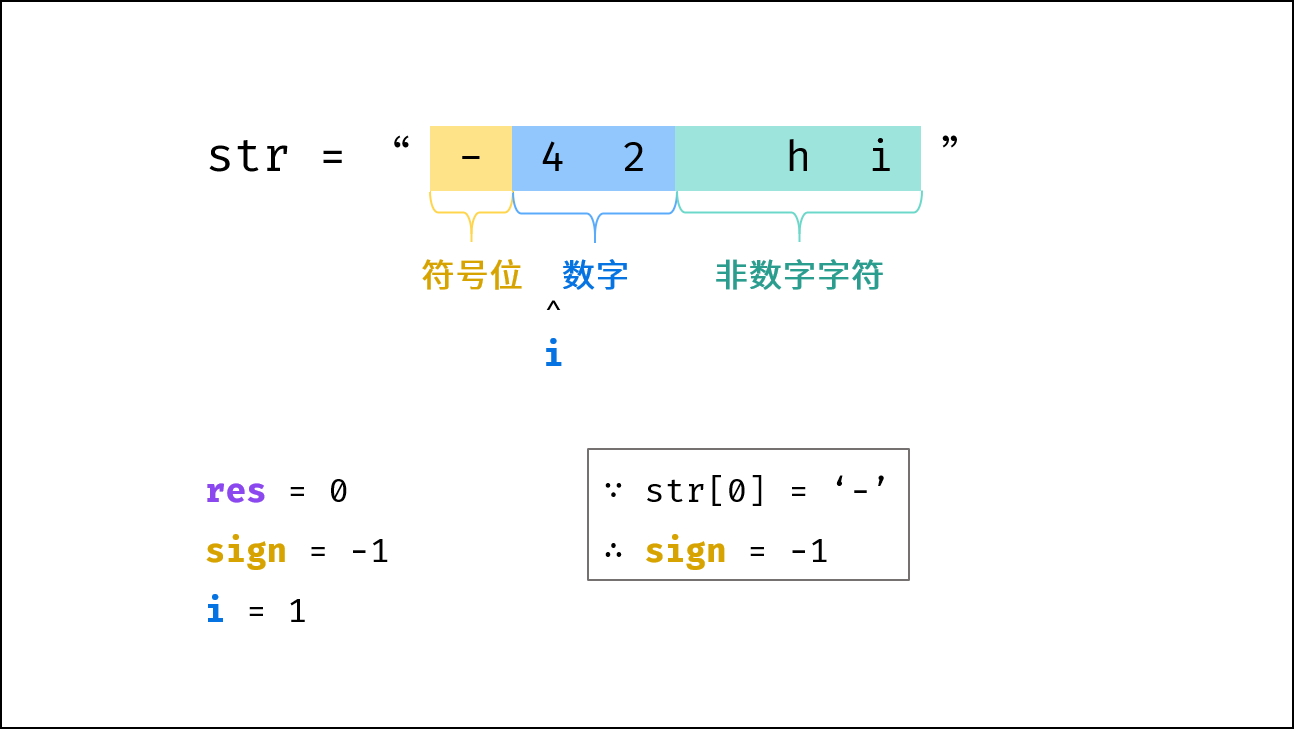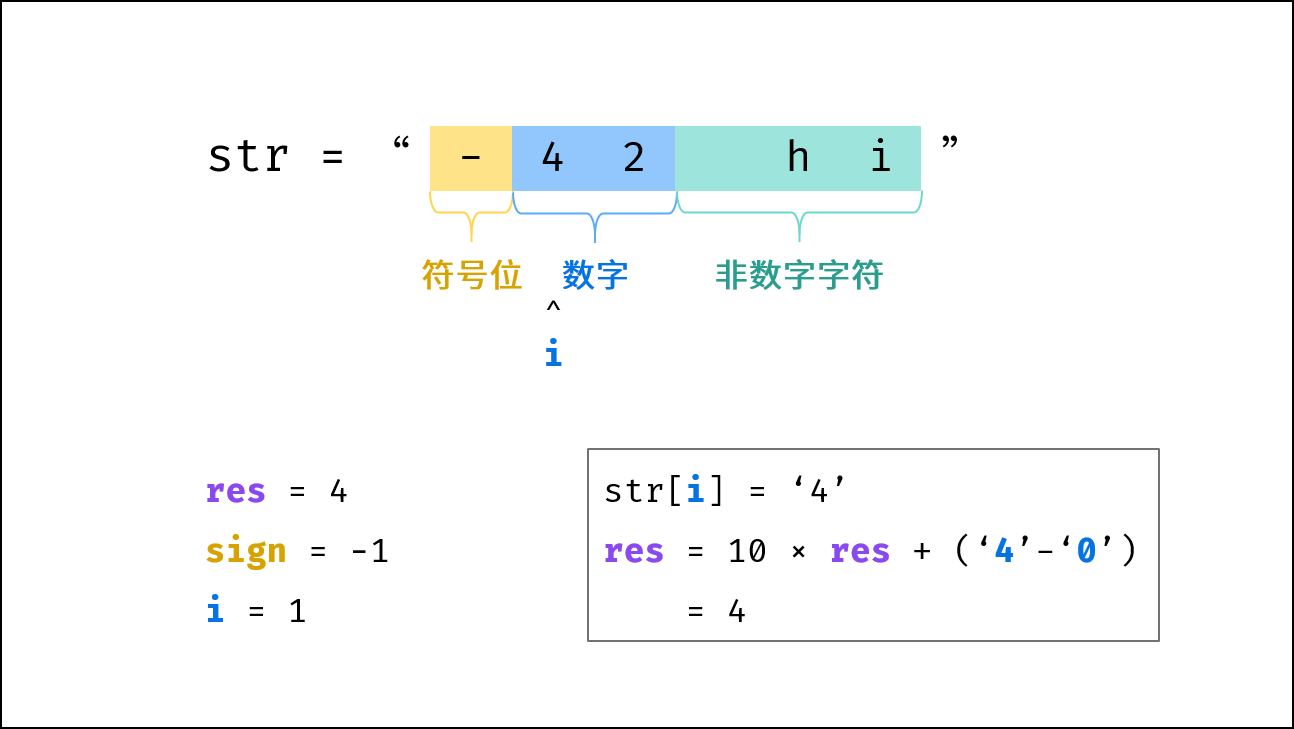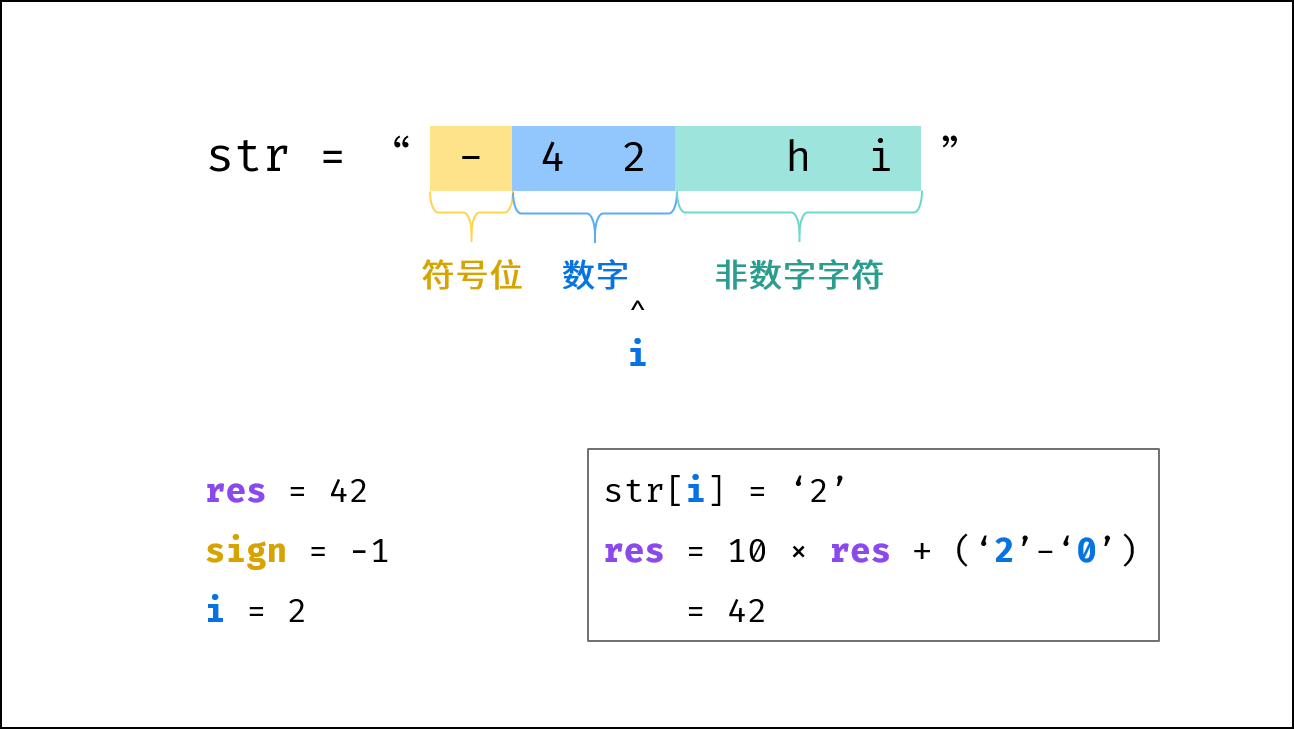<![Picture3.png](https://pic.leetcode-cn.com/1600793383-Lcevlh-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1600793383-tvCmJR-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1600793383-gfdFaU-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1600793383-hBxeGd-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1600793383-EWntxO-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1600793383-jUXVjN-Picture8.png),![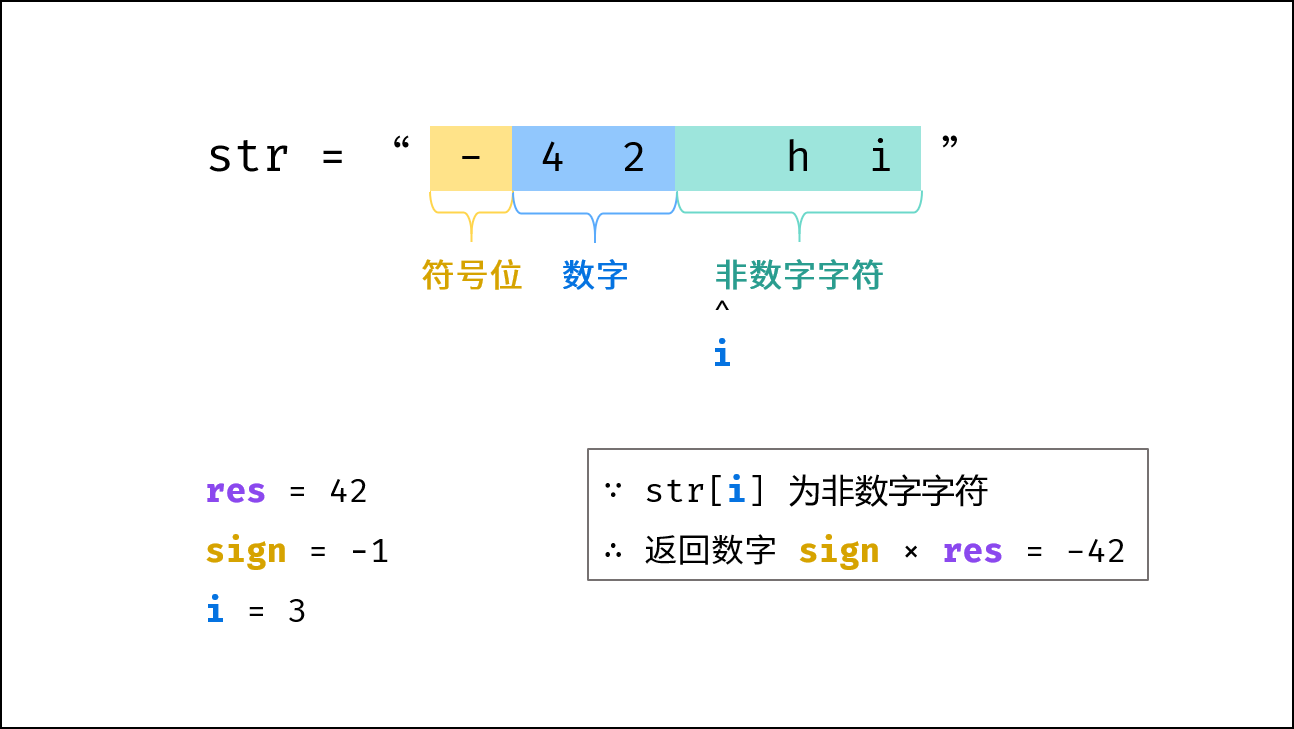Picture9.png](https://pic.leetcode-cn.com/1600793383-FShoDM-Picture9.png)>
## 代码：
```Python []
class Solution:
def myAtoi(self, str: str) -> int:
str = str.strip() # 删除首尾空格
if not str: return 0 # 字符串为空则直接返回
res, i, sign = 0, 1, 1
int_max, int_min, bndry = 2 ** 31 - 1, -2 ** 31, 2 ** 31 // 10
if str[0] == '-': sign = -1 # 保存负号
elif str[0] != '+': i = 0 # 若无符号位，则需从 i = 0 开始数字拼接
for c in str[i:]:
if not '0' <= c <= '9' : break # 遇到非数字的字符则跳出
if res > bndry or res == bndry and c > '7': return int_max if sign == 1 else int_min # 数字越界处理
res = 10 * res + ord(c) - ord('0') # 数字拼接
return sign * res
```
```Java []
class Solution {
public int myAtoi(String str) {
char[] c = str.trim().toCharArray();
if(c.length == 0) return 0;
int res = 0, bndry = Integer.MAX_VALUE / 10;
int i = 1, sign = 1;
if(c[0] == '-') sign = -1;
else if(c[0] != '+') i = 0;
for(int j = i; j < c.length; j++) {
if(c[j] < '0' || c[j] > '9') break;
if(res > bndry || res == bndry && c[j] > '7') return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
res = res * 10 + (c[j] - '0');
}
return sign * res;
}
}
```
若不使用 `trim() / strip()` 删除首部空格，而采取遍历跳过空格的方式，则可以将空间优化至 $O(1)$ ，代码如下：
```Python []
class Solution:
def myAtoi(self, str: str) -> int:
res, i, sign, length = 0, 0, 1, len(str)
int_max, int_min, bndry = 2 ** 31 - 1, -2 ** 31, 2 ** 31 // 10
if not str: return 0 # 空字符串，提前返回
while str[i] == ' ':
i += 1
if i == length: return 0 # 字符串全为空格，提前返回
if str[i] == '-': sign = -1
if str[i] in '+-': i += 1
for j in range(i, length):
if not '0' <= str[j] <= '9' : break
if res > bndry or res == bndry and str[j] > '7':
return int_max if sign == 1 else int_min
res = 10 * res + ord(str[j]) - ord('0')
return sign * res
```
```Java []
class Solution {
public int myAtoi(String str) {
int res = 0, bndry = Integer.MAX_VALUE / 10;
int i = 0, sign = 1, length = str.length();
if(length == 0) return 0;
while(str.charAt(i) == ' ')
if(++i == length) return 0;
if(str.charAt(i) == '-') sign = -1;
if(str.charAt(i) == '-' || str.charAt(i) == '+') i++;
for(int j = i; j < length; j++) {
if(str.charAt(j) < '0' || str.charAt(j) > '9') break;
if(res > bndry || res == bndry && str.charAt(j) > '7')
return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
res = res * 10 + (str.charAt(j) - '0');
}
return sign * res;
}
}
```
```C++ []
class Solution {
public:
int myAtoi(string str) {
int res = 0, bndry = INT_MAX / 10;
int i = 0, sign = 1, length = str.size();
if(length == 0) return 0;
while(str[i] == ' ')
if(++i == length) return 0;
if(str[i] == '-') sign = -1;
if(str[i] == '-' || str[i] == '+') i++;
for(int j = i; j < length; j++) {
if(str[j] < '0' || str[j] > '9') break;
if(res > bndry || res == bndry && str[j] > '7')
return sign == 1 ? INT_MAX : INT_MIN;
res = res * 10 + (str[j] - '0');
}
return sign * res;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为字符串长度，线性遍历字符串占用 $O(N)$ 时间。
- **空间复杂度 $O(N)$ ：** 删除首尾空格后需建立新字符串，最差情况下占用 $O(N)$ 额外空间。

183
leetbook_ioa/docs/LCR 193. 求二叉搜索树的最近公共祖先.md Executable file
View File

@@ -0,0 +1,183 @@
## 解题思路：
**祖先的定义：** 若节点 `p` 在节点 `root` 的左（右）子树中，或 `p = root`，则称 `root` 是 `p` 的祖先。
**最近公共祖先的定义：** 设节点 `root` 为节点 `p` , `q` 的某公共祖先，若其左子节点 `root.left` 和右子节点 `root.right` 都不是 `p` , `q` 的公共祖先，则称 `root` 是 “最近的公共祖先” 。
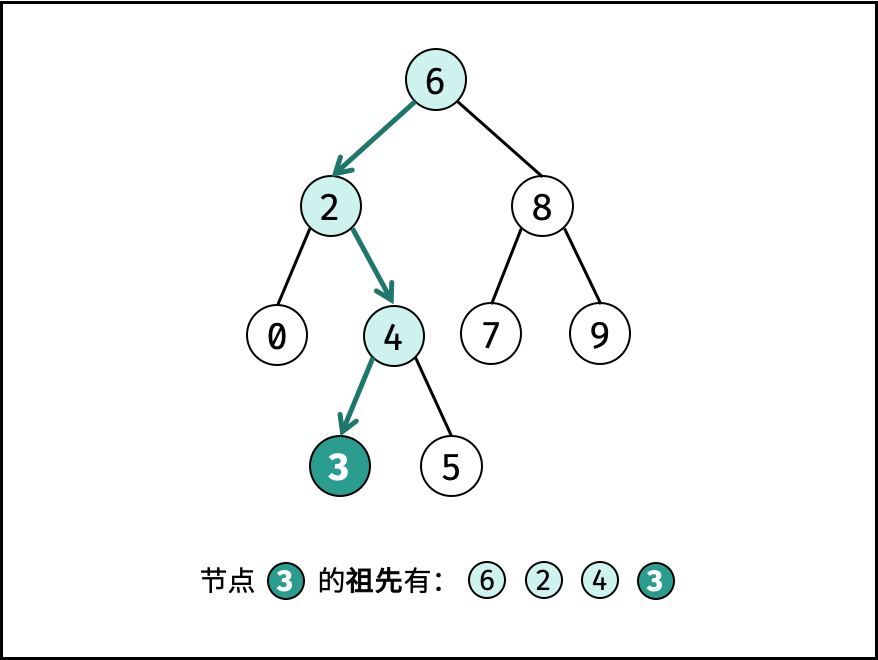![Picture1.png](https://pic.leetcode-cn.com/1599885085-LbAmPd-Picture1.png){:align=center width=450}
根据以上定义，若 `root` 是 `p` , `q` 的 **最近公共祖先** ，则只可能为以下三种情况之一：
1. `p` 和 `q` 在 `root` 的子树中，且分列 `root` 的 **异侧**（即分别在左、右子树中）；
2. `p = root` 且 `q` 在 `root` 的左或右子树中；
3. `q = root` 且 `p` 在 `root` 的左或右子树中；
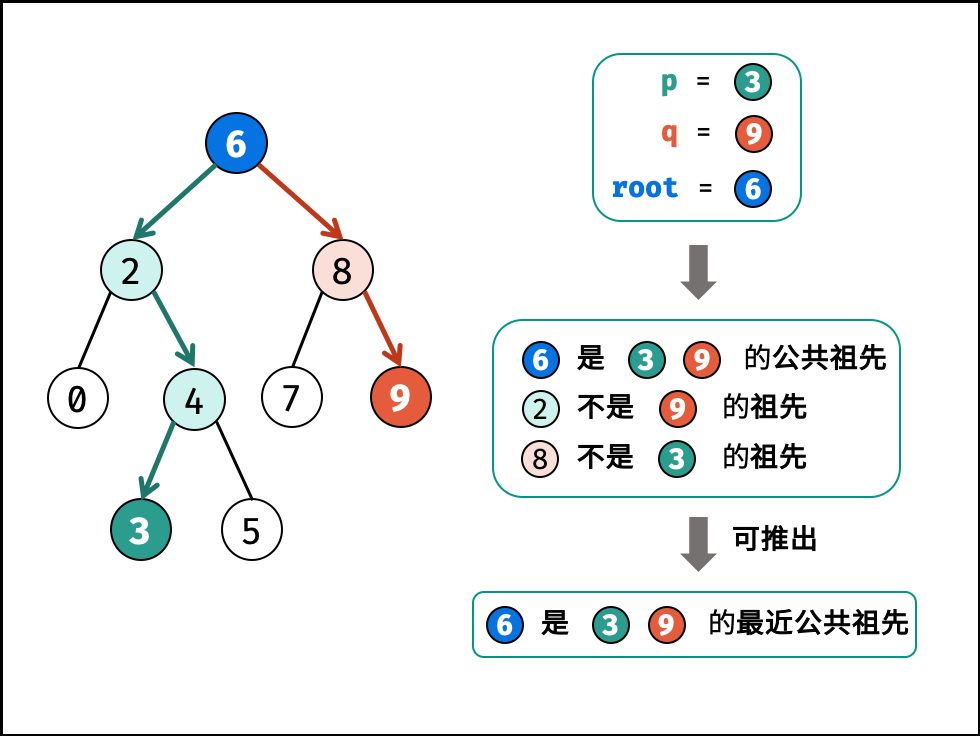![Picture2.png](https://pic.leetcode-cn.com/1599885085-mTpblH-Picture2.png){:align=center width=450}
本题给定了两个重要条件：(1) 树为 **二叉搜索树** ，(2) 树的所有节点的值都是 **唯一** 的。根据以上条件，可方便地判断 `p` , `q` 与 `root` 的子树关系，即：
- 若 `root.val < p.val` ，则 `p` 在 `root` **右子树** 中；
- 若 `root.val > p.val` ，则 `p` 在 `root` **左子树** 中；
- 若 `root.val = p.val` ，则 `p` 和 `root` 指向 **同一节点** ；
## 方法一：迭代
1. **循环搜索：** 当节点 `root` 为空时跳出；
1. 当 `p, q` 都在 `root` 的 **右子树** 中，则遍历至 `root.right` ；
2. 否则，当 `p` , `q` 都在 `root` 的 **左子树** 中，则遍历至 `root.left` ；
3. 否则，说明找到了 **最近公共祖先** ，跳出；
2. **返回值：** 最近公共祖先 `root` ；
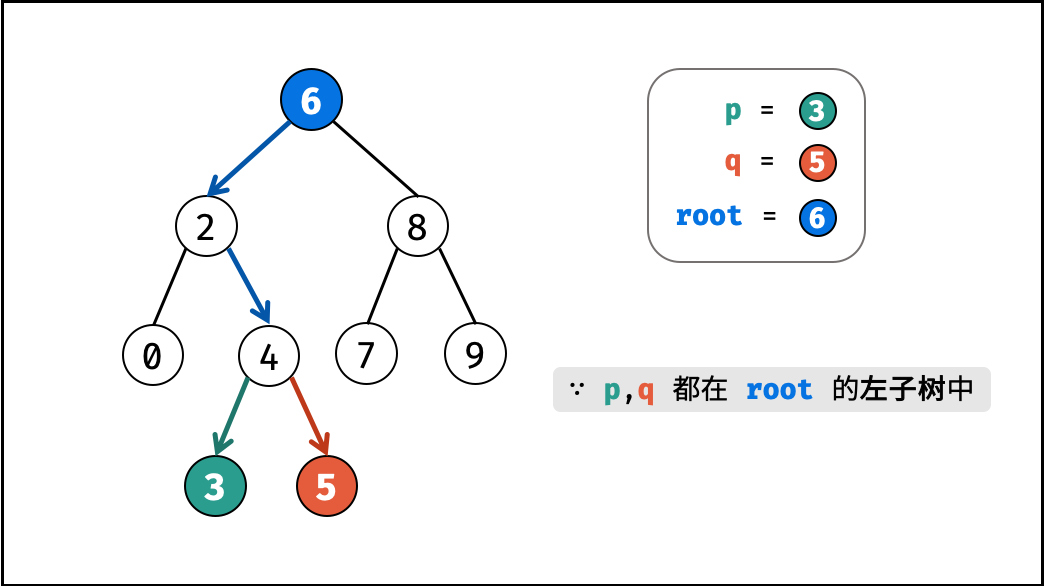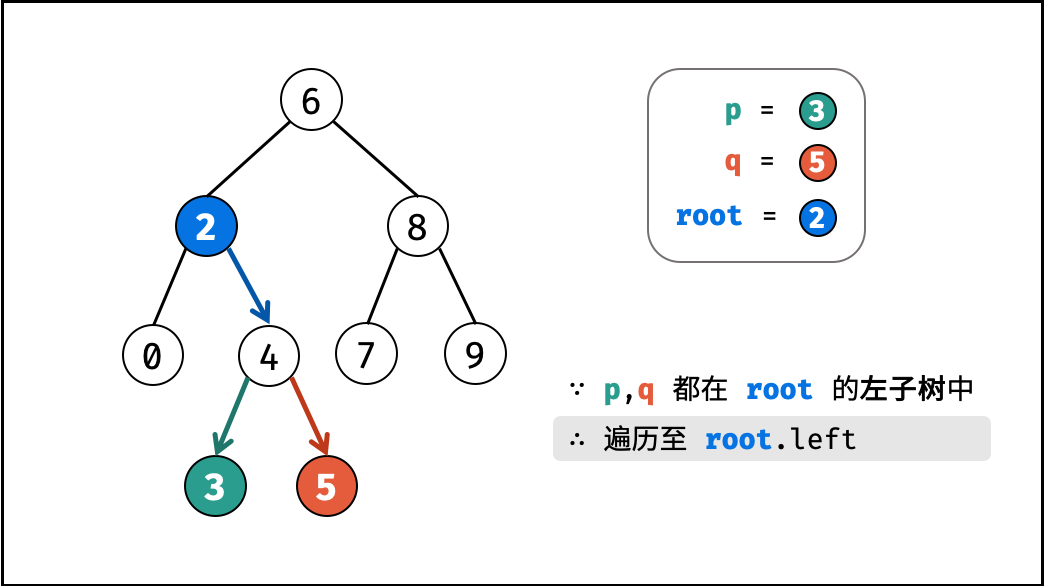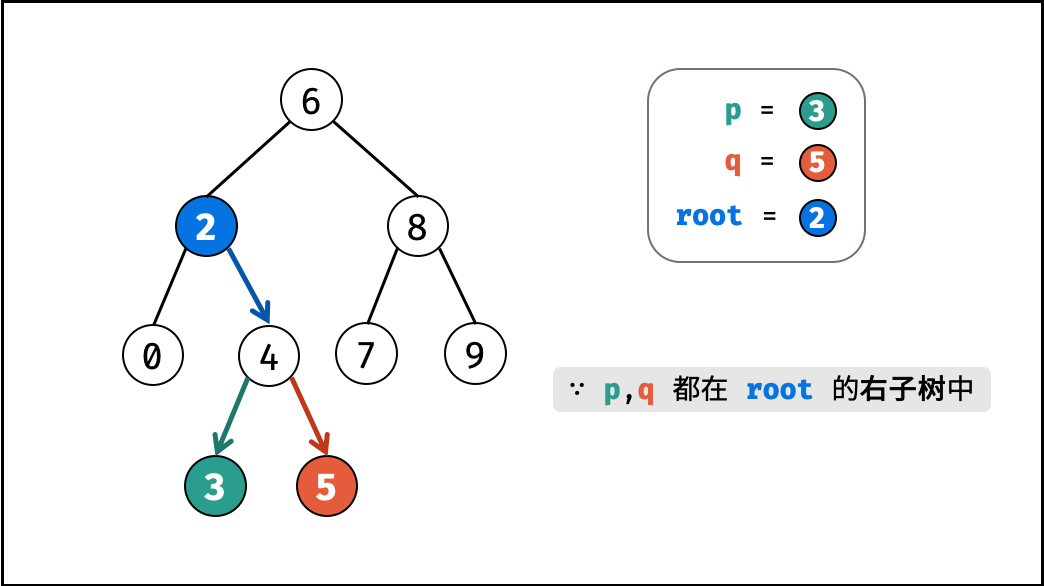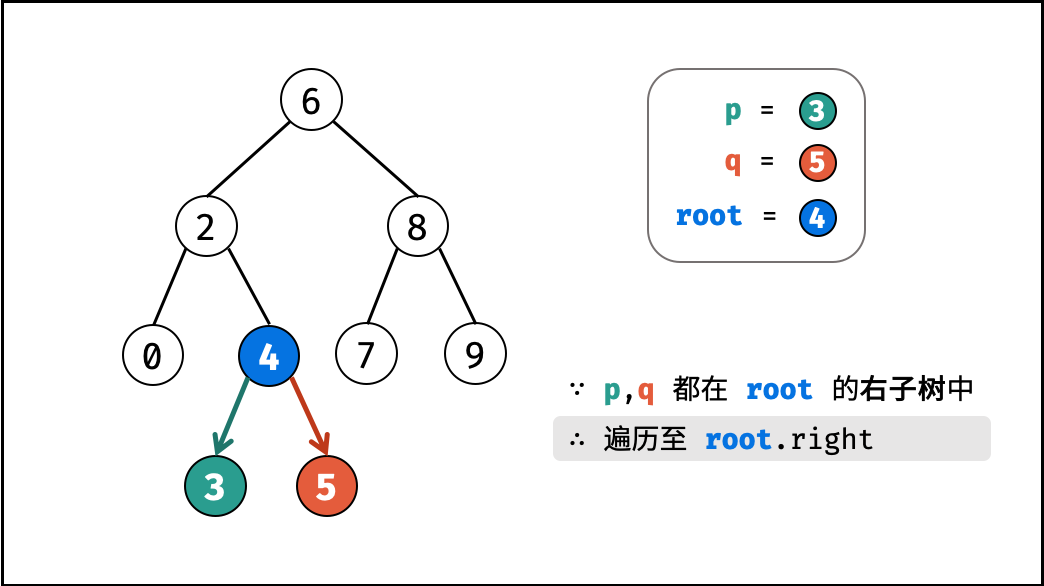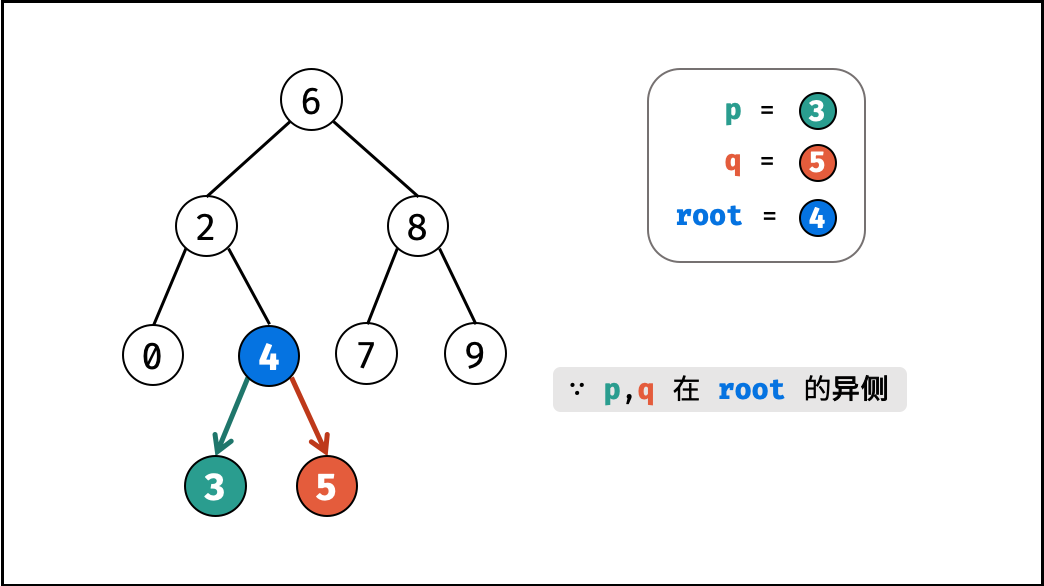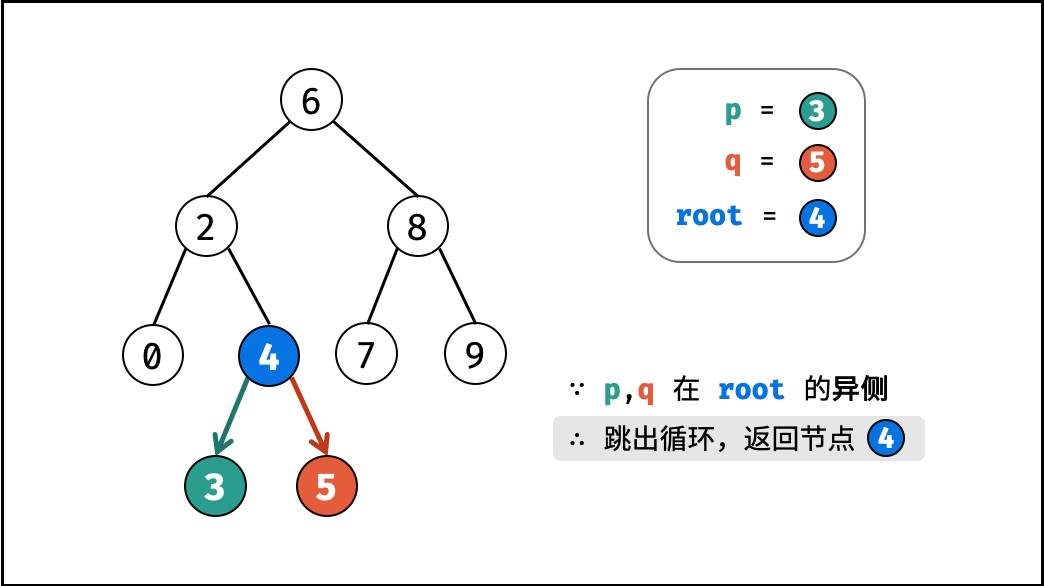<![Picture3.png](https://pic.leetcode-cn.com/1599885085-wQjbOW-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599885085-PcCSVt-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599885085-LOYAWE-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599885085-fRXXTn-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599885085-cdcSND-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599885085-AgCLYq-Picture8.png)>
### 代码：
```Python []
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
while root:
if root.val < p.val and root.val < q.val: # p,q 都在 root 的右子树中
root = root.right # 遍历至右子节点
elif root.val > p.val and root.val > q.val: # p,q 都在 root 的左子树中
root = root.left # 遍历至左子节点
else: break
return root
```
```Java []
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root != null) {
if(root.val < p.val && root.val < q.val) // p,q 都在 root 的右子树中
root = root.right; // 遍历至右子节点
else if(root.val > p.val && root.val > q.val) // p,q 都在 root 的左子树中
root = root.left; // 遍历至左子节点
else break;
}
return root;
}
}
```
```C++ []
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while(root != nullptr) {
if(root->val < p->val && root->val < q->val) // p,q 都在 root 的右子树中
root = root->right; // 遍历至右子节点
else if(root->val > p->val && root->val > q->val) // p,q 都在 root 的左子树中
root = root->left; // 遍历至左子节点
else break;
}
return root;
}
};
```
代码优化：若可保证 `p.val < q.val` ，则在循环中可减少判断条件，提升计算效率。
```Python []
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if p.val > q.val: p, q = q, p # 保证 p.val < q.val
while root:
if root.val < p.val: # p,q 都在 root 的右子树中
root = root.right # 遍历至右子节点
elif root.val > q.val: # p,q 都在 root 的左子树中
root = root.left # 遍历至左子节点
else: break
return root
```
```Java []
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val > q.val) { // 保证 p.val < q.val
TreeNode tmp = p;
p = q;
q = tmp;
}
while(root != null) {
if(root.val < p.val) // p,q 都在 root 的右子树中
root = root.right; // 遍历至右子节点
else if(root.val > q.val) // p,q 都在 root 的左子树中
root = root.left; // 遍历至左子节点
else break;
}
return root;
}
}
```
```C++ []
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(p->val > q->val)
swap(p, q);
while(root != nullptr) {
if(root->val < p->val) // p,q 都在 root 的右子树中
root = root->right; // 遍历至右子节点
else if(root->val > q->val) // p,q 都在 root 的左子树中
root = root->left; // 遍历至左子节点
else break;
}
return root;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为 $\log N$ （满二叉树），最大为 $N$ （退化为链表）。
- **空间复杂度 $O(1)$ ：** 使用常数大小的额外空间。
## 方法二：递归
1. **递推工作：**
1. 当 `p` , `q` 都在 `root` 的 **右子树** 中，则开启递归 `root.right` 并返回；
2. 否则，当 `p` , `q` 都在 `root` 的 **左子树** 中，则开启递归 `root.left` 并返回；
2. **返回值：** 最近公共祖先 `root` ；
### 代码：
```Python []
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if root.val < p.val and root.val < q.val:
return self.lowestCommonAncestor(root.right, p, q)
if root.val > p.val and root.val > q.val:
return self.lowestCommonAncestor(root.left, p, q)
return root
```
```Java []
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
if(root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
return root;
}
}
```
```C++ []
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root->val < p->val && root->val < q->val)
return lowestCommonAncestor(root->right, p, q);
if(root->val > p->val && root->val > q->val)
return lowestCommonAncestor(root->left, p, q);
return root;
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为 $\log N$ （满二叉树），最大为 $N$ （退化为链表）。
- **空间复杂度 $O(N)$ ：** 最差情况下，即树退化为链表时，递归深度达到树的层数 $N$ 。

125
leetbook_ioa/docs/LCR 194. 寻找二叉树的最近公共祖先.md Executable file
View File

@@ -0,0 +1,125 @@
## 解题思路：
**祖先的定义：** 若节点 `p` 在节点 `root` 的左（右）子树中，或 `p = root` ，则称 `root` 是 `p` 的祖先。
**最近公共祖先的定义：** 设节点 `root` 为节点 `p` , `q` 的某公共祖先，若其左子节点 `root.left` 和右子节点 `root.right` 都不是 `p` , `q` 的公共祖先，则称 `root` 是 “最近的公共祖先” 。
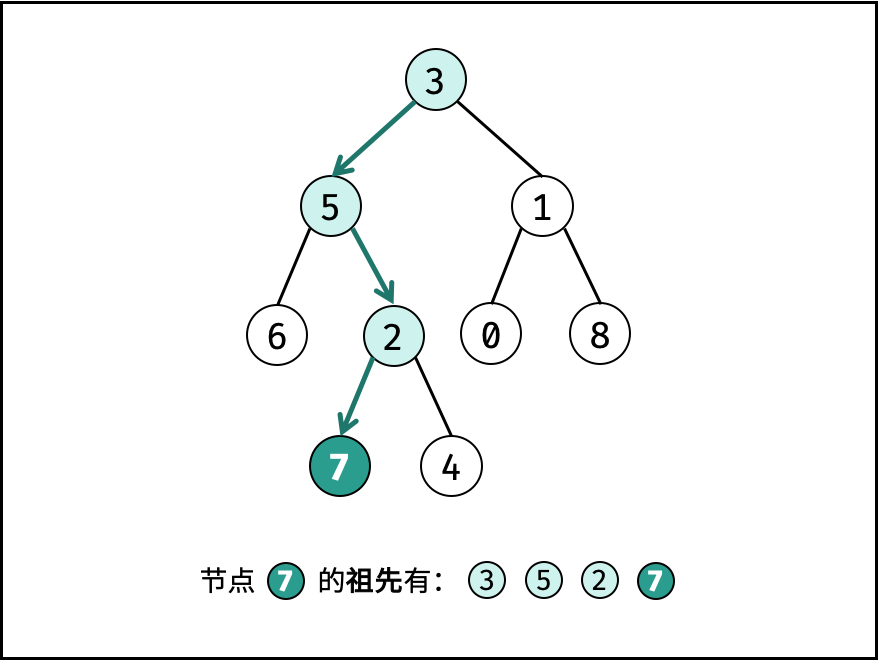![Picture1.png](https://pic.leetcode-cn.com/1599885247-rxcHcZ-Picture1.png){:align=center width=450}
根据以上定义，若 `root` 是 `p` , `q` 的 **最近公共祖先** ，则只可能为以下情况之一：
1. `p` 和 `q` 在 `root` 的子树中，且分列 `root` 的 **异侧**（即分别在左、右子树中）；
2. `p = root` ，且 `q` 在 `root` 的左或右子树中；
3. `q = root` ，且 `p` 在 `root` 的左或右子树中；
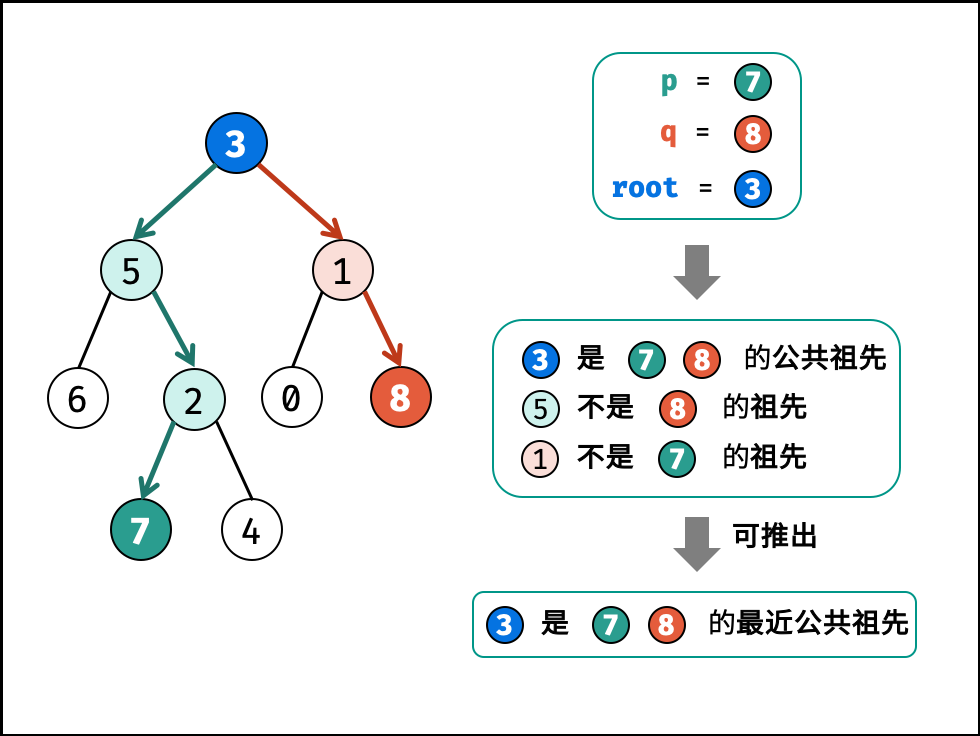![Picture2.png](https://pic.leetcode-cn.com/1599885247-mgYjRv-Picture2.png){:align=center width=450}
考虑通过递归对二叉树进行先序遍历，当遇到节点 `p` 或 `q` 时返回。从底至顶回溯，当节点 `p` , `q` 在节点 `root` 的异侧时，节点 `root` 即为最近公共祖先，则向上返回 `root` 。
### 递归解析：
1. **终止条件：**
1. 当越过叶节点，则直接返回 $\text{null}$ ；
2. 当 `root` 等于 `p` , `q` ，则直接返回 `root` ；
2. **递推工作：**
1. 开启递归左子节点，返回值记为 `left` ；
2. 开启递归右子节点，返回值记为 `right` ；
3. **返回值：** 根据 `left` 和 `right` ，可展开为四种情况；
1. 当 `left` 和 `right` **同时为空** ：说明 `root` 的左 / 右子树中都不包含 `p` , `q` ，返回 $\text{null}$ ；
2. 当 `left` 和 `right` **同时不为空** ：说明 `p` , `q` 分列在 `root` 的 **异侧** （分别在 左 / 右子树），因此 `root` 为最近公共祖先，返回 `root` ；
3. 当 `left` **为空** ，`right` **不为空** ：`p` , `q` 都不在 `root` 的左子树中，直接返回 `right` 。具体可分为两种情况：
1. `p` , `q` 其中一个在 `root` 的 **右子树** 中，此时 `right` 指向 `p`（假设为 `p` ）；
2. `p` , `q` 两节点都在 `root` 的 **右子树** 中，此时的 `right` 指向 **最近公共祖先节点** ；
4. 当 `left` **不为空** ，`right` **为空** ：与情况 `3.` 同理；
> 观察发现，情况 `1.` 可合并至 `3.` 和 `4.` 内，详见文章末尾代码。
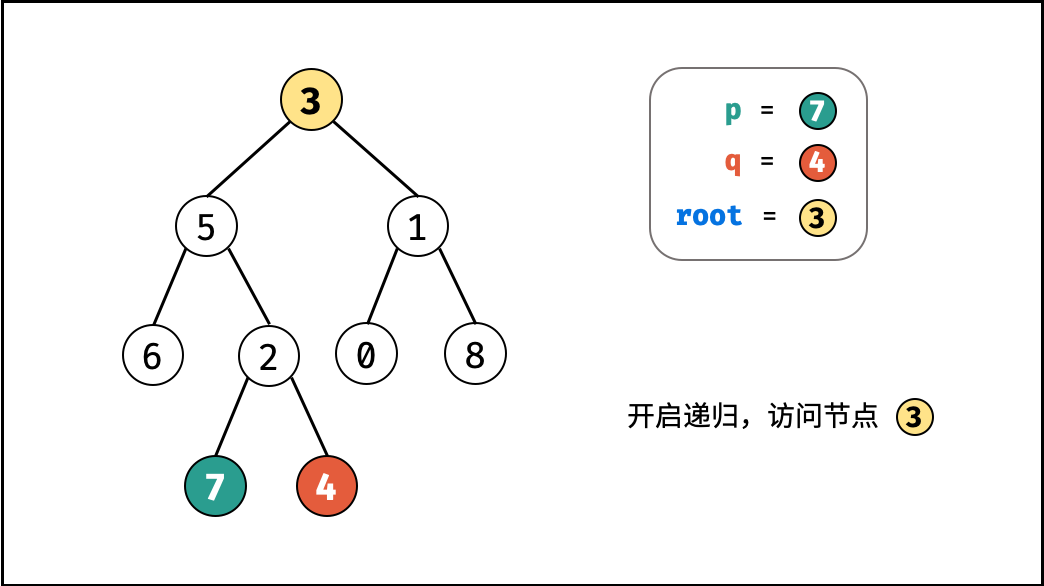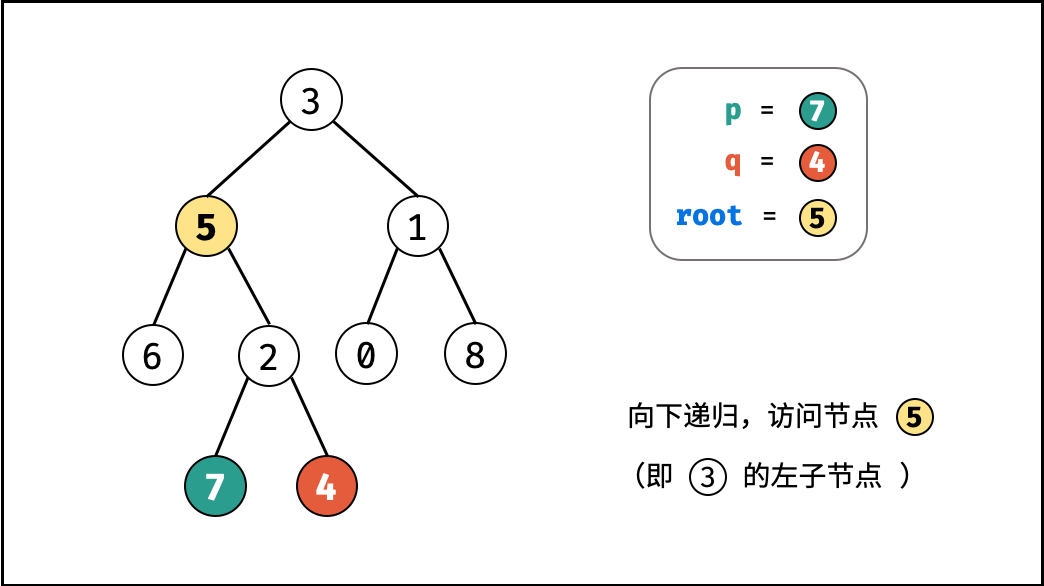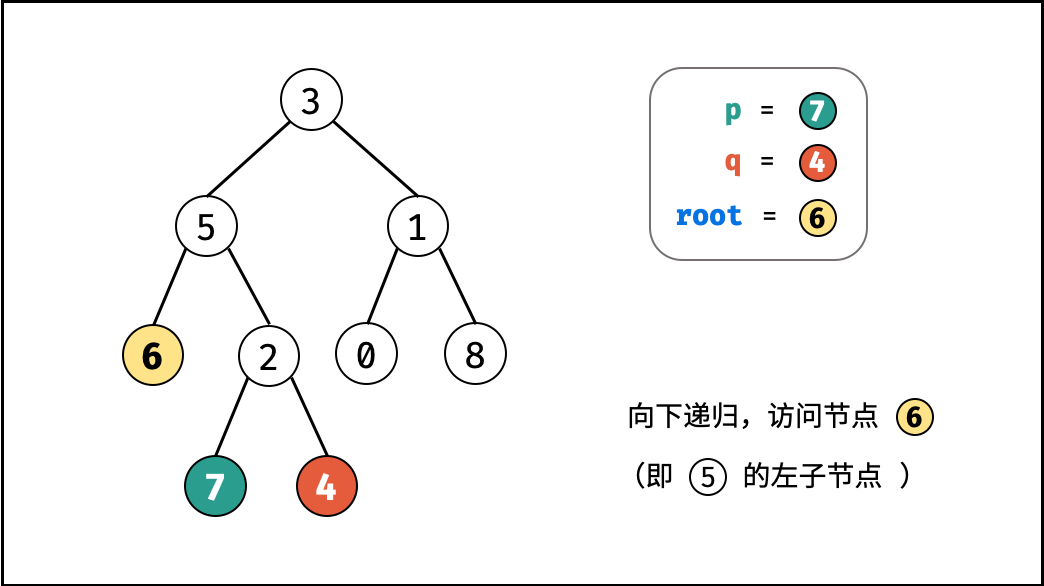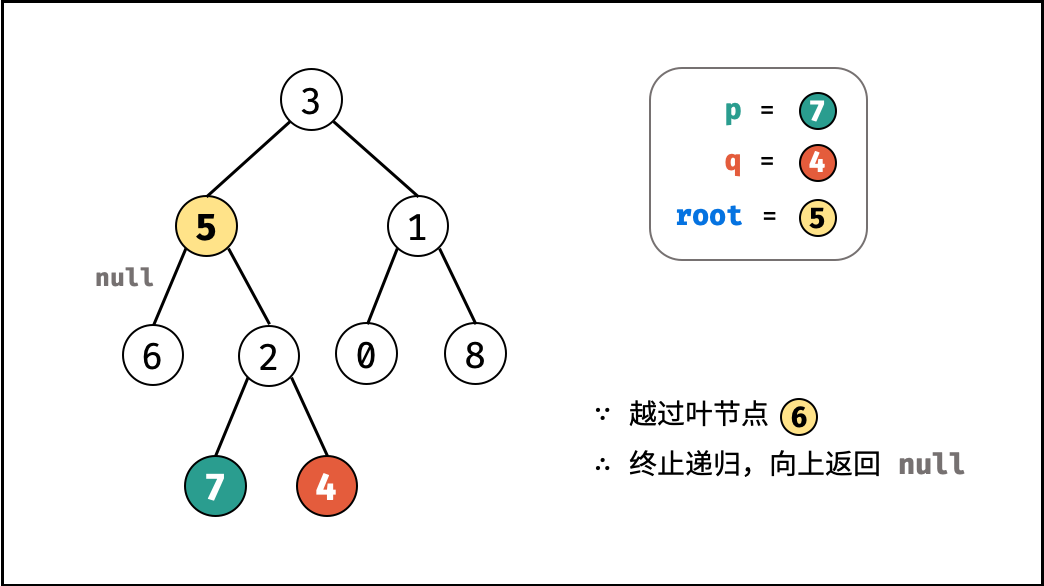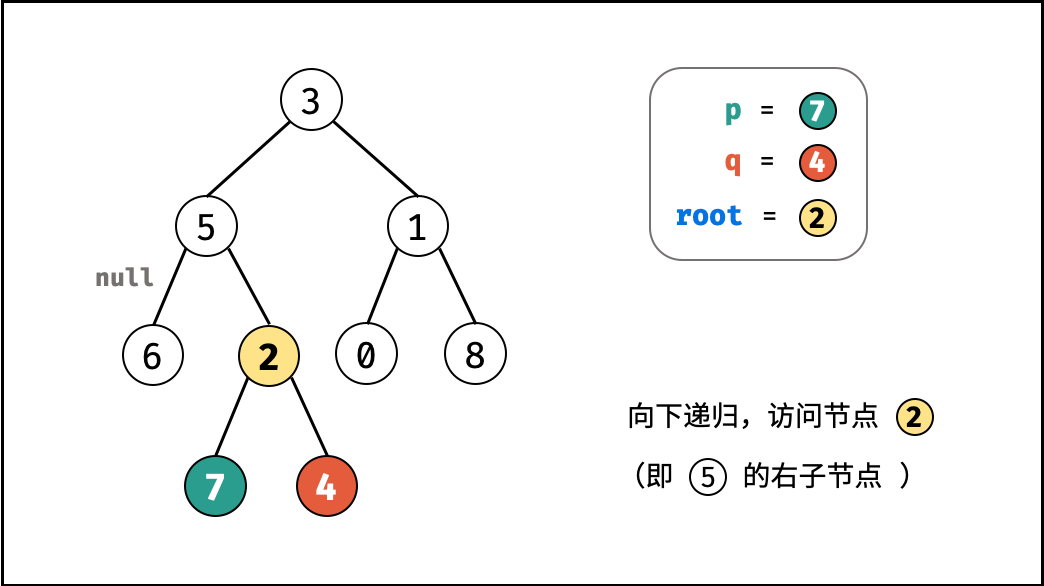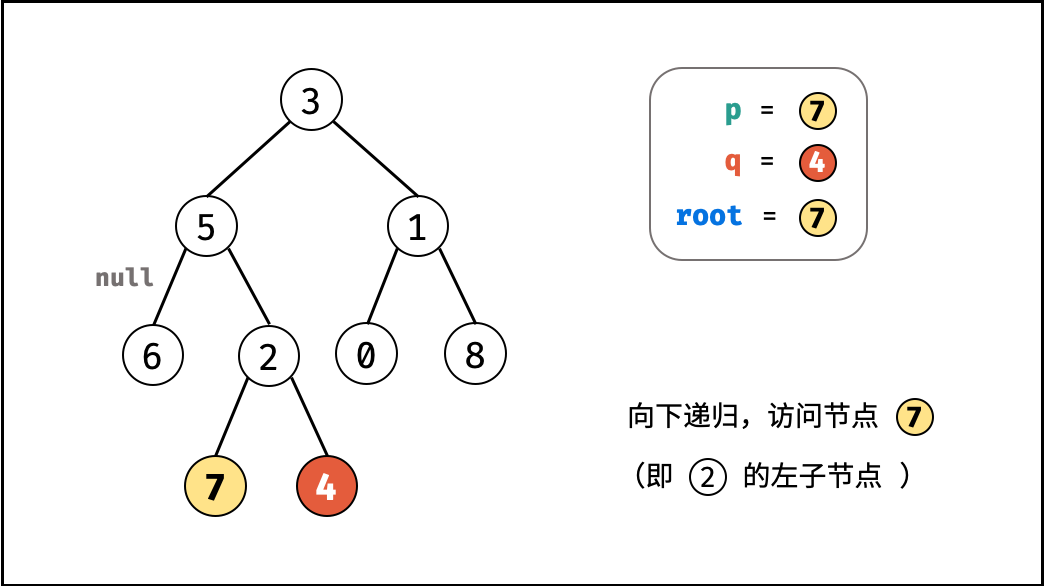<![Picture3.png](https://pic.leetcode-cn.com/1599885247-KpxUys-Picture3.png),![Picture4.png](https://pic.leetcode-cn.com/1599885247-azGPkG-Picture4.png),![Picture5.png](https://pic.leetcode-cn.com/1599885247-hIMEfJ-Picture5.png),![Picture6.png](https://pic.leetcode-cn.com/1599885247-UMCTfd-Picture6.png),![Picture7.png](https://pic.leetcode-cn.com/1599885247-SLOIAX-Picture7.png),![Picture8.png](https://pic.leetcode-cn.com/1599885247-JGxmmL-Picture8.png),![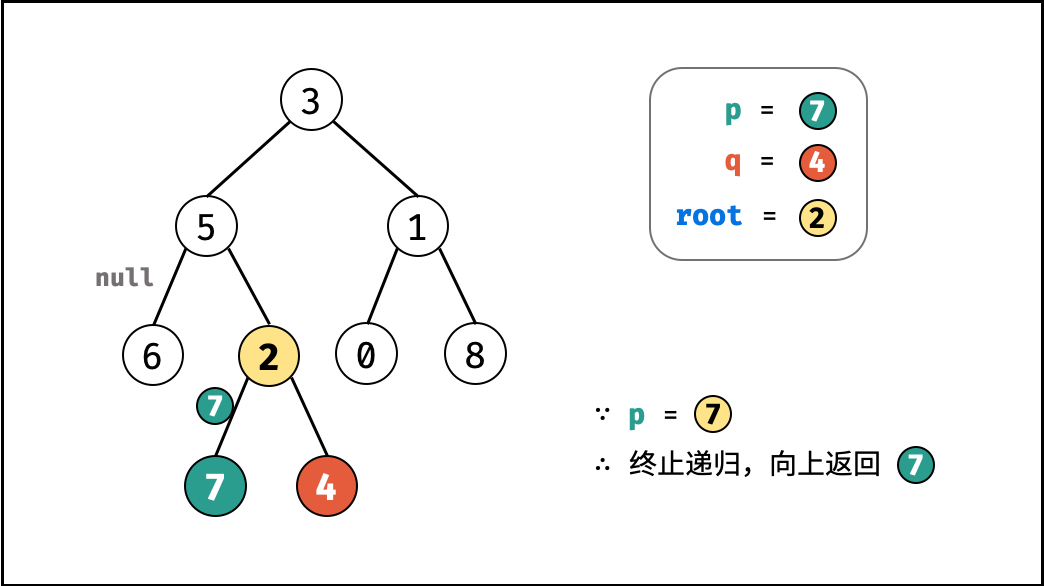Picture9.png](https://pic.leetcode-cn.com/1599885247-lVrUTd-Picture9.png),![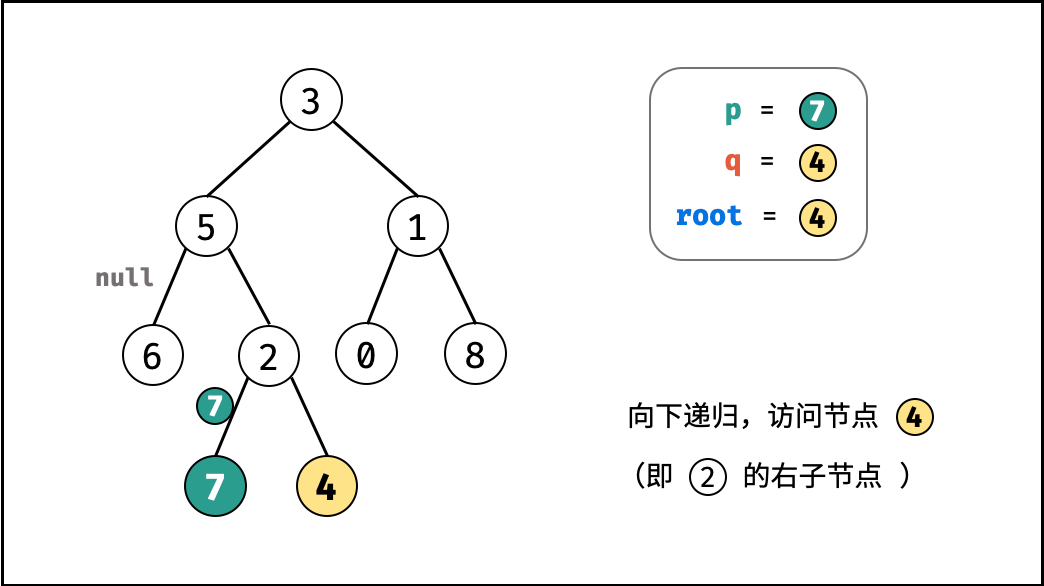Picture10.png](https://pic.leetcode-cn.com/1599885247-VTPazU-Picture10.png),![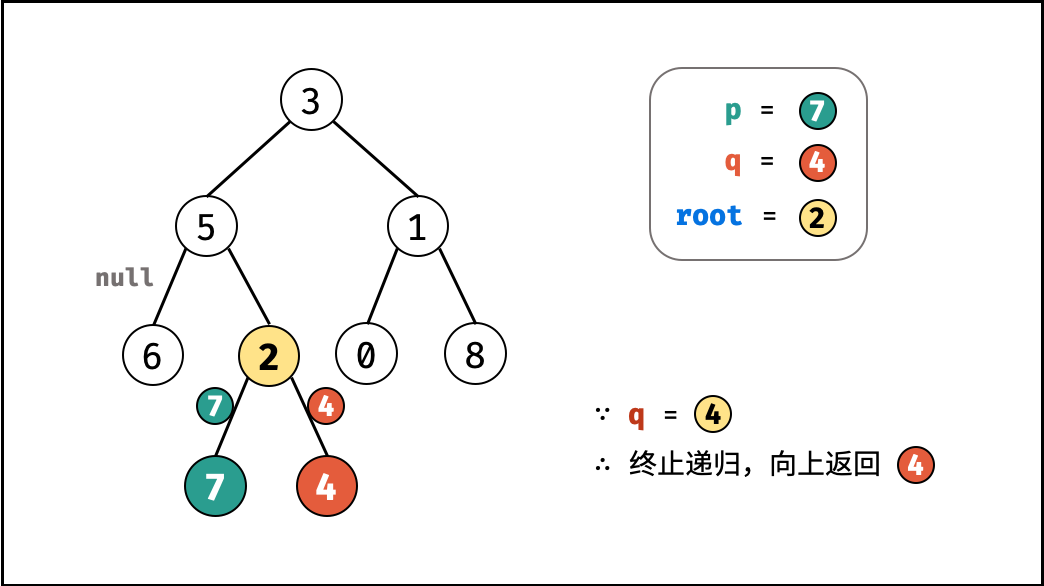Picture11.png](https://pic.leetcode-cn.com/1599885247-KePYfU-Picture11.png),![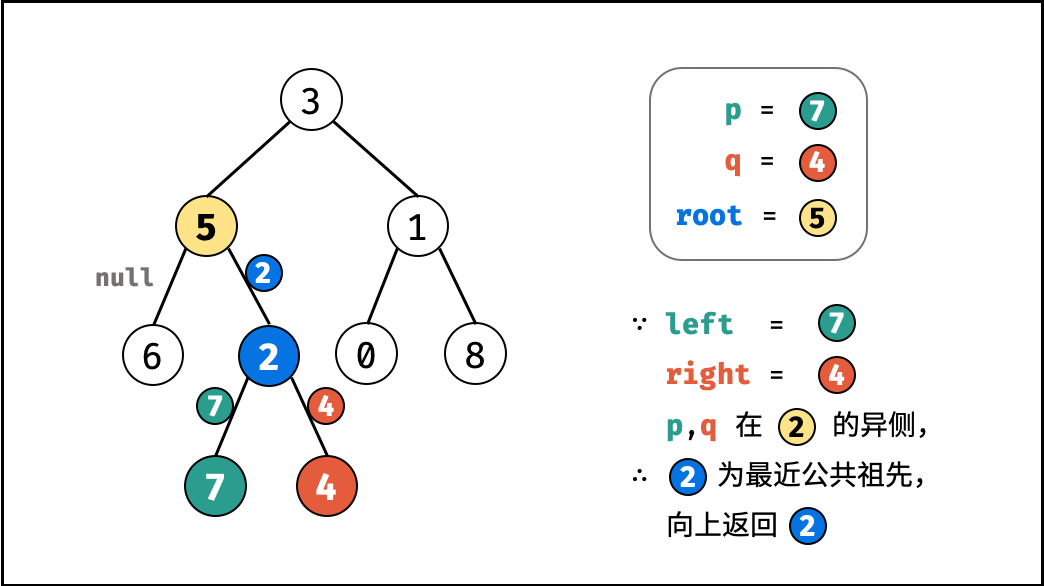Picture12.png](https://pic.leetcode-cn.com/1599885247-xkRUDm-Picture12.png),![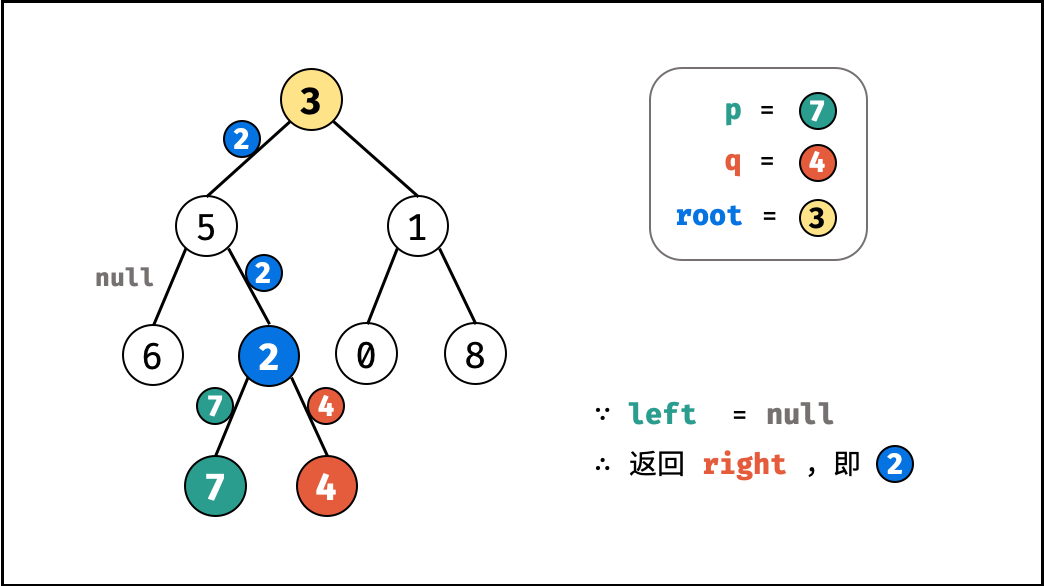Picture13.png](https://pic.leetcode-cn.com/1599885247-SFdLoP-Picture13.png),![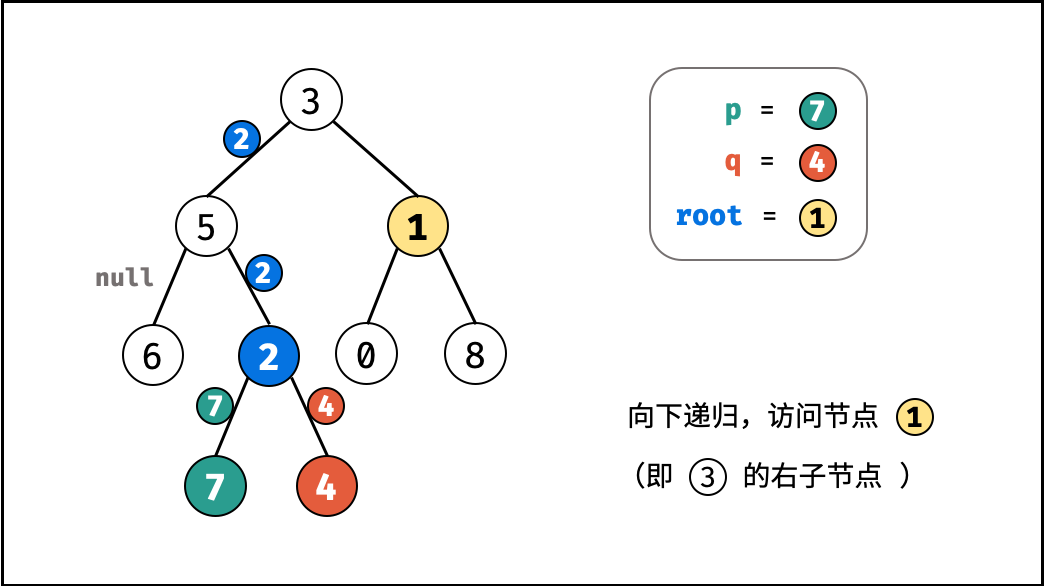Picture14.png](https://pic.leetcode-cn.com/1599885247-YOUEcd-Picture14.png),![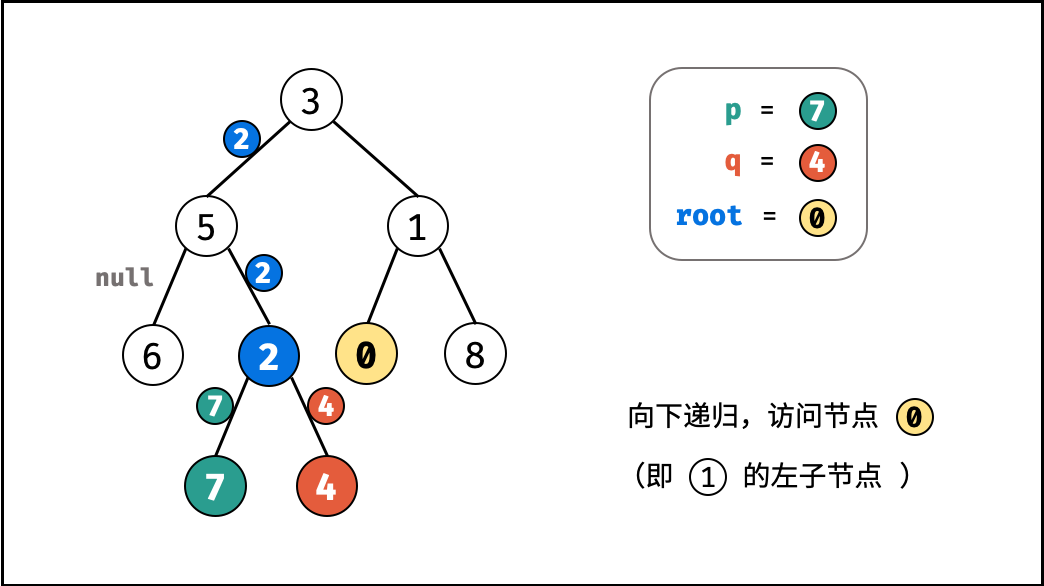Picture15.png](https://pic.leetcode-cn.com/1599885247-HcncTq-Picture15.png),![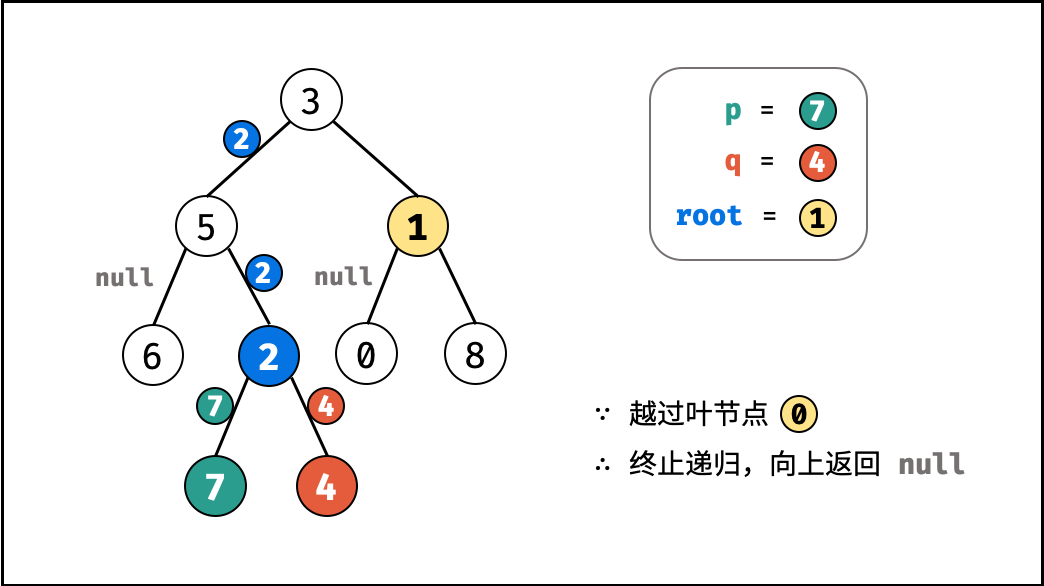Picture16.png](https://pic.leetcode-cn.com/1599885247-oeFNkc-Picture16.png),![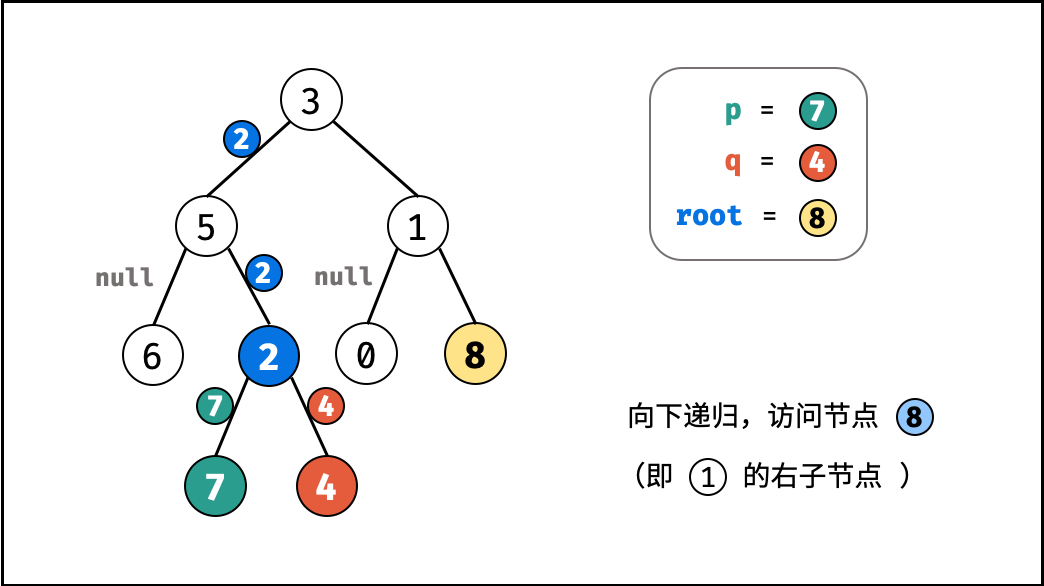Picture17.png](https://pic.leetcode-cn.com/1599885247-DjiiMY-Picture17.png),![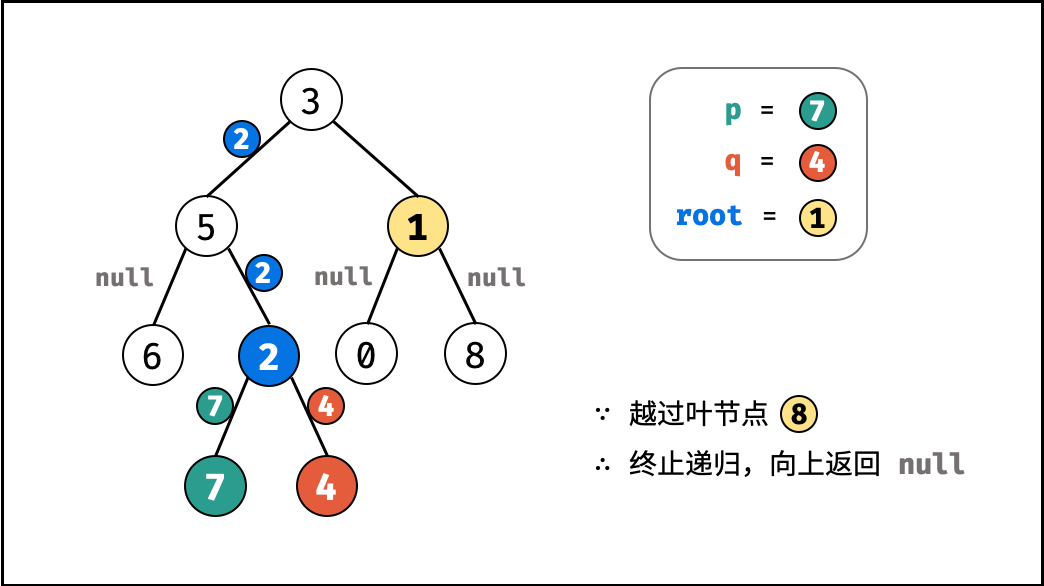Picture18.png](https://pic.leetcode-cn.com/1599885247-SkpSEn-Picture18.png),![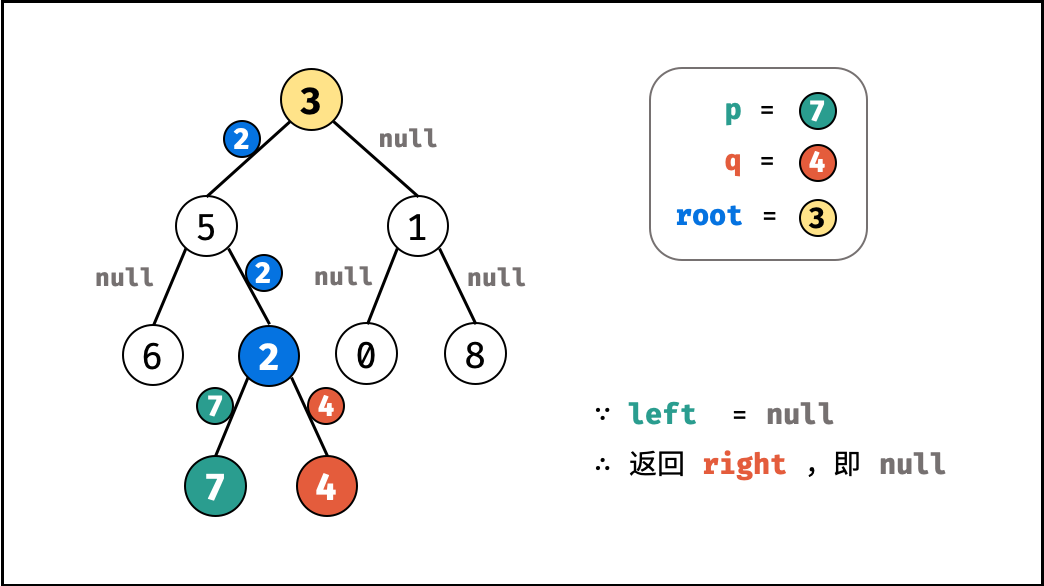Picture19.png](https://pic.leetcode-cn.com/1599885247-jFDBar-Picture19.png),![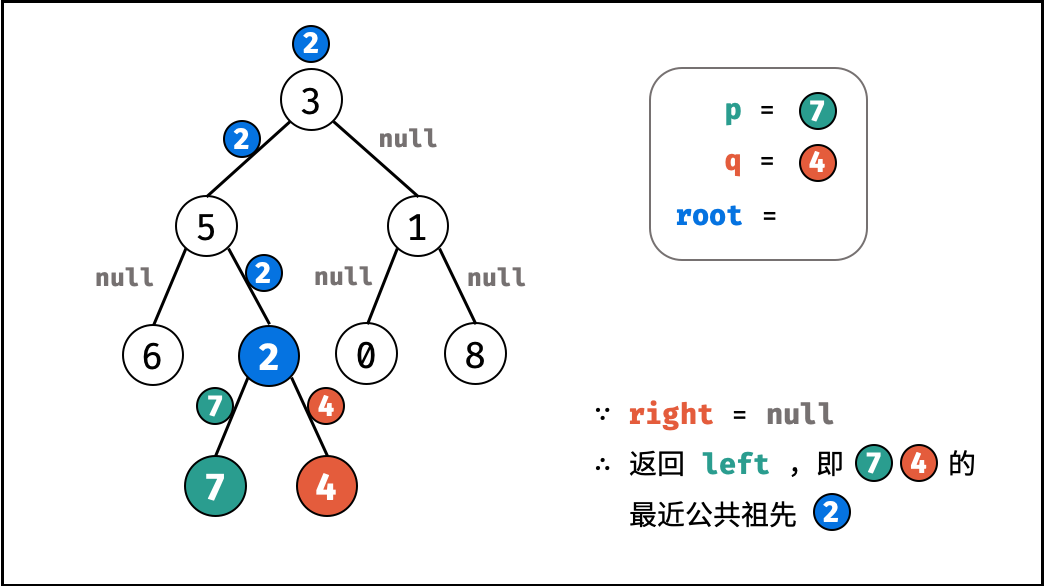Picture20.png](https://pic.leetcode-cn.com/1599885247-GEkXRi-Picture20.png)>
### 代码：
```Python []
class Solution:
def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
if not root or root == p or root == q: return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left: return right
if not right: return left
return root
```
```Java []
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null) return right;
if(right == null) return left;
return root;
}
}
```
```C++ []
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr || root == p || root == q) return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if(left == nullptr) return right;
if(right == nullptr) return left;
return root;
}
};
```
情况 `1.` , `2.` , `3.` , `4.` 的展开写法如下。
```Python []
class Solution:
def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
if not root or root == p or root == q: return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left and not right: return # 1.
if not left: return right # 3.
if not right: return left # 4.
return root # 2. if left and right:
```
```Java []
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null && right == null) return null; // 1.
if(left == null) return right; // 3.
if(right == null) return left; // 4.
return root; // 2. if(left != null and right != null)
}
}
```
```C++ []
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr || root == p || root == q) return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if(left == nullptr && right == nullptr) return nullptr; // 1.
if(left == nullptr) return right; // 3.
if(right == nullptr) return left; // 4.
return root; // 2. if(left != null and right != null)
}
};
```
### 复杂度分析：
- **时间复杂度 $O(N)$ ：** 其中 $N$ 为二叉树节点数；最差情况下，需要递归遍历树的所有节点。
- **空间复杂度 $O(N)$ ：** 最差情况下，递归深度达到 $N$ ，系统使用 $O(N)$ 大小的额外空间。