LeetCode-Book/leetbook_ioa/docs/# 11.1 动态规划解题框架.md

动态规划解题框架

动态规划是算法与数据结构的重难点之一，其包含了「分治思想」、「空间换时间」、「最优解」等多种基石算法思想，常作为笔面试中的中等困难题出现。为帮助读者全面理解动态规划，知晓其来龙去脉，本文将从以下几个角度切入介绍：

1. 动态规划问题特点，动态规划和分治算法的联系与区别；
2. 借助例题介绍重叠子问题和最优子结构分别是什么，以及动态规划是如何解决它们的；
3. 动态规划的解题框架总结；
4. 动态规划的练习例题，从易到难排序；

---

动态规划特点

「分治」是算法中的一种基本思想，其通过将原问题分解为子问题，不断递归地将子问题分解为更小的子问题，并通过组合子问题的解来得到原问题的解。

类似于分治算法，「动态规划」也通过组合子问题的解得到原问题的解。不同的是，适合用动态规划解决的问题具有「重叠子问题」和「最优子结构」两大特性。

重叠子问题

动态规划的子问题是有重叠的，即各个子问题中包含重复的更小子问题。若使用暴力法穷举，求解这些相同子问题会产生大量的重复计算，效率低下。

动态规划在第一次求解某子问题时，会将子问题的解保存；后续遇到重叠子问题时，则直接通过查表获取解，保证每个独立子问题只被计算一次，从而降低算法的时间复杂度。

最优子结构

如果一个问题的最优解可以由其子问题的最优解组合构成，并且这些子问题可以独立求解，那么称此问题具有最优子结构。

动态规划从基础问题的解开始，不断迭代组合、选择子问题的最优解，最终得到原问题最优解。

---

重叠子问题示例：斐波那契数列

斐波那契数形成的数列为 [0, 1, 1, 2, 3, 5, 8, 13, \cdots] ，数学定义如下：

\begin{aligned}
& F_0 = 0 \\
& F_1 = 1 \\
& F_n = F_{n-1} + F_{n-2}
\end{aligned}

题目： 求取第 n 个斐波那契数（从第 0 个斐波那契数开始）。

以下，本文从「暴力递归」$\rightarrow$「记忆化递归」$\rightarrow$「动态规划」三种解法，介绍重叠子问题的概念与解决方案。

方法一：暴力递归

设斐波那契数列第 n 个数字为 f(n) 。根据数列定义，可得 f(n) = f(n - 1) + f(n - 2) ，且第 0 , 1 个斐波那契数分别为 f(0) = 0 , f(1) = 1 。

我们很容易联想到使用分治思想来求取 f(n) ，即将求原问题 f(n) 分解为求子问题 f(n-1) 和 f(n-2) ，向下递归直至已知的 f(0) 和 f(1) ，最终组合这些子问题求取原问题 f(n) 。

# 求第 n 个斐波那契数
def fibonacci(n):
    if n == 0: return 0 # 返回 f(0)
    if n == 1: return 1 # 返回 f(1)
    return fibonacci(n - 1) + fibonacci(n - 2) # 分解为两个子问题求解

// 求第 n 个斐波那契数
int fibonacci(int n) {
    if (n == 0) return 0; // 返回 f(0)
    if (n == 1) return 1; // 返回 f(1)
    return fibonacci(n - 1) + fibonacci(n - 2); // 分解为两个子问题求解
}

int fibonacci(int n) {
    if (n == 0) return 0; // 返回 f(0)
    if (n == 1) return 1; // 返回 f(1)
    return fibonacci(n - 1) + fibonacci(n - 2); // 分解为两个子问题求解
}

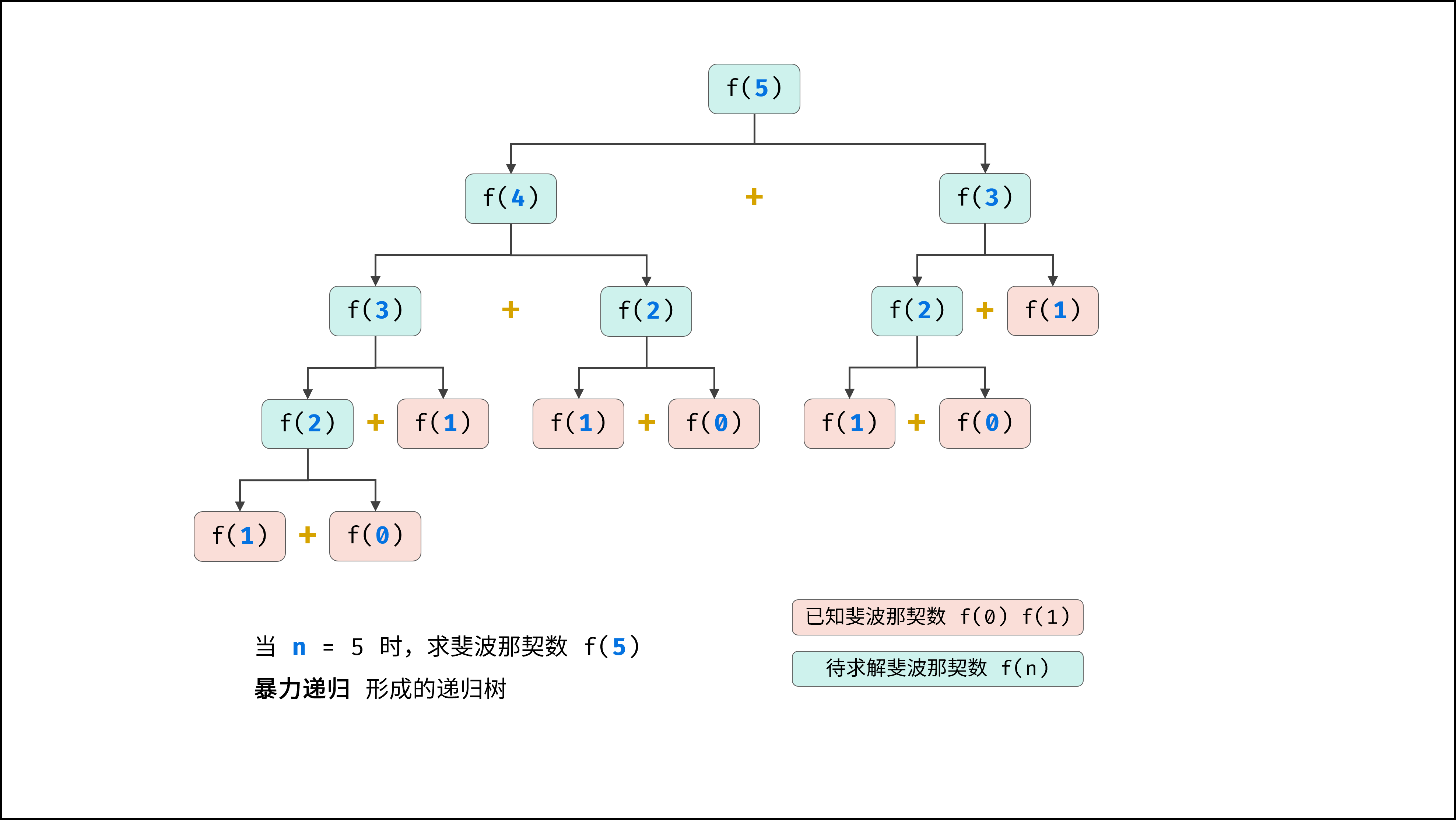
如上图所示，为暴力递归求斐波那契数 f(5) 形成的二叉树，树中的每个节点代表着执行了一次 fibonacci() 函数，且有：

• 执行一次 fibonacci() 函数的时间复杂度为 O(1) ；
• 二叉树节点数为指数级 O(2^n) ；

因此，暴力递归的总体时间复杂度为 O(2^n) 。此方法效率低下，随着 n 的增长产生指数级爆炸。

方法二：记忆化递归

观察发现，暴力递归中的子问题多数都是重叠子问题，即：

\begin{aligned}
& f(n) = f(n - 1) + f(n - 2) & 包含 f(n - 2) \\
& f(n - 1) = f(n - 2) + f(n - 3) & 重复 f(n - 2) \\
& f(n - 2) = f(n - 3) + f(n - 4) & 重复 f(n - 3) \\
& \cdots &以此类推
\end{aligned}

这些重叠子问题产生了大量的递归树节点，其不应被重复计算。实际上，可以在递归中第一次求解子问题时，就将它们保存；后续递归中再次遇到相同子问题时，直接访问内存赋值即可。记忆化递归的代码如下所示。

def fibonacci(n, dp):
    if n == 0: return 0           # 返回 f(0)
    if n == 1: return 1           # 返回 f(1)
    if dp[n] != 0: return dp[n]   # 若 f(n) 以前已经计算过，则直接返回记录的解
    dp[n] = fibonacci(n - 1, dp) + fibonacci(n - 2, dp) # 将 f(n) 则记录至 dp
    return dp[n]

# 求第 n 个斐波那契数
def fibonacci_memorized(n):
    dp = [0] * (n + 1) # 用于保存 f(0) 至 f(n) 问题的解
    return fibonacci(n, dp)

int fibonacci(int n, int[] dp) {
    if (n == 0) return 0;           // 返回 f(0)
    if (n == 1) return 1;           // 返回 f(1)
    if (dp[n] != 0) return dp[n];   // 若 f(n) 以前已经计算过，则直接返回记录的解
    dp[n] = fibonacci(n - 1, dp) + fibonacci(n - 2, dp); // 将 f(n) 则记录至 dp
    return dp[n];
}


// 求第 n 个斐波那契数
int fibonacciMemorized(int n) {
    int[] dp = new int[n + 1]; // 用于保存 f(0) 至 f(n) 问题的解
    return fibonacci(n, dp);
}

int fibonacci(int n, vector<int> dp) {
    if (n == 0) return 0;           // 返回 f(0)
    if (n == 1) return 1;           // 返回 f(1)
    if (dp[n] != 0) return dp[n];   // 若 f(n) 以前已经计算过，则直接返回记录的解
    dp[n] = fibonacci(n - 1, dp) + fibonacci(n - 2, dp); // 将 f(n) 则记录至 dp
    return dp[n];
}


// 求第 n 个斐波那契数
int fibonacciMemorized(int n) {
    vector<int> dp(n + 1, 0); // 用于保存 f(0) 至 f(n) 问题的解
    return fibonacci(n, dp);
}

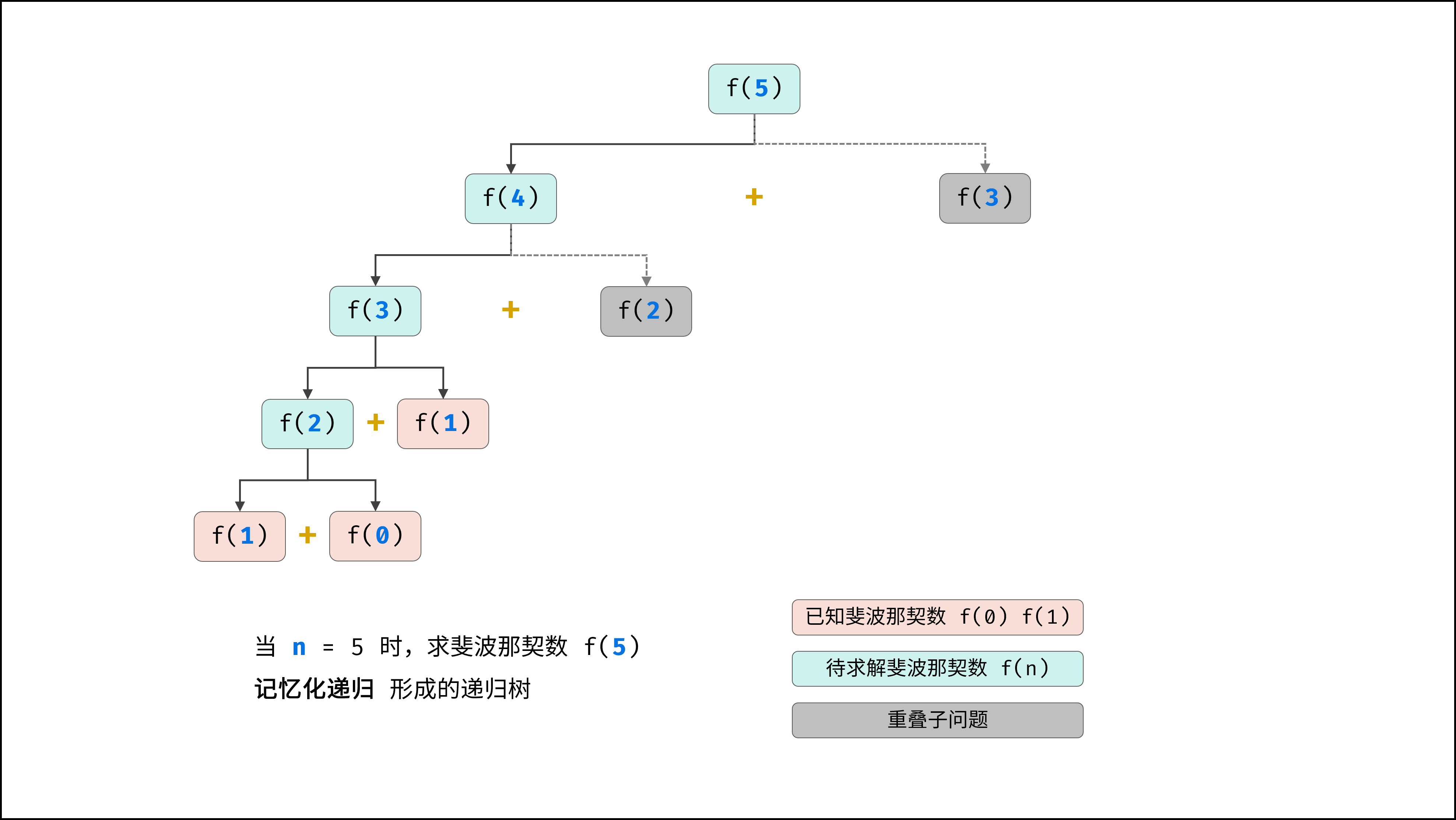
如下图所示，应用记忆化递归方法后，递归树中绝大部分节点被剪枝。此时，fibonacci() 函数的调用次数从 O(2^n) 指数级别降低至 O(n) 线性级别，时间复杂度大大降低。

方法三：动态规划

递归本质上是基于分治思想的从顶至底的解法。借助记忆化递归思想，可应用动态规划从底至顶求取 f(n) ，代码如下所示。

# 求第 n 个斐波那契数
def fibonacci(n):
    if n == 0: return 0       # 若求 f(0) 则直接返回 0
    dp = [0] * (n + 1)        # 初始化 dp 列表
    dp[0], dp[1] = 0, 1       # 初始化 f(0), f(1)
    for i in range(2, n + 1): # 状态转移求取 f(2), f(3), ..., f(n) 
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]              # 返回 f(n)

// 求第 n 个斐波那契数
int fibonacci(int n) {
    if (n == 0) return 0;          // 若求 f(0) 则直接返回 0
    int[] dp = new int[n + 1];     // 初始化 dp 列表
    dp[1] = 1;                     // 初始化 f(0), f(1)
    for (int i = 2; i <= n; i++) { // 状态转移求取 f(2), f(3), ..., f(n) 
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];                  // 返回 f(n)
}

// 求第 n 个斐波那契数
int fibonacci(int n) {
    if (n == 0) return 0;          // 若求 f(0) 则直接返回 0
    vector<int> dp(n + 1, 0);      // 初始化 dp 列表
    dp[1] = 1;                     // 初始化 f(0), f(1)
    for (int i = 2; i <= n; i++) { // 状态转移求取 f(2), f(3), ..., f(n) 
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];                  // 返回 f(n)
}

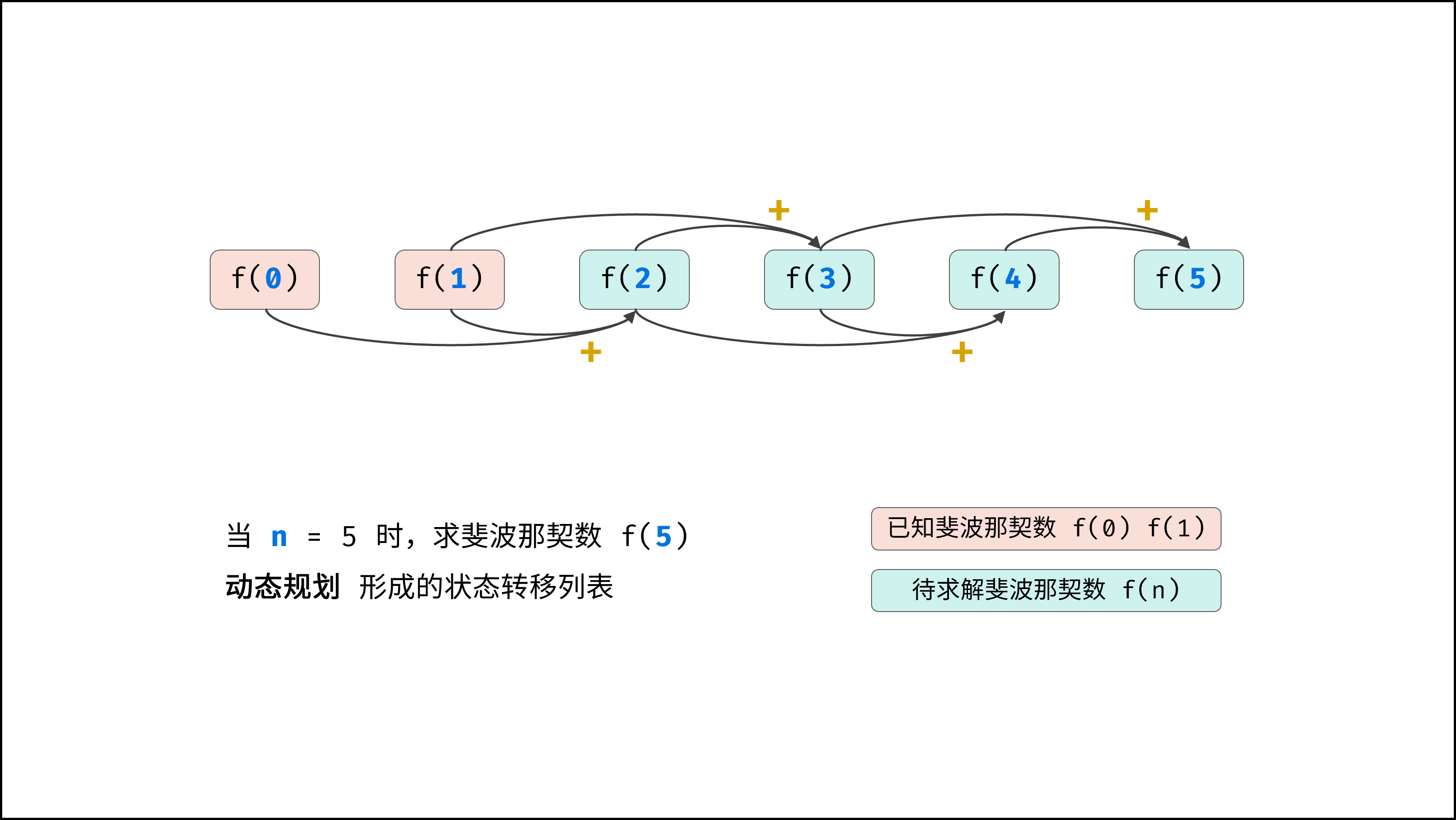
如下图所示，为动态规划求解 f(5) 的迭代流程，其是转移方程 f(n) = f(n - 1) + f(n - 2) 的体现。

上述动态规划解法借助了一个 dp 数组保存子问题的解，其空间复杂度为 O(N) 。而由于 f(n) 只与 f(n - 1) 和 f(n - 2) 有关，因此我们可以仅使用两个变量 a , b 交替前进计算即可。此时动态规划的空间复杂度降低至 O(1) ，代码如下所示。

# 求第 n 个斐波那契数
def fibonacci(n):
    if n == 0: return 0       # 若求 f(0) 则直接返回 0
    a, b = 0, 1               # 初始化 f(0), f(1)
    for i in range(2, n + 1): # 状态转移求取 f(2), f(3), ..., f(n) 
        a, b = b, a + b
    return b                  # 返回 f(n)

// 求第 n 个斐波那契数
int fibonacci(int n) {
    if (n == 0) return 0;           // 若求 f(0) 则直接返回 0
    int a = 0, b = 1;               // 初始化 f(0), f(1)
    for (int i = 2; i <= n; i++) {  // 状态转移求取 f(2), f(3), ..., f(n) 
        int tmp = a;
        a = b;
        b = tmp + b;
    }
    return b;                       // 返回 f(n)
}

// 求第 n 个斐波那契数
int fibonacci(int n) {
    if (n == 0) return 0;           // 若求 f(0) 则直接返回 0
    int a = 0, b = 1;               // 初始化 f(0), f(1)
    for (int i = 2; i <= n; i++) {  // 状态转移求取 f(2), f(3), ..., f(n) 
        int tmp = a;
        a = b;
        b = tmp + b;
    }
    return b;                       // 返回 f(n)
}

示例小结

记忆化递归和动态规划的本质思想是一致的，是对斐波那契数列定义的不同表现形式：

• 记忆化递归 — 从顶至低： 求 f(n) 需要 f(n - 1) 和 f(n - 2) ； \cdots ；求 f(2) 需要 f(1) 和 f(0) ；而 f(1) 和 f(0) 已知；
• 动态规划 — 从底至顶： 将已知 f(0) 和 f(1) 组合得到 f(2) ；\cdots ；将 f(n - 2) 和 f(n - 1) 组合得到 f(n) ；

斐波那契数列问题不包含「最优子结构」，只需计算每个子问题的解，避免重复计算即可，并不需要从子问题组合中选择最优组合。接下来，本文借助「最高蛋糕售价方案」，介绍动态规划的最优子结构概念。

---

最优子结构示例：蛋糕最高售价

小力开了一家蛋糕店，并针对不同重量的蛋糕设定了不同售价，分别为：

蛋糕重量	0	1	2	3	4	5	6
售价	0	2	3	6	7	11	15

问题： 现给定一个重量为 n 的蛋糕，问小力应该如何切分蛋糕，达到最高的蛋糕总售价。

设重量为 n 蛋糕的售价为 p(n) ，切分的最高总售价为 f(n) 。

• 子问题： f(n) 的子问题包括 f(0), f(1), f(2), \cdots, f(n - 1) ，分别代表重量为 0, 1, 2, \cdots, n - 1 蛋糕的最高售价。 已知无蛋糕时 f(0) = 0 ，蛋糕重量为 1 时不可切分 f(1) = p(1) ；

• 最优子结构：

  • 定义： 如果一个问题最优解可以由其子问题最优解组合构成，那么称此问题具有最优子结构。
  • 对于本题： 重量为 n 的蛋糕的总售价可切分为 n 种组合，即重量为 0, 1, 2, ..., n - 1 蛋糕最高售价加上 n, n - 1, n - 2, \cdots, 1 剩余重量蛋糕的售价；从这些组合中，售价最高的组合便是原问题的解 f(n) ，这便是本题的最优子结构。

• 状态转移方程： 找出最优子结构后，易构建出如下的状态转移方程。

f(n) = \max_{0 \leq i < n} (f(i) + p(n - i))

根据以上推导，本题也能使用「暴力递归」$\rightarrow$「记忆化递归」$\rightarrow$「动态规划」三种方法解决。

方法一：暴力递归

暴力递归解法的代码如下，其时间复杂度为指数级 O(2^n) 。

# 输入蛋糕价格列表 price_list ，求重量为 n 蛋糕的最高售价
def max_cake_price(n, price_list):
    if n <= 1: return price_list[n] # 蛋糕重量 <= 1 时直接返回
    f_n = 0
    for i in range(n):  # 从 n 种组合种选择最高售价的组合作为 f(n)
        f_n = max(f_n, max_cake_price(i, price_list) + price_list[n - i])
    return f_n          # 返回 f(n)

max_cake_price(4, [0, 2, 3, 6, 7, 11, 15])

// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, int[] priceList) {
    if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
    int f_n = 0;
    for (int i = 0; i < n; i++)      // 从 n 种组合种选择最高售价的组合作为 f(n)
        f_n = Math.max(f_n, maxCakePrice(i, priceList) + priceList[n - i]);
    return f_n;                      // 返回 f(n)
}

// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, vector<int> priceList) {
    if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
    int f_n = 0;
    for (int i = 0; i < n; i++)      // 从 n 种组合种选择最高售价的组合作为 f(n)
        f_n = max(f_n, maxCakePrice(i, priceList) + priceList[n - i]);
    return f_n;                      // 返回 f(n)
}

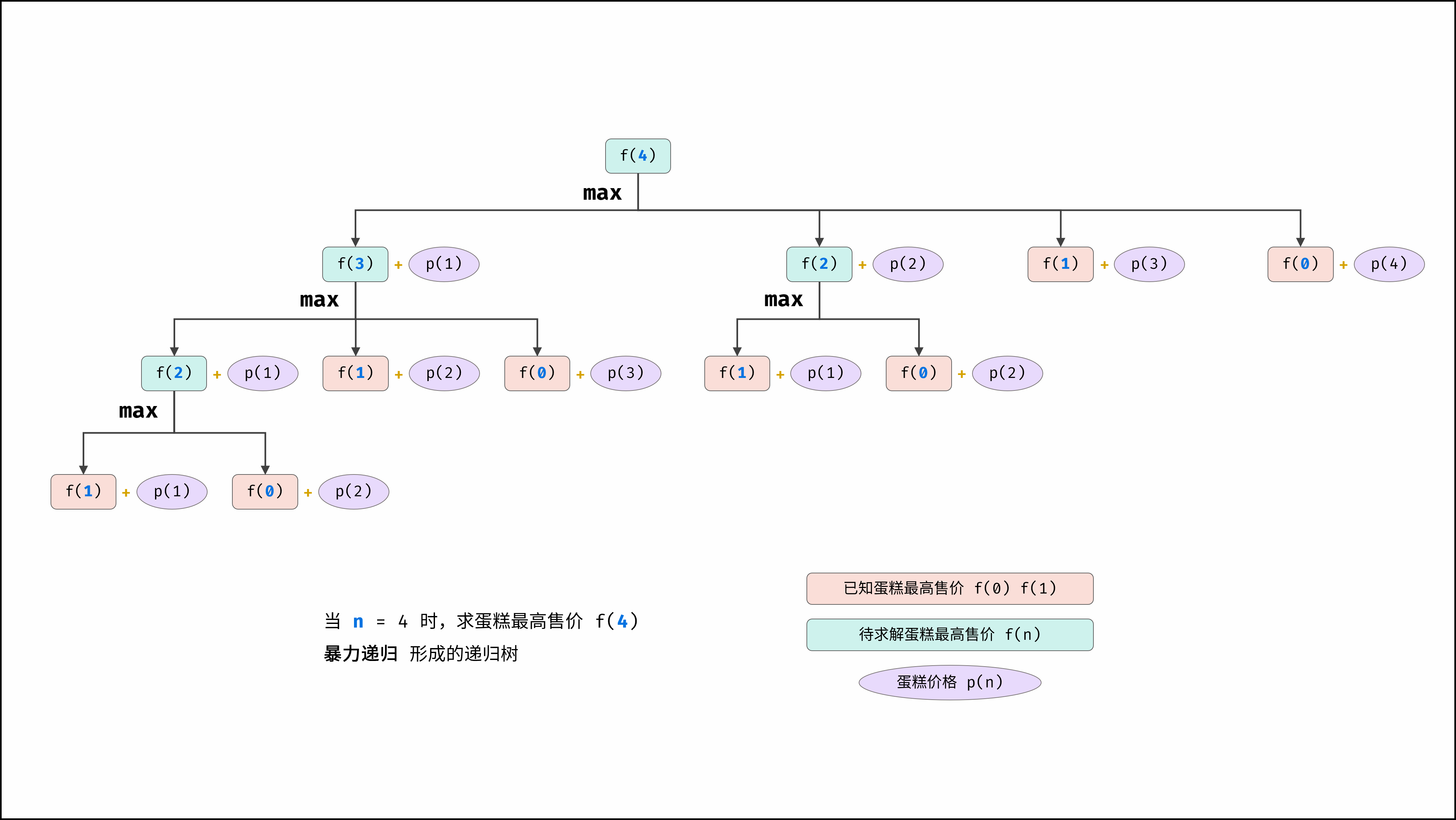
如下图所示，为暴力递归求解 f(4) 形成的多叉树。

方法二：记忆化递归

观察发现，递归树中存在大量重叠子问题，可通过记忆化处理避免重复计算。记忆化递归的算法的时间复杂度为 O(n^2) ，包括：

• f(2) 至 f(n) 共 n - 1 个待计算子问题，使用 O(n) 时间；
• 计算某 f(i) 需遍历 i - 1 种子问题组合，使用 O(n) 时间；

# 输入蛋糕价格列表 price_list ，求重量为 n 蛋糕的最高售价
def max_cake_price(n, price_list, dp):
    if n <= 1: return price_list[n] # 蛋糕重量 <= 1 时直接返回
    f_n = 0
    for i in range(n):  # 从 n 种组合种选择最高售价的组合作为 f(n)
        # 若 f(i) 以前已经计算过，则调取记录的解；否则，递归计算 f(i)
        f_i = dp[i] if dp[i] != 0 else max_cake_price(i, price_list, dp)
        f_n = max(f_n, f_i + price_list[n - i])
    dp[n] = f_n         # 记录 f(n) 至 dp 数组
    return f_n          # 返回 f(n)

def max_cake_price_memorized(n, price_list):
    dp = [0] * (n + 1)
    return max_cake_price(n, price_list, dp)

// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, int[] priceList, int[] dp) {
    if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
    int f_n = 0;
    for (int i = 0; i < n; i++) {    // 从 n 种组合种选择最高售价的组合作为 f(n)
        int f_i = dp[i] != 0 ? dp[i] : maxCakePrice(i, priceList, dp);
        f_n = Math.max(f_n, f_i + priceList[n - i]);
    }
    dp[n] = f_n;                     // 记录 f(n) 至 dp 数组
    return f_n;                      // 返回 f(n)
}

int maxCakePriceMemorized(int n, int[] priceList) {
    int[] dp = new int[n + 1];
    return maxCakePrice(n, priceList, dp);
}

// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, vector<int> &priceList, vector<int> dp) {
    if (n <= 1) return priceList[n]; // 蛋糕重量 <= 1 时直接返回
    int f_n = 0;
    for (int i = 0; i < n; i++) {    // 从 n 种组合种选择最高售价的组合作为 f(n)
        int f_i = dp[i] != 0 ? dp[i] : maxCakePrice(i, priceList, dp);
        f_n = max(f_n, f_i + priceList[n - i]);
    }
    dp[n] = f_n;                     // 记录 f(n) 至 dp 数组
    return f_n;                      // 返回 f(n)
}

int maxCakePriceMemorized(int n, vector<int> priceList) {
    vector<int> dp(n + 1, 0);
    return maxCakePrice(n, priceList, dp);
}

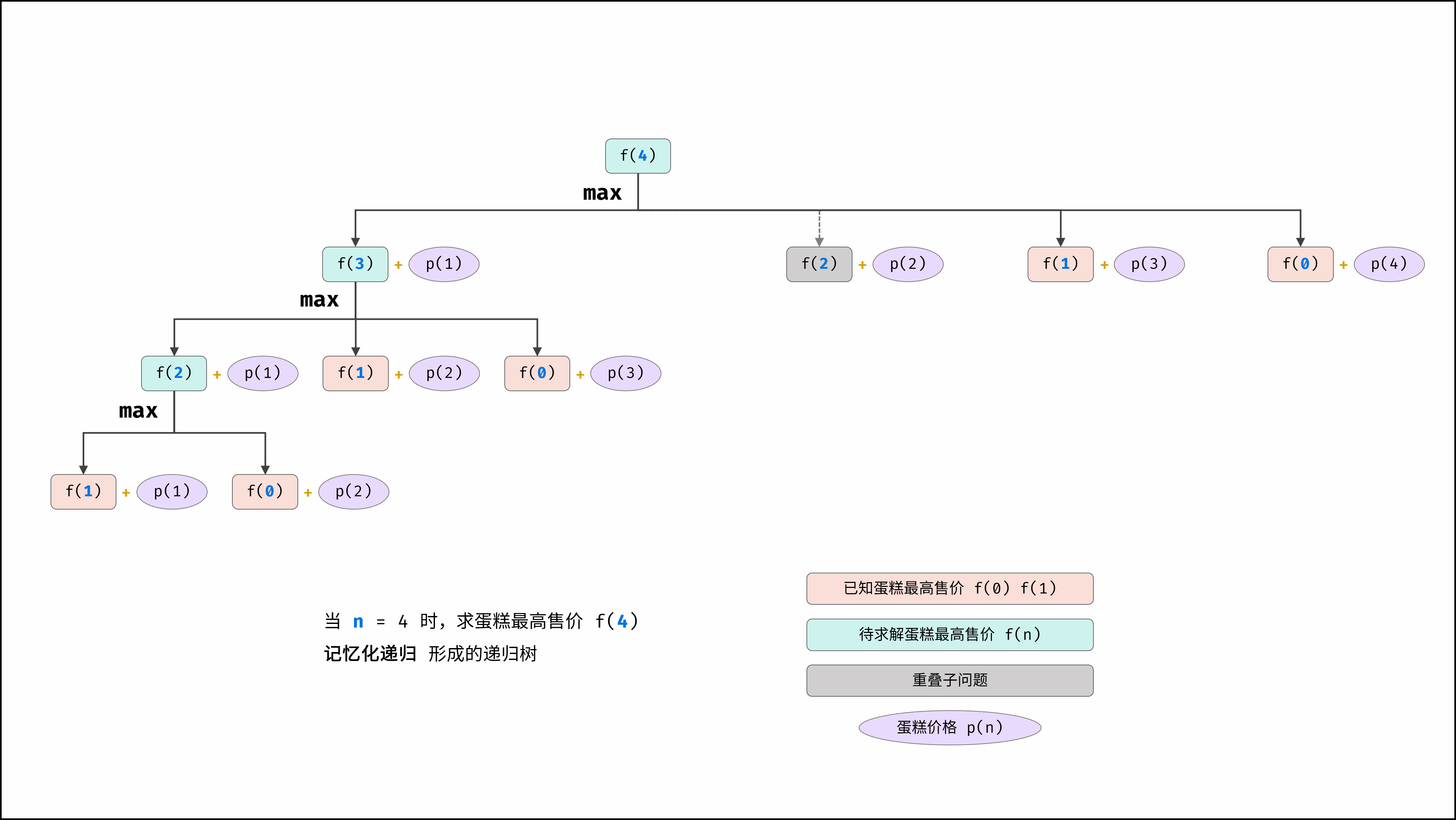
如下图所示，为记忆化递归求解 f(4) 形成的多叉树。观察得知，重叠子问题皆被剪枝。

方法三：动态规划

相较于记忆化递归的从顶至底方法，易得动态规划的从底至顶方法，代码如下所示。

# 输入蛋糕价格列表 price_list ，求重量为 n 蛋糕的最高售价
def max_cake_price(n, price_list):
    if n <= 1: return price_list[n] # 蛋糕重量 <= 1 时直接返回
    dp = [0] * (n + 1)              # 初始化 dp 列表
    for j in range(1, n + 1):       # 按顺序计算 f(1), f(2), ..., f(n)
        for i in range(j):          # 从 j 种组合种选择最高售价的组合作为 f(j)
            dp[j] = max(dp[j], dp[i] + price_list[j - i])
    return dp[n]

// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, int[] priceList) {
    if (n <= 1) return priceList[n];  // 蛋糕重量 <= 1 时直接返回
    int[] dp = new int[n + 1];        // 初始化 dp 列表
    for (int j = 1; j <= n; j++) {    // 按顺序计算 f(1), f(2), ..., f(n)
        for (int i = 0; i < j; i++)   // 从 j 种组合种选择最高售价的组合作为 f(j)
            dp[j] = Math.max(dp[j], dp[i] + priceList[j - i]);
    }
    return dp[n];
}

// 输入蛋糕价格列表 priceList ，求重量为 n 蛋糕的最高售价
int maxCakePrice(int n, vector<int> priceList) {
    if (n <= 1) return priceList[n];  // 蛋糕重量 <= 1 时直接返回
    vector<int> dp(n + 1, 0);         // 初始化 dp 列表
    for (int j = 1; j <= n; j++) {    // 按顺序计算 f(1), f(2), ..., f(n)
        for (int i = 0; i < j; i++)   // 从 j 种组合种选择最高售价的组合作为 f(j)
            dp[j] = max(dp[j], dp[i] + priceList[j - i]);
    }
    return dp[n];
}

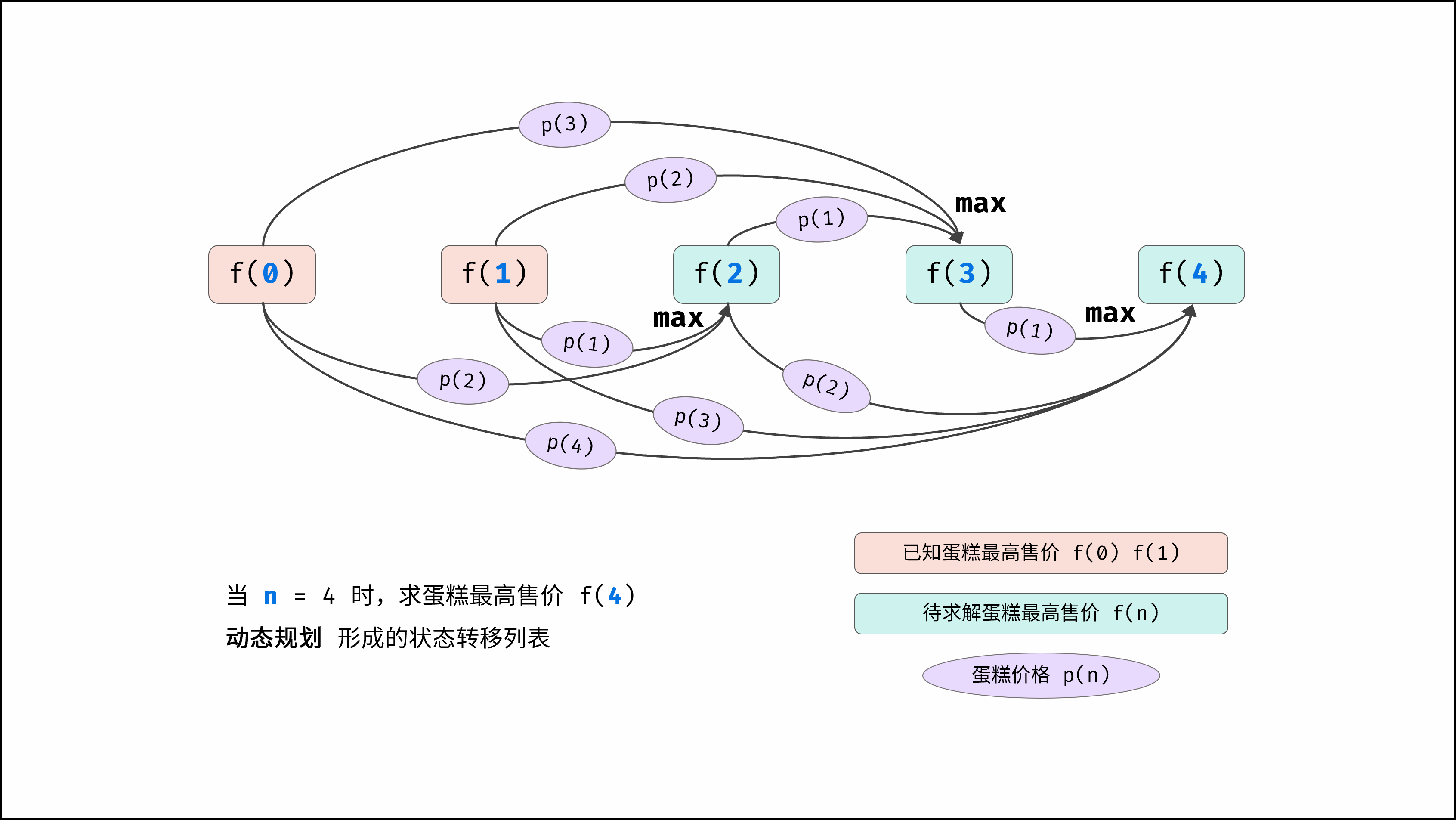
如下图所示，为动态规划求解 f(4) 的迭代流程，其是转移方程 f(n) = \max_{0 \leq i < n} (f(i) + p(n - i)) 的体现。

示例小结

本题同时包含「重叠子问题」和「最优子结构」，为动态规划的典型问题。动态规划通过填表避免了重复计算问题，并通过状态转移方程、初始状态实现对问题的迭代求解。

普遍来看，求最值 的问题一般都具有「重叠子问题」和「最优子结构」特点，因此此类问题往往适合用动态规划解决。

---

动态规划解题框架

若确定给定问题具有重叠子问题和最优子结构，那么就可以使用动态规划求解。总体上看，求解可分为四步：

1. 状态定义： 构建问题最优解模型，包括问题最优解的定义、有哪些计算解的自变量；
2. 初始状态： 确定基础子问题的解（即已知解），原问题和子问题的解都是以基础子问题的解为起始点，在迭代计算中得到的；
3. 转移方程： 确定原问题的解与子问题的解之间的关系是什么，以及使用何种选择规则从子问题最优解组合中选出原问题最优解；
4. 返回值： 确定应返回的问题的解是什么，即动态规划在何处停止迭代；

完成以上步骤后，便容易写出对应的解题代码。

示例：斐波那契数列

• 状态定义：一维 dp 列表，设第 i 个斐波那契数为 dp[i] ；
• 初始状态：已知第 0 , 1 个斐波那契数分别为 dp[0] = 0 , dp[1] = 1 ；
• 转移方程：后一个数字等于前两个数字之和，即

dp[i] = dp[i - 1] + dp[i - 2]

• 返回值：需求取的第 n 个斐波那契数 dp[n] ；

示例：蛋糕最高售价

• 状态定义：一维 dp 列表，设重量为 i 蛋糕的售价为 p(i) ，重量为 i 蛋糕切分后的最高售价为 dp[i] ；
• 初始状态：已知重量为 0 蛋糕的最高售价为 0 ，重量为 1 的蛋糕最高售价为 p(1) ；
• 转移方程：dp[n] 为 n 种切分组合中的最高售价组合，即

dp[n] = \max_{0 \leq i < n} (dp[i] + p(n - i))

• 返回值：需求取的重量为 n 的蛋糕最高售价 dp[n] ；

---

例题练习

动态规划的问题种类多，难度跨度较大，需要充足练习、熟能生巧。以下给出若干典型例题，供读者巩固理解本文内容。

题目	难度	描述
跳跃训练	简单	与本文的斐波那契数列例题等价
连续天数的最高销售额	简单	求最大值问题，关键点在于状态定义
珠宝的最高价值	简单	求最大值问题，特点是其 dp 列表是二维的
统计结果概率	中等	容易想到暴力枚举方法，难点为列出状态转移方程，且正向递推方法比较 tricky
模糊搜索验证	困难	状态定义容易得出，但状态转移方程复杂、选择规则分支多