LeetCode-Book/leetbook_ioa/docs/# 7.4 归并排序.md

归并排序

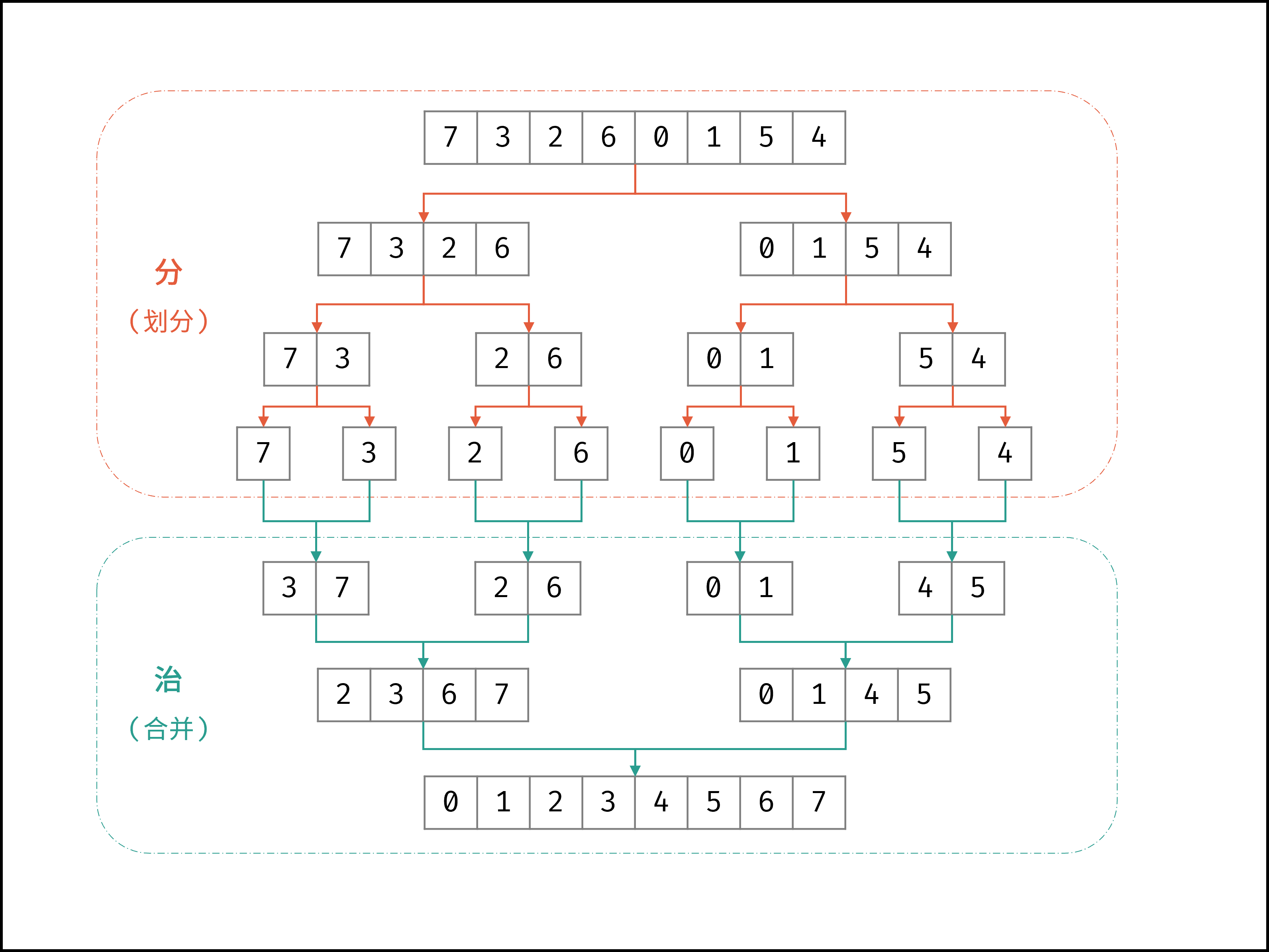
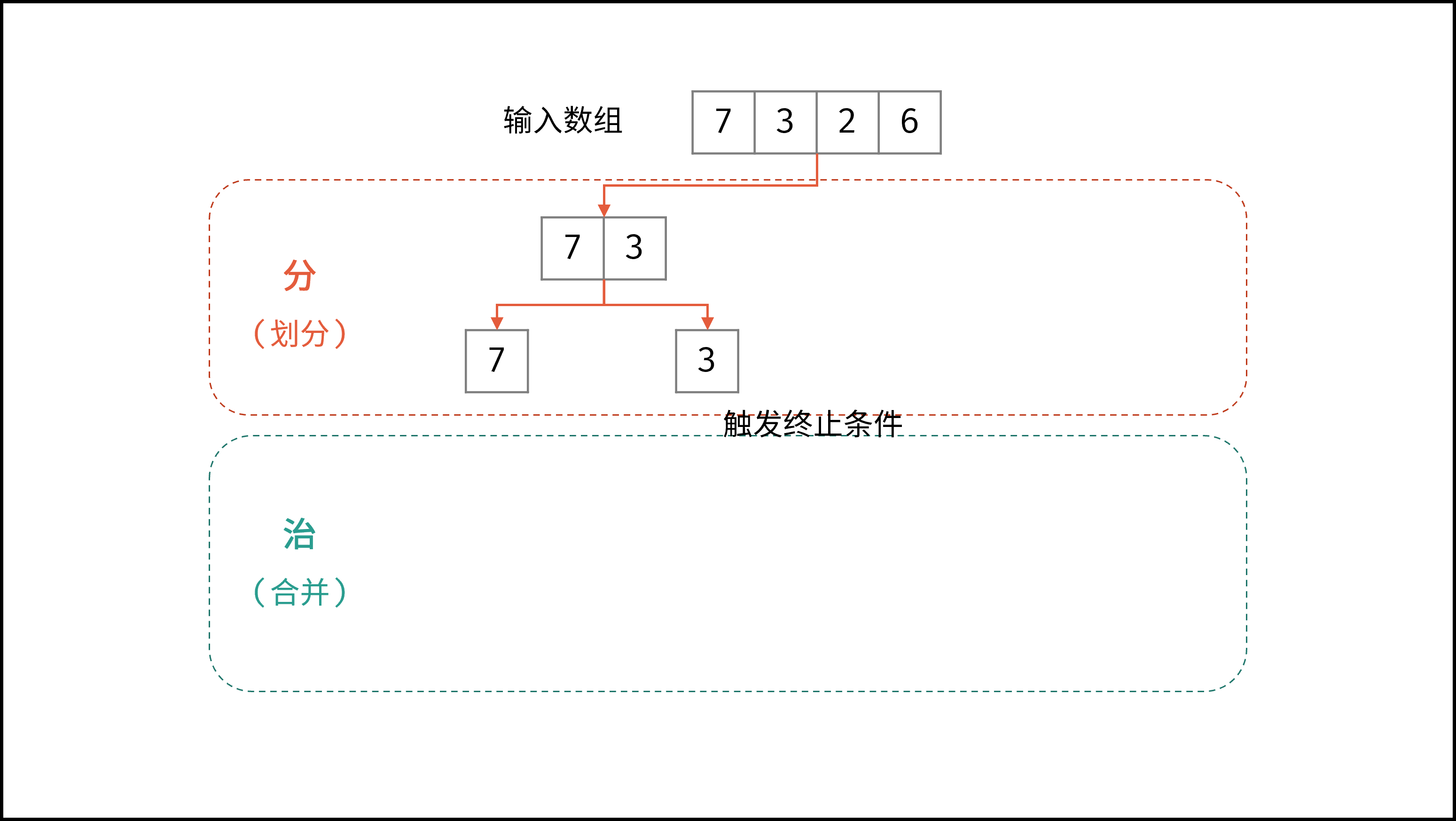
归并排序体现了 “分而治之” 的算法思想，具体为：

• 「分」： 不断将数组从 中点位置 划分开，将原数组的排序问题转化为子数组的排序问题；
• 「治」： 划分到子数组长度为 1 时，开始向上合并，不断将 左右两个较短排序数组 合并为 一个较长排序数组，直至合并至原数组时完成排序；

如下图所示，为数组 [7,3,2,6,0,1,5,4] 的归并排序过程。

{:width=500}

算法流程

1. 递归划分：

   1. 计算数组中点 m ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r) ；
   2. 当 l \geq r 时，代表子数组长度为 1 或 0 ，此时 终止划分 ，开始合并；

2. 合并子数组：

   1. 暂存数组 nums 闭区间 [l, r] 内的元素至辅助数组 tmp ；
   2. 循环合并： 设置双指针 i , j 分别指向 tmp 的左 / 右子数组的首元素；

      注意： nums 子数组的左边界、中点、右边界分别为 l , m , r ，而辅助数组 tmp 中的对应索引为 0 , m - l , r - l ；

      • 当 i == m - l + 1 时： 代表左子数组已合并完，因此添加右子数组元素 tmp[j] ，并执行 j = j + 1 ；
      • 否则，当 j == r - l + 1 时： 代表右子数组已合并完，因此添加左子数组元素 tmp[i] ，并执行 i = i + 1 ；
      • 否则，当 tmp[i] \leq tmp[j] 时： 添加左子数组元素 tmp[i] ，并执行 i = i + 1 ；
      • 否则（即当 tmp[i] > tmp[j] 时）： 添加右子数组元素 tmp[j] ，并执行 j = j + 1 ；

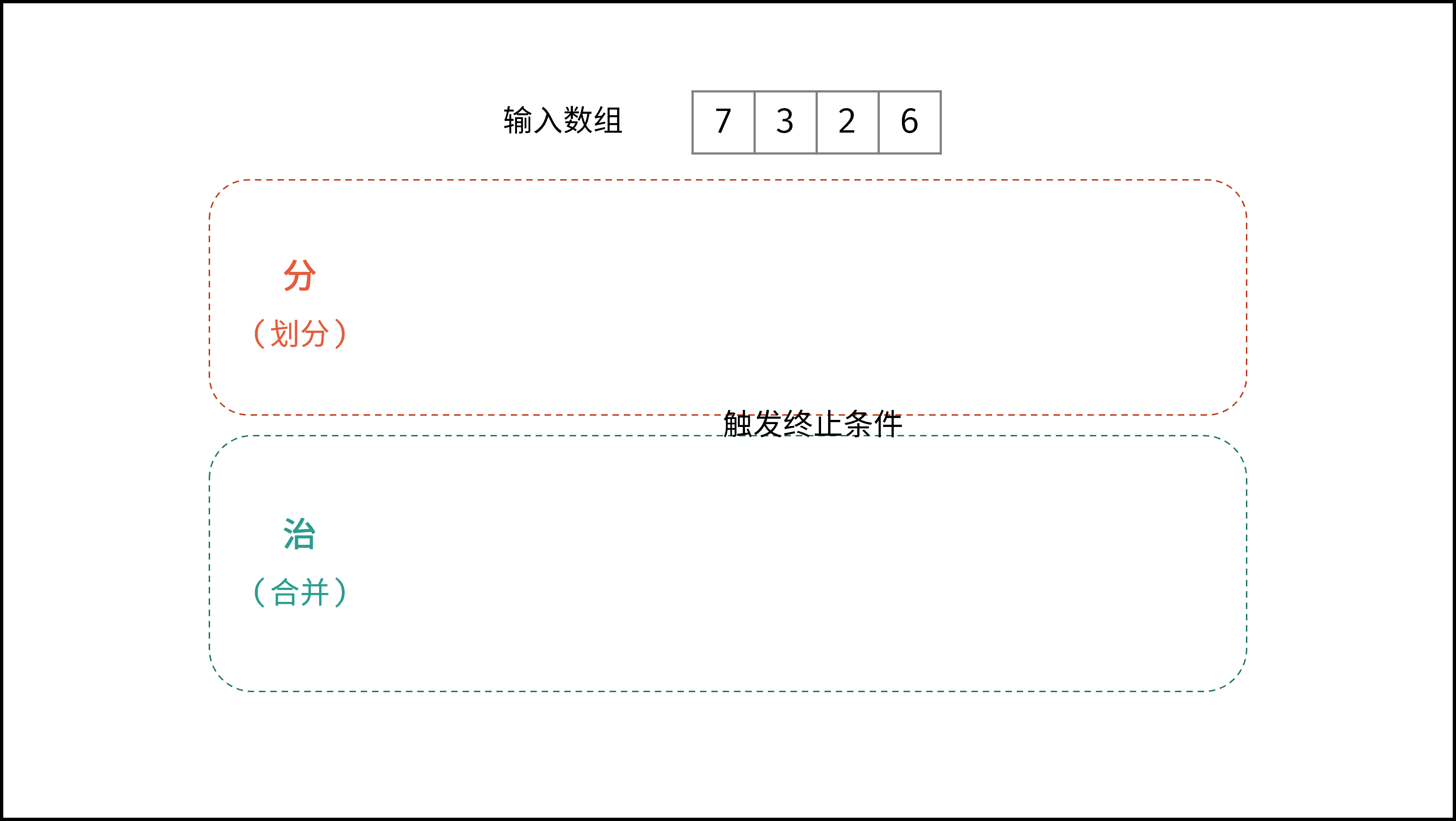
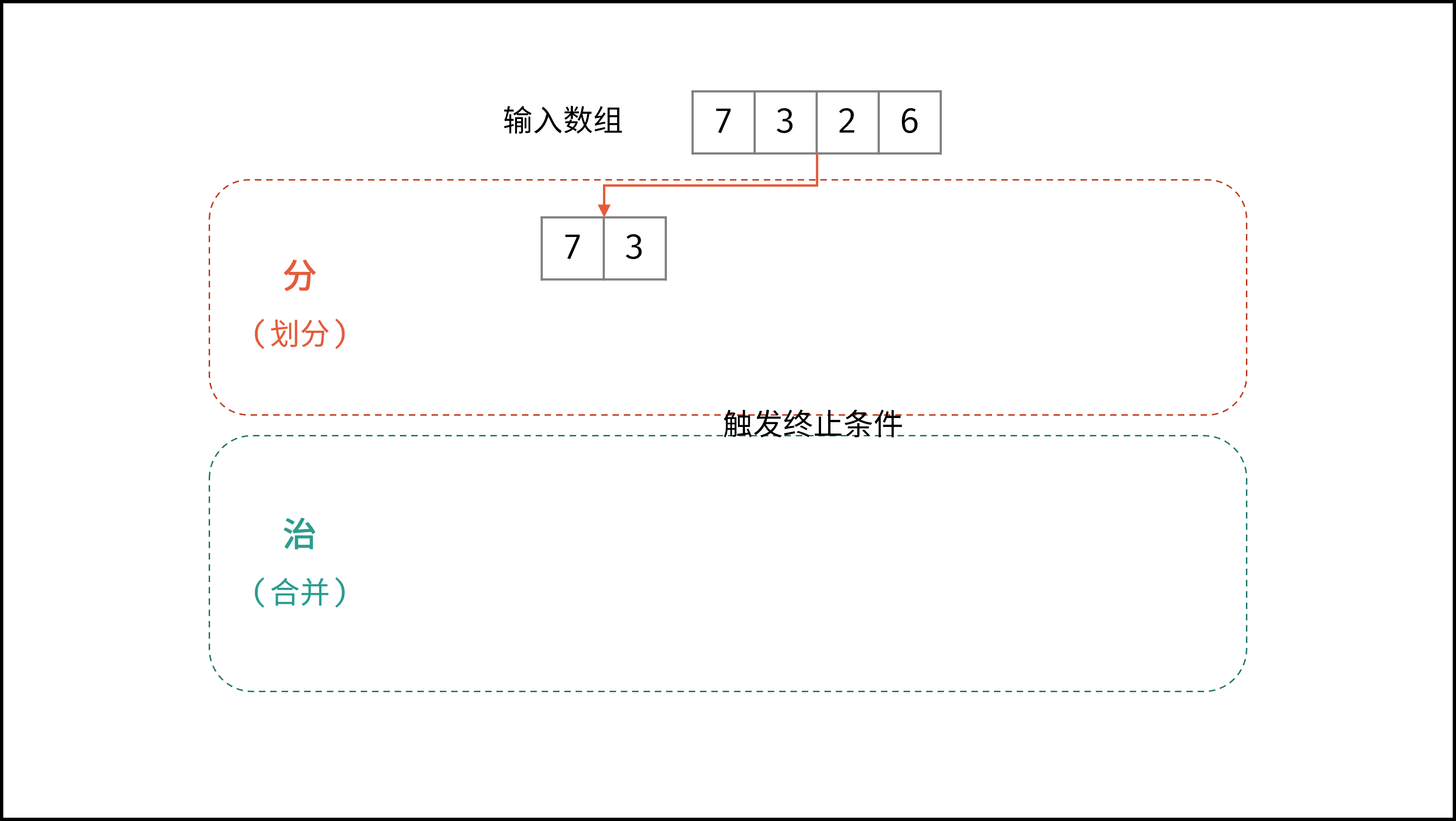
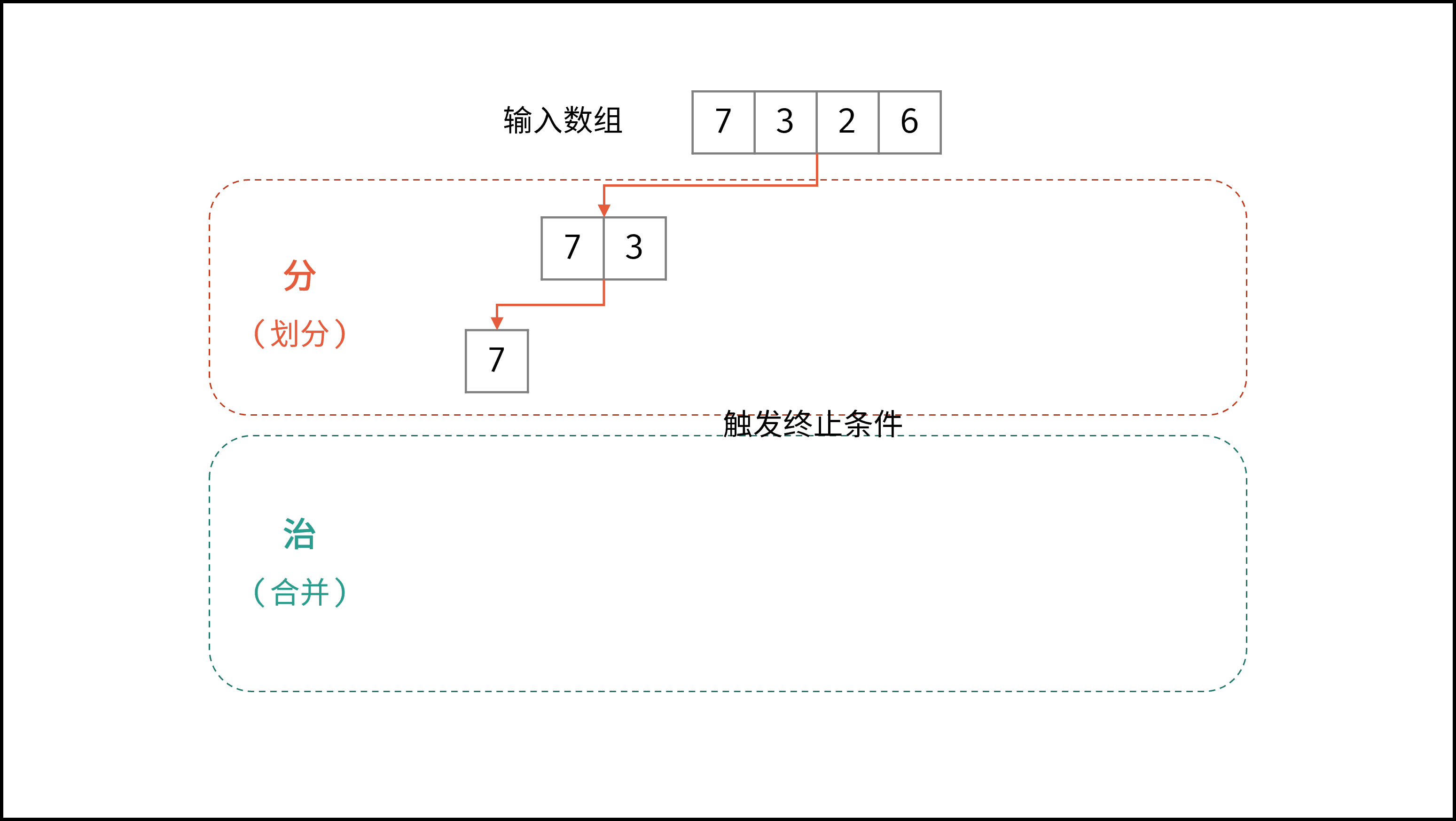
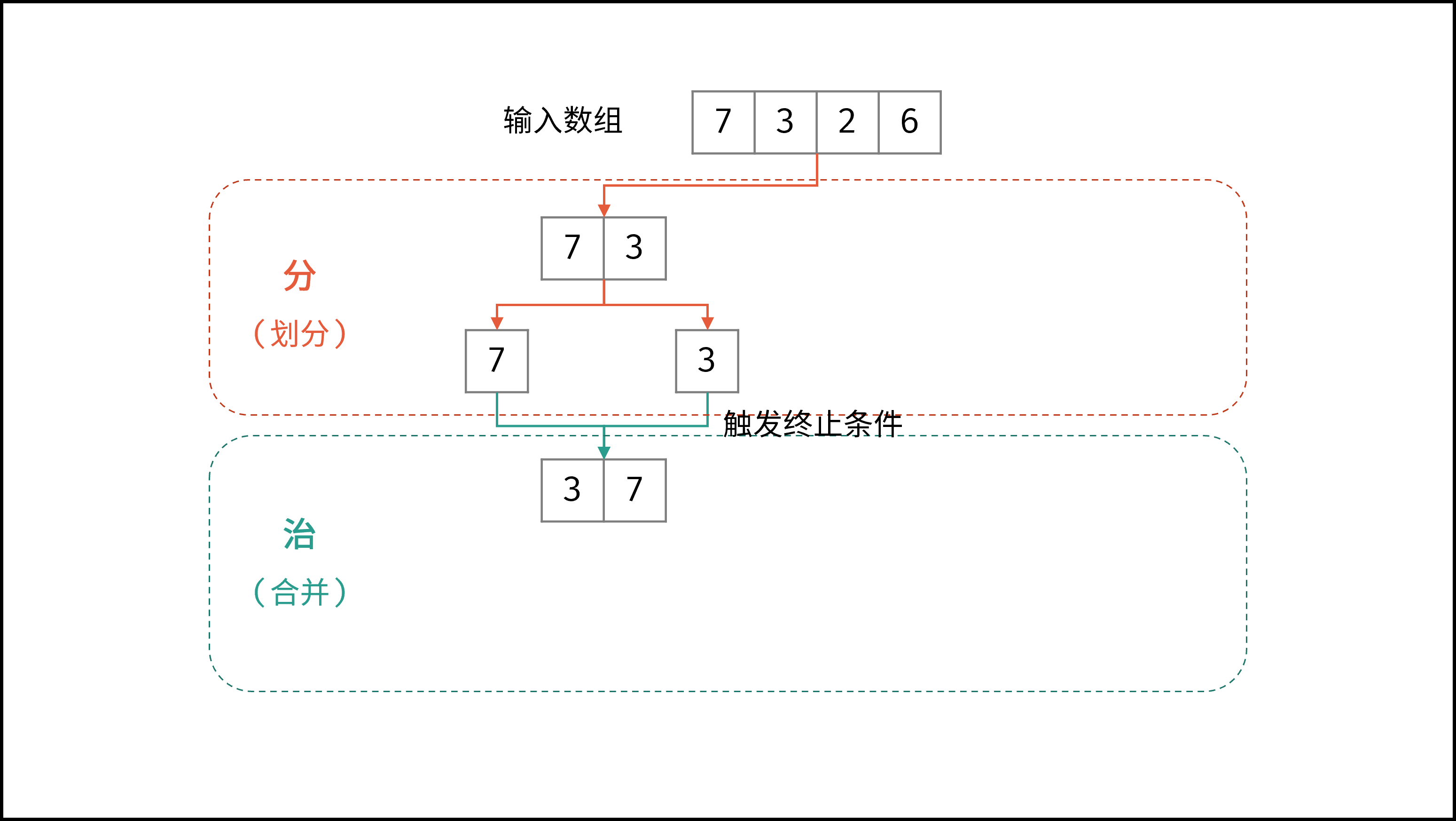
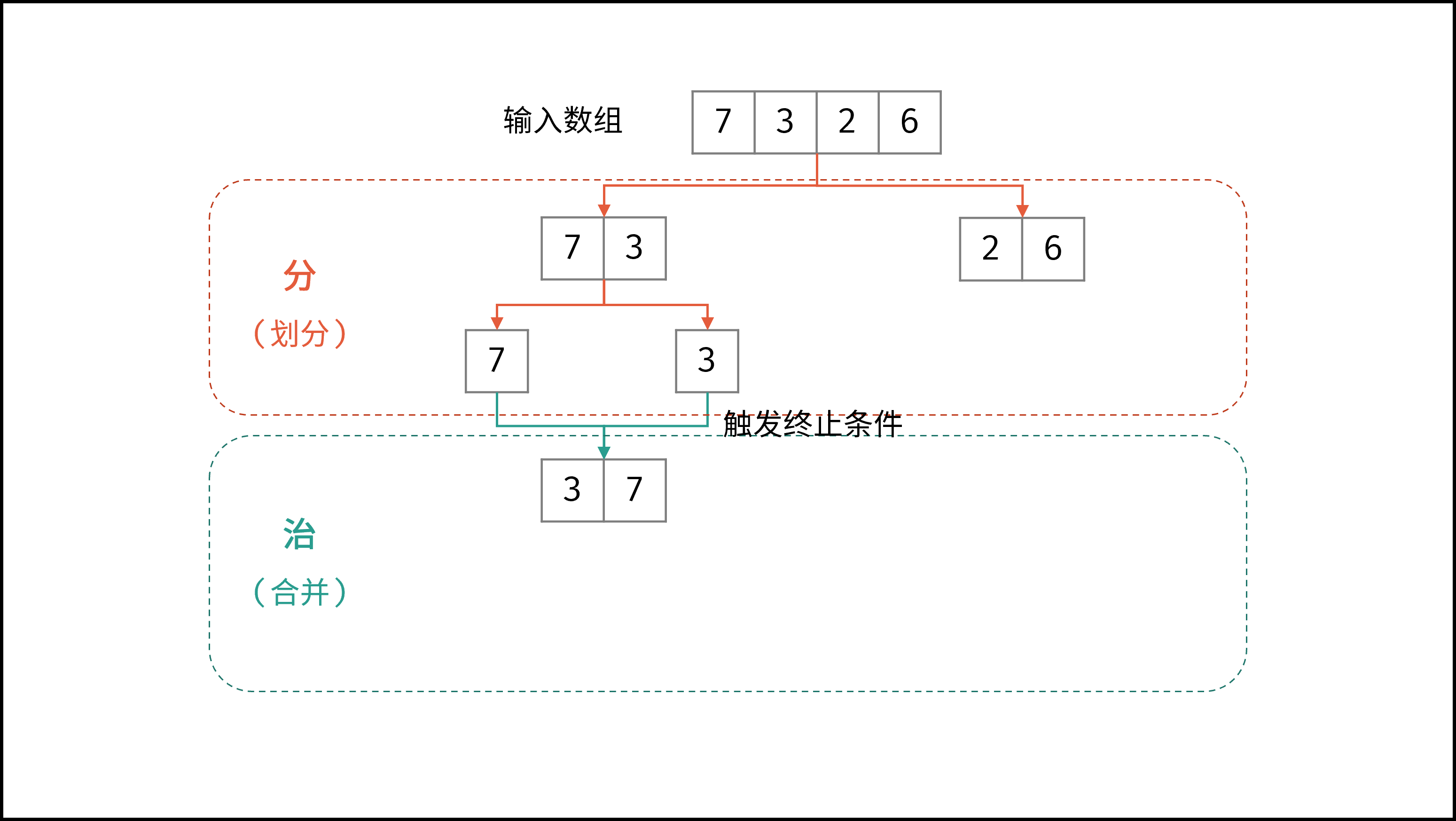
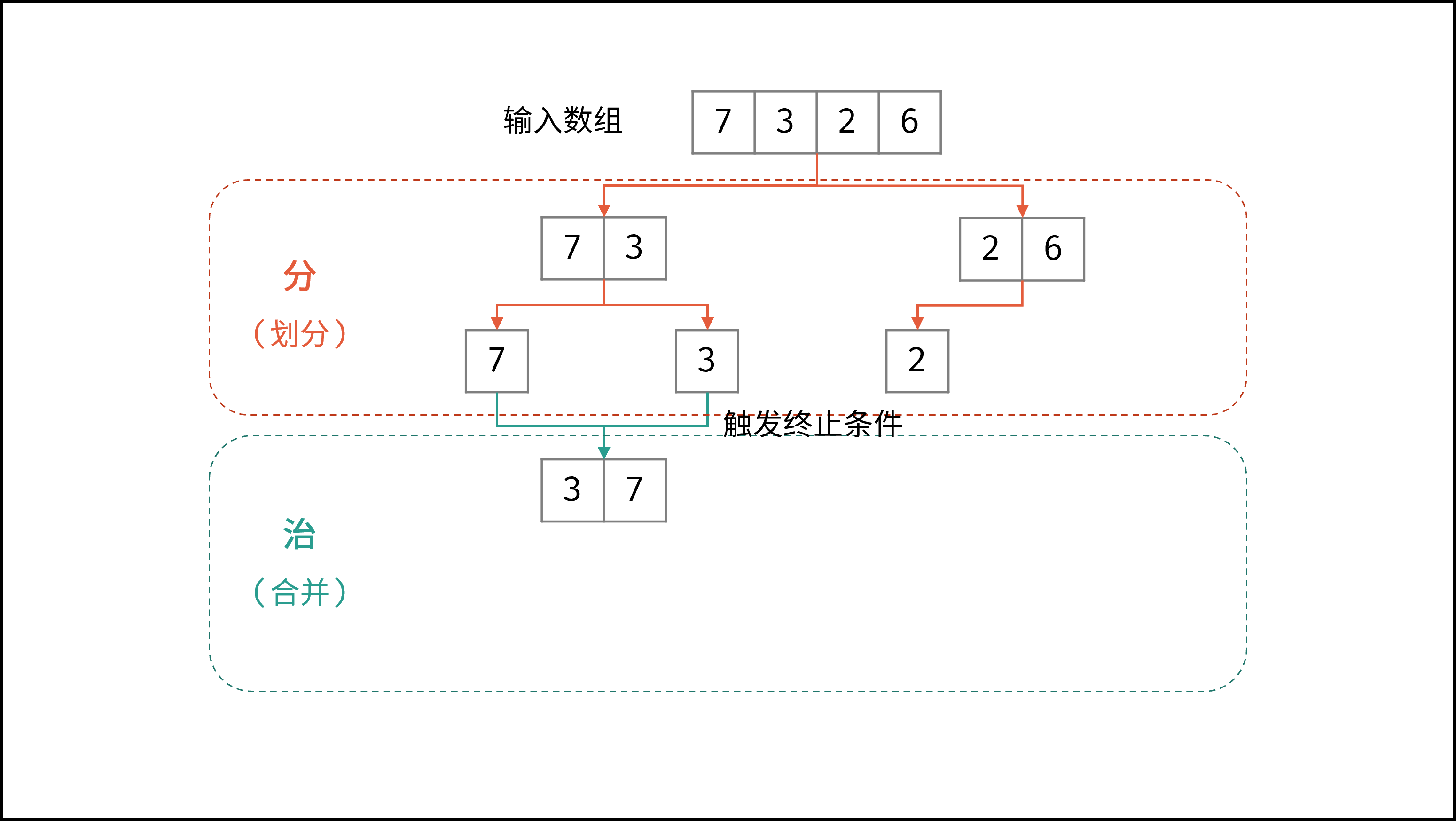
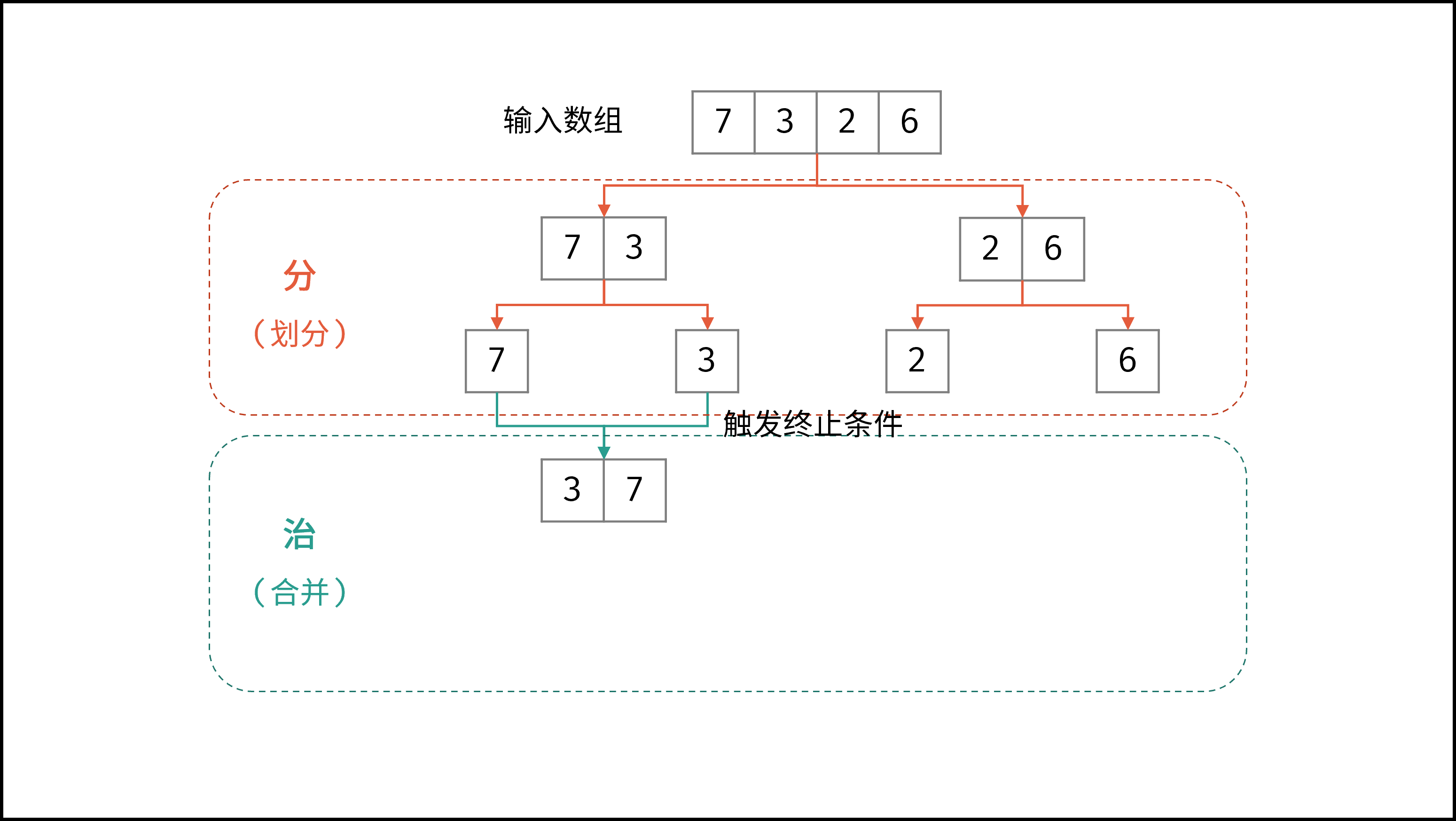
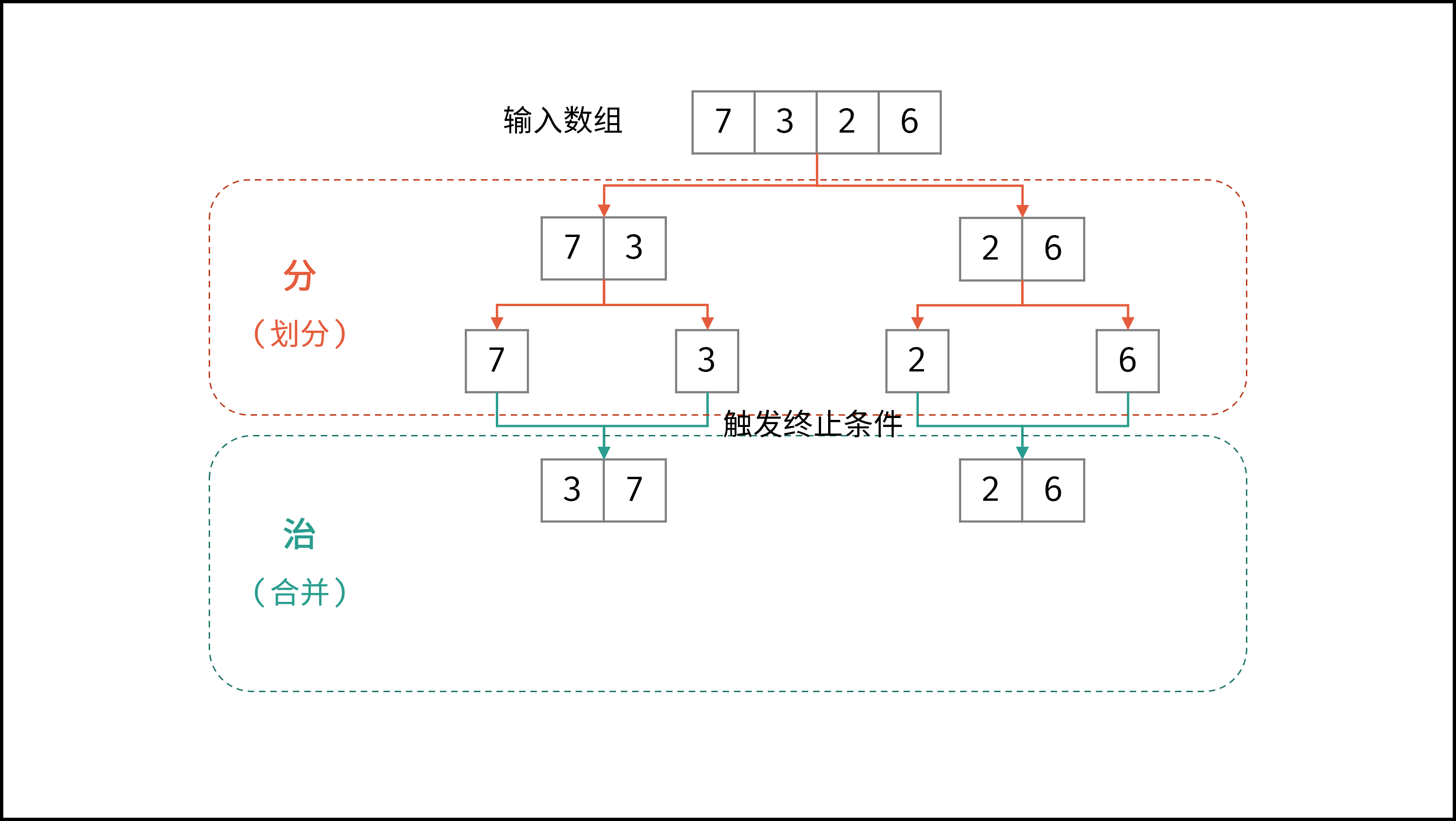
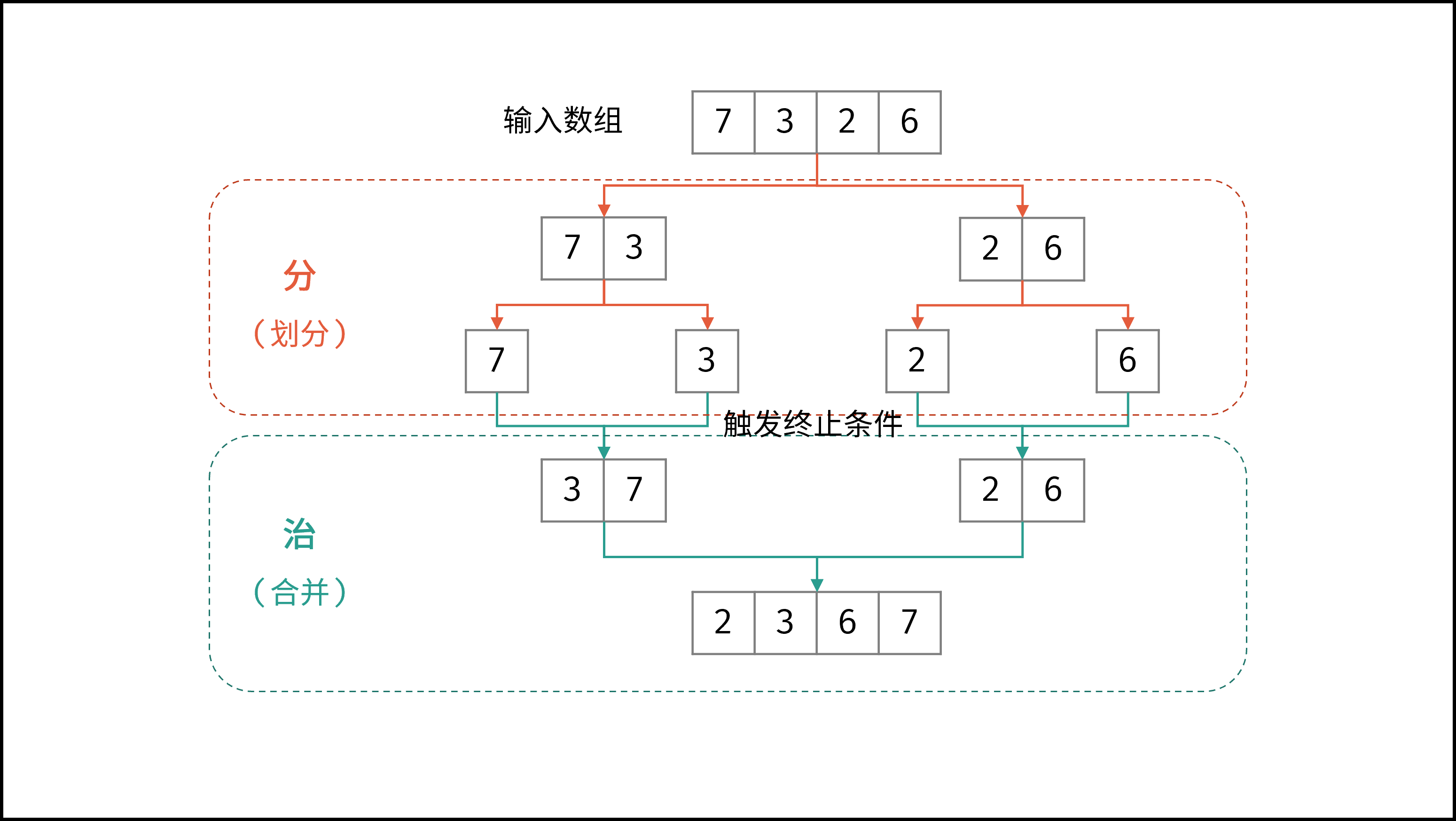
如下动图所示，为数组 [7,3,2,6] 的归并排序过程。

<,,,,,,,,,>

代码

为简化代码，「当 j = r + 1 时」 与 「当 tmp[i] \leq tmp[j] 时」 两判断项可合并。

def merge_sort(nums, l, r):
    # 终止条件
    if l >= r: return
    # 递归划分数组
    m = (l + r) // 2
    merge_sort(nums, l, m)
    merge_sort(nums, m + 1, r)
    # 合并子数组
    tmp = nums[l:r + 1]       # 暂存需合并区间元素
    i, j = 0, m - l + 1       # 两指针分别指向左/右子数组的首个元素
    for k in range(l, r + 1): # 遍历合并左/右子数组
        if i == m - l + 1:
            nums[k] = tmp[j]
            j += 1
        elif j == r - l + 1 or tmp[i] <= tmp[j]:
            nums[k] = tmp[i]
            i += 1
        else:
            nums[k] = tmp[j]
            j += 1

# 调用
nums = [3, 4, 1, 5, 2, 1]
merge_sort(0, len(nums) - 1)

void mergeSort(int[] nums, int l, int r) {
    // 终止条件
    if (l >= r) return;
    // 递归划分
    int m = (l + r) / 2;
    mergeSort(nums, l, m);
    mergeSort(nums, m + 1, r);
    // 合并子数组
    int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
    for (int k = l; k <= r; k++)
        tmp[k - l] = nums[k];
    int i = 0, j = m - l + 1;       // 两指针分别指向左/右子数组的首个元素
    for (int k = l; k <= r; k++) {  // 遍历合并左/右子数组
        if (i == m - l + 1)
            nums[k] = tmp[j++];
        else if (j == r - l + 1 || tmp[i] <= tmp[j])
            nums[k] = tmp[i++];
        else {
            nums[k] = tmp[j++];
        }
    }
}

// 调用
int[] nums = { 3, 4, 1, 5, 2, 1 };
mergeSort(nums, 0, len(nums) - 1);

void mergeSort(vector<int>& nums, int l, int r) {
    // 终止条件
    if (l >= r) return;
    // 递归划分
    int m = (l + r) / 2;
    mergeSort(nums, l, m);
    mergeSort(nums, m + 1, r);
    // 合并阶段
    int tmp[r - l + 1];             // 暂存需合并区间元素
    for (int k = l; k <= r; k++)
        tmp[k - l] = nums[k];
    int i = 0, j = m - l + 1;       // 两指针分别指向左/右子数组的首个元素
    for (int k = l; k <= r; k++) {  // 遍历合并左/右子数组
        if (i == m - l + 1)
            nums[k] = tmp[j++];
        else if (j == r - l + 1 || tmp[i] <= tmp[j])
            nums[k] = tmp[i++];
        else {
            nums[k] = tmp[j++];
        }
    }
}

// 调用
vector<int> nums = { 4, 1, 3, 2, 5, 1 };
mergeSort(nums, 0, nums.size() - 1);

算法特性

• 时间复杂度： 最佳 \Omega(N \log N ) ，平均 \Theta(N \log N) ，最差 O(N \log N) 。
• 空间复杂度 O(N) ： 合并过程中需要借助辅助数组 tmp ，使用 O(N) 大小的额外空间；划分的递归深度为 \log N ，使用 O(\log N) 大小的栈帧空间。
• 若输入数据是 链表 ，则归并排序的空间复杂度可被优化至 O(1) ，这是因为：
  • 通过应用「双指针法」，可在 O(1) 空间下完成两个排序链表的合并，省去辅助数组 tmp 使用的额外空间；
  • 通过使用「迭代」代替「递归划分」，可省去递归使用的栈帧空间；

  详情请参考：148. 排序链表

• 非原地： 辅助数组 tmp 需要使用额外空间。
• 稳定： 归并排序不改变相等元素的相对顺序。
• 非自适应： 对于任意输入数据，归并排序的时间复杂度皆相同。