LeetCode-Book/leetbook_ioa/docs/LCR 132. 砍竹子 II.md

解题思路：

切分规则的推导流程请见上一题「砍竹子 I」。

切分规则：

1. 最优： 3 。把竹子尽可能切为多个长度为 3 的片段，留下的最后一段竹子的长度可能为 0,1,2 三种情况。
2. 次优： 2 。若最后一段竹子长度为 2 ；则保留，不再拆为 1+1 。
3. 最差： 1 。若最后一段竹子长度为 1 ；则应把一份 3 + 1 替换为 $2 + 2$，因为 $2 \times 2 > 3 \times 1$。

算法流程：

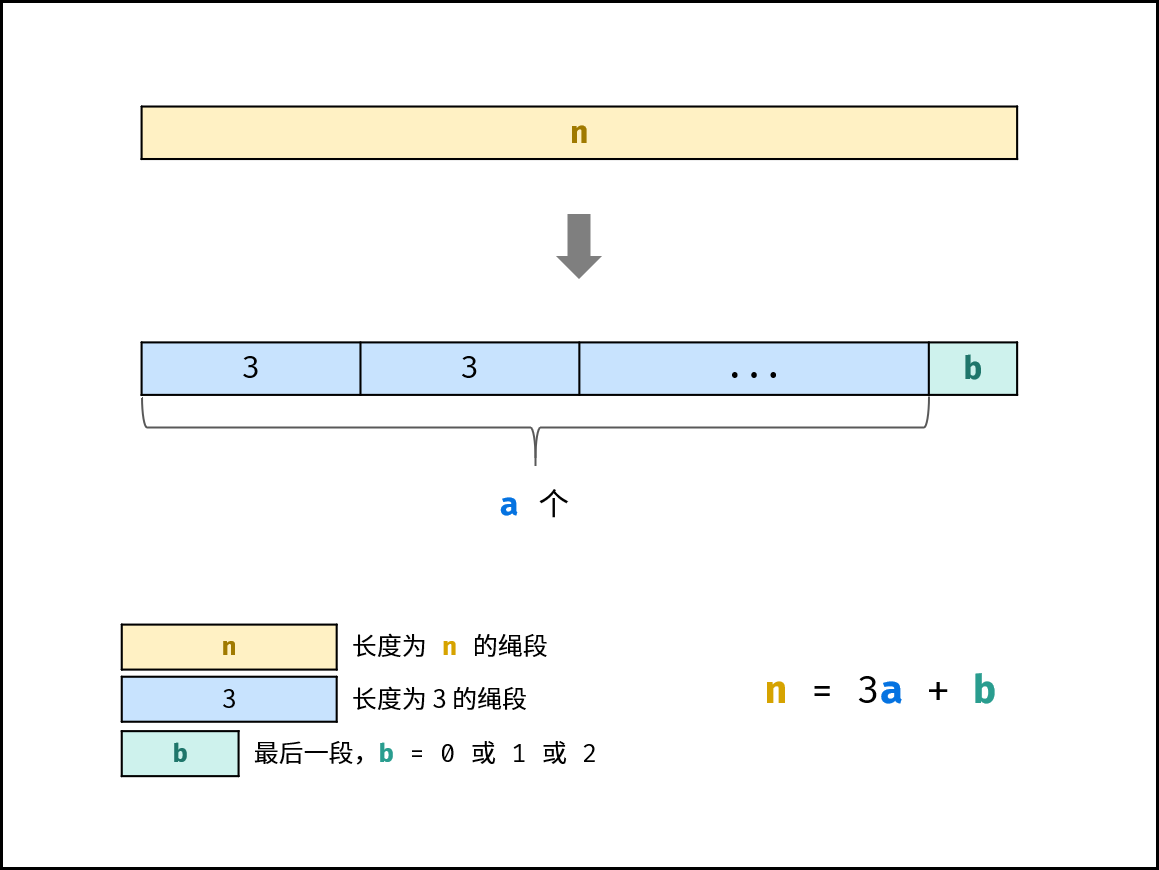
1. 当 n \leq 3 时，按照规则应不切分，但由于题目要求必须剪成 m>1 段，因此必须剪出一段长度为 1 的竹子，即返回 n - 1 。
2. 当 n>3 时，求 n 除以 3 的 整数部分 a 和 余数部分 b （即 n = 3a + b ），并分为以下三种情况（设求余操作符号为 "$\odot$" ）：
   • 当 b = 0 时，直接返回 $3^a \odot 1000000007$；
   • 当 b = 1 时，要将一个 1 + 3 转换为 $2+2$，因此返回 $(3^{a-1} \times 4)\odot 1000000007$；
   • 当 b = 2 时，返回 $(3^a \times 2) \odot 1000000007$。

{:align=center width=600}

大数求余解法：

大数越界： 当 a 增大时，最后返回的 3^a 大小以指数级别增长，可能超出 int32 甚至 int64 的取值范围，导致返回值错误。 大数求余问题： 在仅使用 int32 类型存储的前提下，正确计算 x^a 对 p 求余（即 x^a \odot p ）的值。 解决方案： 循环求余 、 快速幂求余 ，其中后者的时间复杂度更低，两种方法均基于以下求余运算规则推出：

(xy) \odot p = [(x \odot p)(y \odot p)] \odot p

1. 循环求余：

根据求余运算性质推出（∵ 本题中 $x<p$，∴ x \odot p = x ）：

x^a \odot p = [(x ^{a-1} \odot p)(x \odot p)] \odot p=[(x ^{a-1} \odot p)x] \odot p

利用此公式，可通过循环操作依次求 x^1, x^2, ..., x^{a-1}, x^a 对 p 的余数，保证每轮中间值 rem 都在 int32 取值范围中。封装方法代码如下所示。

# 求 (x^a) % p —— 循环求余法
def remainder(x, a, p):
    rem = 1
    for _ in range(a):
        rem = (rem * x) % p
    return rem

时间复杂度 O(N) ： 其中 N=a ，即循环的线性复杂度。

2. 快速幂求余：

根据求余运算性质可推出：

x^a \odot p = (x^2)^{a/2} \odot p = (x^2 \odot p)^{a / 2} \odot p

当 a 为奇数时 a/2 不是整数，因此分为以下两种情况（ ''$//$'' 代表向下取整的除法）：

{x^a \odot p = }
\begin{cases}
(x^2 \odot p)^{a // 2} \odot p &  \text{, $a$ 为偶数} \\
{[(x \odot p)(x ^{a-1} \odot p)] \odot p = [x(x^2 \odot p)^{a//2}] \odot p} & \text{, $a$ 为奇数} \\
\end{cases}

解析： 利用以上公式，可通过循环操作每次把指数 a 问题降低至指数 a//2 问题，只需循环 \log_2(N) 次，因此可将复杂度降低至对数级别。封装方法代码如下所示。

# 求 (x^a) % p —— 快速幂求余
def remainder(x, a, p):
    rem = 1
    while a > 0:
        if a % 2: rem = (rem * x) % p
        x = x ** 2 % p
        a //= 2
    return rem

帮助理解： 根据下表， 初始状态 rem=1, x=3, a=19, p=1000000007 ，最后会将 rem \times (x^a \odot p) 化为 rem \times (x^0 \odot p) = rem \times 1 的形式，即 rem 为余数答案。

n	rem \times (x^a \odot p)	rem_n=rem_{n-1} \times x_{n-1} \odot p	x_n=x_{n-1}^2 \odot p	a_n=a_{n-1}//2
1	1 \times (3^{19} \odot p)	1	3	19
2	3 \times (9^{9} \odot p)	3=1\times3\odot p	9=3^2 \odot p	9=19//2
3	27 \times (81^{4} \odot p)	27 = 3 \times 9 \odot p	81=9^2\odot p	4=9//2
4	27 \times (6561^{2} \odot p)	27	6561=81^2 \odot p	2=4//2
5	27 \times (43046721^{1} \odot p)	27	43046721=6561^2 \odot p	1=2//2
6	162261460 \times (175880701^{0} \odot p)	162261460=27 \times 43046721 \odot p	175880701=43046721^2 \odot p	0=1//2

代码：

Python 代码： 由于语言特性，理论上 Python 中的变量取值范围由系统内存大小决定（无限大），因此在 Python 中其实不用考虑大数越界问题。 Java/C++ 代码： 根据二分法计算原理，至少要保证变量 x 和 rem 可以正确存储 1000000007^2 ，而 2^{64} > 1000000007^2 > 2^{32} ，因此我们选取 long 类型。

class Solution:
    def cuttingBamboo(self, bamboo_len: int) -> int:
        if bamboo_len <= 3: return bamboo_len - 1
        a, b, p, x, rem = bamboo_len // 3 - 1, bamboo_len % 3, 1000000007, 3 , 1
        while a > 0:
            if a % 2: rem = (rem * x) % p
            x = x ** 2 % p
            a //= 2
        if b == 0: return (rem * 3) % p # = 3^(a+1) % p
        if b == 1: return (rem * 4) % p # = 3^a * 4 % p
        return (rem * 6) % p # = 3^(a+1) * 2 % p

class Solution {
    public int cuttingBamboo(int bamboo_len) {
        if(bamboo_len <= 3) return bamboo_len - 1;
        int b = bamboo_len % 3, p = 1000000007;
        long rem = 1, x = 3;
        for(int a = bamboo_len / 3 - 1; a > 0; a /= 2) {
            if(a % 2 == 1) rem = (rem * x) % p;
            x = (x * x) % p;
        }
        if(b == 0) return (int)(rem * 3 % p);
        if(b == 1) return (int)(rem * 4 % p);
        return (int)(rem * 6 % p);
    }
}

class Solution {
public:
    int cuttingBamboo(int bamboo_len) {
        if(bamboo_len <= 3) return bamboo_len - 1;
        int b = bamboo_len % 3, p = 1000000007;
        long rem = 1, x = 3;
        for(int a = bamboo_len / 3 - 1; a > 0; a /= 2) {
            if(a % 2 == 1) rem = (rem * x) % p;
            x = (x * x) % p;
        }
        if(b == 0) return (int)(rem * 3 % p);
        if(b == 1) return (int)(rem * 4 % p);
        return (int)(rem * 6 % p);
    }
};

# 由于语言特性，Python 可以不考虑大数越界问题
class Solution:
    def cuttingBamboo(self, bamboo_len: int) -> int:
        if bamboo_len <= 3: return bamboo_len - 1
        a, b, p = bamboo_len // 3, bamboo_len % 3, 1000000007
        if b == 0: return 3 ** a % p
        if b == 1: return 3 ** (a - 1) * 4 % p
        return 3 ** a * 2 % p

复杂度分析：

以下为 二分求余法 的复杂度。

• 时间复杂度 O(\log N) ： 其中 N=a ，二分法为对数级别复杂度，每轮仅有求整、求余、次方运算。
  • 求整和求余运算：资料提到不超过机器数的整数可以看作是 O(1) ；
  • 幂运算：查阅资料，提到浮点取幂为 O(1) 。
• 空间复杂度 O(1) ： 变量 a, b, p, x, rem 使用常数大小额外空间。