LeetCode-Book/leetbook_ioa/docs/LCR 140. 训练计划 II.md

解题思路：

第一时间想到的解法：

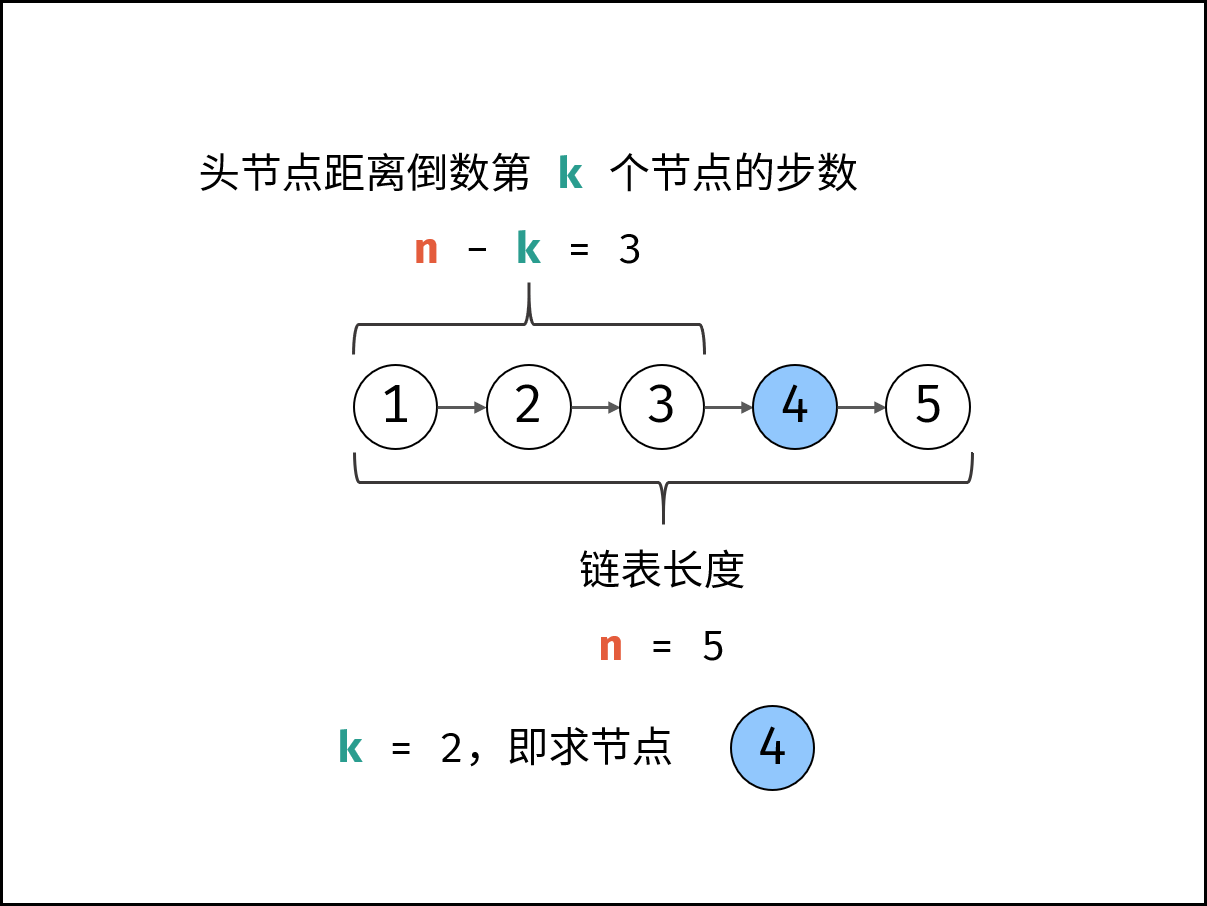
1. 先遍历统计链表长度，记为 n ；
2. 设置一个指针走 (n-cnt) 步，即可找到链表倒数第 cnt 个节点；

使用双指针则可以不用统计链表长度。

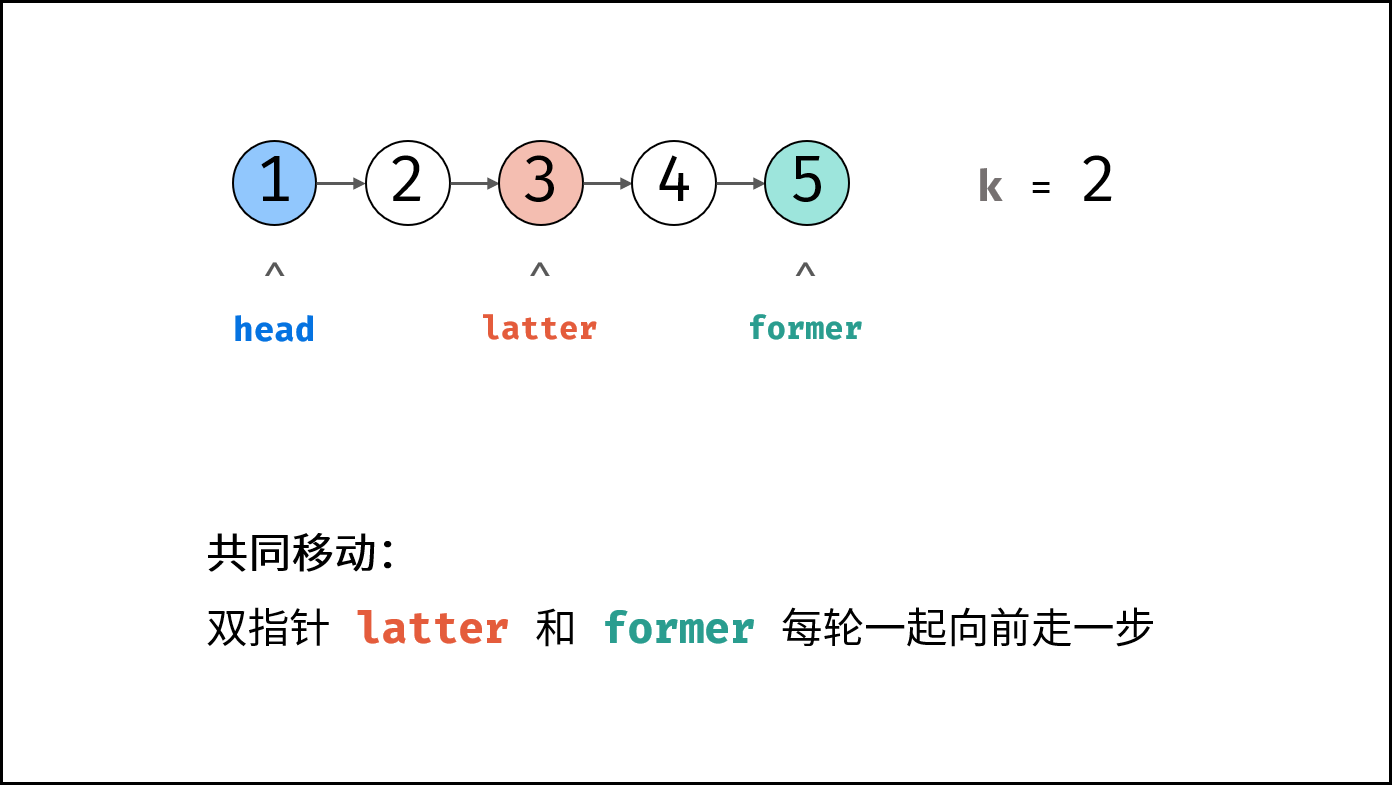
下图中的 k 对应本题的 cnt 。

{:align=center width=450}

算法流程：

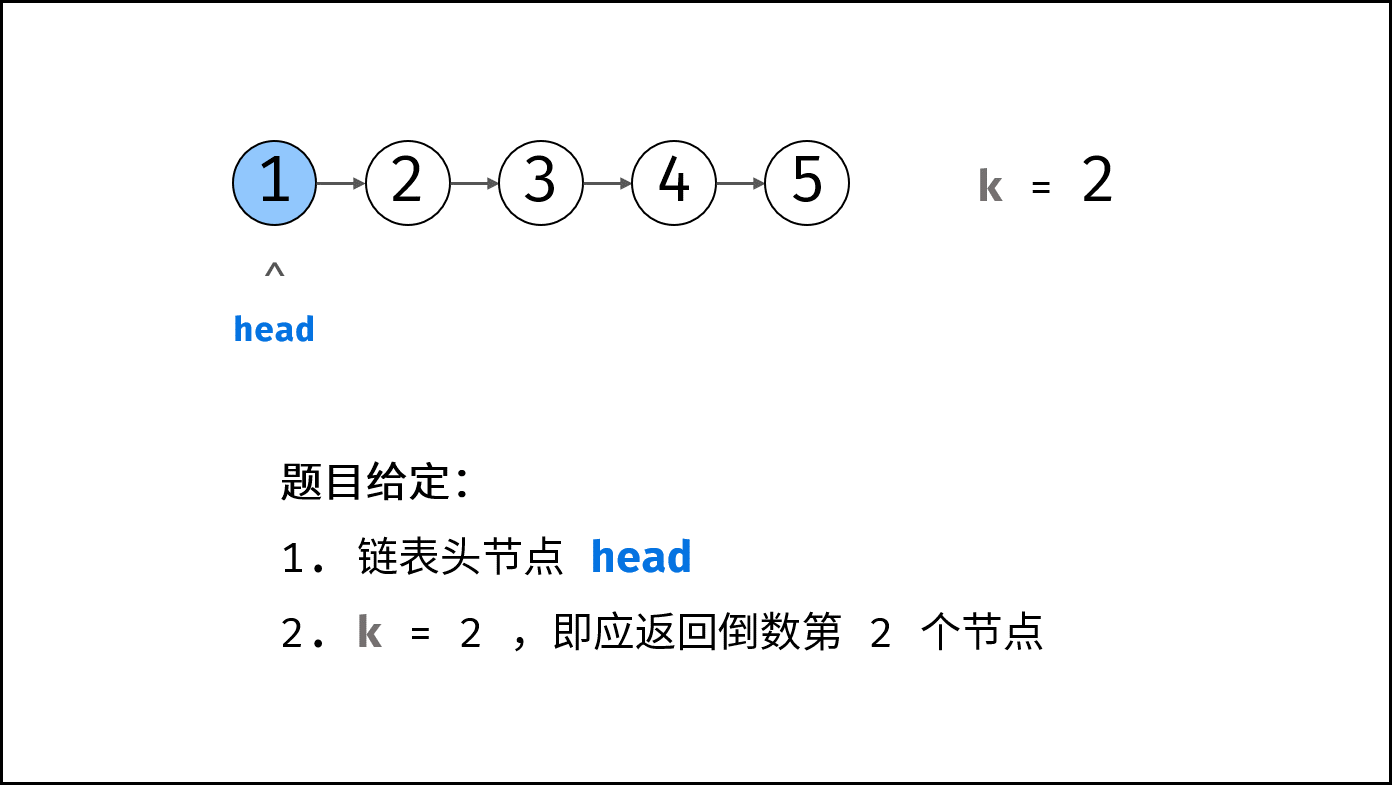
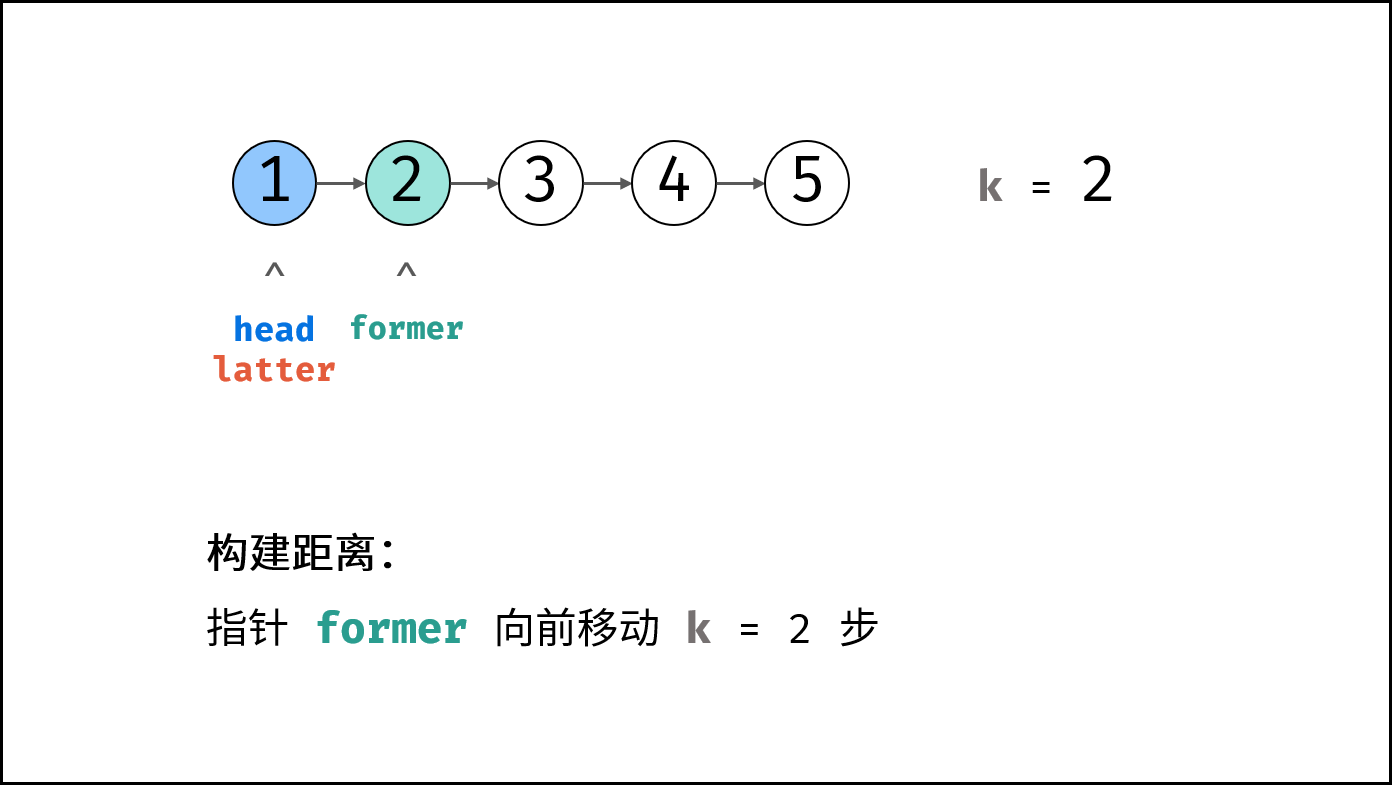
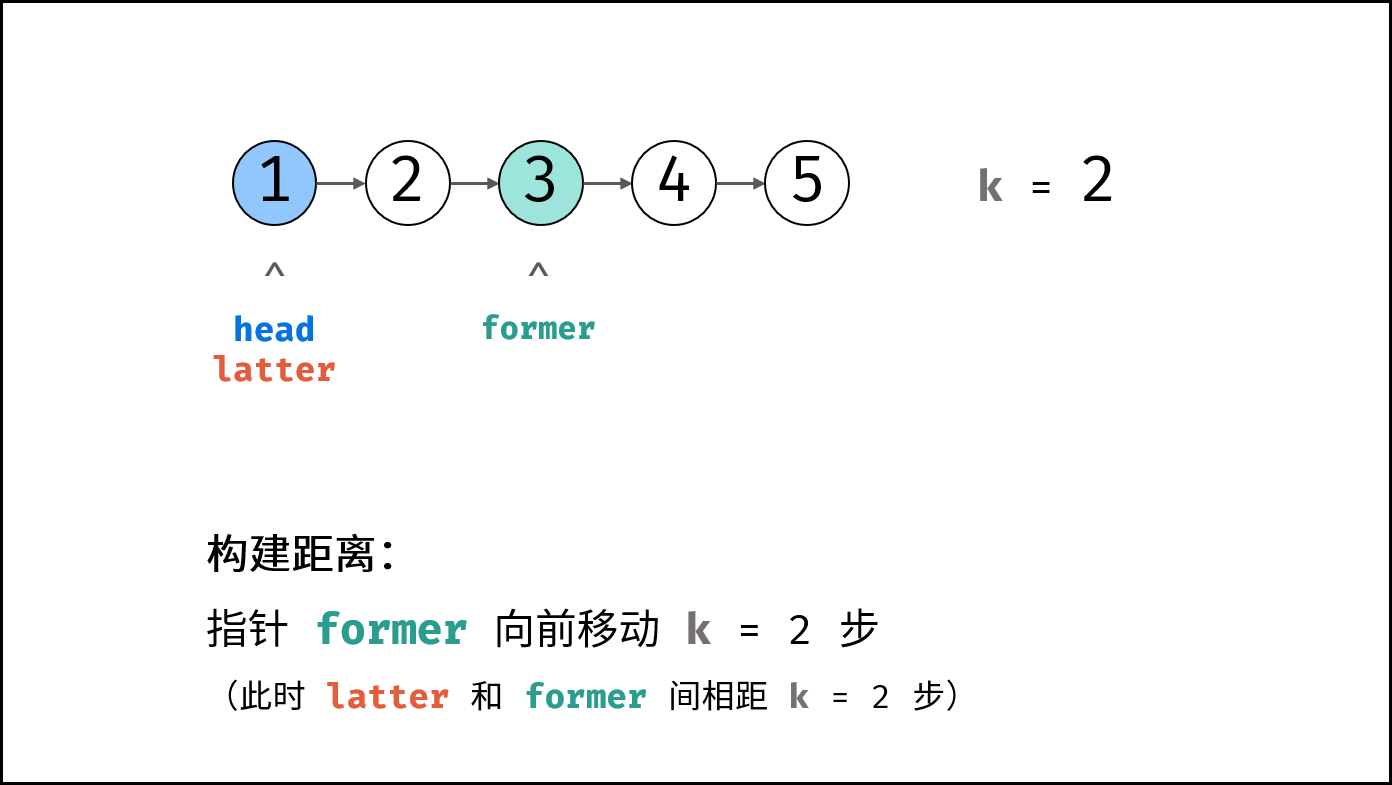
1. 初始化： 前指针 former 、后指针 latter ，双指针都指向头节点 head​ 。
2. 构建双指针距离： 前指针 former 先向前走 cnt 步（结束后，双指针 former 和 latter 间相距 cnt 步）。
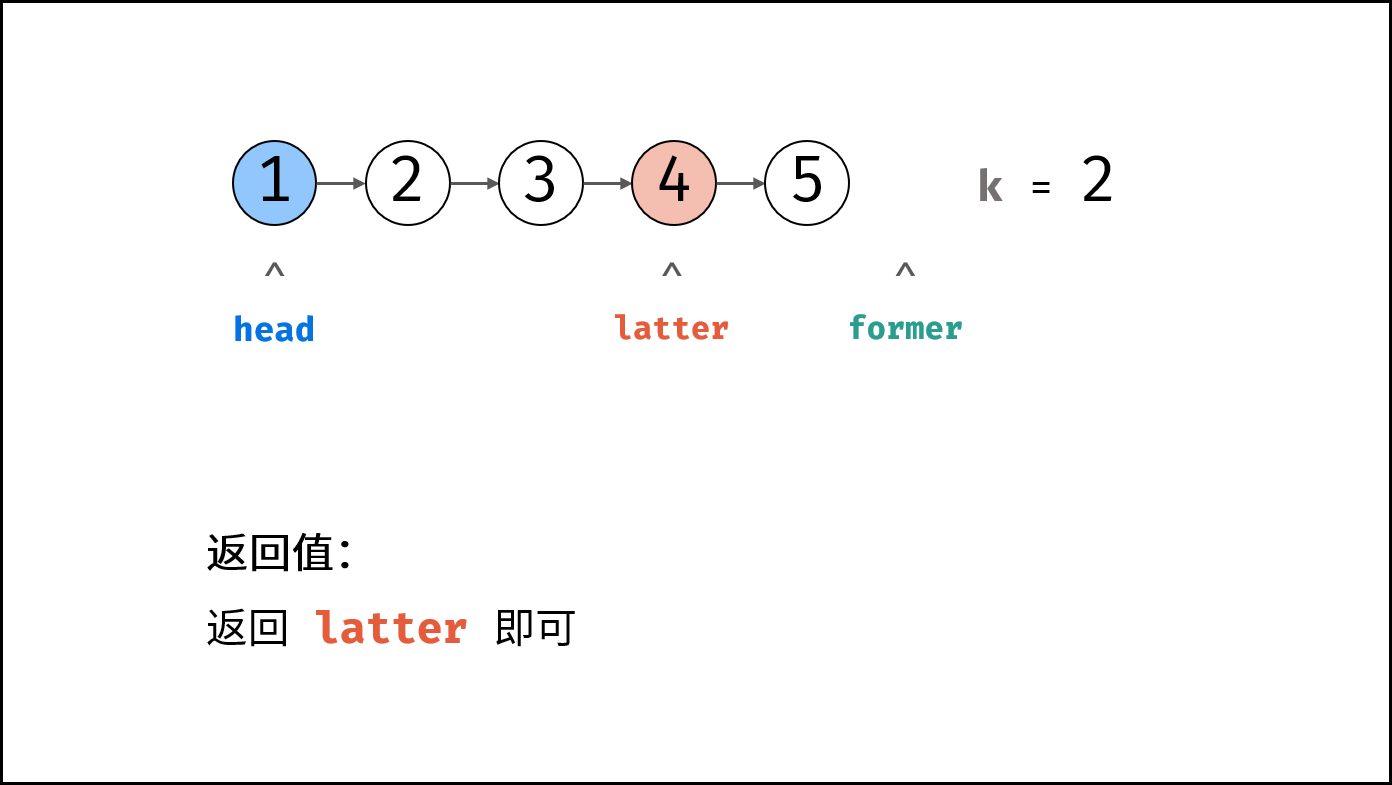
3. 双指针共同移动： 循环中，双指针 former 和 latter 每轮都向前走一步，直至 former 走过链表 尾节点 时跳出（跳出后，latter 与尾节点距离为 $cnt-1$，即 latter 指向倒数第 cnt 个节点）。
4. 返回值： 返回 latter 即可。

<,,,,,,,>

代码：

class Solution:
    def trainingPlan(self, head: ListNode, cnt: int) -> ListNode:
        former, latter = head, head
        for _ in range(cnt):
            former = former.next
        while former:
            former, latter = former.next, latter.next
        return latter

class Solution {
    public ListNode trainingPlan(ListNode head, int cnt) {
        ListNode former = head, latter = head;
        for(int i = 0; i < cnt; i++)
            former = former.next;
        while(former != null) {
            former = former.next;
            latter = latter.next;
        }
        return latter;
    }
}

class Solution {
public:
    ListNode* trainingPlan(ListNode* head, int cnt) {
        ListNode *former = head, *latter = head;
        for(int i = 0; i < cnt; i++)
            former = former->next;
        while(former != nullptr) {
            former = former->next;
            latter = latter->next;
        }
        return latter;
    }
};

本题没有 cnt> 链表长度的测试样例 ，因此不用考虑越界。考虑越界问题的代码如下：

class Solution:
    def trainingPlan(self, head: ListNode, cnt: int) -> ListNode:
        former, latter = head, head
        for _ in range(cnt):
            if not former: return
            former = former.next
        while former:
            former, latter = former.next, latter.next
        return latter

class Solution {
    public ListNode trainingPlan(ListNode head, int cnt) {
        ListNode former = head, latter = head;
        for(int i = 0; i < cnt; i++) {
            if(former == null) return null;
            former = former.next;
        }
        while(former != null) {
            former = former.next;
            latter = latter.next;
        }
        return latter;
    }
}

class Solution {
public:
    ListNode* trainingPlan(ListNode* head, int cnt) {
        ListNode *former = head, *latter = head;
        for(int i = 0; i < cnt; i++) {
            if(former == nullptr) return nullptr;
            former = former->next;
        }
        while(former != nullptr) {
            former = former->next;
            latter = latter->next;
        }
        return latter;
    }
};

复杂度分析：

• 时间复杂度 O(n) ： n 为链表长度；总体看，former 走了 n 步，latter 走了 (-cnt) 步。
• 空间复杂度 O(1) ： 双指针 former , latter 使用常数大小的额外空间。