LeetCode-Book/leetbook_ioa/docs/LCR 158. 库存管理 II.md

解题思路：

请注意，数学中众数的定义为 “数组中出现次数最多的数字” ，与本文定义不同。本文将 “数组中出现次数超过一半的数字” 称为 “众数”。

本题常见的三种解法：

1. 哈希表统计法： 遍历数组 stock ，用 HashMap 统计各数字的数量，即可找出 众数 。此方法时间和空间复杂度均为 O(N) 。
2. 数组排序法： 将数组 stock 排序，数组中点的元素 一定为众数。
3. 摩尔投票法： 核心理念为 票数正负抵消 。此方法时间和空间复杂度分别为 O(N) 和 O(1) ，为本题的最佳解法。

摩尔投票法：

设输入数组 stock 的众数为 x ，数组长度为 n 。

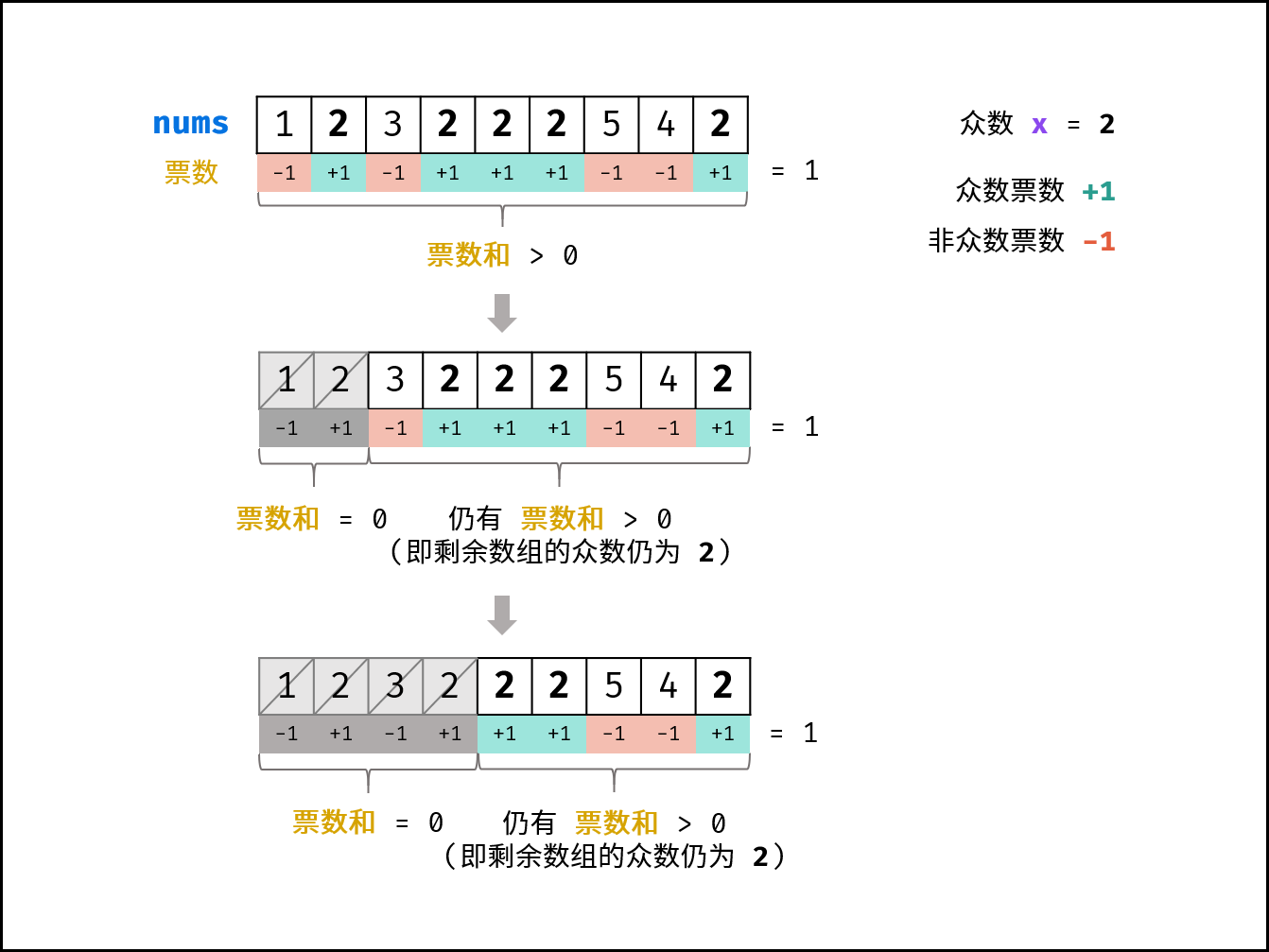
推论一： 若记 众数 的票数为 +1 ，非众数 的票数为 -1 ，则一定有所有数字的 票数和 $> 0$ 。

推论二： 若数组的前 a 个数字的 票数和 $= 0$ ，则 数组剩余 (n-a) 个数字的 票数和一定仍 $>0$ ，即后 (n-a) 个数字的 众数仍为 $x$ 。

下图中的 nums 对应本题的 stock 。

{:align=center width=500}

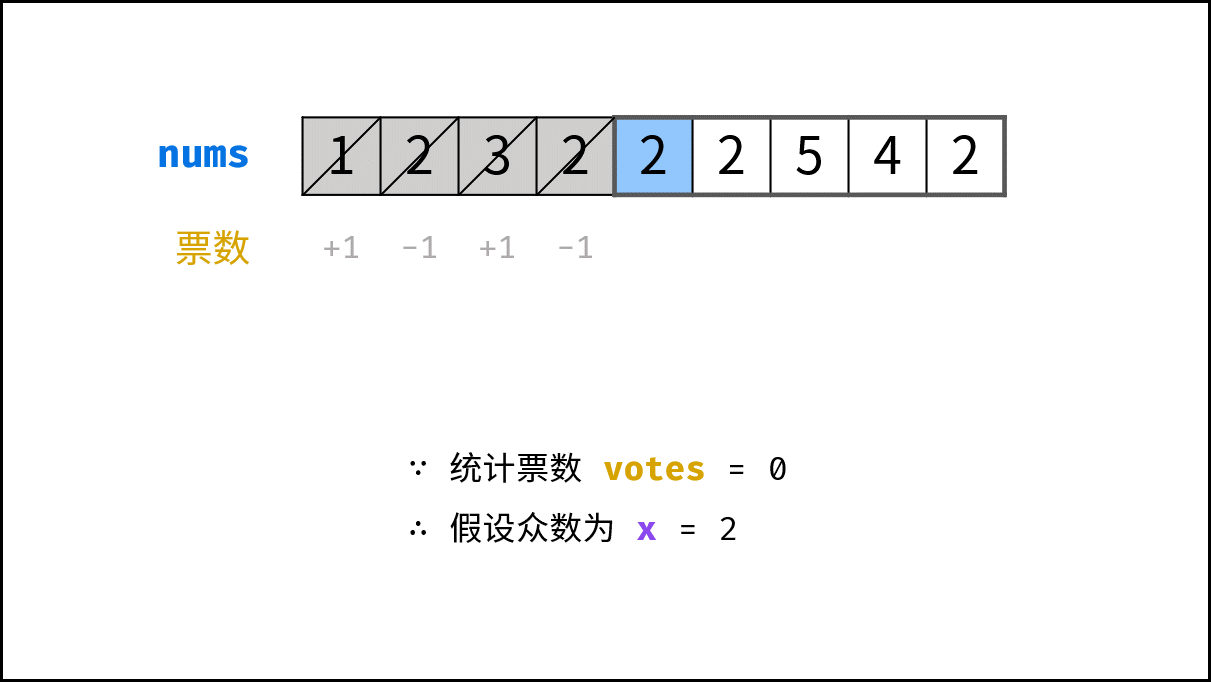
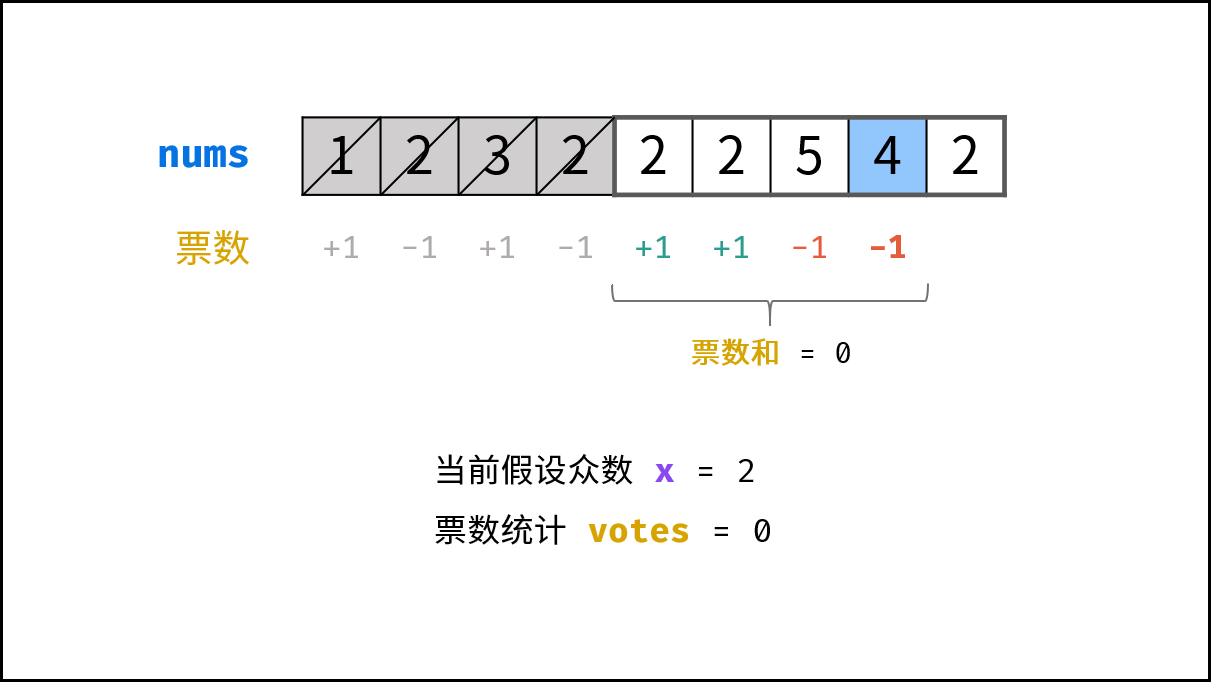
根据以上推论，记数组首个元素为 n_1 ，众数为 x ，遍历并统计票数。当发生 票数和 $= 0$ 时，剩余数组的众数一定不变 ，这是由于：

• 当 n_1 = x ： 抵消的所有数字中，有一半是众数 x 。
• 当 n_1 \neq x ： 抵消的所有数字中，众数 x 的数量最少为 0 个，最多为一半。

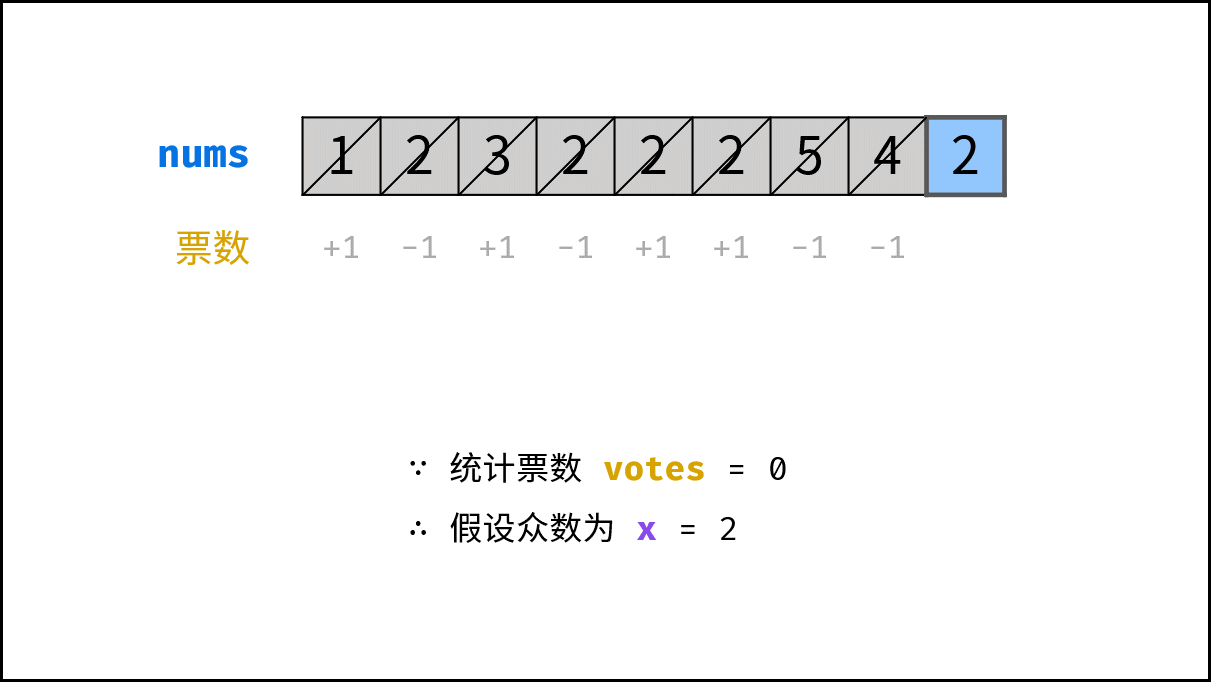
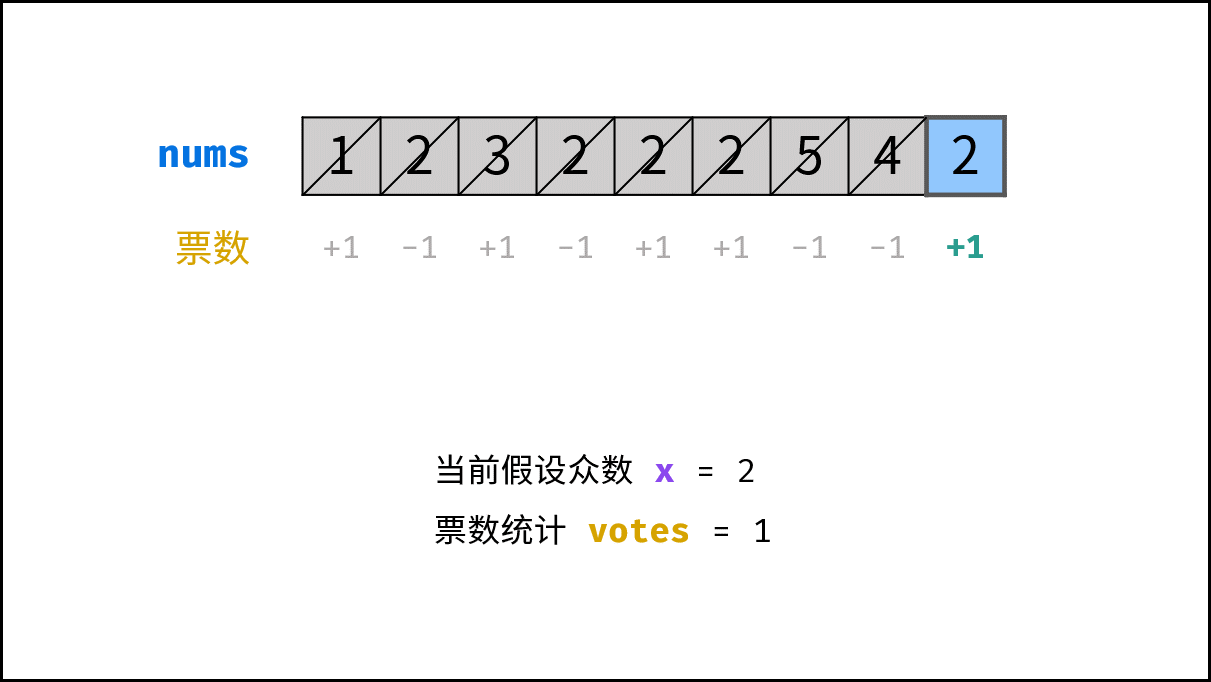
利用此特性，每轮假设发生 票数和 $= 0$ 都可以 缩小剩余数组区间 。当遍历完成时，最后一轮假设的数字即为众数。

算法流程:

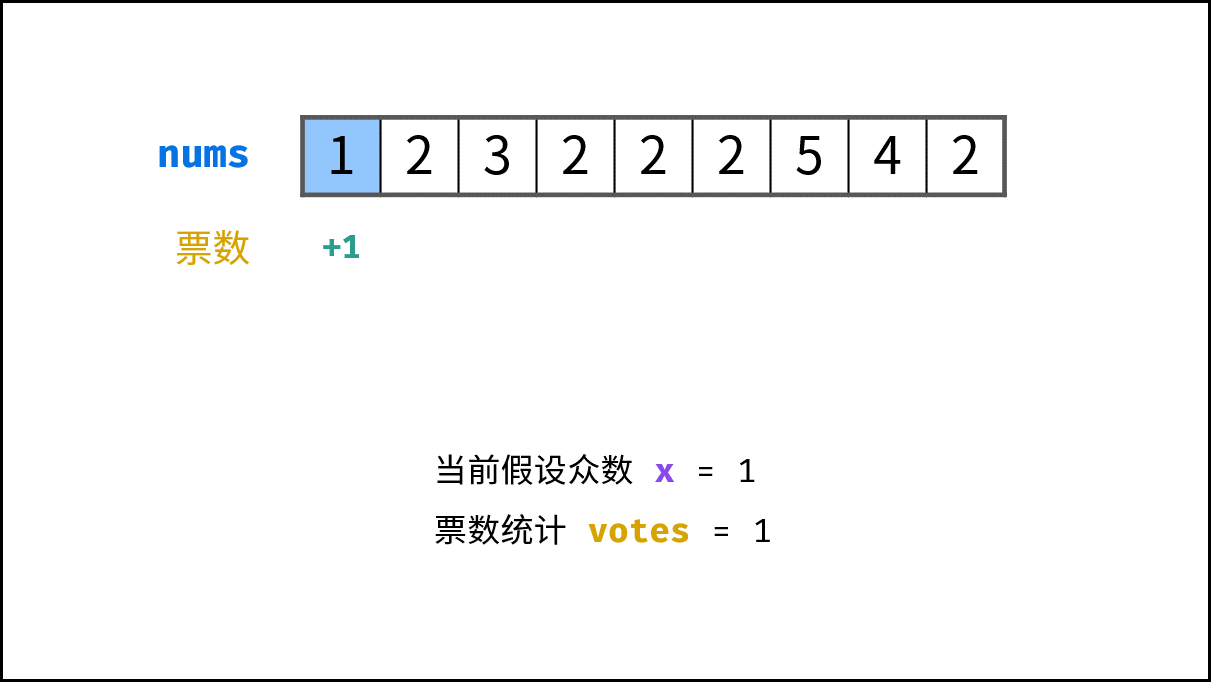
1. 初始化： 票数统计 votes = 0 ， 众数 x；
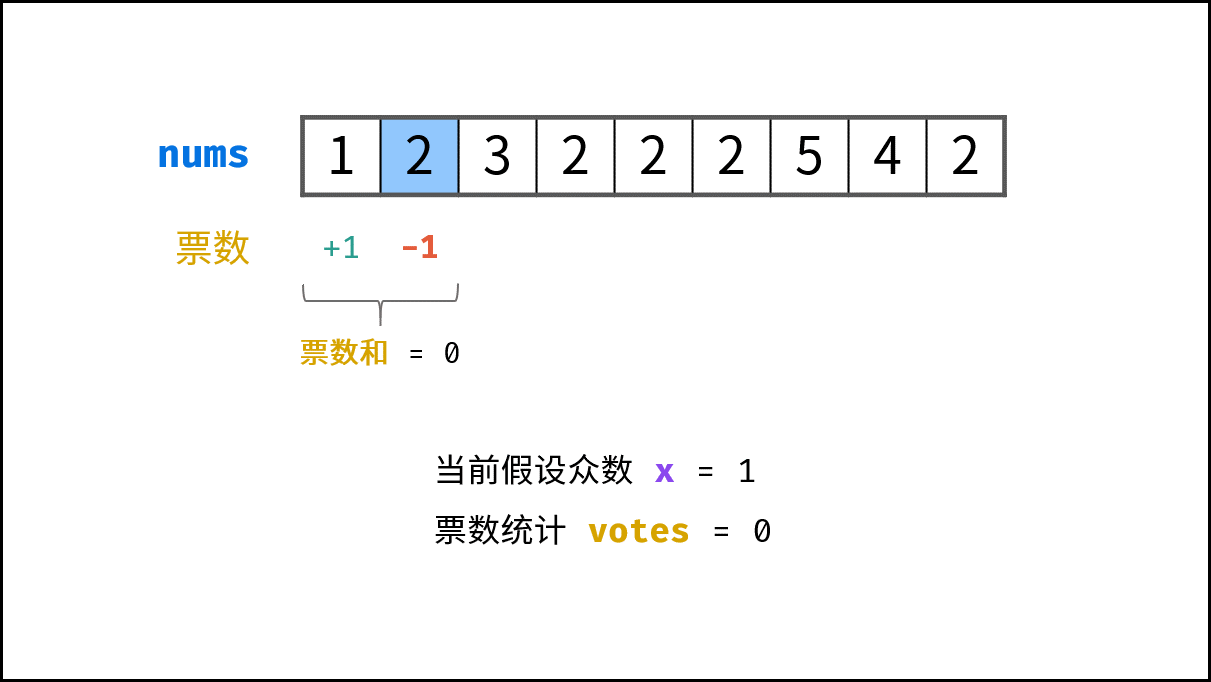
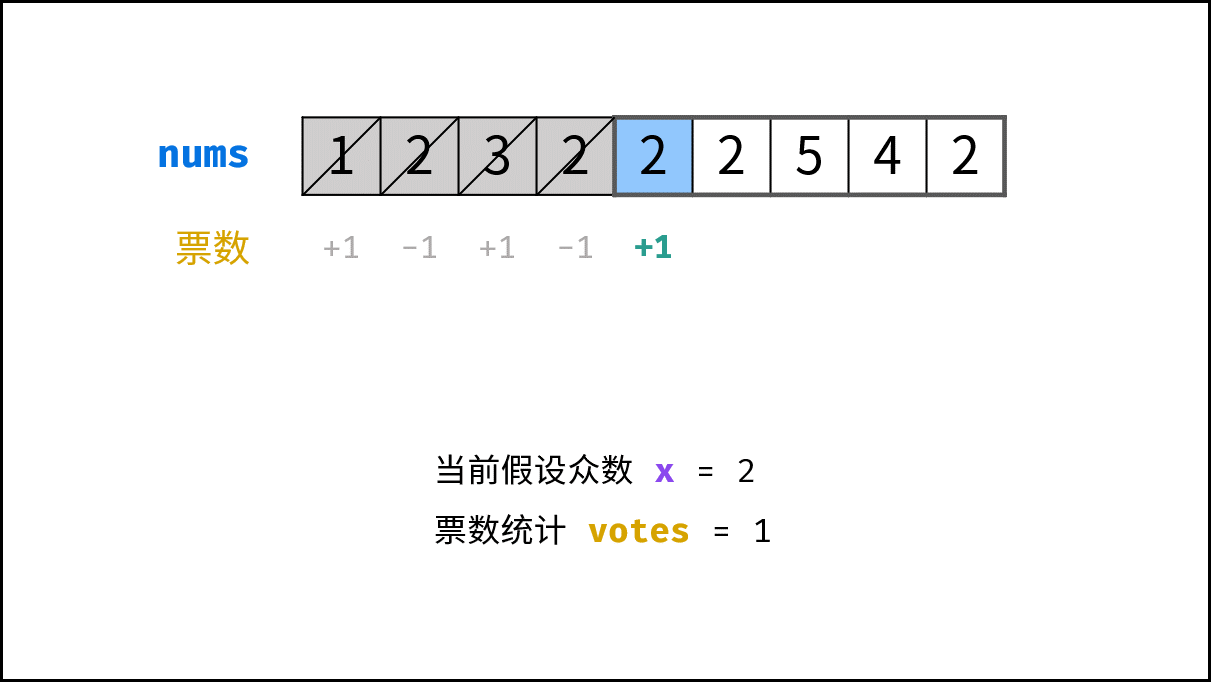
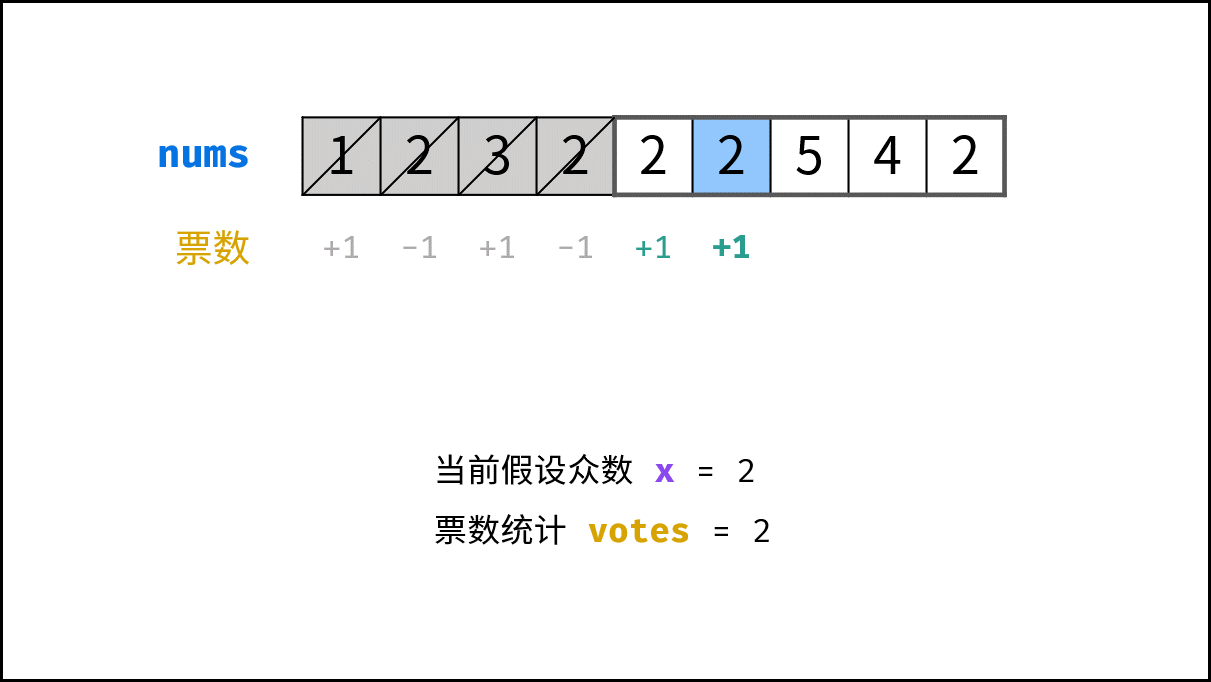
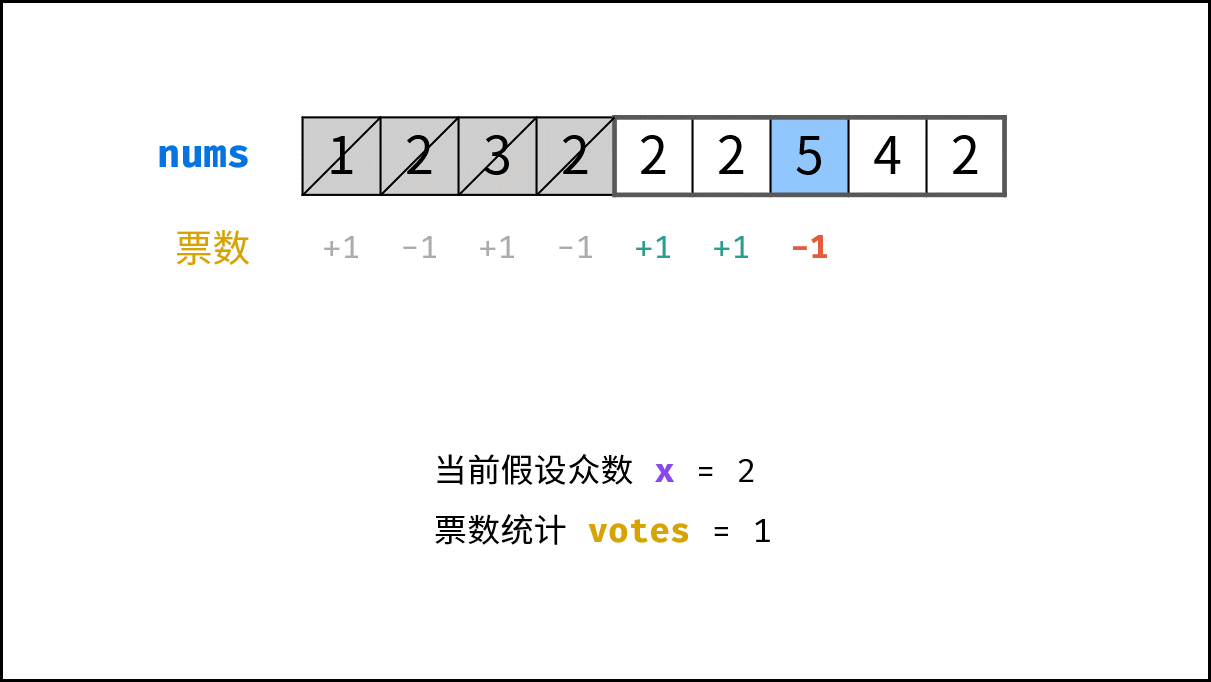
2. 循环： 遍历数组 stock 中的每个数字 num ；
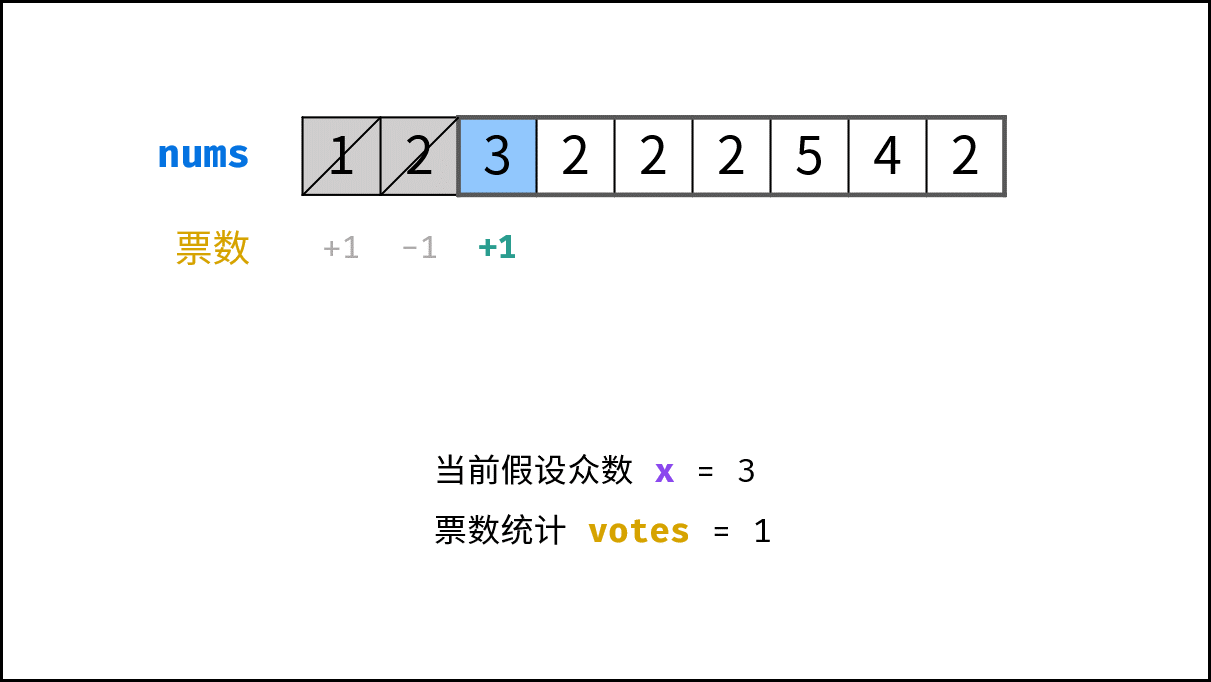
   1. 当 票数 votes 等于 0 ，则假设当前数字 num 是众数；
   2. 当 num = x 时，票数 votes 自增 1 ；当 num != x 时，票数 votes 自减 1 ；
3. 返回值： 返回 x 即可；

<,,,,,,,,,,,,,>

代码：

class Solution:
    def inventoryManagement(self, stock: List[int]) -> int:
        votes = 0
        for num in stock:
            if votes == 0: x = num
            votes += 1 if num == x else -1
        return x

class Solution {
    public int inventoryManagement(int[] stock) {
        int x = 0, votes = 0;
        for(int num : stock){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        return x;
    }
}

class Solution {
public:
    int inventoryManagement(vector<int>& stock) {
        int x = 0, votes = 0;
        for(int num : stock){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        return x;
    }
};

拓展： 由于题目说明 “给定的数组总是存在多数元素” ，因此本题不用考虑 数组不存在众数 的情况。若考虑，需要加入一个 “验证环节” ，遍历数组 stock 统计 x 的数量。

• 若 x 的数量超过数组长度一半，则返回 x ；
• 否则，返回未找到众数；

时间和空间复杂度不变，仍为 O(N) 和 O(1) 。

class Solution:
    def inventoryManagement(self, stock: List[int]) -> int:
        votes, count = 0, 0
        for num in stock:
            if votes == 0: x = num
            votes += 1 if num == x else -1
        # 验证 x 是否为众数
        for num in stock:
            if num == x: count += 1
        return x if count > len(stock) // 2 else 0 # 当无众数时返回 0

class Solution {
    public int inventoryManagement(int[] stock) {
        int x = 0, votes = 0, count = 0;
        for(int num : stock){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        // 验证 x 是否为众数
        for(int num : stock)
            if(num == x) count++;
        return count > stock.length / 2 ? x : 0; // 当无众数时返回 0
    }
}

class Solution {
public:
    int inventoryManagement(vector<int>& stock) {
        int x = 0, votes = 0, count = 0;
        for(int num : stock){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        // 验证 x 是否为众数
        for(int num : stock)
            if(num == x) count++;
        return count > stock.size() / 2 ? x : 0; // 当无众数时返回 0
    }
};

复杂度分析：

• 时间复杂度 O(N) ： N 为数组 stock 长度。
• 空间复杂度 O(1) ： votes 变量使用常数大小的额外空间。