LeetCode-Book/leetbook_ioa/docs/LCR 162. 数字 1 的个数.md

解题思路：

为简化篇幅，本文将 num 记为 n 。

将 1 ~ n 的个位、十位、百位、...的 1 出现次数相加，即为 1 出现的总次数。

设数字 n 是个 x 位数，记 n 的第 i 位为 n_i ，则可将 n 写为 n_{x} n_{x-1} \cdots n_{2} n_{1} ；本文名词规定如下：

• 称 「 n_i 」称为 当前位 ，记为 cur ；
• 将 「 n_{i-1} n_{i-2} \cdots n_{2} n_{1} 」称为 低位 ，记为 low ；
• 将 「 n_{x} n_{x-1} \cdots n_{i+2} n_{i+1} 」称为 高位 ，记为 high ；
• 将 「 10^i 」称为 位因子 ，记为 digit ；

某位中 1 出现次数的计算方法：

根据当前位 cur 值的不同，分为以下三种情况：

1. 当 cur = 0 时： 此位 1 的出现次数只由高位 high 决定，计算公式为：

high \times digit

如下图所示，以 n = 2304 为例，求 digit = 10 （即十位）的 1 出现次数。

{:align=center width=450}

2. 当 cur = 1 时： 此位 1 的出现次数由高位 high 和低位 low 决定，计算公式为：

high \times digit + low + 1

如下图所示，以 n = 2314 为例，求 digit = 10 （即十位）的 1 出现次数。

{:align=center width=450}

3. 当 cur = 2, 3, \cdots, 9 时： 此位 1 的出现次数只由高位 high 决定，计算公式为：

(high + 1) \times digit

如下图所示，以 n = 2324 为例，求 digit = 10 （即十位）的 1 出现次数。

{:align=center width=450}

变量递推公式：

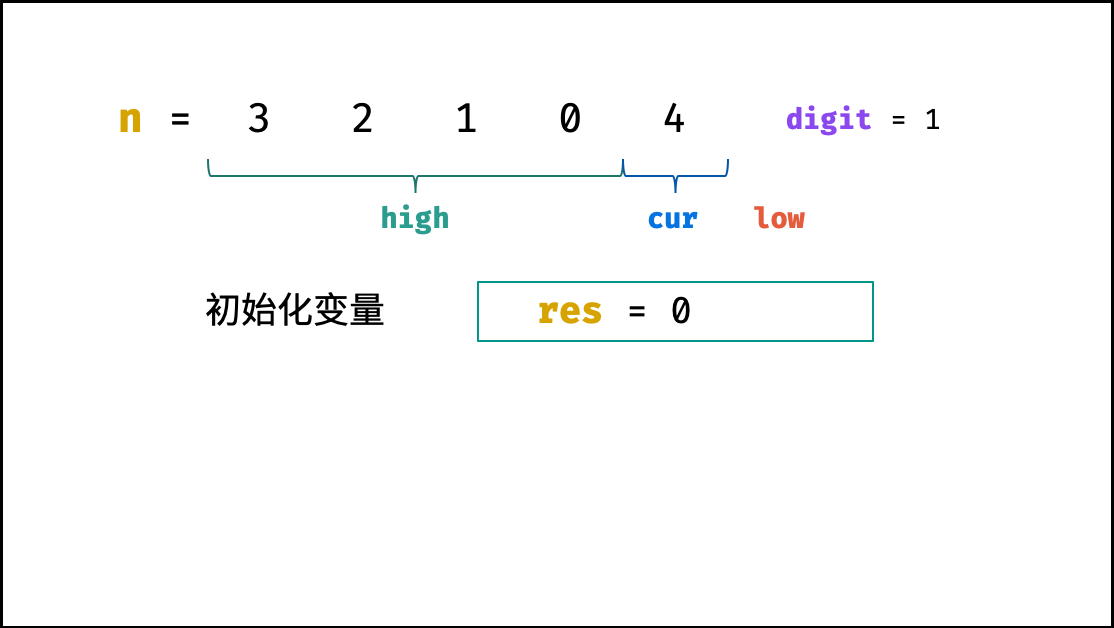
设计按照 “个位、十位、...” 的顺序计算，则 high / cur / low / digit 应初始化为：

high = n // 10
cur = n % 10
low = 0
digit = 1 # 个位

int high = n / 10;
int cur = n % 10;
int low = 0;
int digit = 1; // 个位

int high = n / 10;
int cur = n % 10;
int low = 0;
int digit = 1; // 个位

因此，从个位到最高位的变量递推公式为：

while high != 0 or cur != 0: # 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
    low += cur * digit # 将 cur 加入 low ，组成下轮 low
    cur = high % 10 # 下轮 cur 是本轮 high 的最低位
    high //= 10 # 将本轮 high 最低位删除，得到下轮 high
    digit *= 10 # 位因子每轮 × 10

while(high != 0 || cur != 0) { // 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
    low += cur * digit; // 将 cur 加入 low ，组成下轮 low
    cur = high % 10; // 下轮 cur 是本轮 high 的最低位
    high /= 10; // 将本轮 high 最低位删除，得到下轮 high
    digit *= 10; // 位因子每轮 × 10
}

while(high != 0 || cur != 0) { // 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
    low += cur * digit; // 将 cur 加入 low ，组成下轮 low
    cur = high % 10; // 下轮 cur 是本轮 high 的最低位
    high /= 10; // 将本轮 high 最低位删除，得到下轮 high
    digit *= 10; // 位因子每轮 × 10
}

<,,,,,,>

代码：

class Solution:
    def digitOneInNumber(self, n: int) -> int:
        digit, res = 1, 0
        high, cur, low = n // 10, n % 10, 0
        while high != 0 or cur != 0:
            if cur == 0: res += high * digit
            elif cur == 1: res += high * digit + low + 1
            else: res += (high + 1) * digit
            low += cur * digit
            cur = high % 10
            high //= 10
            digit *= 10
        return res

class Solution {
    public int digitOneInNumber(int n) {
        int digit = 1, res = 0;
        int high = n / 10, cur = n % 10, low = 0;
        while(high != 0 || cur != 0) {
            if(cur == 0) res += high * digit;
            else if(cur == 1) res += high * digit + low + 1;
            else res += (high + 1) * digit;
            low += cur * digit;
            cur = high % 10;
            high /= 10;
            digit *= 10;
        }
        return res;
    }
}

class Solution {
public:
    int digitOneInNumber(int n) {
        long digit = 1;
        int high = n / 10, cur = n % 10, low = 0, res = 0;
        while(high != 0 || cur != 0) {
            if(cur == 0) res += high * digit;
            else if(cur == 1) res += high * digit + low + 1;
            else res += (high + 1) * digit;
            low += cur * digit;
            cur = high % 10;
            high /= 10;
            digit *= 10;
        }
        return res;
    }
};

复杂度分析：

• 时间复杂度 O(\log n) ： 循环内的计算操作使用 O(1) 时间；循环次数为数字 n 的位数，即 \log_{10}{n} ，因此循环使用 O(\log n) 时间。
• 空间复杂度 O(1) ： 几个变量使用常数大小的额外空间。