6.0 KiB
Executable File
方法一：暴力法
此方法超时，但为便于理解「方法二」，建议先理解此方法。
为简化篇幅，本文使用
n代替题目中的num。
给定 n 个骰子，可得：
- 每个骰子摇到
1至6的概率相等，都为\frac{1}{6}。 - 将每个骰子的点数看作独立情况，共有
6^n种「点数组合」。例如n = 2时的点数组合为：
(1,1), (1,2), \cdots, (2, 1), (2, 2), \cdots, (6,1), \cdots, (6, 6)
n个骰子「点数和」的范围为[n, 6n]，数量为6n - n + 1 = 5n + 1种。
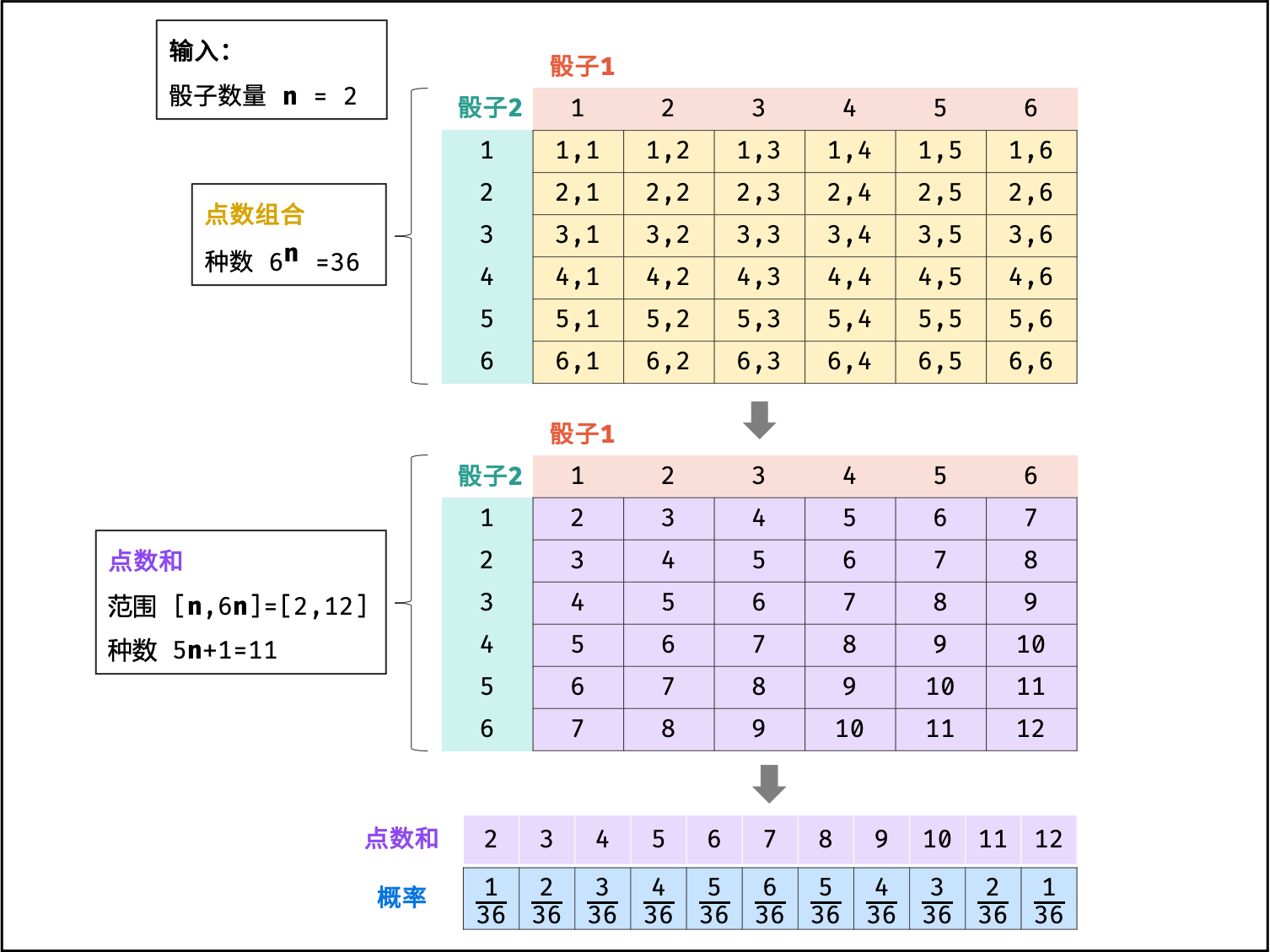
暴力统计： 每个「点数组合」都对应一个「点数和」，考虑遍历所有点数组合，统计每个点数和的出现次数，最后除以点数组合的总数（即除以 6^n ），即可得到每个点数和的出现概率。
如下图所示，为输入
n = 2时，点数组合、点数和、各点数概率的计算过程。
{:align=center width=550}
暴力法需要遍历所有点数组合，因此时间复杂度为 O(6^n) ，观察本题输入取值范围 1 \leq n \leq 11 ，可知此复杂度是无法接受的。
方法二：动态规划
设输入
n个骰子的解（即概率列表）为f(n)，其中「点数和」x的概率为f(n, x)。
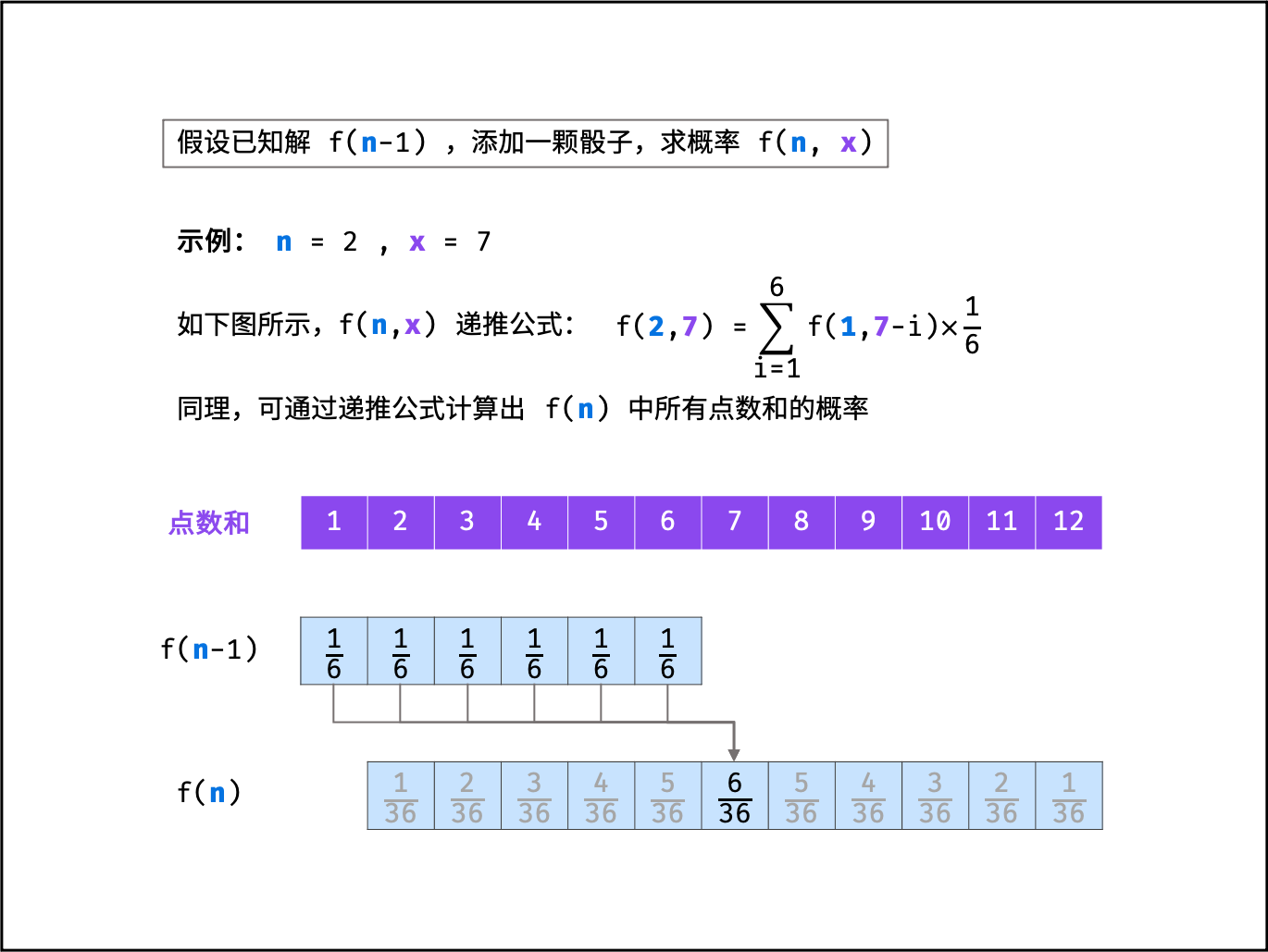
假设已知 n - 1 个骰子的解 f(n - 1) ，此时添加一枚骰子，求 n 个骰子的点数和为 x 的概率 f(n, x) 。
当添加骰子的点数为 1 时，前 n - 1 个骰子的点数和应为 x - 1 ，方可组成点数和 x ；同理，当此骰子为 2 时，前 n - 1 个骰子应为 x - 2 ；以此类推，直至此骰子点数为 6 。将这 6 种情况的概率相加，即可得到概率 f(n, x) 。递推公式如下所示：
f(n, x) = \sum_{i=1}^6 f(n - 1, x - i) \times \frac{1}{6}
根据以上分析，得知通过子问题的解 f(n - 1) 可递推计算出 f(n) ，而输入一个骰子的解 f(1) 已知，因此可通过解 f(1) 依次递推出任意解 f(n) 。
如下图所示，为
n = 2,x = 7的递推计算示例。
{:align=center width=550}
观察发现，以上递推公式虽然可行，但 f(n - 1, x - i) 中的 x - i 会有越界问题。例如，若希望递推计算 f(2, 2) ，由于一个骰子的点数和范围为 [1, 6] ，因此只应求和 f(1, 1) ，即 f(1, 0) , f(1, -1) , ... , f(1, -4) 皆无意义。此越界问题导致代码编写的难度提升。
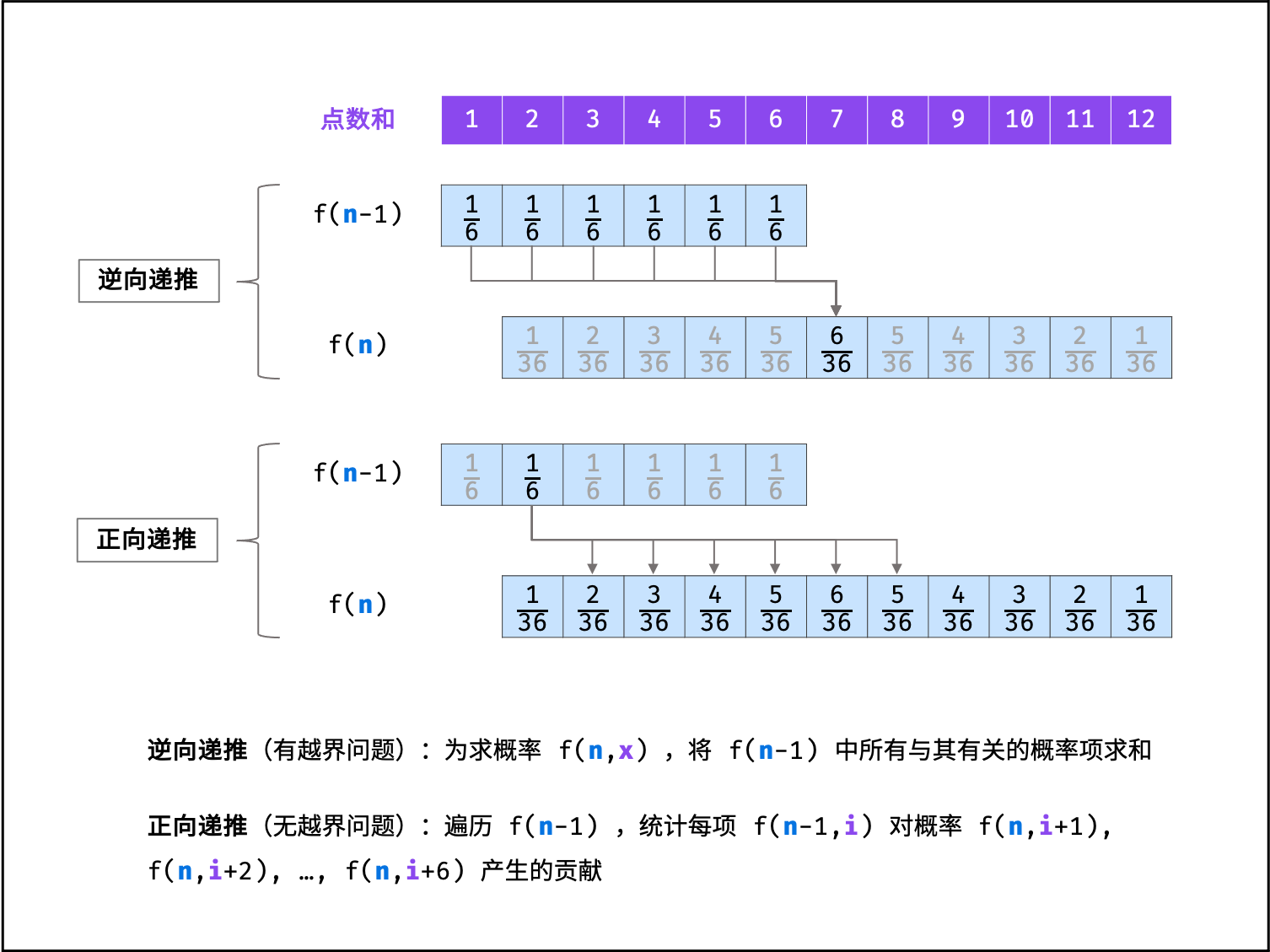
如下图所示，以上递推公式是 “逆向” 的，即为了计算
f(n, x)，将所有与之有关的情况求和；而倘若改换为 “正向” 的递推公式，便可解决越界问题。
{:align=center width=550}
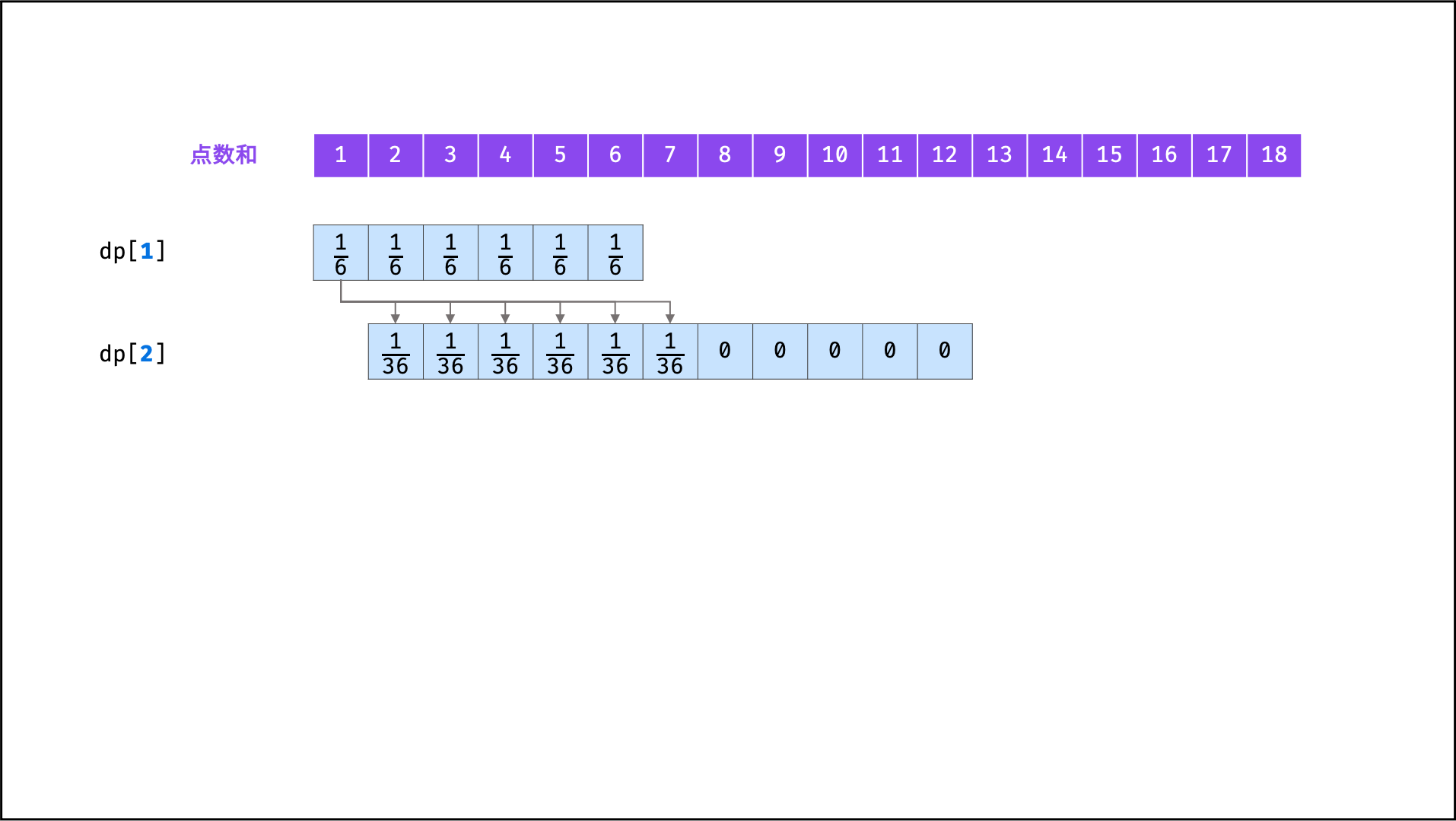
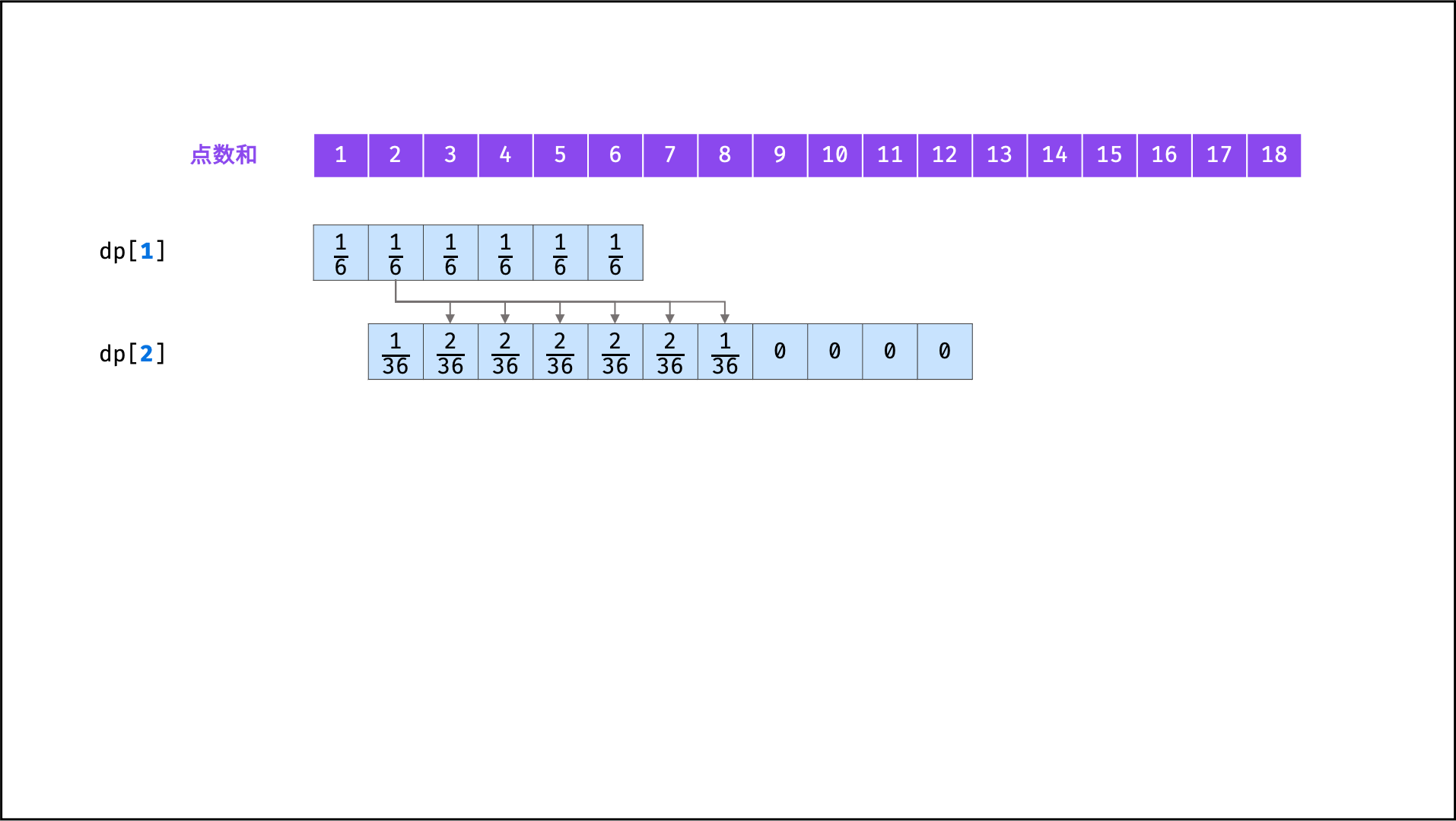
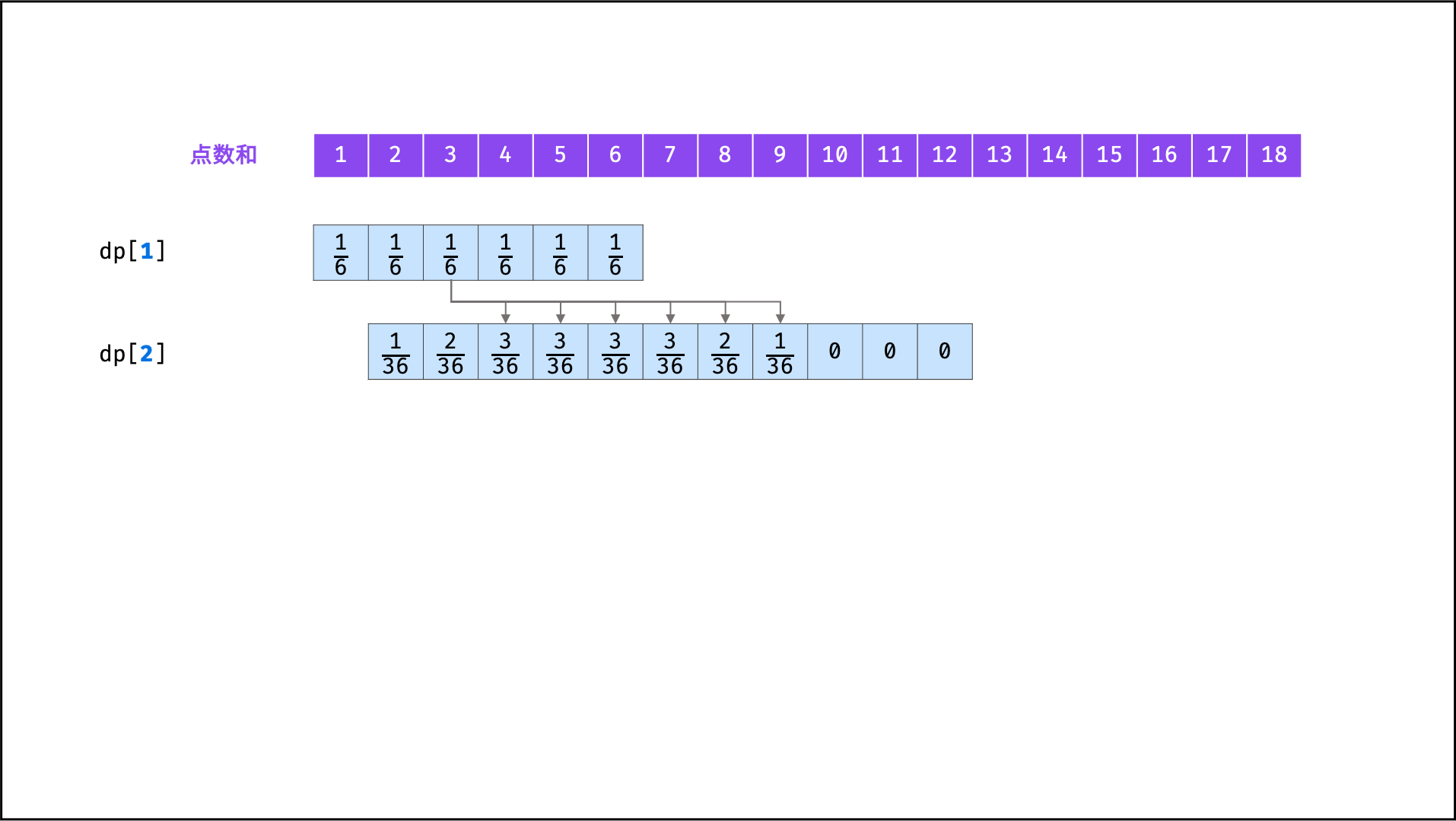
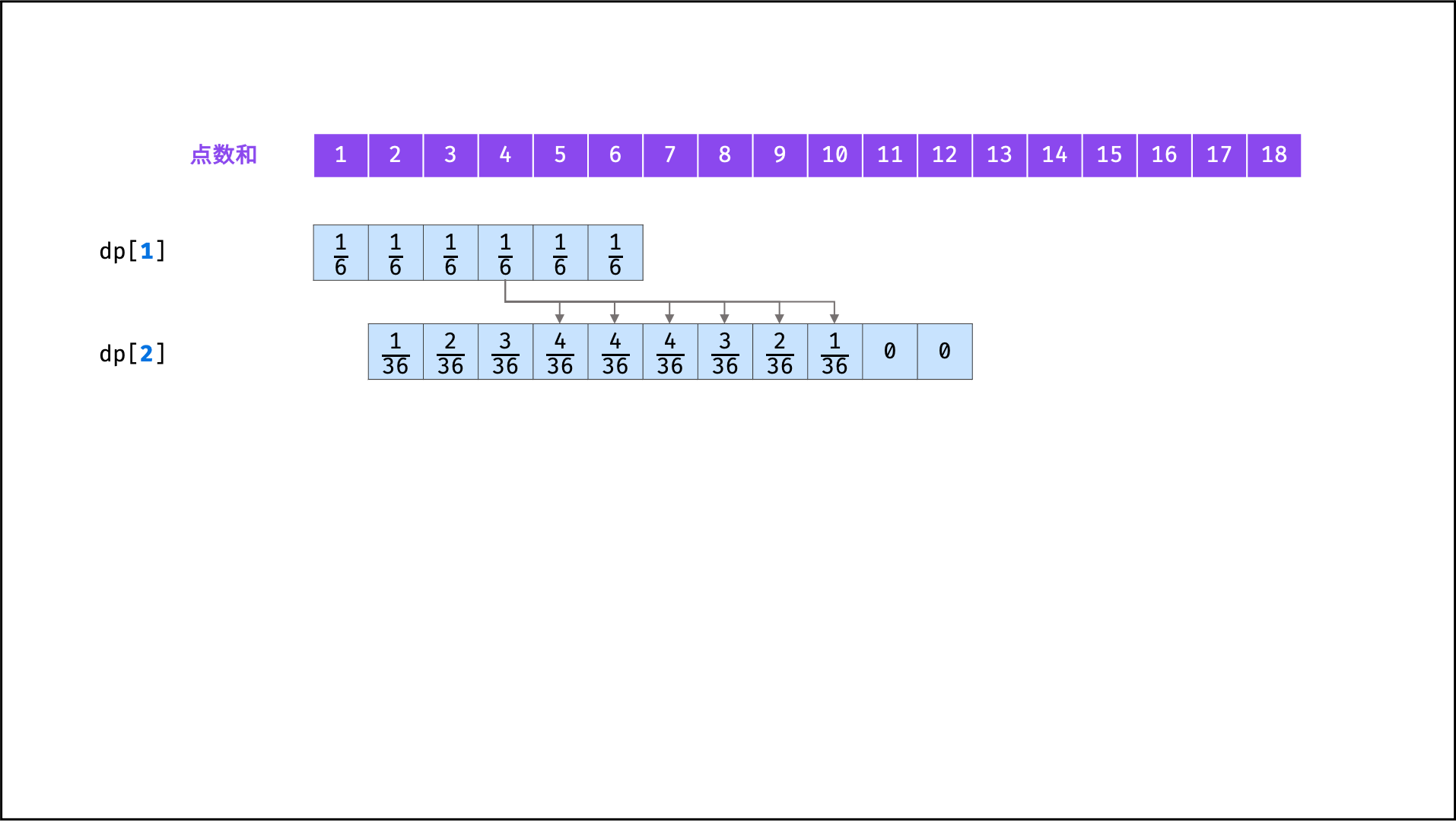
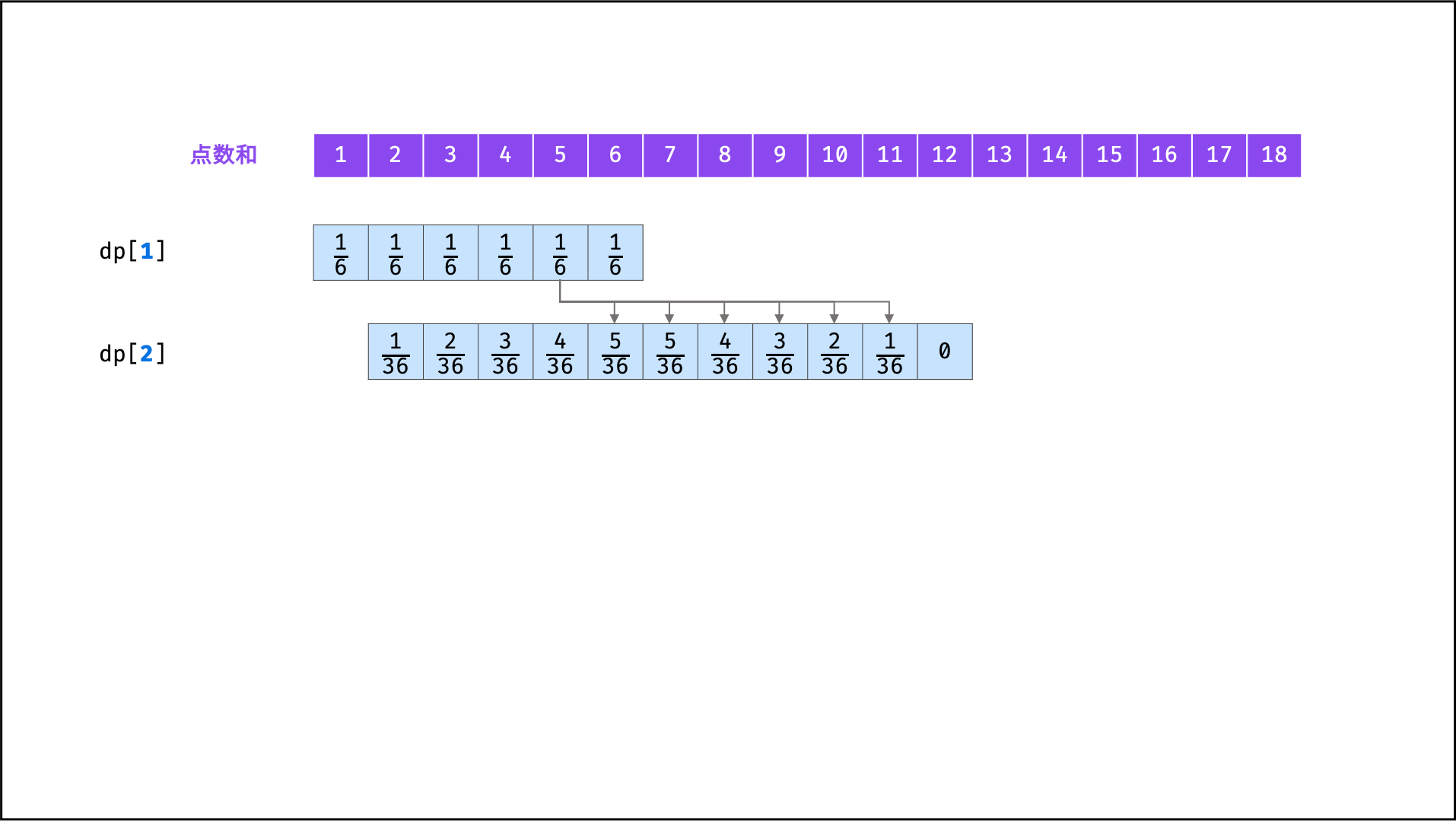
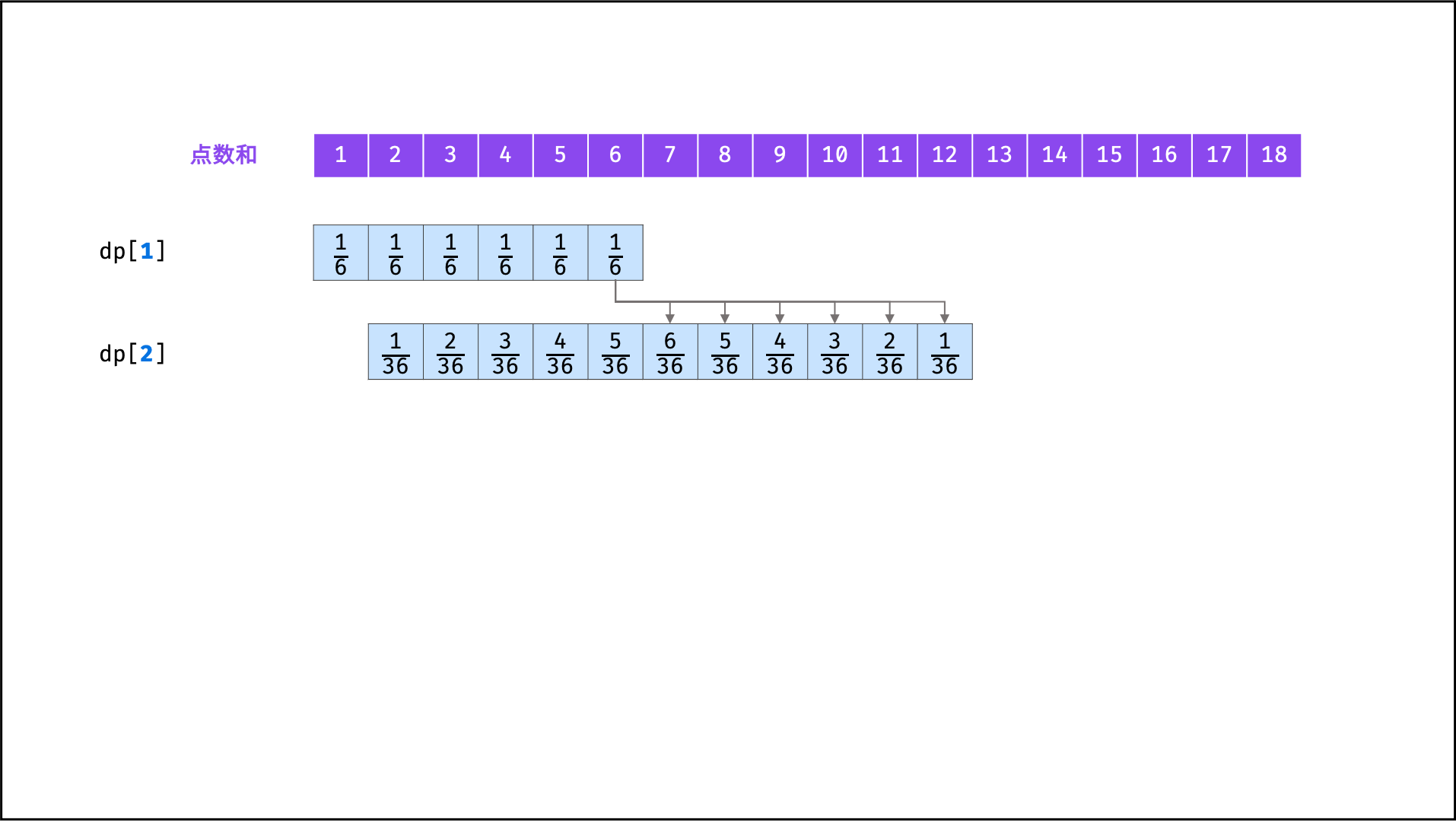
具体来看，由于新增骰子的点数只可能为 1 至 6 ，因此概率 f(n - 1, x) 仅与 f(n, x + 1) , f(n, x + 2), ... , f(n, x + 6) 相关。因而，遍历 f(n - 1) 中各点数和的概率，并将其相加至 f(n) 中所有相关项，即可完成 f(n - 1) 至 f(n) 的递推。
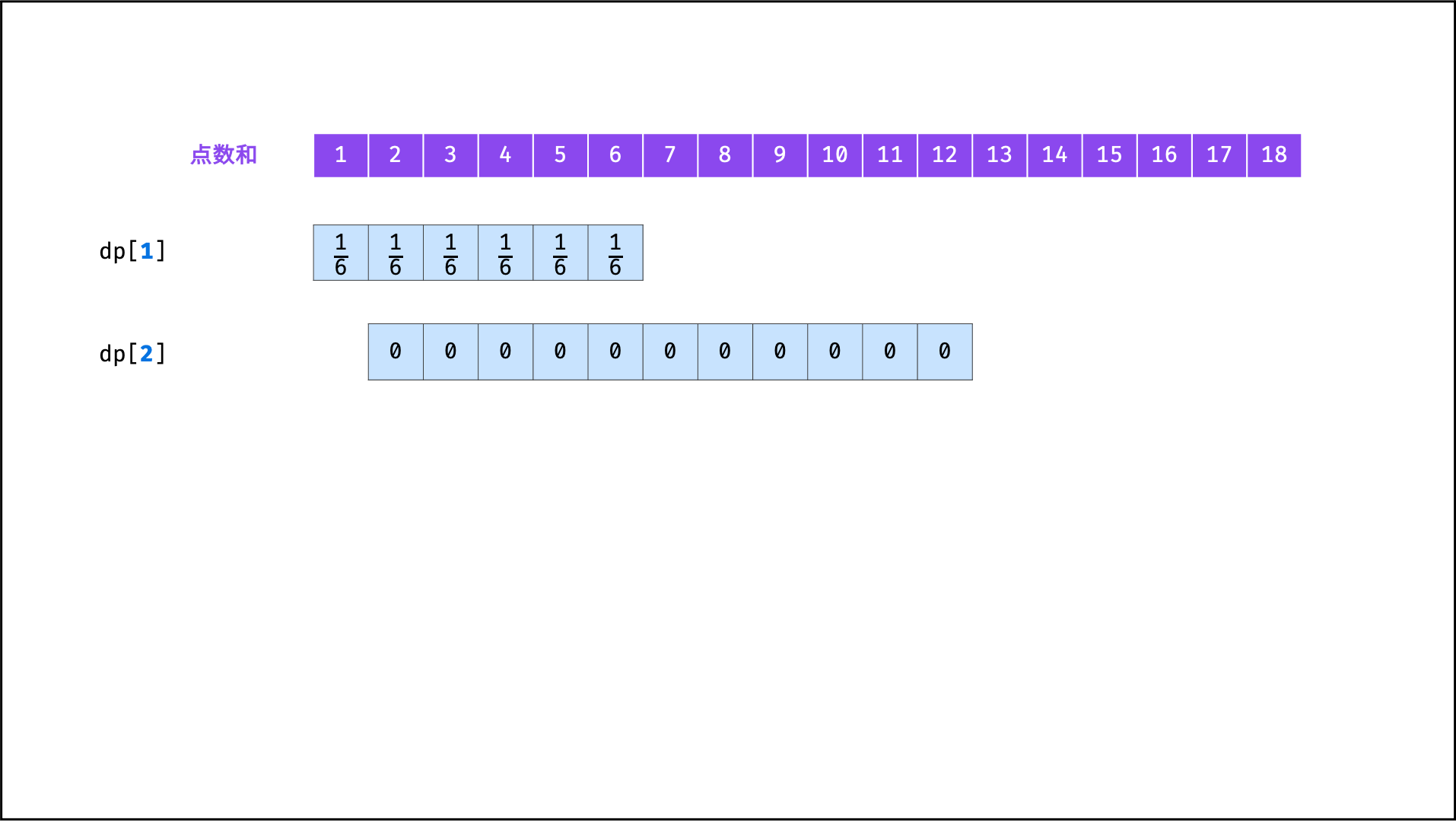
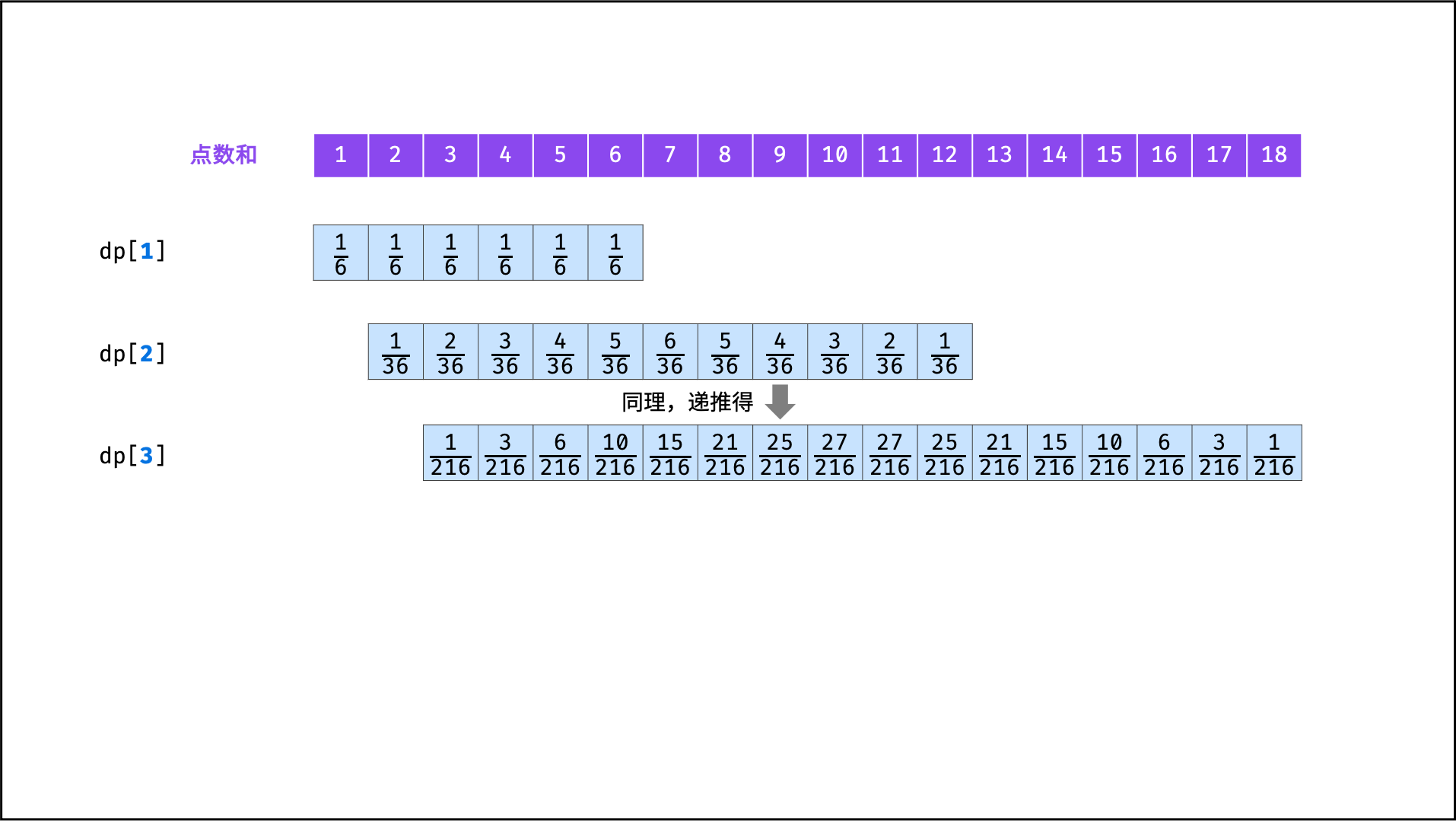
将
f(i)记为动态规划列表形式dp[i]，则i = 1, 2, ..., n的状态转移过程如下图所示。
<
,
,
,
,
,
,
,
,
>
代码：
通常做法是声明一个二维数组 dp ，dp[i][j] 代表前 i 个骰子的点数和 j 的概率，并执行状态转移。而由于 dp[i] 仅由 dp[i-1] 递推得出，为降低空间复杂度，只建立两个一维数组 dp , tmp 交替前进即可。
class Solution:
def statisticsProbability(self, n: int) -> List[float]:
dp = [1 / 6] * 6
for i in range(2, n + 1):
tmp = [0] * (5 * i + 1)
for j in range(len(dp)):
for k in range(6):
tmp[j + k] += dp[j] / 6
dp = tmp
return dp
class Solution {
public double[] statisticsProbability(int n) {
double[] dp = new double[6];
Arrays.fill(dp, 1.0 / 6.0);
for (int i = 2; i <= n; i++) {
double[] tmp = new double[5 * i + 1];
for (int j = 0; j < dp.length; j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += dp[j] / 6.0;
}
}
dp = tmp;
}
return dp;
}
}
class Solution {
public:
vector<double> statisticsProbability(int n) {
vector<double> dp(6, 1.0 / 6.0);
for (int i = 2; i <= n; i++) {
vector<double> tmp(5 * i + 1, 0);
for (int j = 0; j < dp.size(); j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += dp[j] / 6.0;
}
}
dp = tmp;
}
return dp;
}
};
复杂度分析：
- 时间复杂度
O(n ^ 2)： 状态转移循环n - 1轮；每轮中，当i = 2, 3, ..., n时，对应循环数量分别为6 \times 6, 11 \times 6, ..., [5(n - 1) + 1] \times 6；因此总体复杂度为O((n - 1) \times \frac{6 + [5(n - 1) + 1]}{2} \times 6)，即等价于O(n^2)。 - 空间复杂度
O(n)： 状态转移过程中，辅助数组tmp最大长度为6(n-1) - [(n-1) - 1] = 5n - 4，因此使用O(5n - 4) = O(n)大小的额外空间。