LeetCode-Book/leetbook_ioa/docs/LCR 187. 破冰游戏.md

解题思路：

为简化篇幅，本文将 num 和 target 分别记为 n 和 m 。

模拟整个删除过程最直观，即构建一个长度为 n 的链表，各节点值为对应的顺序索引；每轮删除第 m 个节点，直至链表长度为 1 时结束，返回最后剩余节点的值即可。

模拟法需要循环删除 n - 1 轮，每轮在链表中寻找删除节点需要 m 次访问操作（链表线性遍历），因此总体时间复杂度为 O(nm) 。题目给定的 m, n 取值范围如下所示，观察可知此时间复杂度是不可接受的。

1 \leq n \leq 10^5 \\
1 \leq m \leq 10^6

实际上，本题是著名的 “约瑟夫环” 问题，可使用 动态规划 解决。

输入 n, m ，记此约瑟夫环问题为 「n, m 问题」 ，设解（即最后留下的数字）为 f(n) ，则有：

• 「n, m 问题」：数字环为 0, 1, 2, ..., n - 1 ，解为 f(n) ；
• 「n-1, m 问题」：数字环为 0, 1, 2, ..., n - 2 ，解为 f(n-1) ；
• 以此类推……

请注意，数字环是 首尾相接 的，为方便行文，本文使用列表形式表示。

对于「n, m 问题」，首轮删除环中第 m 个数字后，得到一个长度为 n - 1 的数字环。由于有可能 m > n ，因此删除的数字为 (m - 1) \mod n ，删除后的数字环从下个数字（即 m \mod n ）开始，设 t = m \mod n ，可得数字环：

t, t + 1, t + 2, ..., 0, 1, ..., t - 3, t - 2

删除一轮后的数字环也变为一个「n-1, m 问题」，观察以下数字编号对应关系：

\begin{aligned}
「n-1, m 问题」 && \rightarrow && 「n, m 问题」删除后 \\
0 && \rightarrow && t + 0 \\
1 && \rightarrow && t + 1 \\
... && \rightarrow && ... \\
n - 2 && \rightarrow && t - 2 \\
\end{aligned}

设「n-1, m 问题」某数字为 x ，则可得递推关系：

x \rightarrow (x + t) \mod n \\

换而言之，若已知「n-1, m 问题」的解 f(n - 1) ，则可通过以上公式计算得到「n, m 问题」的解 f(n) ，即：

\begin{aligned}
f(n) & = (f(n - 1) + t) \mod n \\
& = (f(n - 1) + m \mod n) \mod n \\
& = (f(n - 1) + m) \mod n
\end{aligned}

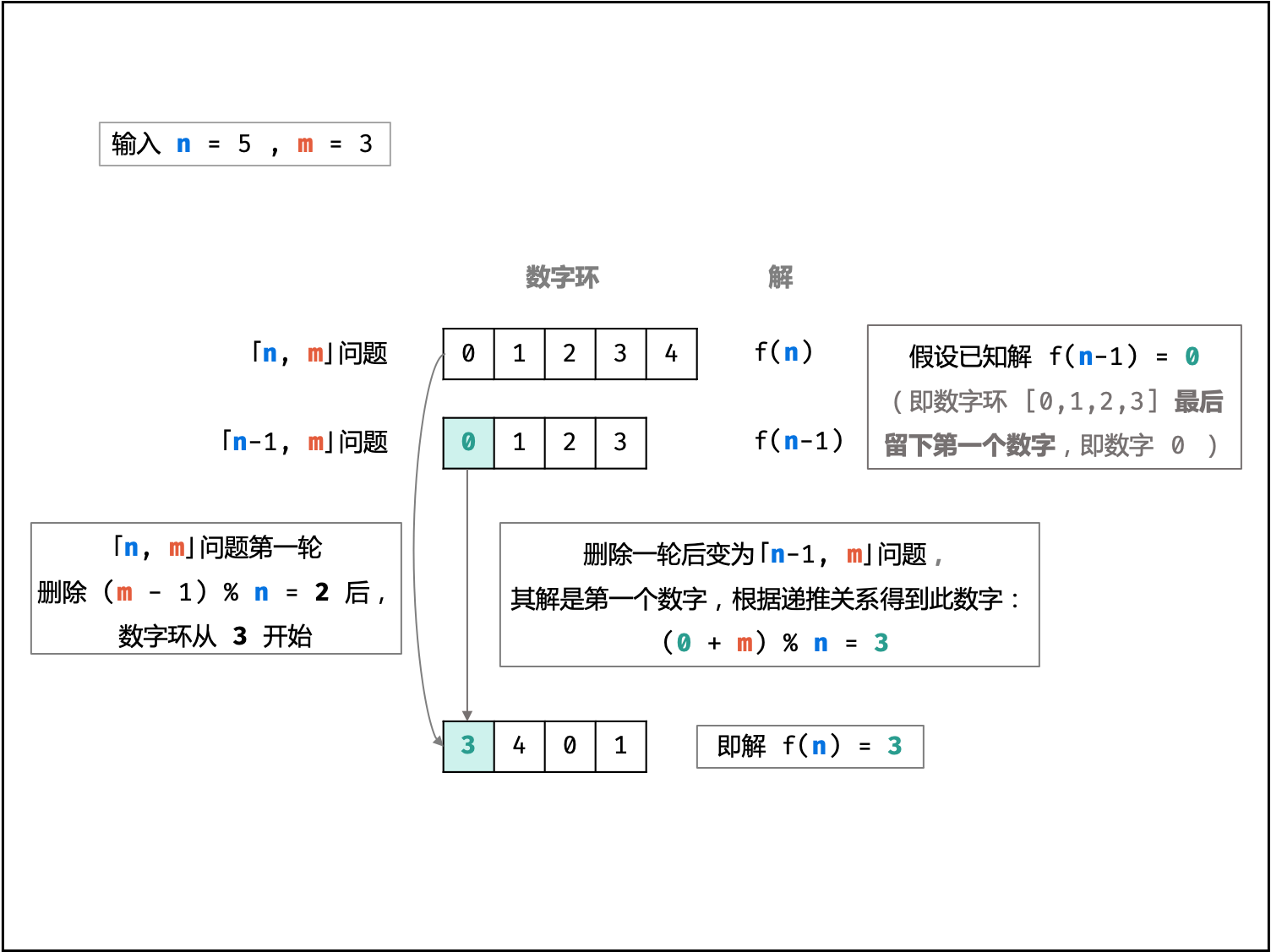
下图中 n , m 分别对应本题的 n , m 。

{:align=center width=550}

f(n) 可由 f(n - 1) 得到，f(n - 1) 可由 f(n - 2) 得到，……，f(2) 可由 f(1) 得到；因此，若给定 f(1) 的值，就可以递推至任意 f(n) 。而「1, m 问题」的解 f(1) = 0 恒成立，即无论 m 为何值，长度为 1 的数字环留下的是一定是数字 0 。

以上数学推导本质是得出动态规划的 转移方程 和 初始状态 。

动态规划解析：

1. 状态定义： 设「i, m 问题」的解为 dp[i] ；
2. 转移方程： 通过以下公式可从 dp[i - 1] 递推得到 dp[i] ；

dp[i] = (dp[i - 1] + m) \mod i

3. 初始状态：「1, m 问题」的解恒为 0 ，即 dp[1] = 0 ；
4. 返回值： 返回「n, m 问题」的解 dp[n] ；

如下图所示，为 n = 5 , m = 3 时的状态转移和对应的模拟删除过程。

代码：

根据状态转移方程的递推特性，无需建立状态列表 dp ，而使用一个变量 x 执行状态转移即可。

class Solution:
    def iceBreakingGame(self, num: int, target: int) -> int:
        x = 0
        for i in range(2, num + 1):
            x = (x + target) % i
        return x

class Solution {
    public int iceBreakingGame(int num, int target) {
        int x = 0;
        for (int i = 2; i <= num; i++) {
            x = (x + target) % i;
        }
        return x;
    }
}

class Solution {
public:
    int iceBreakingGame(int num, int target) {
        int x = 0;
        for (int i = 2; i <= num; i++) {
            x = (x + target) % i;
        }
        return x;
    }
};

复杂度分析：

• 时间复杂度 O(n) ： 状态转移循环 n - 1 次使用 O(n) 时间，状态转移方程计算使用 O(1) 时间；
• 空间复杂度 O(1) ： 使用常数大小的额外空间；