LeetCode-Book/leetbook_ioa/docs/LCR 135. 报数.md

解题思路：

题目要求打印 “从 1 至 cnt 的数字” ，因此需考虑以下两个问题：

1. 最大的 cnt 位数（记为 end ）和位数 cnt 的关系： 例如最大的 1 位数是 9 ，最大的 2 位数是 99 ，最大的 3 位数是 999 。则可推出公式：

end = 10^{cnt} - 1

2. 大数越界问题： 当 cnt 较大时，end 会超出 int32 整型的取值范围，超出取值范围的数字无法正常存储。但由于本题要求返回 int 类型数组，相当于默认所有数字都在 int32 整型取值范围内，因此不考虑大数越界问题。

因此，只需定义区间 [1, 10^{cnt} - 1] 和步长 1 ，通过 for 循环生成结果列表 res 并返回即可。

代码：

class Solution:
    def countNumbers(self, cnt: int) -> List[int]:
        res = []
        for i in range(1, 10 ** cnt):
            res.append(i)
        return res

class Solution {
    public int[] countNumbers(int cnt) {
        int end = (int)Math.pow(10, cnt) - 1;
        int[] res = new int[end];
        for(int i = 0; i < end; i++)
            res[i] = i + 1;
        return res;
    }
}

利用 Python 的语言特性，可以简化代码：先使用 range() 方法生成可迭代对象，再使用 list() 方法转化为列表并返回即可。

class Solution:
    def countNumbers(self, cnt: int) -> List[int]:
        return list(range(1, 10 ** cnt))

复杂度分析：

• 时间复杂度 O(10^{cnt}) ： 生成长度为 10^{cnt} 的列表需使用 O(10^{cnt}) 时间。
• 空间复杂度 O(1) ： 建立列表需使用 O(1) 大小的额外空间（ 列表作为返回结果，不计入额外空间 ）。

大数打印拓展：

实际上，本题的主要考点是大数越界情况下的打印。需要解决以下三个问题：

1. 表示大数的变量类型：

• 无论是 short / int / long ... 任意变量类型，数字的取值范围都是有限的。因此，大数的表示应用字符串 String 类型。

2. 生成数字的字符串集：

• 使用 int 类型时，每轮可通过 +1 生成下个数字，而此方法无法应用至 String 类型。并且， String 类型的数字的进位操作效率较低，例如 "9999" 至 "10000" 需要从个位到千位循环判断，进位 4 次。
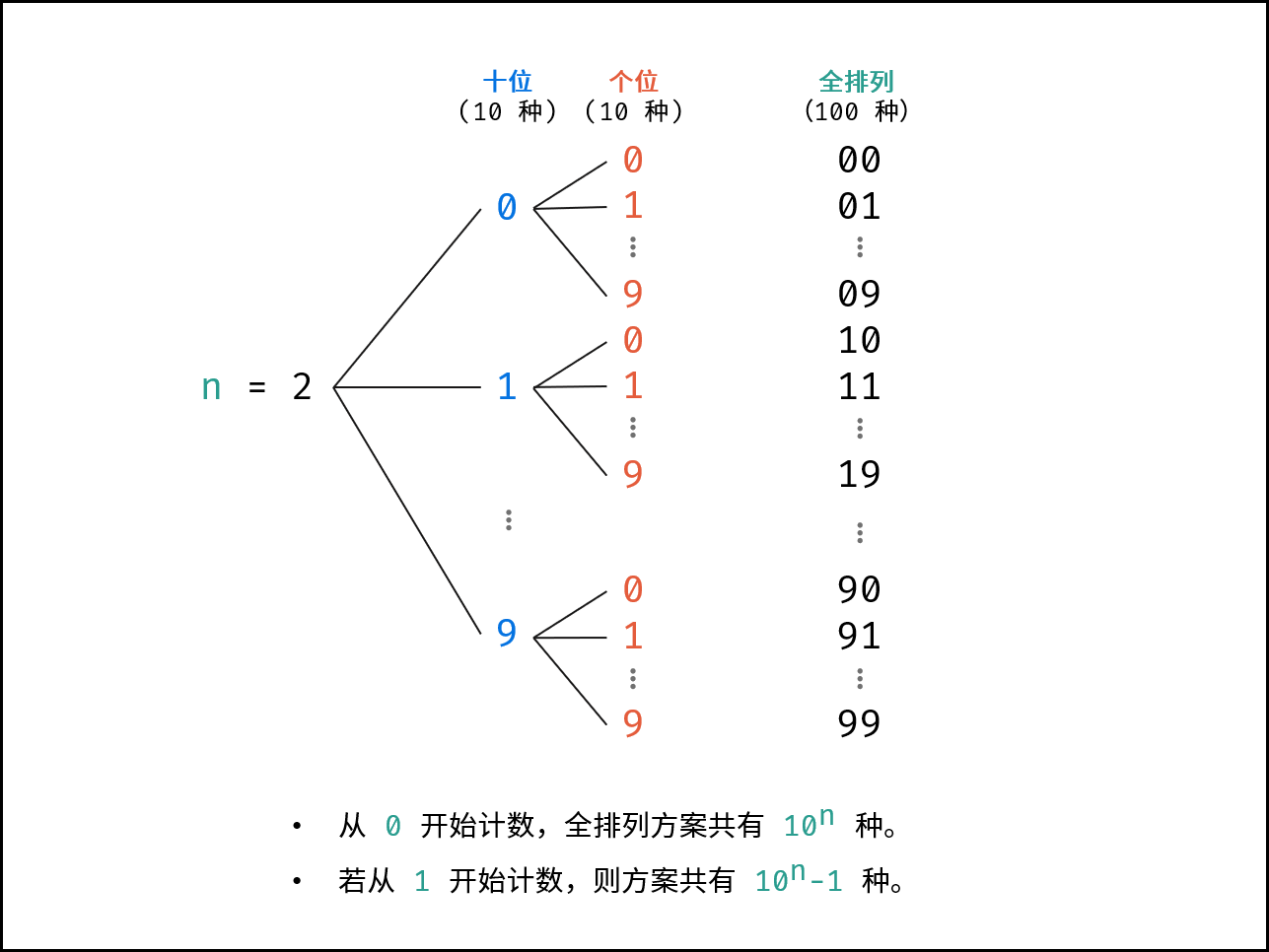
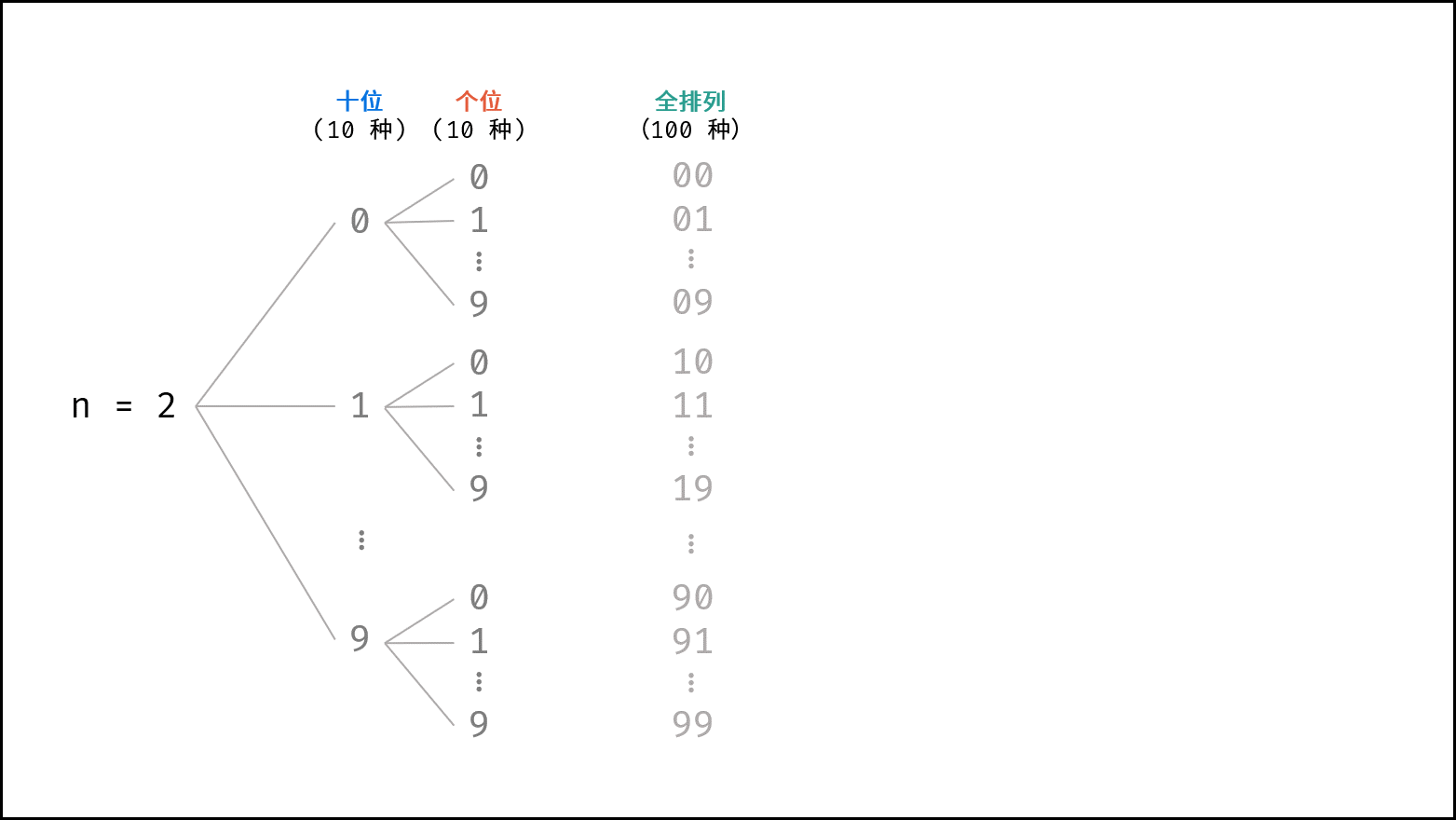
• 观察可知，生成的列表实际上是 cnt 位 0 - 9 的 全排列 ，因此可避开进位操作，通过递归生成数字的 String 列表。

3. 递归生成全排列：

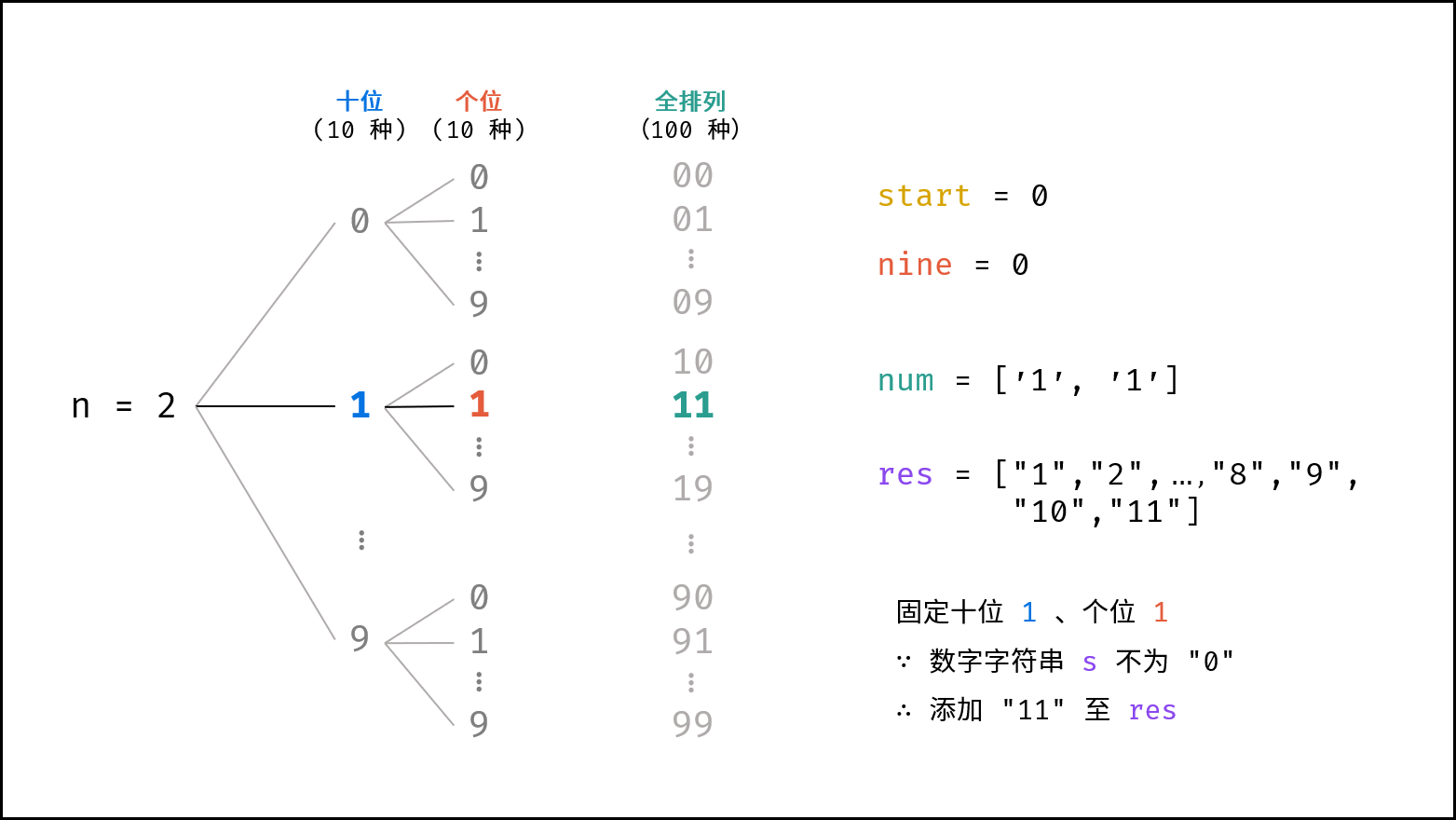
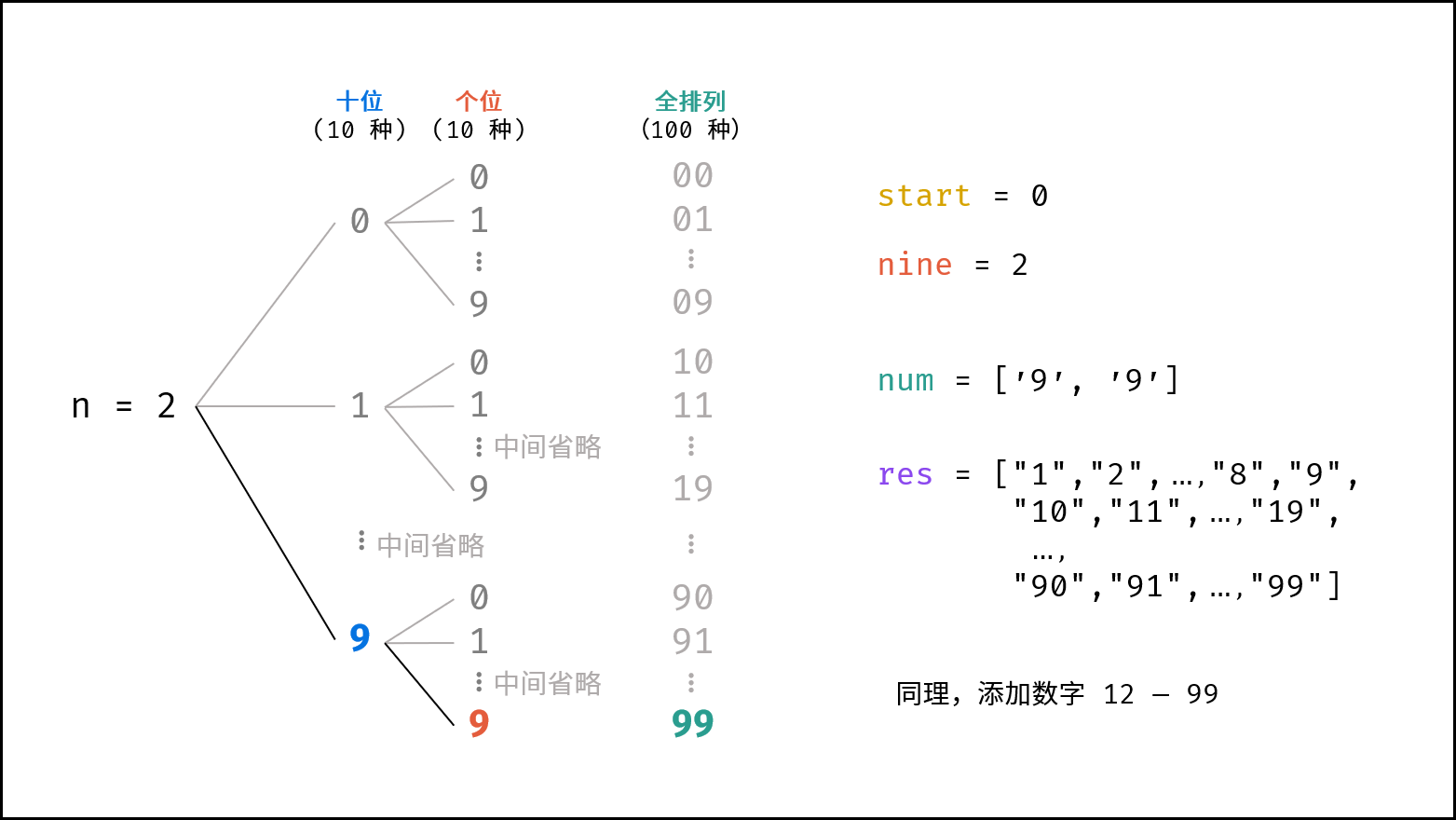
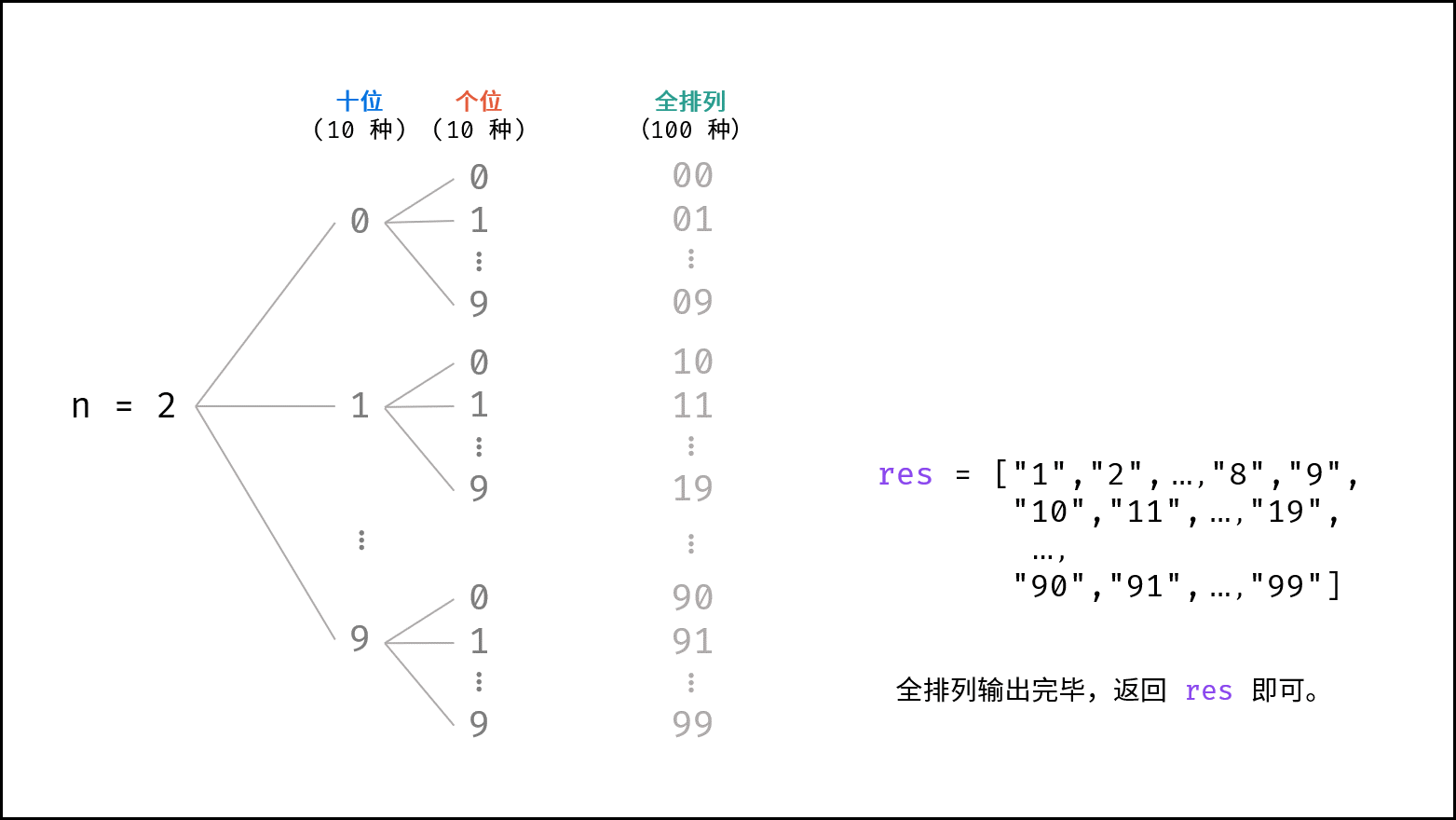
• 基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 cnt = 2 时（数字范围 1 - 99 ），固定十位为 0 - 9 ，按顺序依次开启递归，固定个位 0 - 9 ，终止递归并添加数字字符串。

下图中的 n 对应本题中的 cnt 。

{:align=center width=500}

根据以上方法，可初步编写全排列代码：

class Solution:
    def countNumbers(self, cnt: int) -> [int]:
        def dfs(x):
            if x == cnt: # 终止条件：已固定完所有位
                res.append(''.join(num)) # 拼接 num 并添加至 res 尾部
                return
            for i in range(10): # 遍历 0 - 9
                num[x] = str(i) # 固定第 x 位为 i
                dfs(x + 1) # 开启固定第 x + 1 位
        
        num = ['0'] * cnt # 起始数字定义为 cnt 个 0 组成的字符列表
        res = [] # 数字字符串列表
        dfs(0) # 开启全排列递归
        return ','.join(res)  # 拼接所有数字字符串，使用逗号隔开，并返回

class Solution {
    StringBuilder res;
    int count = 0, cnt;
    char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    public String countNumbers(int cnt) {
        this.cnt = cnt;
        res = new StringBuilder(); // 数字字符串集
        num = new char[cnt]; // 定义长度为 cnt 的字符列表
        dfs(0); // 开启全排列递归
        res.deleteCharAt(res.length() - 1); // 删除最后多余的逗号
        return res.toString(); // 转化为字符串并返回
    }
    void dfs(int x) {
        if(x == cnt) { // 终止条件：已固定完所有位
            res.append(String.valueOf(num) + ","); // 拼接 num 并添加至 res 尾部，使用逗号隔开
            return;
        }
        for(char i : loop) { // 遍历 ‘0‘ - ’9‘
            num[x] = i; // 固定第 x 位为 i
            dfs(x + 1); // 开启固定第 x + 1 位
        }
    }
}

在此方法下，各数字字符串被逗号隔开，共同组成长字符串。返回的数字集字符串如下所示：

输入：n = 1
输出："0,1,2,3,4,5,6,7,8,9"

输入：n = 2
输出："00,01,02,...,10,11,12,...,97,98,99"

输入：n = 3
输出："000,001,002,...,100,101,102,...,997,998,999"

观察可知，当前的生成方法仍有以下问题：

1. 诸如 00, 01, 02, \cdots 应显示为 0, 1, 2, \cdots ，即应 删除高位多余的 $0$ ;
2. 此方法从 0 开始生成，而题目要求 列表从 1 开始 ；

以上两个问题的解决方法如下：

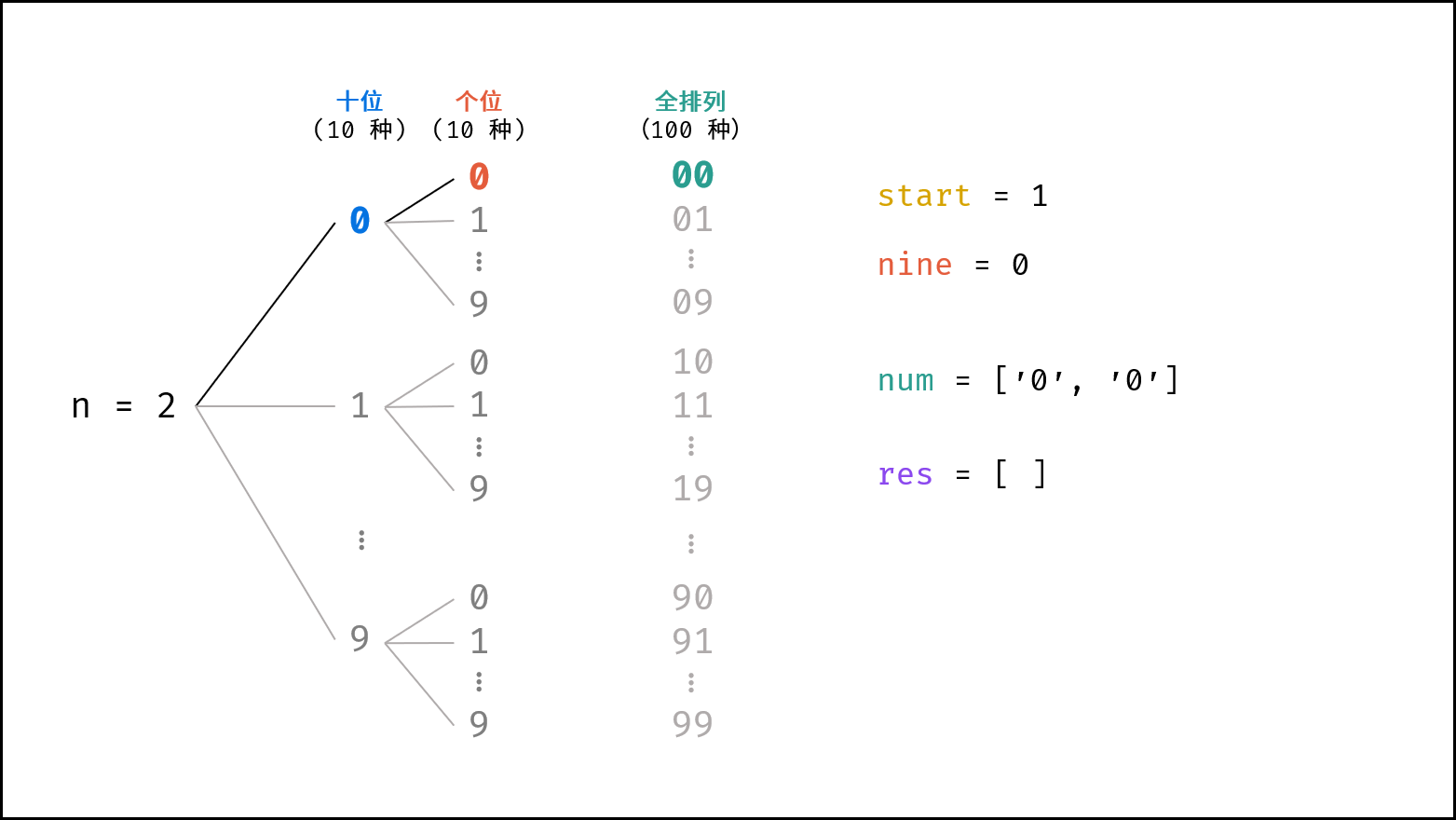
1. 删除高位多余的 0 ：

• 字符串左边界定义： 声明变量 start 规定字符串的左边界，以保证添加的数字字符串 num[start:] 中无高位多余的 0 。例如当 cnt = 2 时，1 - 9 时 start = 1 ，10 - 99 时 start = 0 。

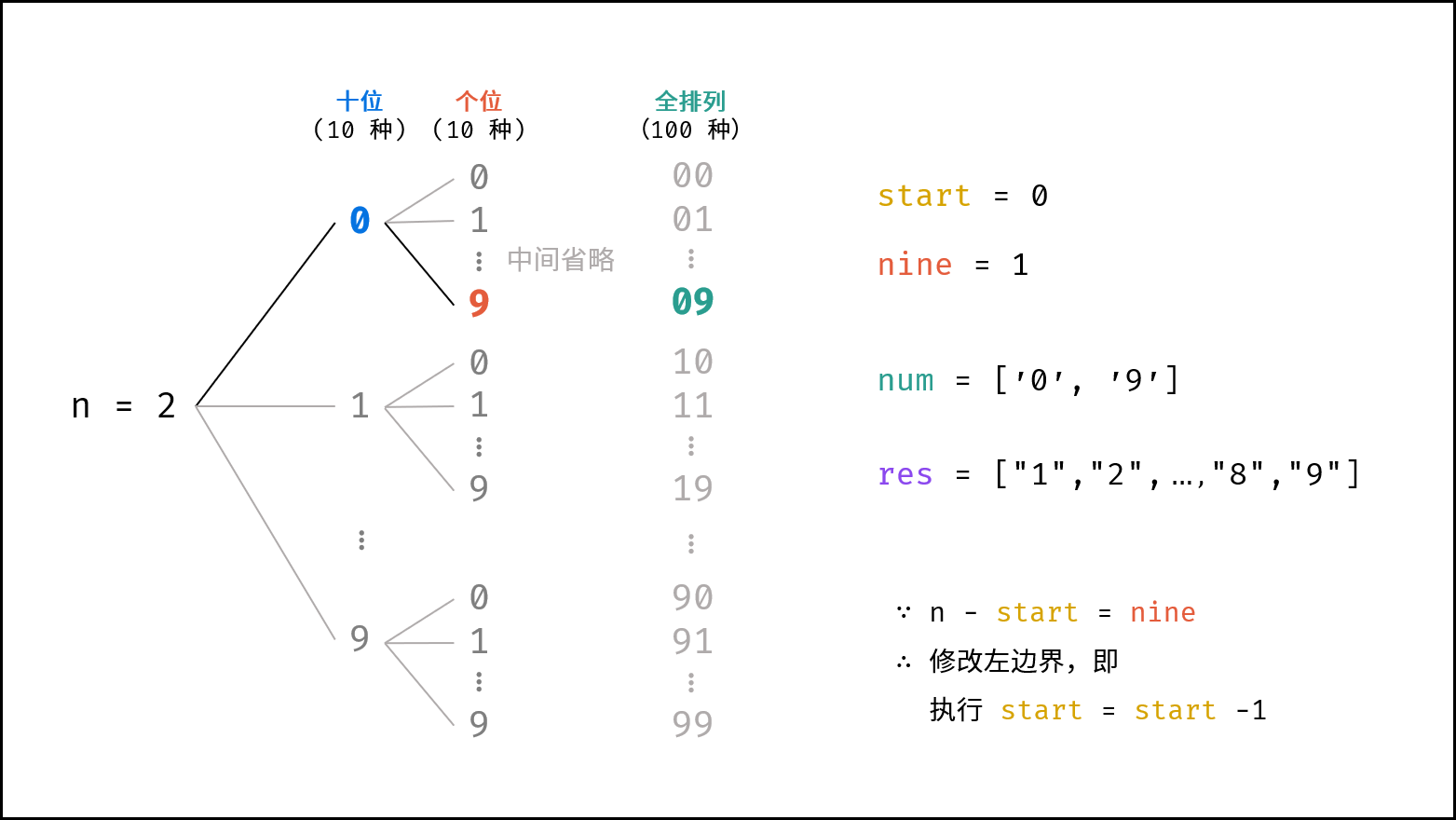
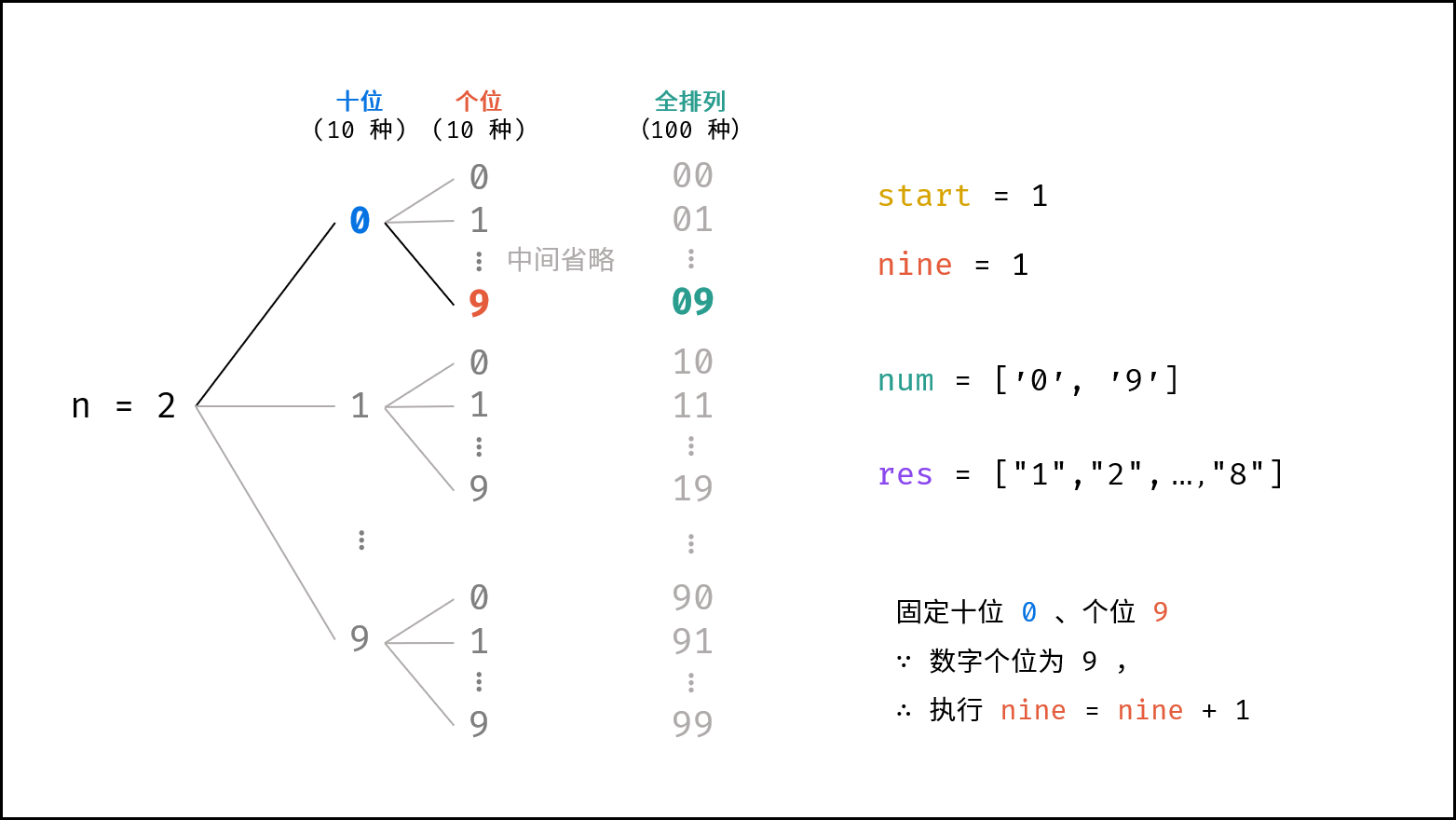
• 左边界 start 变化规律： 观察可知，当输出数字的所有位都是 9 时，则下个数字需要向更高位进 1 ，此时左边界 start 需要减 1 （即高位多余的 0 减少一个）。例如当 cnt = 3 （数字范围 1 - 999 ）时，左边界 start 需要减 1 的情况有： "009" 进位至 "010" ， "099" 进位至 "100" 。设数字各位中 9 的数量为 nine ，所有位都为 9 的判断条件可用以下公式表示：

cnt - start = nine

• 统计 nine 的方法： 固定第 x 位时，当 i = 9 则执行 nine = nine + 1 ，并在回溯前恢复 nine = nine - 1 。

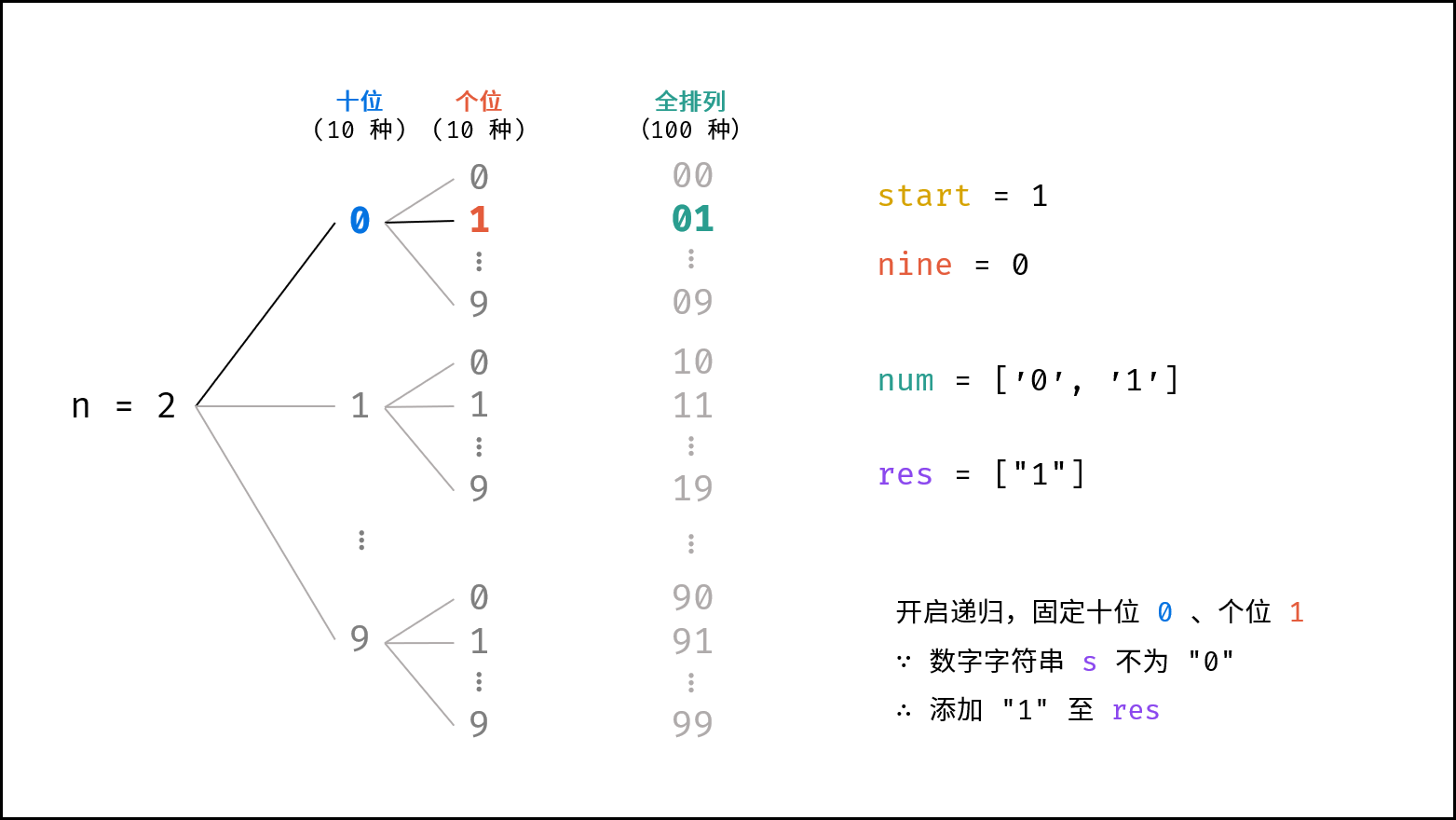
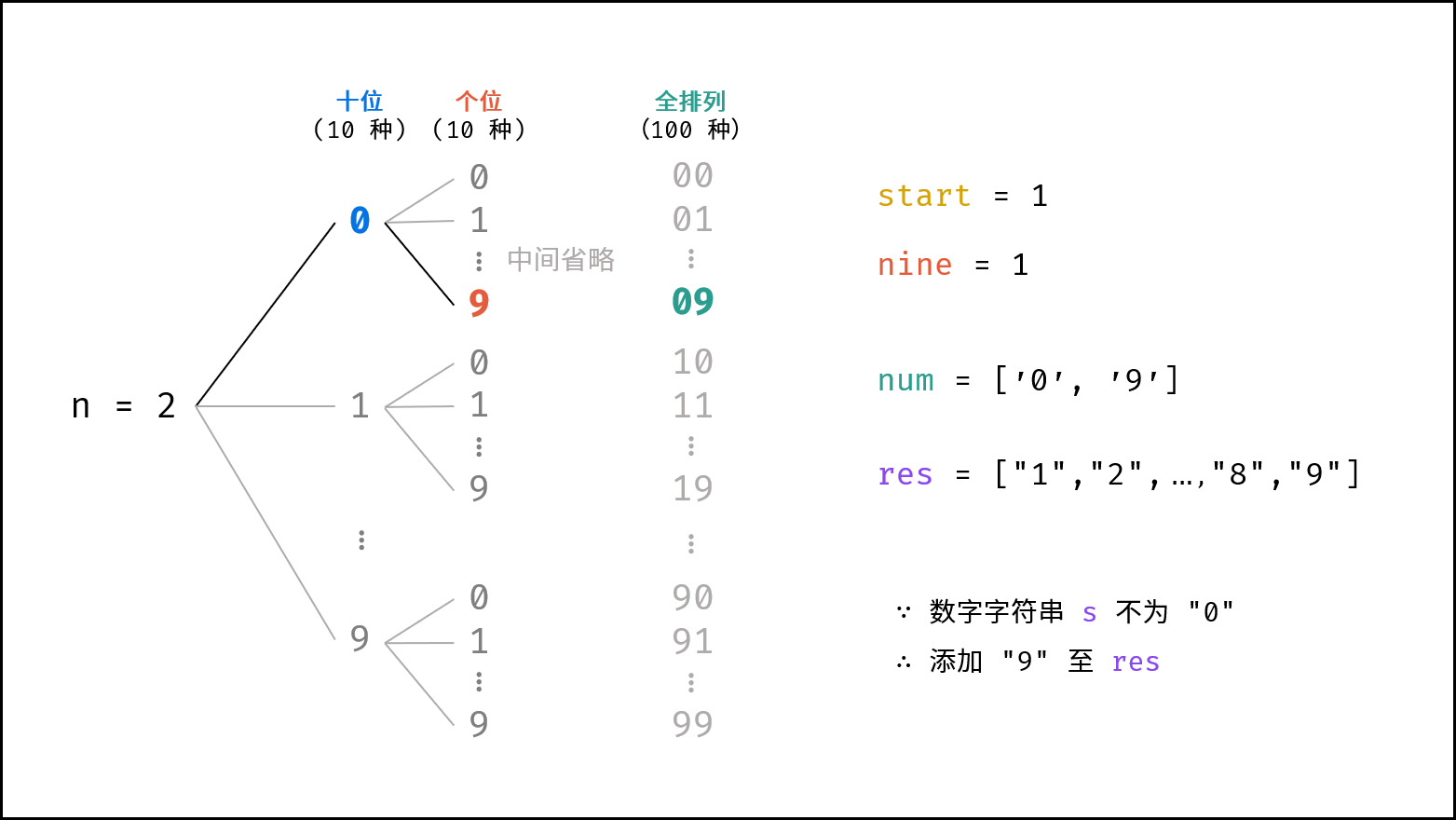
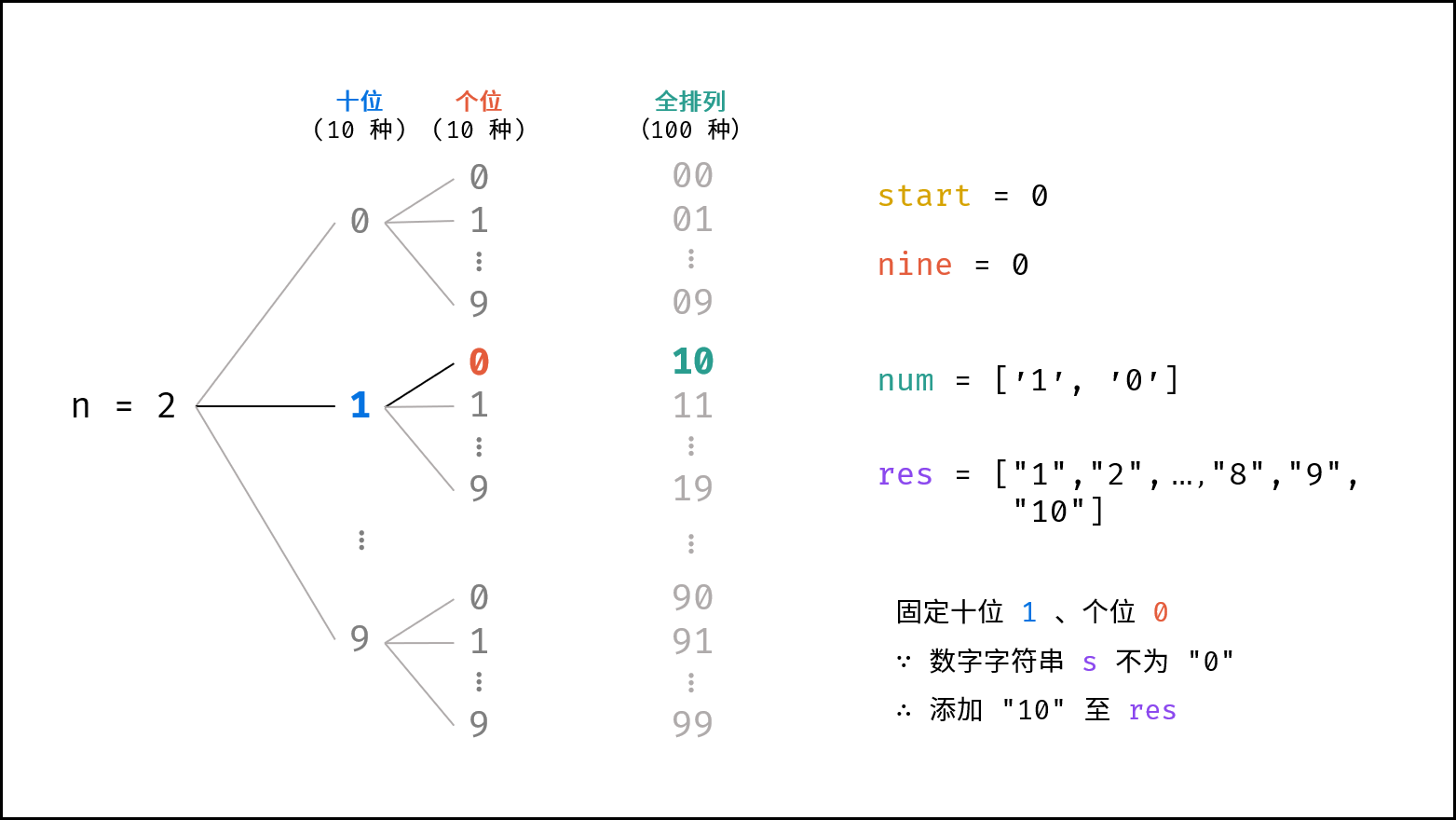
2. 列表从 1 开始：

• 在以上方法的基础上，添加数字字符串前判断其是否为 "0" ，若为 "0" 则直接跳过。

<,,,,,,,,,>

代码：

为 正确表示大数 ，以下代码的返回值为数字字符串集拼接而成的长字符串。

class Solution:
    def countNumbers(self, cnt: int) -> [int]:
        def dfs(x):
            if x == cnt:
                s = ''.join(num[self.start:])
                if s != '0': res.append(s)
                if cnt - self.start == self.nine: self.start -= 1
                return
            for i in range(10):
                if i == 9: self.nine += 1
                num[x] = str(i)
                dfs(x + 1)
            self.nine -= 1
        
        num, res = ['0'] * cnt, []
        self.nine = 0
        self.start = cnt - 1
        dfs(0)
        return ','.join(res)

class Solution {
    StringBuilder res;
    int nine = 0, count = 0, start, cnt;
    char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    public String countNumbers(int cnt) {
        this.cnt = cnt;
        res = new StringBuilder();
        num = new char[cnt];
        start = cnt - 1;
        dfs(0);
        res.deleteCharAt(res.length() - 1);
        return res.toString();
    }
    void dfs(int x) {
        if(x == cnt) {
            String s = String.valueOf(num).substring(start);
            if(!s.equals("0")) res.append(s + ",");
            if(cnt - start == nine) start--;
            return;
        }
        for(char i : loop) {
            if(i == '9') nine++;
            num[x] = i;
            dfs(x + 1);
        }
        nine--;
    }
}

本题要求输出 int 类型数组。为 运行通过 ，可在添加数字字符串 s 前，将其转化为 int 类型。代码如下所示：

class Solution:
    def countNumbers(self, cnt: int) -> [int]:
        def dfs(x):
            if x == cnt:
                s = ''.join(num[self.start:])
                if s != '0': res.append(int(s))
                if cnt - self.start == self.nine: self.start -= 1
                return
            for i in range(10):
                if i == 9: self.nine += 1
                num[x] = str(i)
                dfs(x + 1)
            self.nine -= 1
        
        num, res = ['0'] * cnt, []
        self.nine = 0
        self.start = cnt - 1
        dfs(0)
        return res

class Solution {
    int[] res;
    int nine = 0, count = 0, start, cnt;
    char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    public int[] countNumbers(int cnt) {
        this.cnt = cnt;
        res = new int[(int)Math.pow(10, cnt) - 1];
        num = new char[cnt];
        start = cnt - 1;
        dfs(0);
        return res;
    }
    void dfs(int x) {
        if(x == cnt) {
            String s = String.valueOf(num).substring(start);
            if(!s.equals("0")) res[count++] = Integer.parseInt(s);
            if(cnt - start == nine) start--;
            return;
        }
        for(char i : loop) {
            if(i == '9') nine++;
            num[x] = i;
            dfs(x + 1);
        }
        nine--;
    }
}

复杂度分析：

• 时间复杂度 O(10^{cnt}) ： 递归的生成的排列的数量为 10^{cnt} 。
• 空间复杂度 O(10^{cnt}) ： 结果列表 res 的长度为 10^{cnt} - 1 ，各数字字符串的长度区间为 1, 2, ..., cnt ，因此占用 O(10^{cnt}) 大小的额外空间。